Bayesian Network-Based Earth-Rock Dam Breach Probability Analysis Integrating Machine Learning

Abstract

Earth-rock dams are critical components of hydraulic engineering, undertaking core functions such as flood control and disaster mitigation. However, the potential occurrence of dam breach poses a severe threat to regional socioeconomic stability and ecological security. To address the limitations of traditional Bayesian network (BN) in capturing the complex nonlinear coupling and dynamic mutual interactions among risk factors, they are integrated with machine learning techniques, based on a collected dataset of earth-rock dam breach case samples, the PC structure learning algorithm was employed to preliminarily uncover risk associations. The dataset was compiled from public databases, including the U.S. Army Corps of Engineers (USACE) and Dam Safety Management Center of the Ministry of Water Resources of China, as well as engineering reports from provincial water conservancy departments in China and Europe. Expert knowledge was integrated to optimize the network topology, thereby correcting causal relationships inconsistent with engineering mechanisms. The results indicate that the established hybrid model achieved AUC, accuracy, and F1-Score values of 0.887, 0.895, and 0.899, respectively, significantly outperforming the data-driven model G1. Forward inference identified the key drivers elevating breach risk. Conversely, backward inference revealed that overtopping was the direct failure mode with the highest probability of occurrence and the greatest contribution. The integration of data-driven approaches and domain knowledge provides theoretical and technical support for the probabilistic quantification of earth-rock dam breach and risk prevention and control decision-making.

1. Introduction

Earth-rock dams, owing to their advantages such as utilizing in situ materials and relatively simpler construction techniques, constitute the most numerous and widely distributed dam type globally [1,2,3]. However, since they are constructed using natural earth materials and their construction process is susceptible to constraints from complex geological factors, among others, their dam breach risk is significantly higher than that of other dam types. Once a dam breach event occurs, it will severely threaten people’s lives, property safety, and social stability [4,5,6,7]. Constructing mathematical models through probabilistic quantification methods can systematically analyze the interaction mechanisms and coupling effects of dam breach risk factors. This provides a scientific basis for dam breach early warning, emergency response plan formulation, and engineering reinforcement, holding significant importance for enhancing the safety management level of earth-rock dams.

Due to the inherent structural complexity of earth-rock dam systems and the intricate external conditions, the risk factors influencing their safety are typically characterized by diversity, nonlinearity, and interrelationships. Traditional risk analysis approaches—such as Fault Tree Analysis (FTA); Failure Mode, Effects and Criticality Analysis (FMECA); Analytic Hierarchy Process (AHP); and their extended models—have been wildly applied in practice. Chen et al. [8] proposed a probabilistic risk assessment method for dams under Grey–Stochastic–Fuzzy (GSF) uncertainty, establishing a fault tree model based on fault tree analysis to analyze the failure probability of a roller-compacted concrete dam. He et al. [9] developed a framework and analysis based on fault tree analysis for identifying critical failure paths in gravity dams and earth-rockfill dams. These scholars have made substantial contributions to the analysis of earth-rock dam breach risks, thereby enhancing the risk assessment framework. However, in practical application, traditional dam breach risk analysis methods exhibit several limitations when applied to earth-rock dam systems. For instance, Failure Mode and Effect Analysis (FMEA) can qualitatively summarize and analyze potential failures within a system, but it is cumbersome for describing the comprehensive effects of multiple risk factors; methods such as Analytic Hierarchy Process (AHP) and Fault Tree Analysis (FTA) can intuitively depict causal relationships within the system through constructing logically clear hierarchical structures; however, they struggle to express the correlations among risk factors and cannot achieve the backward inference process [10,11].

Bayesian Networks (BNs) have become a significant tool for dam breach risk modeling due to their ability to intuitively express causal relationships between variables through Directed Acyclic Graphs (DAGs) and perform uncertainty reasoning by combining Conditional Probability Tables (CPT). Oswaldo et al. [12] proposed a nonparametric continuous Bayesian network, effectively applying it to an earth-rock dam in Mexico to deduce the causes, potential consequences, and failure modes of the dam breach. Malekmohammadi B. et al. [13] integrated environmental risk assessment with Bayesian networks and applied this method to the Gabric Dam in Iran. The results demonstrated that the method provided an acceptable and rational risk assessment prioritization when mitigating environmental risks and could serve as a robust decision support system for evaluating environmental risks. Zhang et al. [14] proposes an extended Bayesian network model for calculating the dam failure probability based on fuzzy sets (FSs) and dynamic evidential reasoning. Bayesian networks have become an essential tool for dam breach risk modeling by virtue of their ability to intuitively express causal relationships between variables through DAG and conduct uncertainty reasoning by integrating CPT. However, the current construction of Bayesian networks heavily relies on domain expertise, which introduces substantial subjectivity. This makes it challenging to establish models with unified, objective standards. Furthermore, complex reservoir systems involve numerous interacting factors with intricate relationships. Solely relying on domain expertise makes it difficult to comprehensively and accurately capture the relationships among all influencing factors, potentially leading to incomplete or inaccurate model structures. Concurrently, in-depth dam accident investigations and statistical work have accumulated a wealth of observational data on earth-rock dam safety incidents. These data objectively reflect the state of the dam under the influence of risk factors, laying the foundation for data-driven research. Some studies have attempted to introduce data into Bayesian network-based dam breach risk analysis. However, these studies primarily rely on frequency statistics of data, such as selecting key risk factors for model construction by comparing occurrence frequencies [15]. Statistical analysis inadequately reflects the underlying distribution patterns of the data, making it difficult to effectively characterize the characteristics of earth-rock dam systems, resulting in insufficient accuracy in dam breach risk analysis.

Modern artificial intelligence technologies centered on machine learning (ML), leveraging their powerful data processing and learning capabilities, provide effective approaches for system modeling and prediction in various fields, and also offer advanced computational methods for dam breach risk analysis [16,17]. Algorithms such as Random Forest and Support Vector Machine (SVM) have been applied to dam deformation prediction and seepage monitoring, while ensemble models like XGBoost have demonstrated high accuracy in risk classification [18,19,20]. ML techniques can achieve precise fitting of complex nonlinear systems by uncovering data distribution patterns. However, due to their complex structures and low interpretability, ML techniques struggle to intuitively express and quantify the interactions among variables within earth-rock dam systems, leading to suboptimal performance when used solely for dam breach risk analysis [21]. Considering the advantages of Bayesian Networks in visualization and uncertainty representation, it is feasible to improve BN-based dam breach risk analysis methods by utilizing the data processing and learning capabilities of ML based on available data, while combining them with a strongly interpretable reasoning framework. This approach can enhance the modeling quality of dam breach risk network models and improve the reliability of dam breach risk analysis.

Therefore, to investigate the interactions among earth-rock dam breach risk factors, this study integrates Bayesian Networks with machine learning methods to systematically examine the coupling mechanisms of risk factors, the construction of probabilistic models, and validation methodologies. The work aims to establish a quantifiable and interpretable framework for dam breach probability analysis, providing a novel and effective approach for earth-rock dam risk analysis. This holds significant importance for the efficient and accurate implementation of earth-rock dam risk management and prevention and control measures, ultimately safeguarding the safe operation of earth-rock dams.

2. Materials and Methods

2.1. Data Collection and Preprocessing

Based on historical records of dam failures, the failure scenarios of earth-rock dams are primarily categorized into two major types [22]: One type involves severe incidents that directly lead to dam breach, resulting in the complete structural destruction of the dam. The other type comprises routine dam safety incidents; although these incidents do not directly cause a breach, the dam exhibits safety hazards, such as seepage or cracks in the dam body. If not addressed promptly, these are highly likely to develop into breach incidents. Dam breach incidents often cause irreversible catastrophic impacts, posing direct threats to the life and property of downstream residents and negatively affecting the ecological environment. In contrast, dams with safety hazards can regain their designed functions, such as flood control and power generation, through rehabilitation measures.

This study collected 214 cases of earth-rock dam failure incidents from domestic and international sources to construct a safety incident dataset. These cases were sourced from two main channels: first, public databases, including the U.S. Army Corps of Engineers (USACE) and Dam Safety Management Center of the Ministry of Water Resources of China; second, engineering reports, including accident investigation reports from provincial water conservancy departments in China and Europe. In terms of time range, the cases span from 1980 to 2023. This time frame not only covers recent dam safety management practices but also includes typical historical dam breach events, ensuring both the timeliness and representativeness of the sample set.

Cases lacking key information in the database, such as missing incident type, were excluded. Additionally, data identified as unreasonable, for instance, descriptions of the incident process unrelated to the failure mode of the specific dam, were also discarded. This process resulted in a refined safety incident sample set comprising 166 complete data entries. Among these, 95 cases correspond to dam breach incidents, while 71 cases represent non-breach incidents. The sample set systematically records key information including engineering safety status (breached/non-breached), risk factors, and descriptions of incident causes. Detailed information about these samples is presented in the Supplementary Materials.

2.2. Identification of Risk Factors for Dam Failure in Reservoirs

Risk identification for earth-rock dams constitutes the fundamental work in dam breach risk analysis, with its primary task being the determination of risk factors and failure modes that influence the risk level of earth-rock dam breach. Earth-rock dams are granular structures characterized by low shear strength between particles, rendering them less resistant to water flow impact. Consequently, they exhibit relatively poor resistance to both scouring and seepage. Thus, overtopping, seepage failure, and structural instability are the primary failure modes for earth-rock dams [23,24]. Specific influencing factors are illustrated in

Table 1. Table of factors affecting earth-rock dam failure.

Failure Modes	Influencing Factors	Abbreviation	State Count	State Classification
Overtopping	Exceedance Flood	EFD	2	Yes/No
	Spillway Failure	SF	2	Yes/No
	Management Deficiency	MDA	2	Yes/No
	Gate Failure	GF	2	Yes/No
	Reservoir Over-Filling	ROF	2	Yes/No
	Insufficient Spillway Capacity	ISC	2	Yes/No
Seepage Failure	Exceedance Flood	EFD	2	Yes/No
	Piping	PG	3	Serious/Minor/Normal
	Collapse	SE	3	Serious/Minor/Normal
	Cracks	CK	3	Serious/Minor/Normal
	Internal Erosion	ITE	3	Serious/Minor/Normal
	Seepage Protection Compromise	SPC	2	Yes/No
	Animal Activities or Plant Root Growth	AMT	3	Serious/Minor/Normal
Structural Instability	Settlement	ST	3	Serious/Minor/Normal
	Abutment Deterioration	ATF	2	Yes/No
	Foundation Deterioration	FDI	2	Yes/No
	Slope Instability	SPI	2	Yes/No
	Poor Construction Quality	PCQ	2	Yes/No

.

The primary causes of dam overtopping failure can be attributed to the combined effect of multiple factors spanning hydrology, structure, and management [25]. Primarily, under extreme climate conditions, exceedance flood exceeding the designed flood control standards imposes the initial impact. Structurally, inherent deficiencies in the spillway system manifest as insufficient discharge capacity, potentially stemming from design flow estimation deviations or efficiency degradation due to facility aging. Compounding this, structural damage to the spillway further diminishes its discharge efficiency. Operationally, factors such as over-retention of water, coupled with the absence of real-time hydrological monitoring or errors in operational decision-making, represent critical human elements. Particularly when mechanical failures or electrical malfunctions occur in gate systems, key flood discharge facilities may fail to activate promptly. This cascade of factors can ultimately lead to reservoir water levels surpassing the crest elevation of the parapet wall, triggering catastrophic overtopping incidents. These factors are often interconnected, revealing systemic risks ranging from engineering design to operation and maintenance management.

The causes of dam seepage failure are complex and diverse, primarily involving the dual action of extreme hydrological conditions and compromised structural integrity [26,27]. Exceedance flood induces an instantaneous rise in reservoir water levels, thereby intensifying seepage pressure within the dam body beyond design thresholds, thus causing the failure of the impervious system. Internal erosion and piping phenomena originate from the migration and loss of fine particles under seepage forces, progressively forming continuous seepage pathways. Structural defects, such as cracks, settlements, and damage to impervious elements, directly create preferential paths for seepage, accelerating the development of hydraulic fracturing. Regarding biological activities, animal burrows and plant root penetration into impervious structures weaken the dam’s resistance to seepage through mechanical damage and the creation of water-conducting pathways. These factors often interact synergistically, ultimately triggering progressive or sudden seepage failure under the coupled effects of seepage forces, structural stresses, and material degradation.

The causes of dam structural failure can be traced back to systematic deficiencies in design, construction, and the geological environment. Inadequate construction quality control, such as substandard filling materials, insufficient compaction, or improper joint treatment, directly compromises the compactness and impermeability of the dam body [28]. Dam foundation softening often results from oversights in geological investigation or the failure of impervious measures, leading to a dramatic reduction in the shear strength of weak interlayers upon contact with water, thereby inducing overall sliding. The rock mass at the dam abutments undergoes softening due to weathering, fracture development, or long-term seepage erosion by reservoir water, disrupting the dam’s load transfer mechanism or lateral constraints. Slope instability frequently couples with adverse geological structures and external disturbances such as rainfall infiltration and seismic activity, triggering landslides or collapses that impact the dam structure. Dam body settlement stems from insufficient foundation bearing capacity or internal seepage-induced suffusion forming voids; differential settlement then causes chain reactions such as cracking of impervious elements and concentrated leakage. The superposition and interaction of these factors over time and space often accelerate structural instability and precipitate dam breach risks.

2.3. Construction of Risk Networks for Earth-Rock Dams Integrating Domain Knowledge

Current Bayesian Network model construction heavily relies on domain expertise. However, excessive dependence on expert experience can introduce subjective bias, and knowledge gaps may lead to the misidentification of causal relationships. Moreover, such approaches struggle to adapt to data-driven, dynamically evolving scenarios. In contrast, constructing BNs by integrating structure learning algorithms can uncover latent associations through data mining, automatically optimizing the network topology to effectively compensate for the limitations of purely experience-based modeling. To overcome the constraints inherent in domain knowledge-dependent modeling methods, this study employs a hybrid Bayesian Network modeling approach that fuses data mining with domain knowledge, based on reservoir dam safety incident data. This method divides the modeling process into two aspects: structure construction and parameter learning. By leveraging the strengths of both data mining and domain knowledge approaches, it aims to uncover and quantify causal relationships within the dam system. On this foundation, a dam breach risk network model for reservoirs is constructed.

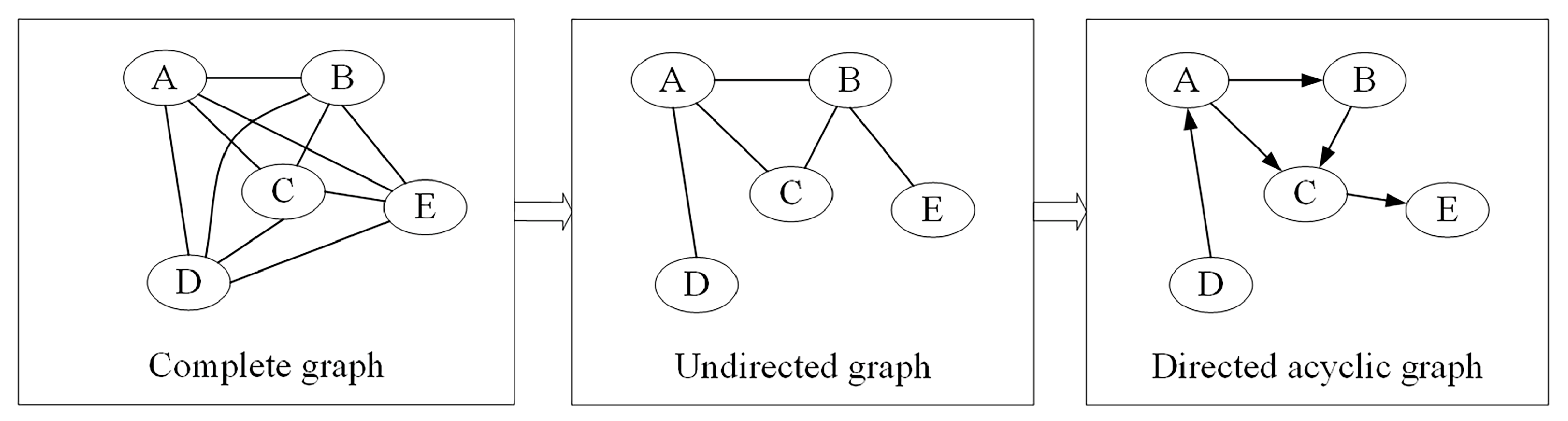
2.3.1. Construction of Risk Network Structures

Structure learning algorithms compensate for the shortcomings of purely domain-knowledge-dependent Bayesian Network model construction, such as subjective bias and misidentification of causal relationships, by mining latent associations between variables from data and automatically optimizing the network topology [29]. Consequently, this approach is well-suited for scenarios where the failure mechanisms of reservoir dams are not yet fully understood, effectively overcoming the limitations of relying solely on domain expertise. Figure 1 illustrates the BN structure learning framework. In this framework, A through E represent five risk factors influencing the safety state of the reservoir dam. The table records the state information of each factor in failure cases (“Y” denotes breach, “N” denotes non-breach). By analyzing these state variation data, the structure learning algorithm can automatically identify association patterns among the factors and determine the number and direction of directed edges. Compared with expert experience, the network structure constructed based on the structure learning algorithm more objectively reflects the true relationships among the variables.

Based on different optimization strategies, structure learning algorithms are primarily categorized into two classes: score-based methods and constraint-based methods [30,31,32]. Score-based algorithms define a scoring function and employ search algorithms to find the network topology that optimizes this score. In contrast, constraint-based methods utilize conditional independence tests to identify dependency relationships between nodes and subsequently construct the corresponding network structure. Constraint-based structure learning algorithms possess a rigorous statistical theoretical foundation and, in principle, align more closely with the semantic characteristics of Bayesian networks. Under certain assumptions, constraint-based structure learning algorithms exhibit higher learning efficiency and can achieve a globally optimal structure, often performing well in practical applications. Hence, the constraint-based PC structure learning algorithm is employed to construct the network structure.

The PC algorithm is a classical constraint-based structure learning algorithm capable of efficiently leveraging conditional independence information within data to construct the structure of a Bayesian Network. The foundation of the PC algorithm lies in conditional independence tests. Specifically, the ${\mathsf{\chi }}^2$-test is employed to verify conditional independence, as it is well-suited for the discrete sample data used in this study and can effectively examine independence between categorical variables. Meanwhile, the significance level α is set to 0.05, a threshold widely adopted in statistical analysis to balance the risk of Type I errors, which involve rejecting a true independence assumption, and Type II errors, which involve accepting a false independence assumption, thereby ensuring the reliability of the learned dependencies [33]. The schematic of the PC structure learning algorithm is illustrated in Figure 2.

2.3.2. Bayesian Network Parameter Learning

After the Bayesian Network structure is established by integrating domain knowledge with a structure learning algorithm, only the dependency topology among variables is determined. To enable the probabilistic reasoning capability of the model, parameter learning is further required. This involves computing the probability distributions of nodes under varying state combinations based on sample data, thereby generating the Conditional Probability Tables.

In the parameter learning phase of Bayesian Networks, although Conditional Probability Tables can theoretically be computed using methods such as Maximum Likelihood Estimation (MLE), these traditional approaches often struggle to provide effective solutions when data is incomplete or contains hidden variables. In contrast, the Expectation-Maximization (EM) algorithm, as an efficient iterative optimization algorithm, leverages its unique two-step alternating strategy of “Expectation” and “Maximization”. This enables it to elegantly handle incomplete data and still converge precisely to a local optimum even in scenarios with missing values, demonstrating superior robustness and adaptability compared to other methods [34,35].

As a classical parameter estimation method, the Expectation–Maximization (EM) algorithm, given a known network topology and observed data, determines the conditional probability distributions of nodes through an iterative optimization process [31]. Starting from initial parameters, the algorithm alternately executes two core steps: the Expectation step (E-step) computes the expected likelihood of the variables given the current parameters; the Maximization step (M-step) maximizes the likelihood function and updates the parameter estimates. This iterative procedure continues until the parameter estimates meet the convergence criteria, thereby obtaining stable probability distribution parameters.

Let the probability density function of the entire sample population Z be $f\left(z|\lambda \right)$. The known data samples within sample Z constitute the observed dataset $D=\left\{d_1,d_2,\dots ,d_n\right\}$, while the unknown data samples constitute the latent dataset $W=\left\{w_1,w_2,\dots ,w_n\right\}$. Thus, the set $Z=\left(D,W\right)$ represents the incomplete dataset, where both the latent data W and the parameters $\lambda$ are unknown. The E-step and M-step in the EM algorithm can be summarized as:

E-step, calculate the expectation:

$$U\left(\lambda ,{\lambda }_{ML}^i\right)={\displaystyle \int f\left(w^i|z,{\lambda }_{ML}^i\right)\ln f\left(\lambda |d\right)dw}$$

(1)

In the equation, ${\lambda }_{ML}$ is the maximum likelihood estimate of $\lambda$, ${\lambda }_{ML}^i$ is the estimated value of parameter ${\lambda }_{ML}$ during the $i+1$ iteration, and $f\left(w^i|z,{\lambda }_{ML}^i\right)$ is the posterior probability density function of the latent data $w$ given the existing datasets Z and $\lambda$.

M-step, calculate the maximum value of $U\left(\lambda ,{\lambda }_{ML}^i\right)$:

$${\lambda }_{ML}^{i+1}=\arg \max U\left(\lambda |{\lambda }_{ML}^i\right)$$

(2)

2.4. Evaluation and Inference of Risk Network Models for Earth-Rock Dams

Bayesian Networks are probabilistic graphical models. During model construction, structural errors and inaccurate parameters may compromise prediction outcomes. Therefore, model evaluation and inference constitute a critical technical step to ensure the reliability of risk quantification results. This process enables the validation and optimization of the model and provides dynamic decision-making support with early warning timeliness under extreme operating conditions.

2.4.1. Predictive Performance Evaluation of Reservoir Dam-Break Models

Upon completing the structure construction and parameter learning of the Bayesian Network model, a scientific evaluation of its predictive performance is essential to verify its reliability and practicality. To this end, the K-fold cross-validation method can be employed. This method randomly partitions the dataset into K mutually exclusive subsets. In each iteration, K-1 subsets are used as the training set for model training, while the remaining one subset serves as the test set to validate the model’s predictive capability. This process is repeated K times, ensuring that each subset has the opportunity to act as the test set. This approach effectively mitigates overfitting issues and yields a more generalizable evaluation result. During each test, the confusion matrix is used to record the number of true positive (TP), false positive (FP), true negative (TN), and false negative (FN) samples predicted by the model. Subsequently, metrics such as precision, recall, F1-score, and accuracy are computed [36,37]. These metrics comprehensively assess the model’s recognition ability for different sample categories from multiple dimensions, intuitively reflecting the accuracy and stability of the model’s predictions, thereby providing a quantitative basis for model optimization and refinement.

The confusion matrix is a standard tool for the quantitative assessment of classification model performance [38]. In this matrix, the rows represent the distribution of the actual observed sample labels, while the columns reflect the distribution of the model’s predicted sample labels. The elements on the main diagonal correspond to True Positive (TP) and True Negative (TN) results, representing the number of samples correctly identified by the model. Conversely, the off-diagonal elements consist of False Negative (FN) and False Positive (FP) results, indicating the number of samples incorrectly predicted by the model. Detailed definitions of specific metrics are provided in

Table 2. Confusion Matrix and Related Metrics.

		Predicted State		Total
		Positive	Negative
Actual State	Positive	True Positive (TP)	False Negative (FN)	Actual Positives
	Negative	False Positive (FP)	True Negative (TN)	Actual Negatives
Total		Predicted Positives	Predicted Negatives	Total Samples

.

The confusion matrix enables the computation of a series of evaluation metrics for a comprehensive assessment of classification model performance. Common metrics include:

Overall Accuracy, which provides a holistic description of the prediction precision across all samples. It is calculated as the proportion of samples correctly classified by the model relative to the total number of samples, with the formula given by:

$$OA={\displaystyle \frac{TP+TN}{TP+FN+FP+TN}}$$

(3)

In the formula, TP is true positive, TN is true negative, FP is false positive, and FN is false negative.

Precision (Prec) measures the prediction accuracy for a single state, specifically the proportion of actual positive samples among those predicted as positive, with its formula given by:

$$Prec={\displaystyle \frac{TP}{TP+FP}}or{\displaystyle \frac{TN}{FN+TN}}$$

(4)

Recall (Rec) is the proportion of actual positive samples that are correctly predicted as positive, reflecting the model’s ability to identify the positive class; its formula is:

$$Rec={\displaystyle \frac{TP}{TP+FN}}or{\displaystyle \frac{TN}{FP+TN}}$$

(5)

The F1-Score is the harmonic mean of Precision (Prec) and Recall (Rec), used to comprehensively evaluate model performance, calculated as:

$$F1-Score={\displaystyle \frac{2\times Prec\times Rec}{Prec+Rec}}$$

(6)

The Receiver Operating Characteristic curve (ROC curve) is a classic visualization tool for assessing classification model performance. This curve plots the True Positive Rate (TPR) on the vertical axis against the False Positive Rate (FPR) on the horizontal axis. By traversing all possible classification thresholds, corresponding coordinate points are generated and connected to form a two-dimensional curve [36]. The formulas for calculating TPR and FPR are as follows:

$$TPR={\displaystyle \frac{TP}{TP+FN}}$$

(7)

$$FPR={\displaystyle \frac{FP}{TN+FP}}$$

(8)

The Area Under the Curve (AUC) is a key parameter quantifying the predictive efficacy of a classification model, defined as the area enclosed by the ROC curve and the coordinate axes [37]. As a dimensionless metric, the AUC value ranges between 0 and 1, and its magnitude is positively correlated with the model’s predictive performance.

2.4.2. Bayesian Network Inference

Risk inference is the process of performing risk probability calculations based on a risk network. Its key steps involve determining the probability parameters within the risk network, such as the prior probabilities of root nodes and the conditional probabilities between parent and child nodes. In the dam risk network, the conditional probabilities between parent and child nodes represent the probabilistic expression of the association degree among various risk factors, serving as crucial evidence for dam risk inference. Bayesian inference is chosen for dam risk assessment due to the complex, dynamic, and interrelated nature of dam risk factors, which traditional methods struggle to handle effectively. Bayesian inference integrates prior knowledge, such as historical data and expert experience, with new evidence from real-time monitoring, enabling a more precise and dynamic reflection of the dam’s risk status.

In dam risk assessment, Bayesian inference is categorized into two types: forward inference and backward inference [39]. Forward inference starts from the basic risk factors in the dam risk network. Utilizing the predefined prior probabilities of root nodes and the conditional probabilities between parent and child nodes, it calculates the probability of risk occurrence for child nodes layer by layer, following the risk propagation path from the bottom to the top level. Ultimately, it completes the probabilistic prediction of target risks, such as dam failure. For example, if we know the prior probabilities of “Exceedance Flood” and “Insufficient Spillway Capacity,” forward inference can compute the probability of “Overtopping” occurring and further estimate the overall probability of dam breach. This helps with proactive risk assessment and early warning. Conversely, backward inference is primarily applied for traceability analysis after the occurrence of a target risk event. When incidents like dam breach or seepage occur, based on the Bayesian inference framework, it inversely computes the contribution degree of each basic risk factor to the target risk event. By comparing the posterior probabilities of different risk factors, it identifies the key risk sources responsible for the incident. For instance, if a dam breach is confirmed, backward inference can calculate how much the probability of each risk factor increases compared to their prior probabilities, thereby pinpointing the most critical causes. This provides a scientifically quantified basis for subsequent risk management, engineering rehabilitation, and other management decisions.

3. Results

3.1. Dam-Break Network Models for Earth-Rock Dams

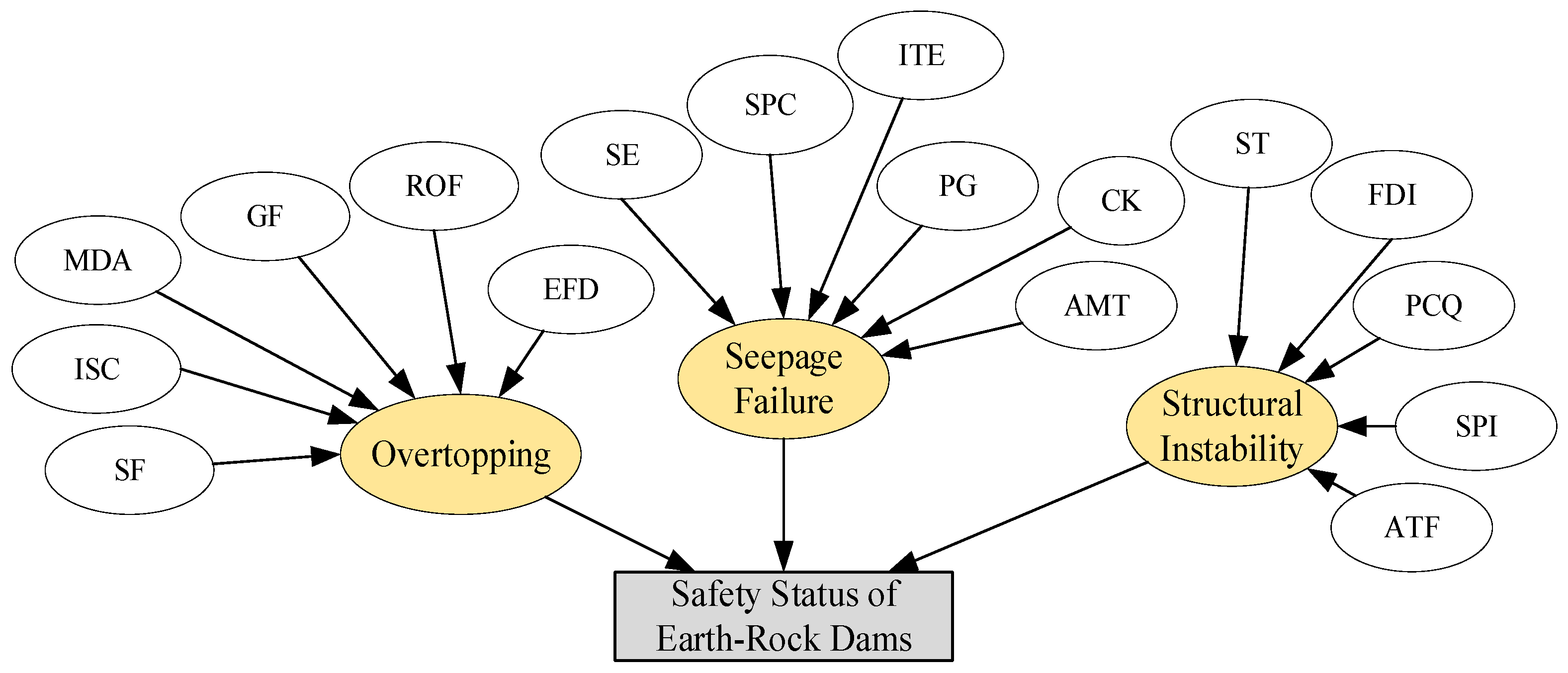
3.1.1. Domain Knowledge-Based Network Structure

By integrating domain expert knowledge, a preliminary Bayesian Network structural model G₁ is constructed, as illustrated in Figure 3. As shown in Figure 3, the manually constructed model relying solely on domain knowledge exhibits a simple network structure with sparse directed arcs. The directionality of these arcs follows a singular pattern: they only point from risk-influencing factors to failure modes, and then from failure modes to the “Reservoir Dam Safety State” node. More critically, except for the “Reservoir Dam Safety State” node, all other nodes have only one child node. This implies that the interaction relationships among various influencing factors are entirely neglected. This simplistic construction approach severely constrains the model’s ability to represent the complex multivariate associations among dam breach risk factors in reality. Consequently, it struggles to accurately reflect the true scenario in actual reservoir operation, where risk factors are intertwined and collectively influence the dam safety state.

3.1.2. Structure Learning Algorithm-Based Network Structure

Based on the safety incident sample set, the PC algorithm was employed to construct the initial network structure of the dam breach risk network model, denoted as model G₂, as shown in Figure 4. Since this algorithm relies entirely on data statistical characteristics for modeling, the directionality of some directed edges lacks practical engineering significance and requires appropriate adjustment. Specific issues include:

(1)

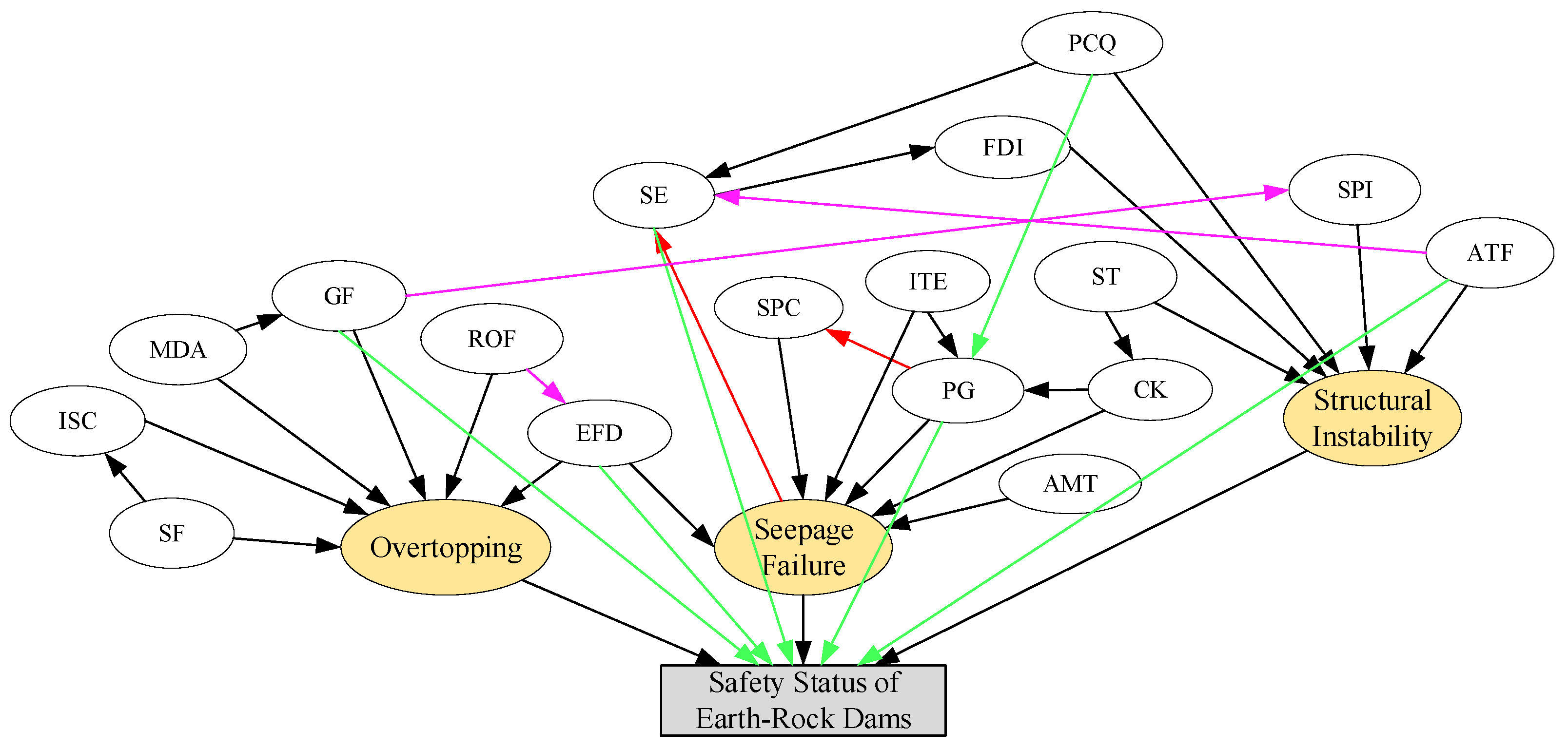
Direct connections between risk factors and the safety state, as indicated by the green arrows in Figure 4. The model contains five risk factors, including gate failure, exceedance flood, collapse, poor construction quality and abutment deterioration, pointing directly to the “Safety State of Earth-Rock Dams”. However, from an engineering mechanism perspective, these risk factors typically affect the safety state indirectly by triggering specific failure modes. Therefore, such connection relationships need adjustment.

(2)

Variable connections lacking causal basis, as indicated by the pink arrows in Figure 4. Although statistical correlations exist between some variables connected by directed edges, clear causal links are absent. Examples include over-retention of water pointing to exceedance flood, gate damage pointing to slope instability, and abutment softening pointing to collapse. These connections require correction based on domain knowledge.

(3)

Connections with incorrect causal direction, as indicated by the red arrows in Figure 4. In the model, seepage failure points to collapse; in fact, collapse is an influencing factor that can lead to seepage failure, thus the direction of the arrow between them is problematic. Additionally, the direction of the directed arc between “piping” and “seepage protection compromise” is also incorrect. “Piping” does not cause “seepage protection compromise”; conversely, damage to impervious facilities creates seepage pathways. Subsequently, fine particles in the soil are gradually carried away by water flow, giving rise to piping.

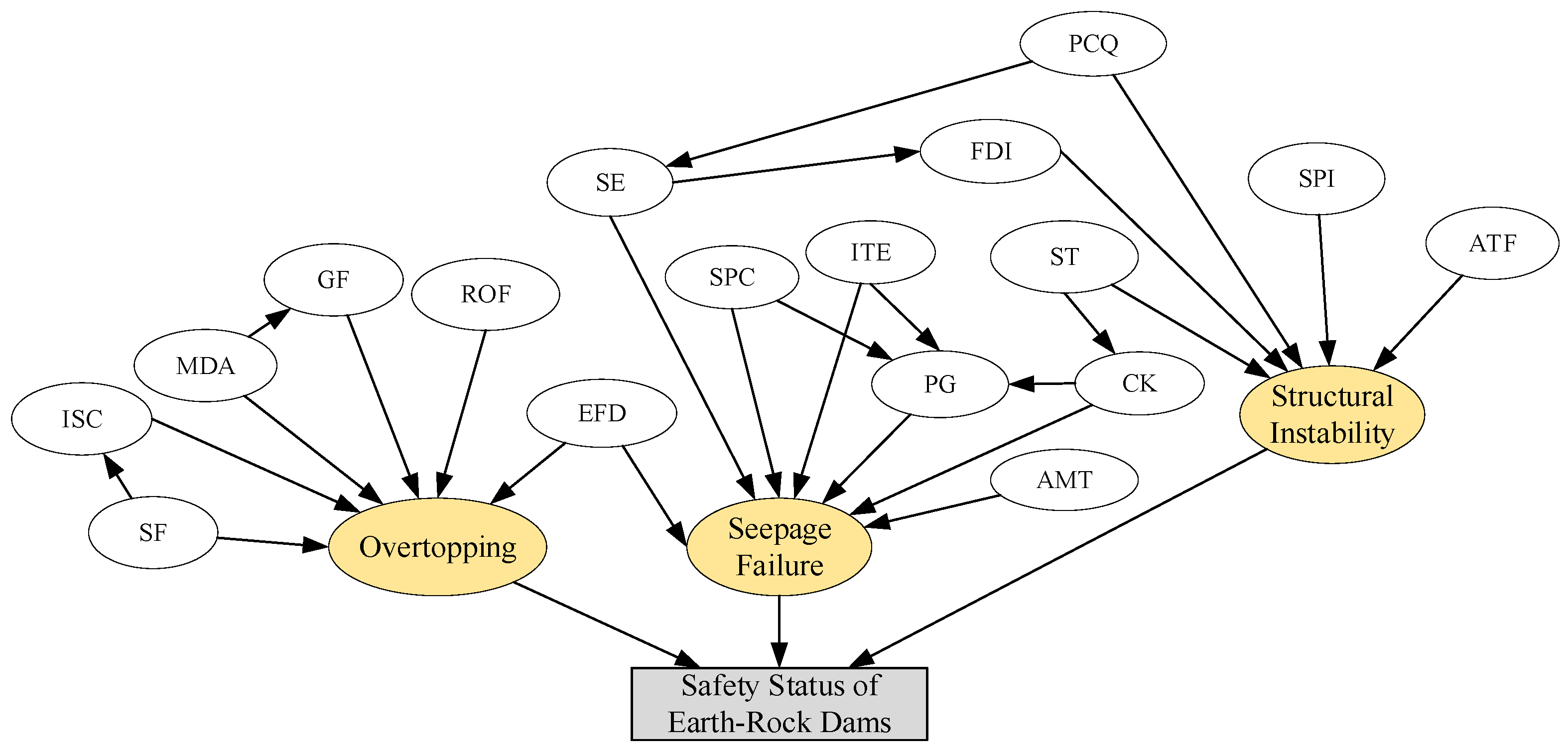
3.1.3. Integrated Network Structure Combining Domain Knowledge and Structure Learning Algorithms

Building upon the initially constructed model, the network structure was optimized through domain expertise, resulting in a hybrid model that integrates domain knowledge with machine learning, denoted as model G₃. The optimization process primarily involved deleting connections lacking a causal basis, removing direct links between risk factors and the safety state, and correcting connections with erroneous causal directions. The optimized network structure, illustrated in Figure 5, exhibits a more concise and reasonable topology, accompanied by a significant reduction in computational complexity.

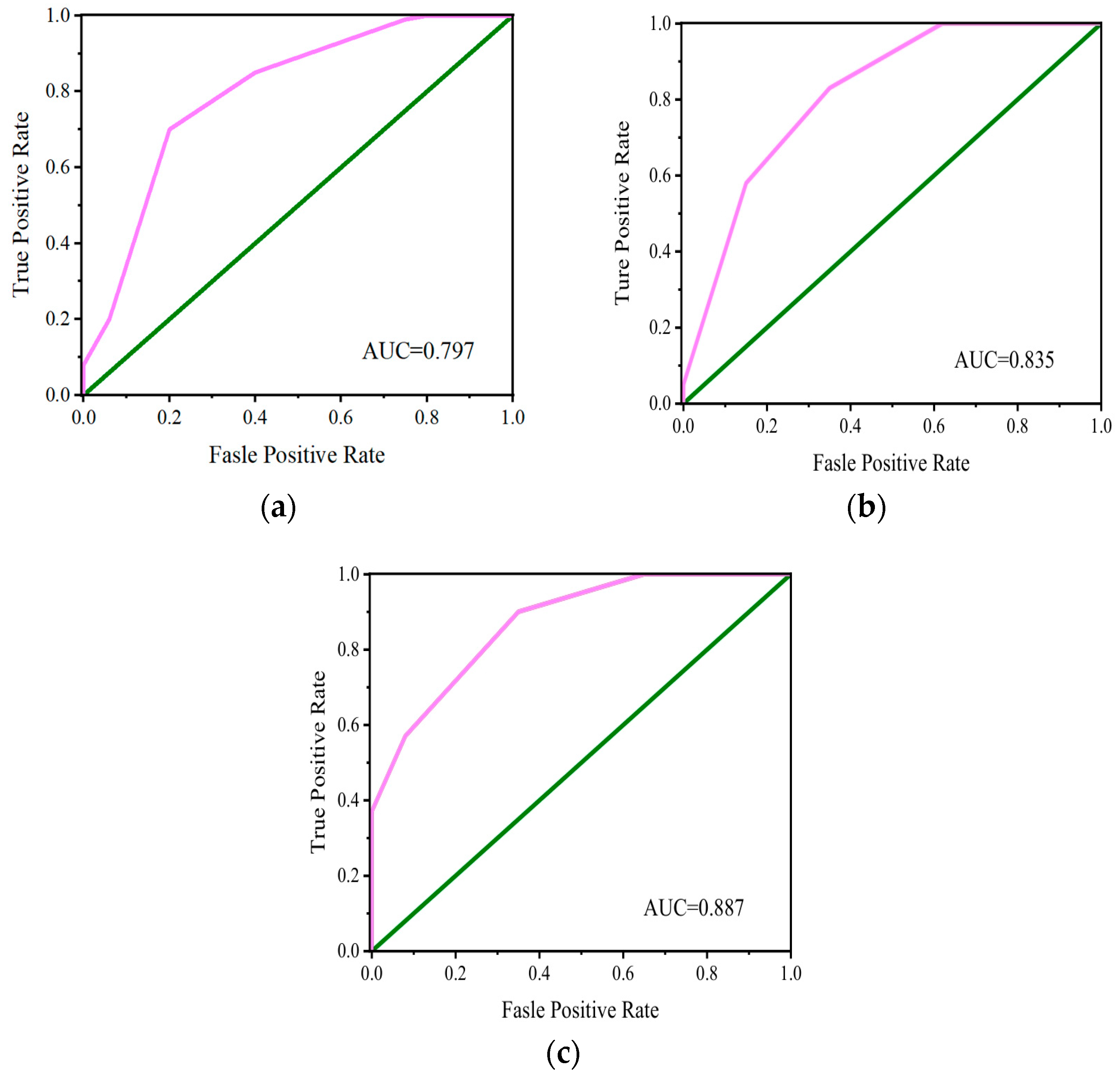
3.2. Model Evaluation Results

Using the aforementioned method, the predictive performance of the three constructed Bayesian Network structural models was assessed. The evaluation selected the “Safety State of Earth-Rock Dams” node as the target variable, making predictions for its two states: breached and non-breached, and the resulting prediction accuracy evaluation metrics are presented in

Table 3. Predictive Performance of Bayesian Network Models.

Model	AUC	OA	Prec	Rec	F1-Score
G1	0.797	0.784	0.782	0.741	0.762
G2	0.835	0.861	0.844	0.834	0.841
G3	0.887	0.895	0.897	0.883	0.899

and Figure 6.

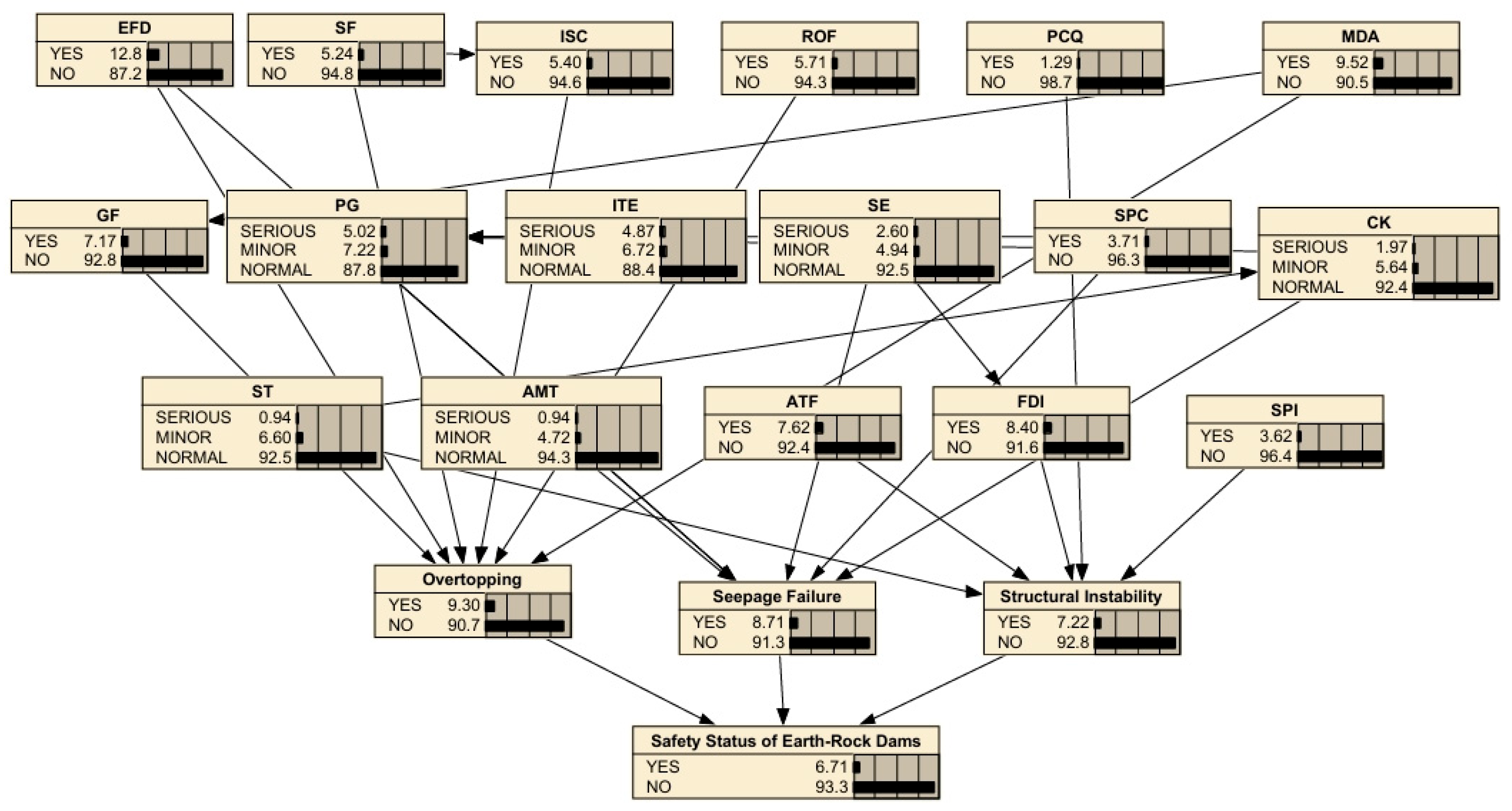
3.3. Inference Results

Based on the comparative model performance evaluation presented in Section 3, probabilistic inference was performed using the risk network model that integrates domain knowledge with a structure learning algorithm. These inferences were conducted using the commercial software Netica Application (Version 5.18, Norsys Software Corp., Vancouver, BC, Canada). Leveraging the probabilistic reasoning mechanism of Bayesian Networks, this approach effectively quantifies the prior probabilities of individual risk factors, the posterior probability distributions of child nodes, and the propagation pathways of failure progression. By running the constructed BN model, the system calculates and presents the prior probabilities of various risk factors in dam breach incidents init systematically calculates the occurrence probabilities of various risk factors in dam breach incidents, with the inference results presented in Figure 7.

The core of the backward inference method lies in reasoning backward from a known event outcome. It systematically traces potential causal elements to reversely derive the key influencing factors that trigger a specific result. In the Bayesian Network model, the state parameter of the “Safety State of Earth-Rock Dams” node was set to confirmed breach state, thereby characterizing the occurrence state of a dam breach incident. Leveraging the backward inference mechanism of this model, the key risk-inducing factors leading to dam breach were systematically identified. The posterior probability increment shown in Figure 8 is obtained by calculating the difference between the posterior probability after establishing breach evidence and the prior probability for each risk factor, clearly demonstrating the relative importance changes in each risk factor under the condition of confirmed dam breach. The specific analysis results are shown in Figure 8.

4. Discussion

(1)

The key performance metrics of model G₃, which integrates domain knowledge with the structure learning algorithm (AUC = 0.887, OA = 0.895, F1-Score = 0.899), significantly outperform those of the domain knowledge-based model G₁ (AUC = 0.797, OA = 0.784, F1-Score = 0.762), as detailed in Table 3. This result reveals that the structure learning algorithm, through data-driven mining of objective associations, effectively compensates for the structural simplification defects inherent in purely domain knowledge-based models caused by excessive reliance on expert experience. These defects include neglecting the coupling effects among risk factors and relying on subjective causal assumptions. The structure learning algorithm significantly optimizes the completeness and causal rationality of the network structure. Consequently, it comprehensively enhances the model’s discrimination accuracy for the dam breach state. This validates the superiority of the strategy integrating machine learning algorithms in constructing high-precision quantitative risk models for earth-rock dams. This strategy leverages the advantage of data-driven approaches in capturing complex associations while utilizing domain knowledge to ensure the engineering rationality of the network topology. It effectively overcomes the subjectivity and limitations of single-domain knowledge modeling, thereby providing reliable methodological support for constructing high-precision and interpretable quantitative risk models for earth-rock dam breach.

(2)

As detailed in Table 3, the key performance metrics of the G₃ model, which integrates domain knowledge: AUC, OA, and F1-Score are 0.887, 0.895, and 0.899, respectively. These values significantly outperform those of the data-driven model G₂ (AUC = 0.835, OA = 0.861, F1-Score = 0.841). This indicates that the model possesses precise discrimination capability for the state of earth-rock dams. The high accuracy and F1-Score demonstrate that the model’s overall classification performance is stable and well-balanced. This result proves the effectiveness of the modeling strategy integrating domain knowledge with machine learning algorithms in enhancing model accuracy and reliability, thereby establishing a credible foundation for practical engineering risk quantification and assessment.

(3)

The forward inference of the Bayesian Network, as quantitatively revealed in Figure 7, identifies the systemic predisposing factors for dam breach and their coupling pathways. The results show that exceedance flood, with an occurrence probability of 12.80%, and insufficient spillway discharge capacity at 5.40%, are the root factors with the highest occurrence probability and the most significant risk contribution. Furthermore, these two factors elevate the probability of dam breach through a cascading effect: “exceedance flood → insufficient spillway discharge capacity → overtopping”. Therefore, in the routine management of earth-rock dams, it is essential to strengthen early warning systems for extreme weather events and optimize reservoir operation plans. Regular assessment of the actual discharge capacity and ensuring the reliable operation of key facilities, such as gates, are critical. Additionally, the coupling and amplification effects must be prioritized, necessitating the implementation of coordinated prevention and control measures.

(4)

Figure 8 employs Bayesian backward inference to quantitatively trace the contributions of direct failure modes under dam-break conditions: The posterior probability increase for flood overtopping is 53.2%, surpassing that of seepage failure (36.09%) and structural failure (24.08%), demonstrating that flood overtopping is the most critical direct failure mode. This result provides a fundamental basis for targeted prevention and control: Preventing flood overtopping must be prioritized, while addressing seepage failure and structural failure also requires attention. The quantified contributions establish an objective priority ranking for the scientific allocation of risk management resources.

(5)

Notwithstanding its demonstrated utility, the proposed model carries inherent limitations that warrant acknowledgment and pave the way for future research. Its performance is contingent upon the representativeness and quality of the historical dataset, which, despite being substantial for the domain, remains limited in size and potentially subject to reporting biases and regional specificity. The static nature of the model, a common characteristic of standard BNs, does not explicitly capture the temporal evolution of risk factors, such as the progressive nature of internal erosion or real-time hydrological changes. Furthermore, the structure learning process, while enhanced by expert knowledge, involves assumptions and discretionary adjustments that influence the final topology. Future work should therefore prioritize augmenting the database with more diverse and granular case histories. A pivotal advancement would be the development of a dynamic BN framework capable of assimilating real-time monitoring data such as seepage pressures, deformation and reservoir levels to enable continuous risk updating and truly proactive early warning. Exploring more advanced, hybrid structure learning methodologies and integrating principles from physics-informed machine learning could further refine the model’s causal fidelity and robustness, ultimately evolving it into a comprehensive, adaptive decision-support tool for dam safety management.

5. Conclusions

This study addresses the challenges of complex coupling among earth-rock dam breach risk factors, the excessive reliance on domain expertise in traditional and existing Bayesian Network (BN) modeling methods, which introduces subjective bias, and the inability of simple statistics to fully uncover underlying data patterns. To overcome these issues, a hybrid Bayesian Network modeling framework integrating domain knowledge with machine learning is proposed and validated. Utilizing global earth-rock dam incident case data, this framework leverages the objective association mining capability of the PC structure learning algorithm and the causal relationship validation and optimization capability of domain expert knowledge. Combined with parameter learning completed via the EM algorithm, it constructs a dam breach probability analysis model characterized by both high accuracy and strong interpretability. The model results indicate that exceedance flood and insufficient spillway discharge capacity are identified as the key risk factors with the highest occurrence probability. Furthermore, overtopping is recognized as the predominant direct failure mode in dam breach events, exhibiting a significantly higher relative risk contribution than seepage failure and structural failure. The integrated framework established in this study effectively reduces the subjectivity in BN model construction and enhances the accuracy of risk quantification. It provides an interpretable scientific basis and a technical pathway for the probabilistic quantification of earth-rock dam breach risk, the identification of key risk-inducing factors, and the formulation of prevention and control strategies.