Development and Comparison of Methods for Identification of Baseflow-Dominant Periods in Streamflow Records

Abstract

Accurately identifying baseflow-dominant (BFD) periods in streamflow records is crucial for evaluating low-flow conditions, groundwater interactions, and other water resource management issues. While baseflow separation methods are widespread, the definition and identification of BFD flows are relatively new areas. Here, we define BFD periods as flow conditions that occur with minimal contribution from quickflow, including periods dominated by bank flow, groundwater interaction, or residual flow routing through the system. We develop a comprehensive, expert-labeled dataset of BFD periods from 182 USGS stream gages across diverse hydrological settings in the continental United States as ground truth. Using this dataset, we evaluate various automated BFD identification methods, including three new approaches, a machine learning classifier, a gradient-based method, and a statistical method, as well as two established techniques: the BN77 and Strict Baseflow methods. Our results demonstrate that the machine learning model (RF-BFD) outperforms all other approaches, achieving an F1 score of 0.92 and 92% accuracy. This study characterizes challenges in identifying BDF periods and establishes benchmarks for improving BFD identification in large-scale hydrological studies. The findings offer a pathway toward more robust and scalable BFD identification techniques, enhancing low-flow forecasting and groundwater-surface water interaction assessments.

1. Introduction

Streamflow has traditionally been divided into quickflow and baseflow contributions [1,2]. Quickflow is the portion of streamflow that results from recent precipitation or snowmelt events and includes surface runoff, snowmelt-driven flow, and other flow components that rapidly enter the stream channel following precipitation or snowmelt events and are routed downstream. Baseflow is the sustained flow fed by delayed subsurface pathways and is present even during periods dominated by quick flow [2,3]. Baseflow is primarily from subsurface sources, including seeps, groundwater aquifers, deeper bank storage, and interconnected geological formations [1,4,5]. Baseflow represents a slow, regulated water release that maintains stream continuity during dry periods and represent the intricate hydrology of watershed landscapes [6,7].

Hydrologists perform flow separation analysis to characterize the two primary components of streamflow to help understand the underlying processes governing a stream’s response in order to better predict the response of streamflow to rainfall or snowmelt in the watershed [5,8]. Researchers have developed various analytical approaches for flow separation, ranging from graphical hydrograph separation to digital filtering techniques, each attempting to separate the baseflow and quickflow contributions to total streamflow [9,10,11]. Existing baseflow separation methods (e.g., digital filters such as Lyne-Hollick [12], UKIH [13], and Eckhardt [11]; graphical methods such as HYSEP [14]) generally focus on quantifying the baseflow component throughout the entire streamflow record but are not specifically designed to identify discrete periods where baseflow dominates the flow regime. These methods often perform poorly during low-flow periods without quickflow, where their estimates become uncertain due to limited dynamic range in the hydrograph and difficulty distinguishing between residual quickflow and true baseflow [7,15].

While precipitation and the resulting quick flow dominate higher streamflow conditions, many stream reaches experience periods where baseflow, primarily from subsurface contributions, dominates the streamflow [2,3]. These baseflow-dominant (BFD) periods mostly occur during low-flow conditions but can occur at other times, for example, during wet periods, but sometimes after a precipitation event. Flow can be BFD, but not necessarily in the low portion of the flow duration curve. Understanding BFD periods is essential for improving flow forecasts at a continental scale when flow conditions are not dominated by precipitation-driven flow, as most hydrologic models route water from precipitation events, with very simple process models, if any, for baseflow. Many different hydrologic processes can contribute to BFD periods. For example, BFD periods could be characterized by the stream either gaining or losing flow to groundwater, bank storage, or residual flow in the channel. Recession curve behavior after a precipitation event may also involve other processes not captured in current routing methods that may be considered as BFD periods [16].

A key challenge in BFD identification is the lack of a universally accepted quantitative definition. Unlike baseflow separation methods that estimate the baseflow component as a proportion of total streamflow, BFD identification requires determining when baseflow is the dominant flow process. We define BFD periods operationally as periods when streamflow exhibits the characteristic signatures of baseflow dominance: (1) minimal contribution from recent precipitation or snowmelt events, (2) relatively stable flow conditions with gradual changes, and (3) hydrograph recession behavior consistent with delayed subsurface drainage rather than rapid surface runoff responses. Importantly, BFD periods are not strictly defined by flow magnitude alone, as a stream can experience BFD conditions at relatively high flows if those flows are sustained by groundwater or delayed subsurface contributions without recent quickflow inputs. This definition recognizes that baseflow dominance is a process-based condition rather than a simple threshold on the baseflow index or flow magnitude, requiring consideration of multiple hydrological indicators simultaneously.

Incorporating these subsurface and other interactions into flow routing models using physics-based deterministic groundwater models remains challenging due to the extensive data requirements for geologic characterization, parametrization, and model calibration, and on a continental scale is generally considered impractical at the resolution required for streamflow interaction. Developing alternative approaches to modeling subsurface interaction with streams requires identifying and characterizing BFD periods.

Hydrologists have used various terms to describe baseflow, including groundwater flow, low flow, percolation flow, underrun, seepage flow, and sustained flow [2], to name a few. Chapman [8] and Eckhardt [11] distinguished baseflow from direct runoff, associating the former with groundwater discharge into the stream while considering direct runoff as the result of overland or near-surface flow. The understanding and quantification of baseflow requires separating different components of streamflow [5,8]. Multiple sources note that baseflow makes up the majority of streamflow during dry periods [3], when quickflow (surface runoff and interflow) is minimal [7,15]. The fraction of streamflow that is baseflow varies by location and climate [2,11,17,18]. For example, baseflow can be a large proportion of streamflow in dry climates [3], and may decrease significantly during wet periods. In a semi-arid sandy area, the baseflow index (ratio of baseflow to total flow) can be as high as 96% [19]. Regarding its dynamics, baseflow responds slowly to rainfall events [20,21], is less variable than streamflow [15], and its peaks are typically delayed relative to streamflow peaks [7].

Numerous algorithms have been developed to separate streamflow into quickflow and baseflow components—a process known as baseflow separation [22]. These methods generally fall into three main categories: graphical methods, recession analysis, and digital filter techniques. Graphical methods rely on hydrograph interpretation to delineate baseflow contributions and are among the earliest approaches developed [2,16]. Common automated tools include the Base Flow Index (BFI) program, which divides streamflow records into distinct periods and assigns minimum flows [9]; Hydrograph Separation Program (HYSEP), which applies a moving window to identify discharge minima [14]; and the United Kingdom Institute of Hydrology (UKIH) method, which identifies turning points in streamflow data [13]. Recession analysis methods study the declining limb of the hydrograph to infer catchment storage properties and baseflow dynamics [16]. An automated implementation is ABIT (Automatic Baseflow Identification Technique), which objectively identifies multiple recession segments for analysis [23]. Digital filter methods, particularly recursive digital filters (RDFs), are widely used due to their simplicity and automation potential. These include the Lyne-Hollick filter, which uses a single recession constant [12]; the UKIH filter [13]; the Chapman-Maxwell filter, developed for ephemeral rivers [8,24]; and the Eckhardt filter, which incorporates both the baseflow index and recession constant as parameters [11]. Despite their utility, RDFs often require subjective parameter choices [25]. While these methods can reveal insights into catchment hydrology, they are generally not based on physical models [26]. Methods that include physical processes include hydrological models that simulate baseflow without relying on fixed separation rules [22]. Other approaches use statistical methods for predicting the baseflow index using catchment characteristics [27], and hybrid methods that calibrate digital filter parameters using auxiliary data or modeling techniques [25,28].

A related, but distinct research focus is identifying periods in a streamflow record when the flow is all or predominantly baseflow (BFD periods). Unlike baseflow separation methods that estimate the baseflow component of streamflow at all times, BFD identification methods specifically detect time intervals when quickflow is insignificant. This is a distinction from separation methods, which generally assume that baseflow is based on contribution from subsurface sources; however, depending on the geology and climate, BFD periods can be characterized by losing reaches, gaining reaches, or reaches where there is little subsurface interaction and can be seen as analogous to emptying a pipe. By identifying BFD periods, these interactions can be characterized and studied, regions where these interactions are important identified, and better models or methods can be created to estimate flow during these periods.

BFD identification differs from both low-flow identification and traditional flow separation approaches. Unlike low-flow identification, BFD periods can occur at higher flow levels when baseflow dominates despite elevated discharge. Unlike flow separation methods, which estimate baseflow components throughout the entire hydrograph but often lack accuracy during low-flow periods, BFD identification specifically targets time periods when baseflow is the dominant flow component. Being able to identify and characterize BFD flow conditions will support the development of alternative methods for incorporating stream subsurface interactions in large-scale hydrologic models, including classifying regions or conditions where current models have difficulties estimating BFD flow, along with areas where current models do well under these conditions.

Research Objectives

The main objectives of this paper are to: (1) define BFD flow conditions, (2) create a comprehensive hand-labeled dataset of BFD periods that serves as ground truth for method development and comparison, (3) develop machine learning, gradient based, and statistical models to classify BFD flow using these data, and (4) evaluate the performance of these new models and existing BFD identification methods. To develop this benchmark dataset, we selected 182 USGS stream gages across diverse hydrogeological settings in the continental United States (CONUS) and hand-labeled daily streamflow records as BFD or non-BFD using graphical hydrograph analysis. We assumed these data were accurate, though we acknowledge variation and differences, and the dataset is somewhat subjective. We used students to generate this dataset, and while we tried to have consistent methods, we acknowledge variation among the gages labeled by different students, though these differences are minimal. We evaluated these differences by having two students label each gage.

We then use this labeled dataset as the basis to evaluate various algorithms for automatically classifying BFD periods in streamflow records. We evaluated two established methods for identifying BFD periods: the Strict method [7], and the BN77 method [23]. We also evaluated three new methods developed as part of this research: a machine learning approach, a threshold gradient method, and a statistical approach. This comparative analysis, using our hand-labeled dataset as ground truth, provides the first comprehensive assessment of how well automated methods align with the hand-labeled BFD periods across diverse hydrological conditions and allows to recommend an automated method that can be applied to very large datasets.

2. Data

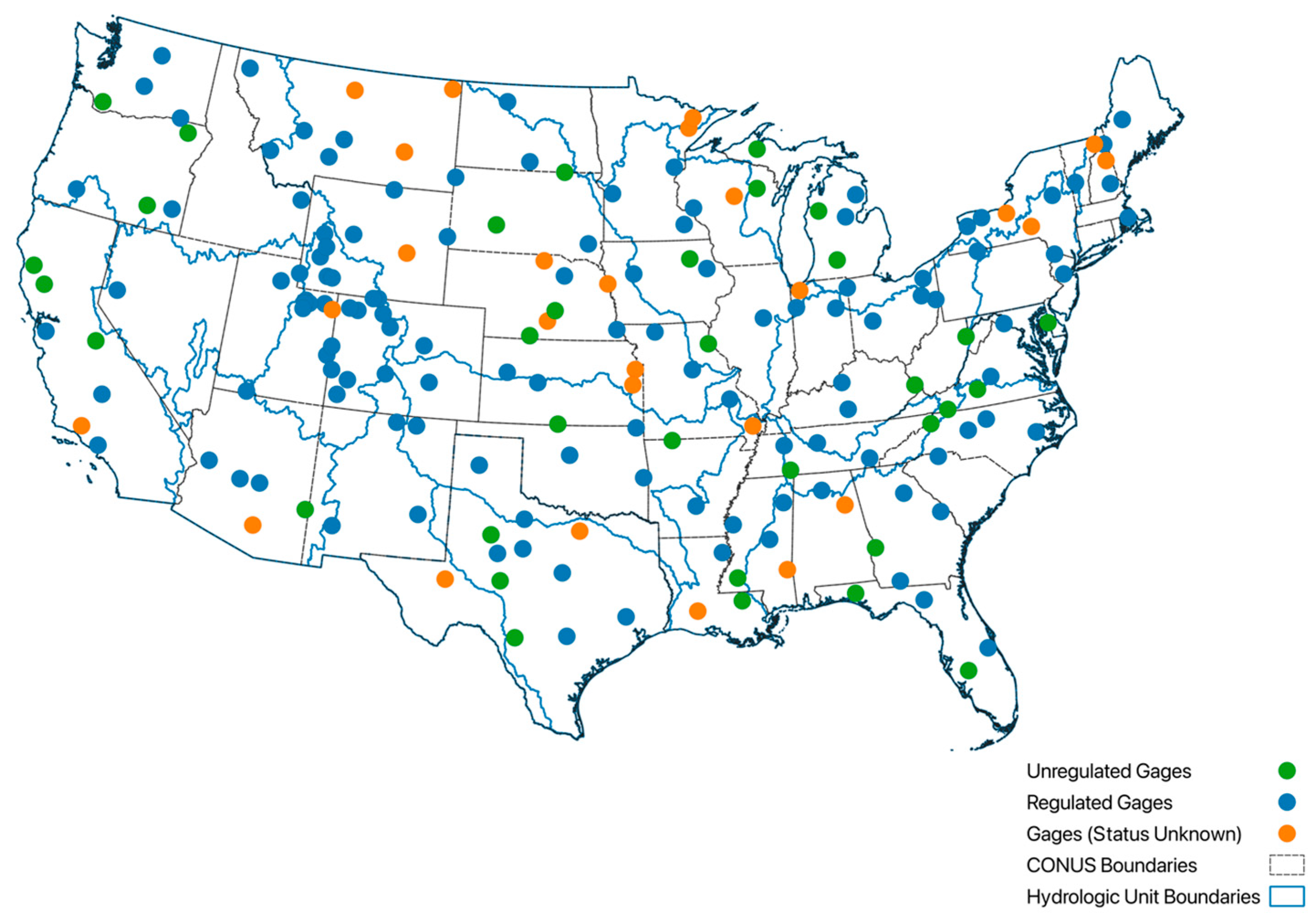
To develop our hand-labeled dataset, we used streamflow data from 182 USGS stream gages selected from across CONUS, with locations shown in Figure 1. To create a representative dataset applicable across all regions of CONUS, we selected gages from multiple areas throughout the country that represent different hydrology and watershed characteristics (Figure 1). We used USGS’s division of the CONUS into 18 regions, which are each further divided into 222 subregions, and tried to select at least one gage for each of the 18 regions.

We prioritized selection for gages located on unregulated rivers based on the unregulated flag in the USGS metadata. The USGS describes these basins as near-reference conditions (i.e., unregulated and unlikely to be altered given associated measures of development). These unregulated gages represent watersheds with minimal human impact, offering insights into near-natural streamflow patterns. This unregulated classification is described by a USGS publication, which provides a comprehensive list of reference-quality gages [29]. While we prioritized unregulated gages, only 34 gages (18%) out of the 182 we selected in the CONUS are considered unregulated by the USGS, as most subregions did not have an unregulated gage. For subregions without unregulated gages, we selected gages with the longest continuous records and minimal missing data to ensure sufficient temporal coverage for model training and evaluation. We handled missing data through exclusion rather than imputation. After computing features, we removed any time steps with NaN or infinite values, ensuring the model was trained only on complete observations.

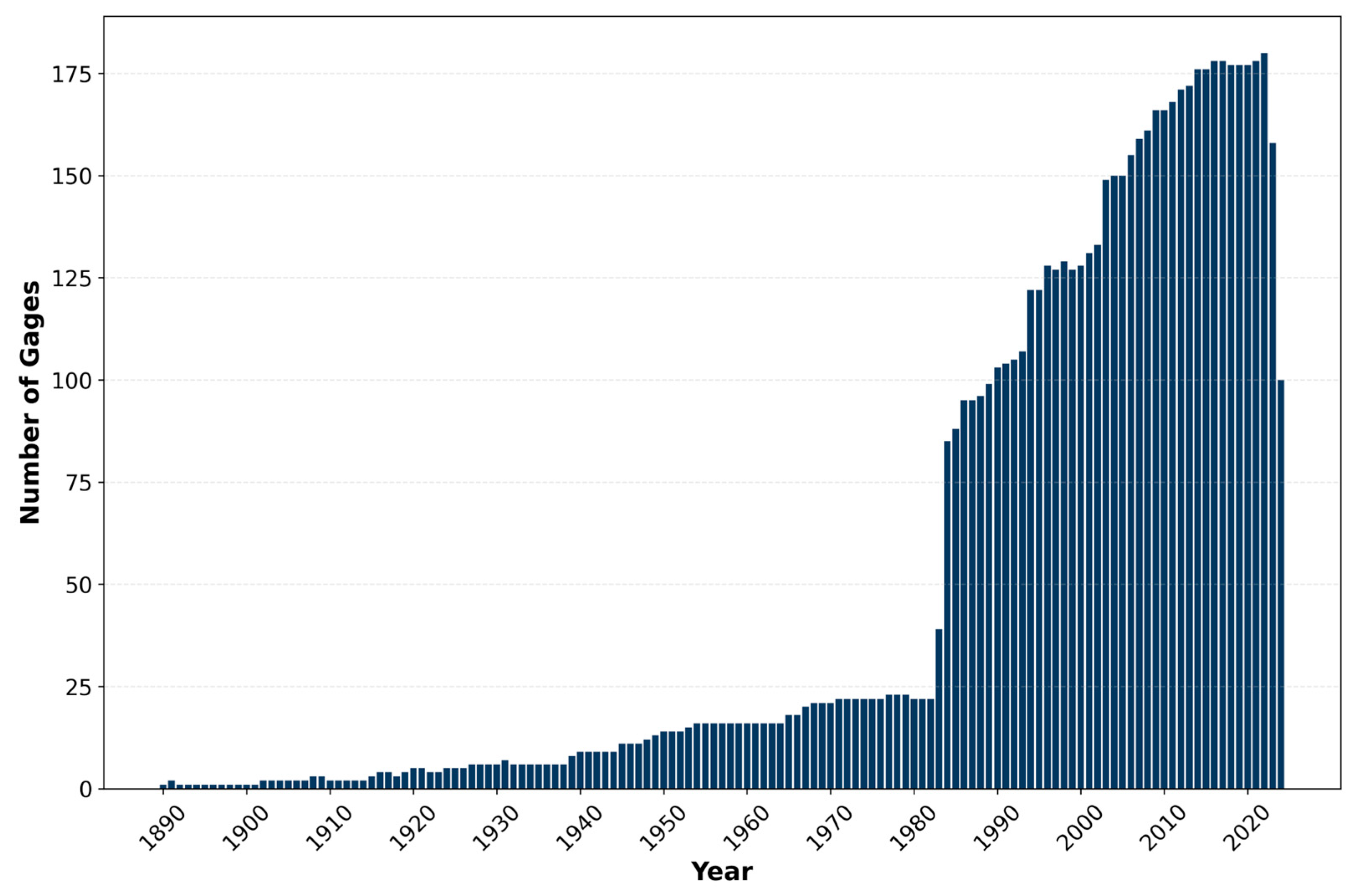
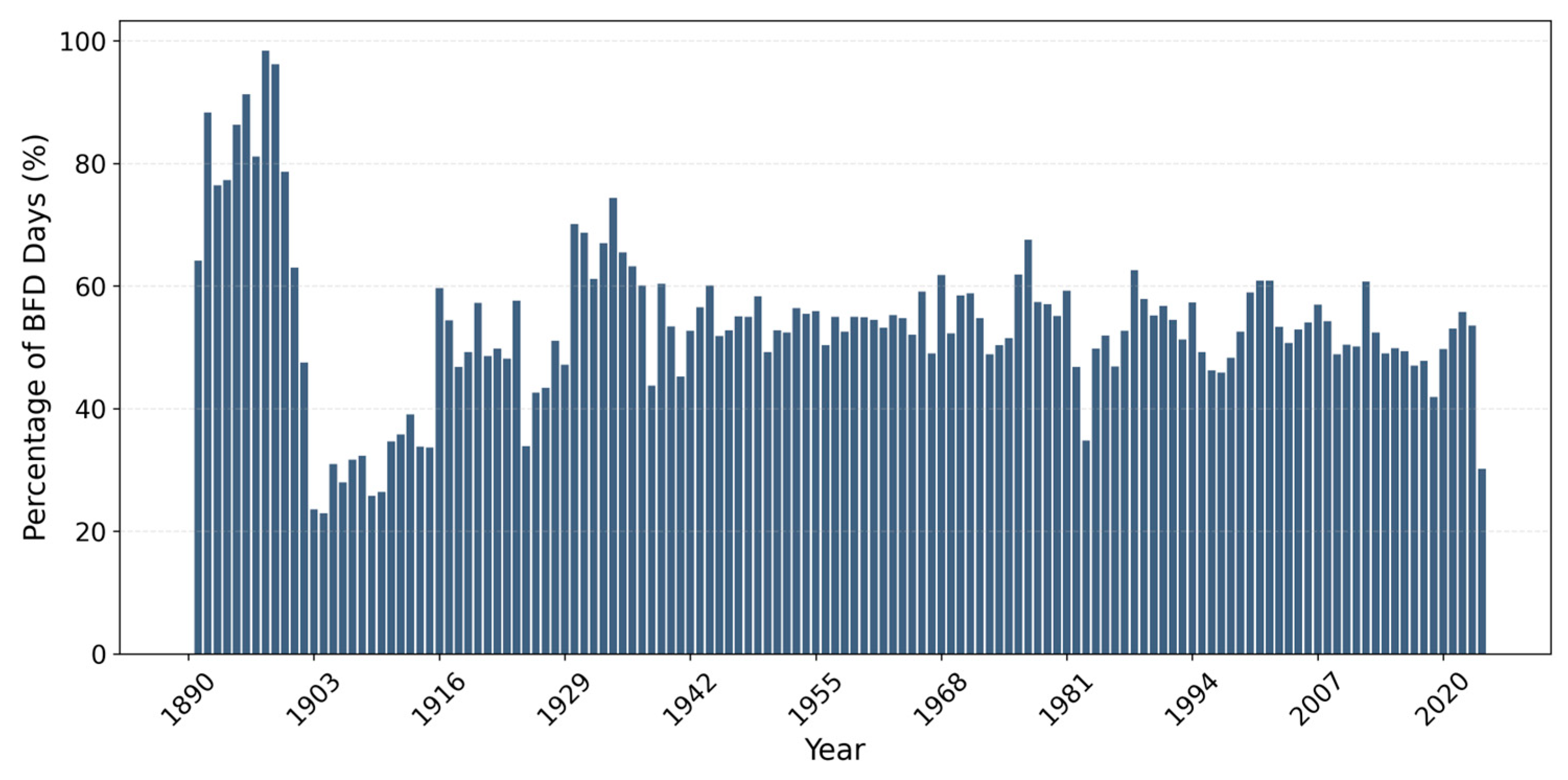
Figure 2 shows the temporal availability of data from our 182 selected USGS stream gages. The figure reveals that significantly more gages have data available in recent decades, with a notable increase beginning around 1985. While some gage deployment began as early as 1890, the number of gages with available data increased substantially around 1980 and continued to grow over time. From the early 2000s onward, data were available from over 150 gages, reaching peak coverage of about 180 gages in the most recent years. This maximum of 180 gages represents the most comprehensive period in our dataset, though the average was 49.7 gages per year across the entire 135-year period from 1890–2024.

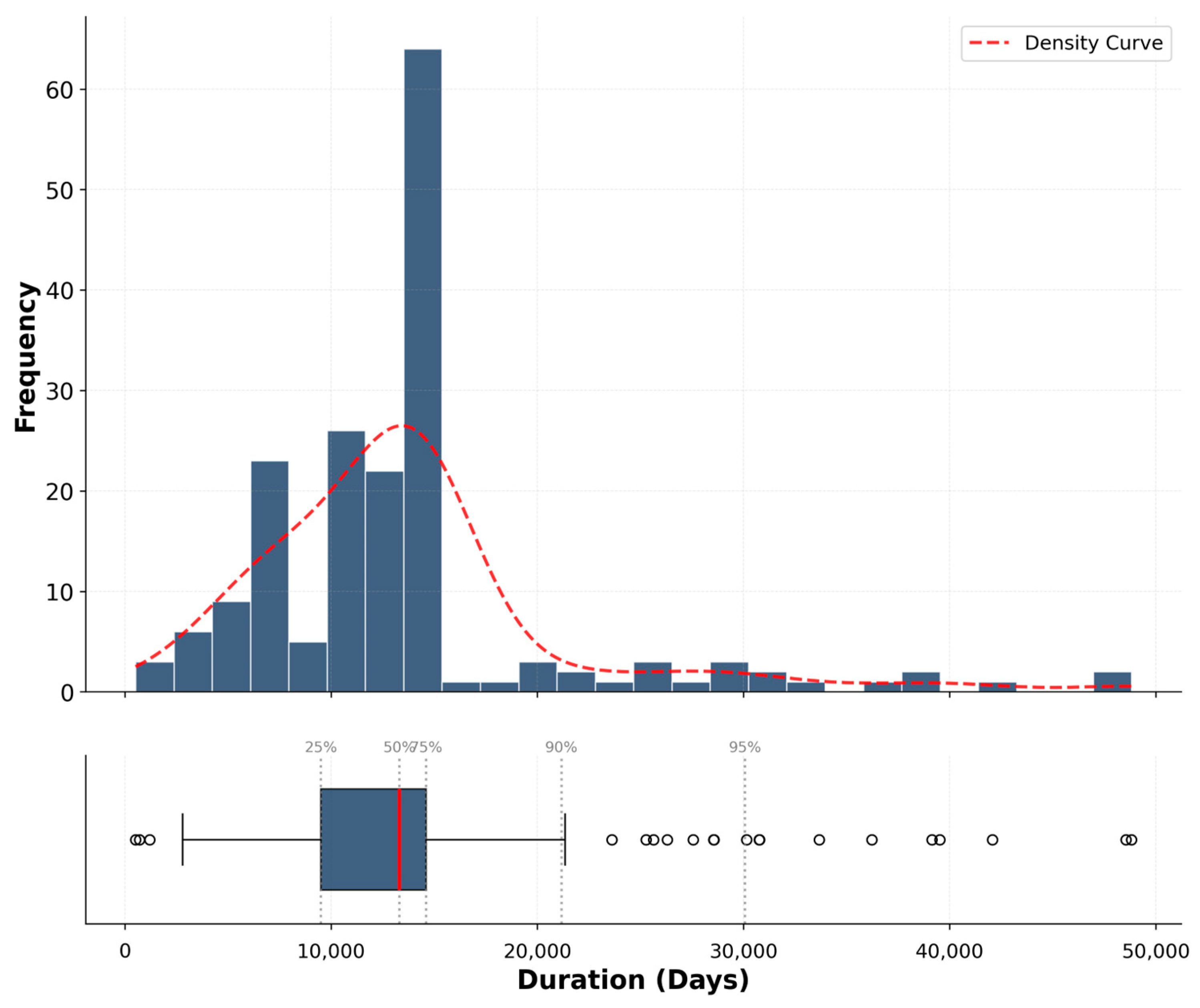
The data from the gages span a considerable range of durations (see

Table 1. Summary statistics of data duration across datasets.

Quantile	Days	Years
Maximum Duration	48,823	134
Minimum Duration	509	1.4
25th Percentile	9943.0	27.2
50th Percentile (Median)	13,694.0	37.5
75th Percentile	14,700.0	40.3

and Figure 3), with the longest continuous record extending 48,823 days (approximately 134 years), while the shortest record is 509 days (about 1.4 years). The median duration of 13,694 days (around 37.5 years) indicates that at least half of the gages have over three decades of data. Furthermore, the interquartile range, spanning from 9943 days (25th percentile) to 14,700 days (75th percentile), suggests that half of the gages have between 27 and 40 years of data, with 75 percent having more than 27 years of data. The mean duration of 13,803 days (37.8 years) closely aligns with the median, indicating a relatively normal distribution of record lengths across the 182 analyzed gages, though the histogram indicates the distribution is right-skewed, with a long tail towards the gages with longer records.

3. Methods

Our methodology consists of five main steps: (1) selection of 182 USGS stream gages across CONUS representing diverse hydrological settings (described in the Section 2 above), (2) Hand-labeling of daily streamflow records to create ground truth BFD classifications, (3) feature selection to extract hydrological characteristics from streamflow time series, (4) development and training of the RF-BFD model using Random Forest classification with cross-validation, and (5) comprehensive performance evaluation comparing RF-BFD against four alternative methods. Figure 4 illustrates this complete methodological workflow from data collection through performance evaluation. Each of these steps is explained in detail in the following sections.

3.1. BFD Hand Labeling

The foundation of our analysis rests on creating a comprehensive hand-labeled dataset of BFD periods from 182 selected USGS gages. Using approximately 10 student hydrologists, we manually classified each daily streamflow record as either BFD (1) or non-BFD (0) through visual analysis of hydrograph data.

The labeling process followed established principles from graphical hydrograph separation methods [9,30]. Our approach involved identifying relatively flat periods or periods without large changes, by visually analyzing recession limbs to determine when quickflow from precipitation events had passed, i.e., the smooth slope characteristics that are typically associated with BFD periods. As illustrated in Figure 5, we classified BFD periods by considering several criteria. Firstly, the streamflow values classified as BFD should typically be lower than the average, indicating periods where quickflow contributions are less prominent. Additionally, flow classified as BFD should be located in sections of the hydrograph where flow values are relatively stable over time with minimal changes, as significant fluctuations typically indicate recent rainfall or other precipitation events. Finally, we considered the slope of the flow curve to help identify the transitions between BFD and precipitation-influenced flow regimes by examining how the streamflow rate transitions from decreasing (negative slope) to stable (near-zero slope) to increasing (positive slope).

BFD periods (labeled as 1, shown in blue) represent flow conditions characterized by stable, gradually declining flows sustained primarily by groundwater discharge or delayed subsurface contributions, with minimal influence from recent precipitation events. These periods typically exhibit smooth recession curves, low variability, and flow magnitudes in the lower portion of the flow duration curve. Non-BFD periods (labeled as 0, shown in red) include rising limbs following precipitation, flow peaks, and the initial steep recession immediately following storm events when quickflow components still dominate streamflow. The transition from non-BFD to BFD occurs when the hydrograph transitions from precipitation-driven responses to groundwater-sustained stable flows.

This approach aligns with graphical hydrograph separation (GHS) methods but proved subjective and sensitive to the scale at which data were examined [10]. We discovered that scaling the graphs to emphasize the baseflow was critical—when graphs included peak flows, we “over-labeled” BFD periods, as periods appearing smooth at larger scales did not meet our criteria when examined at baseflow-focused scales. We also noted that regulated flows from dams and other structures exhibit characteristics similar to BFD flow.

To ensure reliability and reproducibility, we implemented a rigorous validation protocol where 35 gages (20% of the dataset) were independently labeled by two student hydrologists in a double-blind process. This parallel labeling achieved a 90% agreement rate between the labelers, with disagreements primarily occurring during transition periods between flow regimes. Discrepancies were solved through systematic review sessions evaluating against established hydrological principles, including analysis of recession curves, seasonal patterns, and regional characteristics. These sessions harmonized the labels and refined the criteria for the remaining gages.

The resulting dataset, focused on periods of stable recession where baseflow typically dominates streamflow, serves as both training data for our machine learning model and a benchmark for evaluating various BFD identification methods.

3.2. Random Forest Classifier Model

We used a Random Forest classifier, which is an ensemble learning technique that constructs multiple decision trees to improve predictive performance, to develop a model which we call “RF-BFD” to classify flow measurements as BFD or non-BFD [31,32]. We implemented the RF-BFD model using scikit-learn’s RandomForestClassifier with 100 trees, unlimited depth, minimum 2 samples per split, minimum 1 sample per leaf, balanced class weights, and Gini impurity splitting criterion. We used standard Random Forest hyperparameters without extensive tuning, as the algorithm is relatively robust to hyperparameter choices and our primary focus was on feature engineering and interpretability rather than marginal performance optimization through hyperparameter search. We standardized the model features using StandardScaler prior to training. To evaluate model performance, we used 5-fold cross-validation, which provides a stochastic estimate of model performance by iteratively testing the model on different data subsets on 80% of the data, with final evaluation on a held-out 20% test set.

3.2.1. Feature Selection

We explored a number of candidate features to incorporate in the RF-BFD model (

Table 2. Candidate features evaluated for the RF-BFD model, organized by feature category. Features were selected to capture various aspects of baseflow dynamics including flow magnitude, temporal patterns, and hydrograph characteristics relevant to BFD period identification.

Feature Category	Feature Name	Description
Streamflow Magnitude	Q	Daily streamflow/discharge
	Q/Mean	Flow rate normalized by mean flow rate
	Mean_Q	Mean flow rate for each gage
Hydrograph Derivatives	dQ	First derivative of streamflow (rate of change)
	dQ_abs	Absolute value of first derivative
	d2Q	Second derivative of streamflow
	d2Q_abs	Absolute value of second derivative
Baseflow Separation	Q/Chapman	Ratio of total streamflow to Chapman baseflow estimate
	Chapman baseflow	Baseflow estimated using Chapman filter
Moving Window Averages	MW5_Q	5-day moving average of streamflow
	MW5_dQabs	5-day moving average of absolute first derivative
	MW5_d2Qabs	5-day moving average of absolute second derivative
Temporal Indicators	Months	Monthly information (one-hot encoded)
	Q_monthly	Mean monthly streamflow
Percentile-based Ratios	r10m	Ratio of current flow to 10th percentile monthly flow

). We used a systematic approach to identify the most relevant predictors for BFD classification. Our initial feature evaluation included: streamflow magnitude features (Q, Q/Mean, Mean_Q), hydrograph derivatives to capture flow rate changes (dQ, dQ_abs, d2Q, d2Q_abs), baseflow separation ratios derived from the Chapman filter (Q/Chapman, Chapman baseflow), moving window averages to capture short-term patterns (MW5_Q, MW5_dQabs, MW5_d2Qabs), temporal indicators for seasonal patterns (Months, Q_monthly), and percentile-based ratios for long-term context (r10m). We selected this initial feature list to attempt to capture specific aspects of baseflow dynamics, trying to provide a representation of various processes or characteristics of both short-term flow variations and long-term seasonal patterns we thought might be useful in classifying BFD periods.

The following sections (Section Flow Rate–Section R10m) describe each category of features in detail, including their hydrological rationale and computational methods.

Flow Rate

Since baseflow typically corresponds to low-flow periods, we used the flow rate (Q) and the flow rate normalized by the mean flow rate (Q/mean) as candidate features. The mean flow rate represents the central tendency of flow at each stream gage, providing a gage-specific reference point for normalizing flow values. To calculate this adjusted mean value, we excluded measurements beyond two standard deviations from the raw mean, which helped eliminate the influence of extreme flow events that could skew our baseline. The mean flow (Mean_Q) for each gage was also selected as a feature and calculated in the same way.

To reduce noise in the time series data while preserving important patterns, we applied a 5-observation (day) moving window average to the flow rates, creating an additional feature (MW5_Q). This technique enhances the signal-to-noise ratio by dampening short-term fluctuations while highlighting longer-term hydrological trends relevant to baseflow identification. We selected the 5-point window after experimenting with windows ranging from 3 to 10 days, as it optimally balanced noise reduction with retention of significant flow transitions. Our testing showed that larger windows resulted in excessive smoothing that obscured important baseflow transition signals.

Hydrograph Derivatives

Abrupt changes in hydrograph trends can signify transitions into or out of a BFD period. Typically, based on empirical observations, a BFD hydrograph exhibits a characteristic pattern. It initiates with a negative slope, indicating a decreasing flow rate. This is followed by a period of relative stability, characterized by a near-zero slope. The period concludes with a positive slope, suggesting a shift from groundwater-dominated to precipitation-influenced flow. This transition often indicates that external factors, such as precipitation, are beginning to exert a greater influence on streamflow, potentially leading to increased variability. The shift from a groundwater-based flow regime to one more responsive to precipitation can result in notable fluctuations in streamflow.

To capture these nuanced changes in flow dynamics, we incorporated both the first and second derivatives of the hydrograph (dQ, d2Q) into our machine learning model. These derivatives were calculated for each data point with respect to its preceding flow measurements. This approach allows the model to detect subtle changes in flow patterns, potentially improving its ability to identify and predict transitions between baseflow and non-BFD periods. To dampen noise in the data, we used the 5-point moving average of both derivatives (MW5_dQ, MW5_d2Q) as features rather than the actual derivatives. We also used the absolute value of the derivatives (dQ_abs, d2Q_abs) to focus on slope magnitude more than direction. We also calculated the moving average of the absolute values of both first and second derivatives of flow (MW5_dQabs and MW5_d2Qabs). These features capture the stability and rate of change in flow conditions, which are important indicators of BFD, as baseflow periods typically exhibit gradual, consistent changes in flow compared to the more erratic patterns during precipitation-influenced periods.

Baseflow Separation Methods

We included Chapman filter results as candidate features, a common baseflow separation method [8]. The candidate feature was the ratio of total streamflow to the baseflow estimated by the Chapman model (Q/Chapman). This feature provides the model with a dimensionless indicator of the relative contribution of baseflow as estimated by the Chapman filter to total streamflow and represents the temporal dynamics of baseflow variation. We included this feature to include traditional hydrological approaches while bridging the gap between classical hydrological techniques and machine learning methodologies.

Month

Through our analysis of annual hydrographs and the process of identifying BFD periods, we observed that the contribution of baseflow to total streamflow exhibits strong monthly dependence. This temporal variability in baseflow contribution necessitated a feature to incorporate monthly information into our model. We employed the one-hot encoding technique to create a set of binary columns representing each of the twelve months of the year. These features were named month_1 through month_12, corresponding to January through December, respectively. This feature allows the model to capture the distinct characteristics and baseflow patterns associated with individual months. The inclusion of these month-specific features serves multiple purposes in our modeling framework. It enables the model to learn and account for monthly variations in baseflow contribution, potentially improving its accuracy in distinguishing between baseflow and event flow across different times of the year.

R10m

To account for long-term flow characteristics in our model, we incorporated a feature representing the ratio of the current streamflow and the 10th percentile of non-exceedance flow calculated monthly (r10m). We computed r10m by dividing the daily flow value by the 10th percentile flow value. We derived the 10th percentile flow value for each calendar month using data for the entire period of record for each gage. The r10m feature provides a dimensionless indicator that normalizes current flow against historically established low-flow conditions for that specific month, enabling the model to adapt to the varying characteristics of baseflow contribution across different times of year and watershed conditions.

3.2.2. Feature Importance, Sensitivity Analysis, and Final RF-BFD Model

From this set of candidate features, we used the feature importance metrics inherent in the Random Forest algorithm to select the final model features. The feature importance metric in scikit-learn’s RandomForestClassifier calculates importance based on the mean decrease in impurity (MDI), measuring how effectively each feature reduces classification uncertainty across the ensemble of decision trees. Features with higher importance scores demonstrate greater discriminative power in identifying BFD periods, allowing us to systematically eliminate less influential features while maintaining model performance. This data-driven approach to feature selection, combined with hydrological domain knowledge, provided insights into which characteristics most strongly identify BFD periods while ensuring the model remained computationally efficient and interpretable [33].

The results of our feature importance analysis are shown in

Table 3. Selected features and their importance for the machine learning model.

Feature	Importance (%)
Q/Mean	24.86
Mean_Q	18.54
MW5_dQabs	13.93
MW5_d2Qabs	10.95
MW5_Q	10.87
Q	8.56
Q/Chapman	7.25
Months	3.82
r10m	1.21

. Based on our analysis, we selected 9 features for inclusion in the RF-BFD model. The normalized flow rate (Q/Mean) emerged as the most influential feature, contributing 24.86% to the model’s predictive power. Mean flow (Mean_Q) followed at 18.54%, highlighting the significance of overall flow characteristics in identifying BFD periods. Derivatives and moving average features played crucial roles: the 5-point moving average of the absolute value of the first derivative (MW5_dQabs) contributed 13.93%, while the 5-point moving average of the absolute value of the second derivative (MW5_d2Qabs) added 10.95%. The 5-point moving average of the flow rate (MW5_Q) provided a 10.87% contribution, with flow (Q) at 8.56%. Flow normalized by the Chapman baseflow (Q/Chapman) had similar importance with a contribution of 7.25%, with both one-hot encoded month and r10m contributing 3.82% and 1.21%, respectively.

The other features we evaluated had contributions less than 1.21% and made little impact on the model, and so were not included. These included features we expected to be important, such as the derivatives, but were not. However, the smoothed data, both flow and the 1st and 2nd derivatives, were important.

To estimate accuracy, we used 5-fold cross-validation, which systematically trained and tested the model across 5 different data subsets. During cross-validation, we evaluated multiple performance metrics, including accuracy, precision, recall, F1-score, and classification reports for each fold. This approach provides multiple measures of model performance rather than a single accuracy estimate based on one test set. By training the model on different portions of the dataset and evaluating it on the held-out portions, cross-validation helps assess how well the model generalizes to unseen data, providing insight into whether the model is adequately capturing underlying patterns or merely memorizing the training data. This comprehensive evaluation framework enabled us to confidently assess the model’s ability to identify BFD periods across diverse hydrological conditions. The final model was trained on all the available data.

To prevent overfitting, we employed several safeguards: 5-fold cross-validation to validate model stability across different data subsets, evaluation on a hold-out test set (20% of data) never used during training, and balanced class weights to prevent bias toward the majority class. The consistency between cross-validation performance and test set accuracy (92%) indicates the model generalizes well beyond its training data rather than memorizing patterns.

To assess feature dependencies and model robustness, we conducted an ablation study by systematically removing individual features (

Table 4. Feature ablation study results showing model accuracy when individual features are removed. Features are ordered by performance impact.

Feature Removed	Accuracy	Absolute Drop	Relative Drop (%)	Feature Importance (%)
Mean_Q	0.8671	0.0547	5.93	18.54
Months	0.9081	0.0136	1.48	3.82
Q/Mean	0.9100	0.0118	1.28	24.86
Q/Chapman	0.9107	0.0111	1.20	7.25
r10m	0.9160	0.0058	0.63	1.21
Q	0.9159	0.0058	0.63	8.56
MW5_Q	0.9162	0.0055	0.60	10.87
MW5_d2Qabs	0.9187	0.0031	0.33	10.95
MW5_dQabs	0.9192	0.0026	0.28	13.93

). Removing Mean_Q caused the largest performance decrease (5.93%), confirming its critical role in providing gage-specific normalization despite moderate feature importance (18.54%). Months showed the second-largest impact (1.48% drop) despite low feature importance (3.82%), as it captures unique seasonal patterns. Conversely, Q/Mean caused only a 1.28% drop despite having the highest feature importance (24.86%), indicating redundancy with its component features. Derivative features showed minimal impacts (0.28–0.60%), reflecting correlation among smoothed flow gradients. The model maintained over 91.5% accuracy with any single feature removed, demonstrating robustness while confirming that the full feature set achieves optimal performance.

3.3. Gradient Method

The gradient-based approach for identifying BFD periods combines digital filtering with gradient analysis to automatically detect BFD periods in streamflow records. We first apply the Lyne and Hollick digital filter to generate initial baseflow estimates [12]. This filter considers three key components in its operation: the filtered response from the prior time step, the change in streamflow between consecutive measurements, and a filter parameter that controls the degree of separation between quickflow and baseflow components. The filter assesses how current streamflow values change relative to previous measurements, allowing it to distinguish between rapid flow responses and slower baseflow contributions. The filter is calculated as follows:

$$B_t=Q_t-\left(\alpha Q_{t-1}-B_{t-1}\right)+\left({\displaystyle \frac{1+\alpha }{2}}\right)\left(Q_t-Q_{t-1}\right)$$

(1)

where $B_t$ is baseflow at time $t$, $Q_t$ is streamflow at time $t$, $\alpha$ is the filter parameter (0.925), and baseflow is constrained such that 0 ≤ $B_t$≤ $Q_t$. We used α = 0.925, a standard value widely adopted in baseflow separation applications [10,34] that provides reasonable estimates across varied hydrological settings.

Following the initial filtering, we computed daily gradients (i.e., derivative) of the baseflow a using numerical differentiation. This gradient calculation captures the rate of change in baseflow values to allow us to identify periods of minimal variation characteristic of BFD conditions.

$${gradient}_t={\displaystyle \frac{B_t-B_{t-1}}{∆t}}$$

(2)

The absolute values of these gradients serve as indicators of flow stability, as BFD periods typically exhibit minimal fluctuations compared to periods influenced by direct runoff or other rapid flow components.

The identification of BFD periods requires filtering on both flow magnitude and gradient characteristics, as BFD flows are in the lower range of the flow exceedance curve. To include both aspects, we implemented a dual-threshold approach. We established a flow threshold using the Q5 exceedance value (5th percentile of the flow duration curve) to restrict selections to low flows typical of baseflow conditions. This restricts selections to lower flows, even if gradients are low. This flow threshold helps remove periods near peak flows where gradients might temporarily decrease but do not represent true baseflow conditions.

The second threshold uses gradient values and identifies periods with stable flow which are characteristic of BFD flow periods. We determined this gradient threshold as the mean of absolute gradient values between the 25th and 75th percentiles of the sorted gradient distribution for each watershed. Threshold ranges were adjusted for each watershed through visual inspection of hydrographs and gradient distributions, with final values selected to optimize identification of known baseflow periods in each dataset.

The final step to classify BFD periods using this method combines the two flow and gradient thresholds. A streamflow period is classified as BFD only when it satisfies both threshold criteria: the flow magnitude must fall below the established flow threshold, and its gradient must remain below the gradient threshold. This dual-criteria approach helps ensure that identified periods exhibit both the magnitude and stability characteristics expected of BFD conditions, providing a robust method for automated baseflow period identification across diverse hydrological settings.

$${BFD}_t \left\{\begin{array}{c}=1 if \left(Q_t<Q_{threshold}\right) AND \left(\left|{gradient}_t\right|<{gradient}_{threshold}\right)\\ =0 otherwise\end{array}\right.$$

(3)

3.4. Statistical Method

The approach uses a single-parameter digital filter, similar to that of Lyne and Hollick, which is tuned to each gage individually based on the long-term, low-flow characteristics of the gage. We selected the 10th non-exceedance percentile (NEP) to represent low-flow conditions at each gage. For each gage, we constructed an annually repeating sequence of the 10th NEP by matching each Julian Day of the series to the corresponding Julian Day of the streamflow record. The baseflow separation filter was then run on the streamflow timeseries, iteratively changing the filter parameter (β) until the root mean square error (RMSE) between the 10th NEP sequence and the estimated baseflow was minimized.

The “tuning” of the filter parameter to the long-term low-flow behavior of each gage helps to account for differences in the variability of flow observed in the gages. Once the baseflow parameter was tuned for each gage, we compared the separated baseflow to the observed streamflow and computed the baseflow index (BFI) for each day in the period of record. We used the BFI values to estimate when the gage is in a BFD period and when it is not; we classify observed streamflow to be BFD when the BFI is above a threshold. We computed the daily baseflow index (BFI) as:

$$BFI={\displaystyle \frac{Q_{baseflow}}{Q_{total}}}$$

(4)

where $Q_{baseflow}$ is the separated baseflow and $Q_{total}$ is the observed total streamflow for each day.

For this method we used two different moving average windows to smooth the BFI timeseries (5 and 7 days) and three BFI thresholds (0.5, 0.6, and 0.7). We selected these BFI thresholds to test a range of baseflow dominance definitions, where 0.5 represents the minimum condition for baseflow dominance (baseflow greater than 50% of total flow), 0.6 provides an intermediate case, and 0.7 represents strong dominance. We did not test higher thresholds (e.g., 0.8, 0.9) as they would identify only near-pure baseflow periods, which is overly restrictive for our BFD definition that includes bank storage and delayed subsurface contributions beyond groundwater alone. For clarity in presenting results, we refer to each statistical model variant using the format ‘Stat(X.XtYdavg)’ where X.X represents the BFI threshold value (0.5, 0.6, or 0.7) and Y indicates the moving average window in days (5 or 7) used to smooth the BFI timeseries. So, for example, Stat(0.5t6davg) refers to the statistical method with a BFI threshold of 0.5 using a 6-day moving average window to compute the BFI data.

$${BFI}_{smoothed\left(t\right)}=\left({\displaystyle \frac{1}{n}}\right)\sum _{k=0}^{n-1}{BFI}_{t-k}$$

(5)

where $n$ is the moving average window length (5 or 7 days).

$${BFD}_t \left\{\begin{array}{c}=1 if {BFI}_{smoothed\left(t\right)}\ge threshold\\ =0 if {BFI}_{smoothed\left(t\right)}<threshold\end{array}\right.$$

(6)

3.5. Strict Method

The Strict Method described by [7] was originally developed to assist in evaluating various baseflow separation methods. It offers a systematic approach to identify strict baseflow periods from streamflow data. The approach involves identifying days when direct runoff ceases, thus isolating baseflow periods. The algorithm involves removing data points with non-negative quickflow, eliminating two points before and three points after these moments to avoid precipitation and quickflow influence, excluding five points following significant flood events (identified by peaks exceeding the 90th quantile of streamflow observations), and discarding points followed by a smaller streamflow value to mitigate measurement errors. These steps are meant to ensure that only strict baseflow points remain.

This method was designed to select strict baseflow points to serve as a reliable reference for evaluating the performance of different baseflow separation methods. In the original paper, the accuracy of the estimated baseflow from any given method was computed against these strict points. This method relies solely on daily streamflow data and, based on published results, provides a robust and scalable approach for large-scale hydrological studies across multiple catchments [23,35,36].

3.6. BN77 Method

The Brutsaert and Nieber (1977) method (BN77) [37], later automated by Cheng et al. [23], provides a systematic and objective approach for identifying periods of streamflow that represent pure baseflow. The foundation of the method is the observation that, under true baseflow conditions, the relationship between the recession rate (−dQ/dt) and the corresponding discharge (Q) follows predictable power-law patterns when plotted on logarithmic axes. By exploiting these recession characteristics, BN77 distinguishes groundwater-dominated flow from streamflow segments that may still include storm runoff or other non-baseflow components.

Cheng et al. [23] formalized and automated the procedure by introducing nine specific criteria for identifying baseflow points within hydrographs. These include: (1) requiring a positive recession slope (−dQ/dt > 0); (2) enforcing a minimum recession episode length, typically set to eight days; (3–4) discarding the initial points of each episode (at least two points for all recessions, and an additional three points for large events exceeding the 90th percentile of flow); (5) eliminating at least the final point of each episode; (6–7) removing anomalous points and those that violate monotonicity in recession slopes; (8) excluding periods influenced by snow accumulation or freeze–thaw processes; and (9) filtering out points that fall below observational precision thresholds. These criteria collectively ensure that only the segments of the hydrograph governed by aquifer drainage are retained for analysis.

The effectiveness of this automated implementation was evaluated across 26 catchments in the United States, Australia, and China. The comparison focused on the characteristic drainage timescale parameter (K), which describes how quickly groundwater contributes to streamflow during recession. Automated estimates of K (44.5 ± 13.2 days) closely matched those obtained by manual expert selection (45.7 ± 10.5 days), demonstrating that the algorithm can reliably reproduce human judgment. Sensitivity analyses further showed that the choice of minimum recession length and the elimination of points at recession endpoints had little effect on K. By contrast, data quality control measures and the placement of the lower envelope (typically excluding the lowest 5% of data points) exerted a strong influence on parameter estimates, underscoring the importance of rigorous filtering.

The automated BN77 method proceeds in three major stages: recession slope estimation, recession episode identification, and point elimination based on quality control rules. First, the recession slope at time t is computed as follows:

$$S_t={\displaystyle \frac{\left(Q_t-Q_{t+1}\right)}{2}}$$

(7)

where Q_t is the streamflow at time t. Potential recession episodes are then identified when slope conditions are satisfied, specifically when $S_t\le 0$ and $S_{t+1}>0$ marks the start of an episode, or when S_t > 0 indicates continuation of an episode. Episodes must also meet a minimum length criterion (L_min) to be considered valid.

Once recession episodes are defined, a series of elimination steps is applied. Large events are first identified using a threshold defined as the 90th percentile of streamflow (Q_threshold = Quantile(Q, 0.9)). If an episode begins above this threshold, the first three points are discarded; otherwise, the first two points are removed. The last point of each episode is also eliminated to avoid contamination from flow recovery or measurement uncertainty. Anomalous slopes are screened out by retaining only points where the slope ratio

$${ratio}_i={\displaystyle \frac{S_{\left(i+1\right)}}{S_i}}$$

(8)

is less than two, and nonmonotonic behavior is removed by requiring $S_i\ge S_{i+1}$. Finally, all points with discharge below observational precision are excluded. The remaining points are classified as true baseflow, with an indicator variable set to one for selected points and zero otherwise.

Through this systematic procedure, BN77 translates recession theory into a reproducible algorithm for isolating baseflow segments from streamflow records. By combining theoretical scaling laws with rigorous data filtering, the method provides a robust basis for estimating groundwater contributions to streamflow and for calibrating aquifer drainage parameters.

3.7. Model Performance Metrics

We evaluated the effectiveness of baseflow identification methods using several metrics: precision, recall, F1 score, accuracy, mean absolute error (MAE), confusion matrices, and receiver operating characteristic (ROC) curves.

Precision quantifies the proportion of correctly identified baseflow periods among all periods classified as baseflow, helping us assess each model’s reliability in avoiding false positives:

$$Precision={\displaystyle \frac{TP}{TP+FP}}$$

(9)

Recall (sensitivity) measures the proportion of actual baseflow periods correctly identified, indicating how comprehensively each method captures true baseflow conditions:

$$Recall={\displaystyle \frac{TP}{TP+FN}}$$

(10)

F1 Score, the harmonic mean of precision and recall, provides a balanced performance measure particularly valuable for our dataset’s uneven distribution between baseflow and non-baseflow periods.

$$F1 Score=2\times {\displaystyle \frac{Precision\times Recall}{Precision+Recall}}={\displaystyle \frac{2\times TP}{2\times TP+FP+FN}}$$

(11)

Accuracy represents the overall percentage of correct classifications but requires careful interpretation given our class imbalance.

$$Accuracy={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}}$$

(12)

MAE measures the average magnitude of errors without considering their direction, providing a straightforward measure of prediction accuracy in the same units as our streamflow data and enabling direct numerical comparison between different methods [38,39].

$$MAE={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left|y_i-{\widehat{y}}_i\right|$$

(13)

where $n$ is the number of observations, $y_i$ is the actual value (0 for non-BFD, 1 for BFD), and ${\widehat{y}}_i$ is the predicted value.

In these equations, $TP$ represents true positives (correctly identified BFD periods), $TN$ represents true negatives (correctly identified non-BFD periods), $FP$ represents false positives (non-BFD periods incorrectly classified as BFD), and $FN$ represents false negatives (BFD periods incorrectly classified as non-BFD).

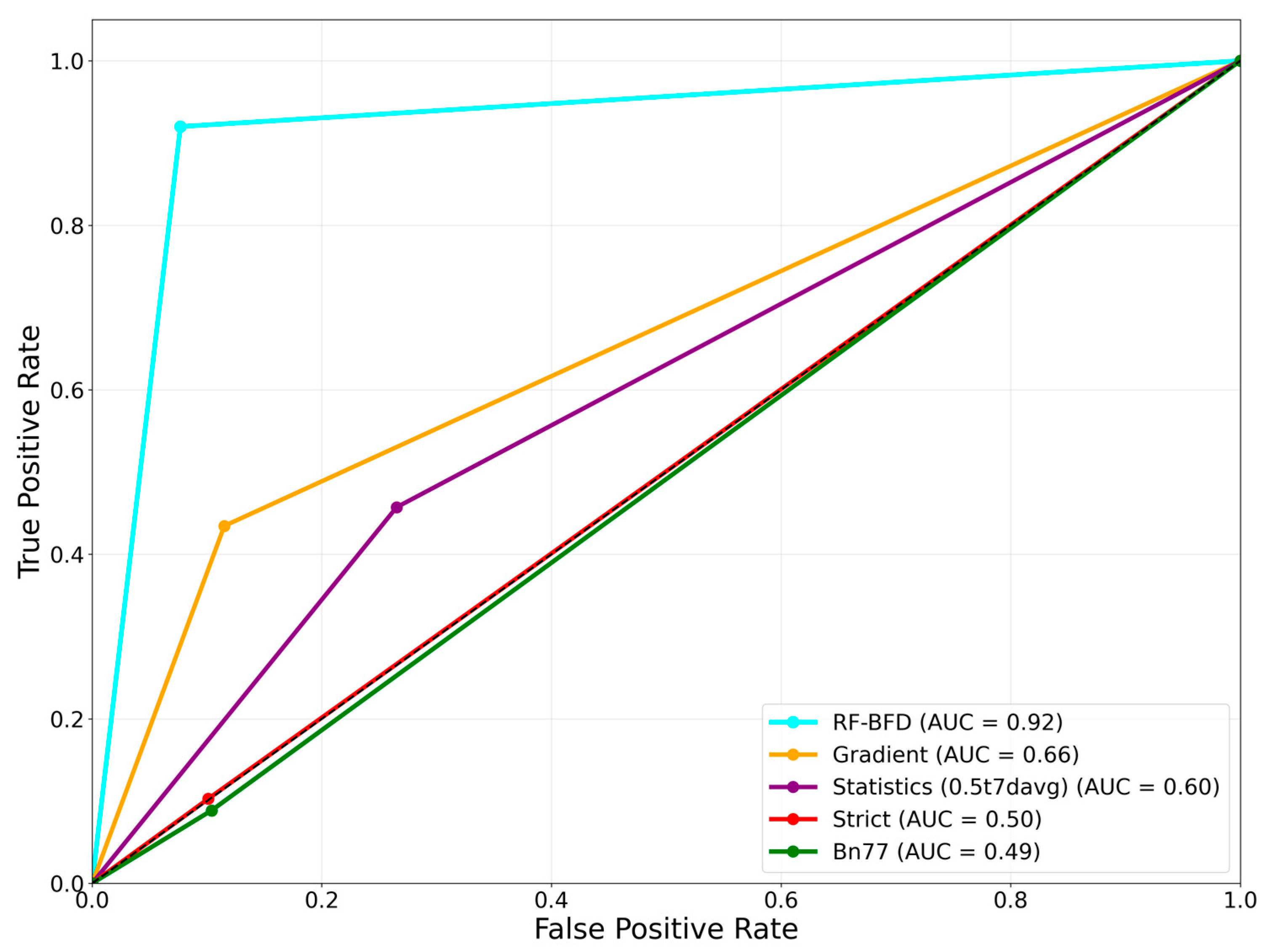
For comprehensive evaluation, we generated confusion matrices—tabular visualizations showing true positive, false positive, true negative, and false negative classifications—and constructed ROC curves that plot true positive rates against false positive rates across various classification thresholds, allowing us to assess each method’s discriminative ability independent of any specific threshold.

4. Results

4.1. Hand Labeling

Figure 6 presents the spatial distribution of the 182 USGS stream gages across CONUS, with colors indicating the percentage of days classified as BFD at each location. The map reveals distinct regional patterns in baseflow occurrence, with gages showing a wide range of baseflow percentages from 6% to 95% of total days. Higher percentages of BFD days (shown in yellow, 74–95%) are predominantly observed in the western United States, particularly in arid and semi-arid regions where groundwater contributions represent a larger proportion of total streamflow. Moderate baseflow percentages (52–74%, shown in lighter colors) are distributed across various regions, including parts of the Great Plains and some eastern locations. Lower percentages (6–52%, shown in darker blue) are more common in humid regions of the eastern United States, where precipitation-driven flow events are more frequent and baseflow periods are proportionally less dominant. This spatial variability reflects the influence of climate, geology, and land use characteristics on the relative importance of groundwater versus surface water contributions to streamflow across different hydrogeological settings.

The hand-labeling process produced a comprehensive dataset of 2,354,237 daily streamflow records across 182 USGS gages, with 1,276,609 (54.23%) classified as BFD and 1,077,628 (45.77%) as non-BFD, indicating that baseflow conditions are the prevalent hydrologic regime in this gage network. Individual gage records ranged from 509 days to 48,823 days (mean: 37.8 years), providing substantial temporal coverage. BFD percentages varied considerably across gages, ranging from 23% to 87% (mean: 54.2% ± 12.8%), with western arid regions showing higher BFD percentages (68% ± 11%) compared to humid southeastern regions (48% ± 15%). Within the flow duration curve, 78% of BFD classifications occurred in the Q50–Q95 range, 15% in the Q95–Q99 range (lowest flows), and only 7% in moderate to high flows (Q0–Q50). Continuous BFD periods averaged 12.3 days in length (median: 8 days, range: 1–127 days), with longer periods during summer/fall (15.7 days) compared to winter/spring (8.9 days).

Figure 7 illustrates the inter-annual variability in baseflow occurrence by showing the percentage of days classified as BFD each year across all gages in the network. The analysis demonstrates considerable year-to-year variation in baseflow occurrence, with some years showing significantly higher or lower percentages of BFD days than others. This is mostly caused by the data from the early years being limited to a few gages (Figure 2) that are not representative of the larger dataset. In later years, significantly more data from a larger set of gages are available.

The early period of the record (1890–1920) exhibits high variability, with several years showing baseflow percentages exceeding 80–90%, though this period is represented by fewer gages in the network. From the 1940s onward, as the gage network expanded, the annual percentages show more consistent patterns, typically ranging between 40 and 70% of days classified as BFD. Notable variations appear to correspond with known climatic events and drought periods, where drier years tend to show higher percentages of BFD days as precipitation-driven flow becomes less frequent.

Temporal and flow regime analysis revealed distinct seasonal patterns in BFD occurrence. Figure 8 demonstrates clear monthly variations that reflect the underlying hydrological processes governing streamflow generation. Winter months (December through February) show moderate BFD percentages, with January exhibiting 56.1% and February showing 52.5% of days classified as BFD. The lowest BFD occurrence is observed during spring months, with April and May showing the minimum values at 32.7% and 32.3%, respectively, corresponding to the typical snowmelt and spring precipitation periods when quickflow components dominate streamflow. Summer and early fall months exhibit the highest BFD percentages, with August, September, and October showing 63.0%, 69.2%, and 68.2%, respectively, reflecting the dominance of subsurface and long-term contributions during dry periods when precipitation-driven flow is minimal. This seasonal pattern aligns with expected hydrological behavior across temperate regions, where BFD flows become the primary source of streamflow during dry summer and fall conditions.

Figure 9 illustrates the relationship between seasonal BFD flow patterns and streamflow magnitude, revealing how BFD percentages vary inversely with total streamflow volumes throughout the year. The analysis shows that winter months maintain moderate baseflow percentages (51.4%) despite relatively high mean streamflow values (14.26 m³/s), indicating the influence of snowpack accumulation and occasional winter precipitation events. Spring exhibits the lowest BFD flow percentage (37.2%) concurrent with the highest mean streamflow (17.71 m³/s), demonstrating the dominance of snowmelt and spring precipitation in driving total streamflow during this period. The summer and fall seasons show the strongest BFD flow dominance, with percentages reaching 63.0% and 64.7%, respectively, while maintaining substantially lower mean streamflow values (10.66 and 10.62 m³/s). This inverse relationship between BFD flow percentage and total streamflow magnitude confirms that BFD conditions are most prevalent during low-flow periods, supporting the hydrological understanding that subsurface contributions become proportionally more significant as surface water inputs from precipitation and snowmelt are reduced.

4.2. Model Performance Analysis

4.2.1. Performance Metrics Results

Table 5. Performance comparison between prediction models and hand labeled data.

Models	Precision	Recall	F1 Score	Accuracy	MAE
RF-BFD	0.92	0.92	0.92	0.92	0.058
BN77	0.50	0.09	0.15	0.46	0.549
Strict	0.54	0.10	0.17	0.47	0.545
Gradient	0.82	0.43	0.57	0.64	0.372
Stat (0.5t5davg)	0.67	0.46	0.54	0.59	0.416
Stat (0.6t5davg)	0.72	0.37	0.49	0.58	0.421
Stat (0.7t5davg)	0.76	0.27	0.40	0.56	0.441
Stat (0.5t7davg)	0.67	0.46	0.54	0.59	0.416
Stat (0.6t7davg)	0.72	0.37	0.49	0.58	0.421
Stat (0.7t7davg)	0.77	0.27	0.40	0.56	0.441

presents the performance metrics for each model compared to the hand-labeled dataset. The RF-BFD model achieved the highest scores across all metrics: Precision (0.92), Recall (0.92), F1 Score (0.92), Accuracy (0.92), and the lowest MAE (0.058). The traditional methods showed substantially lower performance. The Strict method achieved Precision (0.54), Recall (0.10), F1 Score (0.17), and Accuracy (0.47), indicating significant shortcomings in accurately identifying baseflow periods. The BN77 method performed similarly with Precision (0.50), Recall (0.09), F1 Score (0.15), and Accuracy (0.46). Both methods had high MAE values (0.545 and 0.549, respectively) and demonstrated an inability to capture many true baseflow periods due to their low Recall scores. The Gradient method demonstrated intermediate performance with Precision (0.82), Recall (0.43), F1 Score (0.57), Accuracy (0.64), and MAE (0.372). While better than traditional methods, it still fell short of the RF-BFD model’s capabilities.

Among the statistical methods, performance varied by threshold setting, demonstrating a clear trade-off between Precision and Recall. Lower-threshold variants (0.5) achieved the best balance: Stat (0.5t5davg) and Stat (0.5t7davg) models both achieved identical metrics: Precision (0.67), Recall (0.46), F1 Score (0.54), Accuracy (0.59), and MAE (0.416). Higher threshold variants (0.7) showed increased Precision (0.76–0.77) but decreased Recall (0.27), resulting in lower F1 Scores (0.40) and suggesting they miss many true baseflow periods while being more conservative in their identifications.

4.2.2. Practical Method Comparison

To illustrate the practical differences between BFD identification methods, Figure 10 presents a comparative analysis for USGS gage 11,473,900 during 2017, showing how each method performs across varying flow conditions. The hydrograph demonstrates the characteristic challenges of baseflow identification, with multiple precipitation events creating distinct peaks followed by recession periods where BFD transitions occur.

The machine learning model (cyan) demonstrated strong alignment with the hand-labeled periods, successfully identifying most of the extended low-flow periods while showing similar temporal boundaries. The RF-BFD approach exhibited slightly more conservative identification compared to the ground truth, occasionally ending BFD periods earlier during flow transitions. This conservative tendency reflects the model’s training on features that prioritize stability and flow magnitude relationships, resulting in high precision but potentially missing some marginal BFD conditions that human experts might recognize.

The RF-BFD (cyan) demonstrated strong alignment with the hand-labeled periods, successfully identifying most of the extended low-flow periods while showing similar temporal boundaries. The RF-BFD approach captured both the transition periods and the subsequent stable baseflow conditions, showing its ability to recognize the full extent of BFD regimes rather than just recession characteristics. This comprehensive identification reflects the model’s training on features that consider flow stability, magnitude relationships, and temporal patterns beyond simple recession analysis.

Both the Strict method (red) and the BN77 method (green) exhibited a fundamental limitation in their approach to BFD identification. These methods predominantly focused on recession limbs following precipitation events, treating these declining flow periods as baseflow. However, recession limbs often represent transitional periods where quickflow components are still draining from the watershed, rather than true BFD conditions. More critically, both methods consistently failed to identify the extended periods of stable, low flows that followed these recession periods—the very conditions that represent genuine BFD. For example, during the summer period when flows stabilized around 5.7–11.3 m³/s for months, neither the Strict nor BN77 methods identified these obvious BFD conditions, instead focusing only on the initial declining portions of hydrograph limbs.

This limitation highlights a conceptual misunderstanding in traditional approaches: recession limbs are often merely indicators of the beginning of baseflow zones, not the BFD periods themselves. The true BFD conditions typically occur after the recession stabilizes into relatively constant, sustained flows that persist between precipitation events. The Strict and BN77 methods’ focus on recession characteristics causes them to miss these extended stable periods that constitute the majority of actual BFD periods.

The gradient method (orange) and statistical method (purple) showed intermediate performance, with the gradient method demonstrating better capability to identify sustained stable periods beyond recession limbs. The statistical method’s threshold-based approach created more comprehensive identification of extended low-flow periods, though with less precision in temporal boundaries compared to the machine learning approach.

The visualization reveals fundamental philosophical differences between traditional recession-focused methods and comprehensive baseflow identification approaches. While the Strict and BN77 methods prioritize specific hydrograph characteristics associated with recession analysis, they systematically underestimate the temporal extent of BFD periods by missing the stable flow periods that follow recession limbs. This limitation has significant implications for applications requiring accurate quantification of BFD time periods, as traditional methods may underestimate BFD by 50–70% compared to expert identification and more comprehensive automated approaches.

4.2.3. Confusion Matrices and ROC Analysis

Figure 11 shows the confusion matrices for the models. We only included the best-performing statistical model in this figure. The confusion matrices provide detailed breakdowns of classification performance, showing how each method distributes true positives, false positives, true negatives, and false negatives. The RF-BFD model shows the most balanced confusion matrix with high values in both true positive and true negative quadrants, while traditional methods show pronounced imbalances with high false negative rates.

The ROC curves for each model are displayed in Figure 12. For probabilistic methods (RF-BFD, Statistical), curves show performance across different classification thresholds. For deterministic methods (Strict, BN77, Gradient), single points represent their fixed binary classification performance. The RF-BFD, with an area under the ROC curve (AUC) of 0.92, shows a steep curve indicating excellent discriminatory ability. In contrast, the BN77 and Strict models approach the diagonal line, reflecting poor classification capability with AUCs close to 0.49, suggesting near-random performance.

5. Discussion

The decision to develop a comprehensive hand-labeled dataset of BFD periods was driven by several key considerations related to the limitations of existing automated methods and the need for a reliable benchmark against expert judgment. Traditional methods for baseflow identification, while theoretically grounded, have lacked systematic validation against expert-identified periods that reflect the nuanced understanding of baseflow dynamics. The complexity of baseflow processes, which involve multiple pathways including aquifer systems, glacial meltwater, and interconnected geological formations [1,4,5], makes it particularly challenging to assess the accuracy of automated methods without a reliable ground truth.

The creation of a hand-labeled dataset offers distinct advantages in establishing a benchmark that captures the temporal and spatial variability of baseflow processes, while providing a foundation for systematic comparison of automated methods. Unlike purely algorithmic approaches that aim to identify periods where baseflow constitutes the majority of streamflow, such as the BN77 and Strict methods, which rely on fixed parameters or simplistic rules, our dataset incorporates expert knowledge of how baseflow manifests in observed streamflow patterns. This approach is particularly valuable given that baseflow exhibits characteristic patterns, such as a slower response to rainfall events [20,21] and less variability compared to the total streamflow [15]. By codifying these observable patterns through expert labeling rather than attempting to automate the process without validation, we establish a crucial reference point for evaluating various identification methods while still capturing the essential dynamics of baseflow contribution during low-flow conditions.

This approach aligns with recent efforts in hydrological science to develop benchmark datasets for model evaluation [40,41]. Similarly to the CAMELS dataset for catchment attributes [40] and the MOPEX dataset for model parameter estimation [42], our hand-labeled BFD dataset provides a community resource for advancing baseflow identification methods.

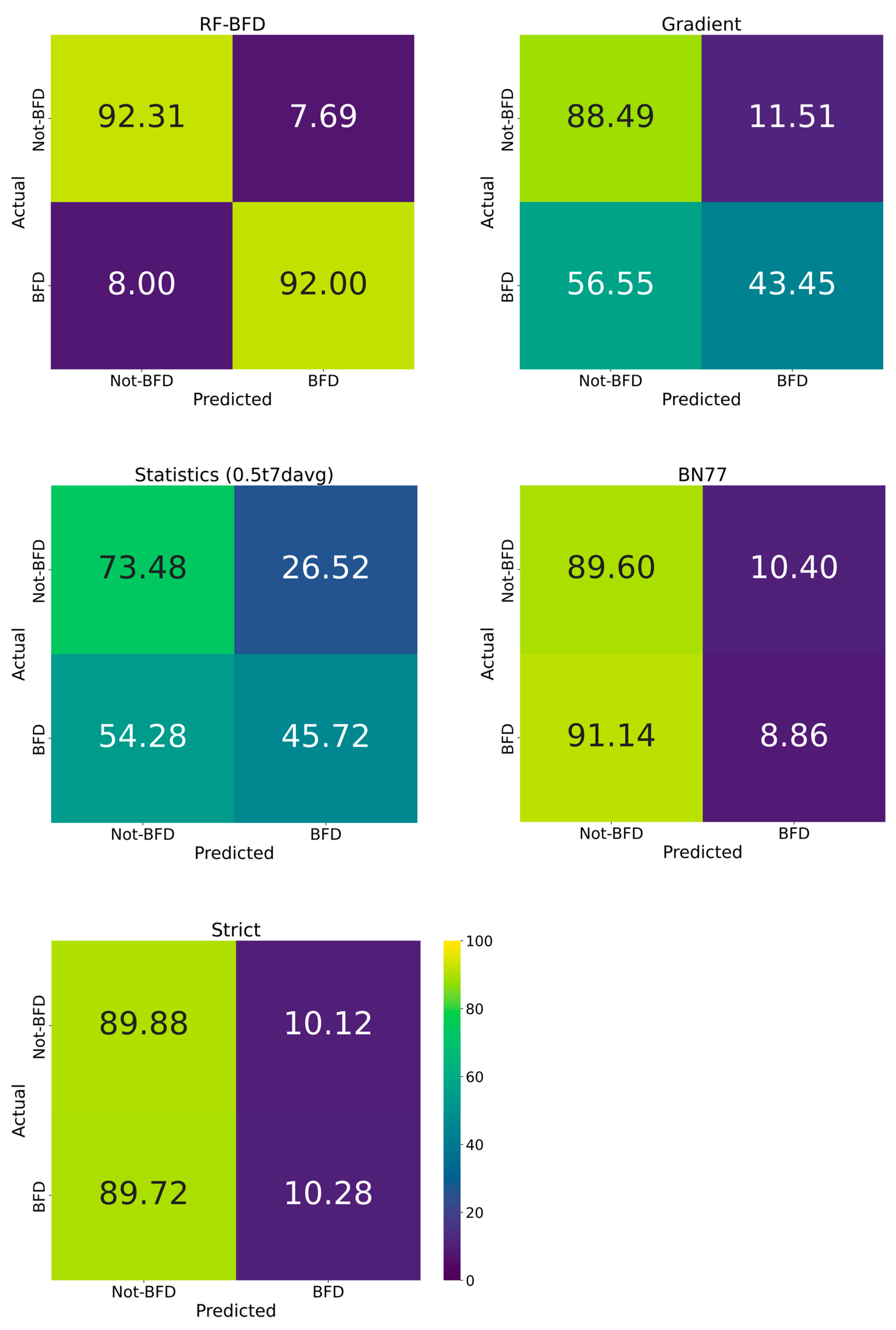
The RF-BFD method showed the best performance of the five methods tested. This superior performance can be attributed to several factors inherent to the RF-BFD approach. First, the RF-BFD method effectively captured the complex, non-linear relationships between multiple hydrological features and BFD, achieving impressive metrics with a Precision of 0.92 and Recall of 0.92. Second, unlike fixed-parameter methods, the RF-BFD method learned from the expert-labeled data to recognize subtle patterns in hydrograph characteristics, including recession curves, flow stability, and relative magnitude compared to long-term averages. Third, the feature importance analysis revealed that the ratio of streamflow to mean flow (Q/Mean) and absolute gradient features (MW5_d2Qabs and MW5_dQabs) contributed significantly to the model’s predictive power, highlighting the value of incorporating multiple indicators rather than relying on single parameters or thresholds. Additionally, the model’s ability to handle seasonal variations through month-based features allowed it to adapt to diverse hydrological conditions across watersheds, outperforming traditional methods that apply fixed criteria regardless of temporal context.

Our feature selection analysis revealed several key insights for BFD identification. The dominance of normalized flow features (Q/Mean: 24.86% importance) over absolute values demonstrates that BFD identification depends on relative flow magnitude within each gage’s regime rather than fixed thresholds, supporting cross-watershed transferability through local normalization. The prominence of smoothed derivative features (MW5_dQabs: 13.93%, MW5_d2Qabs: 10.95%) over raw derivatives (<1% importance) indicates that sustained stability patterns rather than instantaneous conditions characterize BFD periods, aligning with physical understanding of gradually varying groundwater-driven flows. Our ablation study revealed important feature dependencies: Mean_Q caused the largest performance drop when removed (5.93%) despite moderate importance (18.54%), confirming its essential role as a normalization baseline, while Q/Mean caused minimal drop (1.28%) despite the highest importance (24.86%), suggesting feature redundancy that enhances robustness. These findings advance understanding of which hydrological characteristics most effectively distinguish BFD periods and provide practical guidance for developing transferable automated identification methods.

Snow-dominated watersheds present challenges for BFD identification due to complex freeze–thaw dynamics and snowmelt timing [43]. Our simplification in treating snow periods uniformly, while necessary for consistent application across our diverse dataset, likely contributed to some misclassifications in regions where snowmelt drives spring streamflow peaks. Previous baseflow studies in snow-dominated systems have noted that traditional separation methods often fail during snowmelt periods because the gradual release of stored water exhibits characteristics of both quickflow and baseflow [44]. Future improvements to the RF-BFD model could incorporate snow-specific features such as snow water equivalent, degree-day factors, and antecedent temperature conditions to better distinguish between snowmelt-influenced and true baseflow periods [45].

The gradient method showed the second-best performance. This method performs well over shorter time periods; however, its accuracy diminishes when applied to longer time ranges. A likely reason for this drop is related to its third step, where a flow threshold is used to remove high flows. Since the threshold is relative to specific periods, applying it over extended timeframes may result in inconsistencies, as the threshold may vary across different periods, leading to fluctuating results.

The BN77 method performed poorly in our evaluation, with a Precision of only 0.50 and an extremely low Recall of 0.09. This underperformance can be attributed to several factors. First, the method’s strict criteria for identifying pure baseflow conditions resulted in very few periods being classified as BFD, explaining the low Recall. Second, the method’s sensitivity to parameter selection made it challenging to optimize across diverse watershed conditions represented in our dataset. While these implementation details should have been presented in Section 3, we include them here to explain the performance results. In our implementation, we set the minimum length of recession episodes (Lmin) to five days to identify suitable recession periods. While the method typically considers snow-freeze periods, we did not specify a snow-freeze period parameter in our analysis, instead treating all periods uniformly. The observational precision was set to 0.1, and we employed a quantile threshold of 0.9 to identify pure baseflow periods. During snow periods, which present unique challenges for baseflow identification, we classified these intervals as BFD periods. This simplification, while necessary for consistent application across our diverse dataset, likely contributed to misclassifications, particularly in snow-dominated watersheds where baseflow dynamics differ significantly from rainfall-dominated systems.

The Strict Method aims to isolate periods when streamflow consists solely of baseflow, meaning there is no influence from direct runoff caused by rainfall or snowmelt. To achieve this, the method employs a series of stringent criteria to filter out any data points that might be contaminated by quickflow. For instance, it discards data points near flood peaks and excludes points surrounding those identified as having zero direct runoff. This rigorous filtering process ensures that only periods with the purest form of baseflow are retained, leading to a highly conservative identification of BFD periods. This is likely the main reason why this method performed poorly relative to the other methods. Our objective is to find BFD periods, and this method is designed to find periods that are 100% baseflow.

The statistical methods showed moderate performance, with the best variant (0.5 threshold) achieving an F1 score of 0.54, compared to the gradient method’s 0.57. While not achieving the high accuracy of the RF-BFD model, they consistently outperformed both the Strict and BN77 methods across all metrics. The statistical approach with a lower threshold of 0.5 achieved the best balance between Precision (0.67) and Recall (0.46), resulting in an F1 score of 0.54. The performance of the statistical methods did not appear to be significantly affected by the number of averaging days used in the calculations. The Stat (0.5t5davg) and Stat (0.5t7davg) models, which used 5-day and 7-day averaging periods, respectively, achieved nearly identical Precision, Recall, F1 Score, and Accuracy metrics. Similarly, the Stat (0.6t5davg) and Stat (0.6t7davg) models, as well as the Stat (0.7t5davg) and Stat (0.7t7davg) models, showed very comparable results across the evaluation measures. This suggests that the choice of 5-day or 7-day averaging periods did not substantially impact the ability of these statistical methods to identify BFD periods. The consistency in the performance metrics across the different averaging period configurations indicates that the results are not highly dependent on this particular parameter, providing confidence in the reliability and robustness of the statistical approach.

5.1. Spatial Variability and Applications to Large-Scale Modeling

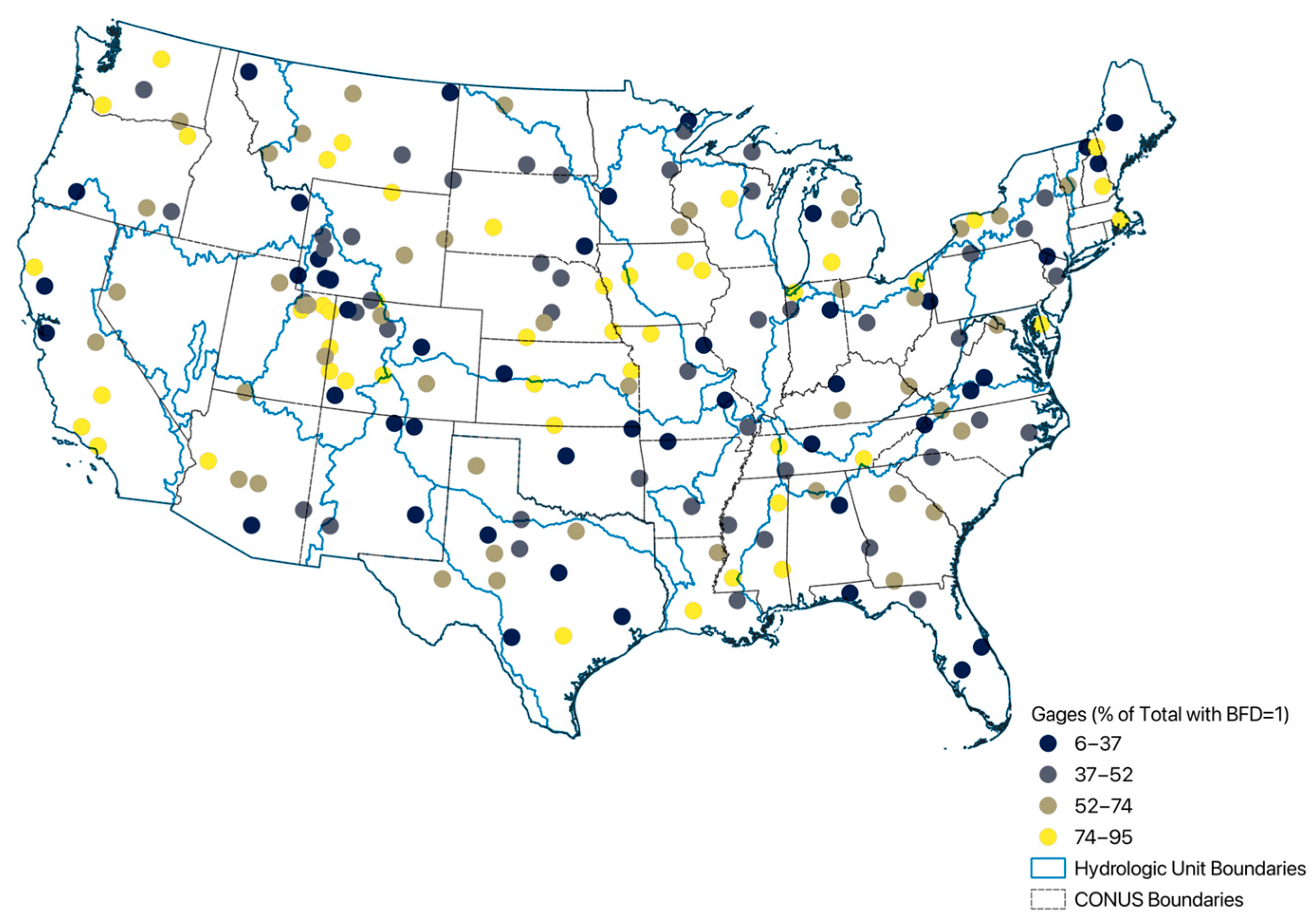
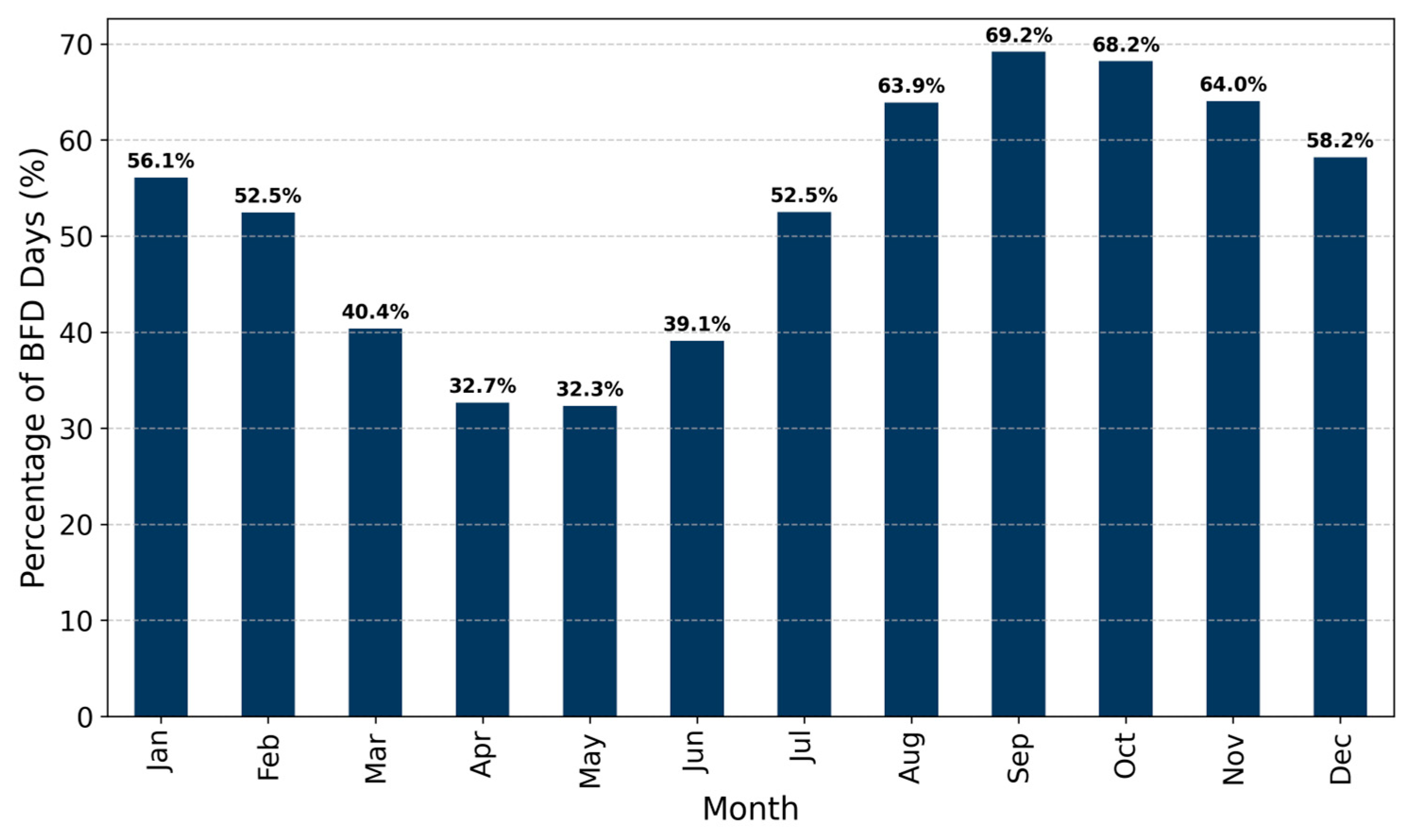
The performance and prevalence of BFD periods varied spatially across our 182-gage network, reflecting diverse hydrological settings in CONUS. As shown in Figure 5, western arid and semi-arid regions exhibited higher BFD percentages (74–95%) compared to humid eastern regions (6–52%), consistent with differing precipitation frequencies and groundwater contributions to streamflow. The RF-BFD model’s ability to adapt to this spatial variability through data-driven learning represents a key advantage over traditional methods with fixed parameters. However, transferability to regions with fundamentally different hydrological characteristics (outside our training dataset) remains a challenge that future work should address through regionalization approaches or region-specific model development. Continental-scale application of BFD identification offers opportunities for improving large-scale hydrological modeling.

By systematically identifying BFD periods in model outputs across stream networks, researchers can diagnose where models fail to capture BFD dynamics, develop targeted bias corrections for BFD versus precipitation-driven periods, and identify regions where improved process representations would most benefit accuracy. The computational efficiency of the RF-BFD approach makes continental-scale application feasible for millions of stream segments. This work introduces a novel framework that, along with subsequent studies building on these methods, is being developed for integration into the National Water Model to implement BFD period identification and improve low-flow prediction accuracy and reliability across CONUS.

5.2. Limitations and Future Research Directions

While the RF-BFD model demonstrates superior performance, several limitations warrant consideration. First, the hand-labeled dataset, though comprehensive, reflects the subjective judgment of human labelers and may not capture all nuances of baseflow dynamics, particularly in highly regulated systems or ephemeral streams where baseflow definitions become ambiguous. Second, our dataset predominantly represents gages in the continental United States, and transferability to regions with fundamentally different hydrogeology (e.g., karst systems, tropical watersheds, or permafrost-dominated basins) remains unvalidated [46]. Third, while our evaluation used a held-out test set (20% of data), this represents temporal holdout within the same gages rather than spatial holdout on completely independent catchments. The model’s high performance may partly reflect learning gage-specific characteristics rather than purely generalizable hydrological patterns. Future work should evaluate spatial transferability through leave-one-region-out cross-validation or application to entirely independent gage networks outside CONUS. However, we note that all gages in our test set span different time periods with varying flow conditions, and the 90% inter-labeler agreement rate suggests our hand-labeled dataset represents consistent hydrological criteria rather than gage-specific idiosyncrasies.

Future research should expand the labeled dataset to include diverse hydrological settings globally, incorporate physically based constraints into machine learning models to improve interpretability and extrapolation, and develop ensemble approaches that combine multiple identification methods weighted by their regional performance [47]. Additionally, integrating remote sensing data (e.g., GRACE groundwater storage anomalies, soil moisture from SMAP) could enhance BFD identification in ungauged basins [48,49]. The application of deep learning architectures, particularly recurrent neural networks that explicitly model temporal dependencies, may further improve BFD identification by better capturing the hydrograph [50]. Finally, coupling BFD identification with process-based hydrological models could enable hypothesis testing about subsurface flow pathways and improve our mechanistic understanding of baseflow generation.

6. Conclusions

This study investigated the effectiveness of various methods for identifying BFD periods in streamflow hydrographs. Five methods were assessed, including two existing methods and three new methods. The performance of each method was evaluated against a meticulously hand-labeled dataset of streamflow measurements from 182 USGS stream gages across the CONUS.

The RF-BFD model, employing a Random Forest classifier, emerged as the most accurate and reliable approach. It achieved an accuracy of 92% and an F1 Score of 0.92, demonstrating its proficiency in distinguishing BFD periods from those influenced by quickflow. This superior performance highlights the potential of data-driven approaches in baseflow identification. The model’s success is attributed to its ability to leverage multiple features derived from the streamflow data, including hydrograph characteristics, moving averages, and baseflow separation outputs.

The Gradient method displayed moderate accuracy with an F1 score of 0.57 and precision of 0.82 but showed a decline in performance when applied over longer timeframes. This limitation may be linked to its reliance on flow thresholds, which can vary significantly across extended periods, leading to inconsistencies in baseflow identification.

The Statistical method, based on baseflow index thresholds, showed varying performance depending on the chosen threshold value. Lower thresholds yielded better results, but the accuracy declined as the threshold increased, indicating a trade-off between precision and recall.

Traditional automated methods (BN77 and Strict) showed consistently poor performance, with recall values below 0.10, indicating a systematic failure to identify true BFD periods. These methods’ reliance on rigid criteria and fixed parameters proved inadequate for capturing the nuanced patterns that characterize baseflow dominance across diverse hydrological settings.

The RF-BFD approach for identifying BFD periods offers a significant advancement over traditional automated methods. While conventional techniques rely on fixed algorithms and conceptual relationships that often struggle to adapt across different catchments, our approach provides a more flexible, data-driven framework. Traditional methods typically employ fixed filtering parameters that vary significantly with soil types, antecedent moisture conditions, and rainfall events, frequently requiring subjective parameter adjustments for each catchment. In contrast, the RF-BFD model leverages labeled data to learn catchment-specific patterns, demonstrating enhanced adaptability when trained with comprehensive datasets covering diverse hydrological conditions.

The study demonstrates the value of creating a comprehensive hand-labeled dataset as a benchmark for evaluating baseflow identification methods at the continental scale. Our systematic comparison of five distinct approaches across 182 diverse USGS gages provides crucial insights into automated baseflow identification performance. Our findings establish the RF-BFD approach as the superior method, opening a door for machine learning methods to be used in BFD period findings. This approach successfully captures the nuanced patterns recognized by human experts while maintaining computational feasibility for large-scale applications. The strong performance of the RF-BFD model establishes it as a new standard for identifying BFD periods—particularly valuable for continental-scale modeling, where optimizing other methods is complex and not feasible without deeper studies of the location. This machine learning framework offers an important tool that preserves accuracy while eliminating the complexities typically associated with traditional methods.