Using a Hydraulic Model for Conceptual Planning of Rural Water Supply Network Reconstruction—Case Study

Abstract

This paper analyses the operation of a water supply system located in the Silesian Voivodeship, serving six small localities covering a rural area of about 50 km² with a total population of 6130. The region’s varied elevation presents challenges to system performance. A hydraulic model was developed in EPANET, then validated and calibrated based on selected measurement points. Previous studies revealed that the network operates under unstable conditions. Although all users receive water under average demand, some areas experience excessive pressure. During peak demand, water shortages occur due to limited inflow to the main reservoir, which the existing pumping system cannot compensate for. In response, the validated model was used in this study to propose a reconstruction strategy to ensure a reliable water supply under all demand conditions. The analysis focused on the introduction of new water intakes, identifying their required capacity and optimal locations. It has been demonstrated that the inclusion of a new water intake positively impacts the stability of the water distribution network, and that a hydraulic model is a valuable tool for supporting the selection of its location. Hydraulic convergence of the model was necessary to optimize and evaluate the proposed solutions. As part of the selection criteria, two parameters were analysed: the percentage of nodes with pressure below 20 m H₂O, and the percentage of nodes where the pressure exceeds 55 m H₂O. Among the evaluated options, the most effective solution was intake no. 1, directly connected to a DN 160 transmission pipe supplying the area with the lowest recorded pressure. The upgraded system operates stably and meets the demands of all users. The obtained results provide valuable support for water utility management in making decisions on the development and operational optimization of water supply networks.

1. Introduction

The water distribution network (WDN) is a key part and at the same time the costliest component of the water supply system (WSS). The primary role of the WDN is to deliver to consumers the water of appropriate quality, in the right quantity, and at the required pressure. The correct design and construction, as well as proper management and maintenance of the WDN, are essential for its operational reliability [1]. The regulation of the network operation and its correct use directly affect the costs associated with water distribution, ultimately influencing the final price of water [2,3,4]. Considering the efficiency of the WSS maintenance, it is essential to minimise total operating costs while ensuring uninterrupted system operation and maintaining its functionality [2].

The hydraulic model is a versatile tool that supports the design of new water distribution networks and the performance analysis of already existing systems. The hydraulic modelling of water distribution networks allows for the simulation of the water flow, taking into account velocities, flow rates, and consumption of water, as well as head losses and operating pressure variations. In principle, it is impossible to measure the above-mentioned parameters for the entire network in operation, due to both the cost and time-consuming nature of such analyses. Developing and calibrating the hydraulic model of the distribution network is more efficient in such a case and allows system performance simulation. At the same time, the inventory of individual network elements, carried out as part of the modelling process, facilitates the validation of the input data. Carrying out numerical analyses enables an assessment of network efficiency and, as a result, allows the operator to make correct decisions [5,6].

In order to achieve high reliability of the hydraulic model, it is necessary to include detailed input data. These include the geometry and type of pipes, the topography, the topology of the network, locations of service connections, the yield of water intakes, the capacity of tanks, and the technical specifications of the pumps and valves [7,8,9,10]. Both verification and calibration are key steps in the model development. The calibration involves matching simulation results (pressure, flow rate) with actual measurement data. Modern techniques, such as Sequential Least Squares Programming (SLSQP), the Genetic Algorithm (GA), or Differential Evolution (DE), allow high precision in determining pipe roughness coefficients [11]. Recent study results also suggest a positive effect of short-burst hydrant trials on improving calibration accuracy [12,13,14].

The optimisation scheme based on the use of the GA allows, for example, the selection of the optimal location, as well as settings of additional valves, to transform the basic district metered area (DMA) layout into adaptive DMA layouts applicable for diversified network management scenarios [15]. Combining the GA with the EPANET Programmer’s Toolkit dynamic link library (DLL) for hydraulic analysis is very beneficial. It allows the creation of an EPANET–GA model that identifies of the optimal solution consistent with the measurement data [16].

Modern water supply systems can be sensitive to accidental contamination. Scenarios for spreading harmful substances can be developed using hydraulic water supply models [17]. Additionally, the EPANET software can be a helpful tool that enables modelling changes in the water age in WDN. The changes in water age can be analysed based on both water pressure and the flow rate [18]. The calibrated model enables advanced operational analyses. Among other things, the model allows identification of reduced pressure zones, areas where acceptable operating parameters are exceeded, the location of bursts and leaks, or the presence of stagnant water. It also allows flushing, inspection planning, and simulation of emergency scenarios [19,20,21,22,23,24,25,26,27]. The understanding of hydraulic parameters, as well as the effective design and operational control, contribute to reducing water losses in the WDS [28]. For example, the hydraulic analysis of changes of operating pressure, carried out using the EPANET model supported by MATLAB software, enables both detection and localization of unreported leaks, contributing to a reduction in water losses [29]. The methodology proposed in [29] supports utilities and employees who are applying both hydraulic modelling and the monitoring of WDN to reduce the water losses and the operating costs. Other modern optimization approaches, utilizing advanced computational methods such as graph theory combined with hybrid optimization algorithms (e.g., GA-COA-SA), offer significant potential for cost minimization while simultaneously meeting all operational requirements [30].

The hydraulic model is also indispensable when carrying out activities to modernise and develop the water distribution system. The hydraulic model makes it possible to verify various investment scenarios, such as replacing pipes or using new pumps, without the risk of costly design errors. The different options for the proposed solutions can be analysed quickly and, based on the results, the most favourable ones can be selected. It is possible to determine the effects of overloading the already existing water supply network and identify errors made designing new sections. The use of the model makes it possible to optimise the electricity used to run the pumps, thus reducing operating costs [5,31]. Smart meters, combined with hydraulic modelling techniques, allow for the reduction of apparent water losses in the water supply network. However, they can also significantly help detect real water losses caused by leaks. Mathematical models can support selecting water meters in multi- and single-family buildings [32]. The use of hydraulic network models can be beneficial in making changes to the division of the network into DMAs, thereby contributing to increasing the system’s energy efficiency [33].

Aim and Scope of the Study

The analysis aimed to determine the optimal conditions for reconstructing the water supply network based on a verified and calibrated hydraulic model. The analysis included potential investment scenarios aimed at improving the operation of the water distribution system under the high hydraulic load conditions.

The analysis of the existing condition of the WDN, conducted based on operational data and the results of model simulations available in [34], showed unstable operation of the water supply network. Therefore, a new water intake has been considered to improve the system’s operating conditions. Two potential locations the water supply system operator identified have been selected for detailed analysis. Based on the hydraulic model, three scenarios of optimization of the network operation were simulated, including:

• Scenario I: operation of the network at the maximum water demand and supply from the new intake located at point no. 1;
• Scenario II: operation of the network at the maximum water demand and supply from the new intake located at point no. 2;
• Scenario III: operation of the network at hydraulic loads exceeding the maximum water demand (simulation of critical conditions), for the more favourable location of the new water intake.

The results of the analyses showed that it is possible to assess the impact of the new intake location on the stability and reliability of system operation under maximum and critical water demand conditions.

2. An Overview of the Existing Condition Model of the Analysed Water Distribution Network

The procedure for developing a hydraulic model for the analysed water supply network is described in detail in the publication [34]. The cited work presents:

• The analysis of the water demand variability;
• The characterization of hydraulic parameters of the existing infrastructure;
• The methodology for preparing input data;
• The verification and calibration of the model using pressure measurements at selected fire hydrants.

This study focuses on aspects relevant to the planned water supply system development. The following is a network characterization that forms the basis for further analysis regarding the optimization of the studied system.

The WDN in question supplies six villages (V1–V6) located in the Silesian Voivodeship, covering an area of about 50 km². These areas are dispersed rural settlements, characterised mainly by single-family housing but also by the presence of public buildings, service and craft companies, commercial and religious facilities, farms (including poultry and cattle farms), and recreational infrastructure. Generally, buildings in the analysed area have no more than three storeys. Some of them are connected to the sanitary sewerage system, while in other cases, septic tanks, cesspools, or domestic sewage treatment plants have been used. Domestic hot water is prepared locally. The population in the study area has remained relatively constant. During the modelling period of six years, only a slight decrease in population (by a maximum of 6%) was observed in one of the villages. The number of serviced inhabitants in the study area during the analysis period was 6131, and the number of service connections was 1075. All service connections were equipped with water meter sets.

The network is supplied with water from a single groundwater intake located in the northern part of the study area (V1). Water is pumped directly from a deep well through the technological system of the Water Treatment Plant. The inverter-driven pumping system maintains the operating pressure of approximately 51 mH₂O, and the maximum flow rate is about 33 m³/h. However, it is not possible to measure hourly and daily flow rates. The network supplies water directly (through a main with a diameter of DN160 mm) from the intake to the first two villages (V1 and V2), and to a centrally located water reservoir in V3. The reservoir’s total capacity is 150 m³, and the effective capacity is approximately 100 m³. This water tank supplies the next four villages (V3–V6) via a second-stage pumping station, which maintains the operating pressure of between 32 and 42 mH₂O, with the average flow rate equal to 13–20 m³/h and the maximum flow rate equal to 45 m³/h. The total length of the network amounts to 58.1 km. The WDN has been constructed from PVC pipes, with the following lengths for each diameter: DN 225–860 m, DN 160–17,100 m, DN 110–16,900 m, DN 90–23,230 m. The water transmission mains are predominantly made from PVC and have a diameter DN160 (with an internal diameter equal to 147 mm).

The water demand included in the model has been calculated based on average annual sales data provided by the network operator. The average daily water demand for the entire network (Q_dśr), estimated based on these data, was equal to 412 m³/d. This value also comprises the non-revenue water (NRW), which accounts for 15% of the supply to the WDS. The NRW comprises the real and apparent water losses (WLs) and unbilled authorised consumption (UAC). The two largest water users (poultry and cattle farms) are located on the major transmission main connecting the water intake to the central reservoir. These two farms’ average daily water demand amounted to 47.2 m³/d and 12.9 m³/d, respectively.

During the study, it was not possible to measure the flow rate variation over time, either for the pumping station at the intake or for the field reservoir. Water peak demand coefficients were therefore estimated based on operational data and the literature, considering the nature of the buildings and the size of the area to be supplied. Due to a shortage of network flow rate during periods of maximum summer consumption, higher values were assumed than would result from the data obtained. During the analysed period, the maximum daily water production reached 755 m³/d. The daily and hourly peak water demand factors were N_dmax = 2 and N_hmax = 3, respectively. These coefficients were the basis for calculating the maximum hourly water demand (Q_hmax), 103 m³/h. Per capita water consumption for household domestic needs ranged from 30–81 dm³/(inhabitant⋅d), depending on the locality. This value increased to 44–171 dm³/(inhabitant·d) after additional consideration of water consumption by farms and other consumers. The highest average consumption of 171 dm³/(inhabitant·d) was recorded in the village where the water tank was located due to the intensive use of water by agriculture.

The area supplied with water by the network is characterised by considerable altitude variation (Figure 1). The difference in ground ordinate between the highest and lowest points is 55.1 m. The water intake is located at an altitude of 228.0 m above sea level, the reservoir is located at 265.8 m above sea level, while the highest located water consumer supplied from the reservoir is placed at 277.1 m above sea level (V4). Therefore, the topography of this area represents a significant impediment to the reliable operation of the water supply system.

3. Materials and Methods

The analysis uses a completed and calibrated hydraulic model developed for the existing condition. The model was created using EPANET 2, a widely recognized software tool created by the United States Environmental Protection Agency (EPA). EPANET 2 allows simulating extended-period hydraulic and water quality behaviour within pressurized pipe networks [35]. The hydraulic model of the network includes 314 nodes connected by 315 sections of PVC pipes with diameters of DN 90–DN 225, as well as the water intake, the water tank and pumping systems with performance curves provided by the operator. The geometrical layout of the network was plotted based on the master map, and water distributions were assigned to nodes based on average demand values.

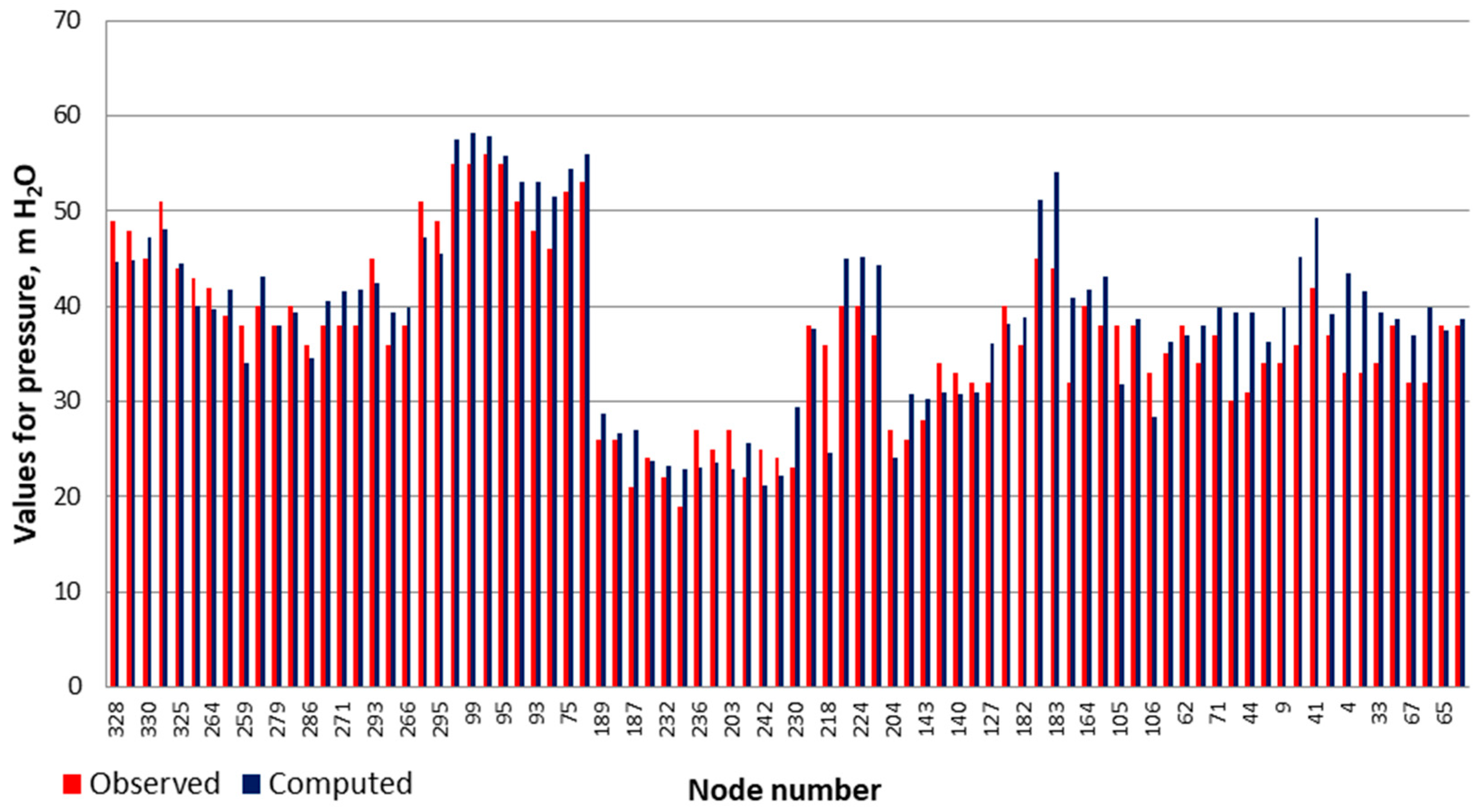
Due to the limited availability of input data provided by the operator, the model calibration was performed based on the pressure height in the nodes. The model was calibrated based on the measurement points in locations of fire hydrants installed in the network. Due to the level of detail in the model, the required number of points should be a minimum of 2% of the nodes. Calibration of the model was carried out using operating pressure values measured at 85 points (27% of nodes), yielding a mean absolute error of 4.5 m H₂O, a mean square error of 3.7 m H₂O, and a correlation coefficient of 0.895. This indicates a strong agreement between the simulated and observed values and a good representation of actual conditions within the network. Only a few nodes exhibited notable deviations between observed and simulated values: in four nodes, the difference approached or slightly exceeded 10 m H₂O, and in seven nodes it was around 7 m H₂O. Despite these local discrepancies at 11 nodes, the model was considered reliable due to the high agreement of the remaining results, as shown in Figure 2.

A sensitivity analysis of the developed hydraulic model was conducted to assess the impact of uncertainty in input parameters on the reliability of the model outputs. The analysis involved varying two key input parameters: pipe roughness coefficients and water demand. The impact of these changes on flow velocity, pressure, and unit head losses was examined. The analysis aimed to identify which parameters most significantly influence critical network indicators. This approach increases the transparency and robustness of the adopted modelling methodology and supports more informed decision-making in system planning. The analysis also provides insights into the model’s stability by evaluating the system’s response to parameter variations. It highlights the areas of the network most sensitive to operational or design changes. The roughness values considered were 0.01 mm, 0.05 mm, and 0.1 mm. Simulations were performed for average and maximum water demand, and water demand increased by 100%. All nodal points and pipe sections were analysed to assess the influence of these variations on the output values.

The most significant deviations from the baseline model were observed in the third scenario, involving a 100% increase in water demand and a roughness coefficient of 0.1 mm. The maximum change in flow velocity was ΔV = 0.01 m/s. Unit head losses increased by Δh = 1.4–3.6 m/km in four pipe sections, and by Δh = 0.61 m/km in three additional sections; however, in most cases, the increase ranged from Δh = 0 to 0.5 m/km. Pressure changes at most nodes (78% of all nodes) did not exceed 2%. For 10% of the nodes, pressure variation ranged between 2% and 5%, and for 11.5% of the nodes it ranged from 5% to 10%. The maximum pressure change, slightly exceeding 10%, was observed at two nodes only.

The hydraulic model allowed testing different scenarios of the water supply network operation. The simulation analysis results presented in the paper [34] indicate that the existing water supply network is not operating stably and needs to be modified. The water supply network ensured a continuous supply of water to all consumers during periods of average water demand, but in some areas, there was excessive pressure reaching 60 mH₂O (V4 and V5). 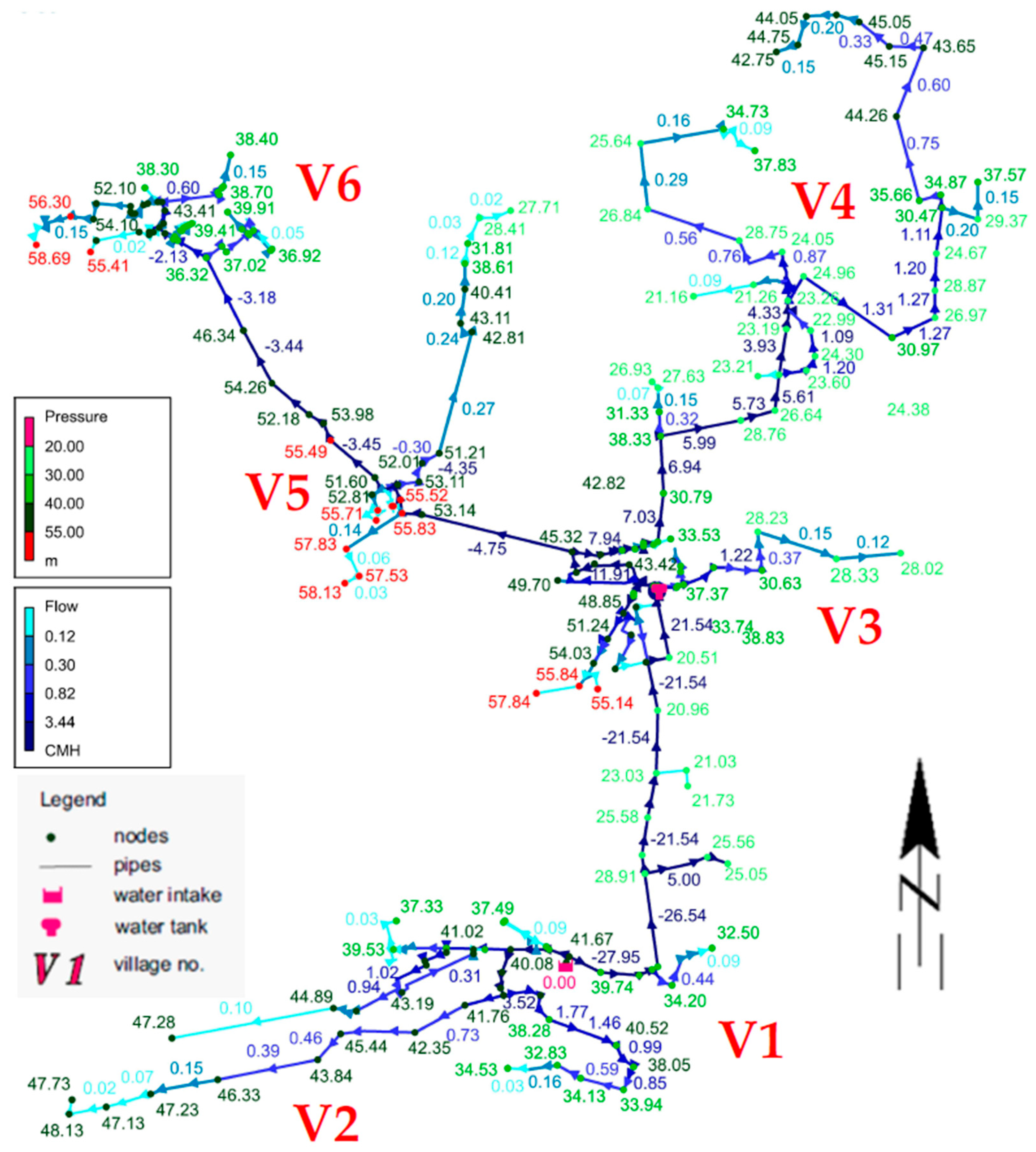Figure 3 shows the water distribution network plan, operating pressures, and flow rates for average daily consumption [34].

The situation worsens during peak demand hours when the water tank’s limited capacity and the existing pumping system cause water shortages in the majority of the network areas. Under the conditions of maximum hourly demand, the hydraulic model fails to converge, generating an error message during the simulation process. Despite operating at maximum capacity, the pumping systems located at the water intake and the storage tank cannot deliver the required water volumes or maintain adequate pressure throughout the network. As a result, calculating and presenting pressure values for the entire system is not feasible. The eastern part of the network experienced the most significant difficulties in obtaining adequate pressure (V4). The primary objective of the analysis, which is the subject of this article, was to improve the water distribution system’s operational performance under elevated demand conditions.

4. Analysis of the Network Operation After Connection to a New Water Source

In order to improve the supply conditions of the existing water distribution network, the inclusion of a deep well as a new water source supplying the WDS was analysed. Following the operator’s guidelines, two possible intake locations were considered in V3. The same capacities of 40 m³/h were assumed for both possible wells, with water pumping heads of 38 m H₂O. Problems with the water supply in the existing WDN occurred at maximum water consumption, so these conditions were taken into account in this analysis scenario.

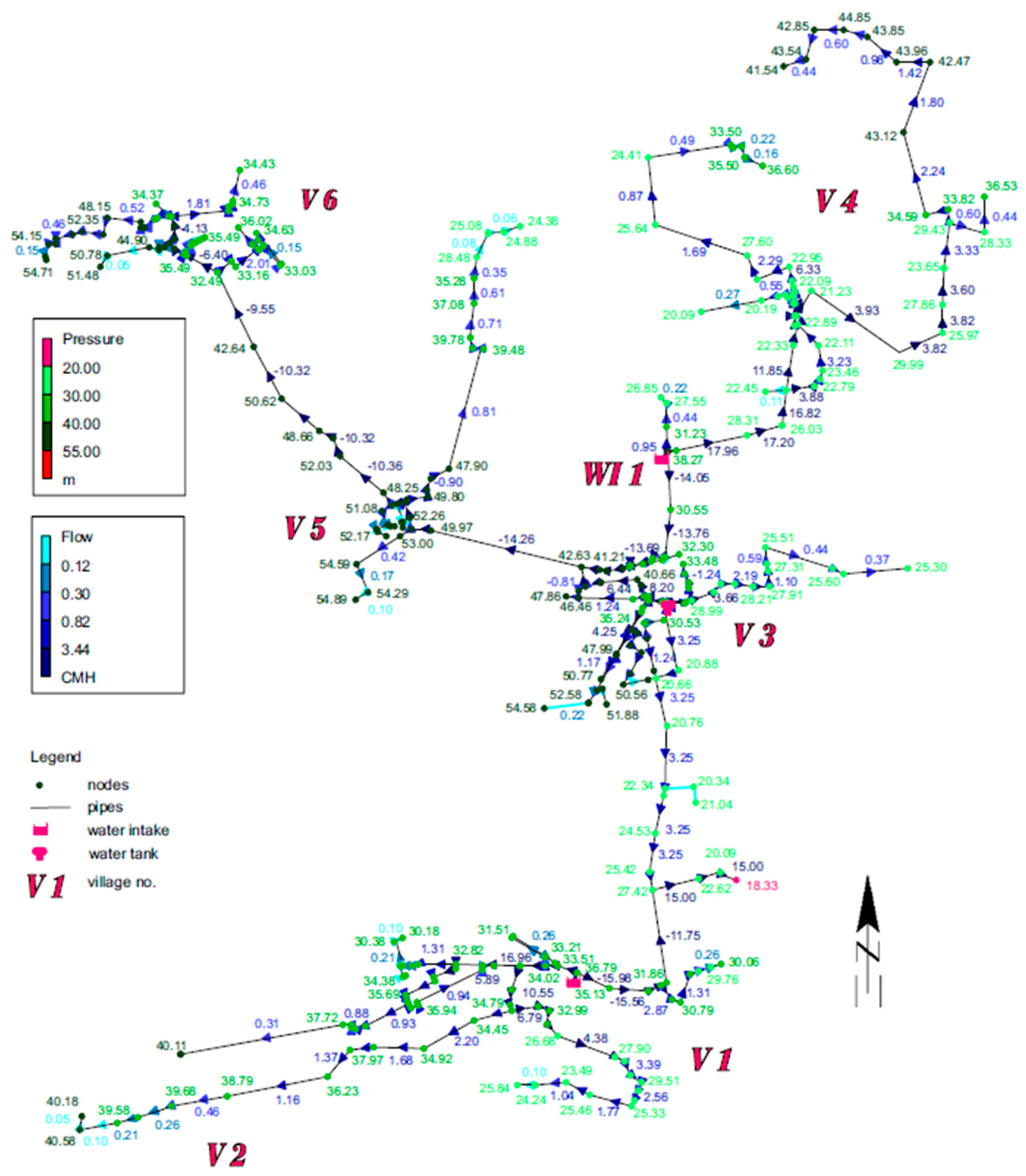
The first scenario involved analysing the impact of the well located at point WI 1 of the water supply system. Figure 4 shows both simulated pressure heads at individual nodes and water flow rates in the network. Values of operating parameters are presented with the use of a variable colour scheme for both pipes and nodes. Operating pressures (given in m H₂O) are presented as numerical values placed on the map at nodes. When the allowable operating pressure is exceeded (above 55 m H₂O), both the nodes and values are marked in red. On the other hand, the excessively low pressure values (lower than 20 m H₂O) are marked in pink. Green colour is used for pressures ranging from 20 m H₂O to 55 m H₂O—the more saturated the colour, the higher the parameter value. The blue numerical values next to the arrows in the middle of the pipe sections refer to the flow rate given in m³/h. The blue colour saturation increases with an increase in flow rate value. The arrows placed in sections indicate the direction of water flow.

In the first scenario of the water intake location, the capacity of the water supply network is sufficient for the assumed maximum consumption, so the simulation runs correctly. The pressure in almost the entire network varies from approximately 20 m H₂O to a maximum value of 55 m H₂O. Only in one node (representing 0.3% of all nodes) does the pressure drop below the required 20 m of water column; however, the solution to this problem is presented in publication [34]. Comparing the above simulation results with the previously conducted analysis of the existing state [34], it was found that the network operation in the V1 and V2 differs only slightly. At the same time, significant differences can be observed in the other localities.

The area supplied directly from the water tank and the planned intake do not show any water shortages, unlike the current situation described in [34]. Water from the new intake is transported towards V3 and V4. It can be observed that after the additional intake was put into operation, despite increased water consumption, the available pressure in both of the above-mentioned locations remains at the required level, above 20 m H₂O, even in the most unfavourably located nodes. The water supply system operates stably and has a capacity that meets the needs of all consumers; the pressure does not exceed 55 m H₂O in any node.

In the second scenario a simulation of the network operation is carried out with a changed location of the pumping well (the supply point WI 2). The assumed water intake operating parameters are the same as in the first scenario: a pumping system capacity of 40 m³/h for a pressure head of 38 m H₂O. The simulation results for V3 and V4 are presented in Figure 5.

In the second scenario, a slightly lower pressure head can be observed in the analysed nodes. The most significant pressure difference between the two scenarios, amounting to approximately 4 m H₂O, is recorded in V4. The pressure does not exceed 55 m H₂O at any node, but at several nodes in the central part of this village (representing 6% of all nodes), the pressure has dropped below the required value of 20 metres. This drop is due to greater pressure losses between the WI 2 intake and water consumers during water distribution. The higher altitude of the well does not compensate for this pressure drop. The land surface altitude for the intake WI 1 is 258.80 m above sea level, and for the intake WI 2 is 264.30 m above sea level, so the difference is 5.5 m. Higher pressure losses during the flow are caused by insufficient diameters of water pipes in the area of the proposed location of the intake WI 2, as in the case of the pipeline section DN90 mm transporting water from the intake between nodes 52 and 120, where the length is approximately 280 m. High pressure losses can also be generated in the network section between transit pipes transporting water to V4 and V5, whose diameter is DN 110. The length of this section is 400 m (nodes no. 120 to 110), with a further narrowing to DN 90 over a length of approximately 220 m (the pipe section from node no. 110 to no. 119). Only in the further sections of the transit pipes are DN 160 pipelines laid.

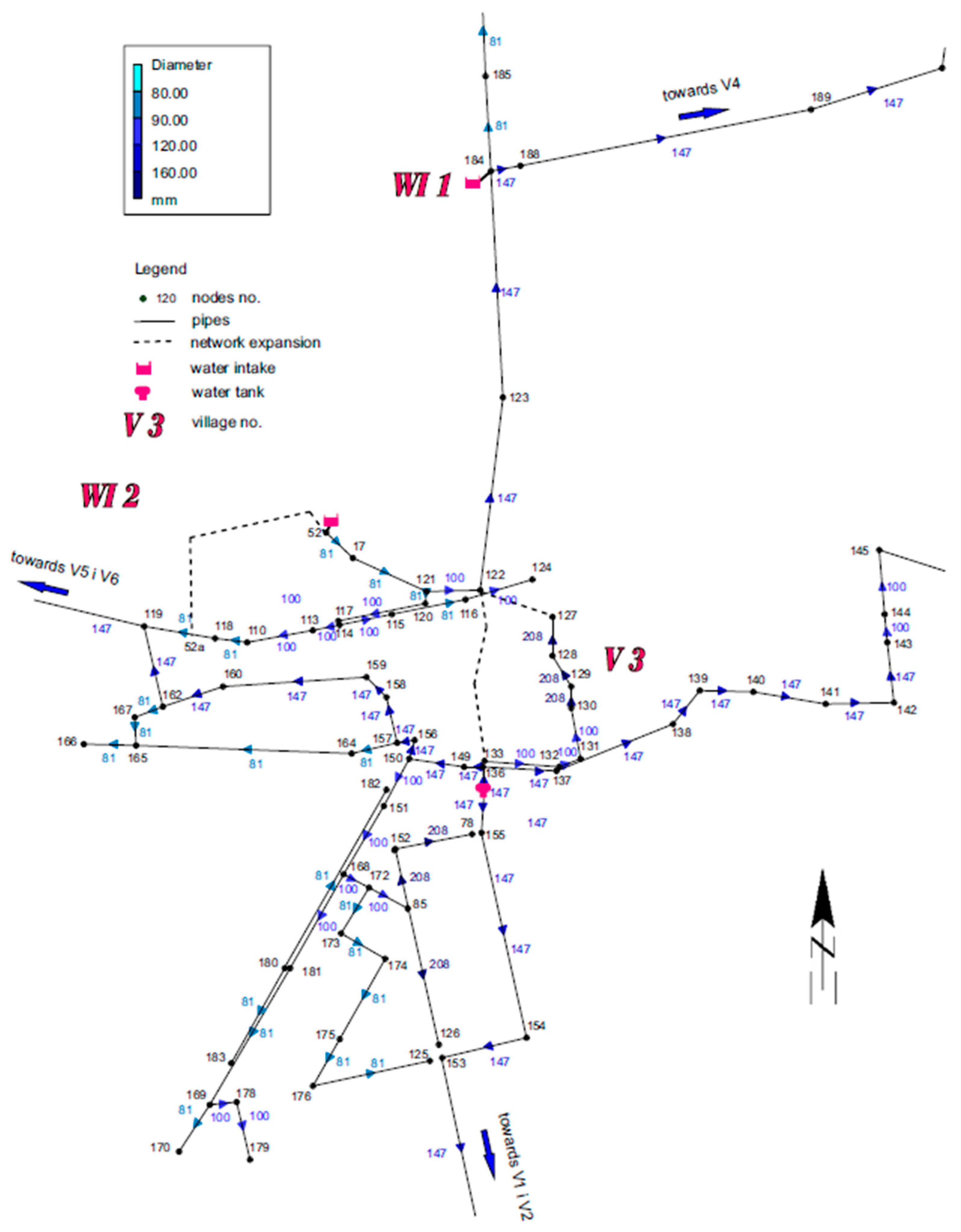
The diameters of the existing network are shown in Figure 6. Due to the model specificity, internal diameters are shown in the drawing (internal diameters were used for calculation). The main transit pipes connecting the individual localities have a diameter of DN 160 mm (internal diameter of 147 mm).

The section between nodes 119 and 122 is one of the main pipelines that needs to be rebuilt first, using an internal diameter of 200 mm. Since the water pipes are located on both sides of the street, connecting the existing DN 90 mm and DN 110 pipes in the section between nodes 117 and 122, instead of constructing a new water main, is possible. The ring created will reduce pressure head losses in this area. However, it is advisable to increase the diameters of pipelines on the remaining part of the street.

Connecting the new intake WI 2 directly to the pipeline transporting water to V5 is also possible, bypassing the existing network: the section marked with a dashed line, between nodes 52 and 52a. This solution would require the construction of a new DN 225 main pipeline with a length of approximately 850 m. However, this does not solve the problem of the insufficient diameter of transit pipelines supplying V3 and V4: the section between nodes 119 and 122. Alternatively, the DN 225 pipeline section on the eastern side (nodes 131 to 127) could be considered (provided its technical condition allows it). The existing water main would have to be connected to the transit pipeline transporting water towards V4. The length of the new section between nodes 122 and 127 will be approximately 250 m. Replacing the existing DN 110 section between nodes 130 and 131 would also be necessary, along with the connection to the DN 160 pipe (to sections 137–128). Another possible option for improving water flow is to route the new DN 225 water main directly towards the existing water tank, between nodes 133 and 122. All the above alternative network routes are marked with a dashed line in Figure 6.

Figure 7 shows the last analysed scenario of the network operation (scenario no. 3), which involves increased water demand concerning maximum consumption, including launching a new intake point: WI 1. The map shows the most problematic area: V4. During the simulation, it was assumed that the maximum hourly consumption for the entire network is 128 m³/h. Despite a slight pressure drop, the network supplies water to the most unfavourably located consumers, with the lowest pressure values observed, as before, in V4. The pressure values are slightly below the required level; however, this is acceptable under critical flow conditions. In such cases, the required minimum pressure value should not fall below 10 m.

Selection between water intakes WI 1 and WI 2 requires an evaluation that considers both capital and operational expenditures and other critical parameters such as water quality and constructability. Based on information the water network operator provided, it was assumed that both variants would exhibit identical yield and water quality. This is due to the proximate locations of the intakes, which will source water from the same aquifer. The yield of the intakes was determined based on the provided geological data. Consequently, water quality and yield were not differentiating factors in the analysis.

Regarding capital expenditures, the direct construction cost of the intake structures themselves is identical for WI 1 and WI 2. However, a significant difference arises in the costs of connecting to the existing distribution network. Connecting the intake WI 2 requires the construction of additional pipeline sections, resulting in higher infrastructure-related costs. In contrast, the location of WI 1 allows for direct connection to the network, significantly enhancing its investment viability. A key aspect of the analysis was the assessment of energy efficiency. Hydraulic simulations demonstrated that, under the assumption of maintaining a minimum pressure of 20 m H₂O at critical nodes (without network modernization), pumping from intake WI 1 is characterized by 5.8% lower energy consumption than variant WI 2. This difference results from a more favourable hydraulic layout and reduced pressure losses. It is noteworthy that an analysis incorporating the modernization of existing infrastructure (replacement of undersized pipes) indicates a slight (0.9%) cost advantage for variant WI 2 in terms of pumping costs. However, it must be emphasized that this configuration leads to excessive pressures (>55 m H₂O) at 10 network nodes, which is associated with an increased risk of failures and negatively impacts infrastructure durability.

In summary, location WI 1 represents a more economically viable and technically justified solution. Despite comparable intake construction costs, WI 1 offers significantly lower connection costs and lower energy consumption in the baseline scenario. Eliminating the risk of excessive pressures in the network further supports the advantage of this variant, ensuring more stable and safer operational conditions.

The findings of this study underscore the critical role of intake location in ensuring reliable water distribution, especially in areas with challenging topography and dispersed settlements. Although the two analysed intake sites—WI 1 and WI 2—are situated relatively close to one another and source water from the same aquifer, simulation results reveal that even small differences in supply point placement can significantly affect pressure and flow conditions throughout the network. The study also emphasizes the importance of considering both hydraulic behaviour and economic factors in infrastructure decision-making. While both intake sites have comparable construction costs and water quality, WI 1 presents clear advantages: lower energy consumption under baseline conditions, easier integration with the existing system, and reduced investment risk. Even when network modernization is considered, the pressure stability of WI 1 remains superior, reinforcing its overall viability. Importantly, this study illustrates the value of hydraulic modelling as a decision-support tool in water infrastructure planning. It enabled the identification of system bottlenecks, assessment of critical areas like V4, and the simulation of complex scenarios that would be difficult or costly to test in real-world conditions. Moreover, the recommendation to implement continuous pressure and flow monitoring addresses a broader issue seen in many rural and semi-rural water systems: a lack of operational data, which limits both real-time response and long-term planning.

The analysis results directly relate to the challenges many other water supply systems face, particularly in smaller towns and areas with dispersed settlements and varied topography. The issues identified in the study—such as unstable network operation, water shortages during peak demand hours, excessive pressure in certain system parts, and insufficient pipe diameters—are typical of many existing water supply networks with limited modernization potential and inadequate monitoring of operating parameters. The study particularly highlights the impact of the water intake location on the reliability of the entire network. A comparison of two scenarios confirmed that even slight differences in the placement of the supply point can lead to significant variations in pressure and flow distribution and thus affect the quality and reliability of water delivery. The findings emphasize that investment decisions regarding the expansion or reconstruction of water supply systems should be based on thorough hydraulic analyses, considering both technical and economic conditions.

Equally important is the role of hydraulic modelling as a decision-support tool—it enables the identification of bottlenecks within the system, evaluation of the impact of proposed changes, and selection of the most effective solutions. The recommendations provided in the study regarding the need for network modernization and continuous pressure and flow monitoring are also applicable to other systems where the lack of operational data hinders day-to-day management and long-term development planning. As such, the methodology presented can be effectively adapted to other regions and conditions, serving as an example of best practices in water supply system planning and performance optimization.

5. Conclusions Resulting from the Conducted Analysis

The conducted analysis confirms that hydraulic modelling is not only an effective tool for assessing the current technical condition of the water supply system but also plays a key role in the investment decision-making process. One of the innovative aspects of this study was the comparison of two water intake location options, taking into account their impact on energy efficiency, pressure stability within the network, and overall investment viability. Currently, the analysed water supply network does not operate stably. Under conditions of average water demand, all consumers are supplied, but in some areas of the network, excessive pressure values (up to almost 60 mH₂O) are recorded. During periods of peak water consumption, shortages occur due to limited inflow to the main water reservoir, which supplies a significant part of the system. The existing pumping system is unable to fully compensate for these shortages. The most significant difficulties in ensuring continuity of supply are observed in V4. A potential upgrade of the pumping system to a higher capacity does not constitute an effective solution to the problem, due to the insufficient capacity of the existing water intake and the inadequate volume of the water reservoir.

In order to solve the above issues, hydraulic modelling was used to analyse possible scenarios of expanding the water supply network with a new water intake. The finished and calibrated model allowed testing two location scenarios for the deep well and assessing their impact on the network functioning. Based on the results of the simulation, the following conclusions were formulated:

1.

Among the two new possible water intake locations indicated by the network operator, the intake location WI 1 is the more advantageous solution. This intake can be directly connected to the DN 160 transit pipeline, which transports water towards V4, where the network’s lowest available pressure is recorded. Choosing the WI 2 location would require rebuilding the existing network—replacing the DN 90 and DN 110 pipes with DN 225 pipes—or building new sections of the water main. Although both intakes are close together and source water from the same aquifer, the study demonstrates that minor differences in spatial placement can lead to significant variations in network performance.

2.

The water pipes located in the central part of V3 need to be modernized. The current pipe diameters (DN 90 and DN 110) are insufficient, resulting in significant pressure losses at maximum flow rates. These pipes, both now and after the planned network expansion, play an important role in water distribution. They are responsible for transporting water to V4, V5, and V6.

3.

In order to improve operating conditions, it is recommended that measuring devices (continuously recording pressure and flow rate) be installed at existing and planned network supply points, particularly at the new water intake and at the existing intake and water tank. This will enable continuous monitoring of network operating parameters, assessment of actual consumption distribution, and effective system management. Installing measuring devices at selected network nodes on transit pipelines supplying individual localities is advisable.

Hydraulic modelling in the analysis proved to be an effective tool in diagnosing current operational problems and evaluating various network expansion scenarios. Thanks to simulations, it was possible to identify critical areas and optimal investment locations and assess the impact of proposed solutions on system performance parameters. Hydraulic modelling thus provides significant support in the strategic planning of water supply system development, enabling decisions based on technical data that lead to improved network reliability and efficiency.