Figure 1.
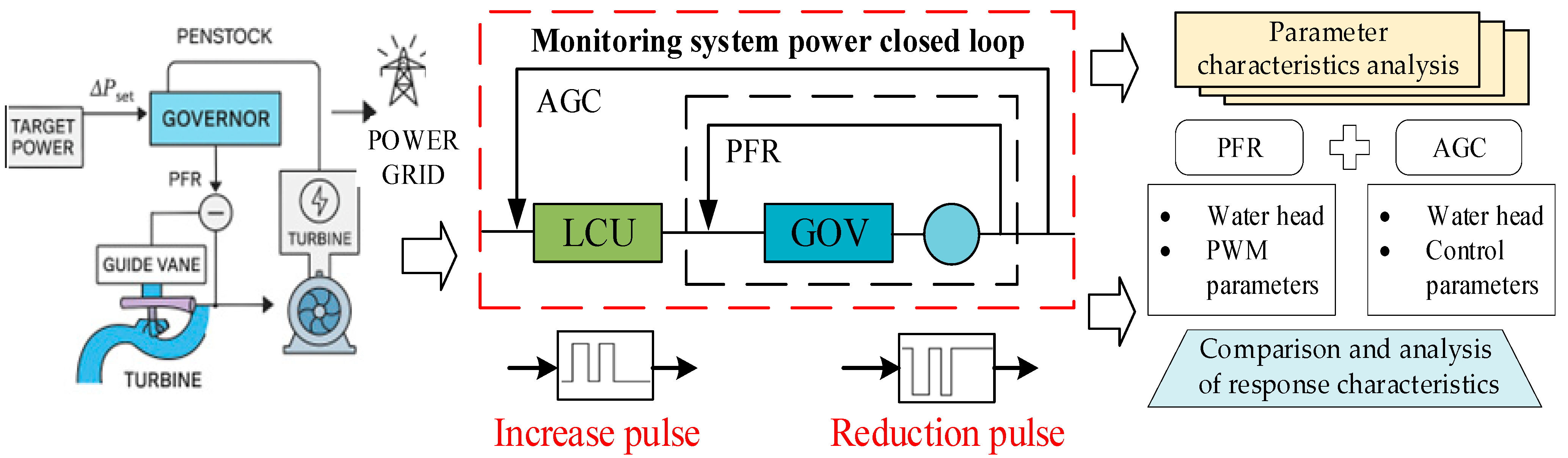
The overall analysis flowchart of regulation characteristics of hydropower units.
Figure 1.
The overall analysis flowchart of regulation characteristics of hydropower units.
Figure 2.
Schematic diagram of the composition of a hydro turbine governor.
Figure 2.
Schematic diagram of the composition of a hydro turbine governor.
Figure 3.
Parallel PID control strategy block diagram.
Figure 3.
Parallel PID control strategy block diagram.
Figure 4.
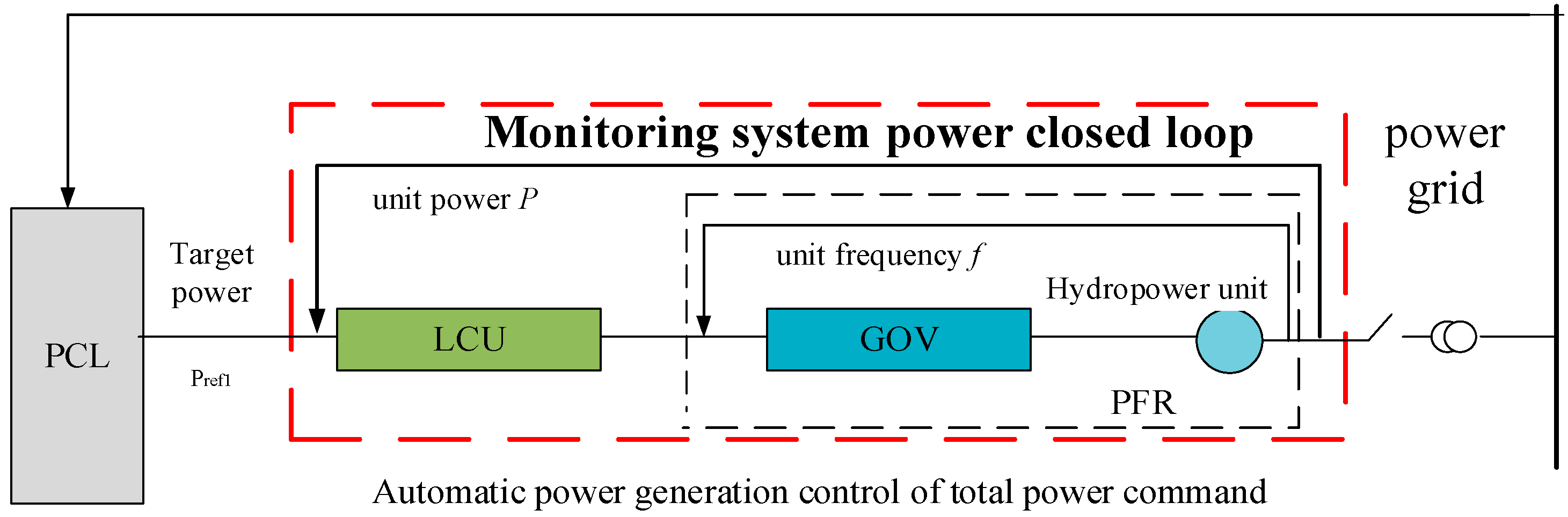
Typical monitoring system control method block diagram for power grids.
Figure 4.
Typical monitoring system control method block diagram for power grids.
Figure 5.
Specific model block diagram of LCU active control. In the figure, Pref represents the active power setpoint of the unit, Pe represents the active power feedback value of the unit, e is the natural logarithm, td1, td2, td3 are the time constants of the delay stages in the figure, Td1, Td2, Td3 are the measurement time constants of the pulse measurement stages in the figure, DZ1 is the deadband of the active power difference, Kpe is the proportional gain coefficient of the power closed-loop control, and Ymax and Ymin are the maximum and minimum values of the active power deviation limits.
Figure 5.
Specific model block diagram of LCU active control. In the figure, Pref represents the active power setpoint of the unit, Pe represents the active power feedback value of the unit, e is the natural logarithm, td1, td2, td3 are the time constants of the delay stages in the figure, Td1, Td2, Td3 are the measurement time constants of the pulse measurement stages in the figure, DZ1 is the deadband of the active power difference, Kpe is the proportional gain coefficient of the power closed-loop control, and Ymax and Ymin are the maximum and minimum values of the active power deviation limits.
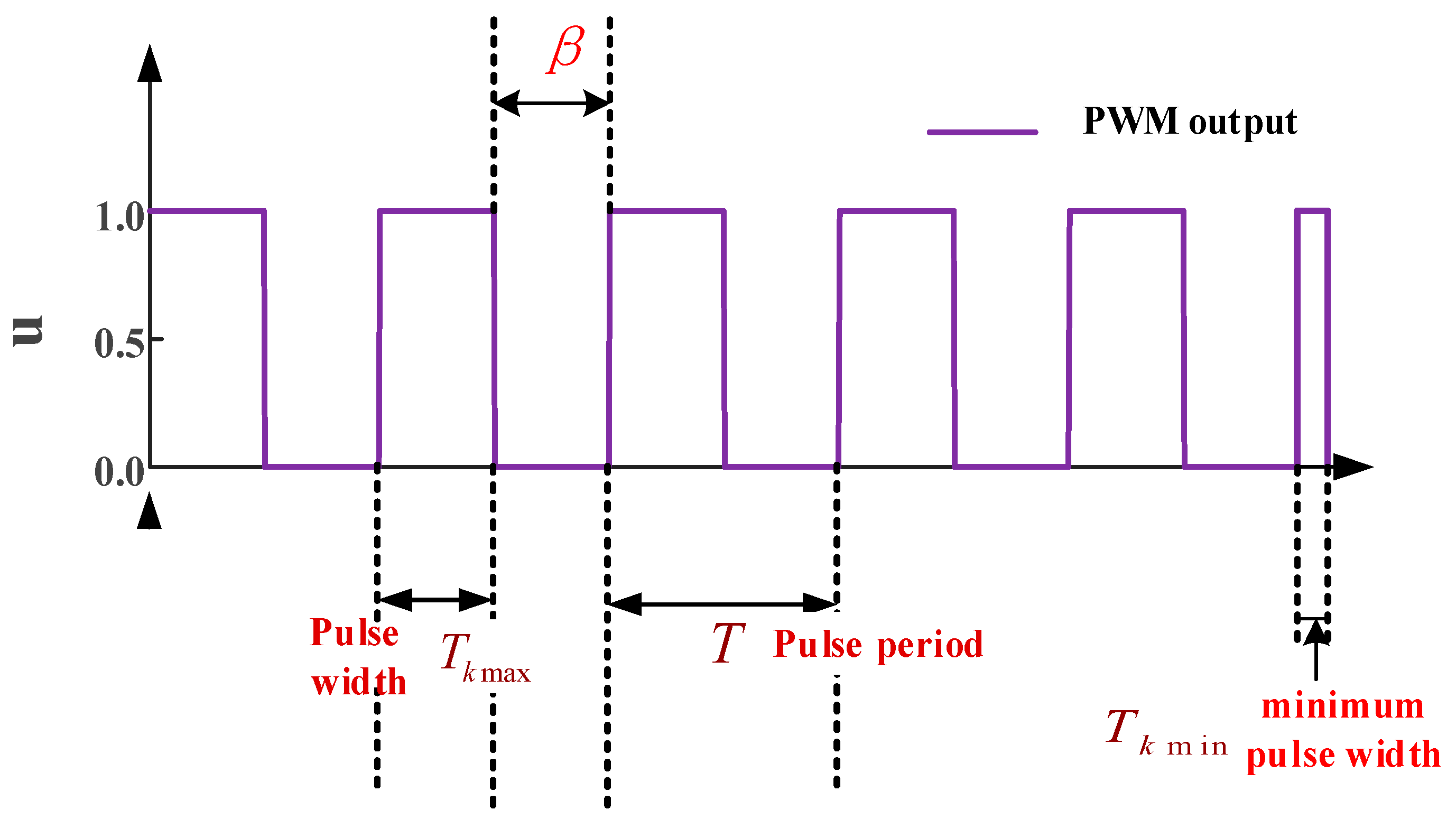
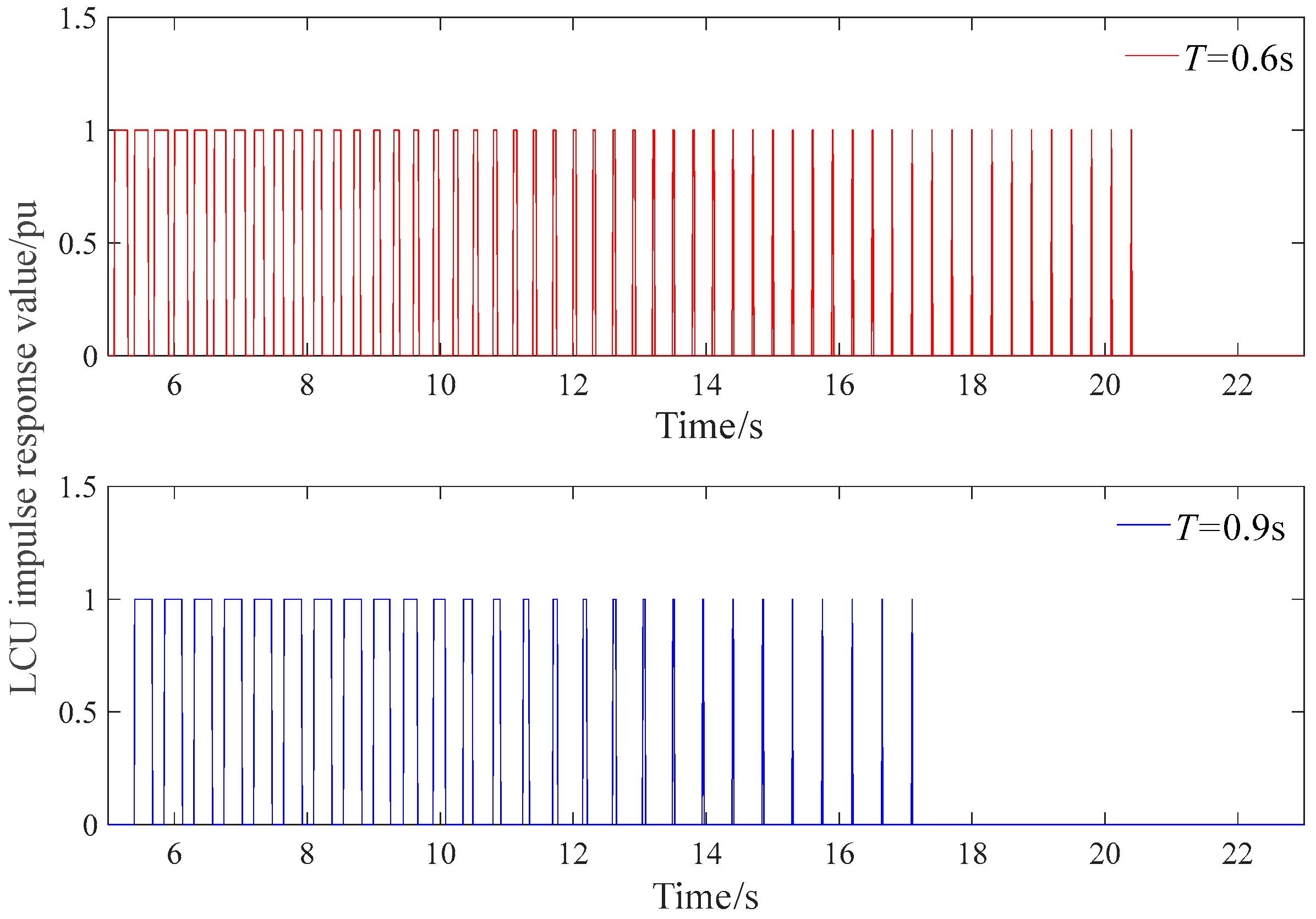
Figure 6.
LCU pulse output diagram.
Figure 6.
LCU pulse output diagram.
Figure 7.
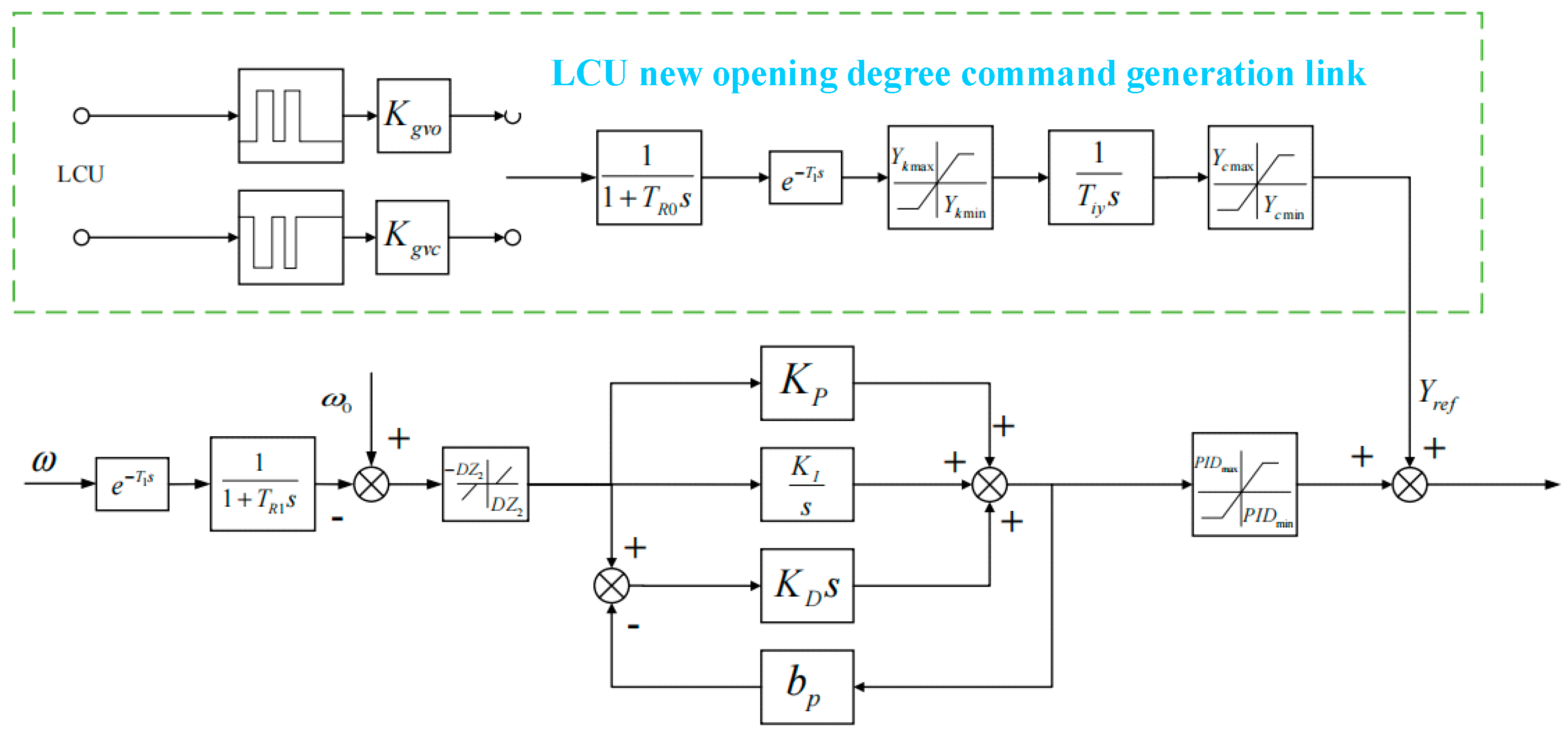
Newly added speed regulator model for the opening degree setpoint generation stage. In the figure, Kgvo and Kgvc are the proportional parameters for increasing and decreasing the guide vane opening at a given point, respectively; Ykmax and Ykmin are the maximum and minimum amplitude limits on the input side of the pulse/opening integral conversion link, respectively; Ykmax and Ykmin are the maximum and minimum amplitude limits on the output side of the pulse/opening integral conversion link, respectively; TR0 is the pulse measurement time constant; and T1 is the delay time constant of the measurement pulse.
Figure 7.
Newly added speed regulator model for the opening degree setpoint generation stage. In the figure, Kgvo and Kgvc are the proportional parameters for increasing and decreasing the guide vane opening at a given point, respectively; Ykmax and Ykmin are the maximum and minimum amplitude limits on the input side of the pulse/opening integral conversion link, respectively; Ykmax and Ykmin are the maximum and minimum amplitude limits on the output side of the pulse/opening integral conversion link, respectively; TR0 is the pulse measurement time constant; and T1 is the delay time constant of the measurement pulse.
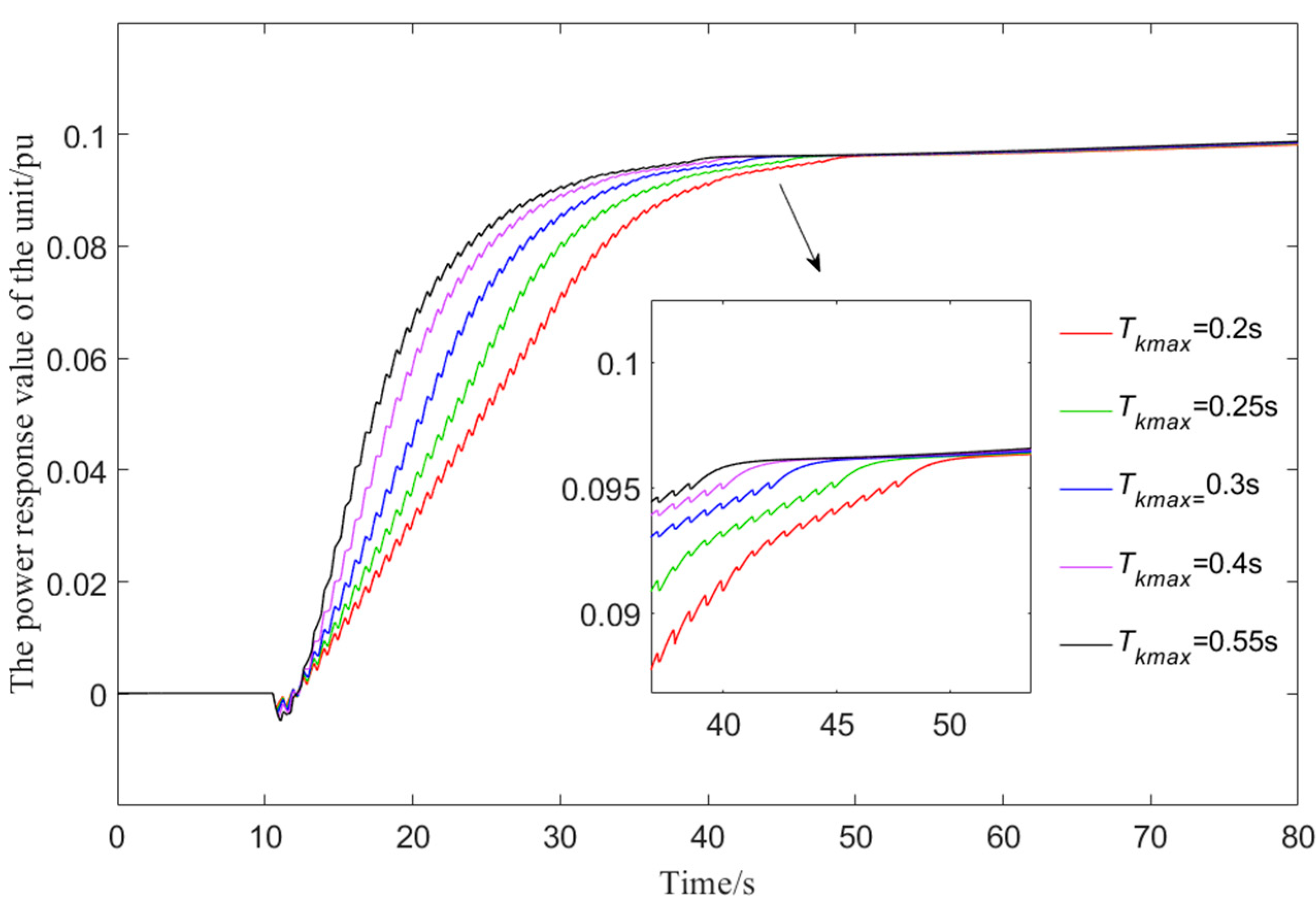
Figure 8.
Active power regulation process of the unit.
Figure 8.
Active power regulation process of the unit.
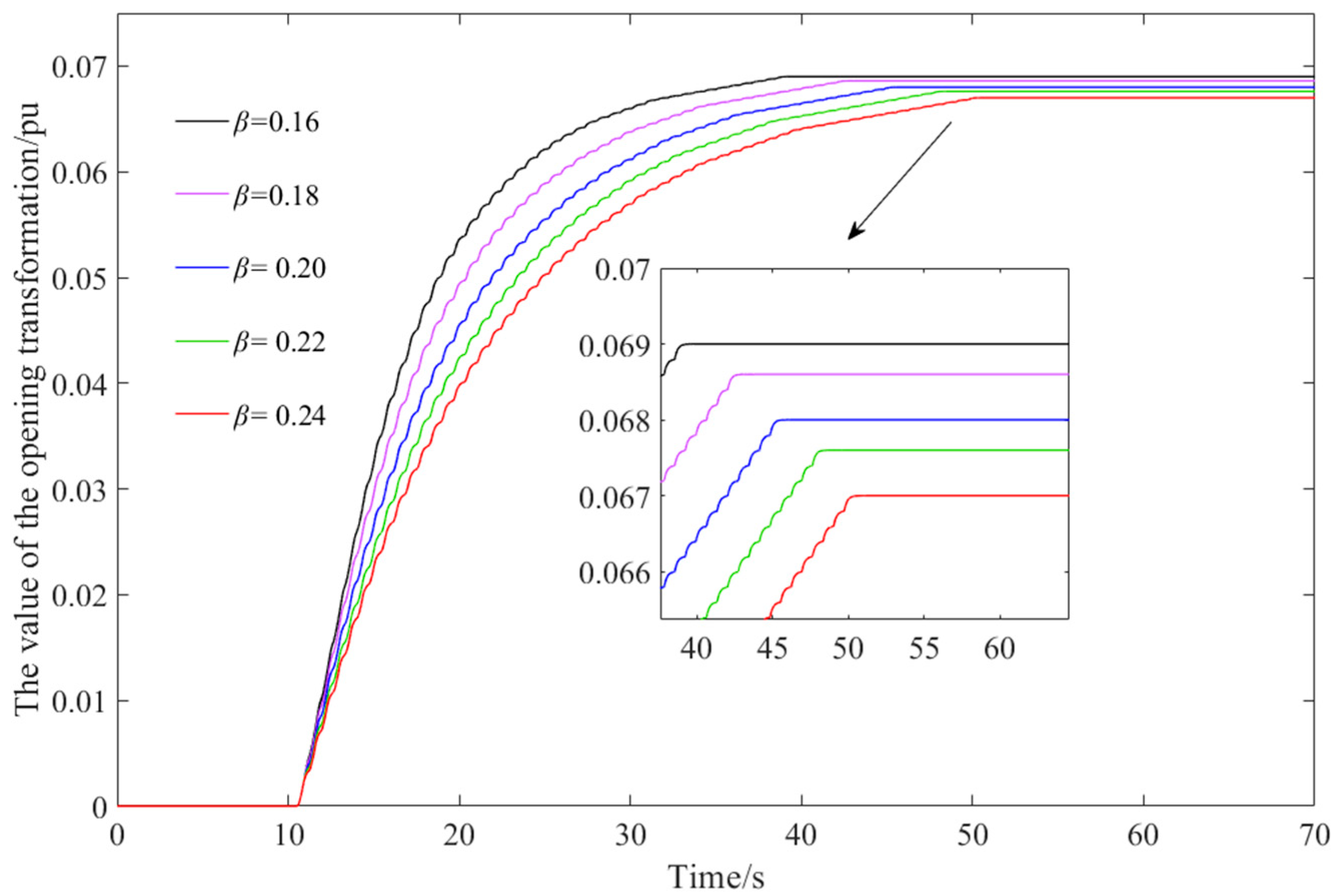
Figure 9.
Effect of various parameters on PWM output.
Figure 9.
Effect of various parameters on PWM output.
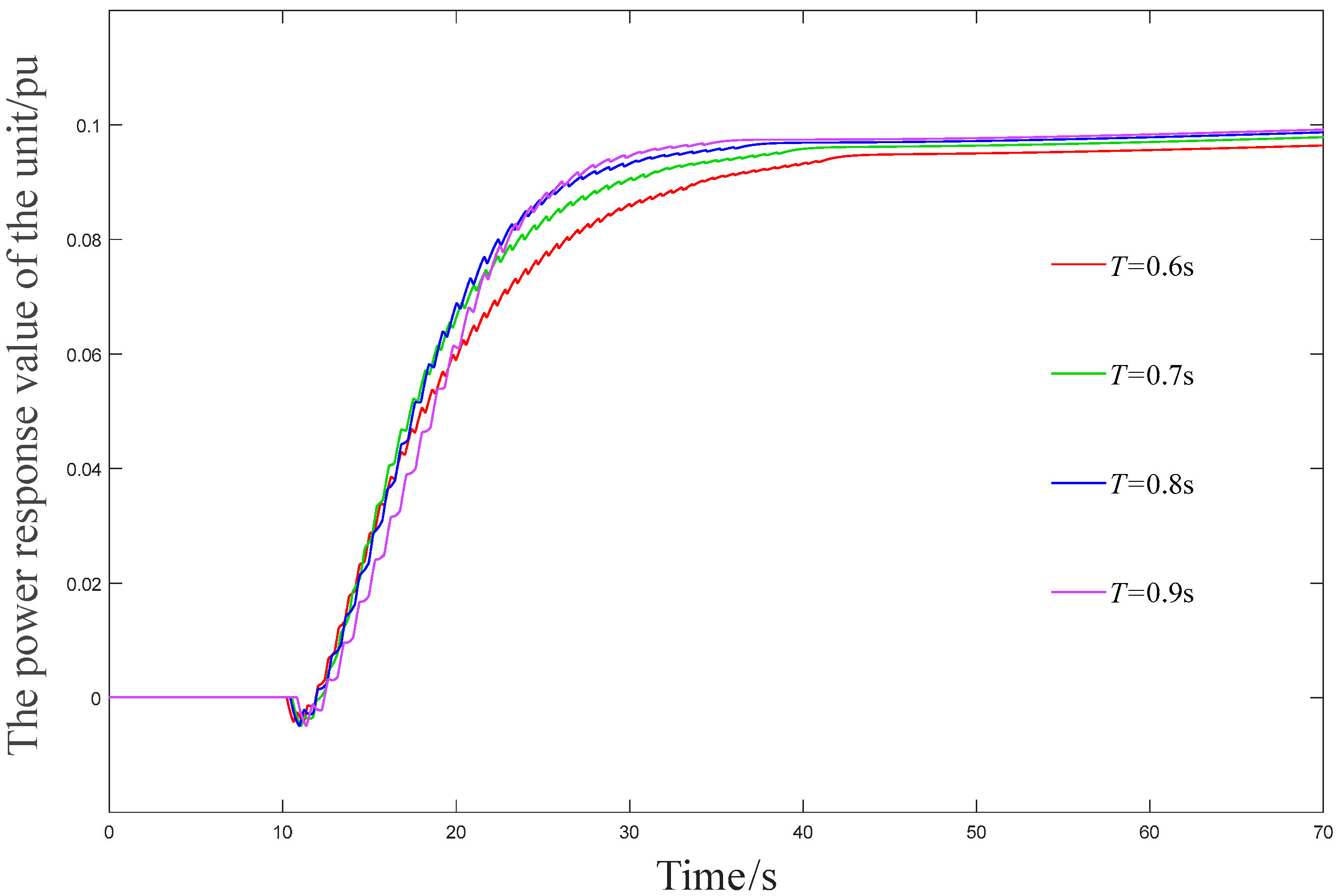
Figure 10.
Active power regulation process of the unit.
Figure 10.
Active power regulation process of the unit.
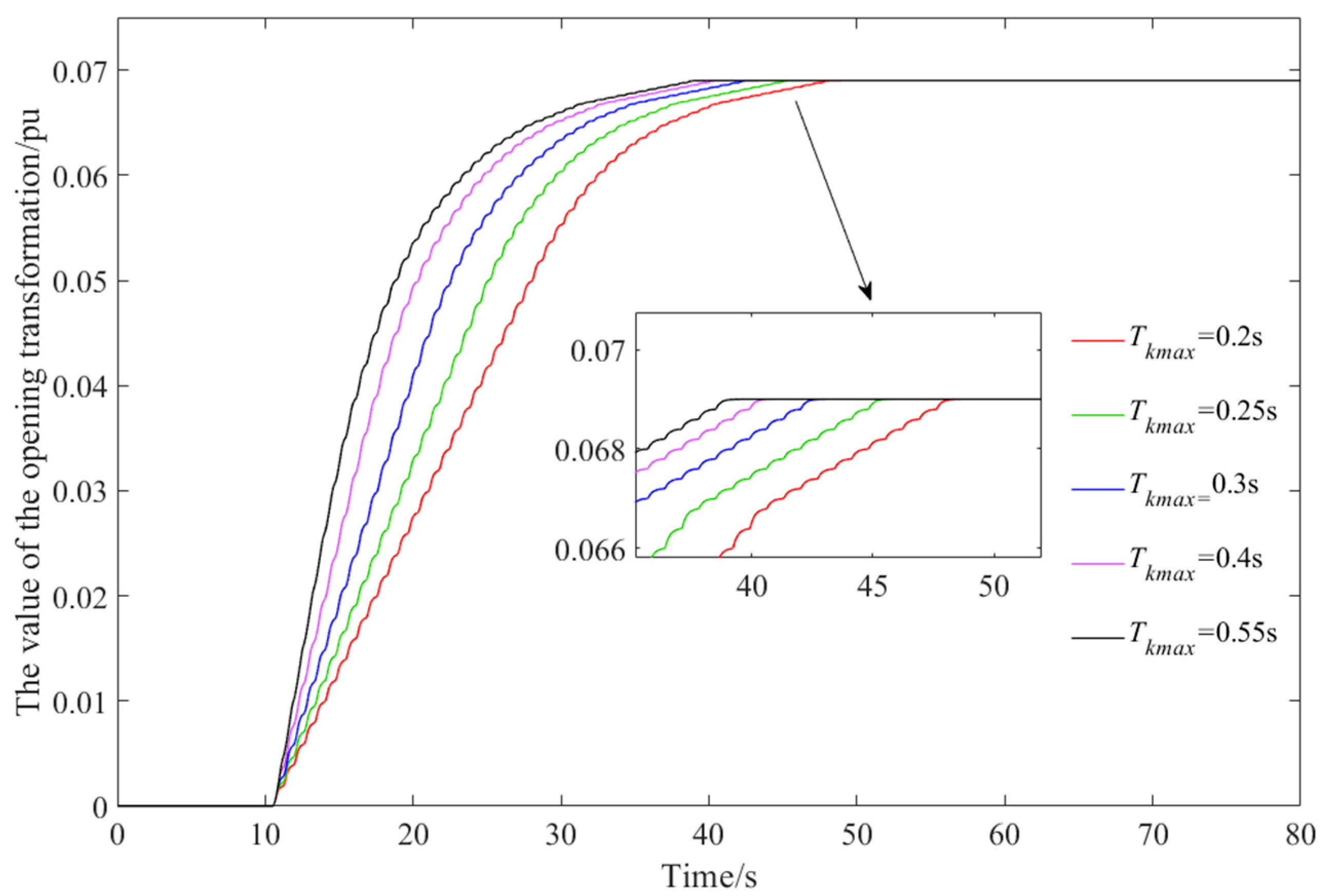
Figure 11.
Turbine guide vane adjustment process.
Figure 11.
Turbine guide vane adjustment process.
Figure 12.
Turbine guide vane adjustment process.
Figure 12.
Turbine guide vane adjustment process.
Figure 13.
Active power regulation process of the unit.
Figure 13.
Active power regulation process of the unit.
Figure 14.
Turbine guide vane adjustment process.
Figure 14.
Turbine guide vane adjustment process.
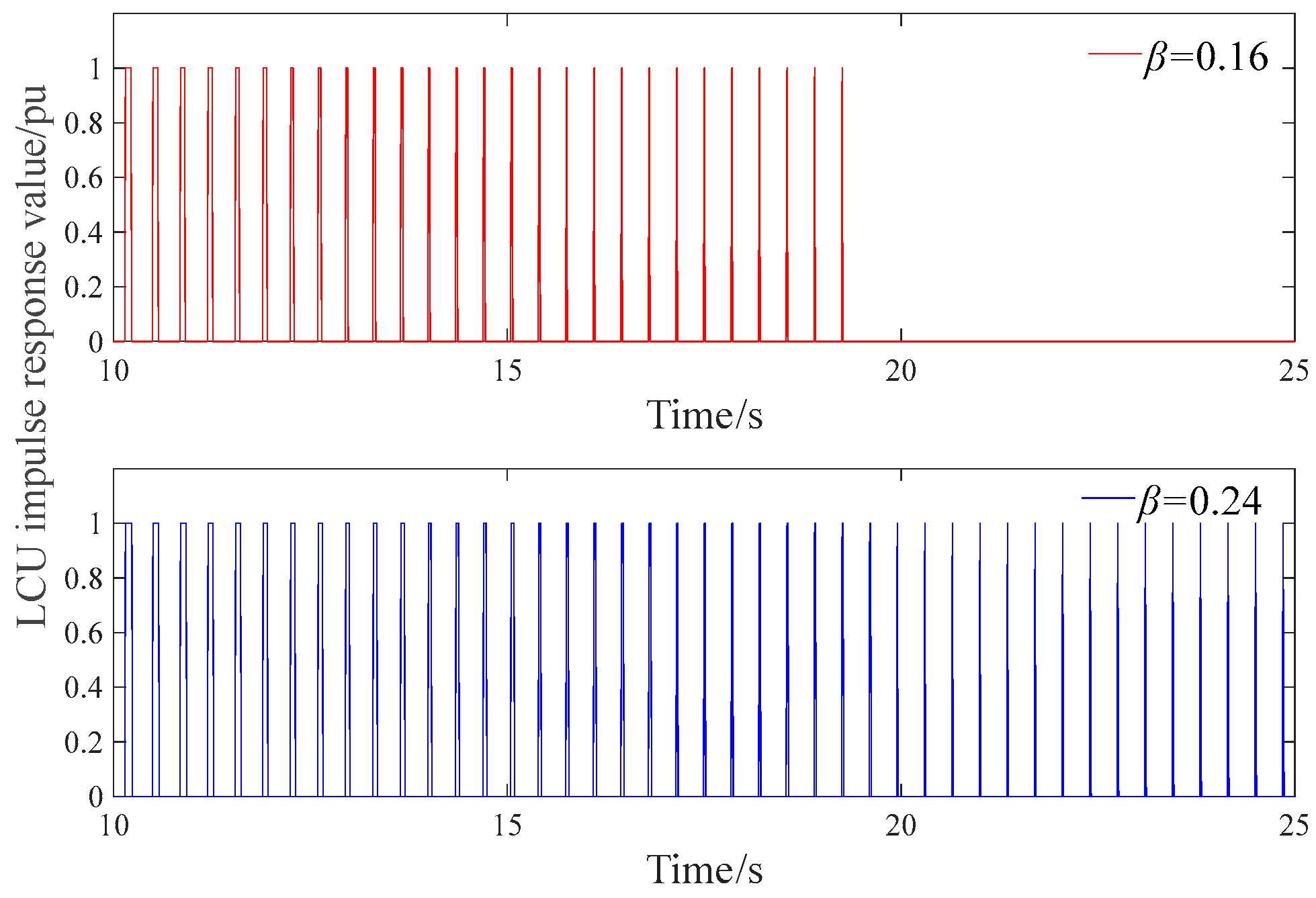
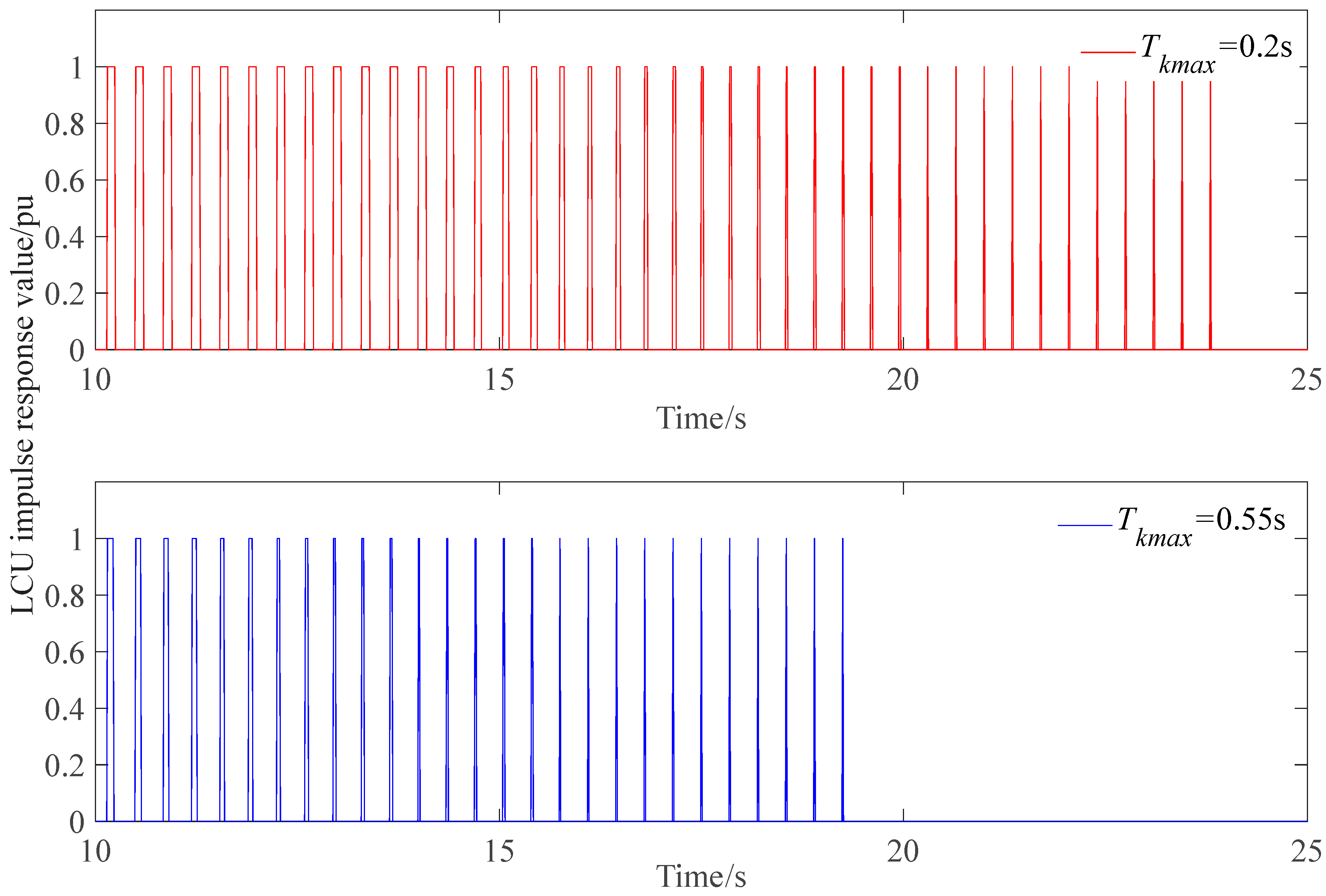
Figure 15.
Unit LCU output pulse diagram.
Figure 15.
Unit LCU output pulse diagram.
Figure 16.
Active power regulation process of the unit.
Figure 16.
Active power regulation process of the unit.
Figure 17.
Turbine guide vane adjustment process.
Figure 17.
Turbine guide vane adjustment process.
Figure 18.
Unit LCU output pulse diagram.
Figure 18.
Unit LCU output pulse diagram.
Figure 19.
Active power regulation process of the unit.
Figure 19.
Active power regulation process of the unit.
Figure 20.
Turbine guide vane adjustment process.
Figure 20.
Turbine guide vane adjustment process.
Figure 21.
Unit LCU output pulse diagram.
Figure 21.
Unit LCU output pulse diagram.
Figure 22.
Active power regulation process of the unit.
Figure 22.
Active power regulation process of the unit.
Figure 23.
Turbine guide vane adjustment process.
Figure 23.
Turbine guide vane adjustment process.
Figure 24.
Active power regulation process of the unit.
Figure 24.
Active power regulation process of the unit.
Figure 25.
Active power regulation process of the unit.
Figure 25.
Active power regulation process of the unit.
Figure 26.
Active power regulation process of the unit.
Figure 26.
Active power regulation process of the unit.
Figure 27.
Active power regulation process of the unit.
Figure 27.
Active power regulation process of the unit.
Figure 28.
Active power regulation process of the unit.
Figure 28.
Active power regulation process of the unit.
Figure 29.
Active power regulation process of the unit.
Figure 29.
Active power regulation process of the unit.
Table 1.
Advantages of this study compared to others.
Table 1.
Advantages of this study compared to others.
| Advantages | Reasons for the Advantage |
|---|
| Modeling | A comprehensive simulation model for hydroelectric units under all operating conditions, incorporating PFR and AGC, has been established to demonstrate the coupled characteristics of water–mechanical–electrical systems. |
| Research Parameters | The parameters studied include hydraulic parameters, control system parameters, and AGC system parameters. The parameters studied are comprehensive. |
| Research Model | The research model incorporates the characteristics of PFR and AGC. |
| Calculation Indicators | The calculated metrics include grid performance indicators, reflecting both responsiveness and stability. |
Table 2.
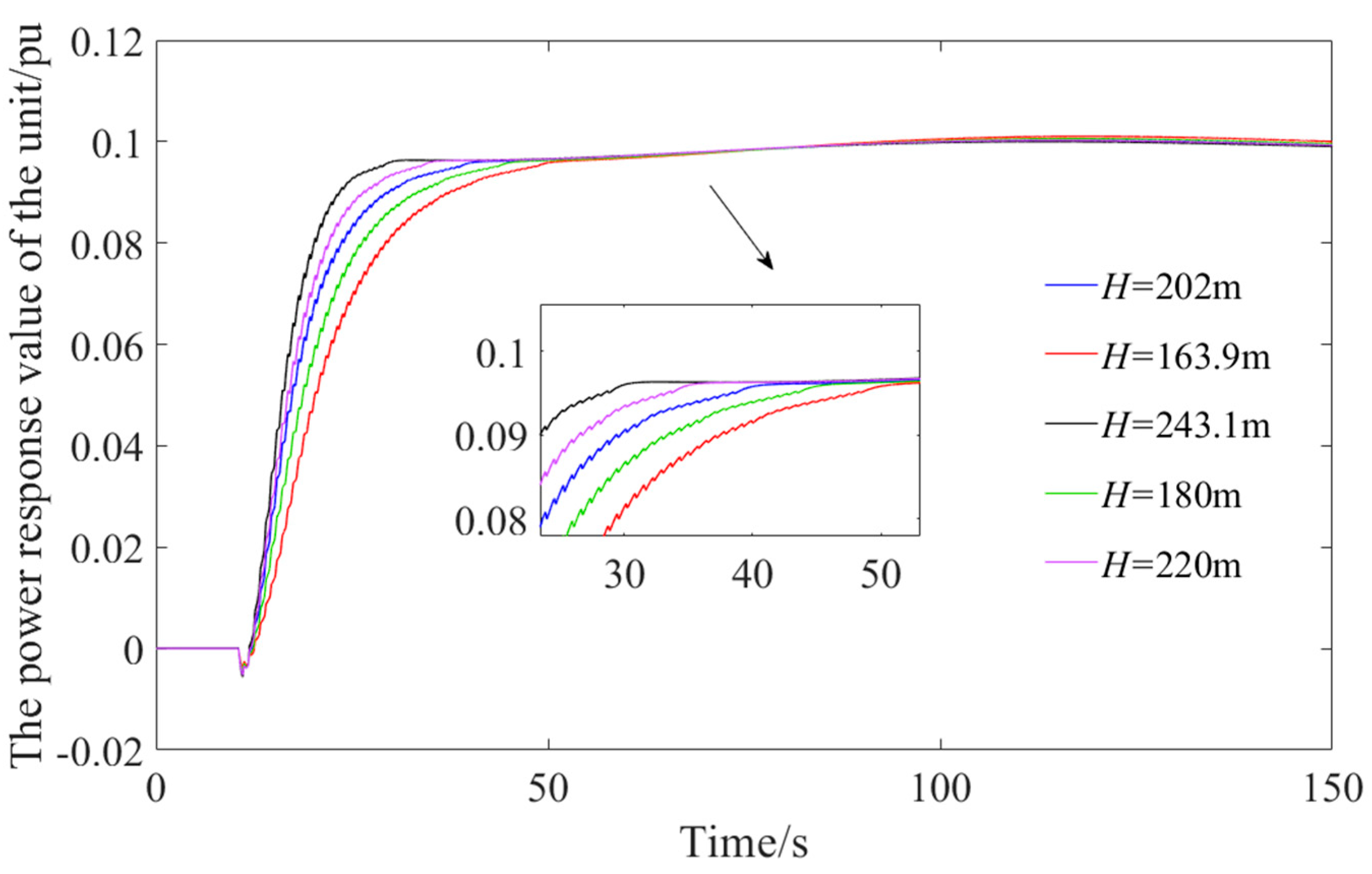
Head response process indicators for active power in hydropower stations.
Table 2.
Head response process indicators for active power in hydropower stations.
| H (m) | Δ (%) | ts (s) |
|---|
| 202 m | 0.0520 | 11.4 |
| 163.9 m | 0.2659 | 19.37 |
| 243.1 m | 0.0024 | 7.45 |
| 180 m | 0.1298 | 15.05 |
| 220 m | 0.0413 | 9.43 |
Table 3.
Fixed pulse width calculation parameters for active power response process indicators in hydropower stations.
Table 3.
Fixed pulse width calculation parameters for active power response process indicators in hydropower stations.
| β | Δ (%) | ts (s) |
|---|
| 0.16 | 0.0520 | 11.4 |
| 0.18 | 0.007 | 12.89 |
| 0.2 | - | 14.82 |
| 0.22 | - | 16.33 |
| 0.24 | - | 17.82 |
Table 4.
Pulse cycle as an indicator of active power response process for hydropower stations.
Table 4.
Pulse cycle as an indicator of active power response process for hydropower stations.
| T (s) | Δ (%) | ts (s) |
|---|
| 0.6 | - | 10.3 |
| 0.7 | 0.0520 | 10.4 |
| 0.8 | 0.2085 | 10.74 |
| 0.9 | 0.3123 | 11.47 |
Table 5.
Indicators of the active power response process of hydropower stations under maximum pulse duration limiting in different cycles.
Table 5.
Indicators of the active power response process of hydropower stations under maximum pulse duration limiting in different cycles.
| Tkmax (s) | Δ (%) | ts (s) |
|---|
| 0.2 | 0.0442 | 20.53 |
| 0.25 | 0.0471 | 17.7 |
| 0.3 | 0.0495 | 15.02 |
| 0.4 | 0.0512 | 12.83 |
| 0.55 | 0.0520 | 11.4 |
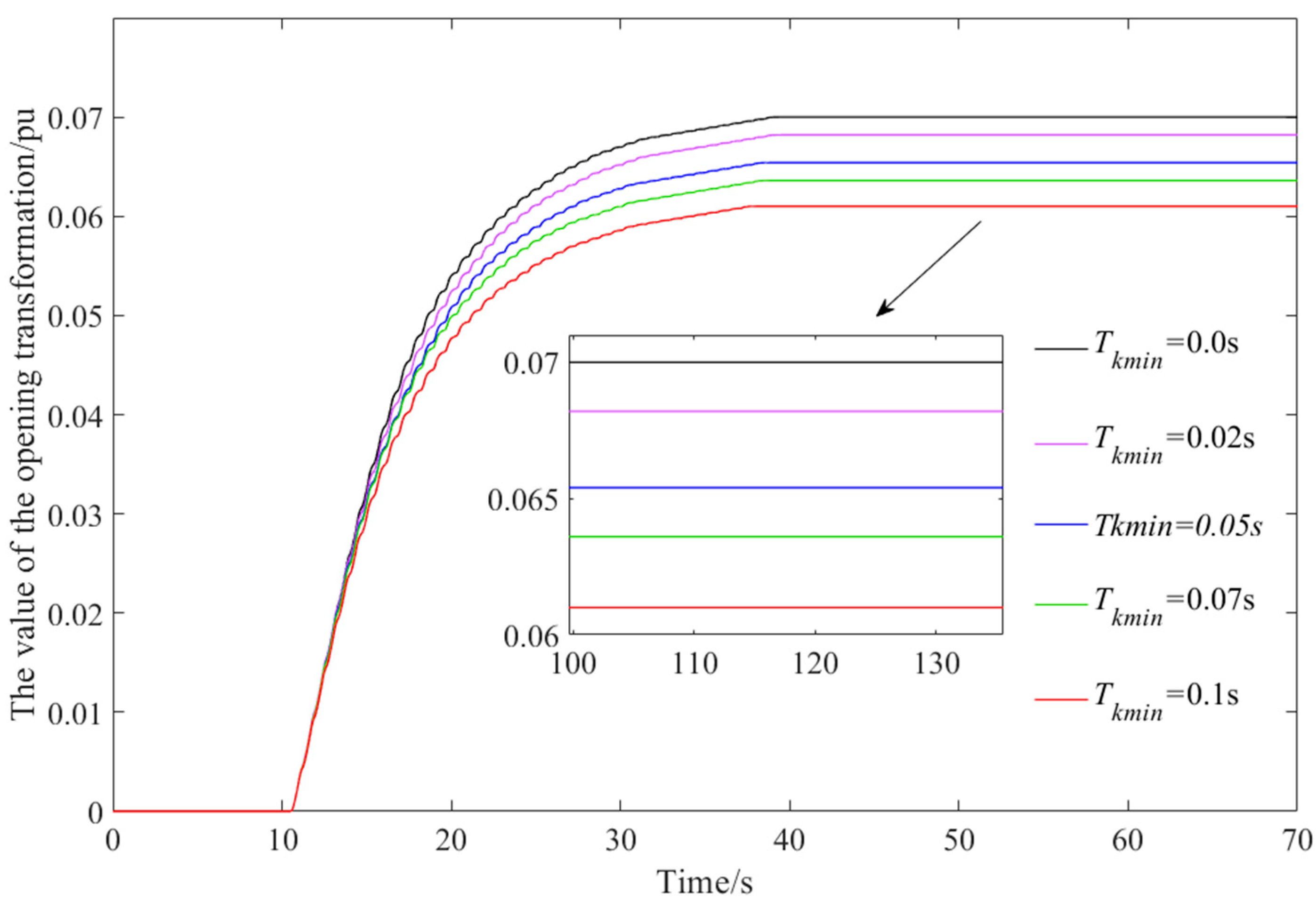
Table 6.
Indicators of active power response process of hydropower stations under minimum pulse duration limiting in different cycle.
Table 6.
Indicators of active power response process of hydropower stations under minimum pulse duration limiting in different cycle.
| Tkmin (s) | Δ (%) | ts (s) |
|---|
| 0 | 0.3094 | 11.33 |
| 0.02 | −0.1545 | 11.64 |
| 0.05 | −0.8771 | 12.29 |
| 0.07 | −1.3512 | 12.89 |
| 0.1 | −2.0272 | 14.2 |
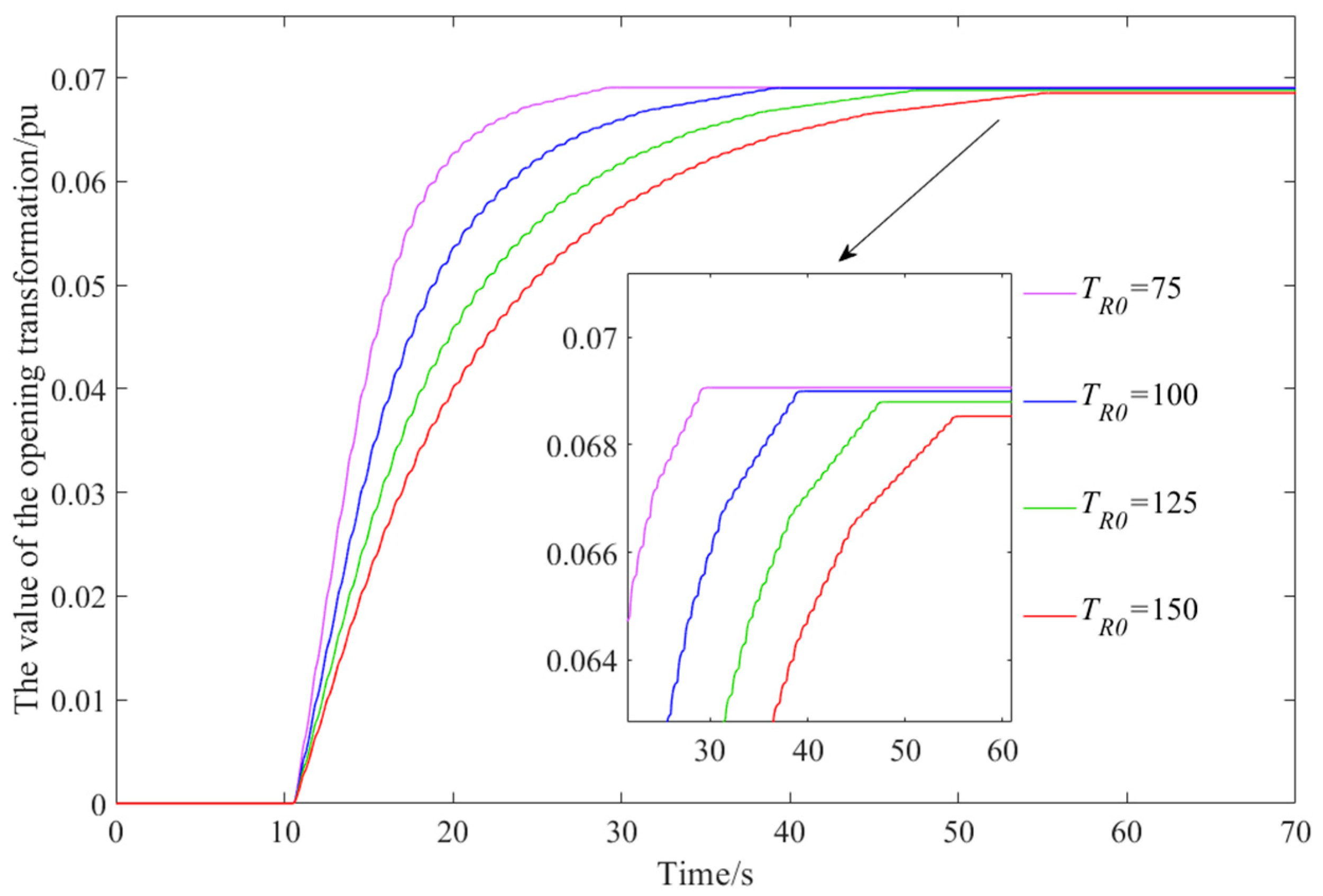
Table 7.
Indicators of active power response process of hydropower stations under different integral conversion parameters of opening degree.
Table 7.
Indicators of active power response process of hydropower stations under different integral conversion parameters of opening degree.
| Tiy (−) | Δ (%) | Ts (s) |
|---|
| 75 | 0.0739 | 8.5 |
| 100 | 0.0520 | 11.4 |
| 125 | - | 14.4 |
| 150 | - | 17.3 |
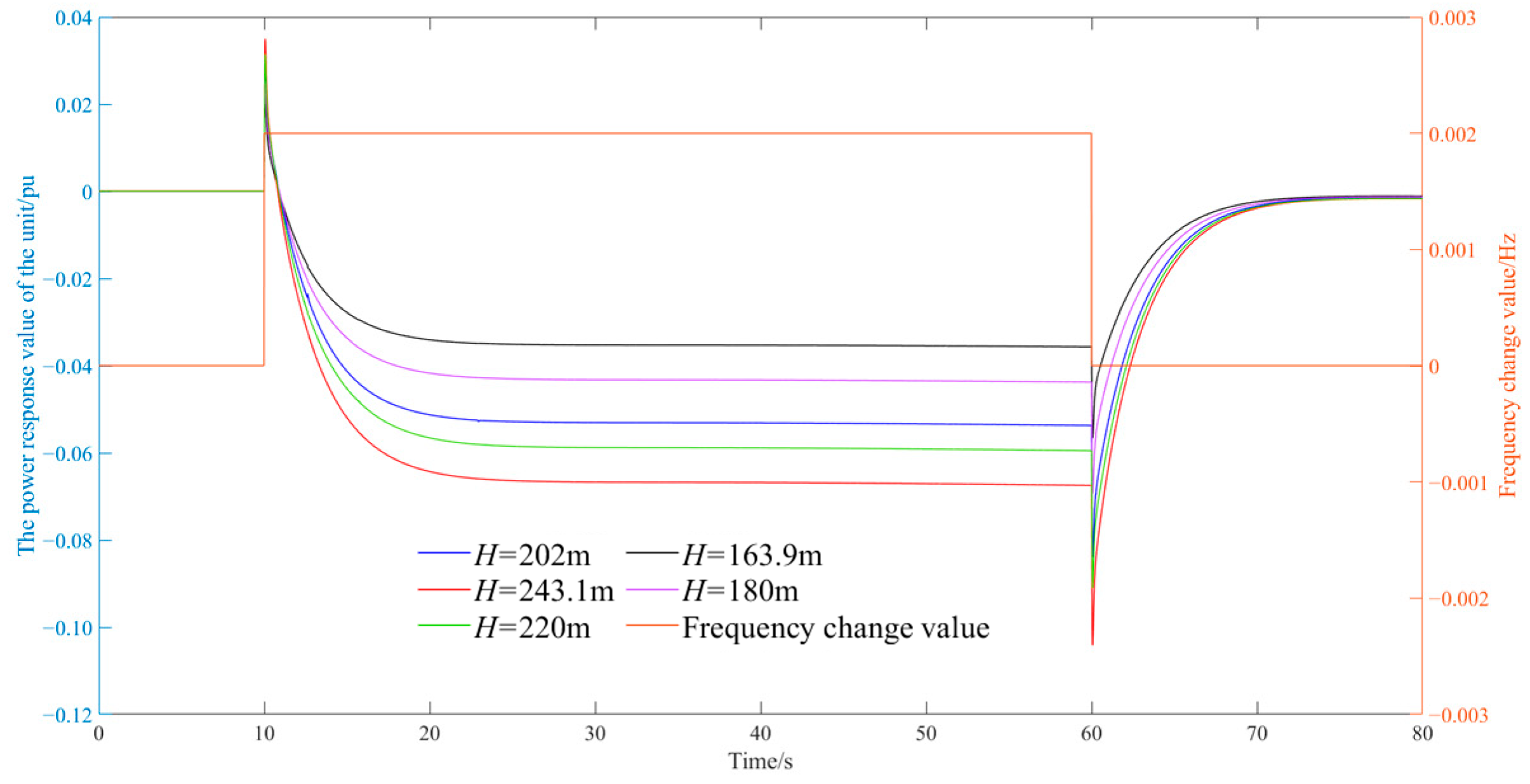
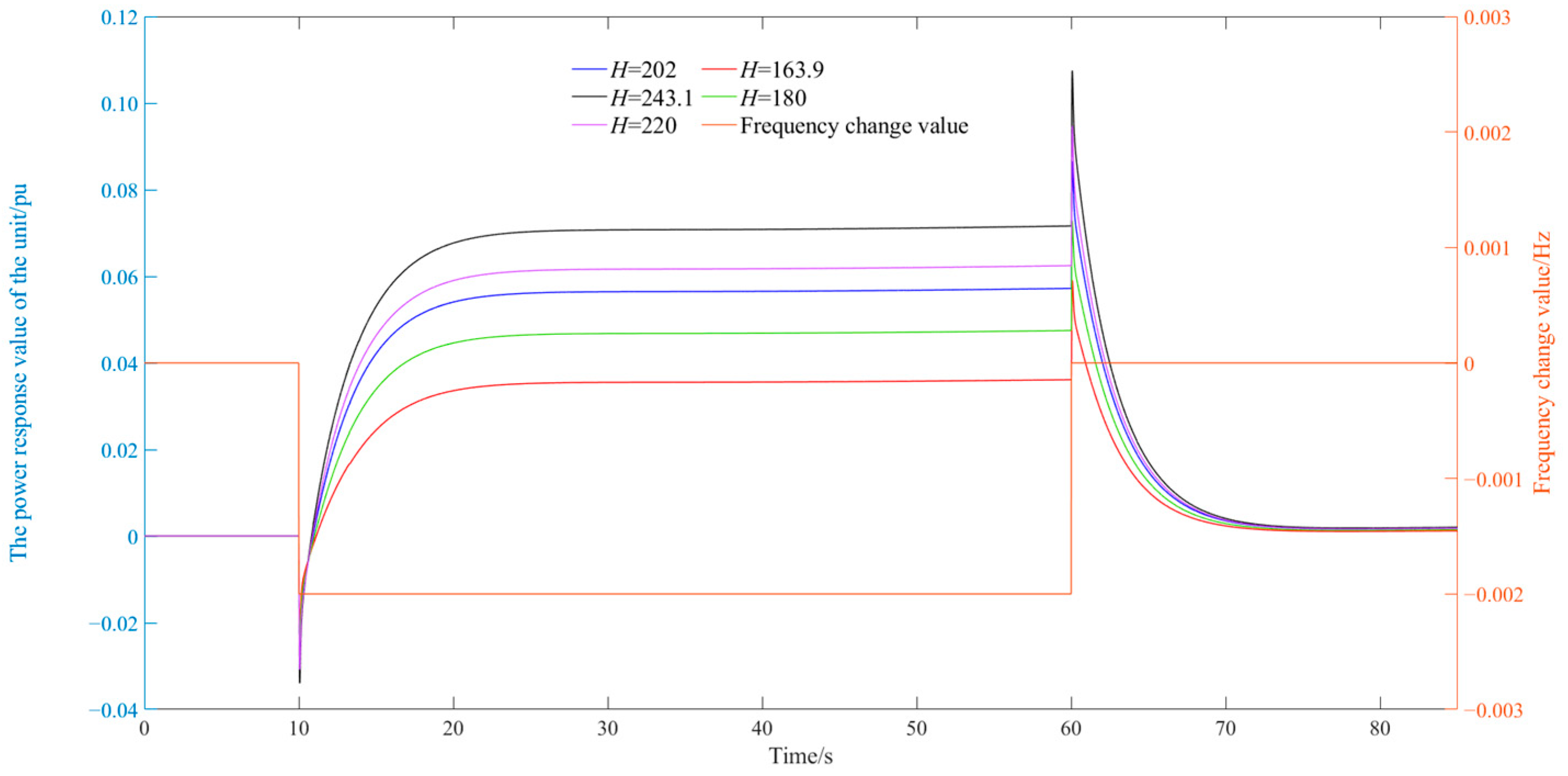
Table 8.
Frequency response process indicators of hydropower stations under different water heads.
Table 8.
Frequency response process indicators of hydropower stations under different water heads.
| Frequency Fluctuation Value | Water Head (m) | Adjustment Time (s) | Load Adjustment Range (%) |
|---|
| +0.1 Hz | 202 | 9.57 | 12.433 |
| 163.9 | 9.5 | 12.017 |
| 243.1 | 9.7 | 10.8894 |
| 180 | 9.64 | 12.6595 |
| 220 | 9.85 | 11.5239 |
| −0.1 Hz | 202 | 10.36 | 12.6573 |
| 163.9 | 11.28 | 12.3089 |
| 243.1 | 10.35 | 11.2523 |
| 180 | 10.7 | 13.278 |
| 220 | 10.35 | 11.735 |
Table 9.
Different steady-state transfer coefficients for hydropower station frequency response process indicators.
Table 9.
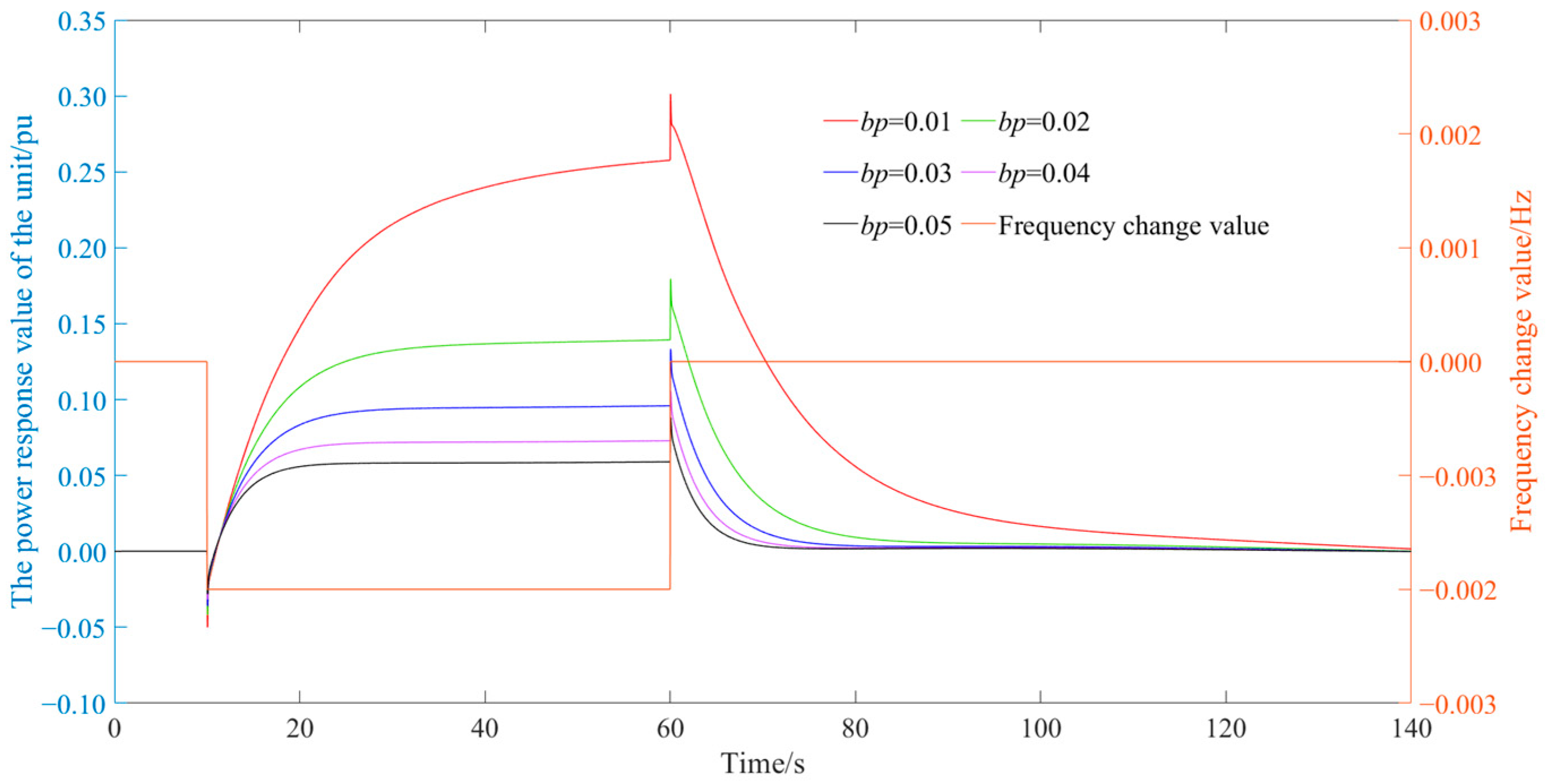
Different steady-state transfer coefficients for hydropower station frequency response process indicators.
| Frequency Fluctuation Value | bp (−) | Adjustment Time (s) | Load Adjustment Range (%) |
|---|
| +0.1 Hz | 0.01 | 31.96 | 53.9 |
| 0.02 | 18.7 | 25.33 |
| 0.03 | 13.55 | 18.28 |
| 0.04 | 11 | 14.65 |
| 0.05 | 9.57 | 12.24 |
| −0.1 Hz | 0.01 | 33.54 | 55.9901 |
| 0.02 | 20.03 | 30.76 |
| 0.03 | 14.84 | 21.215 |
| 0.04 | 11.95 | 16.1234 |
| 0.01 | 31.96 | 53.9 |
Table 10.
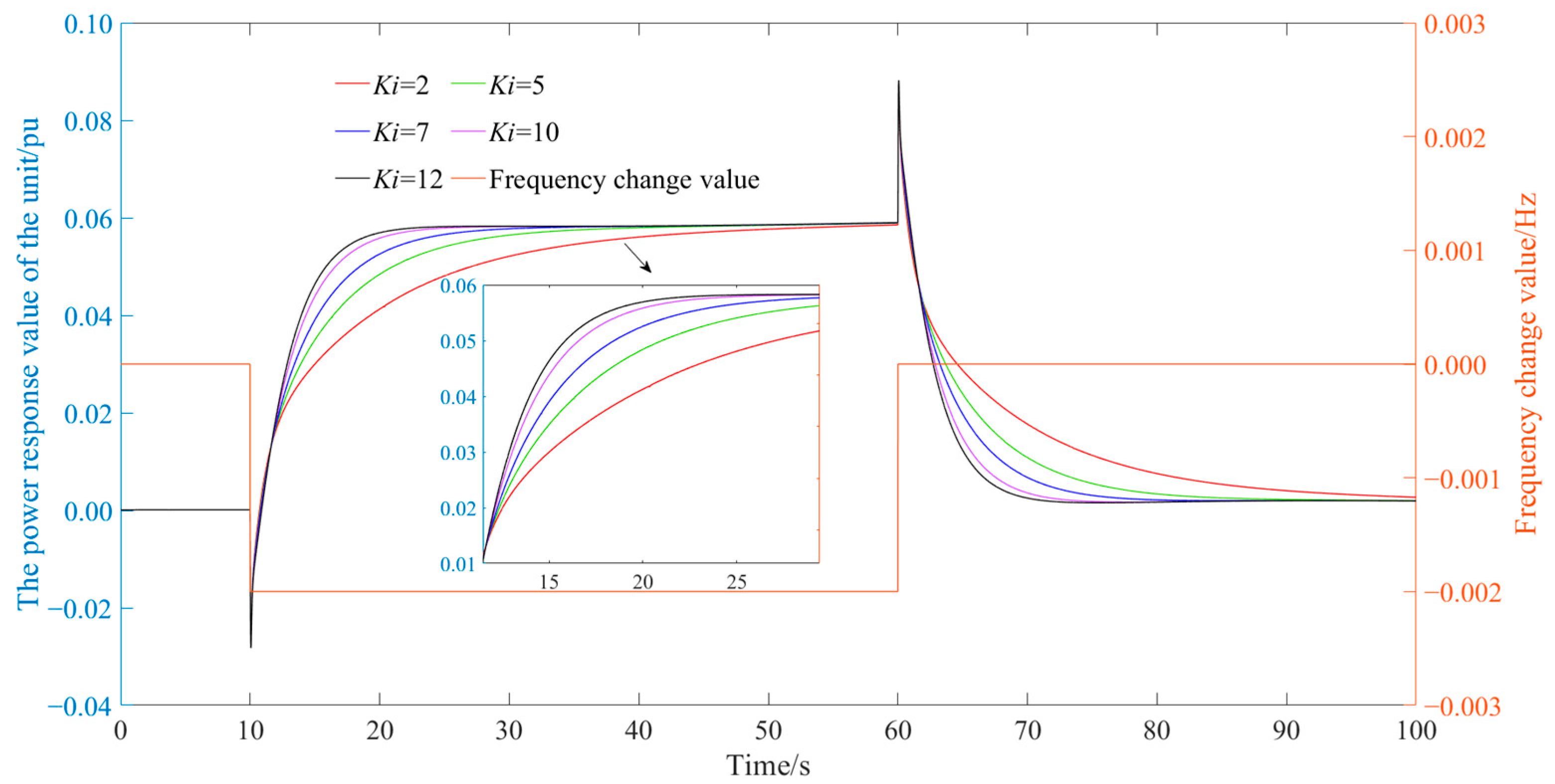
Different gain factors on the frequency response process index of hydropower stations.
Table 10.
Different gain factors on the frequency response process index of hydropower stations.
| Frequency Fluctuation Value | Ki | Adjustment Time (s) | Load Adjustment Range (%) |
|---|
| +0.1 Hz | 3 | 26.76 | 12.09 |
| 5 | 17.4 | 12.22 |
| 7 | 12.92 | 12.23 |
| 10 | 9.57 | 12.24 |
| 12 | 8.28 | 12.24 |
| −0.1 Hz | 3 | 28.32 | 12.84 |
| 5 | 18.55 | 13.02 |
| 7 | 13.81 | 13.04 |
| 10 | 10.25 | 13.05 |
| 3 | 26.76 | 12.09 |