Modeling Total Alkalinity in Aquatic Ecosystems by Decision Trees: Anticipation of pH Stability and Identification of Main Contributors
Abstract
1. Introduction
2. Materials and Methods
2.1. Sampling Campaign and Study Framework
2.2. Physicochemical Analysis Protocol
2.3. Overview of Measured Variables
2.4. Input Variable Selection for TAC Modeling
Building the Training Database
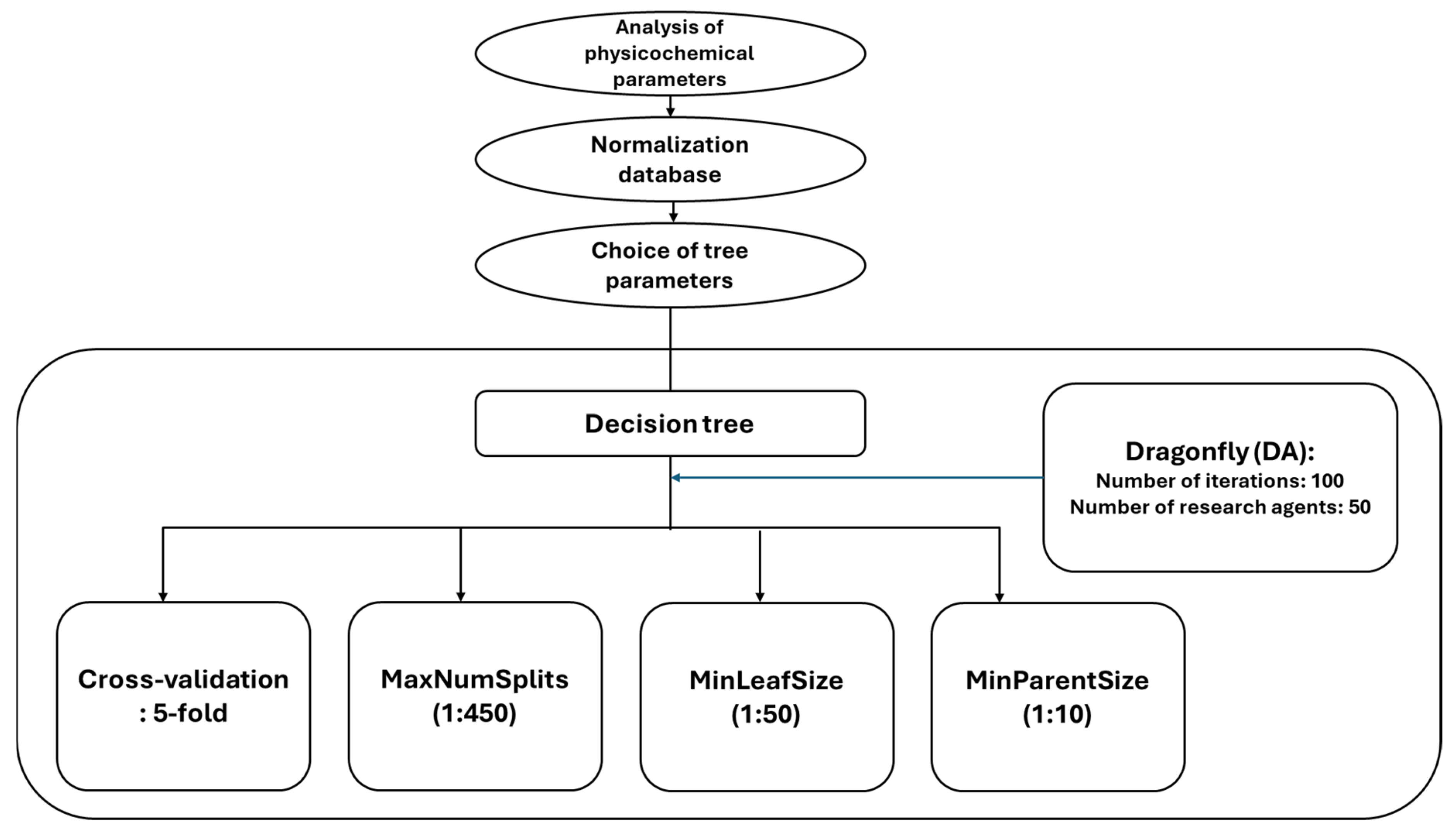
2.5. Decision Tree (DT) Method
2.5.1. Decision Tree Model Development and Validation
Data Preparation
Internal Validation
Hyperparameter Optimization
External Validation
Performance Metrics
3. Results
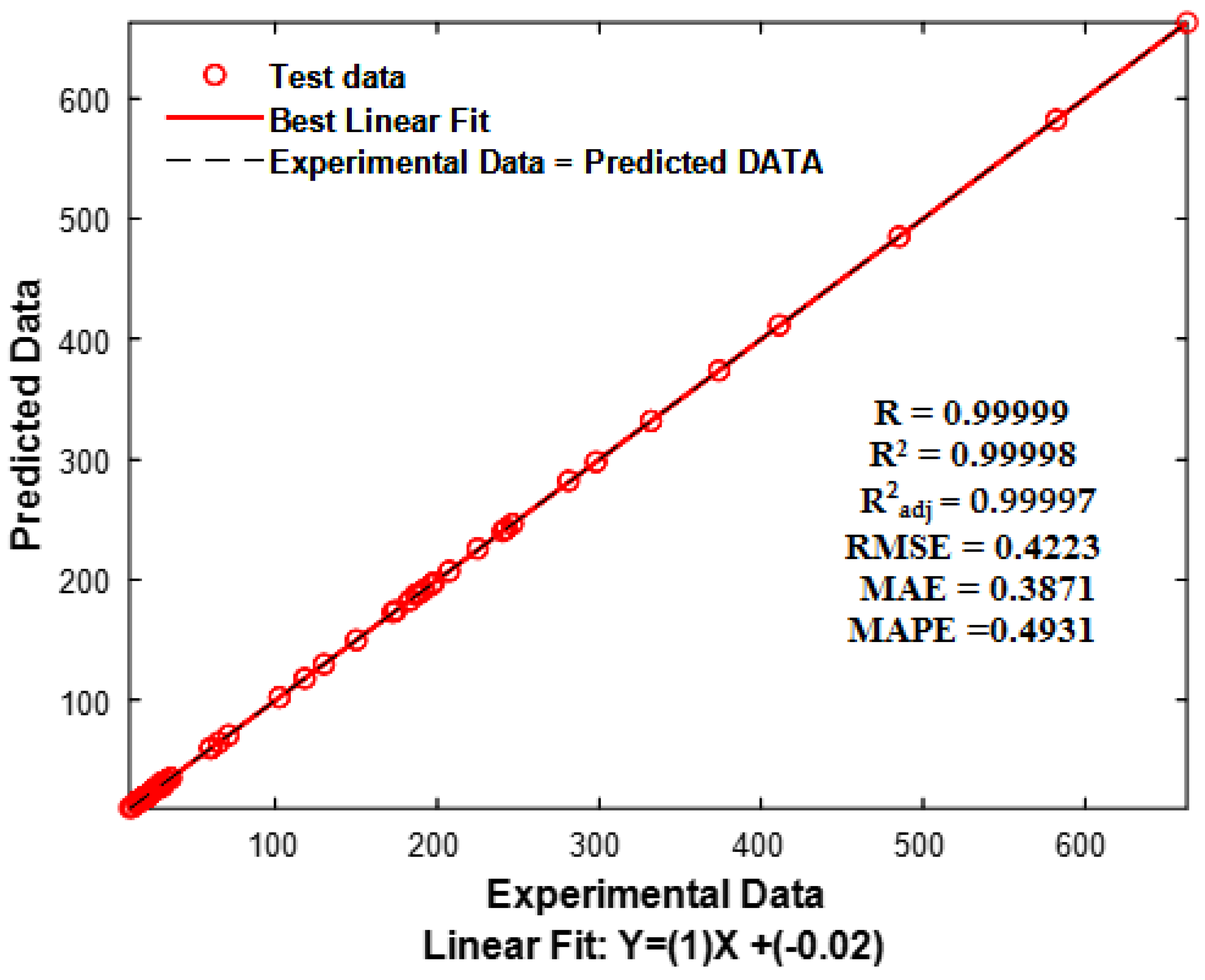
3.1. Decision Tree Modeling
3.2. External Validation
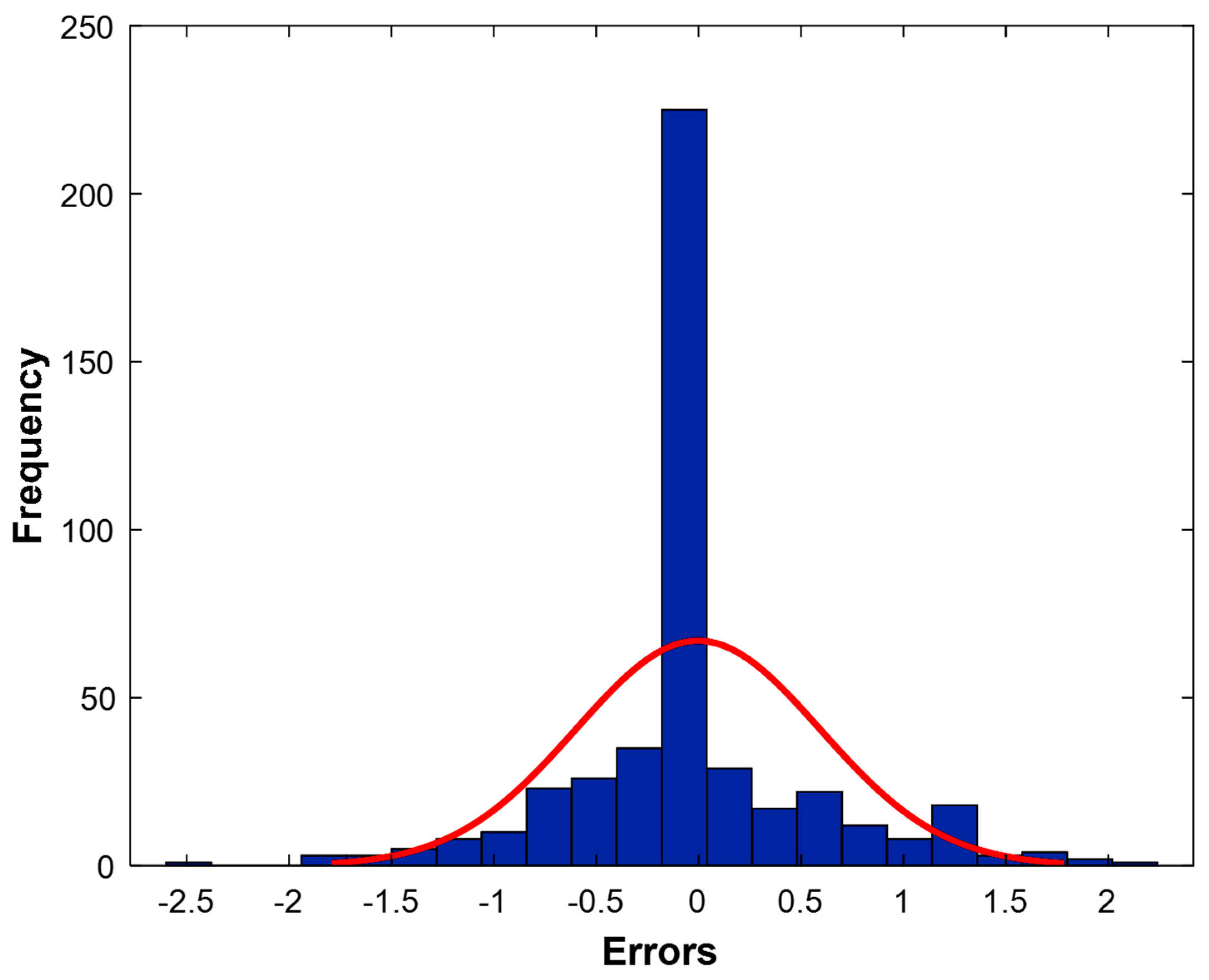
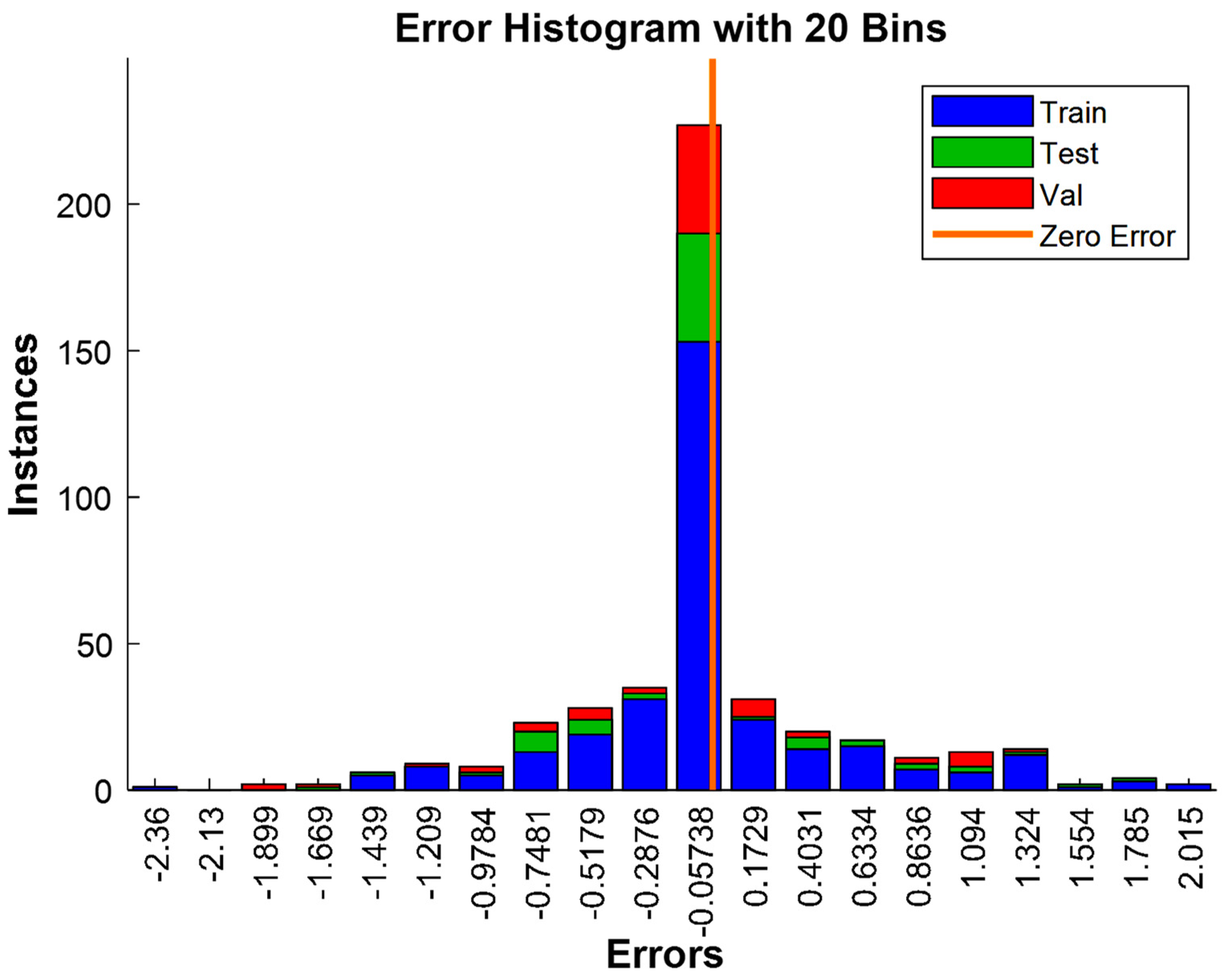
3.3. Analysis of Model Residuals
3.4. Decision Tree
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kasper, S.; Adeyemo, O.K.; Becker, T.; Scarfe, D.; Tepper, J. Aquatic Environment and Life Support Systems. In Fundamentals of Aquatic Veterinary Medicine; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2022. [Google Scholar]
- Pandey, P.K.; Pande, A. Aquatic Environment Management; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar]
- De Paiva Magalhães, D.; Da Costa Marques, M.R.; Baptista, D.F.; Buss, D.F. Metal Bioavailability and Toxicity in Freshwaters. Environ. Chem. Lett. 2015, 13, 69–87. [Google Scholar] [CrossRef]
- Elder, J.F. Metal Biogeochemistry in Surface-Water Systems: A Review of Principles and Concepts; Geological Survey (U.S.): Reston, VA, USA, 1988. [Google Scholar]
- Babaniyi, G.G.; Olagoke, O.V.; Aransiola, S.A. Extracellular Enzymatic Activity of Bacteria in Aquatic Ecosystems. In Microbiology for Cleaner Production and Environmental Sustainability; CRC Press: Boca Raton, FL, USA, 2023; pp. 277–300. [Google Scholar]
- Chu, Y.; Zhang, X.; Tang, X.; Jiang, L.; He, R. Uncovering Anaerobic Oxidation of Methane and Active Microorganisms in Landfills by Using Stable Isotope Probing. Environ. Res. 2025, 271, 121139. [Google Scholar] [CrossRef]
- Muniz, I.P. Freshwater Acidification: Its Effects on Species and Communities of Freshwater Microbes, Plants and Animals. Proc. R. Soc. Edinb. Sect. B Biol. Sci. 1990, 97, 227–254. [Google Scholar] [CrossRef]
- Tahraoui, H.; Toumi, S.; Boudoukhani, M.; Touzout, N.; Sid, A.N.E.H.; Amrane, A.; Belhadj, A.-E.; Hadjadj, M.; Laichi, Y.; Aboumustapha, M. Evaluating the Effectiveness of Coagulation–Flocculation Treatment Using Aluminum Sulfate on a Polluted Surface Water Source: A Year-Long Study. Water 2024, 16, 400. [Google Scholar] [CrossRef]
- Fraga, C.G.; Oteiza, P.I.; Galleano, M. In Vitro Measurements and Interpretation of Total Antioxidant Capacity. Biochim. Biophys. Acta (BBA)-Gen. Subj. 2014, 1840, 931–934. [Google Scholar] [CrossRef]
- Tahraoui, H.; Belhadj, A.-E.; Moula, N.; Bouranene, S.; Amrane, A. Optimisation and Prediction of the Coagulant Dose for the Elimination of Organic Micropollutants Based on Turbidity. Kemija u industriji 2021, 70, 675–691. [Google Scholar] [CrossRef]
- Jothivenkatachalam, K.; Nithya, A.; Mohan, S.C. Correlation Analysis of Drinking Water Quality in and around Perur Block of Coimbatore District, Tamil Nadu, India. Rasayan J. Chem. 2010, 3, 649–654. [Google Scholar]
- Regadío, M.; De Soto, I.S.; Rodríguez-Rastrero, M.; Ruiz, A.I.; Gismera, M.J.; Cuevas, J. Processes and Impacts of Acid Discharges on a Natural Substratum under a Landfill. Sci. Total Environ. 2013, 463, 1049–1059. [Google Scholar] [CrossRef]
- Tuck, I.D.; Pinkerton, M.H.; Tracey, D.M.; Anderson, O.F.; Chiswell, S.M. Ecosystem and Environmental Indicators for Deepwater Fisheries; Ministry for Primary Industries: Wellington, New Zealand, 2014.
- Tahraoui, H.; Belhadj, A.E.; Hamitouche, A.E. Prediction of the Bicarbonate Amount in Drinking Water in the Region of Médéa Using Artificial Neural Network Modelling. Kemija u industriji 2020, 69, 595–602. [Google Scholar] [CrossRef]
- Floegel, A.; Kim, D.-O.; Chung, S.-J.; Song, W.O.; Fernandez, M.L.; Bruno, R.S.; Koo, S.I.; Chun, O.K. Development and Validation of an Algorithm to Establish a Total Antioxidant Capacity Database of the US Diet. Int. J. Food Sci. Nutr. 2010, 61, 600–623. [Google Scholar] [CrossRef]
- Wei, C.; Zhao, T.; Cao, J.; Li, P. Water Quality Prediction Model Based on Interval Type-2 Fuzzy Neural Network with Adaptive Membership Function. Int. J. Fuzzy Syst. 2025. [Google Scholar] [CrossRef]
- Mehrotra, D. Basics of Artificial Intelligence & Machine Learning; Notion Press: Chennai, India, 2019. [Google Scholar]
- Surden, H. Machine Learning and Law: An Overview. In Research Handbook on Big Data Law; Edward Elgar Publishing: Cheltenham, UK, 2021; pp. 171–184. [Google Scholar]
- Wang, Z.; Wang, Q.; Yang, F.; Wang, C.; Yang, M.; Yu, J. How Machine Learning Boosts the Understanding of Organic Pollutant Adsorption on Carbonaceous Materials: A Comprehensive Review with Statistical Insights. Sep. Purif. Technol. 2024, 350, 127790. [Google Scholar] [CrossRef]
- Tahraoui, H.; Toumi, S.; Hassein-Bey, A.H.; Bousselma, A.; Sid, A.N.E.H.; Belhadj, A.-E.; Triki, Z.; Kebir, M.; Amrane, A.; Zhang, J. Advancing Water Quality Research: K-Nearest Neighbor Coupled with the Improved Grey Wolf Optimizer Algorithm Model Unveils New Possibilities for Dry Residue Prediction. Water 2023, 15, 2631. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R.; Taylor, J. Tree-Based Methods. In An Introduction to Statistical Learning; Springer Texts in Statistics; Springer International Publishing: Cham, Switzerland, 2023; pp. 331–366. ISBN 978-3-031-38746-3. [Google Scholar]
- Rodier, J.; Geoffray, C.; Rodi, L. L’analyse de l’eau: Eaux Naturelles, Eaux Residuaires, Eau de Mer: Chimie, Physico-Chimie, Bacteriologie, Biologie; Dunod: Paris, France, 1996. [Google Scholar]
- Zhao, Y.; Wang, H.; Song, B.; Xue, P.; Zhang, W.; Peth, S.; Hill, R.L.; Horn, R. Characterizing Uncertainty in Process-Based Hydraulic Modeling, Exemplified in a Semiarid Inner Mongolia Steppe. Geoderma 2023, 440, 116713. [Google Scholar] [CrossRef]
- Costa, V.G.; Pedreira, C.E. Recent Advances in Decision Trees: An Updated Survey. Artif. Intell. Rev. 2023, 56, 4765–4800. [Google Scholar] [CrossRef]
- Priyanka, N.A.; Kumar, D. Decision Tree Classifier: A Detailed Survey. Int. J. Inf. Decis. Sci. 2020, 12, 246. [Google Scholar] [CrossRef]
- Gupta, B.; Rawat, A.; Jain, A.; Arora, A.; Dhami, N. Analysis of Various Decision Tree Algorithms for Classification in Data Mining. Int. J. Comput. Appl. 2017, 163, 15–19. [Google Scholar] [CrossRef]
- Miller, D.W. Results of a New Classification Algorithm Combining K Nearest Neighbors and Recursive Partitioning. J. Chem. Inf. Comput. Sci. 2001, 41, 168–175. [Google Scholar] [CrossRef]
- Hsieh, W.W. Machine Learning Methods in the Environmental Sciences: Neural Networks and Kernels; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Workie, M.D.; Hailu, B.T.; Birhanu, B.; Suryabhagavan, K.V. Statistical Analysis of Earth Observing Data for Physicochemical Water Quality Parameters Estimation for Lake Beseka, Northern Main Ethiopian Rift, Ethiopia. Geol. Ecol. Landsc. 2024, 1–21. [Google Scholar] [CrossRef]
- Chelghoum, H.; Nasrallah, N.; Tahraoui, H.; Seleiman, M.F.; Bouhenna, M.M.; Belmeskine, H.; Zamouche, M.; Djema, S.; Zhang, J.; Mendil, A. Eco-Friendly Synthesis of ZnO Nanoparticles for Quinoline Dye Photodegradation and Antibacterial Applications Using Advanced Machine Learning Models. Catalysts 2024, 14, 831. [Google Scholar] [CrossRef]
- Guediri, A.; Bouguettoucha, A.; Tahraoui, H.; Chebli, D.; Zhang, J.; Amrane, A.; Khezami, L.; Assadi, A.A. The Enhanced Adsorption Capacity of Ziziphus Jujuba Stones Modified with Ortho-Phosphoric Acid for Organic Dye Removal: A Gaussian Process Regression Approach. Water 2024, 16, 1208. [Google Scholar] [CrossRef]
- Auret, L.; Aldrich, C. Interpretation of Nonlinear Relationships between Process Variables by Use of Random Forests. Miner. Eng. 2012, 35, 27–42. [Google Scholar] [CrossRef]
- Kyriazos, T.; Poga, M. Application of Machine Learning Models in Social Sciences: Managing Nonlinear Relationships. Encyclopedia 2024, 4, 1790–1805. [Google Scholar] [CrossRef]
- Yang, Y.; Morillo, I.G.; Hospedales, T.M. Deep Neural Decision Trees. arXiv 2018, arXiv:1806.06988. [Google Scholar] [CrossRef]
- Shang, Y.; Song, K.; Wen, Z.; Lai, F.; Liu, G.; Tao, H.; Yu, X. Machine Learning Reveals Distinct Aquatic Organic Matter Patterns Driven by Soil Erosion Types. Environ. Sci. Ecotechnol. 2025, 25, 100570. [Google Scholar] [CrossRef]
- Hussain, J. Deep Learning Black Box Problem. 2019. Available online: https://www.diva-portal.org/smash/record.jsf?pid=diva2%3A1353609&dswid=9433 (accessed on 25 June 2025).
- Abellán, J.; Masegosa, A.R. Bagging Decision Trees on Data Sets with Classification Noise. In Foundations of Information and Knowledge Systems; Link, S., Prade, H., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; Volume 5956, pp. 248–265. ISBN 978-3-642-11828-9. [Google Scholar]
- Fritz, M. Decision Tree Classification with Missing Values. Ph.D. Thesis, Technische Universität Wien, Vienna, Austria, 2023. [Google Scholar]
- García, S.; Luengo, J.; Herrera, F. Data Preprocessing in Data Mining; Intelligent Systems Reference Library; Springer International Publishing: Cham, Switzerland, 2015; Volume 72, ISBN 978-3-319-10246-7. [Google Scholar]
- Boorman, D.B.; Hollis, J.M.; Lilly, A. Hydrology of Soil Types: A Hydrologically-Based Classification of the Soils of United Kingdom; Institute of Hydrology: Roorkee, India, 1995. [Google Scholar]
- Pan, W.; Chen, J.; Lv, B.; Peng, L. Lightweight Marine Biodetection Model Based on Improved YOLOv10. Alex. Eng. J. 2025, 119, 379–390. [Google Scholar] [CrossRef]
- Abdelmonaim, M.; Radouane, E.M.; Abdelkader, C.; Mourad, D.; Youssef, O.; Abderrazzaq, B.; Mhamed, K.; Taouraout, A. Evaluating the Quality of Groundwater in the Zagora Region, Southeast Morocco, Using GIS and the Water Quality Index (WQI). Geol. Ecol. Landsc. 2024, 1–17. [Google Scholar] [CrossRef]
- Tahraoui, H.; Belhadj, A.-E. Optimisation de l’élimination Des Micropolluants Organiques. Ph.D. Thesis, Université de Lille, Lille, France, 2021. [Google Scholar]
- Tahraoui, H.; Belhadj, A.-E.; Hamitouche, A.; Bouhedda, M.; Amrane, A. Predicting the Concentration of Sulfate (SO42−) in Drinking Water Using Artificial Neural Networks: A Case Study: Médéa-Algeria. Desalination Water Treat. 2021, 217, 181–194. [Google Scholar] [CrossRef]
- Nedjhioui, M.; Nasrallah, N.; Kebir, M.; Tahraoui, H.; Bouallouche, R.; Assadi, A.A.; Amrane, A.; Jaouadi, B.; Zhang, J.; Mouni, L. Designing an efficient surfactant–polymer–oil–electrolyte system: A multi-objective optimization study. Processes 2023, 11, 1314. [Google Scholar] [CrossRef]
- Li, F.; Lu, H.; Wang, G.; Qiu, J. Long-Term Capturability of Atmospheric Water on a Global Scale. Water Resour. Res. 2024, 60, e2023WR034757. [Google Scholar] [CrossRef]
- Pang, Q.; Zhao, G.; Wang, D.; Zhu, X.; Xie, L.; Zuo, D.; Wang, L.; Tian, L.; Peng, F.; Xu, B. Water Periods Impact the Structure and Metabolic Potential of the Nitrogen-Cycling Microbial Communities in Rivers of Arid and Semi-Arid Regions. Water Res. 2024, 267, 122472. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Li, J.; An, P.; Yan, Z.; Xu, Y.; Pu, S. Enhanced Delivery of Remedial Reagents in Low-Permeability Aquifers through Coupling with Groundwater Circulation Well. J. Hydrol. 2023, 618, 129260. [Google Scholar] [CrossRef]
- Tong, H. Threshold Models in Non-Linear Time Series Analysis; Springer Science & Business Media: Heidelberg, Germany, 2012; Volume 21. [Google Scholar]
- Islam, M.S.; Majumder, S. Alkalinity and Hardness of Natural Waters in Chittagong City of Bangladesh. Int. J. Sci. Bus. 2020, 4, 137–150. [Google Scholar]
- Müller, B.; Meyer, J.S.; Gächter, R. Alkalinity Regulation in Calcium Carbonate-Buffered Lakes: Alkalinity Regulation in Calcium Carbonate-Buffered Lakes. Limnol. Oceanogr. 2016, 61, 341–352. [Google Scholar] [CrossRef]
- Casado, Á.; Ramos, P.; Rodríguez, J.; Moreno, N.; Gil, P. Types and Characteristics of Drinking Water for Hydration in the Elderly. Crit. Rev. Food Sci. Nutr. 2015, 55, 1633–1641. [Google Scholar] [CrossRef]
- Menon, S.V.; Kumar, A.; Middha, S.K.; Paital, B.; Mathur, S.; Johnson, R.; Kademan, A.; Usha, T.; Hemavathi, K.N.; Dayal, S. Water Physicochemical Factors and Oxidative Stress Physiology in Fish, a Review. Front. Environ. Sci. 2023, 11, 1240813. [Google Scholar] [CrossRef]
- Legarra, M.; Blitz, A.; Czégény, Z.; Antal, M.J. Aqueous Potassium Bicarbonate/Carbonate Ionic Equilibria at Elevated Pressures and Temperatures. Ind. Eng. Chem. Res. 2013, 52, 13241–13251. [Google Scholar] [CrossRef]
- Corwin, D.L.; Yemoto, K. Salinity: Electrical Conductivity and Total Dissolved Solids. Soil Sci. Soc. Am. J. 2020, 84, 1442–1461. [Google Scholar] [CrossRef]
- Atanacković, N.; Dragišić, V.; Stojković, J.; Papić, P.; Živanović, V. Hydrochemical Characteristics of Mine Waters from Abandoned Mining Sites in Serbia and Their Impact on Surface Water Quality. Environ. Sci. Pollut. Res. 2013, 20, 7615–7626. [Google Scholar] [CrossRef]
- Laaraj, M.; Benaabidate, L.; Mesnage, V.; Lahmidi, I. Assessment and Modeling of Surface Water Quality for Drinking and Irrigation Purposes Using Water Quality Indices and GIS Techniques in the Inaouene Watershed, Morocco. Model. Earth Syst. Environ. 2024, 10, 2349–2374. [Google Scholar] [CrossRef]
- Bogart, S.J.; Woodman, S.; Steinkey, D.; Meays, C.; Pyle, G.G. Rapid Changes in Water Hardness and Alkalinity: Calcite Formation Is Lethal to Daphnia Magna. Sci. Total Environ. 2016, 559, 182–191. [Google Scholar] [CrossRef]
- Sengupta, P. Potential Health Impacts of Hard Water. Int. J. Prev. Med. 2013, 4, 866. [Google Scholar]
- Abbasi, T.; Abbasi, S.A. Water Quality Indices; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Guo, T.; Yue, Q.; Hou, Y.; Chen, Y.; Yu, D.; Yang, G.; Yu, C.; Zeng, Y.; Feng, Y.; Pu, S. Unveiling the Overlooked Silent Threat: High-Throughput Suspect Screening of Antibiotics and Multidimensional Heterogeneity in Aquatic Ecosystems of Megacity. J. Hazard. Mater. 2025, 493, 138193. [Google Scholar] [CrossRef]
- Randive, P.; Bhagat, M.S.; Bhorkar, M.P.; Bhagat, R.M.; Vinchurkar, S.M.; Shelare, S.; Sharma, S.; Beemkumar, N.; Hemalatha, S.; Kumar, P. Adaptive Optimization of Natural Coagulants Using Hybrid Machine Learning Approach for Sustainable Water Treatment. Sci. Rep. 2025, 15, 16096. [Google Scholar] [CrossRef]
- Blockeel, H.; Devos, L.; Frénay, B.; Nanfack, G.; Nijssen, S. Decision Trees: From Efficient Prediction to Responsible AI. Front. Artif. Intell. 2023, 6, 1124553. [Google Scholar] [CrossRef] [PubMed]
- Haasnoot, M. Anticipating Change: Sustainable Water Policy Pathways for an Uncertain Future. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2013. [Google Scholar]
- Zegaar, A. Classification of Irrigation Water Based on Machine Learning Approach. Ph.D. Thesis, University of Biskra, Biskra, Algeria, 2025. [Google Scholar]
- Santos, H.S.; Nguyen, H.; Venâncio, F.; Ramteke, D.; Zevenhoven, R.; Kinnunen, P. Mechanisms of Mg Carbonates Precipitation and Implications for CO2 Capture and Utilization/Storage. Inorg. Chem. Front. 2023, 10, 2507–2546. [Google Scholar] [CrossRef]
- Thakur, A.; Kumar, A. Electrochemistry Basics and Theory of Scaling in Various Electrolytes: Effect of pH and Other Parameters. In Industrial Scale Inhibition; Yaagoob, I.Y., Verma, C., Eds.; Wiley: Hoboken, NJ, USA, 2024; pp. 36–71. ISBN 978-1-394-19117-8. [Google Scholar]
- Pang, H.; Ben, Y.; Cao, Y.; Qu, S.; Hu, C. Time Series-Based Machine Learning for Forecasting Multivariate Water Quality in Full-Scale Drinking Water Treatment with Various Reagent Dosages. Water Res. 2025, 268, 122777. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.F.; Pan, M.; Beck, H.; Coccia, G.; Serrat-Capdevila, A.; Verbist, K. Satellite Remote Sensing for Water Resources Management: Potential for Supporting Sustainable Development in Data-Poor Regions. Water Resour. Res. 2018, 54, 9724–9758. [Google Scholar] [CrossRef]
- Krivtsov, V. Investigations of Indirect Relationships in Ecology and Environmental Sciences: A Review and the Implications for Comparative Theoretical Ecosystem Analysis. Ecol. Model. 2004, 174, 37–54. [Google Scholar] [CrossRef]
- Harmel, R.D.; Chaubey, I.; Ale, S.; Nejadhashemi, A.P.; Irmak, S.; DeJonge, K.C.; Evett, S.R.; Barnes, E.M.; Catley-Carlson, M.; Hunt, S. Perspectives on Global Water Security. Trans. ASABE 2020, 63, 69–80. [Google Scholar] [CrossRef]




| Variables | Symbol | Unit | Min | Mean | Max | STD |
|---|---|---|---|---|---|---|
| Inputs | ||||||
| Electrical conductivity (Cond) | X1 | µS/cm | 223 | 1263.98 | 3570 | 754.59 |
| Turbidity | X2 | NTU | 0.10 | 7.87 | 1024 | 58.57 |
| pH | X3 | - | 2.10 | 9.62 | 797 | 37.07 |
| Total hardness (TH) | X4 | °F | 8.13 | 53.42 | 160 | 24.27 |
| Calcium (Ca2+) | X5 | mg/L | 16.03 | 121.87 | 360.72 | 47.40 |
| Magnesium (Mg2+) | X6 | mg/L | 0 | 55.20 | 218.70 | 36.91 |
| Bicarbonates (HCO3−) | X7 | mg/L | 6.74 | 200.11 | 495.20 | 117.01 |
| Chlorides (Cl−) | X8 | mg/L | 10.50 | 150.76 | 609.39 | 125.91 |
| Nitrites (NO2−) | X9 | mg/L | 0 | 0.01 | 0.50 | 0.07 |
| Ammonium (NH4+) | X10 | mg/L | 0 | 0.02 | 1.05 | 0.14 |
| Nitrates (NO3−) | X11 | mg/L | 0 | 8.13 | 195.09 | 15.89 |
| Phosphates (PO43−) | X12 | mg/L | 0 | 1.28 | 288 | 19.09 |
| Sulfates (SO42−) | X13 | mg/L | 10.55 | 342.25 | 1457 | 287.37 |
| Sodium (Na+) | X14 | mg/L | 0 | 122.05 | 460 | 121.67 |
| Potassium (K+) | X15 | mg/L | 0.005 | 6.92 | 805 | 37.92 |
| Manganese (Mn2+) | X16 | mg/L | 0 | 0.007 | 0.21 | 0.02 |
| Iron (Fe3+) | X17 | mg/L | 0 | 0.013 | 0.53 | 0.03 |
| Aluminum (Al+) | X18 | mg/L | 0 | 0.005 | 0.90 | 0.04 |
| Total dissolved solids (TDS) | X19 | mg/L | 219.78 | 1036.23 | 2895.74 | 586.87 |
| Organic matter (OM) | X20 | mg/L | 0 | 3.26 | 29.20 | 3.86 |
| Output | ||||||
| Total alkalimetric titre (TAC) | Y1 | °F | 6.50 | 117.71 | 663 | 133.39 |
| DA Number of Iterations: 100 Number of Research Agents: 50 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Min Leaf Size | Surrogate | Min Parent Size | Max Number Splits | Number of Node | R/R2/R2adj | RMSE/MAE/MAPE | ||||
| Train | VAL | ALL | Train | VAL | ALL | |||||
| 1 | ALL | 2 | 450 | 427 | 0.99999 0.99998 0.99997 | 0.99999 0.99998 0.99997 | 0.99999 0.99998 0.99997 | 0.3854 0.3439 0.4392 | 0.4159 0.3794 0.4731 | 0.3957 0.3572 0.4531 |
| R | R2 | R2adj | RMSE | MAE | MAPE |
|---|---|---|---|---|---|
| 0.99999 | 0.99998 | 0.99997 | 0.4223 | 0.3871 | 0.4931 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tahraoui, H.; Bouallouche, R.; Madi, K.; Benkouachi, O.R.; Boudraa, R.; Belkacemi, H.; Lekmine, S.; Moussa, H.; Touzout, N.; Ola, M.S.; et al. Modeling Total Alkalinity in Aquatic Ecosystems by Decision Trees: Anticipation of pH Stability and Identification of Main Contributors. Water 2025, 17, 2939. https://doi.org/10.3390/w17202939
Tahraoui H, Bouallouche R, Madi K, Benkouachi OR, Boudraa R, Belkacemi H, Lekmine S, Moussa H, Touzout N, Ola MS, et al. Modeling Total Alkalinity in Aquatic Ecosystems by Decision Trees: Anticipation of pH Stability and Identification of Main Contributors. Water. 2025; 17(20):2939. https://doi.org/10.3390/w17202939
Chicago/Turabian StyleTahraoui, Hichem, Rachida Bouallouche, Kamilia Madi, Oumnia Rayane Benkouachi, Reguia Boudraa, Hadjar Belkacemi, Sabrina Lekmine, Hamza Moussa, Nabil Touzout, Mohammad Shamsul Ola, and et al. 2025. "Modeling Total Alkalinity in Aquatic Ecosystems by Decision Trees: Anticipation of pH Stability and Identification of Main Contributors" Water 17, no. 20: 2939. https://doi.org/10.3390/w17202939
APA StyleTahraoui, H., Bouallouche, R., Madi, K., Benkouachi, O. R., Boudraa, R., Belkacemi, H., Lekmine, S., Moussa, H., Touzout, N., Ola, M. S., Triki, Z., Zamouche, M., Kebir, M., Nasrallah, N., Assadi, A. A., Benguerba, Y., Zhang, J., & Amrane, A. (2025). Modeling Total Alkalinity in Aquatic Ecosystems by Decision Trees: Anticipation of pH Stability and Identification of Main Contributors. Water, 17(20), 2939. https://doi.org/10.3390/w17202939












