A Machine Learning Approach to Predicting the Turbidity from Filters in a Water Treatment Plant
Abstract
1. Introduction
2. Materials and Methods
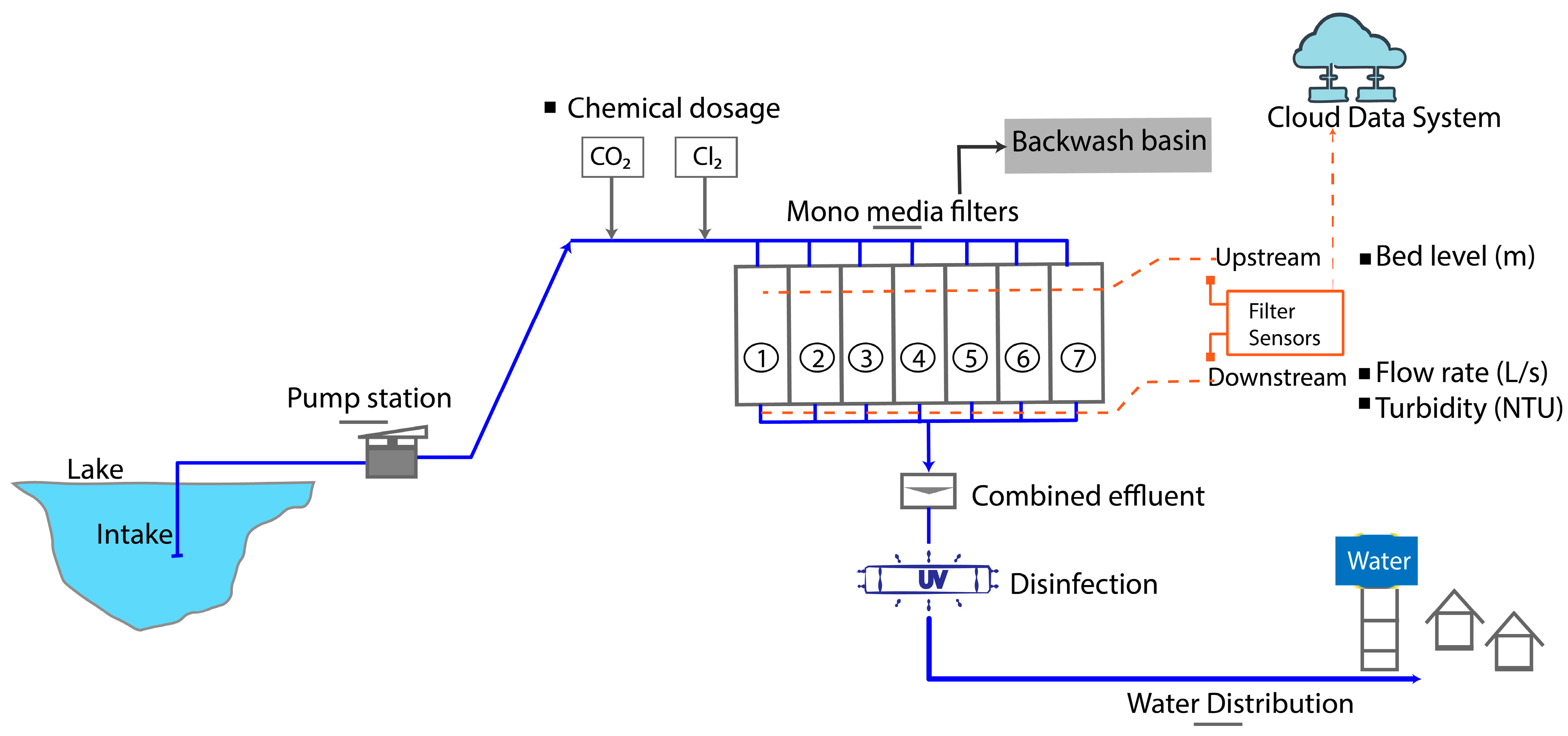
2.1. Overview of Drinking Water Treatment Plant
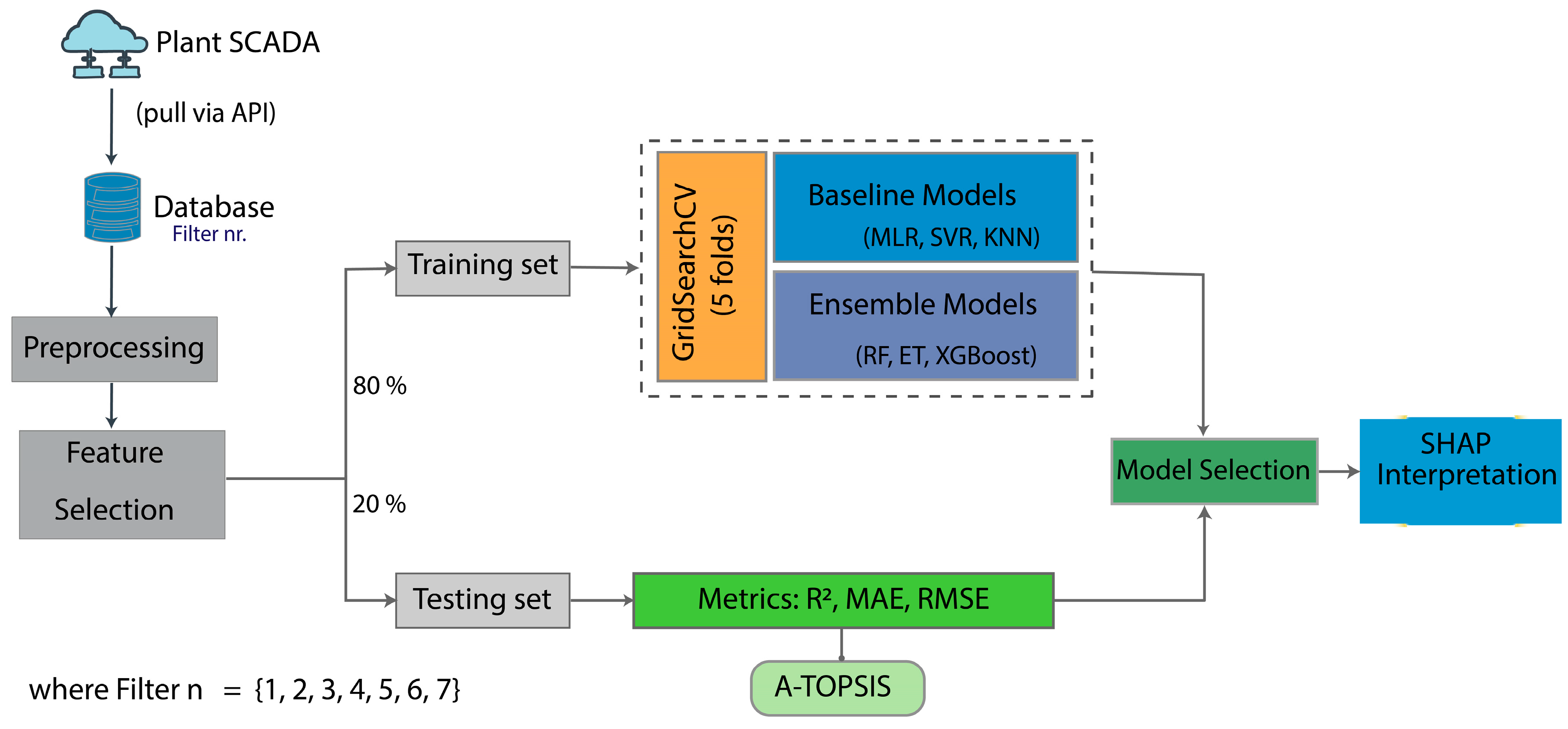
2.2. Conceptual Framework of the Study
2.3. Data Collection, Structuring and Descriptive Analysis
2.4. Machine Learning Models Development
2.4.1. Data Preprocessing and Feature Selection
2.4.2. Model Families and Evaluation
Baseline Models
Ensemble Models
2.5. Model Training, Cross Validation and Hyperparameter Tuning
2.6. Model Evaluation
2.7. TreeSHAP for ML Model Explainability
3. Results and Discussion
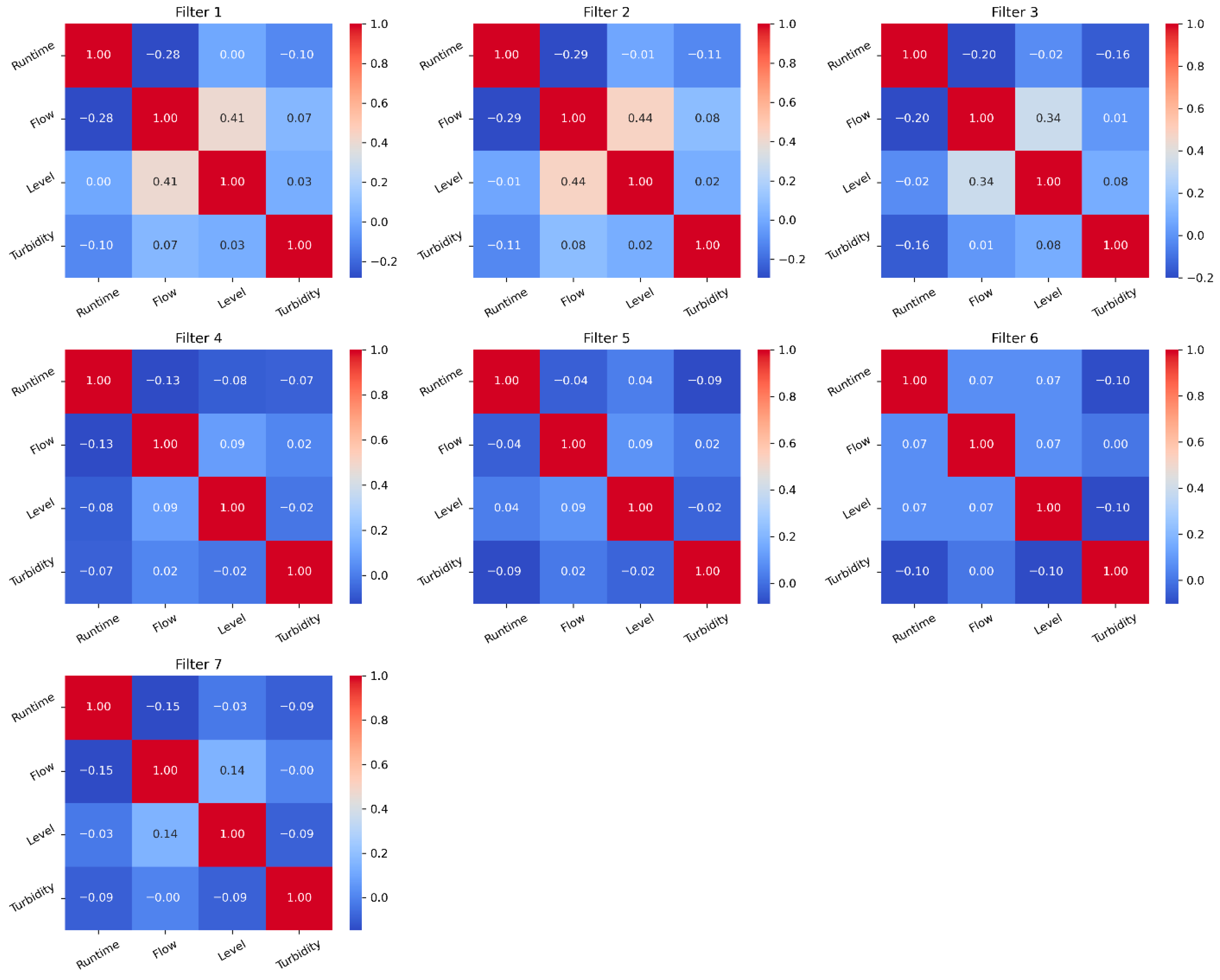
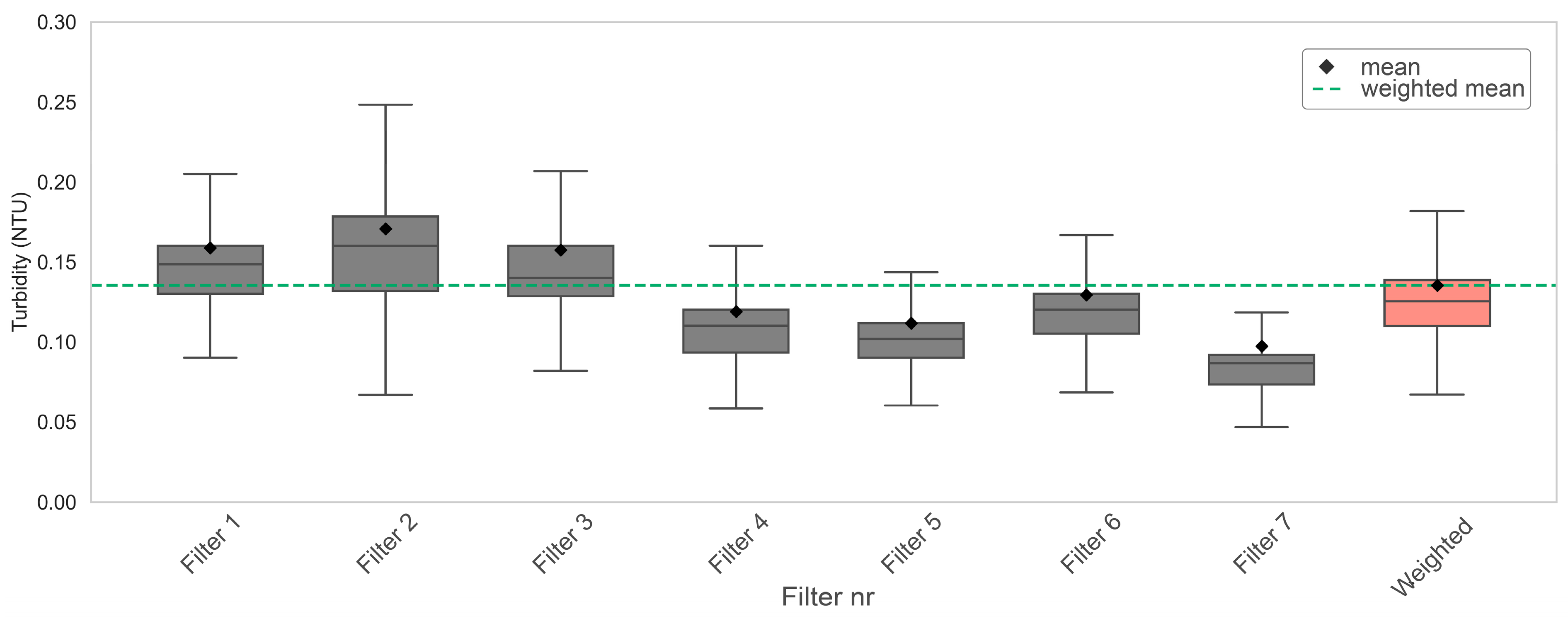
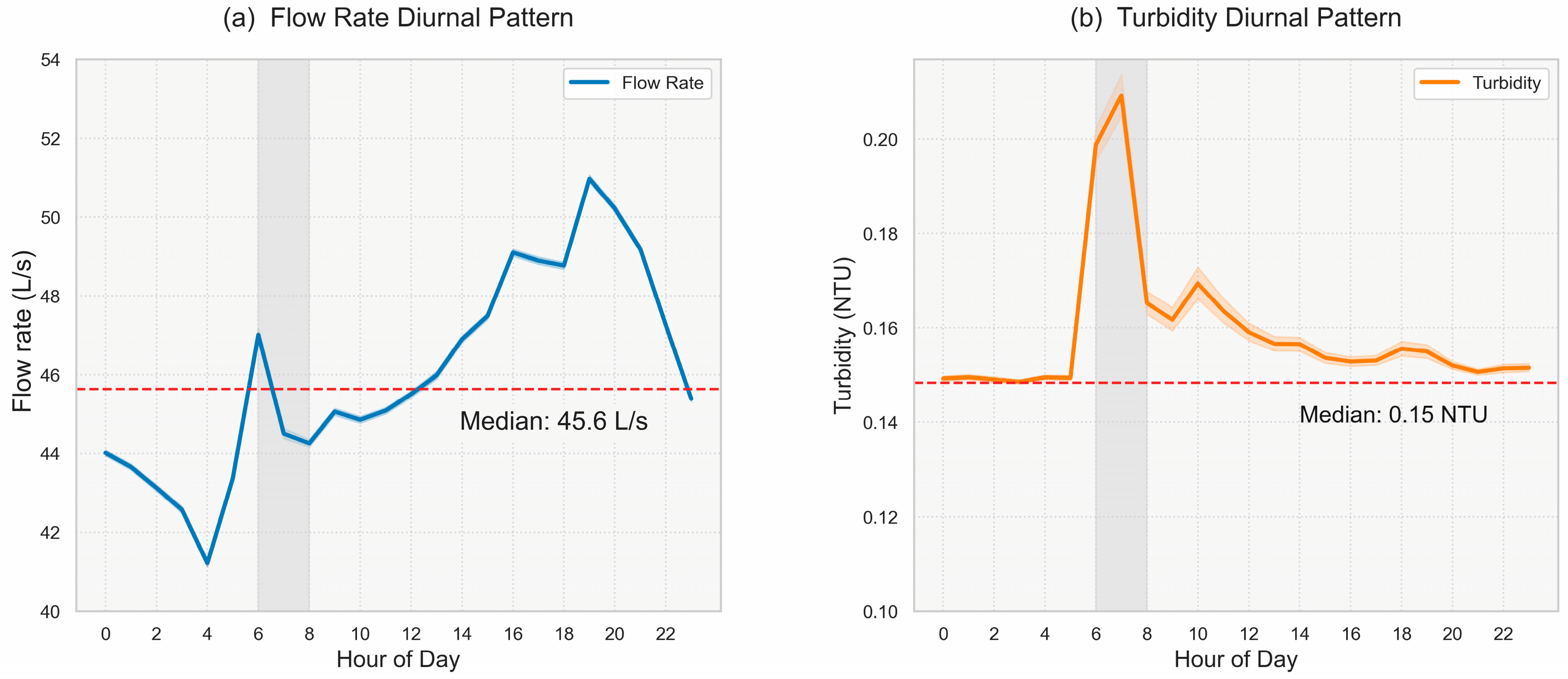
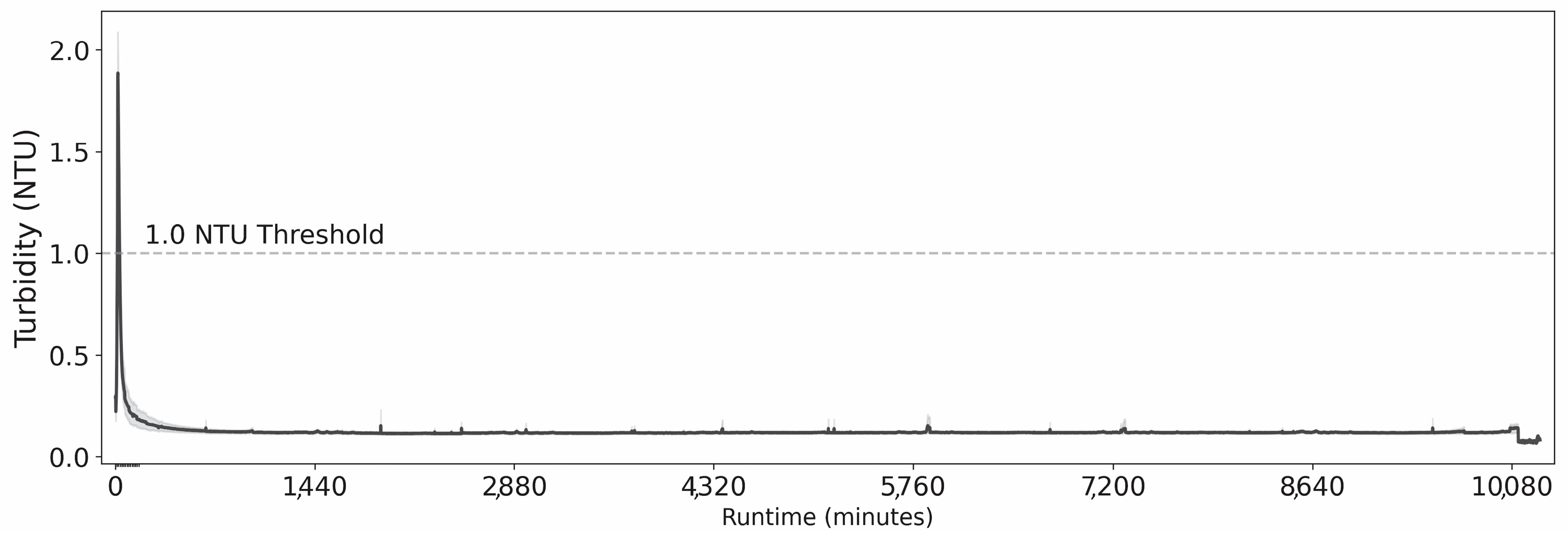
3.1. Feature Characteristics and Correlations
3.2. Model Performance Evaluation for Filtered Water Turbidity Prediction
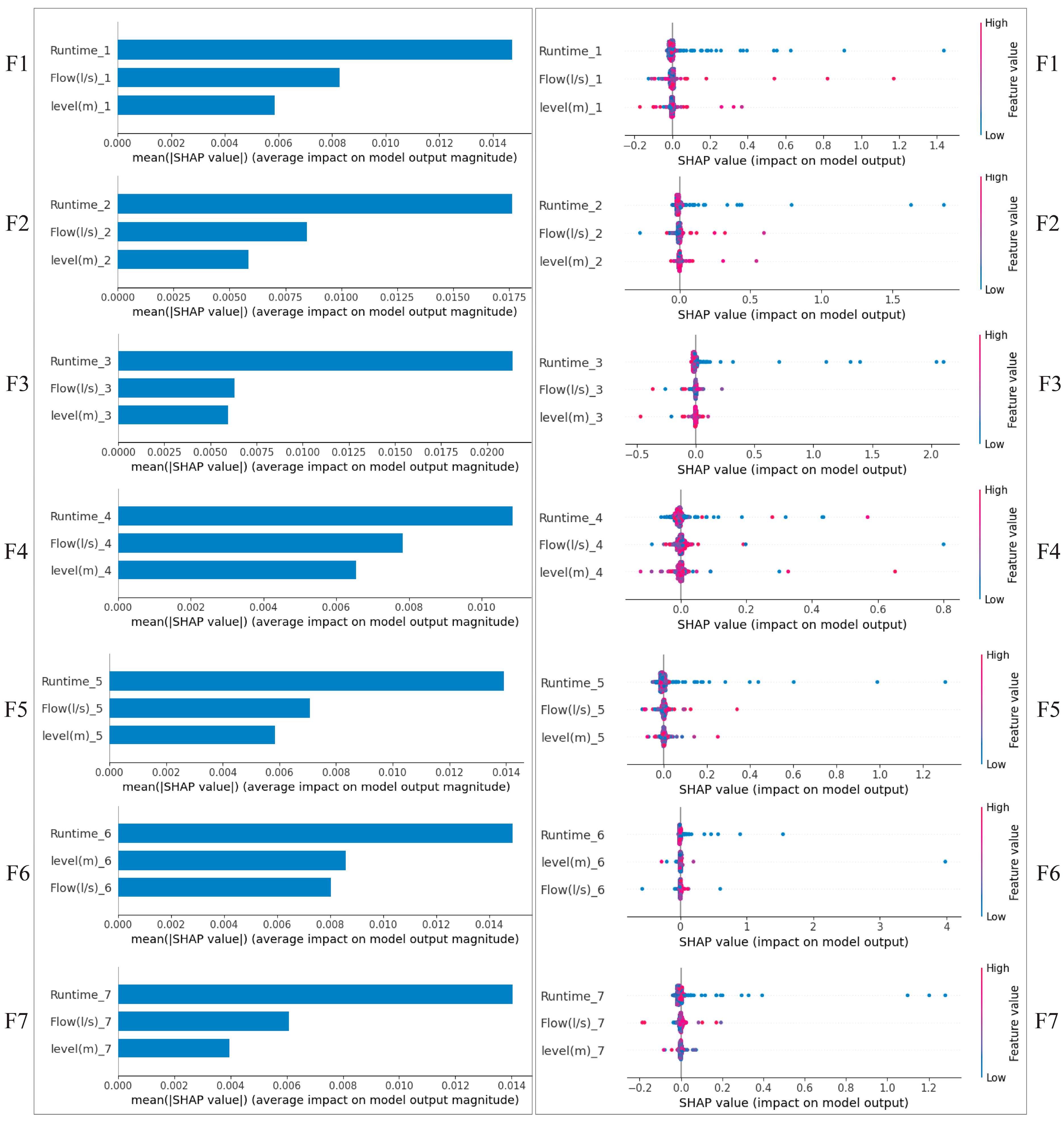
3.3. Model Interpretation and Explainability
3.4. Implication of Predicted Filter Performance on Operation Routines
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| A-TOPSIS | Alternative Technique for Order of Preference by Similarity to Ideal Solution |
| DWTP | Drinking Water Treatment Plants |
| ET | Extra Trees |
| k-NN | K-Nearest Neighbour |
| MAE | Mean Absolute Error |
| ML | Machine Learning |
| MLR | Multiple linear regression |
| NTU | Nephelometric Turbidity Units |
| R2 | R-squared |
| RF | Random Forest |
| RMSE | Root Mean Square Error |
| SCADA | Supervisory Control and Data Acquisition |
| SHAP | SHapley Additive exPlanations |
| SVR | Support Vector Regression |
| USEPA | The U.S. Environmental Protection Agency (EPA) |
| xAI | explainable AI |
| XGBoost | Extreme Gradient Boosting |
References
- Thorne, O.; Fenner, R.A. The impact of climate change on reservoir water quality and water treatment plant operations: A UK case study. Water Environ. J. 2011, 25, 74–87. [Google Scholar] [CrossRef]
- Cornwell, D.A.; MaCphee, M.J.; Brown, R.A.; Via, S.H. Demonstrating Cryptosporidium Removal using spore monitoring at lime-softening plants. J. Am. Water Work. Assoc. 2003, 95, 124–133. [Google Scholar] [CrossRef]
- Elimelech, M.; O’Melia, C.R. Kinetics of deposition of colloidal particles in porous media. Environ. Sci. Technol. 1990, 24, 1528–1536. [Google Scholar] [CrossRef]
- Amirtharajah, A. Some Theoretical and Conceptual Views of Filtration. J. Am. Water Work. Assoc. 1988, 80, 36–46. [Google Scholar] [CrossRef]
- Gregory, J.; Nelson, D.W. Monitoring of aggregates in flowing suspensions. Colloids Surf. 1986, 18, 175–188. [Google Scholar] [CrossRef]
- Hendricks, D.W.; Clunie William, F.; Sturbaum Gregory, D.; Klein Donald, A.; Champlin Tory, L.; Kugrens, P.; Hirsch, J.; McCourt, B.; Nordby George, R.; Sobsey Mark, D.; et al. Filtration Removals of Microorganisms and Particles. J. Environ. Eng. 2005, 131, 1621–1632. [Google Scholar] [CrossRef]
- Kawamura, S. Design and operation of high-rate filters. J. Am. Water Work. Assoc. 1999, 91, 77–90. [Google Scholar] [CrossRef]
- USEPA. Guidance Manual for Compliance with the Surface Water Treatment Rules: Turbidity Provisions; Office of Water: Washington, DC, USA, 2020.
- Hsieh, J.L.; Nguyen, T.Q.; Matte, T.; Ito, K. Drinking Water Turbidity and Emergency Department Visits for Gastrointestinal Illness in New York City, 2002–2009. PLoS ONE 2015, 10, e0125071. [Google Scholar] [CrossRef]
- Benjamin, M.M.; Lawler, D.F. Water Quality Engineering: Physical/Chemical Treatment Processes; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Crittenden, J.C.; Trussell, R.R.; Hand, D.W.; Howe, K.J.; Tchobanoglous, G. Stantec’s Water Treatment: Principles and Design; Wiley: Hoboken, NJ, USA, 2022. [Google Scholar]
- Griffiths, K.; Andrews, R. Application of artificial neural networks for filtration optimization. J. Environ. Eng. 2011, 137, 1040–1047. [Google Scholar] [CrossRef]
- Moradi, S.; Omar, A.; Zhou, Z.; Agostino, A.; Gandomkar, Z.; Bustamante, H.; Power, K.; Henderson, R.; Leslie, G. Forecasting and optimizing dual media filter performance via machine learning. Water Res. 2023, 235, 119874. [Google Scholar] [CrossRef]
- Wan, L.; Gong, K.; Zhang, G.; Yuan, X.; Li, C.; Deng, X. An efficient rolling bearing fault diagnosis method based on spark and improved random forest algorithm. IEEE Access 2021, 9, 37866–37882. [Google Scholar] [CrossRef]
- Gyparakis, S.; Trichakis, I.; Diamadopoulos, E. Using Artificial Neural Networks to Predict Operational Parameters of a Drinking Water Treatment Plant (DWTP). Water 2024, 16, 2863. [Google Scholar] [CrossRef]
- Juntunen, P.; Liukkonen, M.; Lehtola, M.J.; Hiltunen, Y. Dynamic soft sensors for detecting factors affecting turbidity in drinking water. J. Hydroinform. 2012, 15, 416–426. [Google Scholar] [CrossRef]
- Raman, G.S.S.; Klima, M.S. Application of Statistical and Machine Learning Techniques for Laboratory-Scale Pressure Filtration: Modeling and Analysis of Cake Moisture. Miner. Process. Extr. Metall. Rev. 2019, 40, 148–155. [Google Scholar] [CrossRef]
- Kale, S.J.; Khandekar, M.A.; Agashe, S.D. Prediction of Water Filter Bed Backwash Time for Water Treatment Plant using Machine Learning Algorithm. In Proceedings of the 2021 IEEE 6th International Conference on Computing, Communication and Automation (ICCCA), Arad, Romania, 17–19 December 2021; pp. 113–116. [Google Scholar]
- SEKLIMA, Norwegian Centre for Climate Services. Observations and Weather Statistics. Available online: https://seklima.met.no (accessed on 22 April 2025).
- Vann-Net, Map with Waterbodies. Available online: https://vann-nett.no/waterbodies/101-1982-L (accessed on 12 April 2025).
- Mohammed, H.; Longva, A.; Seidu, R. Impact of Climate Forecasts on the Microbial Quality of a Drinking Water Source in Norway Using Hydrodynamic Modeling. Water 2019, 11, 527. [Google Scholar] [CrossRef]
- Elçi, Ş. Effects of thermal stratification and mixing on reservoir water quality. Limnology 2008, 9, 135–142. [Google Scholar] [CrossRef]
- Murray, D.; Stankovic, L.; Stankovic, V. An electrical load measurements dataset of United Kingdom households from a two-year longitudinal study. Sci. Data 2017, 4, 160122. [Google Scholar] [CrossRef]
- Su, X.; Yan, X.; Tsai, C.-L. Linear regression. WIREs Comput. Stat. 2012, 4, 275–294. [Google Scholar] [CrossRef]
- Quan, Q.; Hao, Z.; Xifeng, H.; Jingchun, L. Research on water temperature prediction based on improved support vector regression. Neural Comput. Appl. 2022, 34, 8501–8510. [Google Scholar] [CrossRef]
- Cristianini, N.; Shawe-Taylor, J. Support Vector Machines and Other Kernel-Based Learning Methods; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Györfi, L.; Kohler, M.; Krzyżak, A.; Walk, H. k-NN Estimates. A Distribution-Free Theory of Nonparametric Regression; Springer: New York, NY, USA, 2002; pp. 86–99. [Google Scholar]
- Biau, G.; Scornet, E. A random forest guided tour. Test 2016, 25, 197–227. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Majidi, S.H.; Hadayeghparast, S.; Karimipour, H. FDI attack detection using extra trees algorithm and deep learning algorithm-autoencoder in smart grid. Int. J. Crit. Infrastruct. Prot. 2022, 37, 100508. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Krohling, R.A.; Pacheco, A.G.C. A-TOPSIS—An Approach Based on TOPSIS for Ranking Evolutionary Algorithms. Procedia Comput. Sci. 2015, 55, 308–317. [Google Scholar] [CrossRef]
- Vazquezl, M.Y.L.; Peñafiel, L.A.B.; Muñoz, S.X.S.; Martinez, M.A.Q. A Framework for Selecting Machine Learning Models Using TOPSIS; Springer International Publishing: Cham, Switzerland, 2021. [Google Scholar]
- Nguyen, L.V.; Tornyeviadzi, H.M.; Bui, D.T.; Seidu, R. Predicting Discharges in Sewer Pipes Using an Integrated Long Short-Term Memory and Entropy A-TOPSIS Modeling Framework. Water 2022, 14, 300. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2017; Volume 30. [Google Scholar]
- Molnar, C. Interpretable Machine Learning: A Guide for Making Black Box Models Explainable, 3rd ed.; Leanpub: Victoria, BC, Canada, 2025. [Google Scholar]
- Wang, H.; Marshall, S.D.; Arayanarakool, R.; Balasubramaniam, L.; Jin, X.; Lee, P.S.; Chen, P.C. Optimization of a fluid distribution manifold: Mechanical design, numerical studies, fabrication, and experimental verification. Int. J. Fluid Mach. Syst. 2018, 11, 244–254. [Google Scholar] [CrossRef]
- Lovdata. The Norwegian Regulation on Drinking Water. Available online: https://lovdata.no/dokument/SF/forskrift/2016-12-22-1868 (accessed on 2 August 2025).
- Kramer, O.J.I.; van Schaik, C.; Dacomba-Torres, P.D.R.; de Moel, P.J.; Boek, E.S.; Baars, E.T.; Padding, J.T.; van der Hoek, J.P. Fluidisation characteristics of granular activated carbon in drinking water treatment applications. Adv. Powder Technol. 2021, 32, 3174–3188. [Google Scholar] [CrossRef]
- Kim, J.; Tobiason, J.E. Particles in Filter Effluent: The Roles of Deposition and Detachment. Environ. Sci. Technol. 2004, 38, 6132–6138. [Google Scholar] [CrossRef] [PubMed]
- Tufenkji, N.; Elimelech, M. Correlation Equation for Predicting Single-Collector Efficiency in Physicochemical Filtration in Saturated Porous Media. Environ. Sci. Technol. 2004, 38, 529–536. [Google Scholar] [CrossRef]
- Akkoyunlu, A. Expansion of Granular Water Filters During Backwash. Environ. Eng. Sci. 2003, 20, 655–665. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. Model Assessment and Selection. In The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009; pp. 219–259. [Google Scholar] [CrossRef]
- Futagami, K.; Fukazawa, Y.; Kapoor, N.; Kito, T. Pairwise acquisition prediction with SHAP value interpretation. J. Financ. Data Sci. 2021, 7, 22–44. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.-I. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef] [PubMed]
- Xiao, D.; Nan, J.; He, W.; Zhang, X.; Fan, Y.; Lin, X. Effects of inlet water flow and potential aggregate breakage on the change of turbid particle size distribution during coagulation-sedimentation-filtration (CSF): Pilot-scale experimental and CFD-aided studies. Chem. Eng. Res. Des. 2025, 216, 135–148. [Google Scholar] [CrossRef]
- Templeton, M.R.; Andrews, R.C.; Hofmann, R. Removal of particle-associated bacteriophages by dual-media filtration at different filter cycle stages and impacts on subsequent UV disinfection. Water Res. 2007, 41, 2393–2406. [Google Scholar] [CrossRef] [PubMed]

| Model Type | Hyperparameters |
|---|---|
| K-Nearest Neighbour | ‘n_neighbors’: [3, 5, 7, 9], ‘weights’: [‘uniform’, ‘distance’], ‘p’: [1, 2] |
| Random Forest | ‘n_estimators’: [50, 100, 200], ‘max_depth’: [None], ‘min_samples_split’: [2, 5], ‘min_samples_leaf’: [1, 2], ‘bootstrap’: [True, False] |
| Extra Trees | ‘n_estimators’: [50, 100, 200], ‘max_depth’: [None], ‘min_samples_split’: [2, 5], ‘min_samples_leaf’: [1, 2], ‘bootstrap’: [False] |
| Parameter | Unit | Min | Max | Mean | Std. |
|---|---|---|---|---|---|
| Filtered Water Flow Rate | L/s | 0 | 121.97 | 46.43 | 9.65 |
| Bed Level | m | 3.56 | 5.58 | 4.40 | 0.26 |
| Filtered Water Turbidity | NTU | 0.01 | 10.0 | 0.13 | 0.12 |
| Valve opening | % | 0.00 | 100.0 | 69.4 | 20.9 |
| Filter Runtime | min | 1 | 10,283 | 4806 | 2904 |
| (a) Baseline Models | |||||||||
| R2 | MAE | RMSE | |||||||
| Filter | MLR | SVR | KNN | MLR | SVR | KNN | MLR | SVR | KNN |
| Filter 1 | 0.010 | 0.182 | 0.61 | 0.033 | 0.046 | 0.024 | 0.112 | 0.102 | 0.069 |
| Filter 2 | 0.013 | 0.228 | 0.79 | 0.039 | 0.047 | 0.025 | 0.163 | 0.144 | 0.081 |
| Filter 3 | 0.032 | 0.163 | 0.70 | 0.040 | 0.053 | 0.025 | 0.142 | 0.133 | 0.073 |
| Filter 4 | 0.004 | 0.185 | 0.63 | 0.035 | 0.043 | 0.028 | 0.102 | 0.092 | 0.061 |
| Filter 5 | 0.011 | 0.141 | 0.56 | 0.010 | 0.036 | 0.027 | 0.109 | 0.102 | 0.076 |
| Filter 6 | 0.017 | 0.470 | 0.82 | 0.034 | 0.045 | 0.022 | 0.122 | 0.089 | 0.054 |
| Filter 7 | 0.011 | 0.196 | 0.81 | 0.032 | 0.045 | 0.019 | 0.101 | 0.091 | 0.047 |
| (b) Ensemble Models | |||||||||
| R2 | MAE | RMSE | |||||||
| Filter | XGBoost | RF | ET | XGBoost | RF | ET | XGBoost | RF | ET |
| Filter 1 | 0.61 | 0.81 | 0.86 | 0.025 | 0.017 | 0.016 | 0.071 | 0.048 | 0.016 |
| Filter 2 | 0.65 | 0.85 | 0.90 | 0.027 | 0.018 | 0.017 | 0.098 | 0.062 | 0.017 |
| Filter 3 | 0.66 | 0.89 | 0.92 | 0.025 | 0.016 | 0.016 | 0.084 | 0.048 | 0.016 |
| Filter 4 | 0.35 | 0.79 | 0.80 | 0.029 | 0.019 | 0.019 | 0.082 | 0.047 | 0.019 |
| Filter 5 | 0.49 | 0.79 | 0.82 | 0.029 | 0.018 | 0.017 | 0.078 | 0.052 | 0.017 |
| Filter 6 | 0.74 | 0.89 | 0.91 | 0.023 | 0.016 | 0.016 | 0.063 | 0.040 | 0.016 |
| Filter 7 | 0.75 | 0.87 | 0.87 | 0.021 | 0.014 | 0.014 | 0.051 | 0.037 | 0.014 |
| Algorithm | Ratio | Total | Ranking |
|---|---|---|---|
| ET | 0.29 ± 0.25 | 1.00 | 1 |
| RF | 0.24 ± 0.23 | 0.83 | 2 |
| KNN | 0.20 ± 0.16 | 0.64 | 3 |
| XGBoost | 0.18 ± 0.14 | 0.53 | 4 |
| SVR | 0.06 ± 0.11 | 0.10 | 5 |
| MLR | 0.03 ± 0.11 | 0.01 | 6 |
| Metric | Extra Trees | Random Forest | KNN |
|---|---|---|---|
| Accuracy | High | High | Moderate |
| Stability | Consistent | Consistent | Filter-dependent |
| MAE | ~0.014–0.018 | ~0.014–0.018 | ~0.020–0.030 |
| RMSE | Lowest (~0.036–0.045) | Low (~0.04–0.05) | Higher (~0.07) |
| Training | Medium (~620 s) | Slow (~2100–2500 s) | Fast (~13 s) |
| Prediction | Medium (~1 s) | Medium (~0.4 s) | Fast |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwarko-Kyei, J.; Tornyeviadzi, H.M.; Seidu, R. A Machine Learning Approach to Predicting the Turbidity from Filters in a Water Treatment Plant. Water 2025, 17, 2938. https://doi.org/10.3390/w17202938
Kwarko-Kyei J, Tornyeviadzi HM, Seidu R. A Machine Learning Approach to Predicting the Turbidity from Filters in a Water Treatment Plant. Water. 2025; 17(20):2938. https://doi.org/10.3390/w17202938
Chicago/Turabian StyleKwarko-Kyei, Joseph, Hoese Michel Tornyeviadzi, and Razak Seidu. 2025. "A Machine Learning Approach to Predicting the Turbidity from Filters in a Water Treatment Plant" Water 17, no. 20: 2938. https://doi.org/10.3390/w17202938
APA StyleKwarko-Kyei, J., Tornyeviadzi, H. M., & Seidu, R. (2025). A Machine Learning Approach to Predicting the Turbidity from Filters in a Water Treatment Plant. Water, 17(20), 2938. https://doi.org/10.3390/w17202938






