Exploring the Potential of Multi-Hydrological Model Weighting Schemes to Reduce Uncertainty in Runoff Projections
Abstract
1. Introduction
2. Case Study Background
2.1. Studied Watershed and Observed Data
2.2. Downscaled GCM Data and Uncertainty Assessment
2.2.1. Regional Climate Model Simulations
2.2.2. Statistically Downscaled Simulations
2.2.3. Quantifying Uncertainty in Precipitation and Temperature Projections
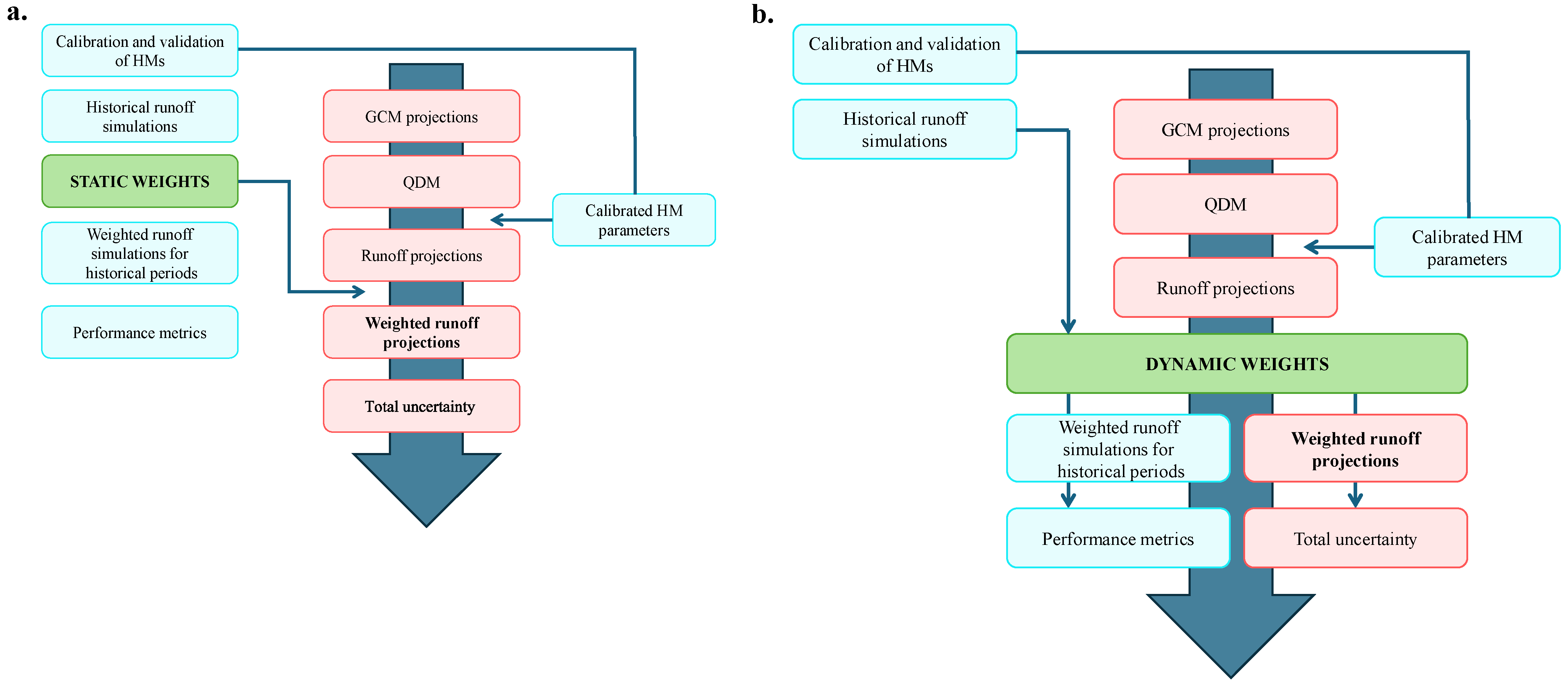
3. Methodology
3.1. Hydrological Models
3.2. Measures for Simulation Performance
3.3. Weighting Methods (WMs)
3.3.1. Equal Weighting (EW)
3.3.2. Bayesian Model Averaging (BMA)
3.3.3. Representation of the Annual Cycle (RAC)
3.3.4. Ordered Weighted Averaging (OWA)
3.3.5. Granger–Ramanathan Averaging (GR)
3.3.6. Uncertainty Optimizing Multi-Model Ensemble (UO-MME)
4. Results and Discussion
4.1. Simulation Performance of HMs
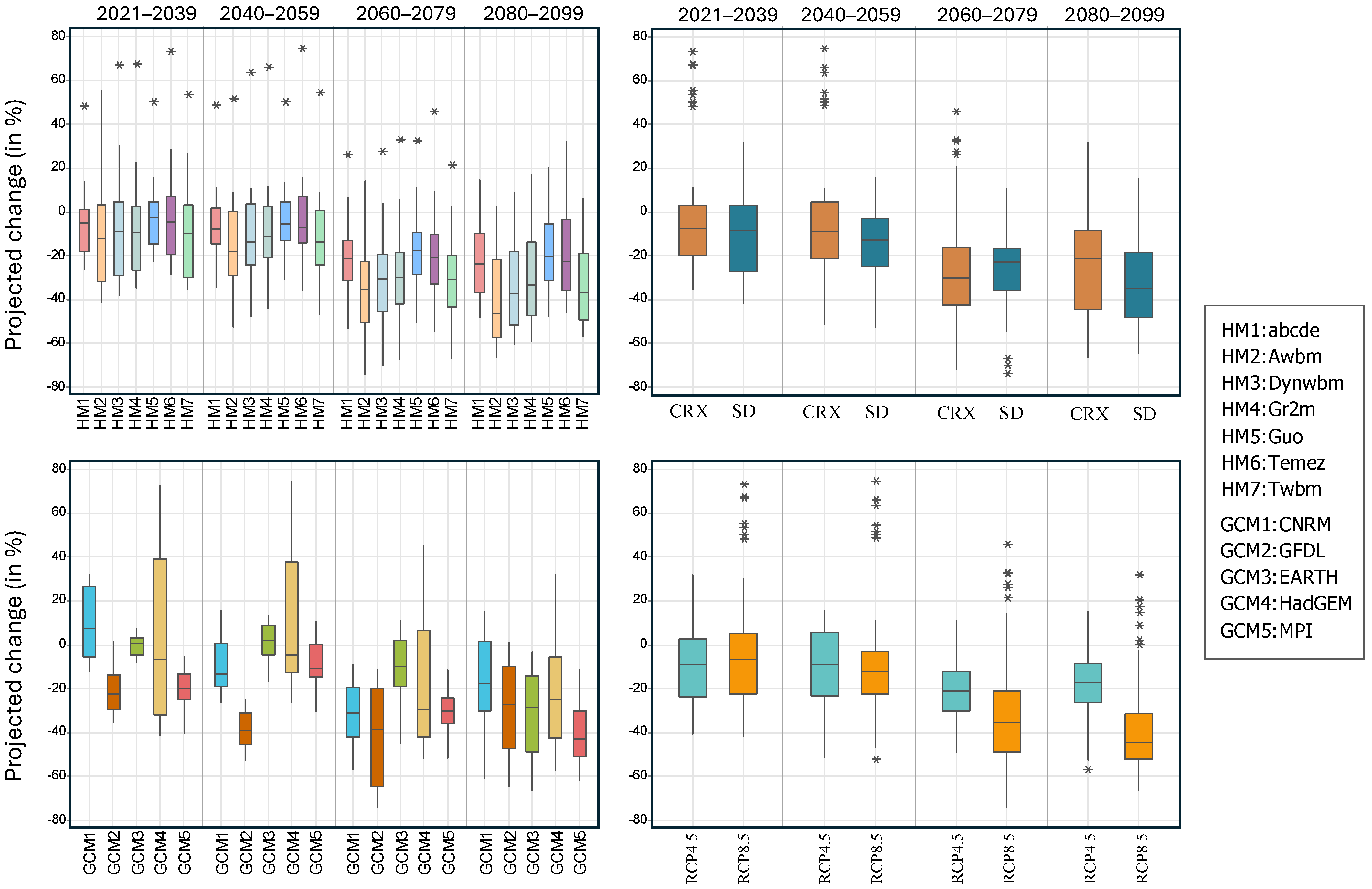
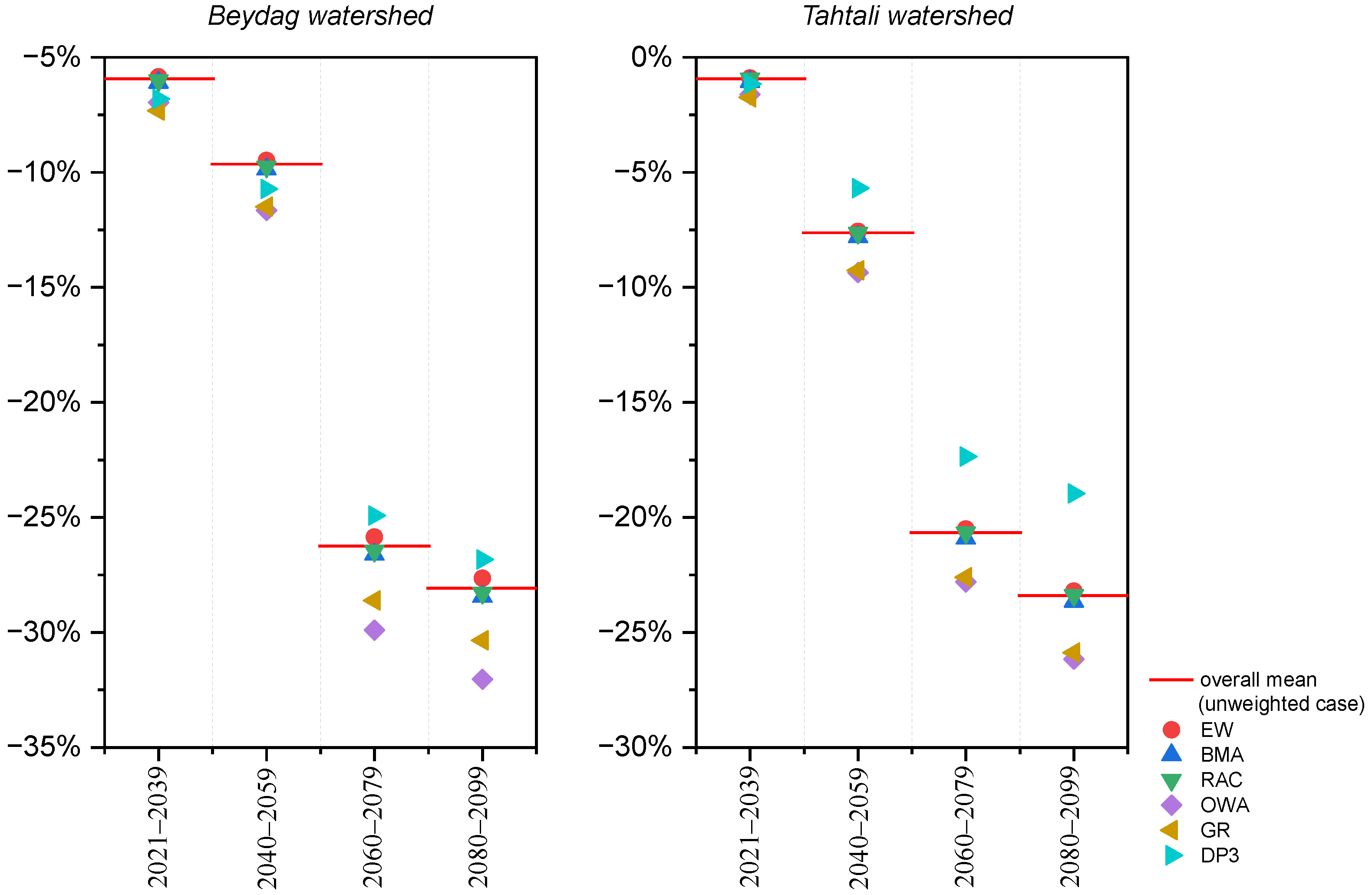
4.2. Projected Changes in Runoff
4.2.1. Statistical Significance of Changes
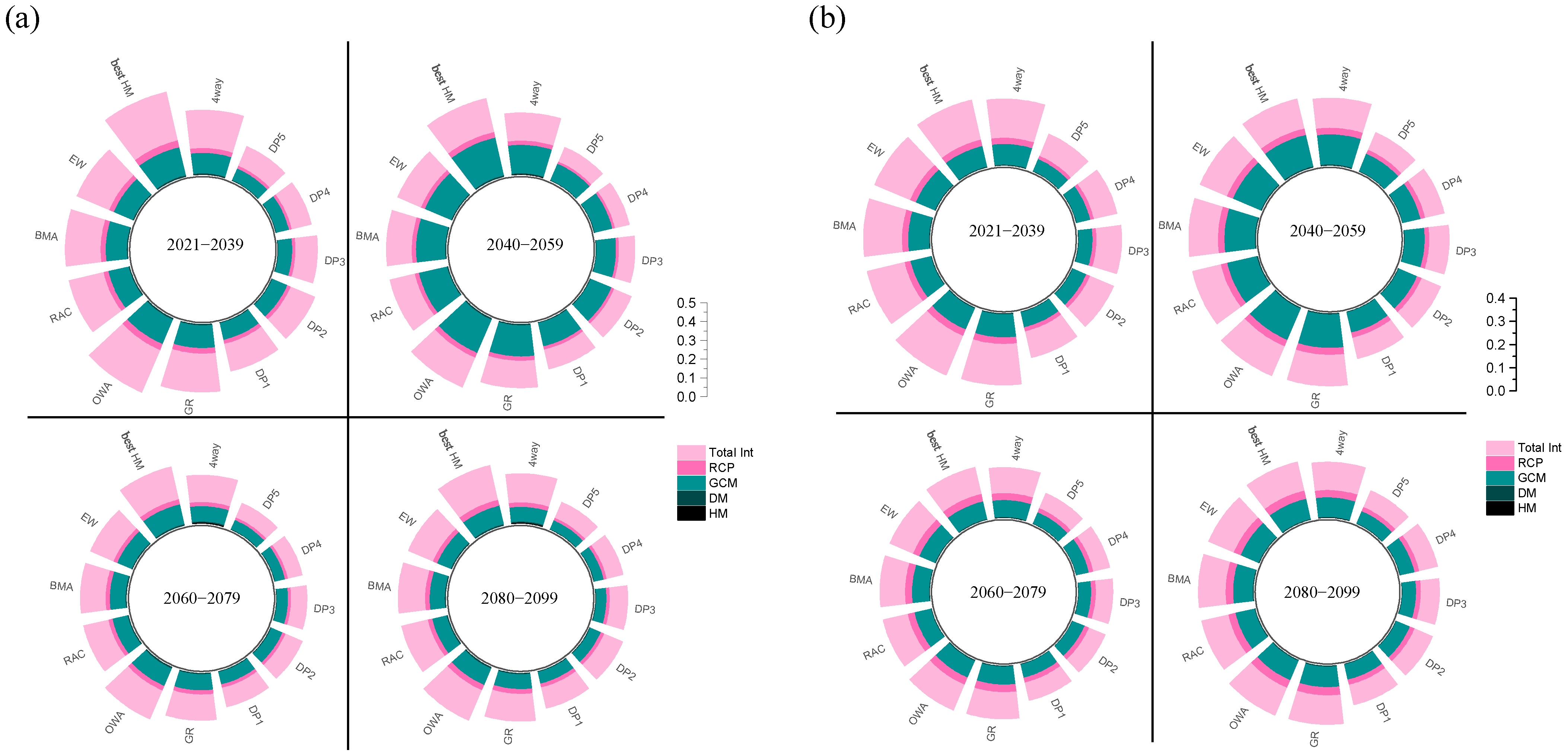
4.2.2. Partitioning Uncertainty in Runoff Projections: Four-Way ANOVA
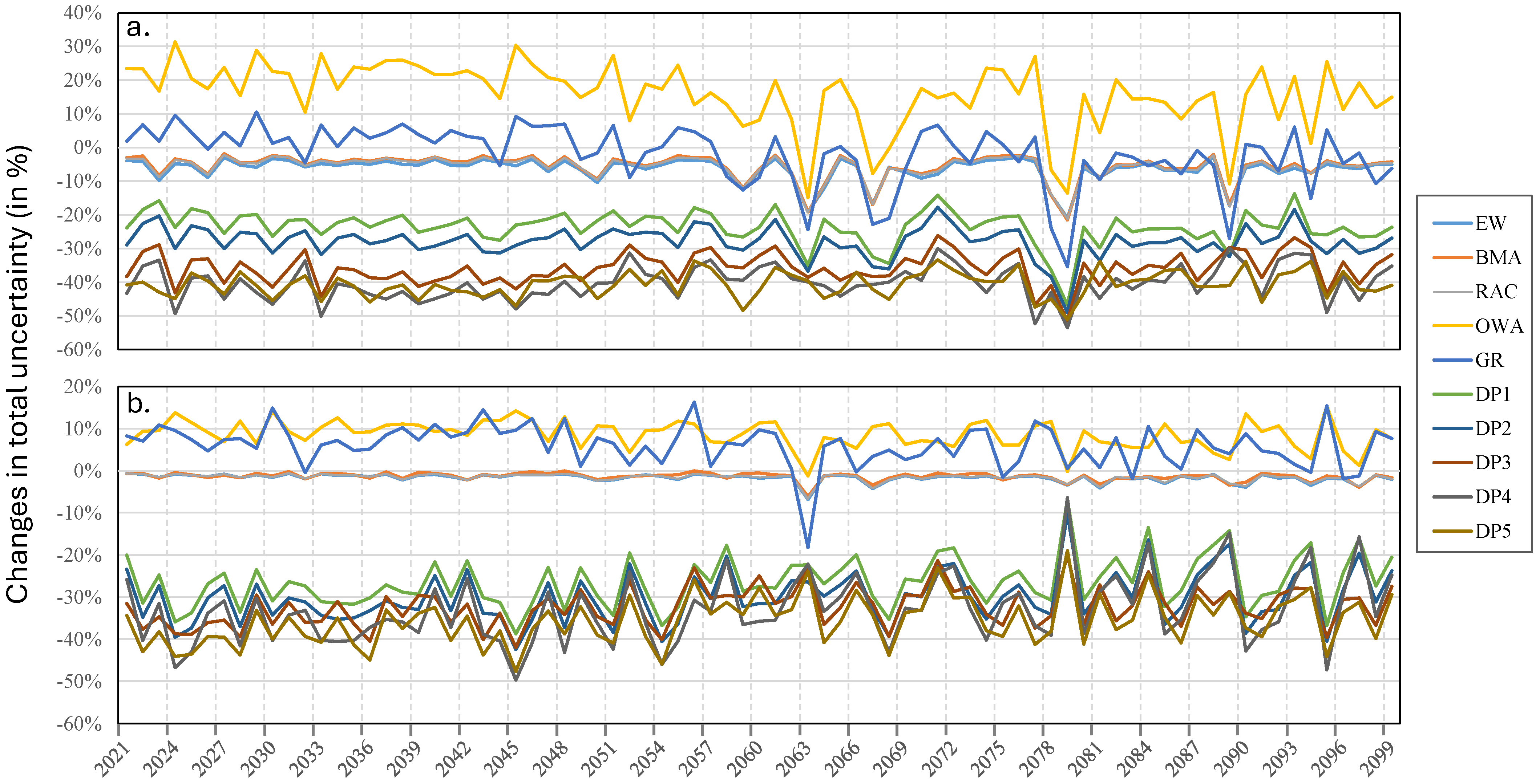
4.3. Multi-Hydrological Model Weighting and Potential Impacts on Uncertainty
4.3.1. Simulation Performance Versus Projected Uncertainty in Standard WMs
4.3.2. Does the UO-MME Framework Effectively Reduce Projection Uncertainty?
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, S.; Shah, H.; Naz, B.S.; Shrestha, N.; Mishra, V.; Daggupati, P.; Ghimire, U.; Vetter, T. Impacts of hydrological model calibration on projected hydrological changes under climate change—A multi-model assessment in three large river basins. Clim. Change 2020, 163, 1143–1164. [Google Scholar] [CrossRef]
- Pastén-Zapata, E.; Pimentel, R.; Royer-Gaspard, P.; Sonnenborg, T.O.; Aparicio-Ibañez, J.; Lemoine, A.; Pérez-Palazón, M.J.; Schneider, R.; Photiadou, C.; Thirel, G.; et al. The effect of weighting hydrological projections based on the robustness of hydrological models under a changing climate. J. Hydrol. Reg. Stud. 2022, 41, 101113. [Google Scholar] [CrossRef]
- Castaneda-Gonzalez, M.; Poulin, A.; Romero-Lopez, R.; Turcotte, R. Hydrological models weighting for hydrological projections: The impacts on future peak flows. J. Hydrol. 2023, 625, 130098. [Google Scholar] [CrossRef]
- Okkan, U.; Fistikoglu, O.; Ersoy, Z.B.; Noori, A.T. Investigating adaptive hedging policies for reservoir operation under climate change impacts. J. Hydrol. 2023, 619, 129286. [Google Scholar] [CrossRef]
- Krysanova, V.; Donnelly, C.; Gelfan, A.; Gerten, D.; Arheimer, B.; Hattermann, F.; Kundzewicz, Z.W. How the performance of hydrological models relates to credibility of projections under climate change. Hydrol. Sci. J. 2018, 63, 696–720. [Google Scholar] [CrossRef]
- Najafi, M.R.; Moradkhani, H.; Jung, I.W. Assessing the uncertainties of hydrologic model selection in climate change impact studies. Hydrol. Process. 2011, 25, 2814–2826. [Google Scholar] [CrossRef]
- Krysanova, V.; Zaherpour, J.; Didovets, I.; Gosling, S.N.; Gerten, D.; Hanasaki, N.; Müller Schmied, H.; Pokhrel, Y.; Satoh, Y.; Tang, Q.; et al. How evaluation of global hydrological models can help to improve credibility of river discharge projections under climate change. Clim. Change 2020, 163, 1353–1377. [Google Scholar] [CrossRef]
- Arsenault, R.; Gatien, P.; Renaud, B.; Brissette, F.; Martel, J.L. A comparative analysis of 9 multi-model averaging approaches in hydrological continuous streamflow simulation. J. Hydrol. 2015, 529, 754–767. [Google Scholar] [CrossRef]
- Duan, K.; Wang, X.; Liu, B.; Zhao, T.; Chen, X. Comparing Bayesian model averaging and reliability ensemble averaging in post-processing runoff projections under climate change. Water 2021, 13, 2124. [Google Scholar] [CrossRef]
- Duan, Q.; Ajami, N.K.; Gao, X.; Sorooshian, S. Multi-model ensemble hydrologic prediction using Bayesian model averaging. Adv. Water Resour. 2007, 30, 1371–1386. [Google Scholar] [CrossRef]
- Diks, C.G.; Vrugt, J.A. Comparison of point forecast accuracy of model averaging methods in hydrologic applications. Stoch. Environ. Res. Risk Assess. 2010, 24, 809–820. [Google Scholar] [CrossRef]
- Wan, Y.; Chen, J.; Xu, C.Y.; Xie, P.; Qi, W.; Li, D.; Zhang, S. Performance dependence of multi-model combination methods on hydrological model calibration strategy and ensemble size. J. Hydrol. 2021, 603, 127065. [Google Scholar] [CrossRef]
- Seiller, G.; Hajji, I.; Anctil, F. Improving the temporal transposability of lumped hydrological models on twenty diversified US watersheds. J. Hydrol. Reg. Stud. 2015, 3, 379–399. [Google Scholar] [CrossRef]
- Broderick, C.; Matthews, T.; Wilby, R.L.; Bastola, S.; Murphy, C. Transferability of hydrological models and ensemble averaging methods between contrasting climatic periods. Water Resour. Res. 2016, 52, 8343–8373. [Google Scholar] [CrossRef]
- Chawla, I.; Mujumdar, P.P. Partitioning uncertainty in streamflow projections under nonstationary model conditions. Adv. Water Resour. 2018, 112, 266–282. [Google Scholar] [CrossRef]
- Reifen, C.; Toumi, R. Climate projections: Past performance no guarantee of future skill? Geophys. Res. Lett. 2009, 36, L13704. [Google Scholar] [CrossRef]
- Wang, H.M.; Chen, J.; Xu, C.Y.; Chen, H.; Guo, S.; Xie, P.; Li, X. Does the weighting of climate simulations result in a better quantification of hydrological impacts? Hydrol. Earth Syst. Sci. 2019, 23, 4033–4050. [Google Scholar] [CrossRef]
- Weigel, A.P.; Knutti, R.; Liniger, M.A.; Appenzeller, C. Risks of model weighting in multimodel climate projections. J. Clim. 2010, 23, 4175–4191. [Google Scholar] [CrossRef]
- Lehner, F.; Wood, A.W.; Vano, J.A.; Lawrence, D.M.; Clark, M.P.; Mankin, J.S. The potential to reduce uncertainty in regional runoff projections from climate models. Nat. Clim. Change 2019, 9, 926–933. [Google Scholar] [CrossRef]
- Ersoy, Z.B.; Fistikoglu, O.; Okkan, U.; Derin, B. Convergence and final performances of optimization algorithms for rainfall–runoff model calibration based on the number of function calls. Earth Sci. Inform. 2025, 18, 382. [Google Scholar] [CrossRef]
- Ekström, M.; Grose, M.R.; Whetton, P.H. An appraisal of downscaling methods used in climate change research. Wiley Interdiscip. Rev. Clim. Change 2015, 6, 301–319. [Google Scholar] [CrossRef]
- Ozturk, T.; Turp, M.T.; Türkeş, M.; Kurnaz, M.L. Future projections of temperature and precipitation climatology for CORDEX-MENA domain using RegCM4.4. Atmos. Res. 2018, 206, 87–107. [Google Scholar] [CrossRef]
- Mesta, B.; Kentel, E. Superensembles of raw and bias-adjusted regional climate models for Mediterranean region, Turkey. Int. J. Climatol. 2022, 42, 2566–2585. [Google Scholar] [CrossRef]
- Cannon, A.J.; Sobie, S.R.; Murdock, T.Q. Bias Correction of GCM Precipitation by Quantile Mapping: How Well Do Methods Preserve Changes in Quantiles and Extremes? J. Clim. 2015, 28, 6938–6959. [Google Scholar] [CrossRef]
- Dunnett, C.W. A multiple comparison procedure for comparing several treatments with a control. J. Am. Stat. Assoc. 1955, 50, 1096–1121. [Google Scholar] [CrossRef]
- Ozturk, T.; Saygili-Araci, F.S.; Kurnaz, M.L. Projected changes in extreme temperature and precipitation indices over CORDEX-MENA domain. Atmosphere 2021, 12, 622. [Google Scholar] [CrossRef]
- Hammami, D.; Lee, T.S.; Ouarda, T.B.; Lee, J. Predictor selection for downscaling GCM data with LASSO. J. Geophys. Res. Atmos. 2012, 117, D17116. [Google Scholar] [CrossRef]
- García-Díez, M.; Fernández, J.; Vautard, R. An RCM multi-physics ensemble over Europe: Multi-variable evaluation to avoid error compensation. Clim. Dyn. 2015, 45, 3141–3156. [Google Scholar] [CrossRef]
- Vetter, T.; Huang, S.; Aich, V.; Yang, T.; Wang, X.; Krysanova, V.; Hattermann, F. Multi-model climate impact assessment and intercomparison for three large-scale river basins on three continents. Earth Syst. Dynam. 2015, 6, 17–43. [Google Scholar] [CrossRef]
- Feng, D.; Beighley, E. Identifying uncertainties in hydrologic fluxes and seasonality from hydrologic model components for climate change impact assessments. Hydrol. Earth Syst. Sci. 2020, 24, 2253–2267. [Google Scholar] [CrossRef]
- Yip, S.; Ferro, C.A.; Stephenson, D.B.; Hawkins, E. A simple, coherent framework for partitioning uncertainty in climate predictions. J. Clim. 2011, 24, 4634–4643. [Google Scholar] [CrossRef]
- Okkan, U.; Fistikoglu, O.; Ersoy, Z.B.; Noori, A.T. Analyzing the uncertainty of potential evapotranspiration models in drought projections derived for a semi-arid watershed. Theor. Appl. Climatol. 2024, 155, 2329–2346. [Google Scholar] [CrossRef]
- Boughton, W. The Australian water balance model. Environ. Model. Softw. 2004, 19, 943–956. [Google Scholar] [CrossRef]
- Zhang, L.; Potter, N.; Hickel, K.; Zhang, Y.; Shao, Q. Water balance modeling over variable time scales based on the Budyko framework—Model development and testing. J. Hydrol. 2008, 360, 117–131. [Google Scholar] [CrossRef]
- Mouelhi, S.; Michel, C.; Perrin, C.; Andréassian, V. Stepwise development of a two-parameter monthly water balance model. J. Hydrol. 2006, 318, 200–214. [Google Scholar] [CrossRef]
- Pérez-Sánchez, J.; Senent-Aparicio, J.; Segura-Méndez, F.; Pulido-Velazquez, D.; Srinivasan, R. Evaluating hydrological models for deriving water resources in peninsular Spain. Sustainability 2019, 11, 2872. [Google Scholar] [CrossRef]
- Pérez-Sánchez, J.; Senent-Aparicio, J.; Jimeno-Sáez, P. The application of spreadsheets for teaching hydrological modeling and climate change impacts on streamflow. Comput. Appl. Eng. Educ. 2022, 30, 1510–1525. [Google Scholar] [CrossRef]
- Elçi, A.; Karadaş, D.; Fıstıkoğlu, O. The combined use of MODFLOW and precipitation-runoff modeling to simulate groundwater flow in a diffuse-pollution prone watershed. Water Sci. Technol. 2010, 62, 180–188. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Maldonado, S.; Merigó, J.; Miranda, J. Redefining support vector machines with the ordered weighted average. Knowl.-Based Syst. 2018, 148, 41–46. [Google Scholar] [CrossRef]
- Granger, C.W.; Ramanathan, R. Improved methods of combining forecasts. J. Forecast. 1984, 3, 197–204. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Parrish, M.A.; Moradkhani, H.; DeChant, C.M. Toward reduction of model uncertainty: Integration of Bayesian model averaging and data assimilation. Water Resour. Res. 2012, 48, W03519. [Google Scholar] [CrossRef]
- Vrac, M.; Allard, D.; Mariéthoz, G.; Thao, S.; Schmutz, L. Distribution-based pooling for combination and multi-model bias correction of climate simulations. Earth Syst. Dynam. 2024, 15, 735–762. [Google Scholar] [CrossRef]
- Dutot, E.; Douville, H. Revisiting the potential to narrow model uncertainty in the projections of Arctic runoff. Geophys. Res. Lett. 2023, 50, e2023GL104039. [Google Scholar] [CrossRef]
- Gholami, H.; Lotfirad, M.; Ashrafi, S.M.; Biazar, S.M.; Singh, V.P. Multi-GCM ensemble model for reduction of uncertainty in runoff projections. Stoch. Environ. Res. Risk Assess. 2023, 37, 953–964. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Xu, C.Y.; Vandewiele, G.L. Sensitivity of monthly rainfall-runoff models to input errors and data length. Hydrol. Sci. J. 1994, 39, 157–176. [Google Scholar] [CrossRef]
- Wang, H.M.; Chen, J.; Xu, C.Y.; Zhang, J.; Chen, H. A framework to quantify the uncertainty contribution of GCMs over multiple sources in hydrological impacts of climate change. Earth’s Future 2020, 8, e2020EF001602. [Google Scholar] [CrossRef]
- Joseph, J.; Ghosh, S.; Pathak, A.; Sahai, A.K. Hydrologic impacts of climate change: Comparisons between hydrological parameter uncertainty and climate model uncertainty. J. Hydrol. 2018, 566, 1–22. [Google Scholar] [CrossRef]
- Wu, Y.; Miao, C.; Fan, X.; Gou, J.; Zhang, Q.; Zheng, H. Quantifying the uncertainty sources of future climate projections and narrowing uncertainties with bias correction techniques. Earth’s Future 2022, 10, e2022EF002963. [Google Scholar] [CrossRef]
- Darbandsari, P.; Coulibaly, P. Inter-comparison of different Bayesian model averaging modifications in streamflow simulation. Water 2019, 11, 1707. [Google Scholar] [CrossRef]
- Coron, L.; Andréassian, V.; Perrin, C.; Bourqui, M.; Hendrickx, F. On the lack of robustness of hydrologic models regarding water balance simulation: A diagnostic approach applied to three models of increasing complexity on 20 mountainous catchments. Hydrol. Earth Syst. Sci. 2014, 18, 727–746. [Google Scholar] [CrossRef]
- Taguela, T.N.; Akinsanola, A.A.; Adeliyi, T.E.; Rhoades, A.; Nazarian, R.H. Understanding drivers and uncertainty in projected African precipitation. npj Clim. Atmos. Sci. 2025, 8, 222. [Google Scholar] [CrossRef]
- Tong, X.; Wang, D.; Singh, V.P.; Wu, J.C.; Chen, X.; Chen, Y.F. Impact of data length on the uncertainty of hydrological copula modeling. J. Hydrol. Eng. 2015, 20, 05014019. [Google Scholar] [CrossRef]
- Tegegne, G.; Park, D.K.; Kim, Y.O. Comparison of hydrological models for the assessment of water resources in a data-scarce region, the Upper Blue Nile River Basin. J. Hydrol. Reg. Stud. 2017, 14, 49–66. [Google Scholar] [CrossRef]
- Zhu, Y.Y.; Yang, S. Evaluation of CMIP6 for historical temperature and precipitation over the Tibetan Plateau and its comparison with CMIP5. Adv. Clim. Change Res. 2020, 11, 239–251. [Google Scholar] [CrossRef]


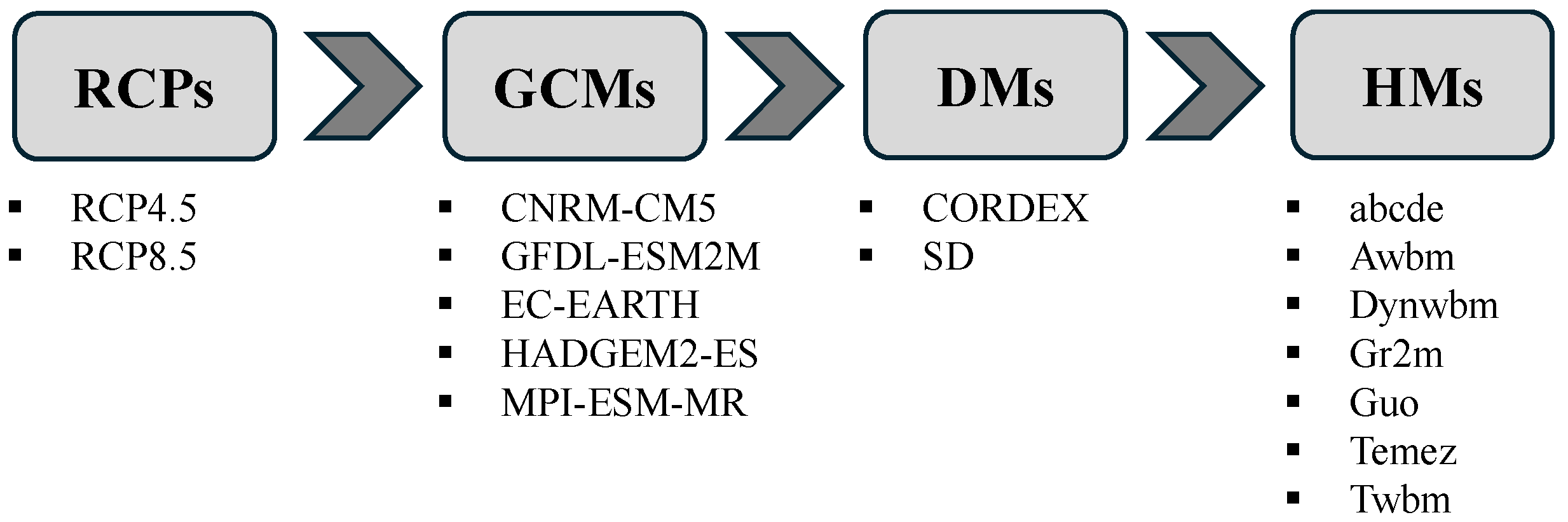


| GCMs | Horizontal Grid Spacing (Lat × Lon) | RCMs | Horizontal Grid Spacing (Lat × Lon) | Acronyms for CORDEX Models Used | Acronyms for Statistically Downscaled CMIP5 Models |
|---|---|---|---|---|---|
| CNRM-CM5 | 1.4° × 1.4° | RCA4 | 0.44° × 0.44° | CNRM-CRX | CNRM-SD |
| GFDL-ESM2M | 2.0° × 2.5° | RCA4 | 0.44° × 0.44° | GFDL-CRX | GFDL-SD |
| EC-EARTH | 1.125° × 1.125° | RCA4 | 0.44° × 0.44° | EARTH-CRX | EARTH-SD |
| HadGEM2-ES | 1.25° × 1.875° | RegCM4.4 | 0.44° × 0.44° | HadGEM-CRX | HadGEM-SD |
| MPI-ESM-MR | 1.875° × 1.875° | RegCM4.4 | 0.44° × 0.44° | MPI-CRX | MPI-SD |
| Weighting Methods | Negative Weight Possible | Constant Term (w0) | Bias Correction | Iterative | Constrained to Sum to Unity |
|---|---|---|---|---|---|
| Equal weight (EW) | X | X | X | X | ✓ |
| Bayesian model averaging (BMA) | X | X | ✓ | ✓ | ✓ |
| Representation of the annual cycle (RAC) | X | X | X | X | ✓ |
| Ordered weighted averaging (OWA) | X | X | ✓ | ✓ | ✓ |
| Granger–Ramanathan (GR) | ✓ | X | X | X | X |
| Uncertainty Optimized Multi-Model Ensemble (UO-MME) | ✓ | ✓ | ✓ | ✓ | X |
| (a) | w0 | w1 | w2 | w3 | w4 | w5 | w6 | w7 | NSEcal | NSEval | LNSEcal | LNSEval | |
| Constraint methods | |||||||||||||
| EW | - | 0.143 | 0.143 | 0.143 | 0.143 | 0.143 | 0.143 | 0.143 | 0.754 | 0.798 | 0.412 | 0.409 | |
| BMA | - | 0.156 | 0.127 | 0.183 | 0.140 | 0.126 | 0.118 | 0.151 | 0.760 | 0.802 | 0.423 | 0.419 | |
| RAC | - | 0.147 | 0.137 | 0.162 | 0.137 | 0.132 | 0.135 | 0.150 | 0.757 | 0.799 | 0.416 | 0.413 | |
| OWA | - | 0.045 | 0.033 | 0.783 | 0.019 | 0.022 | 0.027 | 0.071 | 0.793 | 0.800 | 0.563 | 0.557 | |
| Unconstraint methods | |||||||||||||
| GR | - | 0.603 | −0.143 | 0.629 | −0.135 | −0.317 | 0.000 | 0.359 | 0.804 | 0.814 | 0.668 | 0.685 | |
| DP1 | 0.430 | 0.646 | −0.251 | 0.788 | −0.413 | −0.031 | −0.240 | 0.498 | 0.792 | 0.798 | 0.664 | 0.658 | |
| DP2 | 0.501 | 0.647 | −0.266 | 0.727 | −0.377 | −0.006 | −0.268 | 0.504 | 0.794 | 0.792 | 0.653 | 0.642 | |
| DP3 | 0.576 | 0.673 | −0.279 | 0.712 | −0.403 | 0.130 | −0.388 | 0.509 | 0.789 | 0.788 | 0.648 | 0.632 | |
| DP4 | 0.646 | 0.674 | −0.294 | 0.650 | −0.367 | 0.156 | −0.416 | 0.515 | 0.786 | 0.776 | 0.628 | 0.612 | |
| DP5 | −0.017 | 1.585 | −0.118 | 0.335 | −0.747 | −0.483 | 0.182 | 0.309 | 0.755 | 0.790 | 0.601 | 0.746 | |
| (b) | w0 | w1 | w2 | w3 | w4 | w5 | w6 | w7 | NSEcal | NSEval | LNSEcal | LNSEval | |
| Constraint methods | |||||||||||||
| EW | - | 0.143 | 0.143 | 0.143 | 0.143 | 0.143 | 0.143 | 0.143 | 0.855 | 0.921 | 0.838 | 0.892 | |
| BMA | - | 0.163 | 0.137 | 0.111 | 0.181 | 0.096 | 0.118 | 0.193 | 0.856 | 0.922 | 0.840 | 0.896 | |
| RAC | - | 0.144 | 0.146 | 0.138 | 0.145 | 0.144 | 0.137 | 0.144 | 0.855 | 0.921 | 0.839 | 0.894 | |
| OWA | - | 0.084 | 0.582 | 0.047 | 0.124 | 0.055 | 0.042 | 0.066 | 0.860 | 0.907 | 0.850 | 0.913 | |
| Unconstraint methods | |||||||||||||
| GR | - | 0.559 | 1.256 | −0.113 | −0.088 | 0.151 | −0.076 | −0.689 | 0.866 | 0.901 | −0.341 | 0.154 | |
| DP1 | −0.037 | 1.163 | −0.298 | −0.174 | −0.276 | 0.222 | 0.397 | −0.045 | 0.835 | 0.898 | 0.805 | 0.858 | |
| DP2 | 0.077 | 1.161 | −0.224 | −0.142 | −0.404 | 0.187 | 0.407 | −0.134 | 0.804 | 0.873 | 0.811 | 0.861 | |
| DP3 | −0.234 | 1.742 | −0.482 | −0.310 | −0.578 | −0.570 | 0.402 | 0.716 | 0.815 | 0.873 | 0.809 | 0.863 | |
| DP4 | 0.128 | 1.226 | −0.536 | −0.169 | −0.290 | 0.323 | 0.405 | −0.046 | 0.812 | 0.881 | 0.796 | 0.849 | |
| DP5 | −0.214 | 1.910 | −0.541 | −0.436 | −0.603 | −0.547 | 0.405 | 0.726 | 0.810 | 0.857 | 0.807 | 0.862 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ersoy, Z.B.; Fistikoglu, O.; Okkan, U. Exploring the Potential of Multi-Hydrological Model Weighting Schemes to Reduce Uncertainty in Runoff Projections. Water 2025, 17, 2919. https://doi.org/10.3390/w17202919
Ersoy ZB, Fistikoglu O, Okkan U. Exploring the Potential of Multi-Hydrological Model Weighting Schemes to Reduce Uncertainty in Runoff Projections. Water. 2025; 17(20):2919. https://doi.org/10.3390/w17202919
Chicago/Turabian StyleErsoy, Zeynep Beril, Okan Fistikoglu, and Umut Okkan. 2025. "Exploring the Potential of Multi-Hydrological Model Weighting Schemes to Reduce Uncertainty in Runoff Projections" Water 17, no. 20: 2919. https://doi.org/10.3390/w17202919
APA StyleErsoy, Z. B., Fistikoglu, O., & Okkan, U. (2025). Exploring the Potential of Multi-Hydrological Model Weighting Schemes to Reduce Uncertainty in Runoff Projections. Water, 17(20), 2919. https://doi.org/10.3390/w17202919






