Analysis of Recharge Efficiency Under Barrier Effects Incurred by Adjacent Underground Structures
Abstract
1. Introduction
2. Project Background
3. Pumping Test
4. Numerical Modelling
4.1. Modelling Scheme
4.2. Model Setup
4.2.1. Model Dimension
4.2.2. Constitutive Model
4.3. Boundary Conditions and Simulation of Dewatering and Recharge
4.4. Model Validation
5. Simulation Results and Analysis
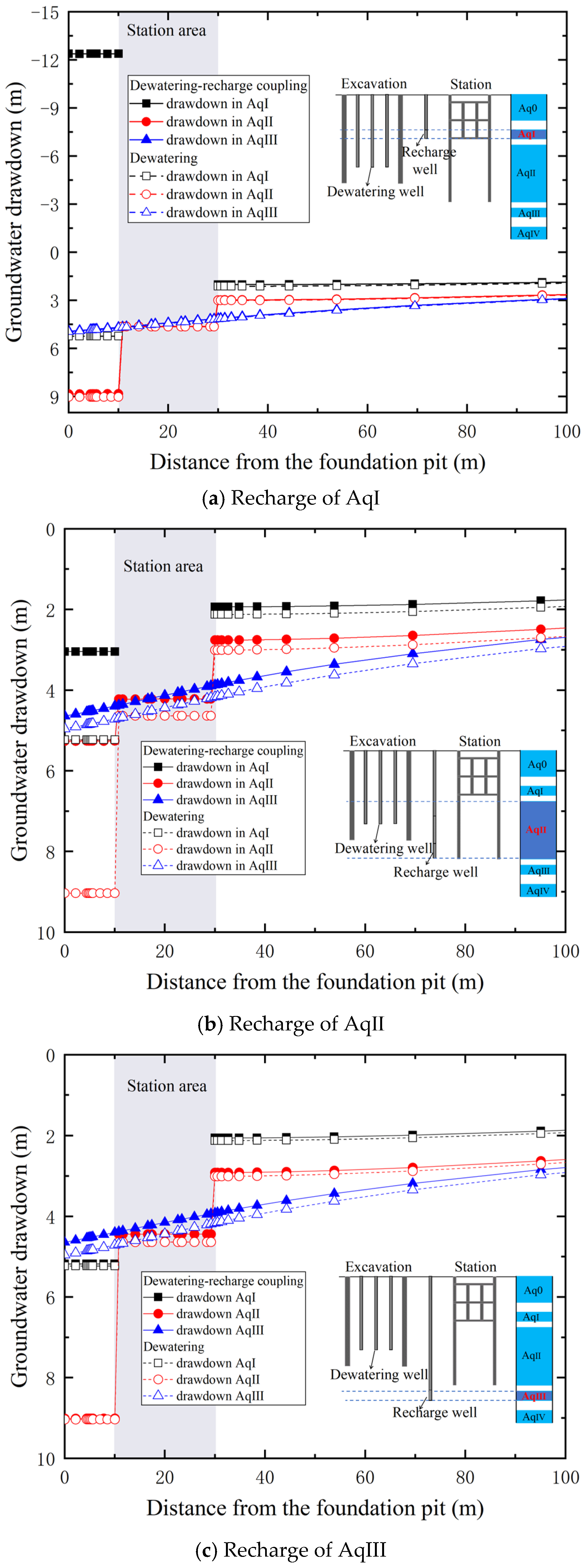
5.1. Response of Groundwater
5.1.1. Groundwater Drawdown
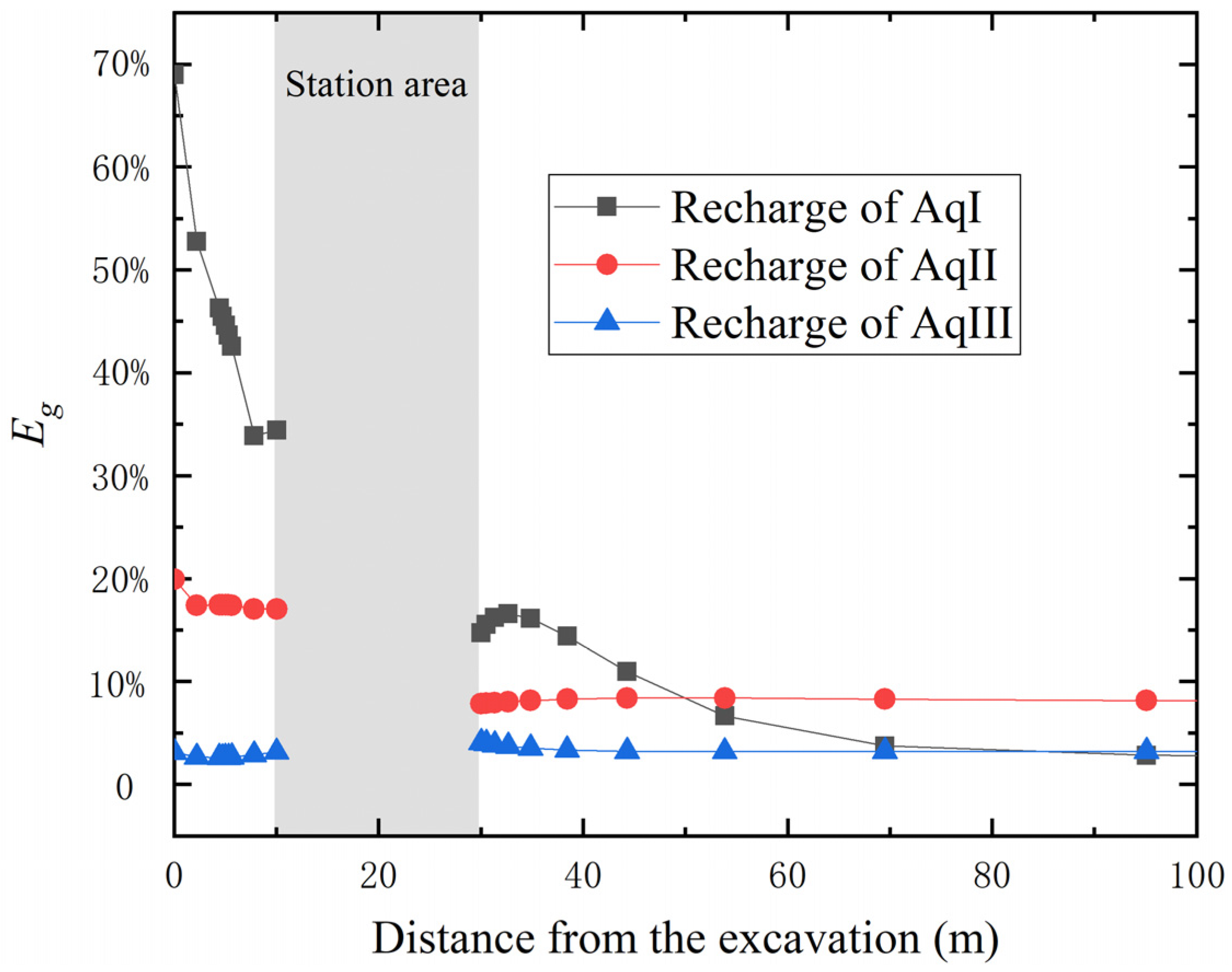
5.1.2. Analysis of Ew
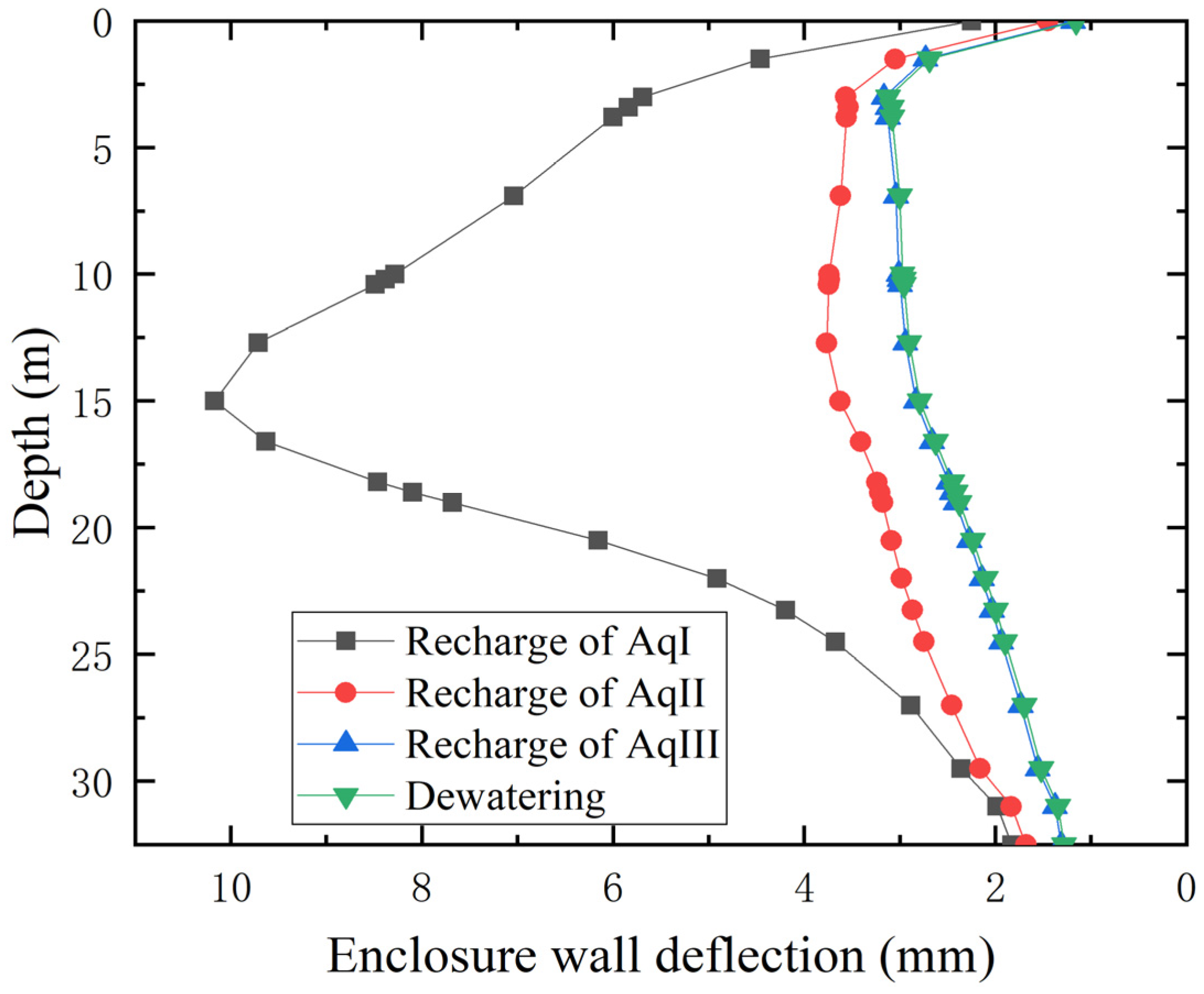
5.2. Response of Enclosure Wall
5.2.1. Enclosure Wall Deflection
5.2.2. Analysis of η
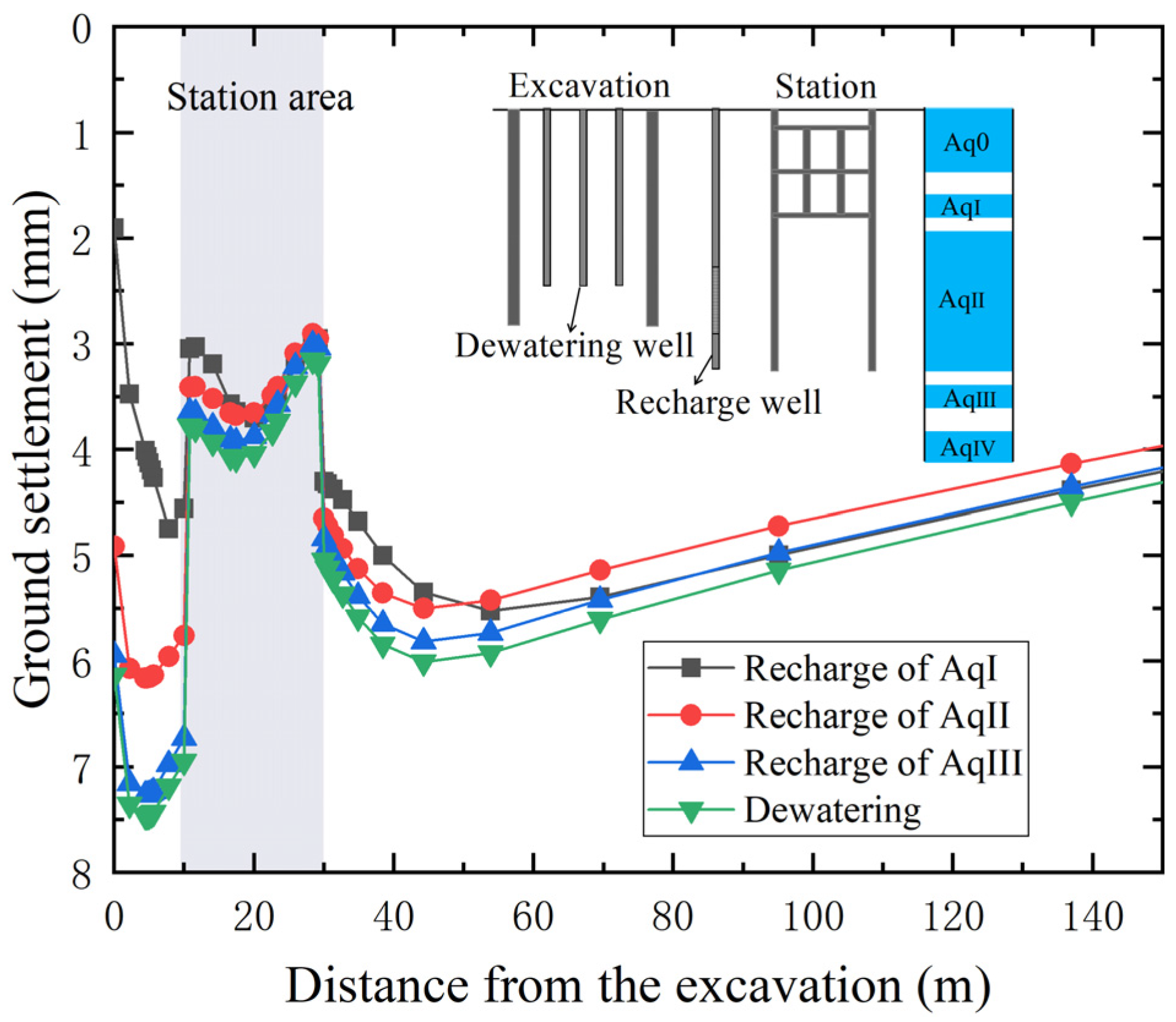
5.3. Response of Soil
5.3.1. Ground Settlement
5.3.2. Analysis of Eg
6. Discussion
7. Conclusions
- In the process of dewatering and the recharge of the foundation pit, the existence of adjacent underground structures will aggravate the fluctuation of groundwater levels. Therefore, the underground barrier should be considered in the design of the recharge to obtain the expected recharge effect.
- When recharging AqI, which is completely cut off by the enclosure and the station, both the groundwater level rise and enclosure deflection induced by recharge are dramatic; therefore, caution should be taken when recharging under this condition to avoid aggravating the deformation of the surrounding environment due to difficulty controlling the recharge process.
- When recharging AqIII, which is not cut off by the underground structure, most of the recharged water flows far away from the foundation pit, resulting in a low recharge efficiency.
- Recharging AqII, which is an aquifer with a hydraulic connection between the inside and outside of the foundation pit, can significantly raise the groundwater of each aquifer, and effectively control the ground settlement without obviously increasing the deflection of the enclosure; engineers could benefit from this recharge scheme to achieve a better recharge effect under the barrier effect.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yin, Z.-Y.; Yin, J.-H.; Huang, H.-W. Rate-Dependent and Long-Term Yield Stress and Strength of Soft Wenzhou Marine Clay: Experiments and Modeling. Mar. Georesources Geotechnol. 2015, 33, 79–91. [Google Scholar] [CrossRef]
- Yin, Z.-Y.; Xu, Q.; Hicher, P.-Y. A simple critical-state-based double-yield-surface model for clay behavior under complex loading. Acta Geotech. 2013, 8, 509–523. [Google Scholar] [CrossRef]
- Wang, J.; Feng, B.; Liu, Y.; Wu, L.; Zhu, Y.; Zhang, X.; Tang, Y.; Yang, P. Controlling subsidence caused by de-watering in a deep foundation pit. Bull. Eng. Geol. Environ. 2012, 71, 545–555. [Google Scholar] [CrossRef]
- Shen, S.L.; Wang, Z.F.; Cheng, W.C. Estimation of lateral displacement induced by jet grouting in clayey soils. Géotechnique 2017, 67, 621–630. [Google Scholar] [CrossRef]
- Luo, Z.; Zhang, Y.; Wu, Y. Finite Element Numerical Simulation of Three-Dimensional Seepage Control for Deep Foundation Pit Dewatering. J. Hydrodyn. 2008, 20, 596–602. [Google Scholar] [CrossRef]
- Wu, Y.-X.; Shen, S.-L.; Yuan, D.-J. Characteristics of dewatering induced drawdown curve under blocking effect of retaining wall in aquifer. J. Hydrol. 2016, 539, 554–566. [Google Scholar] [CrossRef]
- Zeng, C.-F.; Powrie, W.; Xue, X.-L.; Li, M.-K.; Mei, G.-X. Effectiveness of a buttress wall in reducing retaining wall movement during dewatering before bulk excavation. Acta Geotech. 2021, 16, 3253–3267. [Google Scholar] [CrossRef]
- Du, Y.J.; Fan, R.D.; Liu, S.Y.; Reddy, K.R.; Jin, F. Workability, compressibility and hydraulic conductivity of zeolite-amended clayey soil/calcium-bentonite backfills for slurry-trench cutoff walls. Eng. Geol. 2015, 195, 258–268. [Google Scholar] [CrossRef]
- Xu, Y.-S.; Ma, L.; Shen, S.-L.; Sun, W.-J. Evaluation of land subsidence by considering underground structures that penetrate the aquifers of Shanghai, China. Hydrogeol. J. 2012, 20, 1623–1634. [Google Scholar] [CrossRef]
- Wang, Y.; Jiao, J.J. Origin of groundwater salinity and hydrogeochemical processes in the confined Quaternary aquifer of the Pearl River Delta, China. J. Hydrol. 2012, 438–439, 112–124. [Google Scholar] [CrossRef]
- Wang, J.; Feng, B.; Yu, H.; Guo, T.; Yang, G.; Tang, J. Numerical study of dewatering in a large deep foundation pit. Env. Earth Sci. 2013, 69, 863–872. [Google Scholar] [CrossRef]
- Pujades, E.; Vázquez-Suñé, E.; Carrera, J.; Vilarrasa, V.; De Simone, S.; Jurado, A.; Ledesma, A.; Ramos, G.; Lloret, A. Deep enclosures versus pumping to reduce settlements during shaft excavations. Eng. Geol. 2014, 169, 100–111. [Google Scholar] [CrossRef]
- Zeng, C.-F.; Powrie, W.; Chen, H.-B.; Wang, S.; Diao, Y.; Xue, X.-L. Ground Behavior due to Dewatering Inside a Foundation Pit Considering the Barrier Effect of Preexisting Building Piles on Aquifer Flow. J. Geotech. Geoenviron Eng. 2024, 150, 05024004. [Google Scholar] [CrossRef]
- Pujades, E.; Jurado, A. Groundwater-related aspects during the development of deep excavations below the water table: A short review. Undergr. Space 2021, 6, 35–45. [Google Scholar] [CrossRef]
- Xu, Y.-S.; Wu, H.-N.; Wang, B.Z.-F.; Yang, T.-L. Dewatering induced subsidence during excavation in a Shanghai soft deposit. Env. Earth Sci. 2017, 76, 351. [Google Scholar] [CrossRef]
- Figueroa-Miranda, S.; Tuxpan-Vargas, J.; Ramos-Leal, J.A.; Hernández-Madrigal, V.M.; Villaseñor-Reyes, C.I. Land subsidence by groundwater over-exploitation from aquifers in tectonic valleys of Central Mexico: A review. Eng. Geol. 2018, 246, 91–106. [Google Scholar] [CrossRef]
- Shen, S.-L.; Xu, Y.-S. Numerical evaluation of land subsidence induced by groundwater pumping in Shanghai. Can. Geotech. J. 2011, 48, 1378–1392. [Google Scholar] [CrossRef]
- Zeng, C.-F.; Song, W.-W.; Xue, X.-L.; Li, M.-K.; Bai, N.; Mei, G.-X. Construction dewatering in a metro station incorporating buttress retaining wall to limit ground settlement: Insights from experimental modelling. Tunn. Undergr. Space Technol. 2021, 116, 104124. [Google Scholar] [CrossRef]
- Wu, Y.-X.; Wu, H.-N.; Shen, S.-L.; Xu, Y.-S. Behaviour of multi-aquifer system during pumping test. JGS Spec. Publ. 2015, 1, 15–18. [Google Scholar] [CrossRef]
- Xie, Z.-F.; Shen, S.-L.; Arulrajah, A.; Horpibulsuk, S. Environmentally sustainable groundwater control during dewatering with barriers: A case study in Shanghai. Undergr. Space 2021, 6, 12–23. [Google Scholar] [CrossRef]
- Zhang, Y.-Q.; Wang, J.-H.; Chen, J.-J.; Li, M.-G. Numerical study on the responses of groundwater and strata to pumping and recharge in a deep confined aquifer. J. Hydrol. 2017, 548, 342–352. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, J.; Zhang, Y.; Gao, Y. Cause investigation of damages in existing building adjacent to foundation pit in construction. Eng. Fail. Anal. 2018, 83, 117–124. [Google Scholar] [CrossRef]
- He, D.; Zeng, C.; Xu, C.; Xue, X.; Zhao, Y.; Han, L.; Sun, H. Barrier Effect of Existing Building Pile on the Responses of Groundwater and Soil During Foundation Pit Dewatering. Water 2024, 16, 2977. [Google Scholar] [CrossRef]
- Wu, Y.-X.; Zheng, Q.; Zhou, A.; Shen, S.-L. Numerical evaluation of the ground response induced by dewatering in a multi-aquifer system. Geosci. Front. 2021, 12, 101209. [Google Scholar] [CrossRef]
- Zhou, N.; Vermeer, P.A.; Lou, R.; Tang, Y.; Jiang, S. Numerical simulation of deep foundation pit dewatering and optimization of controlling land subsidence. Eng. Geol. 2010, 114, 251–260. [Google Scholar] [CrossRef]
- Pujades, E.; Vàzquez-Suñé, E.; Carrera, J.; Jurado, A. Dewatering of a deep excavation undertaken in a layered soil. Eng. Geol. 2014, 178, 15–27. [Google Scholar] [CrossRef]
- Zeng, C.-F.; Wang, S.; Xue, X.-L.; Zheng, G.; Mei, G.-X. Characteristics of ground settlement due to combined actions of groundwater drawdown and enclosure wall movement. Acta Geotech. 2022, 17, 4095–4112. [Google Scholar] [CrossRef]
- Shen, S.-L.; Lyu, H.-M.; Zhou, A.; Lu, L.-H.; Li, G.; Hu, B.-B. Automatic control of groundwater balance to combat dewatering during construction of a metro system. Autom. Constr. 2021, 123, 103536. [Google Scholar] [CrossRef]
- Wang, X.-W.; Yang, T.-L.; Xu, Y.-S.; Shen, S.-L. Evaluation of optimized depth of waterproof curtain to mitigate negative impacts during dewatering. J. Hydrol. 2019, 577, 123969. [Google Scholar] [CrossRef]
- Lyu, H.-M.; Shen, S.-L.; Wu, Y.-X.; Zhou, A.-N. Calculation of groundwater head distribution with a close barrier during excavation dewatering in confined aquifer. Geosci. Front. 2021, 12, 791–803. [Google Scholar] [CrossRef]
- Attard, G.; Winiarski, T.; Rossier, Y.; Eisenlohr, L. Review: Impact of underground structures on the flow of urban groundwater. Hydrogeol. J. 2016, 24, 5–19. [Google Scholar] [CrossRef]
- Liu, N.-W.; Peng, C.-X.; Li, M.-G.; Chen, J.-J. Hydro-mechanical behavior of a deep excavation with dewatering and recharge in soft deposits. Eng. Geol. 2022, 307, 106780. [Google Scholar] [CrossRef]
- Li, M.-G.; Chen, J.-J.; Xu, Y.-S.; Tong, D.-G.; Cao, W.-W.; Shi, Y.-J. Effects of groundwater exploitation and recharge on land subsidence and infrastructure settlement patterns in Shanghai. Eng. Geol. 2021, 282, 105995. [Google Scholar] [CrossRef]
- Zhang, Y.-Q.; Li, M.-G.; Wang, J.-H.; Chen, J.-J.; Zhu, Y.-F. Field tests of pumping-recharge technology for deep confined aquifers and its application to a deep excavation. Eng. Geol. 2017, 228, 249–259. [Google Scholar] [CrossRef]
- Gödeke, S. Simulation of groundwater mounding at a West Australian mine site. Env. Earth Sci. 2011, 64, 1363–1373. [Google Scholar] [CrossRef]
- Zeng, C.-F.; Zheng, G.; Xue, X.-L.; Mei, G.-X. Combined recharge: A method to prevent ground settlement induced by redevelopment of recharge wells. J. Hydrol. 2019, 568, 1–11. [Google Scholar] [CrossRef]
- Zhang, C.-H.; Wang, B.-T.; Liu, Y. Research on the Effective Control of Ground Settlement during Double-Layered Foundation Pit Dewatering Based on Seepage Control-Recharge Coupling Model. Yuan B, editor. Adv. Civ. Eng. 2022, 2022, 1–8. [Google Scholar] [CrossRef]
- Zheng, G.; Cao, J.R.; Cheng, X.S.; Ha, D.; Wang, F.J. Experimental study on the artificial recharge of semiconfined aquifers involved in deep excavation engineering. J. Hydrol. 2018, 557, 868–877. [Google Scholar] [CrossRef]
- Pujades, E.; López, A.; Carrera, J.; Vázquez-Suñé, E.; Jurado, A. Barrier effect of underground structures on aquifers. Eng. Geol. 2012, 145–146, 41–49. [Google Scholar] [CrossRef]
- Xu, Y.-S.; Shen, S.-L.; Ma, L.; Sun, W.-J.; Yin, Z.-Y. Evaluation of the blocking effect of retaining walls on groundwater seepage in aquifers with different insertion depths. Eng. Geol. 2014, 183, 254–264. [Google Scholar] [CrossRef]
- Zeng, C.-F.; Xue, X.-L.; Zheng, G.; Xue, T.-Y.; Mei, G.-X. Responses of retaining wall and surrounding ground to pre-excavation dewatering in an alternated multi-aquifer-aquitard system. J. Hydrol. 2018, 559, 609–626. [Google Scholar] [CrossRef]
- Font-Capo, J.; Pujades, E.; Vàzquez-Suñé, E.; Carrera, J.; Velasco, V.; Montfort, D. Assessment of the barrier effect caused by underground constructions on porous aquifers with low hydraulic gradient: A case study of the metro construction in Barcelona, Spain. Eng. Geol. 2015, 196, 238–250. [Google Scholar] [CrossRef]
- Tan, Y.; Li, X.; Kang, Z.; Liu, J.; Zhu, Y. Zoned Excavation of an Oversized Pit Close to an Existing Metro Line in Stiff Clay: Case Study. J. Perform. Constr. Facil. 2015, 29, 04014158. [Google Scholar] [CrossRef]
- Ma, L.; Xu, Y.-S.; Shen, S.-L.; Sun, W.-J. Evaluation of the hydraulic conductivity of aquifers with piles. Hydrogeol. J. 2014, 22, 371–382. [Google Scholar] [CrossRef]
- Xue, T.; Xue, X.; Long, S.; Chen, Q.; Lu, S.; Zeng, C. Effect of Pre-Existing Underground Structures on Groundwater Flow and Strata Movement Induced by Dewatering and Excavation. Water 2023, 15, 814. [Google Scholar] [CrossRef]
- Zeng, C.-F.; Liao, H.; Xue, X.-L.; Long, S.-C.; Luo, G.-J.; Diao, Y.; Li, M.-G. Responses of groundwater and soil to dewatering considering the barrier effect of adjacent metro station on multi-aquifers. J. Hydrol. 2022, 612, 128117. [Google Scholar] [CrossRef]
- Bear, J. Hydraulics of Groundwater; Courier Corporation: Mineola, NY, USA, 2012. [Google Scholar]
- Zeng, C.-F.; Chen, H.-B.; Liao, H.; Xue, X.-L.; Chen, Q.-N.; Diao, Y. Behaviours of groundwater and strata during dewatering of large-scale excavations with a nearby underground barrier. J. Hydrol. 2023, 620, 129400. [Google Scholar] [CrossRef]
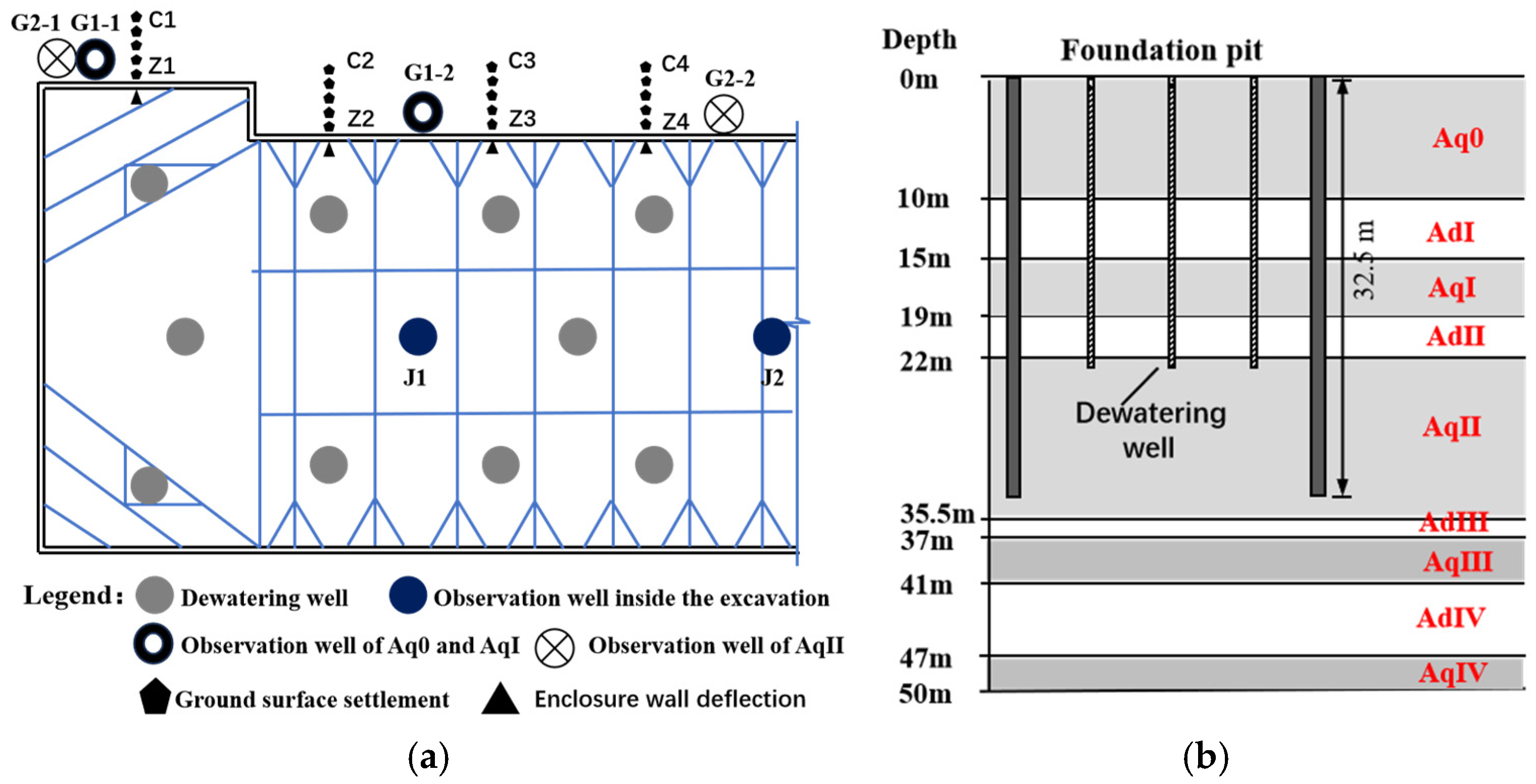

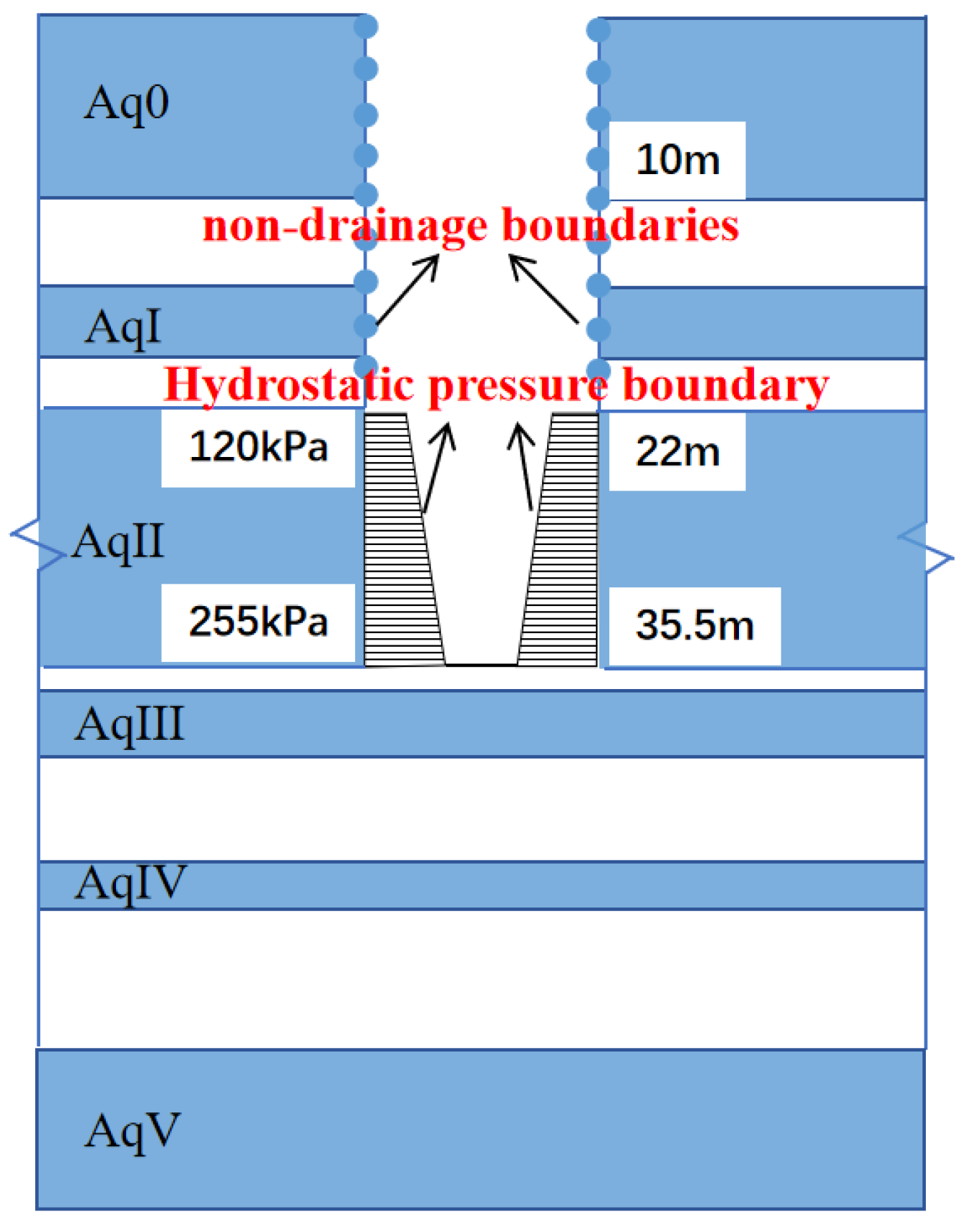
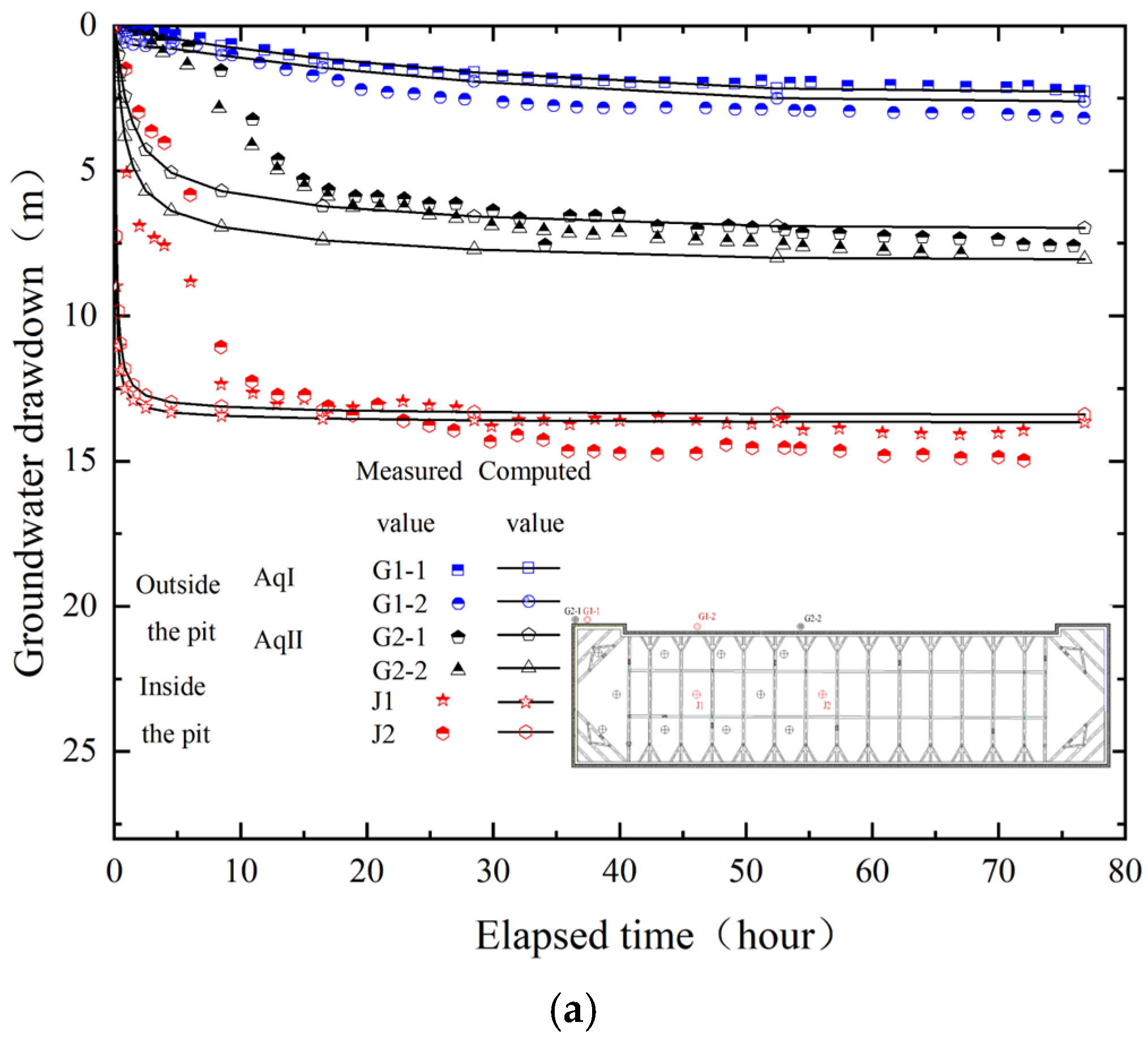
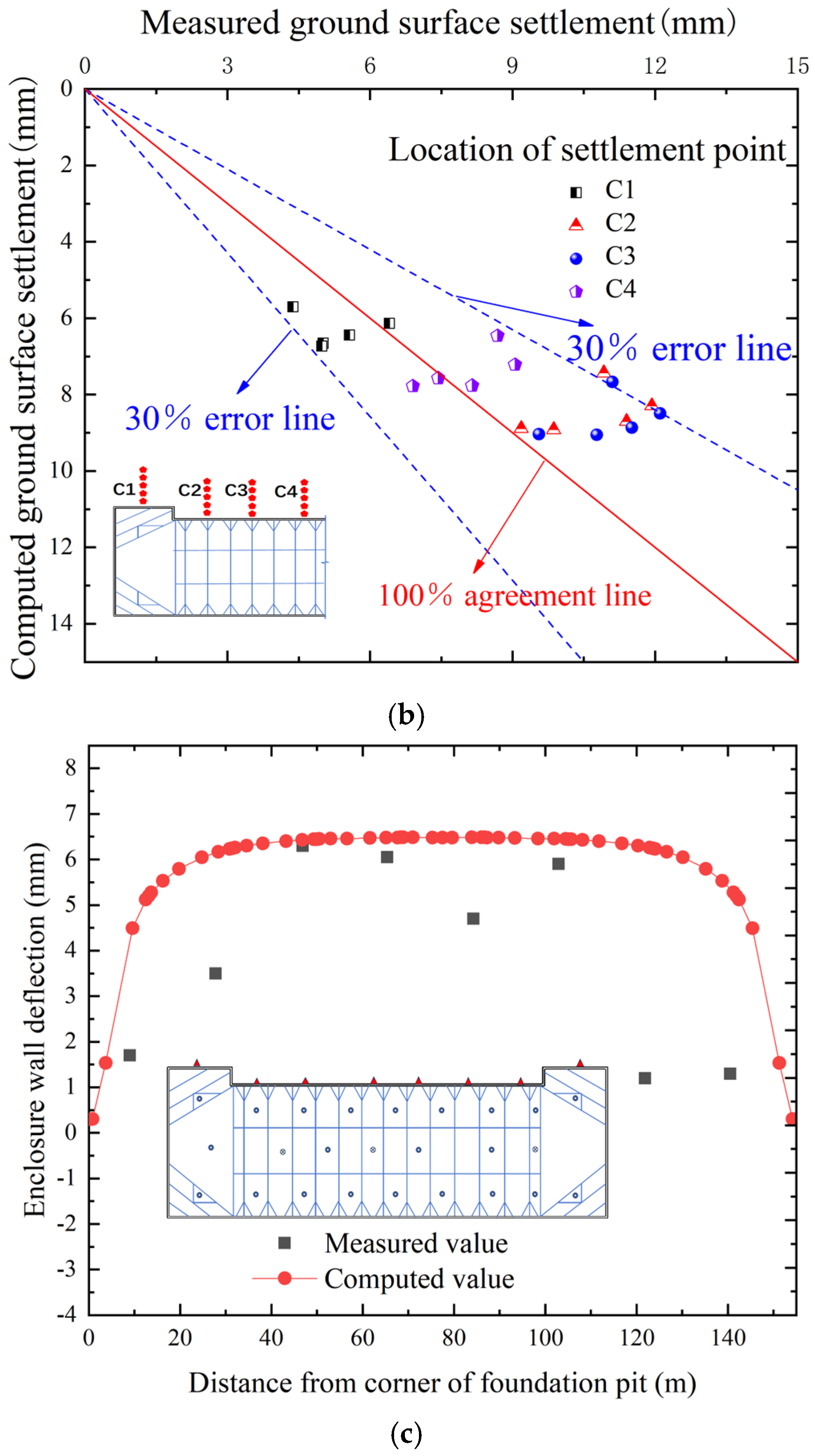


| Hydrological Property | Soil Classification | H (m) | Vs (m/s) | γ (kN/m3) | ω (%) | K0 (m/d) | e | Es (MPa) | φ′ (°) | c′ (kPa) |
|---|---|---|---|---|---|---|---|---|---|---|
| Aq0 | Silty clay | 10 | 152 | 19.1 | 30.4 | 0.577 | 0.85 | 5.9 | 25 | 17 |
| AdI | Silty clay | 15 | 172 | 19.3 | 28.7 | 0.61 | 0.81 | 5.2 | 23 | 18 |
| AqI | Silt | 19 | 266 | 20.2 | 21.7 | 0.44 | 0.62 | 13.6 | 34 | 10 |
| AdII | Silty clay | 22 | 246 | 19.9 | 25.1 | 0.56 | 0.71 | 6.1 | 26 | 19 |
| AqII | Silt | 24.5 | 278 | 20.4 | 22.3 | 0.44 | 0.55 | 11.9 | 34 | 8 |
| Silt | 29.5 | 278 | 20.6 | 20.9 | 0.41 | 0.58 | 13.1 | 36 | 8 | |
| Silty clay | 32.5 | 253 | 20.3 | 23.6 | 0.56 | 0.66 | 7.4 | 26 | 17 | |
| Silty sand | 35.5 | 300 | 20.6 | 16.3 | 0.398 | 0.521 | 16.3 | 37 | 7 | |
| AdIII | Silty clay | 37 | 274.5 | 20.5 | 20.7 | 0.56 | 0.6 | 8.9 | 26 | 19 |
| AqIII | Silt | 41 | 328 | 20.7 | 18.2 | 0.44 | 0.54 | 17 | 34 | 10 |
| AdIV | Silty clay | 47 | 315 | 20.3 | 22.1 | 0.546 | 0.64 | 9.2 | 27 | 18 |
| AqIV | Silty sand | 50 | 360 | 20.6 | 17.5 | 0.384 | 0.53 | 23 | 38 | 7 |
| D/m | H/m | B/m | d/m | q (m3/h) | Recharged Aquifer |
|---|---|---|---|---|---|
| 10 | 35.5 | 40 | 18.4 | 1 | AqI |
| 10 | 35.5 | 40 | 18.4 | 1 | AqII |
| 10 | 35.5 | 40 | 18.4 | 1 | AqIII |
| Soil Classification | Depth (m) | γ (kN/m3) | φ′ (°) | c′ (kPa) | Ss (m−1) | KH (cm/s) | KV (cm/s) | E (MPa) | e |
|---|---|---|---|---|---|---|---|---|---|
| Silty clays with silt seams | 10.0 | 19.1 | 25 | 17 | 2.3 × 10−4 | 3.5 × 10−5 | 3.5 × 10−6 | 43.5 | 0.85 |
| Silty clays | 15.0 | 19.3 | 23 | 18 | 1.8 × 10−4 | 2.9 × 10−5 | 1.2 × 10−6 | 56.3 | 0.81 |
| Clayey silts | 19.0 | 20.2 | 34 | 10 | 7.3 × 10−5 | 2.3 × 10−4 | 1.2 × 10−4 | 137.6 | 0.62 |
| Silty clays | 22.0 | 19.9 | 26 | 19 | 8.4 × 10−5 | 6.9 × 10−6 | 1.2 × 10−6 | 118.6 | 0.71 |
| Sandy silts | 24.5 | 20.4 | 34 | 8 | 6.6 × 10−5 | 2.9 × 10−3 | 5.8 × 10−4 | 151.8 | 0.55 |
| Sandy silts | 29.5 | 20.6 | 36 | 8 | 6.5 × 10−5 | 1.2 × 10−3 | 2.3 × 10−4 | 153.3 | 0.58 |
| Silty clays with silt seams | 32.5 | 20.3 | 26 | 17 | 7.8 × 10−5 | 1.2 × 10−3 | 1.9 × 10−4 | 128.0 | 0.66 |
| Silty sands | 35.5 | 20.6 | 37 | 7 | 5.6 × 10−5 | 3.5 × 10−3 | 6.9 × 10−4 | 178.5 | 0.521 |
| Silty clays | 37.0 | 20.5 | 26 | 19 | 6.6 × 10−5 | 2.3 × 10−5 | 4.6 × 10−6 | 152.2 | 0.6 |
| Sandy silts | 41.0 | 20.7 | 34 | 10 | 4.7 × 10−5 | 3.5 × 10−3 | 1.0 × 10−3 | 214.5 | 0.54 |
| Silty clays | 47.0 | 20.3 | 27 | 18 | 5.0 × 10−5 | 5.8 × 10−7 | 1.2 × 10−7 | 198.4 | 0.64 |
| Silty sands | 50.0 | 20.6 | 38 | 7 | 3.9 × 10−5 | 4.1 × 10−3 | 1.7 × 10−3 | 257 | 0.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, K.; Xu, C.; Zeng, C.; Zhu, L.; Xue, X.; Han, L. Analysis of Recharge Efficiency Under Barrier Effects Incurred by Adjacent Underground Structures. Water 2025, 17, 257. https://doi.org/10.3390/w17020257
Yang K, Xu C, Zeng C, Zhu L, Xue X, Han L. Analysis of Recharge Efficiency Under Barrier Effects Incurred by Adjacent Underground Structures. Water. 2025; 17(2):257. https://doi.org/10.3390/w17020257
Chicago/Turabian StyleYang, Kelang, Changjie Xu, Chaofeng Zeng, Long Zhu, Xiuli Xue, and Lei Han. 2025. "Analysis of Recharge Efficiency Under Barrier Effects Incurred by Adjacent Underground Structures" Water 17, no. 2: 257. https://doi.org/10.3390/w17020257
APA StyleYang, K., Xu, C., Zeng, C., Zhu, L., Xue, X., & Han, L. (2025). Analysis of Recharge Efficiency Under Barrier Effects Incurred by Adjacent Underground Structures. Water, 17(2), 257. https://doi.org/10.3390/w17020257







