Abstract
This work numerically investigates the fully nonlinear evolution of the free surface of a deep non-conducting liquid in a strong tangential electric field based on the method of dynamic conformal transformations. Direct numerical simulation revealed two possible scenarios for the evolution of nonlinear surface electro-hydrodynamic waves: collapse at finite time (in the non-viscous case) and turbulence generated by strongly nonlinear shock-like waves (taking into account both dissipation and pumping of energy). In the process of wave breaking, regions with a steep wave front arise, in which the curvature of the boundary increases infinitely. The inclusion of viscosity prevents the formation of singularities, and the system transfers to a strongly turbulent mode of motion. The spectrum of surface disturbances is very well described by the Kuznetsov spectrum , which corresponds to the second-order singularities in the liquid boundary. The measured probability density functions demonstrate a high level of intermittency in the turbulent regime, i.e., extreme events such as shocks play a dominant role in the evolution of the system. The results of calculations such as the turbulence spectrum, type of surface singularity, and the presence of intermittency are in good qualitative agreement with recent experiments carried out by Ricard and Falcon for a ferrofluid in a magnetic field.
1. Introduction
The problem of the description of free surface water waves is the topic of many studies, starting from classical Stokes works [1,2] and ending with very recent papers; see, e.g., [3,4,5]. By now, the description of water waves has been extended to include a number of problems that take into account the influence of constant vorticity, mean fluid flow, and bottom topography effects [6,7,8,9,10]. It is well known that a stationary gravity wave (Stokes wave) propagating at a constant speed has a limiting amplitude, with which an angle at the wave crest approaches the value . For the limiting amplitude, the slope angles of the boundary undergo a discontinuity at the wave crest, and the curvature of the surface becomes infinite. The process of formation of such a singularity is strongly nonlinear, and its description is impossible within the framework of weakly nonlinear perturbative approaches. The tendency for singularity to occur initiates a strong wave turbulence regime, in which steep-front waves propagate at the fluid boundary [11]. The turbulence spectrum corresponds to , where is the spatial Fourier transform of surface elevations , and k is the wavenumber. Such a spectrum (also called the Kuznetsov spectrum [11]) is strongly nonlinear and is formed due to singularities in the curvature of the boundary. It should be noted that the strong turbulence regime differs significantly from the so-called weak turbulence [12,13,14], which can be realized in systems with small wave amplitudes. While weak turbulence in many wave systems [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30] has been well studied, the strong turbulence regime has been most studied only for acoustic shock waves [31,32,33,34,35]. Thus, the search for new, previously unexplored regimes of strong turbulence is an important and challenging task.
Another type of water wave is an electro-hydrodynamic (EHD) wave, which arises under the influence of an external electric field. Interest in the description of such an EHD flow is due to the possibility of controlling the evolution of the liquid surface using external force fields [36,37,38,39,40]. To date, various coherent structures (solitary waves, solitons, and wave collapses) that arise at the boundaries of liquids in external fields have been well studied; see [41,42,43,44,45]. The complex chaotic behavior of surface waves in external fields (EHD turbulence of surface waves) remains much less understood. Until now, only weak electro- and magneto-hydrodynamic wave turbulence has been investigated in detail, when the amplitudes of surface waves are small [46,47,48,49,50]. In recent experimental work [51,52], a regime of strong magneto-hydrodynamic turbulence on the surface of a ferrofluid in a horizontal magnetic field was observed for the first time. The authors found that in an external magnetic field, surface waves collapse. When waves break, regions with a steep wave front arise, and the curvature of the boundary increases infinitely, i.e., similarly to a Stokes wave. The difference between the observed behavior and classical Stokes waves is that the surface magneto-hydrodynamic waves transform into shocks, but not into corner-type singularities. In fact, the authors observed a regime of strong turbulence with acoustic-like shock waves with the Kuznetsov turbulence spectrum for surface elevations. To theoretically describe the discovered phenomenon, the authors [51,52] used a phenomenological approach based on the model Burgers equation. The authors obtained qualitative agreement with the experimental results. However, a complete theoretical description of the strong turbulence regime within the framework of the initial hydrodynamic equations of liquid flow has not yet been proposed.
In this work, we perform a direct numerical simulation of the fully nonlinear evolution of a dielectric liquid with a free surface placed in an external horizontal electric field to show the possibility of transition to a strong turbulence regime. Melcher and Schwarz showed [53] that the problem of describing such waves is mathematically fully equivalent to waves on a ferrofluid surface in a magnetic field. For this reason, the results obtained in this paper will also be applicable to magneto-hydrodynamic waves. All simulations are performed for the case of a strong external field (the effects of capillarity and gravity are not taken into account). The results of numerical modeling show that in the absence of viscosity, surface waves do tend to break. At singular points, regions with a steep wave front arise (angles of boundary slope tend to 90 degrees), and the curvature of the boundary increases infinitely. These results are in very good agreement with experimental work [51,52] and our earlier studies [54,55]. For the first time, within the framework of the method of dynamic conformal transformations, we carried out calculations taking into account energy dissipation (phenomenological accounting of viscosity). The viscosity effect regularizes the evolution of surface waves, and the addition of an external random force (mechanical pumping) leads to the formation of a quasi-stationary turbulent state. In this strong turbulent regime, large deviations of the probability density functions from the normal Gaussian distribution occur, i.e., a high level of intermittency is observed. The calculated surface turbulence spectrum is well described by the power-law dependence with the exponent , both in wavenumber and frequency regions, indicating the dominant influence of singularities in the boundary curvature. Thus, in this work we have confirmed for the first time the possibility of realizing the strong turbulence regime of electro-hydrodynamic water waves based on the direct numerical simulation of the fully nonlinear hydrodynamic equations.
2. Model Equations
We consider an ideal dielectric (there are no free charges) deep fluid subjected to a strong tangential electric field of a value E. Let the Cartesian coordinate system be such that the equation determines the deviation of the free surface from the unperturbed state . We also assume that the relative dielectric constant of the liquid is high, i.e., , so that electric field lines are directed tangentially to the boundary of the liquid. This assumption allows us to apply the conformal mapping technique for the description of the fluid flow. Such liquids include a wide class of substances, such as distilled water ( at 25 °C) and various alcohols (ethyl alcohol , methanol ), see [56].
The velocity potential and electric field potentials (inside) and (outside) of the liquid satisfy the Laplace equation:
At the liquid surface , the dynamic and kinematic boundary conditions are imposed in the form
where is the nabla operator, g is the gravitational acceleration, is the dielectric constant of vacuum, and and are the surface tension and mass density of the liquid, respectively. The motion of the liquid vanishes with increasing depth; i.e., at . For a tangential electric field, the following boundary condition is satisfied on the surface of the liquid: , where stands for the normal derivative to a free surface. The potentials and are related through the condition of continuity of the electric field strength at the liquid boundary: at . In the trivial case of free surface being flat, we have for the potentials: , , and .
The total energy of the system (Hamiltonian) has the form
The system of Equations (1) and (2) can be represented in terms of the variational derivatives of the Hamiltonian:
where the functions and are the canonically conjugate variables. This system of equations describes the fully nonlinear evolution of capillary–gravity waves on the free surface of the liquid in the presence of an external tangential electric field. The minimum phase velocity of pure capillary–gravity waves is , which is reached at the wavelength corresponding to the period . Below, we will consider the case of a strong electric field: . In such a case, the effects of gravity and capillarity can be neglected. In the linear approximation, the described system is reduced to the dispersion relation [53]:
According to this dispersion law, linear surface waves propagate without dispersion with the speed . It is convenient to introduce the dimensionless variables using the typical wavelength as the horizontal and vertical length, as the velocity potential scale, as the time scale, and as the electric potential scale. Note that in the situation of a strong external tangential field, Zubarev found exact solutions to the above-described system of equations [57,58]. Zubarev’s solutions describe stationary EHD surface waves propagating without distortion along or against the external field.
3. Numerical Model and Parameters
The numerical model used in this work is based on the conformal transformation of the region occupied by a liquid to the half-plane of new conformal variables , i.e., initially independent coordinates are now regarded as functions and . The liquid surface corresponds to the line :
Here, is the Hilbert transform defined in the Fourier space as . The profile of the free surface is determined in the parametric form . Since the procedure of deriving the equations of motion of the liquid in the conformal variables is well known (see [59,60,61]), we just write Equations (1) and (2) in conformal coordinates, adding terms responsible for the action of pumping and dissipation of energy:
where is the Jacobian of the transformation, is the viscosity operator, and is the random driving force acting at large scales. We introduced the terms responsible for the energy dissipation and pumping phenomenologically; in the Fourier space, they are defined as follows:
where are random numbers uniformly distributed in the interval , and are the constants defining the intensity of dissipation and pumping of energy, respectively, is the wavenumber at which the pumping amplitude reaches the maximum, and specifies the width of pumping.
In terms of the conformal variables, the total energy of system (3) is represented in the form
Here, the first term in the integrand corresponds to the kinetic energy of the system, and the second term is the potential energy of surface electro-hydrodynamic waves. In the case of an infinitesimal amplitude of surface waves and the absence of energy pumping and dissipation, Equations (5) and (6) are transformed to the dispersion relation (4).
The numerical solution of system (5) and (6) is based on highly accurate methods of direct numerical simulation. The differential and integral operators are calculated using pseudo-spectral methods with the total number of Fourier harmonics N; as a consequence, the boundary conditions are assumed to be periodic in space. The integration in time is performed by an explicit fourth-order Runge–Kutta method with the step . All calculations are carried out in the periodic region with the length with the following parameters: , and . To suppress the aliasing effect, a low-frequency filter eliminating higher harmonics is used at each step of the integration in time.
4. Simulation Results: Wave Breaking
First of all, we will present the results of modeling the wave breaking process in the absence of external forces (mechanical pumping) and viscosity, i.e., set the parameters: and . Since waves traveling in one direction do not change their shape, interaction is possible only between counter-propagating waves [62]. To describe the interaction of waves, we set the initial conditions as follows:
which describe the interaction of counter-propagating periodic waves with different amplitudes and wavelengths.
Direct numerical simulation shows that, during the interaction of waves, a steep wave front is formed at the liquid boundary; see Figure 1. The inclination angles of the liquid boundary in the shock front region tend to 90 degrees, and the steepness of the waves (the first spatial derivative ) reaches very high values of the order of 10; see Figure 2. The simulations were stopped at the moment in time , when the relative error calculation of the system energy (7) reached the value .
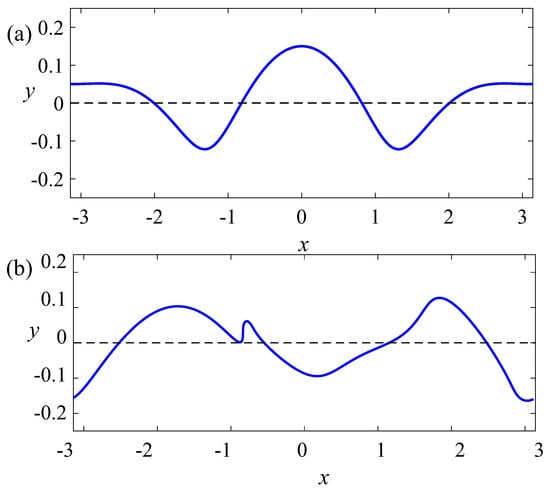
Figure 1.
The shape of the liquid surface is shown (a) at the initial moment and (b) at the end of the calculation interval, .
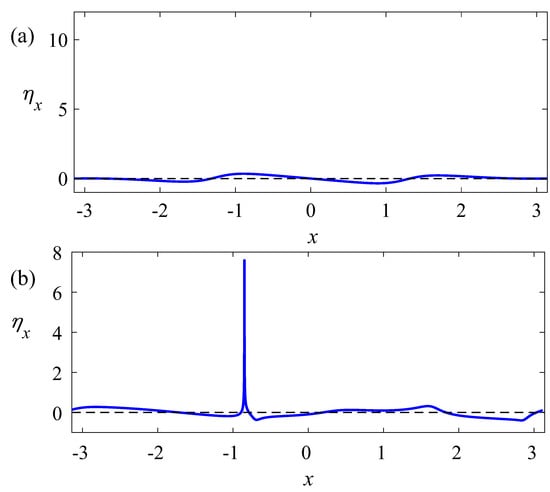
Figure 2.
The first spatial derivative of the surface profile (wave steepness) is shown (a) at the initial moment and (b) at the end of the calculation interval, .
Figure 3 shows the spatial dependence of the boundary curvature K:
at the initial moment of time and at the end of the calculation interval. It can be seen that the curvature of the boundary increases from almost zero to an extremely large value. The observed behavior is a collapse of the surface wave in a finite time. Figure 4 shows the time dependence of the maximum steepness and curvature of the waves. It can be seen that these values increase explosively over time.
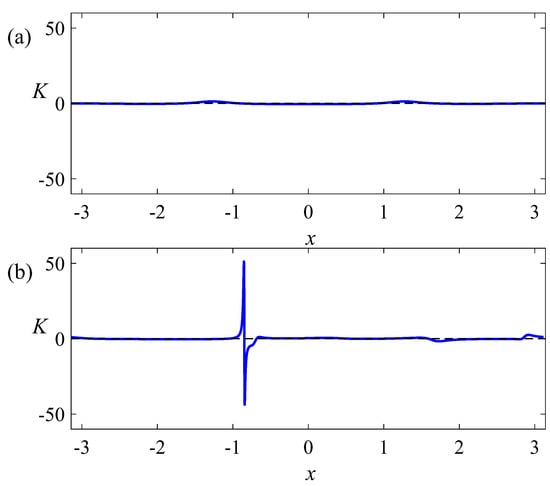
Figure 3.
The curvature of the liquid surface is shown (a) at the initial moment and (b) at the end of the calculation interval, .
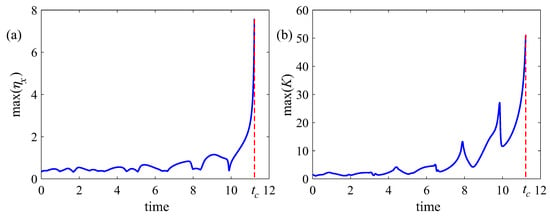
Figure 4.
Time dependencies of the maximum values of steepness (a) and curvature K (b) of the surface in the absence of dissipation and pumping of energy. Here, is the measured collapse time.
Thus, in the non-viscous case, surface electro-hydrodynamic waves break in a finite time. It is important that the collapse of surface waves begins from smooth initial conditions with small amplitude and ends with extremely large values of wave curvature and steepness. The results of the present study are in good agreement with our earlier work [54,55], where it was shown that free-surface electro-hydrodynamic waves tend to break under the influence of a sufficiently strong horizontal field. It should also be noted that similar curvature singularities arise on the fluid surface under the influence of strong vertical electric field [63,64]. It should also be noted that the collapse of electro-hydrodynamic waves differs from the classical breaking of gravity surface waves [65,66,67,68]. In the framework of the present model, we do not take into account the influence of gravity, which corresponds to a much smaller scale of waves.
The numerically observed surface evolution is in very good agreement with the experimental results [51,52] obtained for a magnetic fluid in a strong horizontal magnetic field. These experimental results show that surface magneto-hydrodynamic waves collapse with the formation of regions with high boundary curvature. The authors [51,52] observed the transition of the system of surface magneto-hydrodynamic waves into a regime of strong turbulence with the formation of shock-like waves. In this work, we show that adding viscosity to the key Equations (1) and (2) prevents the formation of singularities in finite time, i.e., the dissipative term regularizes the dynamics of nonlinear waves. The tendency to wave breaking leads to the development of strong electro-hydrodynamic wave turbulence on the liquid surface.
5. Simulation Results: Strong Turbulence Regime
The objective of this section is to simulate the strongly nonlinear dynamics of the fluid surface, taking into account both energy dissipation and pumping. To do this, we define the calculation parameters as follows: , , , and . According to the selected parameters, the free surface oscillations are excited in the long-wave region with random phases. Energy dissipation occurs over the entire range of wavenumbers and its intensity is proportional to .
Figure 5 shows the dependence of the total energy of the system (7) on time. The calculations show that the system of surface waves very quickly, in times of the order of a dimensionless unit, passes into a quasi-stationary regime, in which the energy of the system oscillates around some average value. The inset of Figure 5 shows the probability density function (PDF) for the wave steepness measured relative to its standard deviation . It can be seen that the probability density deviates significantly from the normal Gaussian distribution, which is valid for random uncorrelated processes. To characterize the deviations of the measured PDF from the pure Gaussian distribution, we use the skewness , which is a measure of the asymmetry of the probability distribution, and kurtosis , which is a degree of “tailedness” in the probability distribution, the angle brackets correspond to time averaging. These quantities have the values of and for pure Gaussian distributions. The found skewness is near , and kurtosis reaches the extremely high value of 94.4, demonstrating a high level of intermittency in the system. Thus, long tails appearing in the probability distribution indicate the appearance of a large number of extreme events, which are shock fronts observed in Figure 1. Note that a high level of intermittency is also observed in the experiments [51,52].
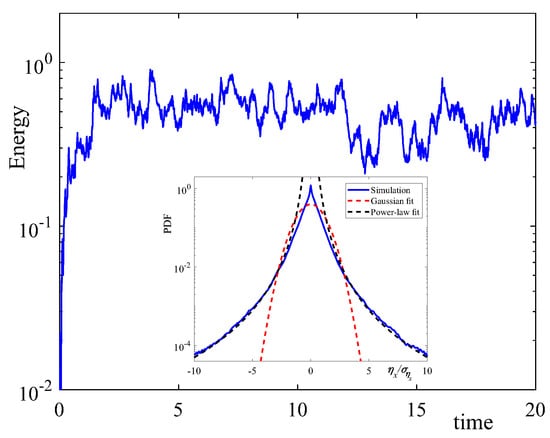
Figure 5.
The evolution of the total energy of the system (7) is shown in the strong turbulence regime. The inset shows the measured probability density function (PDF) for the wave steepness, where is the standard deviation of , the red dashed line corresponds to the Gaussian normal distribution, and the black dashed line corresponds to the power-law distribution: .
Figure 6 shows the main characteristics of the system in the strong turbulence regime: the shape of the surface (a), as well as the steepness (b) and curvature (c) of surface. On can indeed see that regions with steep wave fronts have formed at the liquid boundary that are similar to the structure observed in Figure 1b. The difference between the observed picture and Figure 1b is that, in this case, instead of one shock, a set of randomly distributed shock fronts formed at the liquid boundary.
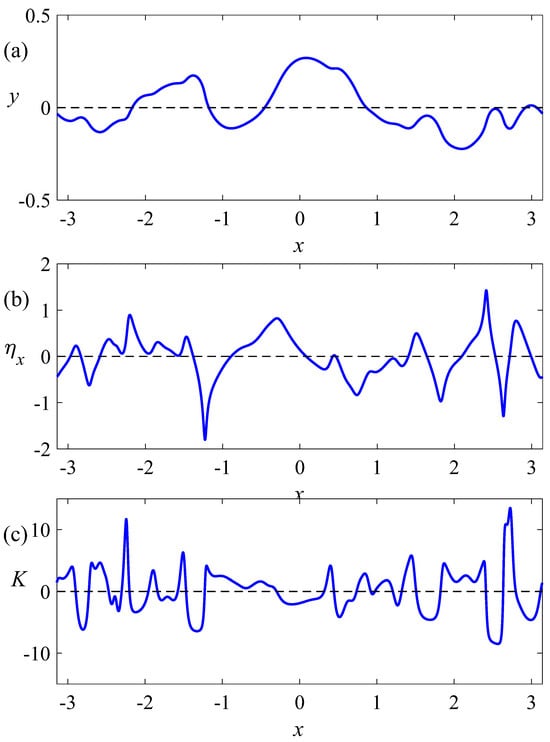
Figure 6.
Snapshots of the free surface (a), wave steepness (b), and the boundary curvature (c) are shown in the strong turbulence regime, .
The evolution of a single shock shown in Figure 1 is completely deterministic: starting from smooth initial conditions with very small amplitude, the surface wave collapses in a finite time. Adding a viscous term to Equations (5) and (6) prevents the formation of singularities, and the dynamics of surface waves become completely regular. Due to the viscosity effect, the forming shocks are dissipated. On the other hand, the energy pumping effect leads to the excitation of new shocks randomly distributed over the liquid boundary. Thus, when the pumping effect is completely compensated by viscosity, the energy balance observed in Figure 5 is achieved.
To demonstrate the complex and chaotic nature of the strong turbulence, Figure 7 shows a section of the evolution of surface waves over the time interval . One can indeed see that the motion of surface waves is quite complex, with new wave fronts appearing and disappearing over time. The steepness of the waves, reaching very high values , also demonstrates a very complex evolution; see Figure 7b. Finally, Figure 7c shows the evolution of the boundary curvature K. It is seen that narrow regions with a high value of K arise on the boundary. The trajectories of shock fronts (high curvature areas) are complex and intricate. Thus, under the combined effect of pumping and dissipation of energy, the system goes from singular behavior with infinite growth of the boundary curvature to a chaotic regime, which is a strong turbulence of random shocks. Note that the observed strong turbulence is very similar to soliton turbulence [69,70,71,72,73,74] (which is also called soliton gas). Each individual soliton is a coherent structure, but the ensemble of interacting solitons, or in our case shocks, exhibits complex chaotic behavior.
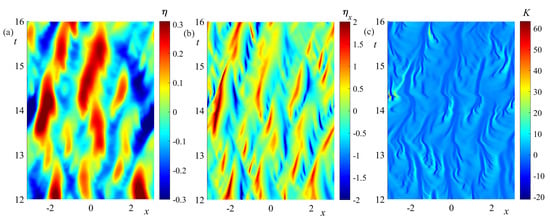
Figure 7.
The evolution of the free surface (a), wave steepness (b), and boundary curvature (c) is shown in the quasi-stationary strong turbulence regime in the time interval .
The main question in the study of turbulent motions is what spectrum is demonstrated by the system. Surface wave turbulence is usually described using the surface elevation spectrum: , where is the spatial Fourier transform of the function . To calculate this spectrum, we need to explicitly find the function . At the same time, the dependence obtained numerically from (5) and (6) does not have a direct physical meaning because it corresponds to the conformal coordinates . For the accurate description of turbulence, it is necessary to explicitly express the function on a uniform grid of the horizontal x axis. The parametric dependence obtained from Equations (5) and (6) is defined at sites i of the calculated nonuniform grid . To obtain the explicit dependence , it is necessary to interpolate the values of the function at new sites j with a fixed step . In this work, we use the cubic splines for the interpolation procedure. This approach was first proposed in our work [75] investigating weak turbulence of collinear capillary waves. As a result, the explicit dependence is determined with very high accuracy.
Figure 8 shows the spatial spectrum of surface elevations averaged over time in the strongly turbulent regime. It can be seen that the obtained spectrum agrees with high accuracy with the power law dependence, , which is the Kuznetsov spectrum for strong turbulence of water waves [11]. The slope of the spectrum corresponds to the singularities in the second spatial derivative, i.e., in the curvature of the boundary K. Indeed, following the work in [11], the discontinuities in the second derivative can be represented as a set of Dirac delta functions:
where is the total number of shocks, is the random position of each shock, is the delta function, and are the amplitudes of the curvature jumps. Using the differentiation rule of the delta functions in Fourier space, one can obtain the following dependence for the Fourier image of the surface shape:
where is a non-dimensional constant defining the normalization of the Fourier transform, in the case, . Finally, squaring the modulus of this expression and averaging over time, we obtain the spectrum of strong electro-hydrodynamic turbulence generated by singularities in the boundary curvature:
where is the number of shocks per unit length, and is the mean square of the curvature jump. The same analysis can be performed for the frequency spectrum . Since the system under study is dispersionless, i.e., the relationship between the wavenumber and frequency is linear (see (4)), the slope of the spectrum in the frequency domain will be the same as in the spectrum (9). Apparently, the forming singularities cause the deviation of the turbulence spectra obtained within the framework of weakly nonlinear models [76,77] from the weak turbulence spectra.
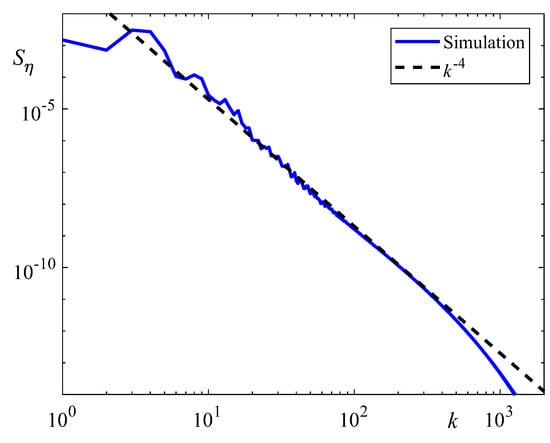
Figure 8.
The surface elevation spectrum averaged over the time interval .
Thus, the obtained results demonstrate the transition from singular behavior with unlimited growth of the boundary curvature to a strongly nonlinear turbulence regime when taking into account dissipation and pumping of energy. It is important that the spectrum of the observed turbulence, see Figure 8, agrees with high accuracy with the estimate (9) obtained under the assumption of the dominant influence of discontinuities in the boundary curvature. In essence, the observed turbulence is an analogue of one-dimensional sound turbulence with a shock-wave spectrum. This fact agrees well with the work in [78], which shows that the system of sound waves in 1D geometry always passes into a strongly nonlinear mode of motion.
6. Discussion
In this work, based on the method of dynamic conformal transformations, a direct numerical simulation of the fully nonlinear evolution of the free surface of a non-conducting liquid in a strong tangential electric field is carried out. To summarize, we present the most important results of this work:
- In the limit of a strong external field (gravity and capillarity forces are negligible) and in the absence of energy dissipation mechanism, the surface electro-hydrodynamic waves collapse in a finite time. The breaking of surface waves corresponds to the formation of a singularity in the second spatial derivative of the liquid surface (the curvature of the boundary increases infinitely).
- Inclusion of the viscosity prevents the formation of singularities in a finite time. Taking into account the external driving force, the system passes into a quasi-stationary mode of motion, when the pumping is completely compensated by dissipative effects.
- The measured probability density functions in the strong turbulence regime deviate significantly from the Gaussian distribution valid for random uncorrelated signals. The measured probability density has elongated tails, which are approximated by a power-law function. Such behavior of the distribution function indicates strong intermittency in the system, when extreme events such as shock waves play a dominant role.
- The shape of the fluid boundary in the strong turbulence regime is a set of second-order shocks randomly distributed along the liquid surface. Despite the fact that each individual shock is a coherent structure, the evolution of the shock wave ensemble becomes chaotic due to the random nature of the energy pumping.
- The calculated turbulence spectrum agrees with high accuracy with the estimate (9) obtained under the assumption of the dominant influence of curvature singularities. It should be noted that the observed spectrum is not derived from the assumption of smallness of nonlinear effects (weak turbulence) but is obtained on the basis of a fully nonlinear approach. Similar spectra of strong turbulence can be realized in acoustic shock waves, large-amplitude ocean and sea waves, and in developed vortex hydrodynamic turbulence [11,31,79,80,81,82].
All the results obtained in the work are obtained for the first time and are original. The simulations conducted open up prospects for further research: a detailed analysis of the statistical properties of turbulence, a spatio-temporal analysis of coherent structures, and a description of turbulence spectra both in the wavenumber and frequency domains.
7. Conclusions
In this work, we have for the first time generalized a fully nonlinear model of free surface flows based on dynamic conformal transformation method for the description of wave collapses leading to the development of strong electro-hydrodynamic wave turbulence. It is especially important to note that the obtained results are in high-accuracy agreement with the results of the experimental studies [51,52] conducted for a magnetic fluid in an external horizontal magnetic field. The calculated statistical characteristics of the turbulent regime, such as the turbulence spectrum, probability density functions, and the type of forming singularities, are in very good agreement with the experiments. Our approach is based on the use of full equations of electro-hydrodynamics, whereas the authors in [51,52] described the turbulence only phenomenologically based on the Burgers equation. In the future, the developed model can be used to describe other types of strong surface turbulence, for example, the turbulence of large-amplitude ocean waves.
Funding
The study was supported by a grant from the Russian Science Foundation No. 23-71-10012, https://rscf.ru/en/project/23-71-10012/, accessed on 10 December 2024.
Data Availability Statement
The data that support the findings of this study are available from the author upon reasonable request.
Acknowledgments
This work is supported by Russian Science Foundation project No. 23-71-10012.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Stokes, G.G. On the theory of oscillatory waves. Trans. Cam. Philos. Soc. 1847, 8, 441–455. [Google Scholar]
- Stokes, G.G. On the theory of oscillatory waves. Math. Phys. Pap. 1880, 1, 197–229. [Google Scholar]
- Dyachenko, S.A.; Lushnikov, P.M.; Korotkevich, A.O. Complex singularity of a Stokes wave. JETP Lett. 2014, 98, 675–679. [Google Scholar] [CrossRef]
- Dyachenko, S.A.; Lushnikov, P.M.; Korotkevich, A.O. Branch cuts of Stokes wave on deep water. Part I: Numerical solution and Padé approximation. Stud. Appl. Math. 2016, 137, 419–472. [Google Scholar] [CrossRef]
- Korotkevich, A.O.; Lushnikov, P.M.; Semenova, A.; Dyachenko, S.A. Superharmonic instability of Stokes waves. Stud. Appl. Math. 2023, 150, 119–134. [Google Scholar] [CrossRef]
- Dyachenko, S.A.; Hur, V.M. Stokes waves with constant vorticity: Folds, gaps and fluid bubbles. J. Fluid Mech. 2019, 878, 502–521. [Google Scholar] [CrossRef]
- Flamarion, M.V. Complex flow structures beneath rotational depression solitary waves in gravity-capillary flows. Wave Motion 2023, 117, 103108. [Google Scholar] [CrossRef]
- Flamarion, M.V.; Nachbin, A.; Ribeiro, R., Jr. Time-dependent Kelvin cat-eye structure due to current–topography interaction. J. Fluid Mech. 2020, 889, A11. [Google Scholar] [CrossRef]
- Flamarion, M.V.; Ribeiro, R., Jr. An iterative method to compute conformal mappings and their inverses in the context of water waves over topographies. Int. J. Numer. Methods Fluids 2021, 93, 3304–3311. [Google Scholar] [CrossRef]
- Flamarion, M.V.; Milewski, P.A.; Nachbin, A. Rotational waves generated by current-topography interaction. Stud. Appl. Math. 2019, 142, 433–464. [Google Scholar] [CrossRef]
- Kuznetsov, E.A. Turbulence spectra generated by singularities. JETP Lett. 2004, 80, 83. [Google Scholar] [CrossRef]
- Nazarenko, S. Wave Turbulence; Springer: Berlin, Germany, 2011. [Google Scholar]
- Zakharov, V.E.; L’vov, V.S.; Falkovich, G. Kolmogorov Spectra of Turbulence I: Wave Turbulence; Springer: Berlin, Germany, 1992. [Google Scholar]
- Newell, A.C.; Rumpf, B. Wave turbulence. Annu. Rev. Fluid Mech. 2011, 43, 59–78. [Google Scholar] [CrossRef]
- Zakharov, V.E. Weak turbulence in media with a decay spectrum. J. App. Mech. Tech. Phys. 1965, 6, 22. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Sagdeev, R.Z. Spectrum of acoustic turbulence. Sov. Phys. Dokl. 1970, 15, 439. [Google Scholar]
- Zakharov, V.E.; Filonenko, N.N. Weak turbulence of capillary waves. J. App. Mech. Tech. Phys. 1967, 8, 37–40. [Google Scholar] [CrossRef]
- Hasselmann, K. Feynman diagrams and interaction rules of wave-wave scattering processes. Rev. Geophys. 1966, 4, 1–32. [Google Scholar] [CrossRef]
- Rosenhaus, V.; Smolkin, V. Feynman rules for forced wave turbulence. J. High. Energy Phys. 2023, 2023, 1–41. [Google Scholar] [CrossRef]
- Rosenhaus, V.; Smolkin, M. Wave turbulence and the kinetic equation beyond leading order. Phys. Rev. E 2024, 109, 064127. [Google Scholar] [CrossRef]
- Galtier, S. Turbulence in space plasmas and beyond. J. Phys. A Math. Theor. 2018, 51, 293001. [Google Scholar] [CrossRef]
- David, V.; Galtier, S.; Meyrand, R. Monofractality in the solar wind at electron scales: Insights from kinetic Alfvén waves turbulence. Phys. Rev. Lett. 2024, 132, 085201. [Google Scholar] [CrossRef]
- Galtier, S.; Nazarenko, S.V.; Newell, A.C.; Pouquet, A. A weak turbulence theory for incompressible magnetohydrodynamics. J. Plasma Phys. 2000, 63, 447–488. [Google Scholar] [CrossRef]
- Tronko, N.; Nazarenko, S.V.; Galtier, S. Weak turbulence in two-dimensional magnetohydrodynamics. Phys. Rev. E 2013, 87, 033103. [Google Scholar] [CrossRef]
- Griffin, A.; Krstulovic, G.; Lvov, V.S.; Nazarenko, S. Energy spectrum of two-dimensional acoustic turbulence. Phys. Rev. Lett. 2022, 128, 224501. [Google Scholar] [CrossRef] [PubMed]
- Shavit, M.; Falkovich, G. Singular measures and information capacity of turbulent cascades. Phys. Rev. Lett. 2020, 125, 104501. [Google Scholar] [CrossRef] [PubMed]
- Frahm, K.M.; Shepelyansky, D.L. Random matrix model of Kolmogorov-Zakharov turbulence. Phys. Rev. E 2024, 109, 044201. [Google Scholar] [CrossRef]
- Semisalov, B.V.; Medvedev, S.B.; Nazarenko, S.V.; Fedoruk, M.P. Numerical analysis of the kinetic equation describing isotropic 4-wave interactions in non-linear physical systems. Commun. Nonlinear Sci. Numer. Simul. 2024, 133, 107957. [Google Scholar] [CrossRef]
- Galtier, S. Fast magneto-acoustic wave turbulence and the Iroshnikov–Kraichnan spectrum. J. Plasma Phys. 2023, 89, 905890205. [Google Scholar] [CrossRef]
- Kochurin, E.A.; Kuznetsov, E.A. Direct numerical simulation of acoustic turbulence: Zakharov–Sagdeev spectrum. JETP Lett. 2022, 116, 863–868. [Google Scholar] [CrossRef]
- Kadomtsev, B.B.; Petviashvili, V.I. On acoustic turbulence. Dokl. Akad. Nauk SSSR 1973, 208, 794–796. [Google Scholar]
- Gupta, P.; Scalo, C. Spectral energy cascade and decay in nonlinear acoustic waves. Phys. Rev. E 2018, 98, 033117. [Google Scholar] [CrossRef]
- Alam, S.; Sahu, P.K.; Verma, M.K. Universal functions for Burgers turbulence. Phys. Rev. Fluids 2022, 7, 074605. [Google Scholar] [CrossRef]
- Kolmakov, G.V.; Efimov, V.B.; Ganshin, A.N.; McClintock, P.V.; Mezhov-Deglin, L.P. Formation of a direct Kolmogorov-like cascade of second-sound waves in He II. Phys. Rev. Lett. 2006, 97, 155301. [Google Scholar] [CrossRef] [PubMed]
- Kochurin, E.A.; Kuznetsov, E.A. Three-Dimensional Acoustic Turbulence: Weak Versus Strong. Phys. Rev. Lett. 2024, 133, 207201. [Google Scholar] [CrossRef] [PubMed]
- Papageorgiou, D.T. Film flows in the presence of electric fields. Annu. Rev. Fluid Mech. 2019, 51, 155–187. [Google Scholar] [CrossRef]
- Medvedev, D.A.; Kupershtokh, A.L. Electric control of dielectric droplets and films. Phys. Fluids 2021, 33, 122103. [Google Scholar] [CrossRef]
- Kupershtokh, A.L.; Medvedev, D.A.; Alyanov, A.V. Heat flux from the surface in the process of the rupture of a thin liquid film by an electric field. Phys. Fluids 2023, 35, 102006. [Google Scholar] [CrossRef]
- Akbari, M.; Mortazavi, S. Three-dimensional numerical simulation of deformation of a single drop under uniform electric field. J. Appl. Fluid Mech. 2017, 10, 693–702. [Google Scholar] [CrossRef]
- Samanta, A. Effect of electric field on an oscillatory film flow. Phys. Fluids 2019, 31, 034109. [Google Scholar] [CrossRef]
- Zubarev, N.M.; Zubareva, O.V. Nondispersive propagation of waves with finite amplitudes on the surface of a dielectric liquid in a tangential electric field. Tech. Phys. Lett. 2006, 32, 886–888. [Google Scholar] [CrossRef]
- Doak, A.; Gao, T.; Vanden-Broeck, J.M. Global bifurcation of capillary-gravity dark solitary waves on the surface of a conducting fluid under normal electric fields. Q. J. Mech. Appl. Math. 2022, 75, 215–234. [Google Scholar] [CrossRef]
- Gao, T.; Doak, A.; Vanden-Broeck, J.M.; Wang, Z. Capillary–gravity waves on a dielectric fluid of finite depth under normal electric field. Eur. J. Mech. B Fluids 2019, 77, 98–107. [Google Scholar] [CrossRef]
- Guan, X.; Wang, Z. Interfacial electrohydrodynamic solitary waves under horizontal electric fields. J. Fluid Mech. 2022, 940, A15. [Google Scholar] [CrossRef]
- Flamarion, M.V.; Gao, T.; Ribeiro, R., Jr.; Doak, A. Flow structure beneath periodic waves with constant vorticity under normal electric fields. Phys. Fluids 2022, 34, 127119. [Google Scholar] [CrossRef]
- Boyer, F.; Falcon, E. Wave turbulence on the surface of a ferrofluid in a magnetic field. Phys. Rev. Lett. 2008, 101, 244502. [Google Scholar] [CrossRef] [PubMed]
- Dorbolo, S.; Falcon, E. Wave turbulence on the surface of a ferrofluid in a horizontal magnetic field. Phys. Rev. E 2011, 83, 046303. [Google Scholar] [CrossRef]
- Kochurin, E.; Ricard, G.; Zubarev, N.; Falcon, E. Three-dimensional direct numerical simulation of free-surface magnetohydrodynamic wave turbulence. Phys. Rev. E 2022, 105, L063101. [Google Scholar] [CrossRef]
- Dmitriev, I.A.; Kochurin, E.A.; Zubarev, N.M. Numerical study of free-surface electro-hydrodynamic wave turbulence. IEEE Trans. Dielectr. Electr. Insul. 2023, 30, 1408–1413. [Google Scholar] [CrossRef]
- Kochurin, E.A. Anisotropy of free-surface wave turbulence induced by a horizontal magnetic (electric) field. Chaos Solitons Fractals 2025, 191, 115828. [Google Scholar] [CrossRef]
- Ricard, G.; Falcon, E. Transition from wave turbulence to acousticlike shock-wave regime. Phys. Rev. Fluids 2023, 8, 014804. [Google Scholar] [CrossRef]
- Ricard, G.; Falcon, E. Experimental evidence of random shock-wave intermittency. Phys. Rev. E 2023, 108, 045106. [Google Scholar] [CrossRef]
- Melcher, J.R.; Schwarz, W.J., Jr. Interfacial relaxation overstability in a tangential electric field. Phys. Fluids 1968, 11, 2604–2616. [Google Scholar] [CrossRef]
- Kochurin, E.A. Formation of weak singularities on the surface of a dielectric fluid in a tangential electric field. Tech. Phys. Lett. 2019, 45, 65–68. [Google Scholar] [CrossRef]
- Kochurin, E.A.; Zubareva, O.V.; Zubarev, N.M. Wave breaking on the surface of a dielectric liquid in a horizontal electric field. IEEE Trans. Dielectr. Electr. Insul. 2020, 27, 1222–1228. [Google Scholar] [CrossRef]
- Maryott, A.A.; Smith, E.R. Table of Dielectric Constants of Pure Liquids (Vol. 514); US Government Printing Office: Washington, DC, USA, 1951. [Google Scholar]
- Zubarev, N.M. Nonlinear waves on the surface of a dielectric liquid in a strong tangential electric field. Phys. Lett. A 2004, 333, 284–288. [Google Scholar] [CrossRef][Green Version]
- Zubarev, N.M. Nonlinear waves on the surface of a dielectric liquid in a horizontal electric field in 3D geometry: Exact solutions. JETP Lett. 2009, 89, 271–274. [Google Scholar] [CrossRef]
- Ovsjannikov, L.V. To the shallow water theory foundation. Arch. Mech. 1974, 26, 6. [Google Scholar]
- Dyachenko, A.I.; Kuznetsov, E.A.; Spector, M.D.; Zakharov, V.E. Analytical description of the free surface dynamics of an ideal fluid (canonical formalism and conformal mapping). Phys. Lett. A 1996, 221, 73–79. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Dyachenko, A.I.; Vasilyev, O.A. New method for numerical simulation of a nonstationary potential flow of incompressible fluid with a free surface. Eur. J. Mech. B Fluids 2002, 21, 283. [Google Scholar] [CrossRef]
- Kochurin, E.A.; Zubarev, N.M. Gravity-capillary waves on the free surface of a liquid dielectric in a tangential electric field. IEEE Trans. Dielectr. Electr. Insul. 2018, 25, 1723–1730. [Google Scholar] [CrossRef]
- Kochurin, E.A.; Zubarev, N.M. Reduced equations of motion of the interface of dielectric liquids in vertical electric and gravitational fields. Phys. Fluids 2012, 24, 072101. [Google Scholar] [CrossRef]
- Gao, T.; Wang, Z.; Papageorgiou, D. Singularities of capillary-gravity waves on dielectric fluid under normal electric fields. SIAM J. Appl. Math. 2024, 84, 523–542. [Google Scholar] [CrossRef]
- Dommermuth, D.G.; Yue, D.K. A high-order spectral method for the study of nonlinear gravity waves. J. Fluid Mech. 1987, 184, 267–288. [Google Scholar] [CrossRef]
- Bayındır, C. Compressive spectral method for the simulation of the nonlinear gravity waves. Sci. Rep. 2016, 6, 22100. [Google Scholar] [CrossRef]
- Akylas, T.R.; Cho, Y. On the stability of lumps and wave collapse in water waves. Philos. Trans. A Math. Phys. Eng. Sci. 2008, 366, 2761–2774. [Google Scholar] [CrossRef]
- McAllister, M.L.; Draycott, S.; Calvert, R.; Davey, T.; Dias, F.; van den Bremer, T.S. Three-dimensional wave breaking. Nature 2024, 633, 601–607. [Google Scholar] [CrossRef]
- Suret, P.; Randoux, S.; Gelash, A.; Agafontsev, D.; Doyon, B.; El, G. Soliton gas: Theory, numerics, and experiments. Phys. Rev. E 2024, 109, 061001. [Google Scholar] [CrossRef]
- Flamarion, M.V.; Pelinovsky, E.; Didenkulova, E. Investigating overtaking collisions of solitary waves in the Schamel equation. Chaos Solitons Fractals 2023, 174, 113870. [Google Scholar] [CrossRef]
- Flamarion, M.V. Solitary wave collisions for the Whitham equation. Comput. Appl. Math. 2022, 41, 356. [Google Scholar] [CrossRef]
- Flamarion, M.V.; Pelinovsky, E. Interaction of interfacial waves with an external force: The Benjamin-Ono equation framework. Symmetry 2023, 15, 1478. [Google Scholar] [CrossRef]
- Flamarion, M.V.; Pelinovsky, E. Soliton interactions with an external forcing: The modified Korteweg–de Vries framework. Chaos Solitons Fractals 2022, 165, 112889. [Google Scholar] [CrossRef]
- Flamarion, M.V.; Pelinovsky, E.; Didenkulova, E. Non-integrable soliton gas: The Schamel equation framework. Chaos Solitons Fractals 2024, 180, 114495. [Google Scholar] [CrossRef]
- Kochurin, E.A. Simulation of the Wave Turbulence of a Liquid Surface Using the Dynamic Conformal Transformation Method. JETP Lett. 2023, 118, 893–898. [Google Scholar] [CrossRef]
- Kochurin, E.A. Wave turbulence of a liquid surface in an external tangential electric field. JETP Lett. 2019, 109, 303–308. [Google Scholar] [CrossRef]
- Kochurin, E.A. Numerical simulation of the wave turbulence on the surface of a ferrofluid in a horizontal magnetic field. J. Magn. Magn. Mater. 2020, 503, 166607. [Google Scholar] [CrossRef]
- Benney, D.J.; Saffman, P.G. Nonlinear interactions of random waves in a dispersive medium. Proc. R. Soc. Lond. 1966, 289, 301–320. [Google Scholar]
- Agafontsev, D.S.; Kuznetsov, E.A.; Mailybaev, A.A.; Sereshchenko, E.V. Compressible vortex structures and their role in the onset of hydrodynamic turbulence. Phys.-Uspekhi. 2022, 65, 189. [Google Scholar] [CrossRef]
- Agafontsev, D.S.; Kuznetsov, E.A.; Mailybaev, A.A. Development of high vorticity structures and geometrical properties of the vortex line representation. Phys. Fluids 2018, 30, 095104. [Google Scholar] [CrossRef]
- Kuznetsov, E.A.; Sereshchenko, E.V. Isotropization of two-dimensional hydrodynamic turbulence in the direct cascade. JETP Lett. 2017, 105, 83–88. [Google Scholar] [CrossRef]
- Kuznetsov, E.A.; Sereshchenko, E.V. Anisotropic characteristics of the Kraichnan direct cascade in two-dimensional hydrodynamic turbulence. JETP Lett. 2015, 102, 760–765. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).