Stack Coupling Machine Learning Model Could Enhance the Accuracy in Short-Term Water Quality Prediction
Abstract
1. Introduction
- To verify the correctness of the gradient boosting method in predicting water quality parameters using the Light GBM algorithm and to analyze the contribution of different sources of data to water quality changes.
- To confirm the effectiveness of LSTM algorithm in the estimation of the parameters of water quality and to identify the stacking lag response period of time-series data in water quality parameters prediction.
- To develop and validate a new method of coupling models to predict the water quality parameters in the Jiuzhoujiang river basin based on the experimental data for the period of 2019–2021.
- Furthermore, to mitigate reduced feature interpretability caused by multicollinearity, we employed the variance inflation factor (VIF) for feature selection prior to model construction and comparison.
2. Methodology
2.1. Model Pre-Processing and Performance Metrics
2.1.1. Data Pre-Processing
2.1.2. Input Selection
2.1.3. Performance Metrics
2.2. Light GBM
| Algorithm 1: Histogram-based Algorithm |
| 1: Input: I: training data, d: max depth |
| 2: Input: m: feature dimension |
| 3: note Set ← {0} ▷ tree nodes in current level |
| 4: row Set ← {{0, 1, 2, …}} ▷ data indices in tree nodes |
| 5: for i = 1 to d do |
| 6: for node in node Set do |
| 7: usedRows ← row Set[node] |
| 8: for k = 1 to m do |
| 9: H ← new Histogram () |
| 10: ▷ Build histogram |
| 11: for j in usedRows do |
| 12: bin ← I.f[k][j].bin |
| 13: H[bin].y ← H[bin].y + I.y[j] |
| 14: H[bin].n ← H[bin].n + 1 |
| 15: Find the best split on histogram H. |
| 16: ... |
| 17: Update rowSet and nodeSet according to the best split points. |
| 18: ... |
| Algorithm 2: Gradient-based One-Side Sampling |
| 1: Input: I: training data, d: iterations |
| 2: Input: a: sampling ratio of large gradient data |
| 3: Input: b: sampling ratio of small gradient data |
| 4: Input: loss: loss function, L: weak learner models ← {}, fact ← (1 − a)/b |
| 5: topN ← a × len(I), randN ← b × len(I) |
| 6: usedRows ← row Set[node] |
| 7: for i = 1 to d do |
| 8: preds ← models.predict(I) |
| 9: g ← loss(I, preds), w ← {1, 1, ...} |
| 10: sorted ← GetSortedIndices(abs(g)) |
| 11: topSet ← sorted[1: topN] |
| 12: randSet ← RandomPick(sorted[topN: len(I)], randN) |
| 13: usedSet ← topSet + randSet |
| 14: w[randSet] × = fact. Assign weight fact to the small gradient data. |
| 15: newModel ← L(I[usedSet], − g[usedSet], w[usedSet]) |
| 16: models.append(newModel) |
| Algorithm 3: Greedy Bundling |
| 1: Input: F: features, K: max conflict count |
| 2: Construct graph G |
| 3: searchOrder ← G.sortByDegree() |
| 4: bundles ← {}, bundlesConflict ← {} |
| 5: for i in searchOrder do |
| 6: needNew ← True |
| 7: for j = 1 to len(bundles) do |
| 8: cnt ← ConflictCnt(bundles[j],F[i]) |
| 9: if cnt + bundlesConflict[i] ≤ K then |
| 10: bundles[j].add(F[i]), needNew ← False |
| 11: break |
| 12: if needNew then |
| 13: Add F[i] as a new bundle to bundles |
| 14: Output: bundles |
| Algorithm 4: Merge Exclusive Features |
| 1: Input: numData: number of data |
| 2: Input: F: One bundle of exclusive features |
| 3: binRanges ← {0}, totalBin ← 0 |
| 4: usedRows ← row Set[node] |
| 5: for f in F do |
| 6: totalBin += f.numBin |
| 7: binRanges.append(totalBin)v |
| 8: newBin ← new Bin(numData) |
| 9: for i = 1 to numData do |
| 10: newBin[i] ← 0 |
| 11: for j = 1 to len(F) do |
| 12: if F[j].bin[i] = 0 then |
| 13: newBin[i] ← F[j].bin[i] + binRanges[j] |
| 14: Output: newBin, binRanges |
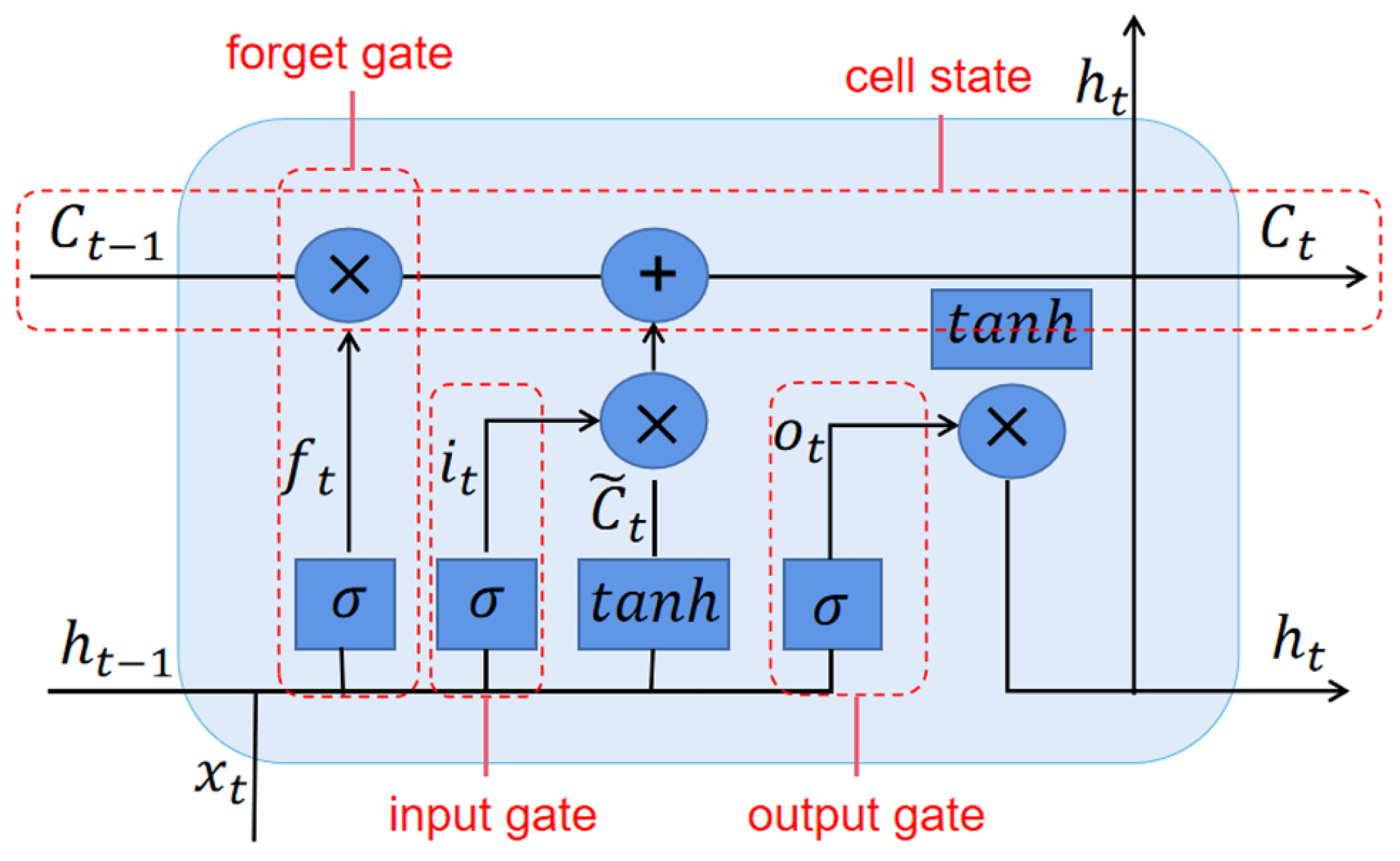
2.3. Long Short-Term Memory
- Forget gate layer: Whether the previous cell state would be forgotten in the current cell is determined in this layer. The current input xt and the previous hidden state ht−1 are passed through and the output of the layer is calculated by Equation (10). A value of ft of 0 or 1 refers to the state of being forgotten or retention.
- Input gate layer: There are two memory vectors to decide the output value in this layer, which can be called as sigmoid vector and tanh vector, and can be calculated by Equation (11) and Equation (12), respectively.
- Output gate layer: The updated hidden cell state and cell state are determined in this layer, which is calculated as follows:
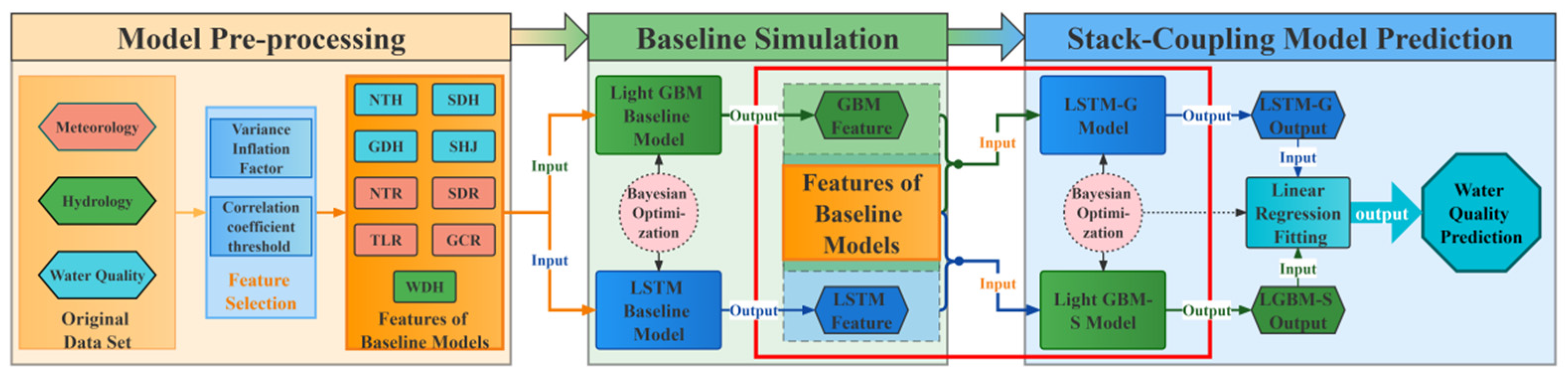
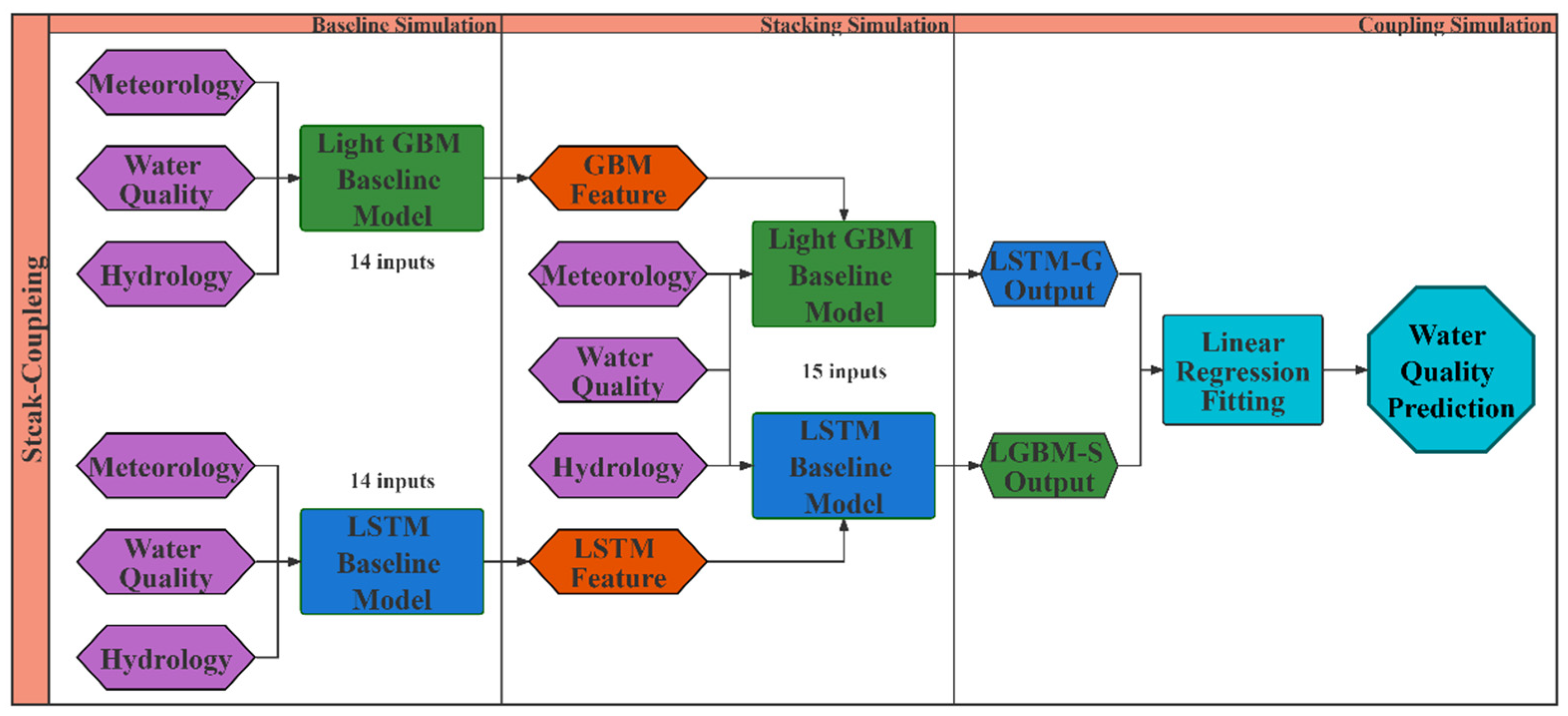
2.4. Stack Coupling Model Framework
- On the other hand, the Bi-LSTM model was used to construct the LSTM baseline model based on the same dataset, in which the continuous data of the previous 10-day was used to predict the 5-day-later COD concentrations. The training process would be iterated many times to achieve the best fitting effect; while early stopping and dropout mechanisms were also introduced to prevent over-fitting [67,71].
- Then the fitted baseline models would be used to fit and predict the 5-day-later COD concentrations water quality data separately, and the results could be regarded as new features and cross-put into the original baseline model dataset to form the reconstructed baseline model dataset.
- Thus, with the first stack coupling process, two new models would be built and fitted with the same steps as the baseline models, which could be called as LGBM-S model and LSTM-G model, respectively.
- When simulation results from two newly fitted models—each applied to the training and validation datasets, respectively—become available, they would be considered as the input features of the second model coupling based on an SVR with linear kernel (SVR-LK) model, where the final prediction of the 5-day-later concentrations could be calculated.
- The data collected by normalization and data filling is preprocessed.
- Model input variables are selected using correlation coefficient threshold screening and variance inflation factor.
- Two baseline models are built and the prediction values obtained; then the values are added into the baseline models as new input variables to build new models.
- The simple linear model is used to take the predicted value of the new models as new inputs to complete the coupling of the model and obtain the final water quality prediction.
3. Example Application
3.1. Study Area and Data
3.2. Model Preparation
3.2.1. Selection of Inputs
3.2.2. Model Construction
3.3. Prediction of Water Quality
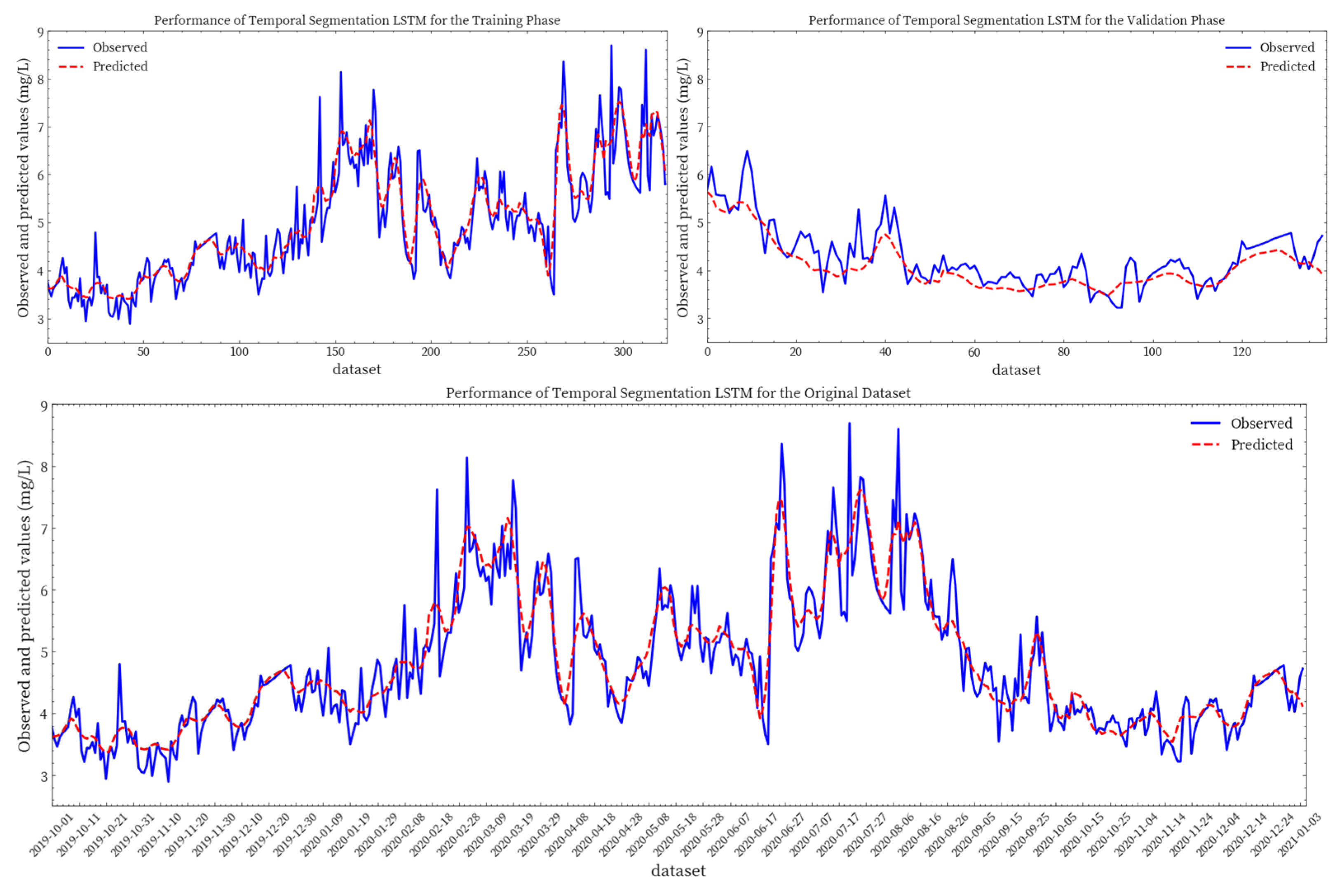
3.3.1. Simulation Results of Baseline Models and Stack Coupling Model
3.3.2. Validation Performance Between All the Five Models
4. Discussion
4.1. Improvement of Water Quality Prediction Model of Stack Coupling Model
4.2. Advantages and Contributions of the Baseline Model in Water Quality Prediction
4.3. Uncertainty Analysis
5. Conclusions
- (1)
- Both the baseline models (LightGBM and LSTM) demonstrated high accuracy in predicting short-term river water quality and exhibited a considerable robustness. The NSE of both models for the validation phase was above 0.75, while the MAPE was below 10%. Furthermore, both “process models” (LGBM-S and LSTM-G) demonstrated modest but consistent improvements in accuracy compared to the baseline model. This suggests that the process models capture information not adequately represented in the baseline simulations, such as spatial dependencies and temporal lag effects.
- (2)
- A Light GBM with Bayesian optimization baseline model was built to predict the river water quality mainly focusing on potential relationships between data with different spatial attributes. The result indicated that the main driving factors of the variation in study area were upstream from Ningtan River, watershed rainfall and background water quality.
- (3)
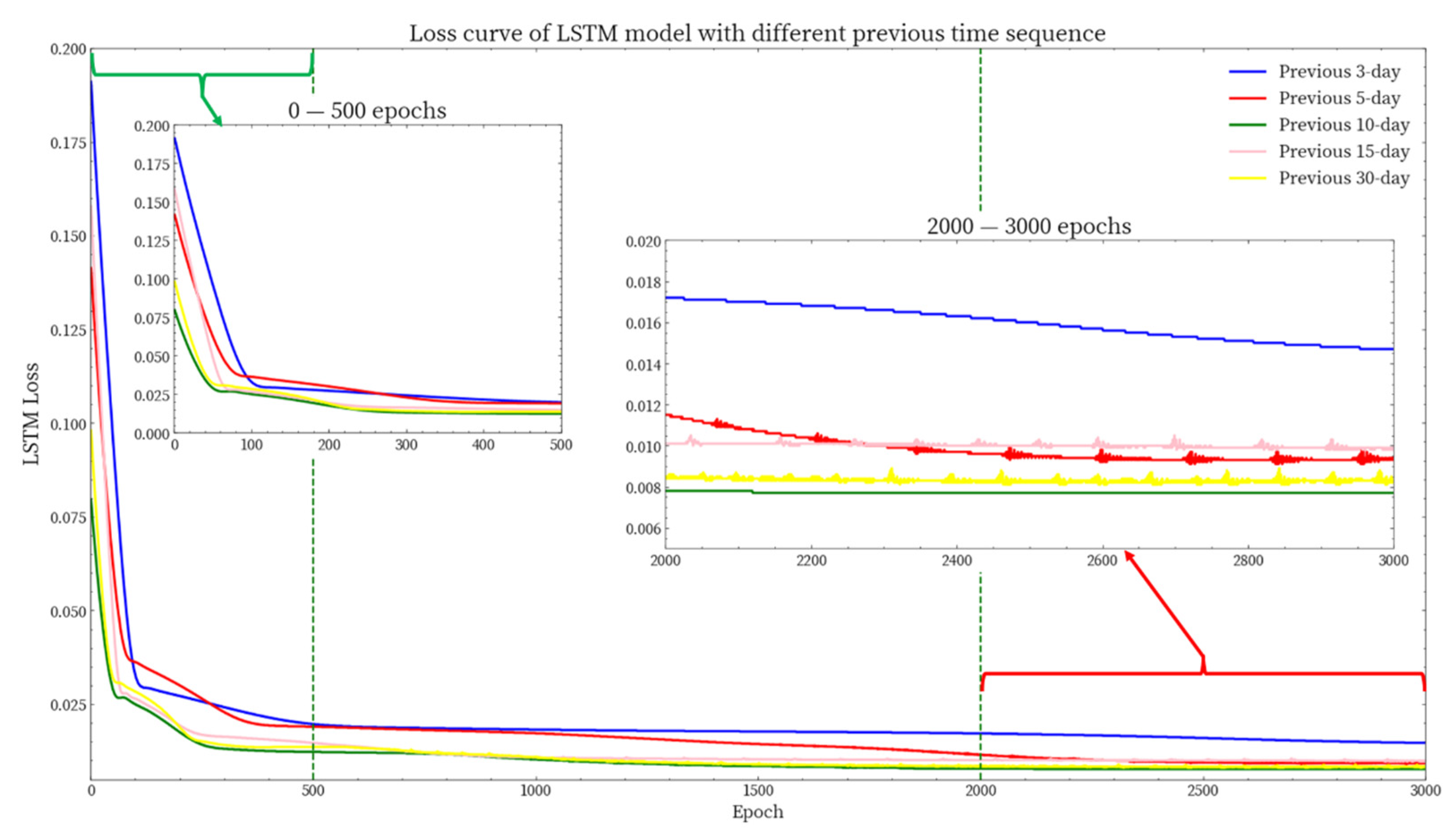
- A LSTM with bidirectional connection baseline model was built to predict the river water quality mainly focusing on the stacking lag effect of time-series data. The result indicated that the short-term river water quality was affected by the stacking lag of the time-series data of the previous 10–15 days.
- (4)
- Owing to the presence of residuals, the predictions deviate somewhat from the observed values. To minimize this deviation and enhance the accuracy of water quality prediction, the simulation results of the two models are recalculated as input variables for one another and then coupled through an SVR-LK model to obtain the final predicted value. It was found that the accuracy of the stack coupling model had increased by 8~12% and the stability of the coupling model had increased by 15–40%. This outcome provides a robust technical foundation for future basin-wide water quality forecasting, early-warning, and real-time environmental management in Guangxi. The approach has already been extended to the Yellow River Basin and the Beijing-Tianjin-Hebei region.
- (5)
- The modeling framework established in this study remains limited in terms of data requirements and physical interpretability. Therefore, a promising direction for future work involves expanding the ensemble to include physics-based models as base learners, while integrating explainable AI (XAI) techniques to enhance transparency and mechanistic insight.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| NSE | Adj. R2 | RMSE (mg/L) | MAPE (%) | CC | |
|---|---|---|---|---|---|
| Overall | 0.841 | 0.837 | 0.479 | 5.618 | 0.931 |
| Train | 0.842 | 0.836 | 0.409 | 5.944 | 0.933 |
| Validation | 0.735 | 0.700 | 0.422 | 5.733 | 0.891 |
| Models | p-Value | Test Statistic | Alpha Level | H0 |
|---|---|---|---|---|
| LSTM model with a strict temporal split | 0.188 | 1.733 | 0.05 | Accept |
References
- Khalil, B.; Ouarda, T.B.M.J.; St-Hilaire, A.; Chebana, F. A statistical approach for the rationalization of water quality indicators in surface water quality monitoring networks. J. Hydrol. 2010, 386, 173–185. [Google Scholar] [CrossRef]
- Grabowski, R.C.; Gurnell, A.M. Hydrogeomorphology—Ecology interactions in river systems. River Res. Appl. 2016, 32, 139–141. [Google Scholar] [CrossRef]
- Singh, A.P.; Dhadse, K.; Ahalawat, J. Managing water quality of a river using an integrated geographically weighted regression technique with fuzzy decision-making model. Environ. Monit. Assess. 2019, 191, 378. [Google Scholar] [CrossRef]
- Vörösmarty, C.J.; McIntyre, P.B.; Gessner, M.O.; Dudgeon, D.; Prusevich, A.; Green, P.; Glidden, S.; Bunn, S.E.; Sullivan, C.A.; Liermann, C.R.; et al. Global threats to human water security and river biodiversity. Nature 2010, 467, 555–561. [Google Scholar] [CrossRef]
- Cheng, H.; Hu, Y.; Zhao, J. Meeting china’s water shortage crisis: Current practices and challenges. Environ. Sci. Technol. 2009, 43, 240–244. [Google Scholar] [CrossRef]
- Tripathi, M.; Singal, S.K. Use of principal component analysis for parameter selection for development of a novel water quality index: A case study of river ganga india. Ecol. Indic. 2019, 96, 430–436. [Google Scholar] [CrossRef]
- Uddin, M.G.; Nash, S.; Rahman, A.; Olbert, A.I. A comprehensive method for improvement of water quality index (WQI) models for coastal water quality assessment. Water Res. 2022, 219, 118532. [Google Scholar] [CrossRef]
- Ahmed, A.N.; Othman, F.B.; Afan, H.A.; Ibrahim, R.K.; Fai, C.M.; Hossain, M.S.; Ehteram, M.; Elshafie, A. Machine learning methods for better water quality prediction. J. Hydrol. 2019, 578, 124084. [Google Scholar] [CrossRef]
- Antanasijević, D.; Pocajt, V.; Povrenovic, D.; Peric-Grujic, A.; Ristic, M. Modelling of dissolved oxygen content using artificial neural networks: Danube River, North Serbia, case study. Environ. Sci. Pollut. Res. 2013, 20, 9006–9013. [Google Scholar] [CrossRef] [PubMed]
- Tchobanoglous, G.; Schroeder, E.E. Water Quality: Characteristics, Modeling, Modification; Addison-Wesley Publishing Co., Ltd.: Reading, MA, USA, 1985; p. 704. [Google Scholar]
- Mohtar, W.H.M.W.; Maulud, K.N.A.; Muhammad, N.S.; Sharil, S.; Zaher Mundher, Y. Spatial and temporal risk quotient based river assessment for water resources management. Environ. Pollut. 2019, 248, 133–144. [Google Scholar] [CrossRef] [PubMed]
- Reichert, P.; Borchardt, D.; Henze, M.; Rauch, W.; Shanahan, P.; Somlyody, L.; Vanrolleghem, P. River Water Quality Model No 1; IWA Publishing: London, UK, 2001. [Google Scholar]
- Chapra, S.; Pellettier, G. QUAL2K: A Modeling Framework for Simulating River and Stream Water Quality; Tufts University: Medford, MA, USA, 2003. [Google Scholar]
- Wool, T.A.; Ambrose, R.B.; Martin, J.L.; Comer, E.A. Water Quality Analysis Simulation Program (WASP) Version 6.0 DRAFT: User’s Manual; US Environmental Protection Agency: Athens, GA, USA, 2006.
- Jothiprakash, V.; Magar, R.B. Multi-time-step ahead daily and hourly intermittent reservoir inflow prediction by artificial intelligent techniques using lumped and distributed data. J. Hydrol. 2012, 450, 293–307. [Google Scholar] [CrossRef]
- Meybeck, M. Global analysis of river systems: From Earth system controls to Anthropocene syndromes. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 2003, 358, 1935–1955. [Google Scholar] [CrossRef]
- Hey, T. The Fourth Paradigm—Data-Intensive Scientific Discovery, IMCW 2012; Springer: Berlin/Heidelberg, Germany, 2012; p. 1. [Google Scholar]
- Tiyasha, T. Tung, T.M.; Yaseen, Z.M. A survey on river water quality modelling using artificial intelligence models: 2000–2020. J. Hydrol. 2020, 585, 124670. [Google Scholar] [CrossRef]
- Turan, M.E.; Yurdusev, M.A. River flow estimation from upstream flow records by artificial intelligence methods. J. Hydrol. 2009, 369, 71–77. [Google Scholar] [CrossRef]
- Quej, V.H.; Almorox, J.; Arnaldo, J.A.; Saito, L. ANFIS, SVM and ANN soft-computing techniques to estimate daily global solar radiation in a warm sub-humid environment. J. Atmos. Sol.-Terr. Phy. 2017, 155, 62–70. [Google Scholar] [CrossRef]
- Huang, W.R.; Foo, S. Neural network modeling of salinity variation in Apalachicola River. Water Res. 2002, 36, 356–362. [Google Scholar] [CrossRef] [PubMed]
- Heddam, S. Multilayer perceptron neural network-based approach for modeling phycocyanin pigment concentrations: Case study from lower Charles River buoy, USA. Environ. Sci. Pollut. Res. 2016, 23, 17210–17225. [Google Scholar] [CrossRef]
- Gebler, D.; Wiegleb, G.; Szoszkiewicz, K. Integrating river hydromorphology and water quality into ecological status modelling by artificial neural networks. Water Res. 2018, 139, 395–405. [Google Scholar] [CrossRef]
- Yan, H.; Zou, Z.; Wang, H. Adaptive neuro fuzzy inference system for classification of water quality status. J. Environ. Sci. 2010, 22, 1891–1896. [Google Scholar] [CrossRef]
- Ahmed, A.A.M.; Syed Mustakim Ali, S. Application of adaptive neuro-fuzzy inference system (ANFIS) to estimate the biochemical oxygen demand (BOD) of Surma River. J. King Saud Univ.-Eng. Sci. 2017, 29, 237–243. [Google Scholar] [CrossRef]
- Kamyab-Talesh, F.; Mousavi, S.-F.; Khaledian, M.; Yousefi-Falakdehi, O.; Norouzi-Masir, M. Prediction of Water Quality Index by Support Vector Machine: A Case Study in the Sefidrud Basin, Northern Iran. Water Resour. 2019, 46, 112–116. [Google Scholar] [CrossRef]
- Ho, J.Y.; Afan, H.A.; El-Shafie, A.H.; Koting, S.B.; Mohd, N.S.; Jaafar, W.Z.B.; Hin, L.S.; Malek, M.A.; Ahmed, A.N.; Mohtar, W.H.M.W.; et al. Towards a time and cost effective approach to water quality index class prediction. J. Hydrol. 2019, 575, 148–165. [Google Scholar] [CrossRef]
- Maier, P.M.; Keller, S. Machine Learning Regression on Hyperspectral Data to Estimate Multiple Water Parameters. In Proceedings of the 9th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Amsterdam, The Netherlands, 23–26 September 2018. [Google Scholar]
- Najah, A.A.; El-Shafie, A.; Karim, O.A.; Jaafar, O. Water quality prediction model utilizing integrated wavelet-ANFIS model with cross-validation. Neural Comput. Appl. 2012, 21, 833–841. [Google Scholar] [CrossRef]
- Jin, T.; Cai, S.B.; Jiang, D.X.; Liu, J. A data-driven model for real-time water quality prediction and early warning by an integration method. Environ. Sci. Pollut. Res. 2019, 26, 30374–30385. [Google Scholar] [CrossRef]
- Faruk, D.O. A hybrid neural network and ARIMA model for water quality time series prediction. Eng. Appl. Artif. Intell. 2010, 23, 586–594. [Google Scholar] [CrossRef]
- Rajaee, T.; Khani, S.; Ravansalar, M. Artificial intelligence-based single and hybrid models for prediction of water quality in rivers: A review. Chemom. Intell. Lab. Syst. 2020, 200, 103978. [Google Scholar] [CrossRef]
- Usman, A.G.; Işik, S.; Abba, S.I. A Novel Multi-model Data-Driven Ensemble Technique for the Prediction of Retention Factor in HPLC Method Development. Chromatographia 2020, 83, 933–945. [Google Scholar] [CrossRef]
- Antanasijević, D.; Pocajt, V.; Peric-Grujic, A.; Ristic, M. Modelling of dissolved oxygen in the Danube River using artificial neural networks and Monte Carlo Simulation uncertainty analysis. J. Hydrol. 2014, 519, 1895–1907. [Google Scholar] [CrossRef]
- Jiawei, H.; Micheline, K.; Jian, P. 3-Data Preprocessing. In Data Mining: Concepts and Techniques, 3rd ed.; Jiawei, H., Micheline, K., Jian, P., Eds.; Morgan Kaufmann: Boston, MA, USA, 2012; pp. 83–124. ISBN 978-0-12-381479-1. [Google Scholar] [CrossRef]
- Abba, S.I.; Hadi, S.J.; Sammen, S.S.; Salih, S.Q.; Abdulkadir, R.A.; Pham, Q.B.; Yaseen, Z.M. Evolutionary computational intelligence algorithm coupled with self-tuning predictive model for water quality index determination. J. Hydrol. 2020, 587, 124974. [Google Scholar] [CrossRef]
- Abba, S.I.; Abdulkadir, R.A.; Saad Sh, S.; Quoc Bao, P.; Lawan, A.A.; Parvaneh, E.; Anurag, M.; Nadhir, A.-A. Integrating feature extraction approaches with hybrid emotional neural networks for water quality index modeling. Appl. Soft Comput. 2022, 114, 108036. [Google Scholar] [CrossRef]
- Zebari, R.; Abdulazeez, A.; Zeebaree, D.; Zebari, D.; Saeed, J. A Comprehensive Review of Dimensionality Reduction Techniques for Feature Selection and Feature Extraction. J. Appl. Sci. Technol. Trends 2020, 1, 56–70. [Google Scholar] [CrossRef]
- Aremu, O.O.; Hyland-Wood, D.; McAree, P.R. A machine learning approach to circumventing the curse of dimensionality in discontinuous time series machine data. Reliab. Eng. Syst. Saf. 2020, 195, 106706. [Google Scholar] [CrossRef]
- Wang, L.; Jiang, S.; Jiang, S. A feature selection method via analysis of relevance, redundancy, and interaction. Expert Syst. Appl. 2021, 183, 115365. [Google Scholar] [CrossRef]
- Myers, J.; Well, A.; Lorch, R. Between-Subjects Designs: Several Factors. In Research Design and Statistical Analysis, 3rd ed.; Routledge: New York, NY, USA, 2010; ISBN 9780203726631. [Google Scholar] [CrossRef]
- Elith, J.; Graham, C.; Anderson, R.; Dudík, M.; Ferrier, S.; Guisan, A.; Hijmans, R.; Huettmann, F.; Leathwick, J.; Lehmann, A.; et al. Novel methods improve prediction of species’ distributions from occurrence data. Ecography 2006, 29, 129–151. [Google Scholar] [CrossRef]
- Dormann, C.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.; Gruber, B.; Lafourcade, B.; Leitao, P.; et al. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Kasraei, B.; Schmidt, M.G.; Zhang, J.; Bulmer, C.E.; Filatow, D.S.; Arbor, A.; Pennell, T.; Heung, B. A framework for optimizing environmental covariates to support model interpretability in digital soil mapping. Geoderma 2024, 445, 116873. [Google Scholar] [CrossRef]
- Salmerón, R.; García, C.; García, J. Variance Inflation Factor and Condition Number in multiple linear regression. J. Stat. Comput. Simul. 2018, 88, 2365–2384. [Google Scholar] [CrossRef]
- Maier, H.R.; Jain, A.; Dandy, G.C.; Sudheer, K.P. Methods used for the development of neural networks for the prediction of water resource variables in river systems: Current status and future directions. Environ. Modell. Softw. 2010, 25, 891–909. [Google Scholar] [CrossRef]
- Kroll, C.N.; Song, P. Impact of multicollinearity on small sample hydrologic regression models. Water Resour. Res. 2013, 49, 3756–3769. [Google Scholar] [CrossRef]
- Demir, V.; Citakoglu, H. Forecasting of solar radiation using different machine learning approaches. Neural Comput. Appl. 2023, 35, 887–906. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H. Boosting and Additive Trees. In The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009; Volume 10, pp. 337–384. [Google Scholar]
- Natekin, A.; Knoll, A. Gradient boosting machines, a tutorial. Front. Neurorobot. 2013, 7, 21. [Google Scholar] [CrossRef]
- Alsabti, K.; Ranka, S.; Singh, V. CLOUDS: A Decision Tree Classifier for Large Datasets. In Proceedings of the Fourth International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 27–31 August 1998; pp. 2–8. [Google Scholar]
- Jin, R.; Agrawal, G. Communication and Memory Efficient Parallel Decision Tree Construction. In Proceedings of the 2003 SIAM International Conference on Data Mining (SDM), San Francisco, CA, USA, 1–3 May 2003; pp. 119–129. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the 31st Conference on Neural Information Processing Systems (NeuraIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 3146–3154. [Google Scholar]
- Li, P.; Wu, Q.; Burges, C. Mcrank: Learning to rank using multiple classification and gradient boosting. In Proceedings of the Conference and Workshop on Neural Information Processing Systems, Vancouver, BC, Canada, 3–6 December 2007. [Google Scholar]
- Gan, M.; Pan, S.; Chen, Y.; Cheng, C.; Pan, H.; Zhu, X. Application of the Machine Learning LightGBM Model to the Prediction of the Water Levels of the Lower Columbia River. J. Mar. Sci. Eng. 2021, 9, 496. [Google Scholar] [CrossRef]
- Chen, T.Q.; Guestrin, C.; Assoc Comp, M. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. In Proceedings of the 32nd Conference on Neural Information Processing Systems (NeuraIPS), Montreal, QC, Canada, 2–8 December 2018. [Google Scholar]
- Collins, M.; Schapire, R.E.; Singer, Y. Logistic regression, AdaBoost and Bregman distances. Mach. Learn. 2002, 48, 253–285. [Google Scholar] [CrossRef]
- Hsu, K.L.; Gupta, H.V.; Sorooshian, S. Artificial Neural Network Modeling of the Rainfall-Runoff Process. Water Resour. Res. 1995, 31, 2517–2530. [Google Scholar] [CrossRef]
- Maier, H.R.; Dandy, G.C. Neural networks for the prediction and forecasting of water resources variables: A review of modelling issues and applications. Environ. Model. Softw. 2000, 15, 101–124. [Google Scholar] [CrossRef]
- Wu, W.; Dandy, G.C.; Maier, H.R. Protocol for developing ANN models and its application to the assessment of the quality of the ANN model development process in drinking water quality modelling. Environ. Model. Softw. 2014, 54, 108–127. [Google Scholar] [CrossRef]
- Singh, K.P.; Basant, A.; Malik, A.; Jain, G. Artificial neural network modeling of the river water quality-A case study. Ecol. Model. 2009, 220, 888–895. [Google Scholar] [CrossRef]
- Yang, S.; Yang, D.; Chen, J.; Zhao, B. Real-time reservoir operation using recurrent neural networks and inflow forecast from a distributed hydrological model. J. Hydrol. 2019, 579, 124229. [Google Scholar] [CrossRef]
- Coulibaly, P.; Anctil, F.; Rasmussen, P.; Bobee, B. A recurrent neural networks approach using indices of low-frenquency climatic variability to forecast regional annual runoff. Hydrol. Process. 2000, 14, 2755–2777. [Google Scholar] [CrossRef]
- Zhang, Y.T.; Li, C.L.; Jiang, Y.Q.; Sun, L.; Zhao, R.B.; Yan, K.F.; Wang, W.H. Accurate prediction of water quality in urban drainage network with integrated EMD-LSTM model. J. Clean. Prod. 2022, 354, 131724. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Tao, Y.; Annan, Z.; Shui-Long, S. Prediction of long-term water quality using machine learning enhanced by Bayesian optimisation. Environ. Pollut. 2023, 318, 120870. [Google Scholar] [CrossRef]
- De’ath, G.; Fabricius, K.E. Classification and regression trees: A powerful yet simple technique for ecological data analysis. Ecology 2000, 81, 3178–3192. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef]
- Abba, S.I.; Pham, Q.B.; Usman, A.G.; Linh, N.T.T.; Aliyu, D.S.; Nguyen, Q.; Bach, Q.-V. Emerging evolutionary algorithm integrated with kernel principal component analysis for modeling the performance of a water treatment plant. J. Water Process Eng. 2020, 33, 101081. [Google Scholar] [CrossRef]
- Bayram, A.; Kankal, M.; Önsoy, H. Estimation of suspended sediment concentration from turbidity measurements using artificial neural networks. Environ. Monit. Assess. 2012, 184, 4355–4365. [Google Scholar] [CrossRef] [PubMed]
- Citakoglu, H.; Demir, V. Developing numerical equality to regional intensity-duration-frequency curves using evolutionary algorithms and multi-gene genetic programming. Acta Geophys. 2023, 71, 469–488. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Ma, M.; Zhao, G.; He, B.; Li, Q.; Dong, H.; Wang, S.; Wang, Z. XGBoost-based method for flash flood risk assessment. J. Hydrol. 2021, 598, 126382. [Google Scholar] [CrossRef]
- Sadayappan, K.; Kerins, D.; Shen, C.P.; Li, L. Nitrate concentrations predominantly driven by human, climate, and soil properties in US rivers. Water Res. 2022, 226, 119295. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Guo, S.Y.; Xin, K.L.; Xu, W.R.; Tao, T.; Yan, H.X. Maintaining the long-term accuracy of water distribution models with data assimilation methods: A comparative study. Water Res. 2022, 226, 119268. [Google Scholar] [CrossRef]
- Waqas, M.; Humphries, U.W. A critical review of RNN and LSTM variants in hydrological time series predictions. Methodsx 2024, 13, 102946. [Google Scholar] [CrossRef] [PubMed]
- Singh, V.K.; Kumar, D.; Singh, S.K.; Pham, Q.B.; Linh, N.T.T.; Mohammed, S.; Anh, D.T. Development of fuzzy analytic hierarchy process based water quality model of Upper Ganga river basin, India. J. Environ. Manage. 2021, 284, 111985. [Google Scholar] [CrossRef] [PubMed]
- Mohammed, H.; Tornyeviadzi, H.M.; Seidu, R. Emulating process-based water quality modelling in water source reservoirs using machine learning. J. Hydrol. 2022, 609, 127675. [Google Scholar] [CrossRef]
- Xia, R.; Wang, G.; Zhang, Y.; Yang, P.; Yang, Z.; Ding, S.; Jia, X.; Yang, C.; Liu, C.; Ma, S.; et al. River algal blooms are well predicted by antecedent environmental conditions. Water Res. 2020, 185, 116221. [Google Scholar] [CrossRef]
- Sharafati, A.; Asadollah, S.B.H.S.; Hosseinzadeh, M. The potential of new ensemble machine learning models for effluent quality parameters prediction and related uncertainty. Process Saf. Environ. Prot. 2020, 140, 68–78. [Google Scholar] [CrossRef]
- Cho, E.; Arhonditsis, G.B.; Khim, J.; Chung, S.; Heo, T.Y. Modeling metal-sediment interaction processes: Parameter sensitivity assessment and uncertainty analysis. Environ. Model. Softw. 2016, 80, 159–174. [Google Scholar] [CrossRef]
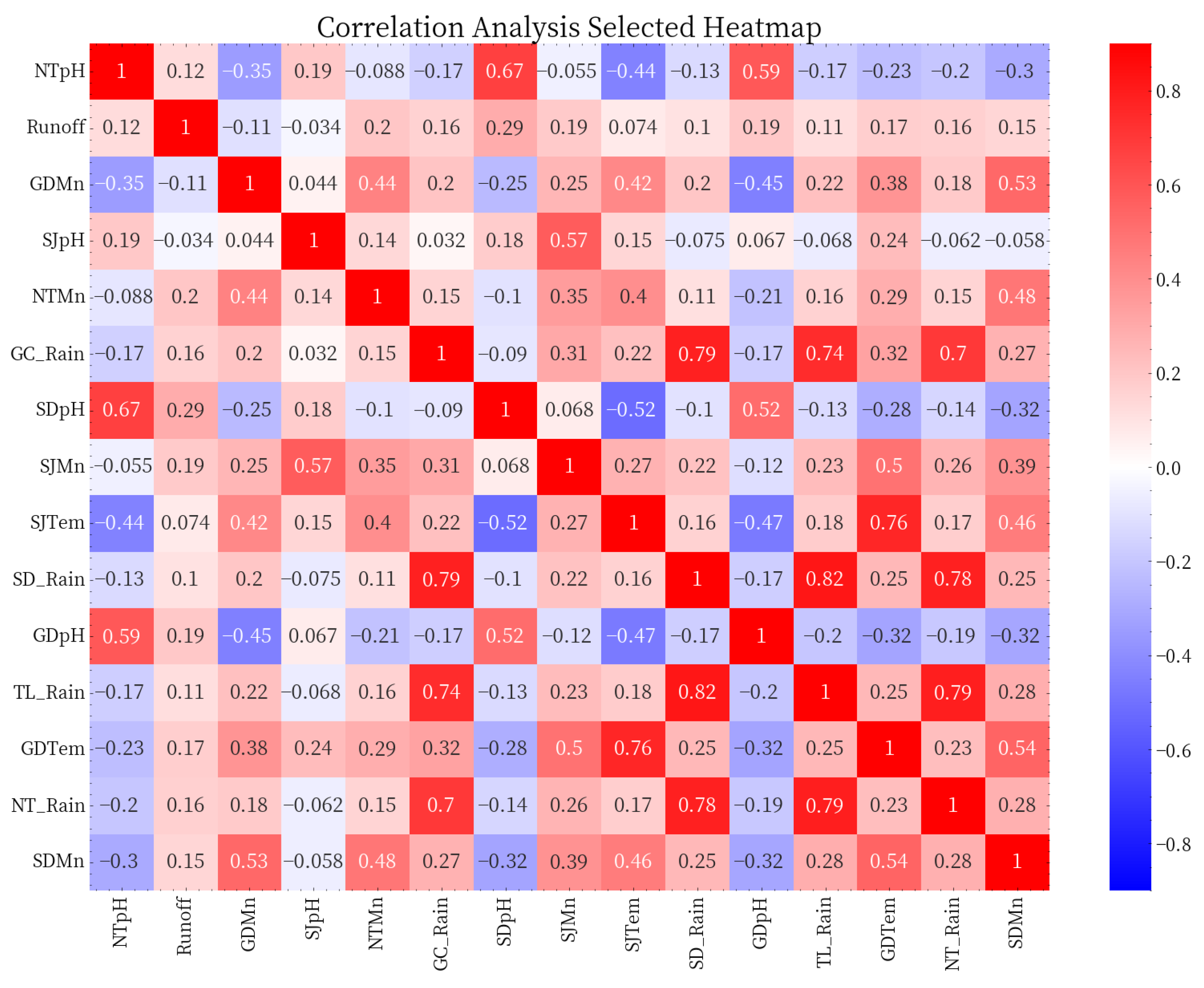
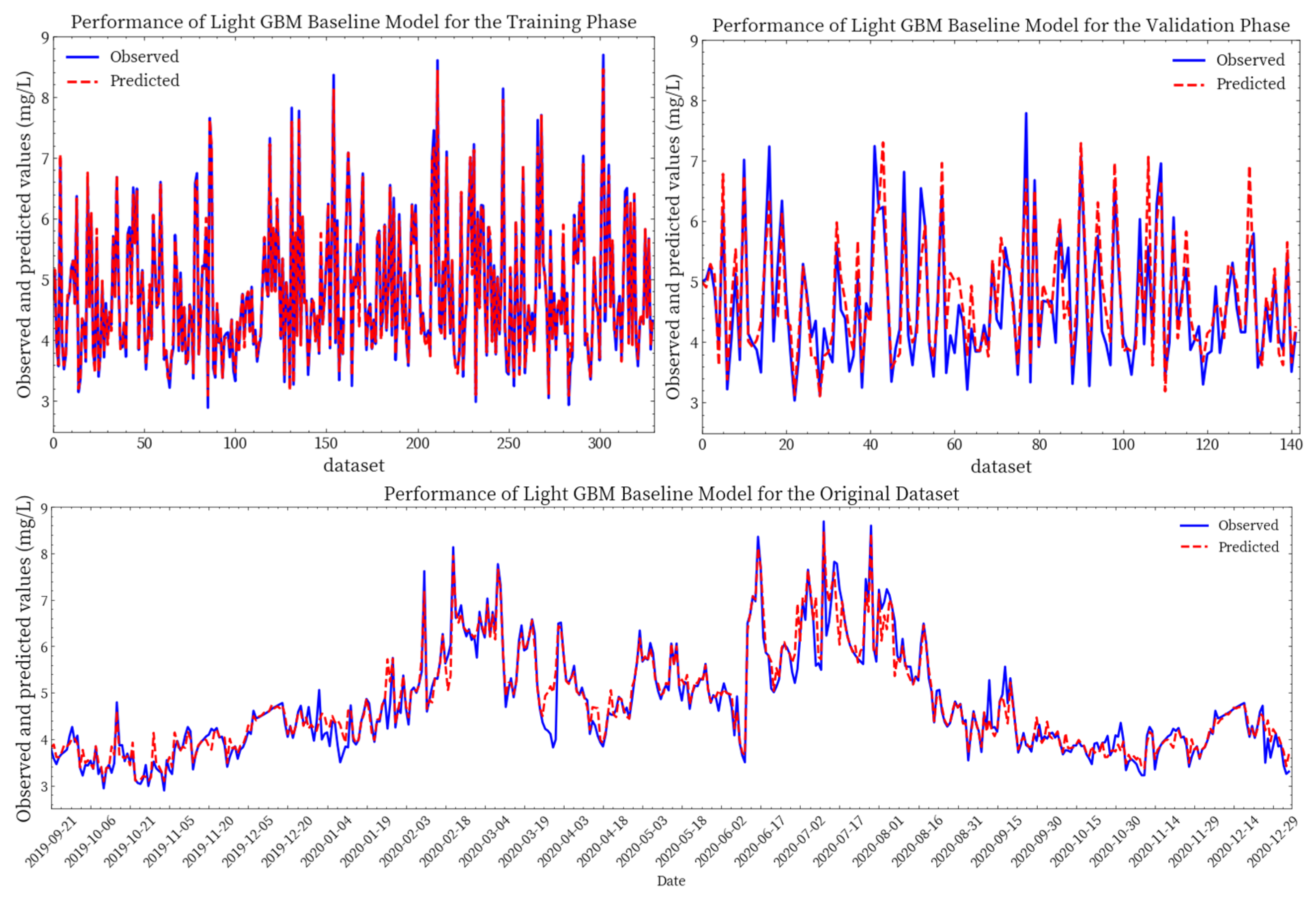





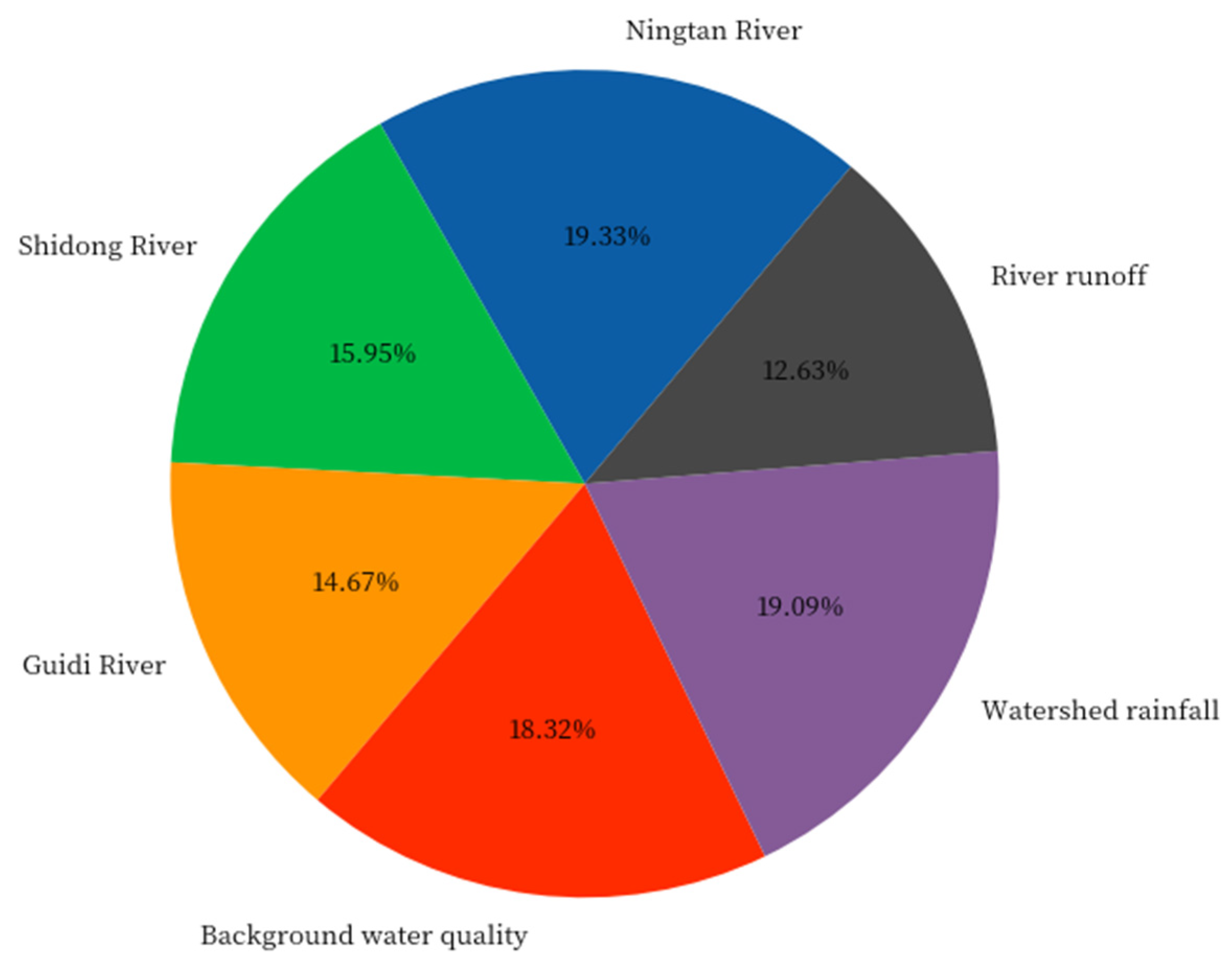
| Sections | Parameters | Unit | Mean | Minimum | Maximum | SD | CV |
|---|---|---|---|---|---|---|---|
| NTH | WT | °C | 24.48 | 13.94 | 34.50 | 4.45 | 5.51 |
| pH | — | 7.54 | 6.21 | 8.80 | 0.56 | 13.36 | |
| COD | mg/L | 2.52 | 0.50 | 7.31 | 1.44 | 1.75 | |
| SDH | WT | °C | 25.14 | 15.00 | 32.50 | 4.58 | 5.49 |
| pH | — | 7.34 | 6.08 | 8.30 | 0.56 | 13.12 | |
| COD | mg/L | 3.90 | 0.50 | 10.04 | 1.93 | 2.02 | |
| GDH | WT | °C | 25.82 | 11.80 | 32.10 | 3.96 | 6.52 |
| pH | — | 7.47 | 6.25 | 8.85 | 0.52 | 14.51 | |
| COD | mg/L | 5.33 | 0.50 | 14.06 | 2.64 | 2.02 | |
| SHJ | WT | °C | 25.82 | 14.80 | 34.42 | 4.75 | 5.43 |
| pH | — | 7.68 | 5.30 | 9.80 | 0.95 | 8.12 | |
| COD | mg/L | 4.72 | 2.89 | 8.69 | 1.10 | 4.27 |
| Type | Unit | Stations | Mean | Minimum | Maximum | SD | CV |
|---|---|---|---|---|---|---|---|
| precipitation | mm | NTR | 3.31 | 0.00 | 86.00 | 9.91 | 0.33 |
| SDR | 2.96 | 0.00 | 56.50 | 8.78 | 0.34 | ||
| CTR | 3.26 | 0.00 | 80.00 | 9.97 | 0.33 | ||
| TLR | 3.81 | 0.00 | 95.00 | 11.46 | 0.33 | ||
| GCR | 3.44 | 0.00 | 136.00 | 11.71 | 0.29 | ||
| flow | m3/s | WDH | 9.63 | 2.62 | 37.4 | 6.82 | 1.41 |
| Feature | VIF | Feature | VIF |
|---|---|---|---|
| NTMn | 1.4798 | NT_Rain | 3.5378 |
| Runoff | 1.6709 | GDTem | 3.8047 |
| GDMn | 1.8735 | SDpH | 4.1896 |
| SJpH | 2.0412 | TL_Rain | 4.6339 |
| SDMn | 2.3295 | SD_Rain | 4.9267 |
| GDpH | 2.3306 | CT_Rain | 6.5421 |
| SJMn | 2.7536 | SDTem | 15.4629 |
| GC_Rain | 2.8449 | SJTem | 16.7376 |
| NTpH | 3.3513 | NTTem | 18.3251 |
| Category | Hyperparameter | Search Spaces |
|---|---|---|
| Core Control | boosting_type | GBDT (Fixed) |
| objective | regression (Fixed) | |
| n_estimators | [1000, 5000] | |
| learning_rate | [0.001, 0.1] | |
| Tree Structure | num_leaves | [2, 100] |
| max_depth | [2, 20] | |
| max_bin | [2, 20] | |
| min_child_samples | [0.01, 1] | |
| colsample_bytree | [0.01, 1] | |
| Others | reg_alpha | [0.001, 1] |
| reg_lambda | [0.001, 1] | |
| stopping_rounds | 500 (Fixed) | |
| eval_metric | RMSE (Fixed) |
| Category | Hyperparameter | Search Spaces |
|---|---|---|
| Model Architecture | hidden Size | [32, 256] |
| number of Layers | [1, 2] | |
| Training Process | epochs | [1000, 5000] |
| learning_rate | [0.00001, 0.01] | |
| batch size | [64, 512] | |
| weight_decay | [0.00001, 0.01] | |
| optimizer | Adam (Fixed) | |
| Regularization | L1_reg | [0.001, 1] |
| dropout rate | [0.01, 0.3] | |
| stopping_rounds | 500 (Fixed) | |
| Loss_metric | RMSE (Fixed) |
| NSE | Adj. R2 | RMSE (mg/L) | MAPE (%) | CC | |
| Overall | 0.935 | 0.933 | 0.282 | 3.496 | 0.967 |
| Training | 0.993 | 0.993 | 0.195 | 1.468 | 0.996 |
| Validation | 0.761 | 0.736 | 0.492 | 8.153 | 0.886 |
| NSE | Adj. R2 | RMSE (mg/L) | MAPE (%) | CC | |
|---|---|---|---|---|---|
| Overall | 0.842 | 0.837 | 0.439 | 6.289 | 0.920 |
| Train | 0.875 | 0.870 | 0.401 | 6.470 | 0.938 |
| Validation | 0.738 | 0.709 | 0.525 | 6.890 | 0.868 |
| NSE | Adj. R2 | RMSE (mg/L) | MAPE (%) | CC | |
| Overall | 0.881 | 0.881 | 0.380 | 5.404 | 0.939 |
| Train | 0.904 | 0.903 | 0.342 | 5.052 | 0.951 |
| Validation | 0.829 | 0.826 | 0.455 | 6.224 | 0.912 |
| Models | p-Value | Test Statistic | Alpha Level | H0 |
| Light GBM | 0.144 | 2.134 | 0.05 | Accept |
| LSTM | 0.234 | 1.419 | 0.05 | Accept |
| LGBM-S | 0.654 | 0.201 | 0.05 | Accept |
| LSTM-G | 0.561 | 0.337 | 0.05 | Accept |
| SVR-LK | 0.773 | 0.121 | 0.05 | Accept |
| Models | NSE | Adj. R2 | RMSE (mg/L) | MAPE (%) |
|---|---|---|---|---|
| Light GBM | 0.761 | 0.736 | 0.492 | 8.153 |
| LSTM | 0.738 | 0.709 | 0.525 | 6.890 |
| LGBM-S | 0.778 | 0.802 | 0.457 | 6.041 |
| LSTM-G | 0.794 | 0.769 | 0.492 | 6.472 |
| SVR-LK | 0.829 | 0.826 | 0.452 | 6.224 |
| Models | Min RMSE | Max RMSE | Medium | Epoch |
|---|---|---|---|---|
| Stack Coupling model | 0.122 mg/L | 0.542 mg/L | 0.389 mg/L | 2000 times |
| Light GBM baseline model | 0.206 mg/L | 0.677 mg/L | 0.454 mg/L | 2000 times |
| LSTM baseline model | 0.278 mg/L | 0.746 mg/L | 0.532 mg/L | 2000 times |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Xia, R.; Wang, Y.; Chen, Y.; Wang, X.; Dou, J. Stack Coupling Machine Learning Model Could Enhance the Accuracy in Short-Term Water Quality Prediction. Water 2025, 17, 2868. https://doi.org/10.3390/w17192868
Zhang K, Xia R, Wang Y, Chen Y, Wang X, Dou J. Stack Coupling Machine Learning Model Could Enhance the Accuracy in Short-Term Water Quality Prediction. Water. 2025; 17(19):2868. https://doi.org/10.3390/w17192868
Chicago/Turabian StyleZhang, Kai, Rui Xia, Yao Wang, Yan Chen, Xiao Wang, and Jinghui Dou. 2025. "Stack Coupling Machine Learning Model Could Enhance the Accuracy in Short-Term Water Quality Prediction" Water 17, no. 19: 2868. https://doi.org/10.3390/w17192868
APA StyleZhang, K., Xia, R., Wang, Y., Chen, Y., Wang, X., & Dou, J. (2025). Stack Coupling Machine Learning Model Could Enhance the Accuracy in Short-Term Water Quality Prediction. Water, 17(19), 2868. https://doi.org/10.3390/w17192868






