Investigating the Frost Cracking Mechanisms of Water-Saturated Fissured Rock Slopes Based on a Meshless Model
Abstract
1. Introduction
2. Fundamental Principles of SPH
2.1. SPH Discretization Approach
2.2. SPH Heat Conduction Equation
3. Implementation Method of Frost Heaving Failure Under SPH Framework
3.1. Fracture Criterion
3.2. Numerical Simulation Method for Frost Heaving and Fracturing
- (1)
- When σ1 > σt, ξ = 0, indicating that the particle has failed and is excluded from mechanical calculations.
- (2)
- When σ1 < σt, ξ = 1, indicating that the particle remains intact and participates in subsequent stress transmission.
- (1)
- Water particles: When the ambient temperature T > 0 °C, the water in fissures remains in a liquid state, defined as “water particles”. At this time, the force exerted by the water on the fracture surfaces can be neglected, and the particle type is marked as Type = W.
- (2)
- Ice–water mixed particles: When −20 °C < T < 0 °C, part of the water in fissures freezes, forming a liquid–solid two-phase coexistence state, defined as “ice–water mixed particles”. At this time, the freezing rate uT changes linearly with temperature, and its expression is:The particle type is marked as Type = WI.
- (3)
- Ice particles: When T < 20 °C, the water in fissures is completely frozen, defined as “ice particles”. At this time, the frost heaving force reaches its maximum value, and the particle type is marked as Type = I.
4. Analysis of Numerical Simulation Results
4.1. Numerical Model, Calculation Scheme, and Parameters
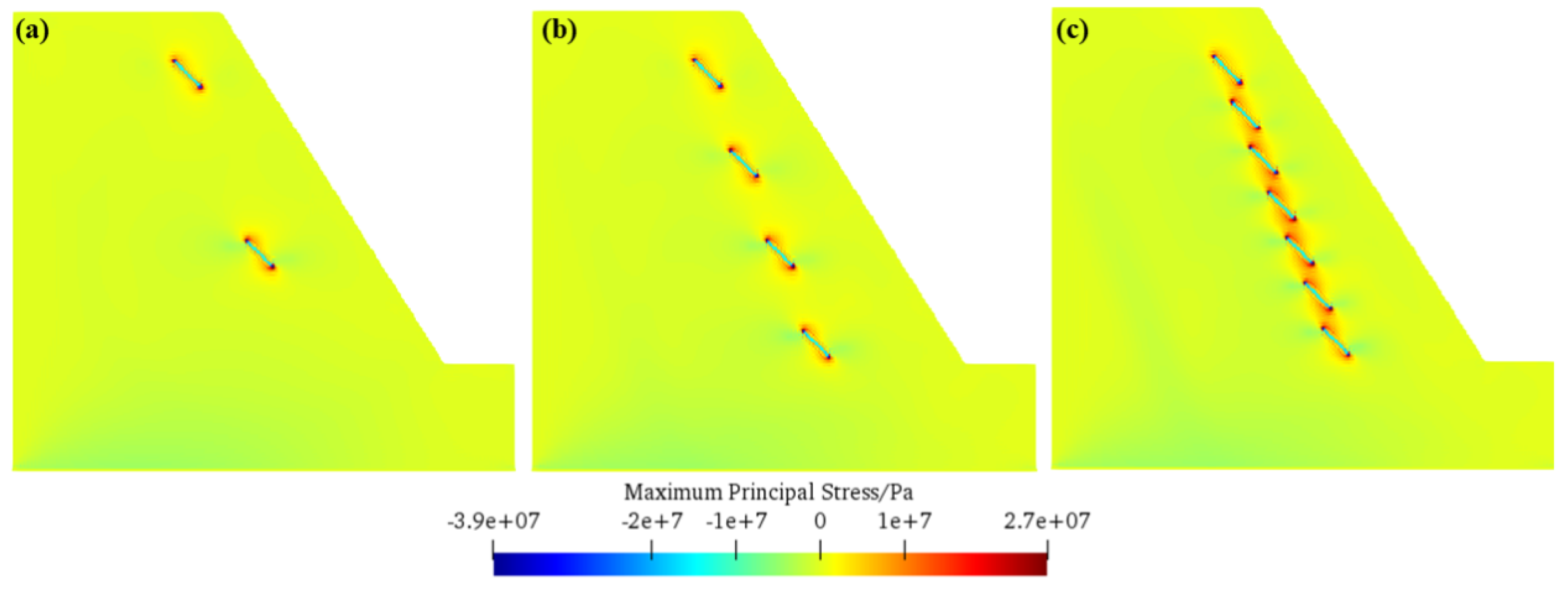
4.2. Influence of Different Fissure Lengths on Slope Frost Heave Failure
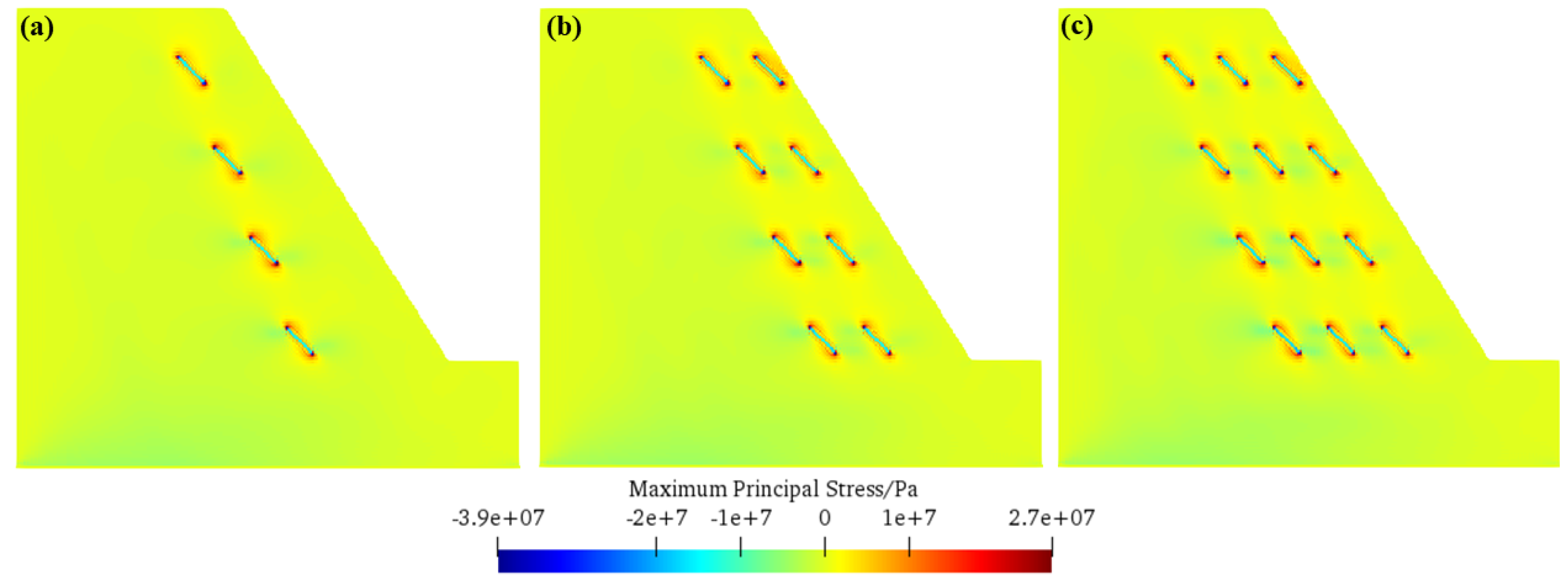
4.3. Influence of Different Numbers of Fissures on Slope Frost Heave Failure
4.4. Influence of Different Fissure Inclination Angles on Slope Frost Heave Failure
4.5. Influence of Different Numbers of Fissure Rows on Rock Slope Frost Heave Failure
5. Discussions
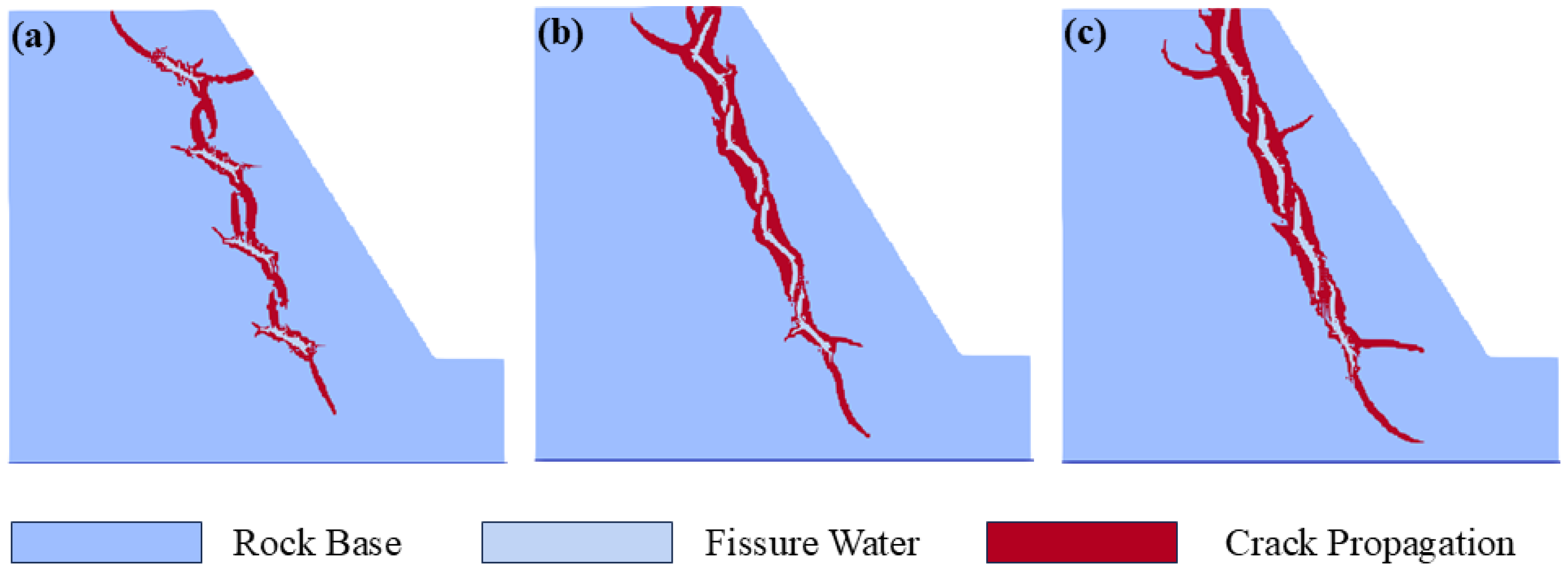
5.1. Mechanism of Action of Different Fissure Lengths on Slope Frost Heave Failure
5.2. Mechanism of Action of Different Numbers of Fissures on Slope Frost Heave Failure
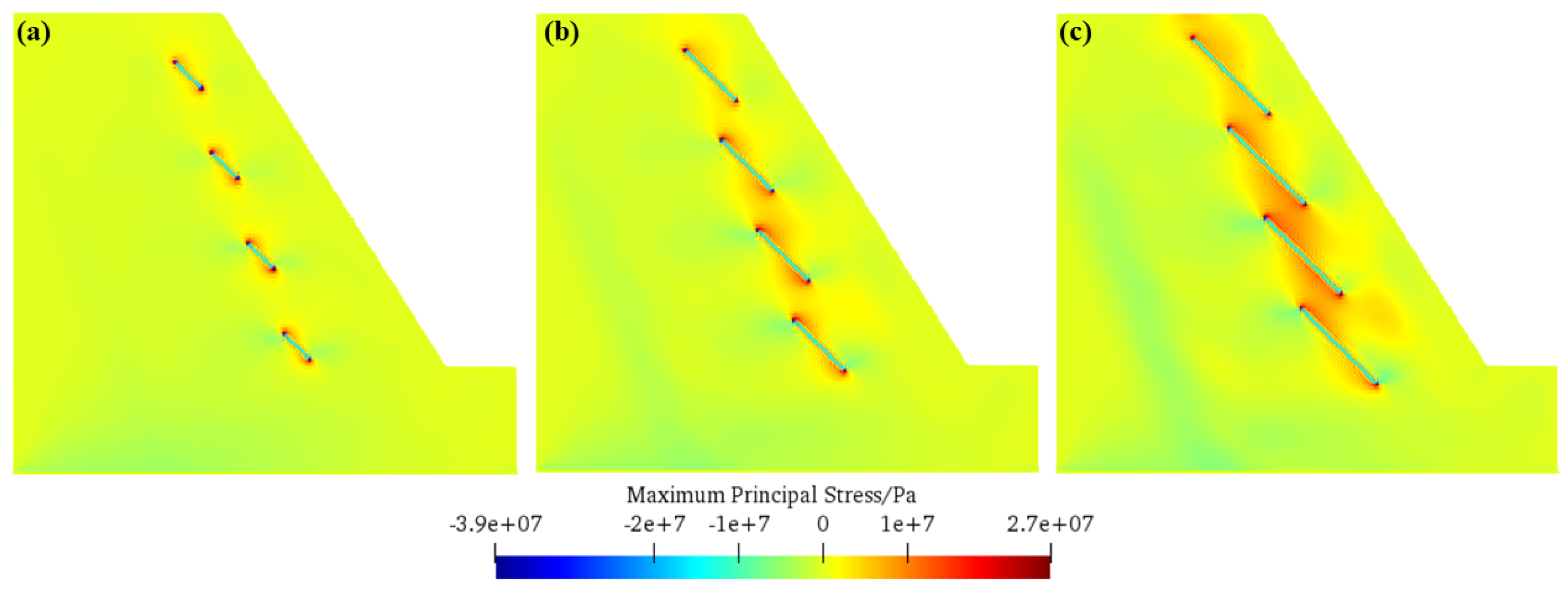
5.3. Mechanism of Action of Different Fissure Inclination Angles on Slope Frost Heave Failure
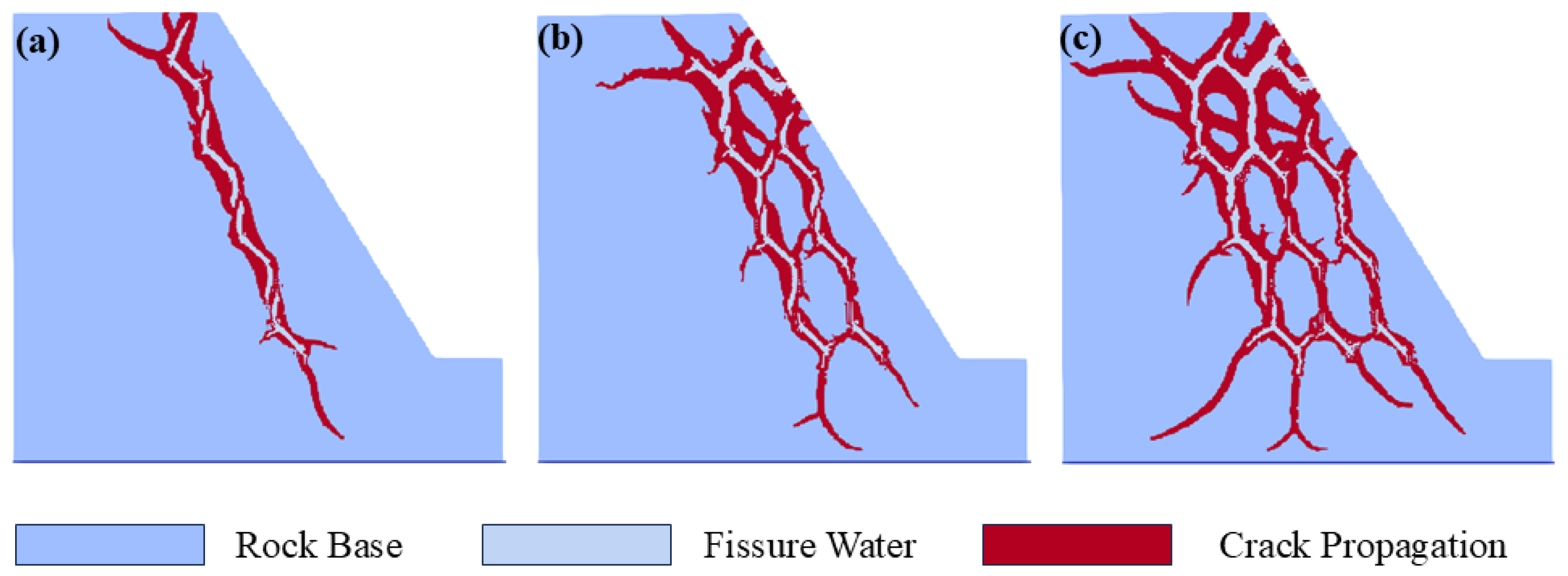
5.4. Mechanism of Action of Different Numbers of Fissure Rows on Rock Slope Frost Heave Failure
5.5. Application Prospects of SPH into Simulating Rock Frost Cracking
6. Conclusions
- (1)
- An innovative SPH-based numerical model for simulating the full process of fissured rock mass frost heave failure has been developed. Aiming at the limitations of traditional numerical methods (e.g., finite element method requiring pre-defined crack paths, discrete element method needing complex parameter calibration), this model integrates the maximum tensile stress criterion as the particle failure criterion and uses a binary fracture marker (ξ) to dynamically characterize the particle failure state (ξ = 0 for failure, ξ = 1 for intact). Combined with thermodynamic phase transition theory, fissure water is classified into water particles (T > 0 °C), ice–water mixed particles (−20 °C < T < 0 °C), and ice particles (T < −20 °C); the equivalent thermal expansion coefficient method is further adopted to quantify the frost heave force on fissure surfaces. This model avoids grid distortion and artificial crack path assumptions, enabling natural simulation of random and sudden crack initiation, propagation, and coalescence under frost heave, which fills the gap in the application of the SPH method in the rock slope frost heave failure simulation mentioned in the document.
- (2)
- The influence law and mechanism of fissure length on slope frost heave failure have been clarified. When the fissure length is small (e.g., 20 m), tensile stress is concentrated only at the tip of prefabricated fissures, secondary cracks develop from both ends of initial fissures and overlap slightly, and the failure mode presents a “strip-like” distribution. As the length increases to 40 m and 60 m, tensile stress concentration areas between fissures gradually connect into a contiguous region, the overlapping position of secondary cracks and initial fissures shifts toward the center of fissures, and the failure mode transforms into “tree-like”. This indicates that the increase in fissure length intensifies the interaction between fissures, promotes the development and coalescence of secondary cracks, and significantly expands the failure scale.
- (3)
- The regulatory effect of fissure number on slope frost heave failure mode and scale has been determined. With a small number of fissures (e.g., 2), the distance between fissures is large, secondary cracks do not overlap, and failure develops independently along each initial fissure in a “sword-like” pattern without penetrating the slope top. When the number increases to four, reduced fissure spacing leads to secondary crack overlap, and failure develops along a quasi-straight line in a “strip-like” pattern with the failure penetrating the slope top. When the number reaches seven, secondary cracks overlap in the early stage of frost heave failure, and the failure mode transforms into “tree-like”. This confirms that the increase in fissure number strengthens the mutual influence between fissures, accelerates crack coalescence, and further expands the failure scale.
- (4)
- The relationship between fissure inclination angle and slope frost heave failure morphology has been revealed. For a small inclination angle (e.g., 30°), tensile stress concentration areas near fissure tips are dispersed, and secondary cracks deviate from initial fissure directions and form multi-branch structures, resulting in a “fishbone-shaped” failure mode with nine secondary cracks. As the inclination angle increases to 45° and 60°, tensile stress concentration areas converge to fissure tips; each fissure is approximately in the same straight line; the failure mode transforms into “strip-like”; and the number of secondary cracks decreases to four and three, respectively. This shows that the increase in fissure inclination angle changes the distribution of tensile stress concentration areas, thereby altering the development direction of secondary cracks and the final failure morphology.
- (5)
- The law of fissure row number affecting the spatial expansion of slope frost heave failure has been supplemented. With a single row of fissures, tensile stress concentration areas connect the tips of a single row of fissures into a continuous zone, and failure presents a “strip-like” distribution. When the row number increases to two, tensile stress concentration areas form a network connection between rows, secondary cracks are more likely to contact the slope surface, the failure mode evolves into “network-like”, and the failure area ratio rises to 12.7%. When the row number reaches three, the network of tensile stress concentration areas becomes denser, the probability of secondary cracks contacting the slope and slope top increases significantly, and the failure scale expands sharply. This indicates that the increase in fissure row number strengthens the interaction between inter-row fissures, promotes the collaborative development of multi-row secondary cracks, and leads to the evolution of failure morphology from “strip-like” to “network-like”.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, L.; Shi, W.; Tian, X.; Li, J.; Zhao, B.; Wang, S.; Tan, J. A plane stress measurement method for CFRP material based on array LCR waves. NDT E Int. 2025, 151, 103318. [Google Scholar] [CrossRef]
- Wang, X.; Li, J.; Zhao, X.; Liang, Y. Propagation characteristics and prediction of blast-induced vibration on closely spaced rock tunnels. Tunn. Undergr. Space Technol. 2022, 123, 104416. [Google Scholar] [CrossRef]
- Wang, X.; Li, Z.; Li, W.; He, C.; Wang, Z. Analysis and prediction of dynamic stress concentration in jointed coal using boundary element method. Theor. Appl. Fract. Mech. 2025, 140, 105136. [Google Scholar] [CrossRef]
- Xiao, W. Analytical theory on instability sliding of surrounding rock blocks in tunnel roof under stress wave actions. Chin. J. Theor. Appl. Mech. 2024, 56, 183–197. [Google Scholar]
- Yu, S.; Ren, X.; Zhang, J. Modeling the rock frost cracking processes using an improved ice—Stress-Damage coupling method. Theor. Appl. Fract. Mech. 2024, 131, 104421. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, X.; Li, W.; Jiang, Y.; Li, Z.; Wang, C. Analytical theoretical study on ultra-low friction characteristics of coal rock interfaces under stress wave action. J. China Coal Soc. 2024, 49, 4495–4507. [Google Scholar]
- Tang, J.; Zhang, M.; Guo, X. Investigation of creep and transport mechanisms of CO2 fracturing within natural gas hydrates. Energy 2024, 300, 131214. [Google Scholar] [CrossRef]
- Zhang, Z.; Tang, J.; Zhang, J. Modeling of scale-dependent perforation geometrical fracture growth in naturally layered media. Eng. Geol. 2024, 336, 107499. [Google Scholar] [CrossRef]
- Zhang, Z.; Tang, J.; Fan, B. An intelligent lithology recognition system for continental shale by using digital coring images and convolutional neural networks. Geoenergy Sci. Eng. 2024, 239, 212909. [Google Scholar] [CrossRef]
- Tang, L.Y.; Wu, D.N.; Zheng, J.G.; Ding, B.; Xu, P.Z.; Yu, Y.T.; Jia, H.L.; Li, H.B.; Qiu, P.Y. A nonlinear viscoelastic-plastic creep constitutive model of soil-rock mixture-concrete interface under freeze-thaw cycles. Res. Cold Arid Reg. 2025; in press. [Google Scholar] [CrossRef]
- Liang, X.; Liu, Z.; Peng, K.; Wang, H.; Zhang, S.; Yuan, C. Failure prediction of fissured rock under freeze-thaw cycles based on critical slowing down theory of acoustic emission multi-parameter. Results Eng. 2025, 5, 103874. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, H.; Liang, L. Freeze-thaw failure characteristics and strength loss of non-penetrating fractured rock mass with different fracture densities. Theor. Appl. Fract. Mech. 2023, 124, 103792. [Google Scholar] [CrossRef]
- Zhou, Z.; Ullah, B.; Rui, Y.; Cai, X.; Lu, J. Predicting the failure of different rocks subjected to freeze-thaw weathering using critical slowing down theory on acoustic emission characteristics. Eng. Geol. 2023, 316, 107059. [Google Scholar] [CrossRef]
- Yu, M.; Wang, Z.; Xu, Y.; Wang, Y.; Wang, L.; Wen, J. Study on mechanical properties and energy evolution characteristics of excavation unloading rock under freeze–thaw temperature range. Eng. Fract. Mech. 2025, 325, 111293. [Google Scholar] [CrossRef]
- Zhang, J.; Du, R.; Zhang, X.; Huang, Z.; Zhang, W. The deformation and failure characteristics of tunnels in layered rock with gentle dip angles after freeze–thaw cycles: Physical model tests and numerical investigation. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2024, 144, 105527. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, L. A fully coupled thermo-mechanical peridynamic model for cracking analysis of frozen rocks. Comput. Geotech. 2023, 164, 105809. [Google Scholar] [CrossRef]
- Guo, L.; Ma, G.; Chen, G. A micro frost heave model for porous rock considering pore characteristics and water saturation. Comput. Geotech. 2024, 166, 106029. [Google Scholar] [CrossRef]
- Deng, Z.; Zhang, X.; Wang, Z.; Min, J.; Wei, J. Analysis of fracture toughness deterioration and instability model of dangerous rock masses under freeze–thaw cycles. Theor. Appl. Fract. Mech. 2024, 131, 104398. [Google Scholar] [CrossRef]
- Sun, L.; Tang, X.; Zeeman, B. Numerical investigation of the path-dependent frost heave process in frozen rock under different freezing conditions. J. Rock Mech. Geotech. Eng. 2025, 17, 637–651. [Google Scholar] [CrossRef]
- Zhou, Y.; Tan, X.; Yang, D. A numerical method to consider the interaction between multiple fractures in frozen rocks based on XFEM. Comput. Geotech. 2024, 169, 106240. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, Q.; Yang, T.; Chen, Y.; Zhang, P.; Liu, H. Investigation of crack propagation and acoustic emission characteristics in jointed rock under freeze–thaw cycles based on DEM. Int. J. Min. Sci. Technol. 2025, 35, 1171–1195. [Google Scholar] [CrossRef]
- Qiu, L.; Shi, C.; Zhang, L.; Zhang, F. Study on meso-deformation and failure mechanism of rock mass with micro-cracks under freeze-thaw loading. Simul. Model. Pract. Theory 2024, 135, 102974. [Google Scholar] [CrossRef]
- Shen, F.; Qiu, W.; Xie, K.; Xing, M.; Zhu, H.; Huang, S. A discrete element-based study of freeze–thaw damage in water-filled fractured rock. Comput. Geotech. 2025, 185, 107343. [Google Scholar] [CrossRef]
- Li, Z.; Liu, X.; Sun, Y.; Jiang, J.; He, Z. A study of the frost heave damage mechanism and numerical simulation of earth-rock dam slope protection in cold regions under the combined effects of moisture migration and ice loads. Cold Reg. Sci. Technol. 2025. [Google Scholar] [CrossRef]
- Li, K.; Li, Y.; Yin, F.; Dai, F.; Wang, C.; Zhang, S.; Wang, K. Mechanical properties and failure mechanism of rock-like specimens with arc-shaped flaws under freeze–thaw cycles. Theor. Appl. Fract. Mech. 2024, 130, 104275. [Google Scholar] [CrossRef]
- Liu, Q.; Kang, Y.; Liu, X. Analysis of stress field and coupling thermos-mechanical simulation of single-fracture freezed rock masses. Chin. J. Rock Mech. Eng. 2011, 30, 217–223. [Google Scholar]
- Yu, S.; Ren, X.; Zhang, J. An Improved Form of SPH Method for Simulating the Thermo-Mechanical-Damage Coupling Problems and Its Applications. Rock Mech. Rock Eng. 2022, 55, 1633–1648. [Google Scholar] [CrossRef]
- Zhang, W.; Xie, X.; Shi, D. Experimental insights into the mechanical properties and constitutive models of coral aggregate seawater concrete mixed with natural aggregates. J. Build. Eng. 2025, 107, 112756. [Google Scholar] [CrossRef]
- Zhang, W.; Li, H.; Shi, D. Determination of Safety Monitoring Indices for Roller-Compacted Concrete Dams Considering Seepage–Stress Coupling Effects. Mathematics 2023, 11, 3224. [Google Scholar] [CrossRef]

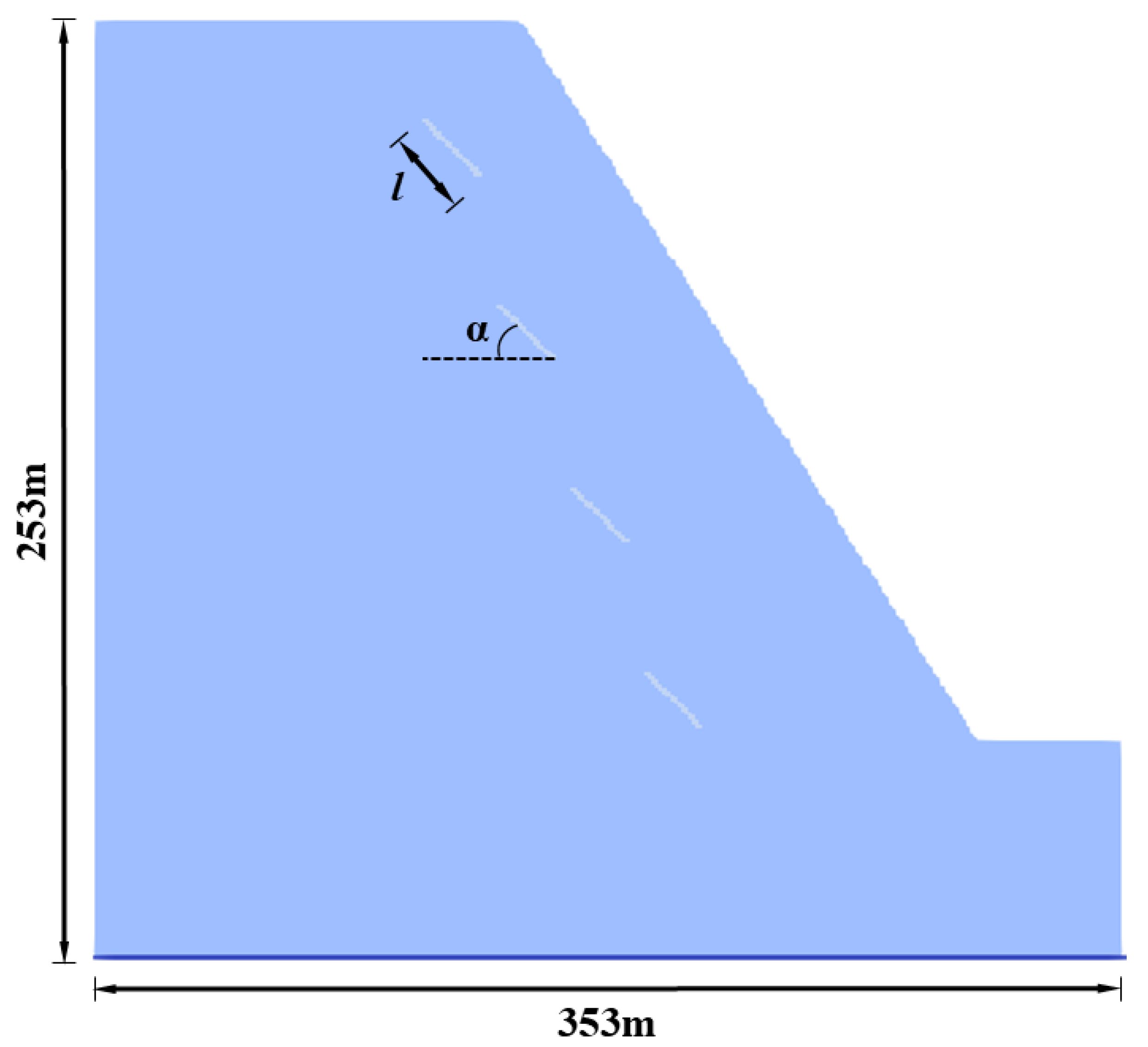



| Numerical Methods | Advantages | Limitations |
|---|---|---|
| FEM |
|
|
| DEM |
|
|
| SPH |
|
| Schemes | Details | Schemes | Details |
|---|---|---|---|
| A1 | l = 20 m | C1 | α = 30° |
| A2 | l = 40 m | C2 | α = 45° |
| A3 | l = 60 m | C3 | α = 60° |
| B1 | n = 2 | D1 | p = 1 |
| B2 | n = 4 | D2 | p = 2 |
| B3 | n = 7 | D3 | p = 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, C.; Zeng, F.; Shao, H.; Zhang, W.; Zhang, B.; Li, W.; Yu, S. Investigating the Frost Cracking Mechanisms of Water-Saturated Fissured Rock Slopes Based on a Meshless Model. Water 2025, 17, 2858. https://doi.org/10.3390/w17192858
Guo C, Zeng F, Shao H, Zhang W, Zhang B, Li W, Yu S. Investigating the Frost Cracking Mechanisms of Water-Saturated Fissured Rock Slopes Based on a Meshless Model. Water. 2025; 17(19):2858. https://doi.org/10.3390/w17192858
Chicago/Turabian StyleGuo, Chunhui, Feixiang Zeng, Han Shao, Wenbing Zhang, Bufan Zhang, Wei Li, and Shuyang Yu. 2025. "Investigating the Frost Cracking Mechanisms of Water-Saturated Fissured Rock Slopes Based on a Meshless Model" Water 17, no. 19: 2858. https://doi.org/10.3390/w17192858
APA StyleGuo, C., Zeng, F., Shao, H., Zhang, W., Zhang, B., Li, W., & Yu, S. (2025). Investigating the Frost Cracking Mechanisms of Water-Saturated Fissured Rock Slopes Based on a Meshless Model. Water, 17(19), 2858. https://doi.org/10.3390/w17192858









