Assessing and Identifying Areas with a High Need for Water Retention Improvement Using the Dematel Method

Abstract

In the integrated management of water resources, which includes protecting and restoring ecosystems that are directly and indirectly dependent on water, a crucial issue is assessing and identifying areas with the greatest need for improved water retention. This study presents an effective and easy-to-apply method based on the multicriteria decision-making approach, which analyses needs and feasibility. Until now, a point bonitation method has been used to evaluate the need to increase the retention capacity of specific areas. Modification of this method involved applying the Decision-Making Trial and Evaluation Laboratory (DEMATEL) approach to estimate the weights of the analysed criteria. The results obtained using the new method were compared with previous studies assessing retention needs in the Masovian Voivodeship (Poland), which relied on the point bonitation method. The final evaluation showed a 74% compliance rate while significantly reducing expert involvement, demonstrating the high applicability of the developed method. Moreover, the DEMATEL method enabled the development of a cause-and-effect model of the criteria and an analysis of their importance. The lowest level of importance (13.6%) was attributed to climatic conditions, while the significance of the remaining criteria (hydrological and hydrogeological conditions, economic use of the catchment area, and catchment area cover) varied within a narrow range, from 20% to 23.5%.

1. Introduction

Protection of water and water-dependent ecosystems is one of the fundamental pillars of the European legal framework shaping water policy—the Water Framework Directive. Climate change has disrupted the global climate system, and its visible effects in Poland include an increase in extreme events and a worsening precipitation deficit [1]. In practice, climate change poses an increasing threat to the country, including droughts, flooding from heavy rainfall, and forest and agricultural fires. Therefore, it is important that, in water management, managers must consider the potential impacts of climate change to achieve sustainable development goals and reduce disaster risk [2]. Adaptation and mitigation are complementary strategies for managing climate change risks and reducing their impacts on water resources [3,4]. Climate change affects the terrestrial water cycle through many different processes. The feedback and interactions between these processes are not fully measurable at appropriate scales, making quantification and consequences difficult to predict [5]. Various anthropogenic factors, including land use and land cover change, and water resource regulation systems, determine the links between climate and water resources.

In the integrated management of water resources, which includes protection and restoration of ecosystems that are directly and indirectly dependent on water, one of the key adaptation and mitigation measures for flood and drought risk is strengthening and restoring water-holding capacity in rural catchment areas. Currently, efforts in this regard are being carried out in Poland through water retention initiatives, understood as the storage of water in small reservoirs, ponds, and waterholes in river valleys and riverbeds, as well as in drainage ditches equipped with damming devices. These activities address various needs, ranging from providing the required water resources on a local scale for agricultural irrigation, fish farming, small hydropower, and recreation, to enriching groundwater resources, mitigating the effects of heavy rainfall and the heat island effect, limiting erosion, and improving water quality (mainly by reducing nutrient loads). Water retention can be achieved through hydrotechnical structures (e.g., weirs, gates, retention reservoirs) or through so-called ‘non-technical’ measures (e.g., wetland restoration, creation of small ponds and oxbows, stream meandering, and floodplain revitalisation). In the past, many of these solutions were already based on concepts derived from ecological engineering [6,7,8,9]. Currently, in line with the advancement of scientific knowledge and in accordance with the global trend and guidelines of the International Union for Conservation of Nature [10,11], the use of nature-based solutions and blue and green infrastructure is being promoted. By influencing both the quantity and quality of stored water, these approaches can significantly enhance biodiversity, provide a range of ecosystem services, reduce flood risk, and mitigate pollution on a large scale [12,13,14,15,16]. Additionally, attitudes toward management are evolving, with an increasing emphasis on a learning-based culture and the incorporation of local communities in decision-making processes [17,18,19,20].

The foundation of rational and sustainable conservation and restoration is the accurate recognition and identification of cause-and-effect relationships within the studied ecosystems [21]. This is a sine qua non requirement of classical management in the terms of Henri Fayol [22], i.e., planning, organising, coordinating, leading, and controlling—in other words, decision-making in a broader sense. Among the commonly used approaches are methods from the group of Multiple Criteria Decision Making (MCDM), which are based on a multi-attribute utility function, as well as Multicriteria Decision Analysis (MCDA), which relies on identifying superiority relationships. Additionally, Multidimensional Comparative Analysis (MCA)—a less complex and more easily implementable method—is primarily used for a multidimensional description of reality in its original application [23]. This approach is reflected in several studies [24,25,26,27,28,29], where the authors present a wide range of applications in water management. These include, among others, assessing groundwater vulnerability to nitrogen pollution, resolving conflicts in water service management, managing rainwater, flood protection, catchment management in agricultural areas, and management of marine coastal zones.

In the context of increasing water scarcity across large areas of Poland and the severe impacts of sudden floods [30,31], efforts to mitigate the negative consequences of these changes are crucial. Therefore, developing effective and easy-to-apply methods for assessing and identifying areas with the greatest need for water retention improvement is essential. Rational decision-making regarding activities aimed at enhancing water retention—under the constant constraint of limited financial resources available to administrative units (e.g., river basins, municipalities)—should be based on a multicriteria analysis of necessity and desirability. One of the methods used for these purposes is the spatial assessment, in which selected spatial units are assessed in terms of environmental conditions conducive to problems, such as droughts and floods, limited water availability, and scarce occurrence of natural habitats. The comparative assessment indicates spatial units with the most significant problems, and the actions taken in these areas will potentially bring the best effects [32].

Spatial assessment is often used in environmental and socio-economic analyses [33]. It is a type of multicriteria analysis in which the final assessment usually depends on many partial assessments (indicators, criteria) and the method of aggregating partial assessments [34]. Almost at every stage of formulating the multicriteria analysis task, the participation of experts, usually from many fields, is necessary. They define the multicriteria problem by establishing a set of criteria and determine the rules for calculating the final scalar assessment by establishing the numerical values of the weighting coefficients describing the relations between individual criteria [35]. Theoretically, it is possible to carry out a “purely expert” assessment, in which a group of experts directly performs the final qualification of objects without defining partial criteria and relations between them. Such a solution will be specific to the selected expert group and devoid of the possibility of any external evaluation or verification. Such an approach is acceptable, although much more difficult to justify and convince interested parties (e.g., local authorities and water users).

The point bonitation method is the most commonly used in area valuation [36] and involves assigning points to basic spatial units that reflect the intensity of the analysed indicators. The assessment score of individual indicators is summed up for each spatial unit and then classified into established value ranges. The advantage of this approach is that it obtains a synthetic objective result, allowing for the comparison of assessments for individual spatial units [33]. The disadvantage is the subjective selection of the range of values (scales) and the weights of the assessed criteria, which depend on experts’ knowledge, experience, and opinions [37]. The results of the point bonitation method depend, to a large extent, on many expert decisions.

Searching for a compromise between experts at the stage of adopting scales and weights of criteria is a laborious and sometimes lengthy process, especially when experts prefer the “importance” of the fields they represent. This problem, as well as the desire to objectify expert assessments, was undoubtedly one of the most important premises for the development of methods that limit the participation of experts to those parts of the analysis in which they are necessary and at a level that generates as few conflict situations as possible [38,39,40]. One such method, which allows for determining weights based on a computational algorithm, is the Decision-Making Trial and Evaluation Laboratory (DEMATEL) method [41,42,43], belonging to the group of tools supporting multicriteria decisions. The method was created to solve contemporary economic, social and financial problems. The DEMATEL method allows for building a cause-effect model of the analysed system’s components (factors, criteria), which allows one to examine and solve complex problems. Its application leads to understanding the interrelationships between factors or criteria, determining key factors considering causal relationships and the degree of interrelationships between factors, and calculating the weights of criteria by considering the interrelationships and levels of criteria influence. Many works have been published showing its usefulness in solving practical issues related to various fields, such as construction and environmental engineering [44], assessment of drought risk [45,46] and flood risk [47,48,49]. The advantages of this method—particularly its ability to account for the influence of difficult-to-measure factors and the interrelations between them—make it suitable for use in combination with other information processing and decision support tools, such as Analytic Hierarchy Process (AHP), entropy method, Delphi method, Analytical Network Process (ANP) [42,50].

This article presents a new method for assessment of the hydrographic units, i.e., river sub-catchments, determined in a specific area (e.g., voivodeship, water management region) in terms of the need (purposefulness) of increasing water retention capacity by the implementation of water retention measures. So far, the point bonitation method was to assess the need to increase the retention of spatial units [32,51]. The novelty of the proposed method consists of using the DEMATEL method to estimate the weights for the analysed criteria (climatic, hydrological, hydrogeological conditions, land cover and development) and introducing continuous standardisation of the values of indicators describing the adopted criteria. The assessment developed with the new method was compared with the research results on the assessment of the need for increasing retention for the Mazovian Voivodeship, referred further as PSWR-2008, in which the point bonitation method was used [32].

2. Materials and Methods

2.1. Study Area

The study covered the area of Mazovian Voivodeship (35,559 km²), located in central Poland. Hydrographic units were evaluated, i.e., sub-catchments or parts of their areas located within the voivodeship. The number of spatial units assessed was 141, with an area from 0.1 to 1228 km² [32].

2.2. Valorisation of SWR Development Needs—PSWR-2008 Approach

The point bonitation method was used to assess the need to increase the water retention of defined spatial units: the spatial units were first evaluated in terms of the selected criteria, and the total assessment was then determined. The analyses used indicators characterising climatic, hydrological (surface water), hydrogeological (groundwater) conditions and land cover and development [32], which affect the quantity and quality of water and its circulation in the landscape.

The area valuation followed a nine-step procedure (Figure 1).

• Step 1. Determination of the purpose of the valorisation: an assessment of the spatial diversity of the need to increase water retention.
• Step 2. Determination of the research area and selection of an adequate spatial unit for the assessment: in the Mazovian Voivodeship, NC = 141 hydrographic units, sub-catchments located entirely or partially within the voivodeship were distinguished.
• Step 3. Selection of evaluation criteria and corresponding indicators related to the valuation objective: the criteria characterised natural and economic conditions related to the need (purposefulness) for SWR development. For each criterion (G), indicators (K) were defined, taking into account the possibility of their calculation based on available data. Five criteria were defined (NG = 5), described by 11 indicators (NK = 11). These were:
  • G1—climatic conditions with two indicators (NGK₁ = 2): K_1,1 climatic precipitation deficit D_clim, and K_1,2 the frequency of precipitation lower than 50% of the multi-year average precipitation sum FPD_50.
  • G2—hydrological conditions with two indicators (NGK₂ = 2): K_2,1 the volume of specific runoff for the mean low flow from the multi-year period MLq, and K_2,2 the ratio of the maximum flow with a probability of exceedance equal to 1% to the mean low flow Q1_MLQ).
  • G3—hydrogeological conditions with two indicators (NGK₃ = 2): K_3,1 water retention of soils RetSoil and K_3,2 the module of renewable groundwater resources MRGR).
  • G4—economic use of the catchment area with three indicators (NGK₄ = 3): K_4,1 share of urbanised areas—W_Urban, K_4,2 share of orchards W_Orcha, and K_4,3 share of arable land W_Arable).
  • G5—catchment land cover with two indicators (NGK₅ = 2): K_5,1 share of forests—W_Forest, K_5,2 share of the area of lakes and artificial water reservoirs—W_Lake.
• Step 4. Calculation of indicator values in spatial units: numerical values of NK = 11 indicators were determined for all NC = 141 sub-catchments. As a result, a matrix of indicator values [k_c,i,j] was obtained (c = 1, …, NC; i = 1, …, NG; j = 1,…, NGK_i).
• Step 5. Adoption of the assessment scale and threshold values for individual indicators: a 3-point scale was used for indicators: 2—high, 1—medium, and 0—low predisposition of the spatial unit to develop water retention. For each indicator, K_ij, an interdisciplinary team of experts established two threshold values separating predisposition classes (L_i,j and H_i,j; i = 1, …, NG; j = 1, …, NGK_i).
• Step 6. Assessment of spatial units in terms of indicators: the partial scores (s_c,i,j) of the sub-catchment c in terms of the j-th indicator in the i-th criterion was calculated:

  $$s_{c,i,j}=\left\{\begin{array}{c}\begin{array}{ccc}0& when& k_{c,i,j}<L_{i,j}\end{array}\\ \begin{array}{ccc} 1& when& L_{i,j}\end{array}\le k_{c,i,j}<\\ \begin{array}{ccc}2& when& k_{c,i,j}\ge H_{i,j}\end{array}\end{array}\right.H_{i,j} i=1,\dots ,NG;j=1,\dots ,{NGK}_i$$

  (1)
  By converting the values of individual indicators, k_c,i,j, into scores, s_z,i,j, following the assumptions of the point bonitation method, the scores of individual indicators can be treated as comparable.
• Step 7. Determination of the overall assessment: the overall assessment V_c of the analysed sub-catchment is equal to the sum of the partial scores s_c,i,j, which means that each of the indicators is equally important:

  $$V_c=\sum _{i=1}^{NG}\sum _{j=1}^{{NGK}_i}{s}_{c,i,j}$$

  (2)
• Step 8. Transformation of the overall assessment to a 3-point scale grade: the V_c scores were transformed to a 3-point scale (V3_c), adopting threshold values for grades at the level of percentiles 70 and 20 as a result of experts’ discussion: grade 2—high priority (development of retention measures is very desirable), when overall assessment V_c ≥ Percentile_70 (12 points), grade 1—medium priority (development of retention is beneficial), when V_c assessment was within the range of Percentile_20 ≤ V_c < Percentile_70, and grade 0—low priority (there is no need to develop retention measures) when the V_c assessment < Percentile_20 (8 points).
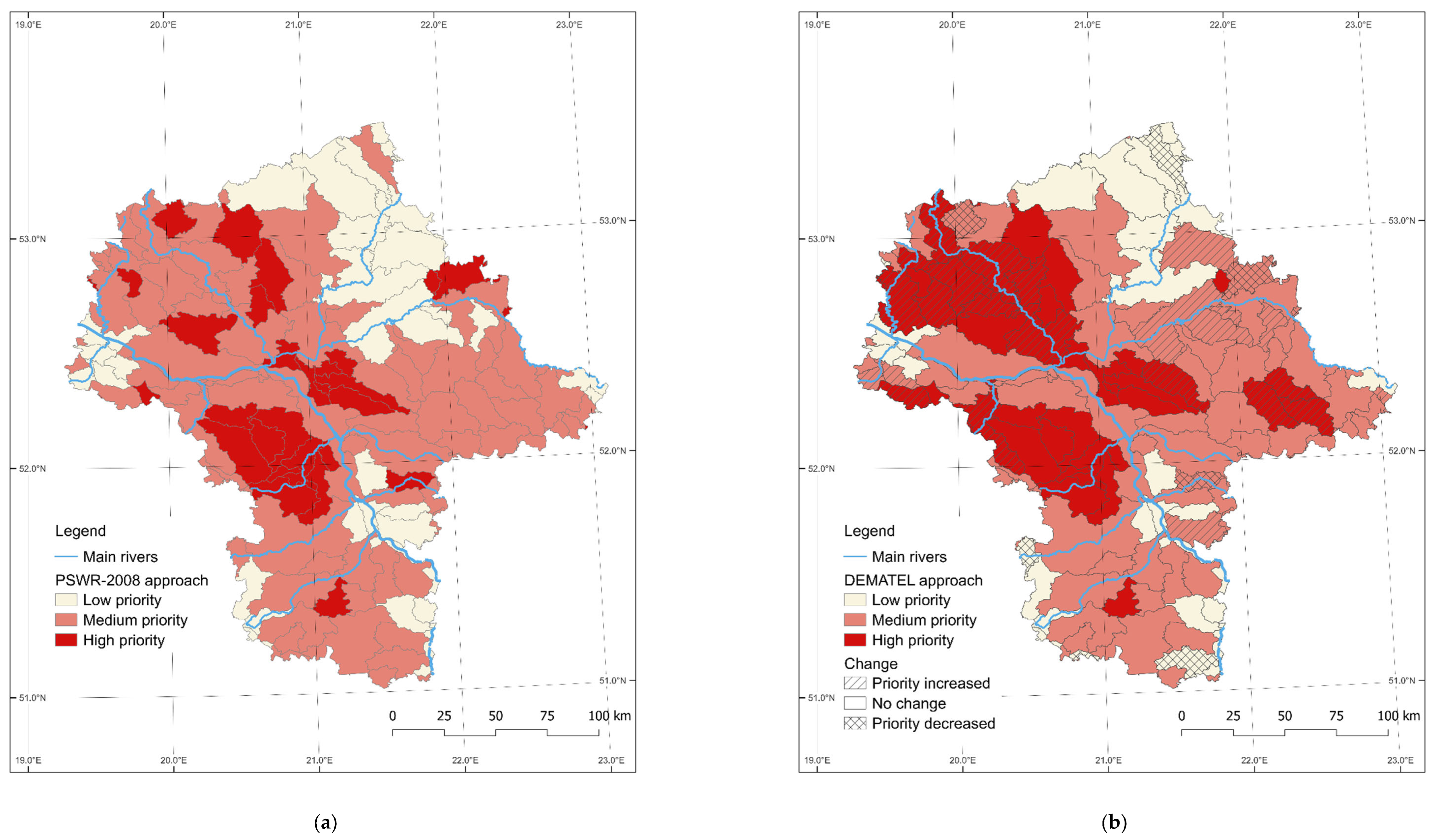
• Step 9. Presentation of the results of valorisation: in tabular form, containing sub-catchments’ overall assessment (V_c) and grades on a 3-point scale (V3_c) and valorisation maps of the Masovian Voivodeship area.

2.3. Valorisation of SWR Development Needs Using the DEMATEL Method

In the new method of assessment of the needs for the development of WR presented here, we have introduced the changes discussed below (Figure 1).

• Use of continuous standardisation of indicator values instead of a 3-point assessment. The values k_c,i,j of individual indicators are standardised according to the relation:

  $$x_{c,i,j}=\left\{\begin{array}{cc}{\displaystyle \frac{k_{c,i,j}-{kmin}_{i,j}}{{kmax}_{i,j}-{kmin}_{i,j}}}& for indicators that are stimulants\\ {\displaystyle \frac{{kmax}_{i,j}-k_{c,i,j}}{{kmax}_{i,j}-{kmin}_{i,j}}}& for indicators that are destimulants\end{array}\right.$$

  (3)

  where kmin_i,j and kmax_i,j are the smallest and largest values of the j-th indicator of the i-th criterion in the set of all 141 spatial units (sub-catchments), respectively.
• Change in the method of calculating the overall assessment of the sub-catchment V_c (c = 1, …, NC) by replacing the sum of the partial scores s_c,i,j (c = 1, …, NC; i = 1, …, NK; j = 1, …, NGK_i) of individual indicators by the weighted sum of standardised values of the (x_c,i,j). In PSWR-2008, all indicators were treated as equally important. The proposed approach introduces weights for the evaluation criteria (β_j; j = 1, …, NG) and weights of indicators within individual criteria (α_i,j; i = 1, …, NG, j = 1, …, NGK_i). The criteria weights are determined using the DEMATEL method (see Section 2.4). The weights for the indicators within each criterion can be arbitrarily determined by experts or using the DEMATEL method. Here, we used the first approach, assuming the same weights for the indicators in each criterion (α_i,j = 1/NGK_i).
• The overall VD_c assessment for the river sub-catchment c was calculated:

  $${VD}_c=\sum _{i=1}^{NG}{\beta }_i·\sum _{j=1}^{{NGK}_i}{\alpha }_{i,j}·x_{c,i,j}$$

  (4)

  where
  ${\sum }_{j=1}^{{NG}_i}{\alpha }_{i,j}·x_{c,i,j}$ means the summary score of the sub-catchment c from the point of view of i-th criterion;
  x_c,i,j for the sub-catchment c is the standardised value of the j-th indicator in the i-th criterion.

2.4. DEMATEL Method

The fundamental goal of the DEMATEL method is to identify and determine the cause–effect relationships between n factors (criteria/indicators) characterising the considered system or decision-making process and the resulting role of these factors (finally—factor weights). The DEMATEL calculation procedure consists of 5 steps [52].

• Step 1—defining the set of factors.

A team of E experts often determines the set of factors characterising the system (problem, decision-making process) based on their experience and literature data.

• Step 2—determining the influence matrix A.

The influence matrix A = [a_i,j]_nxn for n factors is determined based on the opinion of the team of E experts. Each expert determines the degree to which, in their opinion, the i-th factor affects the j-th factor. The direct impact is assessed on a p-degree scale. In this analysis, similarly to the original DEMATEL method, a 4-point scale was adopted: 0—no influence, 1—small influence, 2—medium influence, and 3—large influence. The results of pairwise comparisons between the i-th factor and the j-th factor, made by the k-th expert, are denoted by $b_{i,j}^{\left(k\right)}$. They create individual influence matrices:

$$B^{\left(\mathit{k}\right)}={\left[b_{i,j}^{\left(k\right)}\right]}_{nxn}$$

(5)

where i = 1, 2, …, n; j = 1, 2, … n; k = 1, 2, … E.

These matrices form the basis for calculating the direct influence matrix A, most often as the arithmetic mean of the matrix B^(k):

$$a_{i,j}={\displaystyle \frac{1}{E}}\sum _{k=1}^E{b}_{i,j}^{\left(k\right)}$$

(6)

As a result, the influence matrix A, also called the initial relational matrix, is obtained:

$$A=\left[\begin{array}{cc}\begin{array}{ccc}\begin{array}{c}0\\ a_{\mathrm{2,1}}\\ a_{\mathrm{3,1}}\end{array}& \begin{array}{c}{a}_{\mathrm{1,2}}\\ 0\\ a_{\mathrm{3,2}}\end{array}& \begin{array}{c}{a}_{\mathrm{1,3}}\\ a_{\mathrm{2,3}}\\ 0\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}\dots \\ \dots \\ \dots \end{array}& \begin{array}{c}{a}_{1,n}\\ a_{2,n}\\ a_{3,n}\end{array}\end{array}\\ \begin{array}{ccc}\begin{array}{c}\dots \\ a_{n,1}\end{array}& \begin{array}{c}\dots \\ a_{n,2}\end{array}& \begin{array}{c}\dots \\ a_{n,3}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}\dots \\ \dots \end{array}& \begin{array}{c}\dots \\ 0\end{array}\end{array}\end{array}\right]$$

(7)

The sum of $\left(\sum _{j=1}^n{a}_{i,j}\right)$ elements of the i-th row of matrix A represents the total direct effect of i-th factor on the other factors. Similarly, the sum of $\left(\sum _{i=1}^n{a}_{i,j}\right)$ of the j-th column represents the total direct effect received by j-th factor from the other factors.

• Step 3—determination of a standardised matrix of influences X.

Dividing each element a_i,j by a constant value of s equal to results in the standardisation of matrix A:

$$s=max\left(\underset{1\le i\le n}{\mathit{max}}\sum _{j=1}^n{a}_{i,j}; \underset{1\le j\le n}{\mathit{max}}\sum _{i=1}^n{a}_{i,j}\right)$$

(8)

Standardised Influence Matrix X = [x_i,j]_n×n equals:

$$X={\displaystyle \frac{A}{s}}=\left[\begin{array}{cc}\begin{array}{ccc}\begin{array}{c}0\\ x_{\mathrm{2,1}}\\ x_{\mathrm{3,1}}\end{array}& \begin{array}{c}{x}_{\mathrm{1,2}}\\ 0\\ x_{\mathrm{3,2}}\end{array}& \begin{array}{c}{x}_{\mathrm{1,3}}\\ x_{\mathrm{2,3}}\\ 0\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}\dots \\ \dots \\ \dots \end{array}& \begin{array}{c}{x}_{1,n}\\ x_{2,n}\\ x_{3,n}\end{array}\end{array}\\ \begin{array}{ccc}\begin{array}{c}\dots \\ x_{n,1}\end{array}& \begin{array}{c}\dots \\ x_{n,2}\end{array}& \begin{array}{c}\dots \\ x_{n,3}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}\dots \\ \dots \end{array}& \begin{array}{c}\dots \\ 0\end{array}\end{array}\end{array}\right]$$

(9)

Standardisation carried out in this way ensures that each element x_i,j of matrix X is contained in the closed interval 〈0; 1〉.

• Step 4—Calculation of the total impact matrix T.

The following formula calculates the total impact matrix T:

$$T=\underset{n\to \infty }{\mathit{lim}}\left(X+X^1+X^2+\dots +X^{\infty }\right)=X{(I-X)}^{-1}$$

(10)

It is assumed that X^m for $m\to \infty$ is convergent to the zero matrix [53].

The T matrix, as defined in this way, contains several valuable pieces of information about the interconnections of factors. Summarising the rows and columns of T matrix elements:

$$r_i=\sum _{j=1}^n{t}_{i,j}; c_j=\sum _{i=1}^n{t}_{i,j}; i=1,2,\dots ,n;j=1,2,\dots ,n$$

(11)

allows for defining the amount r_i of total influence (impact), direct and indirect, transferred by the i-th factor to other factors and the size of c_j of the total impact, both direct and indirect, received by the j-th factor from other factors [53,54].

Therefore, when j = i, the sum (r_i + c_i) is an indicator (Prominence) representing the total effect transmitted and received by the i-th factor. In other words, (r_i + c_i) shows the degree of importance the i-th factor plays in the system. However, the difference (r_i − c_i) (Relation) shows the net impact the i-th factor brings to the system. When (r_i − c_i) is positive, the i-th factor is a net agent (sender), and when (r_i − c_i) is negative, the i-th factor is a net recipient [38,53].

• Step 5—Calculation of weights for factors for multicriteria analyses.

The values of the r_i and c_i indicators cannot be directly used as importance coefficients (weights) w_i of individual factors (criteria) in multicriteria optimisation analyses. Most optimisation methods require the weights to be between 0 and 1, and their sum should equal one. In the literature, the weights of the criteria were most often determined by the classic DEMATEL method based on the r_i and c_i indicators as follows [38,52]:

$$w_i={\displaystyle \frac{r_i+c_i}{\sum _{i=1}^n\left(r_i+c_i\right)}} , i=\mathrm{1,2},\dots ,n$$

(12)

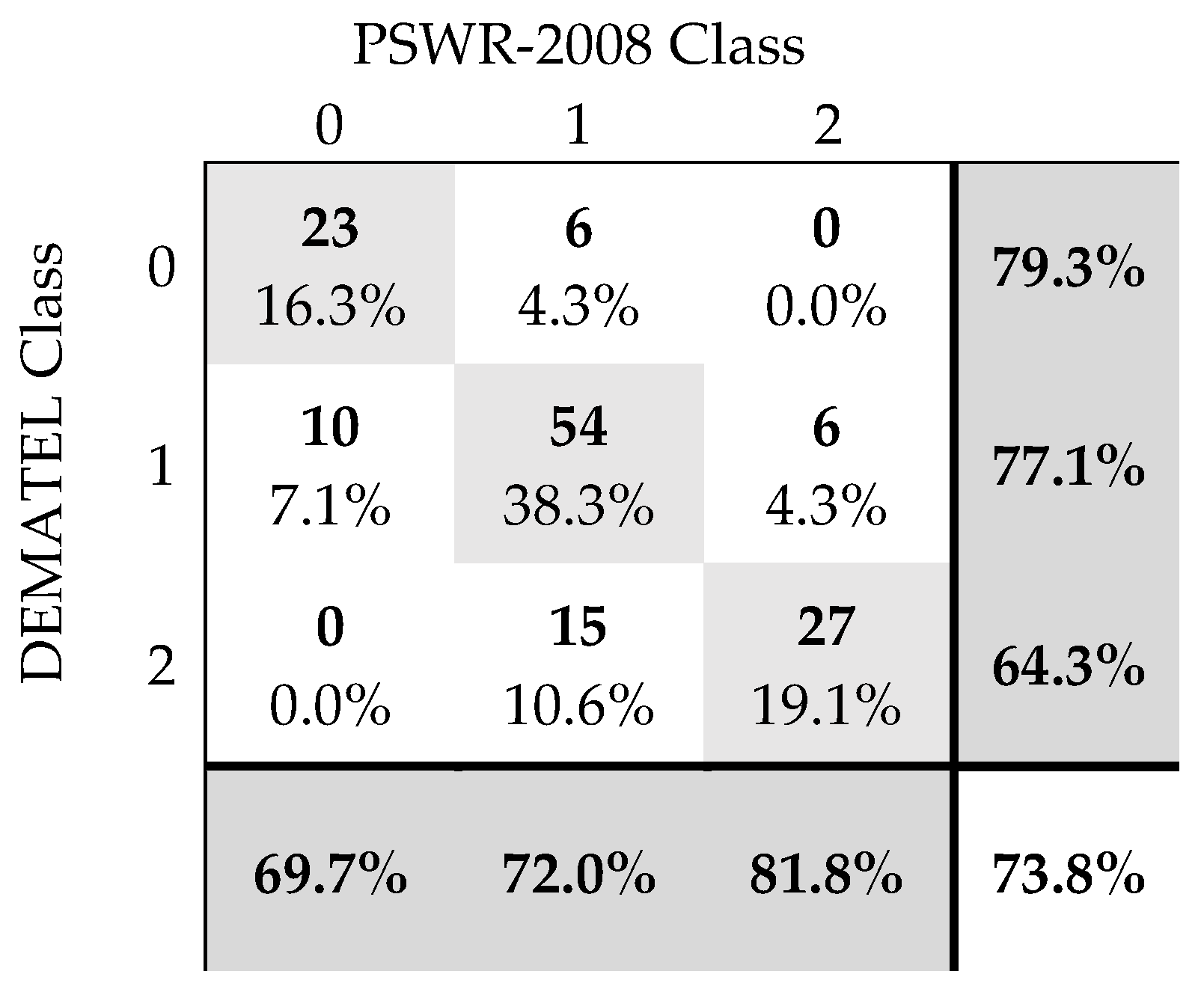
3. Results of Assessment Using the DEMATEL Method

A team of experts (E = 6) in meteorology, hydrology, and water management participated in assessing the Masovian Voivodeship area using the modified method. The experts included experts from academia and people dealing with water retention issues in practice. Following the DEMATEL procedure, each expert assessed the relationships between factors by completing the direct influence matrix $B^{\left(k\right)}$ k = 1,2,…, E. Based on 6 matrices prepared by the experts, an average influence matrix A was determined, containing average values from the experts’ assessments (

Table 1. Averaged influence matrix A.

Factor Description (Criterion)	Factor	G1	G2	G3	G4	G5	Total
Climatic conditions	G1	0.000	3.000	1.833	0.500	1.167	6.500
Hydrological conditions	G2	0.000	0.000	1.500	1.500	1.500	4.500
Hydrogeological conditions	G3	0.000	2.167	0.000	1.167	2.000	5.333
Economic use of the catchment area	G4	0.667	2.500	1.667	0.000	1.833	6.667
Catchment area cover	G5	1.000	2.333	1.833	1.500	0.000	6.667
Total		1.667	10.000	6.833	4.667	6.500

).

The next step was to calculate the standardised influence matrix X. The condition of convergence of the m-th power of the matrix X, with m approaching infinity, to the zero matrix was checked (at the power m = 30, all elements of the X^m matrix were smaller than 10⁻⁷).

Based on the X matrix, the total impact matrix T was calculated (

Table 2. Total influence matrix T.

Factor Description (Criterion)	Factor	G1	G2	G3	G4	G5
Climatic conditions	G1	0.046	0.521	0.364	0.220	0.313
Hydrological conditions	G2	0.047	0.210	0.287	0.261	0.292
Hydrogeological conditions	G3	0.052	0.417	0.179	0.255	0.351
Economic use of the catchment area	G4	0.116	0.496	0.361	0.179	0.376
Catchment area cover	G5	0.142	0.485	0.374	0.307	0.220

) according to the Formula (10).

The T matrix was the basis for calculating the values of the R and C indicators (Formula (11)), Prominence (R + C) showing the degree of importance that the i-th factor plays in the analysed problem (system), and Relation (R − C) indicators showing the net impact that i-th factor contributes to the system. The values of these indicators are summarised in

Table 3. The direct and indirect influence.

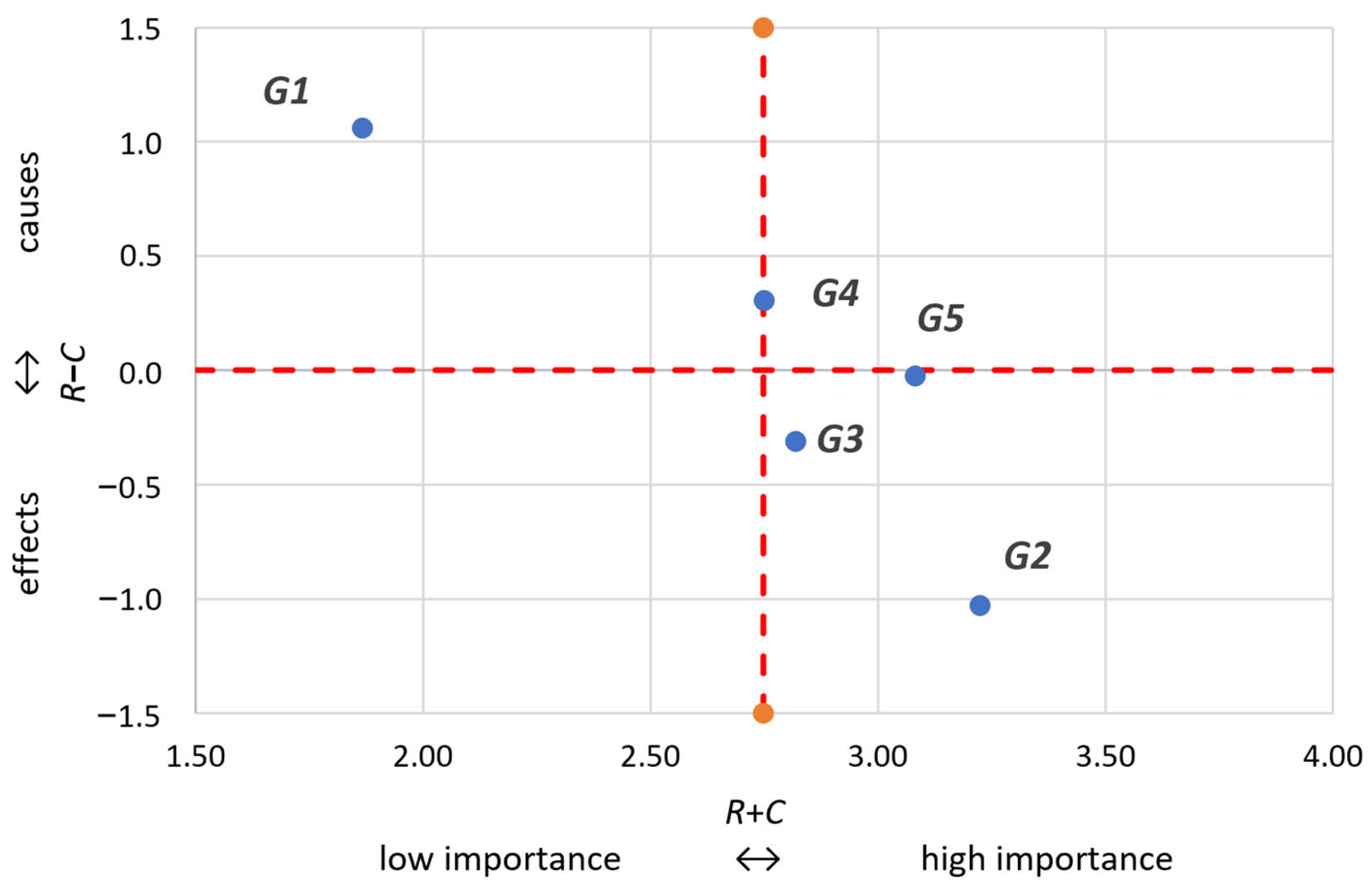
Factor Description (Criterion)	Factor	R	C	R + C	R − C	wi
Climatic conditions	G1	1.464	0.403	1.867	1.060	0.136
Hydrological conditions	G2	1.097	2.120	3.224	−1.031	0.235
Hydrogeological conditions	G3	1.255	1.565	2.820	−0.310	0.205
Economic use of the catchment area	G4	1.528	1.222	2.749	0.306	0.200
Catchment area cover	G5	1.528	1.553	3.081	−0.025	0.224

and shown in Figure 2.

The values of R + C indicators were used to determine the weight coefficients w_i (i = 1, 2, …, n), characterising the importance of individual factors (criteria) in the overall assessment of the needs for the development of the water retention. The weights were calculated according to Formula (12), the numerical values of the obtained weights are presented in Table 3. The results in Table 3 and Figure 2 show that prioritisation of the importance of the criteria is: G2 > G5 > G3 > G4 > G1. The factor with the strongest causal nature is climatic conditions (G1). The r_i − c_i relationship index reaches the highest value for this factor (1.060), but its significance is low (the r_i + c_i position index is the lowest and amounts to 1.867). Another causal factor is G4 (Economic use of the catchment area), which has a significantly higher value of the position index r_i + c_i = 2.749.

The factors illustrating the effects are factors with r_i − c_i < 0: G2 (hydrological conditions) and G3 (hydrogeological conditions)—their relationship indices are −1.031 and −0.310, respectively. However, the G5 factor (land cover) is causal and consequential (relationship index close to 0; r_i − c_i = −0.025).

Comparison of the classification of catchments into priority levels for the development of water retention measures (2—high priority, 1—medium priority, 0—low priority) with the assessment results obtained in PSWR-2008 (where the point bonitation method was used) allowed for assessment of the new method’s effectiveness. The number of catchment areas in individual classes in PSWR-2008 is 33 (class 0), 75 (class 1) and 33 (class 2). The assessment used the confusion matrix [55], which is often applied in classification problems to assess where errors in the model were made (Figure 3). The columns represent the actual classes in which the results should occur, while the rows represent the predictions made by the model (assessment with the DEMATEL method). With the use of this table, it is easy to visualise which predictions are wrong. The confusion matrix shows that the accuracy (which measures how often the model is correct) of the new method for all three classes is 78.3% (in 104 catchments out of 141, the water retention priority classes are the same). Accuracy for individual classes is 69.7%, 72.0%, and 81.8% for classes 0, 1, and 2, respectively. The precision of the correct classification for each class describes what percentage of the catchments in this class truly belong to it (True Positive/(True Positive + False Positive)). Compared to PSWR-2008, the precision of the assessment with the DEMATEL method is 79.3%, 77.1% and 64.3% for classes 0, 1, and 2, respectively (Figure 3). A comparison of the valorisation results is also presented in maps in Figure 4. The comparison of the two maps is a graphical representation of the precision of the new method. It is easy to notice the increased number of catchments with class 2 in the DEMATEL method (42) compared to the map based on the classification in PSWR-2008 (27).

4. Discussion

The results of the valuation assessment carried out using both methods: point bonitation and DEMATEL, are determined by the selection of criteria and indicators, threshold values of indicator assessments, and the method of determining the overall grades. In landscape valorisation, as in other multicriteria assessments, selecting a set of criteria and indicators for the defined objective is a key assessment stage. The indicators should directly or indirectly significantly affect, according to the current state of knowledge and expert opinions, the valorisation objective. In the case of spatial assessment, the size of the analysed area, the size of the assessed spatial units and the spatial variability of the units’ characteristics affect the selection of indicators that should be assessed.

The selection of indicators also depends on practical considerations, particularly the broadly understood availability of data (taking measurements, costs, time). In applying the DEMATEL method to assess retention needs, criteria and indicators were adopted in accordance with PSWR-2008. The indices employed in PSWR-2008 are commonly used in catchment water retention studies [56]. Adopting the same indicators allowed for comparing the assessment carried out in PSWR-2008 with the assessment results based on the new method, in which DEMATEL was used. In order to simplify the analyses, the DEMATEL analysis was applied to the five criteria, which aggregated all 11 indicators. A similar approach consisting of combining appropriate indicators into groups was used in the work of Stoilova [57], where the DEMATEL analysis was performed not only in groups of indicators but also within each of the groups.

The DEMATEL method also allowed the construction of a cause-effect model for the five criteria distinguished (G1—climatic conditions, G2—hydrological conditions, G3—hydrogeological conditions, G4—economic use of the catchment area, G5—catchment land cover). The estimated Prominence index (Table 3) indicates that prioritisation of the importance of the criteria is G2 > G5 > G3 > G4 > G1. The group of causes includes criteria G4 and G1, and the criteria in the effect group are G2, G3 and G5 (Figure 2). Interestingly, factor G5 (land cover) has both a causal and an effect character (relationship index close to 0; r_i − c_i = −0.025). The G2 has negative (R − C) and significant (R + C), indicating that hydrological conditions have a marked impact on the needs for water retention development, but are subject to other factors. Significantly, the use of the DEMATEL method indicated that experts tend to choose criteria that are somewhat influenced by humans, which is illustrated by the outlying values of the impact of the climate factor (Figure 2). This factor is characterised by a high relation and low prominence due to the low total impact (C) received by the G1 from other factors (Table 3). Due to the lack of analyses of prioritisation and cause-and-effect models of criteria relevant to the needs of retention in the literature, it is not easy to relate our results to the research of other authors.

In the new valuation method we proposed, the first change consisted of the standardisation of indicators (Formula (3)). In PSWR-2008, this stage was not performed, but an expert classification of the indicator values on a 3-point scale was carried out. This assessment brought all indicators to the same scale (0, 1 or 2). However, it required the team of experts to determine the threshold values of the assessments, which is one of the most significant difficulties of the point bonitation method [37]. The disadvantages of this approach are: (i) narrowing the spatial differentiation of indicator values to only three values; (ii) using threshold values for evaluation, but at the same time, implicitly, for weighing the importance of indicators; (iii) the possibility of situations in which spatial units (catchments) that differ significantly in terms of the analysed indicator receive the same score on a 3-point scale; or (iv) spatial units that differ slightly receive different scores. Carrying out linear standardisation makes it possible to bring all indicators to the same scale (0–1) without reducing spatial variation to determine the overall score as the sum of partial scores or a weighted sum, where the weights represent the relevance of the indicators. Meanwhile, it relieves the group of experts from difficult task of determining a set of threshold values for indicator scores.

The second change was to use the DEMATEL method to determine the weights for the five criteria analysed. The DEMATEL method enabled elimination of some of the arbitrary decisions of the expert team, simplifying the form of information provided by experts (pairwise comparisons of the importance of criteria) and framed the acquisition of knowledge from the experts in a recognised procedural framework. The formalised procedure did not eliminate the discrepancies in the assessments of individual experts. The influence matrices from experts differed for individual factors: only four relations were assessed unanimously by all experts. A difference of 1 occurred in 9 relations, a difference of 2 in 6 relations and in one case the difference was equal to 3 (on a scale of 0–3).

In the original DEMATEL, it is assumed that expert assessments are precise and have no sources of uncertainty. In practice, uncertainty and ambiguity in assessments often occur (experts are unsure of their assessments). For this reason, modifications have been made to the DEMATEL method: in the fuzzy DEMATEL approach, expert assessments are assigned fuzzy numbers, and in grey-DEMATEL, expert assessments are described by numerical ranges [52]. The first method models fuzziness (linguistic uncertainties in expert assessments), while the second models missing data or information shortages.

Another problem is considering the differences that may arise between experts’ assessments. In the standard approach, the individual influence matrices determined by each expert are aggregated by calculating the arithmetic mean of corresponding elements (the so-called direct influence matrix). This is the most used method in the literature, due to its simplicity and ‘smoothing of differences’ [52]. Less common is the weighted average (if experts have different competencies, they can be assigned different weights). When the experts’ assessments are highly divergent, as well as in studies with a small number of experts (where each extreme assessment could distort the result), the median is used [52]. Determining an aggregated influence matrix as a result of expert discussion and consensus is also applicable [44]. In our study, we presented the results of DEMATEL, in which the direct influence matrix was calculated as the arithmetic mean of the experts’ opinions. A sensitivity analysis shows that using the median instead of the mean does not significantly affect the values of the elements in the aggregated direct influence matrix. The maximum difference in value in the aggregated influence matrix (mean minus median) is 0.5, the minimum is −0.333, and 10 out of 20 elements show no change. The determination of priority levels for developing water retention measures in catchment areas also indicates that the differences between the mean and median are insignificant: two catchment areas were given a priority one class lower, and two others had their priority increased by one class.

Our study used the original DEMATEL method, which does not allow for uncertainty and ambiguity in expert assessments. Such problems would arise when assessing the strength of influence between the 11 accepted indicators. The experts believed they could unambiguously determine the strength of influence between the following criteria: climatic, hydrological, hydrogeological conditions, land use and land cover, to which appropriate indicators were assigned. Therefore, the DEMATEL method was employed to estimate the weights for the five adopted criteria, while the indicators within each criterion were assumed to be equally weighted. In further research, we plan to develop our method to take into account that indicators within a given criterion may differ in their relative importance and to apply a more advanced form of DEMATEL (e.g., fuzzy DEMATEL [52]), which allows for uncertainty and ambiguity in expert assessments.

In the article, we applied a classical approach (Formula (12)) often used in the literature [53,57] in which the weights of the criteria are calculated based on Prominence (R + C) (Table 3). Of course, there are other proposals for estimating weights in the literature on the DEMATEL method, but there are no clear indications of their advantage over the classical approach [38,58]. The weights listed in Table 3 indicate that the smallest weight (0.136) is for the G1 criterion—climatic conditions, the weights of the remaining factors are at a similar level, which varies in the range of 0.200–0.235.

The results of the spatial assessment, according to the new method (including standardisation of indicators and the DEMATEL method), were compared with the results obtained using the expert point bonitation method. The comparative basis (that is, the “ideal” solution) was the result of the point bonitation of sub-catchments of the Mazovian Voivodeship in terms of their assessment of the needs of water retention [32]. All sub-catchments, in the number of 141, were assigned using the expert method to 3 priority classes. The correctness of the new method was assessed based on the confusion matrix (Figure 3), which is often used in assessing the classifier’s quality [55]. Analysing the obtained results presented in Figure 3 and Figure 4, it can be noticed that the final assessment, which is the classification of the catchment for the development of water retention measures (2—high priority, 1—medium priority, 0—low priority), is very similar in both approaches. Out of 141 catchments subjected to valorisation, 104 catchments (74% of catchments; 74.4% of the voivodeship area) obtained the same class, 25 catchments (18%; 21.6% of the voivodeship area) obtained a priority lower by 1 point in the DEMATEL method than in PSWR-2008, and 12 catchments (8%; 4.0% of the voivodeship area) obtained a priority higher by 1 point in the DEMATEL method than in PSWR-2008. There were no discrepancies in the maximum possible difference between classes (±2 points). Approach 2, using the DEMATEL method, indicated a more significant number of sub-catchments with a high priority (2) for implementing measures to increase the retention of the area (42 catchments marked in red in Figure 4b) compared to the number of such Table 1 catchments according to PSWR-2008 (33 catchments marked in red in Figure 4a). Among the 42 catchments with priority 2 indicated in the DEMATEL approach, there were 27 catchments with priority 2 and 15 catchments with priority 1 according to the PSWR-2008 approach. On the other hand, the indications of sub-catchments in which the development of water retention has a low priority (0) included 29 catchments according to the DEMATEL approach and 33 catchments in the PSWR-2008 approach (catchments marked in light yellow in Figure 4b and Figure 4a, respectively). Among the 29 catchments with priority 0 indicated in the DEMATEL approach, there were 23 catchments with priority 0 and 6 catchments with priority 1, according to the PSWR-2008 approach. The achieved accuracy values of the new method (74%) in general and from 70% to 82% in individual classes, as well as precision values from 64% to 79%, indicate good correctness of its operation in classifying the needs of water retention measures. The source of differences in classification by both methods is the introduction of weights, although it is worth noticing that only the weight for criterion G1 differs considerably from the weights of the other criteria. Moving away from threshold values in favour of linear standardisation of indicators is also important.

From the point of view of water management, the changes in the highest priority class for increasing water retention are the most significant. The highest priority indicates the desirability of taking measures to increase landscape retention, so it influences investment programmes. Analysis of the results for catchments that raised the priority showed that in the bonitation method, the values of indicators were close to (or equal to) the adopted threshold values for the priority class, but the catchments were not classified in the higher priority. This was mainly true for hydrological and hydrogeological indicators, but also for climatic indicators, although they received a lower weight in DEMATEL than in bonitation, as well as for the share of arable land. This is a clear indication of the desirability of using continuous (standardised) indicators.

It is worth noting that in the DEMATEL method, it is possible to quantify the impact of the expert’s judgement on the course of the process, and thus, by using the calculated weights, to make the final result more realistic. There is no such possibility in the point bonitation method because all assessments are equally valid. On the other hand, Enríquez-Hidalgo et al. [29] indicate that the DEMATEL method relies heavily on expert judgement, which can introduce biases. Nevertheless, the scope of experts’ engagement in the DEMATEL method is decreased compared to the previously used point bonitation. Two different groups of experts participated in both methods, and even though the DEMATEL method involved experts with less experience, the introduction of linear standardisation and the structural approach in DEMATEL resulted in similar results in the classification of water retention needs as analogous results obtained by a team of very highly qualified experts (PSWR-2008). Considering that only two out of six experts involved in the assessment of the Mazovian Voivodeship catchments using the DEMATEL method participated in the development of PSWR-2008 and a completely different, more straightforward form of articulating expert knowledge, it can be concluded that relatively small discrepancies in the results of the assessment are not due to the experience gained in the previous assessment.

The proposed method is not limited to water retention but can be applied to various issues where assessment is used in the analysis.

5. Conclusions

This research developed a new method of spatial assessment for the need to increase landscape water retention. The modification consisted of introducing linear standardisation of the values of the analysed indicators and using the DEMATEL method to calculate the criteria weights.

The analysed indicators were aggregated into five criteria (G1—climatic conditions, G2—hydrological conditions, G3—hydrogeological conditions, G4—economic use of the catchment area, G5—catchment land cover), for which we calculated the prominence and relation indicators following the DEMATEL method. The Prominence indicator was used to calculate the weights of the criteria.

The DEMATEL multicriteria method allowed creation of a cause-and-effect model of criteria. The group of causes includes criteria G4 and G1; the criteria in the effect group are G2, G3 and G5. The prioritisation of the importance of the criteria is G2 > G5 > G3 > G4 > G1. The G1 criterion has the lowest degree of importance (13.6%). The importance of the remaining criteria varies in a small range from 20% to 23.5%.

The results of the valorisation obtained with the new model were compared with the spatial assessment (river sub-catchments in the Mazovian Voivodeship) obtained with the expert method of point bonitation. The obtained result of the final valuation compliance is 74% (104 catchments), while 37 out of 141 catchments (26%) in the DEMATEL method were classified to a different, but neighbouring, group, compared to the bonitation method. For none of the catchments, the valuation led to the classification to the opposite group (transition between groups “0”—low importance and “2”—high importance or vice versa).

The use of DEMATEL method reduced the participation of experts compared to the previously used point bonitation-based expert valuation. The introduction of a procedure for calculating weights in the form of pairwise comparisons of criteria allows for decomposition of a complex problem, which is arbitrary determination of weights for all criteria. The introduction of such a procedure contributes to greater objectivity and transparency of analyses, which may translate into greater acceptance of the obtained results.

The applicability of the original DEMATEL method may be limited by the dimensionality of the problem. Attempts to assess the strength of influence of 11 factors have shown that experts tend to give ambiguous assessments. In the case of the five criteria, into which we grouped the 11 indicators considered, the relationships between them could already be assessed unambiguously. In further research, we plan to develop our method to consider that indicators within a given criterion may differ in their relative importance and to apply a more advanced form of the DEMATEL (e.g., fuzzy DEMATEL), which allows for uncertainty and ambiguity in expert assessments.

According to the authors of this article, the DEMATEL method can be successfully used to solve similar water management tasks that call for multicriteria analyses.