Studies on the Migration of Metal Ions in the Aquifer and the Seepage Prevention of Intercepting Walls in Lead–Zinc Mining Areas

Abstract

As metal resource extraction increases, heavy metal ion pollution in the saturated zone intensifies. Hence, research on the migration of heavy metal ions in aquifers and the efficacy of protective measures is essential to inform pollution prevention and control engineering. This study focuses on the slag pond and its surrounding area of a smelting plant. Utilizing field hydrological surveys and experiments, and data from previous studies, we employed FEFLOW7.0 simulation software to model the groundwater system of the boulder aquifer in this region. The model divides the domain based on natural topography: the eastern river serves as a constant-head boundary, while other areas are set as specified-flux boundaries. The impermeable layer at the bottom is treated as a no-flow boundary, with a maximum simulation period of 2500 days. The simulation examines the natural movement of zinc ions and how the construction of the wall impacts their migration, as well as the wall’s effectiveness in preventing seepage. Findings indicate that the movement of zinc ions is significantly influenced by the reaction coefficient. When the reaction coefficient exceeds 10⁻⁸ s⁻¹, zinc ions decrease rapidly in the area. After the construction of the cutoff wall, the maximum migration distance of zinc ions within 2500 days decreased from 220 m to 77 m, demonstrating its effectiveness in controlling zinc transport in groundwater.

1. Introduction

As the amount of metals used increases, heavy metal ions such as cadmium, zinc, and lead dissolved in the waste slag from metal mining and smelting [1] under the action of precipitation leaching have become a significant source of soil and groundwater pollution, greatly impacting the surrounding environment and the survival of animals and plants [2]. When untreated waste slag is piled up in the open air, numerous metal ions can leach into the groundwater, contaminating the soil and groundwater in the area [3], and then spread with the movement of groundwater, further impacting the health of local residents [4,5,6].

In the southwestern provinces of China, rich in metal ore resources, smelting plants located near mines produce large amounts of waste slag, which, when left in the open, becomes a significant source of heavy metal pollution in the region [7]. The slag from lead–zinc smelting, in particular, will undergo both horizontal and vertical movements within the soil and groundwater systems, influenced by precipitation, surface runoff, and groundwater flow [8,9]. Addressing zinc contamination in soil and groundwater requires an understanding of the transport and pattern of zinc ions within the groundwater system [10], a crucial aspect in mitigating pollution in slag storage areas [11].

At present, the treatment and remediation of heavy metal pollution areas mainly include physical, chemical, and biological methods, among which the use of biotechnology to remediate zinc-contaminated land and groundwater environment is a research hotspot [12,13,14]. Zuo and others proposed that soil microorganisms in the lead–zinc mining area respond to the pollution of complex heavy metal ions. The results showed that heavy metals significantly affect the metabolism of microorganisms, making them resistant and improving their ability to transport and excrete metal ions. This is the basis for microorganisms to improve heavy metal soil pollution [15]. In addition to microorganisms, the use of various types of phytoremediation is also important [16]. Phytoremediation has attracted attention in metal pollution control due to its green, environmentally friendly, and economic characteristics. However, most plants find it difficult to survive in areas with multiple excessive metal ions. Moreover, it should be noted that the adoption of phytoremediation may also trigger ecological issues such as species invasion. Therefore, phytoremediation technology needs to have a clear understanding of the distribution of pollution in the region. Physical adsorption has many innovations in adsorption materials, such as the swelling of hydrogels. The adsorption capacity can effectively reduce the concentration of heavy metal ions [17]. In traditional chemical methods, the use of hydrothermal sulfiding can separate zinc from sludge [18]. However, these research and governance methods all require controlling polluted ions within a certain range as much as possible. However, in aquifers with high permeability, zinc ions exhibit a rapid transport rate and extensive dispersion. The hydrothermal sulfiding method requires confined migration of zinc ions within a limited range to achieve optimal effectiveness. Consequently, highly permeable aquifers may diminish the remediation efficacy of this technique. Therefore, using cutoff walls to control polluted ions within a certain range is a prerequisite for their governance.

The cutoff wall, depending on its specific location, can be categorized into full cutoff walls, underground cutoff walls, and suspended cutoff walls. This article primarily focuses on the full cutoff wall, which extends from the ground floor to the surface by penetrating the aquifer. Cutoff walls are widely used in water conservancy and groundwater projects [19]. However, most research focuses on the material and structural properties of the wall itself, such as the waterproofing performance of polymer-treated walls [20] or their stress-induced deformation during construction [21]. Nevertheless, there is a scarcity of research examining the effectiveness of cutoff walls in impeding contaminant diffusion within the stratum and exploring the characteristics of contaminant dispersion after the wall’s construction. Additionally, there is a lack of knowledge regarding the criteria required for a cutoff wall to effectively retard contaminant diffusion.

Thus, our research focuses on: (1) examining the transport of zinc in aquifers with moderate to high permeability; (2) assessing the impact of the walls on pollution dispersion and identifying key parameters influencing this process; (3) the lead–zinc mine site primarily contains cadmium, zinc, and lead ions. Our study area is located in its tailings pond, where multiple layers of impermeable membranes are installed at the bottom. Cadmium ions are present in low concentrations and are effectively blocked by the membranes. Lead ions tend to adsorb and precipitate readily within the local aquifer, resulting in limited spread. In contrast, zinc ions enter the groundwater system in larger quantities and can readily migrate and disperse with groundwater flow. Therefore, we selected zinc ions as the primary research subject.

2. Materials and Methods

2.1. Geological Characteristics

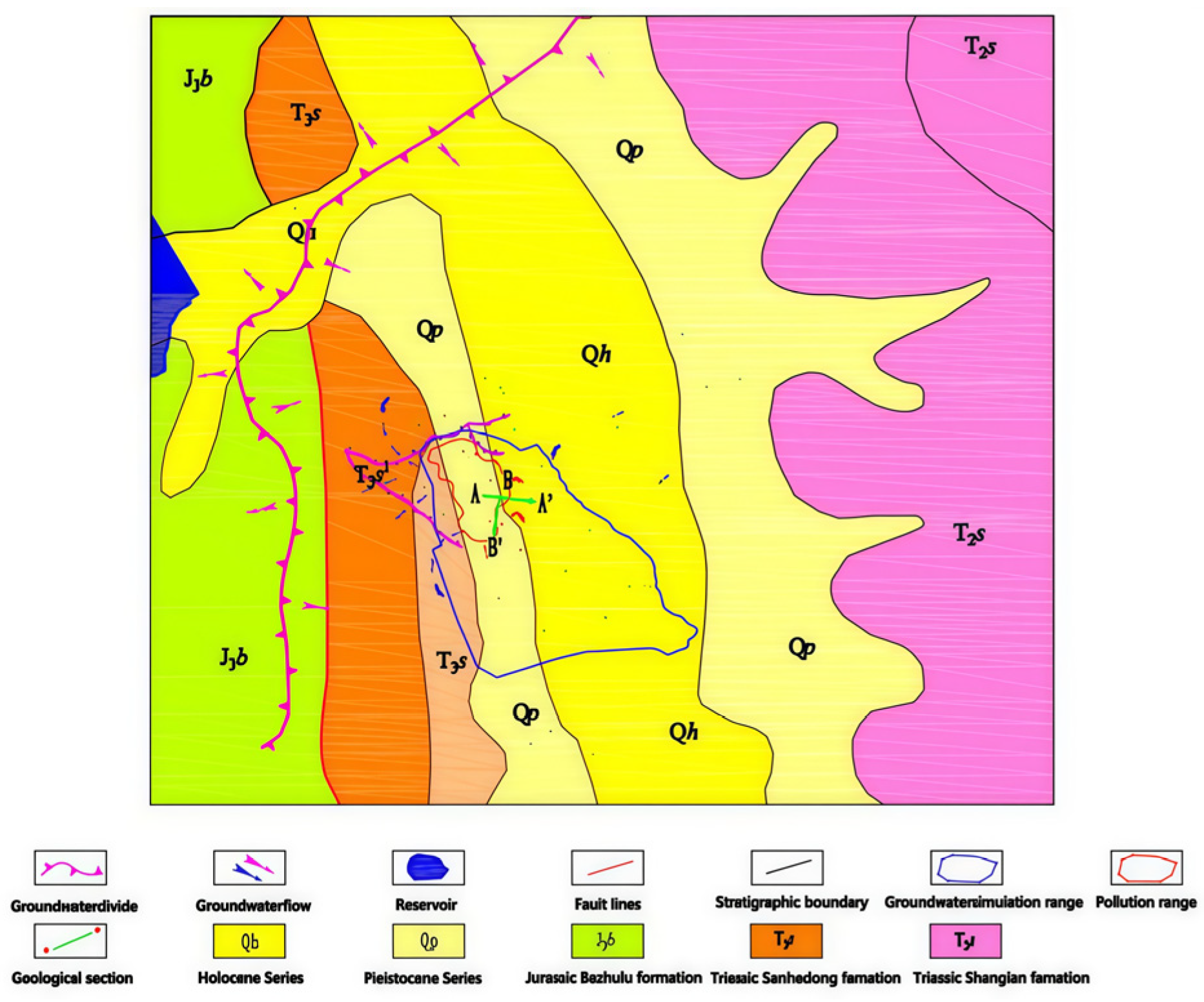
The surface water around the site is developed. The Tongdian River in the north originates from Huangmu village and flows into Tongdian town from south to north. There is the Huangmu reservoir in the northwest, about 1 km away from the slag reservoir. The Pojiao River on the east side is 150 m away from the slag reservoir, which is the main impact water area. The above rivers and reservoirs are the main surface water around the slag reservoir. In addition, there is a flood intercepting ditch on the north side of the slag reservoir, where perennial water flows into the Pojiao River.

The drainage and recharge of regional groundwater are greatly affected by topography and geomorphology and are controlled by formation lithology and geological structure. The topography of the slag storage site is high in the northwest and low in the southeast, so the runoff network flows from northwest to southeast. The crevice water of the giant conglomerate is the water mainly polluted by the leachate of the slag reservoir. Affected by the site supply conditions and topography, the flow direction of this kind of fissure water is generally consistent with the slope direction of the surface gully, flowing from the upstream of the gully to the downstream and flowing into the river. Therefore, the polluted groundwater may affect the surrounding and downstream rivers, which is also the main research content of this article. The crevice water in the site is generally buried deep, and its flow direction is controlled by the Triassic slate rock surface. Due to the certain pressure-bearing property of this layer, it has little hydraulic connection with the crevice water of the upper clastic rocks.

As shown in Figure 1 and Figure 2, the hydrogeological conditions of the study area are relatively complex, and groundwater movement is also influenced by the reservoir located northwest of the study area. The specific stratigraphic and geological conditions are as follows. The strata in the study area are divided into four layers from top to bottom. The first layer is an artificial accumulation layer, which is mainly composed of miscellaneous fill, cohesive soil, gravel, and coarse sand. The layer thickness is 0.8–15.3 m, with weak to medium permeability; the second layer is the quaternary alluvial layer, mainly composed of silty clay, with a thickness of 1.2–18.3 m and weak permeability; the third layer is the strongly weathered boulder, sandy gravel and argillaceous rock layer of the lower tertiary system, with a thickness of 0.9–30.8 m and medium permeability; the fourth layer is the upper member of Sanhedong formation of Upper Triassic system, which is mainly composed of strongly weathered to moderately weathered slate with a thickness of 4.0–15.7 m and a very little to medium permeability.

Based on the site’s groundwater recharge, runoff, and discharge characteristics, this investigation collected 39 water samples and 52 soil samples from various depths to determine the extent and severity of leachate contamination from the slag yard on the surrounding soil and groundwater. The analysis focused on four key parameters: pH, lead, zinc, and cadmium. Water samples underwent analysis using Inductively Coupled Plasma Atomic Emission Spectrometry (ICP-AES) and Atomic Absorption Spectrometry (AAS).

2.2. Model Generalization

The study area covers an area of about 0.68 km² and is a non-complete hydrogeological unit, so there is no complete natural boundary. The solute transport simulation primarily targets the third and fourth highly weathered layers, as defined in the stratigraphic division of Figure 3. Based on the variations in hydraulic conductivity and lithology within the study area (

Table 1. Hydrogeological parameter table.

Parameter	Layer 1
Kxx (cm/s)	5.5 × 10−4
Kyy (cm/s)	5.5 × 10−4
Kzz (cm/s)	5.5 × 10−5
Porosity	0.25

), the conceptual model is generalized into a stratification.

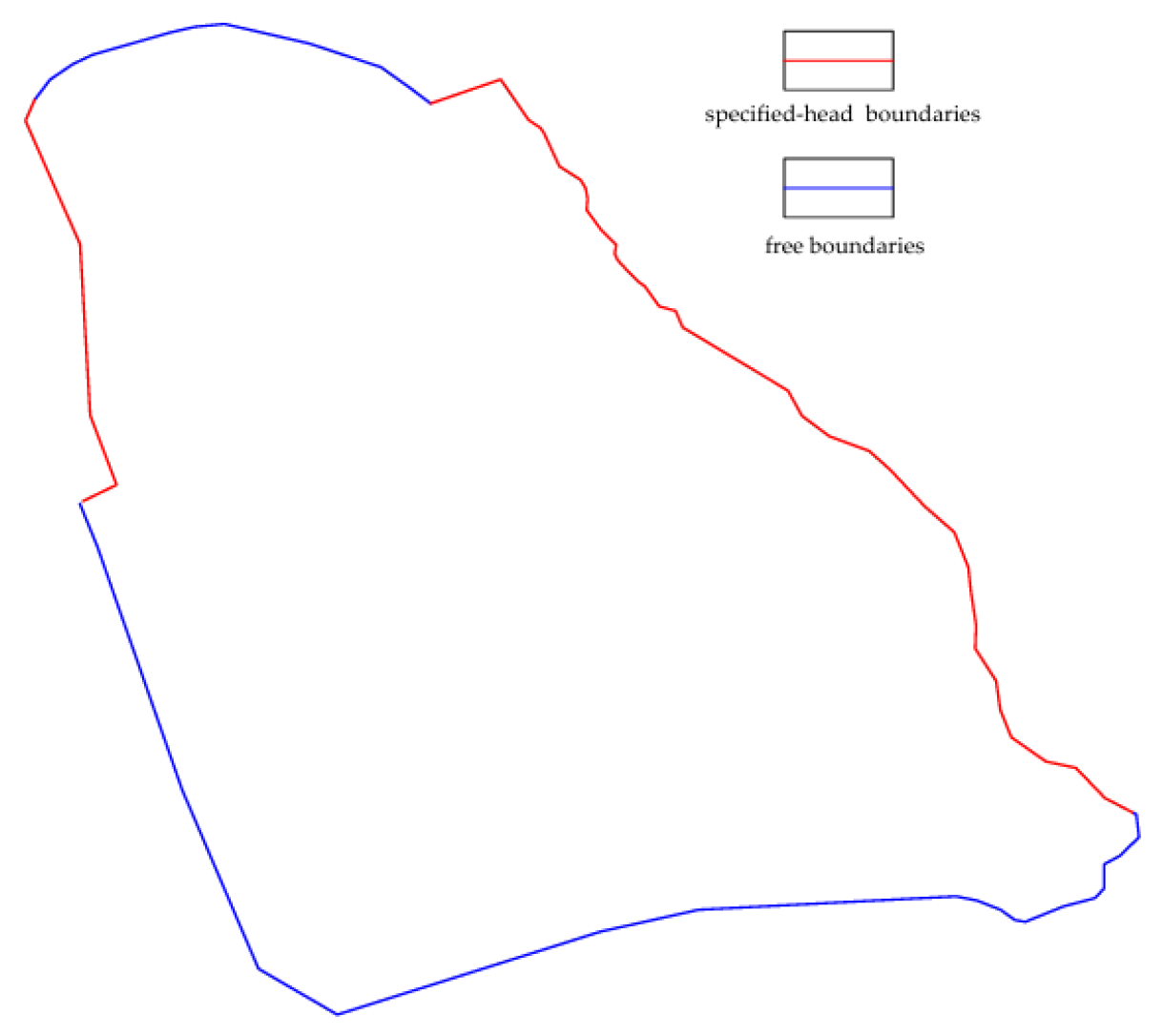
Vertically, the lower model boundary is defined by an impermeable stratigraphic unit, which is implemented as a no-flux boundary condition. The upper boundary incorporates areal recharge from precipitation. Lateral boundaries are delineated by rivers and topographic divides. The eastern river boundary is prescribed as a specified-head condition, as is the western elevated zone due to influence from a reservoir. The northern and southern boundaries are treated as free boundaries, with their flux dynamics controlled by the groundwater flow system (Figure 4).

In the solute transport model, the absence of stored waste materials in the slag repository implies no ongoing external contaminant loading. Both the upper and lower vertical boundaries are assigned as no-flux conditions. Along the lateral margins, the northern boundary is modeled as a no-mass-flux boundary, reflecting the presence of engineered containment structures such as slurry walls and impermeable liners. The remaining boundaries, where containment is absent or compromised, are simulated as free boundaries.

The groundwater contaminant zinc ions primarily originate from the long-term leaching of waste residue from the upper slag storage into the aquifer. For this simulation, the soil water leaching concentration data obtained from the site survey are utilized as the initial conditions, and the simulation models the natural conditions and the temporal and spatial trend of zinc ions after the construction of the cutoff wall.

2.3. Mathematical Model

Based on the groundwater environment obtained from drilling data in the study area, the following hydrogeological mathematical model is established:

$$\left\{\begin{array}{l}{\displaystyle \frac{\partial }{\partial x}}\left[K_x{\displaystyle \frac{\partial h}{\partial x}}\right]+{\displaystyle \frac{\partial }{\partial y}}\left[K_y{\displaystyle \frac{\partial h}{\partial y}}\right]+{\displaystyle \frac{\partial }{\partial z}}\left[K_z{\displaystyle \frac{\partial h}{\partial z}}\right]+W={\mu }_s{\displaystyle \frac{\partial h}{\partial t}}\hspace{1em}\hspace{1em}(x,y,z\in \mathsf{\Omega })\\ h(x,y,z,t)=h_0(x,y,z)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(x,y,z\in \mathsf{\Omega }),t=0\\ h{|}_{B_1}=h_1(x,y,z,t)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(x,y,z)\in B_1,t\ge 0\\ k{\displaystyle \frac{\partial k}{\partial \overrightarrow{n}}}{|}_{B_2}=q(x,y,z,t)=0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(x,y,z)\in B_2,t\ge 0\end{array}\right.$$

(1)

In Equation (1), h is the water head (m); K_x, K_y, and K_z are hydraulic conductivity values (m/d); B₁ is the boundary of a fixed water level; B₂ is the confining boundary; h₁ is the water level (m); W is the source–sink term (d⁻¹); Ω is the seepage zone; μ_s is the coefficient of storage (m⁻¹)—based on the empirical value, it is taken as 0.0009.

The solute transport in aquifers is mainly based on convection dispersion, referring to previous research on the transport of metal ions in moderately permeable rock layers [22]. The mathematical model for solute transport in groundwater can be expressed as follows:

$$\left\{\begin{array}{l}R\theta {\displaystyle \frac{\partial C}{\partial t}}={\displaystyle \frac{\partial }{\partial x_i}}\left(\theta D_{ij}{\displaystyle \frac{\partial C}{\partial x_j}}\right)-{\displaystyle \frac{\partial }{\partial x_i}}(\theta v_{i}C)-W{C}_S-{\lambda }_1\theta C\\ C(x,y,z)=C_0(x,y,z)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(x,y,z)\in \mathsf{\Omega }, t=0\\ C(x,y,z,t){|}_{{\Gamma }_1}=C(x,y,z,t)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(x,y,z)\in {\Gamma }_1, t\ge 0\\ \theta D_{ij}{\displaystyle \frac{\partial C}{\partial x_j}}{|}_{{\Gamma }_1}=f_i(x,y,z,t)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(x,y,z)\in {\Gamma }_2, t>0\end{array}\right.$$

(2)

In Equation (2), R is the hysteresis coefficient; θ is porosity; C is the solute concentration (g/L); t is the simulated time (d); D_ij is the dispersion coefficient (m²/d); v_i is the seepage velocity (m/d); W is the source and sink terms (1/d); C_s is the solute component concentration (mg/L); λ is the first-order reaction rate of dissolution (10⁻⁴ s⁻¹); Ω is the simulated area range; C₀ (x, y, z) is the known concentration distribution of solutes; Γ₁, Γ₂ are the first and second types of boundary conditions and boundaries.

2.4. Parameter Setting and Model Validation

The solute transport model primarily considers the processes of advection, dispersion, adsorption retardation, and reactive decay. The dispersion coefficient is related to the properties of the formation. The longitudinal dispersivity is defined as the ratio of the dispersion coefficient to the average pore water velocity, while the transverse dispersivity is generally set to one-fifth of the longitudinal value. The retardation factor is determined by the product of the partition coefficient and the medium density, with the partition coefficient being ascertained through laboratory tests. The reactive processes mainly focus on the redox reactions and precipitation of zinc ions. These processes are comprehensively defined based on field analysis and synthesis of previous research data. All parameters for the solute transport model are provided in

Table 2. Solute transport model parameter table.

Parameter	Layer 1	Layer 2
Longitudinal Dispersivity	100	100
Transverse Dispersivity	20	20
Decay Constant (10−4)	0.0001	0.0001

.

The hydrological coefficients of the numerical model were determined based on the preliminary survey report, hydrogeological experiments, and relevant literature. In this article, the numerical model is divided into approximately 16,000 triangular grids for calculation. The simulation time is 2500 d, and the time step is 0.001 d.

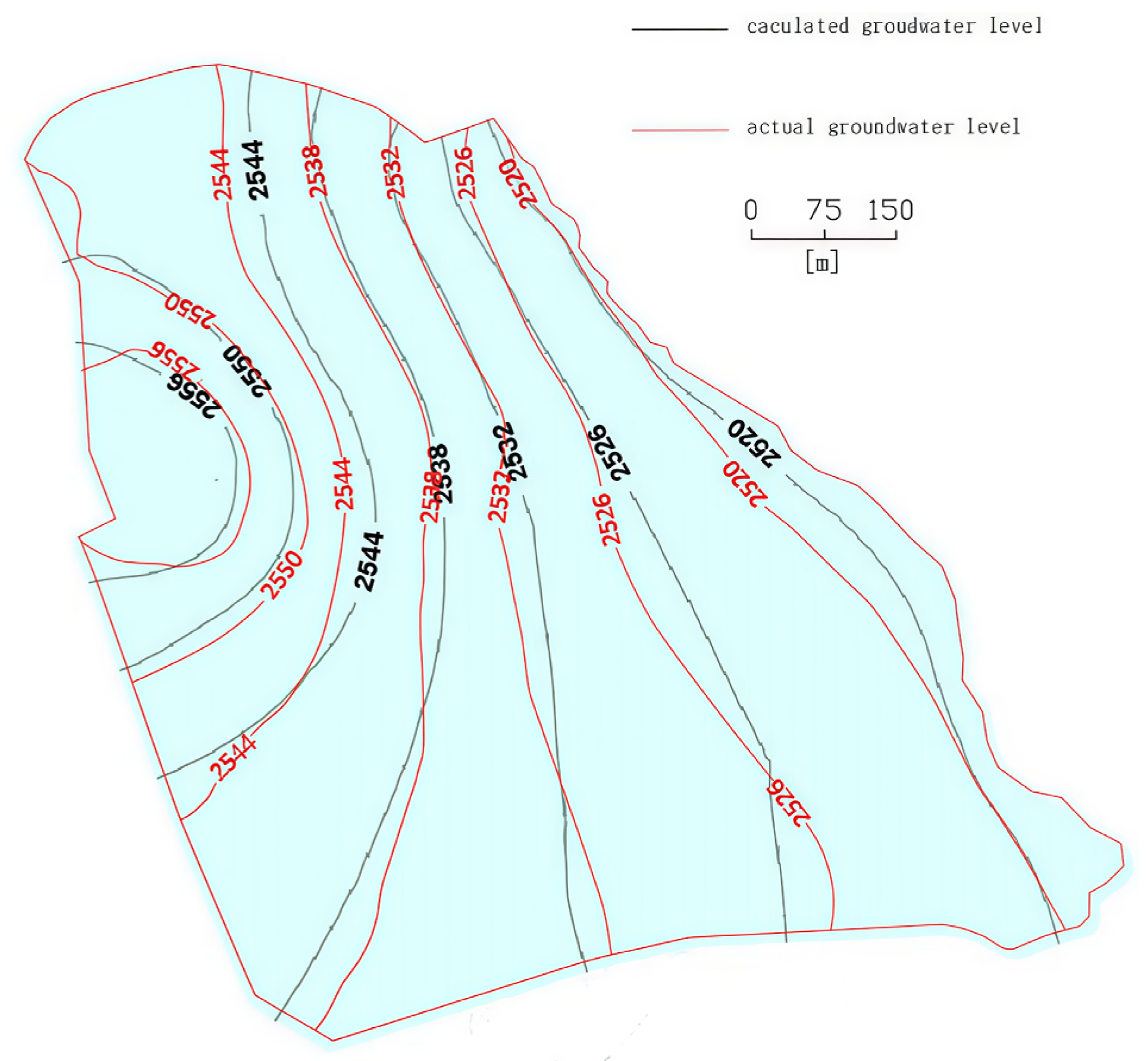
The model parameter verification uses the trial-and-error method. The initial flow field is input into the model with the initial values of parameters obtained from the hydrogeological survey of the study area, and the natural initial flow is obtained through stable flow calculation. 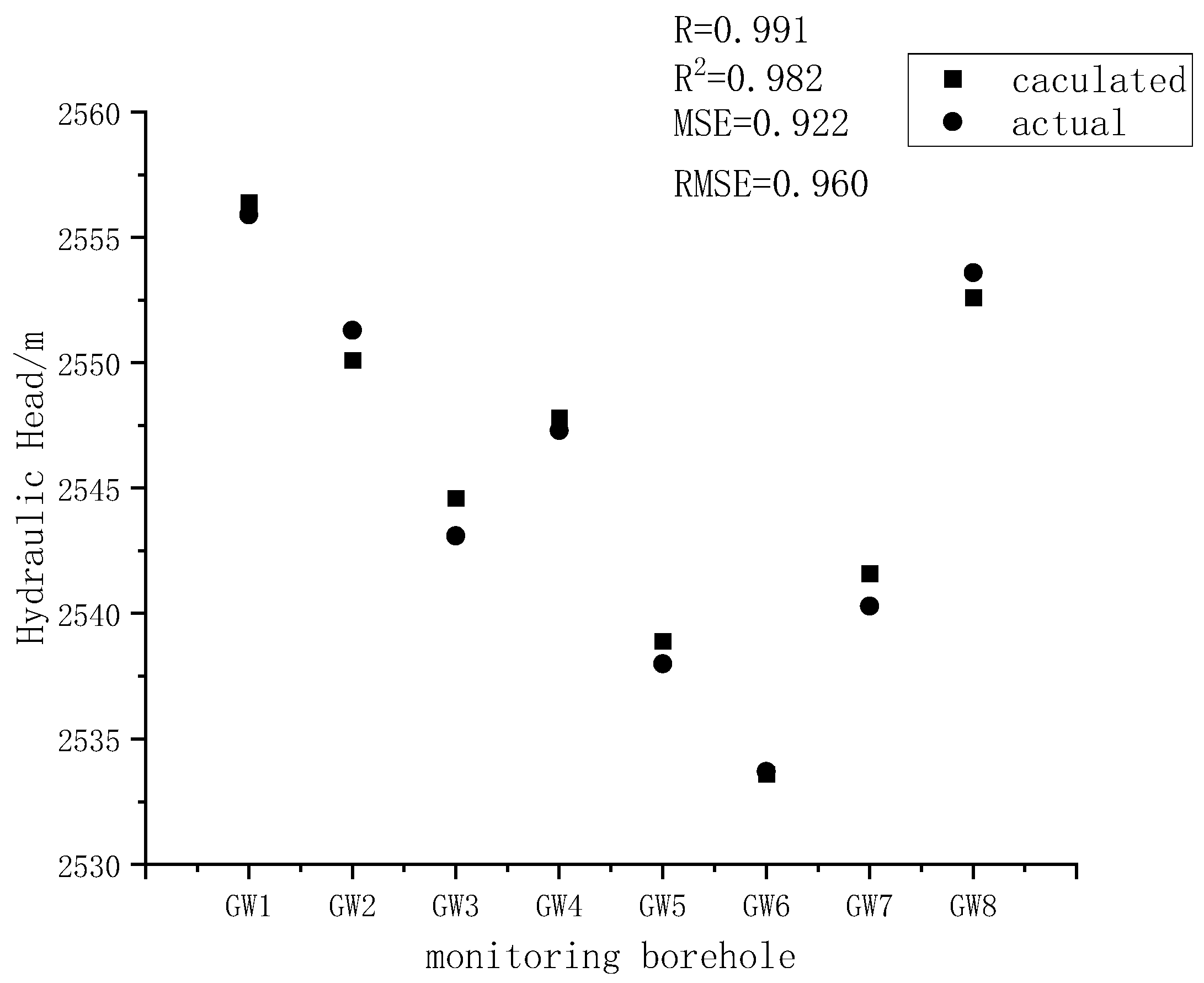Then, the parameters are corrected based on the measured water level, and the corrected initial flow field is obtained (Figure 5). A comparison between the simulated and actual values (Figure 6) yielded a correlation coefficient of 0.991. The mean squared error (MSE) was 0.922, and the root mean squared error (RMSE) was 0.960 when comparing the simulated values to the actual measurements. These results indicate that the initial flow field of the model essentially aligns with the actual hydrogeological conditions of the study area and reflects the characteristics of the real flow field. Therefore, the flow field obtained from this model can be reliably used as the initial condition for transient flow simulations and serves as the basis for subsequent solute transport modeling.

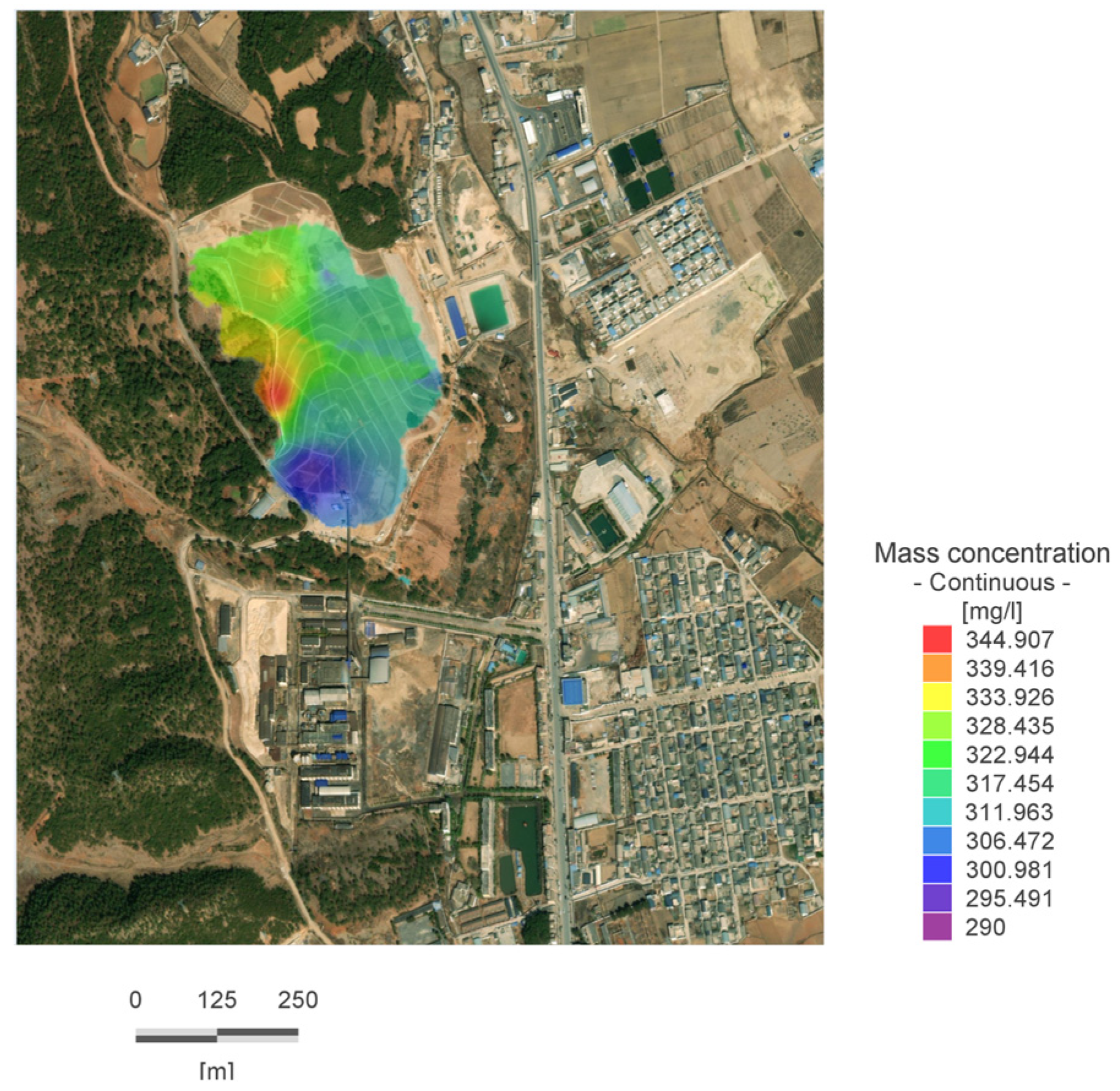
In a natural state, the main sources of zinc ions in groundwater include water pollution caused by substandard wastewater treatment in smelting plants, as well as the leaching of slag into aquifers along unsaturated zones under the action of precipitation. The simulation is based on the initial flow field obtained from stable flow field operation, with the zinc ion concentration distribution obtained from field experiments as the initial concentration, as shown in Figure 7. After removing all pollution sources from the site, the migration of zinc ions in the natural state is studied, and areas with zinc ion concentrations greater than 0.1 mg/L are considered within the scope of pollution diffusion.

3. Results

3.1. The Outcome of Migration in a Natural State

The primary driving forces behind the migration of zinc ions within the aquifer are convection and dispersion. Based on the analysis of the groundwater flow field in the study area, it is evident that the pollutants primarily spread towards the eastern and southern edges of the site, with a direct migration towards the Slope Toe River for discharge. As can be observed from Figure 8, contaminant migration occurs more rapidly in areas with higher flow velocities. Meanwhile, in the direction perpendicular to the groundwater flow, solute transport is predominantly governed by dispersion. As a result, the contaminant ions are continuously migrating toward the southern boundary of the model, albeit at a rate significantly slower than that in the direction of flow.

This occurs for two main reasons: firstly, the intrinsic rate of dispersion within the aqueous medium is relatively low; and secondly, since the overall flow direction in the model is generally from west to east, dispersion in this region primarily manifests as a gradual expansion of the contaminated area with relatively lower concentrations, while the majority of contaminants continue to migrate along the direction of flow.

Therefore, cut-off measures should be installed vertically along the direction of groundwater flow. This approach can more effectively and economically prevent and control contamination.

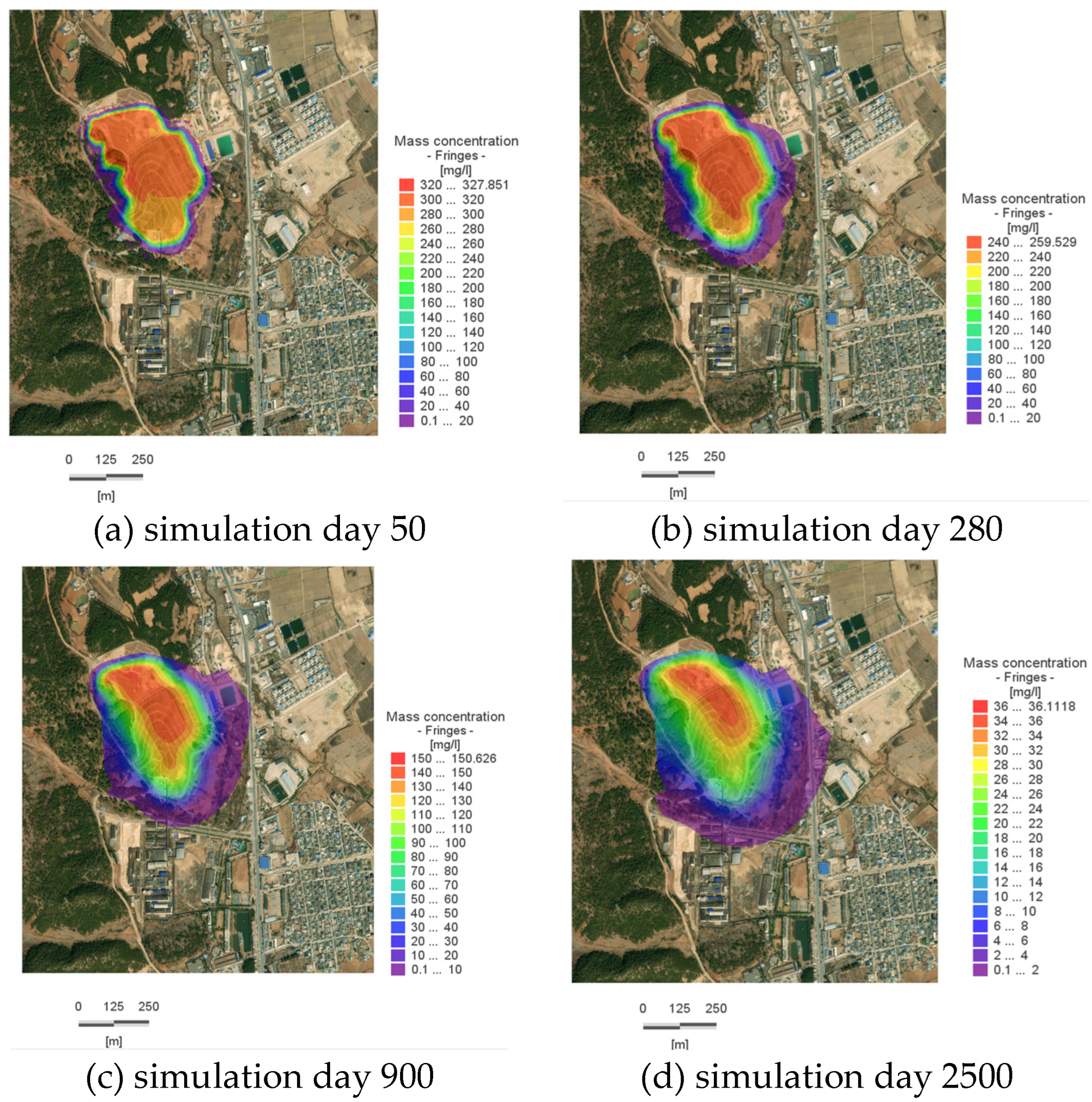
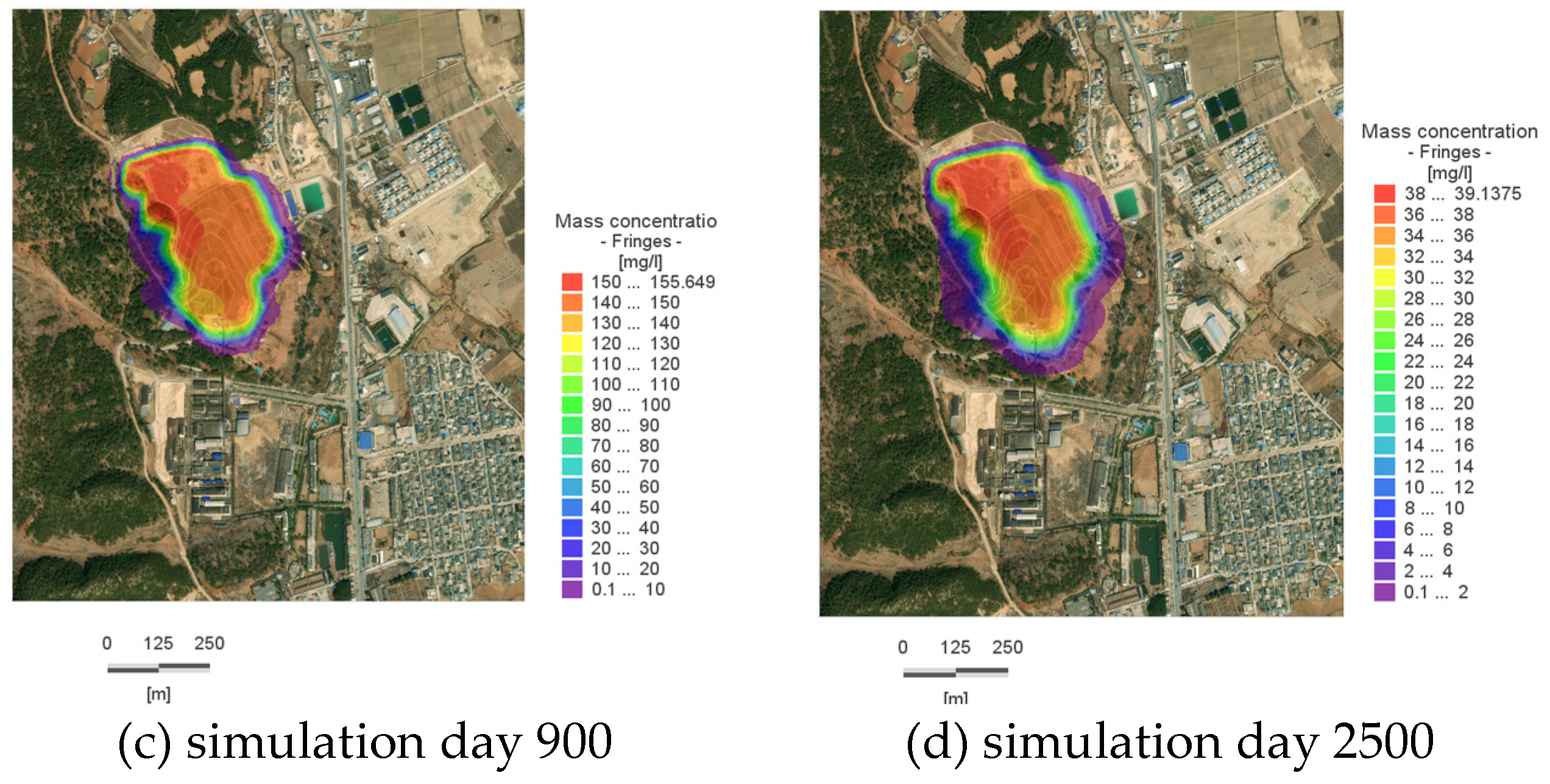
By approximately Day 50, the pollutant plume reaches the vicinity of the Slope Toe River on the eastern boundary (as shown in Figure 8a), with a concentration of 322.68 mg/L at the center of the pollution plume; by Day 280, the plume reaches the western boundary, with a concentration of 257.23 mg/L at its center; by Day 900, the reach of the plume near the Slope Toe River stabilizes, with a concentration of 135 mg/L at its center; by Day 2500, the concentration at the center of the plume within the site is 24 mg/L, indicating that the plume’s spread has essentially ceased, and there has been a significant reduction in the overall amount of pollutants within the site.

3.2. Simulation Results After the Construction of the Cutoff Wall

To contain the expanding contaminated area, underground cutoff walls were constructed on the eastern and southern sides of the slag pond, as indicated in Figure 3. After these walls were put in place, a simulation was run for an equivalent period of time.

By the 50th day of the simulation (as shown in Figure 9a), the maximum dispersion distance without the cutoff walls had reached 95.8 m; after their construction, it was reduced to 15.6 m. By the 2500th day of the simulation, the maximum dispersion distance without the cutoff walls had increased to approximately 220 m; after their construction, it decreased to 77 m, representing a significant reduction (

Table 3. Comparative data on central concentration and maximum contaminant diffusion distance before and after construction.

	Time/day	Natural Conditions	After the Construction of the Cut-Off Wall
Central Concentration (mg/L)	50	322.68	327.85
	280	257.23	250.53
	900	135.00	150.63
	2500	24.10	36.11
Maximum Migration Distance (m)	50	95.80	15.60
	280	136.00	32.00
	900	187.00	51.00
	2500	220.00	77.00

).

Compared to the simulation results under natural conditions, the central concentration of the contaminant plume in the system changes only slightly after the installation of the cutoff wall. However, the extent of the high-concentration zone is significantly larger than that in the natural scenario. This indicates that the contaminants are largely contained within the area restricted by the cutoff wall.

Thus, it is evident that underground cutoff walls significantly contribute to controlling the horizontal movement of pollutants within the aquifer. The installation of cutoff walls effectively mitigates the advection and dispersion of contaminants within groundwater systems, thereby containing the pollution within a defined area. This not only reduces the extent of environmental impact but also facilitates subsequent remediation efforts.

3.3. Engineering Validation

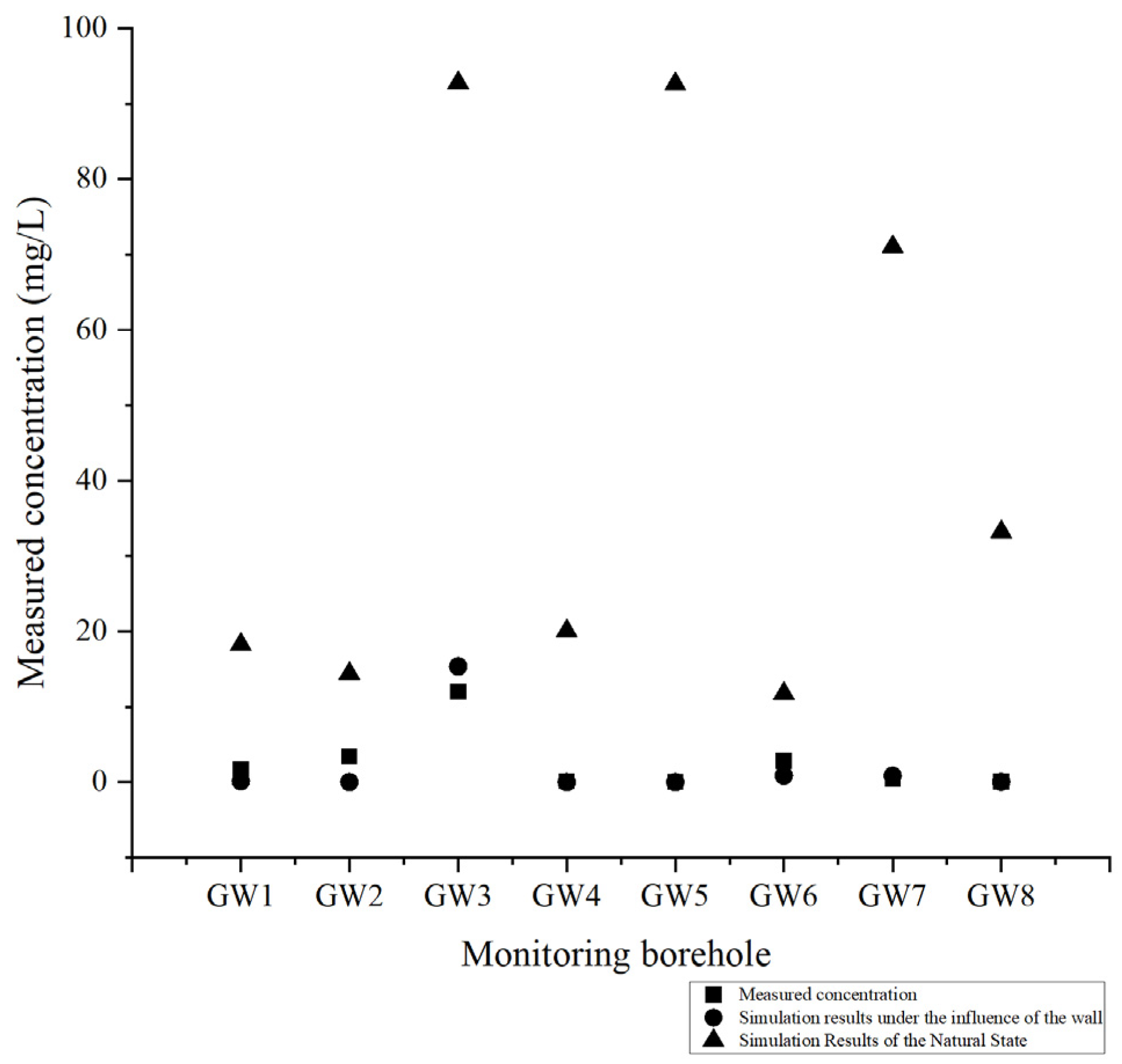
To further validate the efficacy of the cutoff wall and the reliability of the solute transport model, 200 days following the construction and maintenance of the cutoff wall, water samples obtained from hydrological boreholes depicted in Figure 3 were examined. These samples compared the zinc ion concentrations in each borehole under natural conditions, cutoff wall construction, and those actually measured. The findings are presented in Figure 9. Based on the statistical significance test comparing the measured and simulated data, a p-value of 0.943 was obtained. This result indicates that there is no significant difference between the two datasets, suggesting that the simulation outcomes closely align with the actual observed results (Figure 10).

Upon comparing the actual measured concentrations with those predicted under natural conditions, it is evident that the wall’s waterproofing effectiveness is pronounced, with the actual measured zinc ion concentration significantly lower than that predicted for a natural state. When comparing the actual measured concentrations to those predicted under the influence of the cutoff wall, there is minimal variance, with the maximum discrepancy observed in borehole GW3, at 3.34 mg/L, which remains within an acceptable range. This suggests that the cutoff wall has met the anticipated waterproofing standards, marking a successful construction.

After examining the monitoring data from borehole GW3 and comparing it with simulation results, a notably elevated concentration of zinc ions is observed at GW3 compared to other locations. This borehole is situated southwest of the slag storage area, adjacent to the western boundary of the model. The likely cause of this phenomenon is the insufficient coverage of the cut-off wall. During the design phase of the wall, the effect of ionic dispersion was not fully accounted for. As a result, the wall was primarily constructed along the eastern and southern edges of the slag yard, leaving a small section in the southwestern corner unsealed. Due to dispersion, a limited amount of contaminant ions has migrated through this gap, resulting in marginally elevated concentrations of contaminants in the borehole water sample.

To prevent potential contaminant leakage in this area after the future replenishment of slag in the storage facility, it is necessary to reinforce a small section of the cut-off wall at this location. Simultaneously, the sampling frequency of water samples in the area should be increased to closely monitor contamination status and guard against potential acute pollution.

4. Discussion

4.1. Effect of Decay Rate on Ion Transport

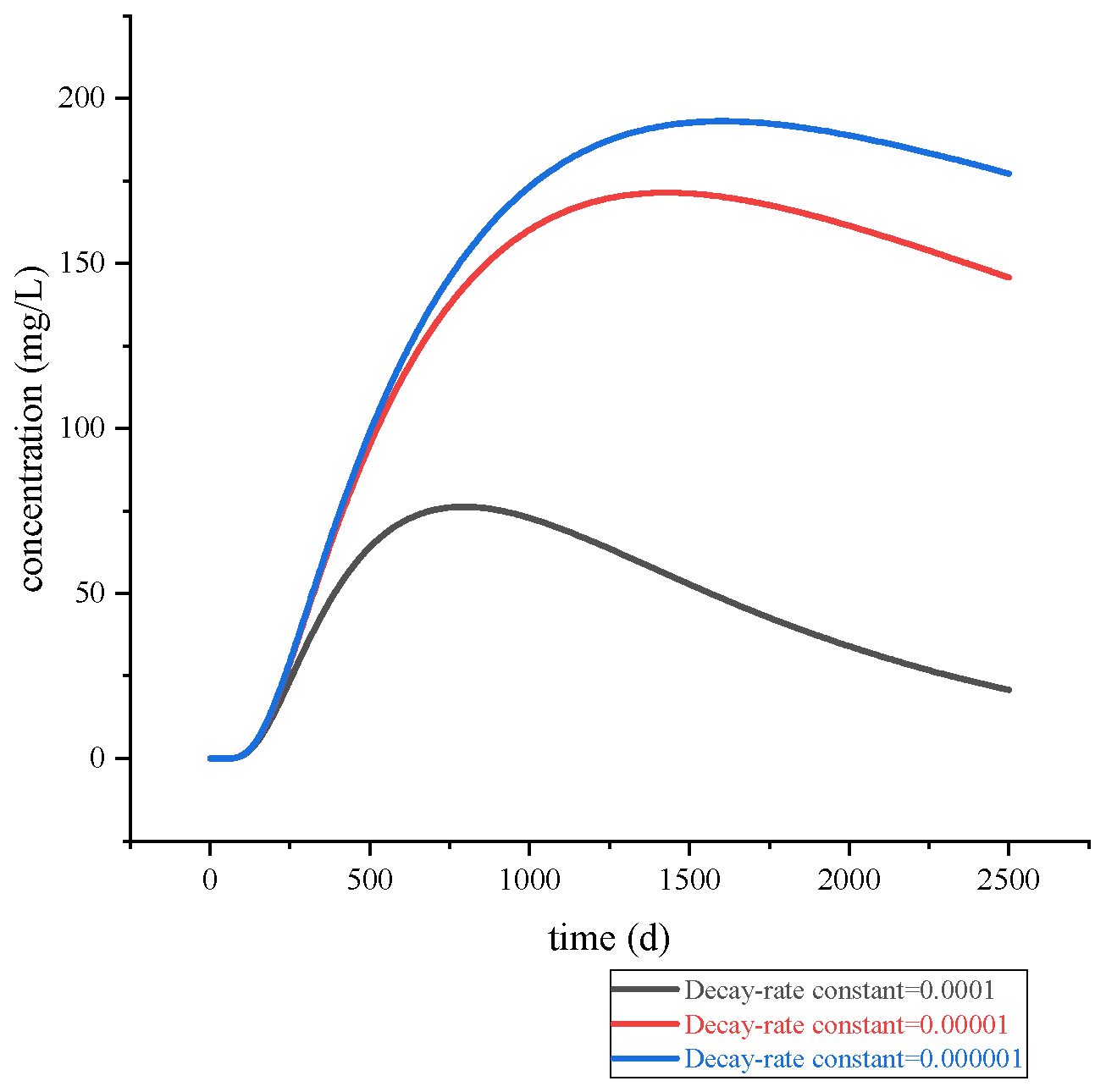
In the article, the consideration of zinc ion decay primarily focuses on the reaction rate of zinc ions in alkaline aqueous environments, with a unit of 10⁻⁴ s⁻¹. As seen in Figure 11 and Figure 12, variations in the reaction constant result in corresponding changes in solute migration rate, exhibiting a negative correlation. Specifically, as the reaction constant increases, the migration rate decreases. Studies have revealed that zinc in natural aquatic environments exists in a soluble complex state. In alkaline environments, zinc may form Zn(OH)₂ flocculent sediments and migrate to the bottom of the aquifer [23], leading to reduced horizontal zinc ion migration and subsequently, a decrease in the concentration of zinc ions in groundwater.

From the perspective of decay time, with a decay rate of 0.0001, the contaminant concentration at the riverside monitoring point shows a significant decrease by day 2500 compared to its peak. In contrast, a lower-order decay rate results in a smaller reduction. This indicates that the decay reaction has a notable effect on reducing zinc ion concentration. Therefore, it is feasible to confine the contamination within a limited area and appropriately adjust the groundwater pH within that zone to influence the reaction rate, thereby further reducing zinc ion levels. However, it is crucial to ensure that this process does not introduce new sources of pollution and cause secondary contamination.

4.2. Effect of Cutoff Wall Parameters on Ion Transport

Due to the construction of underground cutoff walls using grouting, during the actual construction process, the uncontrollable diffusion of grout in the underground environment may result in the cutoff wall’s permeability coefficient failing to meet expected standards. Therefore, the impact of changes in the cutoff wall’s permeability coefficient on solute transport and diffusion is considered. According to Chinese national standards, the zinc ion concentration in groundwater should not exceed 5 mg/L and must not exceed 1 mg/L in drinking water for residents. Since some domestic water sources in the study area may originate from groundwater, such as well water, a zinc ion concentration limit of 1 mg/L is adopted as the criterion for determining whether contamination has occurred.

Figure 12 and Figure 13 indicate that when the permeability coefficient of the cutoff wall varies by an order of magnitude, there is a significant change in its waterproofing efficiency. When the permeability coefficient decreases by an order of magnitude, its waterproofing effect improves significantly. Despite running the simulation for 2500 days, the maximum migration distance remains below 100 m, posing minimal threat to the nearby waterbody. When the permeability coefficient increases by an order of magnitude, its waterproofing effect is notably diminished. By the time the simulation reaches 280 days, the pollution scope has already spilled over to the nearby waterbody. This shows that the permeability coefficient is a crucial factor in determining whether the cutoff wall can effectively contain the leakage of contaminant ions.Therefore, when designing grouting construction plans, sufficient redundancy should be built in to ensure the effective use of the cutoff wall in subsequent prevention and control processes.

However, in practical applications, cutoff walls rarely achieve the idealized conditions assumed in numerical simulations due to constraints in construction and engineering geological conditions. During actual construction, geological heterogeneity often prevents grout from spreading uniformly to the designed extent, resulting in a wall thickness below design standards and/or increased hydraulic conductivity. These imperfections may allow contaminant ions to leak through. Therefore, supplementary measures should be implemented in combination with routine groundwater quality monitoring to ensure long-term effectiveness of the containment system.

4.3. Contaminant Monitoring and Remediation

Based on the above analysis, in aquifers with alkaline conditions, the reaction coefficient for zinc ions is significant, which accelerates their flocculent precipitation and thereby slows down their migration and diffusion within the aquifer. Therefore, in the prevention and control of zinc ion pollution, regions with acidic groundwater and soil environments should adopt quick-acting methods to control the migration of zinc ions as early as possible, such as using pumping technology to extract groundwater from the stratum, purify it, and then re-inject it [24]. The advantage of this approach lies in its rapid effectiveness; however, it requires substantial investment with high engineering costs. This method can be considered for severely contaminated areas requiring urgent remediation.

For areas with pollution in alkaline environments, more gentle approaches can be utilized, such as absorbing and extracting them through the roots of certain plants. This method requires lower investment, but results take longer to manifest. It should therefore be applied in areas with slow contaminant migration rates or be combined with containment measures (such as cutoff walls) to confine and treat the pollution within a confined area.

In controlling the migration of zinc ions, constructing a cutoff wall is feasible. When the permeability coefficient of the cutoff wall reaches 1 × 10⁻⁸ m/s, it can prevent the breakthrough of zinc ions over an extended period. Moreover, to enhance the impermeability of the cutoff wall, the composition of the wall construction materials can be adaptively adjusted. Specifically, chemical additives can be incorporated into conventional cement grouts to specialize their containment effectiveness against specific contaminants [25,26,27].

5. Conclusions

The decay-rate coefficient of solute migration in the aquifer under natural conditions can play a significant role. When the reaction coefficient increases by orders of magnitude, the curve of concentration versus time at the monitoring point on the bank of the Slope Toe River changes significantly, especially when the reaction coefficients are 10⁻¹⁰ s⁻¹ and 10⁻⁹ s⁻¹, respectively. When the reaction coefficient is less than 10⁻⁹ s⁻¹, zinc ions mainly precipitate in the aquifer through reaction, making it difficult for them to enter the local water body and pollute the Slope Toe River.

When the permeability coefficient of the cutoff wall is less than 1 × 10⁻⁶ m/s, the underground cutoff wall has a significant blocking effect on the migration of zinc ions in the aquifer. However, if the permeability coefficient does not meet the expected standard, the blocking effect is poor. Therefore, during actual construction, consideration should be given to increasing the injection volume of grout or increasing the thickness of the cutoff wall to ensure that the cutoff wall meets the anti-seepage standard. Furthermore, careful consideration must be given to the potential environmental impacts of the cutoff wall itself. It is essential to implement mitigation measures during construction and ensure that the completed structure does not cause secondary ecological damage to the local environment.

Using the numerical model of FEFLOW, it is possible to better simulate the transport process of solutes in groundwater and to predict the seepage prevention effect of cutoff walls for engineering projects using it for protection. It can provide effective quantitative parameters for the construction of cutoff walls, improve the seepage prevention ability of the cutoff walls, and reduce the economic cost of engineering projects by improving the construction plan.

In this study, the focus was primarily on the transport of a single ion, without considering potential reactions between other ions and zinc ions that could alter their concentration. Future research should incorporate the transport phenomena within heterogeneous aquifers. Furthermore, since FEFLOW is capable of modeling coupled saturated-unsaturated flow systems, subsequent studies could also integrate the process by which contaminants in the unsaturated zone dissolve into the saturated aquifer due to precipitation or other events. This approach would significantly enhance the targeted mitigation of soil and groundwater contamination caused by leaching from slag reservoir deposits. Additionally, the impact of both normal seasonal rainfall and abnormal rainstorm events on contaminant transport within the saturated–unsaturated groundwater system could be further examined.