A Displacement Monitoring Model for High-Arch Dams Based on SHAP-Driven Ensemble Learning Optimized by the Gray Wolf Algorithm
Abstract
1. Introduction
2. Methodology
2.1. Base Learner Library
- (1)
- Base Learner 1: HST Model
- (2)
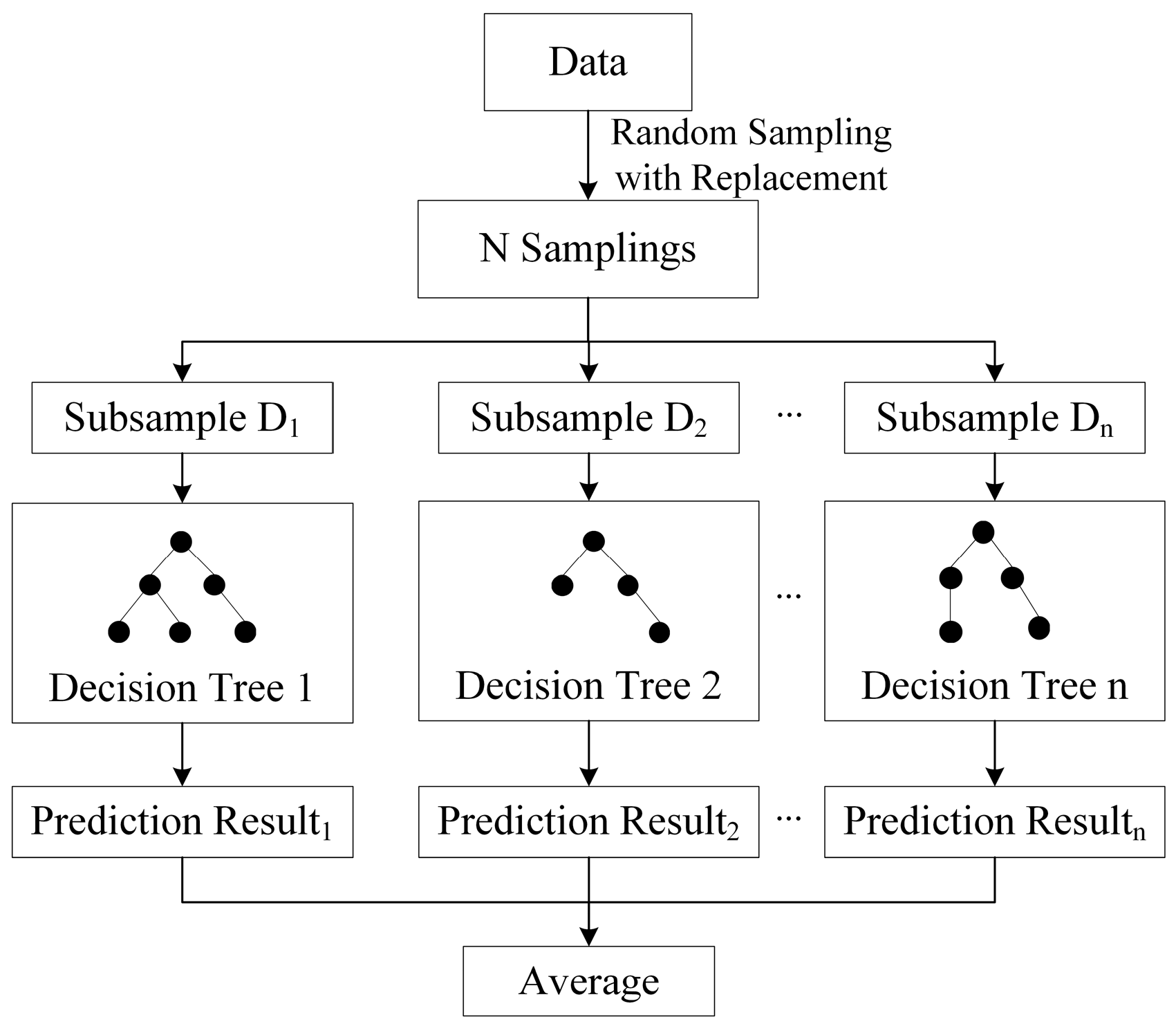
- Base Learner 2: Random Forests
- (3)
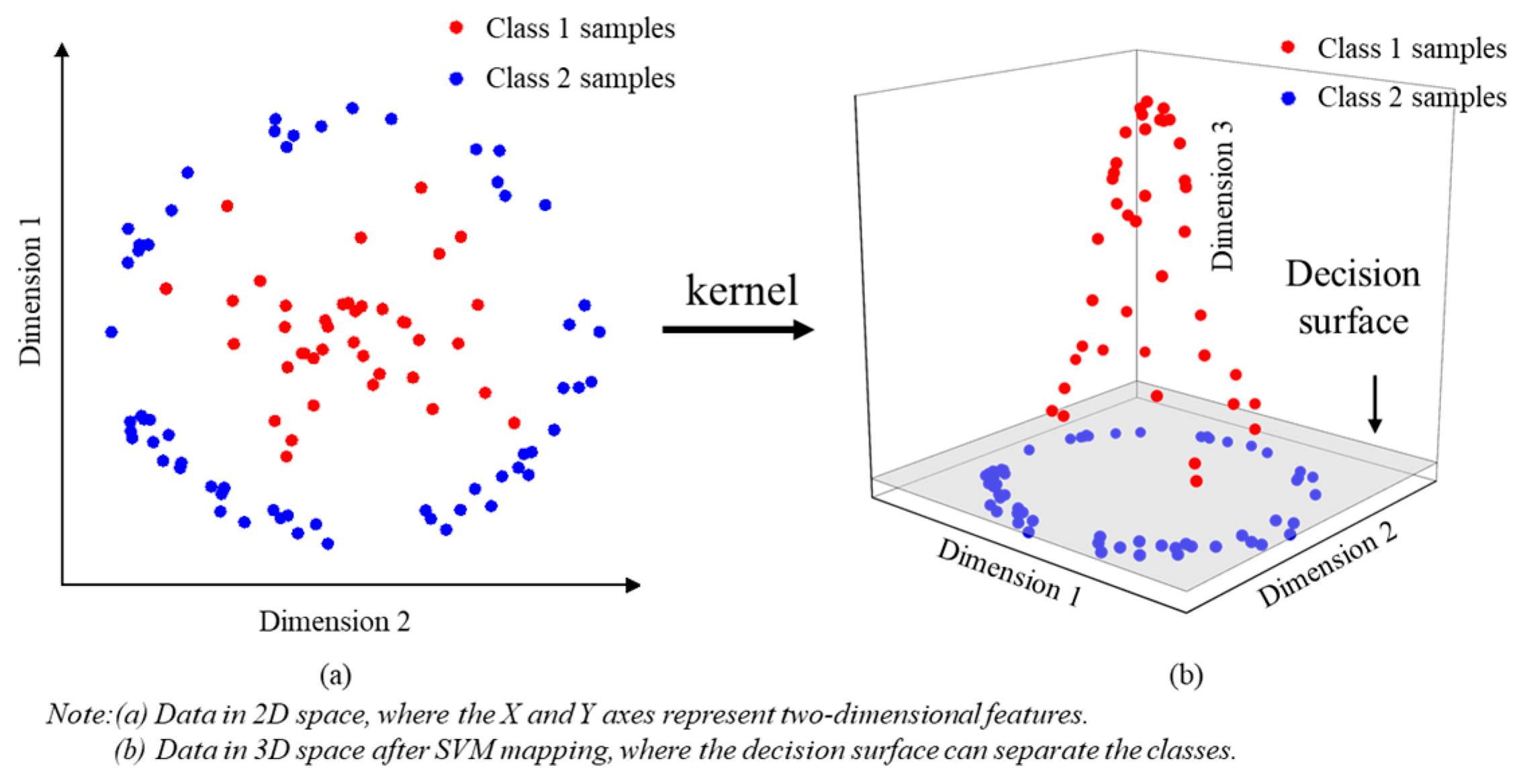
- Base Learner 3: Support Vector Machine
- (4)
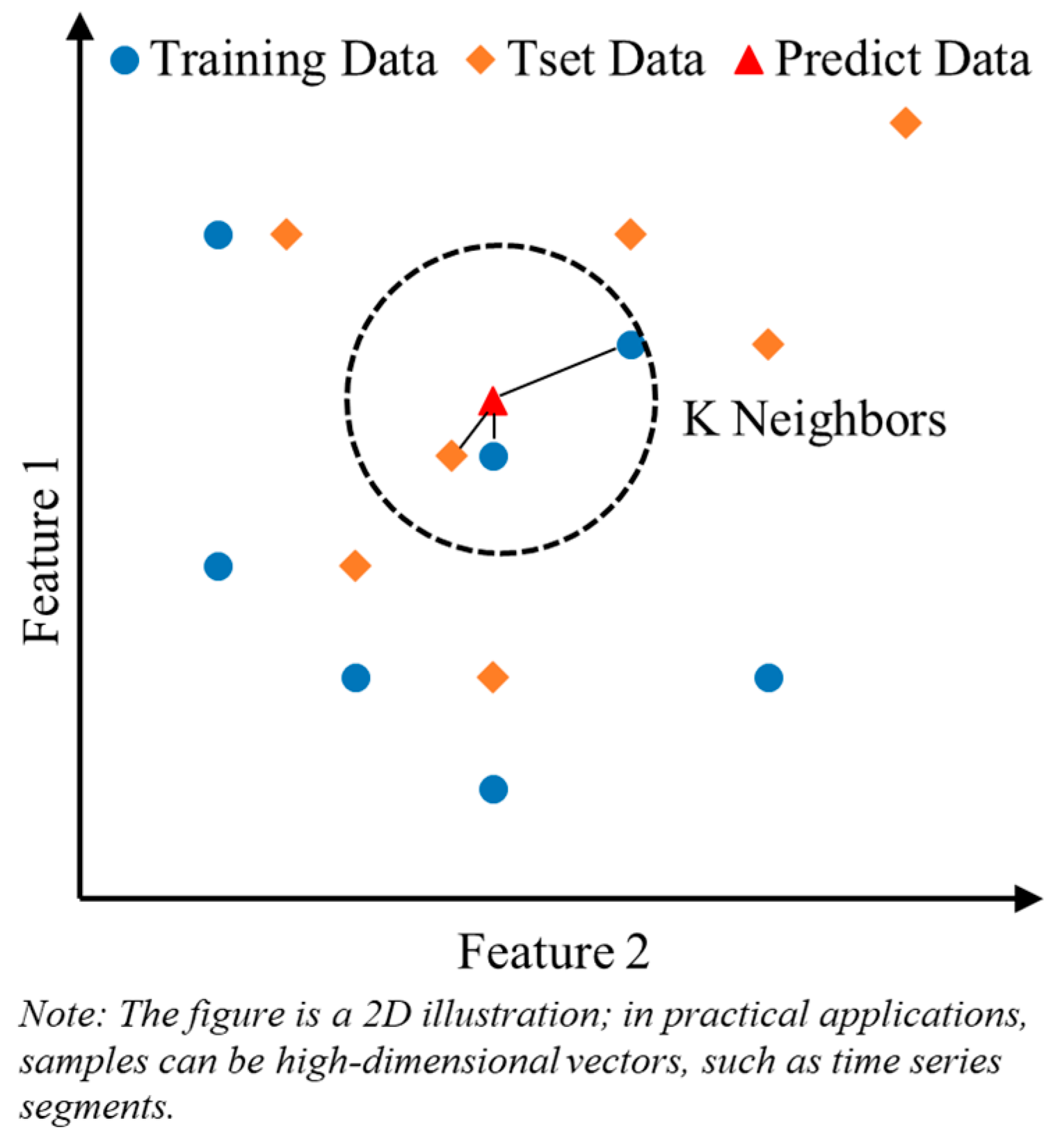
- Base Learner 4: K-Nearest Neighbors(KNN) algorithm
- (5)
- Base Learner 5: The Bidirectional Long Short-Term Memory network
- (6)
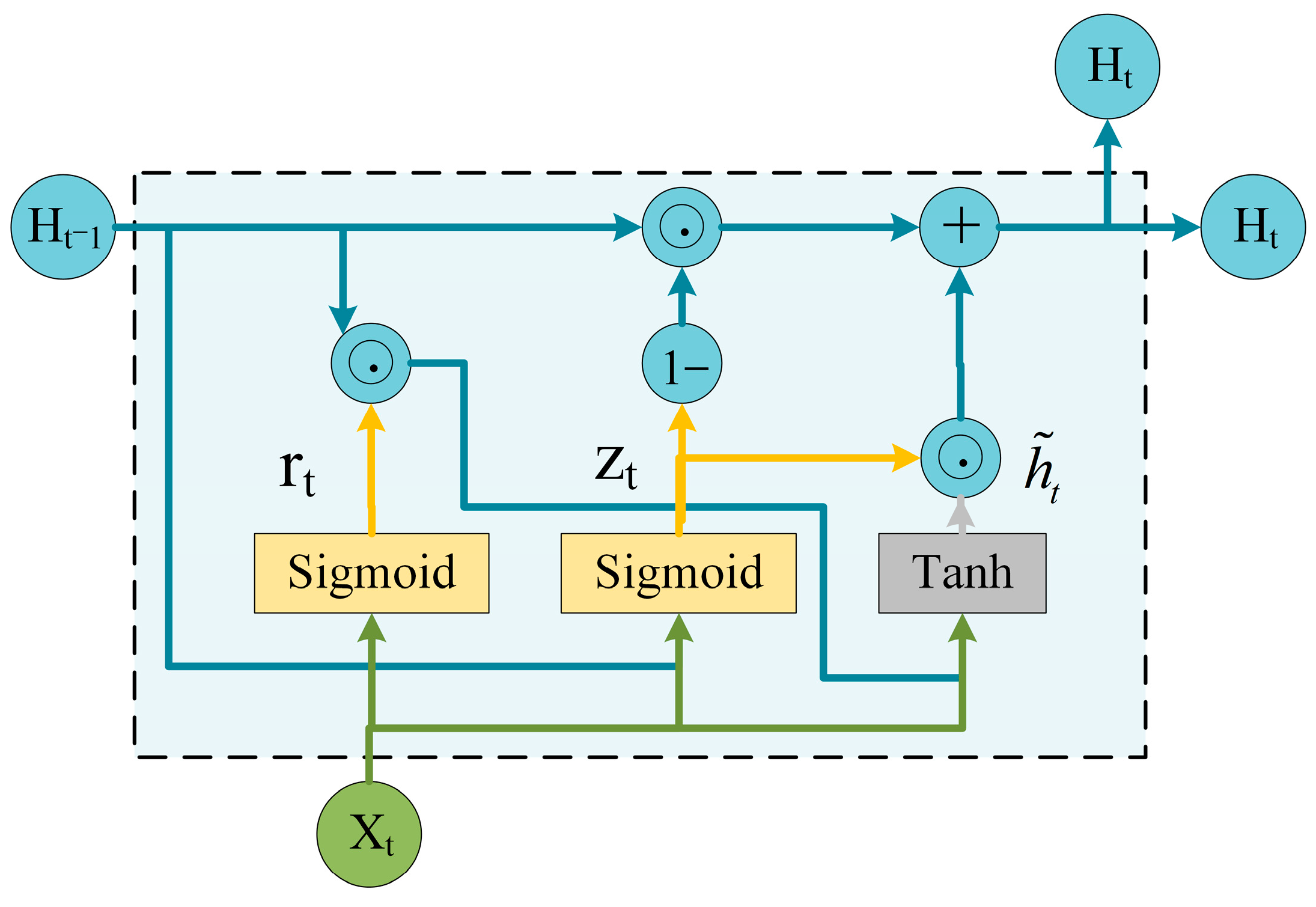
- Base Learner 6: BiGRU
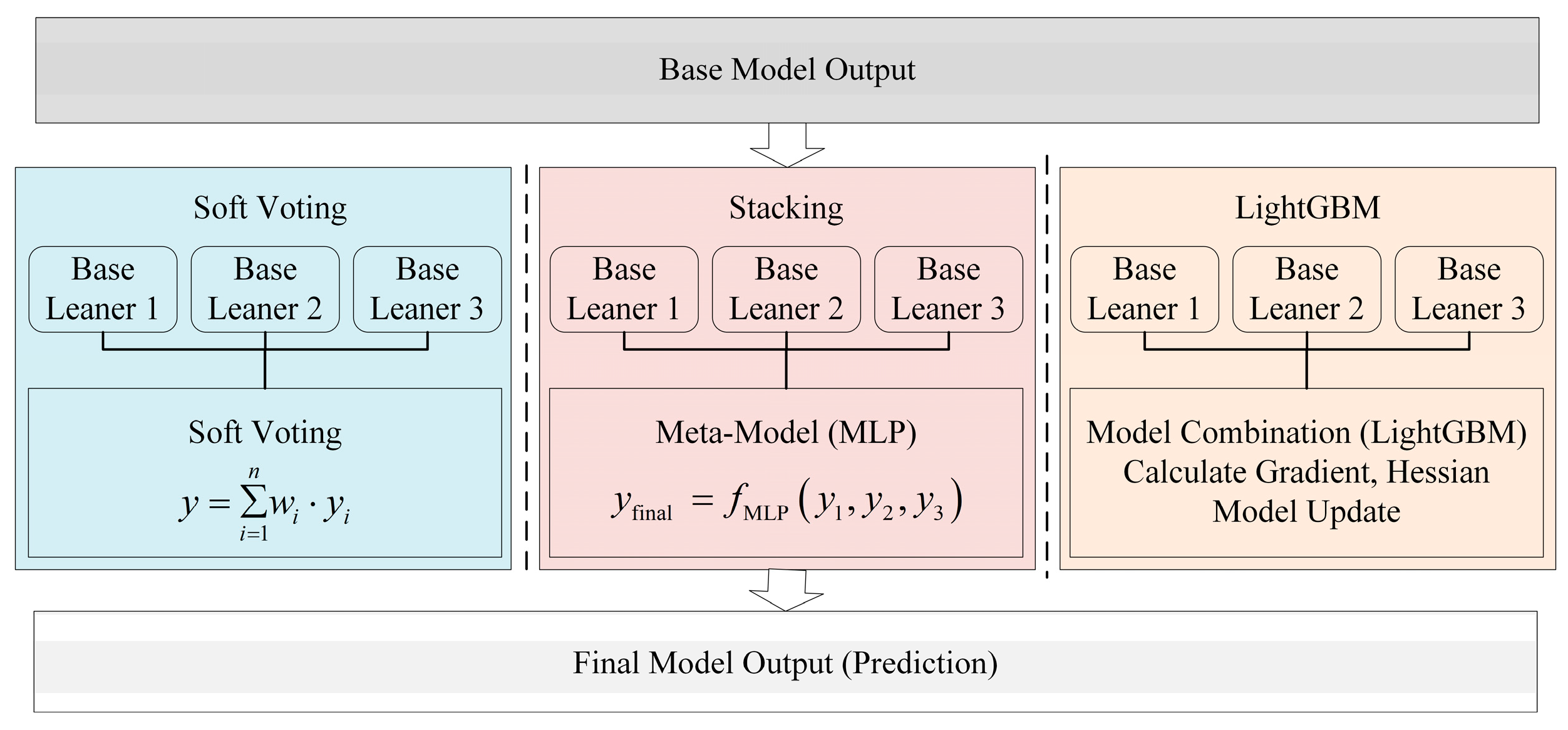
2.2. Model Ensemble Methods
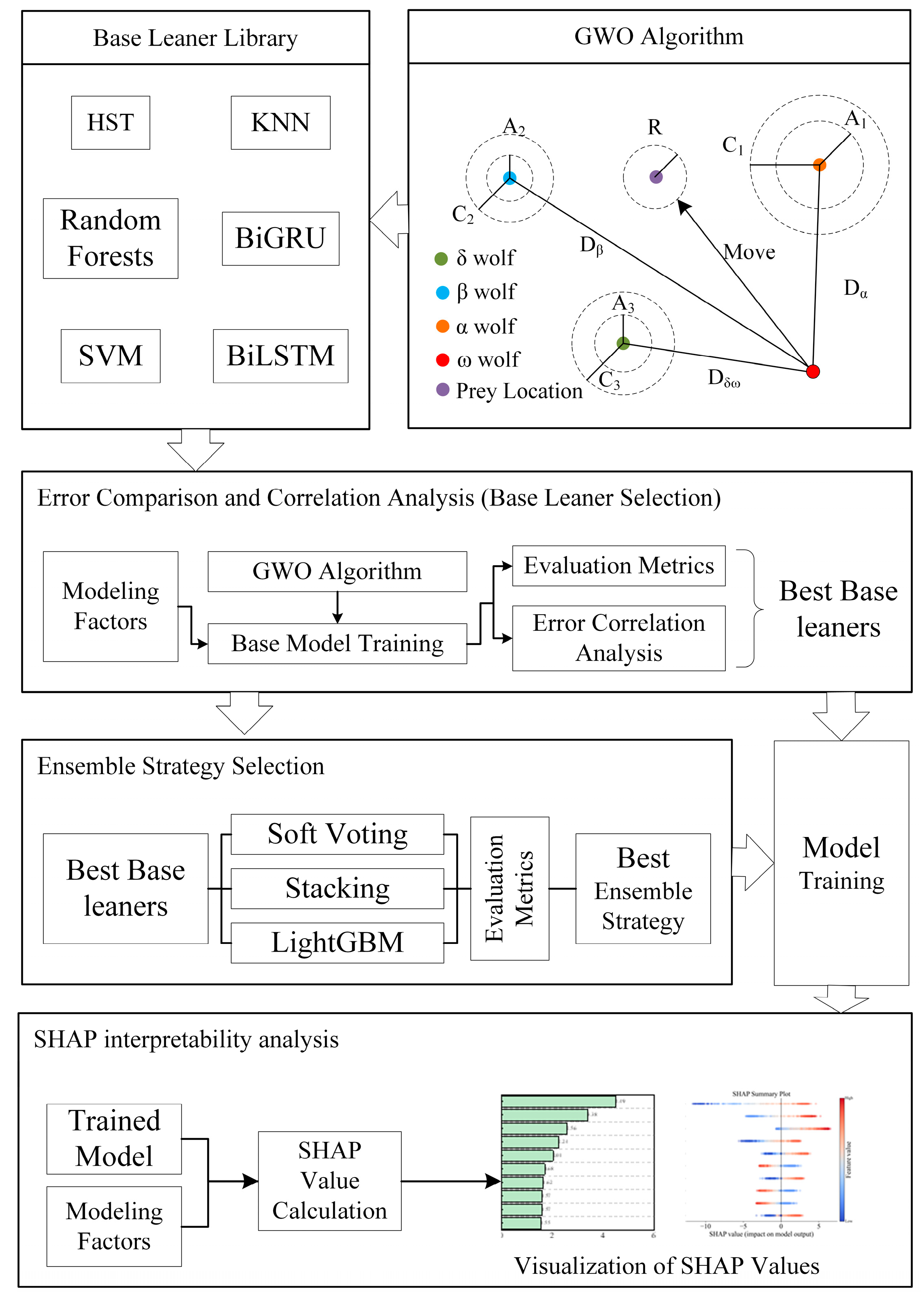
2.3. GWO Optimization Algorithm
2.4. Explainable Machine Learning Framework (SHAP)
3. Ensemble Learning-Based High-Arch Dam Deformation Prediction and Explanation Process
3.1. SHAP-Ensemble Learning Prediction Model Construction
- Data Preprocessing: Outlier detection and missing value interpolation are applied to both displacement monitoring data and corresponding environmental variables to ensure data completeness and accuracy. All input features are subsequently normalized.
- Construction of Modeling Factors: Based on engineering experience, a total of 30 influencing factors—primarily including water pressure, temperature, and time-effect components—are selected for model development.
- Residual Correlation Analysis of Base Models: The correlation coefficients between the prediction residuals of different base models are calculated to assess model complementarity, providing a foundation for subsequent model grouping and ensemble design.
- Selection of Ensemble Strategies: Three ensemble strategies—Bayesian Model Averaging (BMA), Stacking, and LightGBM-based integration—are pre-defined. Model combinations are determined based on residual correlation analysis, and the optimal ensemble method is selected according to overall fitting accuracy.
- Construction of the Ensemble-Based Displacement Prediction Model: Representative base models are integrated using the selected ensemble strategy to construct a predictive model capable of accurately forecasting arch dam displacements.
- SHAP-Based Interpretability Analysis: The SHAP algorithm is employed to quantify the influence of each input factor on the model output, thereby enhancing interpretability and supporting engineering diagnosis and decision-making.
3.2. Prediction Evaluation Metrics
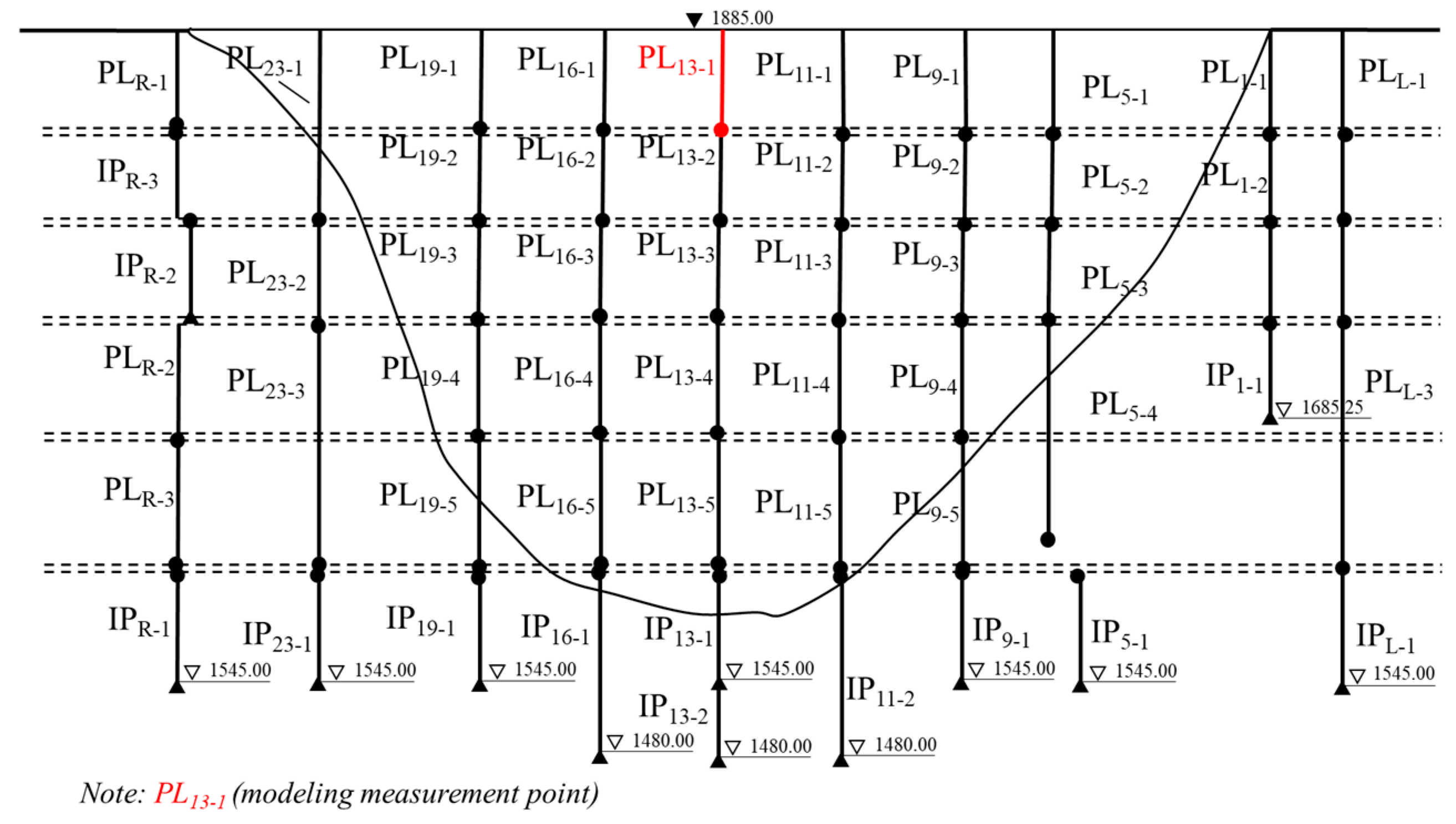
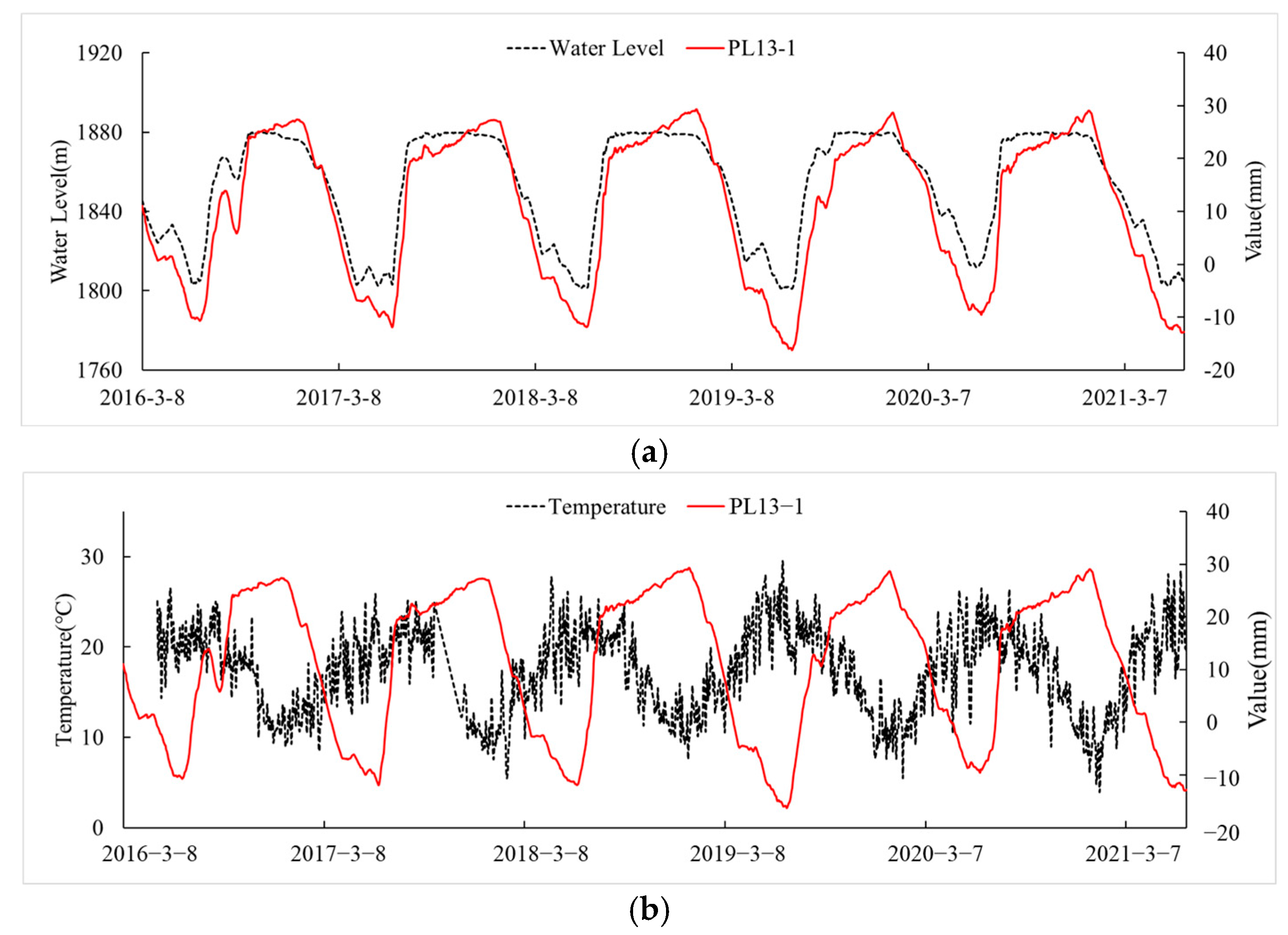
4. Engineering Applications
4.1. Construction of the Ensemble Learning Model
4.1.1. Optimization and Selection of Base Learners
4.1.2. Selection of Meta-Learners
4.1.3. Evaluation of Ensemble Learning Models
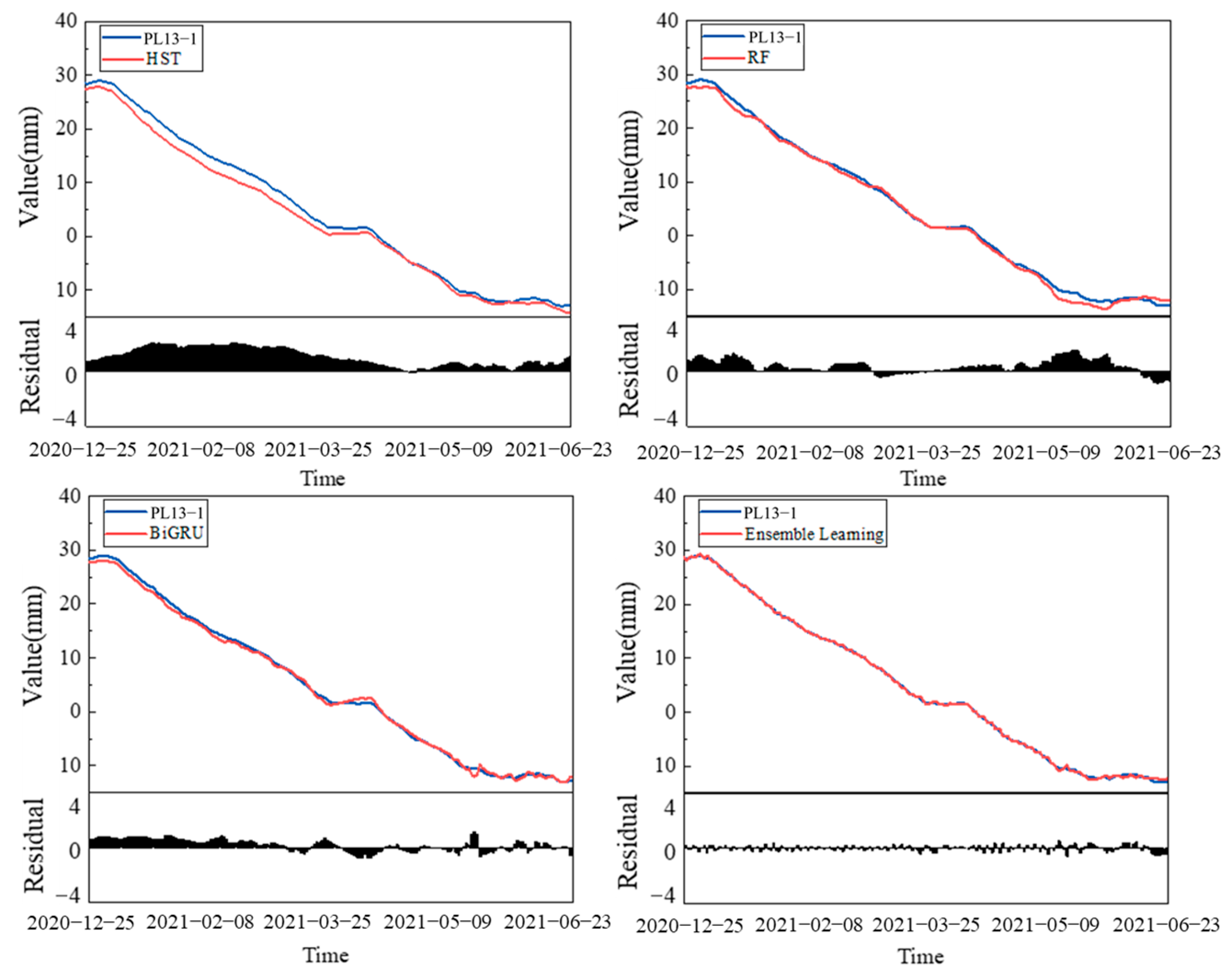
4.1.4. Interpretation of Model Prediction Results
5. Conclusions and Discussion
- The proposed ensemble-learning framework synergistically integrates the merits of multiple base learners. Employing a stacking architecture, it capitalizes on inter-model complementarity and delivers a marked enhancement in the accuracy of arch-dam displacement predictions. AI and ML algorithms, particularly the BiGRU and RF models, demonstrated their effectiveness in anticipating displacement patterns by capturing nonlinear relationships and temporal dependencies that traditional models struggle with.
- GWO algorithm-based hyper-parameter tuning endows each constituent model with near-optimal training conditions while curtailing computational overhead. This procedure secures peak performance for every learner and appreciably shortens the overall training time.
- Coupling the ensemble with SHAP analysis renders the model transparently interpretable. The Shapley values unveil the relative contributions of individual influencing factors, thereby reinforcing the model’s practical utility and engineering reliability.
- Advanced deep-learning architectures. Future studies might incorporate state-of-the-art paradigms—such as Transformers or graph neural networks—as base learners and refine the ensembling strategy to unlock additional predictive gains.
- Distributed computation. Rising computational power could be harnessed through efficient distributed-learning schemes, expediting the training process and enlarging the ensemble’s operational envelope.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, B.; Yang, J.; Hu, D. Dam monitoring data analysis methods: A literature review. Struct. Control Health Monit. 2019, 27, e2501. [Google Scholar] [CrossRef]
- Wen, Z.; Zhou, R.; Su, H. MR and stacked GRUs neural network combined model and its application for deformation prediction of concrete dam. Expert Syst. Appl. 2022, 201, 117272. [Google Scholar] [CrossRef]
- Cheng, M.-Y.; Cao, M.-T.; Huang, I.F. Hybrid artificial intelligence-based inference models for accurately predicting dam body displacements: A case study of the Fei Tsui dam. Struct. Health Monit. Int. J. 2022, 21, 1738–1756. [Google Scholar] [CrossRef]
- Mata, J.; Tavares de Castro, A.; Sá da Costa, J. Constructing statistical models for arch dam deformation. Struct. Control Health Monit. 2014, 21, 423–437. [Google Scholar] [CrossRef]
- Belmokre, A.; Mihoubi, M.K.; Santillan, D. Analysis of Dam Behavior by Statistical Models: Application of the Random Forest Approach. Ksce J. Civ. Eng. 2019, 23, 4800–4811. [Google Scholar] [CrossRef]
- Li, M.; Ren, Q.; Li, M.; Qi, Z.; Tan, D.; Wang, H. Multivariate probabilistic prediction of dam displacement behaviour using extended Seq2Seq learning and adaptive kernel density estimation. Adv. Eng. Inform. 2025, 65, 103343. [Google Scholar] [CrossRef]
- Liu, X.; Li, Z.; Sun, L.; Khailah, E.Y.; Wang, J.; Lu, W. A critical review of statistical model of dam monitoring data. J. Build. Eng. 2023, 80, 108106. [Google Scholar] [CrossRef]
- Papaleontiou, C.G.; Tassoulas, J.L. Evaluation of dam strength by finite element analysis. Earthq. Struct. 2012, 3, 457–471. [Google Scholar] [CrossRef]
- Total stress rapid drawdown analysis of the Pilarcitos Dam failure using the finite element method. Front. Struct. Civ. Eng. 2014, 8, 115–123. [CrossRef]
- Sun, D.; Zhang, G.; Wang, K.; Yao, H. 3D Finite Element Analysis on a 270 m Rockfill Dam Based on Duncan-Chang E-B Model. In Proceedings of the International Conference on Advanced Engineering Materials and Technology (AEMT2011), Sanya, China, 29–31 July 2011; pp. 1213–1216. [Google Scholar]
- Zhu, X.; Wang, X.; Li, X.; Liu, M.; Cheng, Z. A New Dam Reliability Analysis Considering Fluid Structure Interaction. Rock Mech. Rock Eng. 2018, 51, 2505–2516. [Google Scholar] [CrossRef]
- Wei, B.; Chen, L.; Li, H.; Yuan, D.; Wang, G. Optimized prediction model for concrete dam displacement based on signal residual amendment. Appl. Math. Model. 2020, 78, 20–36. [Google Scholar] [CrossRef]
- Chen, S.; Gu, C.; Lin, C.; Zhang, K.; Zhu, Y. Multi-kernel optimized relevance vector machine for probabilistic prediction of concrete dam displacement. Eng. Comput. 2021, 37, 1943–1959. [Google Scholar] [CrossRef]
- Ren, Q.; Li, M.; Kong, R.; Shen, Y.; Du, S. A hybrid approach for interval prediction of concrete dam displacements under uncertain conditions. Eng. Comput. 2023, 39, 1285–1303. [Google Scholar] [CrossRef]
- Yu, X.; Li, J.; Kang, F. A hybrid model of bald eagle search and relevance vector machine for dam safety monitoring using long-term temperature. Adv. Eng. Inform. 2023, 55, 101863. [Google Scholar] [CrossRef]
- He, P.; Pan, J.; Li, Y. Long-term dam behavior prediction with deep learning on graphs. J. Comput. Des. Eng. 2022, 9, 1230–1245. [Google Scholar] [CrossRef]
- Xiong, F.; Wei, B.; Xu, F.; Zhou, L. Deterministic combination prediction model of concrete arch dam displacement based on residual correction. Structures 2022, 44, 1011–1024. [Google Scholar] [CrossRef]
- Zhang, C.; Fu, S.; Ou, B.; Liu, Z.; Hu, M. Prediction of Dam Deformation Using SSA-LSTM Model Based on Empirical Mode Decomposition Method and Wavelet Threshold Noise Reduction. Water 2022, 14, 3380. [Google Scholar] [CrossRef]
- Yuan, D.; Gu, C.; Wei, B.; Qin, X.; Xu, W. A high-performance displacement prediction model of concrete dams integrating signal processing and multiple machine learning techniques. Appl. Math. Model. 2022, 112, 436–451. [Google Scholar] [CrossRef]
- Yu, X.; Li, J.; Kang, F. SSA optimized back propagation neural network model for dam displacement monitoring based on long-term temperature data. Eur. J. Environ. Civ. Eng. 2023, 27, 1617–1643. [Google Scholar] [CrossRef]
- Huang, B.; Kang, F.; Li, J.; Wang, F. Displacement prediction model for high arch dams using long short-term memory based encoder-decoder with dual-stage attention considering measured dam temperature. Eng. Struct. 2023, 280, 115686. [Google Scholar] [CrossRef]
- Bui, K.-T.T.; Torres, J.F.; Gutierrez-Aviles, D.; Nhu, V.-H.; Bui, D.T.; Martinez-Alvarez, F. Deformation forecasting of a hydropower dam by hybridizing a long short-term memory deep learning network with the coronavirus optimization algorithm. Comput. Aided Civ. Infrastruct. Eng. 2022, 37, 1368–1386. [Google Scholar] [CrossRef]
- Yuan, D.; Gu, C.; Wei, B.; Qin, X.; Gu, H. Displacement behavior interpretation and prediction model of concrete gravity dams located in cold area. Struct. Health Monit. Int. J. 2022, 22, 2384–2401. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, W.; Li, Y.; Wen, L.; Sun, X. A multi-output prediction model for the high arch dam displacement utilizing the VMD-DTW partitioning technique and long-term temperature. Expert Syst. Appl. 2025, 267, 126135. [Google Scholar] [CrossRef]
- Li, M.; Pan, J.; Liu, Y.; Wang, Y.; Zhang, W.; Wang, J. Dam deformation forecasting using SVM-DEGWO algorithm based on phase space reconstruction. PLoS ONE 2022, 17, e0267434. [Google Scholar] [CrossRef]
- Liu, D.; Yang, H.; Lu, C.; Ruan, S.; Jiang, S. Prediction of displacement of tailings dams based on MISSA-CNN-BiLSTM model. China Saf. Sci. J. (CSSJ) 2024, 34, 145–154. [Google Scholar]
- Song, C. A novel stability discriminant model of landslide dams based on CNN-BiGRU optimized by attention mechanism. Landslides 2025, 1–15. [Google Scholar] [CrossRef]
- Wu, W.; Su, H.; Feng, Y.; Zhang, S.; Zheng, S.; Cao, W.; Liu, H. A Novel Artificial Intelligence Prediction Process of Concrete Dam Deformation Based on a Stacking Model Fusion Method. Water 2024, 16, 1868. [Google Scholar] [CrossRef]
- Liu, M.; Wen, Z.; Su, H. Deformation prediction based on denoising techniques and ensemble learning algorithms for concrete dams. Expert Syst. Appl. 2024, 238, 122022. [Google Scholar] [CrossRef]
- Wang, R.; Bao, T.; Li, Y.; Song, B.; Xiang, Z. Combined prediction model of dam deformation based on multi-factor fusion and Stacking ensemble learning. J. Hydraul. Eng. 2023, 54, 497–506. [Google Scholar]
- Chithuloori, P.; Kim, J.-M. Soft voting ensemble classifier for liquefaction prediction based on SPT data. Artif. Intell. Rev. 2025, 58, 228. [Google Scholar] [CrossRef]
- Liu, M.; Feng, Y.; Yang, S.; Su, H. Dam Deformation Prediction Considering the Seasonal Fluctuations Using Ensemble Learning Algorithm. Buildings 2024, 14, 2163. [Google Scholar] [CrossRef]
- Yu, H.; Wang, X.; Ren, B.; Zheng, M.; Wu, G.; Zhu, K. IAO-XGBoost ensemble learning model for seepage behavior analysis of earth-rock dam and interpretation of prediction results. J. Hydraul. Eng. 2023, 54, 1195–1209. [Google Scholar]
- Luo, H.; Guo, S.; Bao, W. Random forest model and application of arch dam’s deformation monitoring and prediction. South-to-North Water Transf. Water Sci. Technol. 2016, 14, 116–121. [Google Scholar]
- Fang, C.; Jiao, Y.; Wang, X.; Lu, T.; Gu, H. A Dam Displacement Prediction Method Based on a Model Combining Random Forest, a Convolutional Neural Network, and a Residual Attention Informer. Water 2024, 16, 3687. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, K.; Yu, H.; Cai, Z.; Wang, C. Combinatorial deep learning prediction model for dam seepage pressure considering spatiotemporal correlation. J. Hydroelectr. Eng. 2023, 42, 78–91. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]






| Model | Model Hyperparameter Search Range |
|---|---|
| RF | Estimators number [50, 100, 150, 200, 300]; max depth [None, 5, 10, 15, 20] min samples split [2, 5, 10, 20]; min samples leaf [1, 2, 4, 8] |
| SVM | C [0.1, 1, 10, 100] |
| KNN | Neighbors number [3, 5, 7, 9, 11, 15, 20]; weights [‘uniform’, ‘distance’] |
| BiLSTM | Units [50, 100, 200, 300]; dropout [0.0, 0.1, 0.2, 0.3, 0.5]; Batch size [16, 32, 64, 128]; learning rate [0.001, 0.01, 0.1] |
| BiGRU | Units [50, 100, 200, 300]; dropout [0.0, 0.1, 0.2, 0.3, 0.5]; Batch size [16, 32, 64, 128]; learning rate [0.001, 0.01, 0.1] |
| Model | Train Data Accuracy | Test Data Accuracy | ||||
|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | RMSE | MAE | R2 | |
| HST | 1.0640 | 0.5549 | 0.9972 | 0.7158 | 0.5335 | 0.9865 |
| RF | 0.7145 | 0.4042 | 0.9985 | 0.5288 | 0.4646 | 0.9985 |
| SVM | 0.8322 | 0.3583 | 0.9984 | 0.5335 | 0.4010 | 0.9642 |
| KNN | 0.8468 | 0.2079 | 0.9993 | 0.3450 | 0.2111 | 0.9856 |
| BiLSTM | 0.9881 | 0.3053 | 0.9989 | 0.4549 | 0.3828 | 0.9908 |
| BiGRU | 0.6409 | 0.2735 | 0.9991 | 0.4088 | 0.2377 | 0.9941 |
| Model | Model Optimal Hyperparameters |
|---|---|
| RF | Estimators number: 200; max depth: 10 min samples split: 5; min samples leaf: 2 |
| BiGRU | Units: 200; dropout: 0.3; Batch size: 64; learning rate: 0.01 |
| Model | Test Data Accuracy | ||
|---|---|---|---|
| RMSE | MAE | R2 | |
| HST | 0.7158 | 0.5335 | 0.9865 |
| RF | 0.5288 | 0.4646 | 0.9985 |
| BiGRU | 0.4088 | 0.2377 | 0.9941 |
| Ensemble Learning | 0.2241 | 0.2347 | 0.9993 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Jiang, K.; Yang, S.; Lan, Z.; Qi, Y.; Su, H. A Displacement Monitoring Model for High-Arch Dams Based on SHAP-Driven Ensemble Learning Optimized by the Gray Wolf Algorithm. Water 2025, 17, 2766. https://doi.org/10.3390/w17182766
Li S, Jiang K, Yang S, Lan Z, Qi Y, Su H. A Displacement Monitoring Model for High-Arch Dams Based on SHAP-Driven Ensemble Learning Optimized by the Gray Wolf Algorithm. Water. 2025; 17(18):2766. https://doi.org/10.3390/w17182766
Chicago/Turabian StyleLi, Shasha, Kai Jiang, Shunqun Yang, Zuxiu Lan, Yining Qi, and Huaizhi Su. 2025. "A Displacement Monitoring Model for High-Arch Dams Based on SHAP-Driven Ensemble Learning Optimized by the Gray Wolf Algorithm" Water 17, no. 18: 2766. https://doi.org/10.3390/w17182766
APA StyleLi, S., Jiang, K., Yang, S., Lan, Z., Qi, Y., & Su, H. (2025). A Displacement Monitoring Model for High-Arch Dams Based on SHAP-Driven Ensemble Learning Optimized by the Gray Wolf Algorithm. Water, 17(18), 2766. https://doi.org/10.3390/w17182766







