Quantitative Analysis of Hydraulic Fracture Geometry and Its Relationship with Key Water Hammer Pressure Features
Abstract
1. Introduction
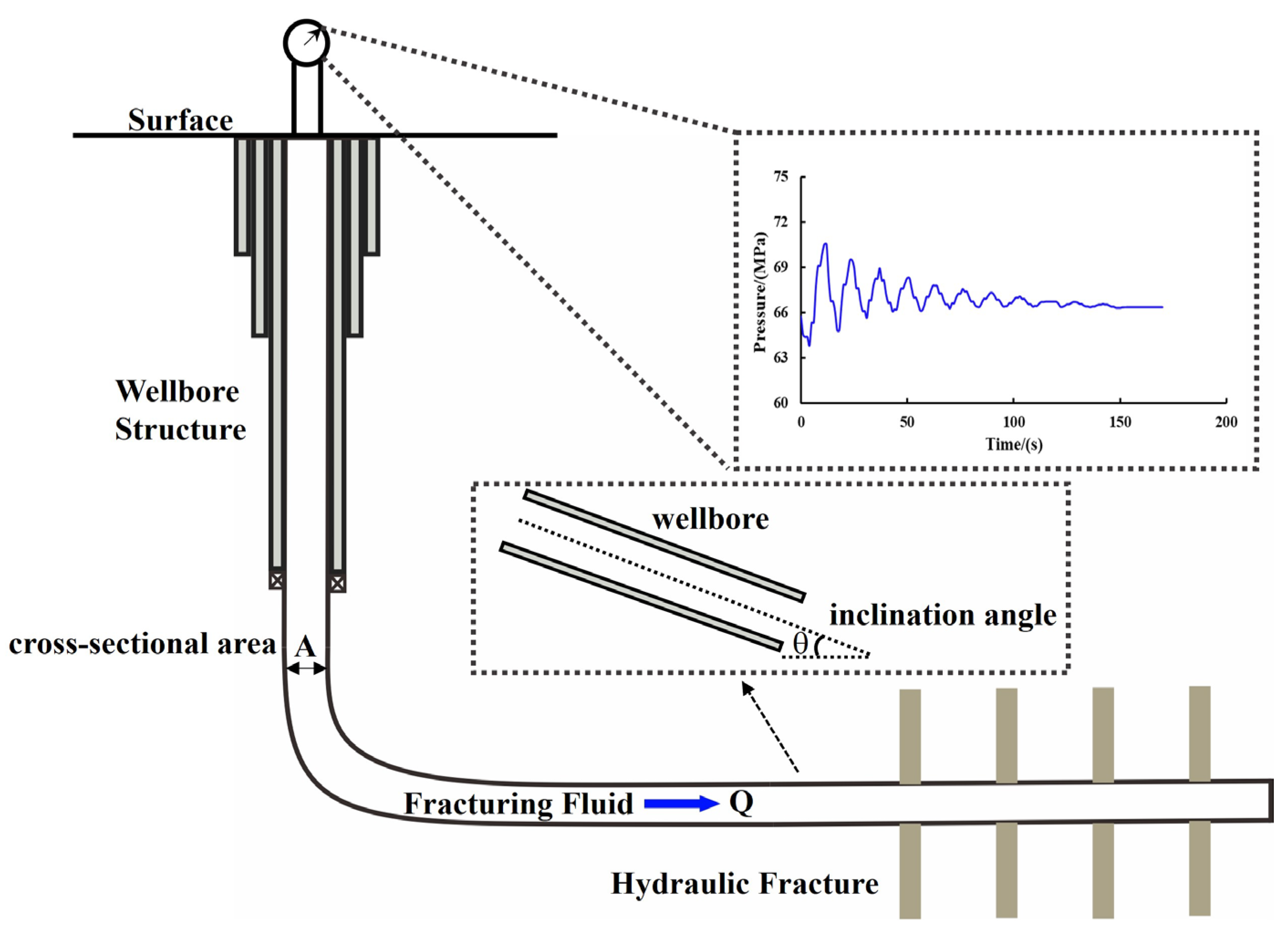
2. Water Hammer Model
2.1. Mathematical Model of Water Hammer Pressure Evolution
2.1.1. Pressure Propagation Model
2.1.2. Initial Conditions
2.1.3. Boundary Conditions
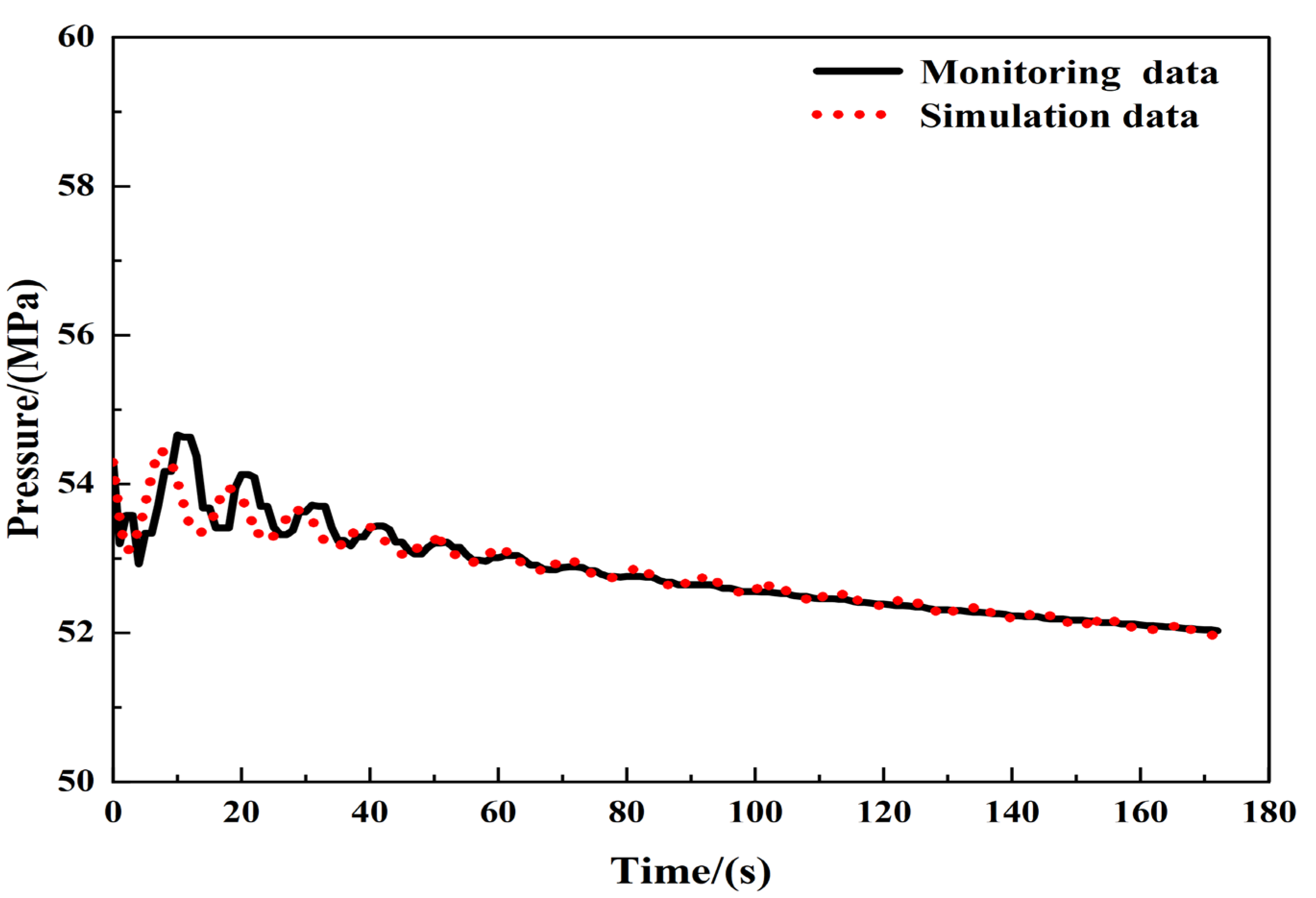
2.1.4. Model Validation
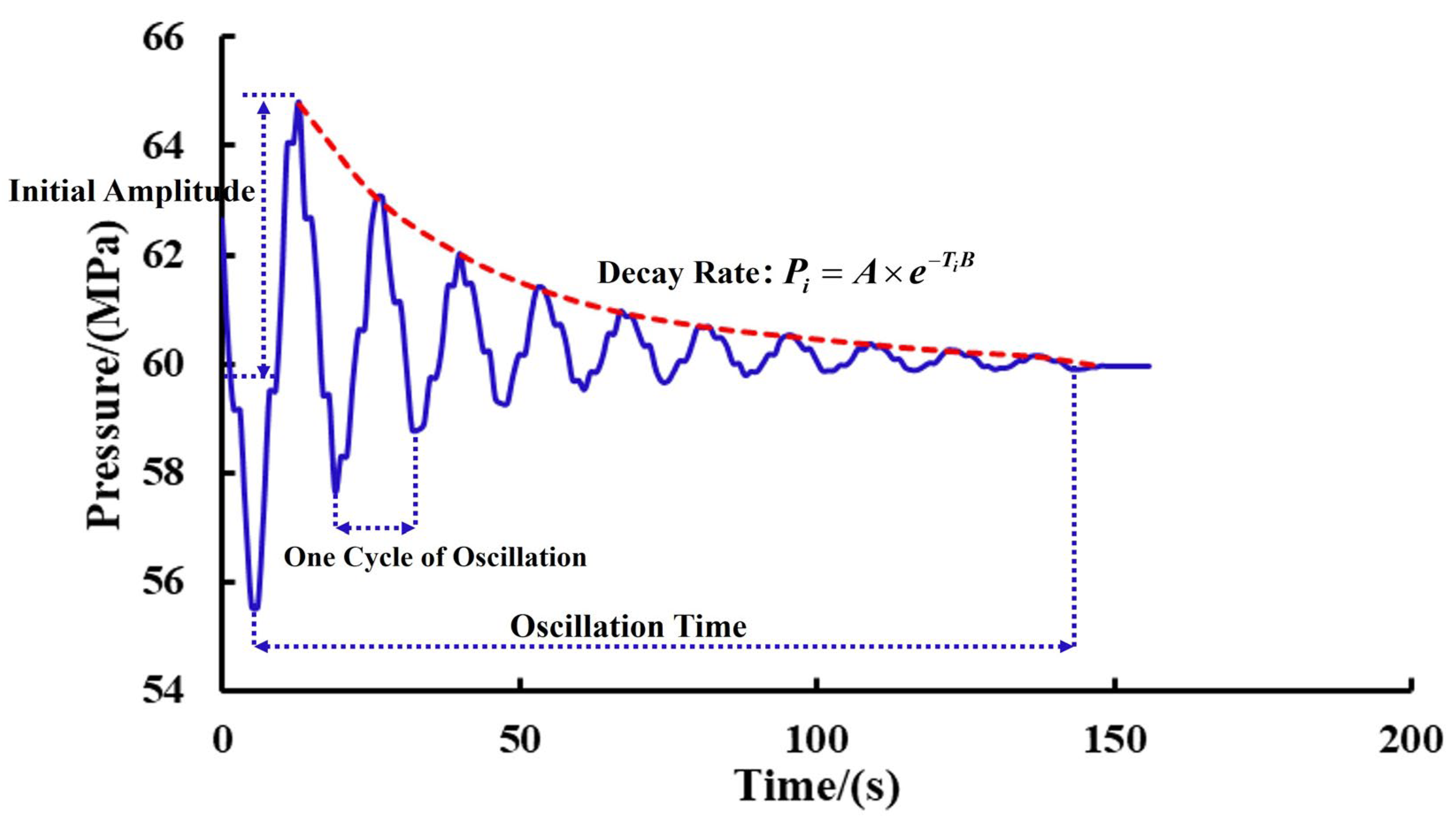
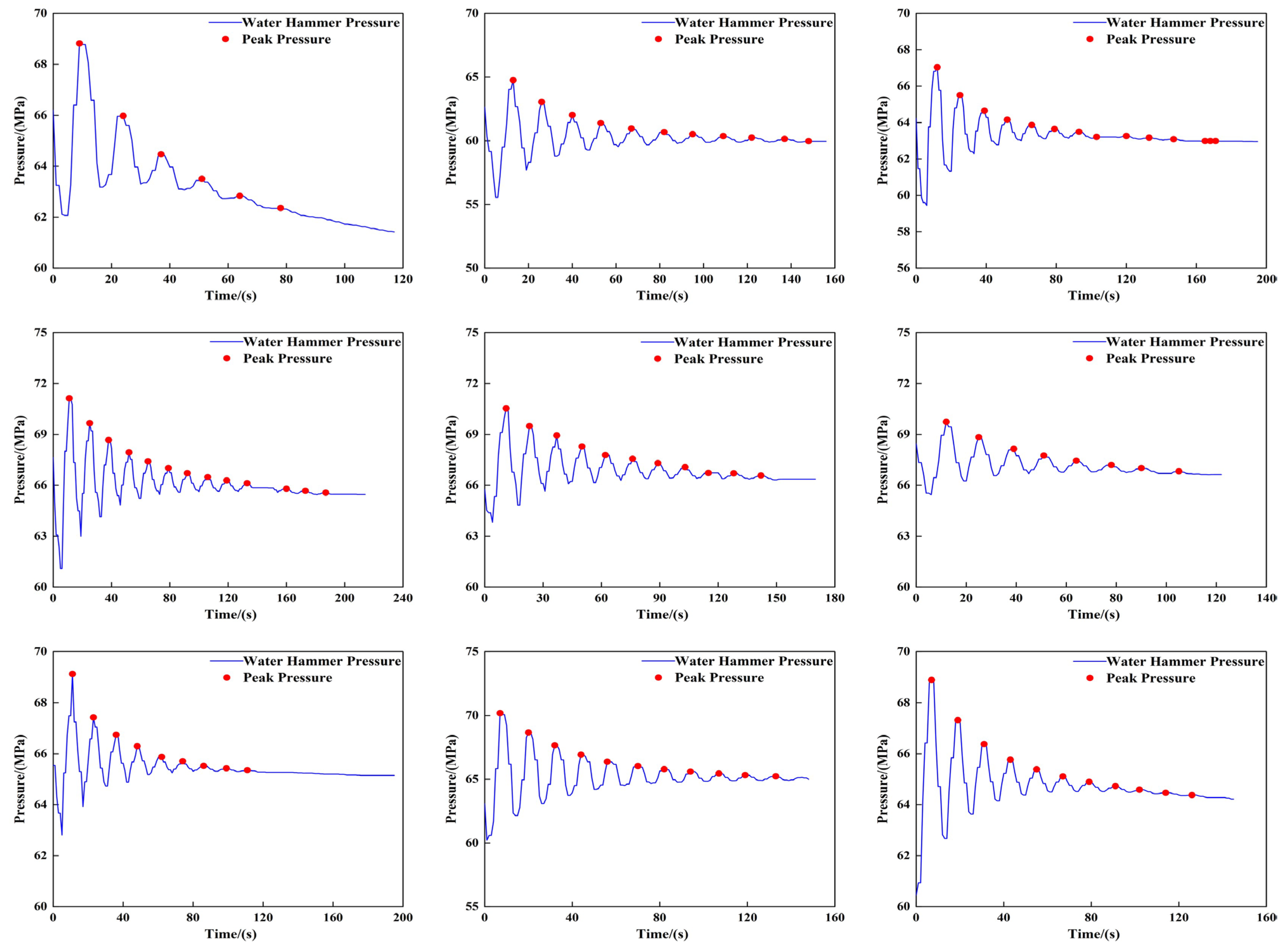
3. Characteristics of Water Hammer Pressure Response
4. Results and Discussion
4.1. Hydraulic Fracture Parameters and Water Hammer Characteristic Parameters
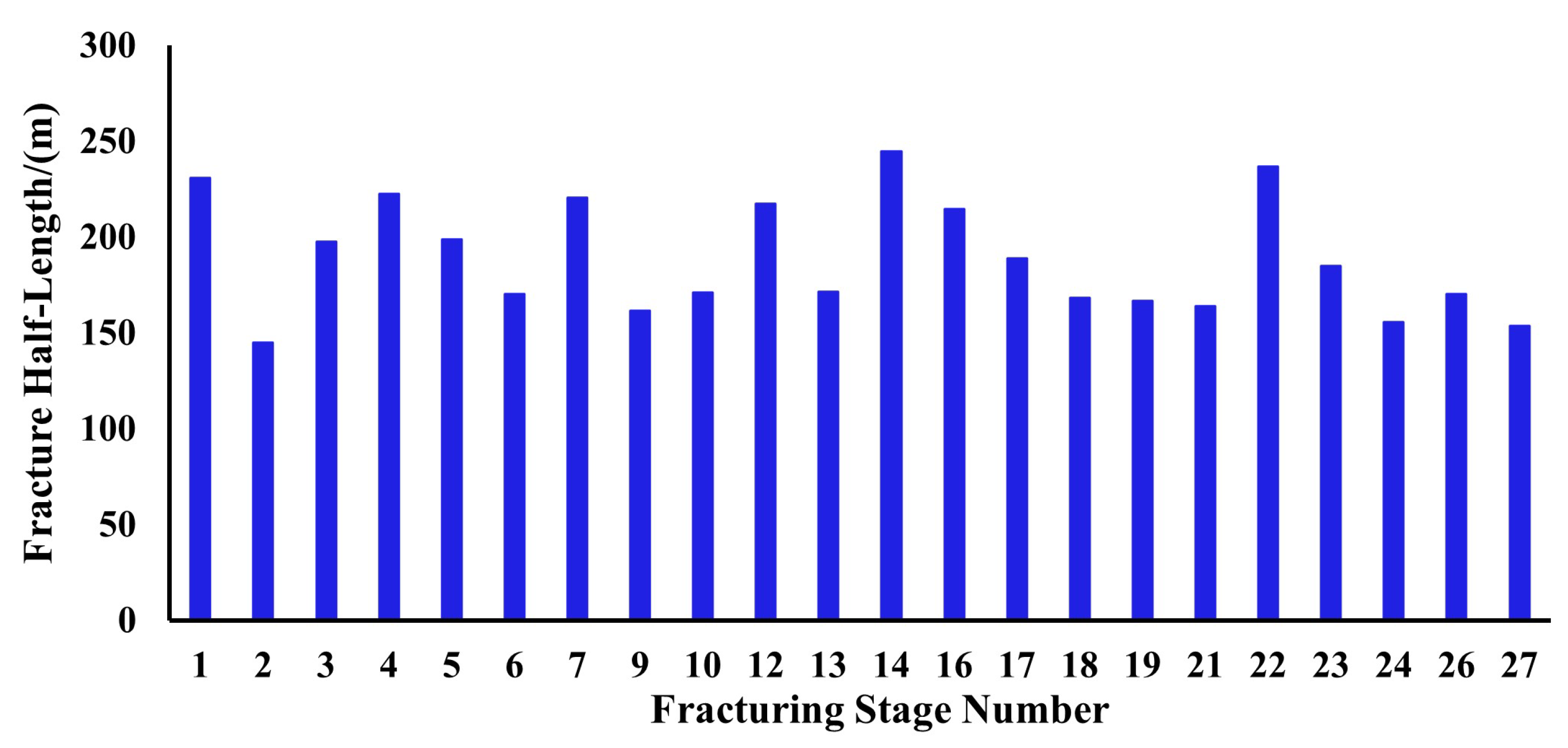
4.1.1. Fracture Geometric Parameters
4.1.2. Water Hammer Characteristic Parameters
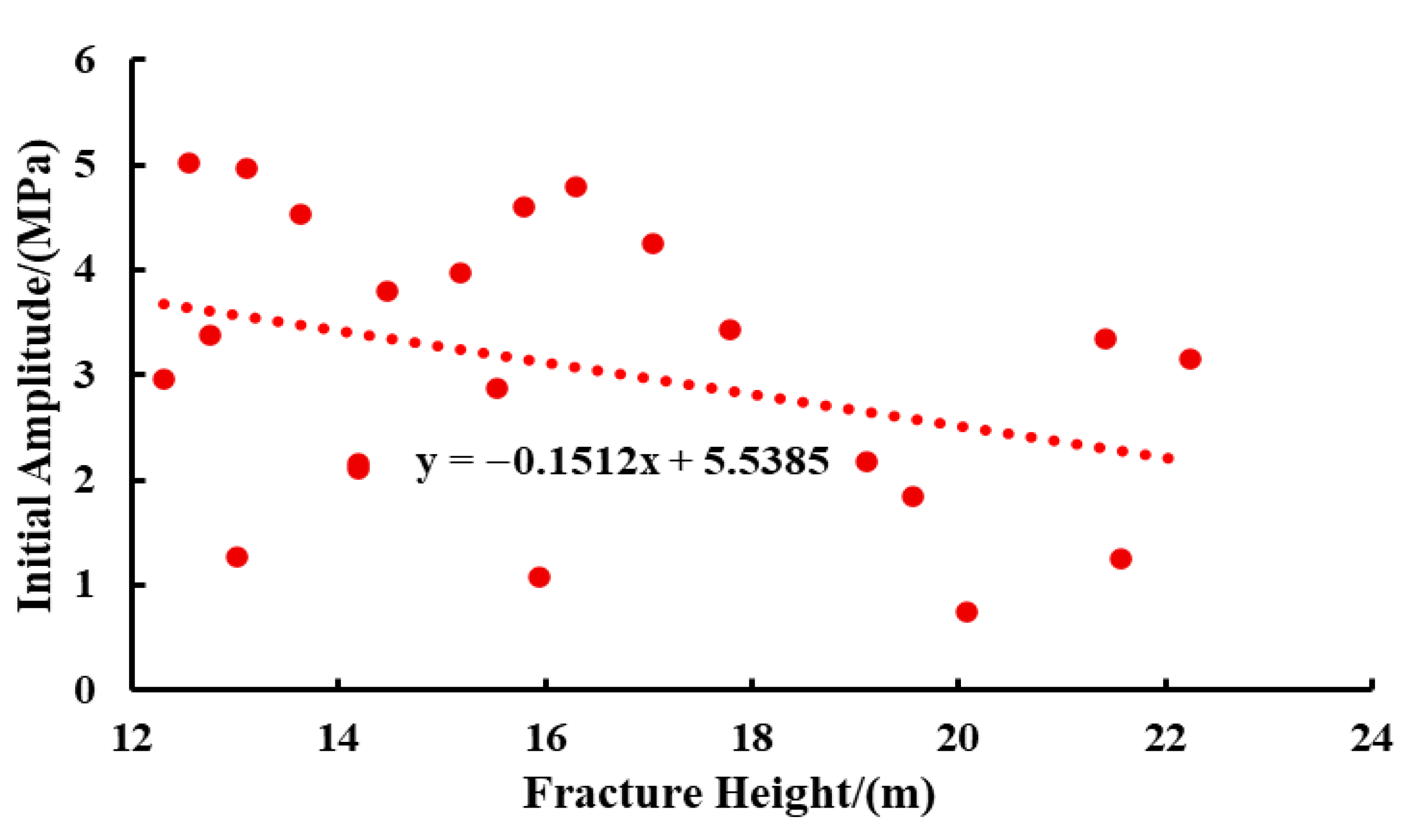
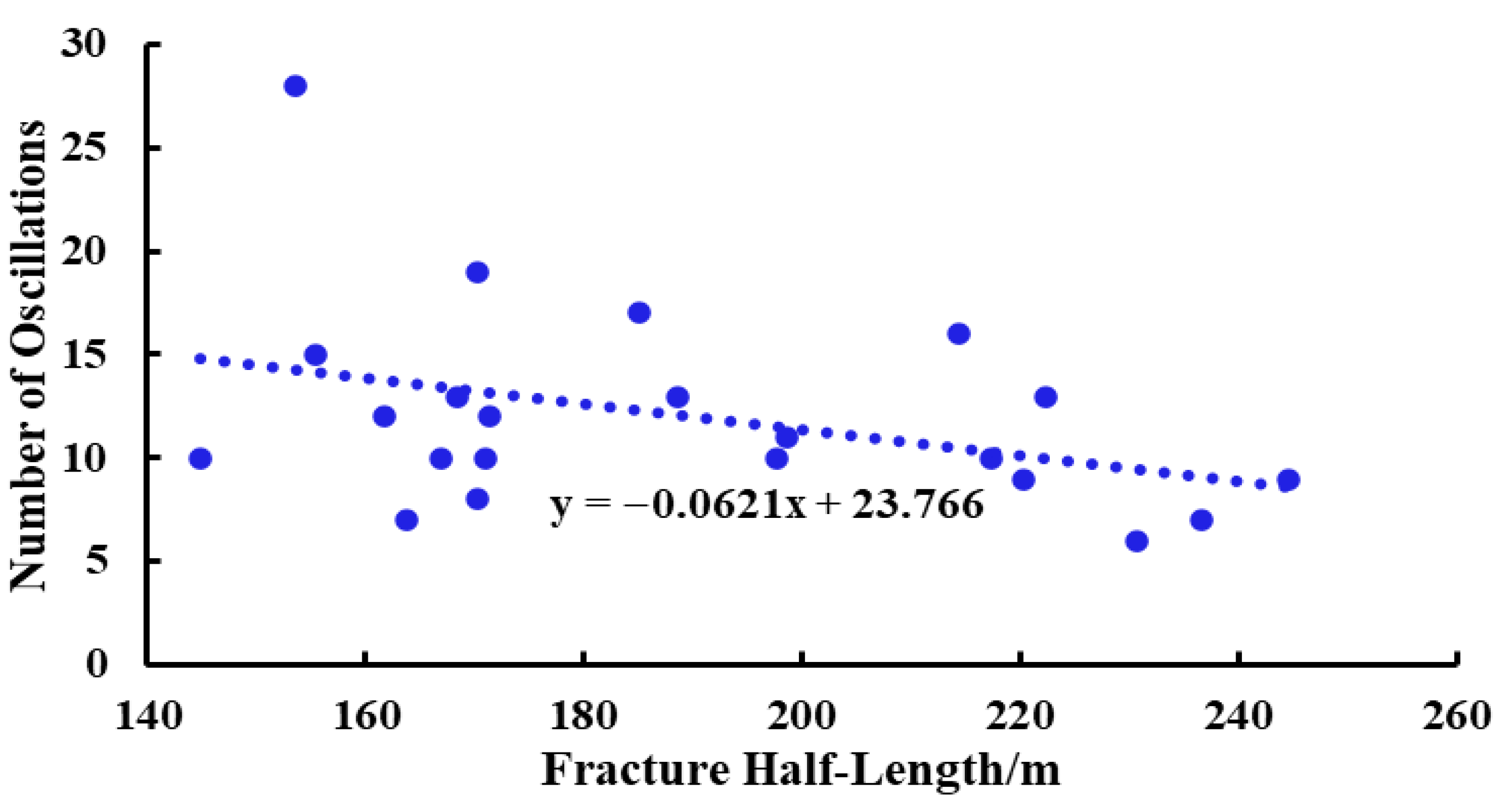
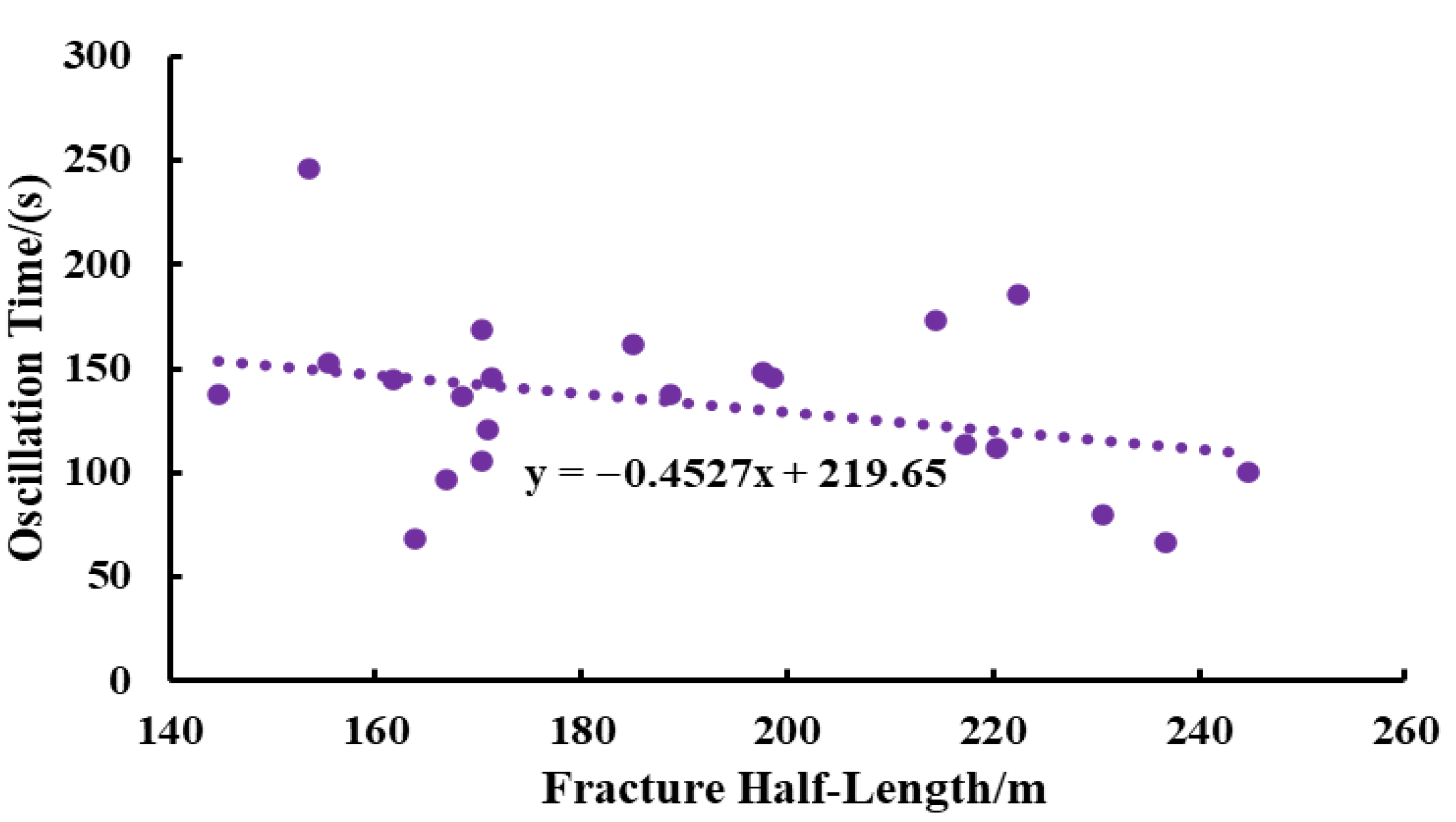
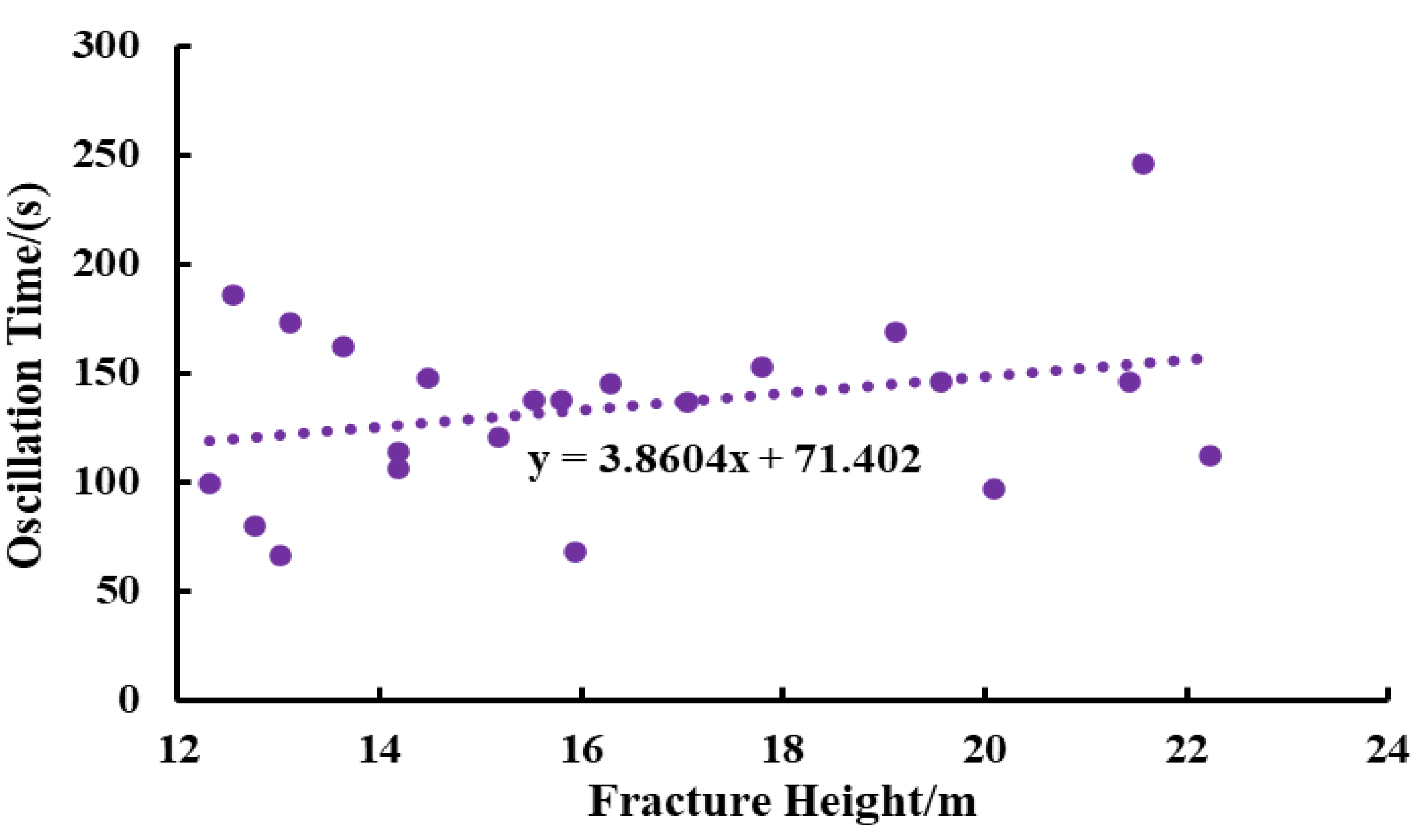
4.2. Correlation Analysis of Water Hammer Characteristics and Fracture Parameters
- (1)
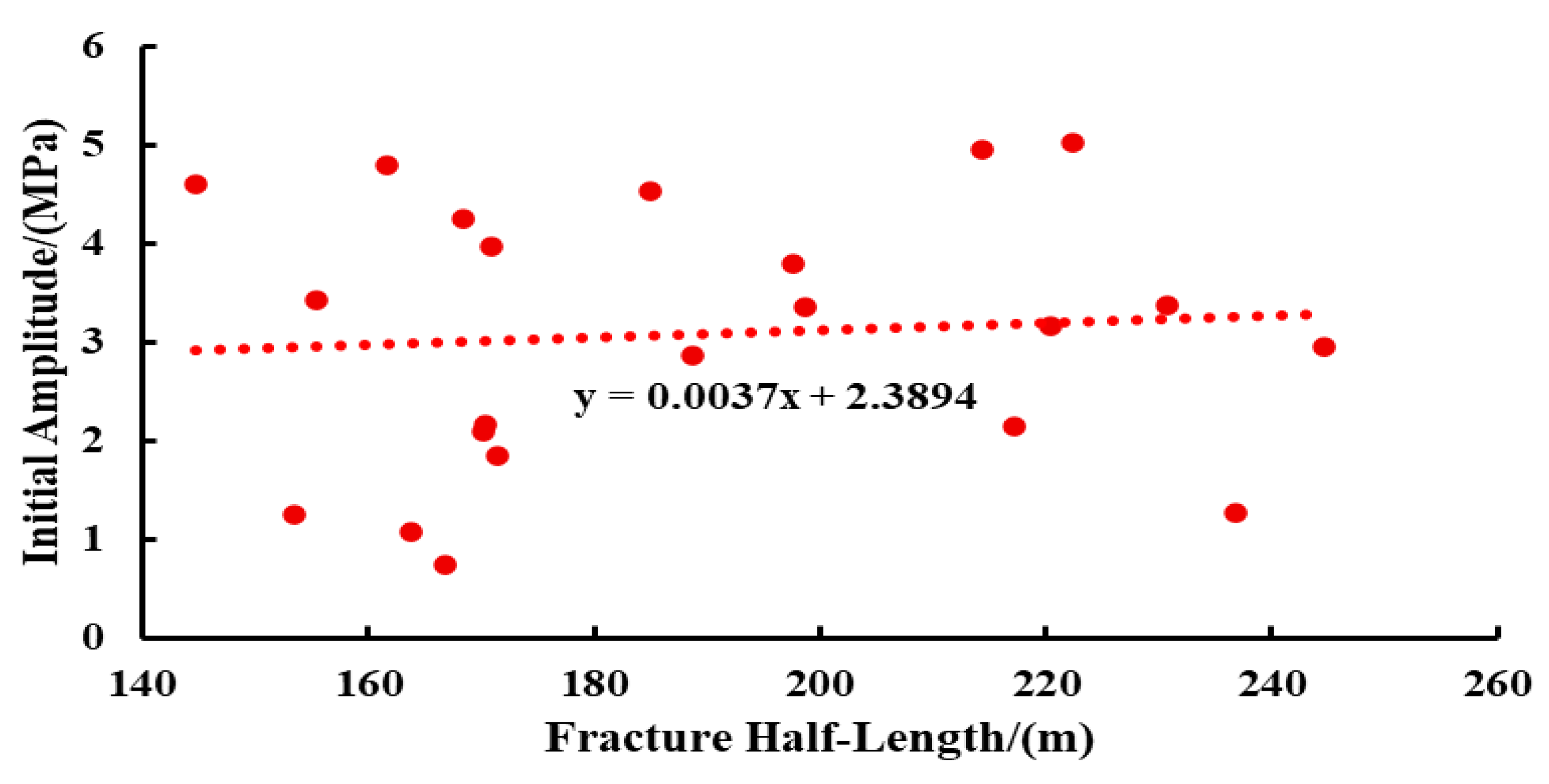
- Initial Amplitude
- (2)
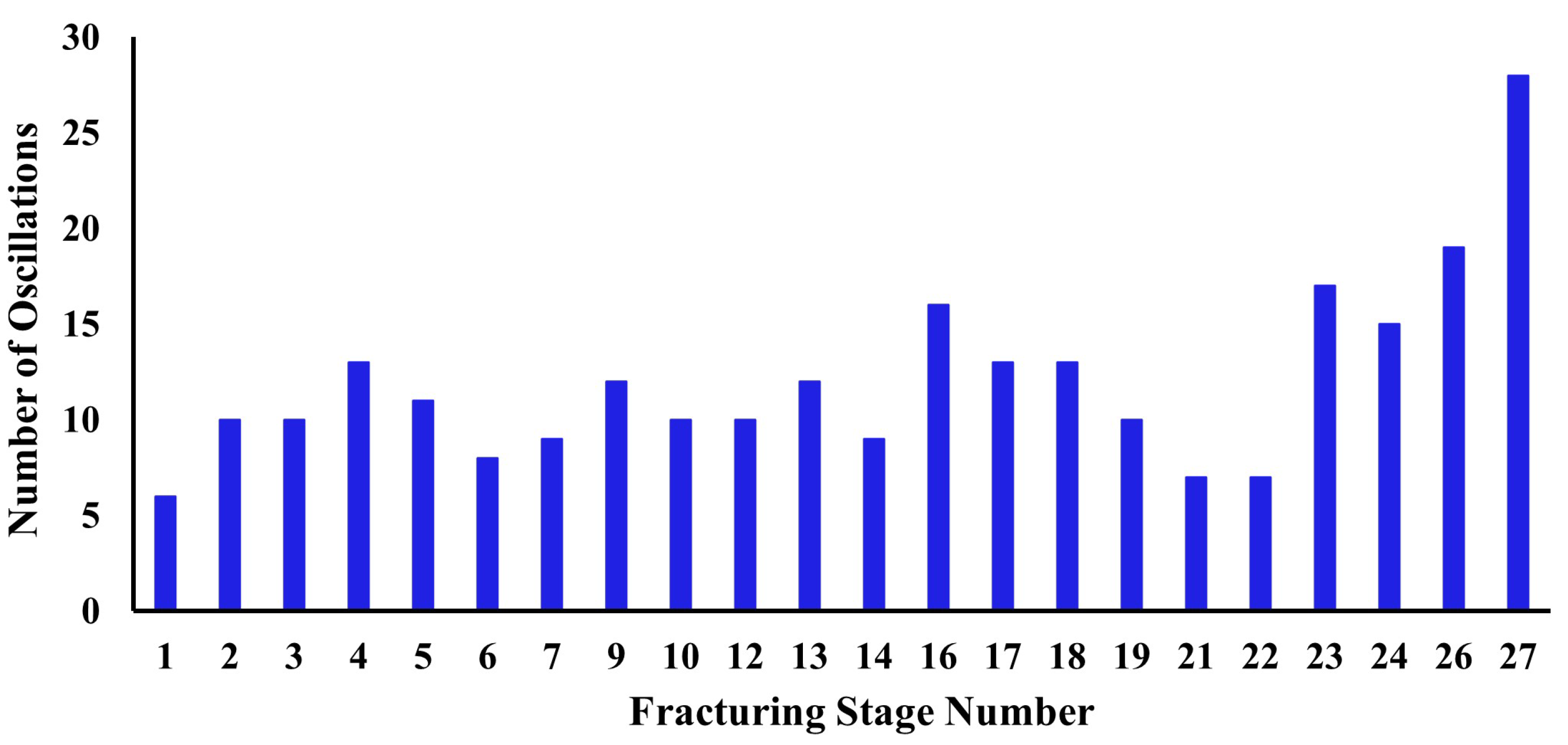
- Number of Oscillations
- (3)
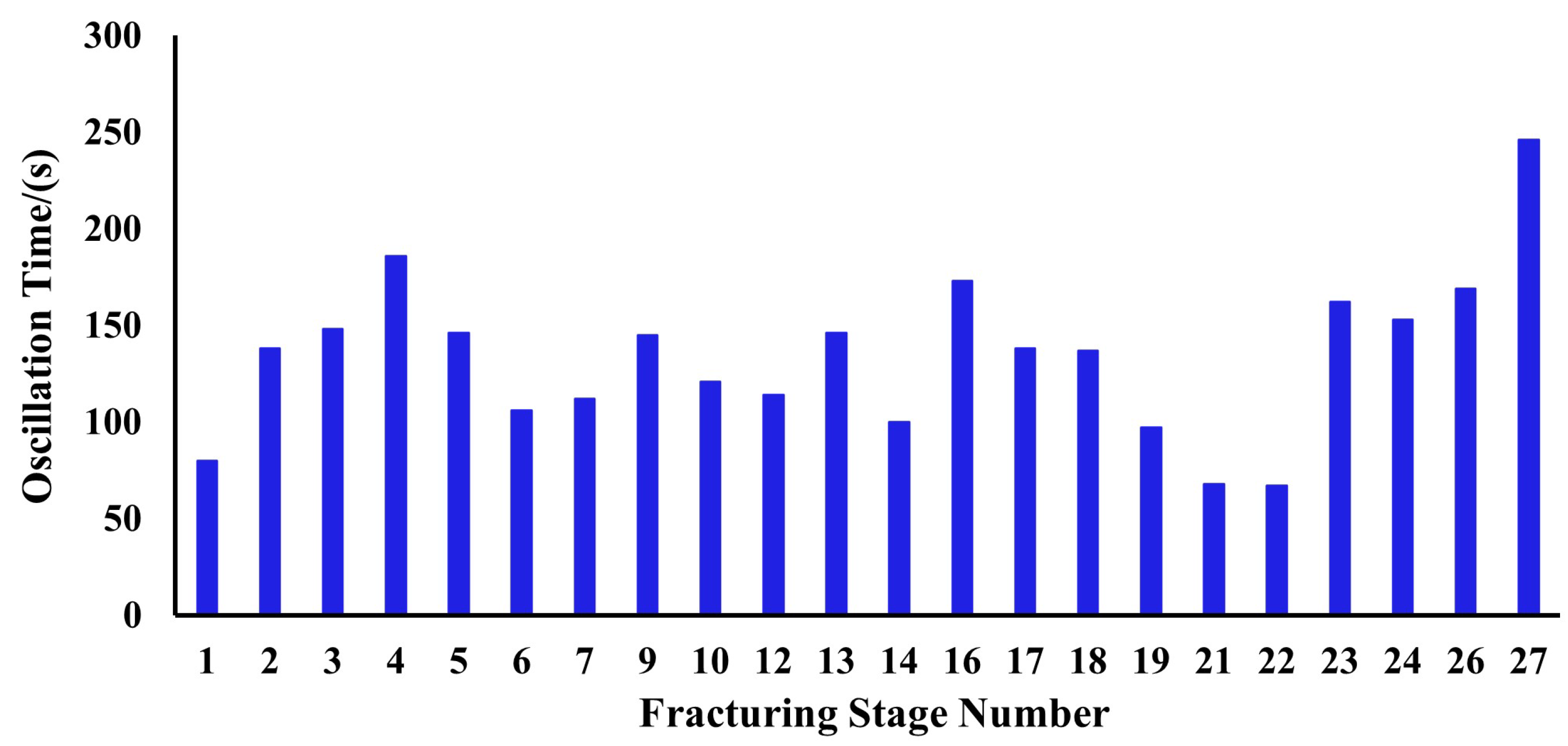
- Oscillation Duration
- (4)
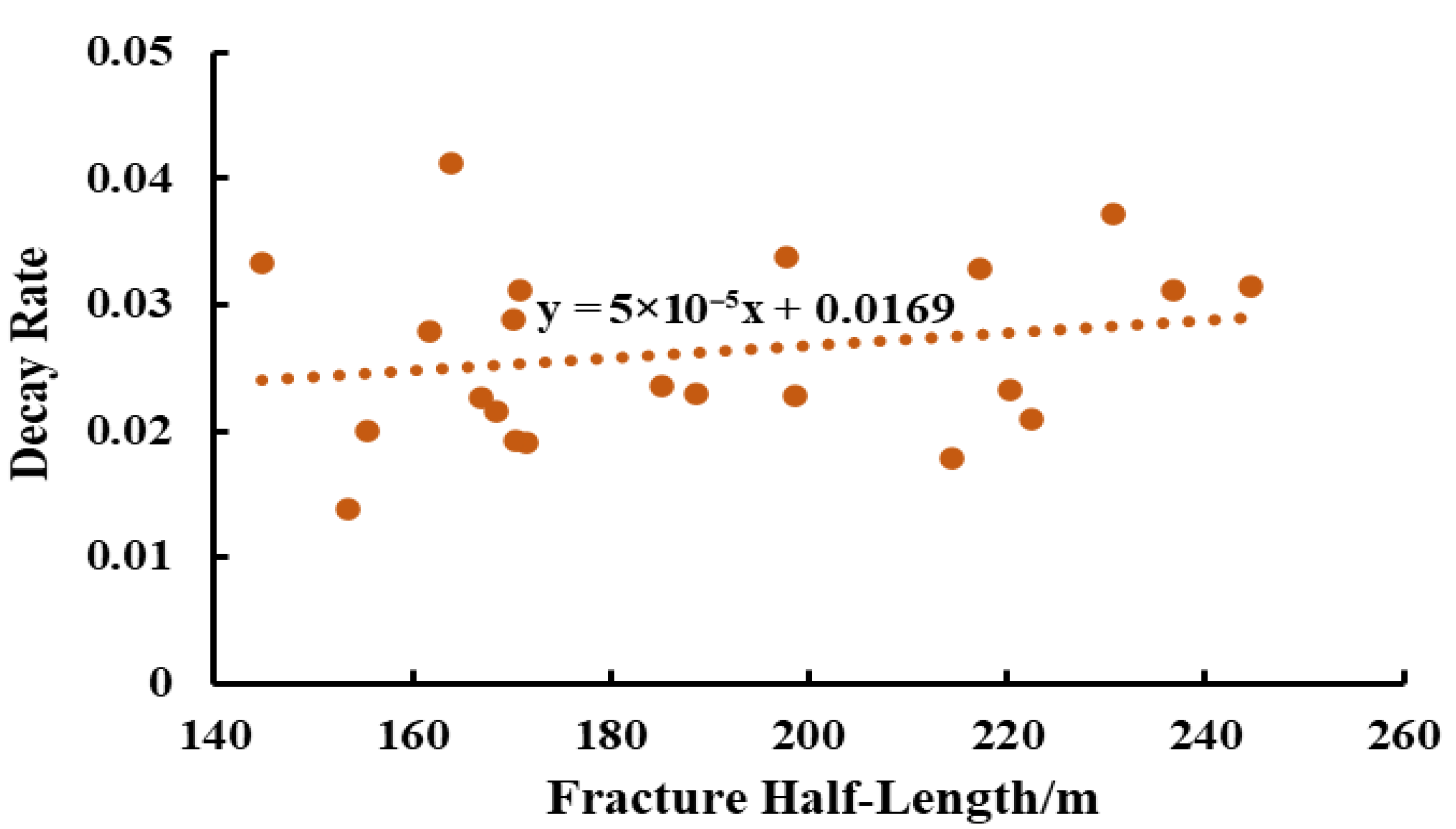
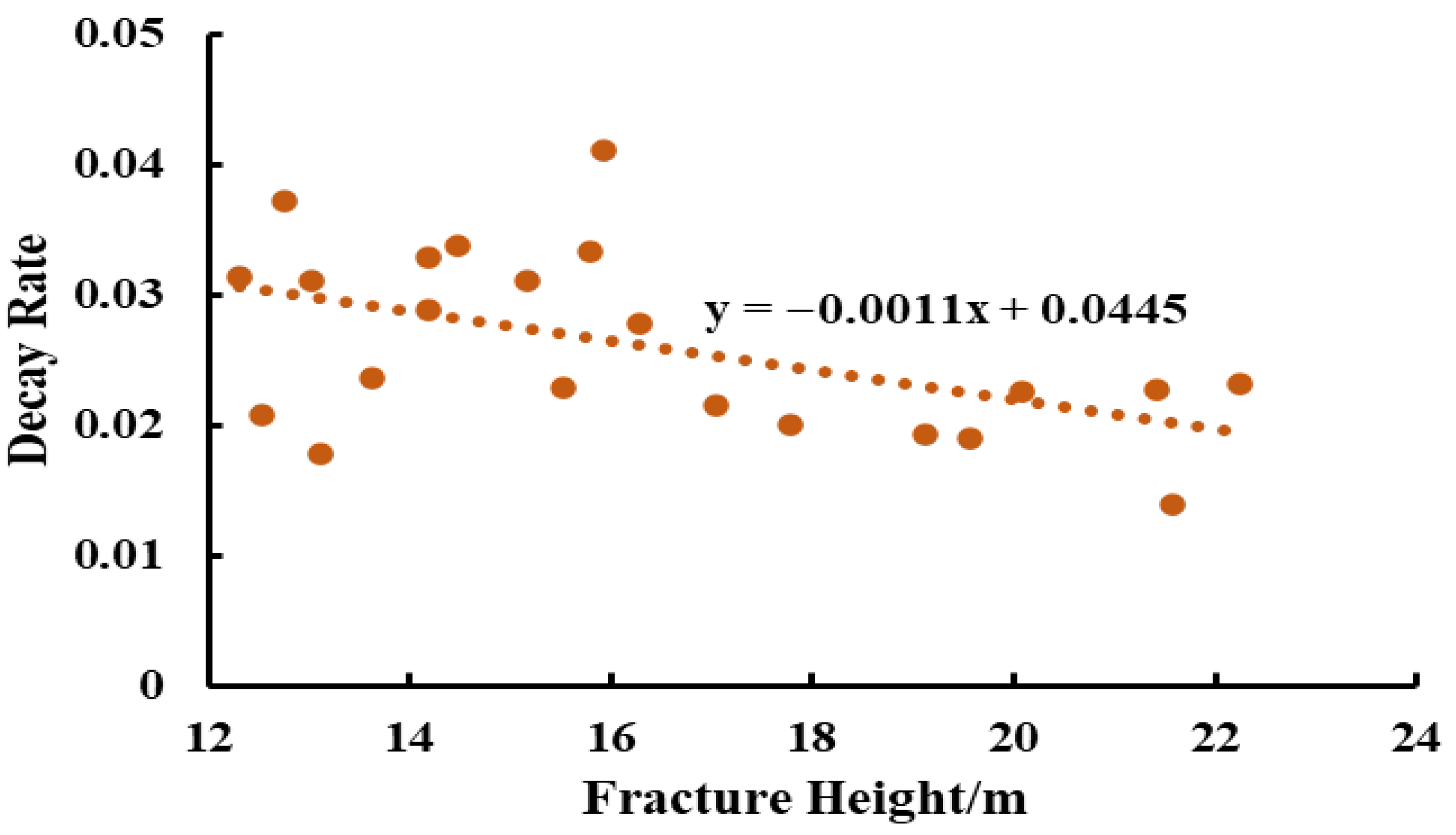
- Water Hammer Pressure Attenuation Rate
4.3. Discussion
5. Conclusions
- (1)
- A mathematical model for the evolution of water hammer pressure during multi-cluster staged fracturing in horizontal wells was established, comprehensively incorporating wellbore friction, perforation friction, and fluid filtration effects within the fractures. Fracture parameters at different fracturing stages were diagnostically analyzed. The inversion results show that the fracture half-length ranges from 144.77 m to 244.68 m, with an average of 188.80 m, while the fracture height varies between 12.31 m and 22.24 m, with an average of 16.26 m.
- (2)
- Based on the measured water hammer pressure data of each fracturing stage, it is found that the initial amplitude of water hammer pressure in this well ranges from 0.74 to 5.02 MPa, with an average value of 3.08 MPa. The number of oscillations varies between 6 and 28, and the average is 12. The oscillation time is between 67 and 246 s, with an average of 134.18 s. The water hammer attenuation rate is in the range of 0.0139 to 0.0412, and the average water hammer attenuation rate is 0.0262.
- (3)
- Correlation analysis between water hammer pressure characteristics and fracture parameters indicates that, under conditions of longer fracture half-length and smaller fracture height, the resulting water hammer pressure exhibits a higher initial amplitude, fewer oscillations, shorter oscillation duration, and a larger attenuation rate.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Zhang, Q.; Shen, J.; Xu, Y.; He, F.; Deng, C.; Xiao, J. volumetric stimulation technology of long-section multi-cluster temporary plugging in shale gas reservoirs. Nat. Gas Ind. 2022, 42, 143–150. [Google Scholar] [CrossRef]
- He, Y.; Huang, H.; Tang, M.; Ni, J.; Li, H.; Babadagli, T.; Zhang, X. Influence mechanisms of pressure difference in fracture ends on dynamic imbibition and displacement in shale reservoirs. J. China Univ. Pet. (Ed. Nat. Sci.) 2024, 48, 114–122. [Google Scholar] [CrossRef]
- Lei, Q.; Weng, D.; Xiong, S.; Liu, H.; Guan, B.; Deng, Q.; Yan, X.; Liang, H.; Ma, Z. Progress and development directions of shale oil reservoir stimulation technology of China National Petroleum Corporation. Pet. Explor. Dev. 2021, 48, 1035–1042. [Google Scholar] [CrossRef]
- Zhao, W.; Jia, A.; Wei, Y.; Wang, J.; Zhu, H. Progress in shale gas exploration in China and prospects for future development. China Pet. Explor. 2020, 25, 31–44. [Google Scholar] [CrossRef]
- Zhu, Z.; Dai, D.; Lu, W.; Wang, S.; Liu, W.; Xiao, J. Numerical Fracture Diagnosis Method for Horizontal Well Fracturing Based on Water Hammer. Chin. J. Comput. Phys. 2023, 40, 735–741. [Google Scholar] [CrossRef]
- Parkhonyuk, S.; Fedorov, A.; Kabannik, A.; Korkin, R.; Nikolaev, M.; Tsygulev, I. Measurements while fracturing: Nonintrusive method of hydraulic fracturing monitoring. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, Woodlands, TX, USA, 23–25 January 2018; p. D031S007R005. [Google Scholar] [CrossRef]
- Haustveit, K.; Dahlgren, K.; Greenwood, H.; Peryam, T.; Kennedy, B.; Dawson, M. New age fracture mapping diagnostic tools-A STACK case study. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, 24–26 January 2017; p. D011S001R002. [Google Scholar] [CrossRef]
- Qiu, Y.; Hu, X.; Zhou, F.; Jiang, Z.; Wang, Y.; Lu, X.; Li, J.; Yi, P. Study on Influence Factors of Wellhead Water Hammer Response Characteristics after Fracturing Pumps Shutdown. Chin. J. Hydrodyn. 2023, 38, 965–973. [Google Scholar] [CrossRef]
- Yong, R.; Qiu, Y.; Zhou, F.; Hu, X.; Song, Y.; Zhou, X. The evaluation of temporary plugging effect in shale gas wells based on high-frequency water hammer pressure. Pet. Sci. Bull. 2024, 09, 789–797. [Google Scholar] [CrossRef]
- Holzhausen, G.R.; Gooch, R.P. Impedance of hydraulic fractures: Its measurement and use for estimating fracture closure pressure and dimensions. In Proceedings of the SPE Rocky Mountain Petroleum Technology Conference/Low-Permeability Reservoirs Symposium, Denver, CO, USA, 19–22 May 1985; p. SPE-13892-MS. [Google Scholar] [CrossRef]
- Hu, X.; Luo, Y.; Zhou, F.; Qiu, Y.; Li, Z.; Li, Y. Evaluation of multi-fractures geometry based on water hammer signals: A new comprehensive model and field application. J. Hydrol. 2022, 612, 128240. [Google Scholar] [CrossRef]
- Qiu, Y.; Hu, X.; Zhou, F.; Li, Z.; Li, Y.; Luo, Y. Water hammer response characteristics of wellbore-fracture system: Multi-dimensional analysis in time, frequency and quefrency domain. J. Pet. Sci. Eng. 2022, 213, 110425. [Google Scholar] [CrossRef]
- Carey, M.A.; Mondal, S.; Sharma, M.M. Analysis of water hammer signatures for fracture diagnostics. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 18–30 September 2015; p. D031S034R003. [Google Scholar] [CrossRef]
- Korkin, R.; Parkhonyuk, S.; Fedorov, A.; Badazhkov, D.; Kabannik, A. High frequency pressure monitoring and data analytics for stimulation efficiency determination: New perspectives or potential limits. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, Woodlands, TX, USA, 4–6 February 2020; p. D031S008R006. [Google Scholar] [CrossRef]
- Panjaitan, M.L.; Moriyama, A.; McMillan, D.; Dunaeva, A.; Rutledge, L.; Xu, J.; Parkhonyuk, S.; Kabannik, A.; Korkin, R.; Warren, M.; et al. Qualifying diversion in multi clusters horizontal well hydraulic fracturing in haynesville shale using water hammer analysis, step-down test and microseismic data. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, Woodlands, TX, USA, 16–18 October 2018; p. D031S007R006. [Google Scholar] [CrossRef]
- Bogdan, A.V.; Keilers, A.; Oussoltsev, D.; Lecerf, B. Real-time interpretation of leak isolation with degradable diverter using high frequency pressure monitoring. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Perth, Australia, 25–27 October 2016; p. SPE-182451-MS. [Google Scholar] [CrossRef]
- Kabannik, A.; Parkhonyuk, S.; Korkin, R.; Litvinets, F.; Dunaeva, A.; Nikolaev, M.; Usoltsev, D. Can we trust the diversion pressure as a decision-making tool: Novel technique reveals the truth. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 11–15 November 2018; p. D021S050R003. [Google Scholar] [CrossRef]
- Ciezobka, J.; Maity, D.; Salehi, I. Variable pump rate fracturing leads to improved production in the marcellus shale. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, Woodlands, TX, USA, 9–11 February 2016; p. D031S008R003. [Google Scholar] [CrossRef]
- Iriarte, J.; Merritt, J.; Kreyche, B. Using water hammer characteristics as a fracture treatment diagnostic. In Proceedings of the SPE Oklahoma City Oil and Gas Symposium/Production and Operations Symposium, Oklahoma City, OK, USA, 27–31 March 2017; p. D031S007R004. [Google Scholar] [CrossRef]
- Dung, N.; David, C.; Tom, D.; Jon, S.; Nico, R.; Annie, O. Practical applications of water hammer analysis from hydraulic fracturing treatments. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, Virtual, 4–6 May 2021; p. D011S002R009. [Google Scholar] [CrossRef]
- Luo, Y.; Hu, X.; Zhou, F.; Qiu, Y.; Lu, X.; Li, J.; Wang, Y. A new water hammer decay model: Analyzing the interference of multiple fractures and perforations on decay rate. SPE J. 2023, 28, 1973–1985. [Google Scholar] [CrossRef]
- Teng, H.; Tang, H.; Ding, Y.; Qin, J.; Cui, E.; Zhang, J.; Niu, Y. Fracture geometry analysis method based on pumping curves: A case study of m well block in Mahu tight conglomerate reservoir. Sci. Technol. Eng. 2024, 24, 14205–14215. [Google Scholar] [CrossRef]
- He, H.; Zou, L.; Li, Y.; Wang, Y.; Li, J.; Wen, H.; Chang, B.; Liu, L. Simulation Method and Feature Analysis of Shutdown Pressure Evolution During Multi-Cluster Fracturing Stimulation. Energy Eng. 2024, 121, 111. [Google Scholar] [CrossRef]
- Brown, G.O. The history of the Darcy-Weisbach equation for pipe flow resistance. In Environmental and Water Resources History; ASCE: New York City, NY, USA, 2002; pp. 34–43. [Google Scholar] [CrossRef]
- Paige, R.W.; Murray, L.R.; Roberts, J.D.M. Field application of hydraulic impedance testing for fracture measurement. SPE Prod. Facil. 1995, 10, 7–12. [Google Scholar] [CrossRef]
- Carter, R. Appendix to Optimum Fluid Characteristics for Fracture Extension; Drilling and Production Practice; Howard, G.C., Fast, C.R., Eds.; American Petroleum Institute: New York, NY, USA, 1957; Volume 267. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Sun, H.; Liu, W.; Zou, L.; Yang, L.; Wu, K.; Liu, L.; Sun, S. Quantitative Analysis of Hydraulic Fracture Geometry and Its Relationship with Key Water Hammer Pressure Features. Water 2025, 17, 2741. https://doi.org/10.3390/w17182741
Li Y, Sun H, Liu W, Zou L, Yang L, Wu K, Liu L, Sun S. Quantitative Analysis of Hydraulic Fracture Geometry and Its Relationship with Key Water Hammer Pressure Features. Water. 2025; 17(18):2741. https://doi.org/10.3390/w17182741
Chicago/Turabian StyleLi, Yanchao, Hu Sun, Wei Liu, Longqing Zou, Liang Yang, Kai Wu, Lijun Liu, and Shuangshuang Sun. 2025. "Quantitative Analysis of Hydraulic Fracture Geometry and Its Relationship with Key Water Hammer Pressure Features" Water 17, no. 18: 2741. https://doi.org/10.3390/w17182741
APA StyleLi, Y., Sun, H., Liu, W., Zou, L., Yang, L., Wu, K., Liu, L., & Sun, S. (2025). Quantitative Analysis of Hydraulic Fracture Geometry and Its Relationship with Key Water Hammer Pressure Features. Water, 17(18), 2741. https://doi.org/10.3390/w17182741





