Air Entrainment of Chute Aerators Under Different Atmospheric Pressures
Abstract
1. Introduction
2. Experimental Setup and Flow Conditions
3. Results and Discussion
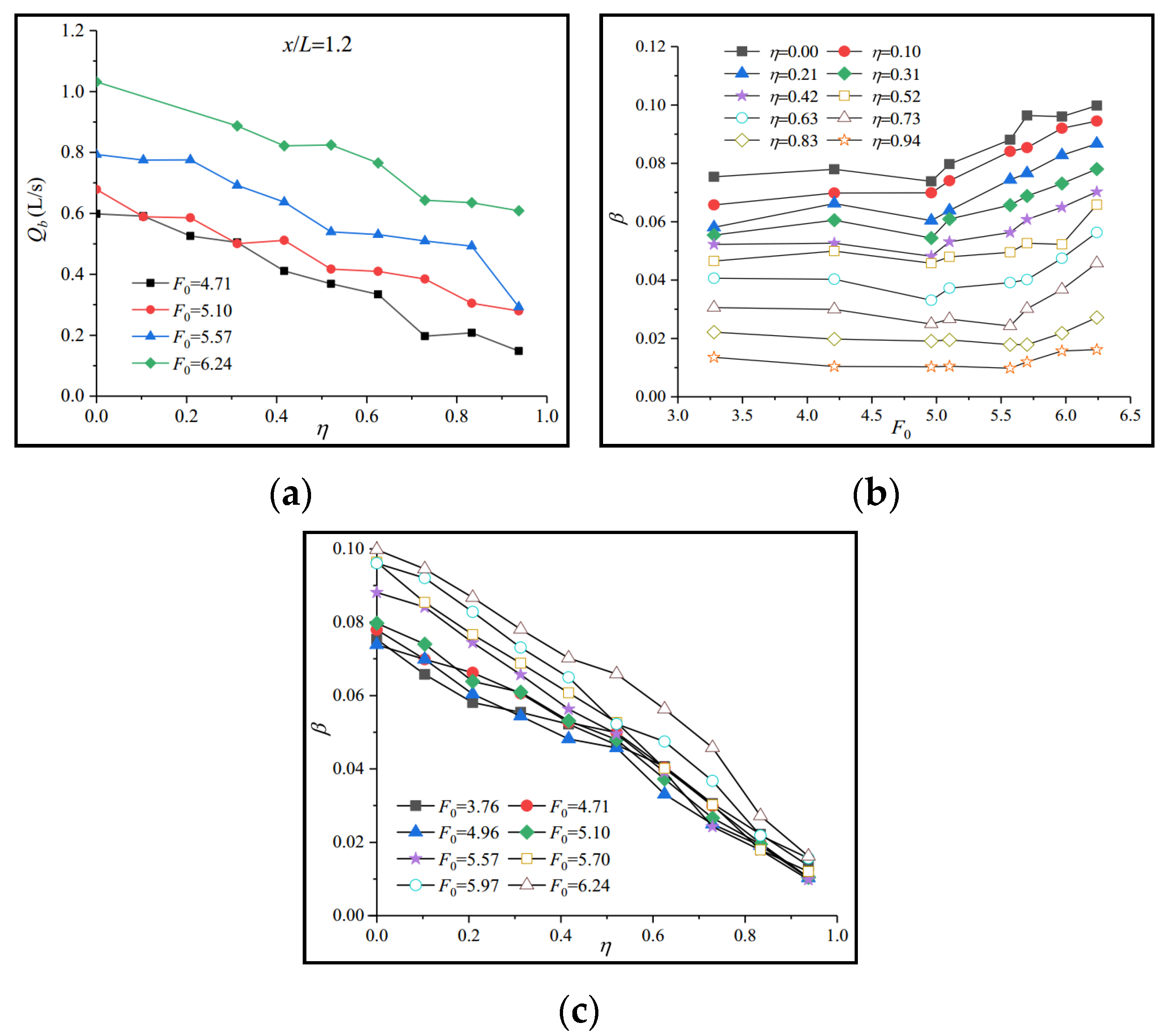
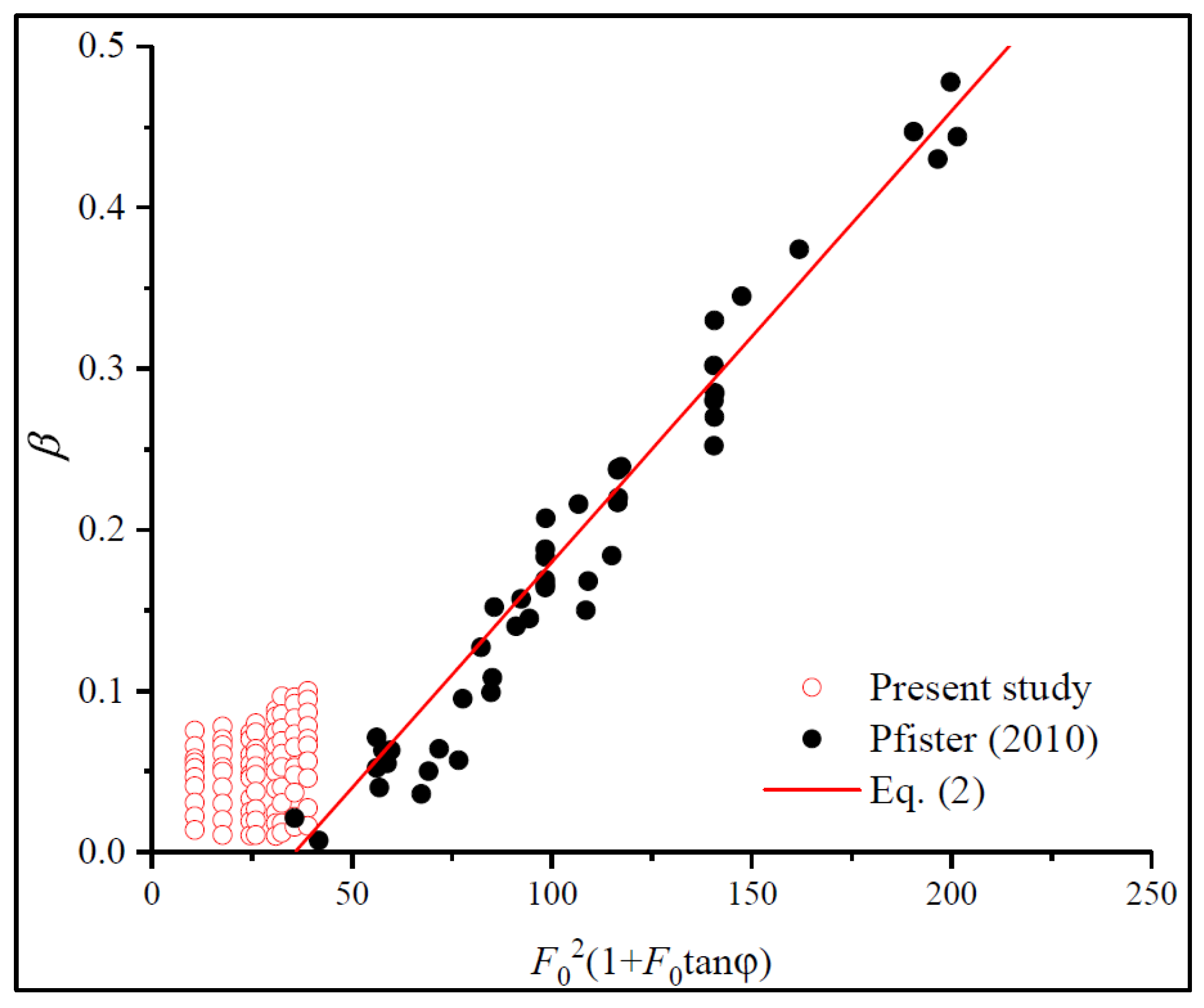
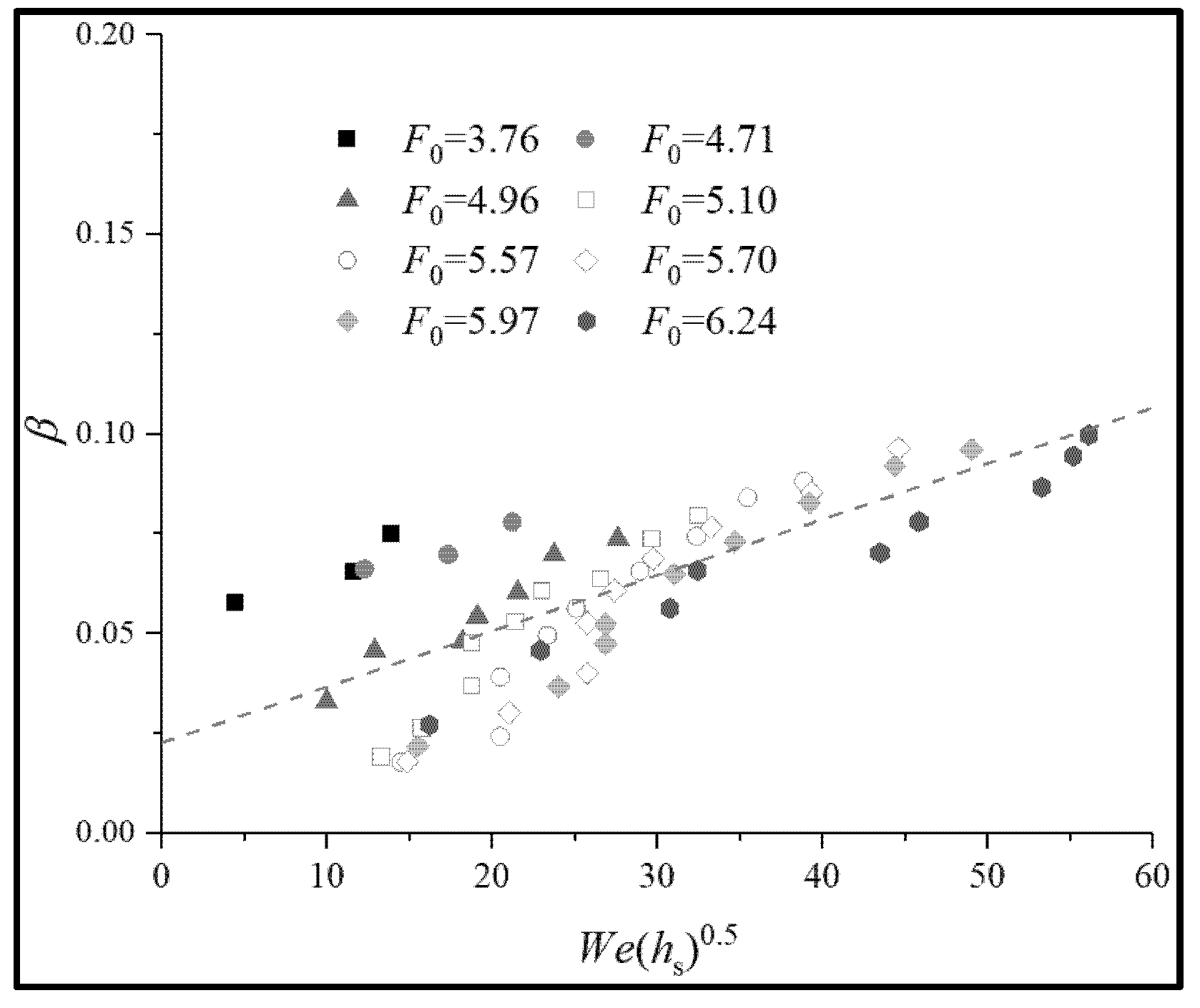
3.1. Air Entrainment Coefficients
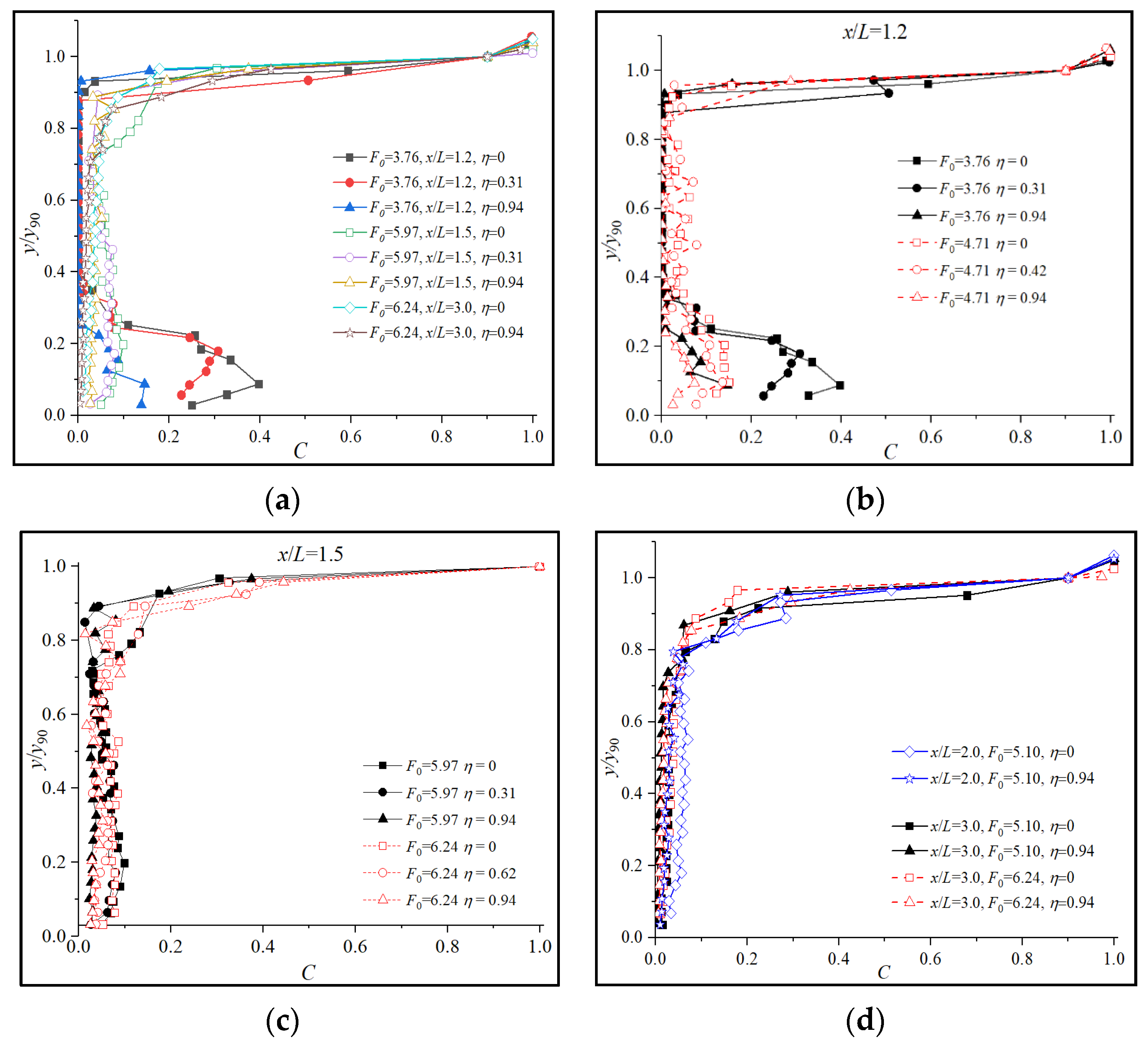
3.2. Air Concentration Distribution
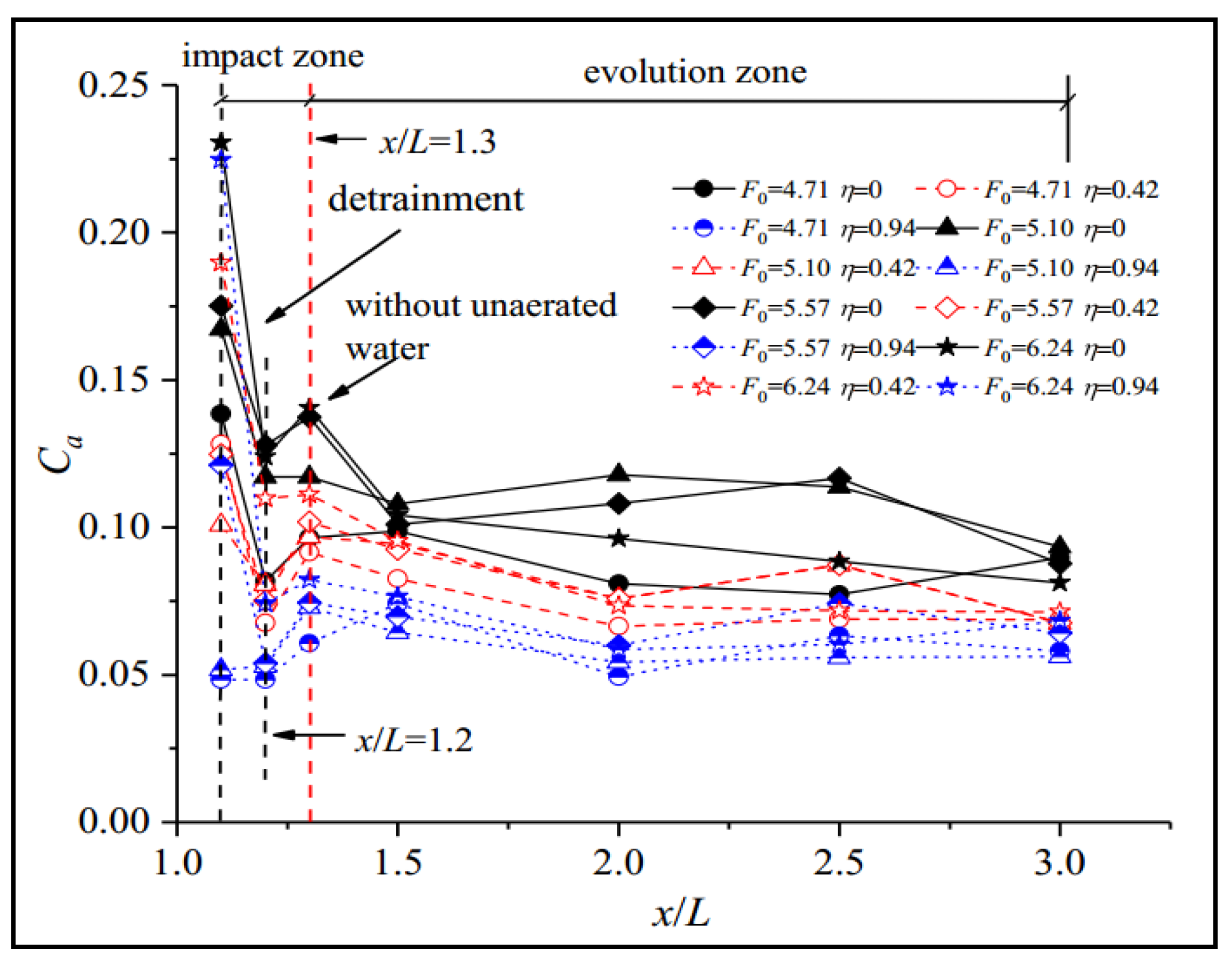
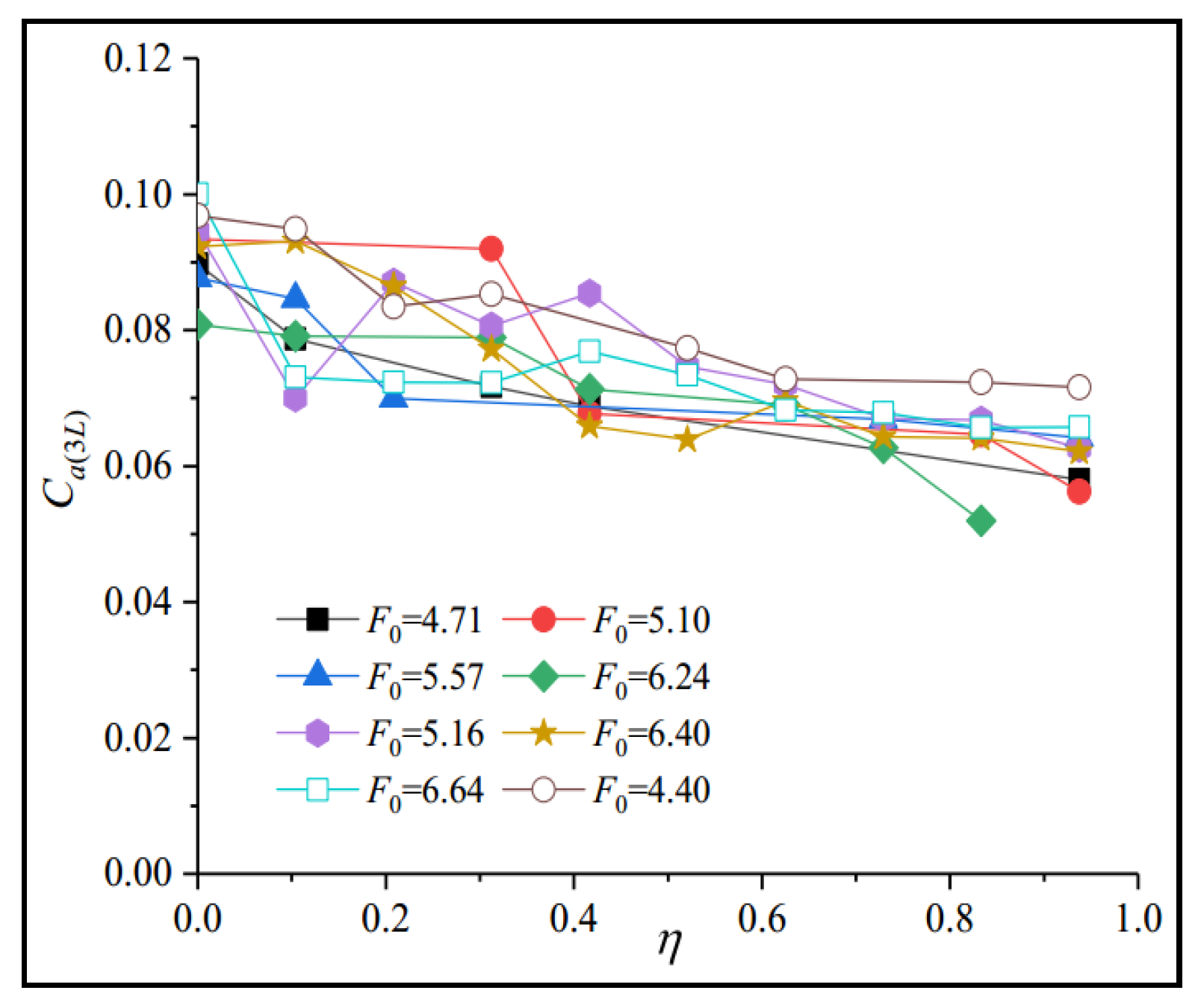
3.3. Average Air Concentration
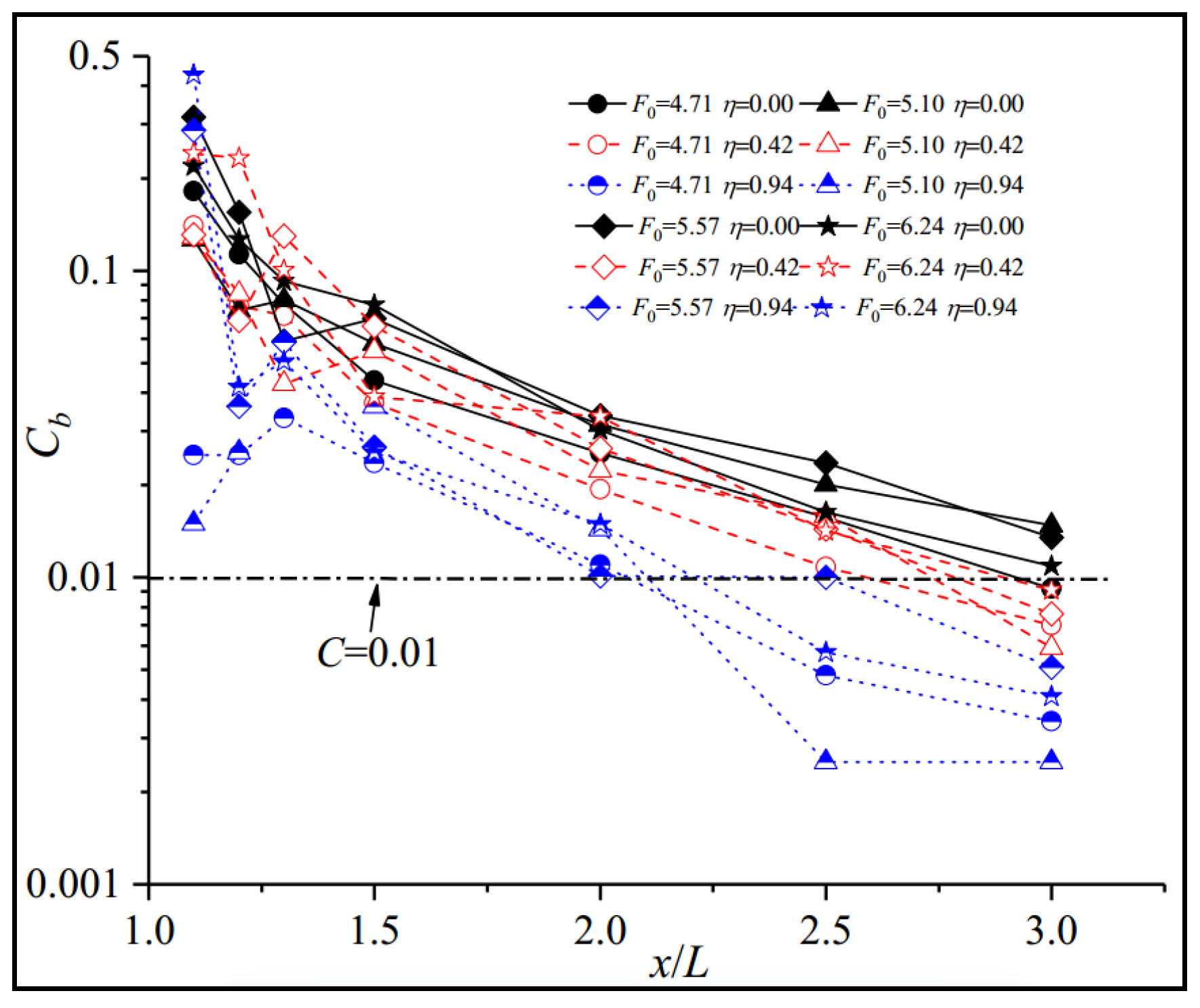
3.4. Bottom Air Concentration
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| A | the cross-sectional area of the shaft (m2) |
| B | chute width (m) |
| C | the air concentration (-) |
| Ca | the average air concentration (-) |
| Cb | the bottom air concentration (-) |
| Ca(3L) | the average air concentration at x = 3L (-) |
| Cb(3L) | the bottom air concentration at x = 3L (-) |
| d | deflector high (m) |
| Fsample | the sampling frequency (kHz) |
| g | gravitational acceleration (m/s2) |
| H | the upstream head (m) |
| h | the approach flow depth (m) |
| h1 | h1 is the position below the blackwater area C = 0 or C < 0.02 (m) |
| hs | the cavity subpressure head (m) |
| L | the jet length (m) |
| Lref | reference length (m) |
| P0 | the atmosphere pressure outside the depression tank (P0 = 960 hPa) |
| Pa | the ambient pressure inside the depression tank (hPa) |
| PN | cavity subpressure index (-) |
| Qa | the ventilation volume in the shaft (m3/s) |
| Qb | air entrainment volume in the bottom water flow (L/s) |
| Qw | water discharge (m3/s) |
| t | sampling time (s) |
| V | the approach flow velocity (m/s) |
| Va | the air velocity in the shaft (m/s) |
| F0 | Froude number (-) |
| Re | Reynolds number (-) |
| We(h) | Weber number, Lref = h (-) |
| We(L) | Weber number, Lref = L (-) |
| We(hs) | Weber number, Lref = hs (-) |
| x | the length of the direction of the flow (m) |
| y | the height of perpendicular to the chute (m) |
| y90 | the height of air-water interface C = 0.9 (m) |
| σw | the surface tension (N/m) |
| α | downstream chute angle (°) |
| β | air entrainment coefficient (-) |
| η | vacuum degree (-) |
| φ | deflect angle (°) |
| ρw | water density (kg/m3) |
References
- Falvey, H.T. Cavitation in chutes and spillways. In Engineering Monograph; No. 42; United States Department of the Interior: Washington, DC, USA, 1990. [Google Scholar]
- Ge, M.M.; Sun, C.Y.; Zhang, G.J.; Coutier-Delgosha, O.; Fan, D. Combined suppression effects on hydrodynamic cavitation performance in Venturi-type reactor for process intensification. Ultrason. Sonochem. 2022, 86, 106035. [Google Scholar] [CrossRef] [PubMed]
- Wilhelms, S.C.; Gulliver, J.S.; Ling, J.T.; Ling, R.S. Gas transfer, cavitation, and bulking in self–aerated spillway flow. J. Hydraul. Res. 2005, 45, 532–539. [Google Scholar] [CrossRef]
- Pfister, M.; Hager, W.H. Self–entrainment of air on stepped spillways. Int. J. Multiph. Flow 2011, 37, 99–107. [Google Scholar] [CrossRef]
- Pfister, M. Chute aerators: Steep deflectors and cavity subpressure. J. Hydraul. Eng. 2011, 137, 1208–1215. [Google Scholar] [CrossRef]
- Brujan, E.A.; Matsumoto, Y. Collapse of micrometer–sized cavitation bubbles near a rigid boundary. Microfluid. Nanofluid. 2012, 13, 957–966. [Google Scholar] [CrossRef]
- Chanson, H. Study of air entrainment and aeration devices. J. Hydraul. Res. 1989, 27, 301–319. [Google Scholar] [CrossRef]
- Chanson, H. Flow downstream of an aerator−Aerator spacing. J. Hydraul. Res. 1989, 27, 519–536. [Google Scholar] [CrossRef]
- Rutschmann, P.; Hager, W.H. Air entrainment by spillway aerators. J. Hydraul. Eng. 1990, 116, 765–782. [Google Scholar] [CrossRef]
- Kramer, K.; Hager, W.H. Air transport in chute flows. Int. J. Multiph. Flow 2005, 31, 1181–1197. [Google Scholar] [CrossRef]
- Kramer, K.; Hager, W.H.; Minor, H.E. Development of air concentration on chute spillways. J. Hydraul. Eng. 2006, 132, 908–915. [Google Scholar] [CrossRef]
- Pfister, M.; Hager, W.H. Chute aerators I: Air transport characteristics. J. Hydraul. Eng. 2010, 136, 352–359. [Google Scholar] [CrossRef]
- Pfister, M.; Hager, W.H. Chute aerators II: Hydraulic design. J. Hydraul. Eng. 2010, 136, 360–367. [Google Scholar] [CrossRef]
- Bai, R.D.; Zhang, F.X.; Wang, W.; Liu, S.J. Air entrainment and detrainment downstream of a chute aerator. J. Hydrodyn. 2019, 31, 76–82. [Google Scholar] [CrossRef]
- Bai, R.D.; Liu, S.J.; Tian, Z.; Wang, W.; Zhang, F. Experimental investigation of bubbly flow and air entrainment discharge downstream of chute aerators. Environ. Fluid Mech. 2019, 19, 1455–1468. [Google Scholar] [CrossRef]
- Kramer, M.; Felder, S.; Hohermuth, B.; Valero, D. Drag reduction in aerated chute flow: Role of bottom air concentration. J. Hydraul. Eng. 2021, 147, 04021041. [Google Scholar] [CrossRef]
- Peterka, A.J. The effect of entrained air on cavitation pitting. In International Hydraulics Convention, Minneapolis; American Society of Civil Engineers: New York, NY, USA, 1953; pp. 507–518. [Google Scholar]
- Chen, X.P.; Deng, J.; Wei, W.R. Development and Application of the velocimeter using air concentration probe of needle–type. In Proceedings of the 16th National Conference of Hydrodynamics/The 32nd National Conference on Hydrodynamics, Wuxi, China, 30 October 2021; pp. 629–635. (In Chinese). [Google Scholar]
- Wei, W.R.; Xu, W.L.; Deng, J.; Guo, Y. Free surface air entrainment and single–bubble movement in supercritical open–channel flow. J. Hydraul. Eng. 2020, 146, 04020050. [Google Scholar] [CrossRef]
- Wang, Y.M.; Deng, J.; Wei, W.R. Investigation on the cavity backwater of chute aerators under various atmospheric pressures. Water 2022, 14, 1513. [Google Scholar] [CrossRef]
- Wu, J.H.; Zhou, Y.; Ma, F. Air entrainment of hydraulic jump aeration basin. J. Hydrodyn. 2019, 30, 962–965. [Google Scholar] [CrossRef]
- Rutschmann, P. Belüftungseinbauten in Schussrinnen [Chute Additions for Air Entrainment]; Mitteilung, D.V., Ed.; ETH–Laboratory of Hydraulics, Hydrology and Glaciology (VAW): Zurich, Switzerland, 1988; p. 97. (In German) [Google Scholar]
- Chanson, H. Study of Air Entrainment and Aeration Devices on Spillway Model. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 1988. [Google Scholar]
- Kökpınar, M.A.; Göğüş, M. High–speed jet flows over spillway aerators. Can. J. Civ. Eng. 2002, 29, 885–898. [Google Scholar] [CrossRef]
- Wei, W.R.; Deng, J.; Zhang, F.X.; Tian, Z. A numerical model for air concentration distribution in self−aerated open channel flows. J. Hydrodyn. 2015, 27, 394–402. [Google Scholar] [CrossRef]
- Aydin, M.C. Aeration efficiency of bottom-inlet aerators for spilways. ISH J. Hydraul. Eng. 2017, 24, 330–336. [Google Scholar] [CrossRef]
- Pfister, M.; Chanson, H. Discussion of scale effects in physical hydraulic engineering models. J. Hydraul. Res. 2012, 50, 244–246. [Google Scholar] [CrossRef]
- Wang, H.; Liu, X.C.; Bai, R.D.; Liu, S. Modified bottom air entrainment estimate by chute offset aerator. J. Hydraul. Eng. 2020, 146, 06020016. [Google Scholar] [CrossRef]
- Wang, H.; Liu, X.; Bai, R.; Liu, S. Bubble characteristics affecting air−water exchange in open–channel flow with a jet forming over a sudden bottom drop. Exp. Therm. Fluid Sci. 2021, 124, 110366. [Google Scholar] [CrossRef]
- Luo, J.; Xu, W.L.; Khoo, B. Stratification effect of air bubble on the shock wave from the collapse of cavitation bubble. J. Fluid Mech. 2021, 919, A16. [Google Scholar] [CrossRef]
- Wei, W.R.; Xu, W.L.; Deng, J.; Tian, Z.; Zhang, F.X. Experimental study of air−water interface properties in self−aerated flows. J. Hydrodyn. 2019, 31, 940–948. [Google Scholar] [CrossRef]
- Rasmussen, R.E.H. Some experiments on cavitation erosion in water mixed with air. In Proceedings of the International Symposium on Cavitation in Hydrodynamics; National Physical Laboratory: London, UK, 1956; pp. 1–25. [Google Scholar]
- Wang, X.; Hu, Y.A.; Zhang, J.M. Experimental study on anti−cavitation mechanism of valve lintel natural aeration of high head lock. J. Hydrodyn. 2019, 32, 337–344. [Google Scholar] [CrossRef]
- Chanson, H. Turbulent air–water flows in hydraulic structures: Dynamic similarity and scale effects. Environ. Fluid Mech. 2009, 9, 125–142. [Google Scholar] [CrossRef]
- Boes, R.M. Scale effects in modelling two−phase stepped spillway flow. In Hydraulics of Stepped Spillways; Minor, H.E., Hager, W.H., Eds.; Balkema: Rotterdam, The Netherlands, 2000; pp. 53–60. [Google Scholar]
- Pinto, N.L. Model evaluation of aerators in shooting flow. In Scale Effects in Modelling Hydraulic Structures; Kobus, H., Ed.; Technische Akademie: Esslingen, Germany, 1984; Volume 4, pp. 1–6. [Google Scholar]
- Ge, M.M.; Sun, C.Y.; Zhang, X.L.; Coutier-Delgosha, O.; Zhang, G. Synchrotron X-ray based particle image velocimetry to measure multiphase streamflow and densitometry. Radiat. Phys. Chem. 2022, 200, 110395. [Google Scholar] [CrossRef]


| Name | Elevation (m) | Dam Height (m) | Atmospheric Pressure (hPa) | η (%) | Country |
|---|---|---|---|---|---|
| Three Gorges Hydroelectric Power Station | 185.00 | 175 | 991 | 2.5 | China |
| Xiluodu Hydropower Plant | 380.00 | 285.5 | 968 | 5 | China |
| Diga del Vajont | 722.50 | 262 | 929 | 9.3 | Italy |
| Nuozhadu Hydropower Station | 812.00 | 261.5 | 919 | 10.4 | China |
| Tehri Dam | 815.00 | 260.5 | 919 | 10.4 | India |
| Baihetan Hydropower Station | 834.00 | 289 | 917 | 10.7 | China |
| Nurek Dams | 855.00 | 304 | 914 | 10.9 | Tajikistan |
| Xiaowan Hydropower Station | 1240.00 | 294.5 | 873 | 15.5 | China |
| Jinping-i Hydropower Station | 1880.00 | 305 | 807 | 22.8 | China |
| The Grande Dixence Dam | 2364.00 | 285 | 759 | 27.9 | The Swiss |
| Banduo Hydropower Station | 2760.00 | 79.7 | 722 | 31.8 | China |
| Lianghekou Hydropower Station | 2865.00 | 295 | 713 | 32.9 | China |
| Jiacha Hydropower Station | 3249.00 | 45.5 | 701 | 34.2 | China |
| Series | V [m/s] | H [m] | F0 | h [m] | Re | We (h) | Pa [hPa] |
|---|---|---|---|---|---|---|---|
| S1 | 3.72 | 1.00 | 3.76 | 0.1 | 3.7 × 105 | 138.02 | 60~960 |
| S2 | 4.67 | 1.50 | 4.71 | 0.1 | 4.6 × 105 | 172.90 | 60~960 |
| S3 | 5.05 | 1.80 | 5.10 | 0.1 | 5.0 × 105 | 187.21 | 60~960 |
| S4 | 5.52 | 2.00 | 5.57 | 0.1 | 5.5 × 105 | 204.47 | 60~960 |
| S5 | 6.18 | 2.40 | 6.24 | 0.1 | 6.1 × 105 | 229.06 | 60~960 |
| S6 | 3.90 | 1.00 | 4.40 | 0.08 | 3.1 × 105 | 129.21 | 60~960 |
| S7 | 4.57 | 1.50 | 5.16 | 0.08 | 3.6 × 105 | 151.53 | 60~960 |
| S8 | 5.67 | 2.00 | 6.40 | 0.08 | 4.5 × 105 | 187.95 | 60~960 |
| S9 | 5.88 | 2.40 | 6.64 | 0.08 | 4.7 × 105 | 195.00 | 60~960 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wei, W.; Song, T.; Deng, J. Air Entrainment of Chute Aerators Under Different Atmospheric Pressures. Water 2025, 17, 2734. https://doi.org/10.3390/w17182734
Wang Y, Wei W, Song T, Deng J. Air Entrainment of Chute Aerators Under Different Atmospheric Pressures. Water. 2025; 17(18):2734. https://doi.org/10.3390/w17182734
Chicago/Turabian StyleWang, Yameng, Wangru Wei, Tantao Song, and Jun Deng. 2025. "Air Entrainment of Chute Aerators Under Different Atmospheric Pressures" Water 17, no. 18: 2734. https://doi.org/10.3390/w17182734
APA StyleWang, Y., Wei, W., Song, T., & Deng, J. (2025). Air Entrainment of Chute Aerators Under Different Atmospheric Pressures. Water, 17(18), 2734. https://doi.org/10.3390/w17182734







