Water Demand Prediction Model of University Park Based on BP-LSTM Neural Network
Abstract
1. Introduction
2. Data Presentation and Evaluation Method
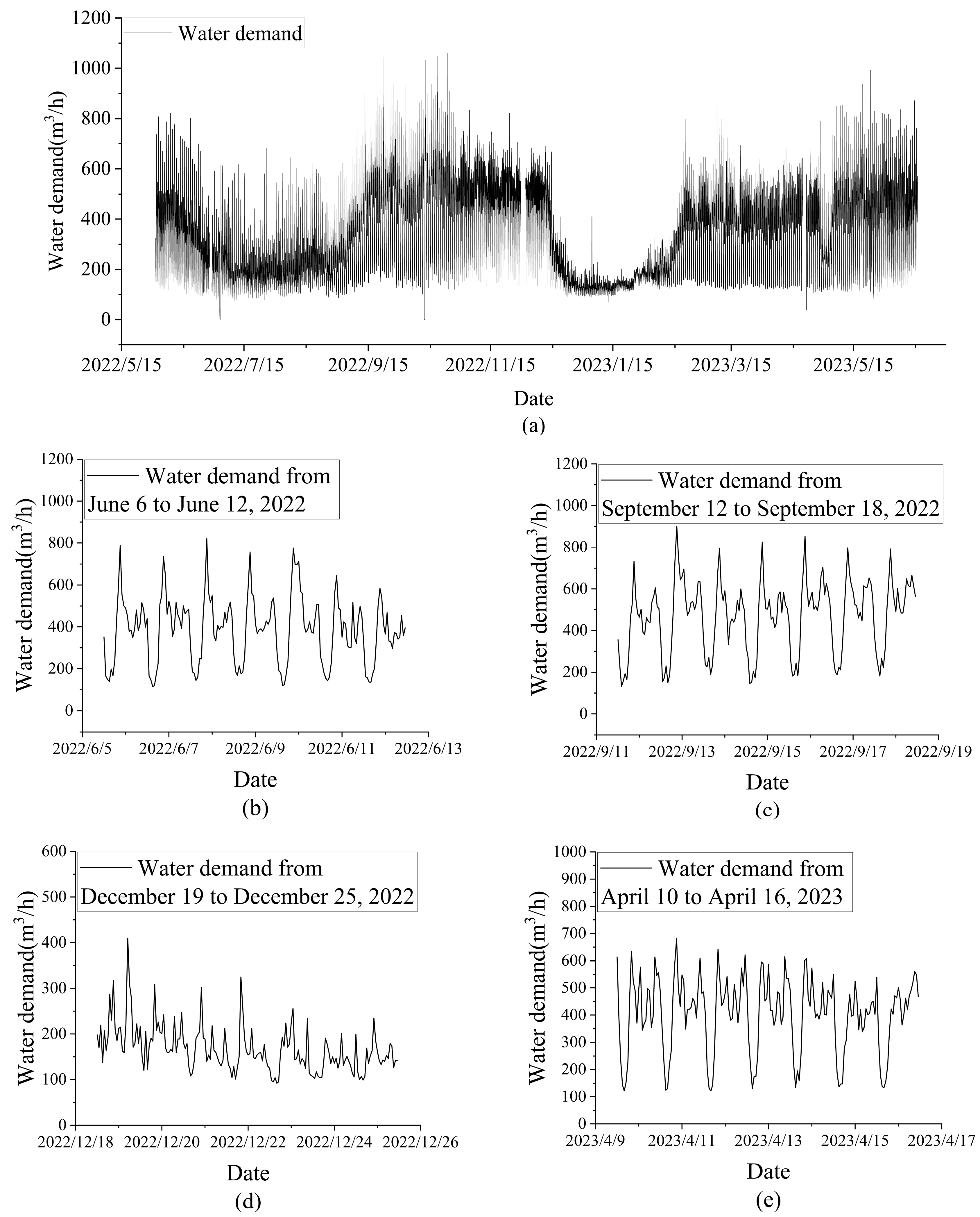
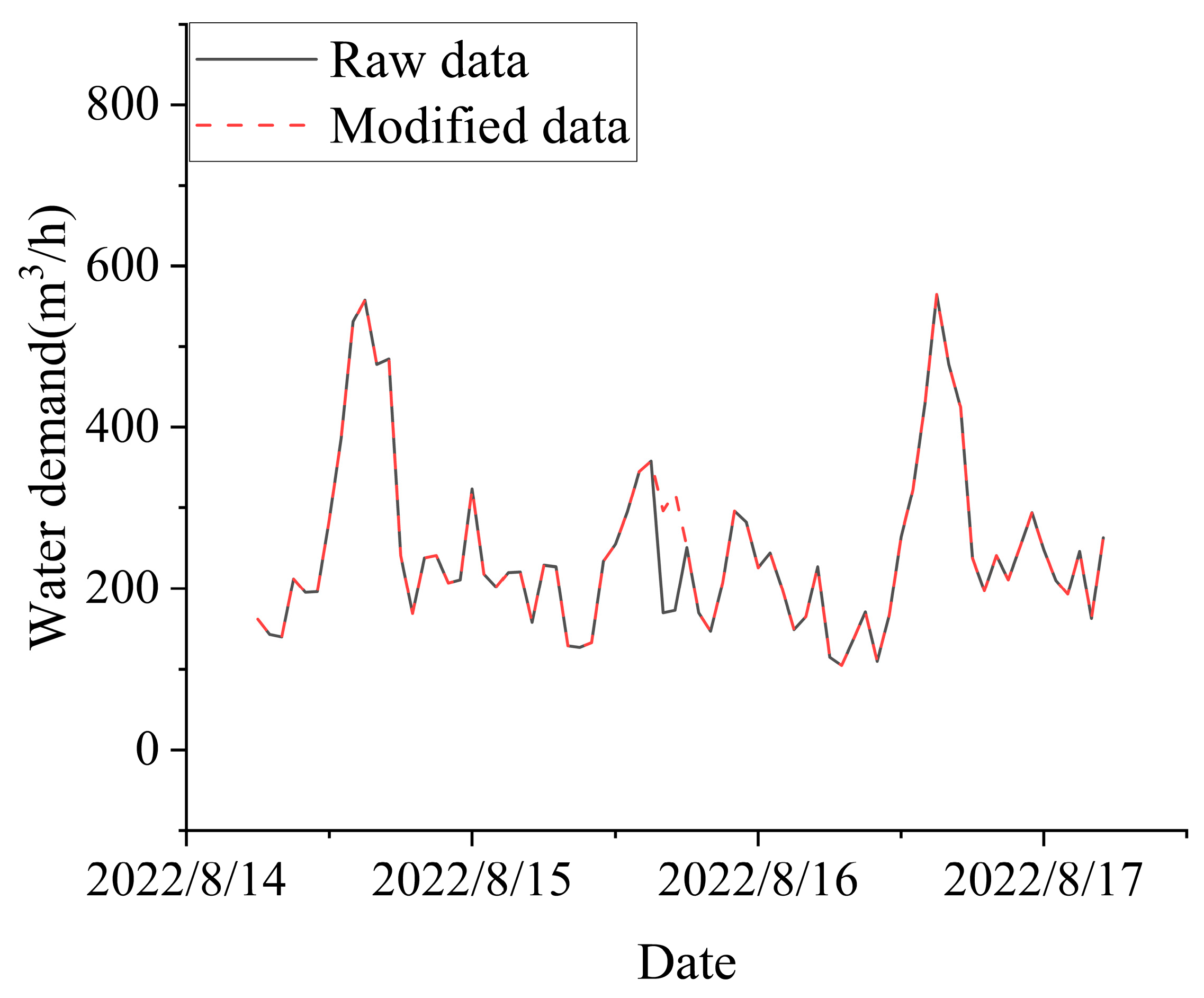
2.1. Data Processing
2.2. Data Analysis
2.2.1. Fast Fourier Transform
2.2.2. Difference and ADF Tests
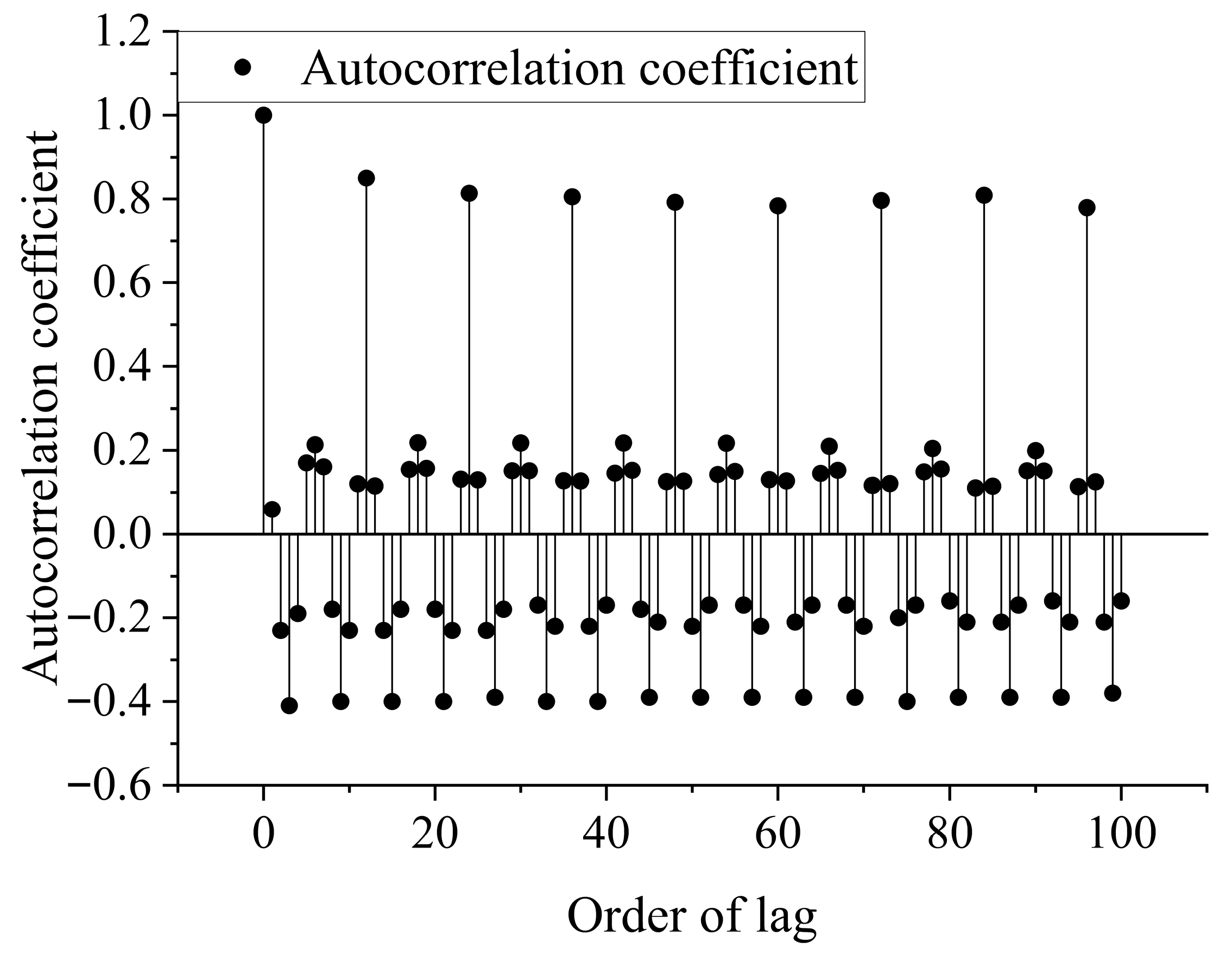
2.2.3. Autocorrelation Coefficient Calculation
3. Model and Method
3.1. Seasonal Autoregressive Differential Moving Average Model
3.2. BP-LSTM Combined Model
3.2.1. BP Neural Network
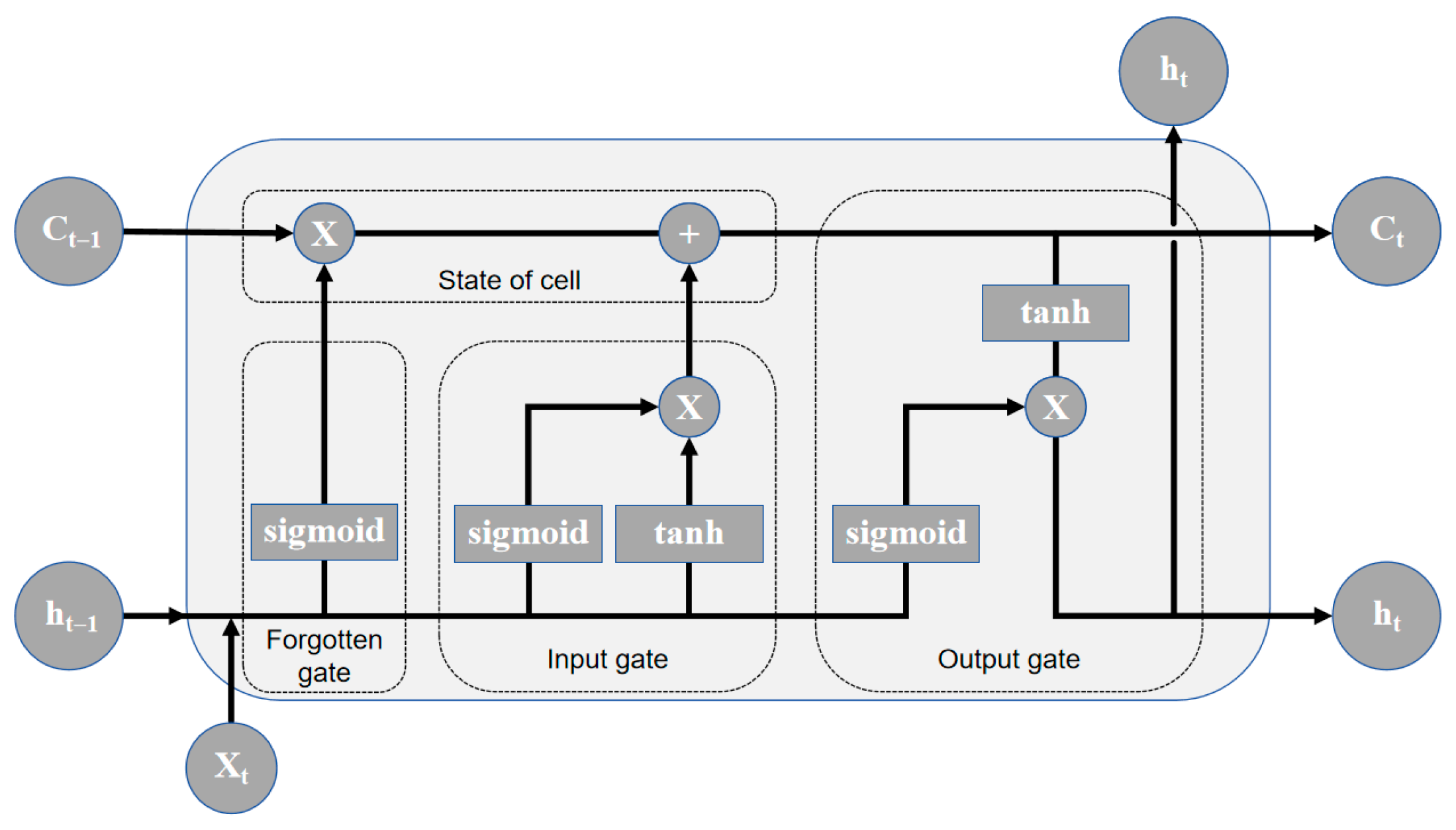
3.2.2. LSTM Neural Network
3.2.3. Ensemble Design
3.3. Determine the Hyperparameters of the Model
3.3.1. SARIMA Model Parameters Determination
3.3.2. BP-LSTM Model Parameters Determination
4. Results and Discussion
4.1. Model Evaluation Metrics
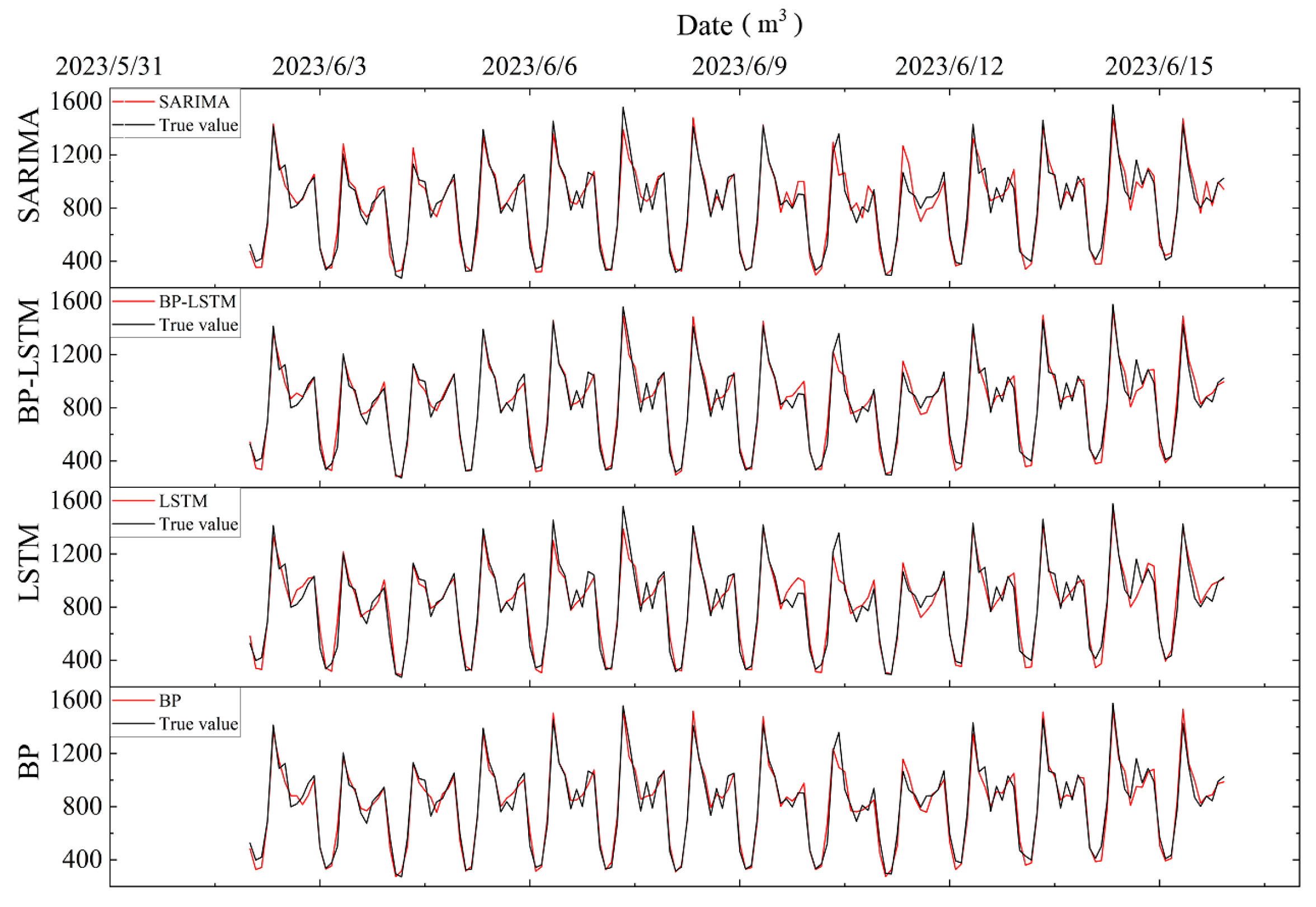
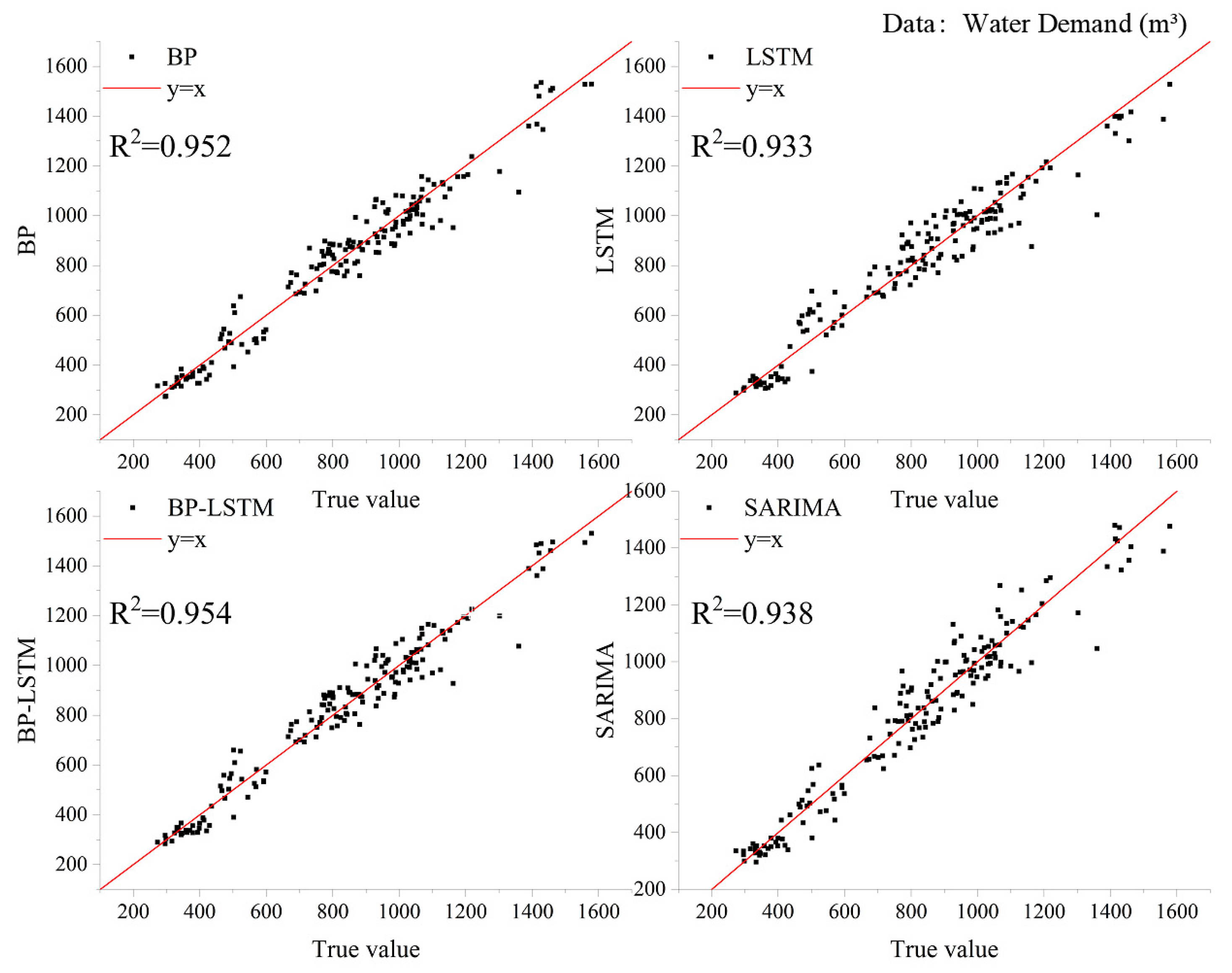
4.2. Forecasting Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shah, W.; Chen, J.; Ullah, I.; Shah, M.H.; Ullah, I. Application of RNN-LSTM in Predicting Drought Patterns in Pakistan: A Pathway to Sustainable Water Resource Management. Water 2024, 16, 1492. [Google Scholar] [CrossRef]
- Mu, L.; Zheng, F.; Tao, R.; Zhang, Q.; Kapelan, Z. Hourly and Daily Urban Water Demand Predictions Using a Long Short-Term Memory Based Model. J. Water Resour. Plan. Manag. 2020, 146, 05020017. [Google Scholar] [CrossRef]
- Howe, C.W.; Linaweaver, F.P. The Impact of Price on Residential Water Demand and Its Relation to System Design and Price Structure. Water Resour. Res. 1967, 3, 13–32. [Google Scholar] [CrossRef]
- Miaou, S. A Stepwise Time Series Regression Procedure for Water Demand Model Identification. Water Resour. Res. 1990, 26, 1887–1897. [Google Scholar] [CrossRef]
- Xue, X.H.; Xue, X.F.; Xu, L. Study on Improved PCA-SVM Model for Water Demand Prediction. Adv. Mat. Res. 2012, 591–593, 1320–1324. [Google Scholar] [CrossRef]
- Zhou, S.; Guo, S.; Du, B.; Huang, S.; Guo, J. A Hybrid Framework for Multivariate Time Series Forecasting of Daily Urban Water Demand Using Attention-Based Convolutional Neural Network and Long Short-Term Memory Network. Sustainability 2022, 14, 11086. [Google Scholar] [CrossRef]
- Chen, J.; Boccelli, D.L. Forecasting Hourly Water Demands with Seasonal Autoregressive Models for Real-Time Application. Water Resour. Res. 2018, 54, 879–894. [Google Scholar] [CrossRef]
- Chen, G.; Long, T.; Xiong, J.; Bai, Y. Multiple Random Forests Modelling for Urban Water Consumption Forecasting. Water Resour. Manag. 2017, 31, 4715–4729. [Google Scholar] [CrossRef]
- Iwakin, O.; Moazeni, F. Improving Urban Water Demand Forecast Using Conformal Prediction-Based Hybrid Machine Learning Models. J. Water Process Eng. 2024, 58, 104721. [Google Scholar] [CrossRef]
- Fu, G.; Jin, Y.; Sun, S.; Yuan, Z.; Butler, D. The Role of Deep Learning in Urban Water Management: A Critical Review. Water Res. 2022, 223, 118973. [Google Scholar] [CrossRef] [PubMed]
- Donkor, E.A.; Mazzuchi, T.A.; Soyer, R.; Roberson, J.A. Urban Water Demand Forecasting: Review of Methods and Models. J. Water Resour. Plan. Manag. 2014, 140, 146–159. [Google Scholar] [CrossRef]
- Liu, X.; Sang, X.; Chang, J.; Zheng, Y. Multi-Model Coupling Water Demand Prediction Optimization Method for Megacities Based on Time Series Decomposition. Water Resour. Manag. 2021, 35, 4021–4041. [Google Scholar] [CrossRef]
- Wang, T. Zhenjiang June 2022 Historical Weather. 2022. Available online: https://lishi.tianqi.com/zhenjiang/202206.html (accessed on 20 August 2025).
- China Meteorological Administration. Official Website. Available online: https://www.cma.gov.cn/ (accessed on 20 August 2025).
- Huang, H.; Zhang, Z.; Song, F. An Ensemble-Learning-Based Method for Short-Term Water Demand Forecasting. Water Resour. Manag. 2021, 35, 1757–1773. [Google Scholar] [CrossRef]
- Ghiassi, M.; Zimbra, D.K.; Saidane, H. Urban Water Demand Forecasting with a Dynamic Artificial Neural Network Model. J. Water Resour. Plan. Manag. 2008, 134, 138–146. [Google Scholar] [CrossRef]
- Wang, K.; Xie, X.; Liu, B.; Yu, J.; Wang, Z. Reliable Multi-Horizon Water Demand Forecasting Model: A Temporal Deep Learning Approach. Sustain. Cities Soc. 2024, 112, 105595. [Google Scholar] [CrossRef]
- Szostek, K.; Mazur, D.; Drałus, G.; Kusznier, J. Analysis of the Effectiveness of ARIMA, SARIMA, and SVR Models in Time Series Forecasting: A Case Study of Wind Farm Energy Production. Energies 2024, 17, 4803. [Google Scholar] [CrossRef]
- Guo, G.; Liu, S.; Wu, Y.; Li, J.; Zhou, R.; Zhu, X. Short-Term Water Demand Forecast Based on Deep Learning Method. J. Water Resour. Plan. Manag. 2018, 144, 04018076. [Google Scholar] [CrossRef]
- Wang, Y.; Qin, L.; Wang, Q.; Chen, Y.; Yang, Q.; Xing, L.; Ba, S. A Novel Deep Learning Carbon Price Short-Term Prediction Model with Dual-Stage Attention Mechanism. Appl. Energy 2023, 347, 121380. [Google Scholar] [CrossRef]
- Almanjahie, I.M.; Chikr-Elmezouar, Z.; Bachir, A. Modeling and Forecasting the Household Water Consumption in Saudi Arabia. Appl. Ecol. Environ. Res. 2019, 17, 1299–1309. [Google Scholar] [CrossRef]
- Tian, Y.; Wu, Q.; Zhang, Y. A Convolutional Long Short-Term Memory Neural Network Based Prediction Model. Int. J. Comput. Commun. Control 2020, 15, 3906. [Google Scholar] [CrossRef]
- Wu, J.; Wang, Z.; Dong, L. Prediction and Analysis of Water Resources Demand in Taiyuan City Based on Principal Component Analysis and BP Neural Network. J. Water Supply Res. Technol.-Aqua 2021, 70, 1272–1286. [Google Scholar] [CrossRef]
- Tang, Z.Q.; Liu, G.; Xu, W.N.; Xia, Z.Y.; Xiao, H. Water Demand Forecasting in Hubei Province with BP Neural Network Model. Adv. Mat. Res. 2012, 599, 701–704. [Google Scholar] [CrossRef]
- Zou, S.; Ren, X.; Wang, C.; Wei, J. Impacts of Temporal Resolution and Spatial Information on Neural-Network-Based PM2.5 Prediction Model. Acta Sci. Nat. Univ. Pekin. 2020, 56, 417–426. [Google Scholar]
- Kavya, M.; Mathew, A.; Shekar, P.R.; Sarwesh, P. Short Term Water Demand Forecast Modelling Using Artificial Intelligence for Smart Water Management. Sustain. Cities Soc. 2023, 95, 104610. [Google Scholar] [CrossRef]
- Du, B.; Zhou, Q.; Guo, J.; Guo, S.; Wang, L. Deep Learning with Long Short-Term Memory Neural Networks Combining Wavelet Transform and Principal Component Analysis for Daily Urban Water Demand Forecasting. Expert. Syst. Appl. 2021, 171, 114571. [Google Scholar] [CrossRef]
- Hu, P.; Tong, J.; Wang, J.; Yang, Y.; Oliveira Turci, L. de A Hybrid Model Based on CNN and Bi-LSTM for Urban Water Demand Prediction. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; IEEE: New York, NY, USA; pp. 1088–1094. [Google Scholar]
- Cao, K.; Kim, H.; Hwang, C.; Jung, H. CNN-LSTM Coupled Model for Prediction of Waterworks Operation Data. J. Inf. Process. Syst. 2018, 14, 1508–1520. [Google Scholar] [CrossRef]
- Hu, S.; Gao, J.; Zhong, D.; Deng, L.; Ou, C.; Xin, P. An Innovative Hourly Water Demand Forecasting Preprocessing Framework with Local Outlier Correction and Adaptive Decomposition Techniques. Water 2021, 13, 582. [Google Scholar] [CrossRef]
- Xenochristou, M.; Kapelan, Z. An Ensemble Stacked Model with Bias Correction for Improved Water Demand Forecasting. Urban Water J. 2020, 17, 212–223. [Google Scholar] [CrossRef]
- Stańczyk, J.; Kajewska-Szkudlarek, J.; Lipiński, P.; Rychlikowski, P. Improving Short-Term Water Demand Forecasting Using Evolutionary Algorithms. Sci. Rep. 2022, 12, 13522. [Google Scholar] [CrossRef]

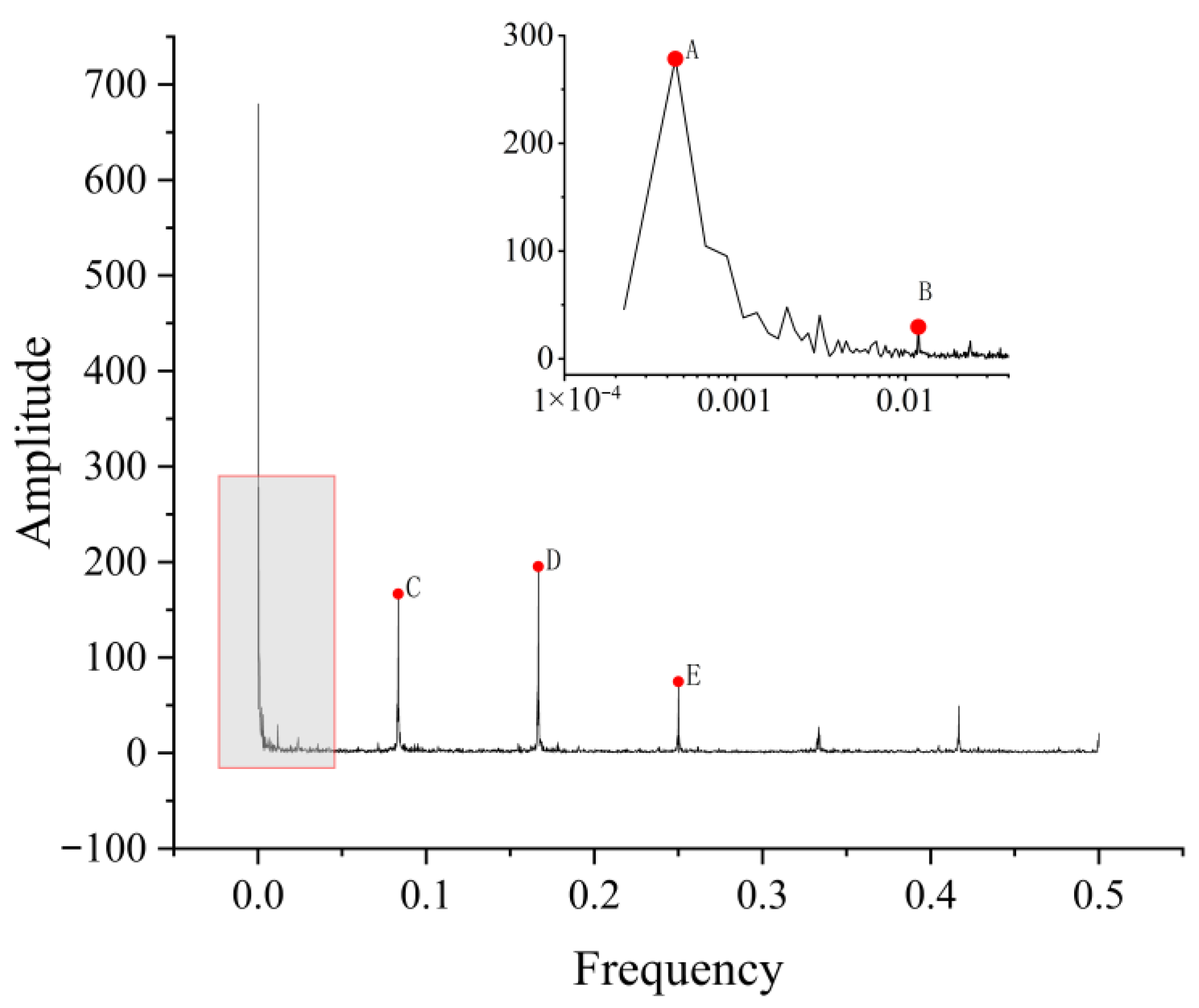



| A | B | C | D | E | |
|---|---|---|---|---|---|
| Period | 186 days | 7 days | 24 h | 12 h | 8 h |
| T-Value | p-Value | Statistical Values for Varying Degrees of Rejection of the Null Hypothesis | |||
|---|---|---|---|---|---|
| 1% | 5% | 10% | |||
| Raw date | −1.92 | 0.32 | −3.43 | −2.86 | −2.57 |
| First-order difference | −19.56 | 0 | −3.43 | −2.86 | −2.57 |
| Second-order difference | −25.89 | 0 | −3.43 | −2.86 | −2.57 |
| Name | Value | Name | Value |
|---|---|---|---|
| The data of the previous week | 1283 | Month | 6 |
| The data of the previous day | 1272 | Date | 8 |
| The data of the previous hour | 450 | Day of week | 5 |
| … | Hours of day | 3 | |
| Data of the previous 12 h | 501 | Maximum temperature | 31 |
| Wind speed | 3 | Minimum temperature | 18 |
| Number of Hidden Layers | The Number of Neurons in Each Hidden Layer | Learning Rate | Batch Size | |
|---|---|---|---|---|
| BP neural network | 3 | (64, 64, 16) | 2.5 × 10−4 | 64 |
| LSTM neural network | 2 | (128, 128) | 10−4 | 32 |
| BP-LSTM neural network | 2 | (16, 8) | 10−5 | 32 |
| SARIMA | BP | LSTM | BP-LSTM | |
|---|---|---|---|---|
| R2 | 0.938 | 0.952 | 0.933 | 0.954 |
| RMSE (m3) | 75.50 | 66.71 | 78.18 | 65.05 |
| MAPE | 7.41% | 6.78% | 7.70% | 6.48% |
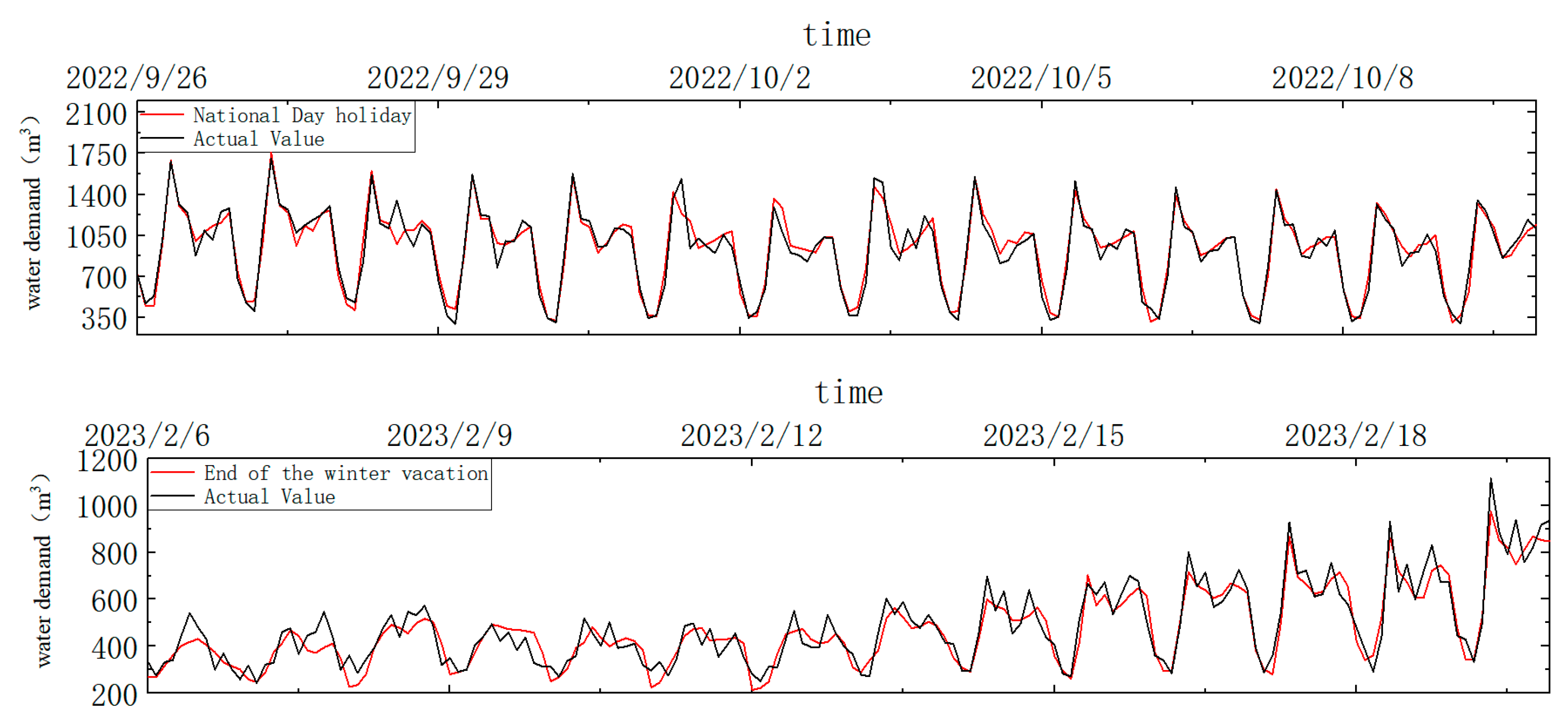
| Backtesting Interval | Number of Data Points | |
|---|---|---|
| National Day | 26 September to 9 October 2022 | 168 |
| Winter Break End | 6 February to 19 February 2023 | 168 |
| R2 | RMSE (m3) | MAPE | |
|---|---|---|---|
| National Day | 0.939 | 6.84 | 2.77 |
| Winter Break End | 0.880 | 1.27 | 5.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, H.; Lv, H.; Yang, Y.; Zhao, R. Water Demand Prediction Model of University Park Based on BP-LSTM Neural Network. Water 2025, 17, 2729. https://doi.org/10.3390/w17182729
Yu H, Lv H, Yang Y, Zhao R. Water Demand Prediction Model of University Park Based on BP-LSTM Neural Network. Water. 2025; 17(18):2729. https://doi.org/10.3390/w17182729
Chicago/Turabian StyleYu, Hanzhi, Hao Lv, Yuhang Yang, and Ruijie Zhao. 2025. "Water Demand Prediction Model of University Park Based on BP-LSTM Neural Network" Water 17, no. 18: 2729. https://doi.org/10.3390/w17182729
APA StyleYu, H., Lv, H., Yang, Y., & Zhao, R. (2025). Water Demand Prediction Model of University Park Based on BP-LSTM Neural Network. Water, 17(18), 2729. https://doi.org/10.3390/w17182729






