Temperature Trends and Seasonality in Neritic and Transitional Waters of the Southern Bay of Biscay from 1998 to 2023
Abstract
1. Introduction
- (a)
- To identify distinct water mass clusters based on temperature variability similarities.
- (b)
- To describe long-term water temperature trends and assess rates of change.
- (c)
- To establish seasonal patterns, phenological changes, and seasonal and monthly differences in interannual temperature variations.
- (d)
- To determine the relationship of air temperature, river flow, and upwelling with water temperature variability at the different spatial and temporal scales studied.
- (e)
- To assess the role of estuarine morphology in shaping thermal conditions in the estuaries under study.
2. Materials and Methods
2.1. Study Area
2.2. Data Acquisition
2.3. Data Selection
2.4. Data Processing
3. Results
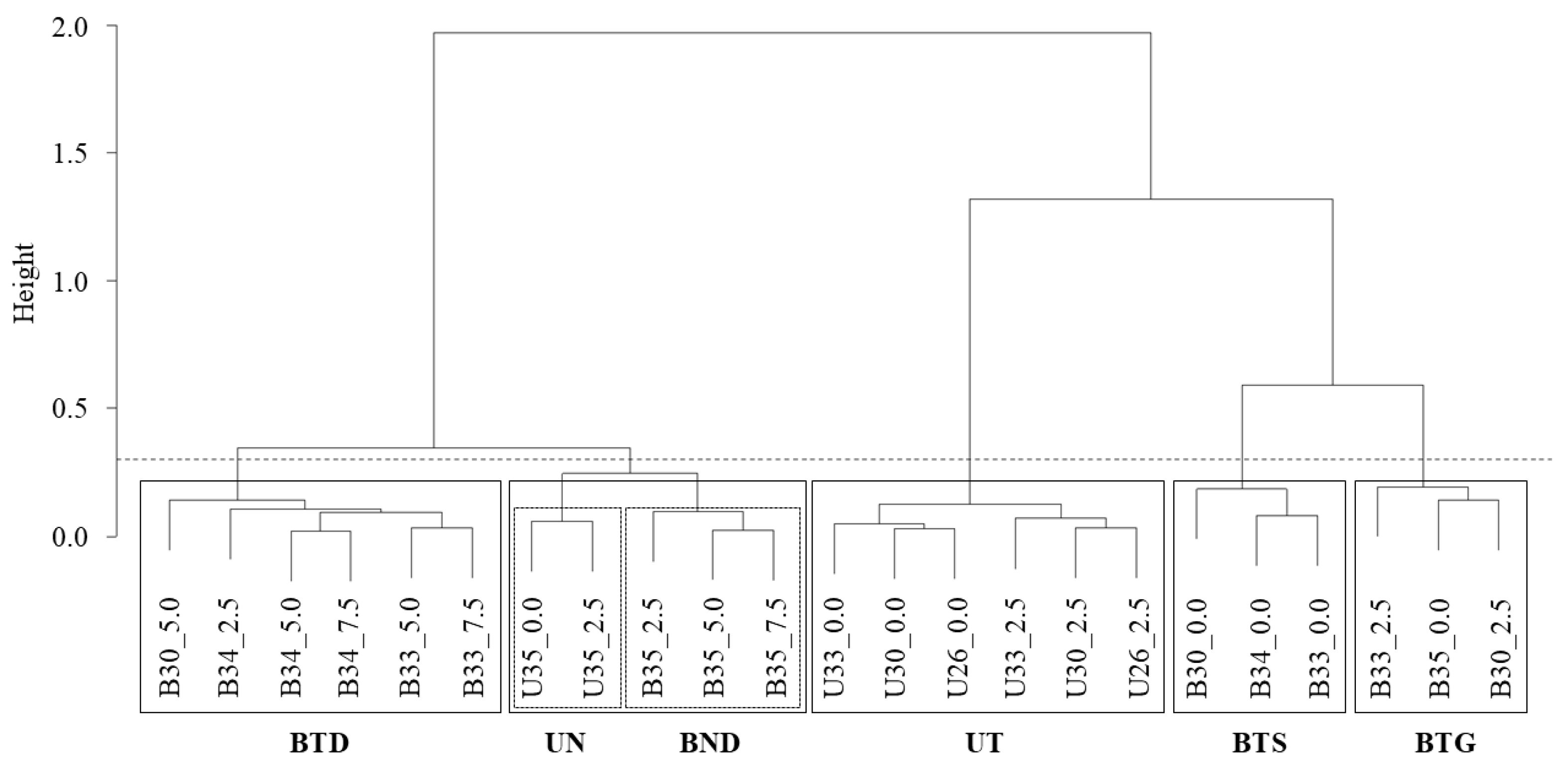
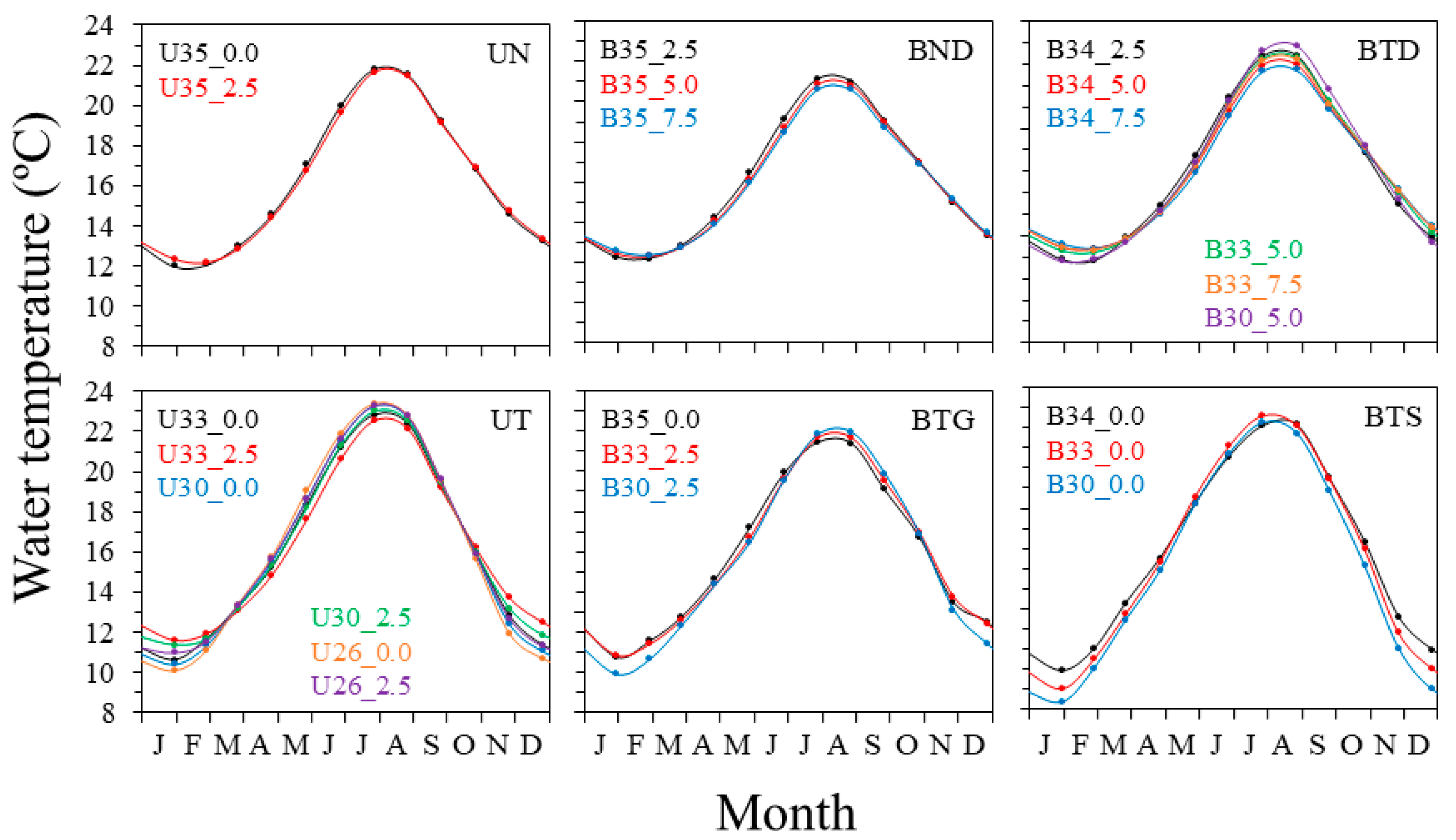
3.1. Water Temperature Time-Series Clustering
- (1)
- BTD (Bilbao-Transitional-Deep). It includes time series from the intermediate and inner (transitional) waters of the estuary of Bilbao, specifically from below the halocline (deep). This water mass cluster comprises data from 2.5, 5.0, and 7.5 m depths at the 34 salinity site; 5.0 and 7.5 m at the 33 salinity site; and 5.0 m at the 30 salinity site.
- (2)
- UN (Urdaibai-Neritic). It includes time series from the neritic waters of the 35 salinity site (both surface and 2.5 m depths) of the estuary of Urdaibai.
- (3)
- BND (Bilbao-Neritic-Deep). It includes time series from the outer zone (neritic) of the estuary of Bilbao, specifically from below the halocline (deep). This group comprises data from 2.5, 5.0, and 7.5 m at the 35 salinity site.
- (4)
- UT (Urdaibai-Transitional). It includes time series from the transitional waters of the estuary of Urdaibai, comprising data from surface and 2.5 m depths at the 33, 30, and 26 salinity sites.
- (5)
- BTS (Bilbao-Transitional-Surface). It includes time series from the intermediate and inner (transitional) surface waters of the estuary of Bilbao. The group comprises data from 0.0 m depth at the 34, 33, and 30 salinity sites.
- (6)
- BTG (Bilbao-Transitional-Gradient). It is a mixed group from the estuary of Bilbao, which includes the time series from the 35 salinity site at the surface and the 33 and 30 salinity sites at 2.5 m depth.
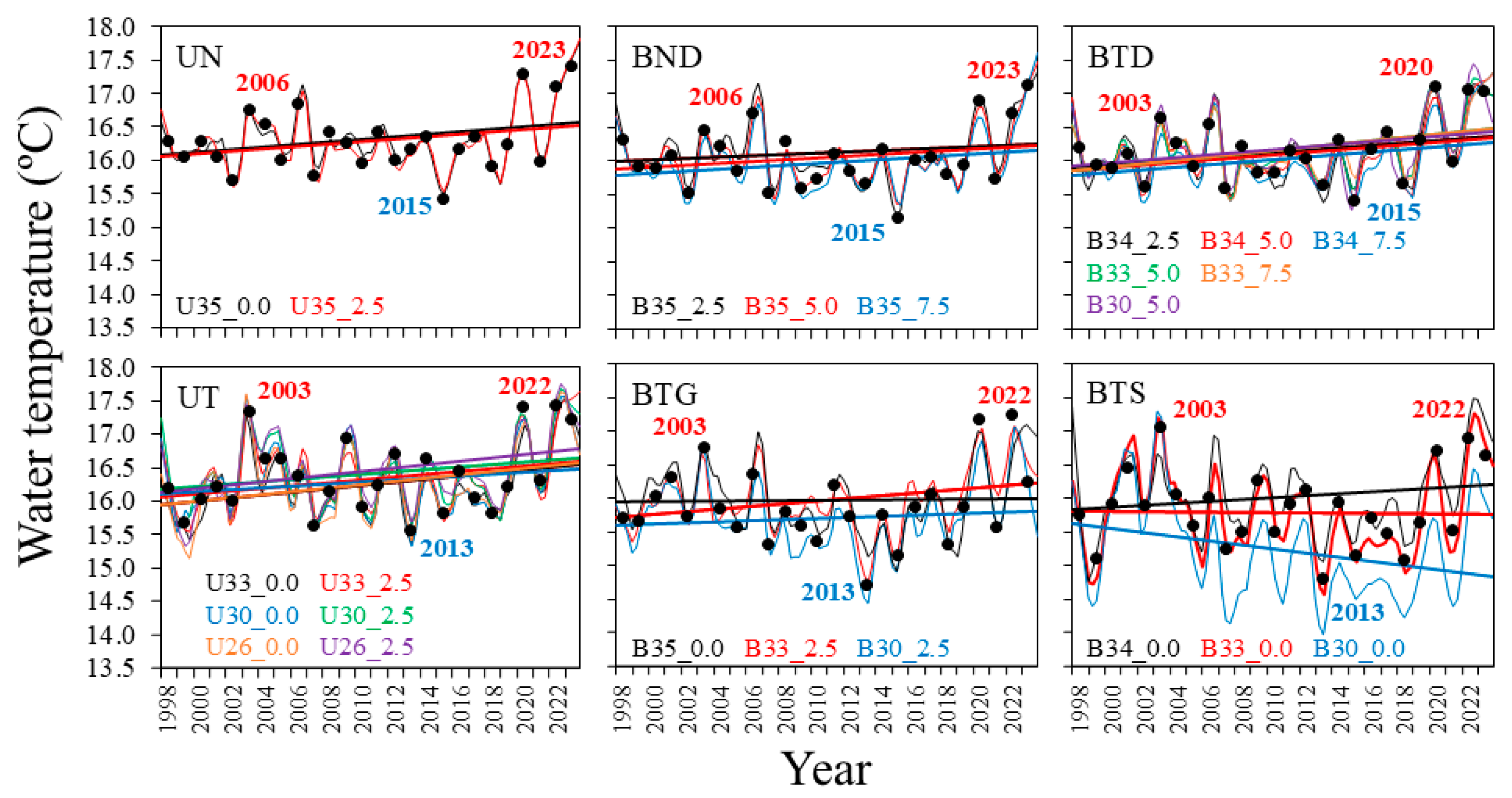
3.2. Interannual Trends in Water Temperature Across Water Masses
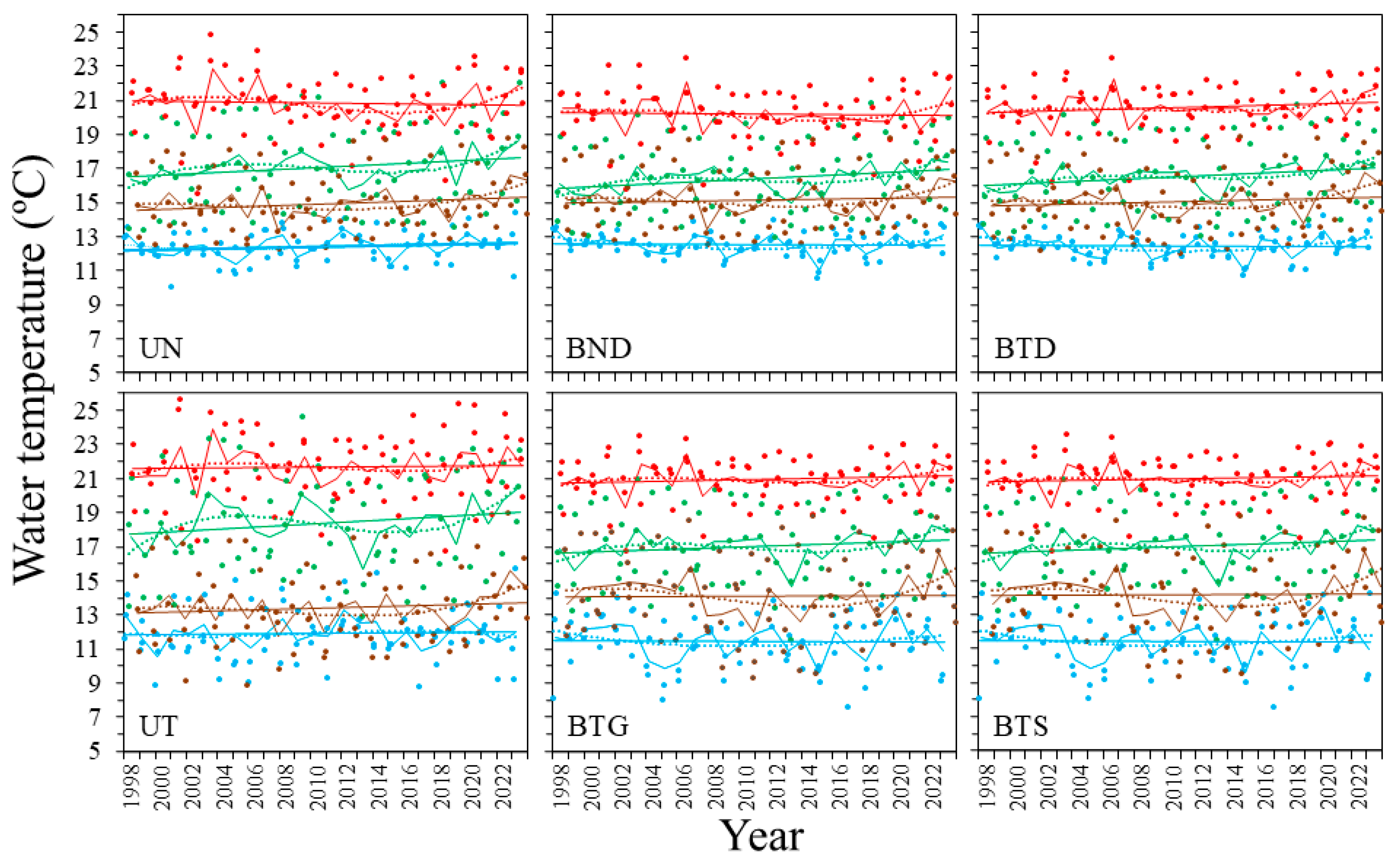
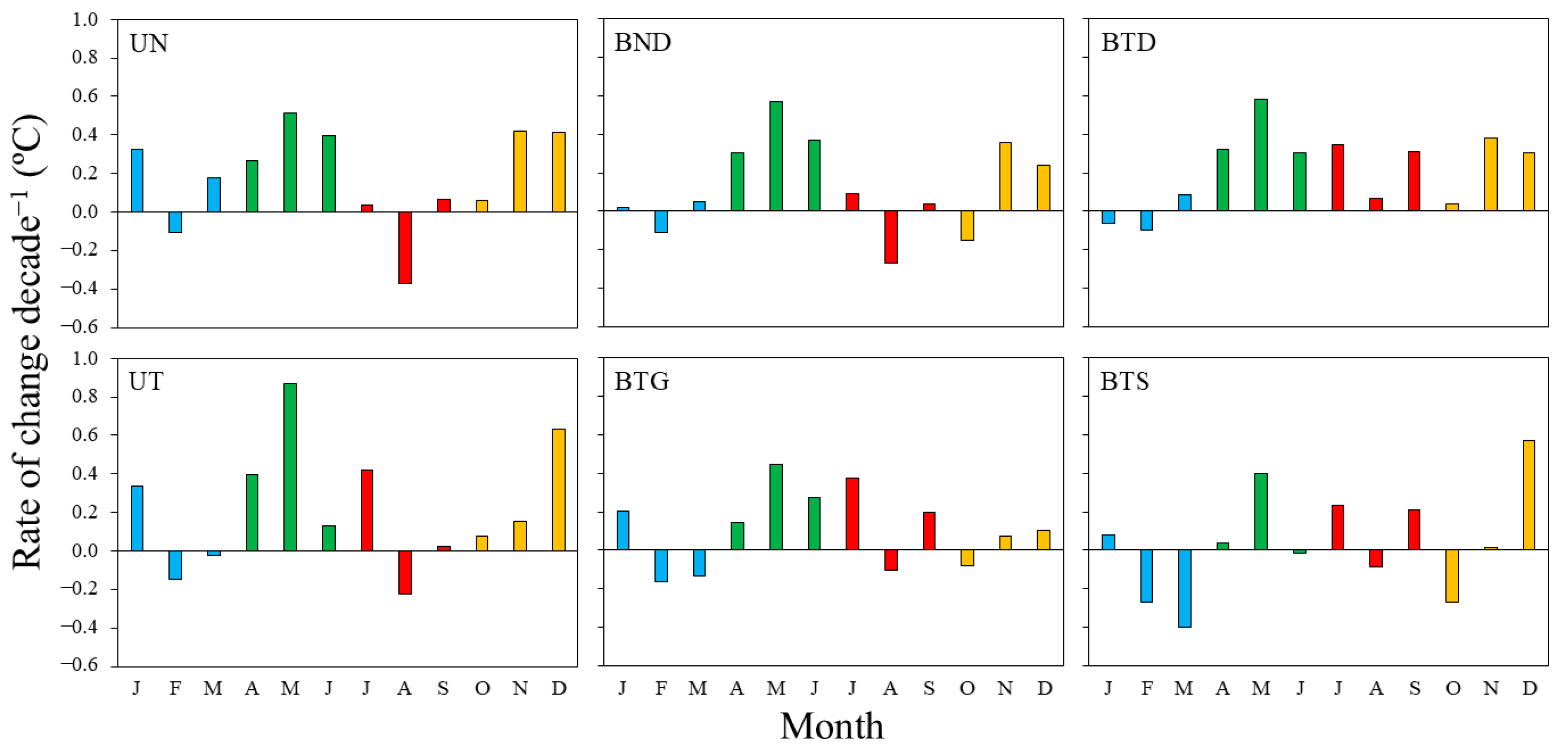
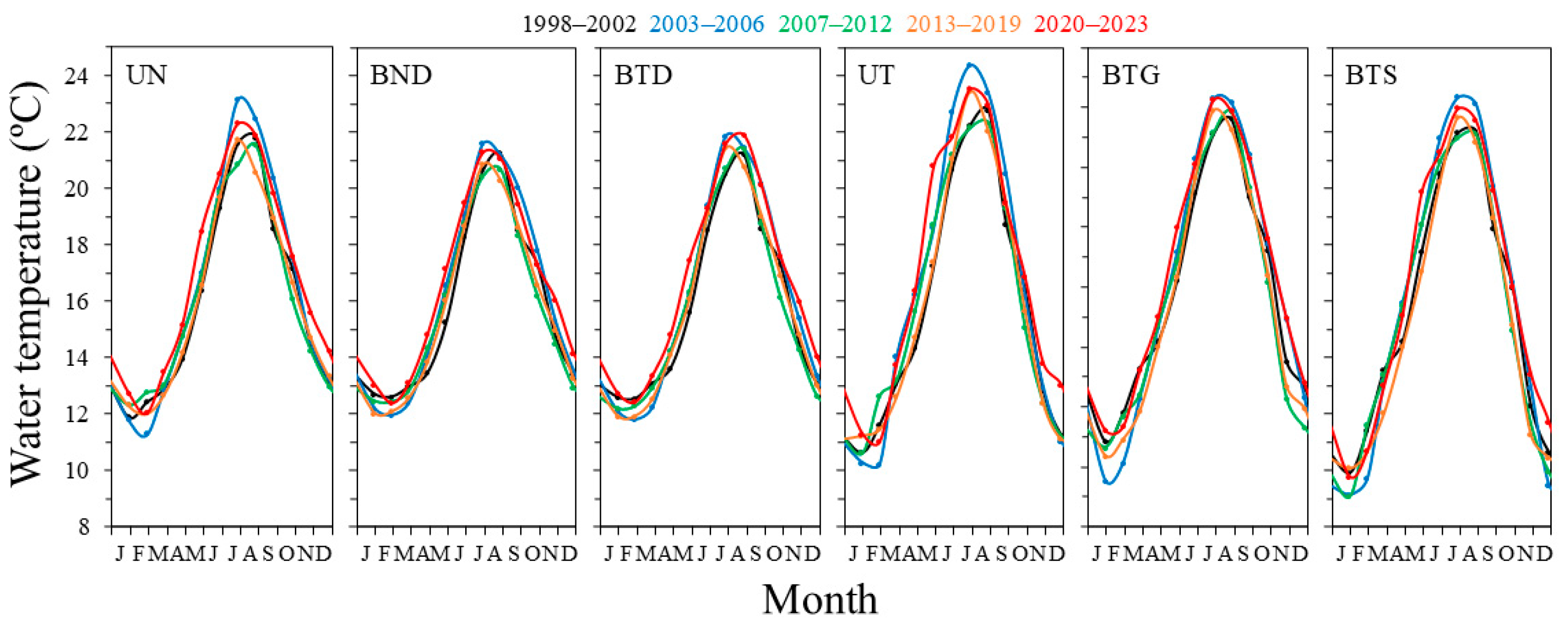
3.3. Seasonal Patterns in Water Temperature Across Water Masses
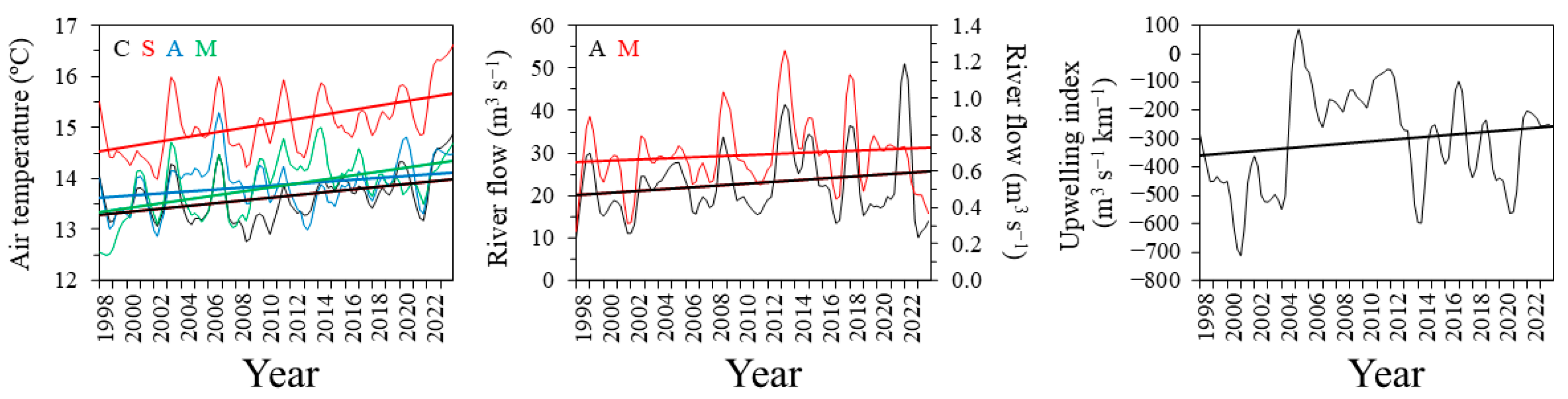
3.4. Relationship of Water Temperature with Environmental Factors
4. Discussion
4.1. Differences in Thermal Environments
4.2. Long-Term Temperature Trends and Change Rates
4.3. Temperature Trends and Change Rates at Intra-Annual Scales
4.4. Interannual Patterns
4.5. Seasonal Patterns
4.6. Relationships with Local Climate and Hydrographic Factors
4.7. Ecological Effects
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Waldock, C.; Dornelas, M.; Bates, A.E. Temperature-driven biodiversity change: Disentangling space and time. BioScience 2018, 68, 873–884. [Google Scholar] [CrossRef]
- Bütikofer, L.; Anderson, K.; Bebber, D.P.; Bennie, J.; Early, R.; Maclean, I.M.D. The problem of scale in predicting biological responses to climate. Glob. Change Biol. 2020, 26, 6657–6666. [Google Scholar] [CrossRef]
- Arroyo, J.I.; Díez, B.; Kempes, C.P.; West, G.B.; Marquet, P.A. A general theory for temperature dependence in biology. Proc. Natl. Acad. Sci. USA 2022, 119, e2119872119. [Google Scholar] [CrossRef]
- Di Cecco, G.J.; Gouhier, T.C. Increased spatial and temporal autocorrelation of temperature under climate change. Sci. Rep. 2018, 8, 14850. [Google Scholar] [CrossRef]
- Hartmann, D.L.; Klein-Tank, A.M.G.; Rusticucci, M.; Alexander, L.V.; Bronnimann, S.; Charabi, Y.; Dentener, F.J.; Edlugokencky, E.J.; Easterling, D.R.; Kaplan, A.; et al. Observations: Atmosphere and Surface, in The Physical Science Basis. In Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK, 2013; pp. 159–254. [Google Scholar]
- Alexander, M.A.; Scott, J.D.; Friedland, K.D.; Mills, K.E.; Nye, J.A.; Pershing, A.J.; Thomas, A.C. Projected sea surface temperatures over the 21st century: Changes in the mean, variability and extremes for large marine ecosystem regions of Northern Oceans. Elem.-Sci. Anthr. 2018, 6, 9. [Google Scholar] [CrossRef]
- Lee, M.A.; Huang, W.P.; Shen, Y.L.; Weng, J.S.; Semedi, B.; Wang, Y.C.; Chan, J.W. Long term observations of interannual and decadal variation of sea surface temperature in the Taiwan Strait. J. Mar. Sci. Technol. 2021, 29, 7. [Google Scholar] [CrossRef]
- Levitus, S.; Antonov, J.I.; Boyer, T.P. Warming of the World Ocean, 1955–2003. Geophys. Res. Lett. 2005, 32, L02604. [Google Scholar] [CrossRef]
- Ginzburg, A.I.; Kostianoy, A.G.; Sheremet, N.A. Seasonal and interanual variability of the Black Sea surface temperature as revealed from satellite data (1982–2000). J. Mar. Syst. 2004, 52, 33–50. [Google Scholar] [CrossRef]
- Santos, A.M.P.; Kazmin, A.S.; Peliz, A. Decadal changes in the Canary upwelling system as revealed by satellite observations: Their impact on productivity. J. Mar. Res. 2005, 63, 359–379. [Google Scholar] [CrossRef]
- Costoya, X.; Decastro, M.; Gómez-Gesteira, M.; Santos, F. Changes in sea surface temperature seasonality in the Bay of Biscay over the last decades (1982–2014). J. Mar. Syst. 2015, 150, 91–101. [Google Scholar] [CrossRef]
- Santos, F.; Gómez-Gesteira, M.; deCastro, M.; Álvarez, I. Variability of coastal and ocean water temperature in the upper 700 m along the western Iberian Peninsula from 1975 to 2006. PLoS ONE 2012, 7, e50666. [Google Scholar] [CrossRef] [PubMed]
- Thomas, A.; Pringle, P.; Pfleiderer, P.; Schleussner, C.F. Tropical Cyclones: Impacts, the Link to Climate Change and Adaptation. Climate Analytics. 6 November 2017. (PDF) Climate Change and Small Island Developing States. Available online: https://climateanalytics.org/publications/tropical-cyclones-impacts-the-link-to-climate-change-and-adaptation/ (accessed on 22 April 2025).
- Varela, R.; de Castro, M.; Días, J.M.; Gómez-Gesteira, M. Coastal warming under climate change: Global, faster and heterogeneous. Sci. Total Environ. 2023, 886, 164029. [Google Scholar] [CrossRef] [PubMed]
- Scanes, E.; Scanes, P.R.; Ross, P.M. Climate change rapidly warms and acidifies Australian estuaries. Nat. Commun. 2020, 11, 1803. [Google Scholar] [CrossRef]
- Shi, J.; Hu, C. South Florida estuaries are warming faster than global oceans. Environ. Res. Lett. 2023, 18, 014003. [Google Scholar] [CrossRef]
- Prum, P.; Harris, L.; Gardner, J. Widespread warming of Earth’s estuaries. Limnol. Oceanogr. Lett. 2024, 9, 268–275. [Google Scholar] [CrossRef]
- BACC Lead Author Group. Assessment of Climate Change for the Baltic Sea Basin. International BALTEX Secretariat. 2006. Available online: https://www.hereon.de/imperia/md/content/baltex/springer_bacc_annexes.pdf (accessed on 22 April 2025).
- Meier, H.E.M. Baltic Sea climate in the late 21st century—A dynamical downscaling approach using two global models and two emission scenarios. Clim. Dyn. 2006, 27, 39–68. [Google Scholar] [CrossRef]
- Brown, C.; Sharp, D.; Mochon Collura, T.C. Effect of climate change on water temperature and attainment of water temperature criteria in the Yaquina estuary, Oregon (USA). Estuar. Coast. Shelf Sci. 2016, 169, 136–146. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.; Xu, J.; Yang, Y.; Lyv, Y.; Luan, K. Seasonal and interannual variations of sea surface temperature and influencing factors in the Yangtze River Estuary. Reg. Stud. Mar. Sci. 2021, 45, 101827. [Google Scholar] [CrossRef]
- Friedland, K.D.; Morse, R.E.; Manning, J.P.; Melrose, D.C.; Miles, T.; Goode, A.G.; Brady, D.C.; Kohut, J.T.; Powell, E.N. Trends and change points in surface and bottom thermal environments of the US Northeast Continental Shelf Ecosystem. Fish. Oceanogr. 2020, 29, 396–414. [Google Scholar] [CrossRef]
- Fernández-Barba, M.; Huertas, I.E.; Navarro, G. Assessment of surface and bottom marine heatwaves along the Spanish coast. Ocean Model. 2024, 190, 102399. [Google Scholar] [CrossRef]
- Lien, V.S.; Raj, R.P.; Chatterjee, S. Surface and bottom marine heatwave characteristics in the Barents Sea: A model study. In 8th Edition of the Copernicus Ocean State Report (OSR8); von Schuckmann, K., Moreira, L., Grégoire, M., Marcos, M., Staneva, J., Brasseur, P., Garric, G., Lionello, P., Karstensen, J., Neukermans, G., Eds.; Copernicus Publications: Göttingen, Germany, 2024; Volume 4-osr8. [Google Scholar] [CrossRef]
- Wolowicz, M.; Sokołowski, A.; Lasota, R. Estuaries—A biological point of view. Oceanol. Hydrobiol. Stud. 2007, 36, 113–130. [Google Scholar] [CrossRef]
- Thrush, S.F.; Townsend, M.; Hewitt, J.E.; Davies, K.; Lohrer, A.M.; Lundquist, C.; Cartner, K. The many uses and values of estuarine ecosystems. In Ecosystems Services in New Zealand—Conditions and Trends; Dymond, J.R., Ed.; Manaaki Whenua Press: Lincoln, New Zealand, 2014; pp. 226–237. [Google Scholar]
- US EPA. Oregon Water Quality Assessment Report. 2006. Available online: https://www.oregon.gov/deq/FilterDocs/0406method.pdf (accessed on 22 April 2025).
- Rabalais, N.N.; Turner, R.E.; Díaz, R.J.; Justic, D. Global change and eutrophication of coastal waters. ICES J. Mar. Sci. 2009, 66, 1528–1537. [Google Scholar] [CrossRef]
- Burge, C.A.; Eakin, C.M.; Friedman, C.S.; Froelich, B.; Hershberger, P.K.; Hofmann, E.E.; Petes, L.E.; Prager, K.C.; Weil, E.; Willis, B.L.; et al. Climate change influences on marine infectious diseases: Implications for management and society. Ann. Rev. Mar. Sci. 2014, 6, 249–277. [Google Scholar] [CrossRef]
- Moore, S.K.; Trainer, V.L.; Mantua, N.J.; Parker, M.S.; Laws, E.A.; Backer, L.C.; Fleming, L.E. Impacts of climate variability and future climate change on harmful algal blooms and human health. Environ. Health 2008, 7, S4. [Google Scholar] [CrossRef]
- Blewett, D.A.; Stevens, P.W. Temperature variability in a subtropical estuary and implications for common snook Centropomus undecimalis, a cold-sensitive fish. Gulf Mex. Sci. 2014, 32, 44–54. [Google Scholar] [CrossRef]
- Alvarez, I.; Gomez-Gesteira, M.; deCastro, M.; Prego, R. Variation in upwelling intensity along the NorthWest Iberian Peninsula (Galicia). J. Atmos. Ocean Sci. 2005, 10, 309–324. [Google Scholar] [CrossRef]
- Wooldridge, T.; Deyzel, S. Variability in estuarine water temperature gradients and influence on the distribution of zooplankton: A biogeographical perspective. Afr. J. Mar. Sci. 2012, 34, 465–477. [Google Scholar] [CrossRef]
- Vroom, J.; van der Wegen, M.; Martyr-Koller, R.C.; Lucas, L.V. What determines water temperature dynamics in the San Francisco Bay-Delta system? Water Resour. Res. 2017, 53, 9901–9921. [Google Scholar] [CrossRef]
- Bashevkin, S.M.; Mahardja, B. Seasonally variable relationships between surface water temperature and inflow in the upper San Francisco Estuary. Limnol. Oceanogr. 2022, 67, 684–702. [Google Scholar] [CrossRef]
- Gross, P.L.; Gan, J.C.L.; Scurfield, D.J.; Frank, C.; Frank, C.; McLean, C.; Bob, C.; Moore, J.W. Complex temperature mosaics across space and time in estuaries: Implications for current and future nursery function for Pacific salmon. Front. Mar. Sci. 2023, 10, 1278810. [Google Scholar] [CrossRef]
- Usabiaga, J.I.; Sáenz-Aguirre, J.; Valencia, V.; Borja, A. Climate and meteorology, variability and its influence on the ocean. In Oceanography and Marine Environment of the Basque Country; Elsevier Oceanography Series 70; Borja, A., Collins, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2004; pp. 75–95. [Google Scholar]
- Barroeta, Z.; Uriarte, I.; Iriarte, A.; Villate, F. Intraregional variability of exotic and native zooplankton in Basque coast estuaries (inner Bay of Biscay): Effect of secondary dispersion, estuary features and regional environmental gradients. Hydrobiologia 2024, 851, 667–687. [Google Scholar] [CrossRef]
- Cearreta, A.; Irabien, M.J.; Pascual, A. Human activities along the Basque coast during the last two centuries: Geological perspective of recent anthropogenic impact on the coast and its environmental consequences. In Oceanography and Marine Environment of the Basque Country; Elsevier Oceanography Series 70; Borja, A., Collins, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2004; pp. 27–50. [Google Scholar]
- Valencia, V.; Borja, A.; Franco, J.; Galparsoro, I.; Tello, E. Medio Físico y Dinámica de los Estuarios de la Costa Vasca. Aplicaciones en Ecología y Gestión; Departamento de Ordenación del Territorio y Medio Ambiente: Gobierno Vasco, Spain, 2024. [Google Scholar]
- Uriarte, I.; Villate, F.; Iriarte, A.; Duque, J.; Ameztoy, I. Seasonal and axial variations of net water circulation and turnover in the estuary of Bilbao. Estuar. Coast. Shelf Sci. 2014, 150, 312–324. [Google Scholar] [CrossRef]
- Fernández-Nóvoa, D.; Costoya, X.; deCastro, M.; Gómez-Gesteira, M. Dynamic characterization of the main Cantabrian River plumes by means of MODIS. Cont. Shelf Res. 2019, 183, 14–27. [Google Scholar] [CrossRef]
- Uriarte, A.; Collins, M.; Cearreta, A.; Bald, J.; Evans, G. Sediment supply, transport and deposition: Contemporary and Late Quaternary evolution. In Oceanography and Marine Environment of the Basque Country; Elsevier Oceanography Series 70; Borja, A., Collins, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2004; pp. 97–131. [Google Scholar]
- Fontán, A.; Valencia, V.; Borja, Á.; Goikoetxea, N. Oceano-meteorological conditions and coupling in the southeastern Bay of Biscay, for the period 2001–2005: A comparison with the past two decades. J. Mar. Syst. 2008, 72, 167–177. [Google Scholar] [CrossRef]
- Hyndman, R.; Athanasopoulos, G.; Bergmeir, C.; Caceres, G.; Chhay, L.; O’Hara-Wild, M.; Petropoulos, F.; Razbash, S.; Wang, E.; Yasmeen, F. Forecast: Forecasting Functions for Time Series and Linear Models. R Package Version 8.21. 2023. Available online: https://pkg.robjhyndman.com/forecast/ (accessed on 3 February 2024).
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2020; p. 818. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. 2024. Available online: https://www.R-project.org/ (accessed on 3 February 2024).
- Barroeta, Z.; García, T.; Uriarte, I.; Iriarte, A.; Villate, F. Response of native and non-indigenous zooplankton to inherent system features and management in two Basque estuaries: A niche decomposition approach. Estuar. Coast. Shelf Sci. 2022, 272, 107878. [Google Scholar] [CrossRef]
- Barroeta, Z.; Villate, F.; Uriarte, I.; Iriarte, A. Differences in the colonization success and impact of non-indigenous and other expanding copepod species on the zooplankton of two contrasting estuaries of the Bay of Biscay. Biol. Invasions 2020, 22, 3239–3267. [Google Scholar] [CrossRef]
- Shen, H.; Zhu, Y.; He, Z.; Li, L.; Lou, Y. Impacts of river discharge on the sea temperature in Changjiang estuary and its adjacent sea. J. Mar. Sci. Eng. 2022, 10, 343. [Google Scholar] [CrossRef]
- Ding, H.; Elmore, A.J. Spatio-temporal patterns in water surface temperature from Landsat time series data in the Chesapeake Bay, U.S.A. Remote Sens. Environ. 2015, 168, 335–348. [Google Scholar] [CrossRef]
- Hutchings, A.M.; De Vries, C.S.; Hayes, N.R.; Orr, H.G. Temperature and dissolved oxygen trends in English estuaries over the past 30 years. Estuar. Coast. Shelf Sci. 2024, 306, 108892. [Google Scholar] [CrossRef]
- Goikoetxea, N.; Borja, Á.; Fontán, A.; González, M.; Valencia, V. Trends and anomalies of sea surface temperature during the last 60 years, within the southeastern Bay of Biscay. Cont. Shelf Res. 2009, 29, 1060–1069. [Google Scholar] [CrossRef]
- Koutsikopoulos, C.; Beillois, P.; Leroy, C.C.; Taillefer, F. Temporal trends and spatial structures of the sea surface temperature in the Bay of Biscay. Oceanol. Acta 1998, 21, 335–344. [Google Scholar] [CrossRef][Green Version]
- Chust, G.; González, M.; Fontán, A.; Revilla, M.; Alvarez, P.; Santos, M.; Cotano, U.; Chifflet, M.; Borja, A.; Muxika, I.; et al. Climate regime shifts and biodiversity redistribution in the Bay of Biscay. Sci. Total Environ. 2022, 803, 149622. [Google Scholar] [CrossRef] [PubMed]
- Michel, S.; Treguier, A.M.; Vandermeirsch, F. Temperature variability in the Bay of Biscay during the past 40 years, from an in situ analysis and a 3D global simulation. Cont. Shelf Res. 2009, 29, 1070–1087. [Google Scholar] [CrossRef]
- Gómez-Gesteira, M.; deCastro, M.; Álvarez, I.; Gesteira, J.L.G. Coastal sea surface temperature warming trend along the continental part of the Atlantic Arc (1985–2005). J. Geophys. Res. 2008, 113, C04010. [Google Scholar] [CrossRef]
- Salat, J.; Pascual, J.; Flexas, M.; Chin, T.M.; Vazquez-Cuervo, J. Forty-five years of oceanographic and meteorological observations at a coastal station in the NW Mediterranean: A ground truth for satellite observations. Ocean Dyn. 2019, 69, 1067–1084. [Google Scholar] [CrossRef]
- Seekell, D.A.; Pace, M.L. Climate change drives warming in the Hudson River Estuary, New York (USA). J. Environ. Monit. 2011, 13, 2321–2327. [Google Scholar] [CrossRef] [PubMed]
- Piecuch, C.G.; Ponte, R.M.; Little, C.M.; Buckley, M.W.; Fukumori, I. Mechanisms underlying recent decadal changes in subpolar North Atlantic Ocean heat content. J. Geophys. Res. Oceans 2017, 122, 7181–7197. [Google Scholar] [CrossRef]
- Costoya, X.; Fernandez-Novoa, D.; deCastro, M.; Santos, F.; Lazure, P.; Gomez-Gesteira, M. Modulation of sea surface temperature warming in the Bay of Biscay by Loire and Gironde Rivers. J. Geophys. Res. Oceans 2016, 121, 966–979. [Google Scholar] [CrossRef]
- Marin, M.J.; Sutherland, D.A.; Helms, A.R. Water temperature variability in the Coos Estuary and its potential link to eelgrass loss. Front. Mar. Sci. 2022, 9, 930440. [Google Scholar] [CrossRef]
- Bradtke, K.M.; Herman, A.; Urbanski, J.A. Spatial and interannual variations of seasonal sea surface temperature patterns in the Baltic Sea. Oceanologia 2010, 52, 345–362. [Google Scholar] [CrossRef]
- Friedland, K.D.; Nielsen, J.M.; Record, N.R.; Brady, D.C.; Morrow, C.J. The phenology of the spring phytoplankton bloom in the North Atlantic does not trend with temperature. Elem. Sci. Anth. 2024, 12, 00111. [Google Scholar] [CrossRef]
- Piedracoba, S.; Pardo, P.C.; Álvarez-Salgado, X.A.; Torres, S. Seasonal, interannual and long-term variability of sea surface temperature in the NW Iberian upwelling, 1982-2020. J. Geophys. Res. Oceans 2024, 129, e2024JC021075. [Google Scholar] [CrossRef]
- Alvarez, I.; Días, J.M.; DeCastro, M.; Vaz, N.; Sousa, M.C.; Gómez-Gesteira, M. Influence of upwelling events on the estuaries of the north-western coast of the Iberian Peninsula. Mar. Freshw. Res. 2013, 64, 1123–1134. [Google Scholar] [CrossRef]
- Barton, E.D.; Largier, J.; Torres, R.; Sheridan, M.; Trasviña, A.; Souza, A.; Pazos, Y.; Valle-Levinson, A. Coastal upwelling and downwelling forcing of circulation in a semi-enclosed bay: Ria de Vigo. Prog. Oceanogr. 2015, 134, 173–189. [Google Scholar] [CrossRef]
- Goela, P.C.; Cordeiro, C.; Danchenko, S.; Icely, J.; Cristina, S.; Newton, A. Time series analysis of data for sea surface temperature and upwelling components from the southwest coast of Portugal. J. Mar. Syst. 2019, 163, 12–22. [Google Scholar] [CrossRef]
- Gramer, L.J.; Zhang, J.A.; Alaka, G.J.; Hazelton, A.T.; Gopalakrishnan, S.G. Coastal downwelling intensifies landfalling hurricanes. Geophys. Res. Lett. 2022, 49, e2021GL096630. [Google Scholar] [CrossRef]
- Pei, Y.H.; Liu, X.H.; He, H.L. Interpreting the sea surface temperature warming trend in the Yellow Sea and East China Sea. Sci. China Earth Sci. 2017, 60, 1558–1568. [Google Scholar] [CrossRef]
- Yeh, S.-W.; Kim, C.-H. Recent warming in the Yellow/East China Sea during winter and the associated atmospheric circulation. Cont. Shelf Res. 2010, 30, 1428–1434. [Google Scholar] [CrossRef]
- Qu, B.; Gabric, A.J.; Zhu, J.; Lin, D.; Qian, F.; Zhao, M. Correlation between sea surface temperature and wind speed in Greenland Sea and their relationships with NAO variability. Water Sci. Eng. 2012, 5, 304–315. [Google Scholar] [CrossRef]
- El-Geziry, T.M.; Elbessa, M.; Tonbol, K. On the relationships between sea surface temperature and atmospheric conditions over the southern Levantine basin. Egypt. J. Aquat. Biol. Fish. 2023, 27, 203–216. [Google Scholar] [CrossRef]
- Venegas, R.M.; Acevedo, J.; Treml, E.A. Three decades of ocean warming impacts on marine ecosystems: A review and perspective. Deep-Sea Res. II 2023, 212, 105318. [Google Scholar] [CrossRef]
- D’Alelio, D.; Rampone, S.; Cusano, L.M.; Morfino, V.; Russo, L.; Sanseverino, N.; Cloern, J.E.; Lomas, M.W. Machine learning identifies a strong association between warming and reduced primary productivity in an oligotrophic ocean gyre. Sci. Rep. 2020, 10, 3287. [Google Scholar] [CrossRef] [PubMed]
- Heneghan, R.F.; Everett, J.D.; Blanchard, J.L.; Sykes, P.; Richardson, A.J. Climate-driven zooplankton shifts cause large-scale declines in food quality for fish. Nat. Clim. Change 2023, 13, 470–477. [Google Scholar] [CrossRef]
- Walther, G.R.; Roques, A.; Hulme, P.E.; Sykes, M.T.; Pyšek, P.; Kühn, I.; Zobel, M.; Bacher, S.; Botta-Dukát, Z.; Bugmann, H.; et al. Alien species in a warmer world: Risks and opportunities. Trends Ecol. Evol. 2009, 24, 686–693. [Google Scholar] [CrossRef]
- Chaudhary, C.; Richardson, A.J.; Schoemane, D.S.; Costello, M.J. Global warming is causing a more pronounced dip in marine species richness around the equator. Proc. Natl. Acad. Sci. USA 2021, 118, e2015094118. [Google Scholar] [CrossRef]
- Benedetti, F.; Vogt, M.; Elizondo, U.H.; Righetti, D.; Zimmermann, N.E.; Gruber, N. Major restructuring of marine plankton assemblages under global warming. Nat. Commun. 2021, 12, 5226. [Google Scholar] [CrossRef]
- Leal Filho, W.; Nagy, G.J.; Martinho, F.; Saroar, M.; Erache, M.G.; Primo, A.L.; Pardal, M.A.; Li, C. Influences of climate change and variability on estuarine ecosystems: An impact study in selected European, South American and Asian countries. Int. J. Environ. Res. Public Health 2002, 19, 585. [Google Scholar] [CrossRef] [PubMed]
- Iriarte, A.; Villate, F.; Uriarte, I.; Bidegain, G.; Barroeta, Z. Shifts in neritic copepod communities off the Basque coast (southeastern Bay of Biscay) between 1998 and 2015. ICES J. Mar. Sci. 2022, 79, 830–843. [Google Scholar] [CrossRef]
- Matthiessen, P.; Law, R.J. Contaminants and their effects on estuarine and coastal organisms in the United Kingdom in the late twentieth century. Environ. Pollut. 2002, 120, 739–757. [Google Scholar] [CrossRef]
- Fowles, A.E.; Edgar, G.J.; Hill, N.; Stuart-Smith, R.D.; Kirkpatrick, J.B. An experimental assessment of impacts of pollution sources on sessile biota in a temperate urbanised estuary. Mar. Pollut. Bull. 2018, 133, 209–217. [Google Scholar] [CrossRef]
- Uriarte, I.; Villate, F.; Iriarte, A. Zooplankton recolonization of the inner estuary of Bilbao: Influence of pollution abatement, climate and non-indigenous species. J. Plankton Res. 2016, 38, 718–731. [Google Scholar] [CrossRef][Green Version]



| Water Cluster | Point | Intercept | Rate of Change Decade−1 | 95% CI (Min–Max) | R2 | p-Value |
|---|---|---|---|---|---|---|
| UN | U35_0.0 | −21.23 | 0.19 | 0.13–0.25 | 0.11 | <0.001 |
| U35_2.5 | −20.91 | 0.18 | 0.12–0.25 | 0.10 | <0.001 | |
| BND | B35_2.5 | −3.21 | 0.10 | 0.03–0.16 | 0.03 | 0.002 |
| B35_5.0 | −9.75 | 0.13 | 0.07–0.19 | 0.06 | <0.001 | |
| B35_7.5 | −13.98 | 0.15 | 0.09–0.21 | 0.07 | <0.001 | |
| BTD | B34_2.5 | −20.81 | 0.18 | 0.12–0.24 | 0.10 | <0.001 |
| B34_5.0 | −20.83 | 0.18 | 0.12–0.24 | 0.11 | <0.001 | |
| B34_7.5 | −22.39 | 0.19 | 0.13–0.25 | 0.11 | <0.001 | |
| B33_5.0 | −32.13 | 0.24 | 0.19–0.29 | 0.20 | <0.001 | |
| B33_7.5 | −32.55 | 0.24 | 0.19–0.29 | 0.22 | <0.001 | |
| B30_5.0 | −24.89 | 0.20 | 0.14–0.27 | 0.12 | <0.001 | |
| UT | U33_0.0 | −30.52 | 0.23 | 0.17–0.30 | 0.14 | <0.001 |
| U33_2.5 | −25.29 | 0.21 | 0.14–0.28 | 0.10 | <0.001 | |
| U30_0.0 | −12.66 | 0.14 | 0.07–0.22 | 0.05 | <0.001 | |
| U30_2.5 | −19.72 | 0.18 | 0.11–0.25 | 0.07 | <0.001 | |
| U26_0.0 | −33.82 | 0.25 | 0.18–0.32 | 0.12 | <0.001 | |
| U26_2.5 | −33.87 | 0.25 | 0.18–0.32 | 0.13 | <0.001 | |
| BTG | B35_0.0 | 11.60 | 0.02 | −0.05–0.10 | 0.00 | 0.570 |
| B33_2.5 | −23.49 | 0.20 | 0.13–0.26 | 0.11 | <0.001 | |
| B30_2.5 | −1.06 | 0.08 | 0.01–0.16 | 0.02 | 0.022 | |
| BTS | B34_0.0 | −13.95 | 0.15 | 0.07–0.23 | 0.04 | <0.001 |
| B33_0.0 | 18.95 | -0.02 | −0.11–0.08 | 0.00 | 0.740 | |
| B30_0.0 | 75.66 | -0.30 | −0.40–−0.20 | 0.10 | <0.001 |
| Rate of Change Decade−1 | ||||
|---|---|---|---|---|
| Water Cluster | Winter | Spring | Summer | Autumn |
| UN | 0.14 | 0.42 | −0.10 | 0.28 |
| BND | −0.01 | 0.44 | −0.05 | 0.13 |
| BTD | −0.02 | 0.43 | 0.23 | 0.22 |
| UT | 0.07 | 0.49 | 0.05 | 0.27 |
| BTG | −0.02 | 0.31 | 0.14 | 0.01 |
| BTS | −0.18 | 0.17 | 0.10 | 0.08 |
| Variable | Type | Intercept | Rate of Change Decade−1 | 95% CI (Min–Max) | R2 | p-Value |
|---|---|---|---|---|---|---|
| Air temperature | Copernicus | −41.03 | 0.27 | 0.21–0.33 | 0.22 | <0.001 |
| Sondika | −73.63 | 0.44 | 0.37–0.51 | 0.34 | <0.001 | |
| Abusu | −26.17 | 0.20 | 0.13–0.27 | 0.10 | <0.001 | |
| Muxika | −63.59 | 0.39 | 0.32–0.45 | 0.28 | <0.001 | |
| River flow | Abusu | −396.56 | 0.21 | 0.91–3.26 | 0.04 | <0.001 |
| Muxika | −5.61 | 0.03 | 0.00–0.06 | 0.02 | 0.023 | |
| Upwelling index | −7985.5 | 38.05 | 12.31–63.78 | 0.03 | 0.004 |
| Water Cluster | Season | ATc | ATs | ATa/m | RFa/m | UPW |
|---|---|---|---|---|---|---|
| UN | Winter | 0.589 | 0.602 | 0.494 | −0.306 | |
| Spring | 0.907 | 0.881 | 0.868 | −0.537 | 0.430 | |
| Summer | 0.593 | 0.514 | 0.521 | |||
| Autumn | 0.871 | 0.861 | 0.780 | −0.483 | ||
| BND | Winter | 0.496 | 0.473 | 0.410 | −0.418 | |
| Spring | 0.893 | 0.874 | 0.882 | −0.442 | 0.398 | |
| Summer | 0.559 | 0.503 | 0.551 | |||
| Autumn | 0.844 | 0.835 | 0.805 | −0.466 | ||
| BTD | Winter | 0.599 | 0.537 | 0.536 | −0.434 | |
| Spring | 0.918 | 0.893 | 0.897 | −0.525 | 0.411 | |
| Summer | 0.645 | 0.609 | 0.647 | |||
| Autumn | 0.868 | 0.858 | 0.833 | −0.509 | ||
| UT | Winter | 0.681 | 0.700 | 0.632 | ||
| Spring | 0.896 | 0.886 | 0.864 | −0.607 | 0.476 | |
| Summer | 0.608 | 0.525 | 0.624 | 0.313 | ||
| Autumn | 0.835 | 0.839 | 0.811 | −0.526 | ||
| BTG | Winter | 0.667 | 0.650 | 0.624 | −0.486 | |
| Spring | 0.925 | 0.904 | 0.907 | −0.504 | 0.448 | |
| Summer | 0.679 | 0.624 | 0.701 | −0.273 | ||
| Autumn | 0.836 | 0.812 | 0.812 | −0.669 | 0.241 | |
| BTS | Winter | 0.737 | 0.737 | 0.722 | −0.267 | |
| Spring | 0.855 | 0.843 | 0.854 | −0.491 | 0.481 | |
| Summer | 0.633 | 0.552 | 0.678 | −0.319 | 0.298 | |
| Autumn | 0.878 | 0.853 | 0.866 | −0.624 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uriarte, I.; Iriarte, A.; Larrinaga, X.; Bidegain, G.; Villate, F. Temperature Trends and Seasonality in Neritic and Transitional Waters of the Southern Bay of Biscay from 1998 to 2023. Water 2025, 17, 2726. https://doi.org/10.3390/w17182726
Uriarte I, Iriarte A, Larrinaga X, Bidegain G, Villate F. Temperature Trends and Seasonality in Neritic and Transitional Waters of the Southern Bay of Biscay from 1998 to 2023. Water. 2025; 17(18):2726. https://doi.org/10.3390/w17182726
Chicago/Turabian StyleUriarte, Ibon, Arantza Iriarte, Xabier Larrinaga, Gorka Bidegain, and Fernando Villate. 2025. "Temperature Trends and Seasonality in Neritic and Transitional Waters of the Southern Bay of Biscay from 1998 to 2023" Water 17, no. 18: 2726. https://doi.org/10.3390/w17182726
APA StyleUriarte, I., Iriarte, A., Larrinaga, X., Bidegain, G., & Villate, F. (2025). Temperature Trends and Seasonality in Neritic and Transitional Waters of the Southern Bay of Biscay from 1998 to 2023. Water, 17(18), 2726. https://doi.org/10.3390/w17182726








