Analysis of Risk Factors for Tunnel Flooding Disasters Based on DEMATEL
Abstract
1. Introduction
2. Data Materials
2.1. Factor Selection
2.2. Basic Data Source
3. Methods
3.1. Construct the Direct Influence Matrix
3.2. Calculation of the Comprehensive Influence Matrix
4. Results
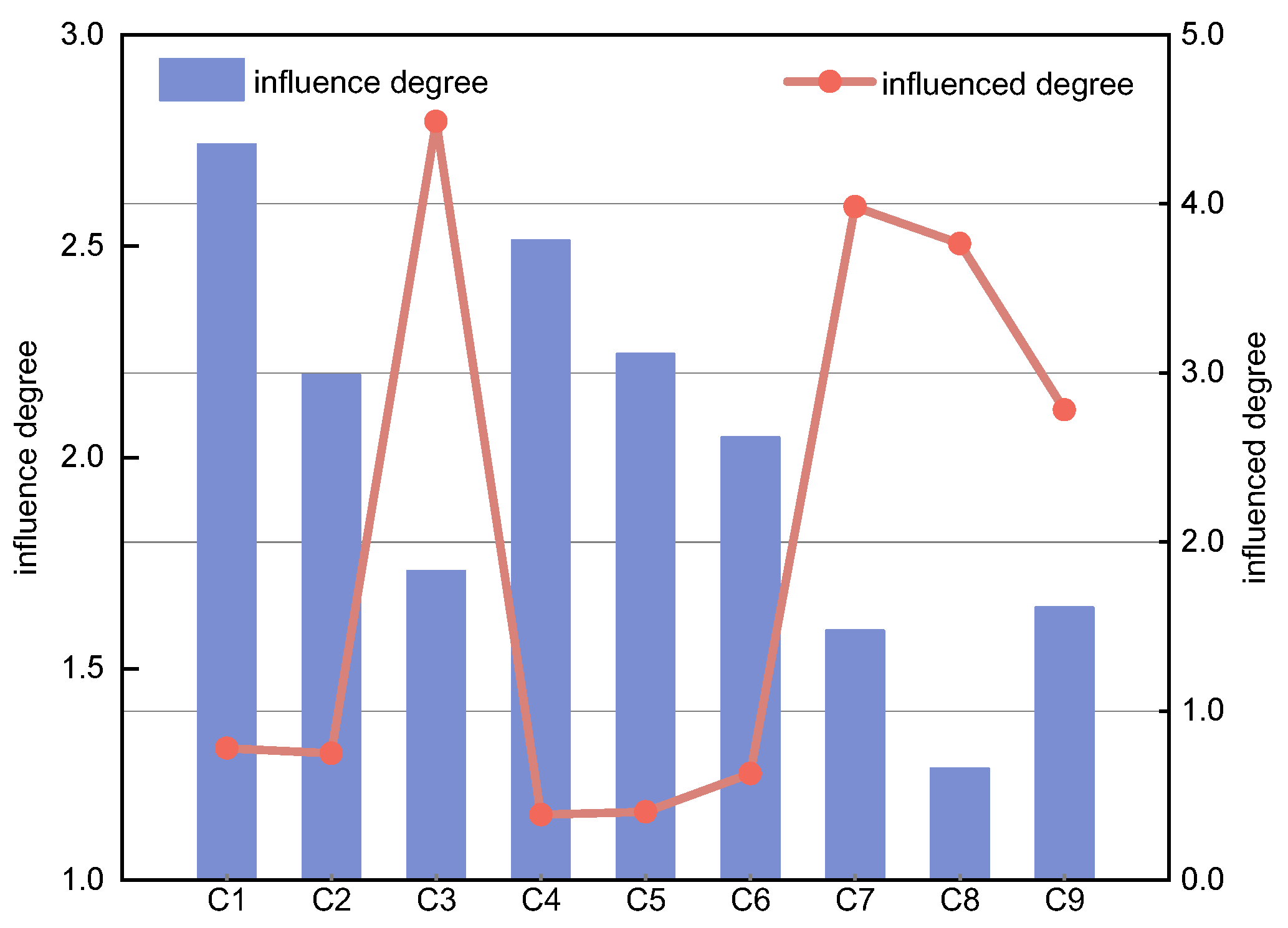
4.1. Influence Degree and Influenced Degree
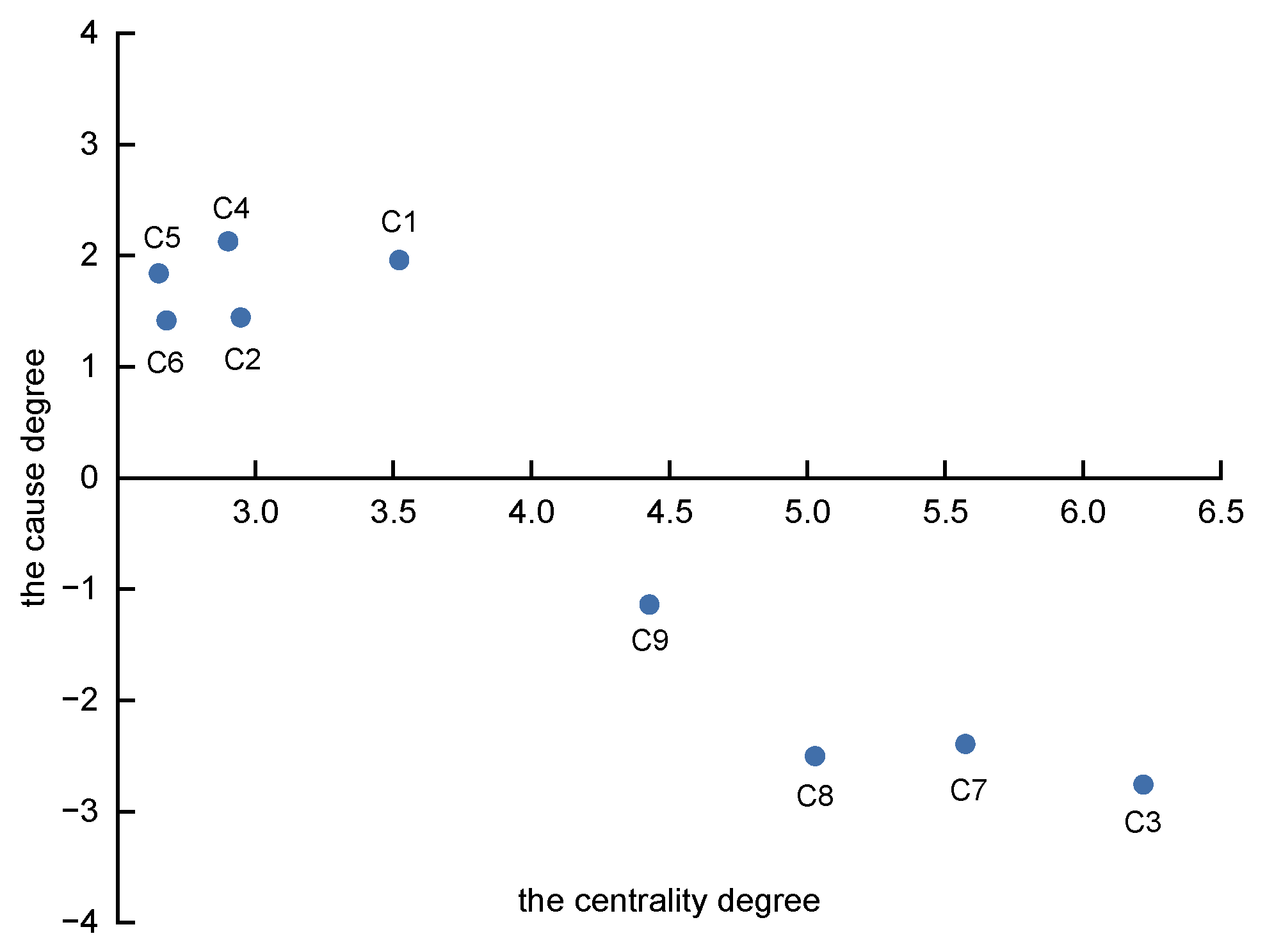
4.2. Central Degree and Cause Degree
5. Discussion
- (1)
- Extreme rainfall represents the primary trigger of tunnel flooding. The formation of a hazard-prone environment within the tunnel area can further amplify the risk of rainfall-induced flooding. Moreover, the tunnel’s exposure and its flood protection capacity directly determine the severity of post-disaster losses. Causal factors such as rainfall intensity, rainfall duration, ground elevation, and road gradient serve as driving forces in the formation of tunnel waterlogging disasters. In contrast, result factors such as water accumulation depth, tunnel drainage capacity, and emergency flood control measures are closely associated with the post-flood severity. According to the evaluation results, improving tunnel flood resilience does not necessarily require the direct enhancement of drainage capacity. Instead, resilience can be effectively improved during the design phase by anticipating rainfall intensity, adjusting ground elevation, and modifying road gradients (e.g., by incorporating reverse slopes at tunnel entrances).
- (2)
- The influence matrix in DEMATEL relies on expert judgment, which introduces subjectivity and potential bias into the analysis of tunnel flooding risks. When multiple factors are strongly correlated, the DEMATEL analysis may amplify or attenuate causal relationships, making it unsuitable for deriving precise conclusions regarding tunnel flood mitigation capability. Therefore, future research should be based on hydrological experiments and numerical simulations to analyze the dynamic evolution of tunnel flooding and to derive the quantitative influence of risk indicators.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gharakhanlou, N.M.; Perez, L. Flood susceptible prediction through the use of geospatial variables and machine learning methods. J. Hydrol. 2023, 617, 129121. [Google Scholar] [CrossRef]
- Xu, K.; Zhuang, Y.; Bin, L.; Wang, C.; Tian, F. Impact assessment of climate change on compound flooding in a coastal city. J. Hydrol. 2023, 617, 129166. [Google Scholar] [CrossRef]
- Alabbad, Y.; Yildirim, E.; Demir, I. A web-based analytical urban flood damage and loss estimation framework. Environ. Model. Softw. 2023, 163, 105670. [Google Scholar] [CrossRef]
- Pariartha, I.G.S.; Aggarwal, S.; Rallapalli, S.; Egodawatta, P.; McGree, J.; Goonetilleke, A. Compounding effects of urbanization, climate change and sea-level rise on monetary projections of flood damage. J. Hydrol. 2023, 620, 129535. [Google Scholar] [CrossRef]
- Ma, C.; Qi, W.; Xu, H.; Zhao, K. An integrated quantitative framework to assess the impacts of disaster-inducing factors on causing urban flood. Nat. Hazards 2022, 113, 1903–1924. [Google Scholar] [CrossRef]
- He, R.; Tiong, R.L.; Yuan, Y.; Zhang, L. Enhancing resilience of urban underground space under floods: Current status and future directions. Tunn. Undergr. Space Technol. 2024, 147, 105674. [Google Scholar] [CrossRef]
- Chen, F.; Liu, S. Research Prospect on Some Scientific and Technological Problems of Water Disaster Prevention and Control in Urban Underground Space. J. Chang. River Sci. Res. Inst. 2024, 41, 90. [Google Scholar]
- Zhao, C.; Wang, J.; Zhang, Y.; Zhang, B. Review of the characteristics, causes and governance of urban flood in China. J. Catastrophol. 2023, 38, 220–228. [Google Scholar]
- Dong, B.; Xia, J.; Li, Q.; Zhou, M. Risk assessment for people and vehicles in an extreme urban flood: Case study of the “7.20” flood event in Zhengzhou, China. Int. J. Disaster Risk Reduct. 2022, 80, 103205. [Google Scholar] [CrossRef]
- Pant, R.; Thacker, S.; Hall, J.; Alderson, D.; Barr, S. Critical infrastructure impact assessment due to flood exposure. J. Flood Risk Manag. 2018, 11, 22–33. [Google Scholar] [CrossRef]
- Lyu, H.-M.; Shen, S.-L.; Zhou, A.; Yang, J. Perspectives for flood risk assessment and management for mega-city metro system. Tunn. Undergr. Space Technol. 2019, 84, 31–44. [Google Scholar] [CrossRef]
- Wu, J.; Fang, W.; Hu, Z.; Hong, B. Application of Bayesian approach to dynamic assessment of flood in urban underground spaces. Water 2018, 10, 1112. [Google Scholar] [CrossRef]
- Li, Z.; Su, H.; Li, Z.; Du, Y. Risk coupling effects on flood-induced hazards in urban underground spaces. Nat. Hazards 2025, 121, 8541–8563. [Google Scholar] [CrossRef]
- O’DOnnell, E.C.; Thorne, C.R. Drivers of future urban flood risk. Philos. Trans. R. Soc. A 2020, 378, 20190216. [Google Scholar] [CrossRef] [PubMed]
- Pathan, A.I.; Agnihotri, P.G.; Said, S.; Patel, D. AHP and TOPSIS based flood risk assessment-a case study of the Navsari City, Gujarat, India. Environ. Monit. Assess. 2022, 194, 509. [Google Scholar] [CrossRef]
- Rafiei-Sardooi, E.; Azareh, A.; Choubin, B.; Mosavi, A.H.; Clague, J.J. Evaluating urban flood risk using hybrid method of TOPSIS and machine learning. Int. J. Disaster Risk Reduct. 2021, 66, 102614. [Google Scholar] [CrossRef]
- Wei, L.; Hu, K.-H.; Hu, X.-D. Rainfall occurrence and its relation to flood damage in China from 2000 to 2015. J. Mt. Sci. 2018, 15, 2492–2504. [Google Scholar] [CrossRef]
- Anni, A.H.; Cohen, S.; Praskievicz, S. Sensitivity of urban flood simulations to stormwater infrastructure and soil infiltration. J. Hydrol. 2020, 588, 125028. [Google Scholar] [CrossRef]
- Sohn, W.; Brody, S.D.; Kim, J.-H.; Li, M.-H. How effective are drainage systems in mitigating flood losses? Cities 2020, 107, 102917. [Google Scholar] [CrossRef]
- Wang, L.; Cui, S.; Li, Y.; Huang, H.; Manandhar, B.; Nitivattananon, V.; Fang, X.; Huang, W. A review of the flood management: From flood control to flood resilience. Heliyon 2022, 8, e11763. [Google Scholar] [CrossRef]
- Xian, S.; Lin, N.; Kunreuther, H. Optimal house elevation for reducing flood-related losses. J. Hydrol. 2017, 548, 63–74. [Google Scholar] [CrossRef]
- Xue, P.; Huang, S.; Xie, K.; Sun, Y.; Fei, L. Identification of the critical factors in flood vulnerability assessment based on an improved DEMATEL method under uncertain environments. Int. J. Disaster Risk Reduct. 2024, 100, 104217. [Google Scholar] [CrossRef]
- Chen, F.; Liu, S.; Liu, W. Causes and characteristics of flooding in urban underground space. J. Chang. River Sci. Res. Inst. 2018, 35, 38. [Google Scholar]
- Yang, K.; Huang, G.Z.; Zhang, L.; Song, Z.; Li, H.X.; Gao, X.H. Analysis of influencing factors of subway system vulnerability under rainstorm conditions based on DEMATEL-AHDT. Water Resour. Hydropower Eng. 2023, 54, 22–33. [Google Scholar]
- Wang, Y.; Li, S.; Hu, C.; Ren, J.; Liu, P.; Zhao, C.; Zhu, M. Analysis of Surface Runoff in Zhengzhou City Under Extreme Rainfall Conditions. Water Resour. Power 2024, 42, 8–10. [Google Scholar]
- Zhong, J.; Li, D.; Jiang, K. Assessment of urban underground spaces inundation during extreme rainfall events. Water Sci. Technol. 2024, 89, 2851–2866. [Google Scholar] [CrossRef]
- Xiao, Z.; Gao, Q.; Hou, X.; Ma, M.; Hu, B.; Song, W.; Jia, L. Rainstorm waterlogging vulnerability assessment of subway stations in the central area of Tianjin. Hydrol. Sci. J. 2023, 68, 2277–2297. [Google Scholar] [CrossRef]
- Salman, A.M.; Li, Y. Flood risk assessment, future trend modeling, and risk communication: A review of ongoing research. Nat. Hazards Rev. 2018, 19, 04018011. [Google Scholar] [CrossRef]
- Hou, X.; Gao, Q.; Xiao, Z.; Ma, M.; Liu, B.; Hu, B.; Jia, L.; Song, W. Rainstorm Flood Risk Assessment of Urban Metro System in Different Operating Periods: A Case Study of the Central Urban Area of Tianjin, China. Nat. Hazards Rev. 2018, 19, 04018011. [Google Scholar] [CrossRef]
- Liu, J.; Zheng, W.; Chen, J.; Zhao, J. Evaluation of Rainstorm Waterlogging Emergency Response Capability of Subway Station for Trio Spaces. J. Catastrophol. 2024, 39, 172–176. [Google Scholar]
- Sun, Y.H.; Han, W.; Duan, W.C. Review on research progress of DEMATEL algorithm for complex systems. Control Decis. 2017, 32, 385–392. [Google Scholar]
- Li, J.; Zhao, J.; Li, Y.; Zhang, Y.; Zhang, S. Risk assessment of urban work safety based on regional disaster system theory. J. Saf. Sci. Technol. 2025, 21, 23–30. [Google Scholar]
- Du, Y.-W.; Zhou, W. New improved DEMATEL method based on both subjective experience and objective data. Eng. Appl. Artif. Intell. 2019, 83, 57–71. [Google Scholar] [CrossRef]
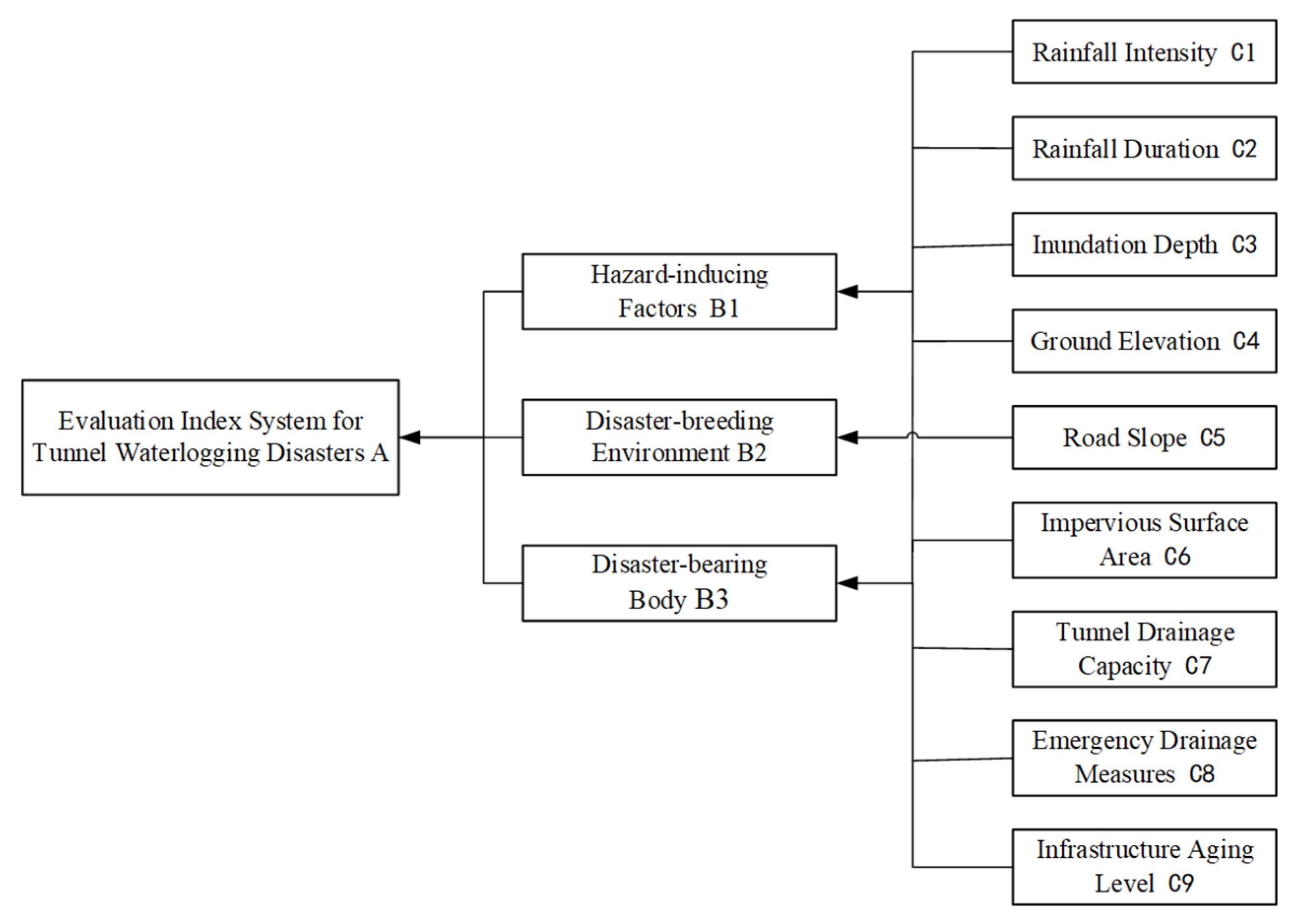
| Factors | Definition Criteria | Standards Referenced | Referenced Literature |
|---|---|---|---|
| Rainfall Intensity C1 | 24 h Cumulative Rainfall (mm) Heavy rain: 50–99.9 mm Torrential rain: 100–249.9 mm Extreme torrential rain: ≥250 mm | GB/T 28592-2012 | [14,22,23,24,25] |
| Rainfall Duration C2 | Rainfall duration refers to the time from the beginning to the end of a rainfall event. It is generally determined by the catchment area of the drainage facility and typically ranges from 3 to 24 hours. | GB/T 28592-2012 | [14,22,26] |
| Inundation Depth C3 | Low risk: less than 27 cm Moderate risk: 27–40 cm High risk: 40–60 cm Very high risk: greater than 60 cm | GB 51222-2017 | [22,23,26,27] |
| Ground Elevation C4 | Tunnel elevation is related to the configuration of drainage pathways. In principle, drainage design follows the concept of “high-level water drains at high points, low-level water drains at low points,” utilizing natural ground elevation to achieve gravity-driven outflow. | GB50015-2019 | [23,27,28,29,30] |
| Road Gradient C5 | The longitudinal slope of the road should be no less than 0.3%. The typical range for road cross-slope is 1.5% to 2.0%, and the shoulder cross-slope may be designed to be 1.0% steeper than the main roadway surface. | CJJ 83-2016 CJJ 37-2012 | [25] |
| Impervious Surface Area C6 | Impervious surfaces are unable to absorb or retain rainfall, making it easier for precipitation to generate surface runoff. The proportion of rainfall that becomes runoff is typically characterized by the runoff coefficient. | GB50015-2019 | [14,23,25] |
| Tunnel Drainage Capacity C7 | The ability of a tunnel entrance to effectively intercept inflowing water and ensure smooth drainage, as well as the degree of connectivity between internal and external drainage systems. | JTG/T 3660—2020 | [24,27] |
| Emergency Flood Control Measures C8 | In the event of a flood disaster, a rapid response capability is essential to implement predefined emergency plans and ensure the operational safety and accessibility of the tunnel. | CJJ 68-2016 | [23,24,26,30] |
| Degree of Infrastructure Aging C9 | Over time, pipelines may deteriorate due to blockages, structural cracks, or corrosion, leading to a marked decline in drainage performance. | GB 55027 | [14,23,28] |
| Scale Value | Degree of Importance |
|---|---|
| 1 | ai has extremely low influence on aj |
| 2 | ai has relatively low influence on aj |
| 3 | ai has a moderate influence on aj |
| 4 | ai has relatively high influence on aj |
| 5 | ai has an extremely high influence on aj |
| 0 | no influence |
| Total | 37 |
| Kendall’s W | 0.811 |
| Asymptotic Significance | 0.5 |
| M9×9 | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 |
|---|---|---|---|---|---|---|---|---|---|
| C1 | 0 | 30 | 29 | 3 | 3 | 1 | 28 | 25 | 14 |
| C2 | 26 | 0 | 22 | 0 | 0 | 1 | 19 | 20 | 14 |
| C3 | 3 | 2 | 0 | 2 | 2 | 2 | 27 | 31 | 20 |
| C4 | 14 | 13 | 27 | 0 | 22 | 2 | 20 | 13 | 3 |
| C5 | 2 | 2 | 26 | 20 | 0 | 9 | 21 | 12 | 13 |
| C6 | 12 | 9 | 24 | 2 | 2 | 0 | 24 | 16 | 8 |
| C7 | 0 | 0 | 34 | 0 | 0 | 4 | 0 | 26 | 18 |
| C8 | 0 | 0 | 28 | 0 | 0 | 0 | 17 | 0 | 18 |
| C9 | 0 | 0 | 24 | 1 | 1 | 9 | 32 | 16 | 0 |
| N9×9 | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 |
|---|---|---|---|---|---|---|---|---|---|
| C1 | 0.00 | 0.23 | 0.22 | 0.02 | 0.02 | 0.01 | 0.21 | 0.19 | 0.11 |
| C2 | 0.20 | 0.00 | 0.17 | 0.00 | 0.00 | 0.01 | 0.14 | 0.15 | 0.11 |
| C3 | 0.02 | 0.02 | 0.00 | 0.02 | 0.02 | 0.02 | 0.20 | 0.23 | 0.15 |
| C4 | 0.11 | 0.10 | 0.20 | 0.00 | 0.17 | 0.02 | 0.15 | 0.10 | 0.02 |
| C5 | 0.02 | 0.02 | 0.20 | 0.15 | 0.00 | 0.07 | 0.16 | 0.09 | 0.10 |
| C6 | 0.09 | 0.07 | 0.18 | 0.02 | 0.02 | 0.00 | 0.18 | 0.12 | 0.06 |
| C7 | 0.00 | 0.00 | 0.26 | 0.00 | 0.00 | 0.03 | 0.00 | 0.20 | 0.14 |
| C8 | 0.00 | 0.00 | 0.21 | 0.00 | 0.00 | 0.00 | 0.13 | 0.00 | 0.14 |
| C9 | 0.00 | 0.00 | 0.18 | 0.01 | 0.01 | 0.07 | 0.24 | 0.12 | 0.00 |
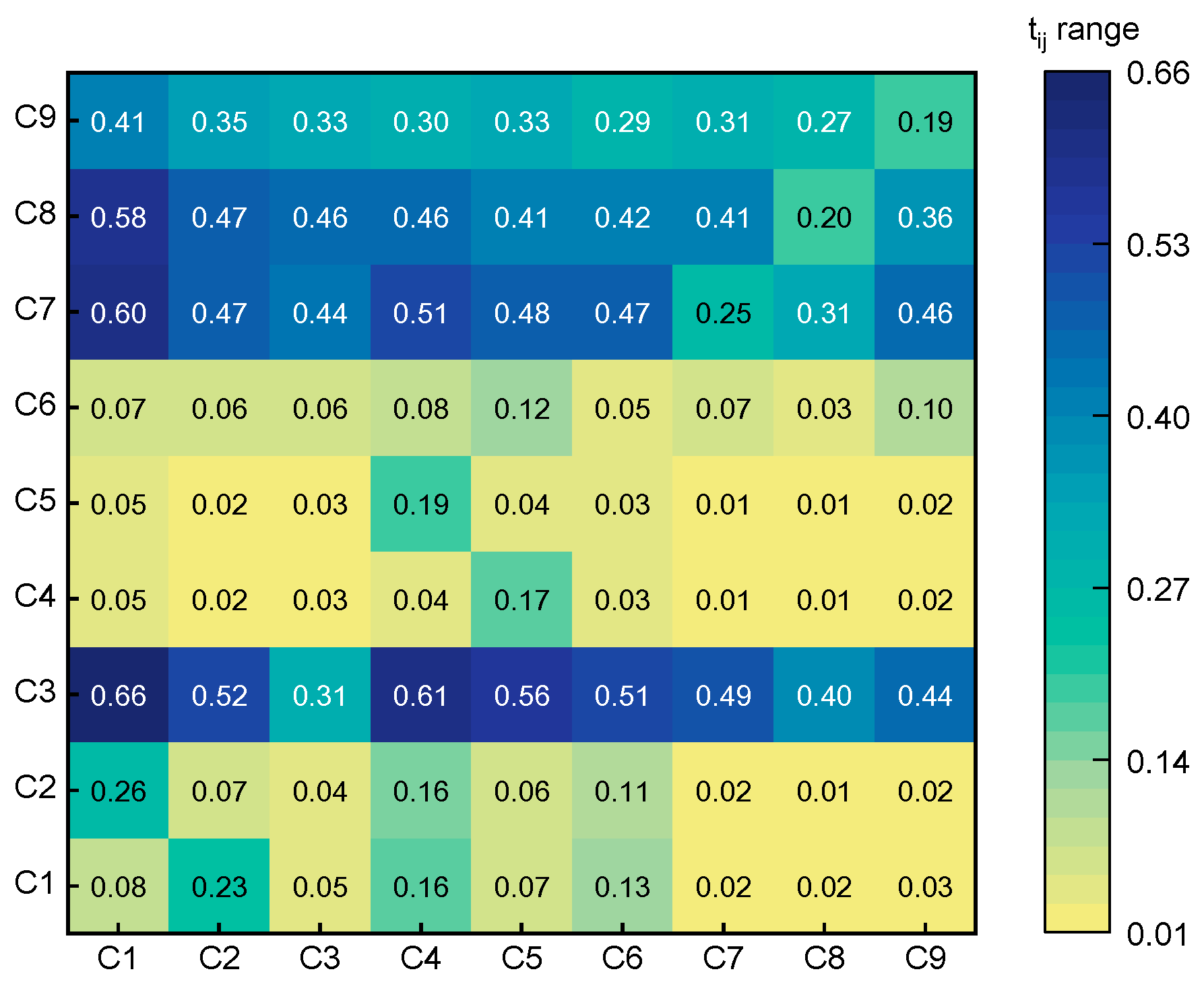
| T9×9 | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 |
|---|---|---|---|---|---|---|---|---|---|
| C1 | 0.08 | 0.26 | 0.66 | 0.05 | 0.05 | 0.07 | 0.60 | 0.58 | 0.41 |
| C2 | 0.23 | 0.07 | 0.52 | 0.02 | 0.02 | 0.06 | 0.47 | 0.47 | 0.35 |
| C3 | 0.05 | 0.04 | 0.31 | 0.03 | 0.03 | 0.06 | 0.44 | 0.46 | 0.33 |
| C4 | 0.16 | 0.16 | 0.61 | 0.04 | 0.19 | 0.08 | 0.51 | 0.46 | 0.30 |
| C5 | 0.07 | 0.06 | 0.56 | 0.17 | 0.04 | 0.12 | 0.48 | 0.41 | 0.33 |
| C6 | 0.13 | 0.11 | 0.51 | 0.03 | 0.03 | 0.05 | 0.47 | 0.42 | 0.29 |
| C7 | 0.02 | 0.02 | 0.49 | 0.01 | 0.01 | 0.07 | 0.25 | 0.41 | 0.31 |
| C8 | 0.02 | 0.01 | 0.40 | 0.01 | 0.01 | 0.03 | 0.31 | 0.20 | 0.27 |
| C9 | 0.03 | 0.02 | 0.44 | 0.02 | 0.02 | 0.10 | 0.46 | 0.36 | 0.19 |
| Factors | Influence Degree Di | Influenced Degree Ci | Central Degree Mi | Cause Degree Ri |
|---|---|---|---|---|
| C1 | 2.74 | 0.78 | 3.52 | 1.96 |
| C2 | 2.20 | 0.75 | 2.95 | 1.44 |
| C3 | 1.73 | 4.49 | 6.22 | −2.76 |
| C4 | 2.51 | 0.39 | 2.90 | 2.13 |
| C5 | 2.24 | 0.41 | 2.65 | 1.84 |
| C6 | 2.05 | 0.63 | 2.68 | 1.42 |
| C7 | 1.59 | 3.98 | 5.57 | −2.39 |
| C8 | 1.26 | 3.76 | 5.03 | −2.50 |
| C9 | 1.65 | 2.78 | 4.43 | −1.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Y.; Zhang, Y.; Zhu, Y.; Tao, Y.; Zhang, R.; Wang, Q. Analysis of Risk Factors for Tunnel Flooding Disasters Based on DEMATEL. Water 2025, 17, 2694. https://doi.org/10.3390/w17182694
Fang Y, Zhang Y, Zhu Y, Tao Y, Zhang R, Wang Q. Analysis of Risk Factors for Tunnel Flooding Disasters Based on DEMATEL. Water. 2025; 17(18):2694. https://doi.org/10.3390/w17182694
Chicago/Turabian StyleFang, Yongxiang, Yanmei Zhang, Yanchang Zhu, Yingying Tao, Rui Zhang, and Qikai Wang. 2025. "Analysis of Risk Factors for Tunnel Flooding Disasters Based on DEMATEL" Water 17, no. 18: 2694. https://doi.org/10.3390/w17182694
APA StyleFang, Y., Zhang, Y., Zhu, Y., Tao, Y., Zhang, R., & Wang, Q. (2025). Analysis of Risk Factors for Tunnel Flooding Disasters Based on DEMATEL. Water, 17(18), 2694. https://doi.org/10.3390/w17182694






