Flood Frequency Analysis and Trend Detection in the Brisbane River Basin, Australia

Abstract

This study presents a comprehensive flood frequency analysis for Australia’s Brisbane River basin using annual maximum flood (AMF) data from 26 stream gauging stations. This evaluates five different probability distributions in fitting the AMF data of the selected stations, which are the Lognormal, Log Pearson Type III (LP3), Gumbel, Generalized Extreme Value (GEV), and Generalized Pareto (GP) distributions (the recommended distributions in FLIKE software (School of Civil Engineering, University of Newcastle Australia, Australia, Release_x86_5.0.306.0). Three different goodness-of-fit tests (Chi-Squared, Anderson–Darling, and Kolmogorov–Smirnov) are adopted. This study also examines trends in the observed AMF data using several trend tests. It is found that the LP3 is the best-fit probability distribution at majority of the selected stations, followed by the GP distribution. Although the AMF data at most of the stations show an increasing linear trend, these trends are generally statistically non-significant.

1. Introduction

Floods cause social, economic, and environmental impacts on both individuals and on urban, suburban, and rural communities [1]. Despite scientific advancements, accurately predicting extreme flood events remains a challenge. Enhanced hydrologic design flood estimation is critical to reducing flood vulnerability and the associated losses. Flood frequency analysis (FFA) serves as a key tool for estimating the probability of flood events, supporting flood risk management, urban planning, and resilient infrastructure design [2]. Since design floods/flood quantiles (a flood discharge associated with a return period) are used in the planning and design of hydraulic structures, its accuracy directly influences economic investments in flood affected regions [3]. FFA is a widely adopted method due to its practicality and straightforward application—requiring only recorded flood data while assuming hydrologic independence [4]. Additionally, FFA provides confidence limits to evaluate reliability of estimated design floods. At-site FFA is the most direct method of design flood estimation, and it also serves as a benchmark for other methods like regional flood frequency analysis (RFFA) and rainfall–runoff modelling.

Selecting an appropriate probability distribution in FFA remains challenging due to limited observational data relative to the long return periods of interest, e.g., 100 years [5,6]. Recent studies highlight regional variations in optimal probability distributions: Wakeby and Kappa perform best in Brazil [7], while Generalized Extreme Value (GEV) outperforms Gumbel in other regions. Globally, Log Pearson Type III (LP3) is preferred in the USA, Generalized Logistic (GLO) in the UK, and Pearson Type III (PE3) in China [8]. In Australia, three-parameter distributions (e.g., LP3, GEV, and Generalized Pareto (GP) distribution) provide more consistent flood quantile confidence intervals than two-parameter ones [9]. The LP3 and GEV with L-moments have proven particularly reliable for design flood estimates [10]. However, the distribution performance can vary by event, as seen in the Swat River, where Cauchy and Log-Logistic distributions were optimal for different floods [11]. Additionally, flood quantile estimates are highly sensitive to maximum recorded flows, especially in block maxima methods [12].

Goodness-of-fit (GoF) tests are commonly used in FFA for evaluating the suitability of probability distributions, where the Chi-Squared (C-S), Kolmogorov–Smirnov (K-S), and Anderson–Darling (A-D) tests are widely used. The A-D test is particularly sensitive to tail behavior—critical for extreme events [13]. Recent studies advocate combining traditional GoF tests with information criteria (e.g., Akaike information criterion (AIC) and Bayesian information criterion (BIC)) and L-moment diagnostics for robust model selection in FFA [14]. For instance, GEV and LP3, when assessed using A-D, provide reliable uncertainty bounds for the estimated design floods [9].

Conventional FFA assumes stationarity—i.e., flood events are independent and identically distributed (IID) over time [15,16]. However, climate change and land-use change can introduce non-stationarity, altering the statistical properties of annual maximum floods (AMFs) [17,18]. Despite this, stationary models remain prevalent in design flood estimation by FFA, underscoring the need for non-stationary FFA approaches [19]. Trend detection in flood data is the critical first step toward non-stationary FFA [20].

In Australia, flooding due to high-intensity rainfall events is one of the costliest natural disasters [21,22], resulting in devastating losses of human life and damage to critical infrastructure and agriculture. For example, the 2010–2011 Australian flood ranks among the nation’s worst natural disaster, impacting its three eastern states badly. In this flood event, approximately 75% of Queensland was declared a disaster zone, with 35 fatalities, over 200,000 people affected, and public infrastructure damages estimated at $5–6 billion [1,23]. The February–March 2022 flood in Southeast Queensland and coastal New South Wales (NSW) is also one of the costliest floods in Australian recent history, causing damage over $6.4 billion [24].

Brisbane, the capital of Queensland, Australia, exhibits high susceptibility to flooding, attributable to its location within the Brisbane River basin and a climate characterized by significant rainfall variability. The devastating historic flood events (e.g., 1893, 1974, 2011, and 2022) serve as stark reminders of the profound social, economic, and environmental impacts of floods on the Brisbane region. Despite this vulnerability, the Brisbane River basin has a paucity of in-depth flood estimation studies and a notable absence of recent investigations into long-term trends in the flood data [25]. Therefore, this study aims to enhance flood estimation through FFA within the Brisbane River basin using observed AMF data. Specifically, this research performs at-site FFA, identifying the best-fit probability distribution via various GoF tests. Additionally, the study investigates the trends within the AMF data, acknowledging that detecting trends in flood data, even if not statistically significant, necessitates reassessment of the flood protection infrastructure [26]. This study will serve as a basis of practical flood risk assessments of the Brisbane River and similar basins in Australia.

2. Material and Methods

This study focuses on the Brisbane River basin in Queensland, Australia—a region highly prone to flooding. Located in southeast Queensland, the catchment spans from the Great Dividing Range upstream to Moreton Bay downstream, covering 13,570 km² (mostly rural) and including the Brisbane River, Lockyer Creek, and Bremer River [27]. Streamflow data from gauges (Figure 1) with records of at least 20 years were analyzed, including some with over 90 years of observed AMF data. Most records are post-1960, with daily and annual maximum flow series, sourced from Queensland’s Department of Natural Resources and Mines.

The overall approach adopted in this study (Figure 2) consists of (i) selection of candidate probability distributions, (ii) selection of suitable parameter estimation methods, (iii) goodness-of-fit (GoF tests) to select suitable probability distributions, (iv) flood quantile estimation and sensitivity analysis, and (v) trend detection using parametric and non-parametric tests.

This study employs two widely used software packages for FFA: EasyFit (Version 5.6) and FLIKE (Release_x86_5.0.306.0). EasyFit offers comprehensive distribution fitting and facilitates robust statistical analysis including GoF tests [28,29]. FLIKE, aligned with ARR (2019), uses Bayesian/L-moment methods to fit five key distributions: Lognormal (LN), LP3, Gumbel (Extreme Value Type I), GP, and GEV [30]. This study employed several parameter estimation methods i.e., Method of Moments (MoM), Maximum Likelihood Estimation (MLE), and L-moments. The parameter estimation using EasyFit software (Version 5.6) [28,29] was carried out with MoM for Gumbel and LP3 distributions; MLE for LN distribution, and Method of L-moments for GEV and GP distributions. The reasons for selecting these five probability distributions are that these are the most commonly used FFA distributions in Australia [2,31] and have been included in the FLIKE software as part of the ARR 2019. This list includes both two- and three-parameter distributions, which are likely to capture the parent distribution at the selected stations in the study area.

Three goodness-of-fit (GoF) tests were adopted, namely the Anderson–Darling (A-D) test, Chi-Squared (C-S) test, and Kolmogorov–Smirnov (K-S) test, to identify the best-fit distribution for the sample of AMF data. The fundamental approach of these tests is similar; however, each test differs in its formulation for calculating the test statistic and determining the critical value, leading to potentially varied results across different tests for the same dataset. For instance, the A-D test might indicate LP3 as the best fit, while the K-S test might rank it as second-best for the identical AMF data series. In such scenarios, visual inspection of the graphical representations (e.g., probability plots, QQ plots, histograms with fitted PDFs) becomes crucial to provide a more holistic and informed decision regarding the most appropriate probability distribution.

The GoF tests in this study were carried out using EasyFit, software [28,29]. Once AMF data have been uploaded, EasyFit evaluates the distributions, and the test statistics and critical values at various significance levels are presented in a tabular form [28,29]. Several FFA studies have been completed using EasyFit software [32,33]. Singo et al. [34] applied this software for FFA in South Africa, and Kamal et al. [35] in the Ganga River at Haridwar and Garhmukteshwar.

The K-S test uses empirical CDFs and theoretical CDFs to calculate the test statistics. The K-S test statistic (D) is the maximum vertical difference between the empirical CDF (P(Xn)) and the theoretical CDF (F(Xn)) and is expressed as D = max|P(Xn) − F(Xn)|, where P(Xn) is the empirical CDF of observed random sample of n ordered observations, and F(Xn) is the theoretical CDF for each of the ordered observations [36]. When the test statistic D becomes smaller than the critical value, then the observed data are considered to have a good fit with the assumed distribution.

The A-D test is a distribution-free or non-parametric test. The A-D test compares expected (theoretical) CDFs to an observed CDFs. The A-D test statistic (A2) can be expressed as [37]

A² = −n − S

(1)

where

$$S={\displaystyle \frac{1}{n}}\sum _{i=1}^n(2i-1)\left[\mathrm{l}\mathrm{n}F(X_{\left(i\right)})+\mathrm{l}\mathrm{n} (1-F (X_{(n+1-i)}))\right]$$

(2)

Here, n is the sample size; Y1, Y2, Y3, Y4, … Yn are the sample data; and F = CDF [37].

If the test statistic A² is higher than critical value, the null hypotheses is rejected.

The C-S statistical hypothesis test is a non-parametric test. In this test, the observed data are grouped into a number of bins (k). Based on the size of sample data, the number of bins can be calculated using an empirical expression where N is the size of the k = 1+ log₂N sample. The Chi-Squared GoF test statistic is

$$\chi 2={\sum }_{i=1}^k{\left(Oi-Ei\right)}^2/E_i$$

(3)

where Ei is the expected frequency for bin i, Oi is the observed frequency for bin i [36] with $F\left(x_2\right)-F\left(x_1\right)$, where x₁ and x₂ are the limits for bin i and F is the CDF of the expected distribution. The null hypothesis is rejected in this test when the test statistic is higher than the critical value, i.e., a statistically significant difference exists between expected and observed value.

Several statistical tests are used to detect non-homogeneities, trends, and change points in hydrological data [38]. Although past studies have examined trends, comprehensive trend analysis of the Brisbane River’s flood data—accounting for recent climate and urbanization impacts—remains limited. A simple quick way to check the presence of a trend in data is to divide the data series into two-time spans and then compute the mean and variance of each time span. If these statistics (mean, variance) of these two sub-data series differ significantly, then there may exist a trend in the data series, and the time series is likely to be non-stationary.

For robust analysis, this study applies 12 parametric and non-parametric tests (e.g., the Mann–Kendall, Spearman’s Rho, Rank-Sum, Rank Difference, Turning Point, distribution-free CUSUM, and Median Crossing non-parametric tests; linear regression, autocorrelation, Student’s t, Worsley Likelihood Ratio, and cumulative deviation parametric tests for trend analysis) using TREND software (Version 1.0.2) [39,40]. These tests assess trends, step changes, and randomness at the 1%, 5%, and 10% significance levels [41,42,43].

Table 1. Different trend tests and their features.

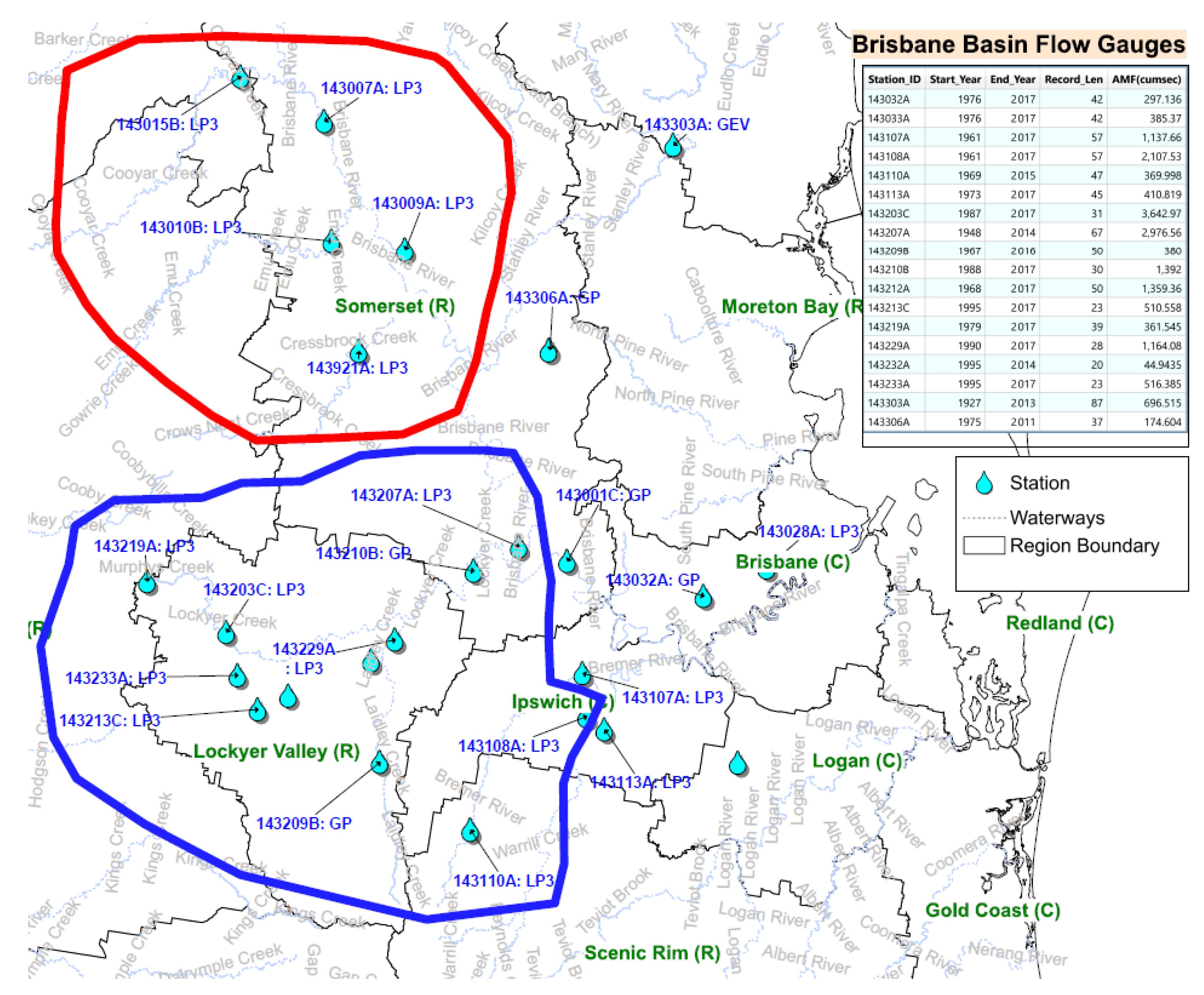
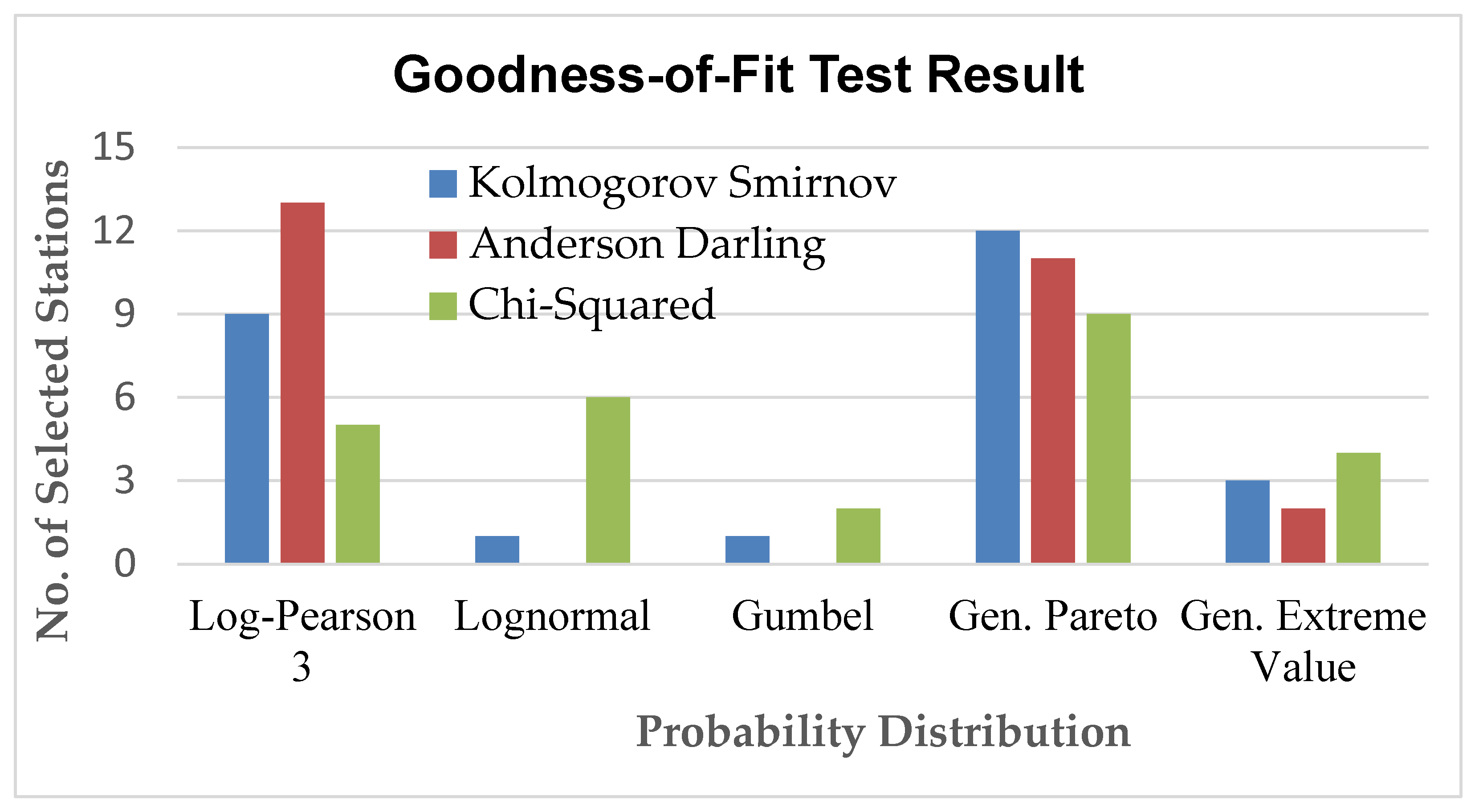
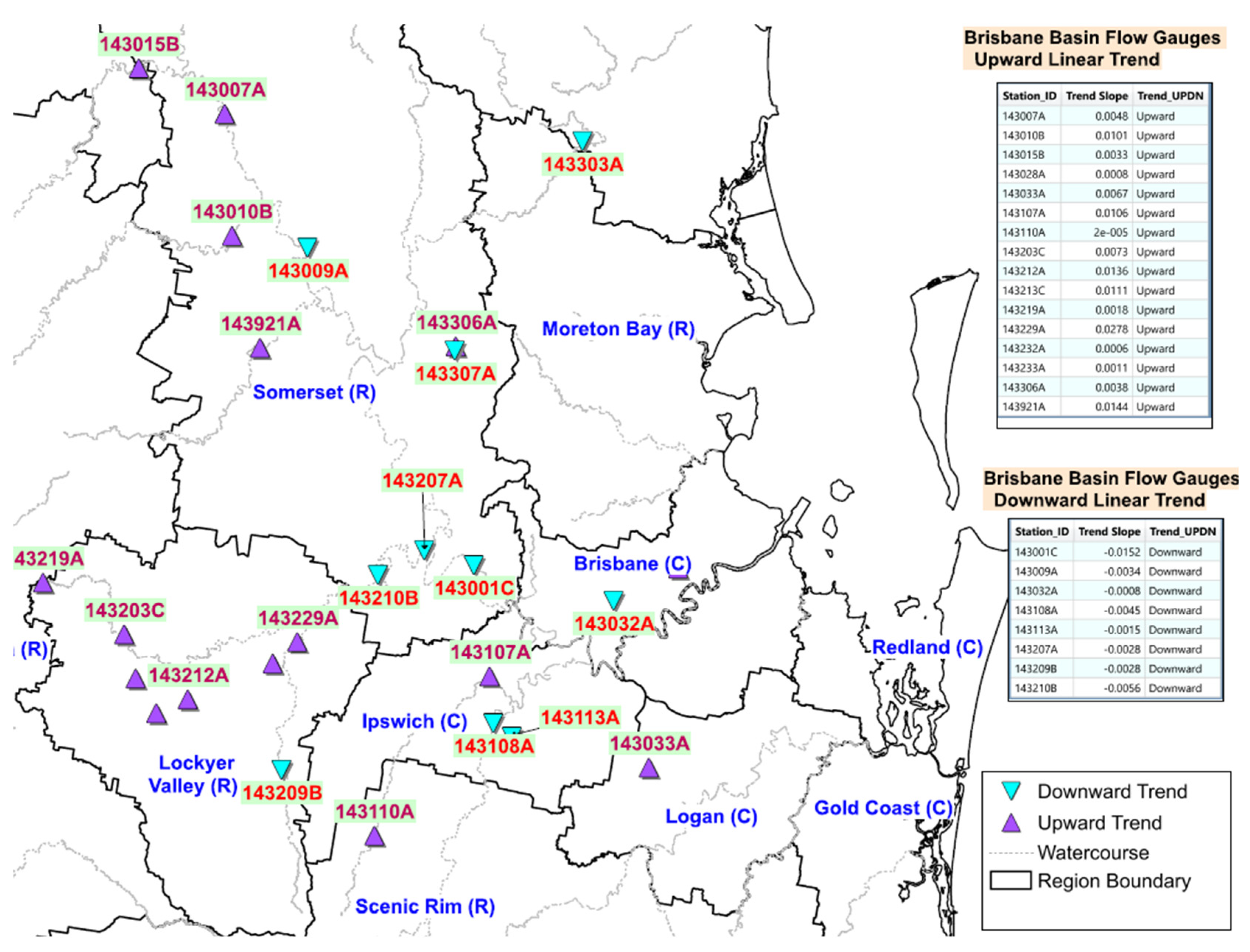
Test	Type	Key Feature	Merits	Demerits
Mann–Kendall	Non-parametric	Rank-based monotonic trend	Robust, handles missing data	Sensitive to autocorrelation
Spearman’s Rho	Non-parametric	Rank correlation	Simple, robust	Less powerful for small datasets
Rank-Sum	Non-parametric	Two-sample shift test	Detects shifts, robust	Cannot detect gradual trends
Rank Difference	Non-parametric	Rank changes over time	Simple, small-sample friendly	Low power
Turning Point	Non-parametric	Randomness test	Easy, detects irregular patterns	Poor for monotonic trends
Distribution-Free CUSUM	Non-parametric	Cumulative deviation from the median	Detects small shifts	Sensitive to autocorrelation
Median Crossing	Non-parametric	Counts median crossings	Very simple	No trend magnitude
Linear Regression	Parametric	Fits straight line	Magnitude and direction	Assumption-heavy
Autocorrelation	Parametric	Lagged correlation	Detects persistence	Not a trend test itself
Student’s t	Parametric	Mean comparison	Simple, powerful	Needs normality
Worsley Likelihood Ratio	Parametric	Change-point detection	Powerful	Complex
Cumulative Deviation	Parametric	Cumulative deviation from the mean	Visual + statistical	Sensitive to outliers

summarizes the features of each of these trend tests. Here, the 10% significance level is used to interpret the results of trend analysis, since this is likely to indicate trends for a greater number of stations.

Table 2. Methods/software used in this study.

Analysis	Software/Method	Reason
Goodness-of-fit test (Anderson–Darling (A-D) test, Chi-Squared (C-S) test, and Kolmogorov–Smirnov (K-S))	EasyFit	A widely used software tool used to carry out goodness-of-fit tests involving numerous probability distributions
Flood frequency analysis (FFA): Lognormal (LN), LP3, Gumbel (Extreme Value Type I), GP, and GEV	FLIKE (Release_x86_5.0.306.0)	This is the recommended software in ARR 2019 [2]
Trend analysis (Mann–Kendall, Spearman’s Rho, Rank-Sum, Rank Difference, Turning Point, distribution-free CUSUM and Median Crossing non-parametric tests; linear regression, autocorrelation, Student’s t, Worsley Likelihood Ratio, and cumulative deviation parametric tests for trend analysis)	TREND (Version 1.0.2)	This is widely used in Australia for trend detection in hydrological time series
Sensitivity analysis	Excel	Easy to use

lists the different software tools and methods used in this study.

3. Results

The GoF test results show that some stations share the same best-fit probability distribution across all three tests—an ideal outcome. However, most stations exhibit variation in the selected probability distribution. To resolve this, a scoring system is applied i.e., ranking the distributions on the basis of their performance across tests. The distribution with the lowest total rank score is selected as the best fit for each station. The results of the A-D, K-S, and C-S tests for station 143009A are summarized in

Table 3. GoF test statistics for five candidate probability distributions used to fit AMF data for Station 143009A (bold values indicate the best-fit probability distribution as per the GoF tests).

Distribution	Kolmogorov–Smirnov (K-S)		Anderson– Darling		Chi-Squared		Avg. Rank
	Statistics	Rank	Statistics	Rank	Statistics	Rank
Log Pearson Type III	0.0709	1	0.4011	1	0.8621	1	1.0
Lognormal	0.0753	2	0.4232	2	1.1246	2	2.0
Generalized Pareto	0.1541	4	1.5218	3	3.5449	3	3.3
Gen. Extreme Value	0.1450	3	1.7200	4	3.6029	4	3.7
Gumbel	0.3079	5	7.1698	5	14.5870	5	5.0

, which shows that the LP3 distribution best fits the AMF data for this station. The test statistics for all other stations are shown in the Supplementary Section (Tables S1–S23).

Figure 3 shows a summary of the GoF test results with Rank 1 for selected stations.

Table 4. Rankings of probability distributions for 26 stations based on the A-D GoF test.

Station	Probability Distribution Corresponding to Ranks of the A-D GoF Test
	I	II	III
143001C	GP	LP3	Lognormal
143007A	LP3	Lognormal	GP
143009A	LP3	Lognormal	GP
143010B	LP3	Lognormal	GP
143015B	LP3	Lognormal	GP
143028A	LP3	GEV	Lognormal
143032A	GP	LP3	GEV
143033A	GP	LP3	Lognormal
143107A	LP3	GEV	Lognormal
143108A	LP3	GEV	Lognormal
143110A	LP3	GEV	Lognormal
143113A	LP3	Lognormal	GEV
143203C	LP3	GEV	Lognormal
143207A	LP3	Lognormal	GP
143209B	GP	GEV	LP3
143212A	LP3	Lognormal	GP
143219A	LP3	Lognormal	GP
143229A	LP3	Lognormal	GP
143303A	GEV	LP3	Gumbel
143921A	LP3	Lognormal	GP
143210B	GP	GEV	LP3
143306A	GP	LP3	GEV
143213C	LP3	Lognormal	GP
143232A	LP3	GEV	Gumbel
143233A	LP3	GP	GEV
143307A	GP	LP3	Lognormal

presents the selected probability distributions for the 26 stations, based on A-D test rankings of first, second, and third place. Table 4 shows that LP3 ranks first for 18 of 26 stations (69%) based on the A-D test, while GP ranks second for 7 stations (23%). Statistics of the probability distribution range for the K-S and for C-S GoF tests are in the Supplementary Section (Tables S24 and S25). The average rankings from three GoF tests (A-D, K-S, and C-S) are computed for Ranks 1, 2, and 3.

Table 5. Summary of GoF results (Rank 1 distribution for all the stations).

Probability Distribution	K-S GoF Test	A-D GoF Test	C-S Test	All Stations
Method	Number of Stations with GoF Test, Rank 1			Avg. No. of Stations
Log Pearson Type III	7	18	7	11
Lognormal	1	0	5	2
Gumbel	1	0	0	0
Generalized Pareto	11	7	5	8
Gen. Extreme Value	6	1	9	5

presents the average Rank 1 results, with LP3 emerging as the most preferred probability distribution for 11 stations, followed by GP for 8 stations. Gumbel was not selected as the best fit for any station. The Supplementary Section (Tables S26 and S27) provides results for Ranks 2 and 3. In

Table 6. Summary of GoF results (Ranks 1, 2, and 3 for all stations with weights for Rank 1, Rank 2, and Rank 3).

Probability Distribution	K-S GoF Test	A-D GoF Test	C-S GoF Test	K-S GoF Test	A-D GoF Test	C-S GoF Test	K-S Gof Test	A-D GoF Test	C-S GoF Test	All Stations
Method	Number of Stations with GoF Test Rank 1			Number of Stations with GoF Test Rank 2			Number of Stations with GoF Test Rank 3			Avg. No. of Stations
	Weight = 3			Weight = 2			Weight = 1
LP3	21	54	21	28	12	16	4	2	10	10
LN	3	0	15	14	22	6	5	8	6	4
Gumbel	3	0	0	2	0	6	1	2	2	1
GP	33	21	15	4	2	10	6	10	5	6
GEV	18	3	21	4	16	14	10	4	3	5

, a weighted scoring system (Rank 1 × 3, Rank 2 × 2, Rank 3 × 1) further confirms LP3 as the most preferred probability distribution for 10 of 26 stations, followed by GP. Gumbel remains the least preferred, selected as Rank 1 by only one station with the K-S test.

Figure 4 illustrates the spatial distribution of best-fit probability distributions based on the A-D test. LP3 is predominantly the best-fit probability distribution in the upper, mountainous regions of the basin, while GP is more common downstream. Overall, LP3 dominates most of the Brisbane River basin, highlighting its suitability across varied terrain within a large river basin. It is seen from the box plot of the catchment area and the best-fit distribution (Figure 5) of the selected stations that there is a weak relationship between catchment area and the best-fit probability distribution, although larger catchments tend to follow the LP3 distribution, as indicated by the higher third quartile value and the high outliers in Figure 5 (right boxplot representing catchment areas associated with the LP3 distribution).

FLIKE-generated probability plots display estimated quantile lines from candidate distributions, the AMF data, and the confidence limit. The Y-axis of the FLIKE probability plot is the estimated quantile and the observed AMF, and the x-axis is an annual exceedance probability (AEP) of 1 in Y. FLIKE-estimated quantile plots for all five probability distributions of Station 143015B are shown in Figure 6. FLIKE-estimated quantiles for the other stations are provided in the Supplementary Section (Figures S1–S25). Figure 6 shows that for Station 143015B, the LP3 distribution provides the best fit for flood quantile estimation, supported by the A-D GoF test. While the results from EasyFit and FLIKE differ slightly, both indicate LP3 as the most suitable distribution for this station. This aligns with the previous studies of Rahman et al. [5], who identified LP3 to be the most appropriate distribution for at-site FFA across Australia. The LP3 was also recommended in the ARR [42], though the later edition [2] does not specify a preferred probability distribution. Similarly, Zaman et al. [44] recommended LP3 and GEV as the best-fit distributions for most Australian stations.

Table 7. Quantile estimates by five different probability distributions for Station 143001C and the percentage difference from the LP3 distribution.

ARI (year)	Quantile Estimate AMF (m3/s)—LP3	Quantile Estimate AMF (m3/s)—LN	Quantile Estimate AMF (m3/s)—Gumbel	Quantile Estimate AMF (m3/s)—Generalized Pareto	Quantile Estimate AMF (m3/s)—GEV
2	315	291 (92%)	545 (173%)	366 (116%)	811 (257%)
5	1549	1379 (89%)	1800 (116%)	1412 (91%)	1953 (126%)
10	3067	3113 (102%)	2632 (86%)	3119 (102%)	3074 (100%)
20	5020	6097 (121%)	3429 (68%)	6469 (129%)	4540 (90%)
50	8134	12,991 (160%)	4461 (55%)	16,297 (200%)	7238 (89%)
100	10,784	21,512 (199%)	5235 (49%)	32,337 (300%)	10,084 (94%)
200	13,598	34,131 (251%)	6005 (44%)	63,821 (469%)	13,892 (102%)
500	17,451	59,714 (342%)	7022 (40%)	156,166 (895%)	20,976 (120%)

shows the estimated flood quantiles for Station 143001C with five different probability distributions. It is seen from the table that flood quantiles with the Gumbel and Lognormal distributions are notably different than those with the LP3, GP, and GEV distributions (a similar result was found for all the stations). The FLIKE flood quantile plot with LP3 shows (Figure 6) that at low return periods, a good match is observed between the observed AMF and quantile values for several distributions. However, for higher return periods, especially the 100-year return period, it becomes more difficult to choose the most preferred distribution. Overall, the majority of stations show that the LP3 distribution fits relatively better to the observed AMF data.

Table 8. Goodness-of-fit test result summary of 26 stations excluding outliers in the data.

Station	Observed Qmax/Q2011 (m3/s)	Estimated Quantile with T = 100 yrs; Q100 (m3/s)	% Difference (Quantile/Observed)
143203C	3643	1989	55
143219A	362	348	96
143108A	2108	2117	100
143303A	710	721	102
143107A	2057	2107	102
143113A	411	434	106
143001C	9533	10,784	113
143028A	133	159	119
143209B	349	416	119
143207A	2977	3582	120
143033A	385	469	122
143010B	2036	2600	128
143015B	2335	3080	132
143306A	175	231	132
143307A	462	624	135
143210B	1401	1958	140
143110A	370	520	141
143232A	45	63	141
143212A	1359	2213	163
143032A	297	533	179
143921A	590	1058	179
143213C	511	927	182
143007A	4404	8240	187
143229A	1395	3606	259

shows that the observed AMF values in 2011 (Q₂₀₁₁) (a devastating flood occurred in the Brisbane region in 2011) are larger than the estimated 100-year flood quantiles for two stations, and three stations are similar to Q₂₀₁₁; however, in 21 cases, the Q₂₀₁₁ values are smaller than the 100-year flood level.

The AMF data of all the 26 stations were analyzed for the presence of outliers, and outliers in data series were identified and removed from the AMF data to evaluate how this removal affects the distributional fitting and parameter estimation. Each station’s AMF data were checked for the presence of outliers using the inbuilt tool of FLIKE software. The GoF test results with and without outliers differ for 12 stations out of 26 stations, although LP3 is the more appropriate probability distribution for both scenarios. The quantile estimation with and without outliers in the AMF data varies up to a maximum of 47%. Rahman et al. [45], in their study on eastern Australia, also found a high difference of up to 60% in quantile estimates due the presence of outliers.

FFA results may be changed if the highest flood record from the AMF data series is ignored. To investigate the sensitivity of the selection of the best-fit probability distribution and quantile estimation, FFA was carried out by removing the highest flood record from the AMF data series at a station, and by removing the two and three highest flood records. Figure 7 shows the best-fit distribution with three different GoF tests without the highest flood event from each of the 26 stations’ AMF data.

Figure 7 demonstrates that removing the highest AMF data point alters the GoF test outcomes, with GP emerging as the preferred distribution, followed by LP3. In contrast, when the full AMF series is retained, LP3 remains the best fit (Figure 3). Further exclusion of the top three AMF values increases the preference for GP across more stations, indicating the sensitivity of distribution selection to extreme values in the AMF data series. Extreme events in AMF data significantly influence flood quantile estimates.

Table 9. Q₅₀ and Q₁₀₀ flood quantiles with the full AMF data and without the highest, second highest, and third highest AMF data points.

Station	Full AMF Data	Full AMF Data	1 Highest AMF Records Removed	1 Highest AMF Records Removed	2 Highest AMF Records Removed	2 Highest AMF Records Removed	3 Highest AMF Record Removed	3 Highest AMF Record Removed
	Q50 m3/s	Q100 m3/s	Q50 m3/s	Q100 m3/s	Q50 m3/s	Q100 m3/s	Q50 m3/s	Q100 m3/s
143001C	8134	10,784	6766	9090	3606	4033	3108	3410
143007A	5389	8240	4252	6228	3726	5408	3263	4704
143009A	11,842	19,085	9982	15,796	8358	12,930	7001	10,607
143010B	1878	2600	1353	1760	1267	1761	980	1313
143015B	2205	3080	1280	1581	1195	1493	1006	1217
143028A	131	159	109	129	97	113	77	85
143032A	379	533	308	422	216	270	186	227
143033A	415	469	370	417	331	370	300	331
143107A	1671	2107	1123	1271	1039	1164	879	937
143108A	1622	2117	1292	1642	1114	1385	913	1083
143110A	447	520	429	499	410	475	392	455
143113A	369	434	224	235	224	238	225	243
143203C	1395	1989	946	1231	670	745	614	678
143207A	3009	3582	2700	3173	2561	3037	2327	2743
143209B	387	416	394	426	366	398	350	379
143210B	1558	1958	1488	2385	1111	1660	820	1108
143212A	1696	2213	1486	1939	1340	1758	1224	1639
143213C	772	927	551	740	336	416	243	302
143219A	212	348	91	123	70	92	60	78
143229A	2305	3606	1134	1372	685	932	423	493
143232A	55	63	43	47	43	49	41	47
143233A	993	1645	344	449	346	478	303	432
143303A	658	721	585	625	607	658	563	605
143306A	208	231	214	238	171	186	163	178
143307A	517	624	446	533	380	450	317	356
143921A	758	1058	641	1000	208	239	172	199

compares quantiles after sequentially removing the highest one, two, and three AMF values. The results show that excluding just the highest value alters Q₁₀₀ estimates by 9% to 86% (mean: 48%), highlighting the sensitivity of flood estimates to high floods. This underscores the need to update FFA following major flood events to ensure infrastructure safety and community resilience. For infrastructure design and flood risk assessment at a given catchment, it is important that the highest AMF data point is not removed in FFA as a high outlier, since its removal would result in much lower design flood estimates for higher return periods (e.g., 100 years). This could lead to under-design of water infrastructure, which is likely to increase future flood damage in the given catchment. To understand the impacts of outliers on FFA results more explicitly, an uncertainty analysis should be conducted using Monte Carlo simulation, as in Khan et al. [9]; however, this is left for future investigation. Care should be exercised so that under-design is not likely to increase the flood damage. For important/sensitive infrastructure (e.g., hospitals and airports), to avoid under-design, several probability distributions to be adopted for FFA, and also RFFA and rainfall runoff models need to be utilized to obtain candidate design flood estimates, which could assist in selecting an optimum design flood estimate for a given infrastructure to reduce the overall flood damage.

We evaluated trends and abrupt changes in AMF data for all 26 stations using 12 statistical tests at the 1%, 5%, and 10% significance levels (

Table 10. Trend test statistics and their critical values for the AMF series at Station 14301B.

Test Name	Test Statistic for Each Test	Critical Values of Trend Test Statistics for Significance Levels			Critical Values of Trend Test Re-Sampling Statistics for Significance Levels			Result
		a = 0.1	a = 0.05	a = 0.01	a = 0.1	a = 0.05	a = 0.01
Mann–Kendall	−1.80	1.65	1.96	2.58	1.64	1.92	2.51	S (0.1)
Spearman’s Rho	−1.73	1.65	1.96	2.58	1.69	1.98	2.57	S (0.1)
Linear regression	0.28	1.68	2.01	2.69	1.72	2.09	2.75	NS
CUSUM	8.00	8.54	9.52	11.41	9.00	10.00	12.00	NS
Cumulative deviation	0.84	1.14	1.27	1.52	1.14	1.28	1.48	NS
Worsley Likelihood Ratio	2.35	2.87	3.16	3.79	3.64	5.98	7.48	NS
Rank-Sum	1.87	1.65	1.96	2.58	1.67	1.99	2.65	S (0.1)
Student’s t	−0.01	1.68	2.01	2.69	1.66	1.92	2.27	NS
Median Crossing	0.58	1.65	1.96	2.58	1.73	2.02	2.31	NS
Turning Point	0.23	1.65	1.96	2.58	1.84	2.19	2.99	NS
Rank Difference	−1.07	1.65	1.96	2.58	1.61	1.85	2.61	NS
Autocorrelation	1.22	1.65	1.96	2.58	1.50	1.77	2.71	NS

Note: ‘NS’ is statistically not significant at the 10% level; ‘S’ is significant at the 10% level.

presents the results for a station). A summary of the trend analysis tests for all selected stations is shown in

Table 11. Trend test summary for all the 26 stations’ AMF data (NS, non-significant trend; S, significant trend).

Station Number	Mann-Kendall	Spearman’s Rho	Linear Regression	Cusum	Cumulative Deviation	Worsley Likelihood	Rank Sum	Student’s t	Median Crossing	Turning Point	Rank Difference	Auto Correlation	Linear Regression Slope
143001C	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	−Ve
143007A	NS	NS	NS	NS	NS	NS	S (0.05)	NS	NS	NS	NS	NS	+Ve
143009A	NS	NS	NS	NS	NS	NS	S (0.1)	NS	NS	NS	NS	NS	−Ve
143010B	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	+Ve
143015B	S (0.1)	S (0.1)	NS	NS	NS	NS	S (0.1)	NS	NS	NS	NS	NS	+Ve
143028A	NS	NS	NS	S (0.1)	S (0.1)	NS	NS	NS	NS	NS	NS	NS	+Ve
143032A	NS	NS	NS	NS	NS	NS	NS	S (0.1)	NS	NS	NS	NS	−Ve
143033A	NS	NS	S (0.1)	NS	S (0.05)	S (0.05)	NS	NS	S (0.1)	NS	S (0.1)	NS	+Ve
143107A	NS	NS	NS	NS	S (0.1)	S (0.1)	NS	NS	NS	NS	NS	NS	+Ve
143108A	NS	NS	NS	NS	NS	NS	NS	NS	S (0.05)	S (0.1)	S (0.1)	NS	−Ve
143110A	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	+Ve
143113A	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	−Ve
143203C	NS	NS	S (0.1)	NS	NS	NS	NS	S (0.1)	NS	NS	NS	NS	+Ve
143207A	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	−Ve
143209B	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	−Ve
143212A	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	+Ve
143219A	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	+Ve
143229A	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	+Ve
143303A	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	S (0.1)	S (0.1)	−Ve
143921A	NS	NS	S (0.1)	NS	S (0.05)	NS	NS	NS	NS	NS	NS	NS	+Ve
143210B	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	−Ve
143306A	NS	NS	NS	NS	NS	S (0.05)	NS	NS	NS	NS	NS	NS	+Ve
143213C	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	+Ve
143232A	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	+Ve
143233A	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	+Ve
143307A	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	NS	−Ve

, where some test statistics show upward (positive) or downward (negative) trends in the AMF data. The presence of a step jump in the data between two subsets of data within the data series is evaluated using the distribution-free CUSUM test, cumulative deviation test, and Worsley Likelihood Ratio test. The summary result (Table 11) shows that a limited number of stations’ AMF data have a step jump at the 10% significance level. It is seen in Table 11 that 21 stations’ AMF data have a mild positive slope in their linear regression line and 5 stations’ data have a negative slope. Figure 8 presents a layout map with statistically significant trends in the AMF data at the 10% significance level for all the stations. Most of the 12 statistical trend tests detected no significant trend in the AMF series across the 26 stations (Table 11). Only Station 143015B (Cooyar Creek, 953 km²) shows a trend at the 10% significance level in the MK and Spearman’s Rho tests. This upstream catchment is largely unaffected by human activity, and its highest AMF (853 m³/s) occurred in 2011.

For Station 143033A (Figure 8) at Oxley Creek (New Beith, Queensland), the linear regression test indicated a trend at the 10% level, while the MK and Spearman’s Rho tests do not (Table 11). This creek, flowing about 50 km into Brisbane River, has experienced extensive sand extraction and modification works, altering its channel geometry [41]. These human-induced changes likely influence flow behavior, suggesting that observed trends may result from land-use changes rather than climate variability.

Across the Brisbane River basin, analyses of the AMF data show no major significant trends or step jumps. The regression lines slope in Figure 8 revels upward/increasing trend for most of the stations (specially stations upstream of the basin). However, a few stations show downward (negative) or decreasing trends, located mainly downstream of the basin. Step-jump tests (distribution-free CUSUM, cumulative deviation and Worsley Likelihood Ratio) detected no significant shifts except for Stations 143028A and 143107A at 10% significance. Similarly, Rank-Sum and Student’s t-tests found no notable median or mean differences across most stations, except for 143009A, 143015B, 143032A, and 143203C. Randomness tests (Turning Points, Median Crossing, Rank Difference, autocorrelation) confirmed consistent patterns in the AMF data, with minor exceptions (143033A, 143108A). Overall, the statistical tests reveal that the consistent/significant trends or step jumps in AMF are not significant at the regional level within the Brisbane River basin. The identified minor trends in the AMF data could be due to land use or climate changes, which are yet to be identified. Similar trends in the AMF data were reported by Haddad and Rahman [46] in Tasmania, Australia, and by Robson et al. [47] in the UK, where few or no significant trends were found in the AMF data. As the trend analysis results (presented above) do not generally detect a statistically significant trend, step jump, mean difference, or median difference for the Brisbane River basin at the 10% significance level, non-stationary FFA was not conducted. Non-stationary FFA is left for future research efforts.

4. Discussion

Our finding of LP3 as the best-fit distribution for 69% of the selected stations in the Brisbane River basin aligns with Rahman et al.’s [45] study. However, Australian studies by Haddad and Rahman [46] found GEV to outperform LP3 in southeastern Australian catchments. The Australian Rainfall and Runoff (ARR) 1989 version (third edition) recommended the LP3 distribution for general use in Australia for FFA [42]. However, the latest version (ARR 2019) did not recommend any particular distribution for FFA in Australia [2]. The recommended candidate distributions for FFA in Australia as per ARR 2019 include LP3, GEV, GPA, Gumbel, and Lognormal (LN) distributions [2,30]. Table 12 summarizes the results from the few recent FFA studies, both those agreeing with and contradicting this study. It should be noted that this study assumes independence in the AMF series and does not examine autocorrelation, spatial correlation, or field significance.

Quantile estimates from FLIKE plots support the choice of LP3 as the preferred probability distribution for the Brisbane River basin, especially for low to medium return periods. However, uncertainty increases significantly at high return periods (e.g., the 100-year return period) which is crucial for long-term planning and infrastructure design. Monte Carlo simulation (as available in FLIKE) was adopted in this study, but Bayesian posterior uncertainty for the model parameters was not explored in depth. The minimum record length of the AMF data is 20 years for a few of our stations. The record length of AMF data in FFA has a significant and often critical impact on the accuracy and uncertainty of quantile estimates, especially for higher return periods [48,49]. Hence, caution should be applied in interpreting the results of this study for the higher return periods (e.g., 100 years and higher).

A uniform probability distribution cannot be recommended for the Brisbane River basin, which indicates that the ARR 2019 [2] recommendation is valid, as this does not recommend using any common probability distribution for Australia, unlike ARR 1989, which suggested LP3 as the common probability distribution for FFA across Australia.

Non-stationary FFA is a growing field that incorporates time-varying covariates (e.g., climate indices and land cover) into the flood estimation procedure, which needs to be adopted in further studies. This will allow for dynamically updating flood risk estimates, aligning better with observed trends. While promising, non-stationary models require longer and higher-quality datasets, which are not always available. Moreover, the incorporation of future climate projections adds further uncertainty, which must be carefully quantified and communicated to decision-makers. Furthermore, combining statistical, hydrological, and machine learning approaches can yield more robust and flexible models capable of handling complex environments and evolving flood risks in a flood-affected region like the Brisbane River basin.

Table 12. Comparison of findings of the present study and other similar studies.

Our Finding	Agreeing Studies	Contradicting Studies	Research Gap Addressed
LP3 as the best-fit probability distribution for the Brisbane River basin	[42,45,50]	[46,51]	Regional distribution suitability
Insignificant AMF trends	[52]	[53]	Trend heterogeneity by region
Quantile estimates under non-stationary conditions	[54,55]	ARR 2019 stationarity assumptions [2]	Non-stationary FFA

Table 12. Comparison of findings of the present study and other similar studies.

Our Finding	Agreeing Studies	Contradicting Studies	Research Gap Addressed
LP3 as the best-fit probability distribution for the Brisbane River basin	[42,45,50]	[46,51]	Regional distribution suitability
Insignificant AMF trends	[52]	[53]	Trend heterogeneity by region
Quantile estimates under non-stationary conditions	[54,55]	ARR 2019 stationarity assumptions [2]	Non-stationary FFA

5. Conclusions

This study presents a comprehensive flood frequency analysis (FFA) for the Brisbane River basin—one of Australia’s most flood-prone regions. By applying several probability distributions and GoF tests, the most suitable probability distributions for characterizing flood events are identified. Trend detection across the basin reveals limited but localized trends in flood magnitudes. The FFA provides insights into temporal variation in the selected best-fit probability distributions, which could be useful for improving flood risk assessments and infrastructure design in the Brisbane River basin. These findings highlight the need for an adaptive approach to flood management in response to ongoing climate change and urban development, supporting more resilient planning and policy decisions in the Brisbane region. The key findings of this study are as follows.

• The LP3 distribution is the most suitable probability distribution for FFA in the Brisbane River basin, followed by the GP distribution.
• The 2011 flood across 26 stations within the basin is generally below the 100-year flood level.
• Goodness-of-fit test results are sensitive to the highest three values of the AMF series and can significantly alter 100-year flood estimates. This suggests that the occurrence of future extreme floods could substantially revise current extreme flood (100-year return level) estimates, necessitating updated FFA after every major flood event to minimize infrastructure and community risks.
• The trend in the AMF data within the Brisbane River basin is not statistically significant.

In light of IPCC AR6 [56] projections of increasing extreme precipitation and flooding under climate change, we recommend periodic FFA updates and non-stationary FFA to improve accuracy and uncertainty quantification in the Brisbane River basin.

FLIKE software, recommended by the ARR, warrants upgradation to include non-stationary FFA. In this regard, the scale parameter of the selected five probability distributions in FLIKE should be made dependent on time and climate change indices.

City councils and relevant government authorities within the Brisbane River basin should conduct flood frequency analysis (FFA) following each major flood event to estimate design floods (e.g., 100-year floods) and assess whether the existing and planned critical flood control infrastructure is sufficient to minimize overall flood damage and strengthen the community’s flood resilience.