Optimal Water Resource Allocation for Urban Water Systems in the Context of Greenhouse Gas Emission Reduction and Recycled Water Utilization
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data Sources
2.1.1. Study Area
2.1.2. Urban Water System in Yiwu City
2.1.3. Data Sources
2.2. Methodology
2.2.1. Estimation of Greenhouse Gas Emission
- (1)
- High-quality water
- (2)
- Recycled water
2.2.2. Estimation of Available Water Resources from Sources
2.2.3. Rime Optimization Algorithm
- (1)
- Soft-rime search strategy
- (2)
- Hard-rime puncture mechanism
- (3)
- Positive greedy selection mechanism
- (4)
- Multiobjective RIME
2.2.4. Regret Theory
2.2.5. Optimal Water Resource Allocation Model
- (1)
- Objective Functions
- (2)
- Constraint conditions
3. Results
3.1. Overview of the Data
3.1.1. Calculation of the Greenhouse Gas Emissions of Different Water Sources
3.1.2. Data on the Available Water Resources and Water Demand
3.2. Optimization of Water Resource Allocation
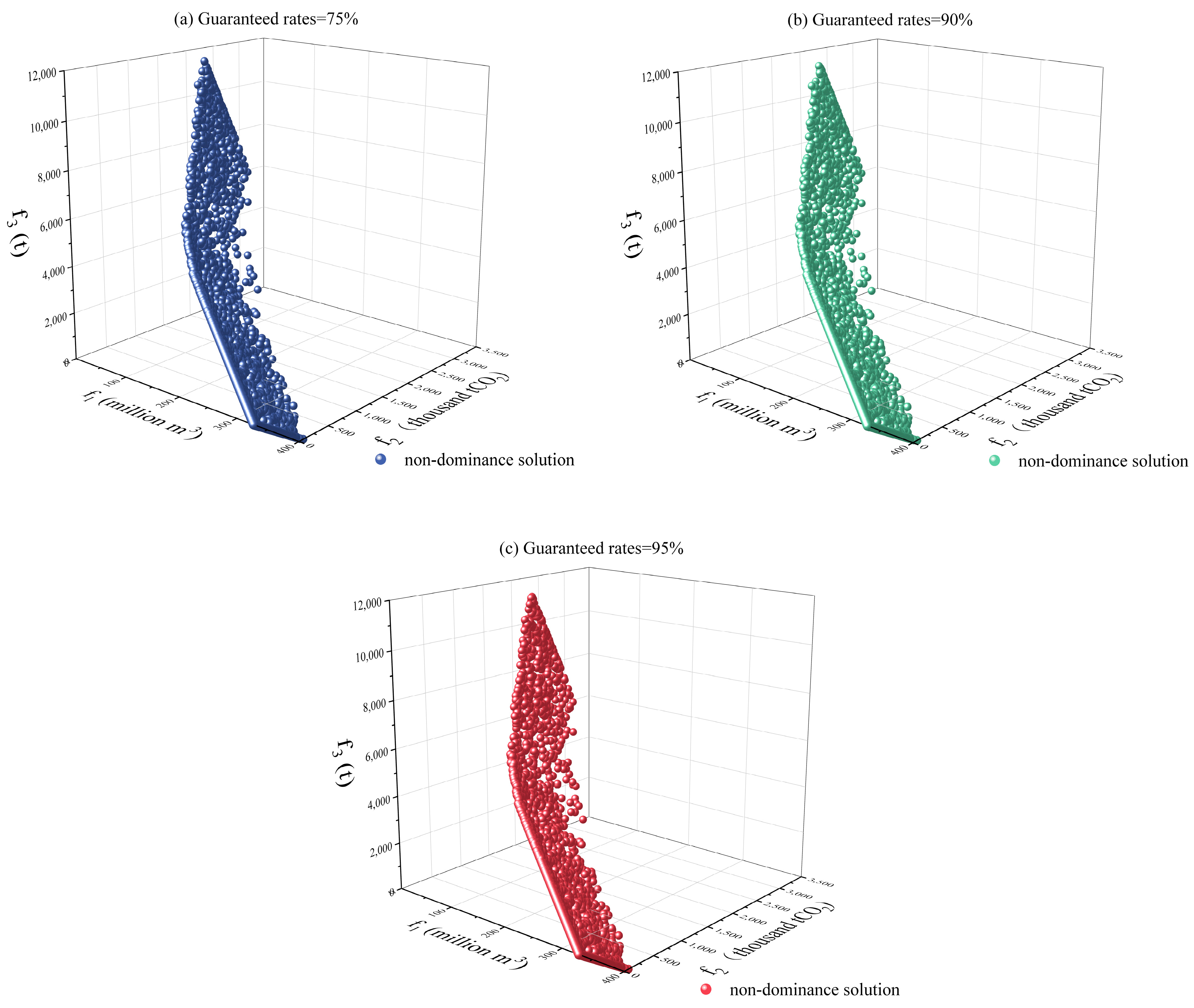
3.2.1. Optimal Results
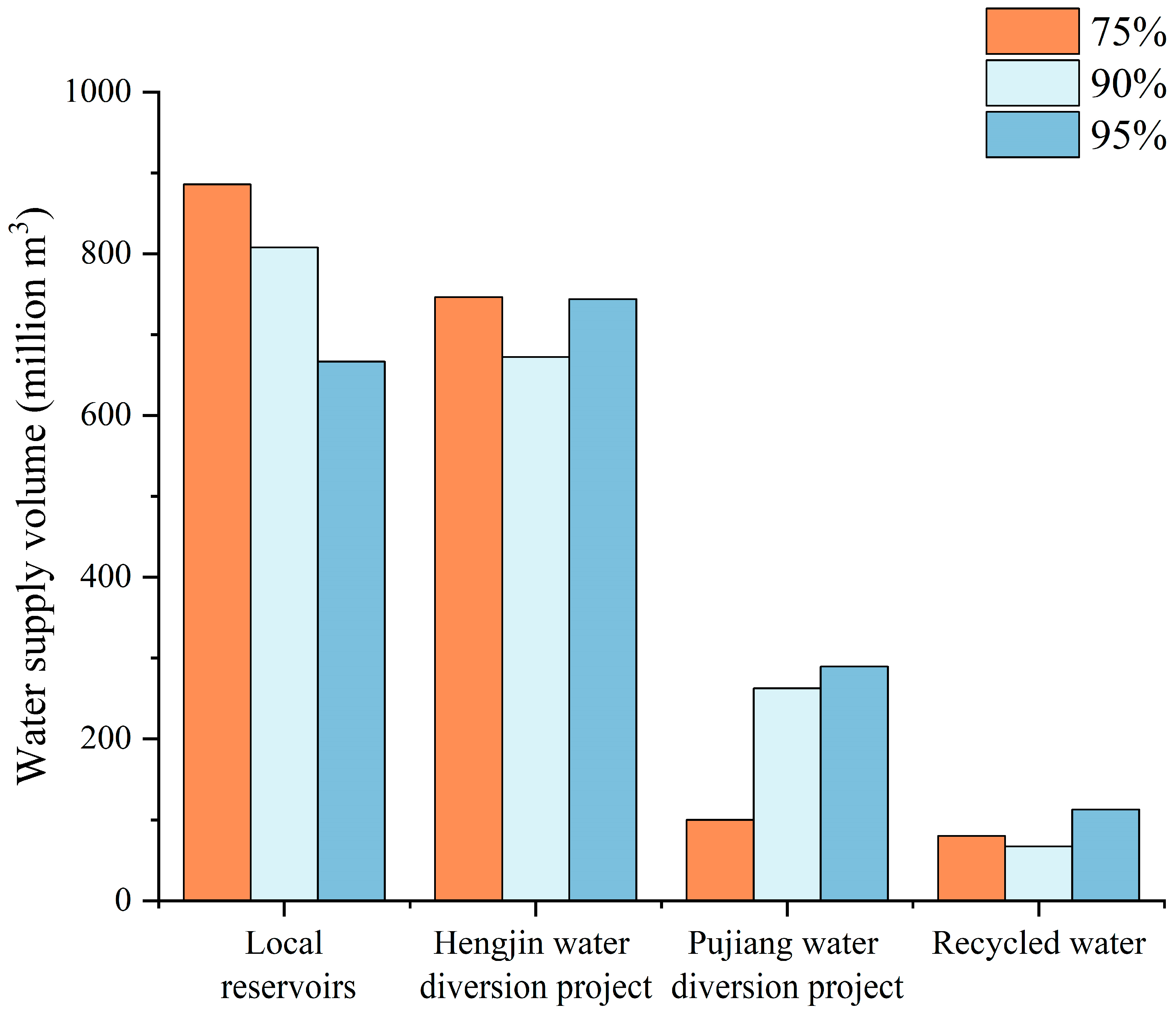
3.2.2. Comparison with the Original Allocation
4. Discussion
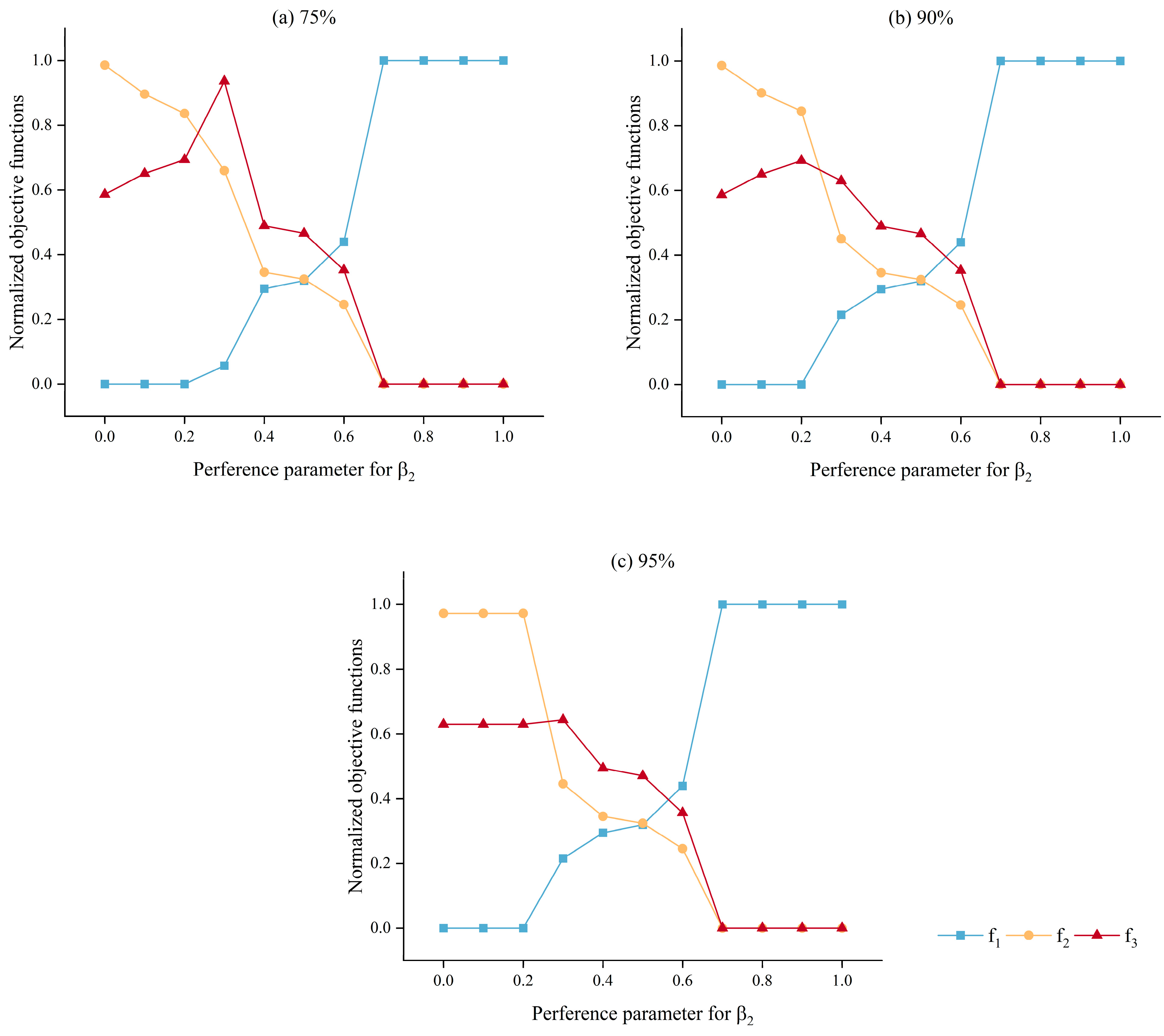
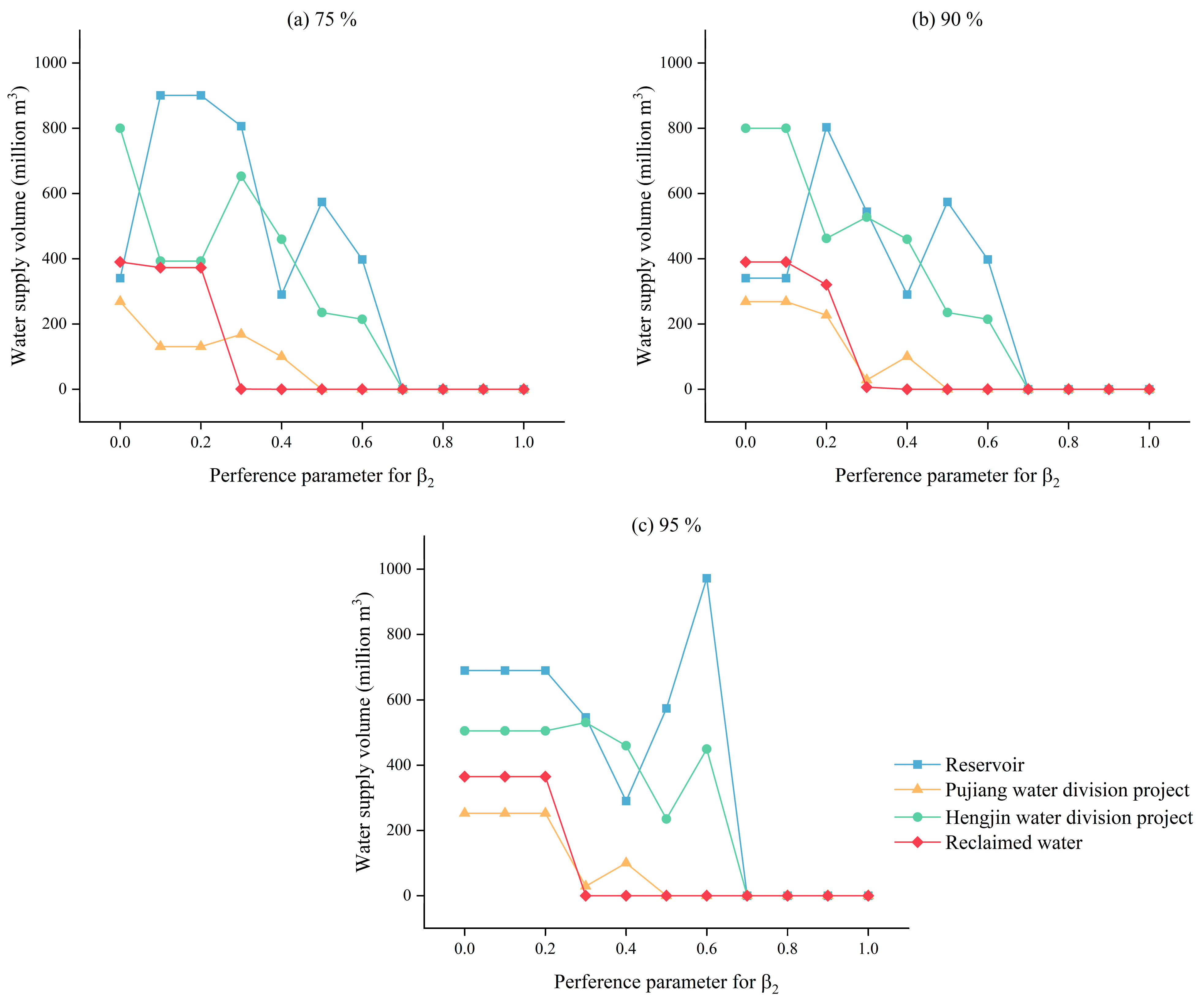
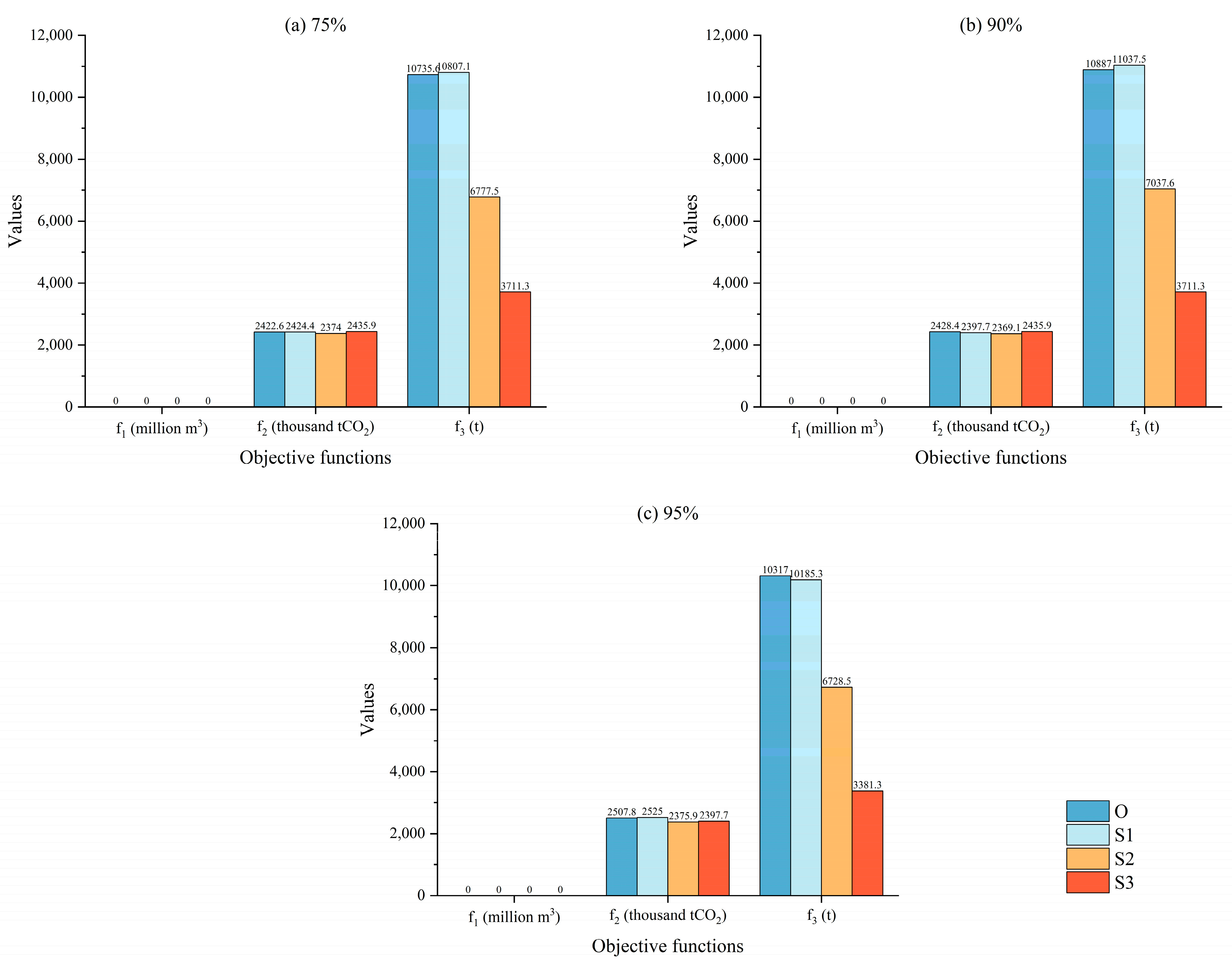
4.1. Impacts of Subjective Preferences on Greenhouse Gas Emission Reductions
4.2. Impacts of Recycled Water Utilization Conditions
4.3. Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LCA | Life cycle assessment |
| MORIME | Multi-objective rime optimization algorithm |
References
- Qiu, X.; Zhang, X.; Zhang, P.; He, M.; Li, F.; Fang, D.; Li, K. Analysis of carbon emission in the whole process of urban water supply. J. Environ. Sci. 2025, 155, 573–582. [Google Scholar] [CrossRef]
- Segurado, R.; Costa, M.; Duić, N.; Carvalho, M. Integrated analysis of energy and water supply in islands. Case study of S. Vicente, Cape Verde. Energy 2016, 29, 639–648. [Google Scholar] [CrossRef]
- He, G.; Zhao, Y.; Wang, J.; Zhu, Y.; Jiang, S.; Li, H.; Wang, Q. The effects of urban water cycle on energy consumption in Beijing, China. J. Geogr. Sci. 2019, 29, 959–970. [Google Scholar] [CrossRef]
- Xiang, X.; Jia, S. China’s water-energy nexus: Assessment of water-related energy use. Resour. Conserv. Recycl. 2019, 144, 32–38. [Google Scholar] [CrossRef]
- Uche, J.; Martínez-Gracia, A.; Círe, F.; Carmona, U. Environmental impact of water supply and water use in a Mediterranean water stressed region. J. Clean. Prod. 2015, 88, 196–204. [Google Scholar] [CrossRef]
- Cho, J.H.; Sung, K.S.; Ha, S.R. A river water quality management model for optimising regional wastewater treatment using a genetic algorithm. J. Environ. Manag. 2004, 73, 229–242. [Google Scholar] [CrossRef]
- Chhipi-Shrestha, G.; Hewage, K.; Sadiq, R. Water–Energy–Carbon Nexus Modeling for Urban Water Systems: System Dynamics Approach. J. Water Resour. Plan. Manag. 2017, 143, 4017016. [Google Scholar] [CrossRef]
- Valek, A.; Sušnik, J.; Grafakos, S. Quantification of the urban water-energy nexus in México City, México, with an assessment of water-system related carbon emissions. Sci. Total Environ. 2017, 590–591, 258–268. [Google Scholar] [CrossRef]
- Venkatesh, G.; Brattebø, H. Assessment of Environmental Impacts of an Aging and Stagnating Water Supply Pipeline Network: City of Oslo, 1991–2006. J. Ind. Ecol. 2012, 16, 722–734. [Google Scholar] [CrossRef]
- Cole, M. Economic growth and water use. Appl. Econ. Lett. 2004, 11, 1–4. [Google Scholar] [CrossRef]
- Ballesteros-Olza, M.; Blanco-Gutiérrez, I.; Esteve, P.; Gómez-Ramos, A.; Bolinches, A. Using reclaimed water to cope with water scarcity: An alternative for agricultural irrigation in Spain. Environ. Res. Lett. 2022, 17, 125002. [Google Scholar] [CrossRef]
- Cai, C.; Yang, C.; Lu, X.; Chen, Y.; Wen, J.; Wang, J.; Wang, R.; Zhang, Z.; Shen, X. Industrial water consumption index: A new bridge between water consumption and socioeconomic development. Water Resour. Ind. 2024, 32, 100270. [Google Scholar] [CrossRef]
- Yi, L.; Jiao, W.; Chen, X.; Chen, W. An overview of reclaimed water reuse in China. J. Environ. Sci. 2011, 23, 1585–1593. [Google Scholar] [CrossRef]
- Santos, A.; Alvarenga, P.; Gando-Ferreira, L.; Quina, M. Urban Wastewater as a Source of Reclaimed Water for Irrigation: Barriers and Future Possibilities. Environments 2023, 10, 10020017. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Li, Y. Research on reclaimed water from the past to the future: A review. Environ. Dev. Sustain. 2021, 24, 112–137. [Google Scholar] [CrossRef]
- Wang, X.; Wu, F. Assessment of reclaimed water utilization in water-scarce regions of China: A multi-dimensional–multi-agent coupling and nesting perspective. J. Clean. Prod. 2024, 450, 141815. [Google Scholar] [CrossRef]
- Marinelli, E.; Radini, S.; Akyol, Ç.; Sgroi, M.; Eusebi, A.L.; Bischetti, G.B.; Mancini, A.; Fatone, F. Water-Energy-Food-Climate Nexus in an Integrated Peri-Urban Wastewater Treatment and Reuse System: From Theory to Practice. Sustainability 2021, 13, 131910952. [Google Scholar] [CrossRef]
- Li, J.; Qiao, Y.; Lei, X.; Kang, A.; Wang, M.; Liao, W.; Wang, H.; Ma, Y. A two-stage water allocation strategy for developing regional economic-environment sustainability. J. Environ. Manag. 2019, 244, 189–198. [Google Scholar] [CrossRef]
- Tian, J.; Guo, S.; Liu, D.; Pan, Z.; Hong, X. A Fair Approach for Multi-Objective Water Resources Allocation. Water Resour. Manag. 2019, 33, 3633–3653. [Google Scholar] [CrossRef]
- Valipour, E.; Ketabchi, H.; Shali, R.S.; Morid, S. Water Resources Allocation: Interactions Between Equity/Justice and Allocation Strategies. Water Resour. Manag. 2023, 38, 505–535. [Google Scholar] [CrossRef]
- Himmelblau, D. Optimization of a water resources system by non-linear programming. Eng. Optim. 1977, 2, 229–238. [Google Scholar] [CrossRef]
- Yakowitz, S. Dynamic programming applications in water resources. Water Resour. Res. 1982, 18, 673–696. [Google Scholar] [CrossRef]
- Nicklow, J.; Reed, P.; Savic, D.; Dessalegne, T.; Harrell, L.; Chan-Hilton, A.; Karamouz, M.; Minsker, B.; Ostfeld, A.; Singh, A.; et al. State of the Art for Genetic Algorithms and Beyond in Water Resources Planning and Management. J. Water Resour. Plan. Manag. 2010, 136, 412–432. [Google Scholar] [CrossRef]
- Jahandideh-Tehrani, M.; Bozorg-Haddad, O.; Loáiciga, H. Application of particle swarm optimization to water management: An introduction and overview. Environ. Monit. Assess. 2020, 192, 281. [Google Scholar] [CrossRef]
- Davijani, M.; Banihabib, M.; Anvar, A.; Hashemi, S. Multi-Objective Optimization Model for the Allocation of Water Resources in Arid Regions Based on the Maximization of Socioeconomic Efficiency. Water Resour. Manag. 2016, 30, 927–946. [Google Scholar] [CrossRef]
- Deng, L.; Guo, S.; Yin, J.; Zeng, Y.; Chen, K. Multi-objective optimization of water resources allocation in Han River basin (China) integrating efficiency, equity and sustainability. Sci. Rep. 2022, 12, 798. [Google Scholar] [CrossRef] [PubMed]
- Baltar, A.; Fontane, D. Use of Multiobjective Particle Swarm Optimization in Water Resources Management. J. Water Resour. Plan. Manag. 2008, 134, 257–265. [Google Scholar] [CrossRef]
- Chen, C.; Zhu, H.; Cai, C.; Wang, S. Research on Impact of Equity Costs and Environmental Costs on Supply-Side Classified Water Pricing. Water 2024, 16, 3275830. [Google Scholar] [CrossRef]
- Gui, Z.; Qi, H.; Wang, S. Study on Carbon Emissions from an Urban Water System Based on a Life Cycle Assessment: A Case Study of a Typical Multi-Water County in China’s River Network Plain. Sustainability 2024, 16, 16051748. [Google Scholar] [CrossRef]
- Terlouw, T.; Bauer, C.; Rosa, L.; Mazzotti, M. Life cycle assessment of carbon dioxide removal technologies: A critical review. Energy Environ. Sci. 2021, 14, 1701–1721. [Google Scholar] [CrossRef]
- Wang, Y.; Pan, Z.; Zhang, W.; Borhani, T.; Li, R.; Zhang, Z. Life cycle assessment of combustion-based electricity generation technologies integrated with carbon capture and storage: A review. Environ. Res. 2022, 207, 112219. [Google Scholar] [CrossRef] [PubMed]
- Nassar, Y.; El-Khozondar, H.; El-Osta, W.; Mohammed, S.; Elnaggar, M.; Khaleel, M.; Ahmed, A.; Alsharif, A. Carbon footprint and energy life cycle assessment of wind energy industry in Libya. Energy Convers. Manag. 2024, 300, 117846. [Google Scholar] [CrossRef]
- GB/T 2589-2008; General Rules for Comprehensive Energy Consumption Calculation. Chinese Standard: Beijing, China, 2008.
- Su, H.; Zhao, D.; Heidari, A.A.; Liu, L.; Zhang, X.; Mafarja, M.; Chen, H. RIME: A physics-based optimization. Neurocomputing 2023, 532, 183–214. [Google Scholar] [CrossRef]
- Zhong, R.; Yu, J.; Zhang, C.; Munetomo, M. SRIME: A strengthened RIME with Latin hypercube sampling and embedded distance-based selection for engineering optimization problems. Neural Comput. Appl. 2024, 36, 6721–6740. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Pandya, S.; Kalita, K.; Jangir, P.; Cep, R.; Migdady, H.; Chohan, J.S.; Abualigah, L.; Mallik, S. Multi-objective RIME algorithm-based techno economic analysis for security constraints load dispatch and power flow including uncertainties model of hybrid power systems. Energy Rep. 2024, 11, 4423–4451. [Google Scholar] [CrossRef]
- Loomes, G.; Sugden, R. Some implications of a more general form of regret theory. J. Econ. Theory 1987, 41, 270–287. [Google Scholar] [CrossRef]
- Bleichrodt, H.; Cillo, A.; Diecidue, E. A Quantitative Measurement of Regret Theory. Manag. Sci. 2009, 56, 217. [Google Scholar] [CrossRef]
- Chorus, C.G. A Generalized Random Regret Minimization model. Transp. Res. Part. B Methodol. 2014, 68, 224–238. [Google Scholar] [CrossRef]
- Wang, L.; Fang, L.; Hipel, K. Basin-wide cooperative water resources allocation. Eur. J. Oper. Res. 2008, 190, 798–817. [Google Scholar] [CrossRef]
- Jinyan, L.; Lanbo, C.; Miao, D.; Ali, A. Water resources allocation model based on ecological priority in the arid region. Environ. Res. 2021, 199, 111201. [Google Scholar] [CrossRef] [PubMed]
- Wei, F.; Zhang, X.; Xu, J.; Bing, J.; Pan, G. Simulation of water resource allocation for sustainable urban development: An integrated optimization approach. J. Clean. Prod. 2020, 273, 122537. [Google Scholar] [CrossRef]
- Zeng, Y.; Liu, D.; Guo, S.; Xiong, L.; Liu, P.; Liu, P.; Yin, J.; Tian, J.; Deng, L.; Zhang, J. Impacts of Water Resources Allocation on Water Environmental Capacity under Climate Change. Water 2021, 13, 1187. [Google Scholar] [CrossRef]
- Abdulbaki, D.; Al-Hindi, M.; Yassine, A.; Najm, M.A. An optimization model for the allocation of water resources. J. Clean. Prod. 2017, 164, 994–1006. [Google Scholar] [CrossRef]


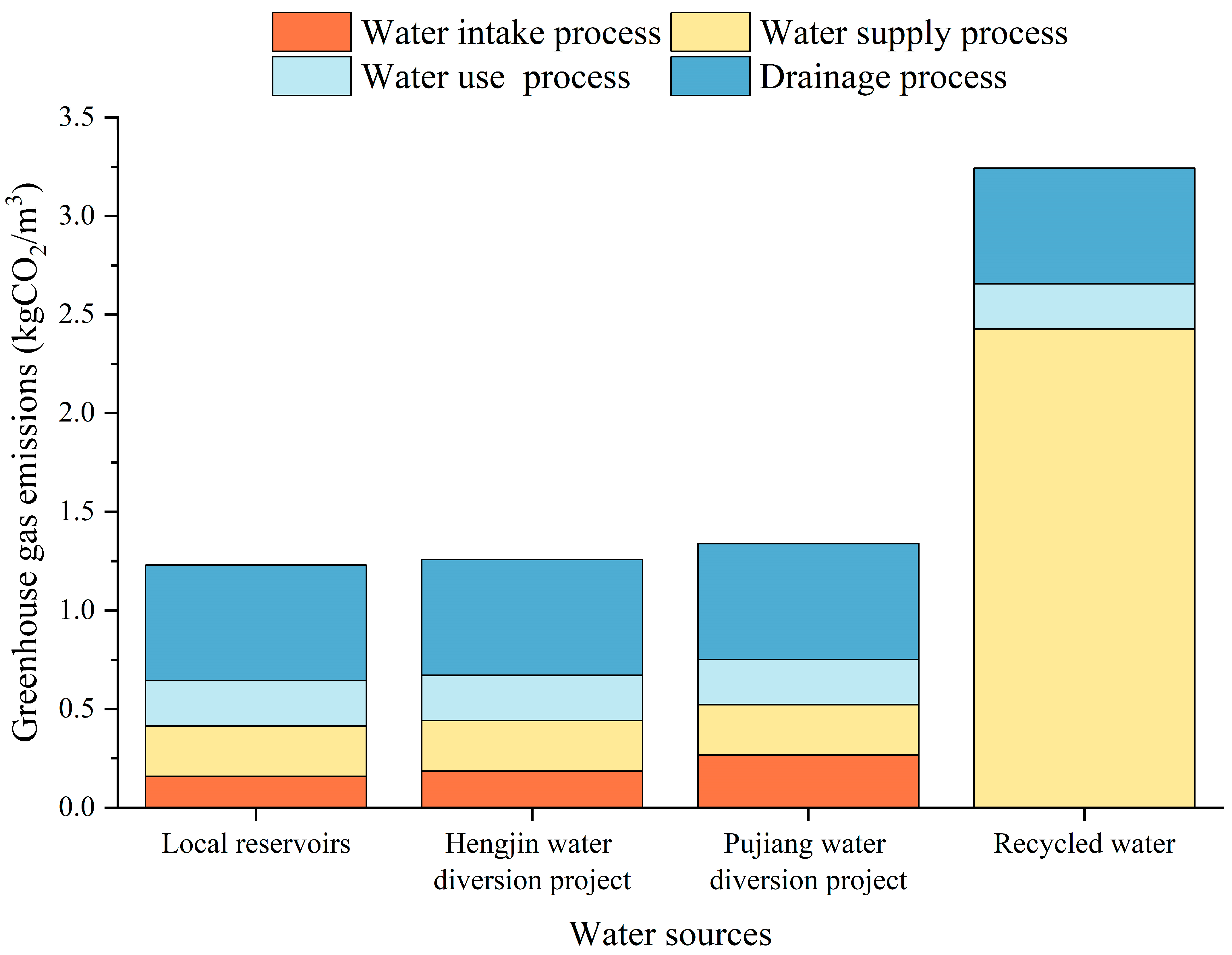


| Water User Name | Description | Water Demand (Million m3) |
|---|---|---|
| Residential water user | Water users from residential daily lives | 612.3 |
| Municipal water user | Water users from construction and tertiary industry | 239.6 |
| Industrial water user | Water users from industry | 960.6 |
| Guaranteed Rates | (Million m3) | (Thousand tCO2) | (t) |
|---|---|---|---|
| 75% | 0.0 | 2422.6 | 10,735.6 |
| 90% | 0.0 | 2428.4 | 10,587.0 |
| 95% | 0.0 | 2507.8 | 10,317.0 |
| Guaranteed Rates | Water Supply Volume (million m3) | |||
|---|---|---|---|---|
| Local Reservoirs | Hengjin Water Diversion Project | Pujiang Water Diversion Project | Recycled Water | |
| 75% | 712.5 | 800 | 300 | 0 |
| 90% | 712.5 | 800 | 300 | 0 |
| 95% | 699.1 | 800 | 300 | 13.4 |
| Objective Functions | Guaranteed Rates | Optimal Water Resource Allocation | Original Water Resource Allocation |
|---|---|---|---|
| (million m3) | 75% | 0.0 | 0.0 |
| 90% | 0.0 | 0.0 | |
| 95% | 0.0 | 0.0 | |
| (thousand tCO2) | 75% | 2422.6 | 2423.3 |
| 90% | 2408.4 | 2409.3 | |
| 95% | 2507.8 | 2508.7 | |
| (t) | 75% | 10,735.6 | 11,781.3 |
| 90% | 10,887.0 | 11,781.3 | |
| 95% | 10,317.0 | 11,607.1 |
| Scenarios | Greenhouse Gas Emission Per m3 of Water (kgCO2/m3) | Upper Limitation of Proportion for Different Water Users (%) | ||
|---|---|---|---|---|
| Residential Water Users | Municipal Water Users | Industrial Water Users | ||
| Original scenario (O) | 3.2429 | 10% | 30% | 40% |
| Greenhouse gas emissions reduction scenario (S1) | 1.5 | 10% | 30% | 40% |
| Water quality improve scenario (S2) | 3.2429 | 30% | 50% | 60% |
| Greenhouse gas emissions reduction and water quality improve scenario (S3) | 1.5 | 30% | 50% | 60% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, C.; Zheng, B.; Wang, J.; Gui, Z.; Qian, H. Optimal Water Resource Allocation for Urban Water Systems in the Context of Greenhouse Gas Emission Reduction and Recycled Water Utilization. Water 2025, 17, 2568. https://doi.org/10.3390/w17172568
Cai C, Zheng B, Wang J, Gui Z, Qian H. Optimal Water Resource Allocation for Urban Water Systems in the Context of Greenhouse Gas Emission Reduction and Recycled Water Utilization. Water. 2025; 17(17):2568. https://doi.org/10.3390/w17172568
Chicago/Turabian StyleCai, Chenkai, Baoxian Zheng, Jianqun Wang, Zihan Gui, and Hao Qian. 2025. "Optimal Water Resource Allocation for Urban Water Systems in the Context of Greenhouse Gas Emission Reduction and Recycled Water Utilization" Water 17, no. 17: 2568. https://doi.org/10.3390/w17172568
APA StyleCai, C., Zheng, B., Wang, J., Gui, Z., & Qian, H. (2025). Optimal Water Resource Allocation for Urban Water Systems in the Context of Greenhouse Gas Emission Reduction and Recycled Water Utilization. Water, 17(17), 2568. https://doi.org/10.3390/w17172568







