Hybrid Decomposition Strategies and Model Combinatorial Optimization for Runoff Prediction

Abstract

Runoff prediction plays a critical role in water resource management and flood mitigation. Traditional runoff prediction methods often rely on single-layer optimization frameworks that process the data without decomposition and employ relatively simple prediction models, leading to suboptimal performance. In this study, a novel two-layer optimization framework is proposed that integrates data decomposition techniques with multi-model combination strategies, establishing a closed-loop feedback mechanism between decomposition and prediction processes. The framework employs the Snow Ablation Optimizer (SAO) to optimize combination weights across both layers. Its adaptive fitness function incorporates three evaluation metrics—Mean Absolute Percentage Error (MAPE), Relative Root Mean Square Error (RRMSE), and Nash–Sutcliffe Efficiency (NSE)—to enable adaptive data processing and intelligent model selection. We validated the framework using observational data from Huangzhuang Hydrological Station in the Hanjiang River Basin. The results demonstrate that, at the decomposition layer, optimal performance was achieved by combining non-decomposition, Singular Spectrum Analysis (SSA), and Complementary Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN) (with coefficients 0.4061, 0.6115, and −0.0063), paired with the long short-term memory (LSTM) model. At the prediction layer, the proposed algorithm achieved a 32.84% improvement over the best single decomposition method and a 30.21% improvement over the best single combination optimization approach. These findings confirm the framework’s effectiveness in enhancing runoff data decomposition and optimizing multi-model selection.

1. Introduction

Accurate and reliable runoff prediction is essential for effective water resource management, playing a critical role in flood prevention, disaster mitigation, optimal water resource allocation, and efficient reservoir operation [1]. High-precision daily runoff prediction remains a particularly challenging problem in hydrological research due to the complex, nonlinear, nonstationary, and stochastic nature of runoff processes. These characteristics arise from the combined influences of meteorological events, watershed attributes, and natural geographic conditions [2]. Consequently, achieving both accuracy and stability in prediction methods continues to be a primary focus for hydrological researchers.

Hydrologic prediction methods are traditionally classified into two primary categories: physically based models and statistical models. Physically based models, such as the Soil and Water Assessment Tool (SWAT) [3] and the Hydrologic Engineering Center’s Hydrologic Modeling System (HEC-HMS) [4], rely on hydrologic process representations and require detailed watershed subsurface parameters. Statistical models, including linear regression and autoregressive moving average (ARMA) time-series methods, operate under linearity assumptions and demonstrate limited effectiveness for complex runoff data due to the inherently nonlinear and nonstationary nature of runoff processes [5]. With advancements in artificial intelligence, machine learning and deep learning models have gained widespread application in runoff prediction. These models can capture nonlinear relationships between predictors and predictions without requiring explicit physical process representations [6]. While Adaptive Neuro-Fuzzy Inference Systems (ANFISs) [7] and Support Vector Machines (SVMs) [8] have been commonly applied, recent studies suggest that deep learning architectures, particularly Convolutional Neural Networks (CNNs) and Long Short-Term Memory (LSTM) networks, demonstrate exceptional potential for daily rainfall–runoff prediction [9]. Nevertheless, the optimal selection and combination of these machine learning and deep learning approaches remains an active research area.

In recent years, advanced decomposition techniques such as Variational Mode Decomposition (VMD) have been increasingly applied to hydrological time series analysis. VMD, an adaptive and data-driven method, decomposes non-stationary signals into intrinsic mode functions (IMFs) through the optimization of a constrained variational model, effectively addressing mode-mixing issues in traditional EMD [10]. For instance, Danandeh Mehr et al. (2023) integrated VMD with a Gaussian Process (GP) model to predict meteorological drought in ungauged catchments [11], while Ahmadi et al. (2023) combined VMD with machine learning for streamflow forecasting [12]. These studies demonstrate VMD’s capability to enhance prediction accuracy by extracting multiscale features. However, VMD requires predefined parameters (e.g., penalty factor and mode number), which may introduce subjectivity. In contrast, CEEMDAN further improves decomposition robustness by adaptively suppressing residual noise and eliminating mode mixing through iterative noise-assisted decomposition [13]. To further improve the prediction effect, hybrid prediction methods combining signal decomposition techniques and machine learning have been gradually introduced into runoff prediction. EMD [10], SSA [14], and CEEMDAN [15] are methods capable of decomposing runoff sequences into multiple components with distinct characteristics, enabling separate prediction and subsequent combination to effectively reduce data complexity. Zhang et al. (2021) applied CEEMDAN combined with LSTM to predict runoff at the Village Beach in the upper reaches of the Yangtze River, achieving a certainty coefficient of 0.94, which meets Class A accuracy standards [15].

However, existing studies demonstrate significant limitations in runoff prediction across diverse hydrological conditions and monitoring stations, particularly regarding (1) the necessity of runoff data decomposition, (2) optimal integration strategies between decomposition methods and prediction models, and (3) oversimplified optimization objectives. Consequently, determining appropriate decomposition techniques, developing context-specific model combinations, and refining optimization frameworks have emerged as pressing research challenges. To address these gaps, in this study, a novel two-layer optimization framework is proposed that synergizes data decomposition techniques with prediction models, departing from conventional single-layer approaches. The framework incorporates (1) a closed-loop feedback mechanism between decomposition and prediction processes, and (2) an innovative weight allocation strategy based on the SAO algorithm [16]. The first optimization layer systematically evaluates data decomposition method combinations. This involves selecting and integrating multiple decomposition techniques, applying the SAO algorithm to optimize combination coefficients, and identifying station-specific optimal decomposition approaches. The second layer focuses on multi-model prediction optimization through developing a collaborative prediction mechanism, implementing adaptive weight adjustment for model combinations, and enhancing overall prediction performance.

2. Method

2.1. Two-Layer Combinatorial Optimization Framework

This study breaks through the traditional single-layer optimization idea by combining the advantages of data decomposition technology and prediction models and constructing a two-layer “data decomposition–model prediction” optimization strategy framework. A closed-loop decomposition–prediction feedback mechanism is developed, and an innovative weight allocation strategy is designed based on the SAO algorithm. The first layer focuses on combination optimization by selecting different data decomposition methods and prediction models and using the SAO algorithm to optimize the combination coefficients of these methods, thus obtaining the best data decomposition method combination scheme that can adapt to the characteristics of the runoff data itself. The second layer focuses on the weight allocation of multiple prediction models, establishes a multi-model cooperative prediction mechanism, realizes the adaptive adjustment of prediction model weights, and obtains the optimal combination of multiple prediction models, which ultimately improves the performance of runoff prediction.

The optimal two-layer combination framework for runoff prediction proposed in this paper is shown in Figure 1, where F1~Fm are the m components obtained through SSA decomposition, and IMF1~IMFn are the n-th modal components obtained using CEEMDAN decomposition.

The two-layer combinatorial optimization model consists of a signal decomposition optimal combination layer and a prediction model optimal combination layer. In the first layer, based on the characteristics of the runoff sequence, the weights of no decomposition and multiple decomposition methods (SSA and CEEMDAN in this study) are configured separately, and the intelligent algorithm seeks the optimal combination. Signal decomposition and model selection are included as part of the initial population, and then optimal weight matching is conducted to achieve signal decomposition model optimization. This process is used to determine the combination of decomposition methods that best fits the characteristics of the runoff data. In the optimal combination of prediction models layer, based on the results of signal decomposition, the weights of different prediction models (linear regression model (LR), back propagation neural network (BP), recurrent neural network (RNN), long short-term memory network (LSTM), and gated recurrent neural network (GRU)) are configured. The specific steps for runoff prediction are as follows:

(1)

Data normalization is performed on the raw runoff sequence to eliminate the difference in magnitude between different data features.

(2)

The original runoff signal is decomposed using SSA and CEEMDAN, respectively.

(3)

The signals are predicted without decomposition, SSA decomposition, and CEEMDAN decomposition using five prediction models, namely, LR, BP, RNN, LSTM, and GRU [5], respectively.

(4)

In the optimal combination layer of signal decomposition, the combination coefficients are assigned to the signals without decomposition, SSA decomposition, and CEEMDAN decomposition in each prediction model, and the formulas containing the MAPE, RRMSE, and NSE metrics are used as the fitness function. Intelligent algorithms are applied to optimize the combination coefficients to obtain the optimal combination strategy for each signal decomposition method.

(5)

The combination coefficients are allocated at the prediction model layer to obtain the optimal combination of the five prediction models, and MAPE, RRMSE, and NSE are utilized to evaluate the prediction effect of the model. The formula of each metric is as follows:

$$MAPE(Q,Q_{pre})={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n\left|Q_i-Q_{pre,i}\right|/Q_i}$$

(1)

$$RRMSE(Q,Q_{pre})=\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n{\left(Q_i-Q_{pre,i}\right)}^2}}/\overline{Q}$$

(2)

$$NSE(Q,Q_{pre})=1-{\displaystyle \frac{{\displaystyle {\sum }_{i=1}^n{(Q_i-Q_{pre,i})}^2}}{{\displaystyle {\sum }_{i=1}^n{(Q_i-\overline{Q})}^2}}}$$

(3)

where Q denotes the measured value of runoff, Q_pre denotes the predicted value of runoff, Q_i denotes the value of runoff at moment i, and $\overline{Q}$ denotes the average value of runoff at n moments.

2.2. Runoff Data Decomposition Methods

2.2.1. SSA

The SSA is a non-parametric time series analysis method that extracts the components of trend, periodicity, and noise in a signal using matrix decomposition techniques. The core idea is to map a one-dimensional time series into a high-dimensional space, capture the intrinsic structure of the data using Singular Value Decomposition (SVD), and then realize component separation through reconstruction. The following is a detailed explanation of the principle of SSA.

For one set of the given trajectory matrix X = (x₁, x₂,.., x_N), its signal decomposition process is as follows:

(1)

Construct the trajectory matrix: according to the given time series x(n)(n = 1,....., N) and embedding dimension L, construct the trajectory matrix X, where the matrix element $X_i={(x(i),x(i+1),\dots ,x(i+L-1))}^T(i=1,\dots ,K,K=N-L+1)$.

(2)

Singular-value decomposition of the trajectory matrix: X = U∑V^T, where U and V are orthogonal matrices, ∑ is a diagonal matrix, and the elements on the diagonal are singular values.

(3)

Grouping reconstruction: according to the magnitude of the singular values or other characteristics, the left singular vector and the right singular vector corresponding to the singular values are grouped, and then different components are obtained through reconstruction.

2.2.2. CEEMDAN

CEEMDAN is selected as the decomposition algorithm for runoff prediction in this study as it can effectively address the nonlinear and nonstationary characteristics of runoff series. By employing an adaptive noise addition strategy, CEEMDAN accurately separates fluctuation components across multiple scales, mitigates mode mixing, and achieves noise reduction through ensemble averaging during decomposition, thereby enhancing decomposition precision. Furthermore, its fully adaptive nature eliminates the need for manual parameter settings, ensuring operational convenience. Utilizing the decomposed Intrinsic Mode Functions (IMFs) and trend components as inputs for the prediction model enables the extraction of multiscale features from runoff series, removes noise interference, and provides richer and more accurate information, consequently improving prediction accuracy significantly. The decomposition process is as follows.

(1)

A certain amount of white noise v_i(t) is introduced into the original signal x(t) to obtain the preprocessing sequence x_i(t). Then, the empirical modal decomposition of x_i(t) is performed, the mean value obtained from the I experiment is taken as the component of the CEEMDAN decomposition, and then the first-order residuals r₁(t) are found.

$$\left\{\begin{array}{l}{x}_i(t)=x(t)+\epsilon {\delta }_i(t)\begin{array}{c}i=1,2,\dots ,I\end{array}\\ \mathrm{IMF}1(t)={\displaystyle \frac{1}{I}}{\displaystyle {\sum }_{i=1}^I\mathrm{IMF}{1}^i(t)}\\ r_1(t)=x(t)-{\displaystyle \frac{1}{I}}{\displaystyle {\sum }_{i=1}^I\mathrm{IMF}{1}^i(t)}\end{array}\right.$$

(4)

where ε is the noise coefficient and δ_i(t) is the noise of the ith experiment.

(2)

The noise is added to the decomposed stage j residual signal and an empirical modal decomposition is performed to find the stage j modal component.

$$\left\{\begin{array}{l}\mathrm{IMF}j(t)={\displaystyle \frac{1}{I}}{\displaystyle {\sum }_{i=1}^I{E}_1[r_{j-1}(t)+\epsilon E_{j-1}{\delta }_i(t)]}\\ r_j(t)=r_{j-1}(t)-\mathrm{IMF}j(t)\end{array}\right.$$

(5)

where $E_{j-1}{\delta }_i(t)$ is the j-1st IMF component after modal decomposition, and r_j(t) and r_j−1(t) are the residual signals of the jth and j-1st stages.

(3)

Cycle steps (1) and (2); when the extreme value point is less than 2 or the number of components n is set by a human, the decomposition process ends. The IMF components and corresponding residuals that meet the requirements are obtained, at which time the original signal x(t) can be expressed as

$$x(t)={\displaystyle {\sum }_{kk=1}^n\mathrm{IMF}kk(t)}+r(t)$$

(6)

where r(t) is the residual signal, and IMFkk(t) is the kkth component.

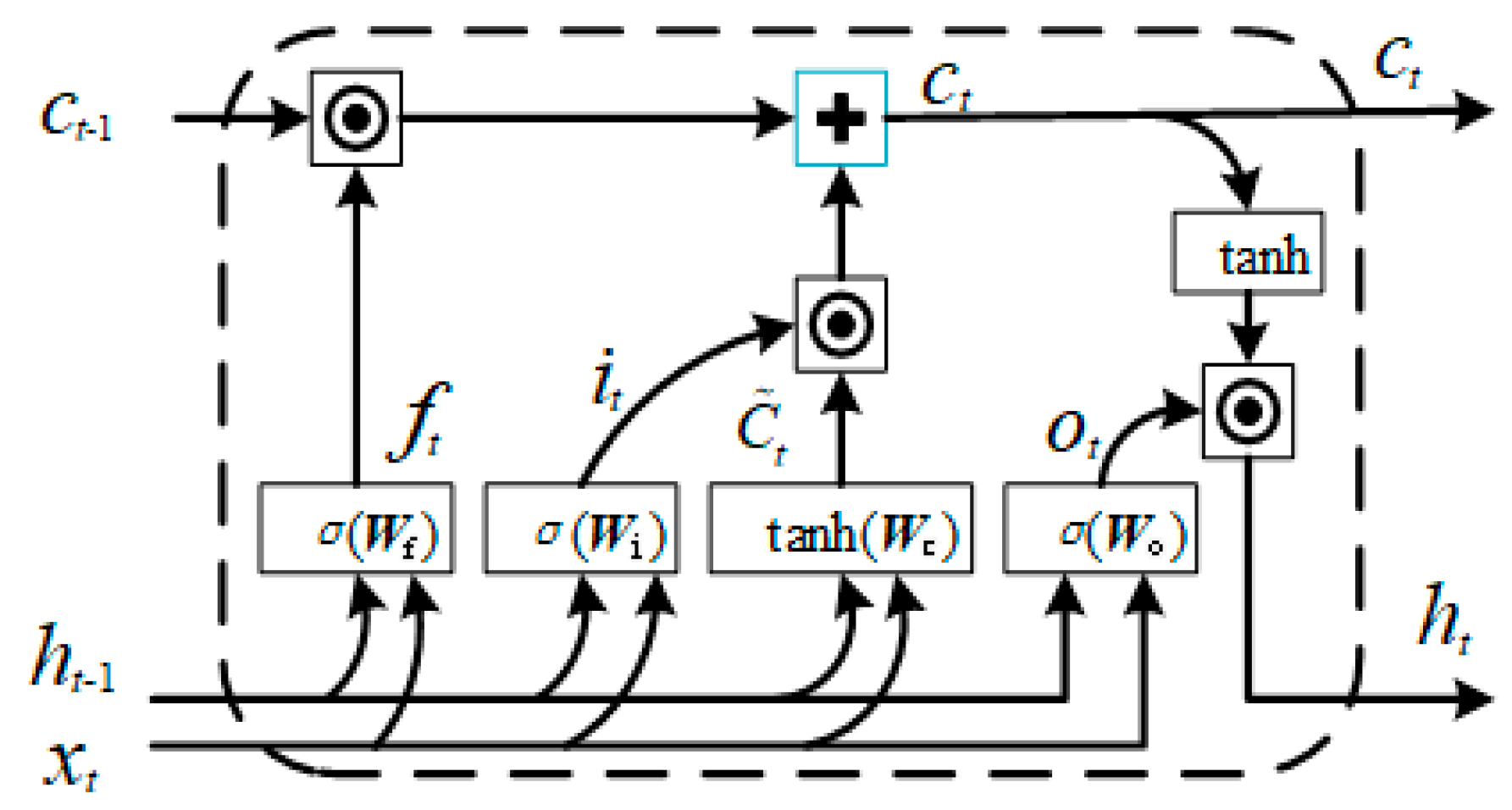
2.3. Runoff Prediction Models

Based on the combination optimization of the data decomposition layer, the second combination optimization is carried out according to the prediction results of five runoff prediction models, namely, LR, BP, RNN, LSTM, and GRU, to achieve the fast and accurate prediction of the runoff sequence. The selection logic of the five models here can be summarized as the hierarchical progression of “traditional statistics (LR) → shallow neural (BP) → basic recurrent (RNN) → long time-series improvement (LSTM) → high efficiency recurrent (GRU)”, which not only covers the nonlinear, time-series-dependent characteristics of hydrological time series, but also meets the benchmark comparison and domain-dependent requirements. Finally, the optimization ability of the framework under different model combinations can be verified through the selection of SAO algorithms and combination optimization. The five models are described in detail below.

The LR model, characterized by its simple structure, fast training speed, and ease of implementation, enables the rapid preliminary fitting of runoff data. However, it exhibits limited capability in modeling complex nonlinear relationships [17]. BP neural networks, while flexible in handling nonlinear relationships through weight adjustments, often suffer from slow convergence and susceptibility to local optima during training [18]. RNNs [19] can process time-dependent data and incorporate historical information for runoff prediction. Nevertheless, they face challenges with gradient vanishing or explosion, which hinder the learning of long-term dependencies. The LSTM network [20], an advanced RNN variant, addresses these issues through its gate mechanism, effectively capturing long-term dependencies while demonstrating strong nonlinear fitting capabilities for runoff prediction. The standard LSTM architecture (Figure 2) consists of (1) input (x_t), previous hidden state (h_t−1), and cell state (C_t−1); (2) gating mechanisms: input gate (i_t), forget gate (f_t), cell state candidate (${\tilde{C}}_t$), and output gate (O_t); (3) weight matrices: W_i, W_f, W_c, and W_O for respective gates; and (4) activation functions: sigmoid and hyperbolic tangent. is multiplication sign. GRU [21] simplifies LSTM by merging the input and forget gates into a single update gate, reducing parameters and training time while maintaining comparable predictive performance.

$$\left\{\begin{array}{l}{i}_t=\sigma (W_i[x_t,h_{t-1},C_{t-1}]+b_i)\\ f_t=\sigma (W_f[x_t,h_{t-1},C_{t-1}]+b_f)\\ C_t=f_t{C}_{t-1}+i_t\tanh (W_C[x_t,h_{t-1}]+b_C)\\ O_t=\sigma (W_O[x_t,h_{t-1},C_t]+b_O)\\ h_t=O_t\tanh (C_t)\end{array}\right.$$

(7)

where b_i, b_f, b_c, and b_o are the bias of the input gate, oblivion gate, cell state, and output gate, respectively. In order to reduce the long training time of the LSTM network, GRU combines the input gate and forgetting gate in the internal structure of the LSTM network into an updating gate r_t, as shown in Figure 3. The reset gate z_t is used to decide the degree of forgetting of the previous information; it is the candidate hidden state at the current moment. W_h is the weight matrix of the hidden layer, and W_z and W_r are the weight matrices of the updating gate and the reset gate, respectively. The GRU network preserves the prediction effect while using fewer training parameters, resulting in a shorter training time. In GRU, r_t (reset gate) controls the effect of historical information on the current candidate state, and z_t (update gate) controls the fusion ratio of the historical state and new candidate state; finally, h_t is the current hidden state weighted by both, reflecting the contextual information of the sequence.

2.4. Optimization Solution Algorithm for Two-Layer Combinatorial Optimization Framework

SAO is used in this study, which is a novel meta-heuristic algorithm inspired by the sublimation (solid directly to gas) and melting (solid to liquid) behaviors of snow [1]. SAO balances the exploratory and exploitative capabilities of the algorithm by simulating these two physical processes to avoid precocious convergence.

The computational flow of the algorithm is as follows (as shown in Figure 4).

Step 1: Initialization phase

Randomly generate the initial population. Each individual position is represented as a matrix Z with dimension N × Dim, where N is the population size and Dim is the problem dimension. For this study, the dimension of the signal layer problem of primary optimization is 3, which corresponds to the combined coefficients of no decomposition, SSA decomposition, and CEEMDAN, respectively. The dimension of the secondary optimization problem at the model layer is 5, which corresponds to the combined coefficients of the five prediction models of LR, BP, RNN, LSTM, and GRU, respectively, after primary optimization. The initial fitness is calculated and the current optimal solution G(t) is recorded. The adaptation function adopted in this study takes into account the three evaluation indexes of MAPE, RRMSE, and NSE, and its formula is as follows:

$$\min f=[MAPE+(1-NSE)+RRMSE]/3$$

(8)

The specific expressions of the three indicators are shown in Equations (1)–(3).

Here, the upper and lower limits of the combination coefficients, according to the method of least squares [22], are determined; that is, according to AW = B to obtain W = A⁻¹B, an optimized LR model prediction is taken as an example of the combination of coefficients W = [W_LR1, W_LR2, W_LR3] and A = [Q_L1, Q_L2, Q_L3]. Under the LR model of three runoff data decomposition methods under the prediction of the runoff value, B = Q is the measured runoff value. Several other single-model data decomposition combined coefficients are also solved in a similar way. The second optimization is the combined coefficients W = [W_LR, W_BP, W_RNN, W_LSTM, W_GRU] and matrix A = [Q_LR, Q_BP, Q_RNN, Q_LSTM, Q_GRU], providing the first optimization of the runoff values predicted by each model. The data used for finding the combination coefficients is from the training set, and then these coefficients are used to test the prediction with the test set data. The obtained least squares combination coefficients are then rounded upward for positive numbers and downward for negative numbers as the upper and lower ranges for the values of the coefficients.

Step 2: Iterative update (until the maximum number of iterations is reached).

(1)

Calculation of snowmelt rate

Calculation of snowmelt rate M based on the degree-per-day model:

$$M=(0.35+0.25{\displaystyle \frac{e^{t/t_{\max }}-1}{e-1}})e^{-t/t_{\max }}$$

(9)

where t is the current iteration number and t_max is the total iteration number.

(2)

Dual population division

The population is dynamically divided into an exploratory subpopulation Pa and an exploitative subpopulation Pb. Initially, the populations are divided 50/50, and gradually the proportion of Pa is increased and that of Pb is decreased with iterations.

(3)

Exploration phase (subpopulation Pa)

For each Z_i ∈ Pa, the position is updated according to the following formula:

$$Z_i(t+1)=Elite(t)+B{M}_i(t)\otimes [{\theta }_1(G(t)-Z_i(t))+(1-{\theta }_1)(\overline{Z}(t)-Z_i(t))]$$

(10)

where Elite(t) is randomly selected from the current optimal, suboptimal, third optimal, and leader centers. BM_i(t) is a Brownian motion random vector, and θ₁ ∈ [0, 1] is a random number. $\overline{Z}(t)$ is the current population center position.

(4)

Development phase (subpopulation Pb)

For each individual Z_i ∈ Pb, the position is updated according to the following equation:

$$Z_i(t+1)=M\times G(t)+B{M}_i(t)\otimes [{\theta }_2(G(t)-Z_i(t))+(1-{\theta }_2)(\overline{Z}(t)-Z_i(t))]$$

(11)

Step 3: Fitness evaluation and update

The fitness of the new position is calculated and the current optimal solution G(t) is updated.

The ratio of the two populations is adjusted: Pa increases by one individual and Pb decreases by one individual (if Pa does not occupy the whole population).

Step 4: Termination condition

The global optimal solution G(t) is outputted after the maximum number of iterations is reached.

3. Case Study

3.1. Study Area and Data

Huangzhuang Hydrological Station in the Han River Basin is selected as a case study, which is located at the demarcation point of the middle (Danjiangkou to Zhongxiang) and lower reaches of the Han River (Zhongxiang to Hankou) (longitude 112.6° E, latitude 31.2° N). This station controls 89% of the catchment area of the whole basin (about 142,000 km²) and is the key control cross section for water and sand transport and flooding evolution in the main stream of the river. The station is positioned 376 km upstream of the river mouth and directly affects the downstream flood safety and water resource allocation in the Jianghan Plain. The data obtained from this station are crucial in determining hydrological models and runoff forecasts in the middle and lower reaches of the Han River.

The daily runoff data from Huangzhuang Hydrological Station from 1 January 2018 to 31 December 2021 were selected for study. The data were obtained from the internal database of the Ministry of Water Resources of China. The data were compiled and processed by the staff in charge of database management at the Ministry of Water Resources, thus guaranteeing the authenticity and quality of the data. The data are kept in an internal database and cannot be made public, but they can be provided privately upon request.

3.2. Experimental Design

The first 70% of the data was divided into a training set for model training and parameter optimization, with the remaining 30% used as a test set to evaluate the model’s prediction performance. Python 3.8 programming was used to realize SSA (the decomposition number, according to the decomposition of the component’s correlation coefficient with the original runoff absolute value, was greater than 0.1, and the last hair component number of 3 was satisfied) and CEEMDAN (using the default parameter adaptive decomposition). The decomposition results are shown in Figure 5. The red line is the raw runoff data and the blue is the decomposed runoff component. The input size of each model was selected as 4 according to the bias correlation coefficient (as shown in Figure 6) and the output was set to 1. The Adam function was used for the learning optimizer: the learning rate of the training model was set to 0.01, and the number of training times was 200. The initial population size of the SAO intelligent optimization algorithm was 100, and the number of iterations was 200.

In this study, we set up experiments according to single-decomposition single-model permutation, single-layer optimization, and two-layer optimization. The details are as follows.

(1)

Single-model single-decomposition: 3 types of data processing (raw data, SSA decomposition, CEEMDAN decomposition) × 5 types of models (LR, BP, RNN, LSTM, GRU);

(2)

Single-layer optimization: optimization of the data decomposition layer only (fixed model);

(3)

Bi-layer optimization (the method adopted in this paper): simultaneous optimization of data layer coefficients (W_single, W_SSA, W_CEEMDAN) and model layer coefficients (W_LR, W_BP, W_RNN, W_LSTM, W_GRU) using the SAO algorithm.

4. Results

4.1. Prediction Results of Single Model in Different Decomposition Modes

Table 1. Prediction evaluation metrics of a single model in different decomposition modes.

Sign	Model	MAPE	RRMSE	NSE	Fitness
single	LR	0.2384	0.2356	0.7644	0.2365
	BP	0.1728	0.1966	0.8034	0.1887
	RNN	0.1211	0.1068	0.8932	0.1116
	LSTM	0.0956	0.0668	0.9332	0.0764
	GRU	0.1373	0.1314	0.8686	0.1334
SSA	LR	0.1581	0.1864	0.8136	0.1769
	BP	0.1407	0.1501	0.8499	0.1470
	RNN	0.1632	0.1848	0.8152	0.1776
	LSTM	0.0915	0.0632	0.9368	0.0726
	GRU	0.1515	0.1461	0.8539	0.1479
CEEMDAN	LR	0.2684	0.1727	0.8273	0.2046
	BP	0.3745	0.2248	0.7752	0.2747
	RNN	0.9499	0.4322	0.5678	0.6048
	LSTM	0.9179	0.3754	0.6246	0.5562
	GRU	0.1924	0.0934	0.9066	0.1264

presents the prediction effects of five prediction models (LR, BP, RNN, LSTM, GRU) under three data processing methods (raw data, no decomposition; SSA decomposition; CEEMDAN decomposition). As seen from the indicators, LSTM achieves the optimal performance under SSA decomposition, with an MAPE of 0.0915, RRMSE of 0.0632, NSE reaching 0.9368, and the lowest adaptation of 0.0726.

The following comparison can be made:

(1)

Deep models are better than shallow models. The average adaptation of LSTM and GRU is much lower than that of LR and BP, indicating that they have advantages in extracting complex temporal features.

(2)

Decomposition mode has a significant impact. SSA improves the prediction accuracy as a whole, especially on LSTM and GRU; CEEMDAN introduces too much noise in some models (e.g., RNN, LSTM), and the performance decreases dramatically.

(3)

There is a coupling effect between model and decomposition. For example, GRU performs better under CEEMDAN than without decomposition (fitness: 0.1264 vs. 0.1334), suggesting that some models are well adapted to high-frequency components.

4.2. Data Decomposition Layer Optimization Results

Table 2. Data decomposition layer (primary) optimization results.

Primary Optimization Method	Model	Data Decomposition Layer Combination Coefficients			Evaluation Metrics
		Wsingle	WSSA	WCEEMDAN	MAPE	RRMSE	NSE	Fitness
Least squares method	LR	1.0451	−0.2152	0.4492	0.3998	0.1002	0.8998	0.2000
	BP	−0.8088	1.4917	0.2661	0.1830	0.1291	0.8709	0.1471
	RNN	1.0705	0.0174	−0.0138	0.1540	0.0990	0.9010	0.1173
	LSTM	0.8698	0.2716	−0.0820	0.1215	0.0567	0.9433	0.0783
	GRU	−0.4594	0.7268	0.5847	0.1552	0.0682	0.9318	0.0972
SAO	LR	0.3819	0.4631	0.2038	0.1777	0.1378	0.8622	0.1511
	BP	−0.4579	1.3616	0.0875	0.1473	0.1363	0.8637	0.1400
	RNN	1.3278	−0.3283	0.0028	0.1184	0.1006	0.8994	0.1065
	LSTM	0.4061	0.6115	−0.0063	0.0896	0.0601	0.9399	0.0699
	GRU	−0.1179	0.5137	0.5347	0.1112	0.0717	0.9283	0.0849

presents the results of each model after data decomposition combination optimization (one optimization). Taking LSTM as an example, the optimal combination obtained by SAO optimization is W_single = 0.4061, W_SSA = 0.6115, W_CEEMDAN = −0.0063. Its fitness is further reduced to 0.0699, which is significantly better than 0.0783 under least squares optimization, with a performance improvement of 10.7%.

The overall trend shows the following:

(1)

SSA components generally gained higher weights in each model, reflecting their greater adaptability to Han River runoff characteristics.

(2)

CEEMDAN component weights are negative in some models (e.g., LSTM), indicating that there is misleading noise in its decomposition results that can be automatically suppressed by SAO with negative weights.

(3)

Intelligent optimization outperforms least squares optimization in all models, with an average reduction in adaptation of 12.2%.

4.3. Model Layer Optimization Results

The results of further model combination optimization (secondary optimization) after optimization based on data decomposition are presented in

Table 3. Model layer optimization results.

Optimization Method	Model Layer Combination Coefficients					Evaluation Metrics
	WLR	WBP	WRNN	WLSTM	WGRU	MAPE	RRMSE	NSE	Fitness
Least squares method	−0.3835	−2.0036	1.9868	1.4872	−0.0808	0.1058	0.0236	0.9764	0.0510
SAO	−0.3150	−1.8176	1.7639	1.3082	0.0613	0.0980	0.0242	0.9758	0.0488

. The optimal combination weights obtained from SAO optimization are WRNN = 1.7639, WLSTM = 1.3082, and WGRU = 0.0613, while the weights of linear models BP and LR are negative.

The key metrics are as follows:

(1)

The fitness value reaches the global minimum, 0.0488, which is 32.84% and 30.21% lower than the optimal single model (0.0726) and single-layer optimization (0.0510), respectively.

(2)

The RRMSE is 0.0242, indicating that the framework has extremely high predictive stability and fitting ability.

(3)

The model combination has a clear preference: the deep recurrent model (RNN/LSTM) dominates the combination, while the shallow model (BP/LR) is significantly suppressed.

4.4. Comprehensive Comparison Results of Prediction Performance

To compare more easily and intuitively, the best results from the method described in this paper were compared with those from various single methods (single runoff prediction without decomposition, SSA decomposition, CEEMDAN decomposition) and one SAO optimization. The results of the comparison are shown below.

Figure 7a shows the effect of the runoff prediction curves for the five methods over the test period (totaling 439 days).

(1)

Peak capture accuracy: At the peak of runoff, the optimal model (Best, red curve) matches the observed values (deviation = −5.94%). The single model (green) and SSA (blue) underestimate the peak by 19.98% and 13%, respectively.

(2)

Low-flow stability: In the low-flow segments from 0 to 250 days and after 400 days, all models have low absolute errors, but Best most closely matches the observed value curve.

Figure 7b (scatter plot) further visually confirms that the predicted values of Best proposed in this study are tightly distributed around the y = x line and closer to the peak.

Figure 7c (bar chart) quantifies and visualizes the error metrics, from which it can be found that the Best model achieves the lowest RRMSE (0.0242) and the highest NSE (0.9758). The single SAO optimization results in 37.2% lower MAPE than the single model.

Figure 7d (box plot) reveals the error distribution characteristics, and the error distribution interval of the Best result proposed in this study is significantly narrower and smaller than that of other methods.

5. Discussion

5.1. Effectiveness and Innovativeness of Dual-Level Optimization Mechanisms

The two-layer combinatorial optimization framework proposed in this study realizes the adaptive coupling of signal processing and model selection through the SAO algorithm, which significantly improves the accuracy of runoff prediction. The key advantages are outlined below.

(1)

Negative weight suppression mechanism (Figure 7d and Table 3)

Negative weights are optimized solutions generated by the SAO algorithm in the process of minimizing the composite fitness function (Equation (8)), whose mathematical essence is minf = (MAPE + (1 − NSE) + RRMSE)/3, which is an objective function that requires the simultaneous reduction in MAPE and RRMSE and the enhancement of NSE. When the prediction result of a component presents a systematic deviation from the true value, the SAO may give it a negative weight to realize bias correction (the reverse correction of noise introduced by over-decomposition through negative coefficients) and model synergy (suppressing the negative impact of low-quality components and strengthening the contribution of dominant components).

In the data decomposition layer, SAO automatically assigns negative weights to CEEMDAN components (e.g., W_CEEMDAN = −0.0063 in LSTM), which effectively suppresses high-frequency noise interference (IQR range of the Best model in Figure 7d is −80~120 m³/s, which is significantly narrower than the single model). The physical significance of the CEEMDAN weights (W_CEEMDAN = −0.0063) of the LSTM model in Table 2, for example, is that the high-frequency components of the CEEMDAN decomposition (IMF1-IMF4) contain unphysical oscillations (Figure 5), and that their predicted values (Q_CEEMDAN) are locally negatively correlated with the true runoff (Q) (e.g., the peak lag phenomenon). Negative weights offset this noise interference by W_CEEMDAN × Q_CEEMDAN.

At the model layer, SAO excludes inefficient models (e.g., W_BP = −1.8176) by negative weighting and strengthens the synergistic effect of RNN (WRNN = 1.7639) and LSTM (W_LSTM = 1.3082) (Table 3). Traditional model combination methods mostly use equal-weighted averaging or empirical weighting, which is difficult to adapt for data features. The intelligent synergy mechanism in this study optimally adjusts the model layer combination coefficients through quadratic optimization. Taking WRNN = 1.7639 and W_LSTM = 1.3082 as an example, it is shown that the combination of short-term dependence (RNN) and long-term dependence (LSTM) is able to extract the runoff time-series information more comprehensively, while the negative weighting of BP and LR automatically excludes its noise influence. This “positive incentive + negative inhibition” weighting strategy significantly improves the adaptive ability of the integrated model.

(2)

Optimization efficiency improvement

SAO’s two-population partitioning strategy balances the exploration and development ability, and the framework adaptation degree is reduced to 0.0488 (Table 3), which is 32.84% lower than that of the optimal single model (SSA + LSTM), which verifies that the two-layer closed-loop optimization is efficient and good at searching the solution space.

(3)

Adaptation function fusion of multiple indicators

The adaptation function integrates three evaluation indicators, MAPE, RRMSE, and NSE, to avoid optimization biased towards a certain indicator (Table 1, Table 2 and Table 3, Figure 7c), so as to equalize and improve the comprehensive performance of the optimized model.

5.2. Analysis of Decomposition Model-Matching Mechanism

(1)

The dominance of SSA (Table 2 and Figure 7a)

SSA generally obtains a high weight (e.g., LSTM layer WSSA = 0.6115) in Han River runoff prediction, as its trajectory matrix reconstruction property can effectively retain the main trend of seasonal flood season runoff (Figure 7a >300-day section). This coincides with the strong seasonal hydrological situation of the Han River. The three main components of the SSA decomposition (see Section 3.2) correspond to the flood season (low-frequency), rainfall (mid-frequency), and evapotranspiration (high-frequency) processes, which is in agreement with the physical mechanism of the basin water cycle.

(2)

Noise problem of CEEMDAN

The essence of CEEMDAN’s performance degradation in some models is the mismatch between decomposition granularity and model architecture (CEEMDAN decomposes the original runoff sequence into too many high-frequency components—in this case (e.g., Figure 5), generating nine IMF components, while SSA decomposes into only three components): the high-frequency noise generated by its over-decomposition interferes with the temporal modeling capability of recurrent neural networks. Additionally, the prediction of more component results via reconstruction may lead to the accumulation of errors. However, through the two-layer optimization of SAO (negative weight suppression + model synergy), this problem is transformed into the adaptive correction capability of the framework, which still contributes positive values to the overall prediction (e.g., 0.5347 for the CEEMDAN weights of GRU). This finding deepens the understanding of the “decomposition–model” coupling mechanism and provides a key design guideline for subsequent research.

In summary, both LSTM and GRU obtain the best performance under SSA, which shows that SSA is more adaptive to the seasonal changes in the Han River Basin in terms of preserving the main trend and cycle characteristics. It is worth noting that CEEMDAN is given negative weight in LSTM, indicating that the method introduces non-negligible high-frequency noise in this case. The ability of SAO to automatically recognize and suppress this type of noise provides a new path for the processing of non-stationary time series.

5.3. Comparison with Existing Methods and Room for Improvement

Compared with physical models (e.g., SWAT), the method proposed in this study does not require a large number of subsurface parameters or high deployment costs, and has a wide range of applicability. Compared with existing combined frameworks (e.g., EMD-LSTM), this method avoids fixed structural errors and possesses migration capability and generalizability. However, there are limitations. First, external uncertainty inputs, such as precipitation forecasts, are not considered. Second, the generalizability of the SSA/CEEMDAN method to other climate zones needs to be further tested. Third, the lack of meteorological inputs such as information on precipitation intensity and spatial and temporal distribution means that the model cannot respond to sudden hydrologic events by relying only on historical runoff series. Neglecting evapotranspiration and soil moisture leads to a surge in errors in the low-flow interval, which is fundamentally caused by reducing the open hydrological system to a closed time series and ignoring the causal chain of precipitation–subsurface–runoff.

Suggestions for future research are as follows:

(1)

The introduction of meteorological forecast data to construct a synergistic prediction system with multi-source inputs.

(2)

An exploration of the applicability of other decomposition methods (e.g., VMD, EWT) in arid or monsoon-type watersheds.

(3)

The coupling of WRF with other meteorological models to construct a cascading prediction framework of “precipitation forecasting → soil moisture updating → runoff response”.

6. Conclusions

To address the lack of synergistic coordination between data decomposition preprocessing and model prediction selection in runoff prediction, a two-layer intelligent optimization framework was proposed in this study that integrates data decomposition techniques with prediction models. Systematic experiments were conducted using Huangzhuang Hydrological Station in the Hanjiang River Basin as the validation case. The key findings are as follows:

(1)

The adaptive decomposition mechanism demonstrates significant improvements in data processing efficacy. SSA decomposition consistently receives high combination weights across most models (e.g., WSSA = 0.6115 in LSTM), effectively capturing the seasonal runoff characteristics of the Hanjiang River. Conversely, CEEMDAN is automatically assigned negative weights in certain models (e.g., WCEEMDAN = −0.0063), which proves effective in suppressing noise interference while still extracting seasonal features. These results confirm the superiority of the proposed decomposition combination strategy over single-method approaches.

(2)

The two-layer optimization framework substantially enhances runoff prediction performance. Under SAO-based co-optimization, the fitness function value improves from 0.0726 (optimal single model: LSTM + SSA) to 0.0488. Error metrics (MAPE, RRMSE) show reductions of 32.84% and 30.21%, respectively, outperforming both the best single model and single-layer optimization approaches. The SAO algorithm strengthens deep recurrent models (WRNN = 1.7639, WLSTM = 1.3082) while mitigating weaknesses in shallow models (e.g., BP, LR), demonstrating the framework’s adaptive capability to identify and regulate model effectiveness. Notably, this data-driven approach requires only historical runoff sequences, making it particularly suitable for rapid deployment scenarios with limited parameter information.