An Interpretable Deep Learning Framework for River Water Quality Prediction—A Case Study of the Poyang Lake Basin
Abstract
1. Introduction
- (1)
- Developing an interpretable deep learning framework driven by multi-source data to enhance both predictive accuracy and model interpretability for water quality management in complex watershed systems.
- (2)
- Evaluating the effectiveness of multi-source data-driven collaborative deep learning methods in improving water quality prediction accuracy across large regions.
- (3)
- Investigating the explanatory variables that dominate the predictive performance of various water quality parameters and quantifying the contribution of key driving factors to water quality impacts.
2. Materials and Methods
2.1. Study Area
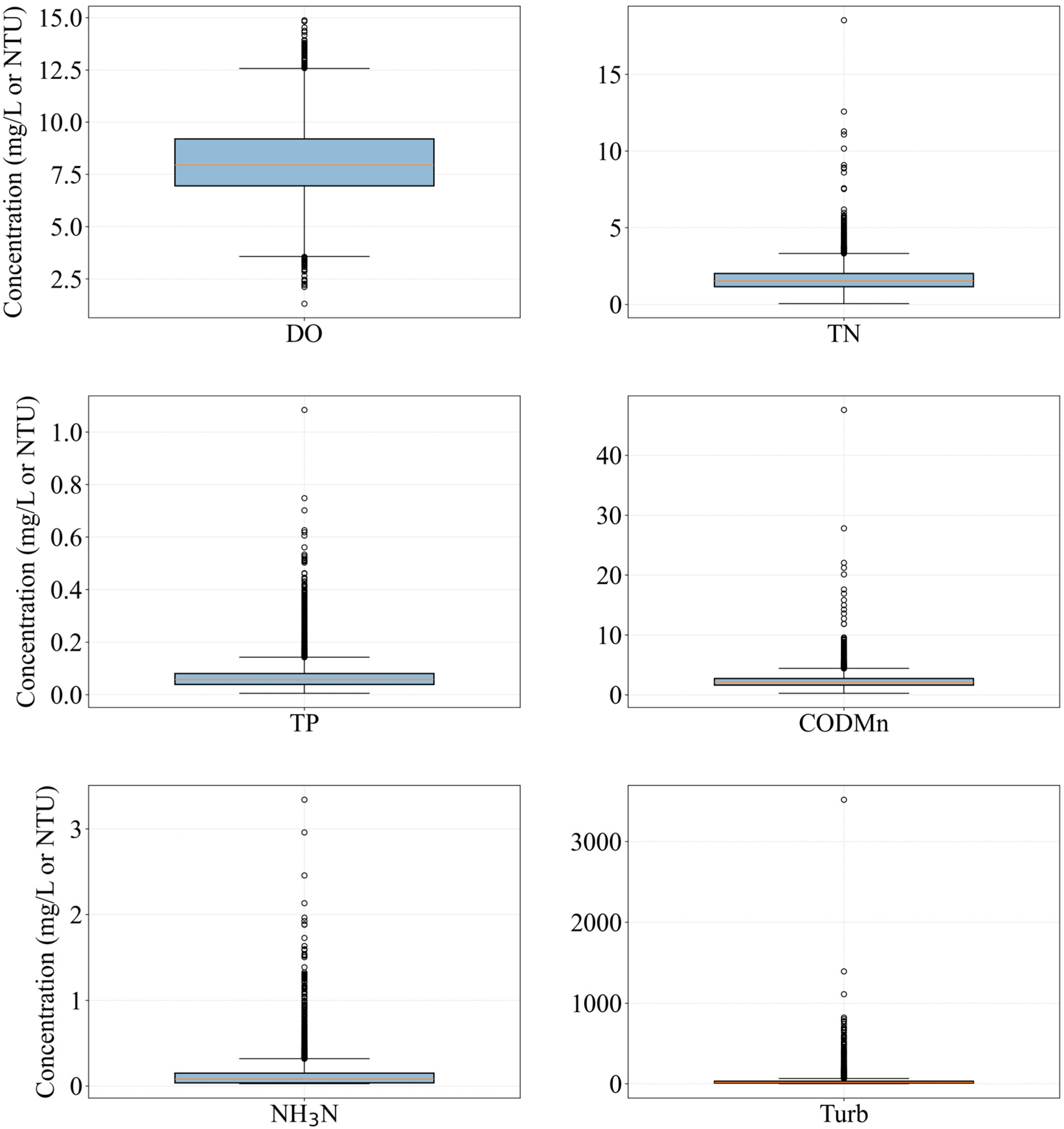
2.2. Data Sources and Preprocessing
2.3. Methodology
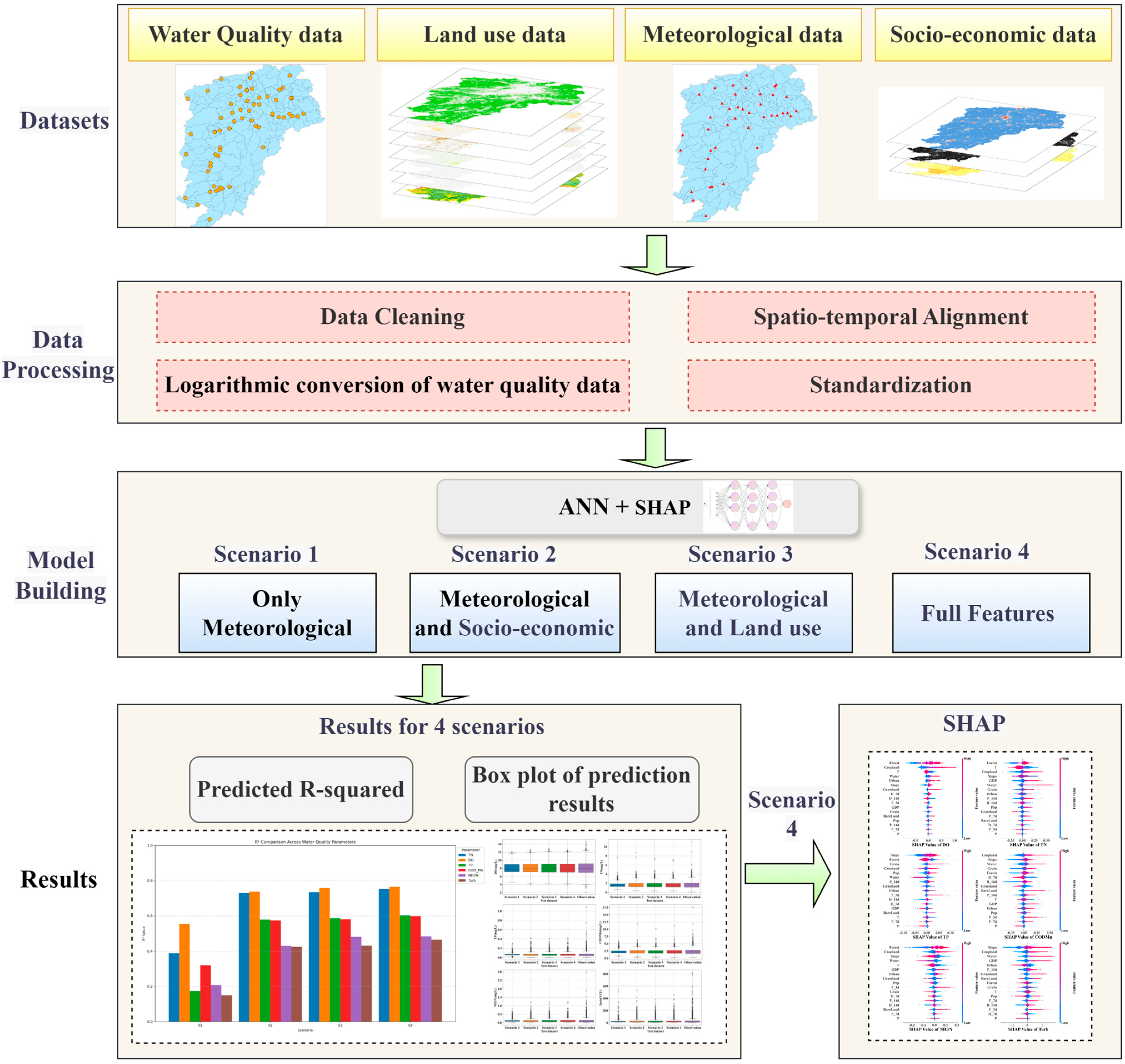
2.3.1. Research Framework
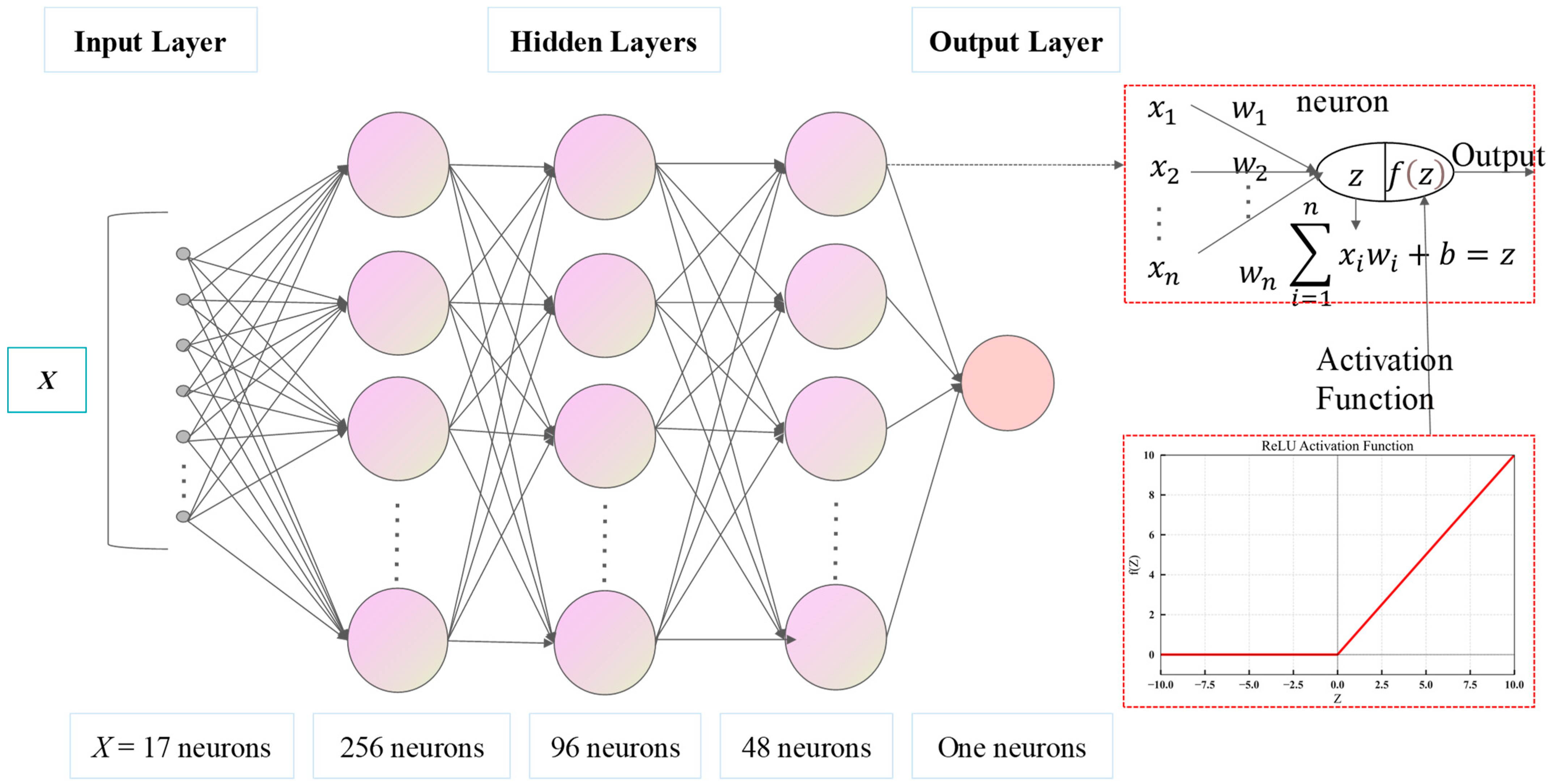
2.3.2. Model Design
2.3.3. Model Training and Evaluation
2.3.4. Modeling Scenarios
2.3.5. Model Interpretability
- -
- is the full set of features (e.g., climate, land use, socioeconomic variables), and is an arbitrary subset without features;
- -
- is the model containing feature i, and is the control model excluding features;
- -
- denotes the feature values in the input vector that retain only a subset of features.
3. Results
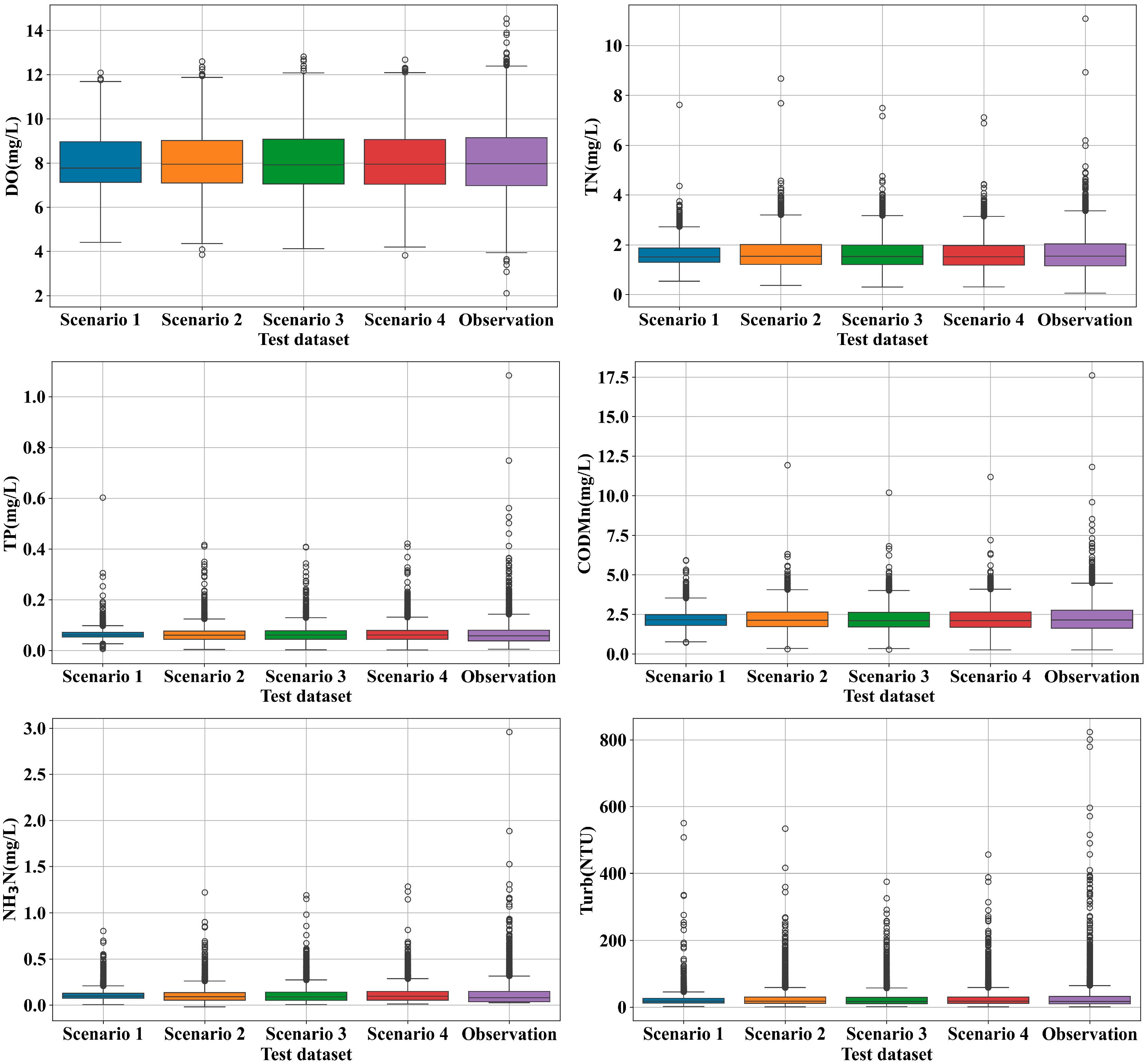
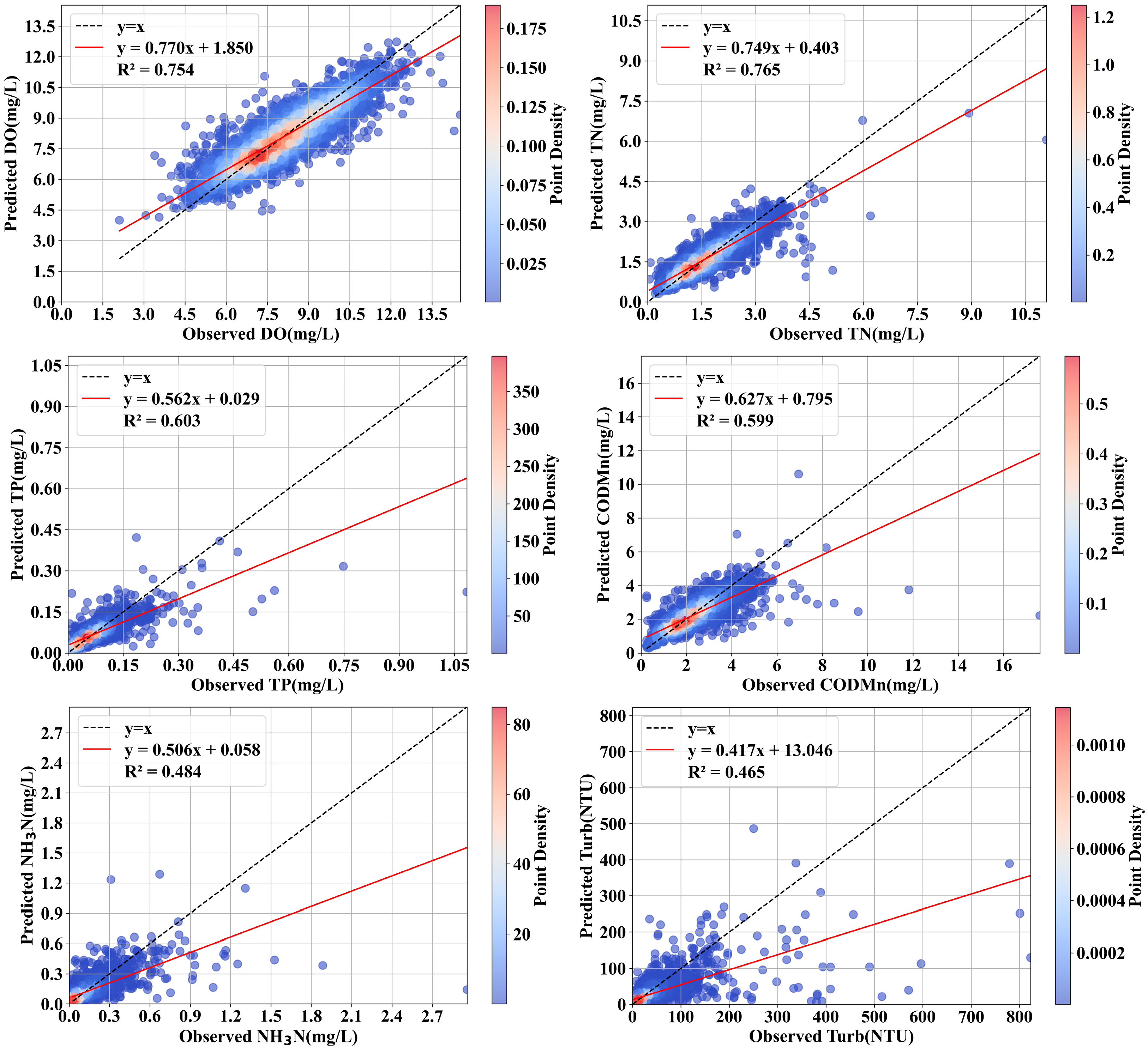
3.1. Accuracy Assessment and Comparison of Water Quality Prediction Under Different Input Scenarios
3.2. Spatial Differences in Water Quality Prediction Accuracy
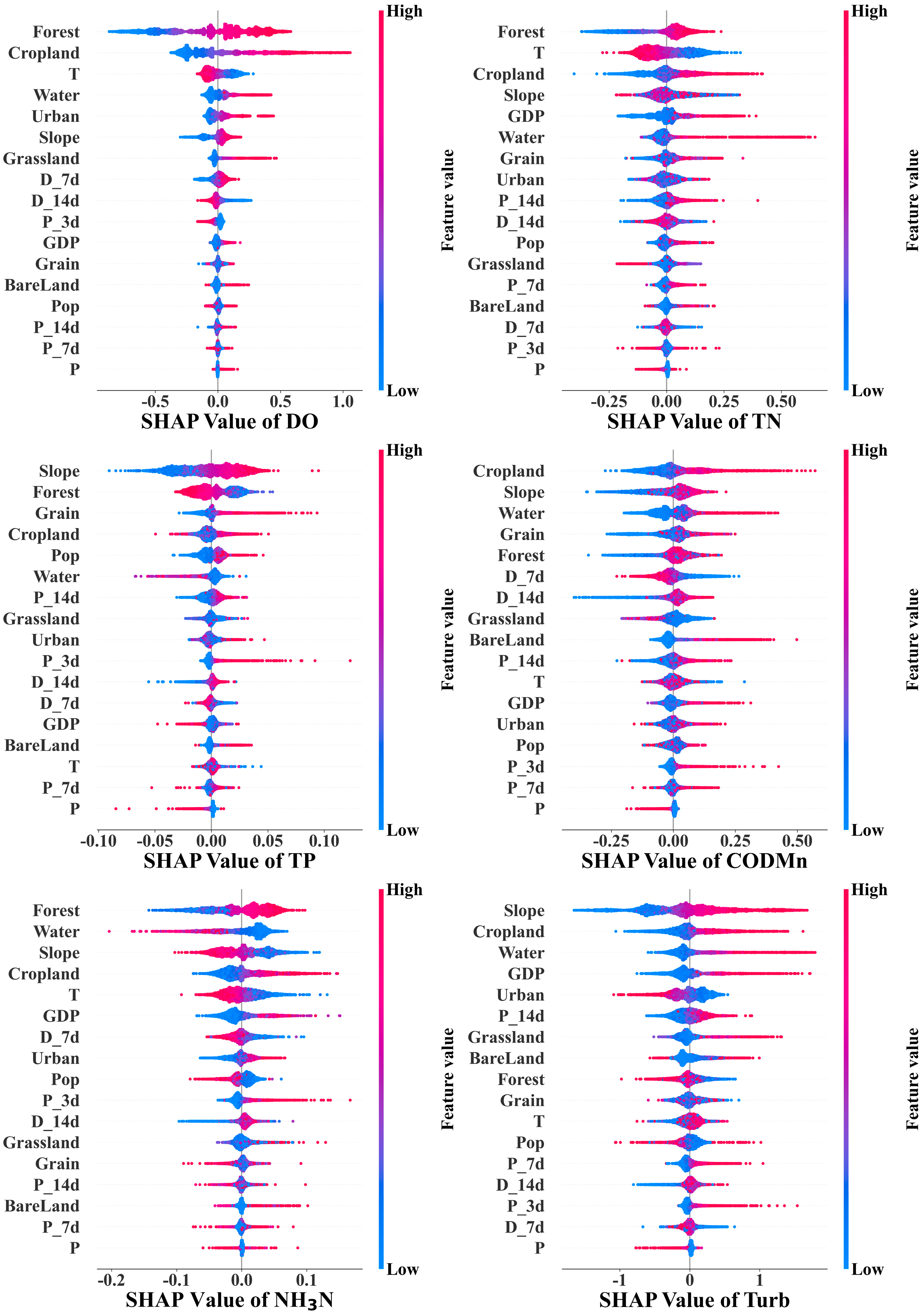
3.3. Driving Forces of Water Quality
4. Discussion
4.1. Advantages of Deep Learning Models That Integrate Multidimensional Data
4.2. Effects of Explanatory Variables on Water Quality Changes
4.3. Limitations and Future Research
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tozer, L. Water pollution ‘timebomb’ threatens global health. Nat. Water 2023, 1, 602–613. [Google Scholar] [CrossRef]
- Wang, M.; Janssen, A.B.G.; Bazin, J.; Strokal, M.; Ma, L.; Kroeze, C. Accounting for interactions between Sustainable Development Goals is essential for water pollution control in China. Nat. Commun. 2022, 13, 730. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Zhao, Y.; Zhu, Y.; Dong, Z.; Wang, F.; Huang, F. Research progress in water quality prediction based on deep learning technology: A review. Environ. Sci. Pollut. Res. 2024, 31, 26415–26431. [Google Scholar] [CrossRef] [PubMed]
- United Nations Environment Programme, U.N.W. Progress on Ambient Water Quality: Mid-term Status of SDG Indicator 6.3.2 and Acceleration Needs, with a Special Focus on Health. Available online: https://wedocs.unep.org/20.500.11822/46105 (accessed on 15 March 2025).
- Bui, H.H.; Ha, N.H.; Nguyen, T.N.D.; Nguyen, A.T.; Pham, T.T.H.; Kandasamy, J.; Nguyen, T.V. Integration of SWAT and QUAL2K for water quality modeling in a data scarce basin of Cau River basin in Vietnam. Ecohydrol. Hydrobiol. 2019, 19, 210–223. [Google Scholar] [CrossRef]
- Tang, P.; Huang, Y.; Kuo, W.; Chen, S. Variations of model performance between QUAL2K and WASP on a river with high ammonia and organic matters. Desalin Water Treat. 2014, 52, 1193–1201. [Google Scholar] [CrossRef]
- Melaku, N.D.; Brown, C.W.; Tavakoly, A.A. Improving process-based prediction of stream water temperature in SWAT using semi-Lagrangian formulation. J. Hydrol. 2025, 651, 132612. [Google Scholar] [CrossRef]
- Noor, S.S.M.; Saad, N.A.; Akhir, M.F.M.; Rahim, M.S.A. QUAL2K water quality model: A comprehensive review of its applications, and limitations. Environ. Model. Softw. 2025, 184, 106284. [Google Scholar] [CrossRef]
- Cui, L.; Wang, Y.; Zhang, H.; Lv, X.; Lei, K. Use of non-linear multiple regression models for setting water quality criteria for copper: Consider the effects of salinity and dissolved organic carbon. J. Hazard. Mater. 2023, 450, 131107. [Google Scholar] [CrossRef]
- Osmane, A.; Zidan, K.; Benaddi, R.; Sbahi, S.; Ouazzani, N.; Belmouden, M.; Mandi, L. Assessment of the effectiveness of a full-scale trickling filter for the treatment of municipal sewage in an arid environment: Multiple linear regression model prediction of fecal coliform removal. J. Water Process Eng. 2024, 64, 105684. [Google Scholar] [CrossRef]
- P Fernandes, A.C.; R Fonseca, A.; Pacheco, F.A.L.; Sanches Fernandes, L.F. Water quality predictions through linear regression-A brute force algorithm approach. Methodsx 2023, 10, 102153. [Google Scholar] [CrossRef]
- Park, N.; Kim, S.; Seo, I.; Yoon, S. Application of LPCF model based on ARIMA model to prediction of water quality change in water supply system. Desalin Water Treat. 2021, 212, 8–16. [Google Scholar] [CrossRef]
- Avila, R.; Horn, B.; Moriarty, E.; Hodson, R.; Moltchanova, E. Evaluating statistical model performance in water quality prediction. J. Environ. Manag. 2018, 206, 910–919. [Google Scholar] [CrossRef] [PubMed]
- Singha, C.; Bhattacharjee, I.; Sahoo, S.; Abdelrahman, K.; Uddin, M.G.; Fnais, M.S.; Govind, A.; Abioui, M. Prediction of urban surface water quality scenarios using hybrid stacking ensembles machine learning model in Howrah Municipal Corporation, West Bengal. J. Environ. Manag. 2024, 370, 122721. [Google Scholar] [CrossRef]
- Wang, F.; Wang, Y.; Zhang, K.; Hu, M.; Weng, Q.; Zhang, H. Spatial heterogeneity modeling of water quality based on random forest regression and model interpretation. Environ. Res. 2021, 202, 111660. [Google Scholar] [CrossRef] [PubMed]
- Niu, C.; Tan, K.; Jia, X.; Wang, X. Deep learning based regression for optically inactive inland water quality parameter estimation using airborne hyperspectral imagery. Environ. Pollut. 2021, 286, 117534. [Google Scholar] [CrossRef]
- Chen, Y.; Song, L.; Liu, Y.; Yang, L.; Li, D. A Review of the Artificial Neural Network Models for Water Quality Prediction. Appl. Sci. 2020, 10. [Google Scholar] [CrossRef]
- Zhi, W.; Appling, A.P.; Golden, H.E.; Podgorski, J.; Li, L. Deep learning for water quality. Nat. Water 2024, 2, 228–241. [Google Scholar] [CrossRef]
- Kasiselvanathan, M.; Venkata Siva Rama Prasad, C.; Vijay Arputharaj, J.; Suresh, A.; Sinduja, M.; Prajna, K.B.; Shanmugm, M. Prediction of ground water quality in western regions of Tamilnadu using LSTM network. Groundw. Sustain. Dev. 2024, 25, 101156. [Google Scholar] [CrossRef]
- Nong, X.; He, Y.; Chen, L.; Wei, J. Machine learning-based evolution of water quality prediction model: An integrated robust framework for comparative application on periodic return and jitter data. Environ. Pollut. 2025, 369, 125834. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, C.; Li, A.; Guo, Y.; Zhang, H.; Tan, C. Spatio-temporal analysis and prediction for raw water quality of drinking water source by improved RNN algorithm. J. Water Process Eng. 2025, 71, 107164. [Google Scholar] [CrossRef]
- Virro, H.; Kmoch, A.; Vainu, M.; Uuemaa, E. Random forest-based modeling of stream nutrients at national level in a data-scarce region. Sci. Total Environ. 2022, 840, 156613. [Google Scholar] [CrossRef]
- Lundberg, S.; Lee, S. A Unified Approach to Interpreting Model Predictions; Cornell University Library: Ithaca, NY, USA, 2017. [Google Scholar]
- Soleymani Hasani, S.; Arias, M.E.; Nguyen, H.Q.; Tarabih, O.M.; Welch, Z.; Zhang, Q. Leveraging explainable machine learning for enhanced management of lake water quality. J. Environ. Manag. 2024, 370, 122890. [Google Scholar] [CrossRef]
- Zheng, H.; Liu, Y.; Wan, W.; Zhao, J.; Xie, G. Large-scale prediction of stream water quality using an interpretable deep learning approach. J. Environ. Manag. 2023, 331, 117309. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Zheng, L.; Wu, J.; Liao, Y. Past and future ecosystem service trade-offs in Poyang Lake Basin under different land use policy scenarios. Arab. J. Geosci. 2020, 13, 46. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, C.; An, T.; Yue, T. Characteristics of Climate Change in Poyang Lake Basin and Its Impact on Net Primary Productivity. Sustainability 2024, 16, 9420. [Google Scholar] [CrossRef]
- Tian, C.; Zhong, J.; You, Q.; Fang, C.; Hu, Q.; Liang, J.; He, J.; Yang, W. Land use modeling and habitat quality assessment under climate scenarios: A case study of the Poyang Lake basin. Ecol. Indic. 2025, 172, 113292. [Google Scholar] [CrossRef]
- Qin, J.; Ye, H.; Lin, K.; Qi, S.; Hu, B.; Luo, J. Assessment of water-related ecosystem services based on multi-scenario land use changes: Focusing on the Poyang Lake Basin of southern China. Ecol. Indic. 2024, 158, 111549. [Google Scholar] [CrossRef]
- Deng, F.; Wen, Y.; Li, L.; Li, Z.; Ma, L.; Lin, J. Design and Application of Control Unit Division Method for Watershed Environmental Management in China in the New Era. Environ. Conform. Assess. 2022, 14, 118–126. [Google Scholar] [CrossRef]
- Guo, D.; Lintern, A.; Webb, J.A.; Ryu, D.; Liu, S.; Bende Michl, U.; Leahy, P.; Wilson, P.; Western, A.W. Key Factors Affecting Temporal Variability in Stream Water Quality. Water Resour. Res. 2019, 55, 112–129. [Google Scholar] [CrossRef]
- Voza, D.; Vuković, M. The assessment and prediction of temporal variations in surface water quality—A case study. Environ. Monit. Assess. 2018, 190, 434. [Google Scholar] [CrossRef] [PubMed]
- Karra, K.; Kontgis, C.; Statman-Weil, Z.; Mazzariello, J.C.; Mathis, M.; Brumby, S.P. Global land use / land cover with Sentinel 2 and deep learning. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; IEEE: New York, NY, USA, 2021; pp. 4704–4707. [Google Scholar]
- Deng, F.; Cao, L.; Li, F.; Li, L.; Man, W.; Chen, Y.; Liu, W.; Peng, C. Mapping China’s Changing Gross Domestic Product Distribution Using Remotely Sensed and Point-of-Interest Data with Geographical Random Forest Model. Sustainability 2023, 15. [Google Scholar] [CrossRef]
- Huang, C. Study on the Spatialization of China’sPopulation by Considering Spatial Nonstationarit. Master’s Thesis, Xiamen University of Technology, Xiamen, China, 2023. [Google Scholar]
- Irwan, D.; Ali, M.; Ahmed, A.N.; Jacky, G.; Nurhakim, A.; Ping Han, M.C.; AlDahoul, N.; El-Shafie, A. Predicting Water Quality with Artificial Intelligence: A Review of Methods and Applications. Arch. Comput. Methods Eng. 2023, 30, 4633–4652. [Google Scholar] [CrossRef]
- Li, J.; Shen, Z.; Liu, G.; Jin, Z.; Liu, R. The effect of social economy-water resources-water environment coupling system on water consumption and pollution emission based on input-output analysis in Changchun city, China. J. Clean. Prod. 2023, 423, 138719. [Google Scholar] [CrossRef]
- Peng, J.; Zhang, Z.; Lin, Y.; Tang, H.; Xu, Z.; Zheng, H. Unveiling Decoupled Social-Ecological Networks of Great Lake Basin: An Ecosystem Services Approach. Earth’s Future 2024, 12, e2024EF004994. [Google Scholar] [CrossRef]
- Xiao, T.; Ran, F.; Li, Z.; Wang, S.; Nie, X.; Liu, Y.; Yang, C.; Tan, M.; Feng, S. Sediment organic carbon dynamics response to land use change in diverse watershed anthropogenic activities. Environ. Int. 2023, 172, 107788. [Google Scholar] [CrossRef] [PubMed]
- Roth, A.E. Lloyd Shapley (1923–2016). Nature 2016, 532, 178. [Google Scholar] [CrossRef]
- Venkateswarlu, T.; Anmala, J. Importance of land use factors in the prediction of water quality of the Upper Green River watershed, Kentucky, USA, using random forest. Environ. Dev. Sustain. 2024, 26, 23961–23984. [Google Scholar] [CrossRef]
- Zhao, Y.; Sun, H.; Wang, X.; Ding, J.; Lu, M.; Pang, J.; Zhou, D.; Liang, M.; Ren, N.; Yang, S. Spatiotemporal drivers of urban water pollution: Assessment of 102 cities across the Yangtze River Basin. Environ. Sci. Ecotechnol. 2024, 20, 100412. [Google Scholar] [CrossRef]
- Wang, L.; Han, X.; Zhang, Y.; Zhang, Q.; Wan, X.; Liang, T.; Song, H.; Bolan, N.; Shaheen, S.M.; White, J.R.; et al. Impacts of land uses on spatio-temporal variations of seasonal water quality in a regulated river basin, Huai River, China. Sci. Total Environ. 2023, 857, 159584. [Google Scholar] [CrossRef]
- Wang, Y.; Junaid, M.; Deng, J.; Tang, Q.; Luo, L.; Xie, Z.; Pei, D. Effects of land-use patterns on seasonal water quality at multiple spatial scales in the Jialing River, Chongqing, China. Catena 2024, 234, 107646. [Google Scholar] [CrossRef]
- Wu, J.; Zeng, S.; Yang, L.; Ren, Y.; Xia, J. Spatiotemporal Characteristics of the Water Quality and Its Multiscale Relationship with Land Use in the Yangtze River Basin. Remote Sens. 2021, 13, 3309. [Google Scholar] [CrossRef]
- McDowell, R.; McNeill, S.J.; Drewry, J.J.; Law, R.; Stevenson, B. Difficulties in using land use pressure and soil quality indicators to predict water quality. Sci. Total Environ. 2024, 935, 173445. [Google Scholar] [CrossRef]
- Wang, W.; Yang, P.; Xia, J.; Huang, H.; Li, J. Impact of land use on water quality in buffer zones at different scales in the Poyang Lake, middle reaches of the Yangtze River basin. Sci. Total Environ. 2023, 896, 165161. [Google Scholar] [CrossRef]
- Hu, Y.; Liu, X.; Zhang, Z.; Wang, S.; Zhou, H. Spatiotemporal Heterogeneity of Agricultural Land Eco-Efficiency: A Case Study of 128 Cities in the Yangtze River Basin. Water 2022, 14, 422. [Google Scholar] [CrossRef]
- Liu, H.; Li, J.; Meng, C.; Ouyang, W.; Wang, X.; Yin, W.; Li, Y. Spatial and hydrological consideration for linking multidimensional landscape metrics to riverine P loading—A case study in an agriculture-forest dominated subtropical watershed, China. Ecol. Indic. 2025, 176, 113678. [Google Scholar] [CrossRef]
- Pakoksung, K.; Inseeyong, N.; Chawaloesphonsiya, N.; Punyapalakul, P.; Chaiwiwatworakul, P.; Xu, M.; Chuenchum, P. Seasonal dynamics of water quality in response to land use changes in the Chi and Mun River Basins Thailand. Sci. Rep. 2025, 15, 7101. [Google Scholar] [CrossRef]
- Xu, Q.; Wang, P.; Shu, W.; Ding, M.; Zhang, H. Influence of landscape structures on river water quality at multiple spatial scales: A case study of the Yuan river watershed, China. Ecol. Indic. 2021, 121, 107226. [Google Scholar] [CrossRef]
- Yao, X.; Zeng, C.; Duan, X.; Wang, Y. Effects of land use patterns on seasonal water quality in Chinese basins at multiple temporal and spatial scales. Ecol. Indic. 2024, 166, 112423. [Google Scholar] [CrossRef]
- Wang, X.; Wu, Y.; Cushman, S.A.; Tie, C.; Lawson, G.; Kollányi, L.; Wang, G.; Ma, J.; Zhang, J.; Bai, T. Spatio-temporal dynamics of water quality and land use in the Lake Dianchi (China) system: A multi-source data-driven approach. J. Hydrol. Reg. Stud. 2025, 59, 102341. [Google Scholar] [CrossRef]
- Lausch, A.; Selsam, P.; Heege, T.; von Trentini, F.; Almeroth, A.; Borg, E.; Klenke, R.; Bumberger, J. Monitoring and modelling landscape structure, land use intensity and landscape change as drivers of water quality using remote sensing. Sci. Total Environ. 2025, 960, 178347. [Google Scholar] [CrossRef] [PubMed]
- Ice, G.G.; Hale, V.C.; Light, J.T.; Muldoon, A.; Simmons, A.; Bousquet, T. Understanding dissolved oxygen concentrations in a discontinuously perennial stream within a managed forest. For. Ecol. Manag. 2021, 479, 118531. [Google Scholar] [CrossRef]
- Ding, J.; Jiang, Y.; Fu, L.; Liu, Q.; Peng, Q.; Kang, M. Impacts of Land Use on Surface Water Quality in a Subtropical River Basin: A Case Study of the Dongjiang River Basin, Southeastern China. Water 2015, 7, 4427–4445. [Google Scholar] [CrossRef]
- Zhang, H.; Ren, X.; Chen, S.; Xie, G.; Hu, Y.; Gao, D.; Tian, X.; Xiao, J.; Wang, H. Deep optimization of water quality index and positive matrix factorization models for water quality evaluation and pollution source apportionment using a random forest model. Environ. Pollut. 2024, 347, 123771. [Google Scholar] [CrossRef]
- Hu, Y.; Peng, Z.; Zhang, Y.; Liu, G.; Zhang, H.; Hu, W. Air temperature effects on nitrogen and phosphorus concentration in Lake Chaohu and adjacent inflowing rivers. Aquat. Sci. 2022, 84, 33. [Google Scholar] [CrossRef]
- Schürings, C.; Globevnik, L.; Lemm, J.U.; Psomas, A.; Snoj, L.; Hering, D.; Birk, S. River ecological status is shaped by agricultural land use intensity across Europe. Water Res. 2024, 251, 121136. [Google Scholar] [CrossRef]
- Xu, H.; Tan, X.; Liang, J.; Cui, Y.; Gao, Q. Impact of Agricultural Non-Point Source Pollution on River Water Quality: Evidence From China. Front. Ecol. Evol. 2022, 10, 858822. [Google Scholar] [CrossRef]
- Lei, C. Evaluating coupled influences of slope class and land use change on water quality using single and composite indices in an agricultural basin. Catena 2025, 248, 108584. [Google Scholar] [CrossRef]
- Lee, J.; Park, S.; Lee, S. Effect of Land Use on Stream Water Quality and Biological Conditions in Multi-Scale Watersheds. Water 2023, 15, 4210. [Google Scholar] [CrossRef]
- Mello, K.D.; Taniwaki, R.H.; Paula, F.R.D.; Valente, R.A.; Randhir, T.O.; Macedo, D.R.; Leal, C.G.; Rodrigues, C.B.; Hughes, R.M. Multiscale land use impacts on water quality: Assessment, planning, and future perspectives in Brazil. J. Environ. Manag. 2020, 270, 110879. [Google Scholar] [CrossRef]
- Huang, S.; Wang, Y.; Xia, J. Which riverine water quality parameters can be predicted by meteorologically-driven deep learning? Sci. Total Environ. 2024, 946, 174357. [Google Scholar] [CrossRef] [PubMed]
- Paule-Mercado, M.C.; Rabaneda-Bueno, R.; Porcal, P.; Kopacek, M.; Huneau, F.; Vystavna, Y. Climate and land use shape the water balance and water quality in selected European lakes. Sci. Rep. 2024, 14, 8049. [Google Scholar] [CrossRef] [PubMed]


| Modeling Scenarios | Predictor Variables |
|---|---|
| Meteorological Factor Coupling Scenario (S1) | Daily average temperature; daily precipitation; cumulative precipitation over the past 3 days, 7 days, and 14 days; and the number of dry days over the past 7 days and 14 days |
| Socioeconomic Expansion Scenario (S2) | S1 + GDP, population density, and grain production |
| Land Use Composite Scenario (S3) | S1 + cropland, forest land, water area, building land, bare land, and grassland |
| Multi-System Synergy Scenario (S4) | All factors |
| Indicators | Scenario | TN | DO | TP | CODMn | NH3N | TURB |
|---|---|---|---|---|---|---|---|
| R2 | S1 | 0.388 | 0.555 | 0.174 | 0.320 | 0.208 | 0.150 |
| S2 | 0.730 | 0.738 | 0.579 | 0.574 | 0.430 | 0.425 | |
| S3 | 0.734 | 0.758 | 0.587 | 0.581 | 0.481 | 0.431 | |
| S4 | 0.754 | 0.765 | 0.603 | 0.599 | 0.484 | 0.465 | |
| MSE | S1 | 0.292 | 1.108 | 0.002 | 0.609 | 0.012 | 1802.509 |
| S2 | 0.132 | 0.622 | 0.001 | 0.388 | 0.009 | 1219.684 | |
| S3 | 0.127 | 0.603 | 0.001 | 0.379 | 0.008 | 1206.893 | |
| S4 | 0.126 | 0.572 | 0.001 | 0.367 | 0.008 | 1135.663 |
| Parameter | F_Value | p_Value |
|---|---|---|
| DO | 14,700.89 | <0.001 |
| TN | 14,821.96 | <0.001 |
| TP | 6950.57 | <0.001 |
| CODMn | 6976.23 | <0.001 |
| NH3N | 4150.01 | <0.001 |
| Turb | 3799.31 | <0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Y.; Zhou, C.; Wu, J.; Deng, F.; Liu, W.; Sun, M.; Li, L. An Interpretable Deep Learning Framework for River Water Quality Prediction—A Case Study of the Poyang Lake Basin. Water 2025, 17, 2496. https://doi.org/10.3390/w17162496
Yuan Y, Zhou C, Wu J, Deng F, Liu W, Sun M, Li L. An Interpretable Deep Learning Framework for River Water Quality Prediction—A Case Study of the Poyang Lake Basin. Water. 2025; 17(16):2496. https://doi.org/10.3390/w17162496
Chicago/Turabian StyleYuan, Ying, Chunjin Zhou, Jingwen Wu, Fuliang Deng, Wei Liu, Mei Sun, and Lanhui Li. 2025. "An Interpretable Deep Learning Framework for River Water Quality Prediction—A Case Study of the Poyang Lake Basin" Water 17, no. 16: 2496. https://doi.org/10.3390/w17162496
APA StyleYuan, Y., Zhou, C., Wu, J., Deng, F., Liu, W., Sun, M., & Li, L. (2025). An Interpretable Deep Learning Framework for River Water Quality Prediction—A Case Study of the Poyang Lake Basin. Water, 17(16), 2496. https://doi.org/10.3390/w17162496







