Creep Tests and Fractional Creep Damage Model of Saturated Frozen Sandstone
Abstract
1. Introduction
2. Frozen Sandstone Creep Test
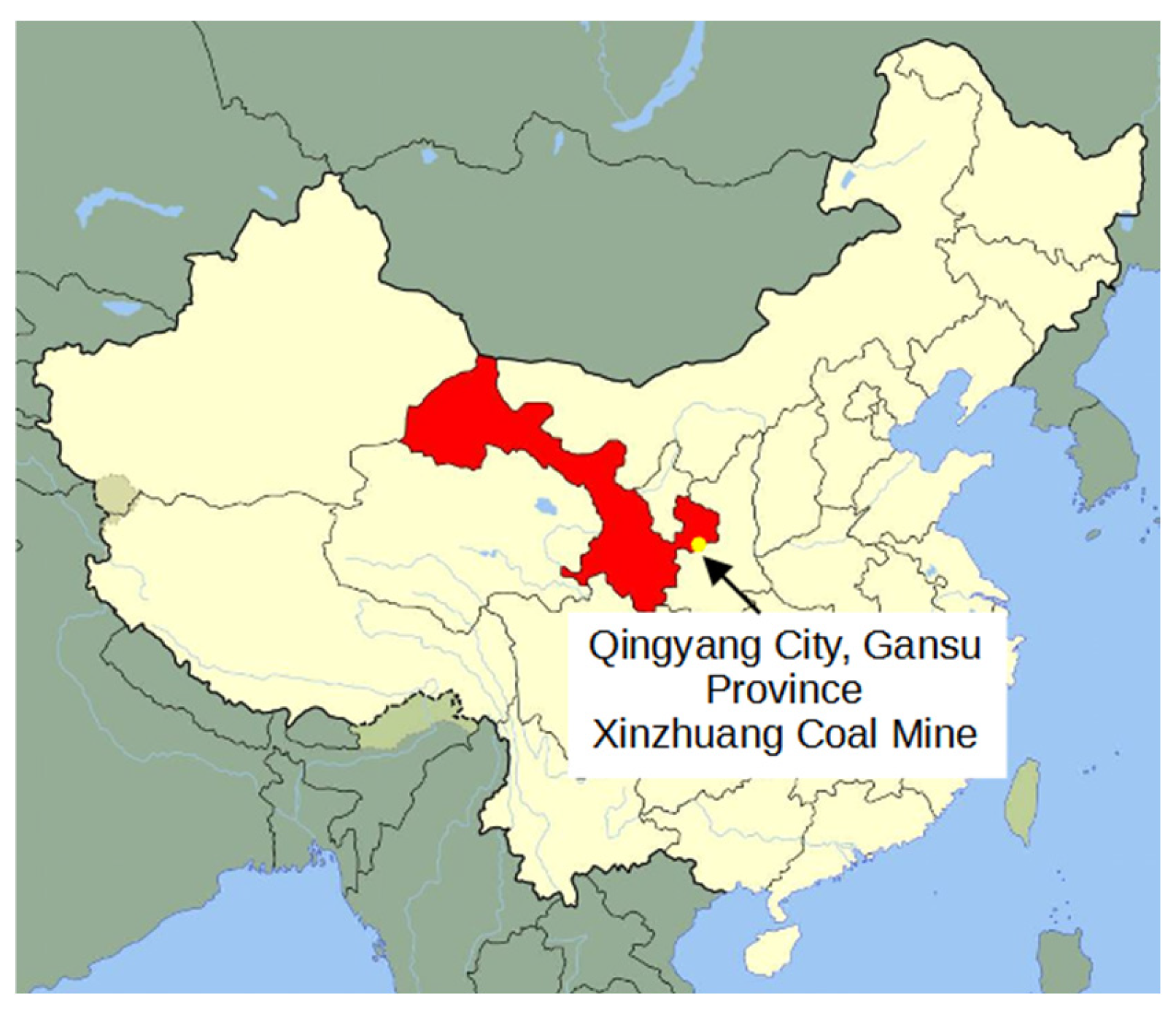
2.1. Engineering Background
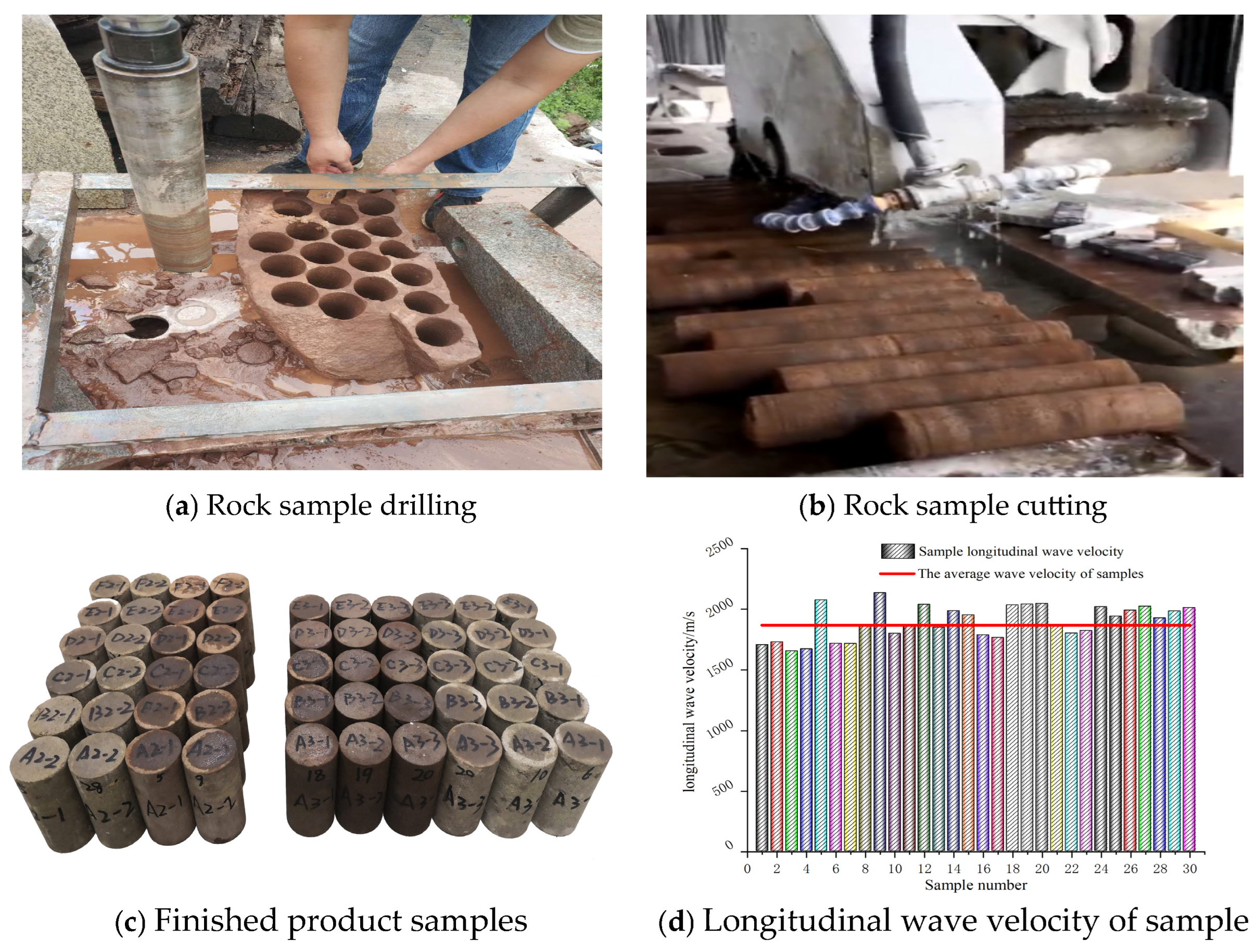
2.2. Selection of Rock Samples
2.3. Test Apparatus
2.4. Pilot Program
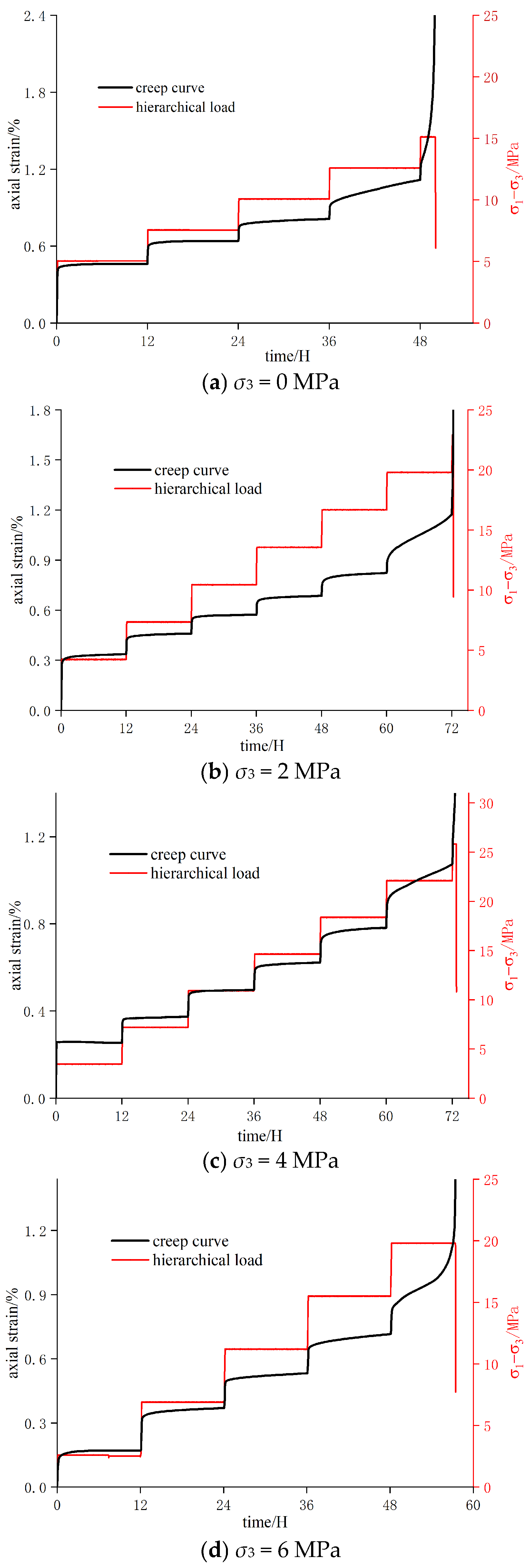
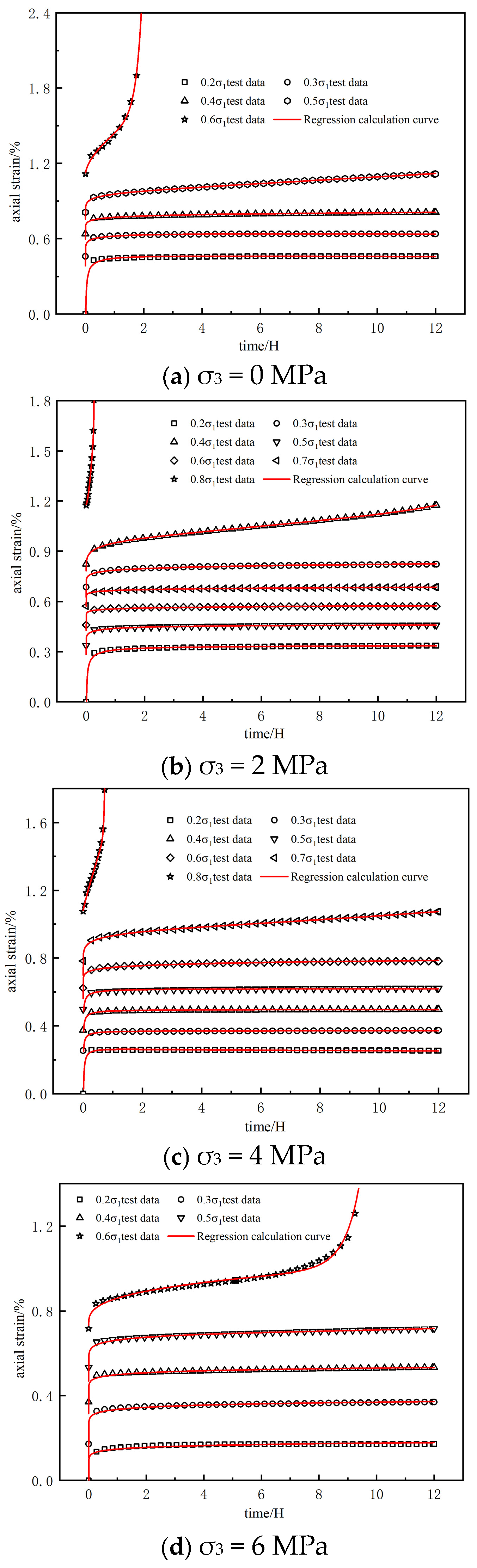
2.5. Creep Characterization Results
3. Damage Characteristics and Creep Evolution of Frozen Sandstone
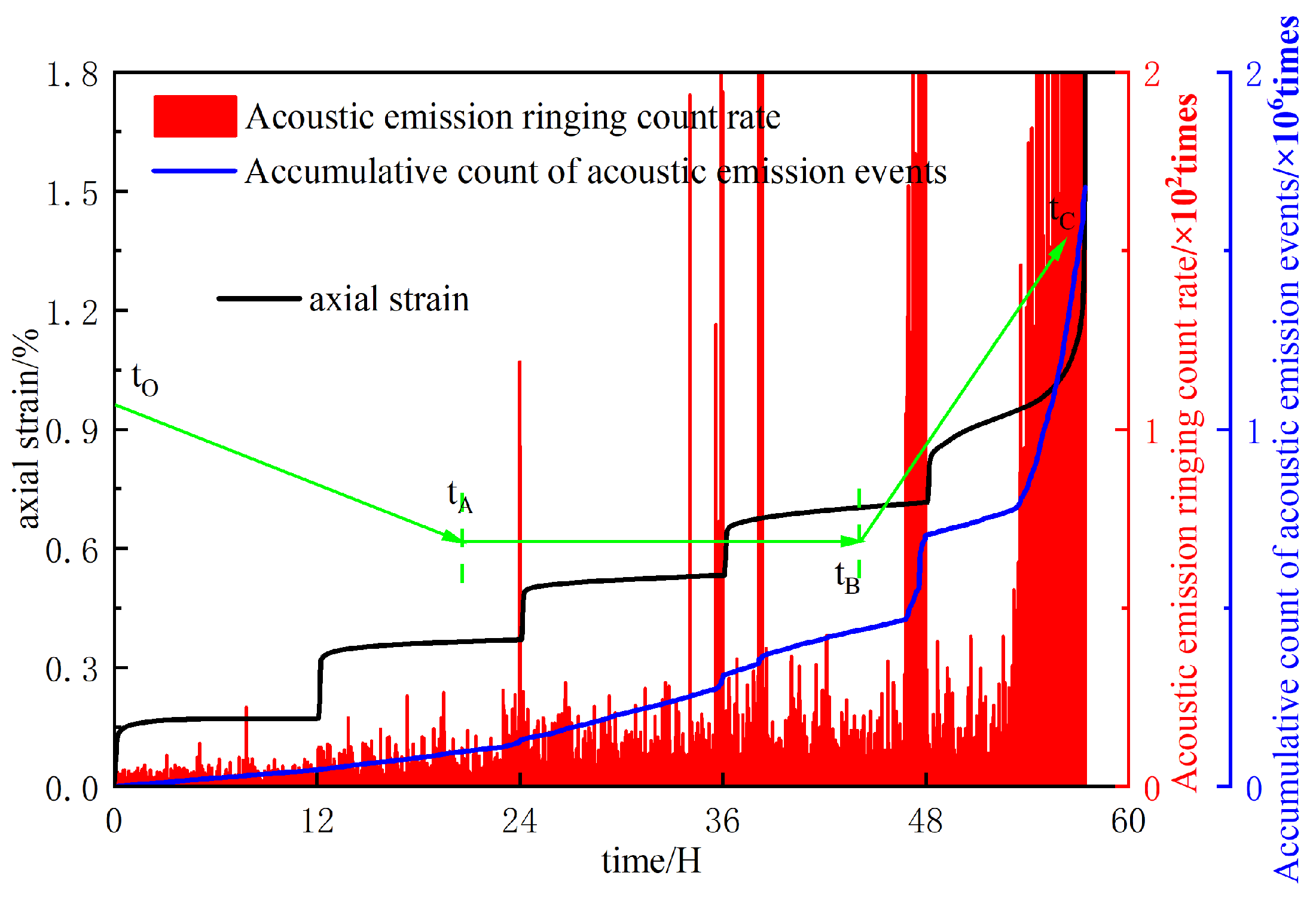
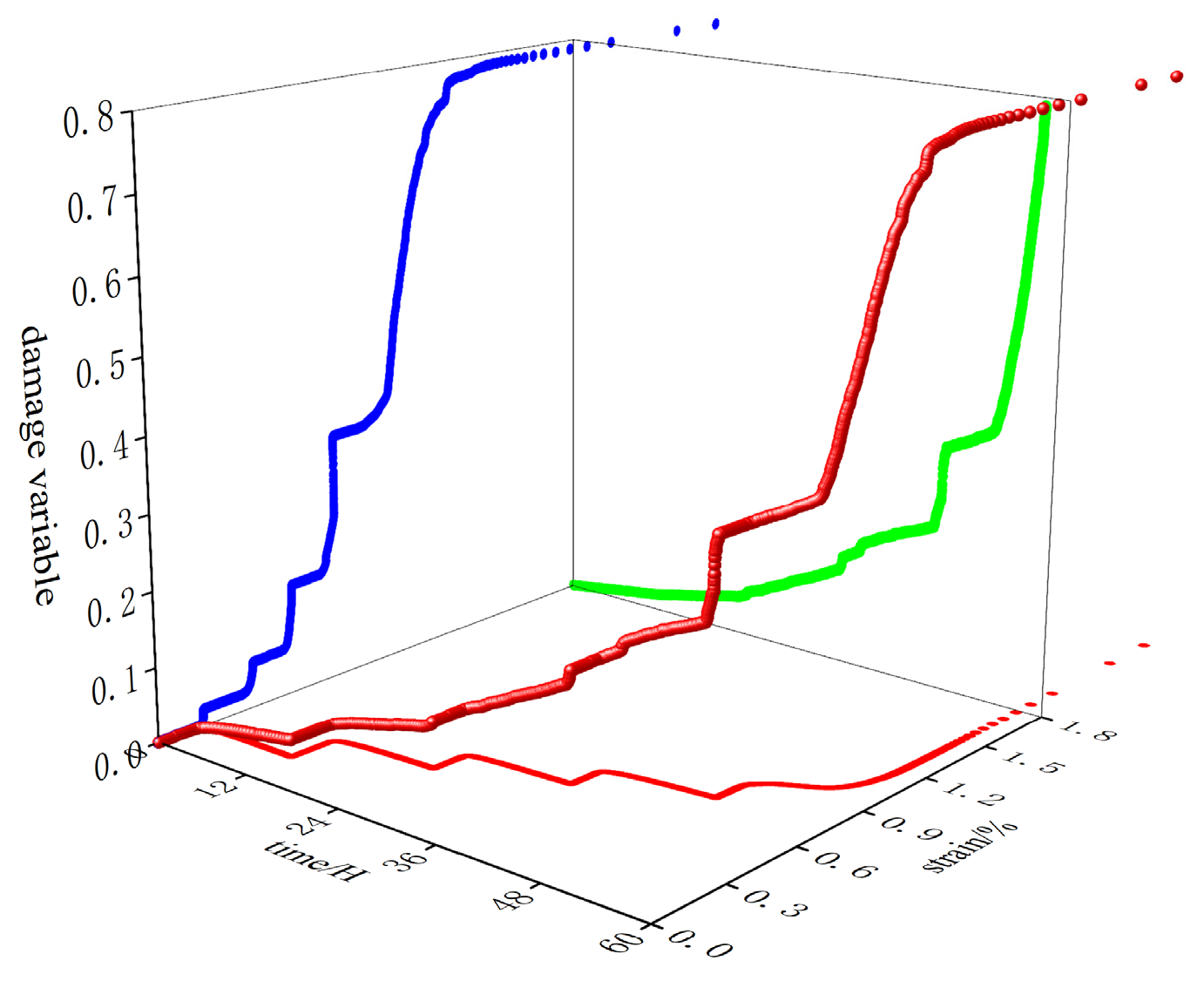
3.1. Damage Characterization Based on Acoustic Emission Energy Parameters
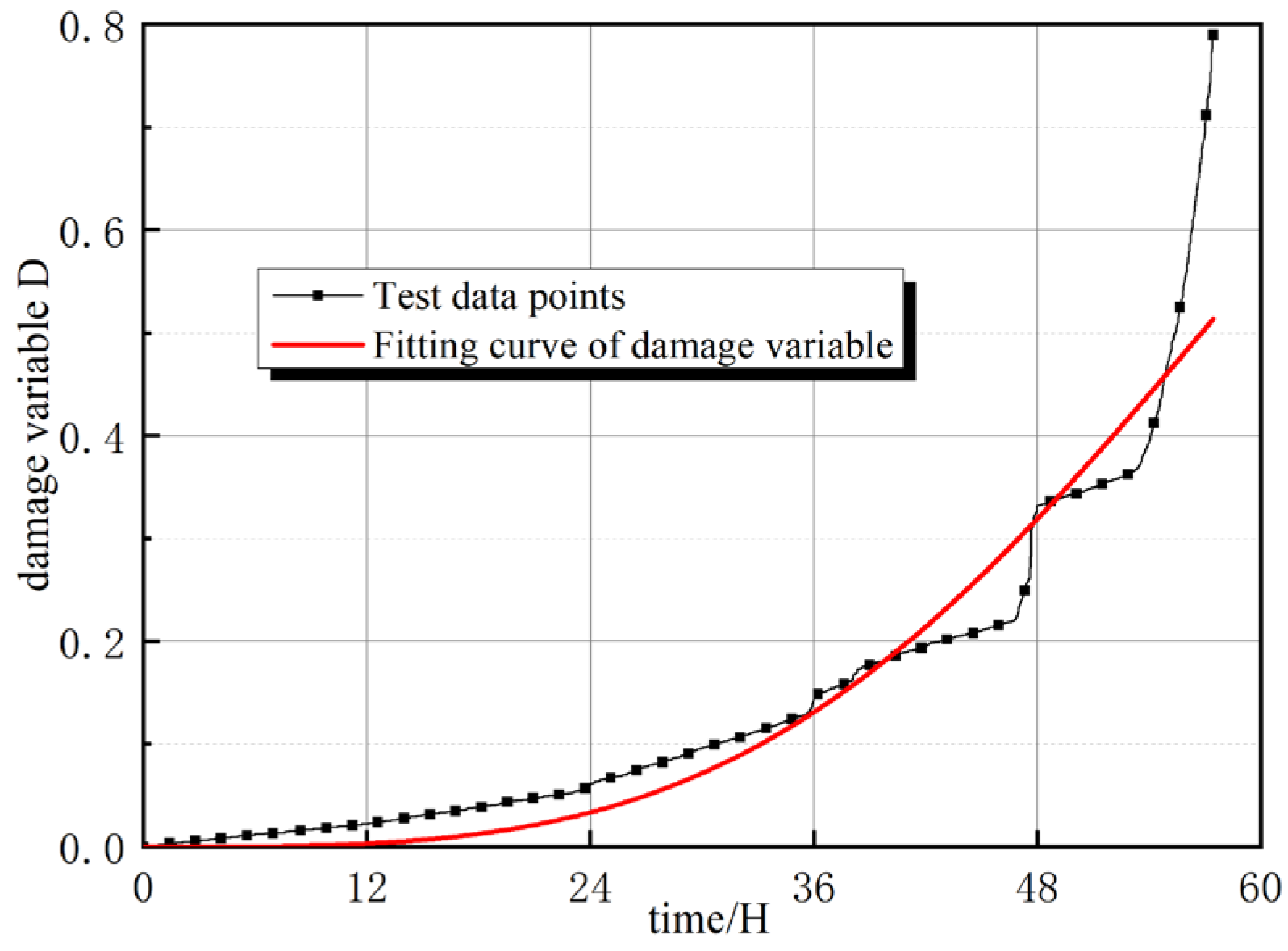
3.2. Damage Evolution During Creep
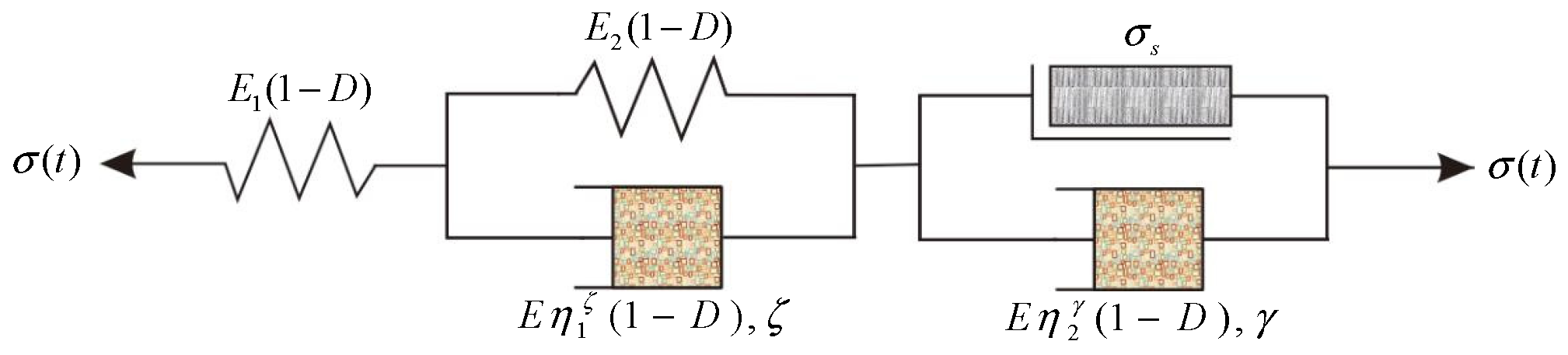
4. Fractional-Order Creep Ontological Model for Saturated Frozen Sandstone Considering Damage
4.1. Fractional Viscous Body
4.2. Fractional Creep Constitutive Model Considering Damage
4.3. Fractional-Order Model Parameter Inversion
5. Fractional-Order Model Creep Parameter Impact Level Analysis
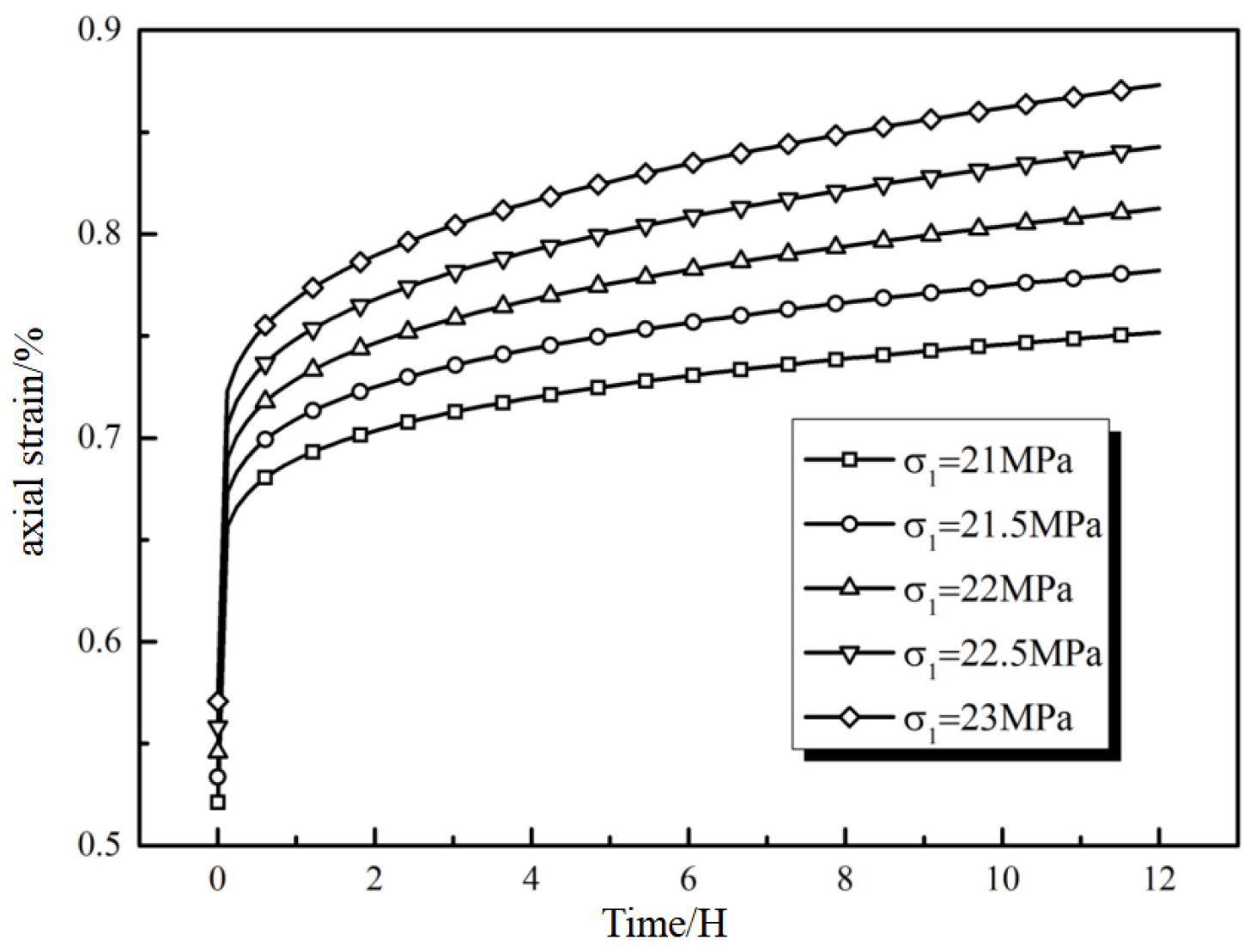
5.1. Effect of Stress Level
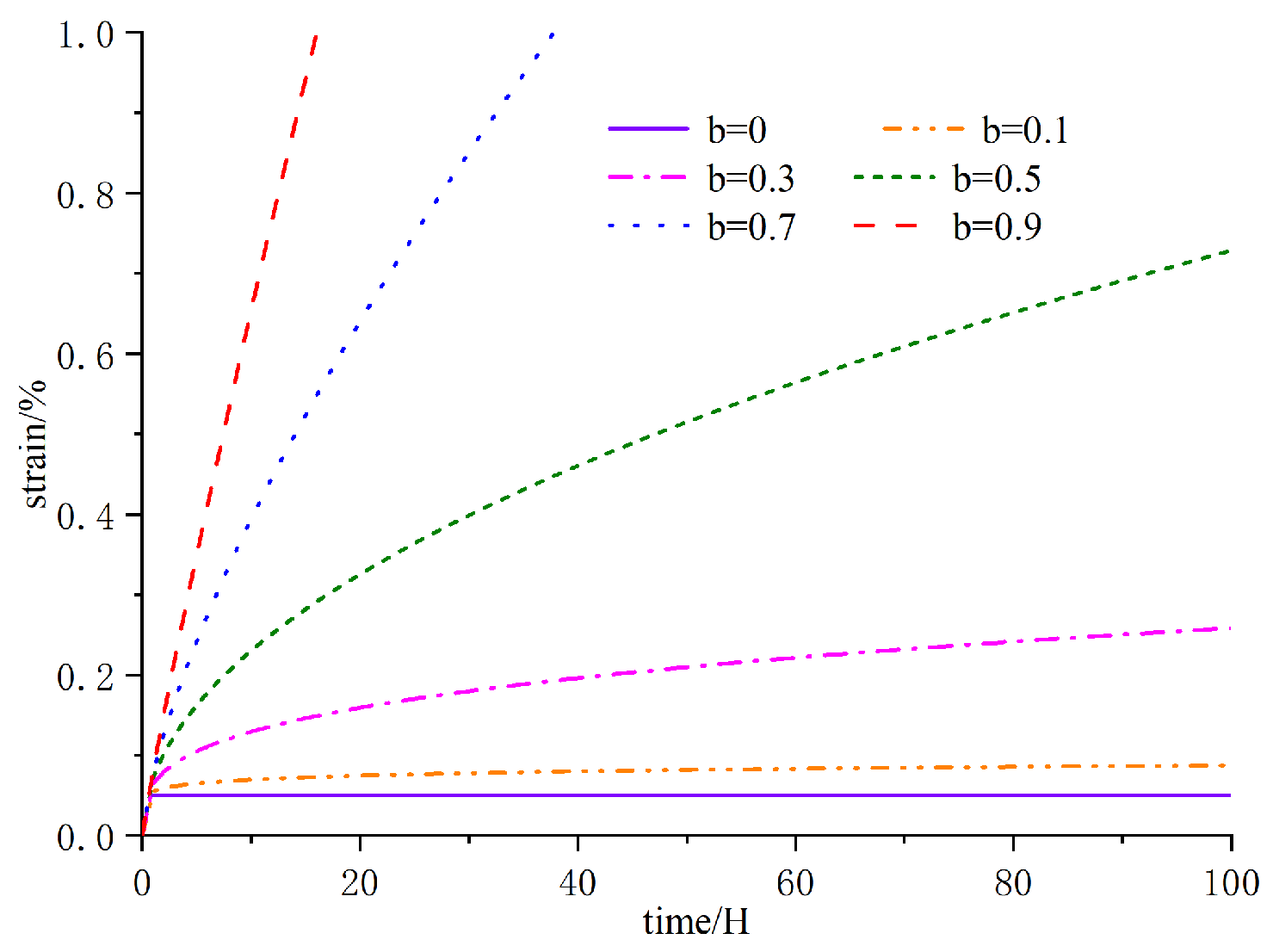
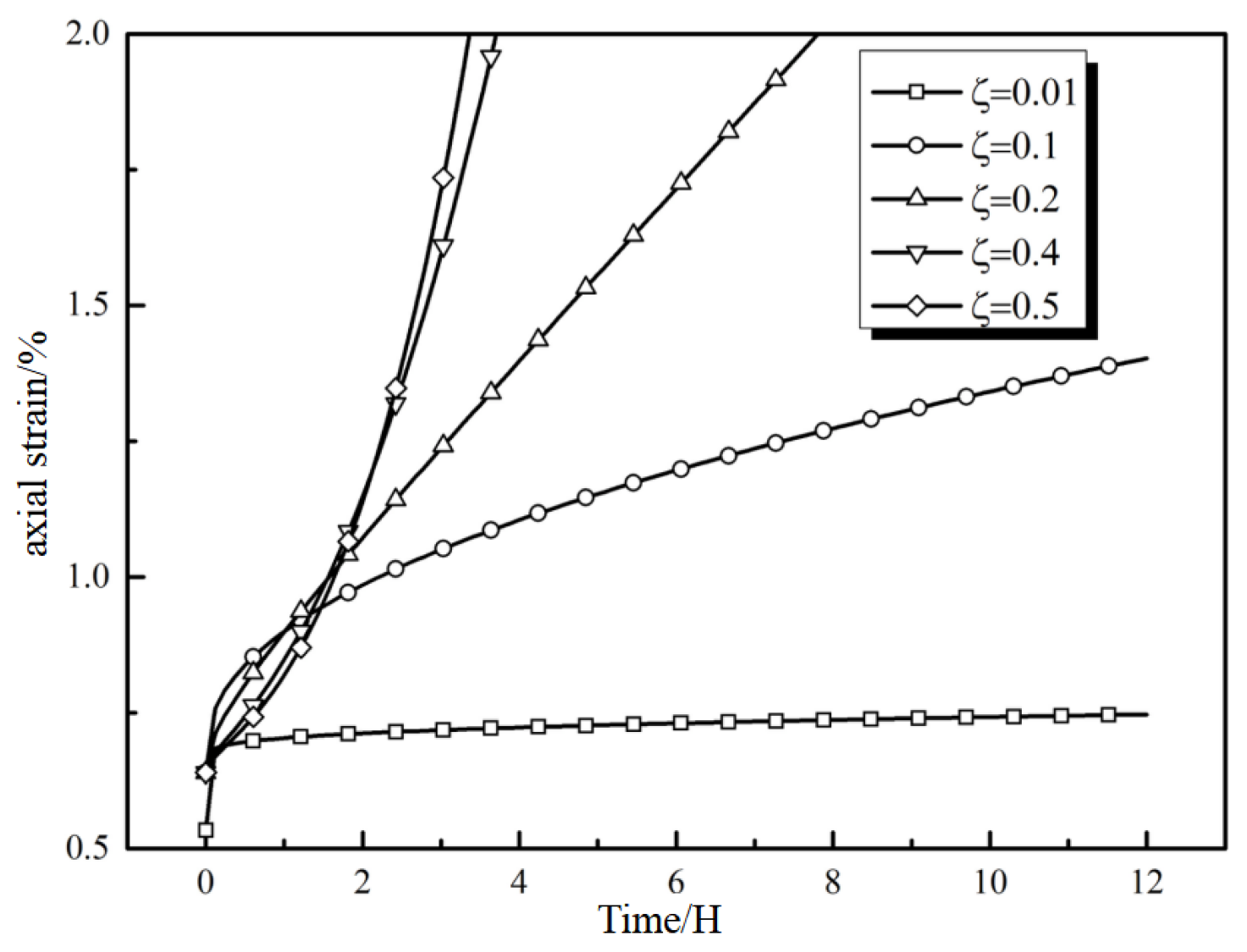
5.2. Effect of Fractional-Order Derivative ζ
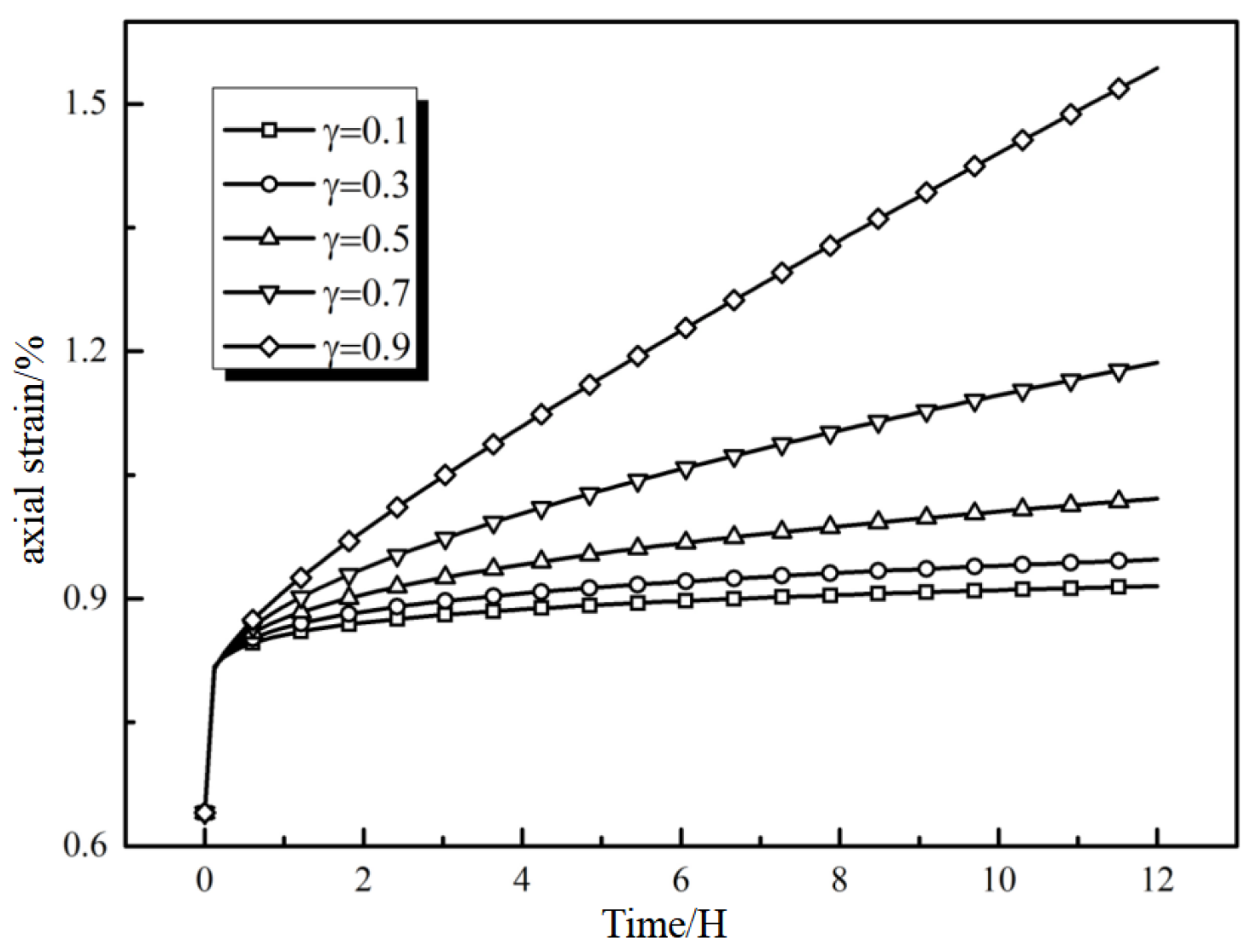
5.3. Effect of Fractional-Order Derivative γ
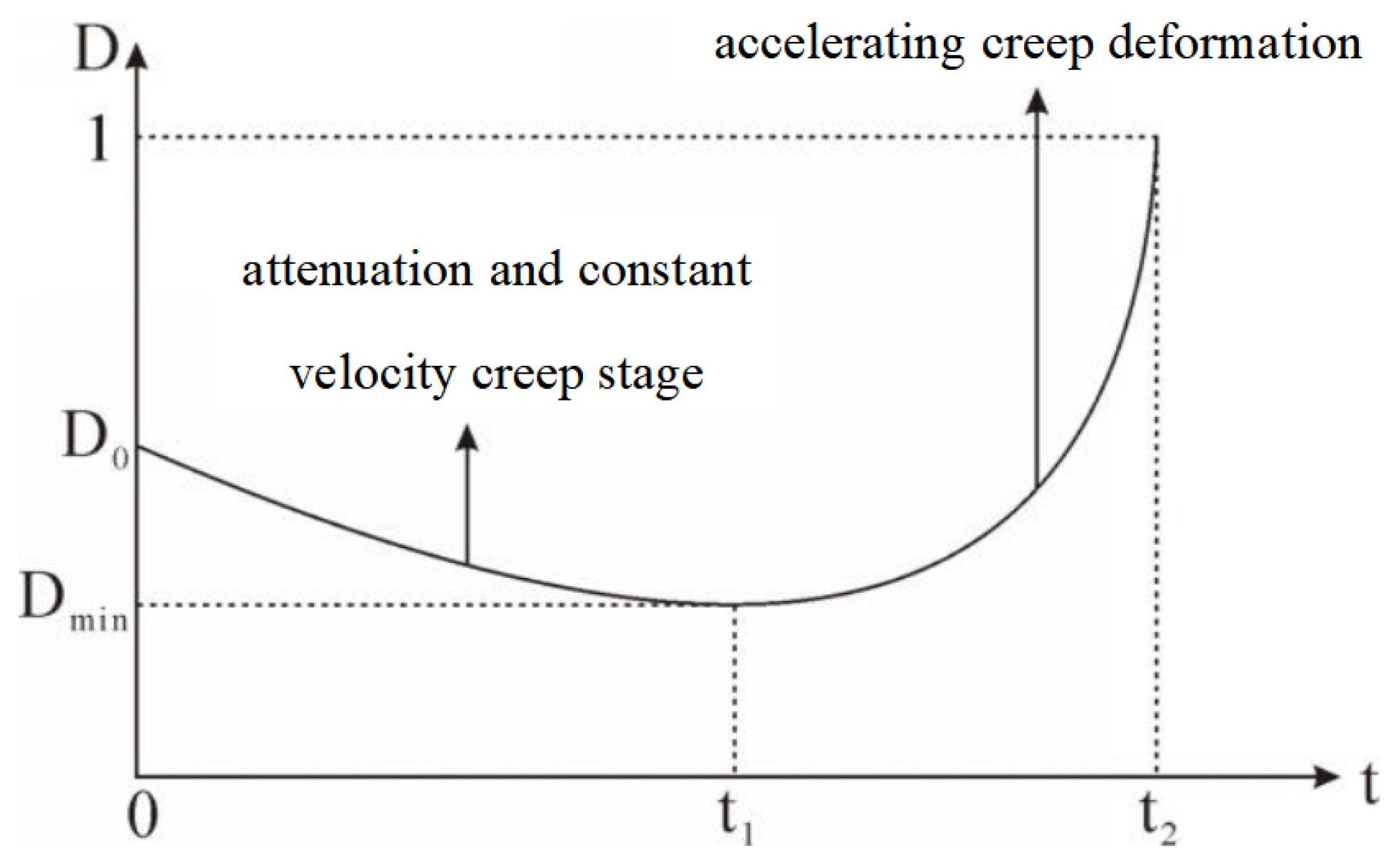
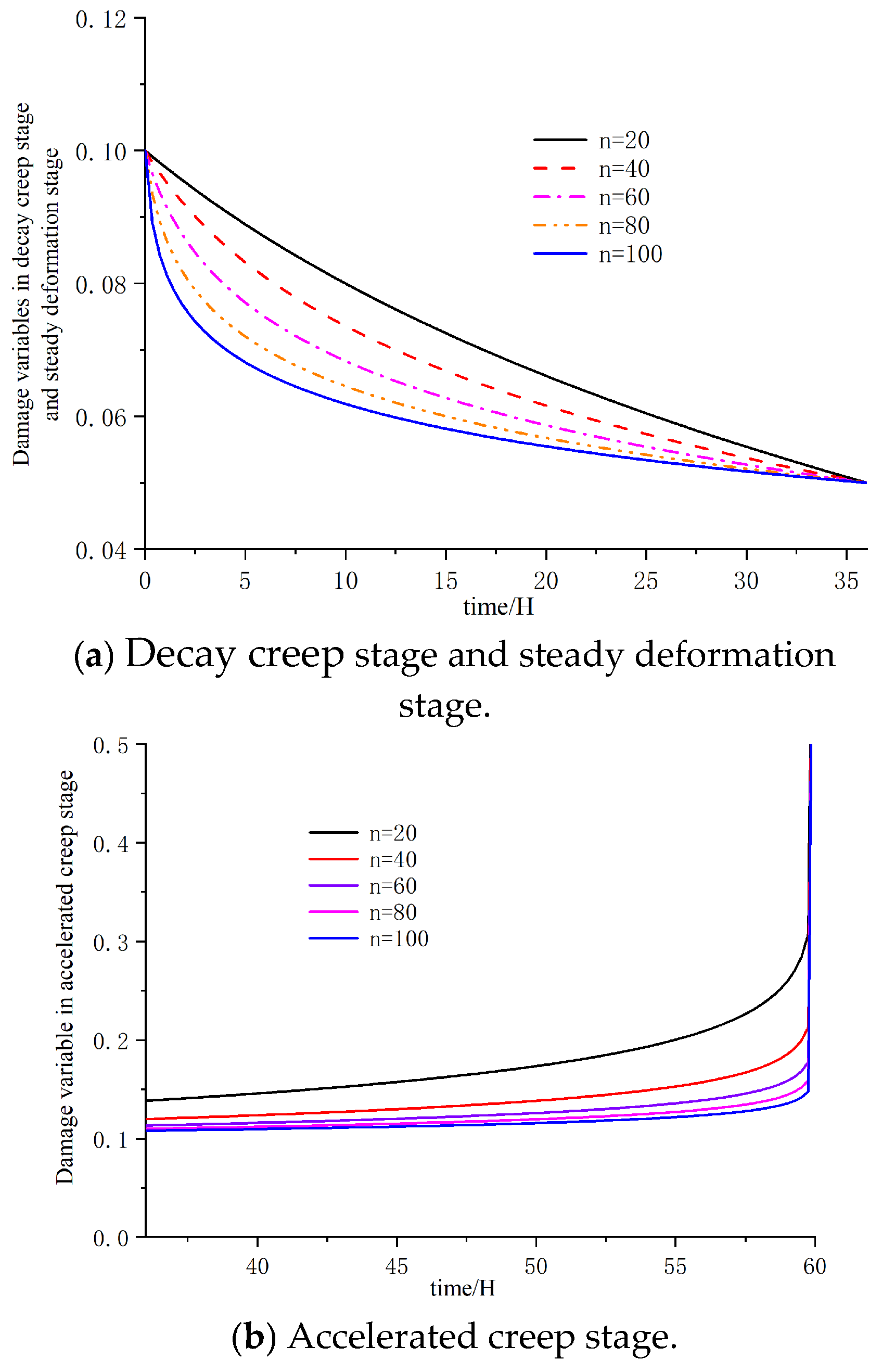
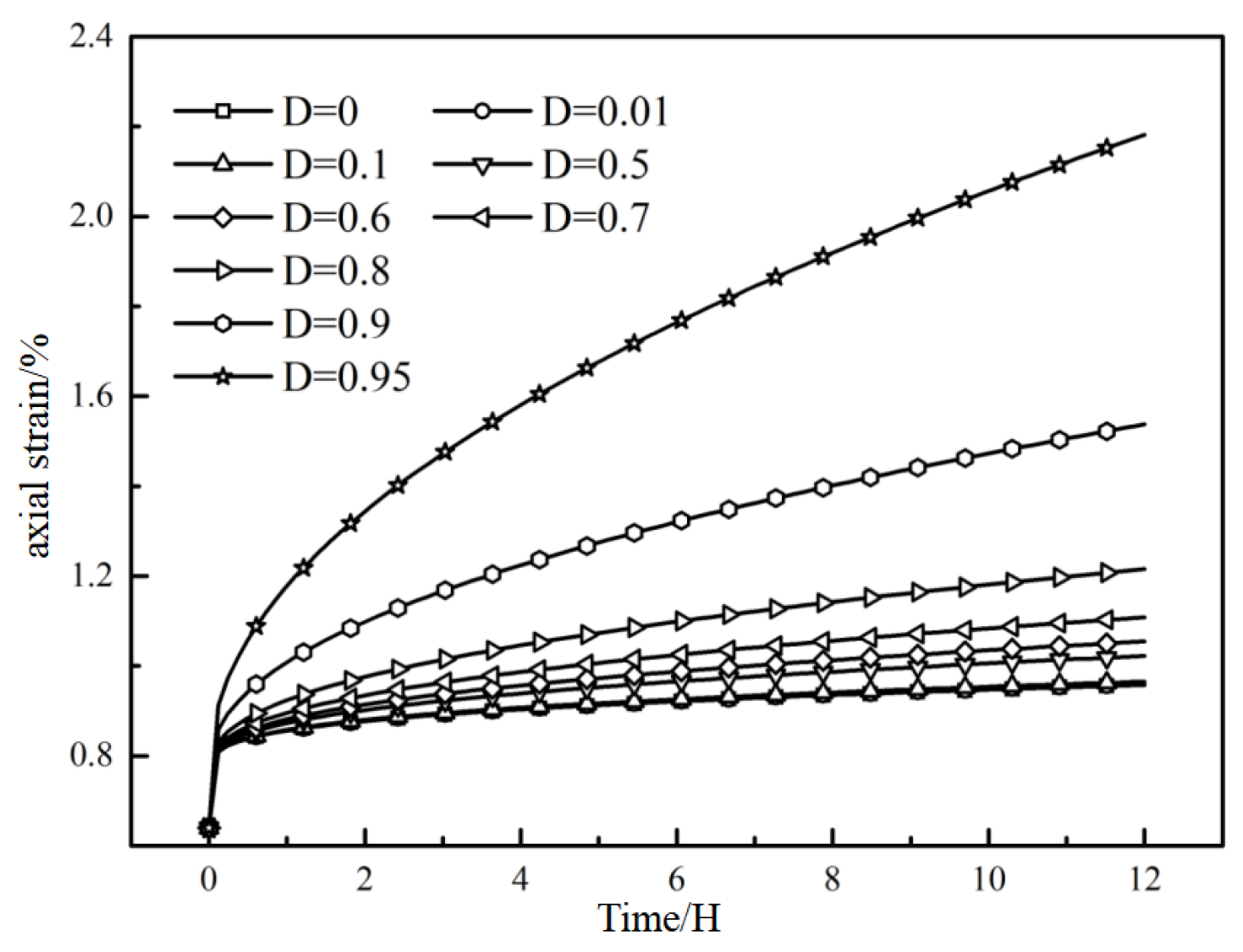
5.4. Impact of Damage Variable
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Griggs, D. Creep of rocks. J. Geol. 1939, 47, 225–251. [Google Scholar] [CrossRef]
- Jun, S.; Wang, S.J. Rock mechanics and rock engineering in China: Developments and current state-of-the-art. Int. J. Rock Mech. Min. Sci. 2000, 37, 447–465. [Google Scholar]
- Zhang, H.M.; Yang, G.S. Damage Constitutive Model of Loaded Rock Under Freeze-thaw Condition. J. Wuhan Univ. Technol. 2013, 35, 79–82. [Google Scholar]
- Li, Z.Y.; Yang, G.S.; Wei, Y. Construction of frozen Sandstone creep damage model and analysis of influencing factors based on fractional-order theory. Arab. J. Sci. Eng. 2021, 46, 11373–11385. [Google Scholar] [CrossRef]
- Li, J.L.; Zhu, L.Y.; Zhou, K.P.; Chen, H.; Gao, L.; Lin, Y.; Shen, Y.-J. Non-linear creep damage model of sandstone under freeze-thaw cycle. J. Cent. South. Univ. 2021, 28, 954–967. [Google Scholar] [CrossRef]
- Chen, K.S. A damage treatment of creep failure in rock salt. Int. J. Damage Mech. 1997, 6, 122–152. [Google Scholar] [CrossRef]
- Bellenger, E.; Bussy, P. Phenomenological modeling and numerical simulation of different modes of creep damage evolution. Int. J. Solids Struct. 2001, 38, 577–604. [Google Scholar] [CrossRef]
- Kranz, R.L. Crack growth and development during creep of Barre granite. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1979, 16, 23–35. [Google Scholar] [CrossRef]
- Atkinson, B.K.; Meredith, P.G. Theory of subcritical crack growth with applications to minerals and rocks. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1988, 25, 111–166. [Google Scholar]
- Miura, K.; Okui, Y.; Horii, H. Micromechanics-based prediction of creep failure of hard rock for long-term safety of high-level radioactive waste disposal system. Mech. Mater. 2003, 35, 587–601. [Google Scholar] [CrossRef]
- Kemeny, J.M. A model for non-linear rock deformation under compression due to sub-critical crack growth. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1991, 28, 459–467. [Google Scholar] [CrossRef]
- Duncan, E.; Lajtai, E.Z. The creep of potash salt rocks from Saskatchewan. Geotech. Geol. Eng. 1993, 11, 159–184. [Google Scholar] [CrossRef]
- Goodwin, A.K.; O’Neill, M.A.; Anderson, W.F. The use of X-ray computer tomography to investigate particulate interactions within opencast coal mine backfills. Eng. Geol. 2003, 70, 331–341. [Google Scholar] [CrossRef]
- Thomachot, C.; Jeannette, D. Evolution of the petrophysical properties of two types of Alsatian sandstone subjected to simulated freeze-thaw conditions. Geol. Soc. Lond. Spec. Publ. 2002, 205, 19–32. [Google Scholar] [CrossRef]
- Ito, H.; Sasajima, S. A ten year creep experiment on small rock specimens. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1987, 24, 113–121. [Google Scholar] [CrossRef]
- Fabre, G.; Pellet, F. Creep and time-dependent damage in argillaceous rocks. Int. J. Rock Mech. Min. Sci. 2006, 43, 950–960. [Google Scholar] [CrossRef]
- Hashiba, K.; Fukui, K. Time-dependent behaviors of granite: Loading-rate dependence, creep, and relaxation. Rock Mech. Rock Eng. 2016, 49, 2569–2580. [Google Scholar] [CrossRef]
- Mishra, B.; Verma, P. Uniaxial and triaxial single and multistage creep tests on coal-measure shale rocks. Int. J. Coal Geol. 2015, 137, 55–65. [Google Scholar] [CrossRef]
- Mansouri, H.; Ajalloeian, R. Mechanical behavior of salt rock under uniaxial compression and creep tests. Int. J. Rock Mech. Min. Sci. 2018, 110, 19–27. [Google Scholar] [CrossRef]
- Wang, X.; Lian, B.; Feng, W. A Nonlinear Creep Damage Model Considering the Effect of Dry-Wet Cycles of Rocks on Reservoir Bank. Water 2020, 12, 2396. [Google Scholar] [CrossRef]
- Yi, S.; Zhang, Y.; Yi, H.; Li, X.; Wang, X.; Wang, Y.; Chu, T. Study on the Instability Activation Mechanism and Deformation Law of Surrounding Rock Affected by Water Immersion in Goafs. Water 2022, 14, 3250. [Google Scholar] [CrossRef]
- Brzesowsky, R.H.; Hangx, S.J.; Brantut, N.; Spiers, C.J. Compaction creep of sands due to time-dependent grain failure: Effects of chemical environment, applied stress, and grain size. J. Geophys. Res. Solid. Earth 2014, 119, 7521–7541. [Google Scholar] [CrossRef]
- Nomikos, P.; Rahmannejad, R.; Sofianos, A. Supported axisymmetric tunnels within linear viscoelastic Burgers rocks. Rock Mech. Rock Eng. 2011, 44, 553–564. [Google Scholar] [CrossRef]
- Zhang, S.; Yun, X.; Song, Y.; Liu, W.; Yang, L. Fluid-Structure Coupling Creep Characteristics of Red-Bed Soft Rock in South China. Water 2022, 14, 4088. [Google Scholar] [CrossRef]
- Zhu, G.; Wang, S.; Zhang, W.; Li, B. Research on the Mechanism and Evolution Law of Delayed Water Inrush Caused by Fault Activation with Mining. Water 2023, 15, 4209. [Google Scholar] [CrossRef]
- Okubo, S.; Fukui, K.; Hashiba, K. Development of a transparent triaxial cell and observation of rock deformation in compression and creep tests. Int. J. Rock Mech. Min. Sci. 2008, 45, 351–361. [Google Scholar] [CrossRef]
- Maranini, E.; Brignoli, M. Creep behaviour of a weak rock: Experimental characterization. Int. J. Rock Mech. Min. Sci. 1999, 36, 127–138. [Google Scholar] [CrossRef]
- Heap, M.; Baud, P.; Meredith, P.; Vinciguerra, S.; Bell, A.F.; Main, I.G. Brittle creep in basalt and its application to time dependent volcano deformation. Earth Planet. Sci. Lett. 2011, 307, 71–82. [Google Scholar] [CrossRef]
- Kranz, R.L.; Scholz, C.H. Critical dilatant volume of rocks at the onset of Tertiary creep. J. Geophys. Res. 1977, 82, 4893–4898. [Google Scholar] [CrossRef]
- Lockner, D.A.; Byerlee, J.D. Changes in complex resistivity during creep in granite. Pure Appl. Geophys. 1986, 124, 659–676. [Google Scholar] [CrossRef]
- Tsai, L.S.; Hsieh, Y.M.; Weng, M.C.; Huang, T.H.; Jeng, F.-S. Time-dependent deformation behaviors of weak sandstones. Int. J. Rock Mech. Min. Sci. 2008, 45, 144–154. [Google Scholar] [CrossRef]
- Heap, M.J.; Baud, P.; Meredith, P.G.; Bell, A.F.; Main, I.G. Time-dependent brittle creep in Darley Dale sandstone. J. Geophys. Res. 2009, 114, B07203. [Google Scholar] [CrossRef]
- Zhang, H.M.; Wang, F.Y.; Yang, G.S. Experimental study on creep characteristics of infiltrated coal-rock under load. Arch. Appl. Mech. 2023, 93, 1331–1349. [Google Scholar] [CrossRef]
- Shan, R.L.; Bai, Y.; Ju, Y.; Han, T.-Y.; Dou, H.-Y.; Li, Z.-L. Study on the Triaxial Unloading Creep Mechanical Properties and Damage Constitutive Model of Red Sandstone Containing a Single Ice-Filled Flaw. Rock. Mech. Rock. Eng. 2021, 54, 833–855. [Google Scholar] [CrossRef]
- Yang, X.; Jiang, A.; Guo, X. Effects of water content and temperature on creep properties of frozen red sandstone: An experimental study. Bull. Eng. Geol. Environ. 2021, 81, 51. [Google Scholar] [CrossRef]
- Li, S.; Tao, W.; Zhang, F.; Yao, X. Experimental study of the dynamic characteristics of sandstone with preexisting creep damage. Mech. Time-Depend. Mater. 2021, 26, 955–973. [Google Scholar] [CrossRef]
- Wang, H.; Xu, Z.; Huai, H.; Yin, Y.; Zeng, J.; Du, Z.; Zhou, H. Experimental study on the mechanical properties of red sandstone with fractures under different loading rates. Int. J. Damage Mech. 2025, 34, 438–467. [Google Scholar] [CrossRef]
- Pan, X.; Berto, F.; Zhou, X. Investigation of creep damage mechanical behaviors of red sandstone considering temperature effect. Fatigue Fract. Eng. Mater. Struct. 2021, 45, 411–424. [Google Scholar] [CrossRef]
- Hu, B.; Wang, Z.Q.; Li, J.; Wei, E.; Ma, L.; Liu, J.; Yu, X. A new shear creep damage model for rock masses after considering initial damage. PLoS ONE 2023, 18, e0280793. [Google Scholar] [CrossRef]
- Jiang, H.; Jiang, A.; Jiang, T. Characterization of the creep behavior and modeling considering viscoelastic-plastic damage of quartz sandstone under thermo-hydro-mechanical conditions. Mech. Time-Depend. Mater. 2023, 28, 185–205. [Google Scholar] [CrossRef]
- Xiu, X.; Wang, Y.; Zhou, Y.; Niu, G.; Zhao, S.; Chang, D. Creep Model and Experimental Verification of Sandstone under the Coupled Effect of Chemical Corrosion and Temperature. Appl. Sci. 2024, 14, 7847. [Google Scholar] [CrossRef]
- Li, T.B.; Chen, C.; Peng, F.; Ma, C.; Li, M.; Wang, Y. Creep damage constitutive model of rock based on the mechanisms of crack-initiated damage and extended. Undergr. Space 2024, 18, 295–313. [Google Scholar] [CrossRef]
- Yu, H.; Wang, Z.; Feng, W.; Wang, Z.; Niu, R.; Cheng, G. Experimental study on the effect of anchors on the creep mechanical properties and acoustic emission characteristics of fractured sandstone under uniaxial compression. Theor. Appl. Fract. Mech. 2023, 126, 103995. [Google Scholar] [CrossRef]
- Pan, X.; Zhou, X. Damage Analysis of Sandstone During the Creep Stage After High-Temperature Heat Treatment Based on NMR Technology. Rock Mech. Rock Eng. 2022, 55, 7569–7586. [Google Scholar] [CrossRef]
- Pan, X.; Zhou, X.; Zou, Y.; Lei, D.; Berto, F. Creep mechanical properties and creep damage model of sandstone considering temperature effect based on acoustic emission. Fatigue Fract. Eng. Mater. Struct. 2023, 47, 35–55. [Google Scholar] [CrossRef]
- Hu, J.; Luge, S.; He, F.; Liu, Z. Experimental Study on Creep of Sandstone under Hydrochemical Corrosion. J. Phys. Conf. Ser. 2022, 2148, 012024. [Google Scholar] [CrossRef]
- GB/T 19222-2003; Sampling of Coal Petrology. Standardization Administration of China: Beijing, China, 2003.
- GB/T 23561; Methods for Determining the Physical and Mechanical Properties of Coal and Rock. China National Standards: Beijing, China, 2009.
- Kachanov, L.M. Rupture time under creep conditions. Int. J. Fract. 1999, 97, 11–18. [Google Scholar] [CrossRef]

| T/°C | σ1/MPa | |||
|---|---|---|---|---|
| σ3 = 0 MPa | σ3 = 2 MPa | σ3 = 4 MPa | σ3 = 6 MPa | |
| −10 | 25.19 | 31.13 | 37.29 | 43.01 |
| Confining Pressure MPa | Axial Compression MPa | E1 | Eη1 | ζ | E2 | D | Eη2 | γ | R2 |
|---|---|---|---|---|---|---|---|---|---|
| GPa | GPa/h | GPa | GPa/h | ||||||
| 0 | 0.2σ1 | 0.0163 | 0.1917 | 0.0037 | 2.1407 | — | — | — | 98.99 |
| 0.3σ1 | 0.0164 | 0.4674 | 0.0093 | 1.5238 | — | — | — | 97.95 | |
| 0.4σ1 | 0.0157 | 0.5002 | 0.0240 | 0.9959 | — | — | — | 96.94 | |
| 0.5σ1 | 0.0155 | 0.5377 | 0.3642 | 0.1438 | 0.4430 | 0.1002 | 0.1541 | 97.99 | |
| 0.6σ1 | 0.01234 | 0.5514 | 0.4651 | 0.0599 | 0.9979 | 0.3771 | 0.6614 | 92.90 | |
| 2 | 0.2σ1 | 0.0277 | 0.2001 | 0.0068 | 1.8698 | — | — | — | 98.99 |
| 0.3σ1 | 0.0276 | 0.5192 | 0.0161 | 1.2305 | — | — | — | 95.94 | |
| 0.4σ1 | 0.0270 | 0.6502 | 0.0140 | 1.0948 | — | — | — | 96.73 | |
| 0.5σ1 | 0.0271 | 0.7035 | 0.0235 | 0.9933 | — | — | — | 93.90 | |
| 0.6σ1 | 0.0272 | 0.8102 | 0.0714 | 0.7814 | 0.4652 | 0.2974 | 0.4278 | 96.99 | |
| 0.7σ1 | 0.0264 | 0.8812 | 0.1557 | 0.3647 | 0.7826 | 0.4271 | 0.6455 | 93.98 | |
| 0.8σ1 | 0.0212 | 0.8834 | 0.4047 | 0.1968 | 0.8088 | 0.6438 | 0.7929 | 91.88 | |
| 4 | 0.2σ1 | 0.0395 | 0.2323 | 0.0035 | 1.9838 | — | — | — | 98.98 |
| 0.3σ1 | 0.0419 | 0.5273 | 0.0078 | 1.1277 | — | — | — | 96.78 | |
| 0.4σ1 | 0.0398 | 0.6889 | 0.0106 | 1.1172 | — | — | — | 93.93 | |
| 0.5σ1 | 0.0374 | 0.7522 | 0.0185 | 1.0186 | — | — | — | 96.89 | |
| 0.6σ1 | 0.0359 | 0.8313 | 0.1470 | 0.9235 | 0.4863 | 0.3045 | 0.1392 | 93.99 | |
| 0.7σ1 | 0.0333 | 0.9002 | 0.2644 | 0.5672 | 0.4892 | 0.7391 | 0.6847 | 96.97 | |
| 0.8σ1 | 0.0277 | 0.2289 | 0.5126 | 0.1686 | 0.9968 | 0.8650 | 0.7355 | 91.93 | |
| 6 | 0.2σ1 | 0.0517 | 0.2674 | 0.0088 | 2.5523 | — | — | — | 98.98 |
| 0.3σ1 | 0.0547 | 0.6402 | 0.0149 | 1.2872 | — | — | — | 98.98 | |
| 0.4σ1 | 0.0494 | 0.7264 | 0.0199 | 1.0985 | — | — | — | 96.83 | |
| 0.5σ1 | 0.0403 | 0.8563 | 0.0253 | 1.0756 | 0.4702 | 0.1675 | 0.5380 | 93.91 | |
| 0.6σ1 | 0.0349 | 0.9100 | 0.4763 | 0.2083 | 0.8102 | 0.3134 | 0.7514 | 90.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Y.; Peng, H. Creep Tests and Fractional Creep Damage Model of Saturated Frozen Sandstone. Water 2025, 17, 2492. https://doi.org/10.3390/w17162492
Wei Y, Peng H. Creep Tests and Fractional Creep Damage Model of Saturated Frozen Sandstone. Water. 2025; 17(16):2492. https://doi.org/10.3390/w17162492
Chicago/Turabian StyleWei, Yao, and Hui Peng. 2025. "Creep Tests and Fractional Creep Damage Model of Saturated Frozen Sandstone" Water 17, no. 16: 2492. https://doi.org/10.3390/w17162492
APA StyleWei, Y., & Peng, H. (2025). Creep Tests and Fractional Creep Damage Model of Saturated Frozen Sandstone. Water, 17(16), 2492. https://doi.org/10.3390/w17162492






