Modeling Hydraulic Transient Process in Long-Distance Water Transfer Systems Using a MUSCL-Type FVM Approach
Abstract
1. Introduction
2. Governing Equations
2.1. Basic Equations for Flow Analysis
2.2. Second-Order MUSCL-Type Scheme
3. Results and Discussions
3.1. Experimental Verification
3.2. Optimal Valve Placement and Operation Strategy
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| a | Acoustic wave speed |
| Cr | Courant number |
| D | Pipe diameter |
| E | Design feasible field |
| , | Fluxes |
| g | Gravitational acceleration |
| H | Water head |
| Hmax1 | Maximum water head upstream of valve |
| Hmax2 | Maximum water head downstream of valve |
| Hmin1 | Minimum water head upstream of valve |
| Hmin2 | Minimum water head downstream of valve |
| Jq | Quasi-steady friction term |
| Ju | Unsteady friction term |
| L | Pipe length |
| L1 | Valve position |
| Nx | Control volumes number along pipe |
| Re | Reynolds number |
| t | Flow time |
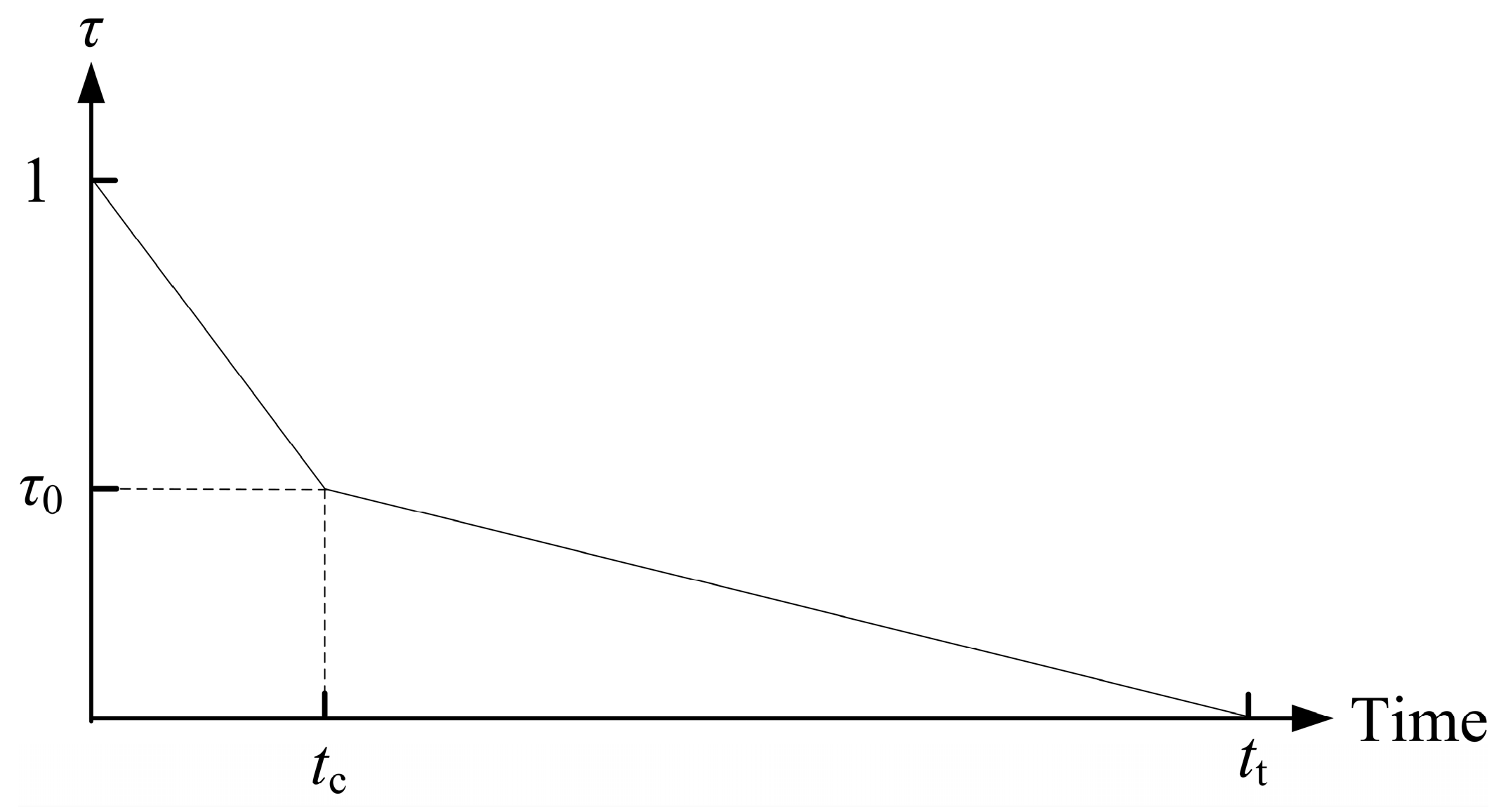
| tc | Valve closure time of first stage |
| V | Flow velocity |
| x | Axial coordinate along pipe |
| τ | Valve opening |
| τ0 | Valve opening of first stage |
| FVM | Finite volume method |
| GTS | Godunov-type scheme |
| MIGA | Multi-Island genetic algorithm |
| MOC | Method of characteristics |
| MUSCL | Monotonic upstream-centered scheme for conservation laws |
| NLPQL | Nonlinear Programming by Quadratic Lagrangian |
| PEPP | Percentage error on pressure peaks |
| RBF | Radial basis function |
Appendix A. Boundary Conditions
References
- Tijsseling, A.S. Water hammer with fluid-structure interaction in thick-walled pipes. Comput. Struct. 2007, 85, 844–851. [Google Scholar] [CrossRef]
- Plouraboué, F. Review on water-hammer waves mechanical and theoretical foundations. Eur. J. Mech. B Fluid. 2024, 108, 237–271. [Google Scholar] [CrossRef]
- Shu, Z.Y.; Lei, G.; Liang, W.Q.; Huang, L.; Che, B.X.; Zheng, X.H.; Qian, H. Rapid prediction of water hammer characteristics in liquid hydrogen storage and transportation systems: A Theoretical model. Renew. Energy 2024, 230, 120781. [Google Scholar] [CrossRef]
- Liu, Z.; Yu, X.D.; Pérez-Díaz, J.I.; Liu, Y.; Martínez-Lucas, G. Influence of water hammer effect on low frequency oscillation of Grid-connected hydropower station system. Renew. Energy 2023, 219, 119530. [Google Scholar] [CrossRef]
- Adel, M.; Kassem, F.A.M.; Fathy, I. Reducing the water hammering, surges, and slamming caused by check valve closure in a wastewater pumping station by using a swing flex check valve. Flow Meas. Instrum. 2025, 104, 102870. [Google Scholar] [CrossRef]
- Wylie, E.B.; Streeter, V.L. Fluid Transients, 1st ed.; McGraw-Hill: New York, NY, USA, 1978. [Google Scholar]
- Lian, J.J.; Yang, X.W.; Wang, H.J. Propagation characteristics analysis of high-frequency vibration in pumped storage power station based on a 1D fluid-solid coupling model. J. Energy Storage 2023, 68, 107869. [Google Scholar] [CrossRef]
- Wu, G.H.; Zhu, J.H.; Han, H.; Liu, Z.K.; Li, X.Q.; Tang, X.L. Dynamics of large cavity induced by valve closure in an undulating pipeline. Phys. Fluids 2023, 35, 123312. [Google Scholar] [CrossRef]
- Zhao, M.; Ghidaoui, M.S. Godunov-type solutions for water hammer flows. J. Hydraul. Eng. 2004, 130, 341–348. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, H.; Liu, D.Y.; Ma, J.J.; Wang, P.; Xia, L. A second-order finite volume method for pipe flow with water column separation. J. Hydro-Environ. Res. 2017, 17, 47–55. [Google Scholar] [CrossRef]
- Zhou, L.; Li, Y.J.; Karney, B.; Cheng, Y.G.; Liu, D.Y. Godunov-type solutions for transient pipe flow implicitly incorporating Brunone unsteady friction. J. Hydraul. Eng. 2021, 147, 04021021. [Google Scholar] [CrossRef]
- Zhou, L.; Li, Y.J.; Zhao, Y.; Ou, C.Q.; Zhao, Y. An accurate and efficient scheme involving unsteady friction for transient pipe flow. J. Hydroinform. 2021, 23, 879–896. [Google Scholar] [CrossRef]
- Li, H.Y.; Zhang, Y.; Cui, J.G.; Zhang, F.; Yang, X.Y.; Shi, W.T.; Mao, L.B. Optimization of water hammer protection against sudden pump stoppage using machine learning models and intelligent algorithms. J. Hydraul. Res. 2025, 63, 265–277. [Google Scholar] [CrossRef]
- Yazdi, J.; Hokmabadi, A.; JaliliGhazizadhe, M.R. Optimal size and placement of water hammer protective devices in water conveyance pipelines. Water Resour. Manag. 2019, 33, 569–590. [Google Scholar] [CrossRef]
- Henclik, S. Numerical modeling of water hammer with fluid-structure interaction in a pipeline with viscoelastic supports. J. Fluid. Struct. 2018, 76, 469–487. [Google Scholar] [CrossRef]
- Li, R.; Gao, Y.Q.; Jiang, B.Y.; Lv, M.; Li, H. Intelligent parameter optimization of sealed airbag vessels with preventing water hammer in cascaded pressurized water transmission system: Based on MOPSO algorithm. J. Water Process Eng. 2025, 70, 106915. [Google Scholar] [CrossRef]
- Ma, J.; Wu, J.D.; Wang, X.D. Simulation of computation and experimental investigations about water hammer in high lift water transmission pipeline. In Proceedings of the International Conference on Advances in Mechanical Engineering and Industrial Informatics, Zhengzhou, China, 11–12 April 2015. [Google Scholar]
- Xin, Q.L.; Du, J.Y.; Liu, M.; Liu, Y.; Huang, J.K.; Yu, W.; Yuan, F.Y.; Wang, D.X.; Yang, X.J. Experimental study on the effects of two-stage valve closure on the maximum water hammer pressure in micro-hydroelectric system. J. Water Process Eng. 2024, 65, 105886. [Google Scholar] [CrossRef]
- Yao, E.; Kember, G.; Hansen, D. Analysis of water hammer attenuation in applications with varying valve closure times. J. Eng. Mech. 2015, 141, 04014107. [Google Scholar] [CrossRef]
- Wang, P.; Yu, J. Numerical simulation of water hammer boundary conditions based on nozzle outflow law. J. Drain. Irrig. Mach. Eng. 2020, 38, 814–818. [Google Scholar]
- Van Leer, B. Towards the Ultimate Conservative Difference Scheme. V. A Second-order Sequel to Godunov’s Method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Zhao, J.H.; Özgen-Xian, I.; Liang, D.F.; Wang, T.; Hinkelmann, R. An improved multislope MUSCL scheme for solving shallow water equations on unstructured grids. Comput. Math. Appl. 2019, 77, 576–596. [Google Scholar] [CrossRef]
- Leveque, R.J. Finite Volume Methods for Hyperbolic Problems, 1st ed.; World Publishing Beijing Corporation Limited: Beijing, China, 2004. [Google Scholar]
- Sohn, S.I. A new TVD-MUSCL scheme for hyperbolic conservation laws. Comput. Math. Appl. 2005, 50, 231–248. [Google Scholar] [CrossRef]
- Hou, J.M.; Liang, Q.H.; Zhang, H.B.; Hinkelmann, R. Multislope MUSCL method applied to solve shallow water equations. Comput. Math. Appl. 2014, 68, 2012–2027. [Google Scholar] [CrossRef]
- Guinot, V.; Delenne, C. MUSCL schemes for the shallow water sensitivity equations with passive scalar transport. Comput. Fluids 2012, 59, 11–30. [Google Scholar] [CrossRef]
- Leng, Y.; Li, X.L.; Fu, D.X.; Ma, Y.W. Optimization of the MUSCL scheme by dispersion and dissipation. Sci. China Phys. Mech. 2012, 55, 844–853. [Google Scholar] [CrossRef]
- Hubbard, M.E. Multidimensional slope limiters for MUSCL-type finite volume schemes on unstructured grids. J. Comput. Phys. 1999, 155, 54–74. [Google Scholar] [CrossRef]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Bergant, A.; Simpson, A.R.; Vìtkovsk, J. Developments in unsteady pipe flow friction modeling. J. Hydraul. Res. 2001, 39, 249–257. [Google Scholar] [CrossRef]
- Li, Y.F.; Yin, Y.H.; Yang, H.; Liu, X.E.; Mo, J.; Cui, H.L. Modeling for Optimization of Circular Flat Pad Aerostatic Bearing with A Single Central Orifice-Type Restrictor Based on CFD Simulation. Tribol. Int. 2017, 109, 206–216. [Google Scholar] [CrossRef]



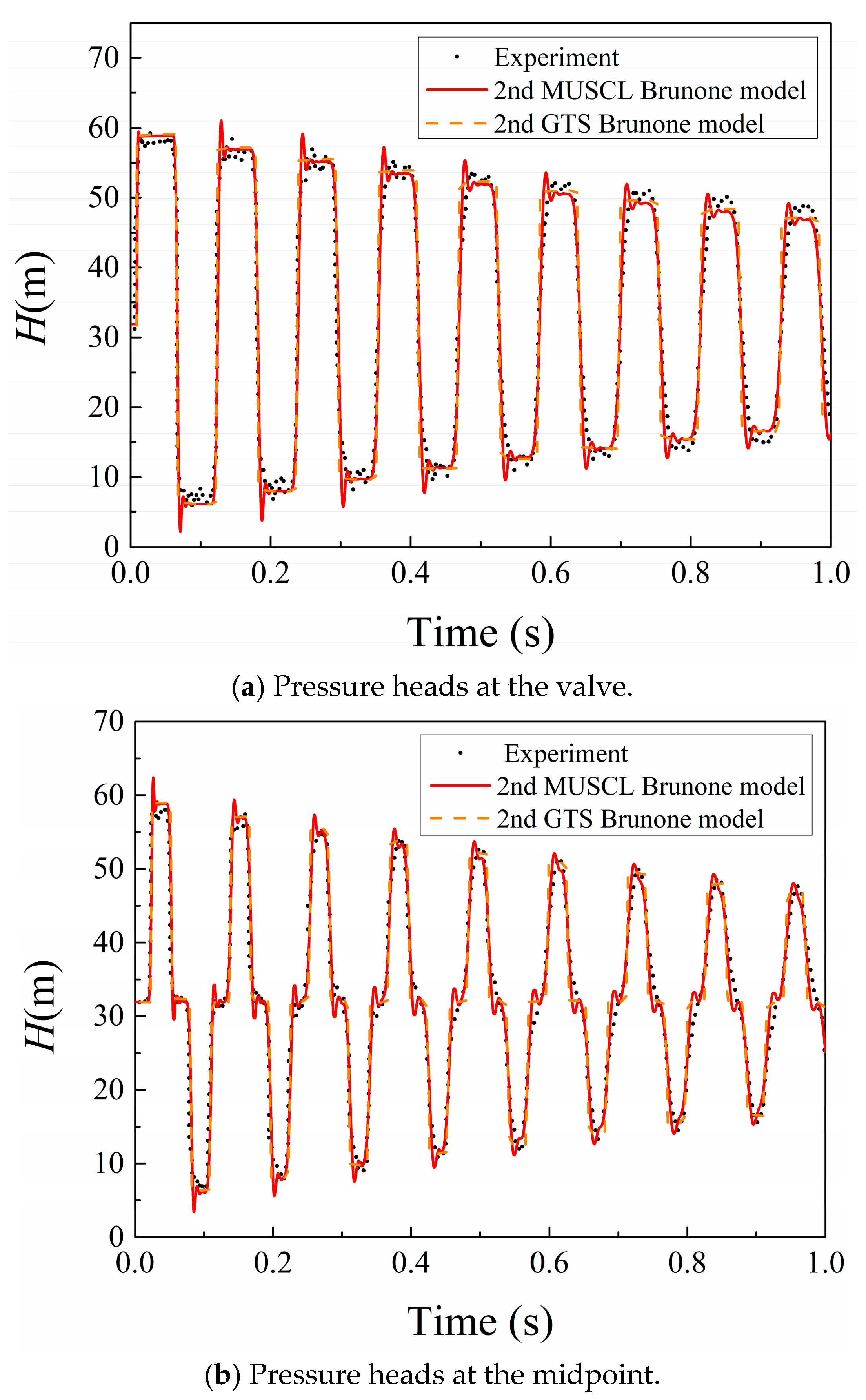
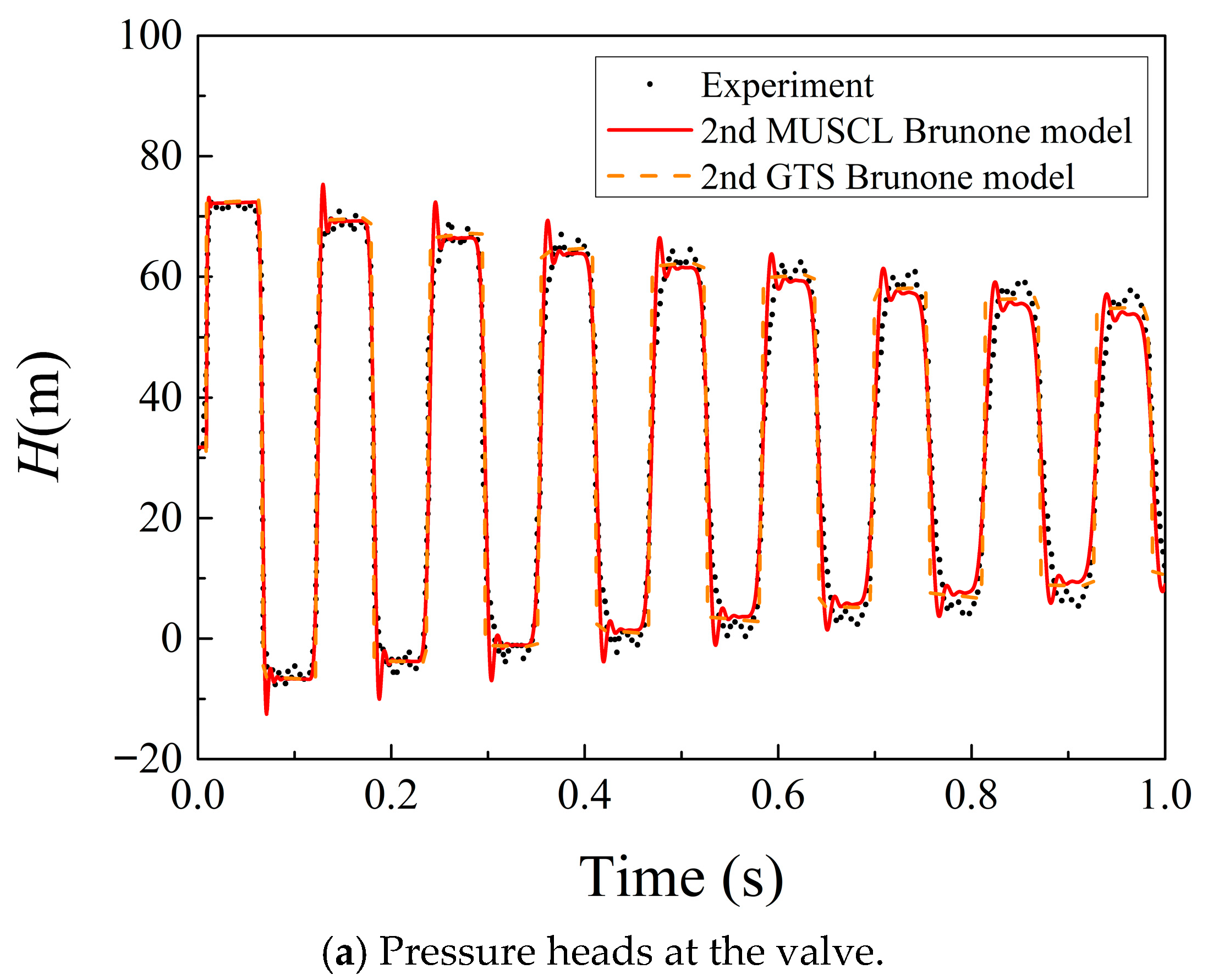
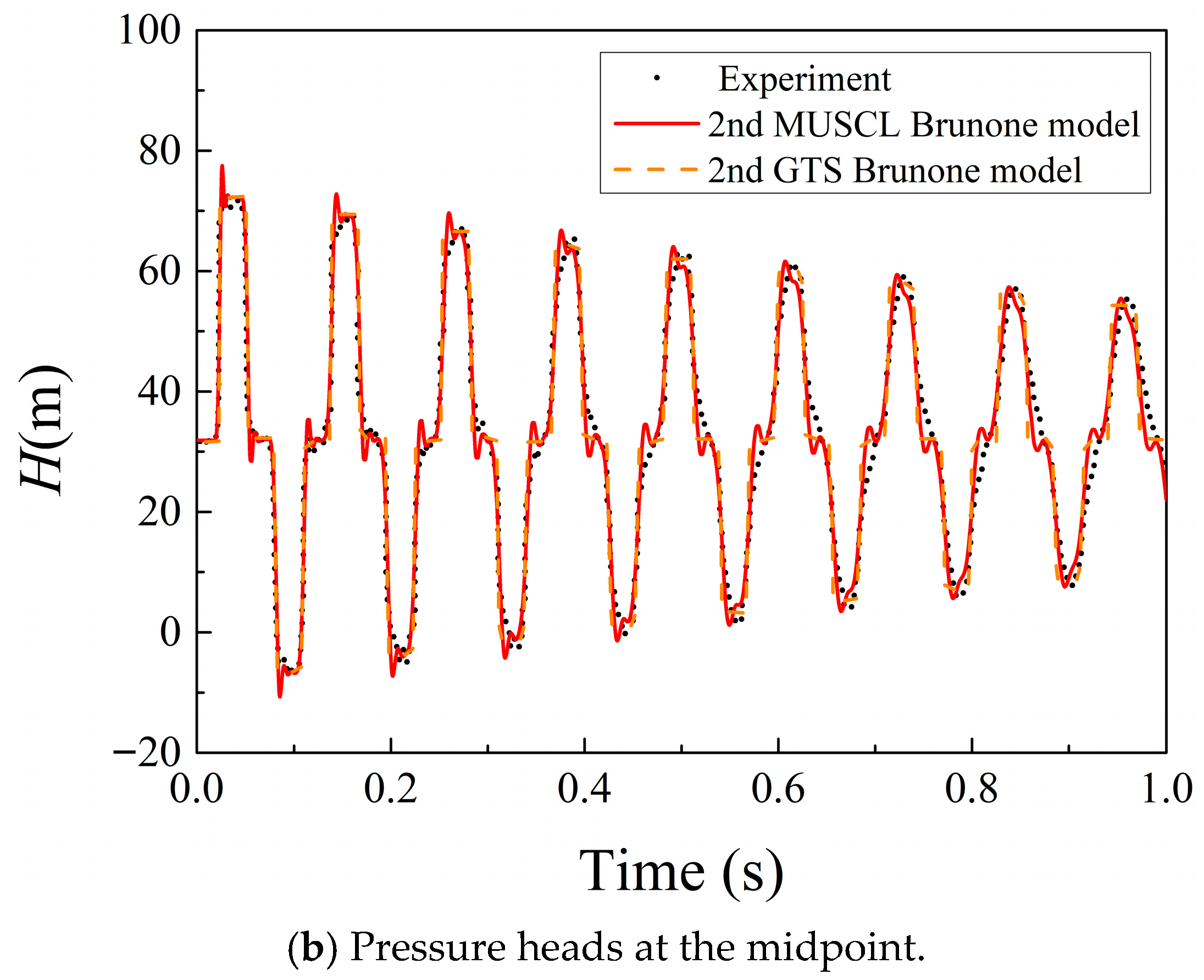

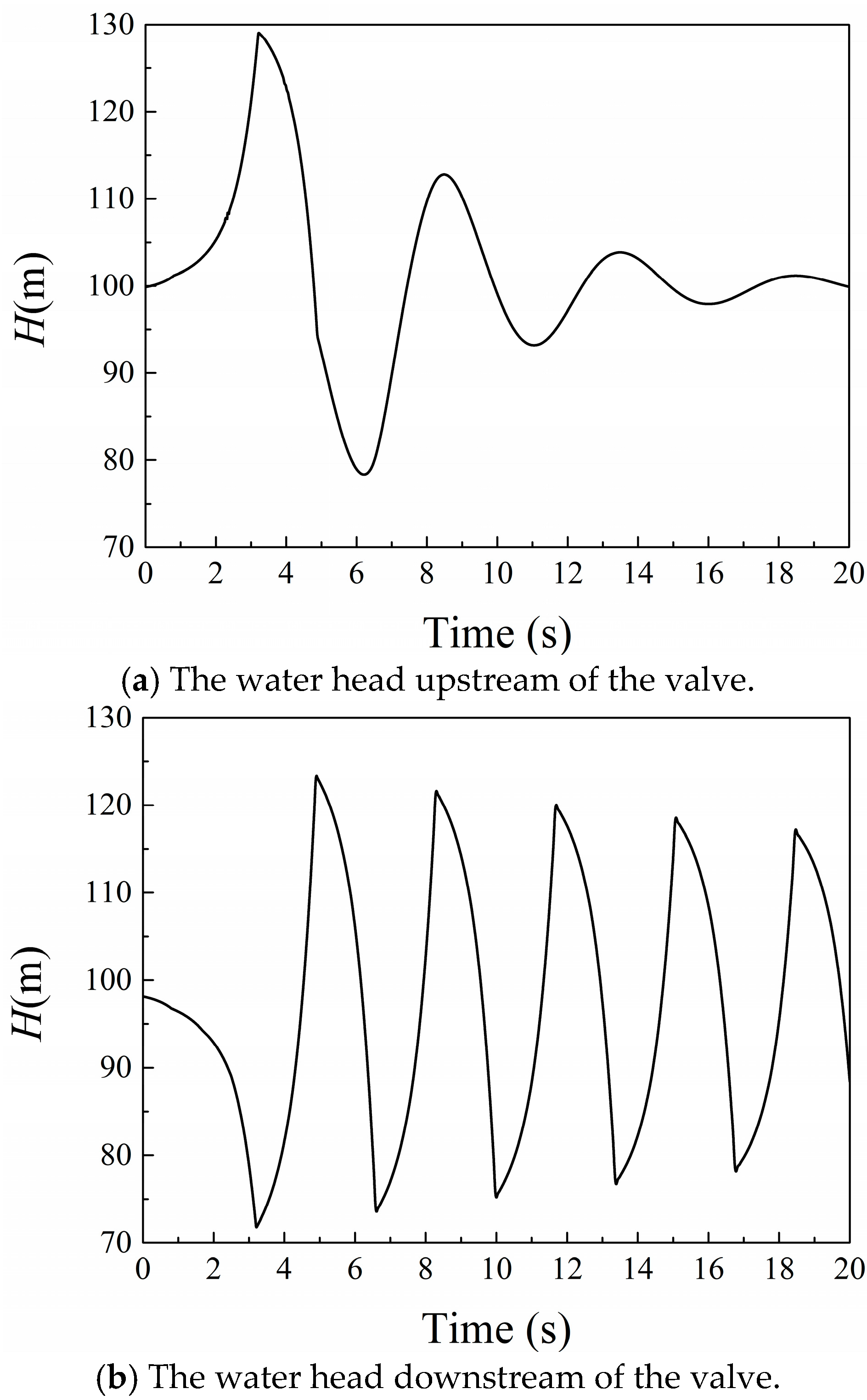
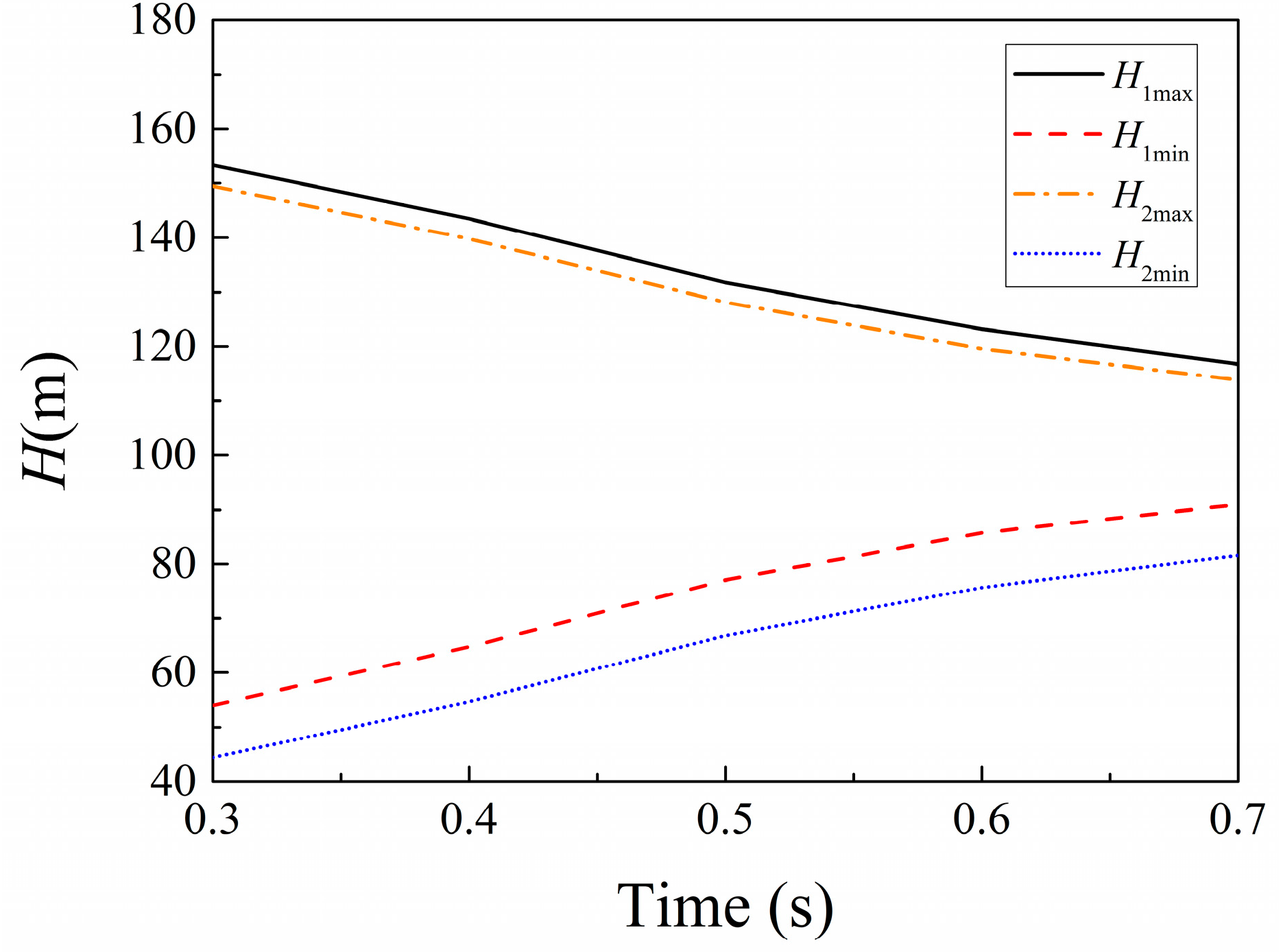
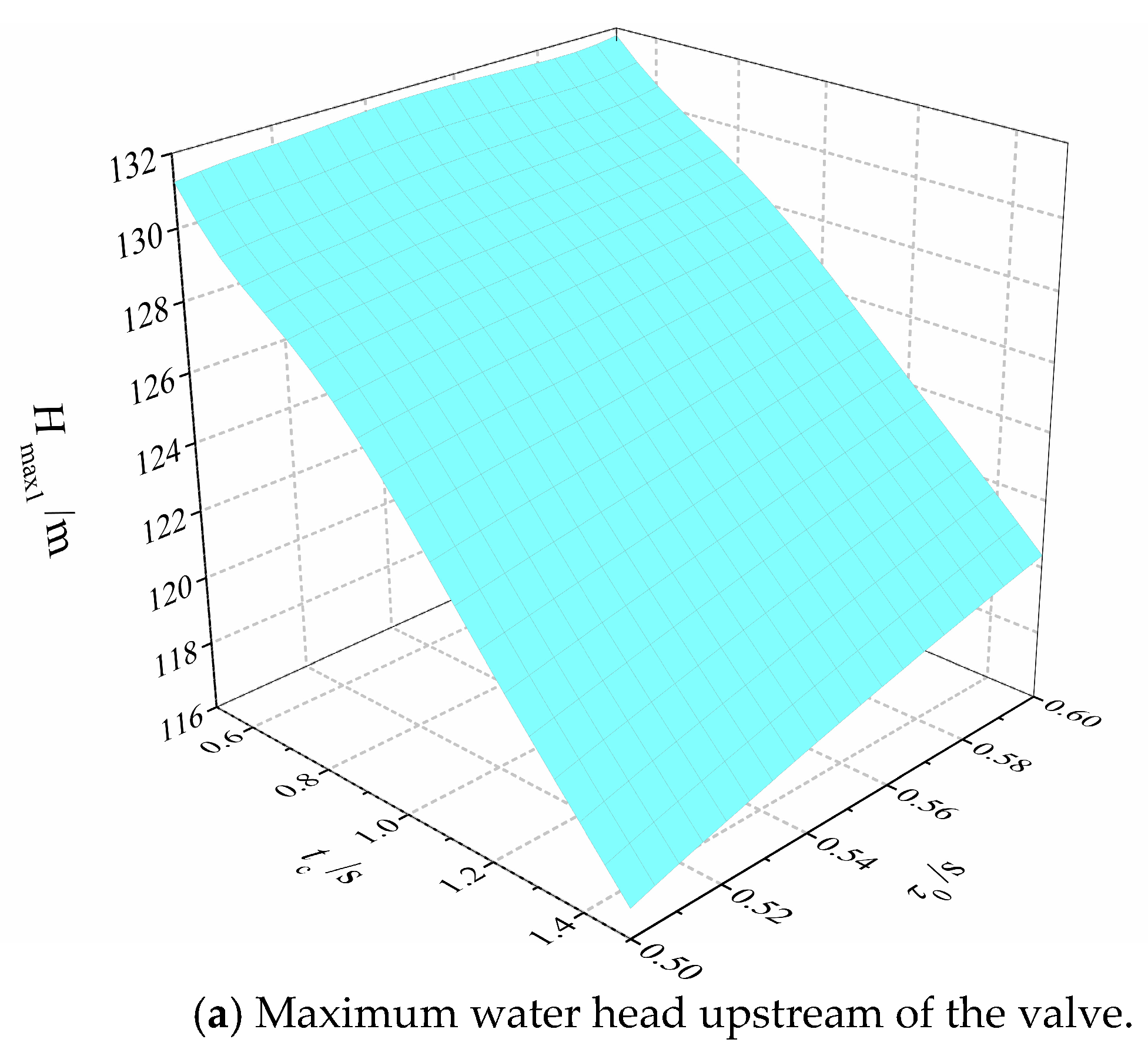
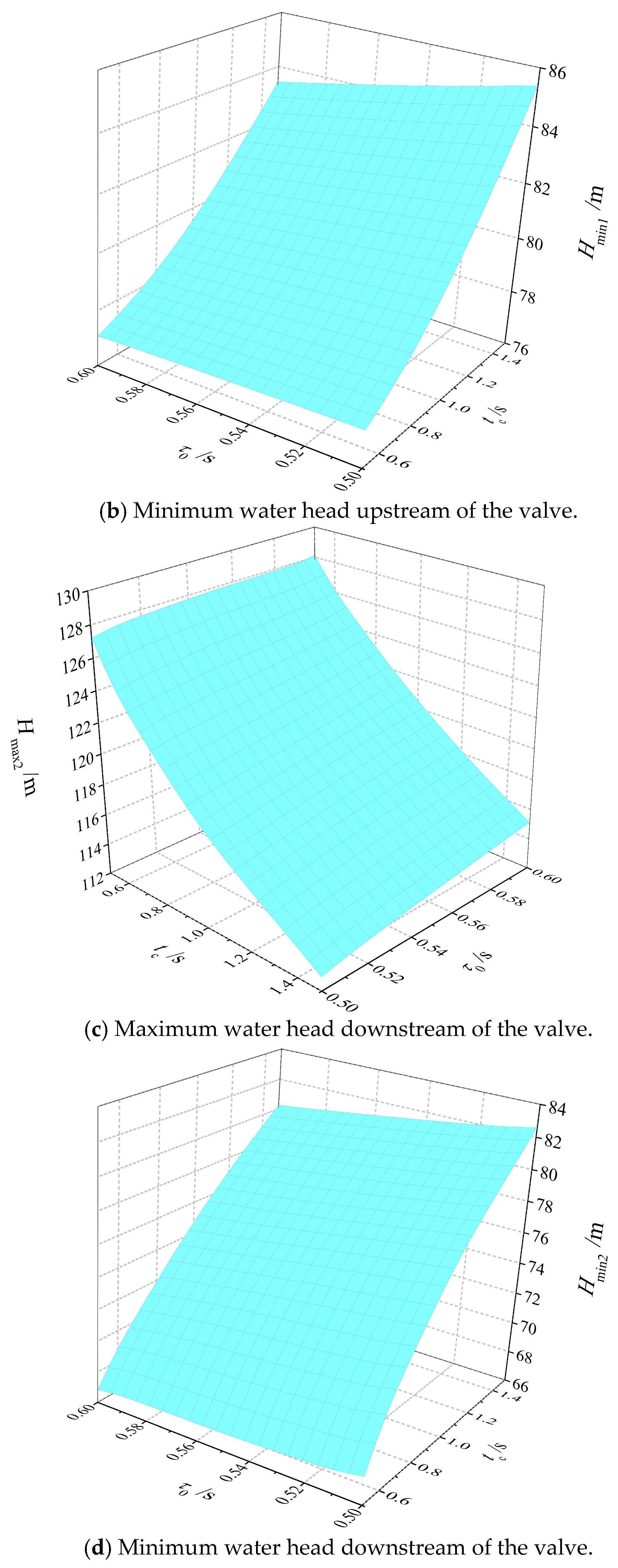
| Position | Initial Velocity | MUSCL | GTS |
|---|---|---|---|
| PEPP (At the valve) | v0 = 0.1 m/s | 0.707 | 3.779 |
| v0 = 0.2 m/s | 1.548 | 2.484 | |
| v0 = 0.3 m/s | 1.649 | 3.196 | |
| PEPP (At the midpoint) | v0 = 0.1 m/s | 0.659 | 1.441 |
| v0 = 0.2 m/s | 2.467 | 1.176 | |
| v0 = 0.3 m/s | 1.673 | 1.434 |
| Effect of tc | Effect of L1 | Effect of τ0 | |
|---|---|---|---|
| Hmax1 | 76.5% | 12.5% | 11.0% |
| Hmax2 | 73.2% | 14.1% | 12.7% |
| Hmin1 | 71.6% | 18.4% | 10.0% |
| Hmin2 | 73.1% | 14.2% | 12.7% |
| L1 | τ0 | tc | Hmax1 | Hmax2 | Hmin1 | Hmin2 |
|---|---|---|---|---|---|---|
| 1100 | 0.5 | 0.56 | 131.03 | 124.46 | 76.84 | 70.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Lian, J. Modeling Hydraulic Transient Process in Long-Distance Water Transfer Systems Using a MUSCL-Type FVM Approach. Water 2025, 17, 2480. https://doi.org/10.3390/w17162480
Li Y, Lian J. Modeling Hydraulic Transient Process in Long-Distance Water Transfer Systems Using a MUSCL-Type FVM Approach. Water. 2025; 17(16):2480. https://doi.org/10.3390/w17162480
Chicago/Turabian StyleLi, Yifei, and Jijian Lian. 2025. "Modeling Hydraulic Transient Process in Long-Distance Water Transfer Systems Using a MUSCL-Type FVM Approach" Water 17, no. 16: 2480. https://doi.org/10.3390/w17162480
APA StyleLi, Y., & Lian, J. (2025). Modeling Hydraulic Transient Process in Long-Distance Water Transfer Systems Using a MUSCL-Type FVM Approach. Water, 17(16), 2480. https://doi.org/10.3390/w17162480






