Spatiotemporal Dynamics of Drought Propagation in the Loess Plateau: A Geomorphological Perspective
Abstract
1. Introduction
2. Study Area and Data Sources
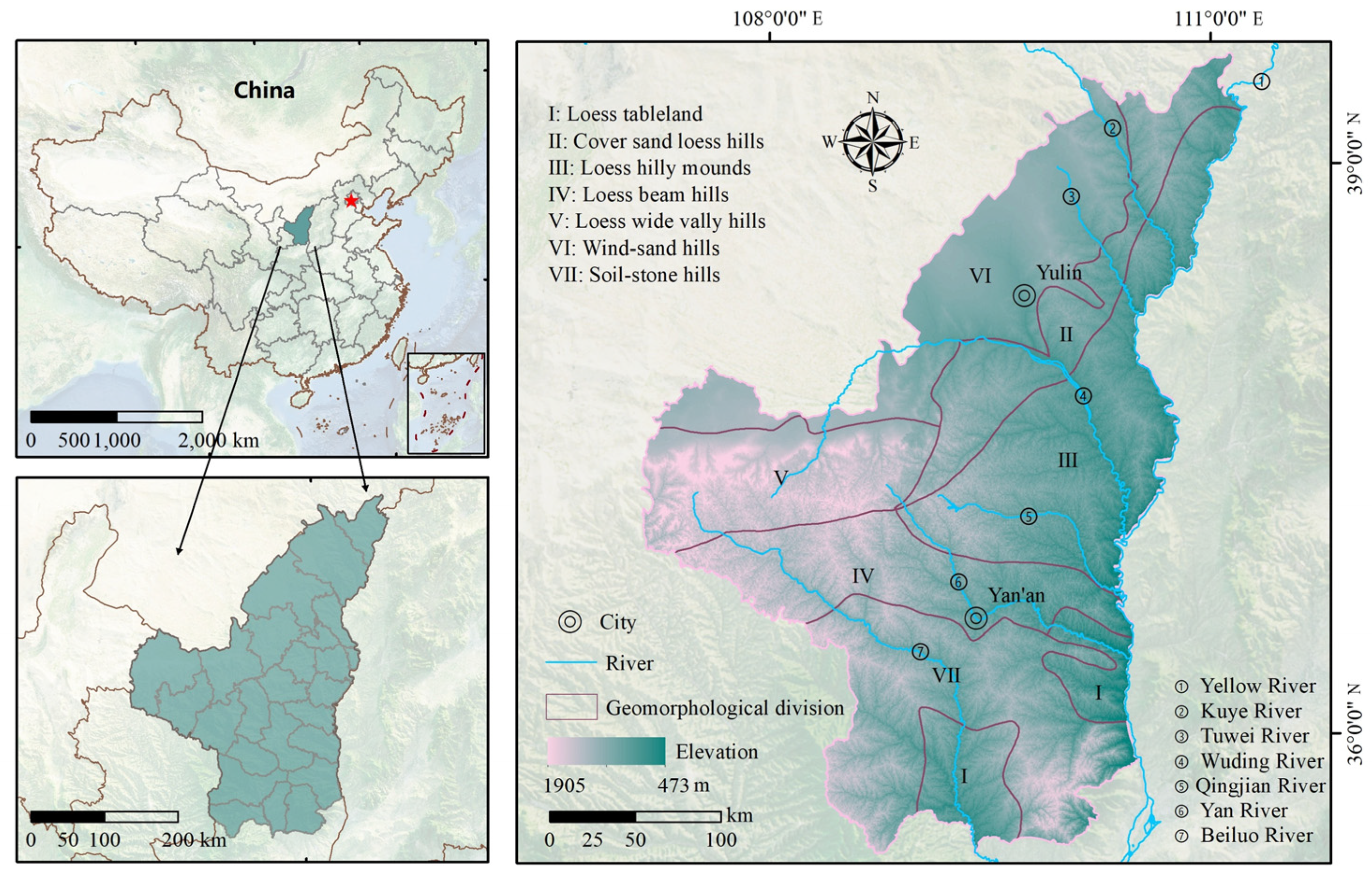
2.1. Study Area
2.2. Data Source
3. Methodology
3.1. Drought Indicators
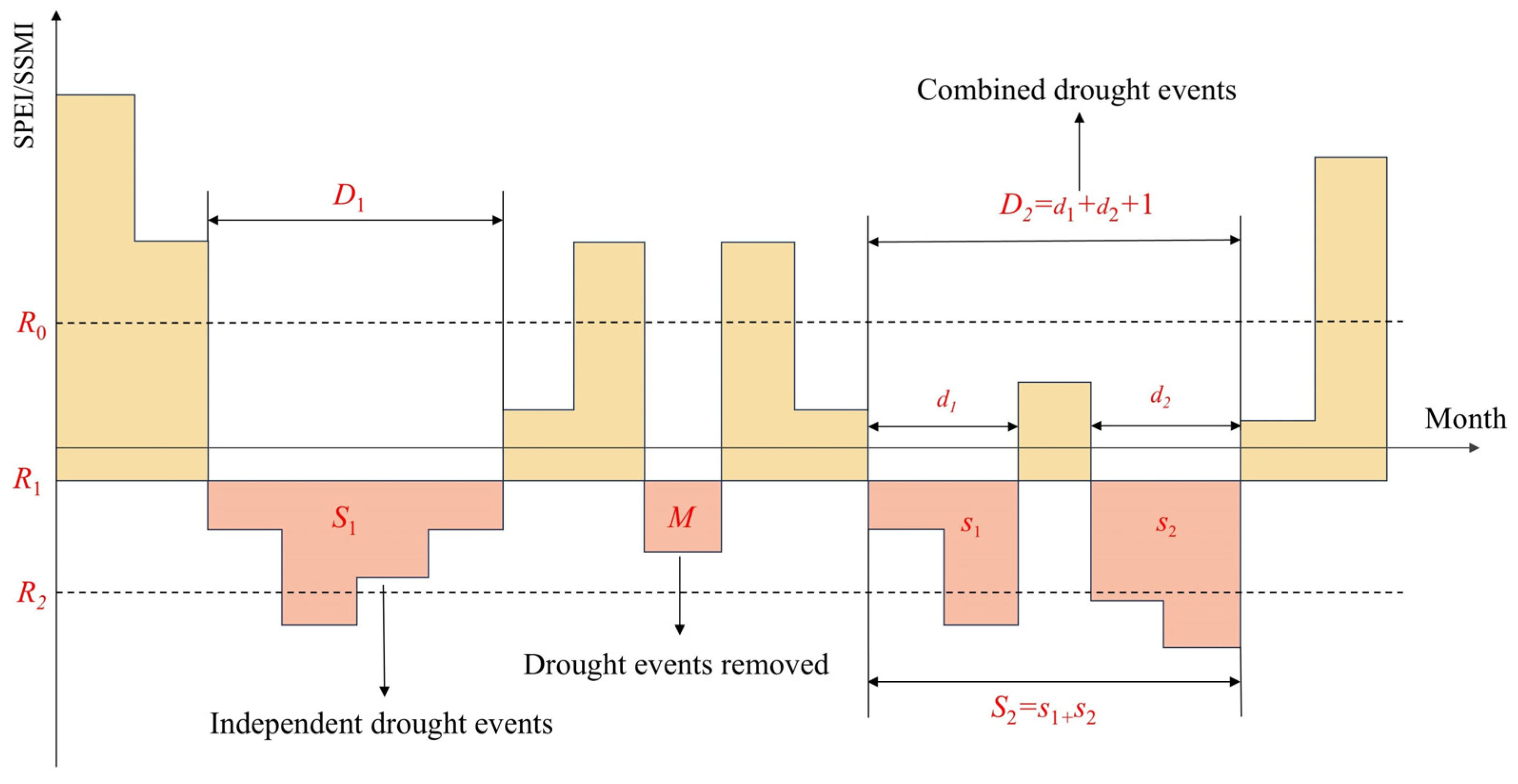
3.2. Drought Event Identification
3.3. Cross-Wavelet Analysis
3.4. Grey Relational Analysis
- (1)
- The 1-month scale SSMI was selected as the reference sequence , while the SPEI at time scales of 1 to 12 months was used as the comparison sequence , where i = 1, 2, …, 12.
- (2)
- The grey relational coefficients between the reference sequence and each comparison sequence were then calculated:where denotes the grey relational coefficients, and is the resolution coefficient, which is set to 0.5 in this study.
- (3)
- The average of the grey relational degree coefficients is calculated to obtain the overall grey relational degree, using the following formula:where n is the number of samples. The closer it is to 1, the stronger the association between the SPEI and the SSMI at this timescale.
3.5. Drought Effective Propagation Rate
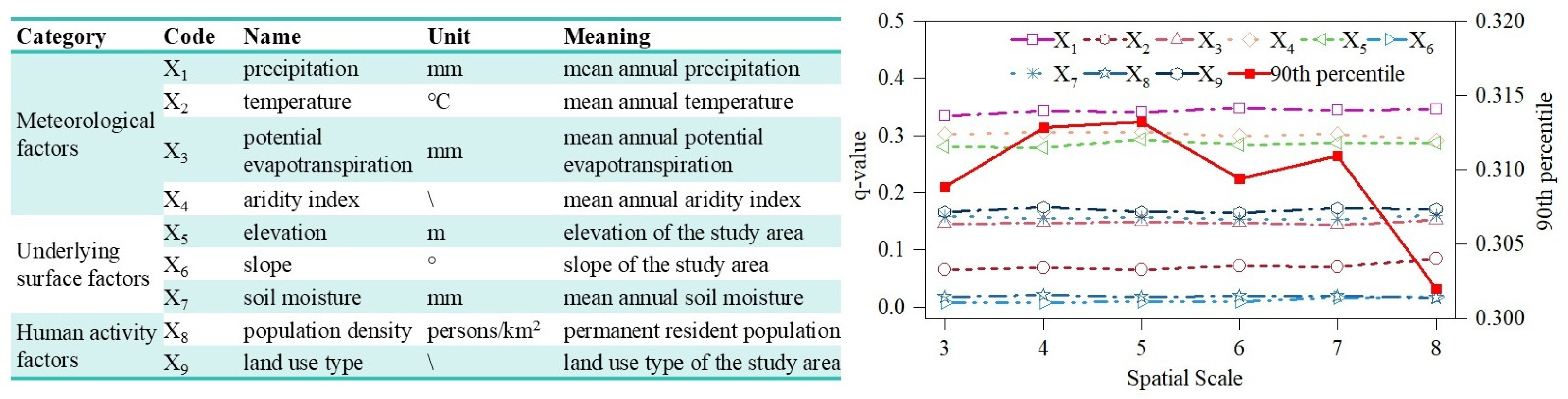
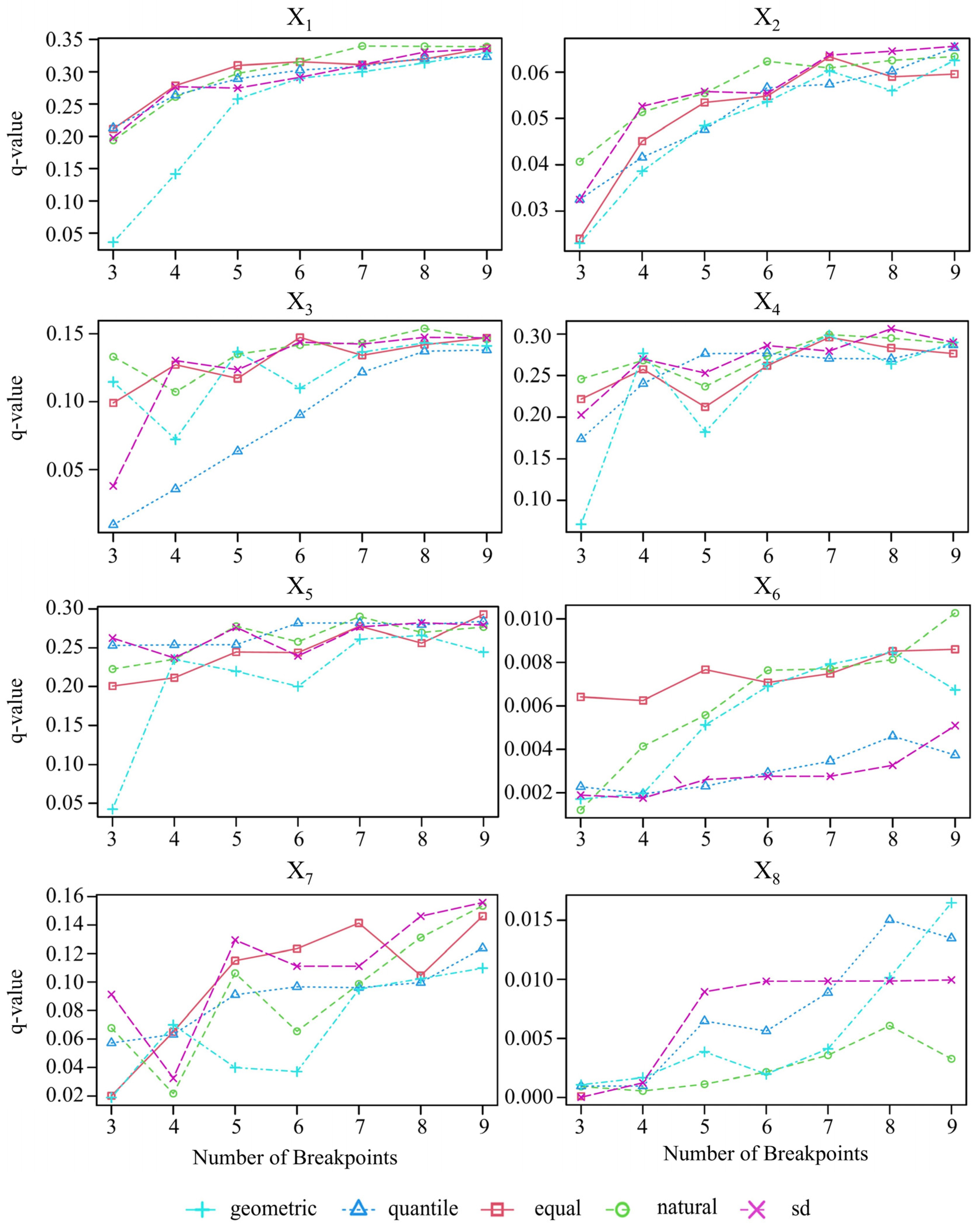
3.6. Optimal Parameter-Based Geographical Detector Model
- (a)
- Factor detector
- (b)
- Parameter optimization
- (c)
- Interaction detector
- (d)
- Risk detector
4. Results and Analysis
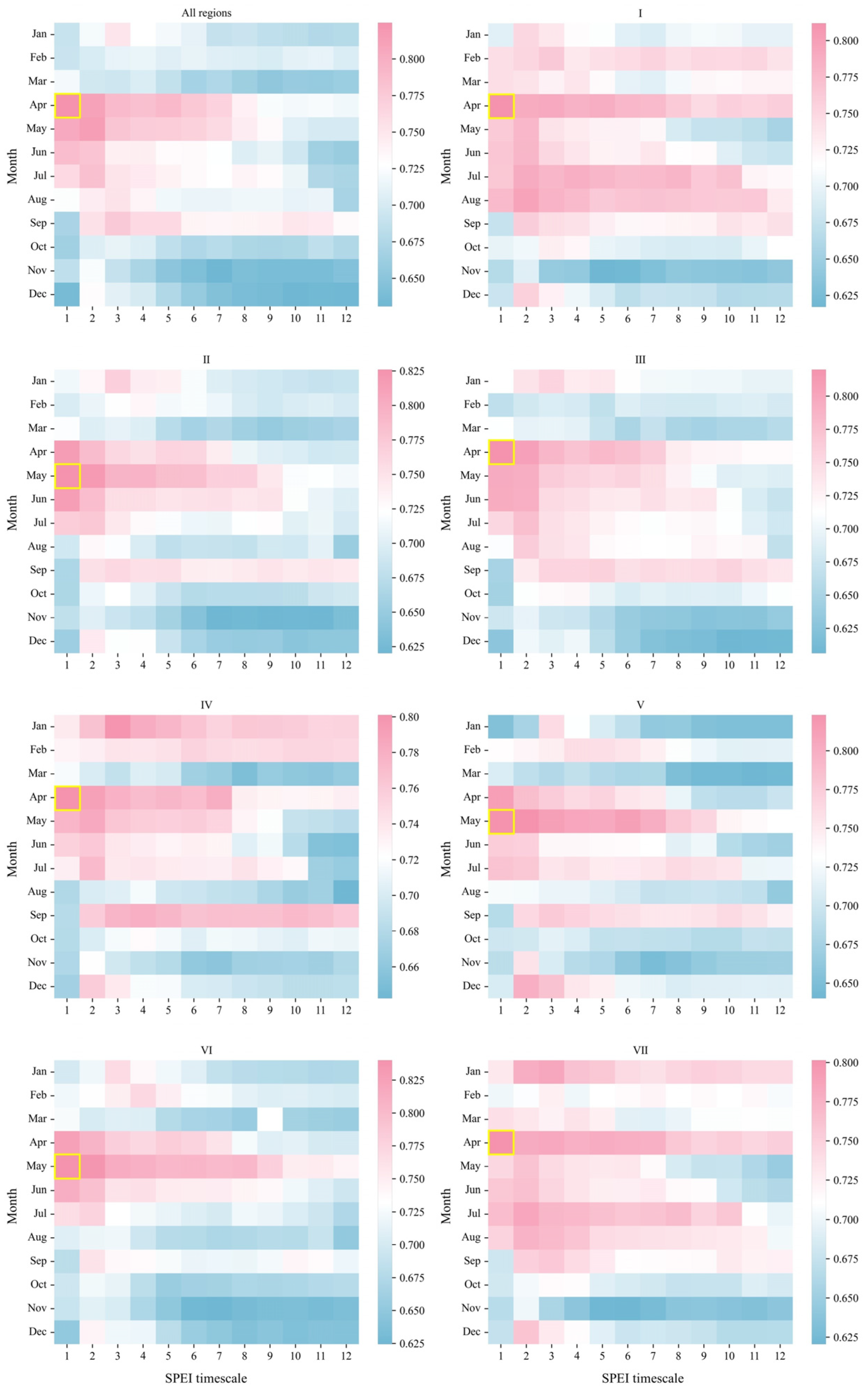
4.1. Estimation of the Propagation Lag from Meteorological Drought to Agricultural Drought
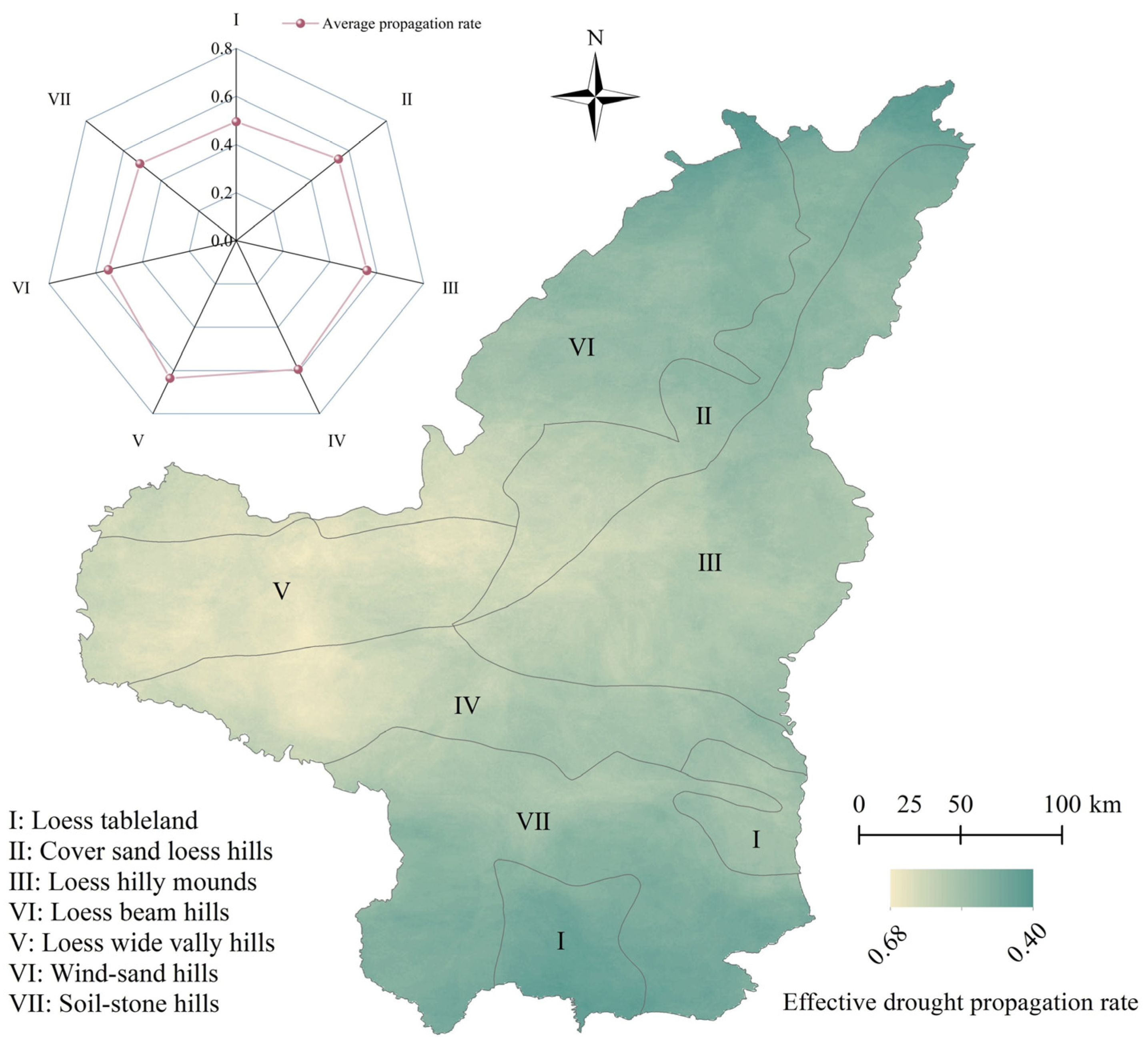
4.2. Assessment of the Effective Propagation Rate from Meteorological to Agricultural Drought
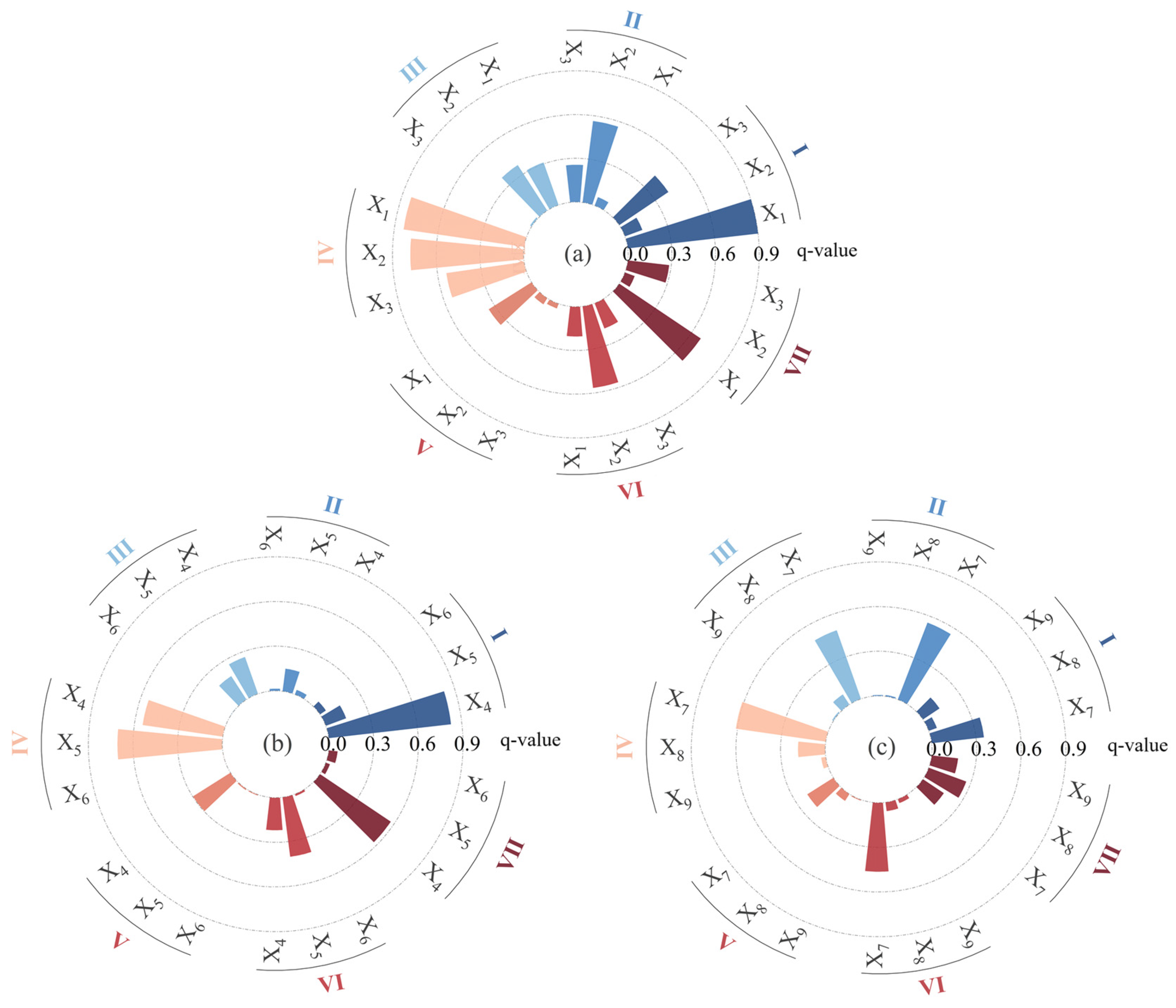
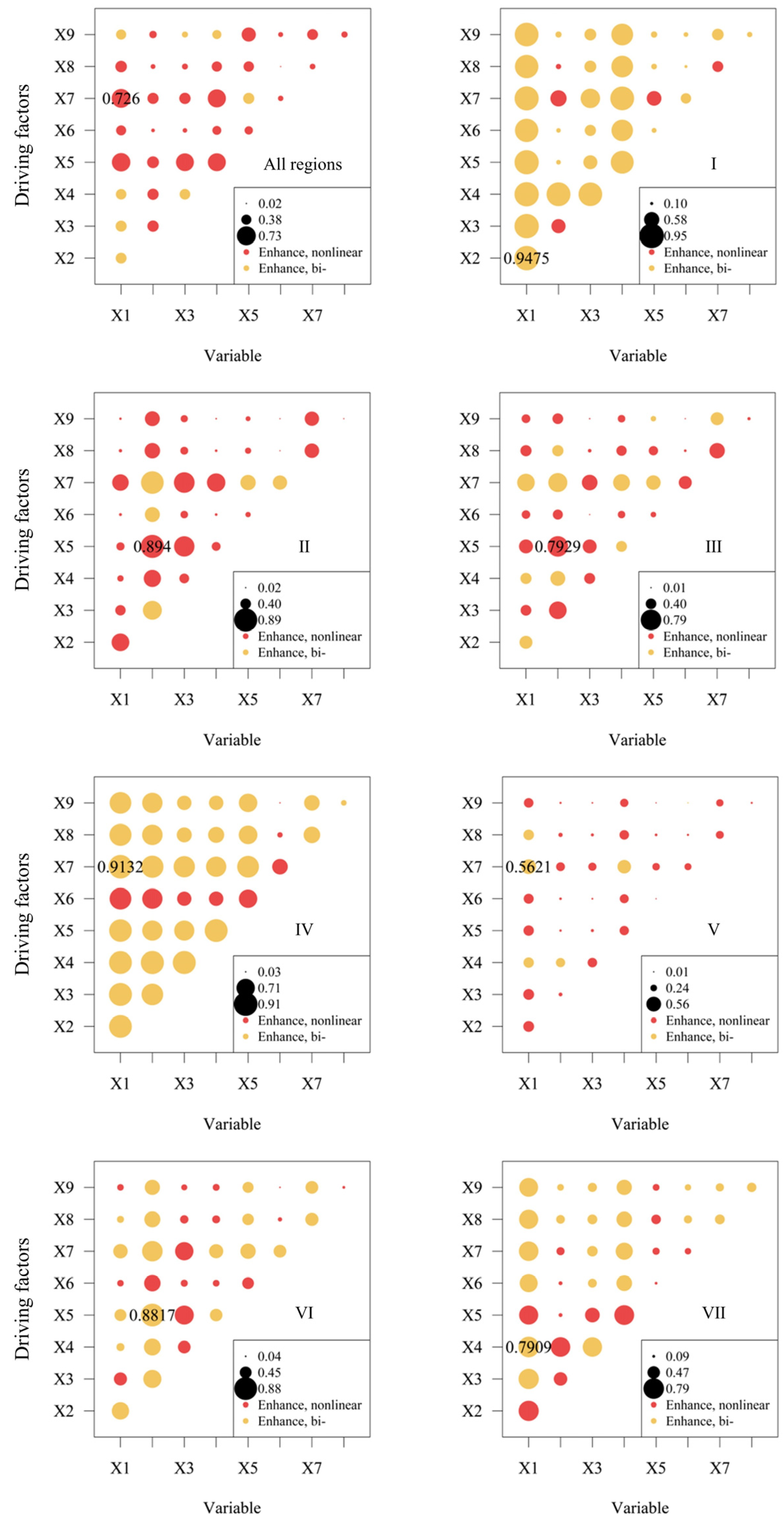
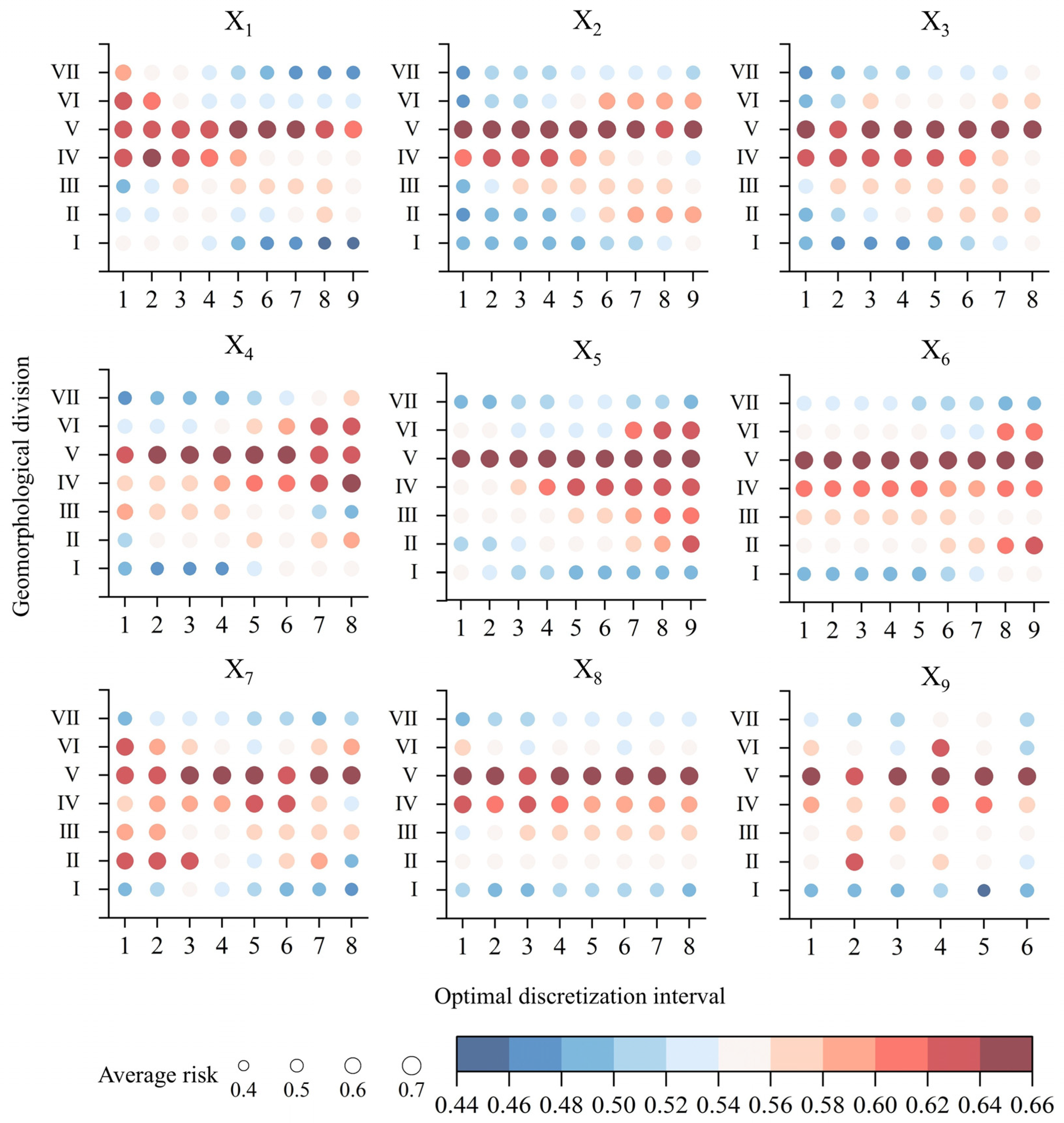
4.3. Detection and Analysis of Factors Influencing the Effective Propagation Rate from Meteorological to Agricultural Drought
5. Discussion
6. Conclusions
- (1)
- Meteorological drought and agricultural drought exhibit significant positive correlations during spring, summer, and autumn, whereas the correlation in winter is relatively weak. The overall drought propagation lag is short, with the seasonal propagation lag concentrated in 1–3 months. Spring demonstrates the shortest lag (average of 1.2 months), while winter exhibits the longest lag (average of 3.1 months).
- (2)
- The propagation rate of drought exceeds 0.4 on the Loess Plateau in northern Shaanxi, exhibiting distinct regional heterogeneity. The propagation rate is higher in the west and central regions (up to 0.68) but lower in the north and south. Among the various geomorphological divisions, the loess wide valley hills and the loess beam hills exhibit stronger propagation effects (rates of 0.64 and 0.59, respectively), whereas the loess tableland and the earth and soil–stone hills demonstrate weaker propagation (around 0.50).
- (3)
- The OPGD results demonstrate that the dominant driving factors vary across geomorphological types. Precipitation and soil moisture are the main contributors in most regions, whereas temperature exerts the greatest influence on the wind-sand hills. Synergistic enhancement effects are present among driving factors: elevated temperature, potential evapotranspiration, and aridity significantly promote drought propagation, while precipitation exerts a suppressive effect in certain areas. Soil moisture and land use types exhibit spatial heterogeneity in their effects. Additionally, the impact of population density differs by region: in the loess beam hills division, it is negatively correlated with drought propagation, likely due to regional interventions such as artificial precipitation enhancement and ecological restoration; conversely, a positive correlation is noted in the soil–stone hills division.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Van Loon, A.F. Hydrological drought explained. Wiley Interdiscip. Rev. Water 2015, 2, 359–392. [Google Scholar] [CrossRef]
- Yao, N.; Li, Y.; Lei, T.J.; Peng, L. Drought evolution, severity and trends in mainland China over 1961–2013. Sci. Total Environ. 2018, 616–617, 73–89. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.Q.; Ye, A.Z.; Zhang, Y.H.; Zhou, J. The peer-to-peer type propagation from meteorological drought to soil moisture drought occurs in areas with strong land-atmosphere interaction. Water Resour. Res. 2022, 58, e2022WR032846. [Google Scholar] [CrossRef]
- Zhao, X.W.; Yang, T.Z.; Zhang, H.B.; Lan, T.; Xue, C.; Li, T.; Ye, Z.; Yang, Z.; Zhang, Y. GTDI: A game-theory-based integrated drought index implying hazard-causing and hazard-bearing impact change. Nat. Hazards Earth Syst. Sci. 2024, 24, 3479–3495. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Pricope, N.G.; Toreti, A.; Morán-Tejeda, E.; Spinoni, J.; Ocampo-Melgar, A.; Archer, E.; Diedhiou, A.; Mesbahzadeh, T.; Ravindranath, N.H.; et al. The Global Threat of Drying Lands: Regional and Global Aridity Trends and Future Projections. A Report of the Science-Policy Interface; United Nations Convention to Combat Desertification (UNCCD): Bonn, Germany, 2024. [Google Scholar]
- Su, B.D.; Huang, J.L.; Mondal, S.K.; Zhai, J.; Wang, Y.; Wen, S.; Gao, M.; Lv, Y.; Jiang, S.; Jiang, T.; et al. Insight from CMIP6 SSP-RCP scenarios for future drought characteristics in China. Atmos. Res. 2021, 250, 105375. [Google Scholar] [CrossRef]
- Dai, M.; Huang, S.Z.; Huang, Q.; Zheng, X.; Su, X.; Leng, G.; Li, Z.; Guo, Y.; Fang, W.; Liu, Y. Propagation characteristics and mechanism from meteorological to agricultural drought in various seasons. J. Hydrol. 2022, 610, 127897. [Google Scholar] [CrossRef]
- Wu, J.W.; Miao, C.Y.; Zheng, H.Y.; Duan, Q.; Lei, X.; Li, H. Meteorological and hydrological drought on the Loess Plateau, China: Evolutionary characteristics, impact, and propagation. J. Geophys. Res. Atmos. 2018, 123, 11569–11584. [Google Scholar] [CrossRef]
- Ashraf, M.S.; Shahid, M.; Waseem, M.; Azam, M.; Rahman, K.U. Assessment of variability in hydrological droughts using the improved innovative trend analysis method. Sustainability 2023, 15, 9065. [Google Scholar] [CrossRef]
- Ashraf, M.; Arshad, A.; Patel, P.M.; Khan, A.; Qamar, H.; Siti-Sundari, R.; Ghani, M.U.; Amin, A.; Babar, J.R. Quantifying climate-induced drought risk to livelihood and mitigation actions in Balochistan. Nat. Hazards 2021, 109, 2127–2151. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Glantz, M.H. Understanding: The drought phenomenon: The role of definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef]
- Hao, Z.H.; Singh, P.V. Drought characterization from a multivariate perspective: A review. J. Hydrol. 2015, 527, 668–678. [Google Scholar] [CrossRef]
- Dai, M.; Huang, S.Z.; Huang, Q.; Leng, G.; Guo, Y.; Wang, L.; Fang, W.; Li, P.; Zheng, X. Assessing agricultural drought risk and its dynamic evolution characteristics. Agric. Water Manag. 2020, 231, 106003. [Google Scholar] [CrossRef]
- Azam, M.; Nauman Altaf, M.; Waseem, M.; Anjum, M.N.; Afzal, A.; Hussain, F.; Eun Lee, J.; Ahmed, R.; Latif, M.; Kwon, S.A.; et al. Bivariate risk evaluation of drought across Balochistan, Pakistan. Heliyon 2025. under review. [Google Scholar] [CrossRef]
- Tu, X.J.; Wu, H.O.; Singh, V.P.; Chen, X.; Lin, K.; Xie, Y. Multivariate design of socioeconomic drought and impact of water reservoirs. J. Hydrol. 2018, 566, 192–204. [Google Scholar] [CrossRef]
- Barker, L.J.; Hannaford, J.; Chiverton, A.; Svensson, C. From meteorological to hydrological drought using standardised indicators. Hydrol. Earth Syst. Sci. 2016, 20, 2483–2505. [Google Scholar] [CrossRef]
- Jehanzaib, M.; Sattar, M.N.; Lee, J.; Kim, T.-W. Investigating effect of climate change on drought propagation from meteorological to hydrological drought using multi-model ensemble projections. Stoch. Environ. Res. Risk Assess. 2020, 34, 7–21. [Google Scholar] [CrossRef]
- Wu, J.F.; Chen, X.H.; Yao, H.X.; Zhang, D. Multi-timescale assessment of propagation thresholds from meteorological to hydrological drought. Sci. Total Environ. 2021, 765, 144232. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, X.; Hao, Z.C.; Singh, V.P.; Hao, F. Characterization of agricultural drought propagation over China based on bivariate probabilistic quantification. J. Hydrol. 2021, 598, 126194. [Google Scholar] [CrossRef]
- Sarwar, A.N.; Waseem, M.; Azam, M.; Abbas, A.; Ahmad, I.; Lee, J.E.; Haq, F.U. Shifting of Meteorological to Hydrological Drought Risk at Regional Scale. Appl. Sci. 2022, 12, 5560. [Google Scholar] [CrossRef]
- Han, H.M.; Sun, J.H. An analysis of the meteorological and hydrological drought propagation characteristics in Ganjiang River Basin. China Rural Water Hydropower 2022, 12, 101–106. [Google Scholar]
- Sattar, M.N.; Lee, J.Y.; Shin, J.Y.; Kim, T.W. Probabilistic characteristics of drought propagation from meteorological to hydrological drought in South Korea. Water Resour. Manag. 2019, 33, 2439–2452. [Google Scholar] [CrossRef]
- Dehghani, M.; Saghafian, B.; Zargar, M. Probabilistic hydrological drought index forecasting based on meteorological drought index using Archimedean copulas. Hydrol. Res. 2019, 50, 1230–1250. [Google Scholar] [CrossRef]
- Geng, G.P.; Zhang, B.; Gu, Q.; He, Z.; Zheng, R. Drought propagation characteristics across China: Time, probability, and threshold. J. Hydrol. 2024, 631, 130805. [Google Scholar] [CrossRef]
- Huang, S.Z.; Huang, Q.; Chang, J.X.; Leng, G.; Xing, L. The response of agricultural drought to meteorological drought and the influencing factors: A case study in the Wei River Basin, China. Agric. Water Manag. 2015, 159, 45–54. [Google Scholar] [CrossRef]
- Gevaert, A.I.; Veldkamp, T.I.; Ward, P.J. The effect of climate type on timescales of drought propagation in an ensemble of global hydrological models. Hydrol. Earth Syst. Sci. 2018, 22, 4649–4665. [Google Scholar] [CrossRef]
- Wu, J.W.; Miao, C.Y.; Tang, X.; Duan, Q.; He, X. A nonparametric standardized runoff index for characterizing hydrological drought on the Loess Plateau, China. Glob. Planet. Change 2018, 161, 53–65. [Google Scholar] [CrossRef]
- Guo, J.; Xiao, D.Y.; Sun, X.L.; Guo, F.; Xue, S.; Fan, L. Drought risk assessment on arid region under different socioeconomic scenarios: A case of Loess Plateau, China. Ecol. Indic. 2024, 167, 112728. [Google Scholar] [CrossRef]
- Ding, Z.M.; Yao, S.B. Assessing the ecological effectiveness of Sloping Land Conversion Programme to identify vegetation restoration types: A case study of Northern Shaanxi Loess Plateau, China. Ecol. Indic. 2022, 145, 109671. [Google Scholar] [CrossRef]
- Yan, Z.J.; Wang, Y.R.; Hu, X.; Luo, W. Assessment and enhancement of ecosystem service supply efficiency based on production possibility frontier: A case study of the Loess Plateau in northern Shaanxi. Sustainability 2023, 15, 14314. [Google Scholar] [CrossRef]
- Wen, X. Temporal and spatial relationships between soil erosion and ecological restoration in semi-arid regions: A case study in northern Shaanxi, China. GISci. Remote Sens. 2020, 57, 572–590. [Google Scholar] [CrossRef]
- Li, C.; Wu, P.T.; Li, X.L.; Zhou, T.; Sun, S.; Wang, Y.; Luan, X.; Yu, X. Spatial and temporal evolution of climatic factors and its impacts on potential evapotranspiration in Loess Plateau of Northern Shaanxi, China. Sci. Total Environ. 2017, 589, 165–172. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Hu, Y.F. Simulation of biocapacity and spatial-temporal evolution analysis of Loess Plateau in northern Shaanxi based on the CA–Markov model. Sustainability 2021, 13, 5901. [Google Scholar] [CrossRef]
- Yang, Q.K. Graphs of Geographical Division on the Loess Plateau (2000); Data Sharing Infrastructure of Earth System Science_Data Sharing Infrastructure of Loess Plateau: 2013. Available online: https://www.geodata.cn/main/face_science_detail?typeName=face_science&guid=155336412721281 (accessed on 1 August 2025).
- Peng, S.Z.; Ding, Y.X.; Wen, Z.M.; Chen, Y.; Cao, Y.; Ren, J. Spatiotemporal change and trend analysis of potential evapotranspiration over the Loess Plateau of China during 2011–2100. Agric. For. Meteorol. 2017, 233, 183–194. [Google Scholar] [CrossRef]
- Peng, S.Z.; Gang, C.C.; Cao, Y.; Chen, Y. Assessment of climate change trends over the Loess Plateau in China from 1901 to 2100. Int. J. Climatol. 2018, 38, 2250–2264. [Google Scholar] [CrossRef]
- Peng, S.Z.; Ding, Y.X.; Liu, W.Z.; Li, Z. 1 km monthly temperature and precipitation dataset for China from 1901 to 2017. Earth Syst. Sci. Data 2019, 11, 1931–1946. [Google Scholar] [CrossRef]
- Ding, Y.X.; Peng, S.Z. Spatiotemporal trends and attribution of drought across China from 1901–2100. Sustainability 2020, 12, 477. [Google Scholar] [CrossRef]
- Ding, Y.X.; Peng, S.Z. Spatiotemporal change and attribution of potential evapotranspiration over China from 1901 to 2100. Theor. Appl. Climatol. 2021, 145, 79–94. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Hao, Z.; AghaKouchak, A. Multivariate standardized drought index: A parametric multi-index model. Adv. Water Resour. 2013, 57, 12–18. [Google Scholar] [CrossRef]
- Oertel, M.; Meza, F.J.; Gironás, J.; Scott, C.A.; Rojas, F.; Pineda-Pablos, N. Drought propagation in semi-arid river basins in Latin America: Lessons from Mexico to the Southern Cone. Water 2018, 10, 1564. [Google Scholar] [CrossRef]
- Khan, M.I.; Zhu, X.Y.; Arshad, M.; Zaman, M.; Niaz, Y.; Ullah, I.; Anjum, M.N.; Uzair, M. Assessment of spatiotemporal characteristics of agro-meteorological drought events based on comparing Standardized Soil Moisture Index, Standardized Precipitation Index and Multivariate Standardized Drought Index. J. Water Clim. Change 2020, 11 (Suppl. S1), 1–17. [Google Scholar] [CrossRef]
- He, J.; Yang, X.H.; Li, Z.; Zhang, X.; Tang, Q. Spatiotemporal variations of meteorological droughts in China during 1961–2014: An investigation based on multi-threshold identification. Int. J. Disaster Risk Sci. 2016, 7, 63–76. [Google Scholar] [CrossRef]
- Ma, Q.; Li, Y.; Liu, F.G.; Feng, H.; Biswas, A.; Zhang, Q. SPEI and multi-threshold run theory based drought analysis using multi-source products in China. J. Hydrol. 2023, 616, 128737. [Google Scholar] [CrossRef]
- Palagiri, H.; Pal, M. Agricultural drought risk assessment in Southern Plateau and Hills using multi threshold run theory. Results Eng. 2024, 22, 102022. [Google Scholar] [CrossRef]
- GB/T20481-2006; Classification of Meteorological Drought. China Standardization Association: Beijing, China, 2006.
- Li, C.D.; Wang, L.; Li, X.X.; Li, Q.; Chang, Z.; Ma, Z. Temporal and spatial characteristics of droughts and floods in the Loess Plateau based on standardized precipitation index. Torrential Rain Disasters 2020, 39, 524–531. [Google Scholar]
- Wang, X.F.; Zhang, Y.; Feng, X.M.; Feng, Y.; Xue, Y.; Pan, N. Analysis and application of drought characteristics based on run theory and Copula function. Trans. Chin. Soc. Agric. Eng. 2017, 33, 206–214. [Google Scholar]
- Maraun, D.; Kurths, J. Cross wavelet analysis: Significance testing and pitfalls. Nonlinear Process. Geophys. 2004, 11, 505–514. [Google Scholar] [CrossRef]
- Marques de Souza, A.; Echer, E.; Bolzan, M.J.A.; Hajra, R. Cross-correlation and cross-wavelet analyses of the solar wind IMF Bz and auroral electrojet index AE coupling during HILDCAAs. Ann. Geophys. 2018, 36, 205–211. [Google Scholar] [CrossRef]
- Li, R.H.; Chen, N.C.; Zhang, X.; Zeng, L.; Wang, X.; Tang, S.; Li, D.; Niyogi, D. Quantitative analysis of agricultural drought propagation process in the Yangtze River Basin by using cross wavelet analysis and spatial autocorrelation. Agric. For. Meteorol. 2020, 280, 107809. [Google Scholar] [CrossRef]
- Muraja, D.O.S.; Klausner, V.; Prestes, A.; da Silva, I.R. Ocean–atmosphere interaction identified in tree-ring time series from southern Brazil using cross-wavelet analysis. Theor. Appl. Climatol. 2023, 153, 1177–1189. [Google Scholar] [CrossRef]
- Kadier, A.; Abdeshahian, P.; Simayi, Y.; Ismail, M.; Hamid, A.A.; Kalil, M.S. Grey relational analysis for comparative assessment of different cathode materials in microbial electrolysis cells. Energy 2015, 90, 1556–1562. [Google Scholar] [CrossRef]
- Rehman, E.; Ikram, M.; Feng, M.T.; Rehman, S. Sectoral-based CO2 emissions of Pakistan: A novel Grey Relation Analysis (GRA) approach. Environ. Sci. Pollut. Res. 2020, 27, 29118–29129. [Google Scholar] [CrossRef] [PubMed]
- Bai, J.Z.; Zhou, Z.X.; Zou, Y.F.; Pulatov, B.; Siddique, K.H. Watershed drought and ecosystem services: Spatiotemporal characteristics and gray relational analysis. ISPRS Int. J. Geo-Inf. 2021, 10, 43. [Google Scholar] [CrossRef]
- Guo, Y.; Huang, S.Z.; Huang, Q.; Leng, G.; Fang, W.; Wang, L.; Wang, H. Propagation thresholds of meteorological drought for triggering hydrological drought at various levels. Sci. Total Environ. 2020, 712, 136502. [Google Scholar] [CrossRef]
- Song, Y.Z.; Wang, J.F.; Ge, Y.; Xu, C. An optimal parameters-based geographical detector model enhances geographic characteristics of explanatory variables for spatial heterogeneity analysis: Cases with different types of spatial data. GISci. Remote Sens. 2020, 57, 593–610. [Google Scholar] [CrossRef]
- Sun, Y.J.; Liu, X.F.; Ren, Z.Y.; Li, S. Spatiotemporal variations of multi-scale drought and its influencing factors across the Loess Plateau from 1960 to 2016. Geogr. Res. 2019, 38, 1820–1832. [Google Scholar]
- Wang, J.R.; Sun, C.J.; Zheng, Z.J.; Li, X.M. Drought characteristics of the Loess Plateau in the past 60 years and its relationship with changes in atmospheric circulation. Acta Ecol. Sin. 2021, 41, 5340–5351. [Google Scholar] [CrossRef]
- Huang, S.Z.; Li, P.; Huang, Q.; Leng, G.; Hou, B.; Ma, L. The propagation from meteorological to hydrological drought and its potential influence factors. J. Hydrol. 2017, 547, 184–195. [Google Scholar] [CrossRef]
- Wang, J.S.; Wang, W.; Cheng, H.; Wang, H.; Zhu, Y. Propagation from meteorological to hydrological drought and its influencing factors in the Huaihe River Basin. Water 2021, 13, 1985. [Google Scholar] [CrossRef]
- Li, M.; Ge, C.H.; Deng, Y.Y.; Wang, G.; Chai, X. Meteorological and agricultural drought characteristics and their relationship across the Loess Plateau. Sci. Geogr. Sin. 2020, 40, 2105–2114. [Google Scholar]
- Zhang, Y.; Hao, Z.C.; Feng, S.F.; Zhang, X.; Xu, Y.; Hao, F. Agricultural drought prediction in China based on drought propagation and large-scale drivers. Agric. Water Manag. 2021, 255, 107028. [Google Scholar] [CrossRef]
- Xu, Z.G.; Wu, Z.Y.; Shao, Q.X.; He, H.; Guo, X. From meteorological to agricultural drought: Propagation time and probabilistic linkages. J. Hydrol. Reg. Stud. 2023, 46, 101329. [Google Scholar] [CrossRef]
- Feng, K.; Yuan, H.B.; Wang, Y.Y.; Li, Y.; Wang, X.; Wang, F.; Su, X.; Zhang, Z. Propagation Dynamics from Meteorological to Agricultural Drought in Northwestern China: Key Influencing Factors. Agronomy 2024, 14, 1987. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, X.; Wang, X.; Hao, Z.; Singh, V.P.; Hao, F. Propagation from meteorological drought to hydrological drought under the impact of human activities: A case study in northern China. J. Hydrol. 2019, 579, 124147. [Google Scholar] [CrossRef]
- Wang, W.X.; Cui, C.F.; Yu, W.H. Response of drought index to land use types in the Loess Plateau of Shaanxi, China. Sci. Rep. 2022, 12, 8668. [Google Scholar] [CrossRef]
- Murugesan, E.; Shanmugamoorthy, S.; Veerasamy, S.; Sivakumar, V. Drought assessment in Coimbatore South region, Tamil Nadu, India, using remote sensing and meteorological data. J. Earth Syst. Sci. 2025, 134, 40. [Google Scholar] [CrossRef]
- Liu, M.C.; Jian, H.F.; Han, H.M.; Long, P. Analyzing the droughts and their determinants in the Fuhe River Basin using the SWAT model. J. Irrig. Drain. 2024, 43, 114–120. [Google Scholar]
- Yuan, X.C.; Zhou, Y.L.; Jin, J.L.; Wei, Y.-M. Risk analysis for drought hazard in China: A case study in Huaibei Plain. Nat. Hazards 2013, 67, 879–900. [Google Scholar] [CrossRef]
- Fowé, T.; Yonaba, R.; Mounirou, L.A.; Ouédraogo, E.; Ibrahim, B.; Niang, D.; Karambiri, H.; Yacouba, H. From meteorological to hydrological drought: A case study using standardized indices in the Nakanbe River Basin, Burkina Faso. Nat. Hazards 2023, 119, 1941–1965. [Google Scholar]

| Name | Data Length | Resolution | Source | |
|---|---|---|---|---|
| Meteorological data | Precipitation | 1901–2021 | 1 km | 1 km monthly precipitation dataset for China (1901–2021) http://data.tpdc.ac.cn (Accessed on 4 March 2024) |
| Temperature | 1901–2021 | 1 km | 1 km monthly mean temperature dataset for China (1901–2021) http://data.tpdc.ac.cn (Accessed on 4 March 2024) | |
| Evapotranspiration | 1901–2022 | 1 km | 1 km monthly potential evapotranspiration dataset for China (1901–2022) http://data.tpdc.ac.cn (Accessed on 4 March 2024) | |
| Aridity index | 1901–2022 | 1 km | 1 km annual aridity index dataset for China (1901–2022) http://data.tpdc.ac.cn (Accessed on 4 March 2024) | |
| Underlying surface data | DEM | 30 m | http://www.gscloud.cn (Accessed on 4 March 2024) | |
| Slope | 30 m | |||
| Soil moisture | 1948–2022 | 0.25° | Global Land Data Assimilation System (GLDAS) https://disc.gsfc.nasa.gov/datasets/ (Accessed on 4 March 2024) | |
| Geomorphological zoning data of the Loess Plateau | Geographical zoning map of the Loess Plateau region (2000) http://www.geodata.cn (Accessed on 4 March 2024) | |||
| Human activity data | Population density | 2000–2022 | 1 km | LandScan dataset https://landscan.ornl.gov/ (Accessed on 4 March 2024) |
| Land use | 1990–2020 | 30 m | Annual China land cover dataset (CLCD) https://zenodo.org/records/4417810 (Accessed on 4 March 2024) |
| Results of q-Value Comparison | Interaction Type |
|---|---|
| q (X1∩X2) < Min [q (X1), q (X2)] | nonlinear weakening |
| Min [q (X1), q (X2)] < q (X1∩X2) < Max [q (X1), q (X2)] | single-factor nonlinear weakening |
| q (X1∩X2) > Max [q (X1), q (X2)] | bi-factor enhancement |
| q (X1∩X2) = q (X1) + q (X2) | Independence |
| q (X1∩X2) > q(X1) + q (X2) | nonlinear enhancement |
| Propagation Time/Month | All Regions | I | II | III | IV | V | VI | VII |
|---|---|---|---|---|---|---|---|---|
| January | 3 | 2 | 3 | 3 | 3 | 3 | 3 | 3 |
| February | 4 | 3 | 4 | 6 | 6 | 4 | 4 | 3 |
| March | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| April | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| May | 2 | 2 | 1 | 1 | 2 | 1 | 1 | 2 |
| June | 1 | 2 | 1 | 1 | 2 | 1 | 1 | 2 |
| July | 2 | 2 | 2 | 2 | 2 | 1 | 2 | 2 |
| August | 3 | 2 | 2 | 2 | 4 | 1 | 3 | 2 |
| September | 3 | 2 | 3 | 5 | 4 | 3 | 2 | 3 |
| October | 3 | 3 | 3 | 4 | 4 | 3 | 2 | 3 |
| November | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| December | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| Propagation Time/Month | All Regions | I | II | III | IV | V | VI | VII |
|---|---|---|---|---|---|---|---|---|
| Spring | 1.3 | 1.3 | 1.0 | 1.0 | 1.3 | 1.0 | 1.0 | 1.3 |
| Summer | 2.0 | 2.0 | 1.7 | 1.7 | 2.7 | 1.0 | 2.0 | 2.0 |
| Autumn | 2.7 | 2.3 | 2.7 | 3.7 | 3.3 | 2.7 | 2.0 | 2.7 |
| Winter | 3.0 | 2.3 | 3.0 | 3.7 | 3.7 | 3.0 | 3.0 | 2.7 |
| Area | Meteorological Drought | Agricultural Drought | ||||||
|---|---|---|---|---|---|---|---|---|
| Start Time | End Time | Duration | Severity | Start Time | End Time | Duration | Severity | |
| I | 1965-06 | 1966-03 | 10 | 12.55 | 1965-08 | 1966-07 | 12 | 12.01 |
| 1997-05 | 1997-12 | 8 | 12.87 | 1997-06 | 1998-02 | 9 | 15.62 | |
| 1998-10 | 1999-04 | 7 | 18.18 | 1998-11 | 1999-05 | 7 | 11.12 | |
| II | 1950-07 | 1950-11 | 5 | 6.85 | 1950-07 | 1951-08 | 14 | 17.4 |
| 1998-09 | 1999-10 | 14 | 21.92 | 1998-10 | 1999-08 | 11 | 14.46 | |
| 2010-07 | 2010-08 | 2 | 2.03 | 2010-08 | 2011-10 | 15 | 12.73 | |
| III | 1950-06 | 1950-09 | 4 | 4.66 | 1950-06 | 1951-03 | 10 | 11.89 |
| 1973-11 | 1973-12 | 2 | 2.25 | 1973-12 | 1974-11 | 12 | 11.07 | |
| 1997-05 | 1997-10 | 6 | 7.56 | 1997-05 | 1997-11 | 7 | 10.94 | |
| IV | 1950-07 | 1950-10 | 4 | 5.48 | 1950-07 | 1951-09 | 15 | 15.33 |
| 1970-11 | 1971-01 | 3 | 2.64 | 1970-11 | 1971-07 | 9 | 12.33 | |
| 2008-05 | 2008-08 | 4 | 4.54 | 2008-06 | 2009-11 | 18 | 18.43 | |
| V | 1966-02 | 1966-04 | 3 | 3.51 | 1966-02 | 1966-08 | 7 | 6.7 |
| 2004-02 | 2004-06 | 5 | 8.26 | 2004-01 | 2004-06 | 6 | 8.02 | |
| 2008-05 | 2008-08 | 4 | 4.94 | 2008-04 | 2009-09 | 18 | 22.73 | |
| VI | 1950-07 | 1950-11 | 5 | 7.08 | 1950-07 | 1951-08 | 14 | 17.46 |
| 1965-07 | 1965-12 | 6 | 11.43 | 1965-07 | 1966-02 | 8 | 15.24 | |
| 2010-07 | 2010-08 | 2 | 1.63 | 2010-08 | 2011-10 | 15 | 15.87 | |
| VII | 1957-08 | 1957-12 | 5 | 8.47 | 1957-09 | 1958-04 | 8 | 10.98 |
| 1997-05 | 1997-12 | 8 | 12.63 | 1997-06 | 1998-01 | 8 | 13.81 | |
| 1998-10 | 1999-03 | 6 | 16.68 | 1998-11 | 1999-05 | 7 | 10.66 | |
| Division | I | II | III | IV | V | VI | VII |
|---|---|---|---|---|---|---|---|
| Mean | 0.50 | 0.54 | 0.56 | 0.59 | 0.64 | 0.55 | 0.51 |
| SD | 0.04 | 0.05 | 0.03 | 0.04 | 0.01 | 0.05 | 0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhang, H.; Ye, Z.; Lyu, J.; Ma, H.; Zhang, X. Spatiotemporal Dynamics of Drought Propagation in the Loess Plateau: A Geomorphological Perspective. Water 2025, 17, 2447. https://doi.org/10.3390/w17162447
Zhang Y, Zhang H, Ye Z, Lyu J, Ma H, Zhang X. Spatiotemporal Dynamics of Drought Propagation in the Loess Plateau: A Geomorphological Perspective. Water. 2025; 17(16):2447. https://doi.org/10.3390/w17162447
Chicago/Turabian StyleZhang, Yu, Hongbo Zhang, Zhaoxia Ye, Jiaojiao Lyu, Huan Ma, and Xuedi Zhang. 2025. "Spatiotemporal Dynamics of Drought Propagation in the Loess Plateau: A Geomorphological Perspective" Water 17, no. 16: 2447. https://doi.org/10.3390/w17162447
APA StyleZhang, Y., Zhang, H., Ye, Z., Lyu, J., Ma, H., & Zhang, X. (2025). Spatiotemporal Dynamics of Drought Propagation in the Loess Plateau: A Geomorphological Perspective. Water, 17(16), 2447. https://doi.org/10.3390/w17162447








