Estimation of Hydraulic Conductivity from Well Logs for the Parameterization of Heterogeneous Multilayer Aquifer Systems
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.1.1. Location
2.1.2. Geological Setting
2.1.3. Hydrogeological Context
2.2. Methodology and Data Acquisition
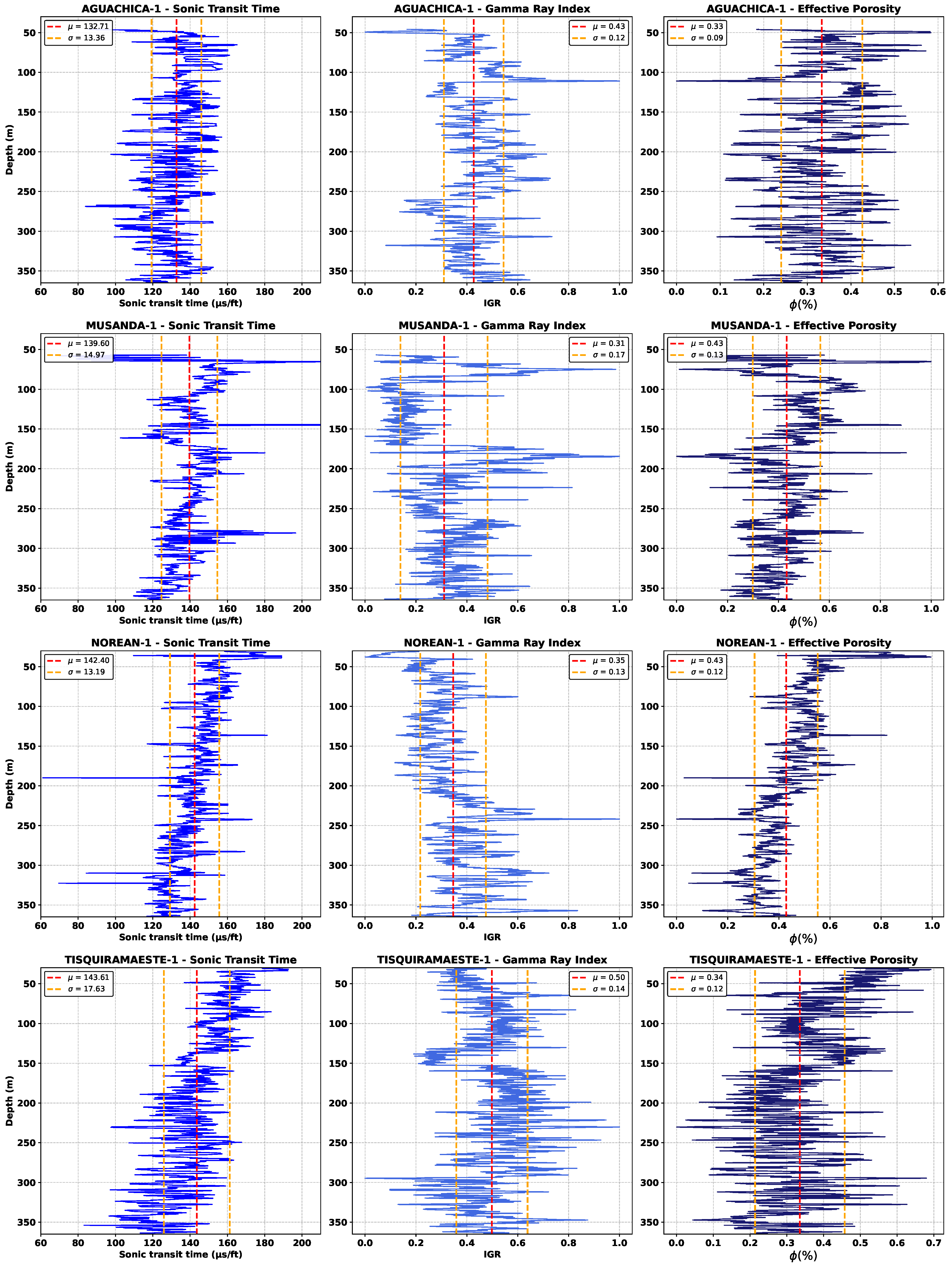
2.2.1. Porosity Estimation
2.2.2. Gamma Ray Index Calculation
2.2.3. Clay Volume Estimation
2.2.4. Effective Porosity Estimation
2.2.5. Temperature
2.2.6. Hydraulic Conductivity Estimation
2.2.7. Pumping Tests
2.2.8. Regional-Scale Groundwater Flow Model
- Modeling ObjectivesTo validate the methodology proposed in this study, a regional-scale groundwater flow model was developed for the study area. The primary objective of the model is to evaluate the estimated hydraulic conductivity values by calibrating them through inverse modeling. The calibration targets consist of observed hydraulic heads at multiple groundwater monitoring points across the region, including wells, piezometers, and hand-dug wells.
- Conceptual ModelThe conceptual model is defined as a graphical and qualitative representation of the aquifer system based on hypotheses regarding its hydrodynamic behavior. It describes the main characteristics of the hydrogeological system, such as boundary conditions, hydrogeological units, and other relevant features [22,86].The proposed conceptual model (Figure 3) represents the regional aquifer system of the MMV, exclusively considering the Neogene–Quaternary deposits of the sedimentary system. Accordingly, the hydrogeological basement is assumed to be composed of the Colorado Formation, which underlies the Real Group.Based on piezometric data collected from 434 water points, a main regional groundwater flow direction with a south-to-north flow direction was identified, discharging into swampy bodies located in the northern part of the study area. Additionally, intermediate flow paths were observed in an east–west direction, originating from the alluvial fans of Aguachica and discharging into the Magdalena River.Annual average precipitation ranges from 3700 mm/year in the south to 1000 mm/year in the north [62]. For this reason, recharge was considered as a spatially distributed input, accounting for both the precipitation variability and land use/land cover conditions described by Lora et al. (2024) [3]. Recharge constituted one of the parameters calibrated during the numerical modeling process.
- Numerical Modeling CodeFEFLOW version 8.1 was used as the modeling code for the implementation of the numerical model. This software applies the finite element method and is designed for simulating flow and transport processes in porous and fractured media [87,88]. It supports both manual and automatic calibration through integration with FEPEST, the FEFLOW-integrated module for PEST [89,90]. This helps to facilitates the adjustment of model parameters, particularly hydraulic conductivity, making it appropriate for the modeling objectives.
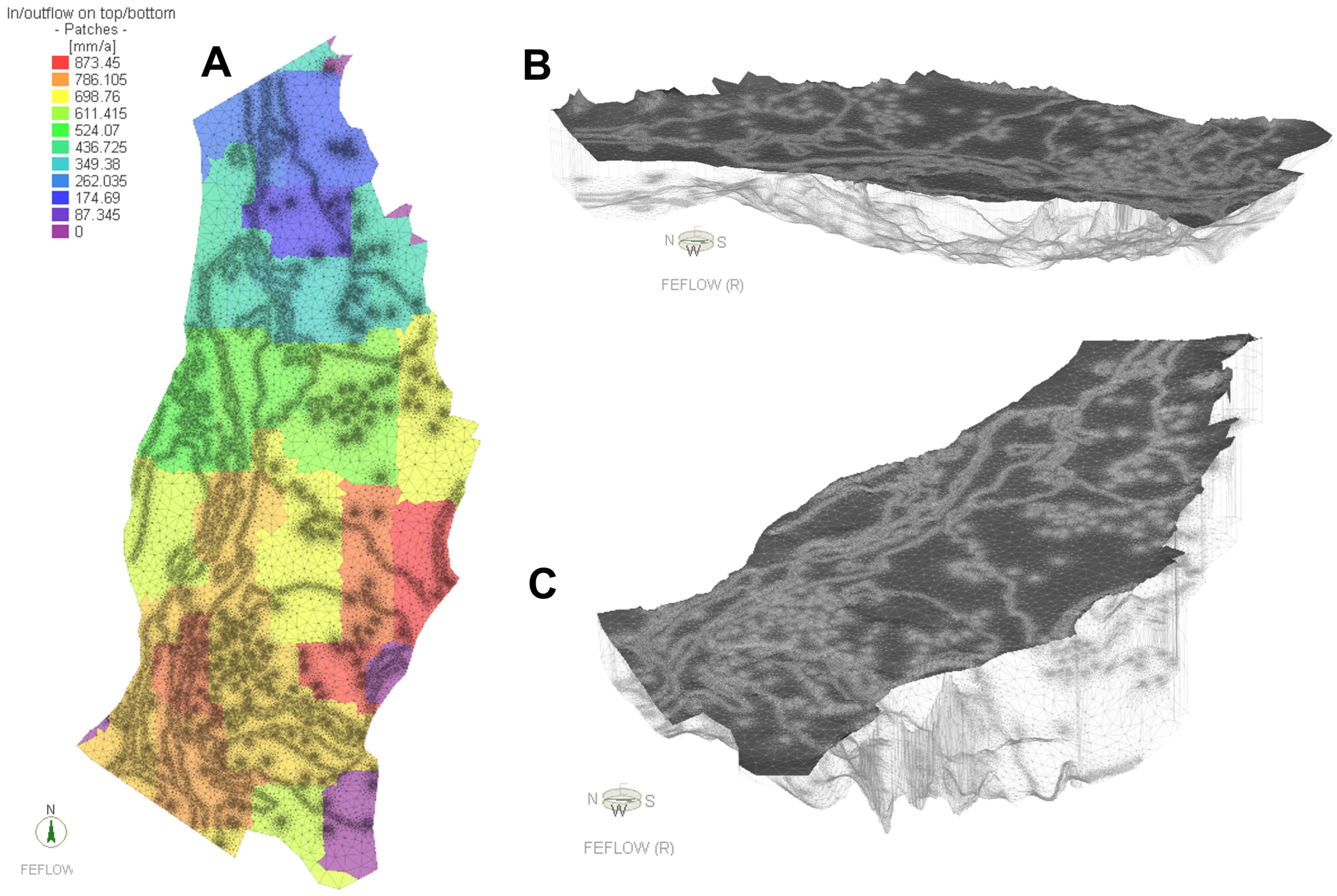
- Numerical ModelImplementation of the numerical model was based on the structural components defined in the conceptual model. Initially, a two-dimensional unstructured mesh composed of 124,397 triangular elements and 62,431 nodes was created (Figure 4A). This mesh was refined in areas with higher data density. From this 2D mesh, a three-dimensional mesh was generated to represent the Neogene–Quaternary hydrogeological units, including the four units of the Real Group and the Quaternary deposits. The upper boundary of the 3D mesh corresponded to the topographic surface, derived from the Shuttle Radar Topography Mission (SRTM) Digital Elevation Model (DEM) provided by NASA and specifically reprocessed for the study area. The lower boundary was defined based on the base of the Real Group. The resulting 3D mesh consisted of 621,985 elements and 374,586 nodes (Figure 4B,C).As described in the conceptual model, the precipitation regime and land use/land cover patterns vary significantly between the southern and northern parts of the study area. To estimate the effective recharge, a hydrological model based on Hydrological Response Units (HRUs) was applied [64]. Recharge rates were determined through an inverse calibration process, resulting in values ranging from 12% to 33% of the annual average precipitation, depending on the HRU. Higher annual recharge values were observed in the southern sector, in line with the spatial distribution of precipitation (Figure 4A).The boundary conditions of the numerical model were established according to the conceptual understanding of the regional hydrogeological system. A Neumann-type condition was applied at the southern boundary to represent regional inflow into the aquifer. On the eastern boundary, a prescribed flow condition was assigned in the northern sector, associated with the Aguachica alluvial fans, while a no-flow condition was set in the southern sector due to the presence of Cretaceous outcrops from the Eastern Cordillera that dip eastward (away from the study area), and as such do not contribute flow to the model domain. Similarly, the western boundary was defined as no-flow in the northern sector due to the presence of low-permeability Cretaceous units such as the La Luna Formation, while a prescribed flow condition was assigned to the southern sector. At the northern boundary, a Dirichlet-type condition was implemented using piezometric levels derived from the available water table data.According to secondary data provided by the Regional Environmental Authorities (CARs) responsible for granting water abstraction licenses in Colombia, 3962 groundwater points were identified within the model domain; however, only 12.95% of these (513 points) had records of permitted discharge rates, defined as the maximum authorized extraction. These discharge values were incorporated into the model as outflows (BC Type IV—Single Well), totaling 83,911.8 m3/day.The model was constructed using five layers. The top layer represents the Quaternary deposits, while the four underlying layers correspond to the sub-units of the Real Group. The model was then parameterized on the basis of this structure. The uppermost layer was subdivided into different Quaternary geomorphological units, each considered a zone of uniform hydraulic conductivity (Figure 5). Similarly, each sub-unit of the Real Group was divided into northern and southern sectors to account for the marked differences in granulometric composition across the study area, where sandy materials predominate in the north and clayey materials in the south [64,91].
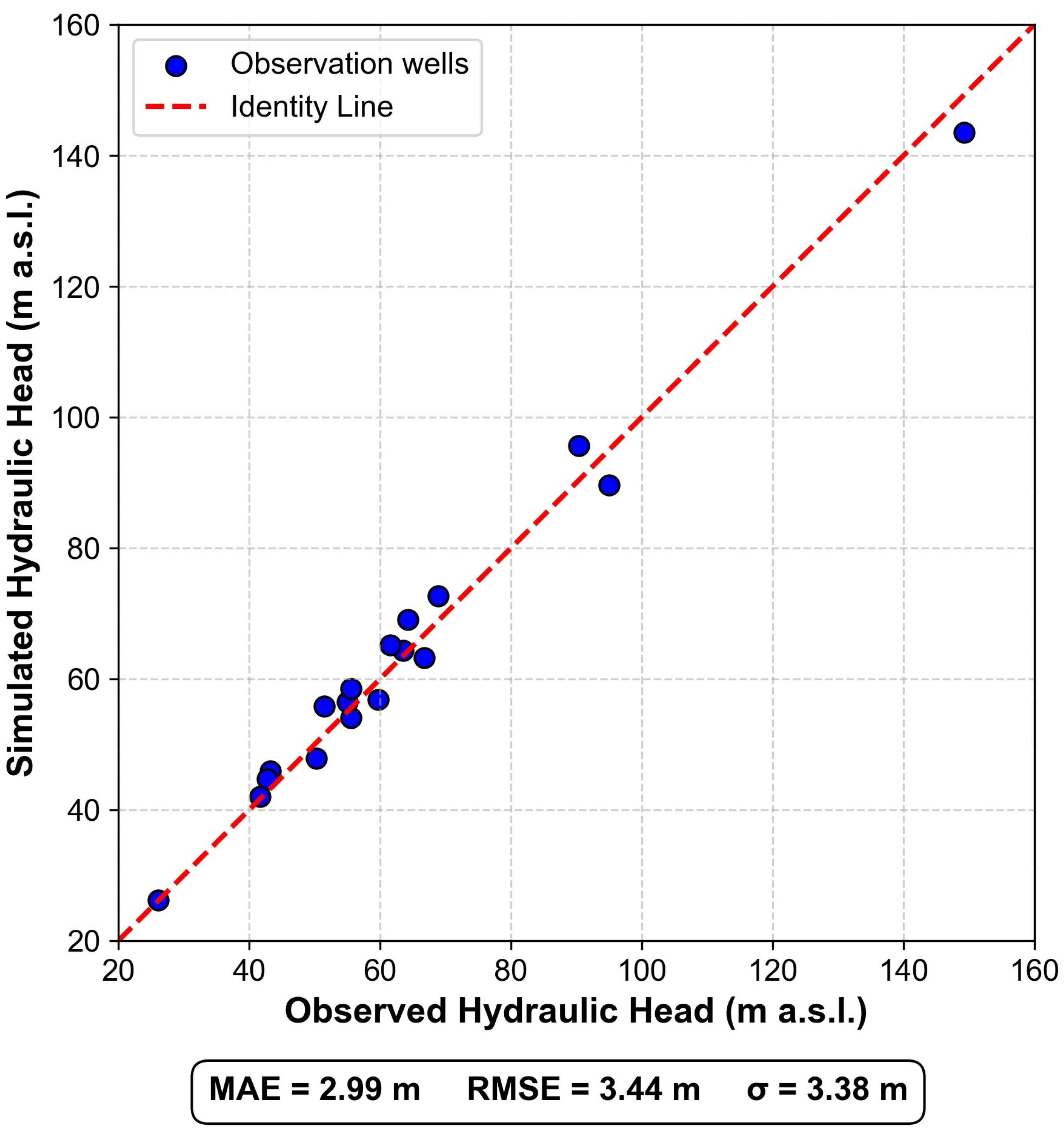
- Model CalibrationCalibration of the model was carried out using an iterative trial-and-error approach, supported by results from previous modeling conducted in the study area [64]. Calibration yielded an RMSE of 3.44 m and an MAE of 2.99 m, indicating good agreement between simulated and observed piezometric levels (Figure 6). This level of accuracy is considered acceptable when taking into account the various sources of uncertainty involved, such as the precision of the digital elevation model (DEM), the zonation used for parameterization, and the simplifications made in the hydrogeological conceptualization.The water balance of the model showed a total imbalance of , which is considered numerically negligible. This result confirms adequate conservation of water mass in the system and consistent implementation of the boundary conditions, recharge, and discharge terms according to the conceptual model. Regarding the flow distribution, the main inflow corresponds to infiltration recharge, with a total rate of 53.33 m3/s, while the most significant outflow takes place through the northern boundary, with 52.61 m3/s.Given that the main objective of this simulation was to estimate hydraulic conductivity values for comparison with the proposed methodology, the calibrated values of K are presented in the results section (Section 3).
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mekonnen, M.M.; Pahlow, M.; Aldaya, M.M.; Zarate, E.; Hoekstra, A.Y. Sustainability, efficiency and equitability of water consumption and pollution in Latin America and the Caribbean. Sustainability 2015, 7, 2086–2112. [Google Scholar] [CrossRef]
- Aranguren-Díaz, Y.; Galán-Freyle, N.J.; Guerra, A.; Manares-Romero, A.; Pacheco-Londoño, L.C.; Romero-Coronado, A.; Vidal-Figueroa, N.; Machado-Sierra, E. Aquifers and groundwater: Challenges and opportunities in water resource management in Colombia. Water 2024, 16, 685. [Google Scholar] [CrossRef]
- Lora-Ariza, B.; Piña, A.; Donado, L.D. Assessment of groundwater quality for human consumption and its health risks in the Middle Magdalena Valley, Colombia. Sci. Rep. 2024, 14, 11346. [Google Scholar] [CrossRef]
- Carrard, N.; Foster, T.; Willetts, J. Groundwater as a source of drinking water in southeast Asia and the Pacific: A multi-country review of current reliance and resource concerns. Water 2019, 11, 1605. [Google Scholar] [CrossRef]
- Jakeman, A.J.; Barreteau, O.; Hunt, R.J.; Rinaudo, J.-D.; Ross, A.; Arshad, M.; Hamilton, S. Integrated groundwater management: An overview of concepts and challenges. In Integrated Groundwater Management: Concepts, Approaches and Challenges; Springer: Cham, Switzerland, 2016; pp. 3–20. [Google Scholar]
- Gaye, C.B.; Tindimugaya, C. Challenges and opportunities for sustainable groundwater management in Africa. Hydrogeol. J. 2019, 27, 1099–1110. [Google Scholar] [CrossRef]
- Qureshi, A.S. Challenges and opportunities of groundwater management in Pakistan. In Groundwater of South Asia; Springer: Cham, Switzerland, 2018; pp. 735–757. [Google Scholar]
- Ahamad, F.; Tyagi, S.K.; Singh, M.; Sharma, A.K. Groundwater in arid and semi-arid regions of India: A review on the quality, management and challenges. In Groundwater in Arid and Semi-Arid Areas: Monitoring, Assessment, Modelling, and Management; Springer: Cham, Switzerland, 2023; pp. 11–52. [Google Scholar]
- Bashandy, A.M.; Bekhit, H.M.; Radwan, H.G. Uncertainty assessment of aquifer hydraulic parameters from pumping test data. Appl. Water Sci. 2024, 14, 84. [Google Scholar] [CrossRef]
- Singh, A. Groundwater resources management through the applications of simulation modeling: A review. Sci. Total Environ. 2014, 499, 414–423. [Google Scholar] [CrossRef] [PubMed]
- West, L.J.; Odling, N.E. Characterization of a multilayer aquifer using open well dilution tests. Groundwater 2007, 45, 74–84. [Google Scholar] [CrossRef]
- Van der Gun, J. Large Aquifer Systems Around the World; The Groundwater Project: Guelph, ON, Canada, 2022. [Google Scholar]
- Shepley, M.G. Vertical hydraulic conductivity and layered heterogeneity: From measurements to models. Hydrogeol. J. 2024, 32, 1017–1042. [Google Scholar] [CrossRef]
- Kim, J.-W.; Choi, H.; Lee, J.-Y. Characterization of hydrogeologic properties for a multi-layered alluvial aquifer using hydraulic and tracer tests and electrical resistivity survey. Environ. Geol. 2005, 48, 991–1001. [Google Scholar] [CrossRef]
- Maliva, R.G. Aquifer Characterization Techniques; Springer International Publishing: Fort Myers, FL, USA, 2016; Volume 4, pp. 1–632. [Google Scholar]
- Senthilkumar, M.; Gnanasundar, D. Aquifer characterization and hydrogeological modeling for devising groundwater management strategies for the Chennai aquifer system, southern India. Environ. Earth Sci. 2022, 81, 187. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, W. A review of regional groundwater flow modeling. Geosci. Front. 2011, 2, 205–214. [Google Scholar] [CrossRef]
- Hill, M.C.; Tiedeman, C.R. Effective Groundwater Model Calibration: With Analysis of Data, Sensitivities, Predictions, and Uncertainty; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Guillaume, J.H.A.; Hunt, R.J.; Comunian, A.; Blakers, R.S.; Fu, B. Methods for exploring uncertainty in groundwater management predictions. In Integrated Groundwater Management: Concepts, Approaches and Challenges; Springer: Cham, Switzerland, 2016; pp. 711–737. [Google Scholar]
- Refsgaard, J.C.; van der Sluijs, J.P.; Højberg, A.L.; Vanrolleghem, P.A. Uncertainty in the environmental modelling process—A framework and guidance. Environ. Model. Softw. 2007, 22, 1543–1556. [Google Scholar] [CrossRef]
- Cui, T.; Sreekanth, J.; Pickett, T.; Rassam, D.; Gilfedder, M.; Barrett, D. Impact of model parameterization on predictive uncertainty of regional groundwater models in the context of environmental impact assessment. Environ. Impact Assess. Rev. 2021, 90, 106620. [Google Scholar] [CrossRef]
- Anderson, M.P.; Woessner, W.W.; Hunt, R.J. Applied Groundwater Modeling: Simulation of Flow and Advective Transport; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Doherty, J. Calibration and Uncertainty Analysis for Complex Environmental Models; Watermark Numerical Computing: Brisbane, Australia, 2015. [Google Scholar]
- Kourakos, G.; Mantoglou, A. Inverse groundwater modeling with emphasis on model parameterization. Water Resour. Res. 2012, 48, W05544. [Google Scholar] [CrossRef]
- Moore, C.; Doherty, J. The cost of uniqueness in groundwater model calibration. Adv. Water Resour. 2006, 29, 605–623. [Google Scholar] [CrossRef]
- Doherty, J.E.; Hunt, R.J. Approaches to Highly Parameterized Inversion—A Guide to Using PEST for Groundwater-Model Calibration; US Geological Survey: Reston, VA, USA, 2010. [Google Scholar]
- Watson, T.A.; Doherty, J.E.; Christensen, S. Parameter and predictive outcomes of model simplification. Water Resour. Res. 2013, 49, 3952–3977. [Google Scholar] [CrossRef]
- Hunt, R.J.; Doherty, J.; Tonkin, M.J. Are models too simple? Arguments for increased parameterization. Groundwater 2007, 45, 254–262. [Google Scholar] [CrossRef]
- Piña, A.; Donado, L.D.; Blessent, D. Analysis of the scale-dependence of the hydraulic conductivity in complex fractured media. J. Hydrol. 2019, 569, 556–572. [Google Scholar] [CrossRef]
- Neuman, S.P. Universal scaling of hydraulic conductivities and dispersivities in geologic media. Water Resour. Res. 1990, 26, 1749–1758. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Panzeri, M.; Tartakovsky, G.D.; Guadagnini, A. Uncertainty quantification in scale-dependent models of flow in porous media. Water Resour. Res. 2017, 53, 9392–9401. [Google Scholar] [CrossRef]
- Kulander, B.R.; Dean, S.L.; Ward, B.J. Fractured Core Analysis: Interpretation, Logging, and Use of Natural and Induced Fractures in Core; American Association of Petroleum Geologists: Tulsa, OK, USA, 1990. [Google Scholar]
- Ngo, V.T.; Lu, V.D.; Nguyen, M.H.; Hoang, T.M.; Nguyen, H.M.; Le, V.M. A comparison of permeability prediction methods using core analysis data. In Proceedings of the SPE Reservoir Characterisation and Simulation Conference and Exhibition, Abu Dhabi, United Arab Emirates, 14–16 September 2015. [Google Scholar]
- Zhang, F.; Zhang, Q.; Zhang, Z.; Rui, Z.; Liu, Y.; Zhang, W.; Zheng, X.; Torabi, F.; Afanasyev, A. A New Experimental Core Analysis Method for Formation Permeability Measurement Under Two-Phase Condition. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 1–4 May 2023. [Google Scholar]
- Renard, P. The future of hydraulic tests. Hydrogeol. J. 2005, 13, 259–262. [Google Scholar] [CrossRef]
- Dashti, Z.; Nakhaei, M.; Vadiati, M.; Karami, G.H.; Kisi, O. A literature review on pumping test analysis (2000–2022). Environ. Sci. Pollut. Res. 2023, 30, 9184–9206. [Google Scholar] [CrossRef]
- Mace, R.E. Estimation of hydraulic conductivity in large-diameter, hand-dug wells using slug-test methods. J. Hydrol. 1999, 219, 34–45. [Google Scholar] [CrossRef]
- Yeh, T.-C.J.; Liu, S. Hydraulic tomography: Development of a new aquifer test method. Water Resour. Res. 2000, 36, 2095–2105. [Google Scholar] [CrossRef]
- Chen, C.-S.; Sie, Y.-C.; Lin, Y.-T. A review of the multilevel slug test for characterizing aquifer heterogeneity. Terr. Atmos. Ocean Sci. 2012, 23, 123–132. [Google Scholar] [CrossRef]
- Wendt, W.A.; Sakurai, S.T.; Nelson, P.H. Permeability prediction from well logs using multiple regression. In Reservoir Characterization; Elsevier: Amsterdam, The Netherlands, 1986; pp. 181–221. [Google Scholar]
- Glover, P.W.; Zadjali, I.I.; Frew, K.A. Permeability prediction from MICP and NMR data using an electrokinetic approach. Geophysics 2006, 71, F49–F60. [Google Scholar] [CrossRef]
- Kasenow, M. Determination of Hydraulic Conductivity from Grain Size Analysis; Water Resources Publication: Highlands Ranch, CO, USA, 2002. [Google Scholar]
- Li, P.-N.; Xu, Y.-S.; Wang, X.-W. Estimation of hydraulic conductivity by the modified Kozeny—Carman equation considering the derivation principle of the original equation. J. Hydrol. 2023, 621, 129658. [Google Scholar] [CrossRef]
- Abdel Azim, R.; Aljehani, A. Neural network model for permeability prediction from reservoir well logs. Processes 2022, 10, 2587. [Google Scholar] [CrossRef]
- Helle, H.B.; Bhatt, A.; Ursin, B. Porosity and permeability prediction from wireline logs using artificial neural networks: A North Sea case study. Geophys. Prospect. 2001, 49, 431–444. [Google Scholar] [CrossRef]
- Trejo-Alonso, J.; Fuentes, C.; Chávez, C.; Quevedo, A.; Gutierrez-Lopez, A.; González-Correa, B. Saturated hydraulic conductivity estimation using artificial neural networks. Water 2021, 13, 705. [Google Scholar] [CrossRef]
- Carrera, J.; Alcolea, A.; Medina, A.; Hidalgo, J.; Slooten, L.J. Inverse problem in hydrogeology. Hydrogeol. J. 2005, 13, 206–222. [Google Scholar] [CrossRef]
- Tsai, F.T.-C.; Li, X. Inverse groundwater modeling for hydraulic conductivity estimation using Bayesian model averaging and variance window. Water Resour. Res. 2008, 44, W09403. [Google Scholar] [CrossRef]
- Perdomo, S.; Ainchil, J.E.; Kruse, E. Hydraulic parameters estimation from well logging resistivity and geoelectrical measurements. J. Appl. Geophys. 2014, 105, 50–58. [Google Scholar] [CrossRef]
- Khalil, M.A.; Santos, F.A.M. Hydraulic conductivity estimation from resistivity logs: A case study in Nubian sandstone aquifer. Arab. J. Geosci. 2013, 6, 205–212. [Google Scholar] [CrossRef]
- Szabó, N.P. Hydraulic conductivity explored by factor analysis of borehole geophysical data. Hydrogeol. J. 2015, 23, 869. [Google Scholar] [CrossRef]
- Ministerio de Ambiente y Desarrollo Sostenible; Instituto de Hidrología, Meteorología y Estudios Ambientales (IDEAM); Universidad Nacional de Colombia (UNAL); Instituto de Investigaciones Marinas y Costeras (INVEMAR). Programa Nacional de Monitoreo del Recurso Hídrico; Minambiente: Bogotá, Colombia, 2024; ISBN 978-628-7598-24-9. Available online: https://www.minambiente.gov.co/ (accessed on 10 July 2025).
- Little, K.E.; Hayashi, M.; Liang, S. Community-based groundwater monitoring network using a citizen-science approach. Groundwater 2016, 54, 317–324. [Google Scholar] [CrossRef]
- Condon, L.E.; Kollet, S.; Bierkens, M.F.P.; Fogg, G.E.; Maxwell, R.M.; Hill, M.C.; Hendricks Fransen, H.-J.; Verhoef, A.; Van Loon, A.F.; Sulis, M.; et al. Global groundwater modeling and monitoring: Opportunities and challenges. Water Resour. Res. 2021, 57, e2020WR029500. [Google Scholar] [CrossRef]
- Agencia Nacional de Hidrocarburos (ANH). Cuenca Valle Medio del Magdalena: Integración geológica de la digitalización y análisis de núcleos; Agencia Nacional de Hidrocarburos: Bogotá, Colombia, 2012. [Google Scholar]
- Nie, J.; Horton, B.K.; Mora, A.; Saylor, J.E.; Housh, T.B.; Rubiano, J.; Naranjo, J. Tracking exhumation of Andean ranges bounding the Middle Magdalena Valley basin, Colombia. Geology 2010, 38, 451–454. [Google Scholar] [CrossRef]
- Lozano, E.; Zamora, N. Anexo n Compilación de la Cuenca del Valle Medio del Magdalena. Available online: http://recordcenter.sgc.gov.co (accessed on 13 July 2025).
- Sarmiento-Rojas, L.F.; Van Wess, J.D.; Cloetingh, S. Mesozoic transtensional basin history of the Eastern Cordillera, Colombian Andes: Inferences from tectonic models. J. S. Am. Earth Sci. 2006, 21, 383–411. [Google Scholar] [CrossRef]
- Diaz Hoyos, S. Análisis Electrofacial y Petrofísico de los Pozos Cagüi-1 y Guane-1 y sus Implicaciones Identificando Sweet Spots en el Valle Medio del Magdalena. Master’s Thesis, Universidad EAFIT, Medellín, Colombia, 2022. [Google Scholar]
- Arenas Bautista, M.C. Integration of Hydrological and Economical Aspects for Water Management in Tropical Regions. Case Study: Middle Magdalena Valley, Colombia. Ph.D. Thesis, Universidad Nacional de Colombia, Bogotá, Colombia, 2019. [Google Scholar]
- Gómez, E.; Jordan, T.E.; Allmendinger, R.W.; Hegarty, K.; Kelley, S. Syntectonic Cenozoic sedimentation in the northern middle Magdalena Valley Basin of Colombia and implications for exhumation of the Northern Andes. Geol. Soc. Am. Bull. 2005, 117, 547–569. [Google Scholar] [CrossRef]
- Piña, A.; Donado, L.D.; Silva, L.; Pescador, J. Seasonal and deep groundwater-surface water interactions in the tropical Middle Magdalena River basin of Colombia. Hydrol. Process. 2022, 36, e14764. [Google Scholar] [CrossRef]
- Sarmiento, G.; Puentes, J.; Sierra, C. Evolución geológica y estratigrafía del Sector Norte del Valle Medio del Magdalena. Geol. Norandina 2015, 12, 51–82. [Google Scholar]
- Universidad Nacional de Colombia. Modelo Hidrodinámico Multiescala; Producto No. 7, Contrato RC No. FP44842-157-2018. Proyecto MEGIA; Universidad Nacional de Colombia: Bogotá, Colombia, 2024. [Google Scholar]
- Lora, B.; Silva, L.; Castro, E.; Donado, L. Characterization of spatial heterogeneity in sedimentary aquifer systems at regional scale by using hydrogeological modeling: A case study of the Middle Magdalena Valley basin-Colombia. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 23–27 May 2022. EGU22-10680. [Google Scholar]
- Malagón, J.P.; Piña, A.; Argüello, S.; Donado, L.D. Análisis hidrogeoquímico-multivariado del agua subterránea del sistema acuífero del Valle Medio del Magdalena, Colombia: Estudio a escala regional. Bol. Soc. Geol. Mex. 2021, 73, 3. [Google Scholar] [CrossRef]
- Wyllie, M.R.J.; Gregory, A.R.; Gardner, L.W. Elastic wave velocities in heterogeneous and porous media. Geophysics 1956, 21, 41–70. [Google Scholar] [CrossRef]
- Szabó, N.P. Shale volume estimation based on the factor analysis of well-logging data. Acta Geophys. 2011, 59, 935–953. [Google Scholar] [CrossRef]
- Kamel, M.H.; Mabrouk, W.M.; Bayoumi, A.I. Porosity estimation using a combination of Wyllie–Clemenceau equations in clean sand formation from acoustic logs. J. Pet. Sci. Eng. 2002, 33, 241–251. [Google Scholar] [CrossRef]
- Poupon, A.; Gaymard, R. The evaluation of clay content from logs. In Proceedings of the SPWLA Annual Logging Symposium, Los Angeles, CA, USA, 3–6 May 1970. [Google Scholar]
- George, J.; Oloruntobi, O.; Butt, S. Development of a Probabilistic Correlation between the Gamma Ray Index and Shale Volume Factor to Improve Resource Estimation for the Niger Delta Basin, Nigeria. MIST Int. J. Sci. Technol. 2024, 12, 11–28. [Google Scholar] [CrossRef]
- Díaz-Curiel, J.; Miguel, M.J.; Biosca, B.; Arévalo-Lomas, L. Gamma ray log to estimate clay content in the layers of water boreholes. J. Appl. Geophys. 2021, 195, 104481. [Google Scholar] [CrossRef]
- Asquith, G.B.; Krygowski, D.; Gibson, C.R. Basic Well Log Analysis; American Association of Petroleum Geologists: Tulsa, OK, USA, 2004; Volume 16. [Google Scholar]
- Kennedy, D. Gamma Ray Index-Shale Volume Transforms. In Proceedings of the SPWLA Annual Logging Symposium, Virtual, 17–20 May 2021. [Google Scholar]
- Twfiq, M.Z.; Zarif, F.M.; Massoud, A.; Al-Temamy, A.M. Determination the petrophysical and natural radioactivity properties of Nubian sandstone aquifer at the area of northwest El Ain Village, Sharq El-Oweinat Area, Southwestern Desert, Egypt. Asian J. Environ. Ecol. 2021, 15, 37–55. [Google Scholar] [CrossRef]
- Alfaro, C.; Alvarado, I.; Quintero, W.; Vargas, C.; Briceño, L.A. Mapa Preliminar de Gradientes Geotérmicos de Colombia; Instituto Colombiano de Geología y Minería (INGEOMINAS), Ministerio de Minas y Energía de Colombia: Bogotá, Colombia, 2009.
- Csókás, J. Determination of yield and water quality of aquifers based on geophysical well logs. Magy. Geofiz. 1995, 35, 176–203. [Google Scholar]
- Szabó, N.P.; Kormos, K.; Dobróka, M. Evaluation of hydraulic conductivity in shallow groundwater formations: A comparative study of the Csókás’ and Kozeny–Carman model. Acta Geod. Geoph. 2015, 50, 461–477. [Google Scholar] [CrossRef]
- Renard, P.; Glenz, D.; Mejias, M. Understanding diagnostic plots for well-test interpretation. Hydrogeol. J. 2009, 17, 589–600. [Google Scholar] [CrossRef]
- Erer, K.S. Adaptive usage of the Butterworth digital filter. J. Biomech. 2007, 40, 2934–2943. [Google Scholar] [CrossRef]
- Renard, P. Hytool: An open source matlab toolbox for the interpretation of hydraulic tests using analytical solutions. J. Open Source Softw. 2017, 2, 441. [Google Scholar] [CrossRef]
- Mobarra, M.; Rezkallah, M.; Ilinca, A. Variable speed diesel generators: Performance and characteristic comparison. Energies 2022, 15, 592. [Google Scholar] [CrossRef]
- Duffield, G.M. AQTESOLV for Windows Version 4.5 User’s Guide; HydroSOLVE: Reston, VA, USA, 2007. [Google Scholar]
- Yao, Y.; Zheng, C.; Tian, Y.; Liu, J.; Zheng, Y. Numerical modeling of regional groundwater flow in the Heihe River Basin, China: Advances and new insights. Sci. China Earth Sci. 2015, 58, 3–15. [Google Scholar] [CrossRef]
- De Marsily, G.; Delay, F.; Teles, V.; Schafmeister, M.T. Some current methods to represent the heterogeneity of natural media in hydrogeology. Hydrogeol. J. 1998, 6, 115–130. [Google Scholar] [CrossRef]
- Enemark, T.; Peeters, L.J.M.; Mallants, D.; Batelaan, O. Hydrogeological conceptual model building and testing: A review. J. Hydrol. 2019, 569, 310–329. [Google Scholar] [CrossRef]
- Karmakar, S.; Tatomir, A.; Oehlmann, S.; Giese, M.; Sauter, M. Numerical benchmark studies on flow and solute transport in geological reservoirs. Water 2022, 14, 1310. [Google Scholar] [CrossRef]
- Diersch, H.-J.G. FEFLOW: Finite Element Modeling of Flow, Mass and Heat Transport in Porous and Fractured Media; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Doherty, J.E.; Hunt, R.J.; Tonkin, M.J. Approaches to Highly Parameterized Inversion: A Guide to Using PEST for Model-Parameter and Predictive-Uncertainty Analysis; U.S. Department of the Interior, U.S. Geological Survey: Reston, VA, USA, 2011; Volume 2010.
- Gatto, B.; Furlanetto, D.; Camporese, M.; Trentin, T.; Salandin, P. Quantifying groundwater recharge in the Venetian high plain between the Brenta and Piave Rivers through integrated surface–subsurface hydrological modeling. J. Hydrol. Reg. Stud. 2023, 50, 101550. [Google Scholar] [CrossRef]
- Vargas Quintero, J.A. Modelamiento de la Estructura Resistiva del Valle Medio del Magdalena a Partir de la Interpretación de Estudios Magnetotelúricos; Universidad Nacional de Colombia: Bogotá, Colombia, 2021; Available online: https://repositorio.unal.edu.co/items/8154d03b-3d41-4982-b4e1-22707e5e225b (accessed on 12 June 2025).
- Rubin, Y. Applied Stochastic Hydrogeology; Oxford University Press: Oxford, UK, 2003. [Google Scholar]



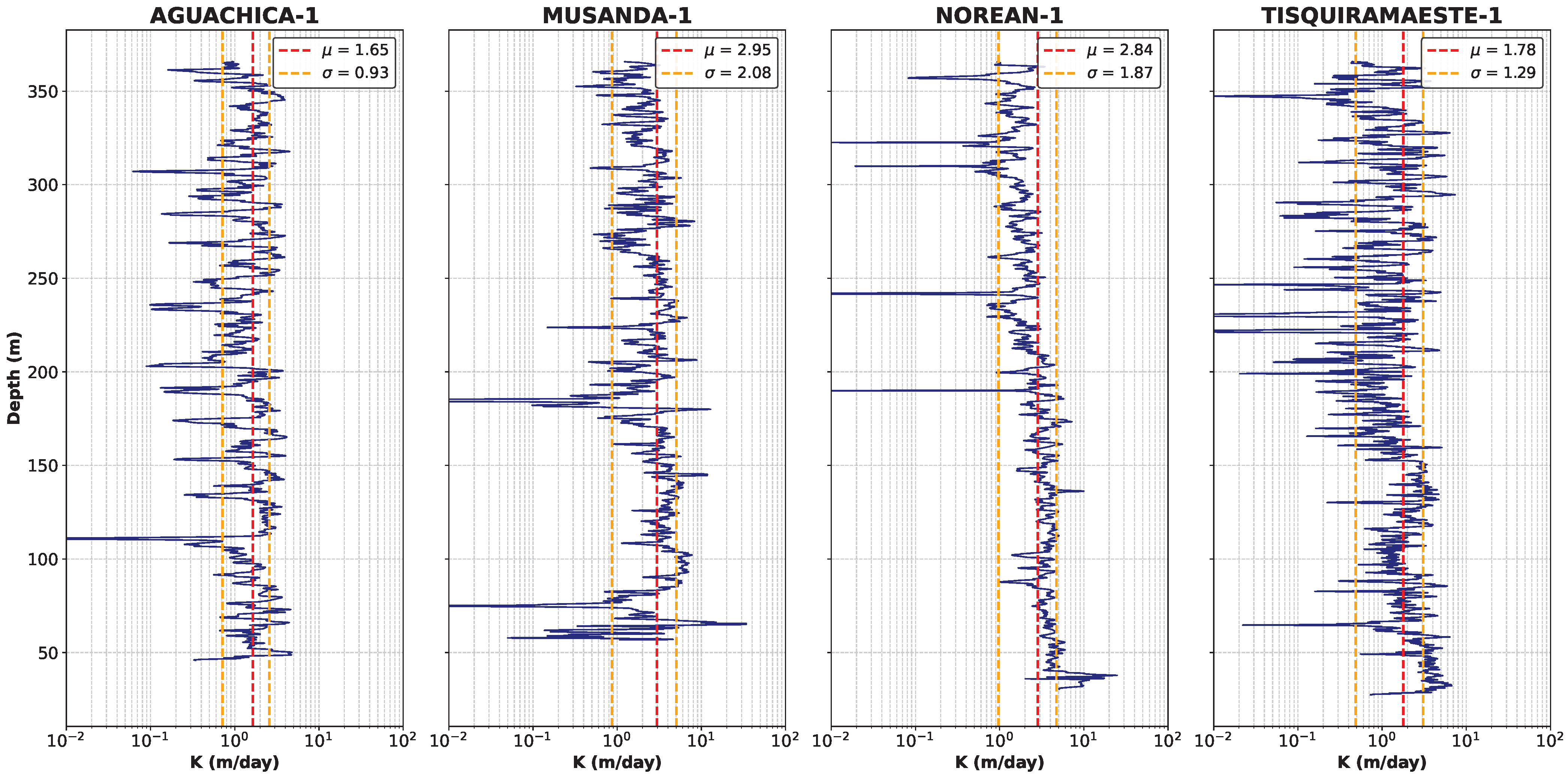
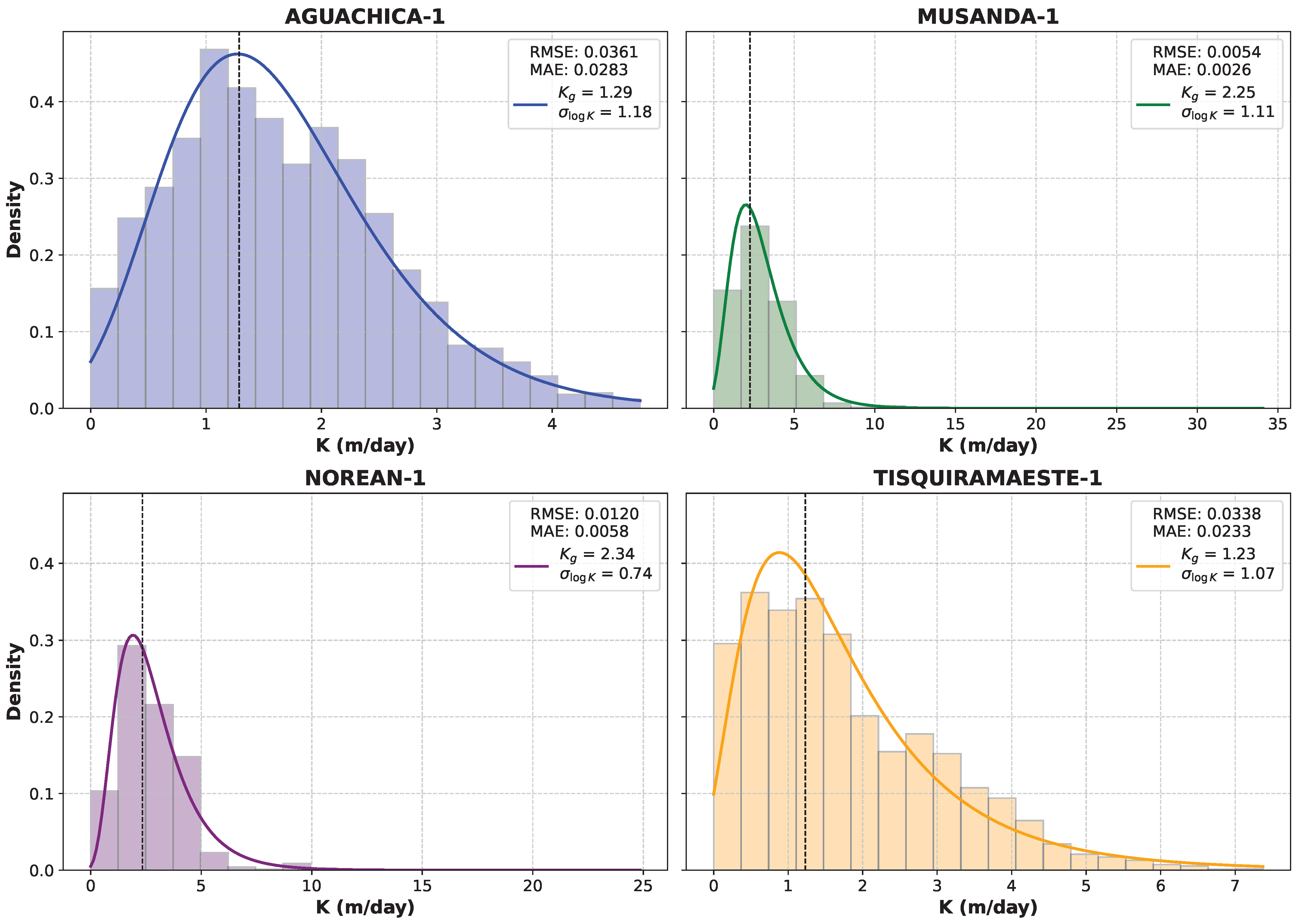


| Well | [m/day] | [m/day] | |
|---|---|---|---|
| AGUACHICA-1 | 1.29 | 1.18 | 1.12 |
| MUSANDA-1 | 2.25 | 1.11 | 1.06 |
| NOREAN-1 | 2.34 | 0.74 | 1.00 |
| TISQUIRAMA ESTE-1 | 1.23 | 1.07 | 1.06 |
| Hydrogeological Units | Hydraulic Transmissivity (m2/Day) | Hydraulic Conductivity (m/Day) | ||||||
|---|---|---|---|---|---|---|---|---|
| Mean () | Max | Min | Std Dev. | Mean () | Max | Min | Std Dev. | |
| QTf | 16.63 | 86.51 | 1.89 | 33.01 | 0.53 | 8.65 | 0.08 | 3.72 |
| QFl | 15.85 | 261.90 | 0.08 | 116.96 | 0.56 | 4.45 | 0.01 | 1.80 |
| QFc | 70.06 | 1104.40 | 2.45 | 289.56 | 1.65 | 23.50 | 0.05 | 5.91 |
| QFal | 42.00 | 2627.10 | 0.65 | 409.06 | 1.56 | 154.92 | 0.02 | 21.63 |
| QCal | 5.67 | 24.06 | 0.97 | 7.69 | 0.22 | 1.81 | 0.02 | 0.55 |
| QAt | 4.45 | 78.58 | 0.30 | 44.22 | 0.07 | 0.99 | 0.00 | 0.54 |
| Quaternary total | 32.54 | 2627.10 | 0.08 | 347.49 | 1.09 | 154.92 | 0.00 | 17.29 |
| Real U4 | 87.17 | 2627.10 | 0.65 | 571.13 | 1.36 | 154.92 | 0.02 | 30.00 |
| Real U3 | 69.88 | 1104.40 | 2.81 | 335.93 | 0.96 | 9.67 | 0.05 | 3.38 |
| Real U2 | 8.36 | 25.93 | 1.43 | 12.31 | 0.21 | 2.59 | 0.05 | 1.46 |
| Real U1 | 24.18 | 190.00 | 1.74 | 60.40 | 1.00 | 12.93 | 0.01 | 4.37 |
| Real total | 55.25 | 2627.10 | 0.65 | 447.61 | 1.06 | 154.92 | 0.01 | 21.65 |
| Hydrogeological Unit | (m/day) | (m/day) | (m/day) |
|---|---|---|---|
| QFal | 1.5 | 1.5 | 0.15 |
| QCal | 1.0 | 1.0 | 0.10 |
| QTf | 1.0 | 1.0 | 0.10 |
| QAt | 0.4 | 0.4 | 0.04 |
| QFl | 0.8 | 0.8 | 0.08 |
| QFc | 1.6 | 1.6 | 0.16 |
| Real U4 North | 0.1 | 0.1 | 0.01 |
| Real U3 North | 0.7 | 0.7 | 0.07 |
| Real U2 North | 0.2 | 0.2 | 0.02 |
| Real U1 North | 0.05 | 0.05 | 0.005 |
| Real U4 South | 1.3 | 1.3 | 0.13 |
| Real U3 South | 0.9 | 0.9 | 0.09 |
| Real U2 South | 0.3 | 0.3 | 0.03 |
| Real U1 South | 0.1 | 0.1 | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lora-Ariza, B.; Silva Vargas, L.; Donado, L.D. Estimation of Hydraulic Conductivity from Well Logs for the Parameterization of Heterogeneous Multilayer Aquifer Systems. Water 2025, 17, 2439. https://doi.org/10.3390/w17162439
Lora-Ariza B, Silva Vargas L, Donado LD. Estimation of Hydraulic Conductivity from Well Logs for the Parameterization of Heterogeneous Multilayer Aquifer Systems. Water. 2025; 17(16):2439. https://doi.org/10.3390/w17162439
Chicago/Turabian StyleLora-Ariza, Boris, Luis Silva Vargas, and Leonardo David Donado. 2025. "Estimation of Hydraulic Conductivity from Well Logs for the Parameterization of Heterogeneous Multilayer Aquifer Systems" Water 17, no. 16: 2439. https://doi.org/10.3390/w17162439
APA StyleLora-Ariza, B., Silva Vargas, L., & Donado, L. D. (2025). Estimation of Hydraulic Conductivity from Well Logs for the Parameterization of Heterogeneous Multilayer Aquifer Systems. Water, 17(16), 2439. https://doi.org/10.3390/w17162439







