Extra Tree Regression Algorithm for Simulation of Iceberg Draft and Subgouge Soil Characteristics
Abstract
1. Introduction
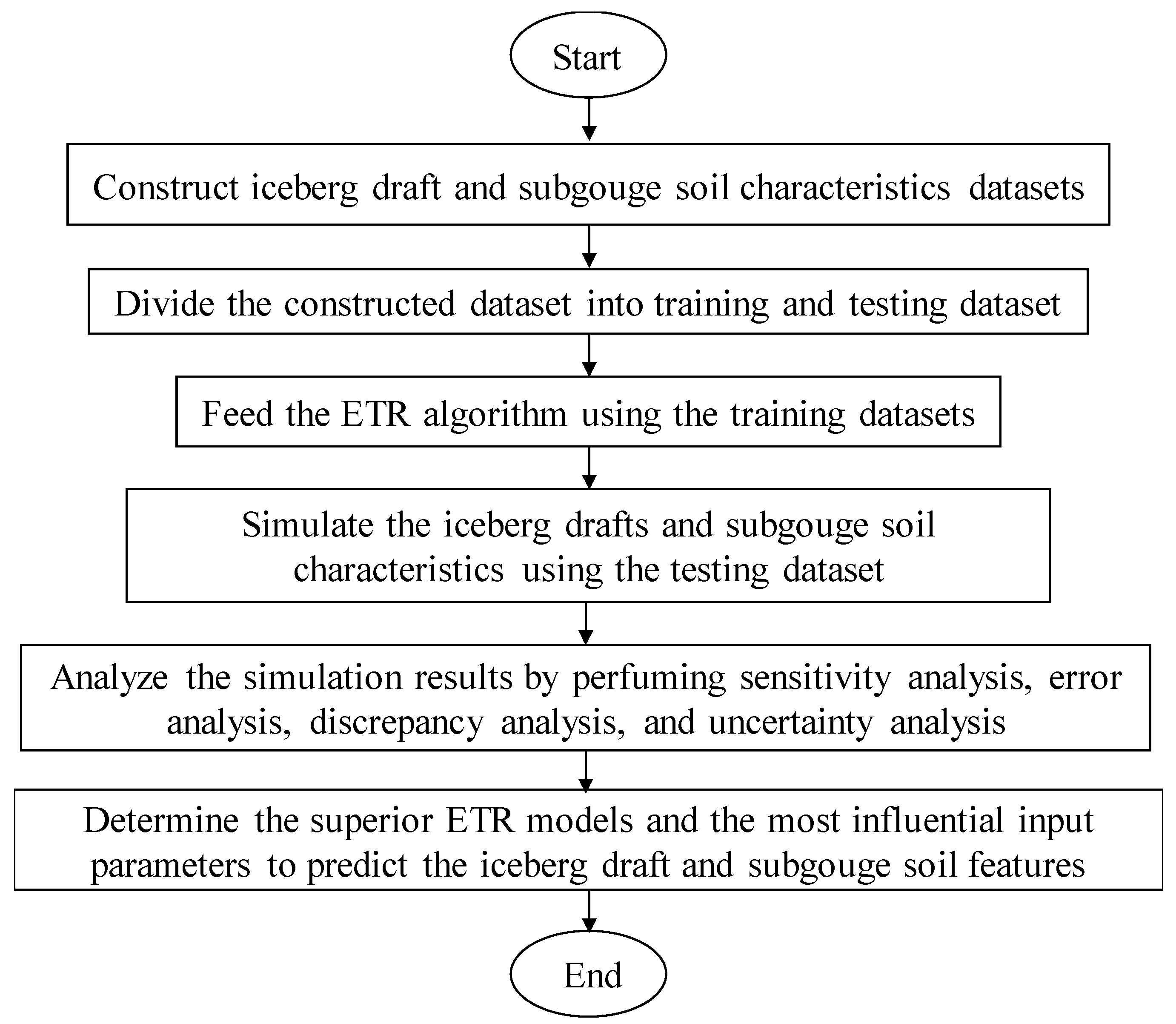
- Establishing an ETR model to simulate the iceberg draft and subgouge soil features simultaneously.
- Analyzing the simulation results to identify the superior ETR models.
- Determination of the most influential input parameters to predict the iceberg draft and subgouge soil characteristics in clay and sandy seabed.
- (1)
- the development of cross-parameter dependencies that capture the complex relationships between draft characteristics and seabed interactions, which were previously ignored in isolated models;
- (2)
- the implementation of a multi-output prediction system that enables real-time assessment of multiple iceberg parameters simultaneously, significantly improving operational efficiency;
- (3)
- the creation of seabed-agnostic modeling capabilities that can adapt to varying geological conditions without requiring separate model deployments; and
- (4)
- enhanced prediction accuracy through synergistic modeling, where draft predictions inform seabed interaction calculations and vice versa.
2. Materials and Methods
2.1. Extra Tree Regression (ETR)
- Removed redundancy while preserving technical precision
- Improved flow between concepts
- Maintained all critical technical details (κ, ռ parameters, bias reduction)
- Clarified the relationship between RF and ETR
- Kept all essential citations
- Structured the information more logically
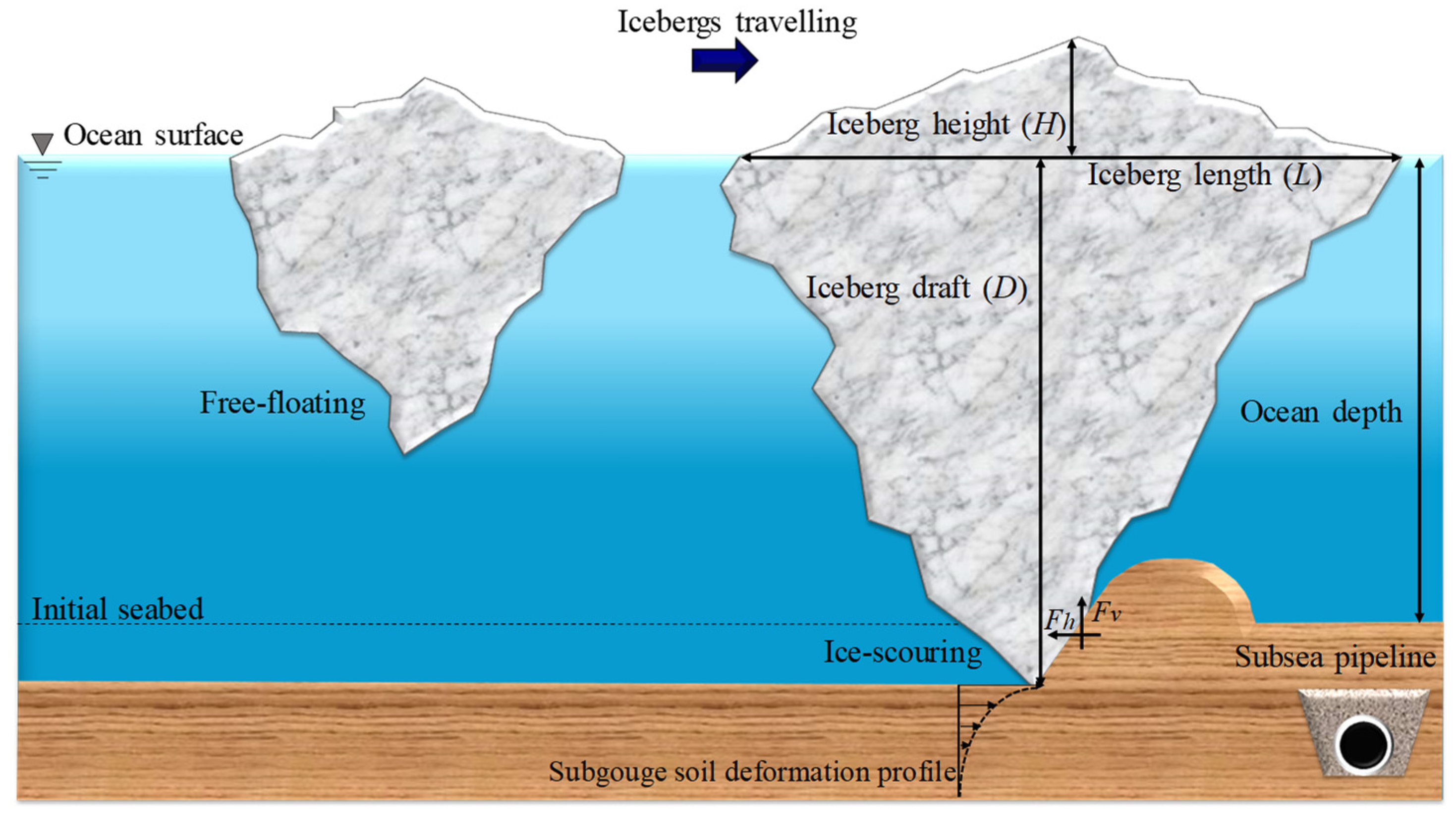
2.2. Iceberg Draft
2.3. Constructed Dataset
2.3.1. Iceberg Draft Dataset
2.3.2. Iceberg–Seabed Interaction
2.4. Goodness of Fitness
3. Results and Discussion
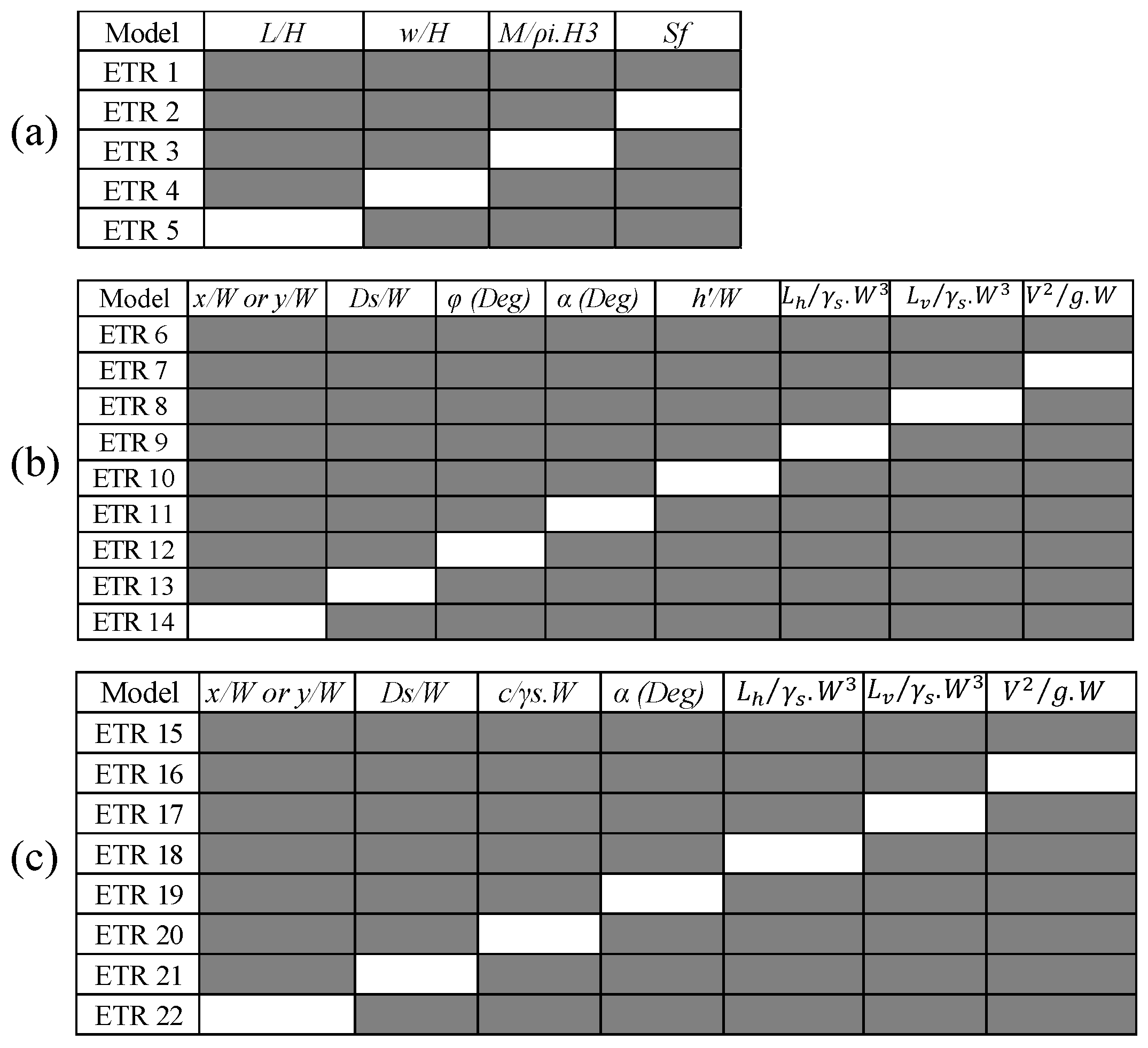
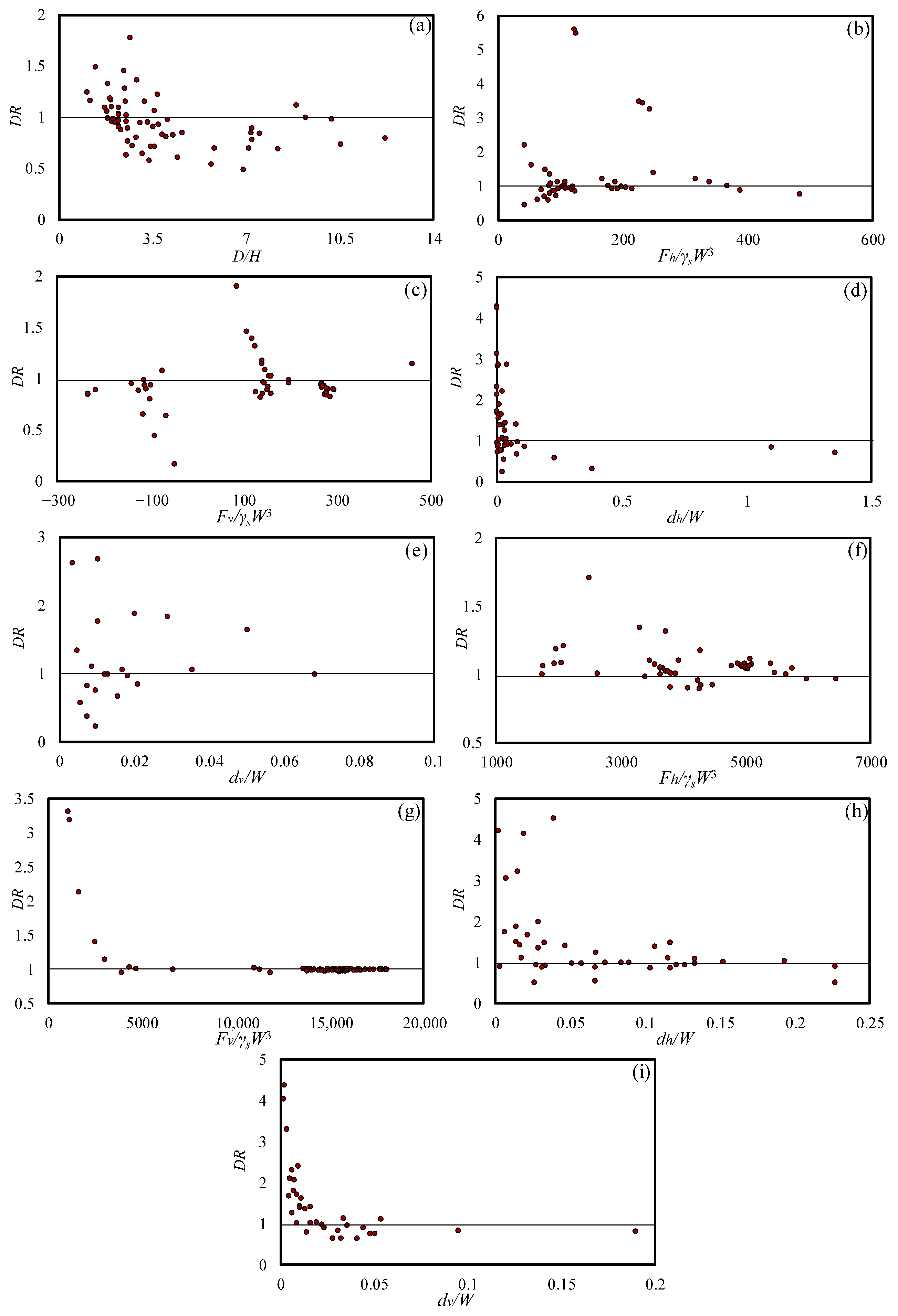
3.1. Sensitivity Analysis
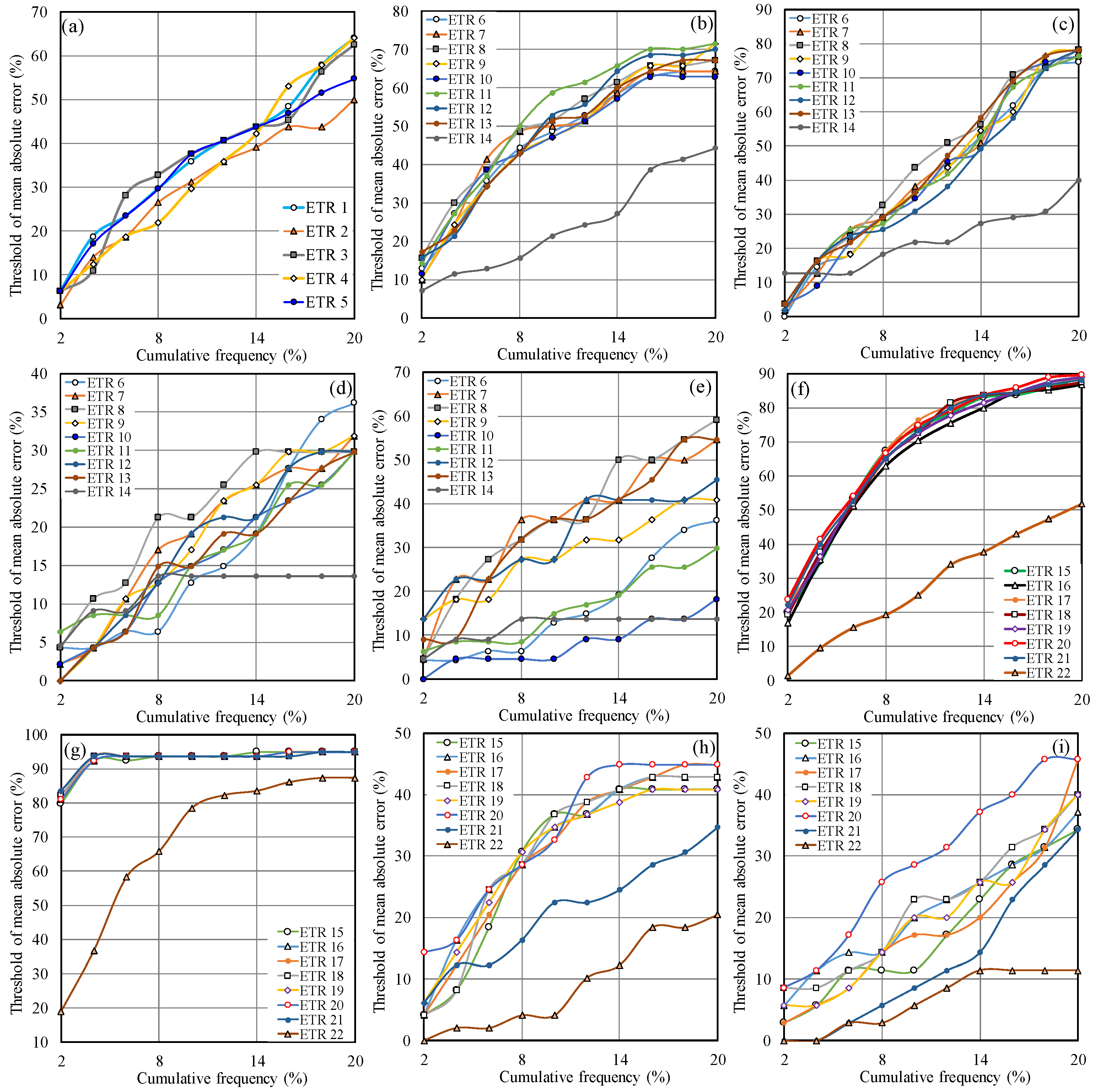
3.2. Uncertainty Analysis
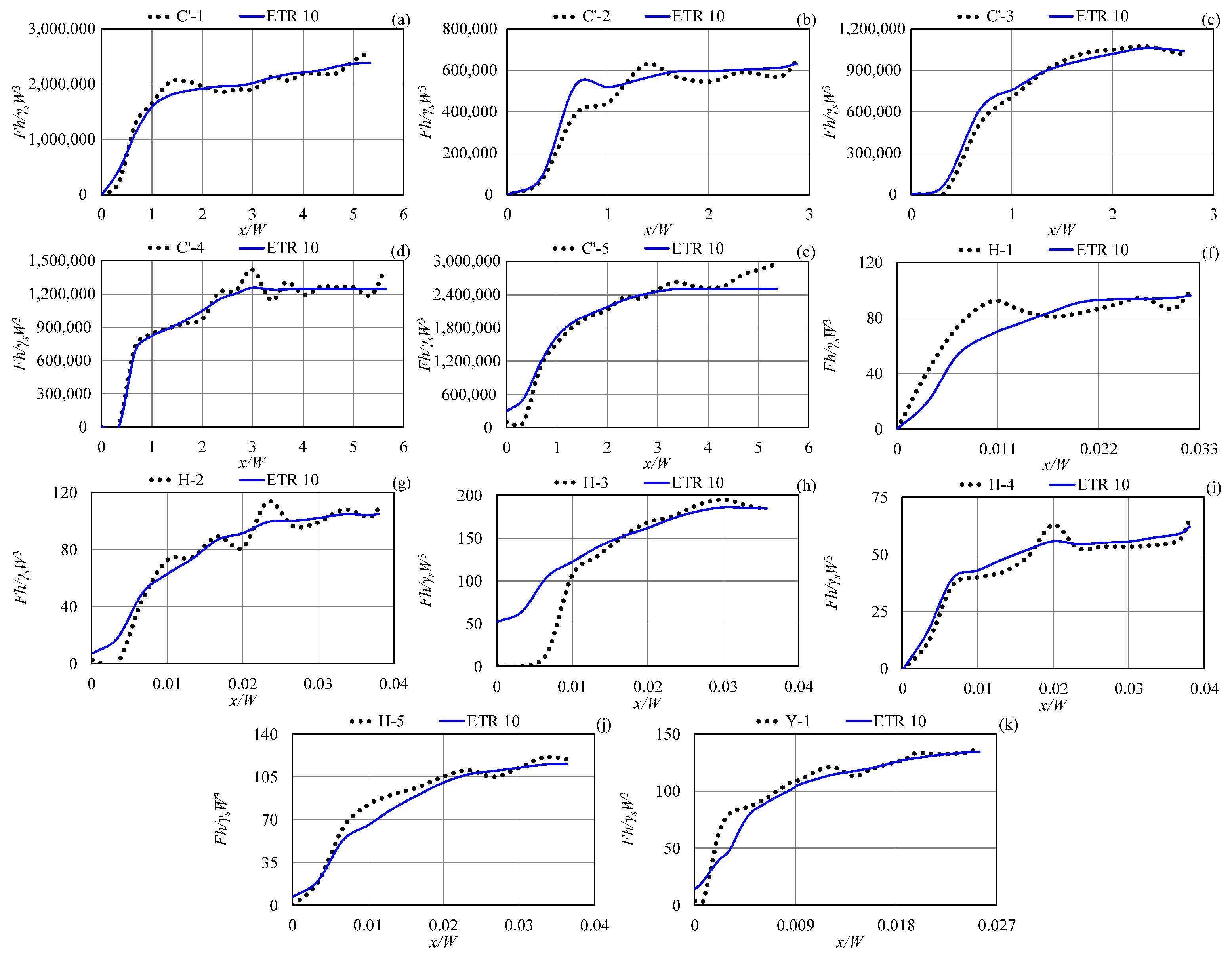
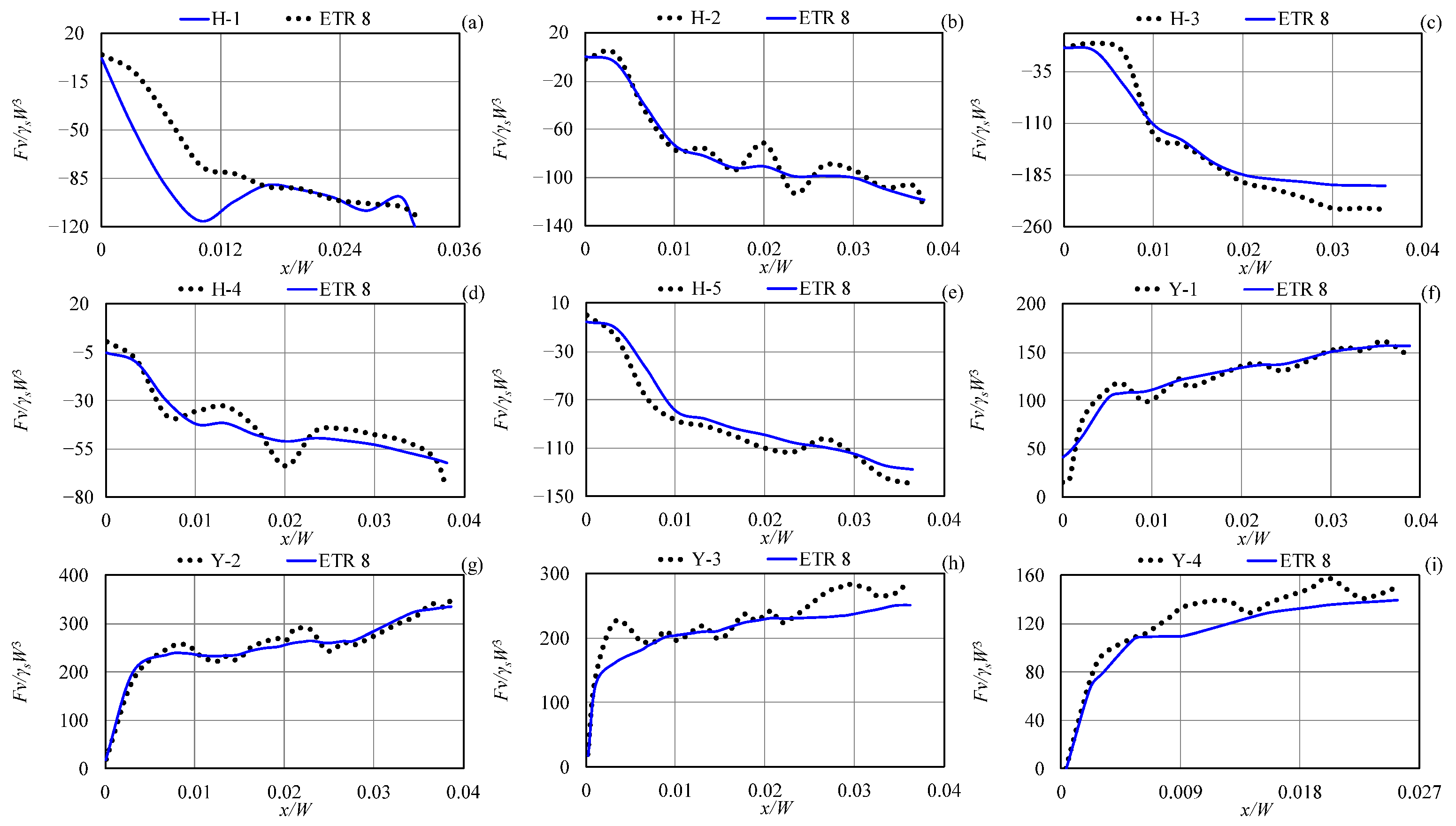
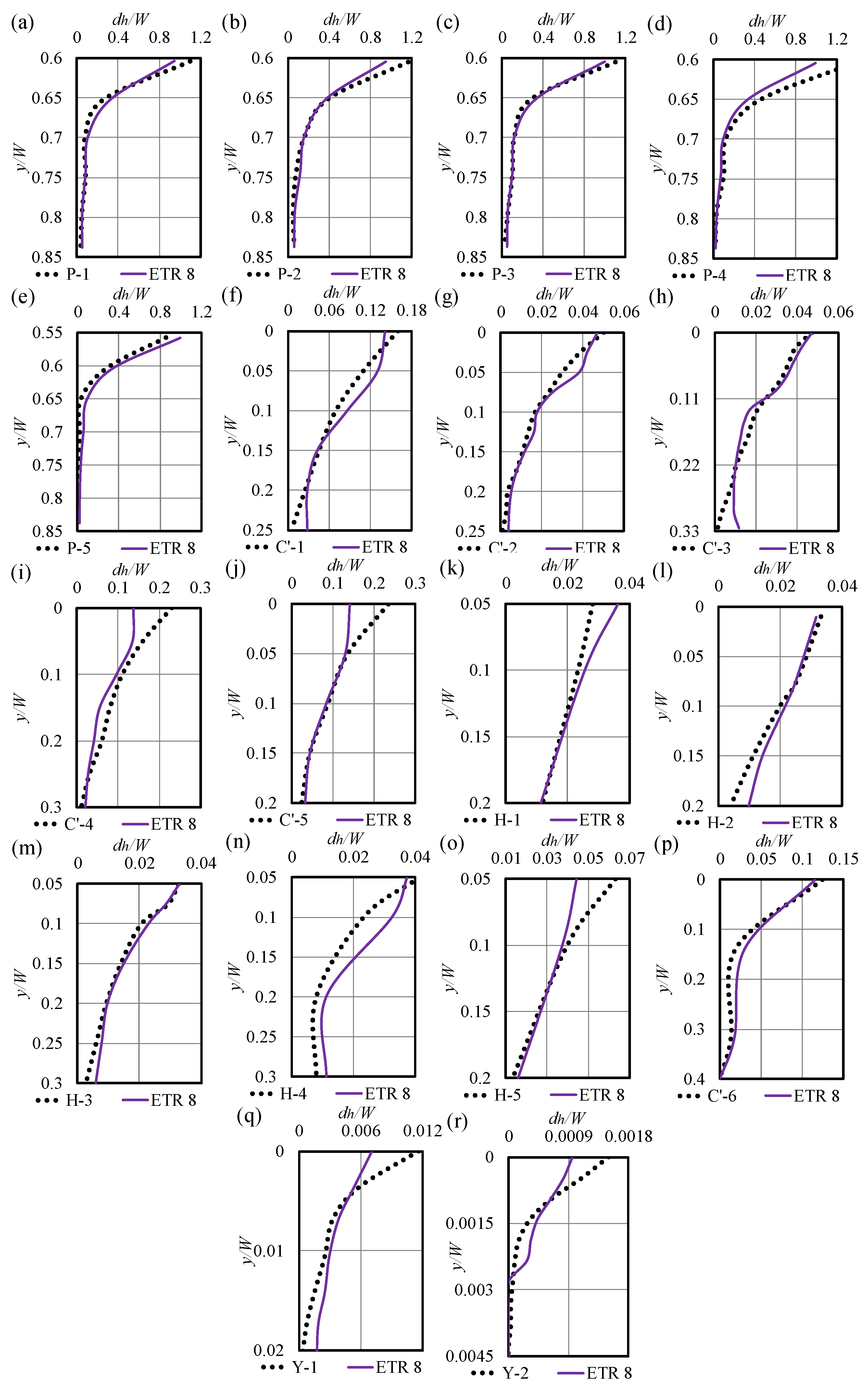
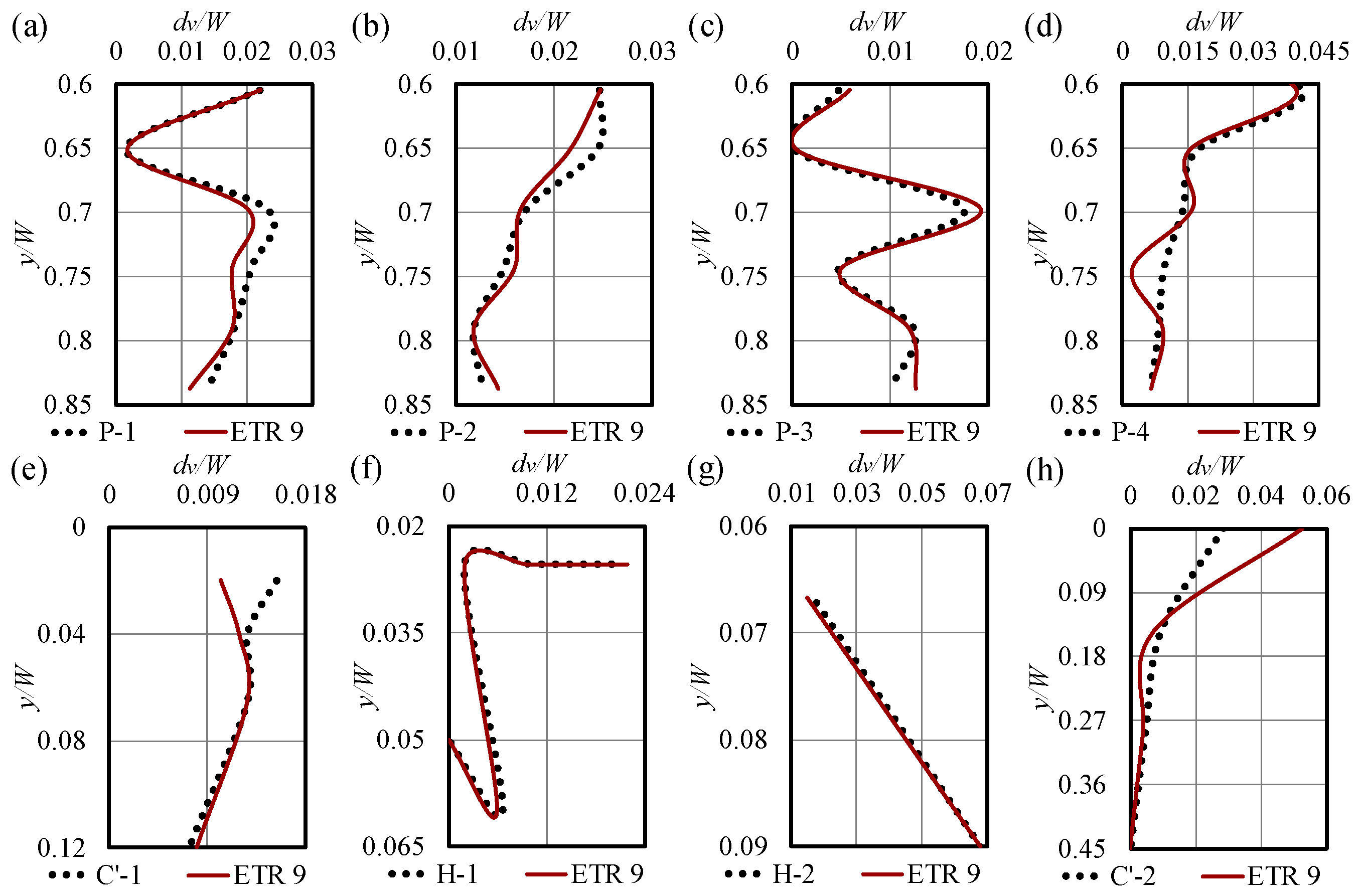
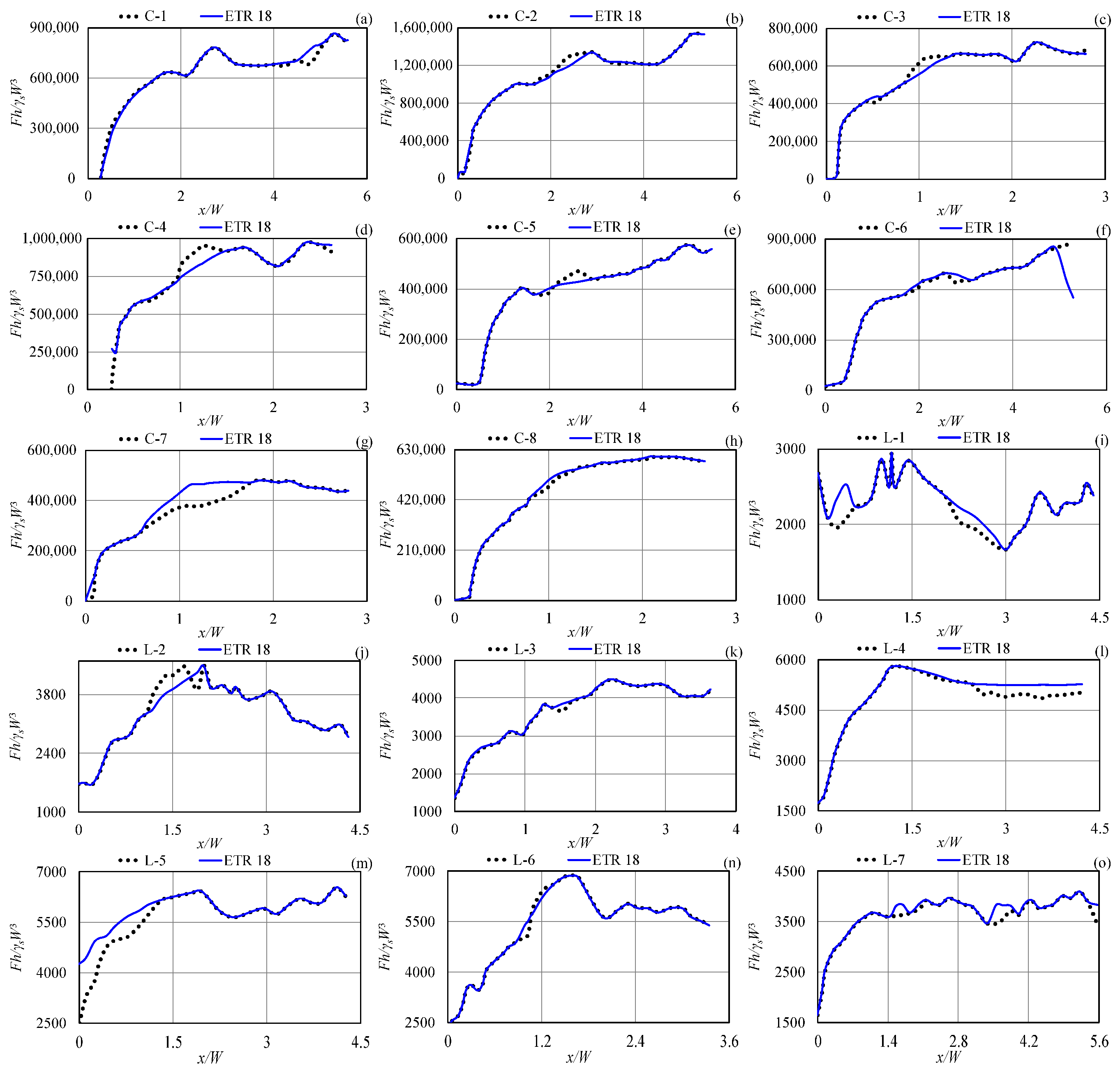
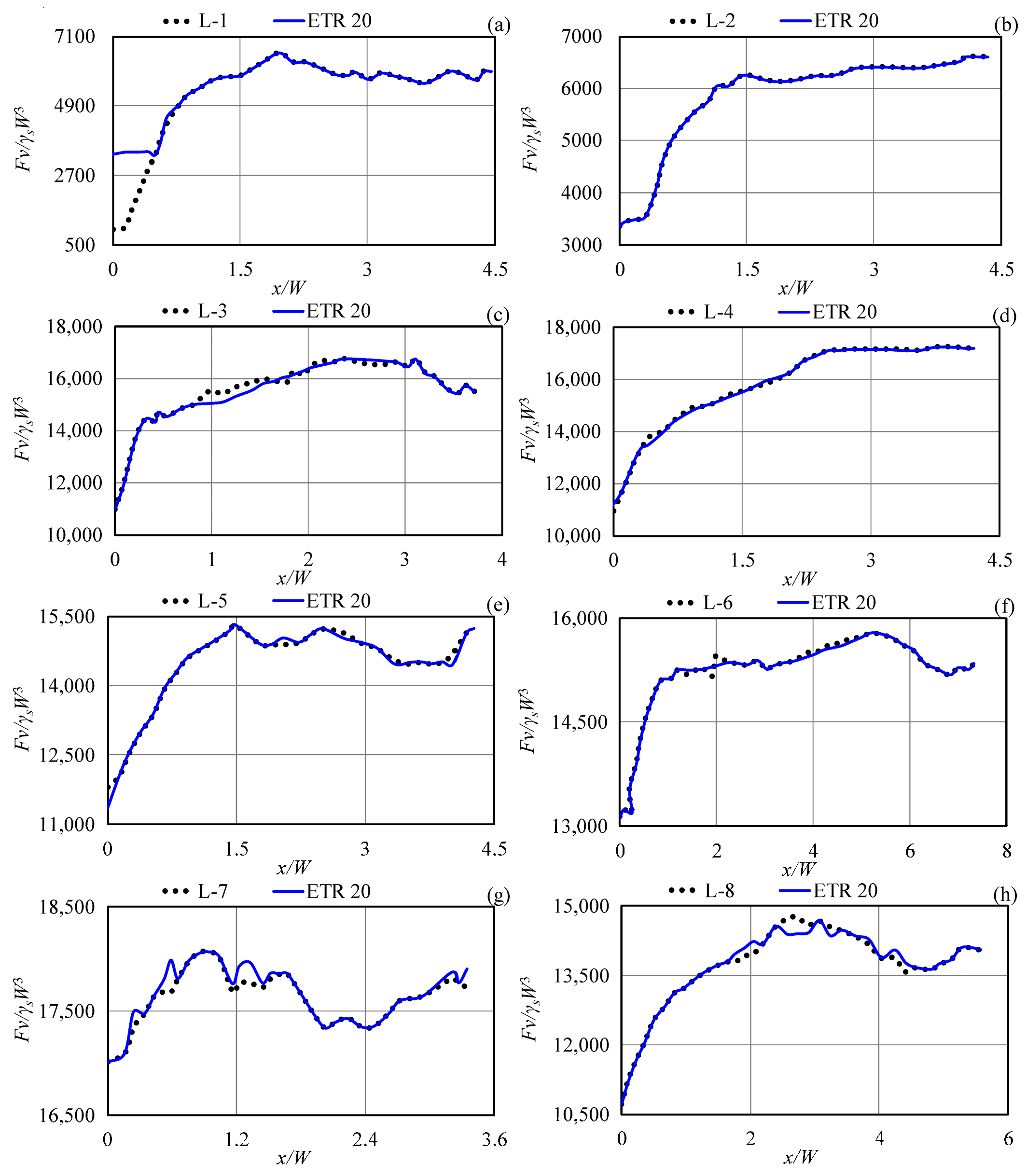
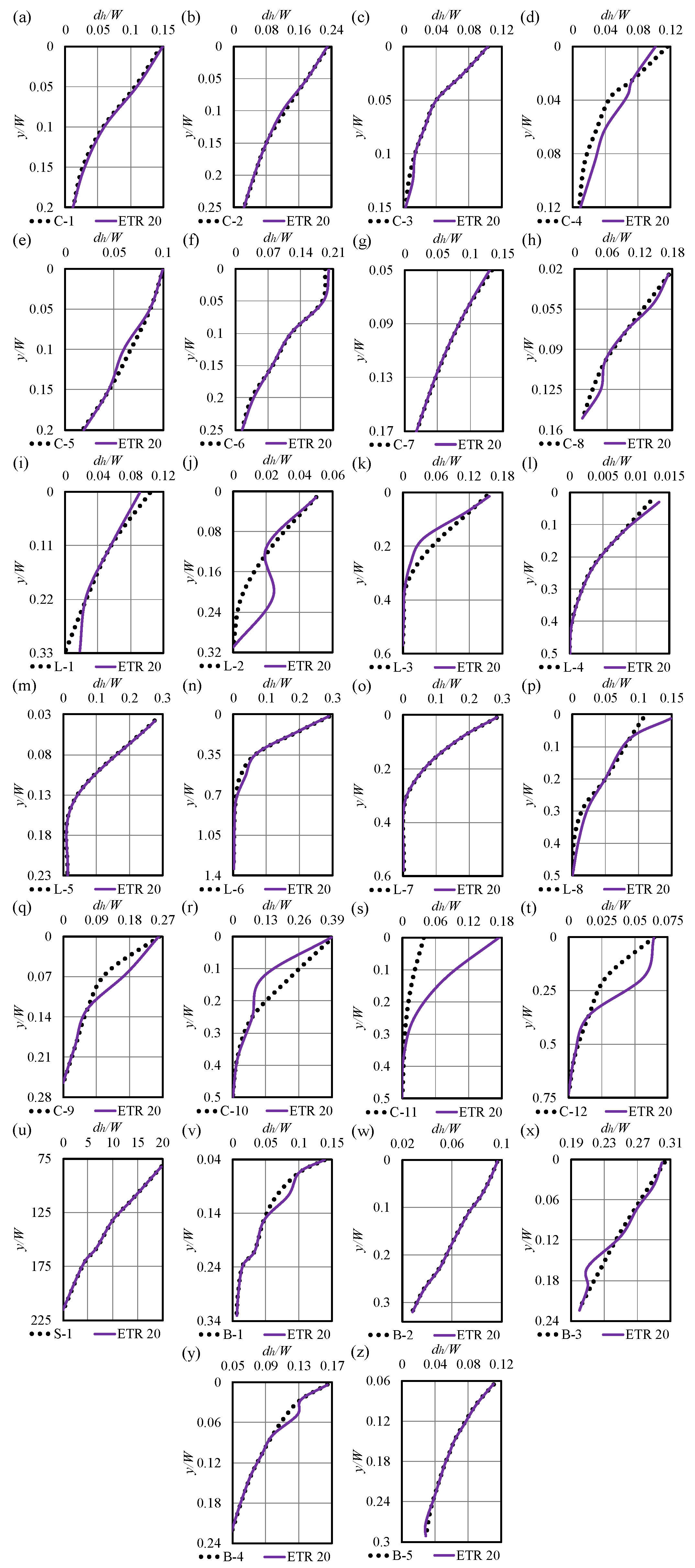
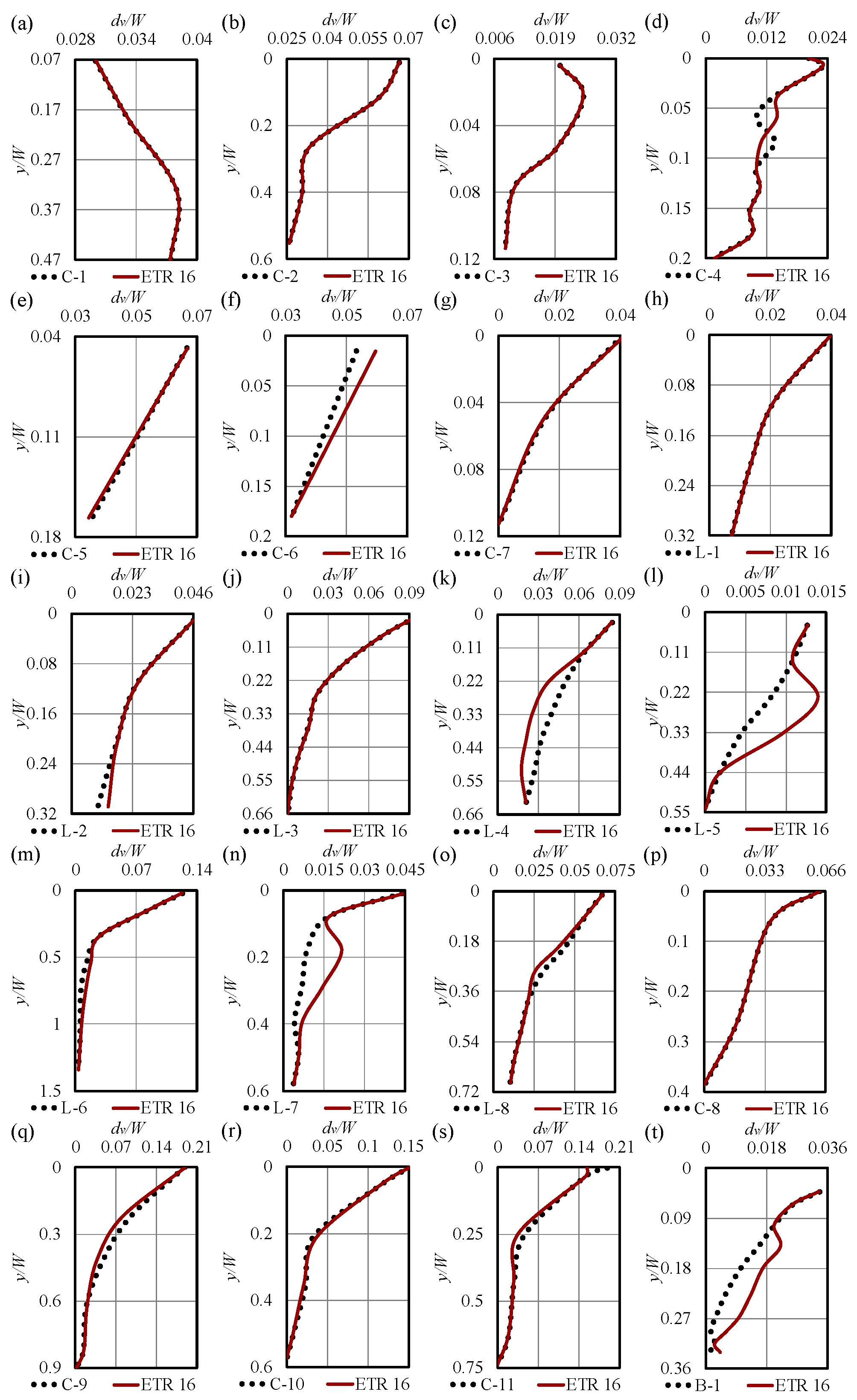
3.3. Superior ETR Models
4. Conclusions
- ETR 1, incorporating all input parameters, delivered the highest accuracy in iceberg draft estimation.
- The iceberg length ratio (L/H) emerged as the most critical factor in predicting iceberg drafts using the ETR algorithm.
- The top-performing ETR models achieved exceptional accuracy, strong correlation, and computational efficiency in estimating subgouge soil parameters across both seabed types.
- For clay seabeds, the best ETR model exhibited a slight underestimation tendency but maintained the narrowest uncertainty range in predicting horizontal deformations.
- Error analysis indicated that approximately one-third of vertical displacements in clay, simulated by the leading ETR model, had errors below 16%.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Blažauskas, N.; Włodarski, M.; Paulauskas, S. Perspectives for Offshore Wind Energy Development in the South-East Baltics. Klaip. Univ. 2013, 1, 1–54. [Google Scholar] [CrossRef]
- Tsvetkova, A. The Role of Supply Vessels in the Development of Offshore Field Projects in Arctic Waters. In Arctic Marine Sustainability Arctic Maritime Businesses and the Resilience of the Marine Environment; Springer: Cham, Switzerland, 2020; pp. 249–273. [Google Scholar]
- Erokhina, O.; Mikolajewicz, U. A New Eulerian Iceberg Module for Climate Studies. J. Adv. Model. Earth Syst. 2024, 16, e2023MS003807. [Google Scholar] [CrossRef]
- Marson, J.M.; Myers, P.G.; Garbo, A.; Copland, L.; Mueller, D. Sea Ice–Driven Iceberg Drift in Baffin Bay. J. Geophys. Res. Oceans 2024, 129, e2023JC020697. [Google Scholar] [CrossRef]
- Allaire, P.E. Stability of Simply Shaped Icebergs. J. Can. Pet. Technol. 1972, 11, PETSOC-72-04-02. [Google Scholar] [CrossRef]
- Robe, R.Q.; Farmer, L.D. Physical Properties of Icebergs. Part I. Height to Draft Ratios of Icebergs. Part II. Mass Estimation of Arctic Icebergs. Coast Guard Res. Dev. Cent. 1976. [Google Scholar]
- Bass, D.W. Stability of Icebergs. Ann. Glaciol. 1980, 1, 43–47. [Google Scholar] [CrossRef]
- Hotzel, I.S.; Miller, J.D. Icebergs: Their Physical Dimensions and the Presentation and Application of Measured Data. Ann. Glaciol. 1983, 4, 116–123. [Google Scholar] [CrossRef]
- C-CORE. Documentation of Iceberg Grounding Events from the 2000 Season; C-CORE Report.: Kanata, ON, Canada, 2001; 01-C10, Revision 0. [Google Scholar]
- Barker, A.; Sayed, M.; Carrieres, T. Determination of Iceberg Draft, Mass and Cross-Sectional Areas. In Proceedings of the 14th International Offshore and Polar Engineering Conference, Toulon, France, 23–28 May 2004. [Google Scholar]
- Dowdeswell, J.A.; Bamber, J.L. Keel Depths of Modern Antarctic Icebergs and Implications for Sea-Floor Scouring in the Geological Record. Mar. Geol. 2007, 243, 120–131. [Google Scholar] [CrossRef]
- Stuckey, P.D. Drift Speed Distribution of Icebergs on the Grand Banks and Influence on Design Loads. Master’s Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, 2008. [Google Scholar]
- McKenna, R.; King, T. Modelling Iceberg Shape, Mass and Draft Changes. In Proceedings of the 20th International Conference on Port and Ocean Engineering under Arctic Conditions, Luleå, Sweden, 9–12 June 2009. [Google Scholar]
- King, T. Iceberg Interaction Frequency Model for Subsea Structures. In Proceedings of the OTC Arctic Technology Conference, Houston, TX, USA, 3–5 December 2012. OTC-23787-MS. [Google Scholar]
- Turnbull, I.D.; Fournier, N.; Stolwijk, M.; Fosnaes, T.; McGonigal, D. Operational Iceberg Drift Forecasting in Northwest Greenland. Cold Reg. Sci. Technol. 2015, 110, 1–18. [Google Scholar] [CrossRef]
- King, T.; Younan, A.; Richard, M.; Bruce, J.; Fuglem, M.; Phillips, R. Subsea Risk Update Using High Resolution Iceberg Profiles. In Proceedings of the Arctic Technology Conference, St. John’s, NL, Canada, 24–26 October 2016. OTC-27358-MS. [Google Scholar]
- Turnbull, I.D.; King, T.; Ralph, F. Development of a New Operational Iceberg Drift Forecast Model for the Grand Banks of Newfoundland. In Proceedings of the OTC Arctic Technology Conference, Houston, TX, USA, 5–7 November 2018. OTC-29109-MS. [Google Scholar]
- McKenna, R.; King, T.; Crocker, G.; Bruneau, S.; German, P. Modelling Iceberg Grounding on the Grand Banks. In Proceedings of the 25th International Conference on Port and Ocean Engineering under Arctic Conditions, Delft, The Netherlands, 9–13 June 2019; pp. 9–19. [Google Scholar]
- Stuckey, P.; Fuglem, M.; Younan, A.; Shayanfar, H.; Huang, Y.; Liu, L.; King, T. Iceberg Load Software Update Using 2019 Iceberg Profile Dataset. In Proceedings of the ASME 2021 40th International Conference on Ocean, Offshore and Arctic Engineering, Glasgow, UK, 21–30 June 2021; Volume 85178. V007T07A018. [Google Scholar]
- Azimi, H.; Mahdianpari, M.; Shiri, H. Determination of Parameters Affecting the Estimation of Iceberg Draft. China Ocean Eng. 2023, 37, 62–72. [Google Scholar] [CrossRef]
- Paulin, M.J. Preliminary Results of Physical Model Tests of Ice Scour; Memorial University of Newfoundland: St. John’s, NL, Canada; Centre for Cold Ocean Resources Engineering (C-CORE): St. John’s, NL, Canada, 1991. [Google Scholar]
- Paulin, M.J. Physical Model Analysis of Iceberg Scour in Dry and Submerged Sand; Memorial University of Newfoundland: St. John’s, NL, Canada, 1992. [Google Scholar]
- Lach, P.R. Centrifuge Modelling of Large Soil Deformation due to Ice Scour; Memorial University of Newfoundland: St. John’s, NL, Canada, 1996. [Google Scholar]
- Woodworth-Lynas, C.; Nixon, D.; Phillips, R.; Palmer, A. Subgouge Deformations and the Security of Arctic Marine Pipelines. In Proceedings of the OTC Offshore Technology Conference, Houston, TX, USA, 6–9 May 1996. OTC-8222-MS. [Google Scholar]
- C-CORE. Phase 3: Centrifuge Modelling of Ice Keel Scour; C-CORE Report.: St. John’s, NL, Canada, 1995; p. 95-Cl2. [Google Scholar]
- C-CORE. PRISE Phase 3c: Extreme LEE Gouge Event-Modeling and Interpretation; C-CORE Report.: St. John’s, NL, Canada, 1996; p. 96-C32. [Google Scholar]
- Hynes, F. Centrifuge Modelling of Ice Scour in Sand; Memorial University of Newfoundland: St. John’s, NL, Canada, 1996. [Google Scholar]
- Schoonbeek, I.S.; van Kesteren, W.G.; Xin, M.X.; Been, K. Slip Line Field Solutions as an Approach to Understand Ice Subgouge Deformation Patterns. In Proceedings of the 16th International Offshore and Polar Engineering Conference, San Francisco, CA, USA, 28 May–2 June 2006. ISOPE-I-06-289. [Google Scholar]
- Been, K.; Sancio, R.B.; Ahrabian, D.; van Kesteren, W.; Croasdale, K.; Palmer, A. Subscour Displacement in Clays from Physical Model Tests. In Proceedings of the IPC2008 7th International Pipeline Conference, Calgary, Alberta, Canada, 29 September–3 October 2008; Volume 48609, pp. 239–245. [Google Scholar]
- Yang, W. Physical Modeling of Subgouge Deformations in Sand; Memorial University of Newfoundland: St. John’s, NL, Canada, 2009. [Google Scholar]
- Arnau Almirall, S. Ice Gouging in Sand and the Associated Rate Effects; University of Aberdeen: Aberdeen, UK, 2017. [Google Scholar]
- Kioka, S.D.; Kubouchi, A.; Saeki, H. Training and Generalization of Experimental Values of Ice Scour Event by a Neural-Network. In Proceedings of the 13th International Offshore and Polar Engineering Conference, Honolulu, HA, USA, 25–30 May 2003. ISOPE-I-03-081. [Google Scholar]
- Kioka, S.; Kubouchi, A.; Ishikawa, R.; Saeki, H. Application of the Mechanical Model for Ice Scour to a Field Site and Simulation Method of Scour Depths. In Proceedings of the 14th International Offshore and Polar Engineering Conference, Toulon, France, 23–28 May 2004. ISOPE-I-04-107. [Google Scholar]
- Azimi, H.; Shiri, H. Dimensionless Groups of Parameters Governing the Ice-Seabed Interaction Process. J. Offshore Mech. Arctic Eng. 2020, 142, 051601. [Google Scholar] [CrossRef]
- Azimi, H.; Shiri, H. Ice-Seabed Interaction Analysis in Sand Using a Gene Expression Programming-Based Approach. Appl. Ocean Res. 2020, 98, 102120. [Google Scholar] [CrossRef]
- Azimi, H.; Shiri, H. Assessment of Ice-Seabed Interaction Process in Clay Using Extreme Learning Machine. Int. J. Offshore Polar Eng. 2021, 31, 411–420. [Google Scholar] [CrossRef]
- Azimi, H.; Shiri, H.; Zendehboudi, S. Ice-Seabed Interaction Modeling in Clay by Using Evolutionary Design of Generalized Group Method of Data Handling. Cold Reg. Sci. Technol. 2022, 193, 103426. [Google Scholar] [CrossRef]
- Azimi, H.; Shiri, H.; Mahdianpari, M. Simulation of Subgouge Sand Deformations Using Robust Machine Learning Algorithms. In Proceedings of the OTC Offshore Technology Conference, Houston, TX, USA, 2–5 May 2022. OTC-31937-MS. [Google Scholar]
- Azimi, H.; Shiri, H.; Mahdianpari, M. Iceberg-Seabed Interaction Evaluation in Clay Seabed Using Tree-Based Machine Learning Algorithms. J. Pipeline Sci. Eng. 2022, 2, 100075. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely Randomized Trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Hammed, M.M.; AlOmar, M.K.; Khaleel, F.; Al-Ansari, N. An Extra Tree Regression Model for Discharge Coefficient Prediction: Novel, Practical Applications in the Hydraulic Sector and Future Research Directions. Math. Probl. Eng. 2021. [Google Scholar] [CrossRef]
- El-Tahan, M.; El-Tahan, H.; Courage, D.; Mitten, P. Documentation of Iceberg Groundings; Environmental Studies Revolving Funds report; Environmental Studies Revolving Funds: Ottawa, ON, Canada, 1985; Volume 7. [Google Scholar]
- Woodworth-Lynas, C.M.T.; Simms, A.; Rendell, C.M. Iceberg Grounding and Scouring on the Labrador Continental Shelf. Cold Reg. Sci. Technol. 1985, 10, 163–186. [Google Scholar] [CrossRef]
- Løset, S.; Carstens, T. Sea Ice and Iceberg Observations in the Western Barents Sea in 1987. Cold Reg. Sci. Technol. 1996, 24, 323–340. [Google Scholar] [CrossRef]
- McKenna, R. Development of Iceberg Shape Characterization for Risk to Grand Banks Installations; PERD/CHC Report; National Research Council Canada: Ottawa, ON, Canada, 2004; p. 20473.
- Sonnichsen, G.; Hundert, T.; Myers, R.; Pocklington, P. Documentation of Recent Iceberg Grounding Events and a Comparison with Older Events of Known Age; Environmental Studies Research Funds: Ottawa, ON, Canada, 2006; Volume 157.
- McGuire, P.; Younan, A.; Wang, Y.; Bruce, J.; Gandi, M.; King, T.; Keeping, K.; Regular, K. Smart Iceberg Management System–Rapid Iceberg Profiling System. In Proceedings of the OTC Arctic Technology Conference, St. John’s, NL, Canada,, 24–26 October 2016. OTC-27473-MS. [Google Scholar]
- Younan, A.; Ralph, F.; Ralph, T.; Bruce, J. Overview of the 2012 Iceberg Profiling Program. In Proceedings of the OTC Arctic Technology Conference, St. John’s, NL, Canada, 24–26 October 2016. OTC-27469-MS. [Google Scholar]
- Talimi, V.; Ni, S.; Qiu, W.; Fuglem, M.; MacNeill, A.; Younan, A. Investigation of Iceberg Hydrodynamics. In Proceedings of the OTC Arctic Technology Conference, St. John’s, NL, Canada, 24–26 October 2016. OTC-27493-MS. [Google Scholar]
- Zhou, M. Underwater Iceberg Profiling and Motion Estimation Using Autonomous Underwater Vehicles. Ph.D. Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, 2017. [Google Scholar]
| Hyperparameter | Value |
|---|---|
| min_samples_leaf | 1 |
| min_samples_split | 8 |
| max_features | 1 |
| random_state | None |
| max_depth | None |
| min_impurity_decrease | 0 |
| max_leaf_nodes | None |
| min_weight_fraction_leaf | 0 |
| ccp_alpha | 0 |
| Research | Number of Case Studies |
|---|---|
| El-Tahan et al. [42] | 38 cases |
| Woodworth-Lynas et al. [43] | One case |
| Løset and Carstens [44] | 52 cases |
| Barker et al. [8] | 14 cases |
| McKenna [45] | Two cases |
| Sonnichsen et al. [46] | Nine cases |
| Turnbull et al. [13] | Two cases |
| McGuire et al. [47] | Eight cases |
| Younan et al. [48] | 29 cases |
| Talimi et al. [49] | One case |
| Zhou [50] | Three cases |
| Turnbull et al. [15] | Two cases |
| Parameter | Model | R | RMSE | AIC | CRM | WI |
|---|---|---|---|---|---|---|
| Draft | ETR 1 | 0.920 | 1.081 | 10.165 | 0.101 | 0.943 |
| ETR 2 | 0.906 | 1.150 | 9.882 | 0.087 | 0.933 | |
| ETR 3 | 0.917 | 1.109 | 8.888 | 0.108 | 0.940 | |
| ETR 4 | 0.923 | 1.161 | 10.138 | 0.107 | 0.926 | |
| ETR 5 | 0.887 | 1.234 | 11.837 | 0.102 | 0.926 | |
| Sand-Horizontal reaction force | ETR 6 | 0.985 | 154,280.556 | 379.182 | −0.030 | 0.992 |
| ETR 7 | 0.983 | 167,992.998 | 379.770 | −0.035 | 0.991 | |
| ETR 8 | 0.982 | 168,842.614 | 379.924 | −0.033 | 0.991 | |
| ETR 9 | 0.983 | 165,178.002 | 379.257 | −0.035 | 0.991 | |
| ETR 10 | 0.994 | 99,805.670 | 363.941 | 0.004 | 0.997 | |
| ETR 11 | 0.982 | 171,349.321 | 380.372 | −0.040 | 0.991 | |
| ETR 12 | 0.982 | 169,286.105 | 380.003 | −0.038 | 0.991 | |
| ETR 13 | 0.986 | 150,379.199 | 376.403 | −0.033 | 0.993 | |
| ETR 14 | 0.880 | 439,271.280 | 408.991 | −0.058 | 0.938 | |
| Sand-Vertical reaction force | ETR 6 | 0.970 | 46.348 | 107.632 | −0.059 | 0.983 |
| ETR 7 | 0.973 | 44.818 | 104.830 | −0.066 | 0.984 | |
| ETR 8 | 0.974 | 43.953 | 104.364 | −0.079 | 0.985 | |
| ETR 9 | 0.972 | 45.123 | 104.992 | −0.059 | 0.984 | |
| ETR 10 | 0.973 | 44.460 | 104.638 | −0.065 | 0.984 | |
| ETR 11 | 0.972 | 45.189 | 105.027 | −0.062 | 0.984 | |
| ETR 12 | 0.972 | 44.911 | 104.880 | −0.064 | 0.984 | |
| ETR 13 | 0.972 | 45.027 | 104.941 | −0.061 | 0.984 | |
| ETR 14 | 0.926 | 70.017 | 115.486 | −0.044 | 0.959 | |
| Sand-Horizontal deformation | ETR 6 | 0.739 | 0.187 | −18.256 | −0.094 | 0.849 |
| ETR 7 | 0.980 | 0.073 | −39.551 | 0.180 | 0.974 | |
| ETR 8 | 0.984 | 0.072 | −39.618 | 0.193 | 0.973 | |
| ETR 9 | 0.982 | 0.079 | −37.901 | 0.197 | 0.968 | |
| ETR 10 | 0.981 | 0.079 | −37.872 | 0.211 | 0.968 | |
| ETR 11 | 0.981 | 0.078 | −38.078 | 0.199 | 0.968 | |
| ETR 12 | 0.982 | 0.074 | −39.172 | 0.204 | 0.972 | |
| ETR 13 | 0.981 | 0.074 | −39.015 | 0.179 | 0.972 | |
| ETR 14 | 0.278 | 0.245 | −14.719 | 0.416 | 0.307 | |
| Sand-Vertical deformation | ETR 6 | 0.828 | 0.009 | −28.827 | −0.001 | 0.913 |
| ETR 7 | 0.826 | 0.009 | −30.733 | −0.012 | 0.912 | |
| ETR 8 | 0.818 | 0.009 | −30.560 | 0.147 | 0.879 | |
| ETR 9 | 0.905 | 0.011 | −29.462 | −0.227 | 0.916 | |
| ETR 10 | 0.818 | 0.011 | −29.495 | −0.313 | 0.849 | |
| ETR 11 | 0.828 | 0.010 | −30.027 | −0.230 | 0.897 | |
| ETR 12 | 0.828 | 0.009 | −30.699 | −0.089 | 0.911 | |
| ETR 13 | 0.828 | 0.009 | −30.776 | 0.056 | 0.912 | |
| ETR 14 | 0.277 | 0.016 | −25.467 | 0.329 | 0.207 | |
| Clay-Horizontal reaction force | ETR 15 | 0.988 | 57,795.569 | 656.856 | 0.011 | 0.994 |
| ETR 16 | 0.988 | 57,521.716 | 656.577 | 0.004 | 0.994 | |
| ETR 17 | 0.988 | 56,914.968 | 655.956 | 0.006 | 0.994 | |
| ETR 18 | 0.989 | 54,630.154 | 653.553 | −0.003 | 0.995 | |
| ETR 19 | 0.988 | 58,744.465 | 657.811 | 0.011 | 0.994 | |
| ETR 20 | 0.988 | 56,624.436 | 655.656 | 0.012 | 0.994 | |
| ETR 21 | 0.989 | 55,408.261 | 654.383 | 0.010 | 0.994 | |
| ETR 22 | 0.794 | 227,462.840 | 737.183 | −0.020 | 0.899 | |
| Clay-Vertical reaction force | ETR 15 | 0.995 | 475.567 | 225.500 | −0.005 | 0.997 |
| ETR 16 | 0.996 | 478.300 | 225.696 | −0.005 | 0.997 | |
| ETR 17 | 0.996 | 478.067 | 225.680 | −0.004 | 0.997 | |
| ETR 18 | 0.996 | 473.733 | 225.367 | −0.006 | 0.997 | |
| ETR 19 | 0.996 | 476.092 | 225.538 | −0.008 | 0.997 | |
| ETR 20 | 0.996 | 472.658 | 225.289 | −0.006 | 0.997 | |
| ETR 21 | 0.996 | 473.307 | 225.336 | −0.006 | 0.997 | |
| ETR 22 | 0.951 | 1512.420 | 265.194 | 0.002 | 0.959 | |
| Clay-Horizontal deformation | ETR 15 | 0.999 | 0.091 | −36.939 | 0.007 | 0.999 |
| ETR 16 | 0.999 | 0.043 | −53.137 | −0.032 | 0.999 | |
| ETR 17 | 0.999 | 0.046 | −51.624 | −0.043 | 0.999 | |
| ETR 18 | 0.999 | 0.066 | −43.745 | −0.057 | 0.999 | |
| ETR 19 | 0.999 | 0.038 | −55.679 | −0.027 | 0.999 | |
| ETR 20 | 0.999 | 0.037 | −56.264 | −0.036 | 0.999 | |
| ETR 21 | 0.999 | 0.057 | −46.891 | −0.045 | 0.999 | |
| ETR 22 | 0.999 | 0.529 | 0.463 | 0.221 | 0.973 | |
| Clay-Vertical deformation | ETR 15 | 0.963 | 0.012 | −53.633 | 0.098 | 0.962 |
| ETR 16 | 0.983 | 0.009 | −57.192 | 0.035 | 0.977 | |
| ETR 17 | 0.974 | 0.011 | −54.854 | 0.122 | 0.968 | |
| ETR 18 | 0.971 | 0.011 | −54.597 | 0.118 | 0.967 | |
| ETR 19 | 0.920 | 0.015 | −49.616 | 0.137 | 0.933 | |
| ETR 20 | 0.980 | 0.010 | −56.382 | 0.073 | 0.974 | |
| ETR 21 | 0.936 | 0.014 | −51.091 | 0.138 | 0.946 | |
| ETR 22 | 0.432 | 0.033 | −37.753 | −0.417 | 0.521 |
| Parameter | Model | Mean | StDev | 95%CI | WUB | |
|---|---|---|---|---|---|---|
| Draft | ETR 1 | 0.39 | 1.016 | 0.136 | 0.644 | ±0.254 |
| ETR 2 | 0.335 | 1.109 | 0.059 | 0.612 | ±0.277 | |
| ETR 3 | 0.415 | 1.037 | 0.156 | 0.674 | ±0.259 | |
| ETR 4 | 0.411 | 1.094 | 0.137 | 0.684 | ±0.274 | |
| ETR 5 | 0.395 | 1.178 | 0.1 | 0.689 | ±0.295 | |
| Sand-Horizontal reaction force | ETR 6 | 7010.948 | 94,635.970 | −16,823 | 30,845 | ±23,834 |
| ETR 7 | 6948.011 | 98,479.210 | −17,854 | 31,750 | ±24,802 | |
| ETR 8 | 8940.125 | 92,871.530 | −14,449 | 32,330 | ±23,389.500 | |
| ETR 9 | 7094.299 | 95,202.510 | −16,882 | 31,071 | ±23,976.500 | |
| ETR 10 | 12,830.91 | 85,894.21 | −8801 | 34,436 | ±21,618.500 | |
| ETR 11 | 5328.068 | 97,348.02 | −19,189 | 29,845 | ±24,517 | |
| ETR 12 | 6038.568 | 97,902.03 | −18,618 | 30,695 | ±24,656.500 | |
| ETR 13 | 4120.492 | 98,780.39 | −20,757 | 28,998 | ±24,877.500 | |
| ETR 14 | 38,833.970 | 238,386.700 | −21,203 | 98,871 | ±60,037 | |
| Sand-Vertical reaction force | ETR 6 | 0.453 | 33.726 | −8.940 | 9.840 | ±9.390 |
| ETR 7 | −0.586 | 32.718 | −9.690 | 8.520 | ±9.105 | |
| ETR 8 | −2.060 | 31.235 | −10.760 | 6.640 | ±8.700 | |
| ETR 9 | 0.195 | 32.835 | −8.950 | 9.340 | ±9.145 | |
| ETR 10 | −0.472 | 32.171 | −9.430 | 8.480 | ±8.955 | |
| ETR 11 | −0.167 | 32.783 | −9.290 | 8.960 | ±9.125 | |
| ETR 12 | −0.278 | 32.495 | −9.330 | 8.770 | ±9.050 | |
| ETR 13 | 0.087 | 32.607 | −8.990 | 9.160 | ±9.075 | |
| ETR 14 | 5.049 | 56.605 | −10.710 | 20.810 | ±15.760 | |
| Sand-Horizontal deformation | ETR 6 | 0.019 | 0.084 | −0.007 | 0.045 | ±0.026 |
| ETR 7 | 0.016 | 0.074 | −0.007 | 0.040 | ±0.024 | |
| ETR 8 | 0.018 | 0.074 | −0.006 | 0.041 | ±0.024 | |
| ETR 9 | 0.018 | 0.081 | −0.007 | 0.043 | ±0.025 | |
| ETR 10 | 0.019 | 0.081 | −0.006 | 0.045 | ±0.026 | |
| ETR 11 | 0.018 | 0.080 | −0.007 | 0.043 | ±0.025 | |
| ETR 12 | 0.018 | 0.075 | −0.005 | 0.042 | ±0.024 | |
| ETR 13 | 0.016 | 0.077 | −0.008 | 0.040 | ±0.024 | |
| ETR 14 | 0.038 | 0.258 | −0.042 | 0.119 | ±0.081 | |
| Sand-vertical deformation | ETR 6 | 0.001 | 0.008 | −0.002 | 0.005 | ±0.004 |
| ETR 7 | 0.001 | 0.008 | −0.003 | 0.005 | ±0.004 | |
| ETR 8 | 0.003 | 0.008 | −0.0003 | 0.007 | ±0.004 | |
| ETR 9 | −0.004 | 0.010 | −0.009 | 0.0007 | ±0.005 | |
| ETR 10 | −0.004 | 0.008 | −0.008 | −0.0006 | ±0.004 | |
| ETR 11 | −0.003 | 0.008 | −0.006 | 0.0008 | ±0.003 | |
| ETR 12 | −0.0003 | 0.008 | −0.004 | 0.003 | ±0.004 | |
| ETR 13 | 0.002 | 0.008 | −0.001 | 0.006 | ±0.004 | |
| ETR 14 | 0.006 | 0.015 | −0.001 | 0.013 | ±0.007 | |
| Clay-Horizontal reaction force | ETR 15 | 6936.124 | 53,473.540 | −2271 | 16,143 | ±9207 |
| ETR 16 | 4131.597 | 53,311.010 | −5048 | 13,311 | ±9179.500 | |
| ETR 17 | 4786.232 | 52,530.400 | −4259 | 13,831 | ±9045 | |
| ETR 18 | 1655.058 | 50,082.490 | −6968 | 10,278 | ±8623 | |
| ETR 19 | 6782.686 | 54,190.590 | −2548 | 16,113 | ±9330.500 | |
| ETR 20 | 7050.163 | 52,443.450 | −1980 | 16,080 | ±9030 | |
| ETR 21 | 6556.398 | 50,604.960 | −2157 | 15,270 | ±8713.500 | |
| ETR 22 | 8330.371 | 202,623.600 | −26,558 | 43,219 | ±34,888.500 | |
| Clay-Vertical reaction force | ETR 15 | −71.925 | 473.101 | −177.900 | 34 | ±105.950 |
| ETR 16 | −66.530 | 476.6775 | −173.300 | 42.200 | ±107.750 | |
| ETR 17 | −55.842 | 477.829 | −162.900 | 51.200 | ±107.050 | |
| ETR 18 | −78.119 | 470.233 | −183.400 | 27.200 | ±105.300 | |
| ETR 19 | −106.604 | 466.960 | −211.200 | −2 | ±104.600 | |
| ETR 20 | −86.388 | 467.666 | −191.100 | 18.400 | ±104.750 | |
| ETR 21 | −80.068 | 469.467 | −185.200 | 25.100 | ±105.150 | |
| ETR 22 | 35.192 | 1521.672 | −306 | 376 | ±341 | |
| Clay-Horizontal deformation | ETR 15 | 0.007 | 0.098 | −0.023 | 0.038 | ±0.031 |
| ETR 16 | −0.007 | 0.040 | −0.019 | 0.006 | ±0.012 | |
| ETR 17 | −0.012 | 0.045 | −0.026 | 0.002 | ±0.014 | |
| ETR 18 | −0.017 | 0.068 | −0.039 | 0.004 | ±0.022 | |
| ETR 19 | −0.006 | 0.037 | −0.017 | 0.005 | ±0.011 | |
| ETR 20 | −0.009 | 0.034 | −0.019 | 0.002 | ±0.011 | |
| ETR 21 | −0.011 | 0.056 | −0.028 | 0.006 | ±0.017 | |
| ETR 22 | 0.092 | 0.570 | −0.085 | 0.270 | ±0.177 | |
| Clay-Vertical deformation | ETR 15 | 0.003 | 0.012 | −0.001 | 0.007 | ±0.004 |
| ETR 16 | 0.001 | 0.009 | −0.002 | 0.004 | ±0.003 | |
| ETR 17 | 0.003 | 0.010 | −0.0003 | 0.007 | ±0.004 | |
| ETR 18 | 0.003 | 0.011 | −0.0005 | 0.007 | ±0.004 | |
| ETR 19 | 0.004 | 0.015 | −0.001 | 0.009 | ±0.005 | |
| ETR 20 | 0.002 | 0.010 | −0.001 | 0.006 | ±0.004 | |
| ETR 21 | 0.004 | 0.013 | −0.0009 | 0.008 | ±0.004 | |
| ETR 22 | −0.011 | 0.032 | −0.022 | −0.0003 | ±0.011 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azimi, H.; Shiri, H. Extra Tree Regression Algorithm for Simulation of Iceberg Draft and Subgouge Soil Characteristics. Water 2025, 17, 2425. https://doi.org/10.3390/w17162425
Azimi H, Shiri H. Extra Tree Regression Algorithm for Simulation of Iceberg Draft and Subgouge Soil Characteristics. Water. 2025; 17(16):2425. https://doi.org/10.3390/w17162425
Chicago/Turabian StyleAzimi, Hamed, and Hodjat Shiri. 2025. "Extra Tree Regression Algorithm for Simulation of Iceberg Draft and Subgouge Soil Characteristics" Water 17, no. 16: 2425. https://doi.org/10.3390/w17162425
APA StyleAzimi, H., & Shiri, H. (2025). Extra Tree Regression Algorithm for Simulation of Iceberg Draft and Subgouge Soil Characteristics. Water, 17(16), 2425. https://doi.org/10.3390/w17162425







