1. Introduction
In recent years, the government has introduced the concept that ‘green mountains and clear waters are as valuable as mountains of gold and silver,’ highlighting the significance of a comprehensive green transformation in socio-economic development and the coordinated progress of ecological protection and economic growth. As imbalances in regional economic development and mismatches in the spatiotemporal distribution of water resources intensify in China, inter-basin water diversion projects have become a key strategic measure for ensuring national water security and optimizing spatial resource allocation [
1]. However, while inter-basin water diversion alleviates water resource pressures in water-receiving areas, it also exerts profound impacts on the ecology and land use patterns of water-sourcing areas, exacerbating developmental imbalances [
2]. As ecological civilization construction and high-quality development continue to advance, how to establish a scientific, fair, and sustainable ecological compensation mechanism has become a core issue for achieving regional coordinated development [
3].
The ecological compensation system is rooted in public goods theory [
4], the internalization of externalities [
5], and the principle of payment for ecosystem services (PES) [
6], aiming to monetize the ecological sacrifices made by donor regions and allocate the associated costs among beneficiary regions. Calculating basin compensation standards is crucial to establishing a functional ecological compensation mechanism. The challenge lies in designing standards that are not only scientifically accurate, reflecting ecological costs and benefits, but also fair, accounting for the fiscal disparities among regions, and operational, ensuring they are acceptable to both parties and adaptable over time. However, existing valuation methods often fail to meet these criteria. Cost-based methods estimate compensation amounts by aggregating direct protection expenditures [
7,
8] or opportunity costs [
9,
10,
11] in contributor regions, but they overlook the fiscal constraints of beneficiary regions and the economic value of abandoned downstream ecosystem services. From the perspective of ecosystem service value, Costanza et al. [
12] first proposed a global estimation method for ecosystem service value, advancing research on the monetization of ecological compensation standards. Xie Gaodi et al. [
13] improved and revised the equivalence factors based on China’s national conditions, enhancing regional applicability. While this method can quantify ecosystem service values, it fails to effectively account for local consumption spillovers, leading to inflated compensation standards. Additionally, econometric analyses of willingness to pay (WTP) and willingness to accept (WTA) [
14,
15] comprehensively consider the payer’s willingness to pay and the recipient’s willingness to accept, making compensation standards more acceptable. Zhao Jingjing et al. [
16] used water footprint estimation to assess the ecosystem services consumed by the protected area in the Dawan River basin. Wang Jiefang et al. [
17] quantified the upper and lower limits of water pollution compensation standards between upstream and downstream regions from the perspective of pollution rights transfer. While the introduction of quantitative compensation models has made ecological compensation calculations more reasonable, they are often based on a single perspective of the cost or benefit calculation and rely on static adjustment models, making them difficult to adapt to the multidimensional complexity of inter-basin water diversion projects. Li Hengchen et al. [
18] used price negotiation to shift compensation standards from “single quantification” to “negotiated bargaining,” but regional differences in allocation rely on subjective weighting, failing to achieve a scientific integration of subjective and objective weights. To address these issues, some scholars have attempted to introduce more complex efficiency measurement tools and priority identification methods. Ma Jun et al. [
19] used a four-stage DEA model to measure the efficiency of ecological compensation in the Yangtze River Economic Belt, considering the differentiated allocation of compensation funds. Sun Fuhua et al. [
20] introduced ECPS to quantify the ecological compensation priorities of various districts in Yangzhou, the water-source area of the East Route of the South-to-North Water Diversion Project. However, overall, the current construction of ecological compensation standards still largely relies on static assessment models, lacking dynamic adjustment mechanisms and pathways for coordinating diverse interests [
21]. This makes it difficult to adapt to the reality of cross-basin water resource allocation when diverse stakeholders and complex ecosystems coexist. There is an urgent need to establish an ecological compensation standard system that combines multidimensionality, fairness, and dynamic adaptability to shift cross-basin water resource allocation toward a more scientific, coordinated, and sustainable direction.
To address the above issues, this study conducts the following work: First, the direct and indirect costs of losses are calculated to determine the cost of losses in the water-source area. Next, the equivalent factor method is used to calculate the value of the ecosystem services obtained by the water-receiving area from the perspective of revenue. This determines the scope of negotiation between the water-source and -receiving areas. Second, the Rubinstein bargaining model is used to analyze ecological compensation quotas under different scenarios and explore the dynamic bargaining process between the two parties. Third, the AHP-entropy method is used to reasonably allocate compensation amounts, considering the differences in economic development levels, ecology, and water resources between the water-receiving areas.
In summary, the potential contributions of this paper are as follows: First, it establishes a theoretical and practical ecological compensation standard optimization mechanism to effectively address the issue of inflated compensation standards caused by regional value spillover effects, thereby enhancing the accuracy of ecological service value assessment. Second, it overcomes the limitations of existing research by introducing a price-bargaining mechanism to enhance the operability and acceptability of the compensation system, thereby strengthening the practicality of compensation standards. Third, by analyzing the heterogeneity of water resources’ ecological and economic levels in water-receiving regions, this study explores ecological compensation calculation methods using regional differentiation, breaking through the fairness bottleneck of traditional “equal allocation” configurations. This provides methodological support and decision-making references for the scientific design, dynamic adjustment, and regional collaborative governance of ecological compensation systems in inter-basin water diversion projects.
2. Materials and Methods
2.1. Study Area
The South-to-North Water Diversion Project is one of China’s major inter-basin water resource allocation projects, with a total length of 1467 km. The first phase of the Eastern Route is a key component of the overall plan for the South-to-North Water Diversion Project, aimed at addressing water shortages in Shandong Province. The first phase of the Eastern Route draws water from the Jiangdu Water Conservancy Hub in Yangzhou, Jiangsu Province, at the lower reaches of the Yangtze River, and distributes it via two routes. One branch flows northward across the Yellow River to northern Shandong Province; the other branch flows eastward to the Jiaodong Peninsula. The water diversion volume for 2023 is 1.48 billion cubic metres. This study selected Yangzhou City (32°15′–33°25′ N, 119°01′–119°54′ E) as the water-source area, which is located in the lower reaches of the Yangtze River in eastern China. Considering the water diversion volume of the East Route of the South-to-North Water Diversion Project in 2023 and the ratio of water diversion volume to local water resources, six cities—Jinan and Qingdao on the Jiaodong Line, and Dongying, Dezhou, Liaocheng, and Binzhou on the Lubei Line—were selected as the primary water-recipient areas (
Figure 1).
2.2. Cost–Benefit Calculation
2.2.1. Cost Method
Currently, the academic community generally adopts a cost-based approach to calculating ecological compensation. The calculation of ecological compensation for water-source areas generally includes both direct and indirect costs [
22]. In Equation (1), C is the total cost, while
is the direct cost, which mainly includes the costs of water conservancy project construction, water pollution treatment, forestry development, and natural ecological restoration [
23].
is the indirect cost, which refers to opportunity costs arising from the lost development opportunities associated with the ecological protection of water resources in source areas, primarily affecting primary and secondary industries. These costs are generally measured by comparing the differences in industrial development speeds before and after ecological protection in water-source areas between the water-source area and a reference area [
24].
This study draws on scholars’ research on opportunity costs in river basins [
25] and selects cities with comparable geographical locations and economic development foundations to the water-source area as references for cost estimation.
where
is the loss-of-opportunity cost per capita in the primary industry in the kth year after the opening of the water transfer project in the water-source area;
and
represent the per capita added value of the primary industry before and after the water diversion project was launched, respectively;
is the growth rate of the primary industry in the kth year after the opening of the water transfer project in the water-source area;
is the parameter for the loss-of-opportunity cost;
and
represent the average annual growth rate of the primary industry in the water-source area before and after the water diversion project was launched, respectively;
and
represent the average annual growth rate of the primary industry in the reference area before and after the water diversion project was launched, respectively;
is the number of permanent residents in the kth year of the water area;
is the adjustment coefficient, which is expressed by the ratio of the financial revenue of the kth year of the water area to the GDP of the year.
The calculation of opportunity costs in the secondary industry is the same as above.
2.2.2. Equivalent Factor Method
Referring to the ecosystem service value equivalent factor method of Xie Gao Di, the net profit of ecological food production of farmland in unit area was taken as the ecosystem service value of one standard equivalent factor. The calculation of grain crops is mainly based on data on the planting area, yield, and price of the three major grain crops: rice, wheat, and corn [
26].
The formula is as follows. D denotes the value of ecosystem services for 1 standard equivalent factor (CNY/
); k is the crop species;
is the area planted with the kth crop (
);
is the average price of the kth crop (CNY/t);
is the unit yield of the kth crop (t/
).
In Formula (6),
is the value of services per unit of ecosystem service function i corresponding to the jth land type (CNY/
);
is the equivalent factor of ecosystem service function i corresponding to the jth land type.
In Equation (7), is the area of the jth land type (); ESV is the total ecosystem service value (CNY).
In actual water diversion projects, the results are adjusted to take into account the impact of water quantity and water quality in the water-source area on ecological service value.
- (1)
Water quality correction factor
Based on Zhang Yihua et al.’s research on water volume correction [
27], in order to ensure that the ecological compensation standards are scientifically and reasonably calculated, a water volume correction coefficient
is introduced, as shown in the following formula:
where
is the annual water transfer from the receiving area (billion cubic metres);
is the total water resources of the water-source area (billion cubic metres).
- (2)
Water quality correction factor is represented by .
Water quality directly affects water use efficiency. Based on the six different water quality classifications (Class I–V and sub-Class V) specified in GB 3838-2002 “Surface Water Environmental Quality Standards,” and referencing the water quality coefficient values assigned by Zhou Shenbei et al. [
28], if the water quality is to reach or surpass Class III, k = 1; if the water quality reaches IV, k = 0.8; if the water quality reaches V, k = 0.55; if the water quality is poor, k = 0. The final water quality correction factor can be calculated based on the water quality conditions and their proportions.
In Formula (9), is the water quality correction coefficient; is the corresponding value for different water quality conditions; is the proportion of water volume corresponding to this type of water quality.
- (3)
Adjustment factor L
The ecological and social value of water resources is dynamic and subject to change. People’s willingness to pay for the ecosystem compensation costs associated with inter-basin water transfers is correlated with their economic living standards and tends to increase as living standards improve. This recognition process follows an S-shaped curve, which can be modelled using R. Pearl’s S-shaped growth curve [
29,
30]. To avoid setting compensation standards too high and exceeding the payment capacity of the water-receiving areas, an adjustment coefficient is introduced to modify the standards. The formula is as follows:
where L is the adjustment coefficient of the value of water ecosystem services;
is the Engel’s coefficient of the study area in the current year; t is the social development coefficient.
In summary, the corrected ecosystem service value of the water area can be calculated as follows:
- (4)
Water footprint method
Since the benefits to the water-receiving areas derive from the spillover service value of upstream ecosystems, the ecosystem service value, calculated using the equivalent factor method, includes the portion consumed by the water source. Considering that water-source areas are both providers of ecosystem services and beneficiaries of ecological protection, the traditional equivalent factor method does not distinguish between local consumption and spillover value. This paper refers to the research of Tu Z et al. [
31,
32] and uses the water footprint method to correct the value of ecosystem services. The formula is as follows:
In Formula (13), CH is the actual ecosystem service value of the water-source area, WDi is the water demand, calculated based on the water footprint method, and WSi is the amount of water resources available in the basin.
2.3. Price Negotiation Standards Based on the Rubinstein Bargaining Model Game
Rubinstein used the method of fully informed, dynamic, cooperative games to construct a bargaining model between two participants who take turns bidding to divide a cake. By simulating the process of the two parties taking turns bidding and bargaining indefinitely under fully informed conditions, the negotiation range gradually narrowed throughout the game. Ultimately, the perfect equilibrium result of the subgame was obtained, proving the existence of a unique equilibrium solution.
When applied to ecological compensation negotiations for inter-basin water transfers, the model calculates the minimum compensation that the water-source area should accept based on the cost principle, denoted as
, and the maximum compensation that can be obtained based on the benefit principle, denoted as
. The negotiation process between the water-source area and the water-recipient area essentially involves allocating the net present value of costs and benefits, i.e.,
. The final outcome depends on the bargaining power of the negotiating parties [
33]. The discount factor is considered an important factor influencing the bargaining power of both parties, indicating patience levels and significantly impacting negotiation outcomes. A higher discount factor implies that participants are more willing to wait, potentially leading to more rounds of negotiations [
34]. Let
and
represent the discount factors for the water-source area and water-recipient area, respectively, with values ranging from 0 to 1.
- (1)
The basic premises for establishing the model include the following points:
Premise 1: Both parties to the negotiation are rational brokers who seek to maximize their own net profits during the negotiation process.
Premise 2: Both parties have complete information and sufficient patience to engage in indefinite negotiations.
Premise 3: Since environmental protection measures in the water-source area are voluntary, the water-source area has relative initiative in the negotiation process and makes the first offer.
- (2)
The gaming process:
Assume that the water district’s allocated share in the first round of offers is x, and the share received by the receiving district is (1 − x). If the receiving district rejects the proposal, the game proceeds to the second round of the game, where the receiving district makes an offer, assuming that the share it receives from its own allocation in the offer is y, and the share the water district receives is (1 − y). Since the game is infinite and symmetric, in equilibrium, the outcome of the game from the second round should have the same structure as the outcome of the game from the first round. Considering the discount factor, the solution accepted by the water district in the first round and the solution accepted in the second round should be equivalent after discounting, i.e., x = 1 − y = , which reduces to the optimal solution of , The share of compensation received by the water district is . Reducing the compensation share to the interval [,] yields the equilibrium optimal solution .
2.4. Hierarchical Analysis (AHP) and Entropy Approach
AHP assigns different weights to influencing factors through subjective evaluation, quantifying the importance of each factor. The entropy value rule extracts objective information using the internal dispersion of sample data. The combination of the two can achieve subjective–objective unity of the weight allocation [
35], significantly improving the scientific nature and rationality of the distribution of ecological compensation.
2.4.1. Hierarchical Analysis to Determine Subjective Weights
American scholar Saaty T. L. proposed the AHP [
36], which involves breaking down factors related to decision-making into target levels, criteria levels, and indicator levels and developing a complete set of mathematical calculation tools. This method is characterized by its systematic, flexible, and concise features. Its core steps are as follows [
37]:
- (1)
Constructing a Hierarchical Model: The target level in this study is the evaluation of ecological compensation standards. The criterion layer includes several influencing factors, which are summarized as the ecological and economic development level of water resources. In the study of Lv Zhixian et al. [
38] on the ecological compensation standard of Xiangjiang River Basin, per capita GDP, per capita tertiary industry gross output value, per capita industrial gross product, resident population, and per capita primary industry gross output value are selected as the relevant indicator factors of economic development level. Compensation in the receiving area was related to the residents’ willingness to pay. Based on the above, the hierarchy is constructed as shown in
Table 1:
- (2)
Constructing a Judgement Matrix
A judgement matrix
is formed by comparing factors
through expert scoring and determining their importance values.
In the judgement matrix, indicates the relative importance of the indicator compared to the indicator. It is common to use a scale of 1–9 to indicate the results of a comparison between the two, where the larger the number, the more important the number corresponding to the risk factor.
- (3)
Weight calculation and consistency test
The matrix is first normalized by columns, summed by rows and normalized again to obtain the weight vector. Then, the vector Xi = (x1, x2, x3, ……, xn)
T is normalized:
The obtained
W = (
W1,
W2,
W3, ……,
Wn)
T are the eigenvectors of the judgement matrix and then the maximum eigenvalue λ of the judgement matrix is calculated as follows:
where
is the eigenvector and
.
Finally, a consistency test of the judgement matrix was conducted:
where
is the scalar value of the matrix consistency test.
where
is a random consistency index, according to the judgement criterion. If
= 0, the judgement matrix has consistency; the smaller
is, the greater the consistency; when
0.1, this means that it passes the consistency test; when
0.1, it does not pass the consistency test, and the judgement matrix-related element values need to be adjusted and a re-examination conducted, until it passes.
2.4.2. Entropy Approach to Determine Objective Weights
Since the traditional AHP belongs to the subjective weight calculation method, there are subjective human factors when comparing the relative importance of indicators, the entropy weight method, first introduced by Shannon, is used to improve the indicator weights of AHP [
39]. The process is shown below:
Positive indicators (larger values are better):
Negative indicators (smaller values are better):
where
is the evaluation data of the jth evaluation indicator normalized by the ith evaluator, x
ij is the original evaluation data of the jth evaluation indicator by the ith evaluator, min x
ij is the minimum value in the original data, and max x
j and min x
(j) are the maximum and minimum values in the jth evaluation indicator, respectively.
- (2)
Calculate the entropy value and coefficient of variation:
The weight of the th evaluator under the th indicator , where n is the number of evaluators. Entropy value of the jth indicator .
This leads to the coefficient of variation for the jth indicator .
- (3)
Calculate the portfolio weights:
The weight of the jth indicator , where p is the number of indicators.
The combined weight of the jth indicator is .
2.5. Data Sources
Based on CNLUCC, Landsat 8 remote sensing images were used, and ArcGIS software version 10.2 was used to pre-process and decipher the remote sensing images and raster data to derive the land use- and land cover-type data for the major water sources in Yangzhou City and the six major water-receiving areas in Shandong Province in 2023. The sown area and production data of the three major grain crops (wheat, rice, and corn) were obtained from the 2023–2024 Statistical Yearbook of each city, and the prices were obtained from the 2023 National Compendium of Agricultural Product Cost-Effectiveness Data. The economic profile and national income of provinces and cities are from provincial and municipal statistical yearbooks. Data on water supply for the South-to-North Water Diversion are from the Water Resources Bulletin of Jiangsu Province and the Water Resources Bulletin of Shandong Province, 2023, and water quality is from the monitoring reports of the General Administration of Environmental Monitoring of China (GAMEMC), the yearbook of the South-to-North Water Diversion Project, and the website.
3. Results
3.1. Cost Accounting
The relevant data of Yangzhou Municipal Water Resources Bureau, Ecology and Environment Bureau, Natural Resources and Planning Bureau were referred to, as well as the public report of Yangzhou Municipal Government on water pollution control and ecological protection and construction in 2023, and the National Development and Reform Commission on the use of special funds for the South-to-North Diversion of Water East Route Project in 2023. The ecological protection of Yangzhou City mainly focuses on the protection of the water quality of water sources, as well as pollution prevention and control, and includes the integration of mountains, water, forests, fields, lakes, grasses and sands, rivers, and lake wetlands, and water ecological restoration projects that are carried out throughout the year. River desilting, ecological slope protection, and the interception of sewage projects are also implemented to protect the water quality of the water transmission trunk line. The direct cost of ecological protection is about CNY 578 million (
Table 2).
When calculating opportunity costs, the reference region is usually chosen as an area with a similar geographical location and economic level as the study region [
40]. After reviewing statistical yearbooks of cities in Jiangsu Province and making comparisons, we determined that Nantong City most closely resembles Yangzhou City in terms of industrial structure and per capita GDP. Additionally, Yangzhou City is located in the central part of Jiangsu Province, and like Nantong City, it belongs to the middle reaches of the Yangtze River region in Jiangsu Province. After comprehensively considering geographical location, industrial structure, per capita GDP, and policy background, we selected Nantong City as the reference region (
Table 3). In order to exclude the specificity of single-year data, the industrial growth rate data of the two cities in the three years before and three years after the water transfer project were taken as the average value. Two periods were selected: before the implementation of the water diversion project (2010–2013) and after its implementation (2020–2023). According to the local statistical yearbook, the main economic and industrial data of Yangzhou and Nantong City for the periods 2010–2013 and 2020–2023 can be calculated.
The differences in the annual per capita growth rates of the primary and secondary industries between the two regions were calculated (
Figure 2). The results show that from 2010 to 2013, the annual average growth rates of the primary and secondary industries per capita in Yangzhou were 9.70% and 11.77%, respectively, while from 2020 to 2023, they decreased to 3.90% and 9.34%, respectively; during the same period, the corresponding growth rates in Nantong were 8.91% and 11.07% for the primary industry, and 5.00% and 7.27% for the secondary industry. According to Equation (4), the average annual growth rates of the added value of the primary and secondary industries lost by Yangzhou City after water diversion were 1.89% and 1.37%, respectively. Combining the actual growth rates of Yangzhou City’s primary and secondary industries in 2023 (3.7% and 6.6%), substituting into Equations (2) and (3) yields opportunity costs of CNY 26 million and CNY 608 million, respectively, resulting in a total indirect cost of CNY 634 million. In summary, based on Equation (1), the ecological compensation amount for Yangzhou City calculated using the cost method is approximately CNY 1.212 billion.
3.2. Accounting for Earnings
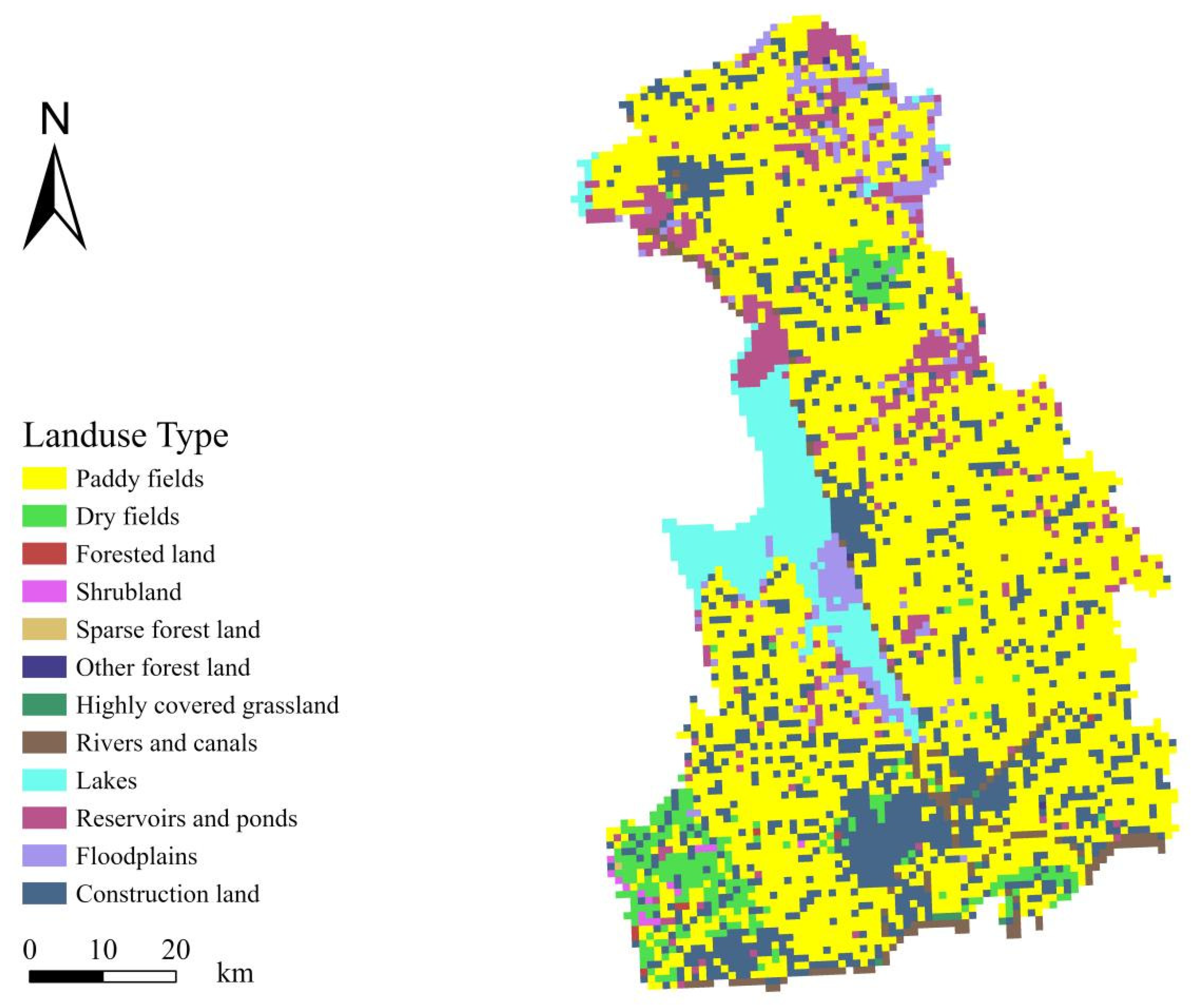
Using ArcGIS software, remote sensing imagery and land cover raster data were preprocessed and interpreted to extract the distribution of major land use types in Yangzhou City for 2023 (
Figure 3). Combined with data on the planting area and yield of grain crops, the total ecosystem service value corresponding to different land use types was calculated using the ecosystem service value calculation model based on Equations (5)–(7), amounting to CNY 44.54 billion (
Table 4). According to the public data of the China South-to-North Water Diversion Group and the water resources bulletin of Shandong Province, the amount of water to transferred via the South-to-North Water Diversion Project in six cities of Shandong Province in 2023 was 688 million cubic metres. The total water resources of Yangzhou city for the whole year comprised 3.038 billion cubic metres, and the water quantity coefficient adjustment
can be calculated as 0.28 according to Equation (8). Data from the 2023 Yangzhou City Annual Environmental Quality Bulletin shows that the ratio of the 47 sections of the provincial examination (including the national examination) in Yangzhou city for the whole year is 95.7% of the excellent III, the ratio of the excellent II is 42.4%, and there is no inferior V class water body. Jiangdu Hub, in 2023, used real-time water quality monitoring to ensure that the transmission of water quality was stable, obtaining three south-to-north water transfer cross-section water quality results of up to III, according to Equation (9) when using the water quality correction coefficient
as an approximation for 1. In terms of social development, the per capita food expenditure in Yangzhou City in 2023 was CNY 8751, accounting for 28.9% of per capita total consumption expenditure. Based on this, the Engel coefficient is 0.289, corresponding to a social development coefficient of 0.45 based on Equation (10). Further calculations yield the water ecosystem service value adjustment coefficient L of 0.61, based on Equation (11). Finally, the dynamically adjusted ecological service value of Yangzhou City estimated using Equation (12) is approximately CNY 6.17 billion.
In order to make the compensation rate more reasonable, the water footprint method was used to exclude the impact of own consumption on ecological compensation. The measurement of water footprint usually focuses on the four aspects of re-agriculture, industry, residential life, and ecological maintenance [
41]. Among them, the water consumption of agricultural production is the core influence factor, and various agricultural products contain a large amount of virtual water. The Penman–Monteith formula calculates reference crop evapotranspiration based on meteorological data, and the CROPWAT 8.0 model outputs an accurate water consumption sequence by integrating crop coefficients with soil moisture correction factors. The calculation of virtual water content per unit product can be obtained from the standard Penman formula and the CROPWAT model [
42]. The total amount of industrial virtual water consumption in Yangzhou City is 305 million cubic metres, but the local consumption accounts for 92% of the total, with weak spatial mobility, the spillover portion is only 0.24 billion cubic metres, the indirect consumption of water resources in the whole life cycle of the product generally accounts for less than 5% of the total water footprint, and the amount of virtual water can be negligible, and can be replaced by the actual water consumption of industry. The total amount of virtual agricultural water is as follows:
where Q
i is the production of agricultural products of category i; VWC
i is the virtual water content per unit of agricultural products of category i.
Based on the data of the production of each agricultural product in the development yearbook of Yangzhou City in 2023 and the data of industrial, domestic, and ecological water use in the water resources bulletin, the water footprint of Yangzhou City in 2023 is obtained (
Table 5).
From the above table, the water footprint method accounted for about 2.128 billion cubic metres of water use in Yangzhou City in 2023, accounting for 0.59 of the available water resources. Therefore, in 2023, the value of ecological services in Yangzhou City will account for 0.59 of its own consumption, and the spillover will account for 0.41 according to Equation (13). The actual benefit to the six cities in Shandong Province will be CNY 2.53 billion.
3.3. Ecological Compensation Standards Based on the Price Negotiation Game
Based on the above calculations, it is found that the cost of providing ecological service value in the water-source area is lower than the benefit of the ecological service value obtained by the receiving area. Therefore, the final ecological compensation standard is based on the dual perspective of cost and benefit, and is determined by the negotiation game between the two parties. According to the above calculation results, it can be seen that, in the Rubinstein game model, the impact of the discounting factor on the compensation standard is crucial. The current research on the discount factor is broadly divided into two categories: one is that of Yuan Hang et al. [
43], using a bilateral stochastic model to analyze the bargaining power of the game parties, and the other is that of Niqi et al. [
44], listing different discount factors and analyzing their impacts on ecological compensation. This paper enumerates different combinations of discounting factors and discusses the negotiation shares obtained by water-source and -receiving areas under different degrees of patience (
Table 6).
The water-source districts and the receiving districts allocate the NPV of CNY 1.318 billion. According to
Table 6, when the water-source district makes the first offer, it has a clear advantage in the allocation of net benefits, and the share of net benefits received by the water-source district exceeds 0.5 by as much as 68.3%. This also verifies the theory of the first-mover advantage in the Rubinstein bargaining model, i.e., the negotiation subject who is the first to make a proposal in the bargaining process tends to have more advantages, and the first bidder obtains a higher share of the quota in the presence of the discount factor.
All other things being equal, both parties’ allocations of net gains increases with the increase in the discount factor. In Rubinstein’s game model, the discount factor represents the time cost of bargaining, which is also a reflection of the degree of patience of the game participants. The essence of the game lies in the psychological and economic acceptability of both parties: the higher their degree of patience, the more favourable their position in the negotiation. In the water-source or receiving area, if or is 1, you can receive the full share of the net benefit.
If this is a symmetric case, i.e., the water-source area and the receiving area have the same discount factor, then , and the equilibrium result is that the water-source area obtains the share and the receiving area obtains the share . Since takes the value of (0, 1), the water-source area must be able to receive more than the general share, which shows that if the two sides have a similar degree of patience during bargaining, they are in a relatively equal position regarding future benefits. The negotiated ecological compensation standards take the interests of both sides into account. If an asymmetric case is considered, i.e., at , the water-source area receives a share of and the receiving area receives a share of , an increase in both and leads to an increase in the share. This means that the present value of the future benefits becomes higher, and the parties in the game have more capital to delay negotiations in order to obtain better terms.
In order to more accurately reflect the impact of the discount factor on the ecological compensation standard, we refer to the study of the upstream and downstream bargaining power of the Bridge Reservoir by Wang New Year et al. [
45]. Assuming that the discount factor of the water-source area and the receiving area is the same,
= 0.8, the ecological compensation standard is CNY 2.108 billion. When the discount factor of the receiving area remains unchanged and the discount factor of the water-source area fluctuates by 10%, i.e., when the value of
ranges from 0.72 to 0.88, the ecological compensation standard fluctuates by CNY 159 million. When the discount factor of the water-source area remains unchanged and the discount factor of the water-receiving area fluctuates by 10%, i.e., when the value of
ranges from 0.72 to 0.88, the ecological compensation standard fluctuates by CNY 198 million. The sensitivity analysis indicates that the compensation standard is more sensitive to the negotiation strategy of the water-receiving area, so the system design should try to guide the water-source area to remain patient and make a rational bid. In practical applications, the calibration of
needs to be combined with empirical data and behavioural analyses to accurately reflect the real preferences of the negotiating parties.
3.4. Allocation of Ecological Compensation Amount Based on AHP-Entropy Method
Exploring the consultation process with the help of the Rubinstein model answers the question of how much compensation is required, but in order to ensure the fairness of the compensation, it is still necessary to consider the differences between different water-receiving areas when determining the actual compensation amount.
By constructing a judgement matrix, the results of the experts’ assessments based on the importance of the indicators are compared using Equation (14). Using the eigenvector method, the weight values for each level are calculated based on Equation (15). Finally, the maximum eigenvalue, CI value, and CR value are calculated according to Equations (16)–(18) to ensure the consistency of the judgement matrix. The weights obtained based on hierarchical analysis are obtained (
Table 7).
When determining objective weights using the entropy method, the data are first processed based on Equations (19) and (20) to calculate the weights for both positive and negative indicators separately. The entropy value of each indicator is then computed to reflect its variability. The indifference coefficient is derived from the entropy value, and finally, the comprehensive weights for each indicator are calculated based on the indifference coefficient (
Table 8).
Combining the subjective AHP weights and the objective entropy weighting method, this paper uses a weighted average method to calculate the final combination weights to reduce the bias of a single method. The combination of hierarchical analysis and entropy method yields the portfolio weights, as shown in
Table 9:
According to the combination of weights and the actual data of the six cities in Shandong Province on the factors affecting the ecological compensation standard (
Table 10), the ecological compensation standards of the six cities in Shandong Province are 14.53% in Jinan and 20.97% in Qingdao on the Jiaodong line, and 23.98% in Dongying, 13.68% in Dezhou, 9.47% in Liaocheng, and 17.37% in Binzhou on the North Lu line (
Figure 4). From the apportionment results, Dongying and Binzhou, as high-water-consuming cities, bear 23.98% and 17.37% of the compensation ratio, respectively, reflecting the principle of “who uses, who compensates” of the ecological compensation system. At the same time, Qingdao and Jinan, cities with a higher economic development level, also bear a higher proportion of the compensation due to their per capita GDP and ability to pay indicators in the weighting system, reflecting the corrective function of the “ability to pay adjustment mechanism” in the regional distribution. This structure not only avoids the tendency towards egalitarianism, but also effectively responds to the reality of ecological pressure and financial capacity, which varies from region to region.
In the actual process, the compensation standard after the game will be distributed according to the combination of weights in the six municipalities to avoid blind egalitarianism, making the ecological compensation standard more reasonable.
4. Discussion
This study employs a dual perspective of costs and benefits to develop a cross-regional ecological compensation framework that integrates dynamic adjustments, game theory analysis, and weighted allocation, aiming to enhance the scientific rigour, fairness, and practicality of compensation standards. Specifically, the cost-based calculation of ecological compensation covers both the direct ecological protection costs of CNY 578 million in Yangzhou City and the indirect opportunity costs of CNY 634 million resulting from restricted industrial development. This ensures that the ecological sacrifices made by water-source areas are compensated with corresponding economic benefits, avoiding the “development sacrifice dilemma.” For water-receiving areas, compensation standards are allocated differently, based on the dual principles of water resource ecology and economic development levels, ensuring that high-water-consuming regions bear corresponding costs while avoiding the compensation pressures that hinder regional economic development. Through this mechanism, water-source areas can leverage ecological compensation to drive upgrades to and transformation of industrial structures, while water-receiving areas obtain stable water resource support at reasonable costs. Both parties form a long-term cooperative economic foundation within a mutually beneficial framework, aligning with the requirement of “balancing efficiency and fairness” in sustainable development.
To overcome the limitations of static calculations, this study further proposes a dynamic adjustment mechanism, suggesting that ecological compensation standards should be dynamically adjusted based on factors such as water resource quantity, water quality, and economic development in water-receiving areas. Adjustment coefficients should be regularly updated to ensure compensation levels remain aligned with long-term ecological and economic changes. Additionally, the Rubinstein model places the ecological compensation negotiation process within a dynamic game-theoretic context, promoting long-term collaborative governance consensus through multiple rounds of price negotiations, thereby reducing the potential risks of regional conflicts. An analysis of discount factors indicates that if water-source regions demonstrate greater patience during negotiations, they can secure more favourable compensation to sustain ongoing protection; additionally, water-recipient regions can achieve a balance between short-term expenditures and long-term benefits through stable water supply arrangements. Overall, the interest coordination and calculation framework proposed in this study helps balance ecological protection and regional development in inter-basin water diversion projects, providing a solid foundation for the long-term sustainable operation of such projects.
This paper has the following limitations. First, although this study established a relatively systematic framework for calculating ecological compensation, several limitations remain. First, in the actual negotiation game process, the discount factor is also associated with the negotiation ability of the negotiating subject, negotiation cost, offer strategy, and the degree of deviation in water demand [
46]. This study did not further calculate the value of the discount factor to measure the bargaining power between negotiating parties, but only analyzed and demonstrated the first-mover advantage of water-source areas. Second, the model primarily targets water resource inter-regional allocation scenarios, and its applicability to other types of ecological services, such as carbon sinks and biodiversity, remains to be tested. Third, while the AHP-entropy weighting method balances subjective and objective factors, it is still difficult to completely avoid subjective bias in expert scoring and indicator selection.
Based on this, future research can be focused on the following areas: (1) introducing a government entity into a three-party dynamic evolutionary game model with multiple agents to explore whether it is possible to determine the monetary value of future economic deficits or benefits when calculating ecological compensation standards; (2) studying the negotiation capabilities and influencing factors in bilateral negotiation games to accurately quantify values and better address issues such as unfairness in cross-regional ecological compensation; (3) incorporating behavioural economics factors such as social preferences and residents’ willingness to pay (WTP) into the model framework to further enhance public participation and social acceptance of the compensation mechanism.
5. Conclusions
This study focuses on the quantification of cross-regional ecological compensation standards, taking Yangzhou City as the water-source area and six cities in Shandong Province as the water-receiving areas. It integrates multiple methods to form a systematic analytical framework and constructs a scientific and feasible ecological compensation analysis framework.
Firstly, this study accounts for the lower limit of ecological compensation based on the cost principle. In 2023, the direct costs of ecological conservation in Yangzhou City totaled approximately CNY 578 million. The loss of development opportunities due to water resource ecological protection amounted to CNY 634 million, totaling CNY 1.212 billion, which constitutes Yangzhou City’s costs. The upper limit of ecological compensation was calculated based on the benefit principle. Using ArcGIS software to preprocess and interpret remote sensing images and raster data, we obtained land use and land cover type data for the main water sources in Yangzhou City in 2023 and quantitatively estimated the value of ecosystem services. Further introducing water volume contribution coefficients, water quality coefficients, and payment capacity adjustment coefficients, a multi-factor correction model was constructed to achieve the transformation of ecological value from static measurement to dynamic adjustment. Subsequently, the water footprint method was used to exclude the impact of self-consumption, yielding the proportion of externalities, resulting in a corrected actual benefit of CNY 2.53 billion. This represents the benefit for the water-receiving area.
Secondly, water-source districts and water-receiving districts negotiated the value of ecosystem services based on the cost and benefit perspectives in the range of CNY 1.21 billion to 2.53 billion, respectively. Assuming that water-source districts bid first, based on the enumerated combination of discounting factors, water-source districts have a 68.3% probability of obtaining more than half of the net benefit share, verifying the first-mover advantage. The exact share of the compensation is primarily influenced by the discount factor. Whichever side has a larger discount factor, i.e., is more patient, will experience an increase in their share of benefits. When the water-source area is completely patient (discount factor = 1) or the receiving area has no patience (discount factor = 0), the two extreme conditions, the water-source area obtains all the net benefits, and the compensation rate is CNY 2.53 billion. When the water-source area discount factor = 0 and the receiving area discount factor = 0.5, both parties will share the net benefits equally, with an ecological compensation rate of CNY 1.871 billion per year. The finite-stage bargaining model was constructed so that the subject and object of ecological compensation in the watershed can negotiate the compensation amount within the acceptable range, which makes the standard of ecological compensation more reasonable.
Thirdly, using the AHP-entropy value combination weighting method to optimize regional allocation, we analyzed the spatial differentiation of compensation shares among the six cities in Shandong Province and obtained the specific compensation allocation ratios for the six cities in Shandong Province. The ratios are as follows: Qingdao 20.97%, Jinan 14.53%, Dongying 23.98%, Dezhou 13.68%, Liaocheng 9.47%, and Binzhou 17.37%. By optimizing the allocation ratios for Shandong Province, the scientific rigour of the compensation distribution was enhanced.
6. Policy Recommendations
Based on the above study, the following policy recommendations are provided for differentiated ecological compensation for inter-basin water transfer projects:
First, ecological compensation standards should be dynamically adjusted in response to changes in water quantity, water quality, and the economic development of the recipient regions. Using the dynamic adjustment coefficients identified in this study, governments can establish a linkage mechanism that ties compensation rates to the costs of protecting and restoring aquatic ecosystems, the opportunity costs of foregone development, and fluctuations in water supply and demand—thereby aligning incentives and obligations. During cost allocation, the ratios derived from the AHP-entropy method should integrate diversion volume, water resource entitlement, and the payment capacity of recipient regions to ensure that high-consuming areas shoulder a proportionately greater share of the compensation burden. These standards must be reviewed and revised periodically to maintain long-term relevance and effectiveness.
Second, during price negotiations between water-source areas and water-recipient areas, both parties are encouraged to explore the use of ecological product value calculation results as a reference basis for determining compensation standards in accordance with the principle of voluntary negotiation. This requires promoting information-sharing and cooperation between regions and strengthening information exchange between water-source areas and water-recipient areas. A water resources, ecological environment, and socio-economic data-sharing platform can be established to enable both parties to obtain real-time information on water resource dynamics, pollution emissions, industrial development, etc., thereby improving negotiation efficiency and promoting coordinated development.
Third, referring to the latest local standard for calculating the ecological product value of cross-regional water diversion systems issued by Yangzhou City, Jiangsu Province, water-source areas may sacrifice some development opportunities for the sake of ecological protection. Water-recipient areas can collaborate with water-source areas to establish ecological industrial parks, develop green industries such as ecological agriculture and ecological tourism, enhance the economic vitality of water-source areas, transform ecological advantages into economic advantages, and promote the coordinated advancement of long-term ecological protection and economic growth.