Integrated Assessment of Groundwater Quality Using Water Quality Indices, Geospatial Analysis, and Neural Networks in a Rural Hungarian Settlement
Abstract
1. Introduction
- Construction of a geodatabase involving 37 dug groundwater wells based on sampling and measurement data. Determination of water quality indices using the Water Quality Index (WQI), Contamination degree (Cd), and Canadian Council of the Ministers of the Environment Water Quality Index (CCME WQI).
- Creation and training of a neural network based on water chemistry parameters for the estimation and performance evaluation of the groundwater quality.
- Mapping, interactive data visualization, and cloud-based sharing of the settlement using three water quality indicators.
2. Materials and Methods
2.1. Study Area and Previous Research Results
2.2. Water Sampling and Analysis
2.3. Applied Water Quality Indices
2.4. Artificial Neural Network
- Training algorithm: trainlm—Levenberg–Marquardt; trainscg—Scaled Conjugate Gradient; trainbr—Bayesian Regularization [48];
- Number of neurons: 10-17-19-21-25;
- Activation function: radbas, tribas, and tansig;
- Initial learning rate: 0.01 (adaptive).
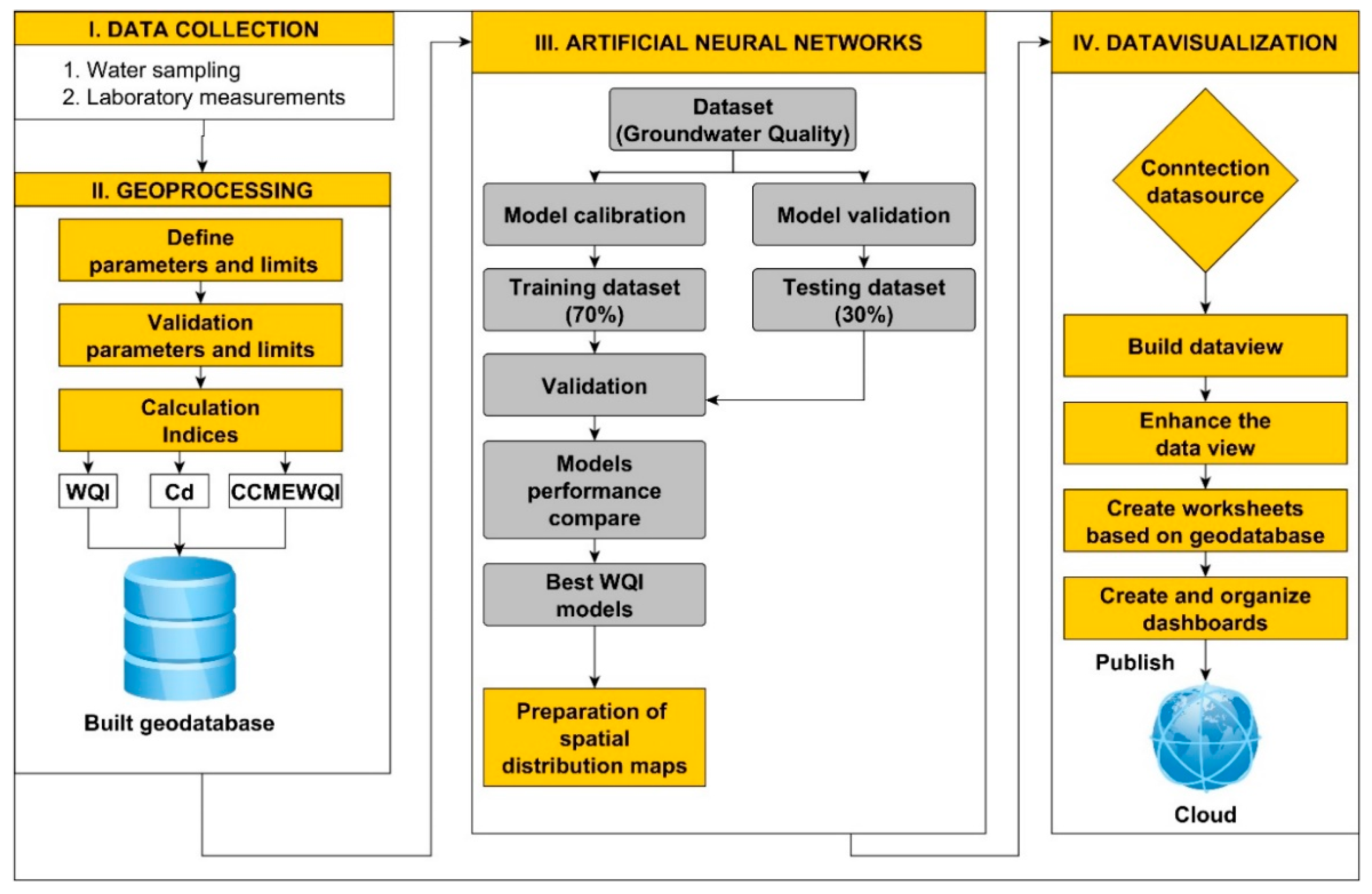
2.5. GIS Process and Data Visualization
3. Results
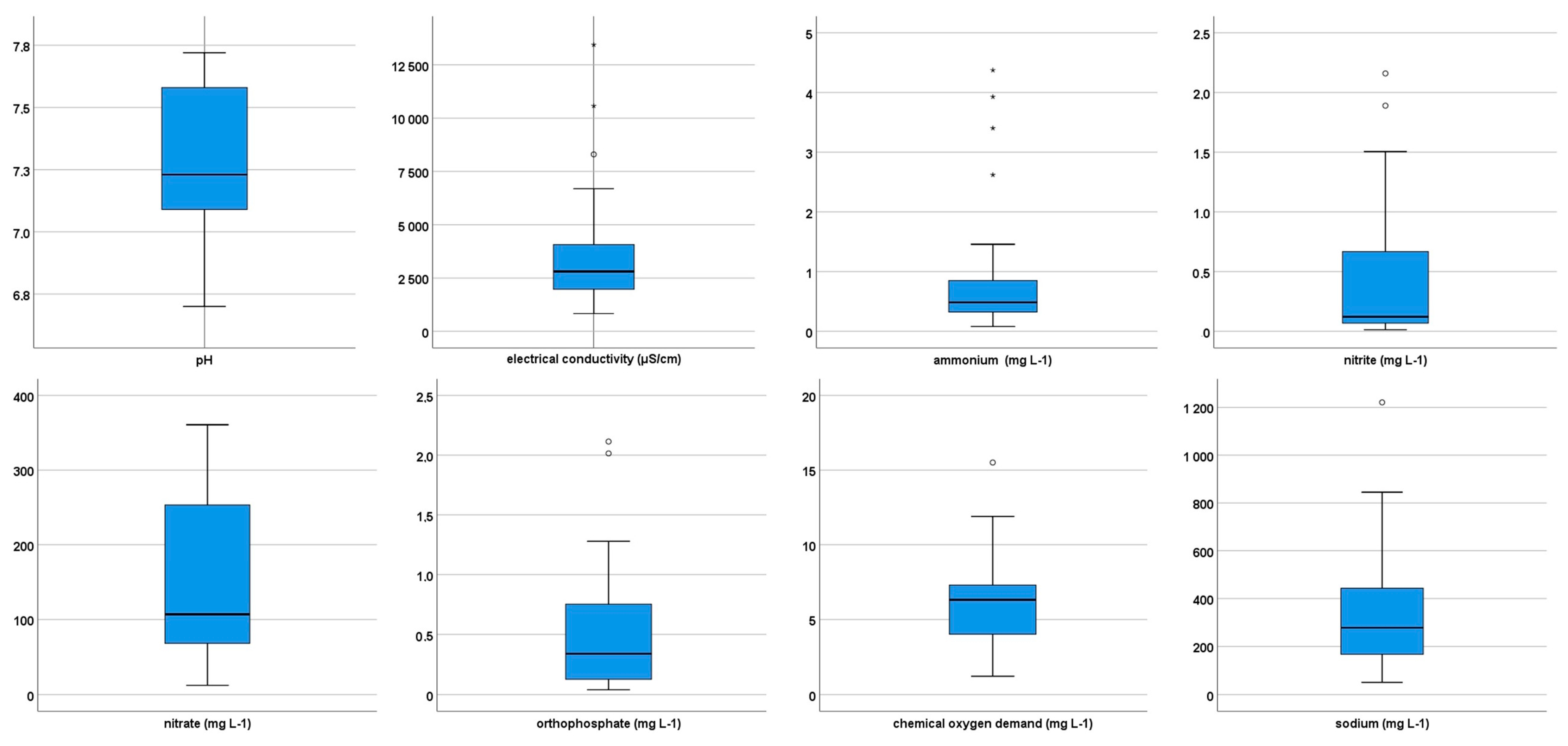
3.1. Assessment of Water Chemistry Parameters
3.2. Spatial Distribution of Groundwater Quality Using Different Indices
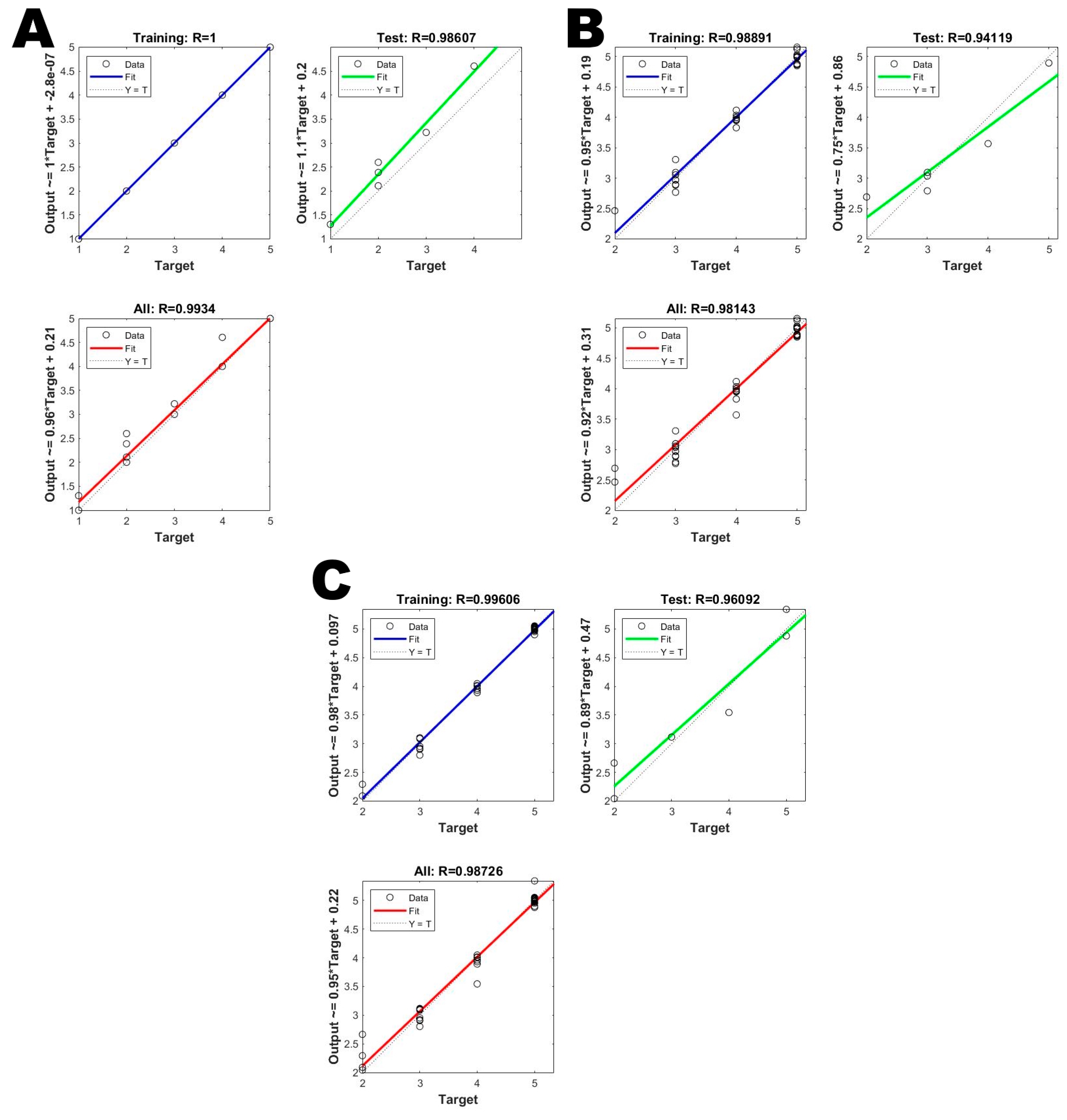
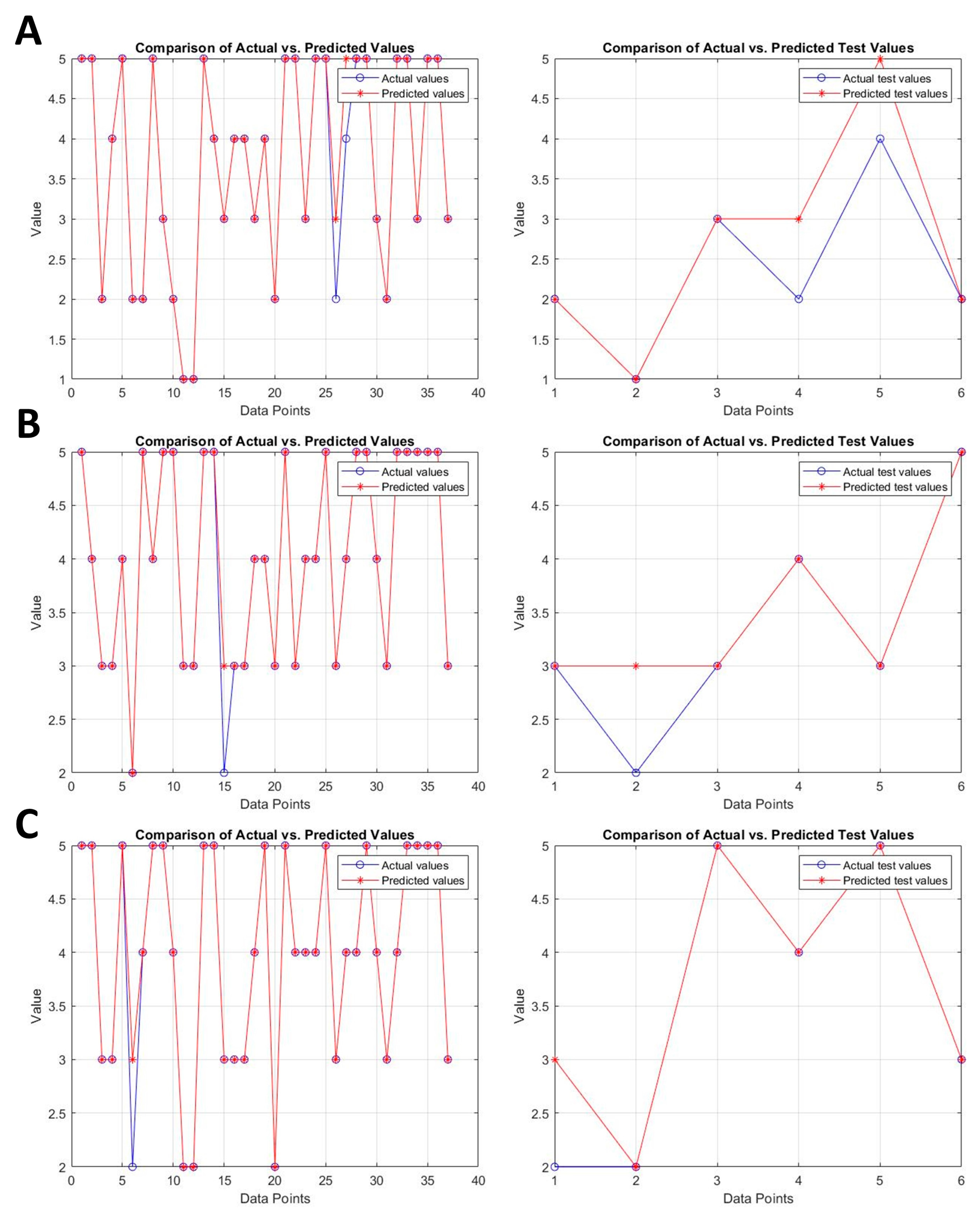
3.3. Performance Assessment of Water Quality Indicators Using Artificial Intelligence
3.4. Interactive Data Visualization of Spatial Water Quality Data
- The sample area dashboard provides a point map showing the location of the sample area in the interface of a Google basemap. By pointing to the monitoring wells, the pop-up bubble help (tooltip) displays the ID and coordinates of the monitoring wells. The view was also connected to distribution maps that depicted the groundwater level and relief conditions of the sample area.
- The data source dashboard displays the attribute data of the connected geodatabase in tabular format.
- The parameters and limits in metered groundwater wells dashboard plots water chemistry parameters on bar charts with a reference line per groundwater well that indicates the contamination limit for each water chemistry parameter.
- Dashboards showing the status of the water quality and degree of pollution can display five different views simultaneously:
- a.
- A point map showing the water quality status of groundwater wells;
- b.
- A summary table of the number of water quality/pollution categories;
- c.
- A donut chart of the % distribution of the categories;
- d.
- A tree map of the proportions of the categories;
- e.
- A bar chart showing the index values for each well.
- The spatial distribution dashboard presents distribution maps of water chemistry parameters and water quality indices edited by Kriging interpolation.
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| ANN | Artificial Neural Network |
| BCWQI | British Columbia Water Quality Index |
| CCME WQI | Canadian Council of Ministers of the Environment Water Quality Index |
| Cd | Contamination Degree |
| COD | Chemical Oxygen Demand |
| CORINE CLC | Coordination of Information on the Environment Land Cover |
| EC | Electrical Conductivity |
| EQ | Equity Index |
| FFNN | Feed-Forward Neural Network |
| GIS | Geographic Information System |
| Na+ | Sodium |
| NH4+ | Ammonium |
| NO2− | Nitrite |
| NO3− | Nitrate |
| NSFWQ | US National Sanitation Foundation Water Quality Index |
| OIP | Overall Index of Pollution |
| OWQI | Oregon Water Quality Index |
| PO43− | Orthophosphate |
| R2 | Determination Coefficient |
| RF | Random Forest |
| RMSE | Root-Mean-Square Error |
| SVM | Support Vector Machine |
| WQI | Water Quality Index |
| WRB | World Reference Base For Soil Resources |
Appendix A
Appendix A.1. Water Quality Index (WQI)
Appendix A.2. CCME Water Quality Index (CCME WQI)
Appendix A.3. Contamination Degree (Cd)
References
- Kerényi, A.; McIntosh, R.W. Sustainable Development in Changing Complex Earth Systems; Sustainable Development Goals Series; Springer International Publishing: Cham, Swizerland, 2020; ISBN 978-3-030-21644-3. [Google Scholar]
- Keraita, B.; Drechsel, P.; Amoah, P. Influence of Urban Wastewater on Stream Water Quality and Agriculture in and around Kumasi, Ghana. Environ. Urban. 2003, 15, 171–178. [Google Scholar] [CrossRef]
- Rutkowski, T.; Raschid-Sally, L.; Buechler, S. Wastewater Irrigation in the Developing World—Two Case Studies from the Kathmandu Valley in Nepal. Agric. Water Manag. 2007, 88, 83–91. [Google Scholar] [CrossRef]
- Aulakh, M.S.; Khurana, M.P.S.; Singh, D. Water Pollution Related to Agricultural, Industrial, and Urban Activities, and Its Effects on the Food Chain: Case Studies from Punjab. J. New Seeds 2009, 10, 112–137. [Google Scholar] [CrossRef]
- Tytła, M. Assessment of Heavy Metal Pollution and Potential Ecological Risk in Sewage Sludge from Municipal Wastewater Treatment Plant Located in the Most Industrialized Region in Poland—Case Study. Int. J. Environ. Res. Public Health 2019, 16, 2430. [Google Scholar] [CrossRef]
- Livia, S.; María, M.-S.; Marco, B.; Marco, R. Assessment of Wastewater Reuse Potential for Irrigation in Rural Semi-Arid Areas: The Case Study of Punitaqui, Chile. Clean. Techn Env. Policy 2020, 22, 1325–1338. [Google Scholar] [CrossRef]
- Bano, H.; Rather, R.A.; Malik, S.; Bhat, M.A.; Khan, A.H.; Américo-Pinheiro, J.H.P.; Mir, I.A. Effect of Seasonal Variation on Pollution Load of Water of Hokersar Wetland: A Case Study of Queen Wetland of Kashmir, J&K, India. Water Air Soil. Pollut. 2022, 233, 518. [Google Scholar] [CrossRef]
- Zolfaghary, P.; Zakerinia, M.; Kazemi, H. A Model for the Use of Urban Treated Wastewater in Agriculture Using Multiple Criteria Decision Making (MCDM) and Geographic Information System (GIS). Agric. Water Manag. 2021, 243, 106490. [Google Scholar] [CrossRef]
- Bugajski, P.M.; Kurek, K.; Mlyński, D.; Operacz, A. Designed and Real Hydraulic Load of Household Wastewater Treatment Plants. J. Water Land. Dev. 2019, 40, 155–160. [Google Scholar] [CrossRef]
- Mester, T.; Szabó, G.; Bessenyei, É.; Karancsi, G.; Barkóczi, N.; Balla, D. The Effects of Uninsulated Sewage Tanks on Groundwater. A Case Study in an Eastern Hungarian Settlement. J. Water Land. Dev. 2017, 33, 123–129. [Google Scholar] [CrossRef]
- Horton, R.K. An Index Number System for Rating Water Quality. J. Wat Pollut. Contr Fed. 1965, 37, 292–315. [Google Scholar]
- Brown, R.M.; McClelland, N.I.; Deininger, R.A.; Tozer, R.G. A Water Quality Index-Do We Dare? Water Sew. Work. 1970, 117, 1–5. [Google Scholar]
- Dunnette, D.A. A Geographically Variable Water Quality Index Used in Oregon. J. Water Pollut. Control Fed. 1979, 51, 53–61. [Google Scholar]
- Dinius, S.H. Design of an Index of Water Quality1. JAWRA J. Am. Water Resour. Assoc. 1987, 23, 833–843. [Google Scholar] [CrossRef]
- Smith, D.G. A Better Water Quality Indexing System for Rivers and Streams. Water Res. 1990, 24, 1237–1244. [Google Scholar] [CrossRef]
- Cude, C.G. Oregon Water Quality Index a Tool for Evaluating Water Quality Management Effectiveness 1. JAWRA J. Am. Water Resour. Assoc. 2001, 37, 125–137. [Google Scholar] [CrossRef]
- Sargaonkar, A.; Deshpande, V. Development of an Overall Index of Pollution for Surface Water Based on a General Classification Scheme in Indian Context. Env. Monit. Assess. 2003, 89, 43–67. [Google Scholar] [CrossRef]
- Liou, S.-M.; Lo, S.-L.; Wang, S.-H. A Generalized Water Quality Index for Taiwan. Env. Monit. Assess. 2004, 96, 35–52. [Google Scholar] [CrossRef]
- Lumb, A.; Halliwell, D.; Sharma, T. Application of CCME Water Quality Index to Monitor Water Quality: A Case Study of the Mackenzie River Basin, Canada. Env. Monit. Assess. 2006, 113, 411–429. [Google Scholar] [CrossRef]
- Luh, J.; Baum, R.; Bartram, J. Equity in Water and Sanitation: Developing an Index to Measure Progressive Realization of the Human Right. Int. J. Hyg. Environ. Health 2013, 216, 662–671. [Google Scholar] [CrossRef]
- Uddin, M.G.; Nash, S.; Olbert, A.I. A Review of Water Quality Index Models and Their Use for Assessing Surface Water Quality. Ecol. Indic. 2021, 122, 107218. [Google Scholar] [CrossRef]
- Simsek, C.; Gunduz, O. IWQ Index: A GIS-Integrated Technique to Assess Irrigation Water Quality. Env. Monit. Assess. 2007, 128, 277–300. [Google Scholar] [CrossRef] [PubMed]
- Şener, Ş.; Şener, E.; Davraz, A. Evaluation of Water Quality Using Water Quality Index (WQI) Method and GIS in Aksu River (SW-Turkey). Sci. Total Environ. 2017, 584–585, 131–144. [Google Scholar] [CrossRef] [PubMed]
- Jha, M.K.; Shekhar, A.; Jenifer, M.A. Assessing Groundwater Quality for Drinking Water Supply Using Hybrid Fuzzy-GIS-Based Water Quality Index. Water Res. 2020, 179, 115867. [Google Scholar] [CrossRef] [PubMed]
- Dandge, K.P.; Patil, S.S. Spatial Distribution of Ground Water Quality Index Using Remote Sensing and GIS Techniques. Appl. Water Sci. 2021, 12, 7. [Google Scholar] [CrossRef]
- Saravani, M.J.; Saadatpour, M.; Shahvaran, A.R. A Web GIS Based Integrated Water Resources Assessment Tool for Javeh Reservoir. Expert. Syst. Appl. 2024, 252, 124198. [Google Scholar] [CrossRef]
- Habeeb, R.; Gupta, Y.; Chinwan, H.; Barker, E. Assessing Demographic and Water Sensitivities Arising Due to Urban Water Insecurity in Haldwani, Uttarakhand (India): A GIS-Based Spatial Analysis. J. Geovis Spat. Anal. 2019, 3, 8. [Google Scholar] [CrossRef]
- Taşan, S. Estimation of Groundwater Quality Using an Integration of Water Quality Index, Artificial Intelligence Methods and GIS: Case Study, Central Mediterranean Region of Turkey. Appl. Water Sci. 2022, 13, 15. [Google Scholar] [CrossRef]
- Mustafa, H.M.; Mustapha, A.; Hayder, G.; Salisu, A. Applications of IoT and Artificial Intelligence in Water Quality Monitoring and Prediction: A Review. In Proceedings of the 2021 6th International Conference on Inventive Computation Technologies (ICICT), Coimbatore, India, 20–22 January 2021; pp. 968–975. [Google Scholar]
- Prohászka, V.; Tormáné Kovács, E.; Grósz, J.; Waltner, I. Az Ásott Kutak Vízminősége Két Ökofaluban: Visnyeszéplakon És Gyűrűfűn. Tájökológiai Lapok 2022, 20, 41–58. [Google Scholar] [CrossRef]
- Vadas, A.; Ferenczi, L. Small Urban Waters and Environmental Pressure before Industrialization: The Case of Hungary. J. Hist. Geogr. 2023, 82, 98–109. [Google Scholar] [CrossRef]
- Kirschner, A.K.T.; Schachner-Groehs, I.; Kavka, G.; Hoedl, E.; Kovacs, A.; Farnleitner, A.H. Long-Term Impact of Basin-Wide Wastewater Management on Faecal Pollution Levels along the Entire Danube River. Env. Sci. Pollut. Res. 2024, 31, 45697–45710. [Google Scholar] [CrossRef]
- HCSO Hungarian Central Statistical Office. Available online: https://www.ksh.hu/?lang=en (accessed on 29 August 2024).
- Michéli, E.; Fuchs, M.; Hegymegi, P.; Stefanovits, P. Classification of the Major Soils of Hungary and Their Correlation with the World Reference Base for Soil Resources (WRB). Agrokémia és Talajt. 2006, 55, 19–28. [Google Scholar] [CrossRef]
- Balla, D.; Kiss, E.; Zichar, M.; Mester, T. Evaluation of Groundwater Quality in the Rural Environment Using Geostatistical Analysis and WebGIS Methods in a Hungarian Settlement, Báránd. Environ. Sci. Pollut. Res. 2023, 31, 57177–57195. [Google Scholar] [CrossRef] [PubMed]
- Mester, T.; Balla, D.; Karancsi, G.; Bessenyei, É.; Szabó, G. Eects of Nitrogen Loading from Domestic Wastewater on Groundwater Quality. Water SA 2019, 45, 349–358. [Google Scholar] [CrossRef]
- Mester, T.; Szabó, G.; Balla, D. Assessment of Shallow Groundwater Purification Processes after the Construction of a Municipal Sewerage Network. Water 2021, 13, 1946. [Google Scholar] [CrossRef]
- Balla, D.; Zichar, M.; Kiss, E.; Szabó, G.; Mester, T. Possibilities for Assessment and Geovisualization of Spatial and Temporal Water Quality Data Using a WebGIS Application. ISPRS Int. J. Geo-Inf. 2022, 11, 108. [Google Scholar] [CrossRef]
- Mester, T.; Balla, D.; Szabó, G. Assessment of Groundwater Quality Changes in the Rural Environment of the Hungarian Great Plain Based on Selected Water Quality Indicators. Water Air Soil. Pollut. 2020, 231, 536. [Google Scholar] [CrossRef]
- MSZ 21464; Hungarian Standards Board: 1998. Sampling from Groundwater, 1998. Available online: https://ugyintezes.mszt.hu/webaruhaz/szabvany-adatok?standard=95049 (accessed on 13 July 2025).
- HS 448-18; Hungarian Standard Water Quality. Part 18: Drinking Water Analysis. Determination of Orthophosphate and Total Phosphorus Using Spectrophotometric Method. Hungarian Standards Institution (MSZT): Budapest, Hungary, 2009.
- HS 1484-13; Hungarian Standard Water Quality. Part 12: Determination of Nitrate and Nitrite. Content by Spectrophotometric Method. Hungarian Standards Institution (MSZT): Budapest, Hungary, 2009.
- HS ISO 7150-1; Hungarian Standard Water Quality. Determination of Ammonium. Part 1: Manual Spectrophotometric Method. Hungarian Standards Institution (MSZT): Budapest, Hungary, 1992.
- Backman, B.; Bodiš, D.; Lahermo, P.; Rapant, S.; Tarvainen, T. Application of a Groundwater Contamination Index in Finland and Slovakia. Environ. Geol. 1998, 36, 55–64. [Google Scholar] [CrossRef]
- Csábrági, A.; Molnár, S.; Tanos, P.; Kovács, J.; Szabó, I.; Molnár, M. Neurális Hálózatok Alkalmazása Hazai Vízminőségi Vizsgálatok Során. Mezőgazdasági Tech. 2019, 60, 2–5. [Google Scholar]
- Alrowais, R.; Abdel Daiem, M.M.; Li, R.; Maklad, M.A.; Helmi, A.M.; Nasef, B.M.; Said, N. Groundwater Quality Assessment for Drinking and Irrigation Purposes at Al-Jouf Area in KSA Using Artificial Neural Network, GIS, and Multivariate Statistical Techniques. Water 2023, 15, 2982. [Google Scholar] [CrossRef]
- The MathWorks Inc. MathWorks—Maker of MATLAB and Simulink; The MathWorks Inc.: Natick, MA, USA, 2024. [Google Scholar]
- Hagan, M.T.; Menhaj, M.B. Training Feedforward Networks with the Marquardt Algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef]
- Golden Software LLC. Surfer® [Computer software]. Golden Software LLC: Golden, CO, USA. Available online: https://www.goldensoftware.com/products/surfer (accessed on 7 August 2025).
- Tableau, P. Báránd Water_Quality. 2023. Available online: https://public.tableau.com/app/profile/d.niel.balla/viz/BrndWater_Quality2023/BrndWaterQuality (accessed on 4 July 2025).
- Zhang, Z. Artificial Neural Network. In Multivariate Time Series Analysis in Climate and Environmental Research; Zhang, Z., Ed.; Springer International Publishing: Cham, Swizerland, 2018; pp. 1–35. ISBN 978-3-319-67340-0. [Google Scholar]
- Trowsdale, S.A.; Lerner, D.N. A Modelling Approach to Determine the Origin of Urban Ground Water. J. Contam. Hydrol. 2007, 91, 171–183. [Google Scholar] [CrossRef]
- Stuart, M.; Lapworth, D.; Crane, E.; Hart, A. Review of Risk from Potential Emerging Contaminants in UK Groundwater. Sci. Total Environ. 2012, 416, 1–21. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Jolly, I.; Sophocleous, M.; Zhang, L. Global Impacts of Conversions from Natural to Agricultural Ecosystems on Water Resources: Quantity versus Quality. Water Resour. Res. 2007, 43, W03437. [Google Scholar] [CrossRef]
- Debrewer, L.M.; Ator, S.W.; Denver, J.M. Temporal Trends in Nitrate and Selected Pesticides in Mid-Atlantic Ground Water. J. Environ. Qual. 2008, 37, S296–S308. [Google Scholar] [CrossRef]
- Ward, M.H.; deKok, T.M.; Levallois, P.; Brender, J.; Gulis, G.; Nolan, B.T.; VanDerslice, J. Workgroup Report: Drinking-Water Nitrate and Health—Recent Findings and Research Needs. Environ. Health Perspect. 2005, 113, 1607–1614. [Google Scholar] [CrossRef] [PubMed]
- WHO 2017, 2017 Guidelines for Drinking-Water Quality, 4th Edition, Incorporating the 1st Addendum. Available online: https://www.who.int/publications/i/item/9789241549950 (accessed on 4 July 2025).
- Balla, D.; Kiss, E.; Zichar, M.; Mester, T. Ásott talajvízkutak vízminőségének tér- és időbeli változásainak értékelése egy alföldi településen a CCME WQI vízminőségi mutató alkalmazásával. TÁJÖKOLÓGIAI LAPOK|J. Landsc. Ecol. 2024, 22, 3–24. [Google Scholar] [CrossRef]
- Pesce, S.F.; Wunderlin, D.A. Use of Water Quality Indices to Verify the Impact of Córdoba City (Argentina) on Suquía River. Water Res. 2000, 34, 2915–2926. [Google Scholar] [CrossRef]
- Gazzaz, N.M.; Yusoff, M.K.; Aris, A.Z.; Juahir, H.; Ramli, M.F. Artificial Neural Network Modeling of the Water Quality Index for Kinta River (Malaysia) Using Water Quality Variables as Predictors. Mar. Pollut. Bull. 2012, 64, 2409–2420. [Google Scholar] [CrossRef] [PubMed]
- Zandbergen, P.A.; Hall, K.J. Analysis of the British Columbia Water Quality Index for Watershed Managers: A Case Study of Two Small Watersheds. Water Qual. Res. J. 1998, 33, 519–550. [Google Scholar] [CrossRef]
- Tyagi, S.; Sharma, B.; Singh, P.; Dobhal, R. Water Quality Assessment in Terms of Water Quality Index. Am. J. Water Resour. 2013, 1, 34–38. [Google Scholar] [CrossRef]
- Ghasemlounia, R.; Gharehbaghi, A.; Ahmadi, F.; Saadatnejadgharahassanlou, H. Developing a Novel Framework for Forecasting Groundwater Level Fluctuations Using Bi-Directional Long Short-Term Memory (BiLSTM) Deep Neural Network. Comput. Electron. Agric. 2021, 191, 106568. [Google Scholar] [CrossRef]
- Alnuwaiser, M.A.; Javed, M.F.; Khan, M.I.; Ahmed, M.W.; Galal, A.M. Support Vector Regression and ANN Approach for Predicting the Ground Water Quality. J. Indian. Chem. Soc. 2022, 99, 100538. [Google Scholar] [CrossRef]
- Bishop, C.M.; Nasrabadi, N.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4. [Google Scholar]
- Wang, L.-P.; Ochoa-Rodríguez, S.; Van Assel, J.; Pina, R.D.; Pessemier, M.; Kroll, S.; Willems, P.; Onof, C. Enhancement of Radar Rainfall Estimates for Urban Hydrology through Optical Flow Temporal Interpolation and Bayesian Gauge-Based Adjustment. J. Hydrol. 2015, 531, 408–426. [Google Scholar] [CrossRef]
- Ibrahim, A.; Ismail, A.; Juahir, H.; Iliyasu, A.B.; Wailare, B.T.; Mukhtar, M.; Aminu, H. Water Quality Modelling Using Principal Component Analysis and Artificial Neural Network. Mar. Pollut. Bull. 2023, 187, 114493. [Google Scholar] [CrossRef]
- Khan, M.; Almazah, M.M.A.; Eilahi, A.; Niaz, R.; Al-Rezami, A.Y.; Zaman, B. Spatial Interpolation of Water Quality Index Based on Ordinary Kriging and Universal Kriging. Geomat. Nat. Hazards Risk 2023, 14, 2190853. [Google Scholar] [CrossRef]
- Ali, S.A.; Ahmad, A. Analysing Water-Borne Diseases Susceptibility in Kolkata Municipal Corporation Using WQI and GIS Based Kriging Interpolation. GeoJournal 2020, 85, 1151–1174. [Google Scholar] [CrossRef]
- Xu, H.; Gao, Q.; Yuan, B. Analysis and Identification of Pollution Sources of Comprehensive River Water Quality: Evidence from Two River Basins in China. Ecol. Indic. 2022, 135, 108561. [Google Scholar] [CrossRef]
- Loucks, D.P.; Van Beek, E. Water Resource Systems Planning and Management; Springer International Publishing: Cham, Swizerland, 2017; ISBN 978-3-319-44232-7. [Google Scholar]

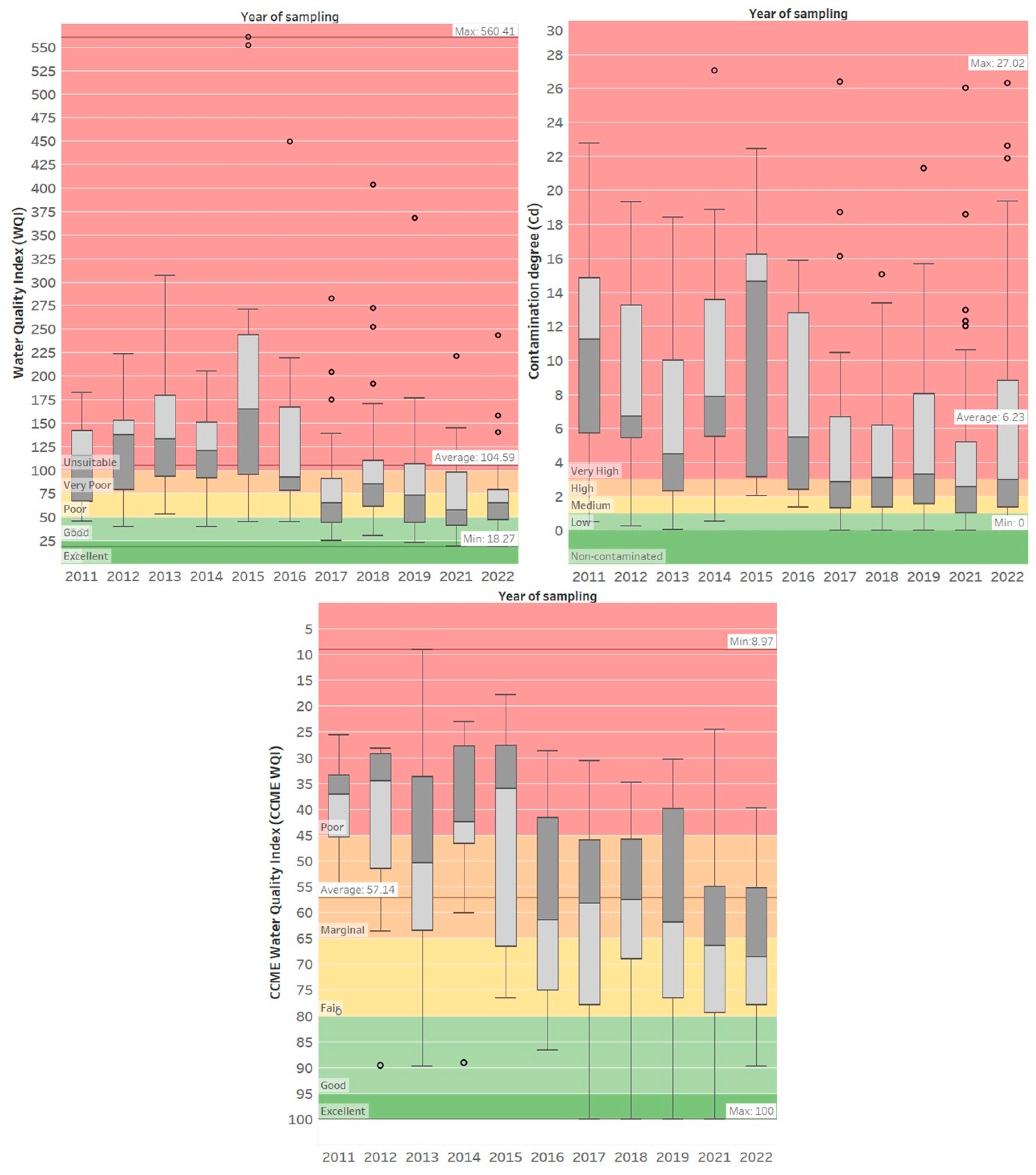

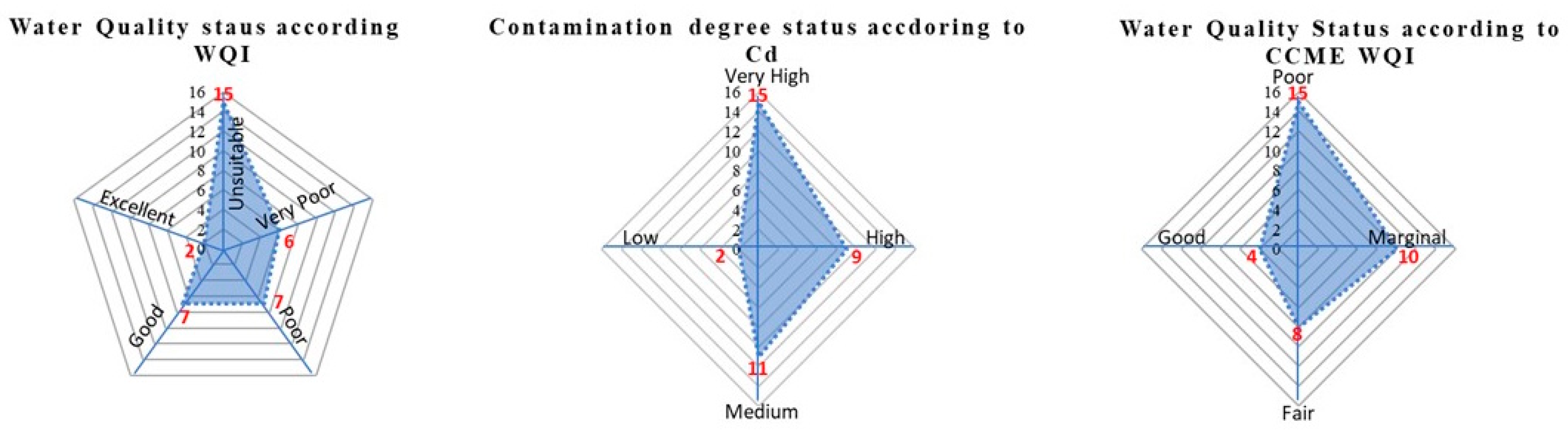


| WQI | Water Quality Status (WQS) | CCME WQI | CCME Water Quality Status (WQS) | Cd | Cd Status | Possible Use |
|---|---|---|---|---|---|---|
| 0–25 | Excellent water quality | 95–100 | Excellent | 0 | Excellent | Drinking, irrigation, and industrial |
| 26–50 | Good water quality | 80–94 | Good | <1 | Low | Irrigation and industrial |
| 51–75 | Poor water quality | 65–79 | Fair | 3–1 | Medium | Irrigation and industrial |
| 76–100 | Very poor water quality | 45–64 | Marginal | 3–6 | High | Irrigation |
| Above 100 | Unsuitable for any use | 0–44 | Poor | >6 | Very High | Proper treatment required before use |
| Parameter | Limit | Mean | SD | Min. | Max. | Lower Q | Upper Q |
|---|---|---|---|---|---|---|---|
| pH | 6.5–8.5 | 7.31 | 0.27 | 6.7 | 7.72 | 7.09 | 7.58 |
| EC (μS/cm) | 2500 | 3625 | 2659.42 | 833 | 13,440 | 1915 | 4075 |
| NH4+ (mg L−1) | 0.5 | 0.86 | 1.03 | 0.08 | 4.37 | 0.32 | 0.86 |
| NO2− (mg L−1) | 0.5 | 0.46 | 0.61 | 0.01 | 2.16 | 0.07 | 0.8 |
| NO3− (mg L−1) | 50 | 154.3 | 104.61 | 12.46 | 360.8 | 68.22 | 264.37 |
| PO43− (mg L−1) | 0.5 | 0.5 | 0.5 | 0.04 | 2.11 | 0.12 | 0.77 |
| COD (mg L−1) | 4.5 | 6.12 | 3.03 | 1.23 | 15.51 | 4.02 | 7.71 |
| Na+ (mg L−1) | 200 | 335.2 | 237.6 | 51.2 | 1221 | 166 | 451.5 |
| Groundwater Quality Index | ||||||||
|---|---|---|---|---|---|---|---|---|
| Parameter | pH | EC | NH4+ | NO2− | NO3− | PO43− | COD | Na+ |
| pH | 1 | |||||||
| EC | −0.445 ** | 1 | ||||||
| NH4+ | −0.24 | 0.27 | 1 | |||||
| NO2− | −0.13 | 0.445 ** | 0.492 ** | 1 | ||||
| NO3− | −0.507 ** | 0.577 ** | 0.24 | 0.342 * | 1 | |||
| PO43− | 0.08 | −0.23 | 0.15 | 0.06 | −0.369 * | 1 | ||
| COD | −0.08 | 0.01 | 0.392 * | 0.475 ** | 0.06 | 0.363 * | 1 | |
| Na+ | −0.16 | 0.604 ** | 0.27 | 0.530 ** | 0.373 * | −0.01 | 0.20 | 1 |
| Model | Measure | Number of Neurons | ||||
|---|---|---|---|---|---|---|
| 10 | 17 | 19 | 21 | 25 | ||
| WQI | RMSE | 0.2179 | 0.1668 | 0.178 | 0.1205 | 0.1933 |
| R2 | 0.9726 | 0.9839 | 0.9817 | 0.9916 | 0.9784 | |
| Cd | RMSE | 0.1621 | 0.1944 | 0.2106 | 0.2021 | 0.2033 |
| R2 | 0.9714 | 0.9589 | 0.9518 | 0.9556 | 0.955 | |
| CCME WQI | RMSE | 0.1305 | 0.1498 | 0.1562 | 0.1377 | 0.1367 |
| R2 | 0.9838 | 0.9787 | 0.9768 | 0.982 | 0.9823 | |
| Model | Measure | Trainlm | Trainscg | Trainbr |
|---|---|---|---|---|
| WQI | RMSE | 0.5397 | 0.5222 | 0.1205 |
| R2 | 0.8319 | 0.8426 | 0.9916 | |
| Cd | RMSE | 0.3261 | 0.2748 | 0.1621 |
| R2 | 0.8843 | 0.9178 | 0.9714 | |
| CCME WQI | RMSE | 0.2801 | 0.3831 | 0.1305 |
| R2 | 0.9255 | 0.8606 | 0.9838 |
| Model | Measure | Radbas | Tribas | Tansig |
|---|---|---|---|---|
| WQI | RMSE | 0.2726 | 0.4061 | 0.1205 |
| R2 | 0.9571 | 0.9048 | 0.9916 | |
| Cd | RMSE | 0.1954 | 0.2402 | 0.1621 |
| R2 | 0.9584 | 0.9372 | 0.9714 | |
| CCME WQI | RMSE | 0.2169 | 0.3383 | 0.1305 |
| R2 | 0.9553 | 0.8914 | 0.9838 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balla, D.; Tari, L.; Hajdu, A.; Kiss, E.; Zichar, M.; Mester, T. Integrated Assessment of Groundwater Quality Using Water Quality Indices, Geospatial Analysis, and Neural Networks in a Rural Hungarian Settlement. Water 2025, 17, 2371. https://doi.org/10.3390/w17162371
Balla D, Tari L, Hajdu A, Kiss E, Zichar M, Mester T. Integrated Assessment of Groundwater Quality Using Water Quality Indices, Geospatial Analysis, and Neural Networks in a Rural Hungarian Settlement. Water. 2025; 17(16):2371. https://doi.org/10.3390/w17162371
Chicago/Turabian StyleBalla, Dániel, Levente Tari, András Hajdu, Emőke Kiss, Marianna Zichar, and Tamás Mester. 2025. "Integrated Assessment of Groundwater Quality Using Water Quality Indices, Geospatial Analysis, and Neural Networks in a Rural Hungarian Settlement" Water 17, no. 16: 2371. https://doi.org/10.3390/w17162371
APA StyleBalla, D., Tari, L., Hajdu, A., Kiss, E., Zichar, M., & Mester, T. (2025). Integrated Assessment of Groundwater Quality Using Water Quality Indices, Geospatial Analysis, and Neural Networks in a Rural Hungarian Settlement. Water, 17(16), 2371. https://doi.org/10.3390/w17162371







