Next Article in Journal
Inland Flood Analysis in Irrigated Agricultural Fields Including Drainage Systems and Pump Stations
Previous Article in Journal
Integrated Flushing and Corrosion Control Measures to Reduce Lead Exposure in Households with Lead Service Lines
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 17
Issue 15
10.3390/w17152298
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Mapping Wet Areas and Drainage Networks of Data-Scarce Catchments Using Topographic Attributes

by
Henrique Marinho Leite Chaves
1,*,
Maria Tereza Leite Montalvão
2 and
Maria Rita Souza Fonseca
1
1
Watershed Management Laboratory-EFL, University of Brasilia, Brasilia 70910-900, DF, Brazil
2
The Nature Consevancy-TNC, Brasilia 70714-900, DF, Brazil
*
Author to whom correspondence should be addressed.
Water 2025, 17(15), 2298; https://doi.org/10.3390/w17152298
Submission received: 11 June 2025 / Revised: 17 July 2025 / Accepted: 31 July 2025 / Published: 2 August 2025
(This article belongs to the Section Hydrogeology)
Browse Figures
Versions Notes

Abstract

Wet areas, which are locations in the landscape that consistently retain moisture, and channel networks are important landscape compartments, with key hydrological and ecological functions. Hence, defining their spatial boundaries is an important step towards sustainable watershed management. In catchments of developing countries, wet areas and small order channels of river networks are rarely mapped, although they represent a crucial component of local livelihoods and ecosystems. In this study, topographic attributes generated with a 30 m SRTM DEM were used to map wet areas and stream networks of two tropical catchments in Central Brazil. The topographic attributes for wet areas were the local slope and the slope curvature, and the Topographic Wetness Index (TWI) was used to delineate the stream networks. Threshold values of the selected topographic attributes were calibrated in the Santa Maria catchment, comparing the synthetically generated wet areas and drainage networks with corresponding reference (map) features, and validated in the nearby Santa Maria basin. Drainage network and wet area delineation accuracies were estimated using random basin transects and multi-criteria and confusion matrix methods. The drainage network accuracies were 67.2% and 70.7%, and wet area accuracies were 72.7% and 73.8%, for the Santa Maria and Gama catchments, respectively, being equivalent or higher than previous studies. The mapping errors resulted from model incompleteness, DEM vertical inaccuracy, and cartographic misrepresentation of the reference topographic maps. The study’s novelty is the use of readily available information to map, with simplicity and robustness, wet areas and channel initiation in data-scarce, tropical environments.

1. Introduction

1.1. Wet Areas

Wet areas, which are locations in landscapes that consistently retain moisture, play a fundamental role in the regulation of stream water quality, reducing sediment and nutrient loading [1] through increased deposition and nutrient uptake [2]. Wet areas also fulfil important ecological functions in catchments, including groundwater recharge and nutrient cycling [3]. In the Cerrado biome of Central Brazil, gallery forests and grassy wetlands form the hydromorphic zones of valley bottoms, along stream channels [4], and are associated with the seasonal fluctuation of the water table [5]. In the Brazilian savanna, low-lying grasslands occur over hydric soils, and gallery forests cover well-drained and hydromorphic soils [6], forming the wet areas of the river basins.
However, data on hydromorphic processes, functions, and their location in tropical catchments are scarce, even though they provide a crucial component of local livelihoods [7]. Therefore, defining the spatial boundaries between well-drained/upslope and poorly drained/valley-bottom areas is an important step towards riparian-area management [8].
Due to the high spatial pedological and groundwater variability, soil and vegetation mapping in wet areas is challenging [4], particularly when the original gallery forest, an indicator of wet areas, is removed [1]. Since shallow water tables in landscape bottoms are associated with hydromorphic soils [1,9], gallery forests [6,10], and stream heads [11,12], and because soil wetness is a function of hillslope convergence [13], different topographic attributes that predict soil wetness can be used to map hydromorphic zones [14], particularly in data-scarce locations [15].
However, most mapping studies of hydromorphic areas and drainage networks were carried out in temperate regions. In an American catchment, it was reported that the upslope area and the Topographic Wetness Index (TWI) [16,17] were correlated with shallow water table persistence. It was also recognized that the product of primary topographic attributes, such as upslope area, slope gradient, and slope curvature, was a good predictor of soil wetness and water table depth [18]. TWI was found to be positively correlated with soil wetness in agricultural fields in the USA, particularly when high-resolution DEMs were used [19].
In Sweden, the upslope contributing area, the slope curvature, and the TWI were used to predict the distribution of wetlands in the landscape, utilizing geobotanical and pedological criteria [20]. In that study, the upslope contributing area was the most important explanatory factor of saturated areas. In a different Swedish basin, a model-derived wetness index proved to be accurate in the prediction of the spatial distribution of saturated areas [21].
In Taiwan, TWI correlated well with runoff-generating areas [22]. In that country, the TWI together with the slope gradient and the slope curvature predicted the spatial distribution of soil types and their properties at fine scales [23]. However, wetness indices worked only when wet areas covered more than 30% of the catchment [24].
In eastern Brazil, slope grade, valley bottom flatness, and the wetness index were used to map the soils of hydromorphic areas, with mapping accuracy depending on the soil drainage conditions [25]. In the Brazilian savanna, the use of gallery forests as a proxy for hydric soils overestimated the distribution of the latter [4], since that type of vegetation also occurred on well-drained soils. This finding was corroborated elsewhere [26], indicating that local slope and the distance from the stream were useful attributes in riparian soil mapping.

1.2. Stream Initiation

Stream heads are the boundaries between hillslopes and river channels [27], and commonly occur at topographic convergences (hollows) where enough runoff accumulates and exceeds an erosion threshold [28]. In steep terrains, landsliding and seepage erosion are the dominant factors controlling channel initiation [29], whereas in gentle slopes, the main driving process is overland flow [30]. The ability to determine the location in the landscape where channels initiate is important for understanding hydrologic and geomorphologic processes, and for managing headwater streams [31]. However, because of the dense canopy of the gallery forests, the conventional photogrammetric mapping of stream heads and the corresponding drainage network is a subjective task, often resulting in inaccurate channel representations [32].
In Oregon (USA), the hypothesis that the channelization threshold is a distance just shorter than the hillslope length was confirmed [29]. In an earlier study, it was concluded that the location of channel heads on steep slopes is controlled by the subsurface flow-induced instability of the colluvial fill [33].
Channel initiation in the landscape can be predicted by the square root of the contributing area times the slope gradient [27]. Local slope, local plan curvature, and average profile curvature are good predictors of channel heads, but the predictive effectiveness depends on the type of catchment [28]. Channel heads can be mapped using TWI thresholds [12], but successful drainage network mapping should strike a reasonable balance between channel density, headward extent, and positional accuracy. It was found that the TWI threshold value for channel initiation is 12 [34], but this value is dependent on the DEM grid size.
In a Korean catchment, the TWI channel initiation threshold was integrated with a spatially distributed flow-apportioning algorithm to delineate channel networks [35], with reasonable results. In another study, a critical support area was used to define channel initiation and drainage position, indicating that the DEM routing method (D8 or D∞) did not matter in steeper slopes [36], provided that the pixel size was smaller than the hillslope length. Conversely, when TWI and different flow direction algorithms were applied to six catchments in southern Brazil, the single-direction D8 algorithm concentrated runoff along the main channel, whereas the D∞ method dispersed it [37].
Considering that topographic attributes are useful proxies for wet areas and river networks in river basins, and that very limited information about the topic exists in the tropics, the objective of this study was to select, calibrate, and validate appropriate topographic attributes, and use them to map wet areas and drainage networks of two Brazilian catchments, assessing the corresponding mapping accuracy with unbiased methods.

2. Materials and Prediction Models

2.1. Study Area

Two small and hydrologically similar catchments of the Brazilian Cerrado biome were studied: The Santa Maria and the Gama river basins, situated 20 km apart (Figure 1), in the vicinity of the city of Brasília (Brazil). The former basin was used to calibrate the threshold values of the selected topographic attributes used for mapping wet areas and stream heads, and the latter catchment was used to validate them. Table 1 presents the hydrologic characteristics of both catchments. In that table, rainfall and runoff were obtained from official raingages and streamgages located in both basins, respectively.
Detailed (1:10,000) and semi-detailed (1:50,000) digital maps of hydrography, soils, and land-use were available for the Santa Maria and Gama basins and were used as a reference. However, since these maps were produced with aerial photogrammetry and remote sensing, they are subject to cartographic errors and misrepresentations [32], and consequently were not taken as ground truth, but used only as a reference. Since the studied basins are natural protected areas with very limited access, ground-truthing through field verification, which could improve confidence in results, was difficult.
Both catchments have gentle slopes, well-drained (Oxisols) and poorly drained soils (Entisols), and are covered with different gradations of savanna vegetation [38]. In the upslope areas, open savanna occurs over well-drained soils. In valley bottoms, gallery forests cover poorly and well-drained soils, and grassy marshes occur over hydric soils (Figure 2 and Figure 3). Two types of valley bottoms exist in the catchments studied: V-type bottoms, where gallery forests predominate, and U-type bottoms, where marshy flats are dominant.

2.2. Selected Topographic Attributes

The selection of topographic attributes favored simplicity and data availability, requiring only the 30 m DEM as input. After a thorough search in the literature, the chosen attributes for the wet area delineation were the local slope and the slope curvature. The Topographic Wetness Index (TWI) was selected for the delineation of the drainage networks. In the case of the local slope, flatter areas are associated with hydric soils of humid basins [26], whereas the slope curvature is associated with areas of flow accumulation [15]. Although basin wetness is a time-dependent process, and despite the static nature of the TWI, key landscape markers of wetness, such as gallery forests and wetlands, are permanent and easily mapped features.
The Topographic Wetness Index (TWI) is an integrated indicator of concentrated flow paths [13,17], and is more suitable for drainage delineation. The TWI is simply [17]
TWI = ln (α/tan β)
where TWI = the wetness index (non-dimensional); α = the upslope contributing area per unit contour length (m), reflecting the tendency of the site to receive upslope water; and β = the local slope gradient (radians), indicating the tendency of the site to drain/retain water. In Equation (1), soil transmissivity was assumed to be constant throughout the catchment [39]. When the slope β in Equation (1) was smaller than 0.001, a constant value of 0.001 was added to avoid division by zero [40].
Considering that the D∞ flow routing algorithm tends to disperse water in gentle slopes, creating a feathering effect in the synthetic drainage network [12], the D8 flow direction routine [41], which concentrates runoff along a channel [37], was selected for the TWI computation. The DEM used in the calculation of the topographic attributes was the 1-arc-second, 30 m SRTM-Topodata, since it can capture enough topographical complexity [42], being available in all tropical regions of the world. All spatial calculations of the three topographic attributes, including their intermediary coverages (flow direction, filling, and flow accumulation), were performed with the ArcGIS 10.8.1® v.1 Spatial Analyst/ESRI package.

2.3. Drainage Network Delineation

Different simulated drainage networks were obtained with distinct TWI thresholds in the Santa Maria (calibration) basin [12,35]. The resulting synthetic stream networks were compared to the reference (map) hydrography. Following recommendations in the literature [34], the calibrated (optimal) TWI threshold in the Santa Maria catchment was obtained by balancing two mapping criteria: (i) the drainage network accuracy and (ii) the channel initiation accuracy, namely
A d = B p / T p + ( O 1 / T 1 ) 2
where Ad = drainage delineation accuracy, with a given TWI threshold; Bp = number of pixels of a given TWI drainage falling inside a 150 m buffer (sufficient to include most valley bottoms), built around the reference drainage network [43]; Tp = the total number of pixels of the TWI drainage network in the basin; O1 = number of first order streams of the reference map matched by TWI pixels; and T1 = total number of first order streams of the reference drainage network (map).
The left term in the numerator of Equation (2) represents the drainage delineation accuracy, and the right term indicates the channel initiation accuracy. The calibrated TWI threshold in the Santa Maria catchment, obtained by the maximization of Equation (2), was subsequently applied to the TWI in the Gama basin to validate the methodology. Finally, the delineation accuracy of both basins was compared with the accuracies of other drainage delineation studies in the literature.

2.4. Wet Area Delineation

The reference wet areas of both catchments were obtained by merging the features of ‘gallery forests’ and ‘grassy marshes’ in both land-use maps in the GIS [44]. Considering that wet areas in the landscape are associated with flats and hollows [4,26], a combination of local slope and slope curvature was used to delineate them [18,45,46], using the following thresholds:
Sc ≤ k1        and          Sl ≤ k2
where Sc = slope curvature; Sl = local slope grade, both obtained with the GIS, using the 30 m DEM; and k1 and k2 are calibrated threshold values. In Equation (3), the constant k1 is negative, since convergent landscape features, such as hollows and concave slopes, were sought. The value of k2, on the other hand, is small and positive, to assess valley flats.
The maps of local slope and slope curvature of the Santa Maria and Gama catchments are shown in Figure 4 and Figure 5, respectively. To assess the accuracy of the wet areas delineated by Equation (3), ten topographic transects [47] were randomly laid across riparian areas of both catchments (Figure 4).
Subsequently, the 10 gridded transects shown in Figure 4 were intersected in the GIS with the predicted and reference wet areas of both basins, and a corresponding confusion matrix was obtained. This matrix was used to assess the accuracy of the wet areas classification, comparing predicted and measured values. The wet area prediction accuracy was given by [47]:
A w = ( T p + T n ) ( T p + T n + F p + F n )
where Aw = wet area prediction accuracy; Tp = number of true positive pixels; Tn = number of true negative pixels; Fp = number of false positive pixels; and Fn = number of false negative pixels. A ‘true positive’ pixel was obtained when a predicted wet area in the transect lines matched a reference wet area. Conversely, a ‘true negative’ pixel occurred when a dry area was correctly predicted. A ‘false-positive’ (Type I error) was obtained when a predicted wet area in the transect was actually dry. Finally, a ‘false-negative’ (Type II error) occurred when a predicted dry area was actually wet.
In the calibration phase, carried out in the Santa Maria catchment, the thresholds k1 and k2, which maximized Equation (4), were obtained by trial and error. The calibrated values of k1 and k2 were then applied to the validation (Gama) catchment, and its prediction accuracy was calculated using Equation (4). Finally, the wet area delineation accuracy of both basins was compared with that of similar studies in the literature.

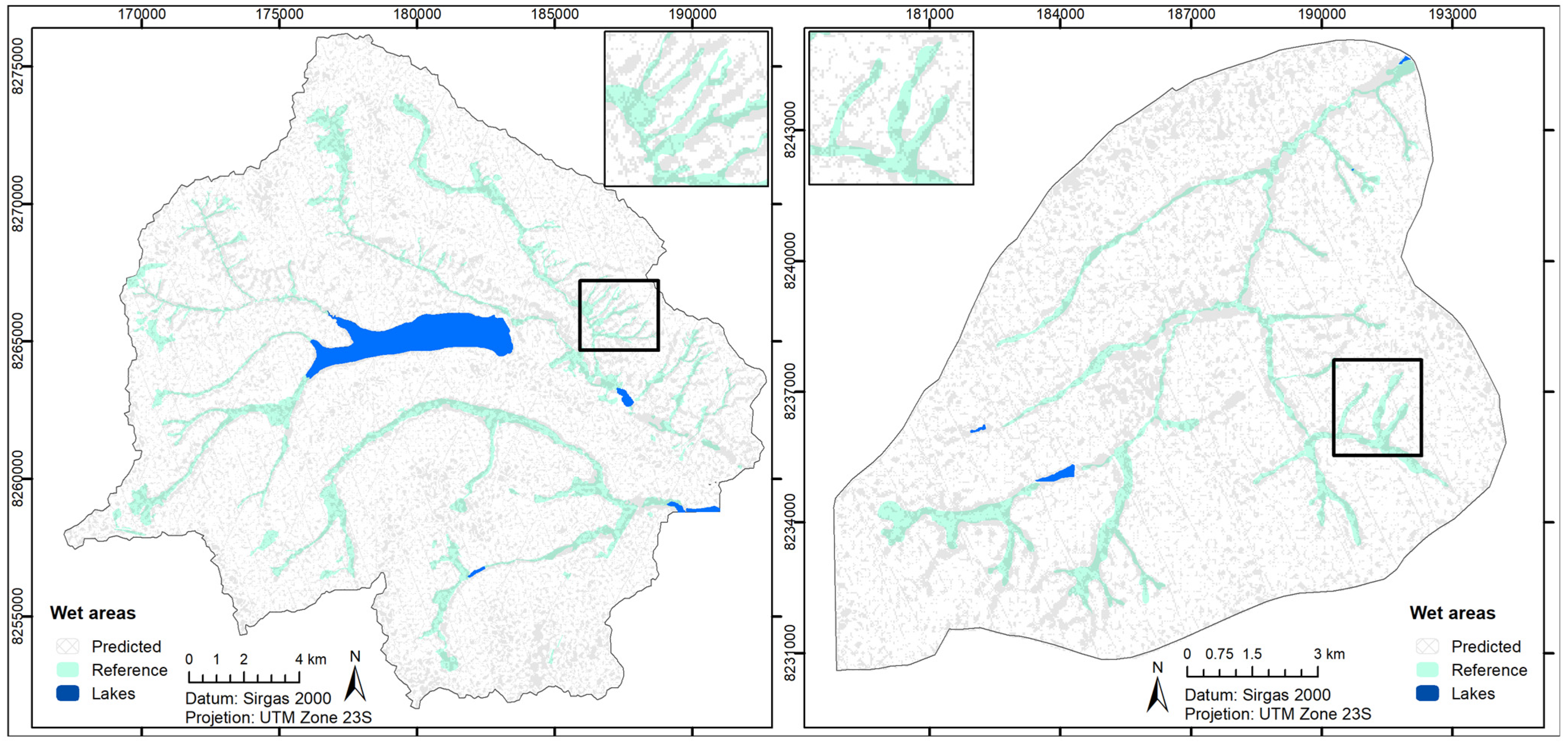
3. Results

3.1. Drainage Network Delineation

The calibrated value of TWI in the Santa Maria basin was TWI = 15, balancing stream initiation and channel delineation accuracies. A similar TWI threshold (TWI = 12) was obtained for a perennial drainage network in England [34]. In Australia, ephemeral gully heads occurred when TWI ≥ 7 [14]. The predicted and reference drainage networks of the calibration and validation catchments are presented in Figure 6. As expected, the synthetic drainage networks were concentrated flow paths, since the D8 single-direction routing algorithm was used [37].
Figure 6 indicates that there is a good agreement between the simulated and reference channel networks, particularly in the Santa Maria catchment. Despite small offsets being observed in the Gama basin, there was a good overall drainage delineation accuracy in both catchments, namely 67.2% and 70.7% for the Santa Maria and Gama basins, respectively (Table 2).

3.2. Wet Area Delineation

The calibrated values of slope curvature (Sc) and local slope (Sl) in the Santa Maria basin were −0.05 and 0.01, respectively, and the simulated and reference wet areas of the Santa Maria and Gama catchments are presented in Figure 7. Table 3 shows the confusion matrix and the overall wet area delineation accuracy for both catchments.
According to Table 3, the overall wet area delineation accuracies in the Santa Maria and Gama catchments were 72.7% and 73.8%, respectively. The predicted wet areas in both catchments were concentrated in the valley bottoms, although some scattered pixels occurred in well-drained upslope areas, since small flat areas also occur in the higher elevations of the watersheds.

4. Discussion

4.1. Drainage Network Delineation

According to Table 2, channel delineation (accuracies of 78.9% and 77.5%) was better predicted than channel initiation (accuracies of 44.4% and 63.9%), in the Santa Maria and Gama basins, respectively. Figure 6 also indicates that higher-order channels were better delineated than first-order streams.
Nevertheless, the overall drainage network prediction accuracies in Table 2 were equivalent to or higher than those found in the literature. In the USA, it was found that stream mapping accuracy using ln(α) varied between 30% and 55% [28], depending on the geology. In Algeria, a Spearman correlation of 0.5 was obtained between the predicted and observed gully heads using the TWI [48].
The homogeneous geology and gentle topography of the Santa Maria and Gama catchments, with corresponding dendritic drainage patterns (Figure 2 and Figure 3), may have contributed to the good TWI mapping accuracy. The discrepancies observed between the synthetic and reference drainage networks resulted from a combination of TWI (model) error and cartographic misrepresentation of the reference maps [35].
Additionally, the large DEM grid size [34,47] and DEM vertical error, the latter resulting from the SRTM radar’s inability to penetrate dense riparian vegetation [48], may have contributed to reducing the accuracies in drainage delineation. Indeed, previous studies in Brazil showed that SRTM errors were linearly related to slope, with the highest vertical errors (RMSE = 8.5 m) occurring in forest areas [48], the same as expected in the present study. Finally, channel initiation was overestimated by the TWI with respect to the reference (map) network because many simulated first-order channels corresponded to temporary streams and ravines in the reference maps [32].

4.2. Wet Area Delineation

Although the overall wet area delineation accuracies of the Santa Maria and Gama catchments were acceptable (72.7% and 73.8%, respectively), wet areas were incorrectly assigned to the basins’ upslope (dry) zones (Figure 7). This may have resulted from model error, large DEM grid size [19], and DEM vertical inaccuracy [48], affecting the overall mapping accuracy. Additionally, since the land-use feature ‘gallery forest’ was taken as a reference wet area, its occurrence over both well- and poorly drained soils [26] may have contributed to reducing the wet area delineation accuracy [4].
In the literature, wet area mapping using topographic attributes showed mixed results. A mapping accuracy of 85.2% was obtained in Sweden, using a combination of TWI and a depth-to-water index [47]. An R2 of 0.61 was obtained between the TWI and wet areas in the USA [19], and a mapping accuracy of 73% was obtained in California [43].
Considering that both studies used DEMs with a higher spatial resolution and secondary topographic attributes, the simplicity and robustness of the proposed method are encouraging, allowing for its utilization in the mapping of drainage networks and wet areas of data-scarce tropical catchments. However, since the proposed method was developed in a specific tropical setting, caution should be utilized in extrapolating it to different landscapes and climatic conditions, without the necessary adjustments.

5. Conclusions

Topographic attributes were used to delineate drainage networks and wet areas in two similar catchments of the Cerrado biome in Central Brazil. The selected attributes were the TWI, the local slope, and the slope curvature, respectively. A 30 m SRTM DEM was used as input, and hydrographic and land-use maps were used as references. The selected topographic attributes were calibrated in the Santa Maria catchment and subsequently validated in the nearby Gama basin, with unbiased multi-criteria metrics.
The accuracies obtained for the simulated drainage networks (67.2% and 70.7%) and wet areas (72.7% and 73.8%), for the Santa Maria and Gama catchments, respectively, were equivalent to or higher than those of similar studies in the literature. The mapping errors were associated with DEM grid size, DEM vertical inaccuracy, and reference map bias. The novelty of the study is the use of readily available information to map, with simplicity and robustness, wet areas and channel initiation in data-scarce, tropical environments.

Author Contributions

Methodology, H.M.L.C.; Software, M.T.L.M. and M.R.S.F.; Validation, M.T.L.M.; Formal analysis, H.M.L.C.; Data curation, M.T.L.M.; Writing—original draft, H.M.L.C.; Writing—review & editing, M.R.S.F. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Research data are available upon request.

Acknowledgments

This research was an initiative of the GRAPHIC/UNESCO Project in Latin America and the Caribbean, with the auspices of The Nature Conservancy-Brazil, and carried out at the Watershed Management Laboratory of the School of Technology of the University of Brasilia-UnB.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Laudon, H.; Kuglerová, L.; Sponseller, M.F.; Nordin, A.; Bishop, K.; Lundmark, T.; Egnell, G.; Anneli, A. The Role of Biogeochemical Hotspots, Landscape Heterogeneity, and Hydrological Connectivity for Minimizing Forestry Effects on Water Quality. Ambio 2016, 45, S152–S162. [Google Scholar] [CrossRef]
  2. Tomer, M.D.; Dosskey, M.G.; Burkart, M.R.; James, D.E.; Helmers, M.J.; Eisenhauer, D.E. Methods to Prioritize Placement of Riparian Buffers for Improved Water Quality. Agrofor. Syst. 2009, 75, 17–25. [Google Scholar] [CrossRef]
  3. Johnson, M.A.; Saraiva, P.M.; Coelho, D. The Role of Gallery Forests in the Distribution of Cerrado Mammals. Rev. Bras. Biol. 1999, 59, 421–427. [Google Scholar] [CrossRef]
  4. Skorupa, A.L.A.; Fay, M.; Zinn, Y.L.; Scheuber, M. Assessing Hydric Soils in a Gallery Forest in the Brazilian Cerrado. Soil Use Manag. 2013, 29, 119–129. [Google Scholar] [CrossRef]
  5. Eiten, G. The Cerrado Vegetation of Brazil. Bot. Rev. 1972, 38, 201–341. [Google Scholar] [CrossRef]
  6. De Oliveira-Filho, A.T.; Shepherd, G.J.; Martins, F.R.; Stubblebine, W.H. Environmental Factors Affecting Physiognomic and Floristic Variation in an Area of Cerrado in Central Brazil. J. Trop. Ecol. 1989, 5, 413–431. [Google Scholar] [CrossRef]
  7. Johnston, R.; Cools, J.; Liersch, S.; Morardet, S.; Murgue, C.; Mahieu, M.; Zsuffa, I.; Uyttendaele, G.P. WETwin: A Structured Approach to Evaluating Wetland Management Options in Data-Poor Contexts. Environ. Sci. Policy 2013, 34, 3–17. [Google Scholar] [CrossRef]
  8. Anaya-Acevedo, J.A.; Escobar-Martínez, J.F.; Massone, H.; Booman, G.; Quiroz-Londoño, O.M.; Cañón-Barriga, C.C.; Montoya-Jaramillo, L.J.; Palomino-Ángel, S. Identificación de Áreas de Humedal En El Contexto Del Desarrollo Agrícola Usando Teledetección y SIG. DYNA 2017, 84, 186–194. [Google Scholar] [CrossRef]
  9. Güntner, A.; Seibert, J.; Uhlenbrook, S. Modeling Spatial Patterns of Saturated Areas: An Evaluation of Different Terrain Indices. Water Resour. Res. 2004, 40, 1–19. [Google Scholar] [CrossRef]
  10. Lenza, E.; Santos, J.O.; Maracahipes-Santos, L. Species Composition, Diversity, and Vegetation Structure in a Gallery Forest-Cerrado Sensu Stricto Transition Zone in Eastern Mato Grosso, Brazil. Acta Bot. Bras. 2015, 29, 327–338. [Google Scholar] [CrossRef]
  11. Dunne, T. Formation and Controls of Channel Networks. Prog. Phys. Geogr. 1980, 4, 28. [Google Scholar] [CrossRef]
  12. Hastings, B.E.; Kampf, S.K. Evaluation of Digital Channel Network Derivation Methods in a Glaciated Subalpine Catchment. Earth Surf. Process. Landf. 2014, 39, 1790–1802. [Google Scholar] [CrossRef]
  13. O’Loughlin, E.M.O.; Resources, L. Natural Catchments by Topographic Analysis Net Drainage Flu x q • i •••. Water Resour. 1986, 22, 794–804. [Google Scholar]
  14. Moore, I.D.; Burch, G.J.; Mackenzie, D.H. Topographic Effects on the Distribution of Surface Soil Water and the Location of Ephemeral Gullies. Trans. Am. Soc. Agric. Eng. 1988, 31, 1098–1107. [Google Scholar] [CrossRef]
  15. Moore, I.D.; Grayson, R.B.; Ladson, A.R. Digital Terrain Modelling: A Review of Hydrological, Geomorphological, and Biological Applications. Hydrol. Process. 1991, 5, 3–30. [Google Scholar] [CrossRef]
  16. Detty, J.M.; McGuire, K.J. Topographic Controls on Shallow Groundwater Dynamics: Implications of Hydrologic Connectivity between Hillslopes and Riparian Zones in a till Mantled Catchment. Hydrol. Process. 2010, 24, 2222–2236. [Google Scholar] [CrossRef]
  17. Beven, K.J.; Kirkby, M.J. A Physically Based, Variable Contributing Area Model of Basin Hydrology. Hydrol. Sci. Bull. 1979, 24, 43–69. [Google Scholar] [CrossRef]
  18. Burt, T.P.; Butcher, D.P. Topographic Controls of Soil Moisture Distributions. J. Soil. Sci. 1985, 36, 469–486. [Google Scholar] [CrossRef]
  19. Buchanan, B.P.; Fleming, M.; Schneider, R.L.; Richards, B.K.; Archibald, J.; Qiu, Z.; Walter, M.T. Evaluating Topographic Wetness Indices across Central New York Agricultural Landscapes. Hydrol. Earth Syst. Sci. 2014, 18, 3279–3299. [Google Scholar] [CrossRef]
  20. Güntner, A.; Krol, M.S.; Araújo, J.C.D.; Bronstert, A. Simple Water Balance Modelling of Surface Reservoir Systems in a Large Data-Scarce Semiarid Region/Modélisation Simple Du Bilan Hydrologique de Systèmes de Réservoirs de Surface Dans Une Grande Région Semi-Aride Pauvre En Données. Hydrol. Sci. J. 2004, 49, 901–918. [Google Scholar] [CrossRef]
  21. Grabs, T.; Seibert, J.; Bishop, K.; Laudon, H. Modeling Spatial Patterns of Saturated Areas: A Comparison of the Topographic Wetness Index and a Dynamic Distributed Model. J. Hydrol. 2009, 373, 15–23. [Google Scholar] [CrossRef]
  22. Chang, C.-H.; Lee, K.T. Analysis of Geomorphologic and Hydrological Characteristcs in Watershed Saturated Areas Using Topographic-Index Threshold and Geomorphology-Based Runoff Model. Hydrol. Process. 2008, 22, 802–812. [Google Scholar] [CrossRef]
  23. Qin, C.Z.; Zhu, A.X.; Pei, T.; Li, B.L.; Scholten, T.; Behrens, T.; Zhou, C.H. An Approach to Computing Topographic Wetness Index Based on Maximum Downslope Gradient. Precis. Agric. 2011, 12, 32–43. [Google Scholar] [CrossRef]
  24. Ali, G.; Birkel, C.; Tetzlaff, D.; Soulsby, C.; Mcdonnell, J.J.; Tarolli, P. A Comparison of Wetness Indices for the Prediction of Observed Connected Saturated Areas under Contrasting Conditions. Earth Surf. Process. Landf. 2014, 39, 399–413. [Google Scholar] [CrossRef]
  25. Silva, B.P.C.; Naves Silva, M.L.; Avalos, F.A.P.; Duarte de Menezes, M.; Curi, N. Author Correction: Digital Soil Mapping Including Additional Point Sampling in Posses Ecosystem Services Pilot Watershed, Southeastern Brazil. Sci. Rep. 2019, 9, 16147. [Google Scholar] [CrossRef]
  26. Marimon, B.S.; Felfili, J.M.; Lima, E.D.S.; Duarte, W.M.G.; Marimon-Júnior, B.H. Environmental Determinants for Natural Regeneration of Gallery Forest at the Cerrado/Amazonia Boundaries in Brazil. Acta Amaz. 2010, 40, 107–118. [Google Scholar] [CrossRef]
  27. Roth, G.; La Barbera, P. Morphological Characterization of Channel Initiation. Phys. Chem. Earth 1997, 22, 329–332. [Google Scholar] [CrossRef]
  28. Julian, J.P.; Elmore, A.J.; Guinn, S.M. Channel Head Locations in Forested Watersheds across the Mid-Atlantic United States: A Physiographic Analysis. Geomorphology 2012, 177–178, 194–203. [Google Scholar] [CrossRef]
  29. Montgomery, D.R.; Dietrich, W.E. Channel Initiation and the Problem of Landscape Scale. Science 1992, 255, 826–830. [Google Scholar] [CrossRef]
  30. Gallon, E.; Lindberg, S. Where Does the Stream Begin? Stream Initiation under Variable Wetness Conditions in a Boreal Landscape; Självständigt Arb.: Upsalla, Sweden, 2014; 34p. [Google Scholar]
  31. Henkle, J.E.; Wohl, E.; Beckman, N. Locations of Channel Heads in the Semiarid Colorado Front Range, USA. Geomorphology 2011, 129, 309–319. [Google Scholar] [CrossRef]
  32. Jaeger, K.L.; Montgomery, D.R.; Bolton, S.M. Channel and Perennial Flow Initiation in Headwater Streams: Management Implications of Variability in Source-Area Size. Environ. Manag. 2007, 40, 775–786. [Google Scholar] [CrossRef] [PubMed]
  33. Montgomery, D.R.; Dietrich, W.E. Source Areas, Drainage Density, and Channel Initiation. Water Resour. Res. 1989, 25, 1907–1918. [Google Scholar] [CrossRef]
  34. Quinn, P.F.; Beven, K.J.; Lamb, R. The in(a/Tan/β) Index: How to Calculate It and How to Use It within the Topmodel Framework. Hydrol. Process. 1995, 9, 161–182. [Google Scholar] [CrossRef]
  35. Kim, S.; Lee, H. A Digital Elevation Analysis: A Spatially Distributed Flow Apportioning Algorithm. Hydrol. Process. 2004, 18, 1777–1794. [Google Scholar] [CrossRef]
  36. McMaster, K.J. Effects of Digital Elevation Model Resolution on Derived Stream Network Positions. Water Resour. Res. 2002, 38, 13-1–13-18. [Google Scholar] [CrossRef]
  37. Ruhoff, A.L.; Castro, N.M.R.; Risso, A. Numerical Modelling of the Topographic Wetness Index: An Analysis at Different Scales. Int. J. Geosci. 2011, 2, 476–483. [Google Scholar] [CrossRef]
  38. Unesco. Vegetação No Distrito Federal: Tempo e Espaço. In Uma Avaliação Multitemporal Da Perda de Cobertura Vegetal No DF e Da Diversidade Florística Da Reserva Da Biosfera Do Cerrado—Fase I, 2nd ed.; UNESCO: Brasilia, Brazil, 2002; ISBN 8587853716. [Google Scholar]
  39. Schneiderman, E.M.; Steenhuis, T.S.; Thongs, D.J.; Easton, Z.M.; Zion, M.S.; Neal, A.L.; Mendoza, G.F.; Walter, M.T. Incorporating Variable Source Area Hydrology into a Curve-Number-Based Watershed Model. Hydrol. Process. 2007, 21, 3420–3430. [Google Scholar] [CrossRef]
  40. O’Neill, M.P.; Schmidt, J.C.; Dobrowolski, J.P.; Hawkins, C.P.; Neale, C.M.U. Identifying Sites for Riparian Wetland Restoration: Application of a Model to the Upper Arkansas River Basin. Restor. Ecol. 1997, 5, 85–102. [Google Scholar] [CrossRef]
  41. Jenson, S.K.; Domingue, J.O. Extracting Topographic Structure from Digital Elevation Data for Geographic Information System Analysis. Photogramm. Eng. Remote Sens. 1988, 54, 1593–1600. [Google Scholar]
  42. Valeriano, M.; Rossetti, D.; Albuquerque, P.C.G. Topodata: Desenvolvimento Da Primeira Versão Do Banco de Dados Geomorfométricos Locais Em Cobertura Nacional. In Proceedings of the Anais XIV Simpdzsio Brasileiro de Sensoriamento Remoto, Natal, Brazil, 25–30 April 2009; pp. 5499–5506. [Google Scholar]
  43. Russell, G.D.; Hawkins, C.P.; O’Neill, M.P. The Role of GIS in Selecting Sites for Riparian Restoration Based on Hydrology and Land Use. Restor. Ecol. 1997, 5, 56–68. [Google Scholar] [CrossRef]
  44. Rinderer, M.; van Meerveld, H.J.; Seibert, J. Topographic Controls on Shallow Groundwater Levels in a Steep, Prealpine Catchment: When Are the TWI Assumpitions Valid? Water Resour. Res. 2014, 50, 6067–6080. [Google Scholar] [CrossRef]
  45. Ågren, A.M.; Lidberg, W.; Strömgren, M.; Ogilvie, J.; Arp, P.A. Evaluating Digital Terrain Indices for Soil Wetness Mapping—A Swedish Case Study. Hydrol. Earth Syst. Sci. 2014, 18, 3623–3634. [Google Scholar] [CrossRef]
  46. Dewitte, O.; Daoudi, M.; Bosco, C.; Van Den Eeckhaut, M. Predicting the Susceptibility to Gully Initiation in Data-Poor Regions. Geomorphology 2015, 228, 101–115. [Google Scholar] [CrossRef]
  47. Capoane, V.; Tiecher, T.; Rasche Alvarez, J.W.R.; Pellegrini, A.; Schaefer, G.L.; Santos, L.J.C.; dos Santos, D.R. Influência Da Resolução Do Modelo Digital de Elevação Na Determinação Do Índice Topográfico de Umidade e Na Capacidade de Predição Dos Teores Carbono Orgânico Do Solo. Geo UERJ 2015, 27, 144–155. [Google Scholar] [CrossRef]
  48. Orlandi, A.G.; de Carvalho Júnior, O.A.; Guimarães, R.F.; de Souza Bias, E.; Corrêa, D.C.; Gomes, R.A.T. Vertical Accuracy Assessment of the Processed SRTM Data for the Brazilian Territory. Bol. Ciênc. Geod. 2019, 25, e2019021. [Google Scholar] [CrossRef]
Water 17 02298 g001
Figure 1. Location of the Santa Maria and Gama catchments, in Central Brazil.
Figure 1. Location of the Santa Maria and Gama catchments, in Central Brazil.
Water 17 02298 g001
Water 17 02298 g002
Figure 2. Elevation, hydrography, soils, and land-use of the Santa Maria catchment.
Figure 2. Elevation, hydrography, soils, and land-use of the Santa Maria catchment.
Water 17 02298 g002
Water 17 02298 g003
Figure 3. Elevation, hydrography, soils, and land-use of the Gama catchment.
Figure 3. Elevation, hydrography, soils, and land-use of the Gama catchment.
Water 17 02298 g003
Water 17 02298 g004
Figure 4. Local slope of the Santa Maria (left) and Gama (right) catchments, and the topographic transects used to assess wet area delineation accuracy.
Figure 4. Local slope of the Santa Maria (left) and Gama (right) catchments, and the topographic transects used to assess wet area delineation accuracy.
Water 17 02298 g004
Water 17 02298 g005
Figure 5. Slope curvatures of the Santa Maria (left) and Gama (right) catchments.
Figure 5. Slope curvatures of the Santa Maria (left) and Gama (right) catchments.
Water 17 02298 g005
Water 17 02298 g006
Figure 6. Predicted (TWI-based) and reference drainage networks of the Santa Maria (left) and Gama (right) catchments. The insets show network in higher detail.
Figure 6. Predicted (TWI-based) and reference drainage networks of the Santa Maria (left) and Gama (right) catchments. The insets show network in higher detail.
Water 17 02298 g006
Water 17 02298 g007
Figure 7. Predicted and reference wet areas of the Santa Maria (left) and Gama (right) catchments. The insets show wet areas in higher detail.
Figure 7. Predicted and reference wet areas of the Santa Maria (left) and Gama (right) catchments. The insets show wet areas in higher detail.
Water 17 02298 g007
Table 1. Main hydrologic characteristics of the Santa Maria and Gama catchments.
Table 1. Main hydrologic characteristics of the Santa Maria and Gama catchments.
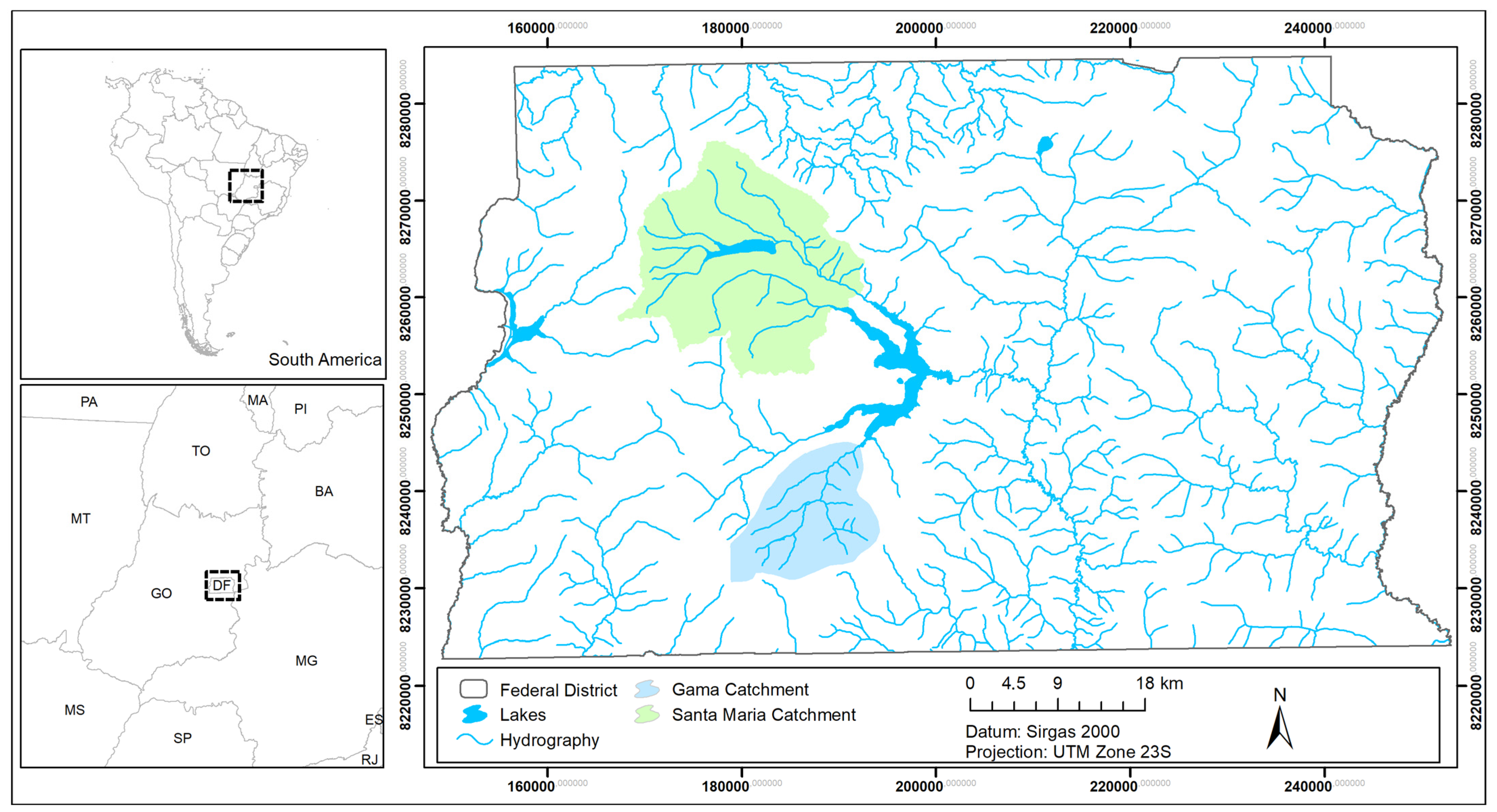
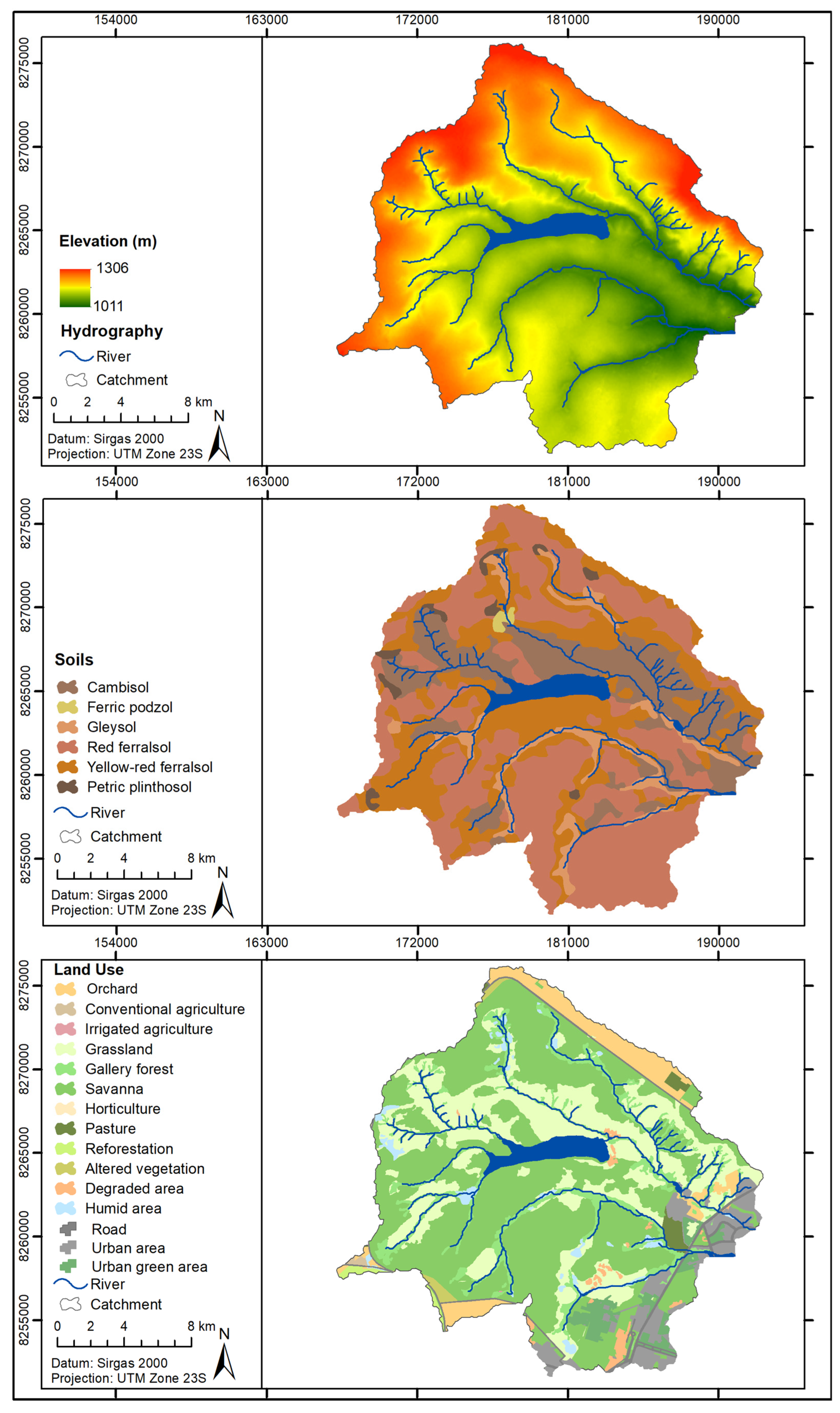
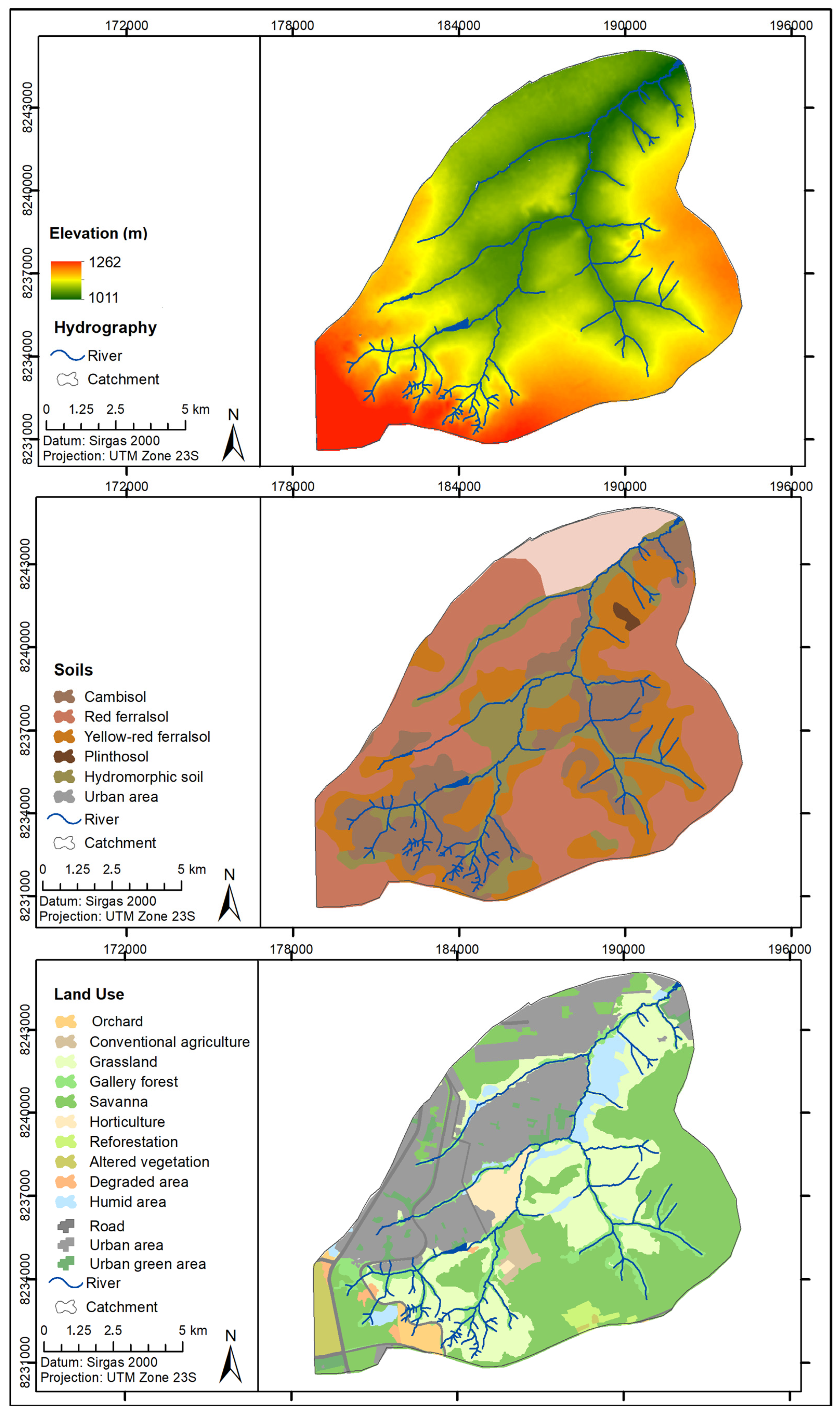
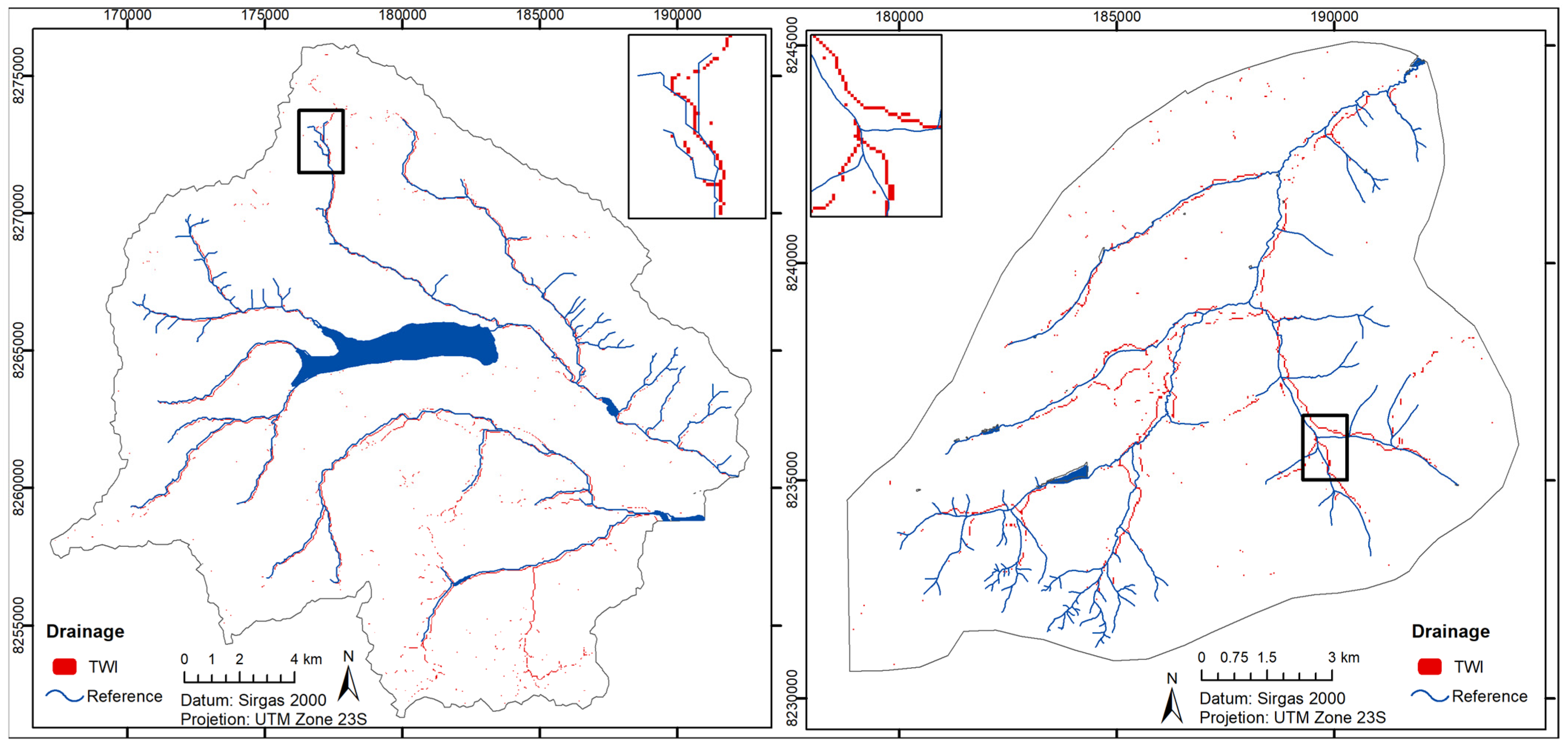
CatchmentArea
(km2)		Hmin
(m)		Hmax
(m)		Slope
(%)		Dd
(km−1)		CrOP
(mm)		Q
(mm)
Santa Maria (C)368.8101213075.040.450.4841400335
Gama (V)144.7101212636.730.580.4441460326
Notes: Hmin = minimum altitude; Hmax = maximum altitude; Dd = drainage density; Cr = Miller’s circularity ratio; O = Strahler’s basin order; P = mean annual precipitation; Q = mean annual runoff; C = calibration catchment; V = validation catchment.
Table 2. Drainage network mapping accuracy of the Santa Maria (calibration) and Gama (validation) catchments, using TWI.
Table 2. Drainage network mapping accuracy of the Santa Maria (calibration) and Gama (validation) catchments, using TWI.
CatchmentNetwork Delineation Accuracy (%)Channel Initiation Accuracy (%)Overall Accuracy
(%)
Santa Maria78.944.467.2
Gama77.563.970.7
Table 3. Confusion matrix and overall wet area delineation accuracy of the Santa Maria and Gama catchments.
Table 3. Confusion matrix and overall wet area delineation accuracy of the Santa Maria and Gama catchments.
Reference Wet Area
S.Maria (N = 2171) Gama (N = 1420)
NoYes NoYes
Predicted Wet AreaNo140683No91180
Yes510172Yes292137
Overall Accuracy 72.7% 73.8%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Chaves, H.M.L.; Montalvão, M.T.L.; Fonseca, M.R.S. Mapping Wet Areas and Drainage Networks of Data-Scarce Catchments Using Topographic Attributes. Water 2025, 17, 2298. https://doi.org/10.3390/w17152298

AMA Style

Chaves HML, Montalvão MTL, Fonseca MRS. Mapping Wet Areas and Drainage Networks of Data-Scarce Catchments Using Topographic Attributes. Water. 2025; 17(15):2298. https://doi.org/10.3390/w17152298

Chicago/Turabian Style

Chaves, Henrique Marinho Leite, Maria Tereza Leite Montalvão, and Maria Rita Souza Fonseca. 2025. "Mapping Wet Areas and Drainage Networks of Data-Scarce Catchments Using Topographic Attributes" Water 17, no. 15: 2298. https://doi.org/10.3390/w17152298

APA Style

Chaves, H. M. L., Montalvão, M. T. L., & Fonseca, M. R. S. (2025). Mapping Wet Areas and Drainage Networks of Data-Scarce Catchments Using Topographic Attributes. Water, 17(15), 2298. https://doi.org/10.3390/w17152298

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop