How Cooperative Are Games in River Sharing Models?

Abstract

There is a long tradition of studying river sharing problems. A central question frequently examined and addressed is how common benefits or costs can be distributed fairly. In this context, axiomatic approaches of cooperative game theory often use contradictory principles of international water law, which are strictly rejected in practice. That leads to the question: Are these methods suitable for a real-world application? First, we conduct a systematic literature review based on the PRISMA approach to categorise the river sharing problems. We identified several articles describing a variety of methods and real-world applications, highlighting interdisciplinary interest. Second, we evaluate the identified axiomatic literature related to TU games with regard to their suitability for real-world applications. We exclude those “standalone” methods that exclusively follow extreme principles and/or do not describe cooperative behaviour. This is essential for a fair distribution. Third, we propose to use the traditional game-theoretical approach of airport games in the context of river protection measures to ensure a better economic interpretation and to enforce future cooperation in the joint implementation of protective measures.

1. Introduction

The equitable use of watercourses with several riparians has long been the subject of scientific discussion under the term river sharing problem (e.g., Rogers [1]; Suzuki & Nakayama [2]; Dinar & Howitt [3]; Ambec & Sprumont [4]). There are 310 international river basins worldwide that have at least two riparian states. The Danube is the river with the most riparian states ($n=19$) in the world. It flows from Germany through Austria, Slovakia, Hungary, Croatia, Serbia, Romania, Bulgaria, the Republic of Moldova, and Ukraine into the Black Sea. Its catchment area also includes the following countries: Albania, Bosnia and Herzegovina, the Czech Republic, Italy, Montenegro, Slovenia, Switzerland, the Republic of North Macedonia, and Poland (McCracken & Wolf [5]). Further selected international rivers and their riparian states are listed in

Table 1. Data on selected international rivers (data from McCracken & Wolf [5]).

River	Number of Riparian States	Continent	Area ${\mathrm{km}}^2$
Oder/Odra	3	Europe	119,252
Elbe	4	Europe	145,157
Tigris-Euphrates/Shatt al Arab	6	Asia	868,989
Amazonas	7	South America	5,952,595
Indus	7	Asia	855,875
Nile	14	Africa	2,961,325
Danube	19	Europe	800,970

.

In this context, the following types of questions arise: How can water resources be distributed fairly?, How can the costs of water pollution be distributed fairly?, How can flood costs be distributed fairly?, etc. The Convention on the Law of the Nonnavigational Uses of International Watercourses as instrument of international water law, provides an answer. Among other things, it codifies an equitable and reasonable utilisation of rivers between countries. A general principle is not to cause significant harm to riparian states through the use of an international watercourse. In that sense a riparian has to avoid the damage costs of downstream riparians. However, even within a country, there are several stakeholders on a river, such as federal states, districts or municipalities. Often, the problem to be observed and solved is that several upstream and downstream riparians have access to the water body and can use and influence this resource to different degrees due to their spatial and geographical location. This leads to the following constellations:

• On the one hand, the upstream riparian has de facto supremacy over the downstream riparian, which leads to a variety of problems:

  -

  In the event of pollution of the watercourse or the discharge or accumulation of water, the downstream party shall bear the damage or the resulting costs. However, the upstream party is responsible for the costs.

  -

  Flood protection measures of the upstream riparian lead to a benefit that is also experienced by the downstream riparian. The upstream riparian often has the most cost-effective flood protection options at its disposal by regulating the volume of water through retention basins and dams. However, the situation is characterised by the fact that the upstream riparian bears the burden and the downstream riparian the benefit of these measures.

• On the other hand, flood protection measures of the downstream riparian can lead to an impairment of the upstream riparian. For example, the raising of dams in the area of the downstream riparian causes a reduced discharge and thus a backwater for the residents further upstream. This phenomenon leads to a “race” of the dams upstream, starting with the downstream riparians and ending with the upstream riparians. One possible solution is for downstream riparians to make areas available to enable rapid runoff and receive compensation payments from upstream riparians in return.

In the context of flooding or pollution, an upstream player has to invest in measures to protect downstream states from harm. If an upstream state causes damage, it should eliminate or mitigate it and, if appropriate, resolve the issues of financial compensation. The game theory literature often targets the second case, i.e., how to fairly share the damage costs caused especially by upstream players (e.g., Ni & Wang [6]; van den Brink et al. [7]; Abraham & Ramachandran [8]). However, for an application, it is necessary to measure the contribution of an upstream state to damage on the riparian player’s territory exactly. Furthermore, two controversial and contradictory principles are often used in the axiomatic literature on international water disputes, since the property rights are not well-defined and thus the Coase theorem [9] cannot be applied. In the meantime, a whole range of different types or classes of river sharing problems have emerged from the original considerations, which use different approaches to modelling. Therefore, we would like to refer to some academic overviews with different focuses: Madani [10]; Beal et al. [11]; Dinar & Hogarth [12] and Dinar [13]. There is an agreement that cooperative measures achieve higher benefits and cause lower costs than isolated measures. The aims of this work are the following:

• Conduct a systematic literature review to categorise the river sharing problems;
• Examine the identified axiomatic literature related to TU games with regard to its suitability for real-world application; and
• Present a unifying approach to share investments in flood or pollution control fairly.

This paper is organised as follows. We begin by describing the different principles of international water law. The development of international water law has been extensively explored and debated by numerous scholars over the decades. While the literature encompasses various perspectives and interpretations, there is a consensus that extreme positions, such as Absolute Territorial Sovereignty and Unlimited Territorial Integrity, are impractical for resolving water conflicts. These doctrines overlook the shared nature of rivers, necessitating a more balanced approach. Modern international water law thus emphasises principles such as Limited Territorial Sovereignty and Limited Territorial Integrity, promoting equitable and reasonable use while minimising significant harm to other states. Then, we describe some necessary definitions of cooperative game theory and explain when the use of TU games for modelling is normatively appropriate. This is necessary to evaluate the results of the following systematic literature review. Next, we describe the methodology (Section 4) and the results of our systematic literature review (Section 5). We follow the PRISMA approach and describe the identified works addressing the river sharing problem. After that, we focus exclusively on axiomatic approaches. First, we examine their research objectives and the principles they follow. We then examine its games and solutions and evaluate them with regard to suitability for a real-world application. Section 6 shows how airport games can be used to share costs for joint river protection measures. Furthermore, Section 7 shows a real case study. Section 8 concludes the paper.

2. Principles of International Water Law

Scholars agree that extreme positions are ineffective for resolving water conflicts due to the shared nature of rivers. Modern international water law therefore adopts balanced approaches that focus on equitable and reasonable use while minimising harm to states. This will be examined in more detail below. The literature on the development of international water law is diverse and is only briefly mentioned here (e.g., Lipper [14]; Lammers [15]; Moermond III & Shirley [16]; McCaffrey [17]; Gleick [18]; Dellapenna [19]; Caponera & Nanni [20]; McIntyre [21]; McCaffrey [22]; De Castro [23]; Mager [24]; Devlaeminck [25]; Kuokkanen [26]; McCaffrey [27]; Meshel [28]; Tortajada & Araral [29]; Zheng & Spijkers [30]; Meshel [31]; Liu [32]). However, the literature agrees on one thing: both the Absolute Territorial Sovereignty (ATS) and the Unlimited Territorial Integrity (UTI) are unsuitable for resolving water conflicts because they ignore the nature of a river as a shared resource (e.g., Lammers [15]; Wolf [33]; Kuokkanen [26]; Tignino & Bréthaut [34]). Furthermore, no case in the modern world is known in which an international court/tribunal has ruled according to these extreme principles (e.g., Moermond III & Shirley [16]; Wolf [33]; Salman [35]; McIntyre [21]; Mohammed [36]). ATS and UTI describe extreme scenarios, and we explain this in more detail below.

ATS, also called Harmon Doctrine, goes back to Judson Harmon (e.g., Wolf [33]; Salman [35]; Mohammed [36]). In 1895, as Attorney General, he advised the United States on the water dispute with Mexico over the Rio Grande. In short, the ATS is described as absolute control over the waters in one’s own territory (Mohammed [36]). However, this does not fully reflect Harmon’s argument. The United States and Mexico concluded the Treaty of Guadalupe Hidalgo in 1848. It guarantees freedom of navigation for both countries in the border region. The starting point of the 1895 dispute was Mexico’s claim that a water diversion in the United States had caused water shortages near El Paso for most of the year (McCaffrey [37]). In Harmon’s [38] view, this agreement only covered the course of the Rio Grande below the New Mexico border (the navigable portions), the section that Mexico shares with Texas. Actions taking place more upstream would not be part of the treaty. Lammers (1984 [15], as cited in Moermond III & Shirley [16]) argues that the Harmon Doctrine in its original form leads to a contradiction:

“It is clear that the unrestricted disposal by State A of the waters of an international watercourse flowing from that State into State B based on the idea of State A’s absolute territorial sovereignty is incompatible with the unrestricted disposal of those waters to which State B would be likewise entitled on the basis of its absolute territorial sovereignty over the natural resources which nature would ordinarily bring into its territory […]. Unlimited disposal by State A of its territory will make the unlimited disposal by State B of its territory impossible and vice versa. Thus, if not already untenable because of the social and economic injustice to which the application of the principle of absolute territorial sovereignty would lead, such application would already seem impossible because of the legal contradiction inherent in the principle itself.”

However, Harmon [38] stated that this case was novel at the time and should therefore be decided solely on a political level and not by his legal opinion. Therefore, the Harmon Doctrine should rather be understood as an expression of the absence of specific rules in international law (Lipper [14]; Moermond III & Shirley [16]). Interestingly, the conflict was resolved a few years later through the construction of a dam and the signing of a treaty on the equitable distribution of the Rio Grande’s water. The United States covered all costs, and in return, Mexico waived any claims for compensation (McCaffrey [37]).

In contrast to ATS, the principle of UTI favors the downstream states. According to this, states can demand the flow of water upstream and may not restrict the natural flow downstream. Wolf [33] stated to ATS and UTI:

“Both absolute principles were effectively dismissed when a 1957 arbitration tribunal ruled in the case that “territorial sovereignty …must bend before all international obligations”, effectively negating the doctrine of absolute sovereignty. Yet the tribunal also admonished the downstream State from the right to veto ‘reasonable’ upstream development, thereby negating the principle of natural flow or absolute riverain integrity. This decision made possible the 1958 Lac Lanoux treaty (revised in 1970), in which it is agreed that water is diverted out-of-basin for French hydropower generation, and a similar quantity is returned before the stream reaches Spanish territory.”

Since these two extreme positions are irreconcilable, only a compromise between the two principles can provide a solution. Restrictions on ATS, respectively, UTI lead to Limited Territorial Sovereignty (LTS), respectively, Limited Territorial Integrity (LTI), which is a fundamental principle of modern international water law (Moermond III & Shirley [16]; Salman [35]; Mohammed [36]). This reinforces the further principle of equitable and reasonable use of water resources. The sovereignty of a state is limited by the fact that it does not cause significant harm to another state. Therefore, it is also called the non-harm principle (Tignino & Bréthaut [34]). However, what constitutes significant harm is not further quantified. In addition to international water law, the principle is also recognised in other areas of international environmental law (e.g., Naderi & Motallebi [39]; Poorhashemi [40]). An extension represents the principle of Territorial Integration of all Basin States (TIBS), which is also called community of co-riparian states or interests. The basic idea of this ideal principle is based on the assumption that all the water of the river belongs to all riparian states as an economic unit. According to this principle, the individual contribution to the flow is irrelevant (Kilgour & Dinar [41]; Salman [35]). However, there are doubts as to whether this principle is established in international water law (Salman [35]; Loures [42]).

3. Cooperative Game Theory

Cooperative game theory examines how players can distribute joint outcomes fairly, whereby cooperation only makes sense normatively if they are better off as a result of cooperation. The following section describes the utilities players can achieve through cooperation and how these utilities can be distributed fairly through solution concepts. The section concludes with a framework for when to use TU games. For related approaches, cf. Appendix A.4.

3.1. Properties of a Game and Solution Concepts

The assumptions of cooperative game theory are numerous. We focus on some necessary preliminary statements. For a detailed discussion, we refer to the appropriate literature (Maschler et al. [43]; Algaba & van den Brink, [44]):

• Players have similar interests and enter into binding agreements so that their goals are to be achieved through cooperation.
• The players’ actions lead to the outcome of the cooperation.
• Every player tries to maximise its utility.
• The outcome of each coalition is known in advance, which requires truthful reporting by the players and reliability of the data.

A TU game (transferable utility game) is a pair $(N,v)$, where $N=\left\{1,2,3,\dots ,n\right\}$ denotes the finite, non-empty set of players (for so-called cost games cf. Appendix A.1). Every subset $S\subseteq N$ is called a coalition. Here, N describes the grand coalition of the TU game. The characteristic function $v:2^N\to \mathbb{R}$ with $v(⌀)=0$ maps a utility value to each subset S, which represents the performance of this coalition. In a TU game, this utility is transferable between all players. We describe a distribution as fair if the shares of the agents involved are based on their performance. These fair shares are determined by axioms (cf. Appendix A.2). However, there are some desirable properties of the coalition function v, which describe whether cooperation between the players is beneficial or not (Peleg & Sudhölter [45]; Mueller [46]):

• A game $(N,v)$ is essential if $v\left(N\right)>{\sum }_{i\in N}v\left(\left\{i\right\}\right).$ Only if this property is fulfilled, then it is a problem of fair sharing. For a so-called inessential game with $v\left(N\right)={\sum }_{i\in N}v\left(\left\{i\right\}\right)$ – an additive game – such a problem does not exist. Inessential games were excluded at the very early stage of game theory development:
  • von Neumann & Morgenstern [47] stated for inessential games: “This is a perfectly trivial case, in which the game is manifestly devoid of further possibilities. There is no occasion for any strategy of coalitions, no element of struggle or competition: each player may play a lone hand, since there is no advantage in any coalition. […] [H]e can get this amount even alone, irrespective of what the others are doing. No coalition could do better in toto.”
  • See Shapley [48] for a similar argumentation: “If v is inessential [the imputation] is a single point …”
  • “It is conceivable that there are games in which no coalition of players is more effective than the several players of the coalition operating alone. […] Such games are called inessential […] Since nothing is gained by forming coalitions in inessential games, it is clear that we cannot expect any theory of coalition formation in that case, and so we shall be concerned only with essential games from now on.” (Luce & Raiffa [49])
  • “Suppose, however, it were always true that $v(S\cup T)=v\left(S\right)+v\left(T\right)$. Again it would be difficult to imagine the occurrence of coalition-formation inasmuch as rational players would not expend energy to change position if the most they could expect would be the same payoff […] It is clear that for a game in which $v(S\cup T)=v\left(S\right)+v\left(T\right)$ there is no point to forming coalitions. Indeed […] there is not much of anything for players to do.” (Riker [50])
• The worth of every coalition is non-negative, so for all $S\subseteq N$ follows $v\left(S\right)\ge 0.$ The utility of at least one coalition should be greater than zero. In particular, coalitions that include multiple players should have a value greater than zero in order to justify cooperation.
• A game $(N,v)$ is superadditive if $v(R\cup S)\ge v\left(R\right)+v\left(S\right)\forall R,S\subseteq N$ for $R\cap S=⌀$. To offer incentives for cooperation, the inequality should hold for at least one coalition.
• A game $(N,v)$ is convex if for all $i\in N$ and all $S\subseteq R\subseteq N\setminus \left\{i\right\}$ follows: $v(S\cup \left\{i\right\})-v\left(S\right)\le v(R\cup \left\{i\right\})-v\left(R\right)$. It claims that a greater coalition generates a higher marginal contribution of player i. Convexity describes a similar effect like superadditivity for coalitions of conjoint elements. Further, convex games are superadditive.

A solution $f:(N,v)\to {\mathbb{R}}^n$ maps to every game $(N,v)$ a share $x_i$ to every player i of the game. The core of a game $(N,v)$ (Gillies [51]) is:

$$Core\left(v\right)=\left\{x\in \mathbb{R}: \sum _{i\in N}{x}_i=v\left(N\right) \mathrm{and} \sum _{i\in T}{x}_i\ge v\left(T\right) \mathrm{for} \mathrm{all} T\subset N\right\}.$$

A convex game is a sufficient condition for a non-empty core. Furthermore, it is a desirable property that a solution lies in the non-empty core of the game. The Shapley value (Shapley [48]) is the weighted average of the marginal contributions of each player i to the coalitions S and the formula is given by:

$${\displaystyle {\varphi }_i\left(v\right)=\sum _{T\subseteq N:i\in T}{\displaystyle \frac{(t-1)!\left(n-t\right)!}{n!}}[v\left(T\right)-v(T\setminus \left\{i\right\})].}$$

For convex games, the Shapley value lies in the non-empty core of the game (Shapley [52]).

3.2. How to Respectively Not Model Cooperative Games

First, the underlying game should be checked for the fulfilment of the desirable properties:

• Essentiality: If the game is inessential, there is no incentive for players to cooperate, so we can stop further analysis.
• Balancedness (game with a non-empty core): If the game is not balanced, at least one coalition has an incentive to leave the grand coalition. This would not ensure cooperation among all players, so we can stop further analysis. For a balanced game, it should be checked whether the proposed solution lies in the core of the game.
• Superadditivity: Describes the state of synergy, which is the incentive for cooperation. A non-superadditive game implies for the Shapley value that it is not necessarily part of the core.
• Convexity: This state is desirable because it describes an analogous relationship to “increasing returns to scale” with respect to marginal contributions (Shapley [52]). Further, it implies that the Shapley value lies in the non-empty core.

In general, the game should be essential and superadditive, and the proposed solution should be a part of the core. If it is the Shapley value or the solution is related to it, it is additionally desirable that the game is convex to guarantee that the solution belongs to the core. Only if these properties are fulfilled can it be ensured that the axiomatically proposed fair solution to the concept is actually realised. This is particularly crucial for real-world cases and for the subsequent analysis of the river sharing problems.

4. Methodology

4.1. Literature Search and Selection Strategy

In the following, we present our strategy for selecting cooperative game theory-related literature in the context of the river sharing problem. In Figure 1 we illustrate our methodological approach for the systematic literature review which is based on the PRISMA approach (Page et al. [53]). Further, the literature selection process is quantified. We use for our research the scientific databases of Web of Science (WoS), ScienceDirect (SD) and EBSCOhost. Therefore, we start by searching with the string

• ((river OR water) AND (share OR sharing) AND problem) AND (allocation OR game OR rule OR cost)

for filtering in titles, abstracts and keywords (respectively, subject terms) of the papers. In addition, we only included scientific articles and reviews (respectively, academic journals) in English, which were published until December 2024, in our research. In the second step, we screened the titles and abstracts of the identified articles, and papers out of the scope were excluded from the further literature review. After that, we removed the duplicates and obtained 57 papers. Additionally, we identified 16 more related papers from Madani [10] and backward search.

Figure 1. Literature selection flow diagram based on the PRISMA approach.

Figure 1. Literature selection flow diagram based on the PRISMA approach.

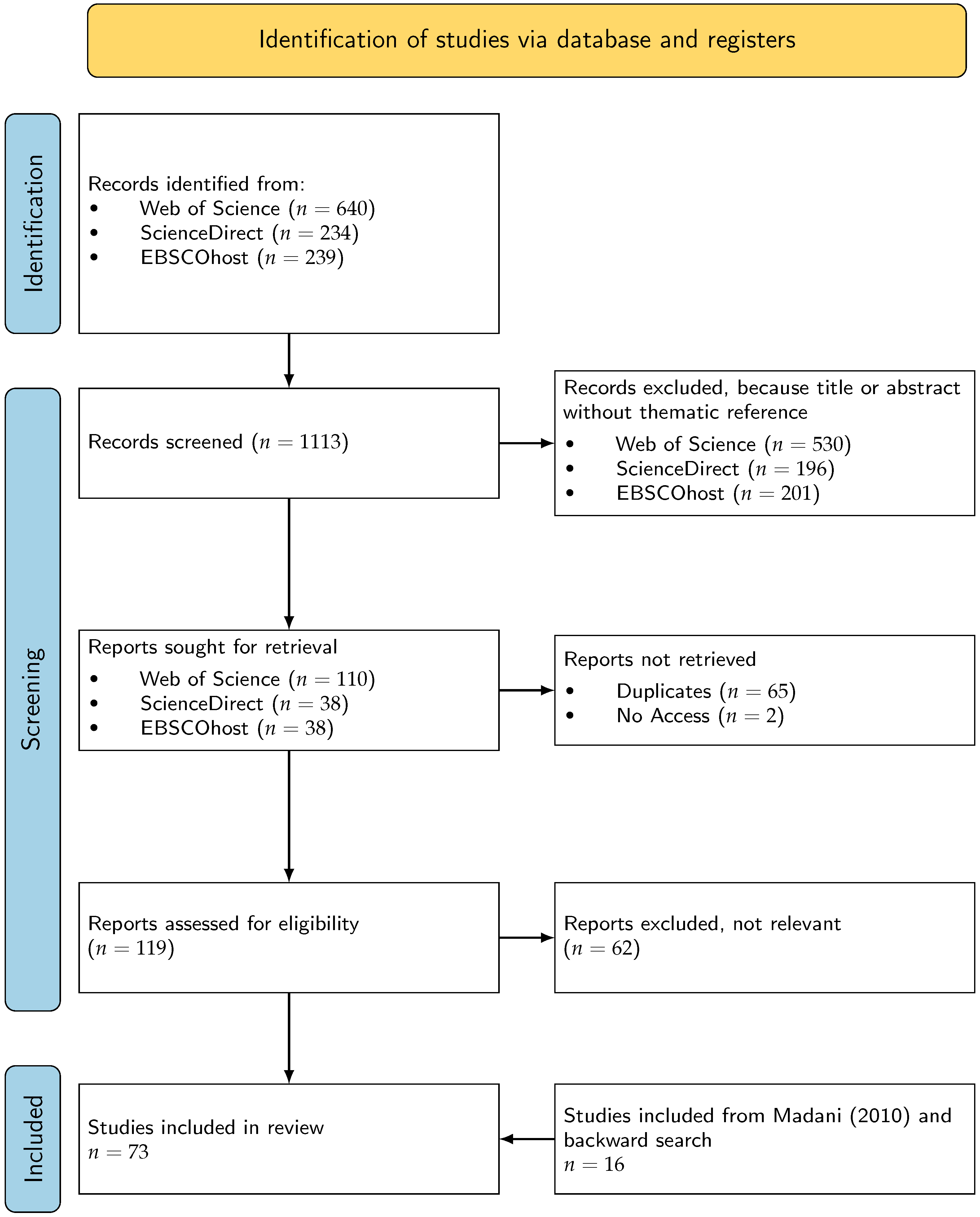
4.2. Sample Description

We initially categorised the selected papers according to the topics of sharing of water resources; cost sharing of infrastructure for water supply or disposal; and cost sharing of flood, flood prevention, pollution or pollution control. We also reviewed the papers to determine whether they aim for a fair distribution of collective benefits or costs. Furthermore, we evaluated the areas in which they made substantial contributions, and we list the game-theoretic concepts they used (methods outside of game theory are also summarised under “others”). Many papers have a purely application-oriented approach to a real-world problem. The technical contribution then consists in constructing a framework for applying existing game-theoretic methods (these are marked with ∗ in

Table A1. Categorisation of the articles from the sample.

Problem

Relevant Contributions

Methods

Published Article

①

②

③

Fair

Techn.

Applic.

Lit. Rev.

$Core\left(v\right)$

${\varphi }_i\left(v\right)$

BA

BS

Other

Rogers (1969)

[1]

X

${\mathrm{X}}^{\ast }$

X

X

Suzuki/Nakayama (1976)

[2]

X

X

${\mathrm{X}}^{\ast }$

X

X

X

Sheehan/Kogiku (1981)

[93]

X

X

X

X

X

X

X

X

Straffin/Heany (1981)

[94]

X

X

X

X

X

Young et al. (1982)

[95]

X

X

${\mathrm{X}}^{\ast }$

X

X

X

X

Lejano/Davos (1995)

[96]

X

X

X

X

X

X

Dinar/Howitt (1997)

[3]

X

X

X

X

X

X

X

Becker/Easter (1999)

[97]

X

X

${\mathrm{X}}^{\ast }$

X

X

X

Frisvold/Caswell (2000)

[98]

X

X

X

X

X

Ambec/Sprumont (2002)

[4]

X

X

X

X

X

Kucukmehmetoglu/Guldmann (2004)

[99]

X

X

${\mathrm{X}}^{\ast }$

X

X

X

X

X

Wu/Whittington (2006)

[100]

X

X

${\mathrm{X}}^{\ast }$

X

X

X

X

X

Ni/Wang (2007)

[6]

X

X

X

X

X

X

Ambec/Ehlers (2008)

[54]

X

X

X

X

X

Kucukmehmetoglu (2009)

[101]

X

X

${\mathrm{X}}^{\ast }$

X

X

X

X

X

Sumaila et al. (2009)

[102]

X

X

Khmelnitskaya (2010)

[71]

X

X

X

X

X

Kucukmehmetoglu et al. (2010)

[103]

X

X

${\mathrm{X}}^{\ast }$

X

X

X

X

X

Mahjouri/Ardestani (2010)

[104]

X

X

${\mathrm{X}}^{\ast }$

X

X

X

X

X

Mahjouri/Ardestani (2011)

[105]

X

X

${\mathrm{X}}^{\ast }$

X

X

X

Ansink/Weikard (2012)

[65]

X

X

X

X

X

X

van den Brink et al. (2012)

[55]

X

X

X

X

X

Dong et al. (2012)

[57]

X

X

X

X

X

X

X

X

Kucukmehmetoglu (2012)

[106]

X

X

${\mathrm{X}}^{\ast }$

X

X

X

X

Ambec et al. (2013)

[107]

X

X

X

X

X

X

X

Beal et al. (2013)

[11]

X

X

X

X

X

X

X

Gómez-Rúa (2013)

[58]

X

X

X

X

X

van den Brink et al. (2014)

[56]

X

X

X

X

X

X

Khmelnitskaya (2014)

[108]

X

X

X

X

X

X

Mianabadi et al. (2014)

[109]

X

${\mathrm{X}}^{\ast }$

X

X

X

Read et al. (2014)

[110]

X

${\mathrm{X}}^{\ast }$

X

X

X

Alcalde-Unzu et al. (2015)

[59]

X

X

X

X

X

Ansink/Weikard (2015)

[66]

X

X

X

X

X

Beal et al. (2015)

[111]

X

X

X

X

X

Houba et al. (2015)

[112]

X

X

X

X

X

X

X

Mianabadi et al. (2015)

[113]

X

X

X

X

X

X

X

Sechi/Zucca (2015)

[114]

X

X

X

X

X

X

Ansink/Houba (2016)

[115]

X

X

X

X

X

Degefu et al. (2016)

[116]

X

X

${\mathrm{X}}^{\ast }$

X

X

X

X

X

Girard et al. (2016)

[117]

X

X

X

X

X

X

Degefu et al. (2017)

[118]

X

X

${\mathrm{X}}^{\ast }$

X

X

X

X

X

Osório (2017a)

[119]

X

X

X

X

X

X

Osório (2017b)

[120]

X

X

X

X

X

X

Zomorodian et al. (2017)

[121]

X

${\mathrm{X}}^{\ast }$

X

X

X

van den Brink et al. (2018)

[7]

X

X

X

X

X

X

Jeong et al. (2018)

[73]

X

X

${\mathrm{X}}^{\ast }$

X

X

X

X

Sedghamiz et al. (2018)

[122]

X

${\mathrm{X}}^{\ast }$

X

X

X

X

Alvarez et al. (2019)

[123]

X

X

X

X

X

X

X

Gudmundsson et al. (2019)

[124]

X

X

X

X

X

X

Qin et al. (2019)

[125]

X

X

${\mathrm{X}}^{\ast }$

X

X

X

X

X

Sun et al. (2019)

[60]

X

X

X

X

X

Abraham/Ramachandran (2020)

[8]

X

X

X

X

X

X

Janjua/Hassan (2020a)

[126]

X

X

${\mathrm{X}}^{\ast }$

X

X

X

X

X

Janjua/Hassan (2020b)

[127]

X

X

${\mathrm{X}}^{\ast }$

X

X

X

X

X

Janjua et al. (2020)

[128]

X

X

${\mathrm{X}}^{\ast }$

X

X

X

X

Öztürk (2020)

[129]

X

X

X

X

X

X

X

Qin et al. (2020)

[130]

X

X

${\mathrm{X}}^{\ast }$

X

X

X

X

Tayebikhorami et al. (2020)

[131]

X

${\mathrm{X}}^{\ast }$

X

X

X

X

X

Abraham/Ramachandran (2021)

[132]

X

${\mathrm{X}}^{\ast }$

X

X

X

X

Estévez-Fernández et al. (2021)

[133]

X

X

X

X

X

Hou et al. (2021)

[61]

X

X

X

X

X

X

X

Liu et al. (2020)

[134]

X

X

${\mathrm{X}}^{\ast }$

X

X

X

X

Nehra/Caplan (2022)

[135]

X

X

${\mathrm{X}}^{\ast }$

X

X

X

X

Wang (2022)

[136]

X

X

X

X

Cano-Berlanga et al. (2023)

[137]

X

X

X

X

Li et al. (2023)

[62]

X

X

X

X

X

X

X

Wan et al. (2023)

[138]

X

X

${\mathrm{X}}^{\ast }$

X

X

X

X

Yuan et al. (2023)

[139]

X

X

${\mathrm{X}}^{\ast }$

X

X

X

X

X

Zhu et al. (2023)

[140]

X

X

${\mathrm{X}}^{\ast }$

X

X

X

X

Hou et al. (2024)

[63]

X

X

X

X

X

X

X

Lowing (2024)

[64]

X

X

X

X

X

X

Qin et al. (2024)

[141]

X

X

${\mathrm{X}}^{\ast }$

X

X

X

X

X

Zhang et al. (2024)

[142]

X

X

${\mathrm{X}}^{\ast }$

X

X

X

X

X

Notes: ①–Sharing of water resources; ②–Cost sharing of infrastructure for water supply or disposal; ③–Cost sharing of flood, flood prevention, pollution or pollution control; Techn.–Technical; ∗–Framework; Applic.–Application; Lit. Rev.–Literature Review; BA–Bankruptcy Approach; BS - Bargaining Solution.

). Further, almost two-thirds of the articles ($n=45$) contain a real-world application, a significant proportion of which ($n=18$) describe transboundary watercourses. Figure 2 shows that most of the empirical studies in the sample focus on rivers in the countries of Turkey, Syria, Iraq, China, USA, Iran, Sudan, Pakistan, Ethiopia and Egypt. The description/analysis of all these papers is beyond the scope of this work; rather, this preliminary selection is intended to illustrate the interdisciplinary interest and importance of the topic. The academic interest in the topic has increased significantly over time, especially since around 2010. A list and classification of the papers can be found in the appendix (cf. Table A1). Here we focus on the axiomatic approaches that relate almost exclusively to river sharing problems. Seventeen papers remain, with van den Brink contributing the most publications (n = 4, cf. Figure 3). These articles have different objectives and use various principles in the context of the river sharing problem; therefore, they will be described in the next section. We then analyse their games and solutions and situate them within the context of real-world applications.

5. Content Analysis Result

5.1. Objectives

The aim of the articles is to determine a fair share of:

• the water resource (Ambec & Sprumont [4]; Ambec & Ehlers [54]; van den Brink et al. [55]; van den Brink et al. [56]);
• the pollution costs (Ni & Wang [6]; Dong et al. [57]; Gómez-Rúa [58]; Alcalde-Unzu et al. [59]; van den Brink et al. [7]; Sun et al. [60]; Hou et al. [61]; Li et al. [62]; Hou et al. [63]; Lowing [64]); or
• the flooding costs (Abraham & Ramachandran [8])

along a river. Further, Ansink & Weikard [65] and Ansink & Weikard [66] analyse the redistribution of a water resource among agents who have a claim to this resource. All papers follow an axiomatic approach but differ in their design and the methods used. In most papers, the riparian states are ordered completely linearly from upstream to downstream; only van den Brink et al. [55]; Dong et al. [57]; van den Brink et al. [7] and Hou et al. [61] deviate from this approach, using a more general network structure. The approach of all articles is described by one or more TU games or can be expressed as such. Some papers explicitly use a utility function for modelling that is differentiable for all agents with a positive water consumption and strictly concave and are either strictly increasing (Ambec & Sprumont [4]) or have a saturation point (Ambec & Ehlers [54]). van den Brink et al. [55] and van den Brink et al. [56] examine both cases, where van den Brink et al. [56] weakens the assumption of differentiability to continuity. The corresponding allocation of the respective problem is determined directly by one or more rules, or by families of rules. The solutions presented in the papers are based on or are discussed in the context of corresponding water principles, which are described in the next chapter.

5.2. Principles

Almost all papers in the sample use either ATS and/or UTI to justify their solution(s). ATS describes that a country has absolute sovereignty over the resources within its territory. As stated in Section 2, ATS is contradictory. Some articles of the sample circumvent this by technically assuming that each riparian state controls only the part of the water that flows exclusively into its territory (e.g., Ambec & Sprumont [4]; Ambec & Ehlers [54]; Ansink & Weikard [66]). However, this does not fully reflect Harmon’s argument. In contrast, UTI theory states that one should not change one’s own conditions to the detriment of a neighboring country. In most cases, this favors downstream agents, such as Ansink & Weikard [66] who, however, interpret it as an extreme form of the no-harm principle. In addition to interpreting the UTI as a Downstream Responsibility (DR), Dong et al. [57] also define an Upstream Responsibility (UR). An agent is responsible for the costs of his own territory and partly also for the costs of upstream agents. This principle is also followed by van den Brink et al. [7]; Sun et al. [60]; Hou et al. [61] and Hou et al. [63]. Ansink & Weikard [65] state that when applying the proportional rule, the constrained equal awards, the constrained equal losses or the Talmud rule, the principle of ATS, respectively, UTI is approximately described in situations where the upstream agent has a very high, respectively, very low water claim compared to the downstream agent. Further, van den Brink et al. [55]; van den Brink et al. [56] and van den Brink et al. [7] use the TIBS principle (cf. Section 2) to justify their solutions. Furthermore, van den Brink et al. [7] use UTI as both a Downstream and Upstream Responsibility to re-axiomatise rules from Dong et al. [57]. Gómez-Rúa [58] follows the “Polluter-Pays” principle of the European Union Water Framework Directive, which can be considered as a specification of UTI. It stipulates that those responsible for environmental pollution must also bear the associated costs of eliminating the pollution. An analogous consideration represents the Extended Producer Responsibility principle. It is the basis of Abraham & Ramachandran [8] to determine their TU game. The manufacturer then bears responsibility for the entire lifespan of a product. Thus, those upstream agents are liable for the damages in proportion to the amount of water they discharged. Another principle used in sampling is that of Solidarity. Lowing [64] formulates this by requiring all agents to contribute (equally) to the cleaning costs.

Table 2. Principles of the sample.

Principles	Published Article
ATS	Ambec/Sprumont [4]; Ni/Wang [6]; Ambec/Ehlers [54]; Ansink/Weikard [65]; Dong et al. [57]; van den Brink et al. [56]; Alcalde-Unzu et al. [59]; Ansink/Weikard [66]; van den Brink et al. [7]; Sun et al. [60]; Hou et al. [61]; Li et al. [62]; Hou et al. [63]; Lowing [64]
UTI: DR	Ambec/Sprumont [4]; Ni/Wang [6]; Ambec/Ehlers [54]; Ansink/Weikard [65]; Dong et al. [57]; Gómez-Rúa [58]; van den Brink et al. [56]; Alcalde-Unzu et al. [59]; Ansink/Weikard [66]; van den Brink et al. [7]; Sun et al. [60]; Li et al. [62]; Hou et al. [63]; Lowing [64]
UTI: UR	Dong et al. [57]; van den Brink et al. [7]; Sun et al. [60]; Hou et al. [61]; Hou et al. [63]
TIBS	van den Brink et al. [55]; van den Brink et al. [56]; van den Brink et al. [7]
Extended Producer Responsibility	Abraham/Ramachandran [8]
Solidarity	Lowing [64]

summarises this section.

5.3. Games, Solutions and Evaluation

Some papers in the sample describe specific TU games, which will be examined in more detail below. However, not all authors follow this path, others immediately establish axioms for their river sharing problem. Ambec & Sprumont [4] determine the Secure Benefit game $(N,v)$ based on ATS and the Aspiration Welfare game $(N,w)$ based on UTI. The Secure Benefit game is essential and superadditive. Interestingly, the defined Aspiration Welfare game describes the maximally legitimate aspirations of a coalition. This is a kind of opportunity cost that agents try to minimise, which is reflected in the restricted form of concavity. The marginal contribution of a downstream agent to a superset is never larger than the agent’s marginal contribution to a subset. Further, Ni & Wang [6] define a Local Responsibility cost game $(N,v^C)$ based on ATS and a Downstream Responsibility cost game $(N,w^C)$ based on UTI. $v^C$ is additive by definition and therefore leads to an additive zero-utility game. The Downstream Responsibility cost game is essential and concave. It is also called the Dual Airport game (van den Brink & van der Laan [67]). Ambec & Ehlers [54] specify the core lower bounds of the Secure Benefit game of Ambec & Sprumont [4] to non-cooperative core lower bounds and cooperative core lower bounds. With more than three agents, the cooperative core is not necessarily non-empty. van den Brink et al. [55] generalise the approaches of Ambec & Sprumont [4] and Ambec & Ehlers [54] to networks. Furthermore, Dong et al. [57] generalise the Local Responsibility and the Downstream Responsibility cost game of Ni & Wang [6] to a network structure. They also introduce the Upstream Responsibility cost game based on UTI which is essential and concave. Gómez-Rúa [58] defines a cost game $(N,c)$, which is inessential. van den Brink et al. [7] use the Local Responsibility, the Downstream Responsibility and the Upstream Responsibility cost game of Dong et al. [57] and further define the Limited Upstream-oriented cost game. For the linear river case, the Downstream Responsibility cost game and the Limited Upstream-oriented cost game coincide. Abraham & Ramachandran [8] determine the Flood Cost Sharing game $(N,v^d)$ which is additive and therefore leads to an additive zero-utility game (Müller & Pisch [68]). Both the River Pollution Responsibility Sharing (cost) game $(N,v^N)$—(Hou et al. [61]) based on the ATS and UTI—and the Polluted River Responsibility cost game $(N,v^C)$—(Hou et al. [63]) based on the ATS and UTI—are essential and concave. The Pollution Cost-Sharing game $(N,v^C)$ of Li et al. [62] based on the ATS and UTI is essential—except that it is the Local Responsibility cost game—and subadditive.

Below we consider the proposed solutions. Ambec & Sprumont [4] develop the Downstream Incremental distribution that satisfies both the core lower bounds and the aspiration upper bounds. An agent is assigned its marginal contribution to the coalition, determined by its predecessors along the river. The solution describes a compromise between ATS and UTI. Ambec & Ehlers [54] show in a generalised approach that the Downstream Incremental distribution also satisfies the non-cooperative core lower bounds. van den Brink et al. [55] proposes the class of Weighted Hierarchical solutions to satisfy the TIBS. These range from Downstream Incremental to Upstream Incremental distributions, with an average hierarchical solution serving as a compromise. The principles are applied to flows with and without satiable agents and potentially multiple springs. Ni & Wang [6] present two counterfactual methods: the Local Responsibility Sharing method and the Upstream Equal Sharing method. According to the Local Responsibility Sharing method, each agent bears the costs in its territory, while in the Upstream Equal Sharing method, costs are distributed equally upstream. Both methods coincides with the Shapley value and lie in the non-empty core of the corresponding game. In addition to the generalisation of the Local Responsibility Sharing method and the Upstream Equal Sharing method to network structures, Dong et al. [57] can also confirm their relationships to the Shapley value and the core. Furthermore, the newly defined Downstream Equal Sharing method generally coincides with the Shapley value of the Upstream Responsibility cost game, and with the solution of the airport game according to Definition 4 in the case of a linear river. Further, Ansink & Weikard [65] address the river sharing problem with resource endowments and claims by transforming it into a sequence of two-agent problems, equivalent to bankruptcy problems, and solve them using bankruptcy rules. This class of solutions is called Sequential Sharing rules. A generalised approach was developed by Ansink & Weikard [66] that uses two opposing rules. The Harmon rule states that each agent is allocated the minimum of the two quantities: the total amount of water available in its territory or its individual claim. The no-harm rule limits the water available on an agent’s territory to downstream claims that cannot be met by the water of downstream agents. The Downstream Incremental distribution of Ambec & Sprumont [4] can also be represented as a claims problem and then coincides with the Harmon rule. van den Brink et al. [56] introduce the UTI incremental solution. In contrast to the Downstream Incremental distribution, an agent’s payoff does not depend on the utility functions of the upstream agents. A special case is also considered where each agent has a saturation point, leading to a river claim problem of Ansink & Weikard [65]. Gómez-Rúa [58] describes two families of rules for distributing the costs of pollution upstream, where the second family of rules takes into account the distance of the agent to the pollution. Furthermore, two additional rules belonging to the first family of rules are described. One of these rules corresponds to the weighted Shapley value of an inessential game. The Upstream Responsibility rule by Alcalde-Unzu et al. [59] is a kind of compromise between ATS and UTI, taking into account a waste transfer rate. van den Brink et al. [7] first show that the Upstream Equal Sharing method and the Downstream Equal Sharing method coincide with the conjunctive permission value of an associated game with a permission structure. Games with a permission structure represent scenarios of a hierarchical structure in which players of a TU game require superior approval to cooperate with other players. Second, they introduce the Upstream Limited Sharing method, which represents a compromise between ATS and UTI. Accordingly, the Downstream Responsibilities of the agents become smaller compared to Upstream Equal Sharing method, but the costs are distributed upstream, although not necessarily equally. A convex combination of Local Responsibility method and Upstream Equal Sharing method is introduced by Sun et al. [60]. They call it the $\alpha$-responsibility method. Here, $\alpha$ represents the share of the cleaning costs of its territory that it is willing to pay. Further, the Sequential Upstream Proportional Allocation of Abraham & Ramachandran [8] coincide with the Shapley value of an additive game. Both the Adjacent Downstream Compensation method (Hou et al. [61]) and the Bilateral Compensation method (Hou et al. [63]) are compromises of ATS and UTI. Li et al. [62] introduce two extensions of the Local Responsibility Sharing method and the Upstream Equal Sharing method. One of these is the Equal Upstream Responsibility method, in which each agent is initially allocated a portion of the costs for cleaning their own territory. The remaining costs are then divided equally among the upstream agents. The $\alpha$-responsibility method from Sun et al. [60] can be represented as Equal Upstream Responsibility method. The second method is the Weighted Upstream Sharing method, where each agent should bear the cleaning costs for its territory and the downstream territories according to its given weight. It is also shown that the $0.5$-responsibility method is equal to the Shapley value of the corresponding game. Lowing [64] introduce the Equal Upstream-Local Responsibility, the Equal Upstream-Solidarity and the Equal Upstream-Solidarity-Responsibility method. The Equal Upstream-Local Responsibility method is quite similar to the Equal Upstream Responsibility method, with the remaining costs then being shared equally with the upstream agents and also with the territory agent itself. The Equal Upstream-Solidarity method represents a compromise between the UTI and the Solidarity principle. The cleaning costs for a segment are then distributed partially among all agents, and the remainder is distributed upstream. The Equal Upstream-Solidarity-Responsibility method is a compromise between ATS, UTI, and the Solidarity principle. In comparison to the Equal Upstream-Solidarity method, an additional portion of the cleaning costs for a segment of an agent is borne by the agent itself.

To evaluate the proposed solutions for their suitability for real-world applications, the principles they pursue are first examined to determine whether they aim for a compromise solution. As described in Section 2, it is crucial for the solution to strike a balance between the ATS and UTI. Furthermore, if it is clear from the outset - without applying the solution concept - which agent causes and bears the damage, then there is no distribution problem in the true sense of the term. Therefore, the following solutions are unsuitable for a real application:

• the Local Responsibility Sharing method
• the Upstream Equal Sharing method
• the Downstream Equal Sharing method
• the Harmon rule
• the UTI incremental solution
• the families of rules of Gómez-Rúa [58]
• the Sequential Upstream Proportional Allocation
• the Equal Upstream-Solidarity method

Ansink & Weikard [66] themselves state:

“Finally, the Harmon rule is a controversial rule and our paper should not be interpreted as an ignorant pledge to implement this rule.”

Our assessment goes beyond the axiomatic description of the rules/methods that describe the agents’ properties for a fair solution. These axioms must be accepted by the agents to be considered fair. Often, relationships are established with a traditional solution concept to increase acceptance. Only if the associated modelling, in this case the TU games, promotes cooperation, is this justification for fairness sufficiently valid. Thus, a method whose associated TU game is inessential appears unsuitable for representing a fair solution, even in a theoretical context. This applies, for example, to the Local Responsibility Sharing method and the Sequential Upstream Proportional Allocation, which lead to a carry-your-own-cost rule. Both cases lead to an additive zero-utility game. These games model a situation where there is nothing to share and no one gains anything. The associated TU game of a “standalone” solution should fulfil the described properties in Section 3.2. Otherwise, this results in paradoxes that undermine the method’s validity, especially if it purports to fairly distribute jointly achieved utilities or costs and the methods are therefore unsuitable for solving the problem. Referring again to the Local Responsibility Sharing method and the Upstream Equal Sharing method. Rather, these solutions represent limits within which a fair solution should operate. Additionally, these methods have served as a foundation for various compromise solutions. However, the following concerns make the Downstream Incremental distribution appear unsuitable. On the one hand, it is assumed that the agent furthest upstream in the river does not seek a higher utility than it can achieve on its own (Ansink & Weikard [65]). And on the other hand, it is not very convincing that all gains from cooperation go to the downstream agents (van den Brink et al. [69]; Houba [70]; Khmelnitskaya [71] and Ansink & Weikard [65]). Overall, the following solutions, which represent a compromise between ATS and UTI or a compromise between two counterfactual rules, appear suitable for a real-world application:

• Weighted Hierarchical solutions
• Sequential Sharing rules
• no-harm rule
• Upstream Responsibility rule
• Upstream Limited Sharing method
• $\alpha$-responsibility method
• Adjacent Downstream Compensation method
• Bilateral Compensation method
• Equal Upstream Responsibility method
• Weighted Upstream Sharing method
• Equal Upstream-Local Responsibility method
• Equal Upstream-Solidarity-Responsibility method

It is notable that none of the proposed solutions addresses the fair distribution of prevention costs, such as for floods or pollution. This will be discussed in the following section.

6. Allocation of Common Costs for River Protection Measures

In the river games exclusively based on the ATS and UTI, there is no incentive for cooperation, which consequently leads to an unsatisfactory result for all parties involved. The costs of preventing all damage are not sufficiently taken into account because there is no incentive for riparian users to find a joint solution. To address this problem, we present a unified approach. Therefore, a different modelling of the same problem is proposed, where investments must be made to avoid damage costs. We thus “automatically” follow the no-harm principle. We propose to use a traditional game-theoretical approach in the context of river protection measures to ensure a better economic interpretation. In the following, the decision-making situations are characterised by the fact that a resource is used by several users. The utilisation is quasi-linear or sequential. Some sections are used jointly, while other sections are used individually. Purely sequential use does not take place. As the usage can be graphically illustrated as a line, the term linear usage is used here. The cost shares for each user in these cases depend on where a player is placed on the usage line and on how many other players are using this resource. One class of these games is known as airport games. The key question in this approach for technical plant and machinery is the determination of the hypothetical overheads of the smaller dimensioned plant variants. In contrast to the real existing plant, which was dimensioned for the largest user type, the small ones are not built. The cost growth laws offer a way out here (Mueller [72]). These can be used to derive the cost ratios on the basis of the technical-physical dimensions. In some cases, investments are required in resources that are shared by different users but are utilised differently. During the construction of the resource, the user with the highest requirement profile is defined as the reference user, and the system is dimensioned according to their profile. However, the entire system is also used by users with a lower requirement profile. This raises the question of a fair allocation of the overhead costs of this system in a period. This question was asked and answered for the first time when determining the allocation of overheads for the use of runways according to the principle of causation. That is why they are also called “airport games”. A technical description can be found in the appendix (cf. Appendix A.3). However, in the following, we show the possibilities for cost sharing of shared resources using this approach. The allocation of costs for investment measures for preventive flood protection is presented below. In this scenario, the upstream riparian(s) invest(s) in flood protection measures from which the downstream riparians also benefit. In order for the upstream riparian to take or accept such measures, it makes sense for them to participate in the benefits they generate or the costs they incur. This can be achieved through compensation payments, which are undertaken by the downstream riparian in favor of the upstream riparian. The mechanism of action is of a compensatory nature: the upstream riparian takes measures for the benefit of the downstream riparian and receives financial resources from the downstream riparian as compensation. Typically, investment or maintenance measures for

• Flood protection and
• Environmental protection, such as water purification or retention

are the main focus. This scenario can be modelled as an airport game, as shown in Example 1.

Example 1.

Along a river, starting from the source downstream, there are the riparian communities A, B and C. Upstream municipality A builds flood protection structures for EUR 9 million. The next downstream municipality B therefore only has to invest EUR 4 million and the following municipality C only EUR 1 million. If municipalities A and B did not take any protective measures, municipality C would have to invest EUR 14 million itself. If municipality A did not invest in flood protection, municipality B would have to raise EUR 13 million. The flood protection measures of municipality A benefit all residents, while the measures of municipality B both B and C. This situation can be modelled as an airport game. The solution results in the cost shares from Definition 4:

$$\begin{array}{cccccc}\hfill x_A=& \hfill {\displaystyle \frac{9}{3}}\hfill & \hfill & \hfill & \hfill & =3,\hfill \\ \hfill x_B=& \hfill {\displaystyle \frac{9}{3}}\hfill & \hfill +{\displaystyle \frac{4}{2}}\hfill & \hfill & \hfill & =5,\hfill \\ \hfill x_C=& \hfill {\displaystyle \frac{9}{3}}\hfill & \hfill +{\displaystyle \frac{4}{2}}\hfill & \hfill +{\displaystyle \frac{1}{1}}\hfill & \hfill & =6,\hfill \\ \hfill & \hfill & \hfill & \hfill & Sum\hfill & =14.\hfill \end{array}$$

The cost function is set up according to Definition 3 and can be seen in

Table 3. Cost function of flood protection investments.

	S	⌀	$\left\{\mathbf{A}\right\}$	$\left\{\mathbf{B}\right\}$	$\left\{\mathbf{C}\right\}$	$\left\{\mathbf{A},\mathbf{B}\right\}$	$\left\{\mathbf{A},\mathbf{C}\right\}$	$\left\{\mathbf{B},\mathbf{C}\right\}$	$\left\{\mathbf{A},\mathbf{B},\mathbf{C}\right\}$
Function
$\mathbf{c}\left(\mathbf{S}\right)$		0	9	13	14	13	14	14	14

.

The following Shapley values result for the cost function: ${\varphi }_A\left(c\right)=3$, ${\varphi }_B\left(c\right)=5$ and ${\varphi }_C\left(c\right)=6$. The Shapley values are consistent with the previously determined results, which was the subject of Theorem 1. Obviously, neighbor C bears the greatest costs, as it also receives the greatest benefit.

The challenge with this solution undoubtedly lies in determining or modelling the hypothetical costs of stand-alone coalitions. This would require calculating or simulating the costs that a downstream user would incur if the upstream users did not take any action. It must be noted that the potential areas of application are primarily to be found in the infrastructure sector, where the investments and the resulting overheads are determined by load- or size-dependent usage characteristics. In operational production, the cost structures are hardly defined by these parameters.

7. Case Study

To strengthen the claim of applicability, we use a case study to show how the problem can be modelled. The starting point is the available data from a suitable project (cf.

Table 4. Input data of study from Jeong et al. [73].

Cost of the Jungnang Underground Floodway	USD 476 Million
Parameter k	0.6913
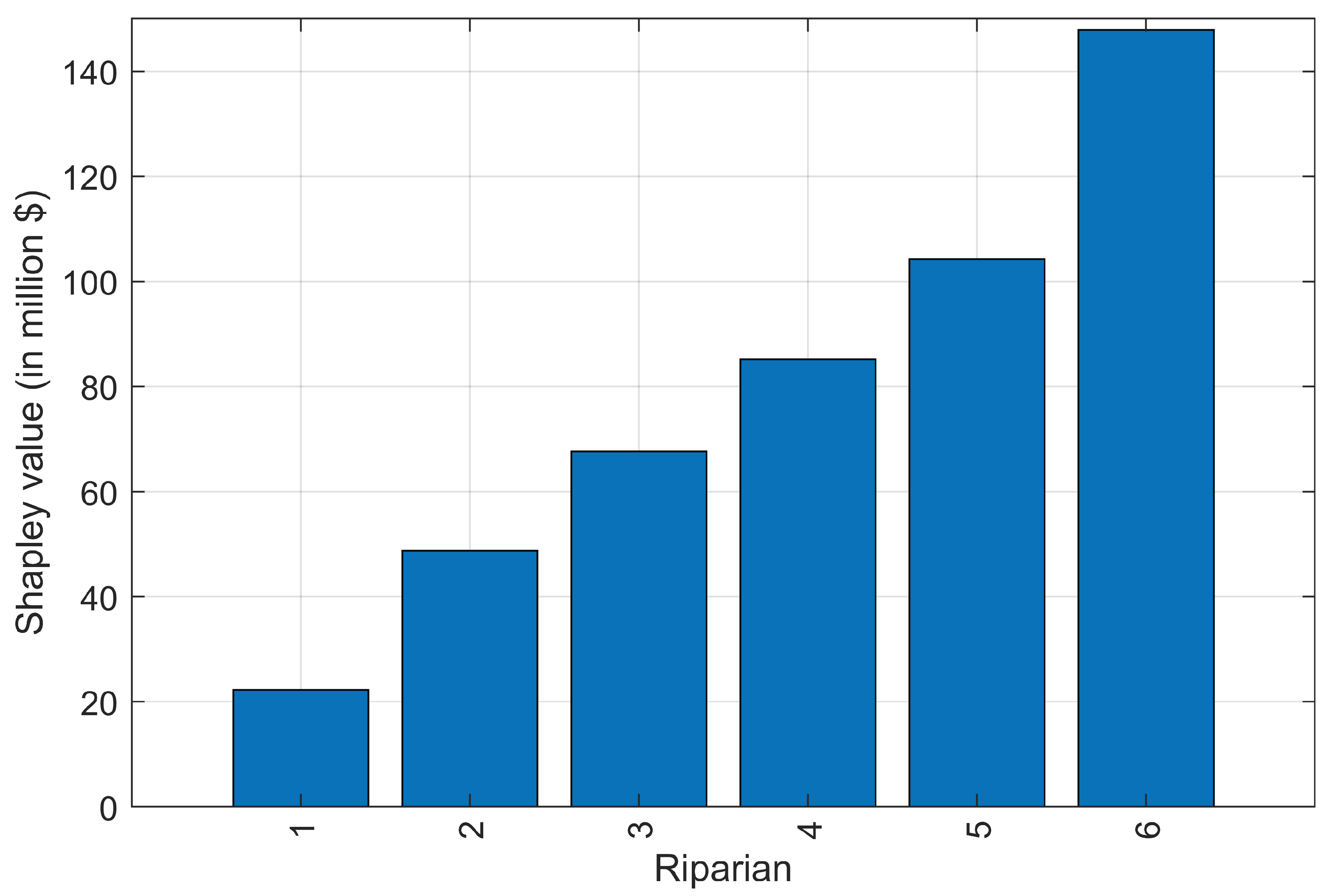
Riparian	Capacity need (${\mathrm{m}}^3$)
Dobong (1)	367,652
Nowon (2)	629,145
Seongbuk (3)	436,177
Jungnang (4)	328,420
Dongdaemun (5)	252,262
Seongdong (6)	299,838

). Jeong et al. [73] studied a similar allocation problem. The aim was to determine a fair distribution of the costs of flood protection measures among six riparians bordering the Jungnang Underground Floodway. Jeong et al. [73] studied the fair cost allocation of flood protection measures using a case study in South Korea. Our approach differs in several ways. We focus only on protection costs, allow all coalitions to cooperate and use an airport game to model this scenario. The simple linear river case is considered (cf. Figure 4).

Next we introduce the notation. The cost game of the problem is $(N,c)$. $w_T$ is the needed capacity of a coalition $T\subseteq N$. k is the parameter that determines the change in the average cost according to capacity. $C_N$ is the whole cost of the project. The cost growth laws are specified by a power-sizing model (Newnan et al. [74]). The cost ratio between two entities A and B is proportional to their capacity ratio raised to a power k. Thus, we are able to determine the costs $c_i$ of the riparians $i\in N$ in the sense of the airport game in ascending order:

$$\begin{array}{c}\hfill 0<c_1={\left({\displaystyle \frac{w_{\left\{1\right\}}}{w_N}}\right)}^k·C_N<c_2={\left({\displaystyle \frac{w_{\left\{1,2\right\}}}{w_N}}\right)}^k·C_N<\dots <c_n=C_N\end{array}$$

The cost function, which represents a pessimistic view, is given in Definition 1. It is pessimistic in the sense that the coalition’s cost will be determined by the most downstream riparian. It is therefore implicitly assumed that for a riparian, capacities of upstream riparians are also needed to maintain the same level of protection. This is consequently also reflected in the fair distribution of the project costs (cf. Figure 5).

Definition 1.

The cost function with $i\in N$ is defined by: $c_p(⌀)=0$ and ${\mathit{c}}_{\mathit{p}}\left(\mathit{T}\right)=\mathit{max}\left\{{\mathit{c}}_{\mathit{i}}|\mathit{T}\cap \left\{\mathit{i}\right\}\ne ⌀\right\}\forall \mathit{T}\subseteq \mathit{N}$.

8. Discussion

The focus of this paper was particularly on approaches to the fair distribution of benefits or costs along a river. These approaches use methods of game theory to represent principles of international water law. Therefore, we conduct a systematic literature review for categorisation (cf. Table A1). We evaluate the identified axiomatic literature related to TU games with regard to their suitability for real-world application and exclude those methods that follow extreme principles or are criticised in the literature. Further, we present a framework for when to use TU games in Section 3.2. One of the central takeaways from this study is that an airport game can be used to share costs for joint river protection measures. With the suggested well-known approach, we want to enforce future cooperation in the joint implementation of protective measures.

This article has emphasised once again that in the real world, ATS and UTI never promote cooperation in absolute terms. Thus, by definition, the principles of ATS and UTI represent non-cooperative behaviour and cannot, in themselves, be considered as a justification for appropriate, fair solutions. Nevertheless, these extreme principles, which are incompatible with international water law, can serve as a strategic starting point for negotiations between riparian states that can lead to a cooperative outcome in accordance with international water law. Therefore, it should be explicitly clarified at this point that the ATS and the UTI are to be rejected in the real interdependent, water-scarce world (Mohammed [36]). In addition, we demonstrate that the corresponding TU games of some rules are inessential. Since inessential games were excluded at a very early stage in the development of game theory, an analysis of these games is not fruitful from a normative perspective. A potential way out could be to base the solution on a descriptive foundation, as Willis [76] noted:

“However, an adequate descriptive theory of coalitions in inessential games will be less simple and more interesting than the normative theory. In fact, such a descriptive theory is of special interest just because of the particular simplicity of the associated normative theory. Just because coalitions are neither advantagous or disadvantagous, extra-normative considerations will have their maximal impact on behaviour. In the absence of logical rationale, psychological factors should be revealed more clearly. The game theorist has good reason to dismiss inessential games as trivial. The behavioural scientist, on the other hand, has good reason to consider them interesting and useful.”

Interestingly, the ATS-based Secure Benefit game of Ambec & Sprumont [4] is essential and superadditive by its nature. In contrast, the Local Responsibility cost game of Ni & Wang [6] is inessential, which describes the real nature of ATS and thus normatively excludes cooperative behaviour.

Future research should further analyse the articles listed in Table A1. For example, the technical frameworks for application-oriented approaches to a real-world problem could be described in detail. It would also be interesting to examine the axiomatic approaches with regard to the similarities and differences of their underlying axioms. In addition to the cooperative approaches to the river sharing problem discussed, non-cooperative or strategic approaches from game theory may also be suitable for mapping and describing the conflicts arising from the opposing principles of ATS and UTI. However, this paper does not cover these non-cooperative approaches.