Modelling of Water Level Fluctuations and Sediment Fluxes in Nokoué Lake (Southern Benin)
Abstract
1. Introduction
2. Materials and Methods
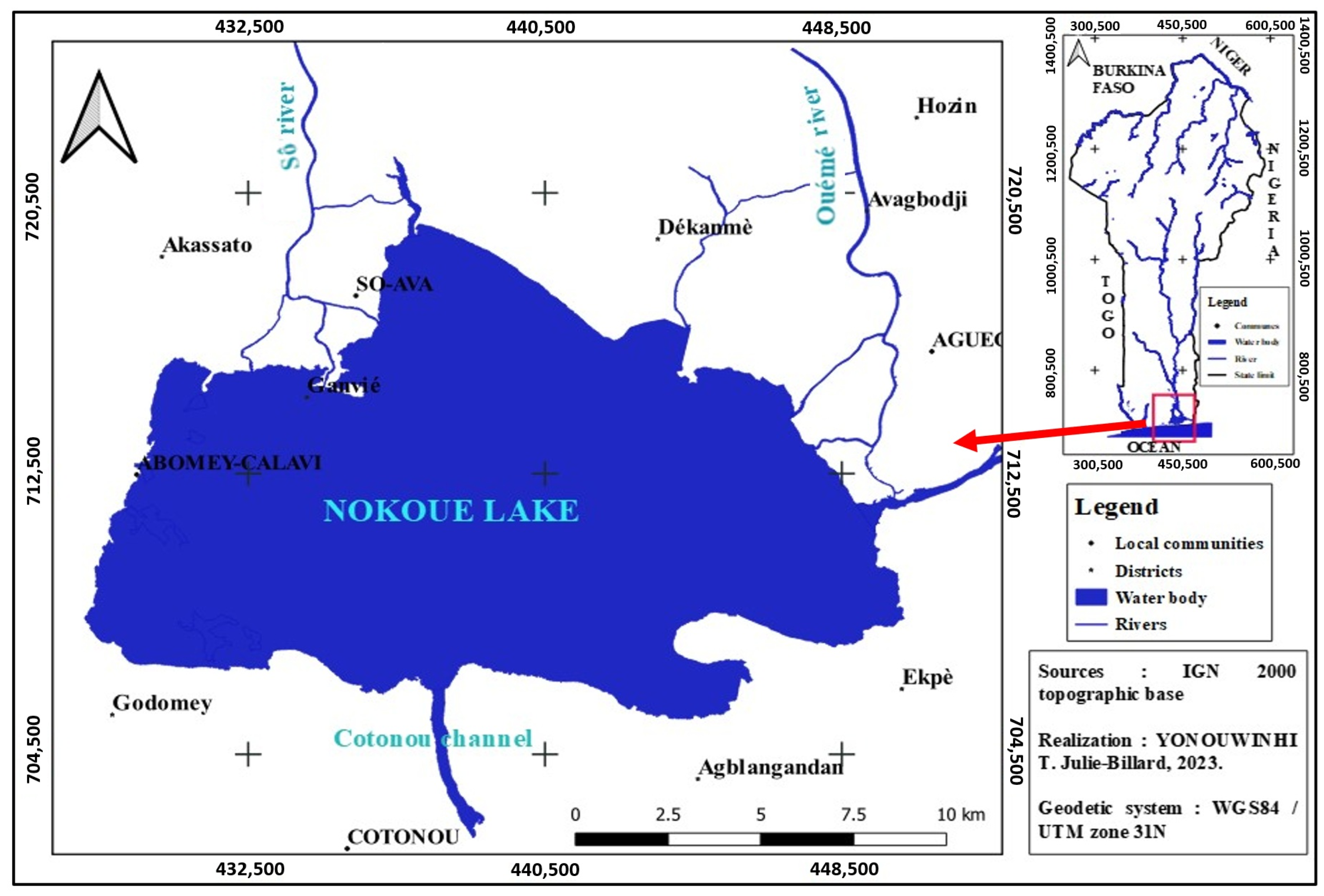
2.1. Study Area
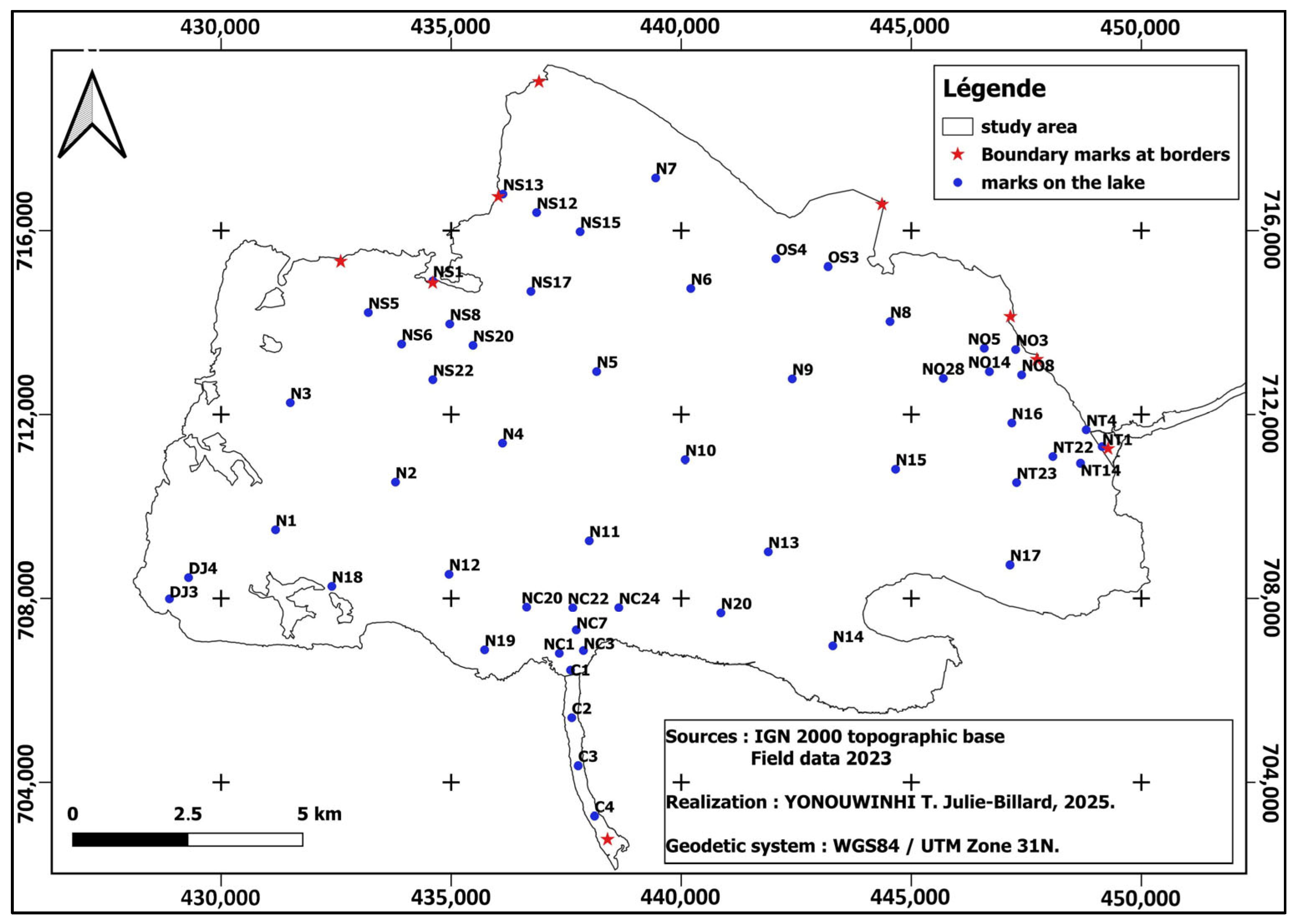
2.2. Field Measurements
2.3. Model Description
2.4. Setting Up the Model
2.5. Model Performance Indicators
3. Results
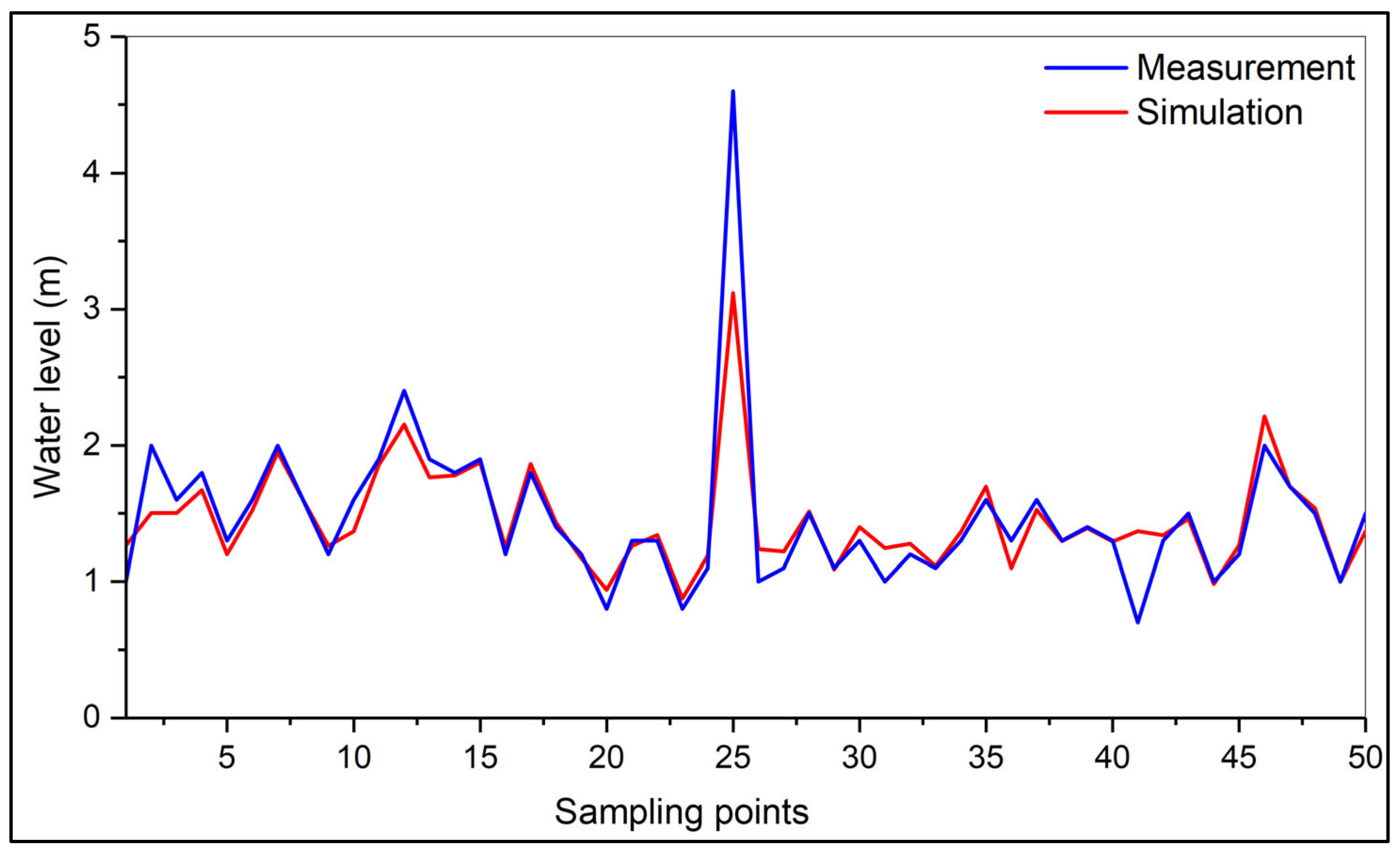
3.1. Calibration and Validation of the Hydrodynamic Model
3.2. Dynamics of Observed and Simulated Streamflow
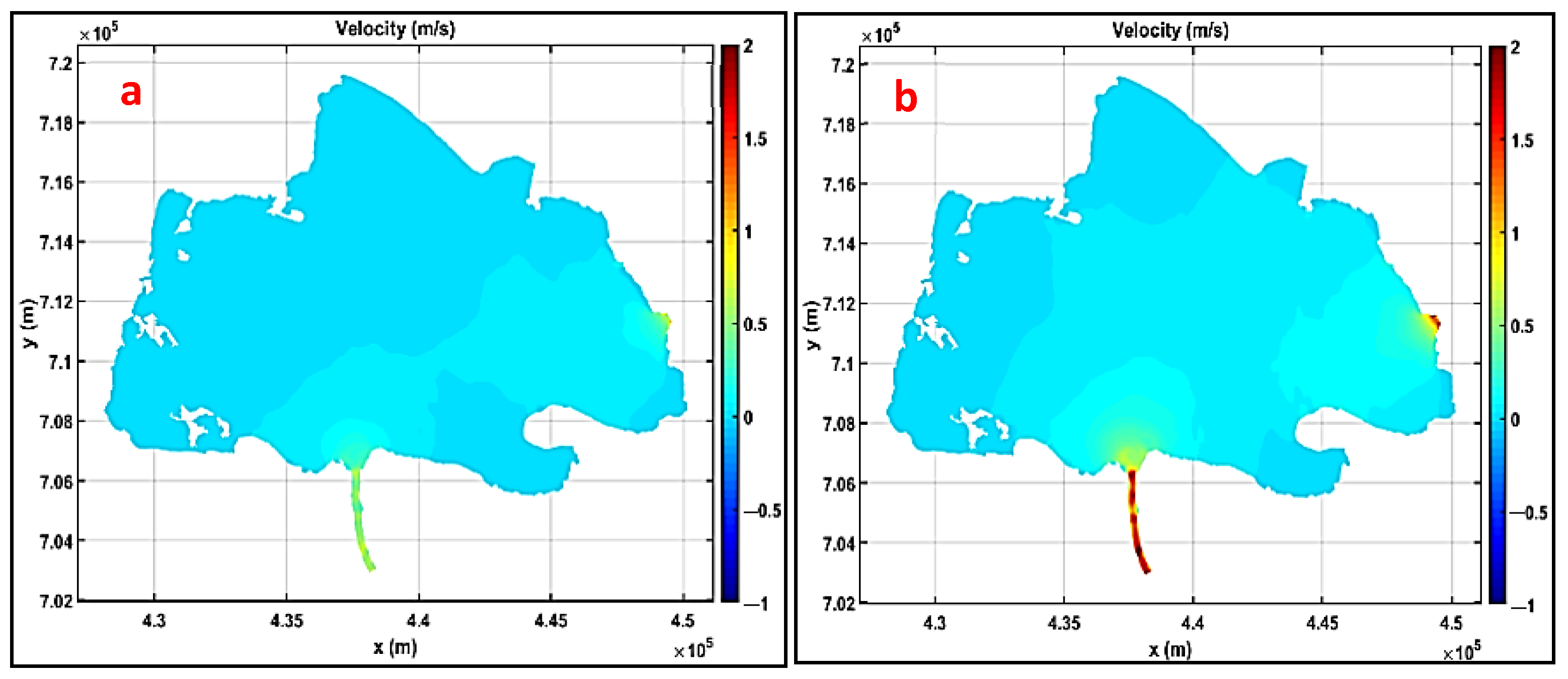
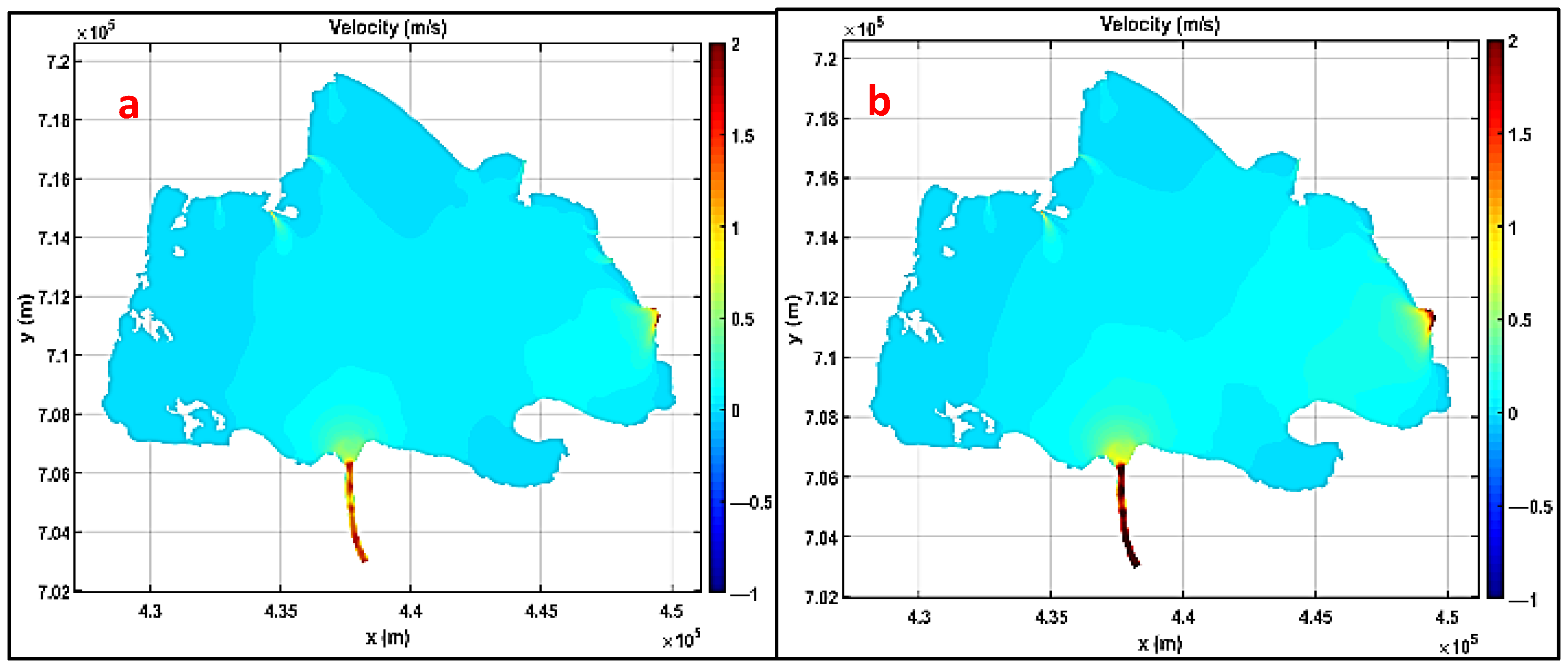
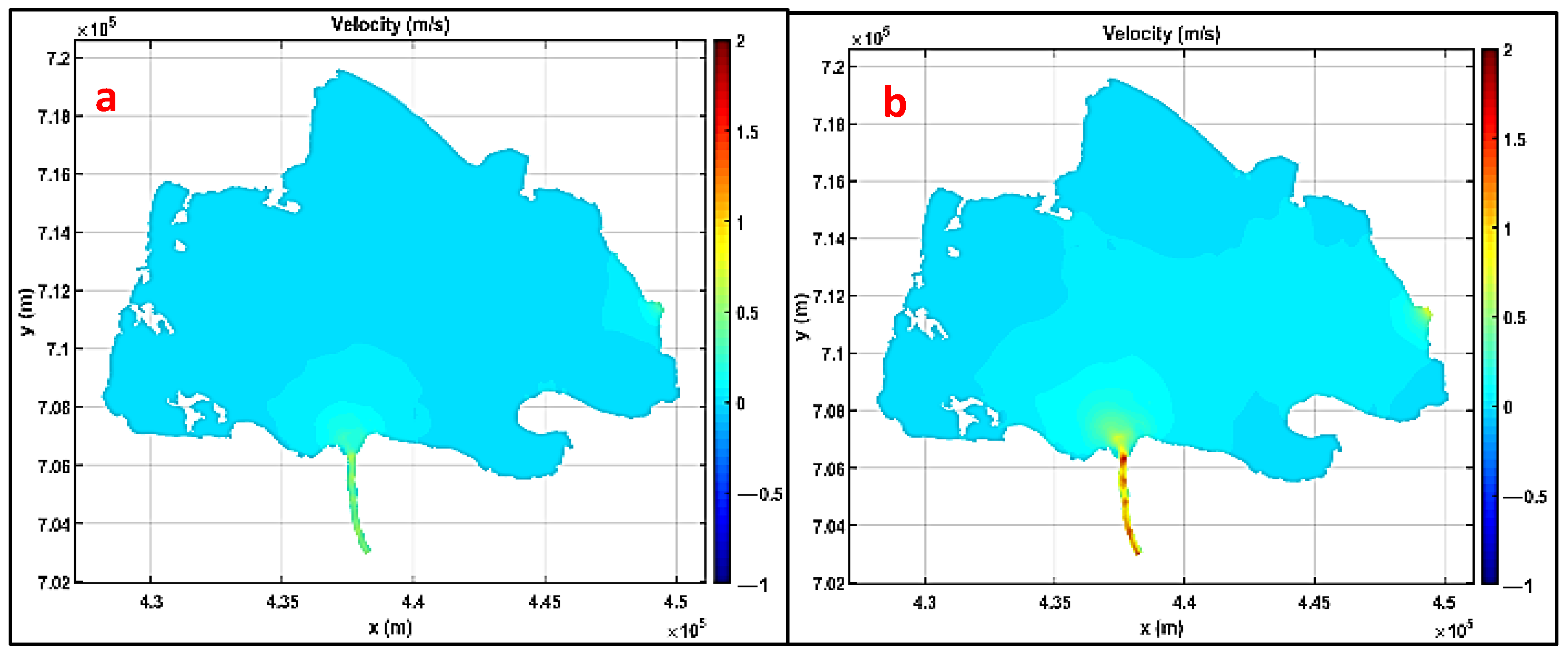
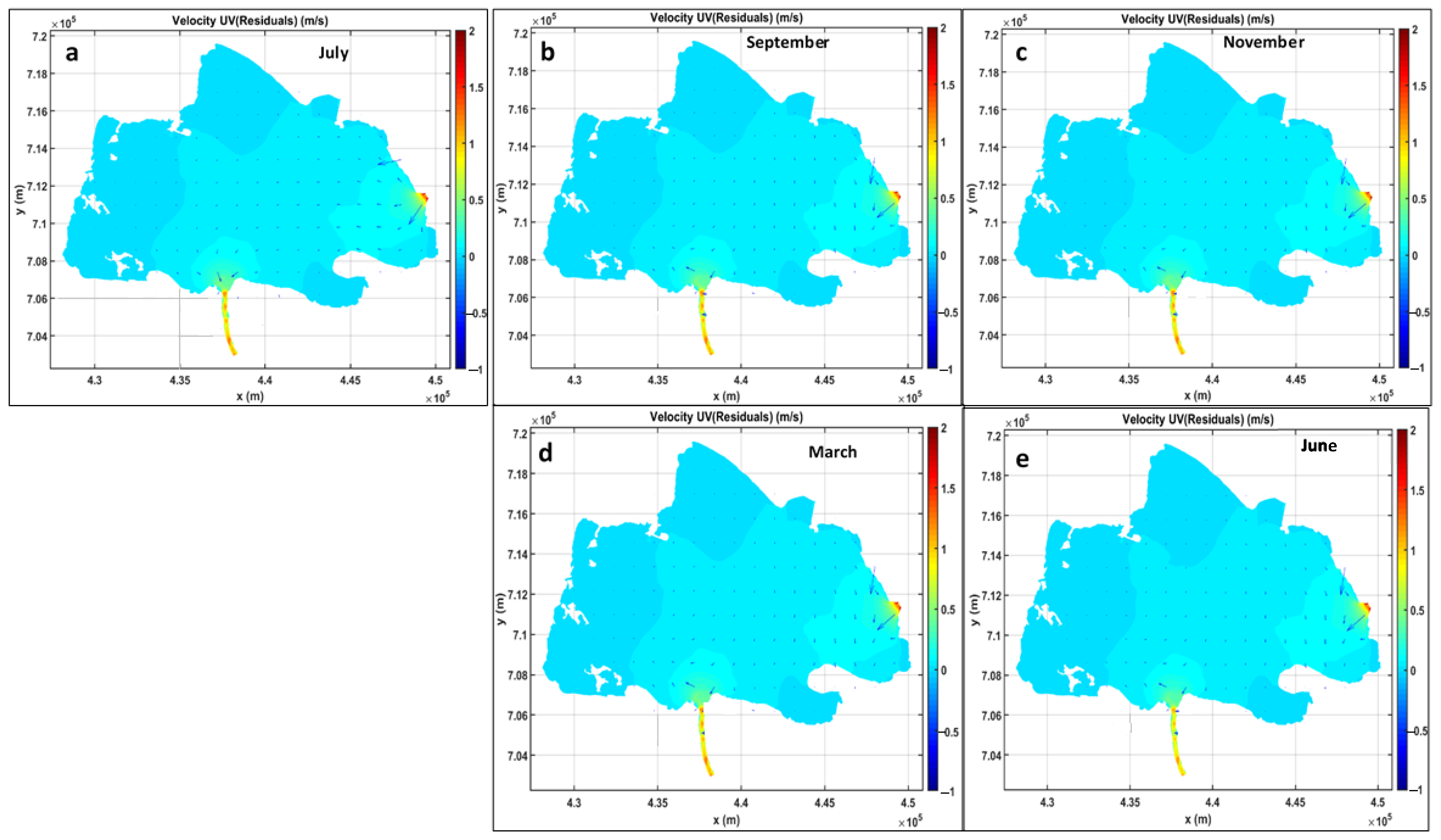
3.3. Velocity Dynamics and Suspended Solids
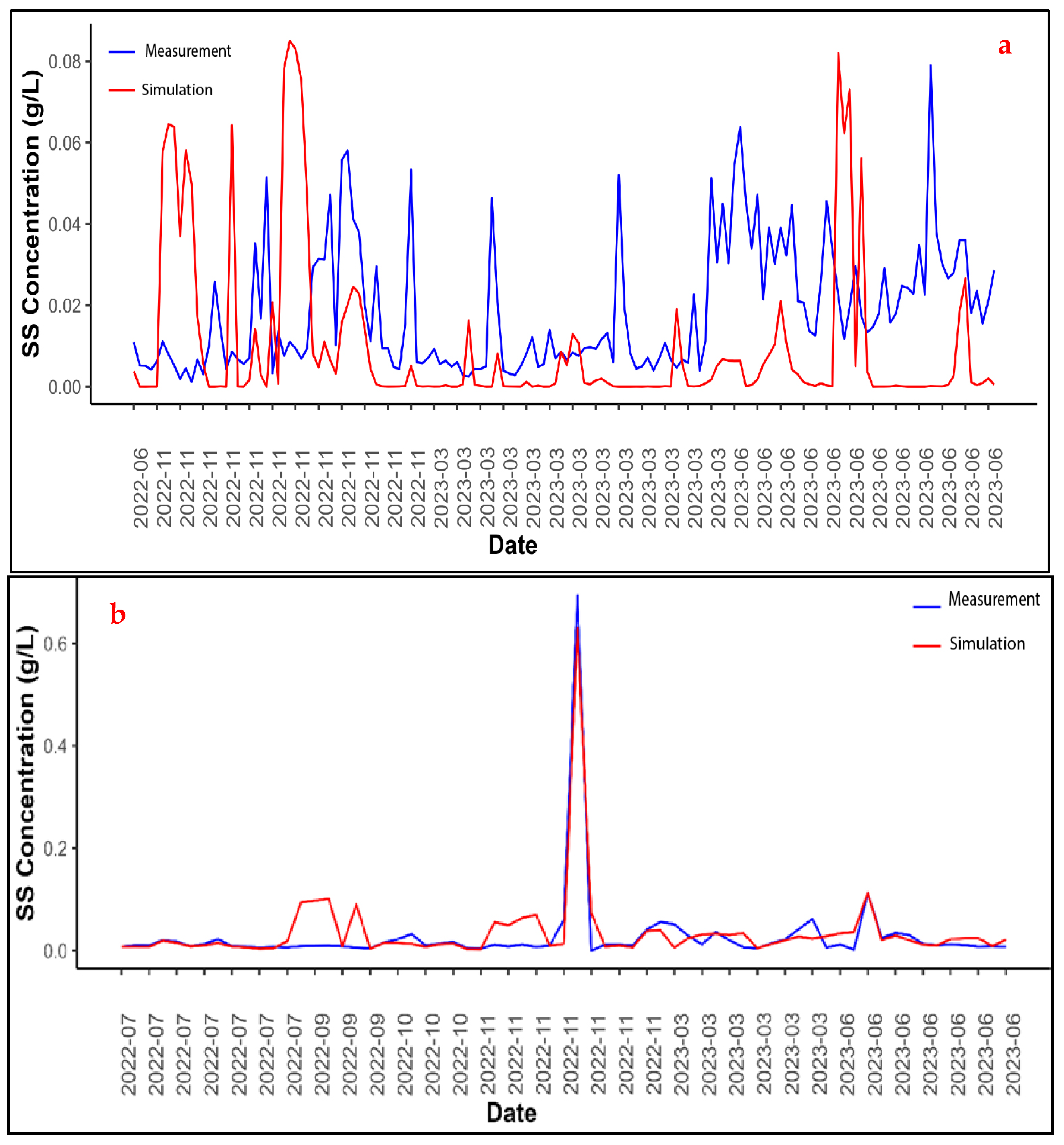
3.4. Validation of the Hydrosedimentary Model
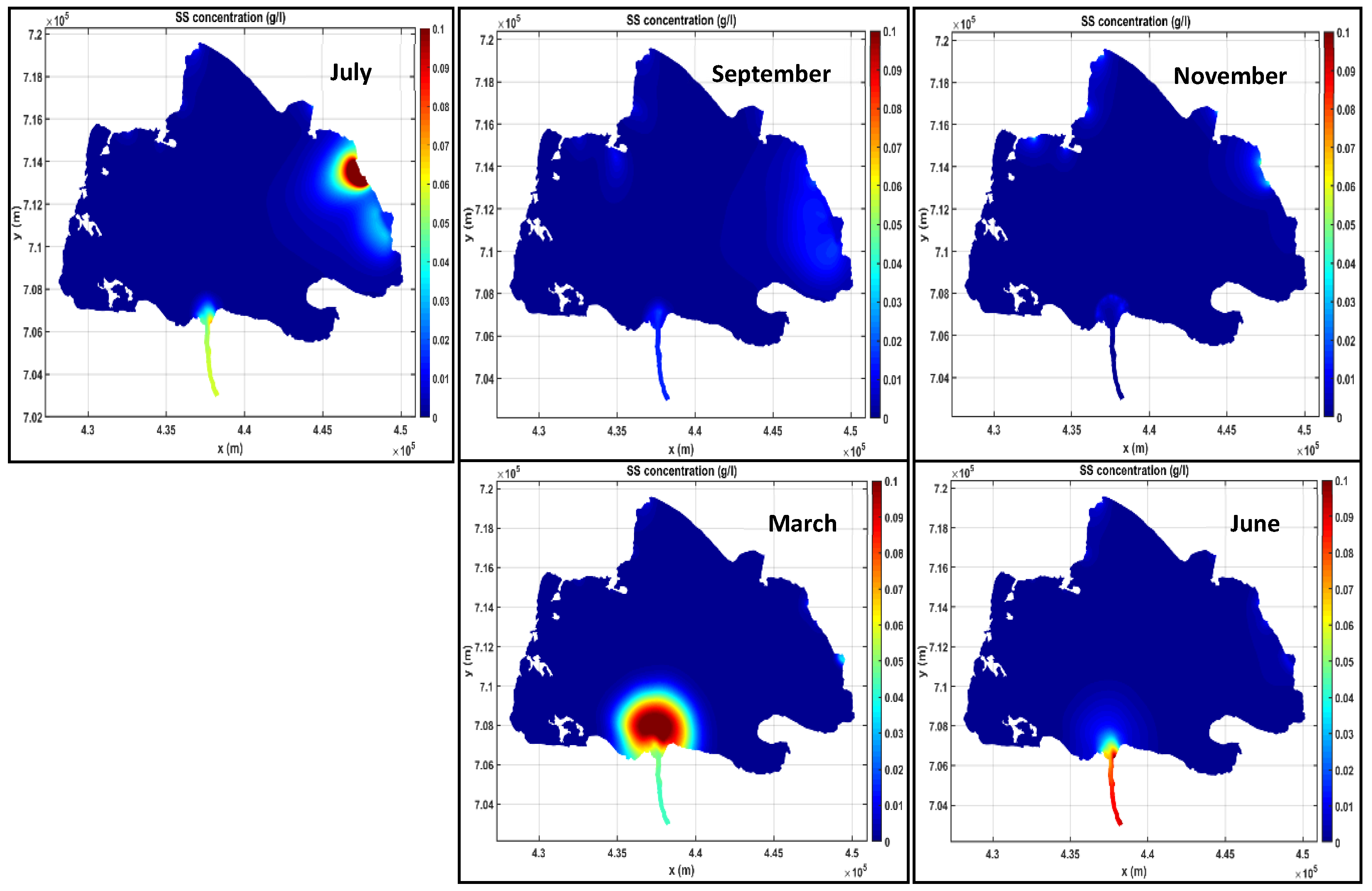
3.5. Distribution of Suspended Solids in the Study Area
3.6. Model Uncertainty
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boukari, O.T.; Dovonou, F.E.; Chouti, W.K.; Dagnon, D.K.; Adjadjihoue, E.; Abou, Y.; Mama, D.; Bawa, L.M. Biomasse planctonique et qualité de l’eau du lac Ahémé au Sud-Ouest du Bénin: Plankton biomass and water quality of Lake Ahémé in south-west of Benin. Int. J. Biol. Chem. Sci. 2022, 16, 1350–1364. [Google Scholar] [CrossRef]
- Whitman, W.B.; Coleman, D.C.; Wiebe, W.J. Prokaryotes: The unseen majority. Proc. Natl. Acad. Sci. USA 1998, 95, 6578–6583. [Google Scholar] [CrossRef] [PubMed]
- Heise, S.; Förstner, U. Risks from Historical Contaminated Sediments in the Rhine Basin. In The Interactions Between Sediments and Water; Kronvang, B., Faganeli, J., Ogrinc, N., Eds.; Springer: Dordrecht, The Netherlands, 2006; pp. 261–272. [Google Scholar]
- Heise, S.; Förstner, U. Risk assessment of contaminated sediments in river basins—Theoretical considerations and pragmatic approach. J. Environ. Monit. 2007, 9, 943. [Google Scholar] [CrossRef] [PubMed]
- Grabowski, R.C.; Droppo, I.G.; Wharton, G. Erodibility of cohesive sediment: The importance of sediment properties. Earth-Sci. Rev. 2011, 105, 101–120. [Google Scholar] [CrossRef]
- Pérez-Ruzafa, A.; Marcos, C.; Bernal, C.M.; Quintino, V.; Freitas, R.; Rodrigues, A.M.; García-Sánchez, M.; Pérez-Ruzafa, I.M. Cymodocea nodosa vs. Caulerpa prolifera: Causes and consequences of a long term history of interaction in macrophyte meadows in the Mar Menor coastal lagoon (Spain, southwestern Mediterranean). Estuar. Coast. Shelf Sci. 2012, 110, 101–115. [Google Scholar] [CrossRef]
- Alongi, D.M. Present state and future of the world’s mangrove forests. Envir. Conserv. 2002, 29, 331–349. [Google Scholar] [CrossRef]
- Zhang, C.; Li, M.; Zhao, G.-R.; Lu, W. Harnessing Yeast Peroxisomes and Cytosol Acetyl-CoA for Sesquiterpene α-Humulene Production. J. Agric. Food Chem. 2020, 68, 1382–1389. [Google Scholar] [CrossRef]
- Rissanen, K. Crystallography of encapsulated molecules. Chem. Soc. Rev. 2017, 46, 2638–2648. [Google Scholar] [CrossRef]
- Ouillon, S. Why and How Do We Study Sediment Transport? Focus on Coastal Zones and Ongoing Methods. Water 2018, 10, 390. [Google Scholar] [CrossRef]
- Larsen, S.; Kristiansen, E.; Van Den Tillaar, R. Effects of subjective and objective autoregulation methods for intensity and volume on enhancing maximal strength during resistance-training interventions: A systematic review. PeerJ 2021, 9, e10663. [Google Scholar] [CrossRef]
- Siviglia, A.; Crosato, A. Numerical modelling of river morphodynamics: Latest developments and remaining challenges. Adv. Water Resour. 2016, 93, 1–3. [Google Scholar] [CrossRef]
- Morel, Y.; Chaigneau, A.; Okpeitcha, V.O.; Stieglitz, T.; Assogba, A.; Duhaut, T.; Rétif, F.; Peugeot, C.; Sohou, Z. Terrestrial or oceanic forcing? Water level variations in coastal lagoons constrained by river inflow and ocean tides. Adv. Water Resour. 2022, 169, 104309. [Google Scholar] [CrossRef]
- Djihouessi, M.B.; Aina, M.P. A review of hydrodynamics and water quality of Lake Nokoué: Current state of knowledge and prospects for further research. Reg. Stud. Mar. Sci. 2018, 18, 57–67. [Google Scholar] [CrossRef]
- Zandagba, J.; Adandedji, F.M.; Mama, D.; Chabi, A.; Afouda, A. Assessment of the Physico-Chemical Pollution of a Water Body in a Perspective of Integrated Water Resource Management: Case Study of Nokou Lake. J. Environ. Prot. 2016, 7, 656–669. [Google Scholar] [CrossRef]
- Chaigneau, A.; Okpeitcha, O.V.; Morel, Y.; Stieglitz, T.; Assogba, A.; Benoist, M.; Allamel, P.; Honfo, J.; Awoulmbang Sakpak, T.D.; Rétif, F.; et al. From seasonal flood pulse to seiche: Multi-frequency water-level fluctuations in a large shallow tropical lagoon (Nokoué Lagoon, Benin). Estuar. Coast. Shelf Sci. 2022, 267, 107767. [Google Scholar] [CrossRef]
- Chaigneau, A.; Ouinsou, F.T.; Akodogbo, H.H.; Dobigny, G.; Avocegan, T.T.; Dossou-Sognon, F.U.; Okpeitcha, V.O.; Djihouessi, M.B.; Azémar, F. Physicochemical Drivers of Zooplankton Seasonal Variability in a West African Lagoon (Nokoué Lagoon, Benin). J. Mar. Sci. Eng. 2023, 11, 556. [Google Scholar] [CrossRef]
- Okpeitcha, O.V.; Chaigneau, A.; Morel, Y.; Stieglitz, T.; Pomalegni, Y.; Sohou, Z.; Mama, D. Seasonal and interannual variability of salinity in a large West-African lagoon (Nokoué Lagoon, Benin). Estuar. Coast. Shelf Sci. 2022, 264, 107689. [Google Scholar] [CrossRef]
- Beighley, J.S.; Hudac, C.M.; Arnett, A.B.; Peterson, J.L.; Gerdts, J.; Wallace, A.S.; Mefford, H.C.; Hoekzema, K.; Turner, T.N.; O’Roak, B.J.; et al. Clinical Phenotypes of Carriers of Mutations in CHD8 or Its Conserved Target Genes. Biol. Psychiatry 2020, 87, 123–131. [Google Scholar] [CrossRef]
- Li, L.; Ni, J.; Chang, F.; Yue, Y.; Frolova, N.; Magritsky, D.; Borthwick, A.G.L.; Ciais, P.; Wang, Y.; Zheng, C.; et al. Global trends in water and sediment fluxes of the world’s large rivers. Sci. Bull. 2020, 65, 62–69. [Google Scholar] [CrossRef]
- Kryzhanouski, Y. Ronan HERVOUET, Le goût des tyrans. Une ethnographie politique du quotidien en Biélorussie. Lormont: Le Bord de l’Eau, 2020, 282 p. Connexe 2021, 7, 228–231. [Google Scholar] [CrossRef]
- Yang, C.; Potts, R.; Shanks, D.R. Enhancing learning and retrieval of new information: A review of the forward testing effect. npj Sci. Learn. 2018, 3, 8. [Google Scholar] [CrossRef]
- Gupta, A.; Rodriguez-Hernandez, J.; Slebi-Acevedo, C.J.; Castro-Fresno, D. Improving Porous Asphalt Mixes by Incorporation of Additives; Finnish Transport and Communications Agency Traficom: Helsinki, Finland, 2020. [Google Scholar]
- Kumar, T.S.; Rao, N.N.M.; Rawat, R.; Rani, H.S.; Sharma, M.; Sadhu, V.; Sainath, A.V.S. Galactopolymer architectures/functionalized graphene oxide nanocomposites for antimicrobial applications. J. Polym. Res. 2021, 28, 196. [Google Scholar] [CrossRef]
- Chen, P.; Shi, W.; Liu, Y.; Cao, X. Slip rate deficit partitioned by fault-fold system on the active Haiyuan fault zone, Northeastern Tibetan Plateau. J. Struct. Geol. 2022, 155, 104516. [Google Scholar] [CrossRef]
- Gadel, F.; Texier, H. Distribution and nature of organic matter in recent sediments of Lake Nokoué, Benin (West Africa). Estuar. Coast. Shelf Sci. 1986, 22, 767–784. [Google Scholar] [CrossRef]
- Luc, L.B.; Alé, G.; Bertrand, M.; Texier, H.; Yves, B.; René, G. Les Ressources en Eaux Superficielles de la République du Bénin; ORSTOM: Paris, France, 1993. [Google Scholar]
- Fink, A.H.; Engel, T.; Ermert, V.; Van Der Linden, R.; Schneidewind, M.; Redl, R.; Afiesimama, E.; Thiaw, W.M.; Yorke, C.; Evans, M.; et al. Mean Climate and Seasonal Cycle. In Meteorology of Tropical West Africa; Parker, D.J., Diop-Kane, M., Eds.; Wiley: Hoboken, NJ, USA, 2017; pp. 1–39. [Google Scholar]
- Ahokpossi, Y. Analysis of the rainfall variability and change in the Republic of Benin (West Africa). Hydrol. Sci. J. 2018, 63, 2097–2123. [Google Scholar] [CrossRef]
- N’Tcha M’Po, Y.; Lawin, E.; Yao, B.; Oyerinde, G.; Attogouinon, A.; Afouda, A. Decreasing Past and Mid-Century Rainfall Indices over the Ouémé River Basin, Benin (West Africa). Climate 2017, 5, 74. [Google Scholar] [CrossRef]
- Guedje, F.K.; Houeto, A.V.V.; Houngninou, E.B.; Fink, A.H.; Knippertz, P. Climatology of coastal wind regimes in Benin. Meteorol. Z. 2019, 28, 23–39. [Google Scholar] [CrossRef]
- Biao, E. Assessing the Impacts of Climate Change on River Discharge Dynamics in Oueme River Basin (Benin, West Africa). Hydrology 2017, 4, 47. [Google Scholar] [CrossRef]
- Lawin, A.E.; Hounguè, R.; N’Tcha M’Po, Y.; Hounguè, N.R.; Attogouinon, A.; Afouda, A.A. Mid-Century Climate Change Impacts on Ouémé River Discharge at Bonou Outlet (Benin). Hydrology 2019, 6, 72. [Google Scholar] [CrossRef]
- Mama, D. Méthodologie et Résultats du Diagnostic de L’eutrophisation du Lac Nokoué (Bénin). Ph.D. Thesis, ÉUniversité de Limoges, Limoges, France, 2010. [Google Scholar]
- Djihouessi, M.B.; Djihouessi, M.B.; Aina, M.P. A review of habitat and biodiversity research in Lake Nokoué, Benin Republic: Current state of knowledge and prospects for further research. Ecohydrol. Hydrobiol. 2019, 19, 131–145. [Google Scholar] [CrossRef]
- Bajamgnigni Gbambie, A.S.; Steyn, D.G. Sea breezes at Cotonou and their interaction with the West African monsoon: SEA BREEZES AT COTONOU. Int. J. Clim. 2013, 33, 2889–2899. [Google Scholar] [CrossRef]
- Hervouet, J. Hydrodynamics of Free Surface Flows: Modelling with the Finite Element Method; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Thiébot, J.; Sedrati, M.; Guillou, S. The Potential of Tidal Energy Production in a Narrow Channel: The Gulf of Morbihan. J. Mar. Sci. Eng. 2024, 12, 479. [Google Scholar] [CrossRef]
- Lepesqueur, J.; Hostache, R.; Martínez-Carreras, N.; Montargès-Pelletier, E.; Hissler, C. Sediment transport modelling in riverine environments: On the importance of grain-size distribution, sediment density, and suspended sediment concentrations at the upstream boundary. Hydrol. Earth Syst. Sci. 2019, 23, 3901–3915. [Google Scholar] [CrossRef]
- Tassi, P.; Benson, T.; Delinares, M.; Fontaine, J.; Huybrechts, N.; Kopmann, R.; Pavan, S.; Pham, C.-T.; Taccone, F.; Walther, R. GAIA—A unified framework for sediment transport and bed evolution in rivers, coastal seas and transitional waters in the TELEMAC-MASCARET modelling system. Environ. Model. Softw. 2023, 159, 105544. [Google Scholar] [CrossRef]
- Krone, R.B. Flume Studies of the Transport of Sediment in Estuarial Shoaling Processes; University of California, Institute of Engineering Research: Pasadena, CA, USA, 1962. [Google Scholar]
- Partheniades, E. Erosion and Deposition of Cohesive Soils. J. Hydraul. Div. Proc. Am. Soc. Civ. Eng. 1965, 91, 105–139. [Google Scholar] [CrossRef]
- Zanke, U. Mitteilungen des Franzius-Instituts für Wasserbau und Küsteningenieurwesen der Technischen Universität Hannover, chap: Berechnung der Sinkgeschwindigkeiten von Sedimenten; Germany, 1977; pp. 231–245. Available online: https://portal.issn.org/resource/ISSN/0340-0077 (accessed on 19 July 2025).
- Thanh, V.Q.; Reyns, J.; Wackerman, C.; Eidam, E.F.; Roelvink, D. Modelling suspended sediment dynamics on the subaqueous delta of the Mekong River. Cont. Shelf Res. 2017, 147, 213–230. [Google Scholar] [CrossRef]
- Letrung, T.; Li, Q.; Li, Y.; Vukien, T.; Nguyenthai, Q. Morphology Evolution of Cuadai Estuary, Mekong River, Southern Vietnam. J. Hydrol. Eng. 2013, 18, 1122–1132. [Google Scholar] [CrossRef]
- Hung, N.N.; Delgado, J.M.; Güntner, A.; Merz, B.; Bárdossy, A.; Apel, H. Sedimentation in the floodplains of the Mekong Delta, Vietnam Part II: Deposition and erosion. Hydrol. Process. 2014, 28, 3145–3160. [Google Scholar] [CrossRef]
- Manh, N.V.; Dung, N.V.; Hung, N.N.; Merz, B.; Apel, H. Large-scale suspended sediment transport and sediment deposition in the Mekong Delta. Hydrol. Earth Syst. Sci. 2014, 18, 3033–3053. [Google Scholar] [CrossRef]
- Jordan, C.; Tiede, J.; Lojek, O.; Visscher, J.; Apel, H.; Nguyen, H.Q.; Quang, C.N.X.; Schlurmann, T. Sand mining in the Mekong Delta revisited—Current scales of local sediment deficits. Sci. Rep. 2019, 9, 17823. [Google Scholar] [CrossRef]
- Hackney, C.R.; Darby, S.E.; Parsons, D.R.; Leyland, J.; Best, J.L.; Aalto, R.; Nicholas, A.P.; Houseago, R.C. River bank instability from unsustainable sand mining in the lower Mekong River. Nat. Sustain. 2020, 3, 217–225. [Google Scholar] [CrossRef]
- Binh, D.V.; Kantoush, S.A.; Ata, R.; Tassi, P.; Nguyen, T.V.; Lepesqueur, J.; Abderrezzak, K.E.K.; Bourban, S.E.; Nguyen, Q.H.; Phuong, D.N.L.; et al. Hydrodynamics, sediment transport, and morphodynamics in the Vietnamese Mekong Delta: Field study and numerical modelling. Geomorphology 2022, 413, 108368. [Google Scholar] [CrossRef]
- Tang, T.; Shindell, D.; Faluvegi, G.; Myhre, G.; Olivié, D.; Voulgarakis, A.; Kasoar, M.; Andrews, T.; Boucher, O.; Forster, P.M.; et al. Comparison of Effective Radiative Forcing Calculations Using Multiple Methods, Drivers, and Models. JGR Atmos. 2019, 124, 4382–4394. [Google Scholar] [CrossRef]
- Wang, Y. An Empirical Study on the Factors Influencing the Effect of Interactive Video Information Dissemination in Science Popularization. Pop. Sci. Res. 2022, 3, 26–37+106. [Google Scholar]
- Banasik, K.; Chojnacki, A.L.; Gebczyk, K.; Grakowski, L. Influence of wind speed on the reliability of low-voltage overhead power lines. In Proceedings of the 2019 Progress in Applied Electrical Engineering (PAEE), Koscielisko, Poland, 17–21 June 2019; IEEE: New York, NY, USA, 2019; pp. 1–5. [Google Scholar]
- Ganju, N.K.; Couvillion, B.R.; Defne, Z.; Ackerman, K.V. Development and Application of Landsat-Based Wetland Vegetation Cover and UnVegetated-Vegetated Marsh Ratio (UVVR) for the Conterminous United States. Estuaries Coasts 2022, 45, 1861–1878. [Google Scholar] [CrossRef]



| Month | Q1 | Q2 | Q3 | Q4 | Q5 | Q6 | Q7 |
|---|---|---|---|---|---|---|---|
| Jul-22 | 40.1 | 0.0 | 9.7 | 4.0 | 6.7 | 4.6 | 3.7 |
| Sep-22 | 112.1 | 37.6 | 46.9 | 93.4 | 77.7 | 137.0 | 60.8 |
| Nov-22 | 83.3 | 9.8 | 5.0 | 7.7 | 8.5 | 3.8 | 1.8 |
| Mar-23 | −31.3 | 3.8 | 3.2 | 6.1 | −4.2 | 3.7 | 2.3 |
| Jun-23 | 14.7 | 0.2 | −4.7 | −3.2 | −6.7 | 6.5 | 6.8 |
| Parameters | References | |||
|---|---|---|---|---|
| (m/s) | (m/s) | M kg/(s.m2) | τce (N/m2) | |
| 10−4–3·10−4 | 8.9·10−3–1.1·10−2 | 5·10−6–1·10−4 | 0.15–1.5 | [45] |
| 2.16·10−4–1.85·10−3 | 4.5·10−3–5.3·10−3 | 5.13·10−6–8·10−6 | 0.028–0.044 | [46] |
| 10−4–1.3·10−3 | 4.4·10−3–5·10−3 | [47] | ||
| 5·10−5–3.3·10−4 | 1.0 | 2·10−5 | 0.2 | [44] |
| Water Level | Velocity | Css | |||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | NSE | RMSE (m) | R2 | NSE | RMSE (m/s) | R2 | NSE | RMSE (g/L) | |
| Model calibration | |||||||||
| 0.86 | 0.78 | 0.26 | 0.82 | 0.77 | 0.07 | 0.97 | 0.96 | 0.03 | |
| Model validation | |||||||||
| 0.91 | 0.93 | 0.08 | 0.94 | 0.95 | 0.06 | 0.88 | 0.87 | 0.03 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yonouwinhi, T.J.-B.; Thiébot, J.; Guillou, S.S.; d’Almeida, G.A.F.A.; Abagale, F.K. Modelling of Water Level Fluctuations and Sediment Fluxes in Nokoué Lake (Southern Benin). Water 2025, 17, 2209. https://doi.org/10.3390/w17152209
Yonouwinhi TJ-B, Thiébot J, Guillou SS, d’Almeida GAFA, Abagale FK. Modelling of Water Level Fluctuations and Sediment Fluxes in Nokoué Lake (Southern Benin). Water. 2025; 17(15):2209. https://doi.org/10.3390/w17152209
Chicago/Turabian StyleYonouwinhi, Tètchodiwèï Julie-Billard, Jérôme Thiébot, Sylvain S. Guillou, Gérard Alfred Franck Assiom d’Almeida, and Felix Kofi Abagale. 2025. "Modelling of Water Level Fluctuations and Sediment Fluxes in Nokoué Lake (Southern Benin)" Water 17, no. 15: 2209. https://doi.org/10.3390/w17152209
APA StyleYonouwinhi, T. J.-B., Thiébot, J., Guillou, S. S., d’Almeida, G. A. F. A., & Abagale, F. K. (2025). Modelling of Water Level Fluctuations and Sediment Fluxes in Nokoué Lake (Southern Benin). Water, 17(15), 2209. https://doi.org/10.3390/w17152209









