Identification of Critical Exposed Elements and Strategies for Mitigating Secondary Hazards in Flood-Induced Coal Mine Accidents
Abstract
1. Introduction
- This paper proposes a two-stage analytical framework for Natech events, centered around the identification of critical exposed elements. By recognizing their dual role as both victims and facilitators of hazard transmission, the framework systematically analyzes key propagation pathways and introduces a tailored link classification and grading method for disaster evolution.
- An enhanced algorithm for node importance identification based on adjacency information entropy is developed. Incorporating the concept of coupling enhancement coefficients, the algorithm captures the inherent multi-hazard coupling features of Natech scenarios. Comparative analyses against classical methods validate its effectiveness and robustness in identifying critical exposed elements.
- To prioritize intervention targets, a dual-dimensional link classification strategy integrating entropy and risk is introduced. This approach adheres to the principle of concentrating efforts on decisive hazards, enabling targeted interventions under limited conditions and enhancing the overall efficiency of Natech disaster mitigation efforts.
- The proposed framework is validated using a comprehensive dataset of real-world coal mine–flood Natech cases. The findings offer actionable insights for emergency decision-making and strategic risk mitigation. Specifically, the results support targeted classification of exposed elements and focused interventions along high-risk propagation routes, facilitating the formulation of differentiated emergency response plans and enhancing the accuracy and timeliness of coal mine disaster governance.
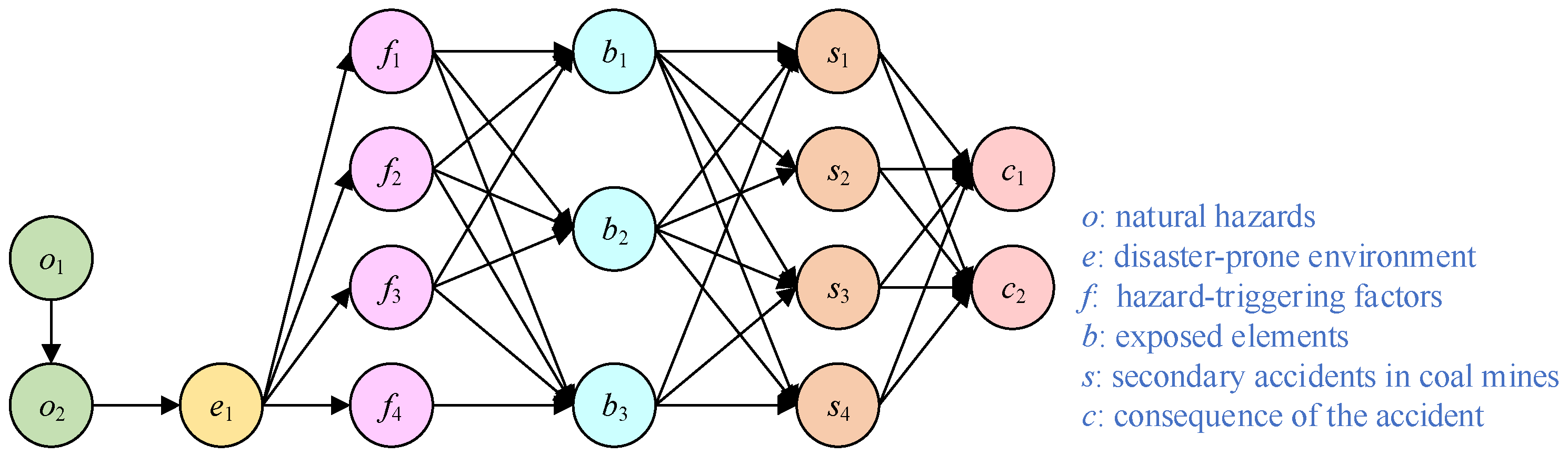
2. Analytical Framework
3. Datas and Methods
3.1. Data Sources
- The National Institute for Occupational Safety and Health (NIOSH) and the Mine Safety and Health Administration (MSHA) in the United States. Accident data are publicly accessible via their official websites (https://www.cdc.gov/niosh/ (accessed on 5 March 2025) and https://www.msha.gov/ (accessed on 6 March 2025));
- China Safety Production Yearbook (2000–2017), compiled by the China Academy of Safety Science and Technology, accessible through the National Library of China and relevant academic databases;
- The Coal Mine Safety Production Network (http://www.mkaq.org (accessed on 9 March 2025)) and the Safety Management Network (http://www.safehoo.com (accessed on 10 March 2025)), both of which provide open-access mining accident cases and safety analysis reports;
- Official websites of emergency management authorities, such as the Ministry of Emergency Management of China (http://www.mem.gov.cn (accessed on 11 March 2025)), where accident bulletins can be retrieved from the “News” or “Accident Alerts” sections.
3.2. Methodology
3.2.1. Problem Description
3.2.2. Coupled Adjacency Information Entropy Model for Key Exposed Element Identification
- Modeling of Enhancement Coefficients Under Coupling Mechanisms
- Enhancement Coefficient Under OR Coupling
- Enhancement Coefficient Under AND Coupling
- Enhancement Coefficient Under CO Coupling
- 2.
- Coupled Adjacency Information Entropy Model
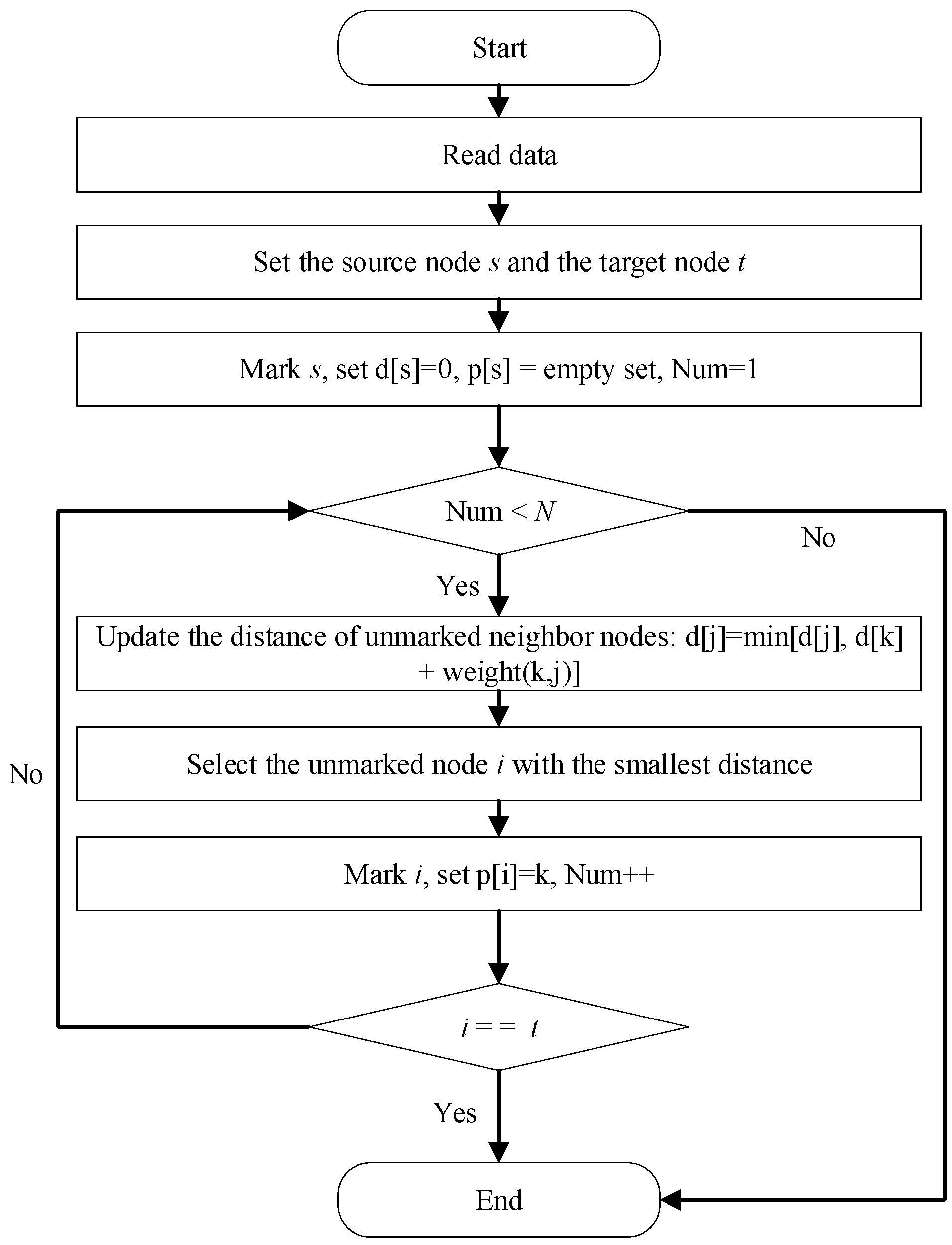
3.2.3. Dijkstra’s Algorithm for Identifying the Shortest Propagation Path of Secondary Hazards
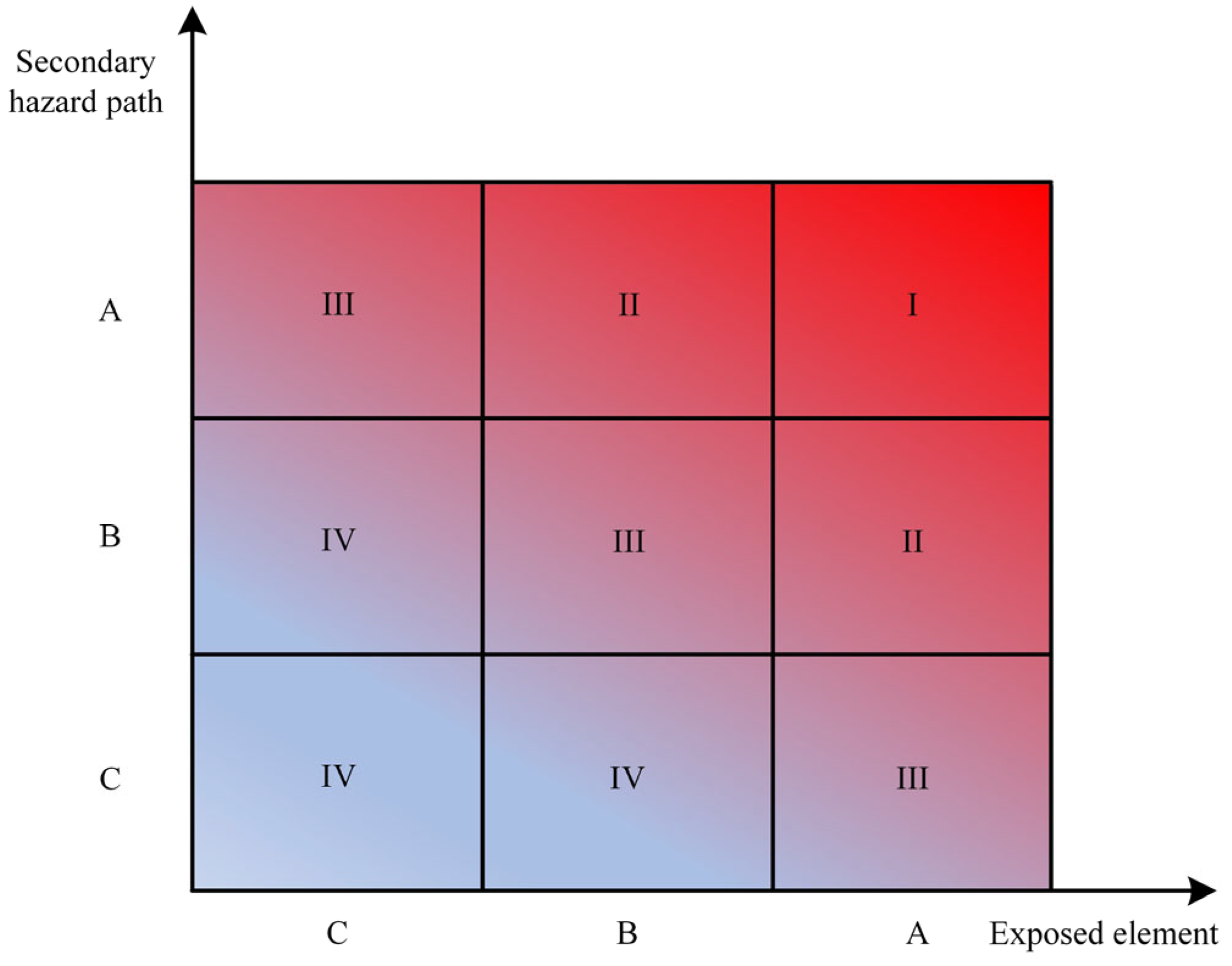
3.2.4. Priority Determination Based on Dual Dimensions of Exposed Element Management and Secondary Hazard Disruption
- (1)
- Classification of Exposed Elements and Secondary Hazard Paths
- (2)
- Priority Determination Based on Combined Dual-Dimensional Classification
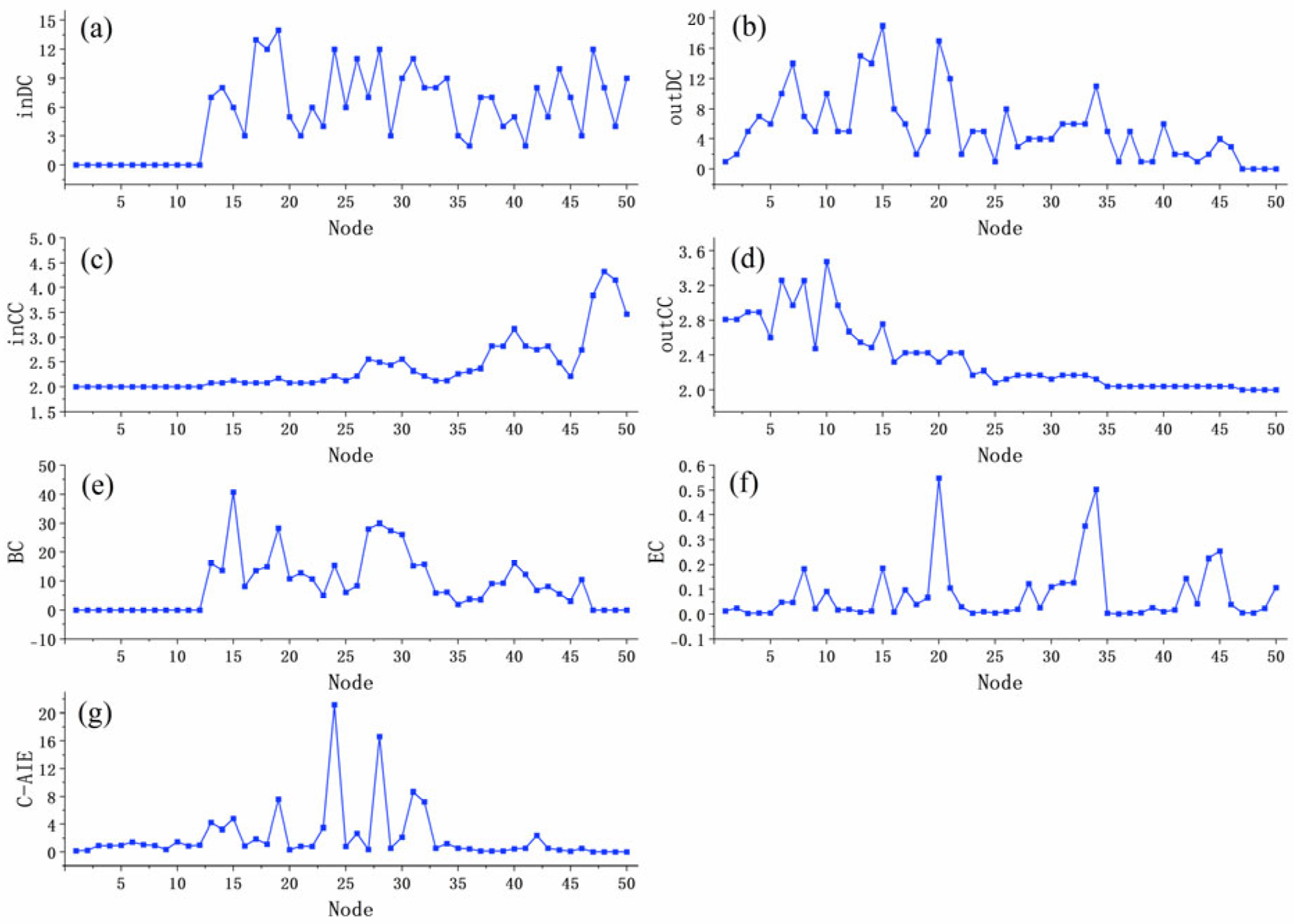
3.3. Numerical Analysis
- (1)
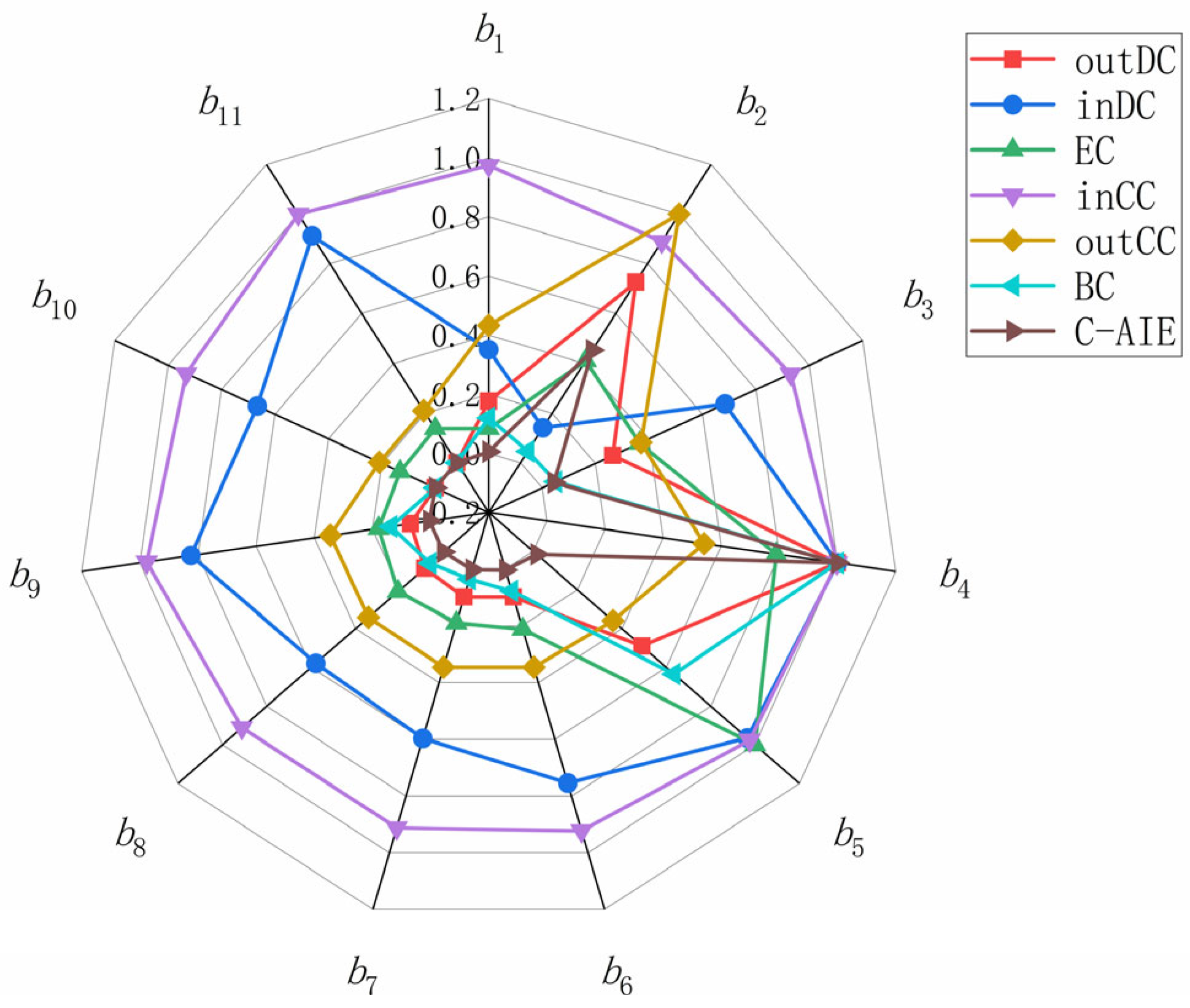
- Degree Centrality focuses on the direct influence between nodes
- (2)
- Closeness Centrality reflects the degree to which a node is positioned at the center of the network; the closer a node is to the center of the network, the higher its importance
- (3)
- Node Betweenness Centrality reflects the extent to which a node (or edge) acts as a “bridge” or “intermediary” between other nodes in the network
- (4)
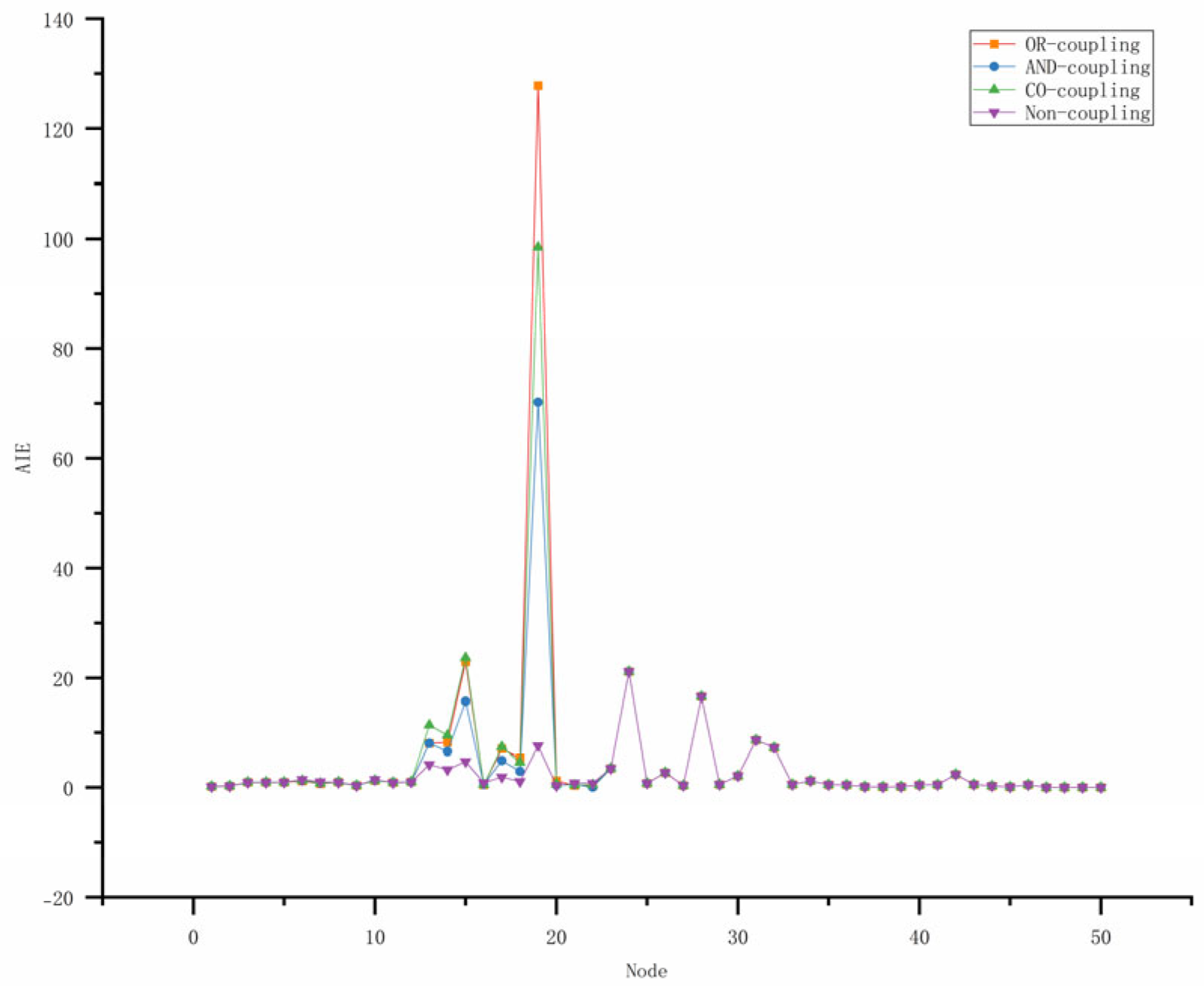
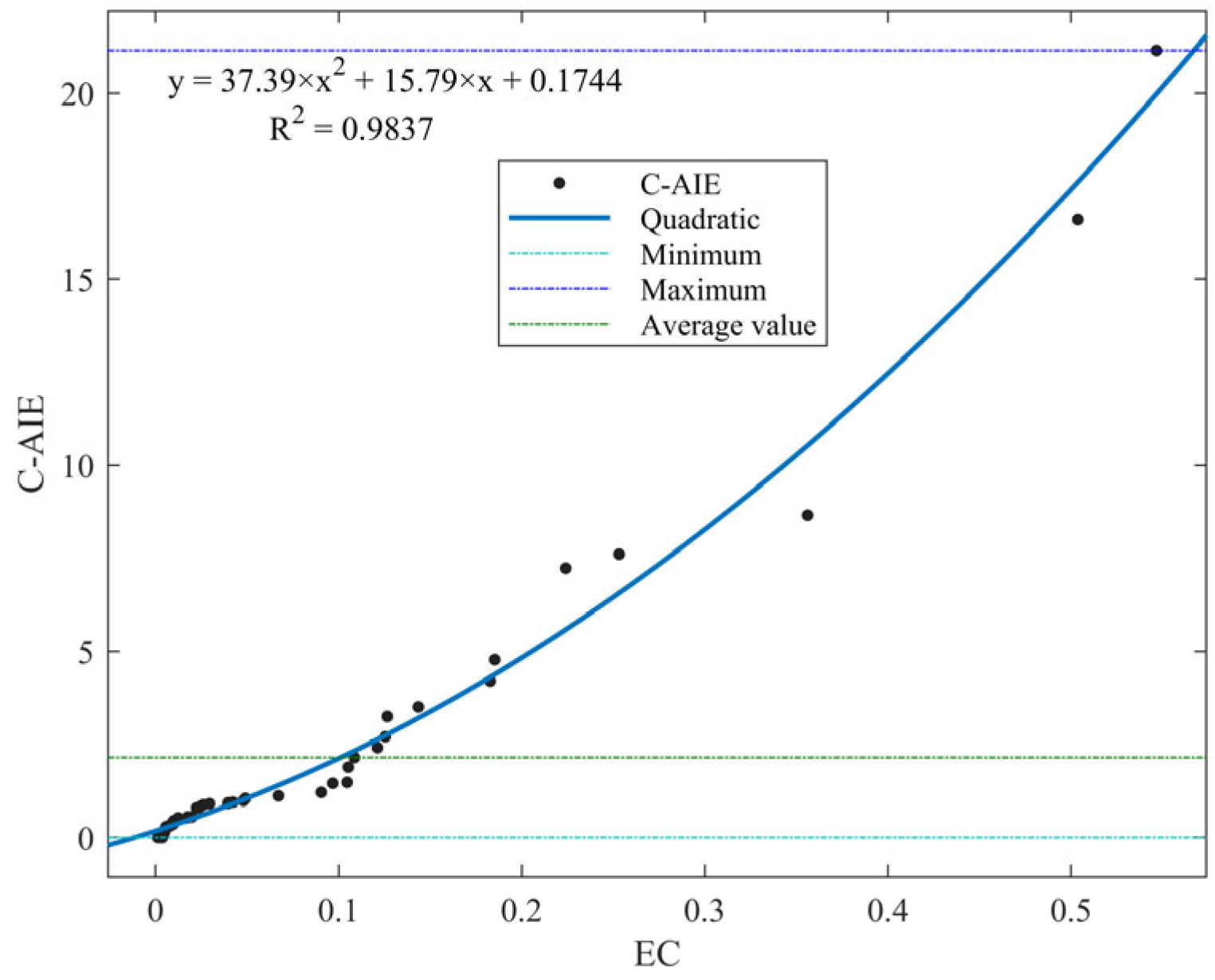
- C-AIE and EC not only focus on the “direct influence” of nodes but also consider the “indirect influence,” so the distribution trends of node importance for both are quite similar, but C-AIE has higher discriminability
3.4. Algorithmic Workflow
4. Results
4.1. Construction of the Coal Mine–Flood Natech Event Chain Network
4.2. Analysis of Exposed Elements
4.2.1. Importance Evaluation and Classification of Exposed Elements Based on the C-AIE Algorithm
4.2.2. Analysis of Key Exposed Elements by Category
- (1)
- Class A exposed elements
- (2)
- Class B exposed elements
- (3)
- Class C exposed elements
4.3. Analysis of Secondary Hazard Propagation Paths
4.3.1. Classification of Secondary Hazard Evolution Paths Based on Dijkstra’s Algorithm
4.3.2. Analysis of Secondary Hazard Propagation Paths by Category
- (1)
- Class A propagation paths
- (2)
- Class B propagation paths
- (3)
- Class C propagation paths
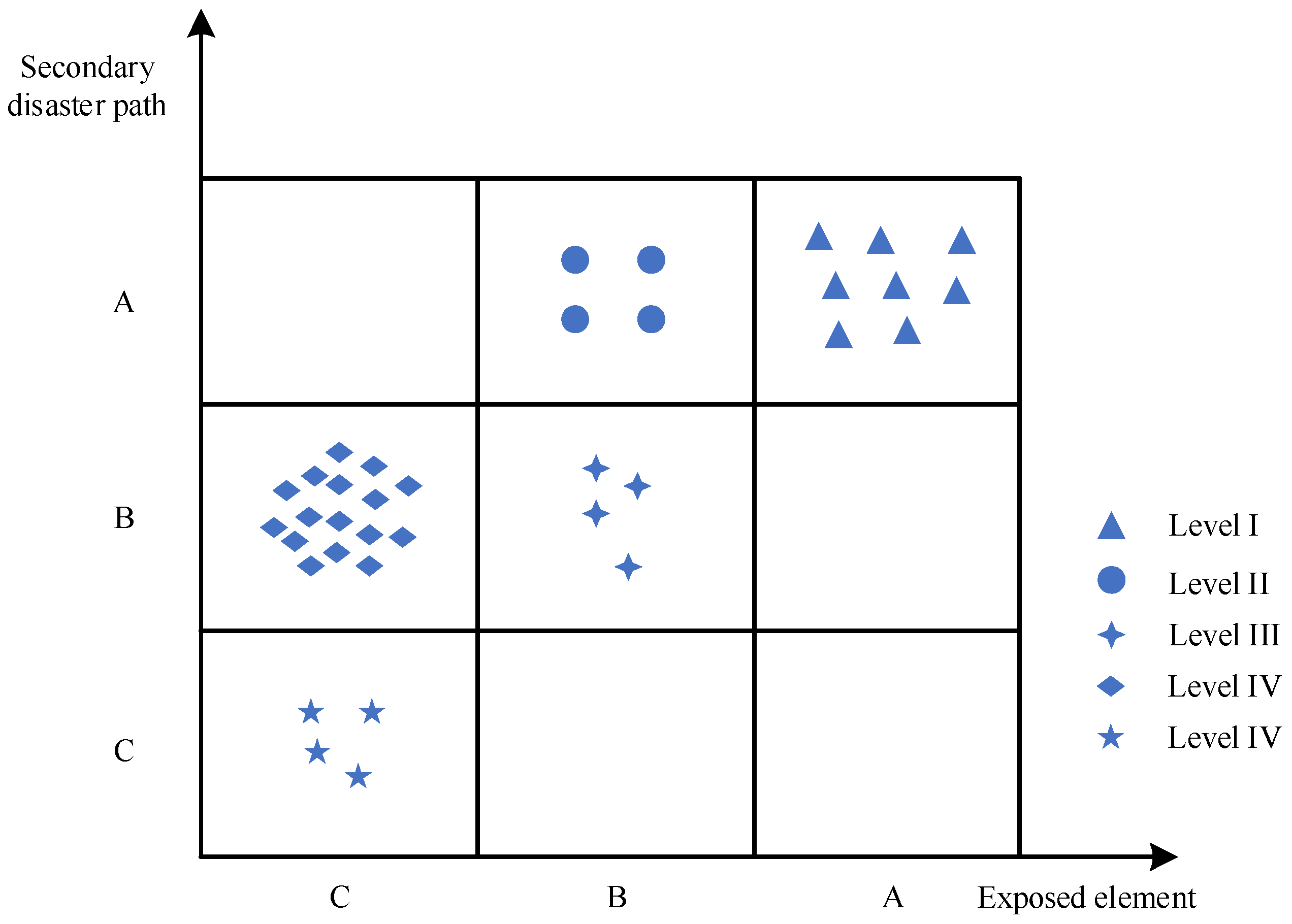
4.4. Management Priority Determination Based on Exposed Elements and Secondary Hazard Propagation Paths
- (1)
- Level I (class A exposed elements and class A paths)
- (2)
- Level II (class B exposed elements and class A paths)
- (3)
- Level III (class B exposed elements and class B paths)
- (4)
- Level IV (class C exposed elements and class B/C paths)
5. Discussion
5.1. Hazard Reduction Strategies for Coal Mine-Flood Natech Events
- Surface facility (b4) and surrounding hydrological systems (b2), as well as the secondary hazard propagation paths that act as conduits between them, should be monitored as the highest priority. After a natural hazard occurs, the status of surface facility and surrounding hydrological systems is most likely to change, easily expanding the hazard scope through the hazard-causing environment, and the rate of destruction is extremely fast. Therefore, in daily protection, surface facility should be reinforced to improve its hazard resistance; real-time monitoring devices (such as hydrological monitoring and ground subsidence monitoring) should be deployed in surrounding hydrological systems to promptly detect anomalies, prevent the failure of surrounding hydrological systems, and thus avoid cascading effects in other hazard-bearing systems.
- The well and tunnel system (b5) and the surrounding geological system (b3), as well as the secondary hazard propagation paths that act as conductive intermediaries, should be monitored as a second-high priority. These systems are highly susceptible to the impacts of surface facility and surrounding hydrological systems; for example, flooding of industrial squares or damage to river channels may directly lead to well and tunnel collapses or geological structure damage. Therefore, geological exploration should be conducted regularly to identify geological risk points such as faults and landslides in advance, optimizing the layout of wells and tunnels; strengthening well and tunnel reinforcement and dynamic monitoring, using high-strength support materials and sensor networks to monitor well and tunnel deformation and pressure changes in real time; and setting up emergency isolation doors or waterproof flood walls at key nodes of the wells and tunnels to prevent the spread of hazards.
- The ecological system of the mining area (b1), power system (b9), ventilation system (b8), mining system (b6), drainage system (b7), and the secondary hazard transmission paths that use them as conduits should be prioritized for management. These systems are at a higher risk of indirect impact from natural hazards and need to comprehensively reduce their indirect risks in natural hazards through technical redundancy design (such as backup power supply, multi-level drainage), intelligent monitoring (real-time fault diagnosis and data linkage), ecological protection measures (vegetation buffer zones and pollution emergency response), and remote automated operations, thereby enhancing the system’s hazard resilience and rapid recovery capabilities, and avoiding secondary hazard transmission caused by equipment failure or ecological damage.
- The transportation lifting system (b10), safety monitoring and communication system (b11), and the secondary hazard propagation paths that serve as conduits for them should be optimized as basic support systems. Although their direct risks are relatively low, the failure of the transportation lifting system and the safety monitoring and communication system may hinder rescue efforts and information transmission. Measures such as planning emergency transportation routes, reinforcing transportation lifting equipment, deploying multi-modal communication redundancy, and implementing hazard linkage response should be taken to ensure smooth transportation and uninterrupted information transmission in extreme environments, providing reliable support for overall emergency response.
5.2. Comparative Analysis with Existing Studies
5.2.1. Comparison with Benchmark Algorithms
5.2.2. Comparison with Other Entropy-Based Node Identification Algorithms
- (1)
- Well-suited for directed and weighted networks, enhancing applicability. The C-AIE algorithm is specifically developed to accommodate directed and weighted networks, aligning well with the structural attributes of hazard chain systems. In contrast, methods proposed in References [25,44,45] are limited to undirected and unweighted networks, rendering them inadequate for capturing asymmetric inter-node influences or varying edge weights. By differentiating the impact of in-degree and out-degree on node significance, the C-AIE algorithm offers a more refined understanding of network structure.
- (2)
- Computationally efficient with reduced data requirements. Unlike the method in reference [45], which necessitates both first-order and second-order neighbor information, the C-AIE algorithm relies solely on a node and its immediate neighbors. This design simplifies the data processing pipeline while preserving high identification accuracy, making it suitable for large-scale or data-constrained scenarios.
- (3)
- Incorporates coupling mechanisms to model compound hazard dynamics. Although reference [26] extends entropy-based methods to various network types, it—like other compared methods—does not account for hazard coupling. The C-AIE algorithm addresses this gap by modeling the collaborative impact of multiple parent nodes on a shared downstream node, thus capturing the cascade amplification effects commonly observed in multi-hazard hazard systems.
5.3. Applicability of the Proposed Method Across Sectors
- Reclassification of exposed elements. The critical infrastructure affected varies across hazard types. Floods typically damage surface-level drainage and shaft systems, whereas earthquakes are more likely to impact underground tunnels and support structures. Hence, the node types and spatial distribution in the network must be redefined accordingly.
- Adjustment of coupling mechanisms. The current model is based on flood-induced cascading effects. However, other hazards differ in their transmission mechanisms and interdependency patterns. Therefore, the inter-node coupling logic and edge weights must be revised to accurately capture the dynamic evolution under alternative disaster scenarios.
- Modification of hazard propagation mechanisms. Spatial and temporal characteristics of hazard spread vary significantly. Floods tend to exhibit terrain-dependent flow paths, while earthquakes propagate damage in a simultaneous, multi-point fashion. As such, model parameters and propagation rules should be recalibrated to reflect these differences.
6. Conclusions and Suggestions
6.1. Conclusions and Future Work
6.2. Suggestions
- (1)
- Develop a multi-hazard Natech knowledge base and dataset. Establishing a comprehensive accident case repository in representative mining regions—including events triggered by floods, earthquakes, landslides, and snow-related hazards—would allow for systematic documentation of exposed element distributions, coupling chains, and historical propagation patterns. Such a database would facilitate effective model transfer and algorithm refinement.
- (2)
- Conduct model adaptation studies for different types of mines. It is suggested to investigate the characteristics of accident chains in different types of mines under the influence of natural disasters, and to explore algorithmic models with high adaptability and generalization ability in broader application scenarios.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| No. | Node | inDC | outDC | inCC | outCC | BC | EC | C-AIE |
|---|---|---|---|---|---|---|---|---|
| 1 | a1 | 0 | 1 | 2.000 | 2.811 | 0 | 0.012 | 0.141 |
| 2 | a2 | 0 | 2 | 2.000 | 2.811 | 0 | 0.025 | 0.228 |
| 3 | a3 | 0 | 5 | 2.000 | 2.896 | 0 | 0.003 | 0.915 |
| 4 | a4 | 0 | 7 | 2.000 | 2.896 | 0 | 0.005 | 0.909 |
| 5 | a5 | 0 | 6 | 2.000 | 2.605 | 0 | 0.005 | 0.951 |
| 6 | a6 | 0 | 10 | 2.000 | 3.260 | 0 | 0.049 | 1.457 |
| 7 | a7 | 0 | 14 | 2.000 | 2.975 | 0 | 0.048 | 1.051 |
| 8 | a8 | 0 | 7 | 2.000 | 3.258 | 0 | 0.183 | 0.934 |
| 9 | a9 | 0 | 5 | 2.000 | 2.476 | 0 | 0.022 | 0.344 |
| 10 | a10 | 0 | 10 | 2.000 | 3.480 | 0 | 0.090 | 1.482 |
| 11 | a11 | 0 | 5 | 2.000 | 2.975 | 0 | 0.018 | 0.878 |
| 12 | a12 | 0 | 5 | 2.000 | 2.670 | 0 | 0.020 | 0.993 |
| 13 | b1 | 7 | 15 | 2.083 | 2.549 | 16.233 | 0.008 | 4.204 |
| 14 | b2 | 8 | 14 | 2.083 | 2.489 | 13.671 | 0.012 | 3.253 |
| 15 | b3 | 6 | 19 | 2.128 | 2.756 | 40.700 | 0.185 | 4.776 |
| 16 | b4 | 3 | 8 | 2.083 | 2.318 | 8.095 | 0.008 | 0.879 |
| 17 | b5 | 13 | 6 | 2.083 | 2.427 | 13.617 | 0.097 | 1.892 |
| 18 | b6 | 12 | 2 | 2.083 | 2.427 | 15.000 | 0.040 | 1.120 |
| 19 | b7 | 14 | 5 | 2.174 | 2.427 | 28.317 | 0.067 | 7.614 |
| 20 | b8 | 5 | 17 | 2.083 | 2.318 | 10.800 | 0.547 | 0.308 |
| 21 | b9 | 3 | 12 | 2.083 | 2.427 | 12.833 | 0.105 | 0.841 |
| 22 | b10 | 6 | 2 | 2.083 | 2.427 | 10.733 | 0.029 | 0.798 |
| 23 | c1 | 4 | 5 | 2.126 | 2.172 | 4.950 | 0.003 | 3.510 |
| 24 | c2 | 12 | 5 | 2.219 | 2.220 | 15.460 | 0.010 | 21.151 |
| 25 | c3 | 6 | 1 | 2.126 | 2.082 | 6.000 | 0.005 | 0.800 |
| 26 | c4 | 11 | 8 | 2.219 | 2.127 | 8.288 | 0.010 | 2.710 |
| 27 | c5 | 7 | 3 | 2.555 | 2.172 | 27.969 | 0.020 | 0.357 |
| 28 | c6 | 12 | 4 | 2.491 | 2.172 | 29.900 | 0.121 | 16.599 |
| 29 | c7 | 3 | 4 | 2.431 | 2.172 | 27.450 | 0.026 | 0.553 |
| 30 | c8 | 9 | 4 | 2.553 | 2.127 | 26.033 | 0.109 | 2.151 |
| 31 | c9 | 11 | 6 | 2.320 | 2.172 | 15.317 | 0.125 | 8.660 |
| 32 | c10 | 8 | 6 | 2.219 | 2.172 | 15.833 | 0.127 | 7.238 |
| 33 | c11 | 8 | 6 | 2.126 | 2.172 | 5.733 | 0.356 | 0.554 |
| 34 | c12 | 9 | 11 | 2.126 | 2.127 | 6.067 | 0.504 | 1.213 |
| 35 | c13 | 3 | 5 | 2.264 | 2.041 | 2.000 | 0.004 | 0.530 |
| 36 | c14 | 2 | 1 | 2.317 | 2.041 | 3.750 | 0.001 | 0.459 |
| 37 | c15 | 7 | 5 | 2.371 | 2.041 | 3.602 | 0.004 | 0.125 |
| 38 | c16 | 7 | 1 | 2.826 | 2.041 | 9.064 | 0.006 | 0.115 |
| 39 | c17 | 4 | 1 | 2.821 | 2.041 | 9.233 | 0.026 | 0.125 |
| 40 | c18 | 5 | 6 | 3.167 | 2.041 | 16.250 | 0.010 | 0.454 |
| 41 | c19 | 2 | 2 | 2.823 | 2.041 | 12.333 | 0.017 | 0.528 |
| 42 | c20 | 8 | 2 | 2.747 | 2.041 | 6.717 | 0.144 | 2.417 |
| 43 | c21 | 5 | 1 | 2.821 | 2.041 | 8.050 | 0.042 | 0.553 |
| 44 | c22 | 10 | 2 | 2.484 | 2.041 | 5.450 | 0.224 | 0.291 |
| 45 | c23 | 7 | 4 | 2.217 | 2.041 | 3.067 | 0.253 | 0.103 |
| 46 | c24 | 3 | 3 | 2.745 | 2.041 | 10.483 | 0.039 | 0.520 |
| 47 | c25 | 12 | 0 | 3.840 | 2.000 | 0 | 0.005 | 0.000 |
| 48 | c26 | 8 | 0 | 4.325 | 2.000 | 0 | 0.004 | 0.000 |
| 49 | c27 | 4 | 0 | 4.149 | 2.000 | 0 | 0.024 | 0.000 |
| 50 | c28 | 9 | 0 | 3.465 | 2.000 | 0 | 0.105 | 0.000 |
| No. | Node | OR Coupling | AND Coupling | CO Coupling | No Coupling (AIE) |
|---|---|---|---|---|---|
| 1 | a1 | 0.1924 | 0.1827 | 0.1931 | 0.1408 |
| 2 | a2 | 0.3006 | 0.2873 | 0.3015 | 0.2275 |
| 3 | a3 | 0.9716 | 0.9590 | 0.9659 | 0.9148 |
| 4 | a4 | 0.9647 | 0.9628 | 0.9822 | 0.9090 |
| 5 | a5 | 0.9817 | 0.9753 | 0.9761 | 0.9508 |
| 6 | a6 | 1.2035 | 1.2927 | 1.2614 | 1.4572 |
| 7 | a7 | 0.6936 | 0.8183 | 0.7774 | 1.0512 |
| 8 | a8 | 1.0131 | 0.9929 | 0.9943 | 0.9341 |
| 9 | a9 | 0.3621 | 0.3602 | 0.3614 | 0.3439 |
| 10 | a10 | 1.2907 | 1.3445 | 1.2835 | 1.4816 |
| 11 | a11 | 0.9162 | 0.9047 | 0.9137 | 0.8779 |
| 12 | a12 | 1.0341 | 1.0271 | 1.0321 | 0.9929 |
| 13 | b1 | 8.0890 | 8.0890 | 11.3855 | 4.2040 |
| 14 | b2 | 8.2462 | 6.5778 | 9.5119 | 3.2529 |
| 15 | b3 | 22.9471 | 15.7376 | 23.6692 | 4.7756 |
| 16 | b4 | 0.5010 | 0.5694 | 0.4988 | 0.8790 |
| 17 | b5 | 7.0632 | 4.9446 | 7.3978 | 1.8916 |
| 18 | b6 | 5.3460 | 2.9699 | 4.5748 | 1.1200 |
| 19 | b7 | 127.9241 | 70.2186 | 98.4316 | 7.6137 |
| 20 | b8 | 1.2225 | 0.4000 | 0.5914 | 0.3081 |
| 21 | b9 | 0.3578 | 0.5434 | 0.4117 | 0.8411 |
| 22 | b10 | 0.3930 | 0.0483 | 0.5210 | 0.7979 |
| 23 | c1 | 3.5096 | 3.5096 | 3.5096 | 3.5096 |
| 24 | c2 | 21.1505 | 21.1505 | 21.1505 | 21.1505 |
| 25 | c3 | 0.8002 | 0.8002 | 0.8002 | 0.8002 |
| 26 | c4 | 2.7100 | 2.7100 | 2.7100 | 2.7100 |
| 27 | c5 | 0.3571 | 0.3571 | 0.3571 | 0.3571 |
| 28 | c6 | 16.5988 | 16.5988 | 16.5988 | 16.5988 |
| 29 | c7 | 0.5534 | 0.5534 | 0.5534 | 0.5534 |
| 30 | c8 | 2.1513 | 2.1513 | 2.1513 | 2.1513 |
| 31 | c9 | 8.6596 | 8.6596 | 8.6596 | 8.6596 |
| 32 | c10 | 7.2381 | 7.2381 | 7.2381 | 7.2381 |
| 33 | c11 | 0.5539 | 0.5539 | 0.5539 | 0.5539 |
| 34 | c12 | 1.2126 | 1.2126 | 1.2126 | 1.2126 |
| 35 | c13 | 0.5299 | 0.5299 | 0.5299 | 0.5299 |
| 36 | c14 | 0.4594 | 0.4594 | 0.4594 | 0.4594 |
| 37 | c15 | 0.1251 | 0.1251 | 0.1251 | 0.1251 |
| 38 | c16 | 0.1151 | 0.1151 | 0.1151 | 0.1151 |
| 39 | c17 | 0.1251 | 0.1251 | 0.1251 | 0.1251 |
| 40 | c18 | 0.4536 | 0.4536 | 0.4536 | 0.4536 |
| 41 | c19 | 0.5283 | 0.5283 | 0.5283 | 0.5283 |
| 42 | c20 | 2.4169 | 2.4169 | 2.4169 | 2.4169 |
| 43 | c21 | 0.5534 | 0.5534 | 0.5534 | 0.5534 |
| 44 | c22 | 0.2905 | 0.2905 | 0.2905 | 0.2905 |
| 45 | c23 | 0.1028 | 0.1028 | 0.1028 | 0.1028 |
| 46 | c24 | 0.5200 | 0.5200 | 0.5200 | 0.5200 |
| 47 | c25 | 0 | 0 | 0 | 0 |
| 48 | c26 | 0 | 0 | 0 | 0 |
| 49 | c27 | 0 | 0 | 0 | 0 |
| 50 | c28 | 0 | 0 | 0 | 0 |
| Grading | Shortest Path Node | Shortest Path Length |
|---|---|---|
| High risk | b4-s16-s45-c1 | 2.2 |
| b4-s16-s45-c3 | 2.2 | |
| b4-s8-s48-c2 | 2.2 | |
| b5-s19-s43-c2 | 2.2 | |
| b4-s15-s54-c4 | 2.3 | |
| b2-b9-s23-s43-c1 | 2.3 | |
| b2-s10-s48-c2 | 2.4 | |
| b5-s19-s45-c1 | 2.5 | |
| b5-s19-s45-c3 | 2.5 | |
| b2-s10-s54-c3 | 2.5 | |
| b2-s10-s53-c4 | 2.5 | |
| b3-s29-s49-c2 | 2.5 | |
| Medium risk | b5-s19-s52-c4 | 2.6 |
| b9-s23-s43-c1 | 2.6 | |
| b9-s23-s43-c2 | 2.6 | |
| b9-s23-s43-c3 | 2.6 | |
| b1-s5-s54-c3 | 2.7 | |
| b1-s5-s48-c2 | 2.8 | |
| b8-s25-s58-c2 | 2.9 | |
| b1-s17-s52-c4 | 3.0 | |
| b3-s29-s60-c3 | 3.0 | |
| b3-b5-s19-s45-c1 | 3.3 | |
| b3-b5-s19-s52-c4 | 3.4 | |
| b6-s26-s31-s60-c3 | 3.5 | |
| b7-s27-s19-s45-c1 | 3.5 | |
| b7-s27-s19-s45-c3 | 3.5 | |
| b7-s27-s19-s52-c4 | 3.6 | |
| b1-s5-s48-s19-s45-c1 | 3.8 | |
| b6-s26-s31-s57-c2 | 4.0 | |
| b7-s27-s19-s43-c2 | 4.0 | |
| b9-s23-s27-s19-s52-c4 | 4.3 | |
| b6-s26-s31-s23-s43-c1 | 4.9 | |
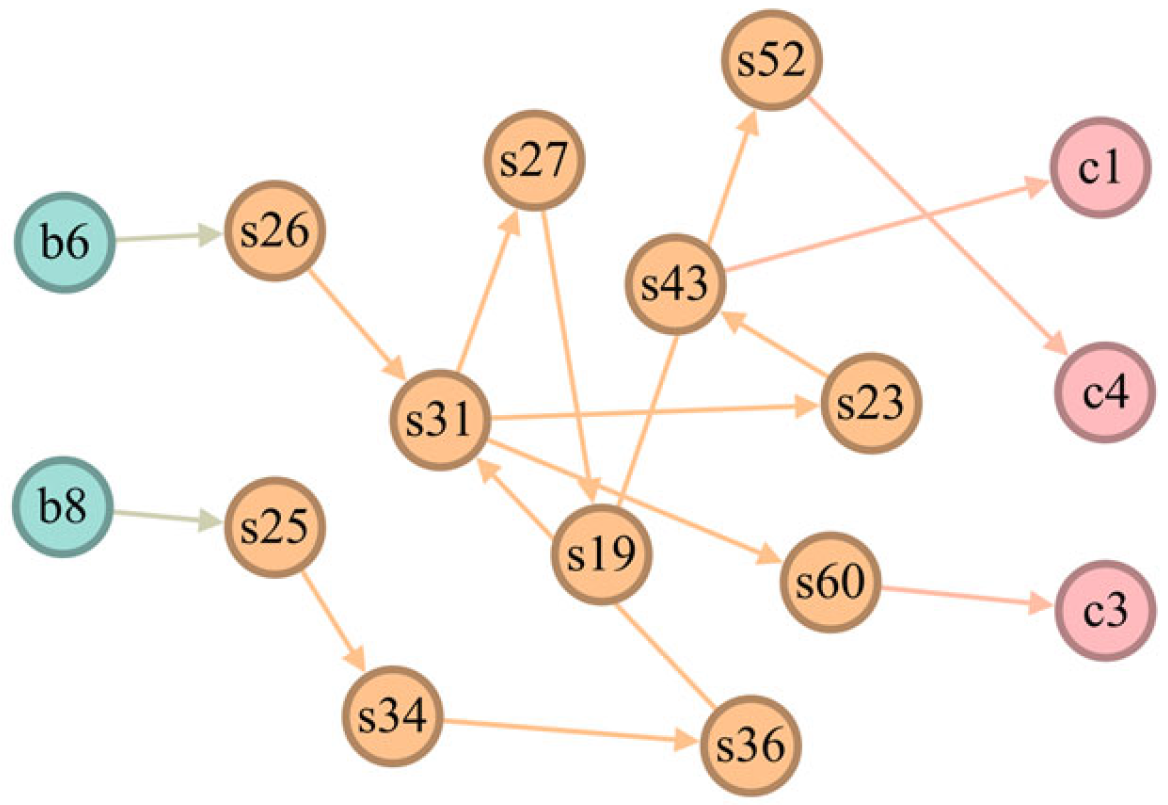
| Low risk | b8-s25-s34-s36-s31-s60-c3 | 5.4 |
| b6-s26-s31-s27-s19-s52-c4 | 5.6 | |
| b8-s25-s34-s36-s31-s27-s19-s52-c4 | 2.0 | |
| b8-s25-s34-s36-s31-s23-s43-c1 | 6.8 |
| Management Priority | Exposed Element Level | Path Level | Exposed Element | Shortest Path Node |
|---|---|---|---|---|
| I | A | A | b4 | b4-s16-s45-c1 |
| b4 | b4-s16-s45-c3 | |||
| b4 | b4-s8-s48-c2 | |||
| b4 | b4-s15-s54-c4 | |||
| b2 | b2-b9-s23-s43-c1 | |||
| b2 | b2-s10-s48-c2 | |||
| b2 | b2-s10-s54-c3 | |||
| b2 | b2-s10-s53-c4 | |||
| II | B | A | b5 | b5-s19-s43-c2 |
| b5 | b5-s19-s45-c1 | |||
| b5 | b5-s19-s45-c3 | |||
| b3 | b3-s29-s49-c2 | |||
| III | B | B | b5 | b5-s19-s52-c4 |
| b3 | b3-s29-s60-c3 | |||
| b3 | b3-b5-s19-s45-c1 | |||
| b3 | b3-b5-s19-s52-c4 | |||
| IV | C | B | b9 | b9-s23-s43-c1 |
| b9 | b9-s23-s43-c2 | |||
| b9 | b9-s23-s43-c3 | |||
| b1 | b1-s5-s54-c3 | |||
| b1 | b1-s5-s48-c2 | |||
| b8 | b8-s25-s58-c2 | |||
| b1 | b1-s17-s52-c4 | |||
| b6 | b6-s26-s31-s60-c3 | |||
| b7 | b7-s27-s19-s45-c1 | |||
| b7 | b7-s27-s19-s45-c3 | |||
| b7 | b7-s27-s19-s52-c4 | |||
| b1 | b1-s5-s48-s19-s45-c1 | |||
| b6 | b6-s26-s31-s57-c2 | |||
| b7 | b7-s27-s19-s43-c2 | |||
| b9 | b9-s23-s27-s19-s52-c4 | |||
| b6 | b6-s26-s31-s23-s43-c1 | |||
| C | C | b8 | b8-s25-s34-s36-s31-s60-c3 | |
| b6 | b6-s26-s31-s27-s19-s52-c4 | |||
| b8 | b8-s25-s34-s36-s31-s27-s19-s52-c4 | |||
| b8 | b8-s25-s34-s36-s31-s23-s43-c1 |
Appendix B
| Algorithm A1 Steps of the priority determination method based on exposed element management and secondary hazard mitigation |
| 1 Start |
| 2 Input: Directed weighted graph G = (V, E, W) |
| 3 where V = set of nodes, E = set of edges, W = edge weights |
| 4 // Step 1: Node activation probability modeling |
| 5 For each node i ∈ V do |
| 6 Compute occurrence probability using Equations (7)–(10): |
| 7 End for |
| 8 // Step 2: Edge-level coupling enhancement coefficient calculation |
| 9 For each edge (j → i) ∈ E do |
| 10 Set e(j→i) ← 0 |
| 11 For each neighbor r ∈ Predecessors(i), r ≠ j do |
| 12 Determine coupling type T ← C(j, r, i) |
| 13 Compute joint probability p(j ∩ r) |
| 14 Switch T: |
| 15 Case OR based on Equation (1): |
| c ← |
| 16 Case AND based on Equation (3): |
| c ← |
| 17 Case CO based on Equation (5): |
| 18 If p(j) × p(r) ≠ 0 then |
| c ← |
| 19 Else: |
| 20 c ← 0 |
| 21 End Switch |
| 22 Accumulate: e(j→i) ← e(j→i) + c |
| 23 End for |
| 24 End for |
| 25 // Step 3: Coupling-adjacency information entropy computation |
| 26 For each node i ∈ V do |
| 27 Compute strength values using Equations (16)–(18) |
| 28 Compute entropy using Equations (19)–(21): |
| 29 End for |
| 30 // Step 4: Shortest path analysis using Dijkstra |
| 31 For each source node s ∈ S do |
| 32 Run Dijkstra(G, source = s) |
| 33 For each destination node t ∈ V do |
| 34 Store l(s, t) ← distance from s to t |
| 35 End for |
| 36 End for |
| 37 // Step 5: Priority classification based on entropy and path risk |
| 38 For each node i ∈ V do |
| 39 If H(i) ≥ θ_high → class_i ← ‘A’ |
| 40 Else if H(i) ≥ θ_mid → class_i ← ‘B’ |
| 41 Else → class_i ← ‘C’ |
| 42 End for |
| 43 For each (s → t) ∈ all stored shortest paths l(s, t) do |
| 44 If l(s, t) ≤ l_short → class_l(s,t) ← ‘A’ |
| 45 Else if l(s, t) ≤ l_mid → class_l(s,t) ← ‘B’ |
| 46 Else → class_l(s,t) ← ‘C’ |
| 47 End for |
| 48 // Step 6: Cross-dimensional priority matrix assignment |
| 49 For each (s → t) do |
| 50 Retrieve c_i = class_s, c_l = class_l(s, t) |
| 51 Assign priority level: |
| 52 If (c_i = A ∧ c_l = A) → priority ← I |
| 53 Else if (c_i =A ∧ c_l = B) ∨ (c_i =B ∧ c_l =A) → priority ← II |
| 54 Else if (c_i =B ∧ c_l = B) → priority ← III |
| 55 Else → priority ← IV |
| 56 End for |
| 57 Output |
| 58 -Node importance classification: EntropyClass(i) ∈ {A, B, C} |
| 59 -Path risk classification: PathRiskClass(s → t) ∈ {A, B, C} |
| 60 -Combined priority matrix: PriorityLevel(s → t) ∈ {I, II, III, IV} |
| 61 End |
References
- Misuri, A.; Cozzani, V. A paradigm shift in the assessment of Natech scenarios in chemical and process facilities. Process Saf. Environ. Prot. 2021, 152, 338–351. [Google Scholar] [CrossRef]
- Krausmann, E.; Cruz, A.M.; Salzano, E. Natech Risk Assessment and Management: Reducing the Risk of Natural-Hazard Impact on Hazardous Installations; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Lan, M.; Gardoni, P.; Qin, R.; Zhang, X.; Zhu, J.; Lo, S. Modeling NaTech-related domino effects in process clusters: A network-based approach. Reliab. Eng. Syst. Saf. 2022, 221, 108329. [Google Scholar] [CrossRef]
- Zou, J.; Ma, T.; He, Y.; Zhao, H.; Chu, Y.; Zhang, D.; Huang, C. Quantitative risk analysis of domino effect and natech accidents triggered by flood in liquor storage tank farms. J. Loss Prev. Process Ind. 2024, 92, 105490. [Google Scholar] [CrossRef]
- Ricci, F.; Moreno, V.C.; Cozzani, V. A comprehensive analysis of the occurrence of Natech events in the process industry. Process Saf. Environ. Prot. 2021, 147, 703–713. [Google Scholar] [CrossRef]
- Ma, T.; Zou, J.; He, Y.; Zhao, H.; Chu, Y.; Zhang, D.; Huang, C. Application of domino effect quantitative risk assessment to Natech accident triggered by earthquakes in a liquor storage tank area. Int. J. Disaster Risk Reduct. 2024, 114, 104957. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, T.; Wang, H.; Zhang, P.; Dong, X.; Zhao, Y.; Liu, Y. Risk assessment of disaster chain in multi-seam mining beneath gully topography. Int. J. Disaster Risk Reduct. 2024, 111, 104750. [Google Scholar] [CrossRef]
- Qi, Q.; Sun, Z.; Liu, W.; Wang, A.; Yang, J.; Liu, S.; Sun, L.; Wang, W. Study on risk assessment model of coal mine water accident induced by flood disaster. Coal Sci. Technol. 2023, 51, 395–402. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, Y.; Li, S.; Li, S.; Chen, W. Bi-objective robust optimisation on relief collaborative distribution considering secondary disasters. Int. J. Prod. Res. 2024, 62, 2435–2454. [Google Scholar] [CrossRef]
- YIlDIz, T.D. Loss of profits occurring due to the halting of mining operations arising from occupational accidents or reasons related to legislation. Gospod. Surowcami Miner. 2021, 37, 153–176. [Google Scholar] [CrossRef]
- Kahraman, M.M. Analysis of Mining Lost Time Incident Duration Influencing Factors Through Machine Learning. Min. Metall. Explor. 2021, 38, 1031–1039. [Google Scholar] [CrossRef]
- Kong, F. Discussion on the Coupling Effect of Disasters from the Perspective of Disaster System. J. Catastrophol. 2024, 39, 1–5. [Google Scholar] [CrossRef]
- Sun, Z.; Liu, Y.; Qi, Q.; Liu, W.; Li, D.; Chai, J. Risk assessment of coal mine flood disasters based on projection pursuit clustering model. Sustainability 2022, 14, 11131. [Google Scholar] [CrossRef]
- Jiao, L.; Luo, Q.; Lu, H.; Huo, X.; Zhang, Y.; Wu, Y. Research on the urban rail transit disaster chain: Critical nodes, edge vulnerability and breaking strategy. Int. J. Disaster Risk Reduct. 2024, 102, 104258. [Google Scholar] [CrossRef]
- Zeng, T.; Chen, G.; Reniers, G.; Hu, K. Resilience assessment of chemical industrial areas during Natech-related cascading multi-hazards. J. Loss Prev. Process Ind. 2023, 81, 104967. [Google Scholar] [CrossRef]
- Chen, C.; Reniers, G.; Khakzad, N. A thorough classification and discussion of approaches for modeling and managing domino effects in the process industries. Saf. Sci. 2020, 125, 104618. [Google Scholar] [CrossRef]
- Ding, L.; Khan, F.; Guo, X.; Ji, J. A novel approach to reduce fire-induced domino effect risk by leveraging loading/unloading demands in chemical industrial parks. Process Saf. Environ. Prot. 2021, 146, 610–619. [Google Scholar] [CrossRef]
- Lan, M.; Shao, Y.; Zhu, J.; Lo, S.; Ng, S.T. A hybrid copula-fragility approach for investigating the impact of hazard dependence on a process facility’s failure. Process Saf. Environ. Prot. 2021, 149, 1017–1030. [Google Scholar] [CrossRef]
- Lan, M.; Zhu, J.; Lo, S. Hybrid Bayesian network-based landslide risk assessment method for modeling risk for industrial facilities subjected to landslides. Reliab. Eng. Syst. Saf. 2021, 215, 107851. [Google Scholar] [CrossRef]
- Zhou, J.; Yu, X.; Lu, J. Node importance in controlled complex networks. IEEE Trans. Circuits Syst. II Express Briefs 2018, 66, 437–441. [Google Scholar] [CrossRef]
- Zhang, Q.; Deng, R.; Ding, K.; Li, M. Structural analysis and the sum of nodes’ betweenness centrality in complex networks. Chaos Solitons Fractals 2024, 185, 115158. [Google Scholar] [CrossRef]
- Tomaselli, C.; Gambuzza, L.V.; Sorrentino, F.; Frasca, M. Control of multiconsensus in multi-agent systems based on eigenvector centrality. Automatica 2024, 164, 111638. [Google Scholar] [CrossRef]
- Shang, Q.; Deng, Y.; Cheong, K.H. Identifying influential nodes in complex networks: Effective distance gravity model. Inf. Sci. 2021, 577, 162–179. [Google Scholar] [CrossRef]
- Guo, H.-x.; He, X.-y.; Lv, X.-b.; Wu, Y. Risk analysis of rainstorm-urban lifeline system disaster chain based on the PageRank-risk matrix and complex network. Nat. Hazards 2024, 120, 10583–10606. [Google Scholar] [CrossRef]
- Huang, W.; Li, H.; Yin, Y.; Zhang, Z.; Xie, A.; Zhang, Y.; Cheng, G. Node importance identification of unweighted urban rail transit network: An Adjacency Information Entropy based approach. Reliab. Eng. Syst. Saf. 2024, 242, 109766. [Google Scholar] [CrossRef]
- Hu, G.; Xu, X.; Gao, H.; Guo, X. Node importance recognition algorithm based on adjacency information entropy in networks. Syst. Eng.-Theory Pract. 2020, 40, 714–725. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, L.; Chen, X. A framework for using event evolutionary graphs to rapidly assess the vulnerability of urban flood cascade compound disaster event networks. J. Hydrol. 2024, 642, 131783. [Google Scholar] [CrossRef]
- Lotero, S.; Androulakis, V.; Khaniani, H.; Hassanalian, M.; Shao, S.; Roghanchi, P. Optimizing fire emergency evacuation routes in underground coal mines: A lightweight network flow approach. Tunn. Undergr. Space Technol. 2024, 146, 105637. [Google Scholar] [CrossRef]
- Bulut, M.; Özcan, E. Optimization of electricity transmission by Ford–Fulkerson algorithm. Sustain. Energy Grids Netw. 2021, 28, 100544. [Google Scholar] [CrossRef]
- Eggimann, S. The potential of implementing superblocks for multifunctional street use in cities. Nat. Sustain. 2022, 5, 406–414. [Google Scholar] [CrossRef]
- Wu, L.; Huang, X.; Cui, J.; Liu, C.; Xiao, W. Modified adaptive ant colony optimization algorithm and its application for solving path planning of mobile robot. Expert Syst. Appl. 2023, 215, 119410. [Google Scholar] [CrossRef]
- Sadaf, T.; Qamar, U.; Khan, S.A.; Almutairi, S. A novel smart street intervention mechanism using clustering-based path optimization for street networks. Knowl.-Based Syst. 2025, 311, 113065. [Google Scholar] [CrossRef]
- Yu, S.; Song, Y. Ripple spreading algorithm: A new method for solving multi-objective shortest path problems with mixed time windows. Complex Intell. Syst. 2024, 10, 2299–2325. [Google Scholar] [CrossRef]
- Hu, H.; Lan, M.; Qin, R.; Zhu, J. Fragility assessment for process pipelines in flood events through physically-based hazard response analysis. J. Loss Prev. Process Ind. 2024, 90, 105349. [Google Scholar] [CrossRef]
- Deng, J.; Liu, S.; Shu, Y.; Hu, Y.; Xie, C.; Zeng, X. Risk evolution and prevention and control strategies of maritime accidents in China’s coastal areas based on complex network models. Ocean Coast. Manag. 2023, 237, 106527. [Google Scholar] [CrossRef]
- Zheng, W.; Li, T.; Jing, Q.; Qi, S.; Li, Y. Real-time quantitative risk analysis and routing optimization of gaseous hydrogen tube trailer transport: A Bayesian network and Dijkstra algorithm combining approach. Process Saf. Environ. Prot. 2024, 192, 1205–1220. [Google Scholar] [CrossRef]
- Li, X.; Ning, X.; Ma, J.; Han, Z. Investigating the Evolution Path of Urban Natural Gas Pipeline Accidents Using a Complex Network Approach. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2024, 10, 06024005. [Google Scholar] [CrossRef]
- Office of the Leading Group of the First National Natural Disaster Comprehensive Risk Survey of the State Council. Technical Specification for the Investigation of Exposed Elements in Coal Mine Natural Hazards. FXPC/YJ G-12. 2021. Available online: https://jz.docin.com/p-2842135927.html (accessed on 15 March 2025).
- Zhu, G.; Sun, R.; Fan, J.; Li, F.; Hou, Y.; Yu, H.; Liu, P.X. Coupling Effect and Chain Evolution of Urban Rail Transit Emergencies. IEEE Trans. Intell. Transp. Syst. 2023, 25, 1044–1053. [Google Scholar] [CrossRef]
- Sentz, K.; Ferson, S. Combination of Evidence in Dempster-Shafer Theory; Sandia National Laboratories: Albuquerque, NM, USA, 2002. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Guo, X.; Zhao, J.; Zong, X.; Song, G.; Du, L.; Lai, C.; Jin, X. Redefining mandibular sub-units: The “ABC” classification and surgical strategies for lower face contouring. Aesthetic Plast. Surg. 2023, 47, 690–699. [Google Scholar] [CrossRef]
- Wang, C.; Ma, J.; Su, C.; Deng, J.; Chen, W. Evolution and risk analysis of flood-induced coal mine disaster chains. J. Saf. Environ. 2025, 1–12. [Google Scholar] [CrossRef]
- Xi, Y.; Cui, X. Identifying influential nodes in complex networks based on information entropy and relationship strength. Entropy 2023, 25, 754. [Google Scholar] [CrossRef] [PubMed]
- Lei, M.; Cheong, K.H. Node influence ranking in complex networks: A local structure entropy approach. Chaos Solitons Fractals 2022, 160, 112136. [Google Scholar] [CrossRef]







| No. | Node Number | Node Information | No. | Node Number | Node Information |
|---|---|---|---|---|---|
| 1 | o1 | Heavy rain and flood | 52 | s22 | Puddle in the tunnel |
| 2 | o2 | Strong wind | 53 | s23 | Damage to power system equipment |
| 3 | o3 | Thunderbolt | 54 | s24 | Safety monitoring and communication system equipment failure |
| 4 | e1 | Lightning current and strong energy | 55 | s25 | Ventilation system equipment malfunction |
| 5 | e2 | Wind pressure | 56 | s26 | Short circuit with electric machinery |
| 6 | e3 | Surface runoff | 57 | s27 | Drainage system damage |
| 7 | e4 | Surface water | 58 | s28 | Mud and slurry collapse in the tunnel |
| 8 | e5 | Old empty water | 59 | s29 | Collapse of mined-out areas |
| 9 | e6 | Groundwater | 60 | s30 | Water accumulation in mined-out areas |
| 10 | f1 | Lightning strike | 61 | s31 | Gas explosion |
| 11 | f2 | Storm | 62 | s32 | Increase in water flow |
| 12 | f3 | Changes in the physical structure | 63 | s33 | Drainage failure |
| 13 | f4 | Landslide and rockfall | 64 | s34 | The fan stops blowing |
| 14 | f5 | Debris flow | 65 | s35 | Toxic gas emissions |
| 15 | f6 | Ground subsidence | 66 | s36 | Gas accumulation |
| 16 | f7 | Mountain flood | 67 | s37 | System false alarm |
| 17 | f8 | Mineral water | 68 | s38 | Residential area damaged |
| 18 | f9 | Mine water inrush, infiltration, and flooding | 69 | s39 | Hot air flow intake |
| 19 | f10 | Goaf | 70 | s40 | Heat wave burns |
| 20 | b1 | Mining area ecosystem | 71 | s41 | Building collapse |
| 21 | b2 | Surrounding hydrological system | 72 | s42 | Damage to machinery and equipment |
| 22 | b3 | Surrounding geological system | 73 | s43 | Power outage |
| 23 | b4 | Surface facility | 74 | s44 | Communication interruption |
| 24 | b5 | Shaft and tunnel system | 75 | s45 | Water supply interruption |
| 25 | b6 | Mining system | 76 | s46 | Road traffic interruption |
| 26 | b7 | Drainage system | 77 | s47 | Electric shock |
| 27 | b8 | Ventilation system | 78 | s48 | The river water level rises |
| 28 | b9 | Power system | 79 | s49 | Object strike |
| 29 | b10 | Transport lifting system | 80 | s50 | Mechanical injury |
| 30 | b11 | Security monitoring and communication system | 81 | s51 | Coal mine material loss |
| 31 | s1 | Damage to ground facilities | 82 | s52 | Environmental pollution |
| 32 | s2 | Industrial site destruction | 83 | s53 | Ecological pollution |
| 33 | s3 | Fire | 84 | s54 | Land degradation |
| 34 | s4 | The spontaneous combustion and collapse of the gangue mountain | 85 | s55 | Crop damage |
| 35 | s5 | Destruction of surface vegetation | 86 | s56 | Drowning |
| 36 | s6 | Damage to roads and bridges | 87 | s57 | Personnel burial |
| 37 | s7 | Industrial site burial | 88 | s58 | Hypoxia asphyxia |
| 38 | s8 | Factory destroyed | 89 | s59 | Shaft and tunnel damage |
| 39 | s9 | Burial of road bridges | 90 | s60 | Work face shutdown |
| 40 | s10 | River channel damage | 91 | s61 | Decline in shaft and tunnel stability |
| 41 | s11 | Reservoir overflow | 92 | s62 | Shock wave impact |
| 42 | s12 | Wellhead embankment collapse | 93 | s63 | Suffocation from poisoning |
| 43 | s13 | Device submerged in water | 94 | s64 | High-pressure impact |
| 44 | s14 | Industrial site flooding | 95 | s65 | High-temperature burning |
| 45 | s15 | Road erosion damage | 96 | s66 | Decreased recoverable reserves |
| 46 | s16 | Cable route damage | 97 | s67 | Missing persons |
| 47 | s17 | Water pollution | 98 | c1 | Social impact |
| 48 | s18 | Soil pollution | 99 | c2 | Casualties |
| 49 | s19 | Mine flooding | 100 | c3 | Property damage |
| 50 | s20 | Water pressure impact on the tunnel | 101 | c4 | Ecological destruction |
| 51 | s21 | Tunnel collapse and blockage |
| Exposed Element level | Secondary Hazard Path Level | Management Priority | Feature Description |
|---|---|---|---|
| A | A | I | High connectivity diversity and shortest propagation path easily trigger multi-chain reactions |
| A | B | II | High connectivity diversity and moderate transmission speed |
| B | A | Local hub function and rapid dissemination | |
| B | B | III | Medium connectivity and medium transmission speed |
| A | C | High connectivity diversity and slow conduction path | |
| C | A | Single connection path but spreads quickly | |
| B | C | IV | Low connectivity or slow transmission |
| C | B | ||
| C | C |
| Parent Node | Child Node | Parent Node | Child Node |
|---|---|---|---|
| f1 - f2 - f3 | b1 | f9 - (f6 = f7) | b8 |
| f4 = f5 = f6 = f7 | b3 | f1 - f2 - f9 - (f6 = f7) | b9 |
| f1 - f2 - f3 - (f4 = f5 = f6 = f7) | b4 | f9 - (f4 = f5 = f6 = f7) | b10 |
| f1 - f9 - (f4 = f5 = f6 = f7) | b5 | f1 - f2 - f9 - (f4 = f5 = f6 = f7) | b11 |
| f9 - (f5 = f6 = f7) | b6 | e4 -- e5 | f9 |
| f9 - (f6 = f7) | b7 |
| Grading | Sorting | Node | Exposed Element | C-AIE |
|---|---|---|---|---|
| High entropy | 1 | b4 | Surface facility | 134.301 |
| 2 | b2 | Surrounding hydrological system | 60.705 | |
| Medium entropy | 3 | b3 | Surrounding geological system | 5.896 |
| 4 | b5 | Shaft and tunnel system | 2.199 | |
| Low entropy | 5 | b1 | Mining area ecosystem | 0.714 |
| 6 | b9 | Power system | 0.491 | |
| 7 | b8 | Ventilation system | 0.485 | |
| 8 | b6 | Mining system | 0.418 | |
| 9 | b7 | Drainage system | 0.350 | |
| Others | 10 | b10 | Transport lifting system | 0 |
| 11 | b11 | Security monitoring and communication system | 0 |
| Benchmark Algorithm | Importance Ranking of Exposed Elements |
|---|---|
| Out-degree Centrality (outDC) | b4-b2-b5-b3-b1-b6-b7-b8-b9-b10-b11 |
| In-degree Centrality (inDC) | b4-b5-b11-b9-b6-b3-b10-b7-b8-b1-b2 |
| Eigenvector Centrality (EC) | b5-b4-b2-b3-b6-b8-b7-b9-b11-b10-b1 |
| In-closeness Centrality (inCC) | b11-b4-b5-b9-b1-b10-b3-b6-b7-b8-b2 |
| Out-closeness Centrality (outCC) | b2-b4-b1-b3-b5-b7-b6-b9-b8-b10-b11 |
| Betweenness Centrality (BC) | b4-b5-b9-b1-b6-b8-b3-b2-b7-b10-b11 |
| Proposed method (C-AIE) | b4-b2-b3-b5-b1-b9-b8-b6-b7-b10-b11 |
| Reference | Main Method | Neighbor Consideration | Directed Network Support | Weighted Network Support | Coupling Mechanism Considered |
|---|---|---|---|---|---|
| [25] | Adjacency information entropy | √ | × | × | × |
| [44] | Information entropy | √ | × | × | × |
| [45] | Local structure entropy | √ | × | × | × |
| [26] | Adjacency information entropy | √ | √ | √ | × |
| Proposed method | C-AIE | √ | √ | √ | √ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Liu, C.; Pan, L.; Su, X.; He, K.; Mao, Z. Identification of Critical Exposed Elements and Strategies for Mitigating Secondary Hazards in Flood-Induced Coal Mine Accidents. Water 2025, 17, 2181. https://doi.org/10.3390/w17152181
Yang X, Liu C, Pan L, Su X, He K, Mao Z. Identification of Critical Exposed Elements and Strategies for Mitigating Secondary Hazards in Flood-Induced Coal Mine Accidents. Water. 2025; 17(15):2181. https://doi.org/10.3390/w17152181
Chicago/Turabian StyleYang, Xue, Chen Liu, Langxuan Pan, Xiaona Su, Ke He, and Ziyu Mao. 2025. "Identification of Critical Exposed Elements and Strategies for Mitigating Secondary Hazards in Flood-Induced Coal Mine Accidents" Water 17, no. 15: 2181. https://doi.org/10.3390/w17152181
APA StyleYang, X., Liu, C., Pan, L., Su, X., He, K., & Mao, Z. (2025). Identification of Critical Exposed Elements and Strategies for Mitigating Secondary Hazards in Flood-Induced Coal Mine Accidents. Water, 17(15), 2181. https://doi.org/10.3390/w17152181







