Future Residential Water Use and Management Under Climate Change Using Bayesian Neural Networks
Abstract
1. Introduction
2. Data and Methodology
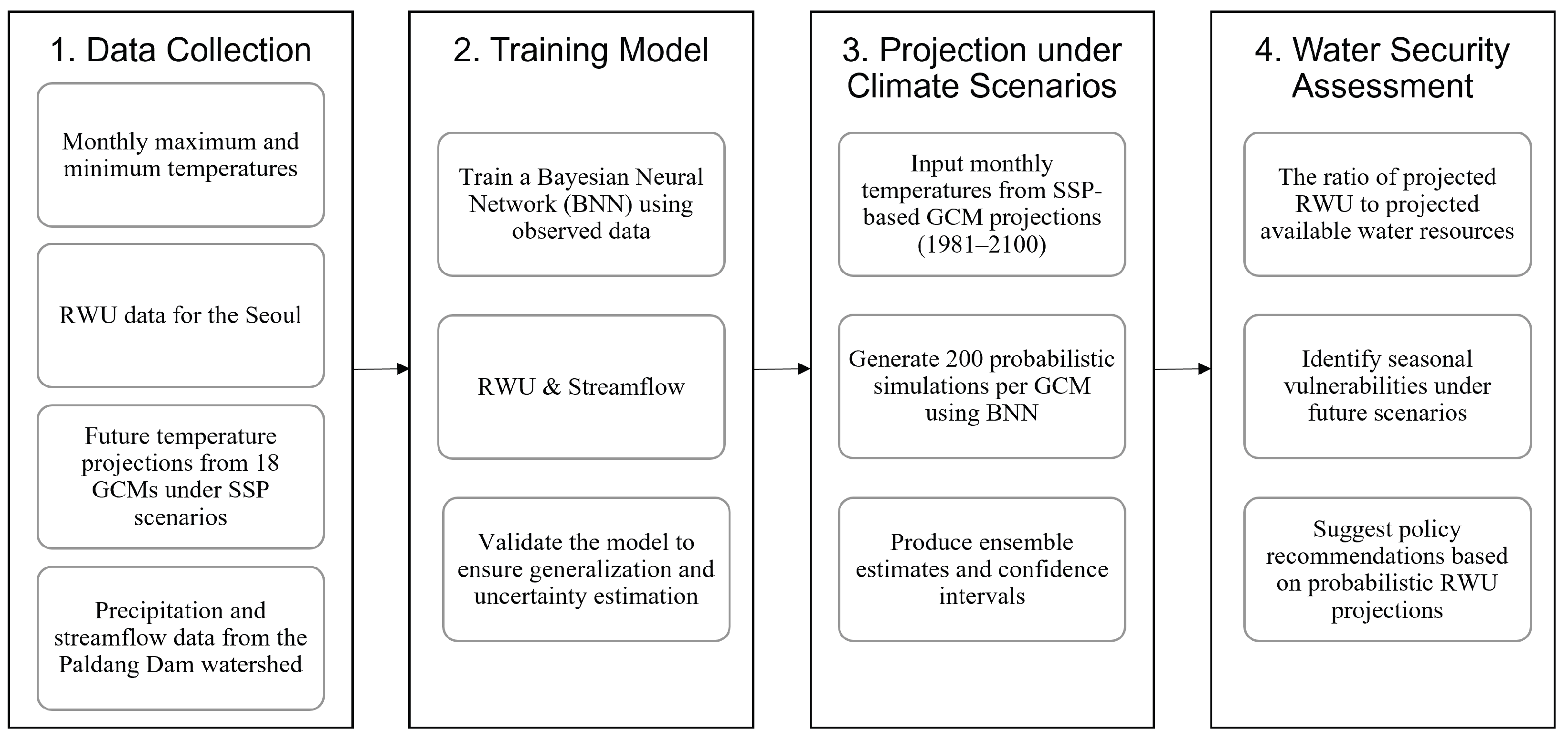
2.1. Study Framework
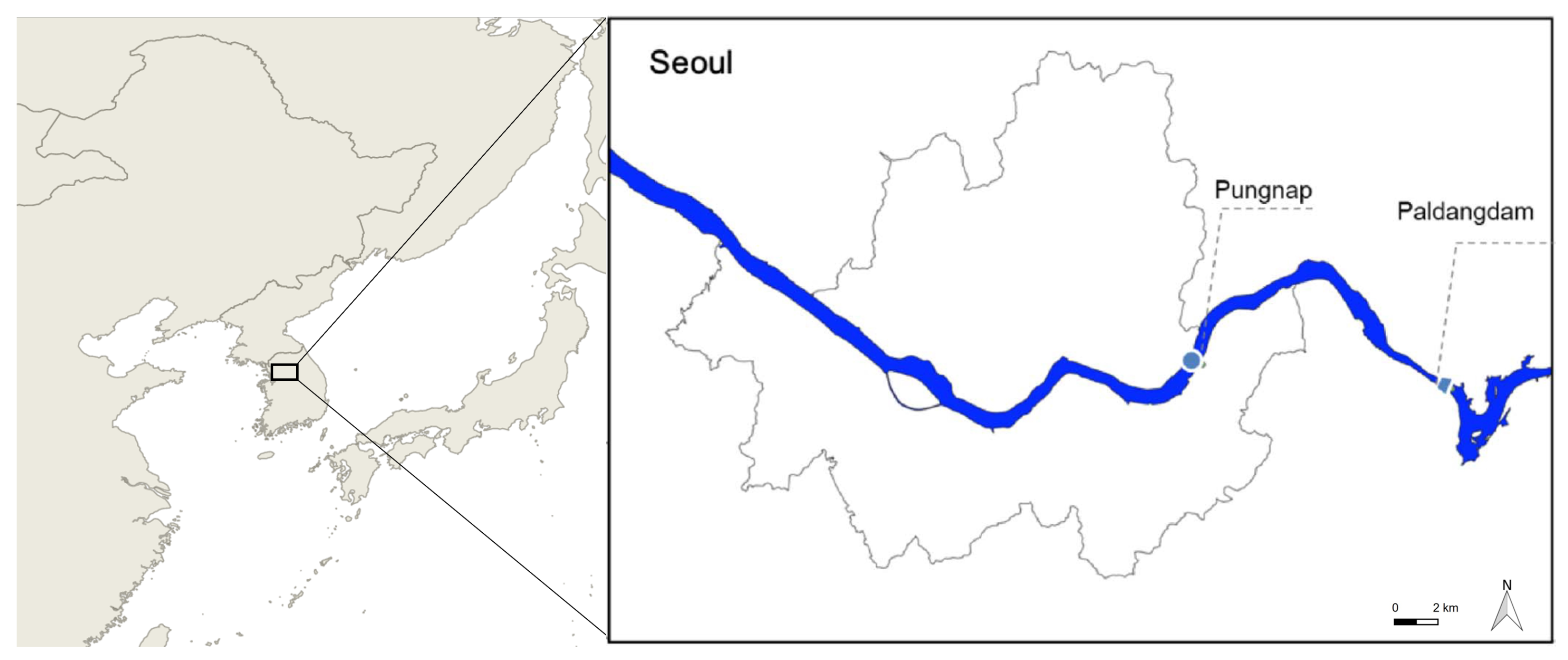
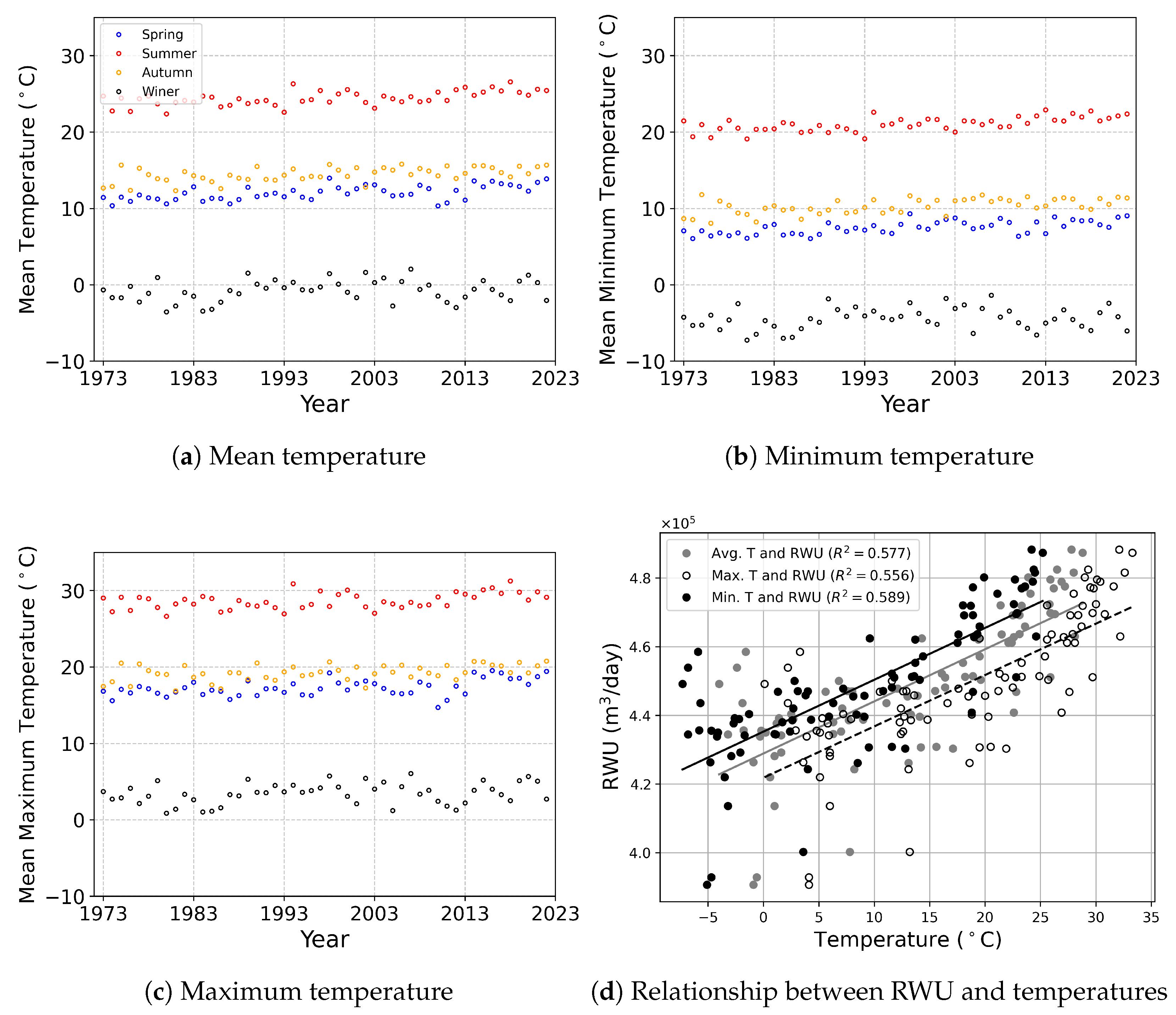
2.2. Study Area and Data
2.3. Bayesian Neural Networks
3. Results
3.1. Training the RWU Estimator with the BNN
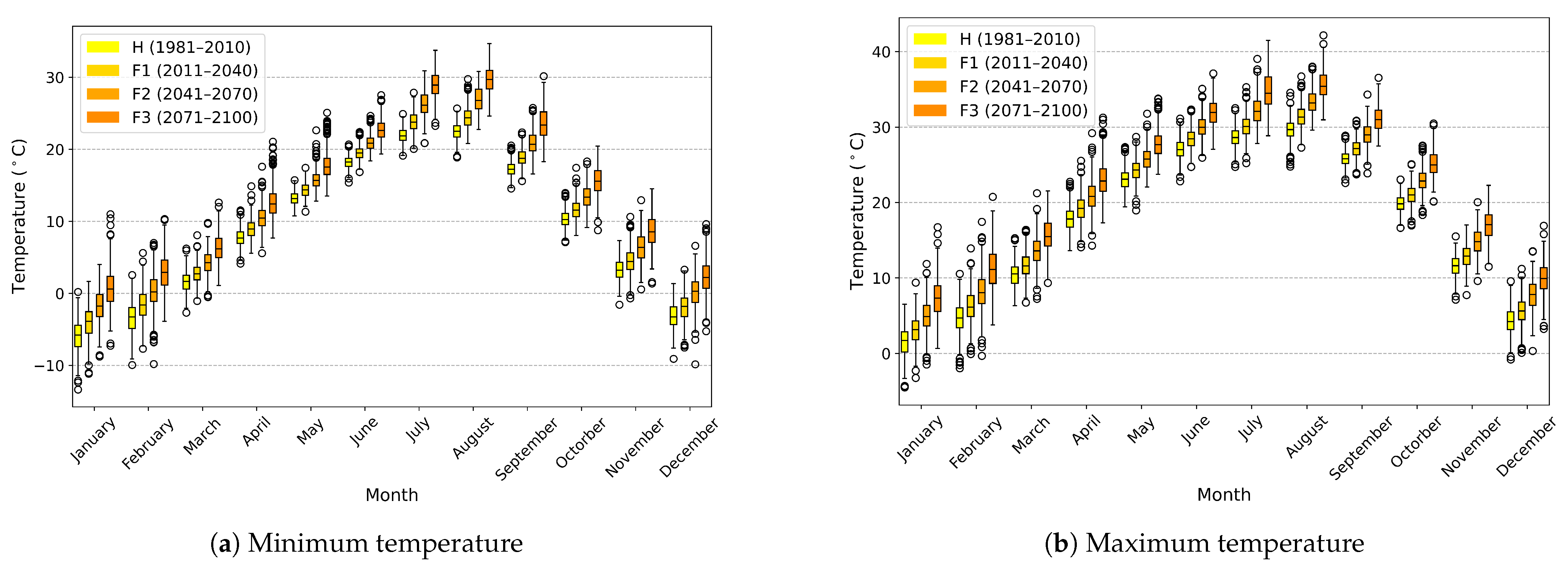
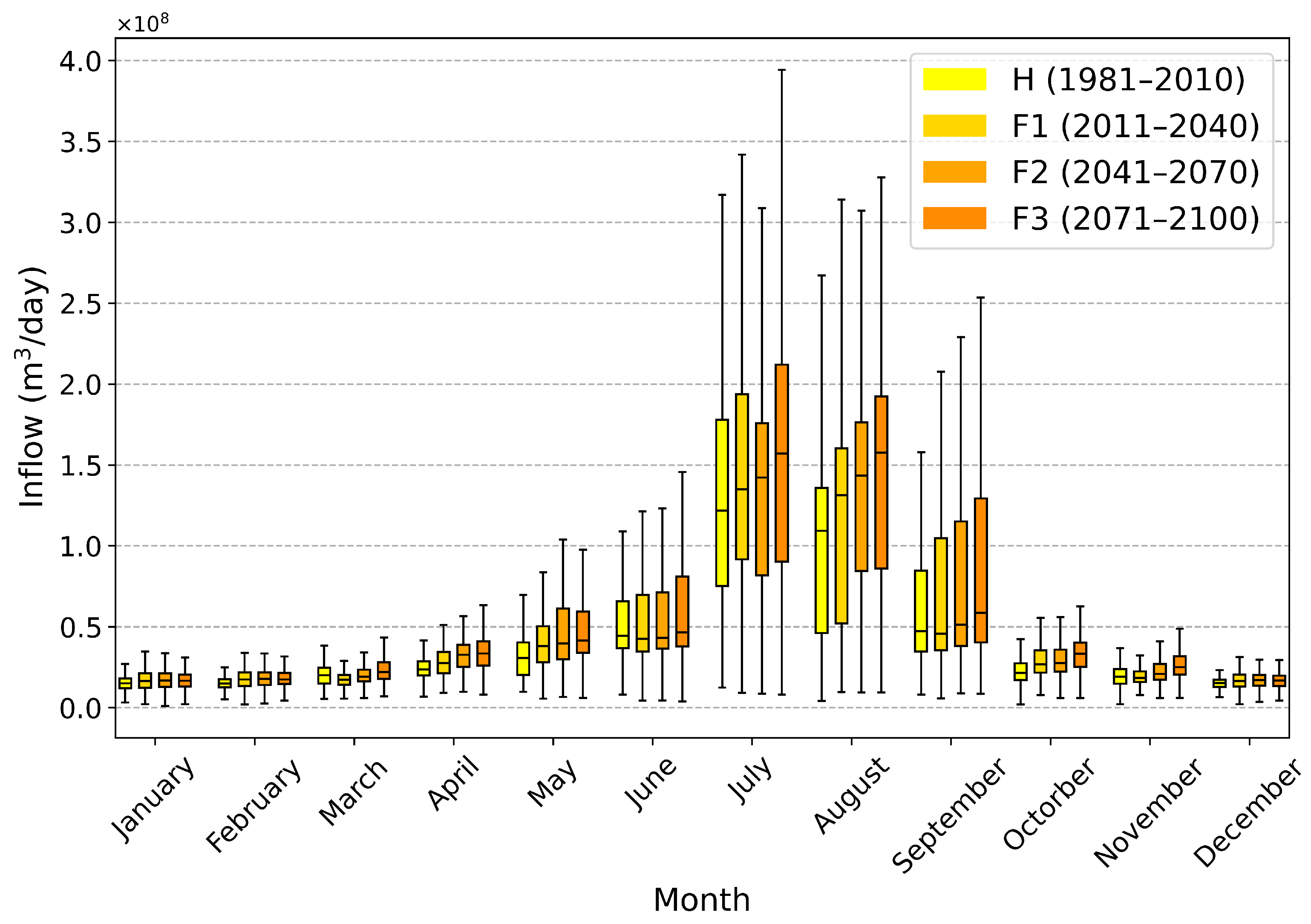
3.2. Future Climate Projections Using CMIP6 GCMs
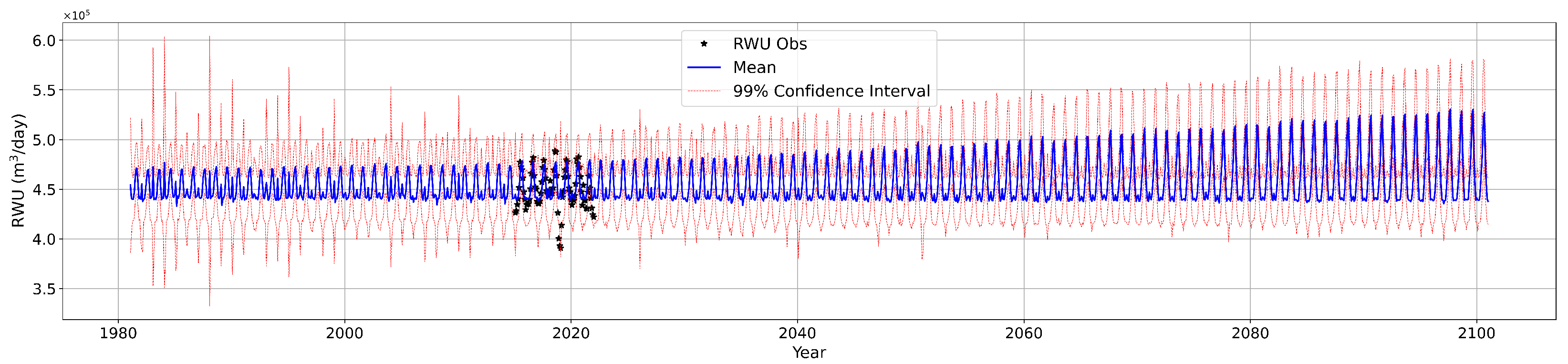
3.3. Residential Water Use Projection Under Climate Change
3.4. Residential Water Use Projection with Water Resources
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, J.; Yang, H.; Gosling, S.N.; Kummu, M.; Flörke, M.; Pfister, S.; Hanasaki, N.; Wada, Y.; Zhang, X.; Zheng, C.; et al. Water scarcity assessments in the past, present, and future. Earth’s Future 2017, 5, 545–559. [Google Scholar] [CrossRef]
- Falkenmark, M.; Lundqvist, J.; Widstrand, C. Macro-scale water scarcity requires micro-scale approaches: Aspects of vulnerability in semi-arid development. In Natural Resources Forum; Wiley Online Library: Hoboken, NJ, USA, 1989; Volume 13, pp. 258–267. [Google Scholar]
- Alcamo, J.; Henrichs, T.; Rösch, T. Global modeling and scenario analysis for the World Commission on Water for the 21st Century. Kassel. World Water Ser. 2000, 2, 48. [Google Scholar]
- Vorosmarty, C.J.; Green, P.; Salisbury, J.; Lammers, R.B. Global water resources: Vulnerability from climate change and population growth. Science 2000, 289, 284–288. [Google Scholar] [CrossRef] [PubMed]
- Mazzoni, F.; Alvisi, S.; Blokker, M.; Buchberger, S.G.; Castelletti, A.; Cominola, A.; Gross, M.P.; Jacobs, H.E.; Mayer, P.; Steffelbauer, D.B.; et al. Investigating the characteristics of residential end uses of water: A worldwide review. Water Res. 2023, 230, 119500. [Google Scholar] [CrossRef]
- House-Peters, L.A.; Chang, H. Urban water demand modeling: Review of concepts, methods, and organizing principles. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Rockaway, T.D.; Coomes, P.A.; Rivard, J.; Kornstein, B. Residential water use trends in North America. J.-Am. Water Work. Assoc. 2011, 103, 76–89. [Google Scholar] [CrossRef]
- Balling, R.C.; Gober, P. Climate variability and residential water use in the city of Phoenix, Arizona. J. Appl. Meteorol. Climatol. 2007, 46, 1130–1137. [Google Scholar] [CrossRef]
- Breyer, B.; Chang, H.; Parandvash, G.H. Land-use, temperature, and single-family residential water use patterns in Portland, Oregon and Phoenix, Arizona. Appl. Geogr. 2012, 35, 142–151. [Google Scholar] [CrossRef]
- Rathnayaka, K.; Malano, H.; Maheepala, S.; George, B.; Nawarathna, B.; Arora, M.; Roberts, P. Seasonal demand dynamics of residential water end-uses. Water 2015, 7, 202–216. [Google Scholar] [CrossRef]
- Mo, X.G.; Hu, S.; Lin, Z.H.; Liu, S.X.; Xia, J. Impacts of climate change on agricultural water resources and adaptation on the North China Plain. Adv. Clim. Change Res. 2017, 8, 93–98. [Google Scholar] [CrossRef]
- Sung, J.H.; Seo, S.B. Estimation of river management flow considering stream water deficit characteristics. Water 2018, 10, 1521. [Google Scholar] [CrossRef]
- Park, J.; Sung, J.H.; Lim, Y.J.; Kang, H.S. Introduction and application of non-stationary standardized precipitation index considering probability distribution function and return period. Theor. Appl. Climatol. 2019, 136, 529–542. [Google Scholar] [CrossRef]
- Kim, J.H.; Sung, J.H.; Shahid, S.; Chung, E.S. Future hydrological drought analysis considering agricultural water withdrawal under SSP scenarios. Water Resour. Manag. 2022, 36, 2913–2930. [Google Scholar] [CrossRef]
- Praskievicz, S.; Chang, H. Identifying the relationships between urban water consumption and weather variables in Seoul, Korea. Phys. Geogr. 2009, 30, 324–337. [Google Scholar] [CrossRef]
- Korea Meteorological Administration. Seoul Climate Change Projection Report 2023; Technical report; KMA: Seoul, Republic of Korea, 2023. [Google Scholar]
- Alcamo, J.; Döll, P.; Henrichs, T.; Kaspar, F.; Lehner, B.; Rösch, T.; Siebert, S. Development and testing of the WaterGAP 2 global model of water use and availability. Hydrol. Sci. J. 2003, 48, 317–337. [Google Scholar] [CrossRef]
- Wada, Y.; Wisser, D.; Bierkens, M.F. Global modeling of withdrawal, allocation and consumptive use of surface water and groundwater resources. Earth Syst. Dyn. 2014, 5, 15–40. [Google Scholar] [CrossRef]
- Mekonnen, M.M.; Hoekstra, A.Y. Four billion people facing severe water scarcity. Sci. Adv. 2016, 2, e1500323. [Google Scholar] [CrossRef]
- Mohor, G.S.; Mendiondo, E.M. Economic indicators of hydrologic drought insurance under water demand and climate change scenarios in a Brazilian context. Ecol. Econ. 2017, 140, 66–78. [Google Scholar] [CrossRef]
- Xie, M.; Zhang, C.; Zhang, J.; Wang, G.; Jin, J.; Liu, C.; He, R.; Bao, Z. Projection of Future Water Resources Carrying Capacity in the Huang-Huai-Hai River Basin under the Impacts of Climate Change and Human Activities. Water 2022, 14, 2006. [Google Scholar] [CrossRef]
- Guo, G.; Liu, S.; Wu, Y.; Li, J.; Zhou, R.; Zhu, X. Short-term water demand forecast based on deep learning method. J. Water Resour. Plan. Manag. 2018, 144, 04018076. [Google Scholar] [CrossRef]
- Mu, L.; Zheng, F.; Tao, R.; Zhang, Q.; Kapelan, Z. Hourly and daily urban water demand predictions using a long short-term memory based model. J. Water Resour. Plan. Manag. 2020, 146, 05020017. [Google Scholar] [CrossRef]
- Hu, P.; Tong, J.; Wang, J.; Yang, Y.; de Oliveira Turci, L. A hybrid model based on CNN and Bi-LSTM for urban water demand prediction. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 1088–1094. [Google Scholar]
- Du, B.; Zhou, Q.; Guo, J.; Guo, S.; Wang, L. Deep learning with long short-term memory neural networks combining wavelet transform and principal component analysis for daily urban water demand forecasting. Expert Syst. Appl. 2021, 171, 114571. [Google Scholar] [CrossRef]
- Seo, Y.H.; Park, J.; Kim, B.S.; Sung, J.H. Projection of Changes in Stream Water Use Due to Climate Change. Sustainability 2024, 16, 10120. [Google Scholar] [CrossRef]
- Sung, J.H.; Chung, E.S. What is the Impact of COVID-19 on Residential Water Use? KSCE J. Civ. Eng. 2023, 27, 5481–5490. [Google Scholar] [CrossRef]
- Yoon, E.H.; Sung, J.H.; Kim, B.S.; Seong, K.W.; Choi, J.R.; Seo, Y.H. Changes in the Urban Hydrological Cycle of the Future Using Low-Impact Development Based on Shared Socioeconomic Pathway Scenarios. Water 2023, 15, 4002. [Google Scholar] [CrossRef]
- Sung, J.H.; Kang, D.H.; Seo, Y.H.; Kim, B.S. Analysis of extreme rainfall characteristics in 2022 and projection of extreme rainfall based on climate change scenarios. Water 2023, 15, 3986. [Google Scholar] [CrossRef]
- Horowitz, L.W.; Naik, V.; Sentman, L.; Paulot, F.; Blanton, C.; McHugh, C.; Radhakrishnan, A.; Rand, K.; Vahlenkamp, H.; Zadeh, N.T.; et al. NOAA-GFDL GFDL-ESM4 Model Output Prepared for CMIP6 AerChemMIP. 2018. Available online: https://www.wdc-climate.de/ui/cmip6?input=CMIP6.AerChemMIP.NOAA-GFDL.GFDL-ESM4 (accessed on 19 July 2025).
- Yukimoto, S.; Kawai, H.; Koshiro, T.; Oshima, N.; Yoshida, K.; Urakawa, S.; Tsujino, H.; Deushi, M.; Tanaka, T.; Hosaka, M.; et al. The Meteorological Research Institute Earth System Model version 2.0, MRI-ESM2. 0: Description and basic evaluation of the physical component. J. Meteorol. Soc. Jpn. Ser. II 2019, 97, 931–965. [Google Scholar] [CrossRef]
- Voldoire, A.; Saint-Martin, D.; Sénési, S.; Decharme, B.; Alias, A.; Chevallier, M.; Colin, J.; Guérémy, J.F.; Michou, M.; Moine, M.P.; et al. Evaluation of CMIP6 deck experiments with CNRM-CM6-1. J. Adv. Model. Earth Syst. 2019, 11, 2177–2213. [Google Scholar] [CrossRef]
- Séférian, R.; Nabat, P.; Michou, M.; Saint-Martin, D.; Voldoire, A.; Colin, J.; Decharme, B.; Delire, C.; Berthet, S.; Chevallier, M.; et al. Evaluation of CNRM Earth system model, CNRM-ESM2-1: Role of Earth system processes in present-day and future climate. J. Adv. Model. Earth Syst. 2019, 11, 4182–4227. [Google Scholar] [CrossRef]
- Boucher, O.; Servonnat, J.; Albright, A.L.; Aumont, O.; Balkanski, Y.; Bastrikov, V.; Bekki, S.; Bonnet, R.; Bony, S.; Bopp, L.; et al. Presentation and evaluation of the IPSL-CM6A-LR climate model. J. Adv. Model. Earth Syst. 2020, 12, e2019MS002010. [Google Scholar] [CrossRef]
- Schupfner, M.; Wieners, K.H.; Wachsmann, F.; Milinski, S.; Steger, C.; Bittner, M.; Jungclaus, J.; Früh, B.; Pankatz, K.; Giorgetta, M.; et al. DKRZ MPI-ESM1.2-LR Model Output Prepared for CMIP6 ScenarioMIP. Available online: https://www.wdc-climate.de/ui/cmip6?input=CMIP6.ScenarioMIP.MPI-M.MPI-ESM1-2-LR.ssp2452023 (accessed on 19 July 2025).
- Dalvi, M.; Abraham, L.; Archibald, A.; Folberth, G.; Griffiths, P.; Johnson, B.; Keeble, J.; Morgenstern, O.; Mulcahy, J.; Richardson, M.; et al. NIWA UKESM1.0-LL Model Output Prepared for CMIP6 AerChemMIP. 2019. Available online: https://www.wdc-climate.de/ui/cmip6?input=CMIP6.AerChemMIP.NIWA.UKESM1-0-LL (accessed on 19 July 2025).
- Dix, M.; Bi, D.; Dobrohotoff, P.; Fiedler, R.; Harman, I.; Law, R.; Mackallah, C.; Marsland, S.; O’Farrell, S.; Rashid, H.; et al. CSIRO-ARCCSS ACCESS-CM2 Model Output Prepared for CMIP6 CMIP Historical. 2019. Available online: https://www.wdc-climate.de/ui/cmip6?input=CMIP6.CMIP.CSIRO-ARCCSS.ACCESS-CM2.historical (accessed on 19 July 2025).
- Ziehn, T.; Chamberlain, M.; Lenton, A.; Law, R.; Bodman, R.; Dix, M.; Wang, Y.; Dobrohotoff, P.; Srbinovsky, J.; Stevens, L.; et al. CSIRO ACCESS-ESM1.5 Model Output Prepared for CMIP6 CMIP. 2019. Available online: https://www.wdc-climate.de/ui/cmip6?input=CMIP6.CMIP.CSIRO.ACCESS-ESM1-5 (accessed on 19 July 2025).
- Swart, N.C.; Cole, J.N.; Kharin, V.V.; Lazare, M.; Scinocca, J.F.; Gillett, N.P.; Anstey, J.; Arora, V.; Christian, J.R.; Hanna, S.; et al. The Canadian earth system model version 5 (CanESM5. 0.3). Geosci. Model Dev. 2019, 12, 4823–4873. [Google Scholar] [CrossRef]
- Volodin, E.; Mortikov, E.; Gritsun, A.; Lykossov, V.; Galin, V.; Diansky, N.; Gusev, A.; Kostrykin, S.; Iakovlev, N.; Shestakova, A.; et al. INM INM-CM5-0 Model Output Prepared for CMIP6 ScenarioMIP. 2019. Available online: https://www.wdc-climate.de/ui/cmip6?input=CMIP6.ScenarioMIP.INM.INM-CM5-0 (accessed on 19 July 2025).
- Döscher, R.; Acosta, M.; Alessandri, A.; Anthoni, P.; Arsouze, T.; Bergman, T.; Bernardello, R.; Boussetta, S.; Caron, L.; Carver, G.; et al. The EC-Earth3 Earth system model for the coupled model intercomparison project 6. Geosci. Model Dev. 2022, 15, 2973–3020. [Google Scholar] [CrossRef]
- Shiogama, H.; Abe, M.; Tatebe, H. MIROC MIROC6 Model Output Prepared for CMIP6 ScenarioMIP. 2019. Available online: https://www.wdc-climate.de/ui/cmip6?input=CMIP6.ScenarioMIP.MIROC.MIROC6 (accessed on 19 July 2025).
- Seland, Ø.; Bentsen, M.; Olivié, D.; Toniazzo, T.; Gjermundsen, A.; Graff, L.S.; Debernard, J.B.; Gupta, A.K.; He, Y.C.; Kirkevåg, A.; et al. Overview of the Norwegian Earth System Model (NorESM2) and key climate response of CMIP6 DECK, historical, and scenario simulations. Geosci. Model Dev. 2020, 13, 6165–6200. [Google Scholar] [CrossRef]
- Byun, Y.H.; Lim, Y.J.; Sung, H.M.; Kim, J.; Sun, M.; Kim, B.H. NIMS-KMA KACE1.0-G Model Output Prepared for CMIP6 CMIP Historical. 2019. Available online: https://www.wdc-climate.de/ui/cmip6?input=CMIP6.CMIP.NIMS-KMA.KACE-1-0-G.historical (accessed on 19 July 2025).
- Ranzato, M.; Boureau, Y.L.; Cun, Y. Sparse Feature Learning for Deep Belief Networks. 2007. Available online: https://proceedings.neurips.cc/paper_files/paper/2007/file/c60d060b946d6dd6145dcbad5c4ccf6f-Paper.pdf (accessed on 19 July 2025).
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Bengio, Y.; Goodfellow, I.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2017; Volume 1. [Google Scholar]
- Sit, M.; Demiray, B.Z.; Xiang, Z.; Ewing, G.J.; Sermet, Y.; Demir, I. A comprehensive review of deep learning applications in hydrology and water resources. Water Sci. Technol. 2020, 82, 2635–2670. [Google Scholar] [CrossRef] [PubMed]
- Shen, C.; Lawson, K. Applications of deep learning in hydrology. In Deep Learning for the Earth Sciences: A Comprehensive Approach to Remote Sensing, Climate Science, and Geosciences; John Wiley & Sons: Hoboken, NJ, USA, 2021; pp. 283–297. [Google Scholar]
- Tripathy, K.P.; Mishra, A.K. Deep learning in hydrology and water resources disciplines: Concepts, methods, applications, and research directions. J. Hydrol. 2024, 628, 130458. [Google Scholar] [CrossRef]
- MacKay, D.J. A practical Bayesian framework for backpropagation networks. Neural Comput. 1992, 4, 448–472. [Google Scholar] [CrossRef]
- Jospin, L.V.; Laga, H.; Boussaid, F.; Buntine, W.; Bennamoun, M. Hands-on Bayesian neural networks—A tutorial for deep learning users. IEEE Comput. Intell. Mag. 2022, 17, 29–48. [Google Scholar] [CrossRef]
- Sung, J.H.; Ryu, Y.; Chung, E.S. Estimation of water-use rates based on hydro-meteorological variables using deep belief network. Water 2020, 12, 2700. [Google Scholar] [CrossRef]
- Sung, J.H.; Kim, J.; Chung, E.S.; Ryu, Y. Deep-learning based projection of change in irrigation water-use under RCP 8.5. Hydrol. Processes 2021, 35, e14315. [Google Scholar] [CrossRef]
- Sung, J.H.; Baek, D.; Ryu, Y.; Seo, S.B.; Seong, K.W. Effects of hydro-meteorological factors on streamflow withdrawal for irrigation in yeongsan river basin. Sustainability 2021, 13, 4969. [Google Scholar] [CrossRef]
- Chang, H.; Praskievicz, S.; Parandvash, H. Sensitivity of urban water consumption to weather and climate variability at multiple temporal scales: The case of Portland, Oregon. Int. J. Geospat. Environ. Res. 2014, 1, 7. [Google Scholar]
- Moon, T.H.; Chae, Y.; Lee, D.S.; Kim, D.H.; Kim, H.g. Analyzing climate change impacts on health, energy, water resources, and biodiversity sectors for effective climate change policy in South Korea. Sci. Rep. 2021, 11, 18512. [Google Scholar] [CrossRef]
- Gosling, S.N.; Arnell, N.W. A global assessment of the impact of climate change on water scarcity. Clim. Change 2016, 134, 371–385. [Google Scholar] [CrossRef]




| Institute | GCMs | Resolution | References |
|---|---|---|---|
| Geophysical Fluid Dynamics Laboratory (USA) | GFDL-ESM4 | 360 × 180 | Horowitz et al. [30] |
| Meteorological Research Institute (Japan) | MRI-ESM2-0 | 320 × 160 | Yukimoto et al. [31] |
| Centre National de Recherches Meteorologiques (France) | CNRM-CM6-1/CNRM-ESM2-1 | 24,572 grids (128 lat. circles) | Voldoire et al. [32]; Séférian et al. [33] |
| Institute Pierre-Simon Laplace (France) | IPSL-CM6A-LR | 144 × 143 | Boucher et al. [34] |
| Max Planck Institute for Meteorology (Germany) | MPI-ESM1-2-HR | 384 × 192 | Schupfner et al. [35] |
| Met Office Hadley Centre (UK) | UKESM1-0-LL | 192 × 144 | Dalvi et al. [36] |
| CSIRO/ARC Centre for Climate System Science (Australia) | ACCESS-CM2 | 192 × 144 | Dix et al. [37] |
| CSIRO (Australia) | ACCESS-ESM1-5 | 192 × 145 | Ziehn et al. [38] |
| Canadian Centre for Climate Modelling and Analysis (Canada) | CanESM5 | 128 × 64 | Swart et al. [39] |
| Institute for Numerical Mathematics (Russia) | INM-CM4-8/INM-CM5-0 | 180 × 120 | Volodin et al. [40] |
| EC-Earth-Consortium | EC-Earth3 | 512 × 256 | Döscher et al. [41] |
| Japan JAMSTEC/AORI/NIES/RIKEN | MIROC6/MIROC-ES2L | 256 × 128 | Shiogama et al. [42] |
| NorESM Climate Modeling Consortium (Norway) | NorESM2-LM | 144 × 96 | Seland et al. [43] |
| NIMS/KMA (Korea) | KACE-1-0-G | 192 × 144 | Byun et al. [44] |
| Dataset | MAE | RMSE | MAPE | PICP (95%) | PICP (99%) |
|---|---|---|---|---|---|
| Train | 4660 | 6760 | 1.05 | 0.970 | 0.985 |
| Validation | 9770 | 11,400 | 2.19 | 0.824 | 1.000 |
| Total | 5690 | 7900 | 1.28 | 0.940 | 0.988 |
| Jan. | Feb. | Mar. | Apr. | May | Jun. | Jul. | Aug. | Sep. | Oct. | Nov. | Dec. | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Max. | Mean (Hist) | 1.5 | 4.7 | 10.4 | 17.8 | 23.0 | 27.0 | 28.6 | 29.6 | 25.8 | 19.8 | 11.6 | 4.3 |
| Std (Hist) | 1.9 | 2.1 | 1.7 | 1.6 | 1.3 | 1.3 | 1.3 | 1.4 | 1.0 | 1.1 | 1.4 | 1.8 | |
| Mean (F1) | 3.0 | 6.2 | 11.7 | 19.2 | 24.3 | 28.4 | 30.1 | 31.4 | 27.1 | 21.0 | 12.9 | 5.6 | |
| Std (F1) | 1.9 | 2.1 | 1.7 | 1.7 | 1.4 | 1.4 | 1.5 | 1.4 | 1.2 | 1.3 | 1.5 | 1.8 | |
| Mean (F2) | 5.0 | 8.2 | 13.5 | 20.9 | 25.8 | 30.0 | 32.2 | 33.3 | 29.0 | 23.0 | 14.8 | 7.7 | |
| Std (F2) | 2.1 | 2.5 | 1.9 | 2.0 | 1.5 | 1.5 | 1.9 | 1.6 | 1.5 | 1.5 | 1.7 | 2.0 | |
| Mean (F3) | 7.4 | 11.2 | 15.7 | 23.0 | 27.8 | 31.9 | 34.9 | 35.6 | 31.1 | 25.2 | 17.0 | 10.0 | |
| Std (F3) | 2.5 | 2.9 | 2.2 | 2.3 | 1.8 | 1.8 | 2.5 | 1.9 | 1.7 | 1.7 | 1.9 | 2.1 | |
| Min. | Mean (Hist) | −6.0 | −3.4 | 1.6 | 7.8 | 13.2 | 18.2 | 21.9 | 22.5 | 17.2 | 10.3 | 3.2 | −3.2 |
| Std (Hist) | 2.2 | 2.2 | 1.4 | 1.2 | 0.9 | 0.8 | 1.0 | 1.1 | 1.0 | 1.1 | 1.4 | 1.8 | |
| Mean (F1) | −4.1 | −1.6 | 2.7 | 8.9 | 14.3 | 19.4 | 23.8 | 24.4 | 18.8 | 11.6 | 4.5 | −1.9 | |
| Std (F1) | 2.3 | 2.1 | 1.4 | 1.3 | 1.0 | 0.9 | 1.4 | 1.4 | 1.2 | 1.4 | 1.7 | 1.9 | |
| Mean (F2) | −1.8 | 0.3 | 4.2 | 10.5 | 15.8 | 20.9 | 26.3 | 27.0 | 20.9 | 13.4 | 6.4 | 0.1 | |
| Std (F2) | 2.2 | 2.3 | 1.6 | 1.6 | 1.2 | 1.1 | 1.7 | 1.8 | 1.6 | 1.6 | 1.9 | 2.1 | |
| Mean (F3) | 0.7 | 2.9 | 6.4 | 12.6 | 17.8 | 22.7 | 28.9 | 29.6 | 23.6 | 15.6 | 8.7 | 2.3 | |
| Std (F3) | 2.7 | 2.5 | 2.1 | 2.2 | 1.8 | 1.5 | 1.9 | 1.9 | 2.2 | 2.0 | 2.3 | 2.4 |
| Jan. | Feb. | Mar. | Apr. | May | Jun. | Jul. | Aug. | Sep. | Oct. | Nov. | Dec. | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hist. | Mean (×105) | 4.55 | 4.41 | 4.41 | 4.41 | 4.47 | 4.62 | 4.71 | 4.72 | 4.57 | 4.42 | 4.41 | 4.43 |
| Std (×104) | 3.13 | 1.63 | 0.90 | 0.86 | 0.96 | 1.03 | 0.99 | 1.02 | 0.94 | 0.87 | 0.90 | 1.34 | |
| CV | 0.0687 | 0.0370 | 0.0204 | 0.0194 | 0.0216 | 0.0224 | 0.0211 | 0.0216 | 0.0206 | 0.0197 | 0.0205 | 0.0303 | |
| F1 | Mean (×105) | 4.47 | 4.40 | 4.40 | 4.42 | 4.50 | 4.67 | 4.79 | 4.80 | 4.61 | 4.43 | 4.40 | 4.41 |
| Std (×104) | 1.89 | 1.16 | 0.93 | 0.89 | 1.00 | 1.11 | 1.26 | 1.23 | 0.96 | 0.89 | 0.90 | 1.23 | |
| CV | 0.0424 | 0.0264 | 0.0211 | 0.0201 | 0.0222 | 0.0238 | 0.0263 | 0.0257 | 0.0208 | 0.0202 | 0.0204 | 0.0279 | |
| F2 | Mean (×105) | 4.45 | 4.40 | 4.38 | 4.45 | 4.56 | 4.74 | 4.94 | 4.97 | 4.68 | 4.47 | 4.39 | 4.40 |
| Std (×104) | 1.37 | 1.05 | 0.91 | 0.99 | 1.10 | 1.26 | 1.72 | 1.69 | 1.07 | 0.95 | 0.87 | 1.10 | |
| CV | 0.0309 | 0.0238 | 0.0206 | 0.0223 | 0.0240 | 0.0265 | 0.0348 | 0.0340 | 0.0230 | 0.0213 | 0.0199 | 0.0249 | |
| F3 | Mean (×105) | 4.41 | 4.39 | 4.39 | 4.49 | 4.66 | 4.84 | 5.15 | 5.19 | 4.78 | 4.54 | 4.39 | 4.39 |
| Std (×104) | 1.31 | 0.95 | 0.89 | 1.16 | 1.30 | 1.47 | 1.95 | 1.93 | 1.41 | 1.08 | 0.86 | 0.93 | |
| CV | 0.0298 | 0.0215 | 0.0203 | 0.0258 | 0.0279 | 0.0304 | 0.0377 | 0.0372 | 0.0294 | 0.0239 | 0.0196 | 0.0213 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seo, Y.-H.; Sung, J.H.; Park, J.-S.; Kim, B.-S.; Park, J. Future Residential Water Use and Management Under Climate Change Using Bayesian Neural Networks. Water 2025, 17, 2179. https://doi.org/10.3390/w17152179
Seo Y-H, Sung JH, Park J-S, Kim B-S, Park J. Future Residential Water Use and Management Under Climate Change Using Bayesian Neural Networks. Water. 2025; 17(15):2179. https://doi.org/10.3390/w17152179
Chicago/Turabian StyleSeo, Young-Ho, Jang Hyun Sung, Joon-Seok Park, Byung-Sik Kim, and Junehyeong Park. 2025. "Future Residential Water Use and Management Under Climate Change Using Bayesian Neural Networks" Water 17, no. 15: 2179. https://doi.org/10.3390/w17152179
APA StyleSeo, Y.-H., Sung, J. H., Park, J.-S., Kim, B.-S., & Park, J. (2025). Future Residential Water Use and Management Under Climate Change Using Bayesian Neural Networks. Water, 17(15), 2179. https://doi.org/10.3390/w17152179






