A Field Study on Sampling Strategy of Short-Term Pumping Tests for Hydraulic Tomography Based on the Successive Linear Estimator

Abstract

Hydraulic tomography (HT) based on the successive linear estimator (SLE) offers the high-resolution characterization of aquifer heterogeneity but conventionally requires prolonged pumping to achieve steady-state conditions, limiting its applicability in contamination-sensitive or low-permeability settings. This study bridged theoretical and practical gaps (1) by identifying spatial periodicity (hole effect) as the mechanism underlying divergences in steady-state cross-correlation patterns between random finite element method (RFEM) and first-order analysis, modeled via an oscillatory covariance function, and (2) by validating a novel short-term sampling strategy for SLE-based HT using field experiments at the University of Göttingen test site. Utilizing early-time drawdown data, we reconstructed spatially congruent distributions of hydraulic conductivity, specific storage, and hydraulic diffusivity after rigorous wavelet denoising. The results demonstrate that the short-term sampling strategy achieves accuracy comparable to that of long-term sampling strategy in characterizing aquifer heterogeneity. Critically, by decoupling SLE from steady-state requirements, this approach minimizes groundwater disturbance and time costs, expanding HT’s feasibility to challenging environments.

1. Introduction

Hydraulic tomography (HT) has emerged as a powerful technique for characterizing aquifer heterogeneity, playing a crucial role in hydrogeological investigations, groundwater contamination remediation, and water resource management [1,2,3,4,5]. HT achieves this by performing sequential pumping/injection tests at multiple locations while monitoring the corresponding hydraulic head responses at various observation points [6]. These extensive transient head datasets, when inverted using appropriate algorithms—such as hydraulic travel time inversion, geostatistical inversion, pilot point inversion, steady shape inversion, and Gaussian mixture methods—enable the reconstruction of spatial distributions of key hydraulic parameters, such as hydraulic conductivity (K) and specific storage (Sₛ).

Among the inversion methods, the successive linear estimator (SLE) has gained prominence due to its computational efficiency and robustness [7,8,9,10,11,12]. SLE addresses the inherent nonlinearity of the inverse problem through iterative linearization and least-squares minimization [13]. However, a significant limitation of conventional SLE lies in its reliance on hydraulic head data reaching steady-state conditions [14]. This requirement necessitates prolonged pumping/injection durations and extended recovery periods, resulting in high operational costs, lengthy experimental timelines, and substantial perturbations to the natural groundwater system. These drawbacks are especially concerning at contaminated sites. Prolonged pumping there may mobilize pollutants. Moreover, in low-permeability aquifers, achieving steady-state conditions can be impractical or take prohibitively long.

Consequently, there is a strong impetus to develop strategies that decouple SLE-based HT from the requirement for steady-state flow attainment in pumping tests. Alternative approaches like Hydraulic Travel-Time Tomography and Hydraulic Attenuation Tomography have demonstrated the potential to characterize aquifer heterogeneity using short-term tests (e.g., slug tests or brief pumping) by focusing on early-time signal propagation (travel times or attenuation) [15,16,17,18,19]. While promising, these methods differ fundamentally from SLE, raising the critical question: Can the widely used SLE algorithm itself be effectively adapted to utilize early-time drawdown data from short-term pumping tests?

The feasibility of such an adaptation hinges on understanding when and where early-time head data contain sufficient information about hydraulic conductivity and specific storage. This is where cross-correlation analysis provides essential theoretical insights. This statistical tool quantifies the spatial–temporal relationships between aquifer parameters and the observed hydraulic head responses during pumping [14,20,21,22,23]. Studies by Sun et al. [14] and Hou et al. [23] employed different methodologies (first-order analysis and Random Finite Element Method, RFEM, respectively) to conduct such analyses. Sun et al. [14] suggested sampling extending to steady/quasi-steady state, while Hou et al. [23] based on RFEM simulations, proposed a short-term strategy utilizing data at specific characteristic times (e.g., maximum first derivative, zero second derivative of drawdown). Critically, however, these insights into early-time data utility for SLE have primarily been derived from numerical experiments, with a notable lack of validation through field studies.

This study bridged the critical gap between theoretical frameworks and field application by validating the feasibility of characterizing aquifer heterogeneity using SLE with early-time drawdown data from short-term HT pumping tests. To achieve this objective, discrepancies in cross-correlation results derived from RFEM versus first-order analysis were first analyzed. Subsequently, HT pumping tests were implemented at the University of Göttingen field site, where experimental data underwent noise-reduction processing prior to the estimation of the spatial distribution of hydraulic parameters using both short-term and long-term sampling strategies. Finally, inversion results from both strategies were comparatively evaluated with rigorous reliability assessments. This research provides a novel and practical approach for HT applications in time-constrained and environmentally sensitive settings. Furthermore, it establishes a foundation for integrating efficient early-time data acquisition with robust inversion algorithms like SLE, advancing the toolkit for aquifer characterization.

2. Cross-Correlation Analysis

Cross-correlation analysis provides the theoretical foundation for optimizing pumping sampling strategies in parameter estimation. It elucidates the dynamic correlation patterns between spatially variable parameters and the transient water levels induced by pumping. This method identifies spatial–temporal domains of high parameter–head correlations, thus guiding the design of efficient sampling strategies.

2.1. Cross-Correlation Analysis Based on the Random Finite Element Method (RFEM)

Hou et al. [23] employed the random finite element method (RFEM) to conduct cross-correlation analyses between observed hydraulic heads and hydraulic parameters (hydraulic conductivity and specific storage). Based on these analyses, they developed a short-term sampling strategy, which was rigorously validated through numerical experiments. A brief overview of the RFEM-based cross-correlation analysis is provided as follows:

RFEM integrates random field theory with the finite element method (FEM) within the framework of Monte Carlo simulation [24,25,26,27]. In this approach, hydraulic conductivity and specific storage at each location within an aquifer are treated as random variables. The collection of these random variables across all spatial locations constitutes a random field, which is characterized by its statistical properties (mean, variance, and correlation scales) [28]. To ensure the non-negativity of hydraulic conductivity and specific storage, we employ their natural logarithmic transformations (lnK and lnS_s) for subsequent analysis.

Given specified mean, variance, and correlation scales, the random field can generate an infinite number of possible spatial distributions, each referred to as a realization. Using the spectral method, a finite set of discrete realizations can be numerically generated [29]. These parameter fields are then sequentially input into an appropriate groundwater flow model, where the corresponding observed water head data are obtained through finite element analysis. The cross-correlation is quantified via Equation (1) [30]:

$${\rho }_{hf}\left(\mathbf{x},t\right)={\displaystyle \frac{{\sum }_{i=1}^n\left(F_{\mathbf{x}}^i-{\overline{F}}_{\mathbf{x}}\right)\left(H_t^i-{\overline{H}}_t\right)}{\sqrt{{\sum }_{i=1}^n{\left(F_{\mathbf{x}}^i-{\overline{F}}_{\mathbf{x}}\right)}^2{\sum }_{i=1}^n{\left(H_t^i-{\overline{H}}_t\right)}^2}}}$$

(1)

where $\mathbf{x}$ denotes the spatial coordinates, and t represents time. ρ_hf quantifies the cross-correlation between the hydraulic head observed at the well at time t and the hydraulic parameter (lnK and lnS_s) at location x, respectively. Here, n is the total number of realizations. $F_x^i$ corresponds to the hydraulic parameter values at x in the i-th realization, while ${\overline{F}}_x$ represents the ensemble mean across all realizations. Similarly, $H_t^i$ is the simulated head at the observation well at time t for the i-th, and ${\overline{H}}_t$ is the mean head at time t over all realizations.

Hou et al. [23] conducted cross-correlation analysis using the Random Finite Element Method (RFEM) on a synthetic 2D confined aquifer model. The model consists of 50 × 50 square elements, each 2 m wide. All boundaries are set as constant head boundaries at 100 m, with an initial head of 100 m throughout. An observation well is located at (x = 34 m, y = 50 m), represented by the white point in Figure 1 and Figure 2, and a pumping well is at (x = 66 m, y = 50 m), represented by the red point in Figure 1 and Figure 2, discharging at a constant rate of 0.0001 m³/s. The log-transformed hydraulic conductivity (lnK) and specific storage (lnS_s) have means of −9 and variances of 1. The correlation lengths in both the x- and y-directions are set to 20 m.

Figure 1 and Figure 2 reveal distinct temporal–spatial correlations between hydraulic parameters (lnK and lnS_s) and observed heads. Specifically, for the cross-correlation between lnK and hydraulic heads, a negative correlation exists in the region between the pumping and observation wells (i.e., higher lnK corresponds to lower hydraulic heads, and vice versa), whereas a positive correlation is observed in the outer regions. The correlation initially increases rapidly, stabilizes, and then slightly declines over time, peaking when the second derivative of the correlation function equals zero (t₂). For the cross-correlation between lnS_s and hydraulic heads, a positive correlation is found between the pumping and observation wells, with no significant correlation in the outer regions. The maximum correlation occurs when the first derivative reaches its extremum (t₁).

2.2. Cross-Correlation Analysis Based on the First-Order Analysis

Prior to the work of Hou et al. [23], Sun et al. [14] employed an alternative approach for cross-correlation analysis—the first-order analysis. A brief description of the cross-correlation based on the first-order analysis is provided below:

$$\begin{gathered} h\left({\mathit{x}}_i,t\right) \approx \left[{\left.{\displaystyle \frac{\partial H\left({\mathit{x}}_i,t\right)}{\partial lnK\left({\mathit{x}}_j\right)}}\right|}_{Y,Z}\right]y\left({\mathit{x}}_j\right)+\left[{\left.{\displaystyle \frac{\partial H\left({\mathit{x}}_i,t\right)}{\partial ln{S}_s\left({\mathit{x}}_j\right)}}\right|}_{Y,Z}\right]y\left({\mathit{x}}_j\right) \\ =J_{hy}\left({\mathit{x}}_i,{\mathit{x}}_j,t\right)y\left({\mathit{x}}_j\right)+J_{hz}\left({\mathit{x}}_i,{\mathit{x}}_j,t\right)z\left({\mathit{x}}_j\right) \end{gathered}$$

(2)

where y(x_j) and z(x_j) represent perturbations of lnK and lnS_s, respectively, at spatial locations x_j, where j = 1, …; N denotes the total number of elements in the finite element domain. Y and Z are the mean values of lnK and lnS_s, respectively. Consequently, the logarithmic hydraulic conductivity and specific storage can be expressed as lnK = Y + y and lnS_s = Z + z. The terms J_hy(x_i,x_j,t) and J_hz(x_i,x_j,t) correspond to the sensitivity coefficients of hydraulic head (h) at location x_j and time t with respect to perturbations in lnK and lnS_s at location x_j, respectively. In this formulation, Einstein’s summation convention is applied to repeated indices. Physically, this implies that the head perturbation observed at (x_i,t) can be expressed as a linear superposition of parameter perturbations (lnK and lnS_s) throughout the entire aquifer domain, with the sensitivity coefficients serving as weighting factors for each parameter’s contribution.

The cross-correlation ρ_hy and ρ_hz at location i and j at time t can be calculated through Equations (3) and (4).

$${\rho }_{hy}\left({\mathit{x}}_i,{\mathit{x}}_j,t\right)={\displaystyle \frac{J_{hy}\left({\mathit{x}}_i,{\mathit{x}}_j,t\right)R_{yy}\left({\mathit{x}}_i,{\mathit{x}}_j\right)}{\sqrt{R_{hh}\left({\mathit{x}}_i,{\mathit{x}}_j,t\right)R_{yy}\left({\mathit{x}}_i,{\mathit{x}}_j\right)}}}$$

(3)

$${\rho }_{hz}\left({\mathit{x}}_i,{\mathit{x}}_j,t\right)={\displaystyle \frac{J_{hz}\left({\mathit{x}}_i,{\mathit{x}}_j,t\right)R_{zz}\left({\mathit{x}}_i,{\mathit{x}}_j\right)}{\sqrt{R_{hh}\left({\mathit{x}}_i,{\mathit{x}}_j,t\right)R_{zz}\left({\mathit{x}}_i,{\mathit{x}}_j\right)}}}$$

(4)

where R_yy and R_zz denote the covariance matrices of the perturbations in lnK and lnS_s, respectively, both modeled using the same exponential covariance function. The head covariance matrix, R_hh, is derived from R_yy, R_zz, and the sensitivity matrices from J_hy and J_hz.

Sun et al. [14] conducted the first-order cross-correlation analysis using a synthetic 2D confined aquifer model (200 m × 200 m), discretized into 100 × 100 square elements (2 m each). All boundaries were assigned a constant head of 100 m. An observation well (white point in Figure 3 and Figure 4) was placed at (80 m, 100 m), and a pumping well (black point in Figure 3 and Figure 4) at (120 m, 100 m), with a constant discharge of 0.0006 m³/s. The geometric means of hydraulic conductivity and specific storage were 0.000116 m/s and 0.00014 m⁻¹, respectively. The variances of lnT and lnS were 1.0 and 0.2. Both parameters followed exponential covariance functions with isotropic correlation lengths of 30 m in x and y directions.

The results of cross-correlation analysis based on the first-order analysis are shown in Figure 3 and Figure 4. The results reveal that the cross-correlation between hydraulic head and lnS_s is predominantly confined to the region bounded by the observation well and the pumping well within the aquifer. The correlation peaks during the early time period (tₘ), followed by a gradual decay to negligible values. The characteristic time tₘ exhibits close correspondence with the intercept time t₀, where t₀ represents the time at which the extrapolated drawdown from the initial linear segment of the observed drawdown-log time curve approaches zero.

During early time conditions, a strong cross-correlation between hydraulic head and lnK is observed exclusively within the inter-well region. This spatial pattern subsequently evolves into two kidney-shaped humps, characterized by two distinct correlation maxima positioned symmetrically about the central axis connecting the observation and pumping wells. As the pumping test progresses toward steady-state conditions, both the spatial extent and magnitude of these correlation peaks increase progressively, attaining their maximum values as flow reach steady-state.

2.3. Mechanistic Comparison of Cross-Correlation Behaviors

The two cross-correlation analysis methodologies demonstrate both convergent and divergent outcomes in characterizing aquifer parameter interactions. Consistency is observed in their temporal–spatial correlation patterns: both approaches identify nearly identical temporal variations in the correlation between lnS_s and observed hydraulic heads, with high-correlation zones occupying consistent spatial positions. Regarding lnK and hydraulic head relationships, both methodologies initially detect a pronounced negative correlation within the inter-well region during early pumping stages, followed by the emergence of dual-kidney-shaped positive correlation zones in peripheral regions as pumping progresses. Divergence becomes evident in the cross-correlation between hydraulic conductivity and observed head under steady-state conditions. The first-order analysis reveals an attenuation of the initial strong negative inter-well correlation, transitioning to a weak positive relationship upon stabilization, whereas the RFEM maintains persistent strong negative correlations throughout the pumping process. This discrepancy underscores a critical gap in our understanding of the mechanisms responsible for divergent steady-state cross-correlations.

Theoretical foundations from Equations (3) and (4) indicate that the first-order cross-correlation outcomes are governed by sensitivity matrices derived via the adjoint state method and covariance matrices defined by an exponential autocorrelation function (Equation (5)).

$$\mathsf{\rho }\left(\xi \right)=e^{-{\left[{\left|{\displaystyle \frac{{\xi }_1}{{\lambda }_1}}\right|}^2+{\left|{\displaystyle \frac{{\xi }_2}{{\lambda }_2}}\right|}^2\right]}^{{\displaystyle \frac{1}{2}}}}$$

(5)

where ξ represents the separation vector with components ξ₁ and ξ₂ in the x- and y-directions, and λ₁ and λ₂ denote the respective correlation scales. Cross-correlation analysis, inherently a sensitivity analysis incorporating correlation scales, is dominated by these covariance structures. While Equation (5) describes idealized exponential decay of correlation with distance, field observations frequently reveal periodic fluctuations in spatial correlations along vertical and lateral direction—termed the hole effect—manifested as non-monotonic oscillatory attenuation rather than smooth decay [31,32]. These periodic patterns likely reflect geological cyclic structures such as sedimentary alternations (e.g., sand-mudstone sequences) or tectonic-induced repetitive fracturing/folding. The hole effect model is provided below:

$$\mathsf{\rho }\left(\xi \right)=e^{-{\left[{\left|{\displaystyle \frac{{\xi }_1}{{\lambda }_1}}\right|}^2+{\left|{\displaystyle \frac{{\xi }_2}{{\lambda }_2}}\right|}^2\right]}^{{\displaystyle \frac{1}{2}}}}\mathrm{c}\mathrm{o}\mathrm{s}({\displaystyle \frac{\pi }{a}}\sqrt{{\left|{\displaystyle \frac{{\xi }_1}{{\lambda }_1}}\right|}^2+{\left|{\displaystyle \frac{{\xi }_2}{{\lambda }_2}}\right|}^2})$$

(6)

where a is a dimensionless constant.

Monte Carlo simulations based on extensive realizations of the parameter fields—using the same statistical properties as in Hou et al. [23], with lnK and lnS_s having means of −9, variances of 1, and correlation lengths of 20 m in both x- and y-directions—produce an ensemble-averaged autocorrelation function curve, derived geostatistically using Equation (7). As shown in Figure 5c, the resulting curve closely aligns with the predictions of the hole effect model, strongly indicating that spatial periodicity (i.e., hole effects) is the primary source of the observed methodological discrepancies.

$$\mathsf{\rho }\left(\xi \right)={\displaystyle \frac{Cov\left(\xi \right)}{Cov\left(0\right)}}={\displaystyle \frac{N\sum _{i=1}^{N-\xi }\left[F\left(i\right)-\overline{F}\right]\left[F\left(i+\xi \right)-\overline{F}\right]}{\left(N-\xi \right)\sum _{i=1}^N\left[F\left(i\right)-\overline{F}\right]\left[F\left(i\right)-\overline{F}\right]}}$$

(7)

where cov denotes the covariance function, N is the number of elements in a row or column, F(i) is the parameter value at location i, ξ is the lag distance, and $\overline{F}$ is the mean of the parameter values along the statistical row or column.

To verify this hypothesis, the study first replicated Sun’s framework under steady-state conditions, yielding consistent cross-correlation patterns between lnK and observed heads (Figure 6b). Sensitivity analysis (Figure 6a) revealed negative correlations between inter-well parameters and hydraulic heads, contrasting with positive correlations in peripheral regions. The subsequent substitution of the conventional exponential covariance model with the hole effect model produced a systematic shift in correlation patterns (Figure 5c): inter-well correlations reverted to negative values while peripheral positivity attenuated, achieving alignment with Monte Carlo-based cross-correlation results. This transformation conclusively demonstrates that the hole effect—manifested as periodic covariance structures—governs the observed discrepancies between the two methodologies. The consistency between geostatistically derived covariance curves (Figure 5c) and the hole effect model predictions further reinforces the critical role of spatial periodicity in modulating cross-correlation behavior, providing mechanistic evidence for the methodological divergence.

Cross-correlation analysis reveals the magnitude of interdependence between observed hydraulic heads and spatially distributed parameters during pumping, providing critical insights for optimizing sampling strategies in parameter inversion. First-order-based cross-correlation results recommend extending pumping operations until steady or quasi-steady states are achieved. In contrast, Monte Carlo simulation-driven cross-correlation analysis proposes terminating pumping when the second derivative of head responses approaches zero.

Since reaching the point where the second-order derivative of head in all observation wells equals zero generally requires less time than achieving full steady-state conditions, the former is referred to as the short-term pumping approach, and the latter as the long-term pumping approach. The long-term sampling strategy involves collecting head data from both the early-time and steady-state phases of the test, which serve as inputs for the SLE. In contrast, the short-term sampling strategy selects head data corresponding to the time when the first-order derivative reaches its extremum and when the second-order derivative equals zero.

Both strategies have been validated through numerical and laboratory experiments: Sun et al. [14] conducted comprehensive numerical simulations for the long-term strategy; Jiang et al. [9] verified the long-term approach using laboratory experiments; and Hou et al. [23] applied Monte Carlo simulations to rigorously test the short-term strategy. However, their effectiveness under field conditions remains unverified. To address this gap, the present study carried out a hydraulic tomography (HT) pumping test at a field site at the University of Göttingen, aiming to systematically evaluate the robustness of these sampling strategies under realistic hydrogeological conditions. To address this gap, this study conducted a HT pumping test at a field site at the University of Göttingen, systematically evaluating the robustness of these strategies under real-world hydrogeological conditions.

3. Hydraulic Tomography Survey at the Test Site

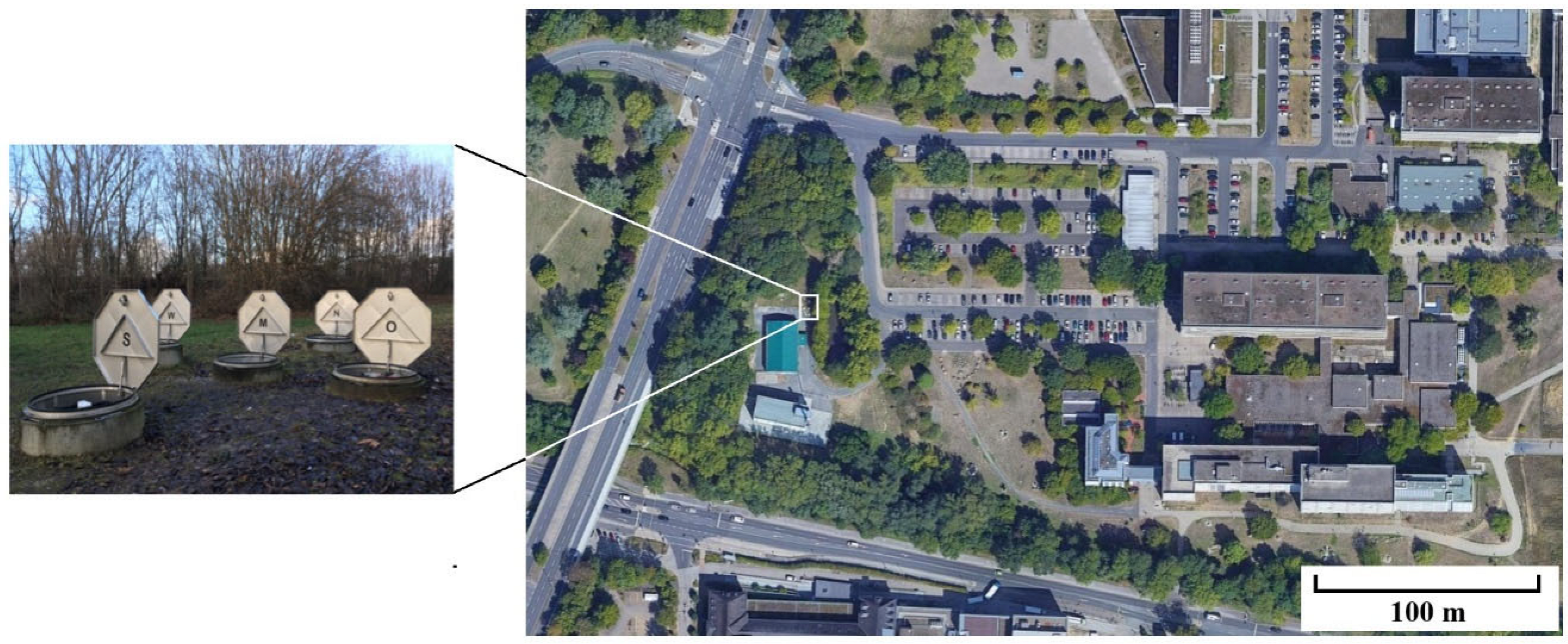
3.1. Site Description

The study site is situated on the North Campus of the University of Göttingen, Germany, adjacent to the Faculty of Geosciences and Geography (Figure 7), covering an area of approximately 25 m². Five monitoring wells—designated O (east), W (west), S (south), N (north), and M (center)—have been installed at the site. Each well is 78 m deep and uniformly constructed, consisting of nine alternating segments of slotted polyethylene (PE) screens (5 m in length, 7.6 cm in diameter) and fully cased PE pipe sections (3 m in length, 7.6 cm in diameter). The screen segments in each well are sequentially numbered from top to bottom (e.g., O1 to O9 in well O). Each screen section is surrounded by a high-permeability gravel pack (6 m in length, 4.5 cm in thickness) that fills the annular space, while each fully cased segment is sealed with a low-permeability clay fill (2 m in length, 4.5 cm in thickness), ensuring hydraulic isolation. Figure 8 presents the well construction details and profiles within the 0–45 m depth interval for wells M and O.

3.2. Previous Research on This Test Site

The experimental site has undergone extensive multidisciplinary characterization since its establishment.

Geophysical investigations by the Göttingen group and LIAG (Leibniz Institute for Applied Geophysics) encompassed comprehensive logging across wells O, W, S, N, and M, including gamma ray, acoustic/optical televiewer, caliper, and vertical deflection measurements. These efforts revealed consistent structural features, such as bedding planes dipping approximately 75° to the southeast [33] and pronounced vertical heterogeneity in fracturing with higher fracture density above 40 m depth.

Hydrogeological characterization further revealed substantial heterogeneity, particularly in the upper 40 m. Laboratory-based permeability tests on core samples from well N showed hydraulic conductivity values ranging from 10⁻¹⁰ to 10⁻⁶ m/s, depending on lithology and fracture characteristics [34], while field-scale investigations reported higher values. Oberdorfer et al. [35] characterized the five-well cluster (O, W, S, N, M) using cross-well multi-level pumping tests at the first screen interval of each well. Analyzing data via the Theis [36] and Cooper and Jacob [37] methods, they estimated hydraulic conductivity (K = 3 × 10⁻⁴ to 5 × 10⁻⁴ m·s⁻¹) and specific storage (S_s = 2 × 10⁻⁶ to 1 × 10⁻³ m⁻¹). Tomographic pumping tests [38] identified variable hydraulic diffusivity (D)—defined as the ratio of hydraulic conductivity to specific storage—ranging from 0.01 to 199 m²/s between wells M and O above a depth of 40 m (Figure 9), and revealed three distinct high-diffusivity layers (D > 5 m²/s).

These diverse and extensive prior studies have provided a solid foundation of background information for this study and offer valuable reference results that can be used for comparison and validation. On the other hand, the noticeable discrepancies among these previous findings highlight a critical challenge in the field-based estimation of heterogeneous parameters—namely, the absence of a unique, definitive reference solution. This inherent uncertainty also represents a key difficulty addressed in this study.

3.3. Pumping Tests

Hydraulic tomography was conducted through a series of cross-well pumping tests, with Well O as the pumping source and Well M as the observation well. The extraction system employed a Grundfos MP1 submersible pump (Bjerringbro, Denmark) with a frequency inverter for precise rate control. Drawdown was monitored using pressure transducers in both wells, logged continuously by a Campbell Scientific CR3000 datalogger (Logan, UT, USA). To isolate specific screen intervals and prevent vertical flow interference, double-packer systems activated by pressurized air were deployed in both wells.

Due to low hydraulic conductivity, Screen 1 (shallowest interval) in wells O and M was excluded. Experiments utilized Screens 2–5 in the pumping well (O) as sources and corresponding screens in the observation well (M) as receivers, forming a 4 × 4 testing matrix (16 source-receiver pairs). Figure 8 illustrates this multi-level array geometry. Pumping durations were 30 min for same-depth tests (O2M2, O3M3, O4M4, O5M5) and 5 min for all other pairs.

4. Results

4.1. Wavelet De-Noising and Data Processing

Field-collected pumping test data are inevitably contaminated by noise (e.g., electrical interference, barometric effects), necessitating effective denoising methodologies to extract meaningful signals. While techniques range from basic filters to neural networks, wavelet denoising has proven to be particularly suitable for hydrogeological applications due to its superior balance of noise suppression and signal feature preservation, alongside computational efficiency. Xiang [39] established the signal-to-noise ratio (SNR) as a robust metric for hydrograph quality assessment, noting wavelet denoising’s efficacy for enhancement. Yang [40] further optimized this approach under white noise assumptions, identifying Coiflets (decomposition level 5, denoising level 6) as optimal. In this study, we applied Yang’s wavelet method followed by polynomial fitting to preprocess multi-level pumping test data, generating smoothed curves for derivative analysis. First and second derivatives of the drawdown data were subsequently computed. The times of maximum first derivative and the zero-crossing point of the second derivative were statistically determined and are summarized in

Table 1. Sampling times (t₁ * and t₂ *) of all pumping tests.

Pumping Tests	t1 (s)	t2 (s)
O2M2	7.6	100
O2M3	9	100
O2M4	22.2	130
O3M2	4	50
O3M3	4.8	100
O3M4	10.4	60
O4M2	22.4	100
O4M3	36	150
O4M4	3	50
O5M2	21.6	100
O5M3	22.6	100
O5M4	19.6	100
O5M5	2.5	50

Notes: * t₁ represents the time when the first derivative of observed head in observation well with respect to time reaches its extreme value; t₂ denotes the time when the second derivative of the observed head becomes zero.

, with datasets O2M5, O3M5, and O4M5 excluded due to irreducible noise.

Generally, identical-depth pumping-observation screen pairs exhibit minimal lateral separation and thus the shortest hydraulic travel times. Paradoxically, the travel time for the O3M2 pair is significantly shorter than for O3M3 despite greater lateral offset (Table 1). This anomaly reveals a high-permeability zone between screens O3 and M2, accelerating groundwater flow—demonstrating pronounced subsurface heterogeneity within the study area.

4.2. Inversion and Validation

A synthetic 2D vertical confined aquifer model (Figure 10) was established to estimate the spatial distribution of hydraulic parameters using SLE. The domain was discretized into a uniform 40 × 12 grid with 1 m × 1 m square elements, with constant-head boundaries (50 m) imposed on all sides and an initial hydraulic head field uniformly initialized at 50 m. The configuration included five pumping wells (O2–O5; red points in Figure 10) operating at a constant rate of 0.0005 m³/s each, and five observation points (M2–M5; white points in Figure 6). Due to SLE’s low sensitivity to input parameter means and variances [6], prior mean values for hydraulic conductivity and specific storage were assigned as 3.0 × 10⁻⁴ m/s and 2.0 × 10⁻⁵ m⁻¹, respectively, based on previous regional studies, with variances set to 3.60 × 10⁻⁷ m²/s² and 1.60 × 10⁻⁹ m⁻². In the absence of site-specific correlation length data, horizontal and vertical correlation scales were conservatively assumed equal to the grid discretization size (1 m).

Given the limited number of pumping and observation wells and their close proximity (M and O wells), our analysis focuses specifically on the parameter distributions within the inter-well region delineated by the blue rectangle in Figure 10.

The inversion results using the short-term sampling strategy are shown in Figure 11a–c. The estimated hydraulic conductivity reaches minimum values between wells O2M2 and O5M5, while maximum values (indicating highest permeability) occur between O3M3, with O4M4 exhibiting intermediate hydraulic conductivity values. Specific storage maxima are observed between O2M2, followed by O3M3, with minima between O5M5. Diffusivity peaks between O3M3, with notably elevated values also present directly beneath O3M3 and O4M4.

Results from the long-term sampling strategy (SLE, Figure 11d–f) reveal a strikingly similar spatial distribution pattern for hydraulic conductivity, specific storage, and hydraulic diffusivity compared to the short-term results, with high-value zones occurring at identical depths, although the absolute maxima exhibit minor variations. Furthermore, comparison with travel-time-based inversion results (Figure 9 and Figure 11c,f) consistently identifies the highest hydraulic diffusivity values (>100 m²/s) near the depth of the O3M3 interval. This convergence of results derived from distinct methodologies and datasets strongly supports the reliability of the inferred parameter distributions.

Figure 12a,b present scatter plots of observed versus simulated hydraulic heads under two different sampling strategies. The associated performance metrics—including the coefficient of determination (R²), L₂-norm, and slope—are summarized in

Table 2. Performance metrics under different observational head input configurations.

Hydraulic Head Input Configurations	R2	L2	Slope
Short-term sampling strategy inversion	0.9560	0.041	0.8792
Long-term sampling strategy inversion	0.9696	0.0384	0.9669
Dense input data validation	0.9627	0.0513	0.9068
Leave-one-out validation	0.9346	0.0733	0.7963

. These results suggest a slightly better performance for the long-term sampling strategy. However, this marginal difference is not sufficient to conclusively establish the superiority of the long-term approach in terms of inversion accuracy, as the performance gap is minimal and may be influenced by the inherent variability of a single field experiment. In contrast, the strong similarity between the results obtained from both strategies provides more convincing evidence of the robustness of the inversion approach.

To further evaluate the robustness of the inversion results, two additional validation analyses were performed.

First, an inversion was conducted using a denser set of observational data—five drawdown measurements per test at 7.6 s, 50 s, 100 s, 200 s, and 500 s, instead of the original two. As shown in Figure 11g–i, this extended dataset confirmed that the zones of maximum hydraulic conductivity and hydraulic diffusivity remained centered around the O3M3 depth. Although specific storage estimates exhibited minor variations (a slight decrease near O2M2 and a slight increase near O3M3, both within ±3 × 10⁻⁵ m⁻¹), these differences are attributed to the inclusion of later-time data (t > t₁), which are less sensitive to specific storage. As shown in Figure 12c and Table 2, the performance metrics for R² and slope fall between those of the long-term and short-term sampling strategies, while the L₂ exhibits a higher error than both. This suggests a possible implication: when using the SLE method, increasing the number of observed head samples does not necessarily lead to improved inversion performance. However, this hypothesis requires further investigation in future studies. Nevertheless, these variations are consistent with the overall spatial trends observed in the initial inversion and do not alter the main interpretation.

Second, a leave-one-out inversion was carried out by omitting the data from well pair O4M4, using the remaining 12 well pairs (each with two drawdown measurements) as input. The resulting parameter fields were then used in a forward simulation to predict the drawdown at O4M4. As illustrated in Figure 11j–l, the simulated drawdown closely matches the observed data, despite minor deviations introduced by excluding O4M4 from the inversion. When one set of pumping data is excluded, the performance metrics deteriorate significantly, as shown in Figure 12d and Table 2. This highlights the critical importance of the number of wells in determining the quality of SLE-based inversion results. The key spatial features, including the high-value parameter zones, remained stable across both inversions.

The further analysis of the simulation performance of the leave-one-out inversion (Figure 13) indicates a slight underestimation of drawdown in the 0–50 s range, likely due to experimental noise associated with pump start-up, as reflected by fluctuations in the observed curve. From 50 to 100 s, the simulation aligns well with observations. Beyond 150 s, the observed drawdown increasingly exceeds the simulated response. This growing late-time mismatch is attributed to the expanding cone of depression reaching regions beyond the instrumented domain, where aquifer heterogeneity remains uncharacterized due to the lack of well coverage and is therefore not captured in the inversion.

5. Conclusions

This study presents cross-correlation analyses using two distinct approaches: RFEM and the first-order analysis. We discuss the consistency and discrepancies in their results, attributing the divergence to the “hole effect” in aquifer heterogeneity. Subsequently, HT pumping tests were conducted at the University of Göttingen field site, yielding observational datasets that underwent rigorous noise reduction. These processed data were then utilized to estimate the spatial distributions of hydraulic parameters (hydraulic conductivity, specific storage, and hydraulic diffusivity) through both long-term and short-term sampling strategies. The results were further validated to ensure robustness.

Key theoretical findings reveal that the divergence in steady-state cross-correlation patterns between RFEM and first-order approaches arises from spatial periodicity (hole effect) in aquifer heterogeneity. This phenomenon, modeled via an oscillatory covariance function Equation (6), resolves methodological discrepancies by demonstrating that periodic structures (e.g., sedimentary cycles or fracturing patterns) govern covariance attenuation, thereby modulating the cross-correlation between hydraulic parameters and observed head.

Field validation at the University of Göttingen field site, employing HT pumping tests with rigorously denoised observational data, confirmed that both short-term and long-term sampling strategies—derived from RFEM and first-order cross-correlation principles, respectively—yield consistent, high-fidelity reconstructions of aquifer heterogeneity. Inversions using early-time (t₁, t₂) and extended-duration data produced spatially congruent hydraulic conductivity, specific storage, and hydraulic diffusivity distributions. Validation via augmented datasets and excluded well-pair analyses further affirmed result robustness. The convergence of these outcomes with travel-time tomography underscores their reliability.

Critically, the short-term strategy reduces pumping durations while preserving inversion accuracy. This efficiency significantly expands HT’s applicability to contamination-sensitive sites and low-permeability aquifers, where prolonged pumping risks mobilizing pollutants or becomes technically infeasible. By decoupling SLE from steady-state requirements and minimizing aquifer disturbance, this work establishes a pragmatic framework for efficient, sustainable aquifer characterization in challenging environments.