Abstract
Sediment accumulation in irrigation channels poses a significant challenge to water resource management, impacting hydraulic efficiency and agricultural sustainability. This study introduces an innovative multidisciplinary framework that integrates advanced image analysis (FIJI/ImageJ 1.54p), statistical validation (RStudio), and vector field modeling with a novel Sinusoidal Morphodynamic Bedload Transport Equation (SMBTE) to predict sediment deposition patterns with high precision. Conducted along the Malacatos River in La Tebaida Linear Park, Loja, Ecuador, the research captured a natural sediment transport event under controlled flow conditions, transitioning from pressurized pipe flow to free-surface flow. Observed sediment deposition reduced the hydraulic cross-section by approximately 5 cm, notably altering flow dynamics and water distribution. The final SMBTE model (Model 8) demonstrated exceptional predictive accuracy, achieving RMSE: 0.0108, R2: 0.8689, NSE: 0.8689, MAE: 0.0093, and a correlation coefficient exceeding 0.93. Complementary analyses, including heatmaps, histograms, and vector fields, revealed spatial heterogeneity, local gradients, and oscillatory trends in sediment distribution. These tools identified high-concentration sediment zones and quantified variability, providing actionable insights for optimizing canal design, maintenance schedules, and sediment control strategies. By leveraging open-source software and real-world validation, this methodology offers a scalable, replicable framework applicable to diverse water conveyance systems. The study advances understanding of sediment dynamics under subcritical (Fr ≈ 0.07) and turbulent flow conditions (Re ≈ 41,000), contributing to improved irrigation efficiency, system resilience, and sustainable water management. This research establishes a robust foundation for future advancements in sediment transport modeling and hydrological engineering, addressing critical challenges in agricultural water systems.
1. Introduction
Sediment accumulation in irrigation channels represents a critical challenge for agricultural water management systems worldwide, significantly compromising hydraulic efficiency and water distribution capacity [1]. The progressive deposition of sediments reduces channel cross-sectional area, increases flow resistance, and leads to uneven water distribution, ultimately threatening agricultural productivity and food security [2]. In regions characterized by complex topography and variable hydrological regimes, such as the Andean highlands of Ecuador, these challenges are particularly pronounced due to high erosion rates and sediment loads. Sediment deposition occurs when flow velocities fall below critical thresholds, typically between 0.3 m/s and 0.5 m/s for fine-grained materials, leading to progressive accumulation that compromises hydraulic performance through reduced conveyance capacity, increased roughness coefficients, and altered flow dynamics [3]. These challenges are further compounded in environments with steep topography and seasonal sediment load variations, such as the Andean valleys of southern Ecuador, where sediment transport significantly impacts irrigation infrastructure.
Traditional approaches to sediment transport analysis have predominantly relied on empirical models and point-based measurement techniques [3,4]. While these methods have provided foundational insights into sediment dynamics, they often lack the spatio-temporal resolution required for precise characterization of complex, spatially variable deposition patterns, particularly periodic bedforms that significantly impact hydraulic resistance [5]. Furthermore, traditional techniques, such as physical sampling and empirical modeling, require substantial field labor and may lack the precision necessary to characterize deposition patterns across diverse environmental conditions [6]. These limitations underscore the critical need for advanced, non-invasive techniques capable of delivering high-resolution morphometric data and predictive models that can capture these specific features with enhanced accuracy and efficiency.
Advances in image processing and computer vision have revolutionized sediment transport research, offering unprecedented opportunities for detailed morphological analysis [7]. Tools like FIJI/ImageJ 1.54p, an open-source platform for scientific image analysis, enable the extraction of high-resolution topographic data from images, facilitating comprehensive characterization of sedimentary structures.
Unlike existing image-based techniques that primarily focus on visual classification or empirical pattern detection [7], the proposed approach introduces a parametric sinusoidal model capable of capturing periodic sediment structures with high spatial resolution [8]. This mathematical formalization allows for the quantification of morphometric descriptors such as wavelength and amplitude—parameters that are not explicitly resolved in most image segmentation or thresholding methods. By integrating sinusoidal curves fitting with high-resolution imaging, this study provides a reproducible and interpretable framework that advances sediment modeling beyond purely empirical or heuristic techniques.
For instance, vector field analysis, three-dimensional surface reconstruction [8], and mathematical modeling [9] provide substantial advantages over traditional methods, facilitating comprehensive morphological characterization across multiple scales without disrupting the sediment bed [10].
High-resolution imagery (6936 × 9248 pixels) captured under controlled conditions enables the quantification of sedimentary structures with enhanced precision, as demonstrated in this study conducted in a controlled channel within the La Tebaida Linear Park along the left bank of the Malacatos River in Loja, Ecuador (Figure 1). This site was selected for its representative flow conditions, moderate slope characteristics, seasonal sediment load variations, and a history of sedimentation issues affecting irrigation infrastructure.
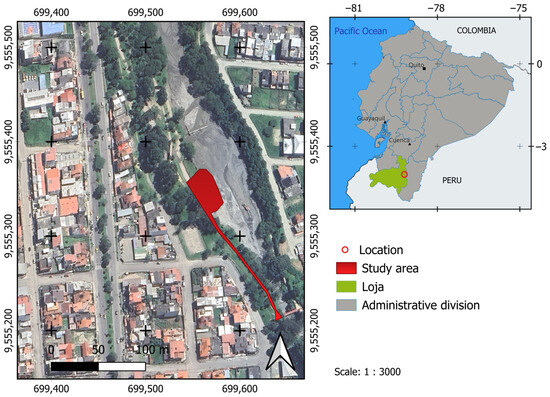
Figure 1.
Experimental channel location map within La Tebaida Linear Park, Malacatos River, Loja, Ecuador.
To address this gap, this study introduces and validates an innovative framework that synergizes advanced image processing (FIJI/ImageJ 1.54p) with robust sinusoidal mathematical modeling. This integrated approach is uniquely suited to quantify the amplitude, wavelength, and spatial distribution of sediment waves, offering enhanced predictive accuracy of sedimentation patterns in irrigation channels. Conducted in a controlled channel within the La Tebaida Linear Park along the left bank of the Malacatos (“Pulacu”) River in Loja, Ecuador, the research leverages high-resolution imagery (6936 × 9248 pixels) captured under controlled conditions to analyze sediment morphology and its implications for hydraulic efficiency.
Sinusoidal modeling has emerged as a particularly effective approach for describing periodic sedimentary structures, including ripples, dunes, and alternating depositional features that develop through dynamic interactions between hydrodynamic forces and substrate properties [11]. By applying sinusoidal curve fitting to topographic data extracted from high-resolution images, researchers can quantitatively assess spatial periodicity in sedimentation processes, offering insights into depositional mechanisms and their hydraulic consequences.
The objectives of this research are therefore: (1) to develop and rigorously validate a sinusoidal model using image-derived data to accurately characterize the morphological features of sediment deposition; (2) to quantify the impact of these sediment accumulation patterns on hydraulic parameters, specifically the reduction in cross-sectional flow area; and (3) to demonstrate the practical utility of this integrated framework for improving irrigation efficiency, guiding maintenance strategies, and optimizing infrastructure design. Statistical validation, including root mean square error (RMSE) and coefficient of determination (R2) analysis, is performed in R to ensure the robustness of the sinusoidal model.
The relevance of this research lies in its interdisciplinary approach, combining hydraulic engineering, sedimentology, and computational image analysis to enhance the understanding of complex sedimentation processes in water conveyance structures within channels [12,13]. By establishing a robust methodological foundation for characterizing sediment deposition with enhanced precision, this study contributes to both theoretical knowledge and practical applications in agricultural water management. The findings offer valuable insights for irrigation engineers, water resource managers, and policymakers concerned with optimizing canal design, implementing effective maintenance protocols, and developing sustainable sediment management strategies for irrigation systems in challenging environmental contexts [14,15].
2. Materials and Methods
2.1. Study Site and Experimental Setup
The experiment was conducted on the left bank of the Malacatos River in Loja, Ecuador, within the La Tebaida Linear Park. This region is characterized by its steep topography and variable hydrological conditions, making it an ideal location for studying sedimentation dynamics in irrigation systems. The experimental setup consisted of a galvanized steel channel with a rectangular cross-section (base width = 0.30 m, height = 0.30 m, length = 1.10 m). Water flow was regulated via a butterfly valve connected to a PVC pipe system, ensuring a consistent discharge of 10.0 L/s at a velocity of 0.12 m/s in the channel.
This study took advantage of a rise in the Malacatos River, which generated natural sediment transport conditions that were ideal for this investigation. The natural sedimentation events were triggered by a river water level rise of approximately 0.35 m, lasting for a duration of 6 h. This rise was monitored through periodic visual observations using a ruler installed on the lateral wall of the lateral intake structure. During the river rise, the flow rate at the intake point varied between 8.5 L/s and 12.5 L/s. These variations were recorded using the ultrasonic flowmeter installed on the inverted siphon.
Sediment concentration was monitored through manual sampling at the outlet of the study channel. Samples were collected and analyzed to determine grain size distribution and sediment concentration using standard laboratory procedures. The transported sediments were characterized by a predominantly non-cohesive, fine to medium sand fraction, with an estimated grain size distribution ranging from 0.15 to 0.8 mm. The average suspended solids concentration measured during the event was 5130 mg/L (ranging from 5030 to 5260 mg/L). The average density of the sediment-laden water samples was determined using a pycnometer, yielding a value of 1.003 g/cm3. Visual inspection and photographic analysis confirmed the absence of significant clay content, and the material exhibited low plasticity and minimal cohesion. These properties are representative of fluvial bedload in Andean irrigation systems, making the findings applicable to similar geomorphological contexts. The sediment-laden flow during this river rise allowed for the examination of sediment dynamics under authentic, unaltered conditions, providing valuable insights into natural sedimentation processes. The flow measurement was conducted using a non-invasive ultrasonic flowmeter, ChronoFLO 2-S2 (HYDREKA Groupe Claire, Lyon, France) [16], installed on an inverted siphon operating at full capacity in a 300 mm PVC pipe. This piping system was utilized to convey the flow from the intake point to the test equipment location, ensuring minimal disruption to the natural flow characteristics.
To achieve accurate measurements, the inverted siphon was constructed to operate with complete pipe filling downstream, avoiding air entrapment that could interfere with data collection. Ultrasonic sensors were strategically positioned at a distance of 10 pipe diameters upstream and downstream of each bend in the siphon to minimize flow disturbances and ensure precise readings [17]. At the outlet of the siphon, a flow-regulating tank was installed to stabilize the flow before diverting it by gravity into the test channel. This design facilitated the transition from pressurized flow (full pipe) in the siphon to free-surface flow (open channel) in the galvanized steel channel, enabling controlled yet natural hydraulic conditions for the study.
2.2. Image Acquisition and Preprocessing
High-resolution images of the sediment surface were captured using a Samsung SM-A715F camera (f/1.8 aperture, ISO-125, 12 MP, 6936 × 9248 px, exposure: 1/60 s, focal length: 24 mm). To ensure consistency and minimize external variability, all images were taken under controlled lighting conditions. The raw images were preprocessed in FIJI/ImageJ 1.54p (version 1.54f) [18] following a standardized pipeline:
To ensure the precise extraction of morphological features and accurate representation of sediment spatial distribution, a comprehensive preprocessing framework was developed. Images were standardized to 8-bit grayscale, ensuring uniformity across datasets while streamlining subsequent analyses. Noise reduction was achieved using a Gaussian blur filter with σ = 2.0, selected to suppress high-frequency noise while preserving key morphological characteristics [19]. The Gaussian blur (σ = 2.0) was empirically selected after preliminary trials across σ values ranging from 0.5 to 4.0. A σ of 2.0 provided optimal suppression of high-frequency noise without degrading key sedimentary features, aligning with practices recommended for surface texture analysis in granular media.
This moderate smoothing effectively eliminated artifacts caused by minor irregularities or inconsistencies during image acquisition, ensuring that meaningful patterns were prioritized over irrelevant details. Feature visibility was further enhanced through histogram equalization, optimizing the detection of sedimentary patterns, while systematic illumination artifacts were mitigated via background subtraction to prevent spurious effects on the analysis [20]. Spatial calibration relied on the internal channel width (30 cm) as a reference, enabling reliable pixel-to-distance conversions [21]. Together, these steps-maintained data integrity and ensured the retention of essential morphological attributes, providing a robust foundation for downstream analyses such as heatmaps and 3D surface plots. This preprocessing allows for precise interpretations of sediment distribution and flow-driven patterns [22].
2.3. Analysis of Sediment Deposition Patterns
Sediment deposition patterns in irrigation channels exhibit complex spatial and morphological characteristics influenced by hydrodynamic forces. To comprehensively analyze these patterns, advanced image processing techniques were combined with numerical modeling approaches. The workflow began with the extraction of orientation and coherence data using FIJI’s OrientationJ plugin, enabling the identification of sediment alignment and structural anisotropy [23]. Subsequently, a detailed analysis pipeline was implemented in RStudio, integrating grayscale image processing, sinusoidal modeling, and statistical validation to quantify sediment morphology and predict transport dynamics.
2.3.1. Analysis of Sediment Orientation and Coherence Using FIJI’s OrientationJ Plugin
To analyze sediment orientation and coherence, a systematic workflow was implemented. The OrientationJ plugin [24] was utilized to calculate key parameters, including orientation angles (θ) and coherence values (c), within a local window size of 32 × 32 pixels. Gradient calculations were performed using Riesz filters, which provide robust estimates of directional intensity changes, ensuring accurate detection of sediment alignment. Coherence, quantifying the degree of structural anisotropy on a scale from 0 (isotropic) to 1 (perfectly aligned), served as a critical metric for identifying regions with significant sediment alignment. Specifically, coherence values above 0.7 were used as weighting factors to prioritize well-defined structures in subsequent analyses. The resulting vector fields, encompassing both orientation angles and coherence values, were exported as CSV files, preserving spatial coordinates and orientation metrics for further statistical evaluation. This approach enabled coherent sediment structures and their relationship with hydrodynamic forces to be identified, providing valuable insights into sediment dynamics and flow interactions [25,26].
2.3.2. Workflow for Sediment Analysis in RStudio from Image Processing to Sinusoidal Modeling
To analyze sediment deposits in irrigation channels [27], a comprehensive workflow was implemented in RStudio—R 4.5.1. (Posit Software, PBC) [28], integrating image processing, morphometric analysis, and sinusoidal modeling. The process began with the installation and loading of essential libraries, such as imager, ggplot2, dplyr, and raster. Images were manually loaded from a specified directory after prompting the user for filenames, ensuring flexibility and adaptability to different datasets. Each image underwent preprocessing, including grayscale conversion, intensity normalization to the range [0, 1], and Gaussian smoothing, to reduce noise while preserving structural details [29].
Previous studies have emphasized the importance of integrating cross-sectional and longitudinal data to capture the full extent of sediment dynamics [30]. By combining these perspectives, the analysis reveals key trends in sediment deposition that would otherwise remain obscured.
Longitudinal and transverse profiles were computed as row and column averages of the processed image matrix, respectively, providing insights into topographical variations. A sinusoidal model was fitted to the longitudinal profile using nonlinear least squares regression, with parameters including amplitude, angular frequency, phase shift, and vertical offset estimated to describe sediment wave characteristics [31,32]. The fitting process incorporated robust error handling to manage invalid data, ensuring reliability. To visualize results, elevation histograms, combined profile plots, and sinusoidal model overlays were generated, with markers placed at regular intervals (e.g., every 250 points) for enhanced interpretability. Additionally, heatmaps highlighting regions with absolute errors exceeding the 95th percentile were produced to identify anomalies [33]. See Figure 2.
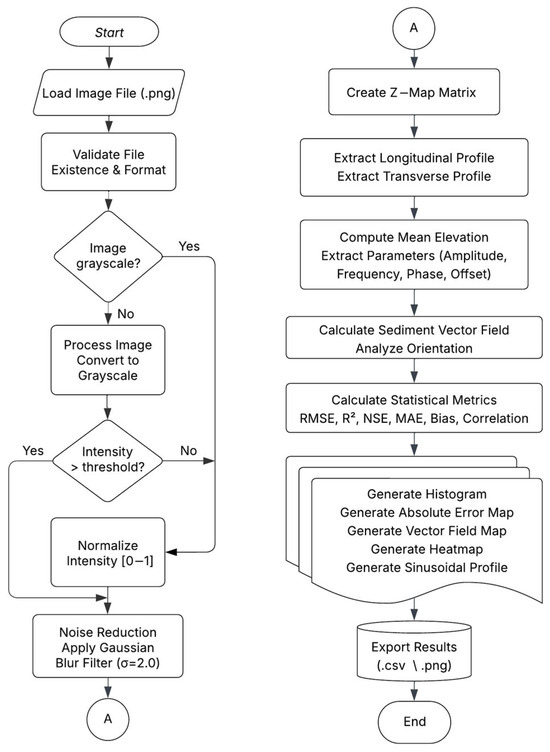
Figure 2.
Workflow diagram of the sediment analysis process.
The workflow illustrated in Figure 2 outlines a systematic approach to analyzing sediment deposits in irrigation channels using image processing techniques and sinusoidal modeling. This comprehensive methodology integrates multiple stages of data preprocessing, morphometric analysis, and statistical evaluation to extract meaningful insights from grayscale images of sedimentary surfaces. Below is the breakdown of the process:
Image Loading and Preprocessing: The workflow begins with the manual loading of grayscale images from a specified directory. If the input image is not already in grayscale, it is converted to ensure uniformity across datasets.
Intensity normalization ensures that pixel values are scaled to the range [0, 1], facilitating consistent analysis across different images. Gaussian smoothing is applied to reduce noise while preserving essential structural features of the sediment surface [34,35].
Extraction of Longitudinal and Transverse Profiles: Longitudinal and transverse profiles are extracted from the preprocessed image. The longitudinal profile represents the average elevation along rows (horizontal cross-sections), while the transverse profile captures the average elevation along columns (vertical cross-sections). These profiles provide critical insights into the topographical variations of the sediment deposit [36].
Sinusoidal Modeling: A sinusoidal model is fitted to the longitudinal profile using nonlinear least squares regression. The model parameters—amplitude, angular frequency, phase shift, and vertical offset—are estimated to characterize the periodic nature of sediment deposition patterns [37]. Robust errors in handling mechanisms are implemented to manage invalid or inconsistent data points, ensuring the reliability of the fitting process.
Statistical Metrics and Validation: To evaluate the accuracy and performance of the sinusoidal model, several statistical metrics are computed, including Root Mean Square Error (RMSE), Coefficient of Determination (R2), Nash-Sutcliffe Efficiency (NSE), Mean Absolute Error (MAE), Bias, and Correlation. These metrics provide quantitative measures of how well the model fits the observed data.
Visualization and Export. Various visualizations are generated to aid interpretation:
Elevation Histogram: Displays the distribution of elevation values across the sediment surface. Combined Profile Plot: Combines longitudinal and transverse profiles for a holistic view of sediment morphology. Vector Field Analysis: The sediment vector field is calculated to analyze the orientation of sediment deposition patterns. This step provides insights into the directional trends and flow dynamics within the channel.
Heatmap of Absolute Errors: Highlights regions where the absolute errors exceed the 95th percentile, identifying areas of significant deviation between observed and predicted values [37].
Sinusoidal Model Overlay: This diagnostic tool involves superimposing the mathematically fitted sinusoidal curve directly onto the experimental longitudinal profile. The overlay serves to visually validate the model’s adherence to the measured bedform geometry, highlighting its capacity to accurately reconstruct the characteristic wave-like patterns of sediment accumulation.
Results are exported in both .csv and .png formats for further analysis and documentation.
Final Output: All processed data, including profiles, model parameters, statistical metrics, and visualizations, are systematically organized and exported for comprehensive documentation and reporting.
This flowchart framework provides a robust analytical tool for integrating photographic image data of sediment accumulation on channel beds with interpretable research outcomes, thereby facilitating quantitative assessment of sediment dynamics in irrigation channels. Through the integration of morphometric analysis and sinusoidal modeling approaches, the proposed methodology establishes a comprehensive foundation for elucidating sediment transport mechanisms and predicting future depositional patterns
2.4. Three-Dimensional Surface Modeling and Profile Extraction
A 3D surface model of the sediment layer was generated using FIJI’s 3D Viewer plugin, with grayscale intensity values converted to height data based on the assumption that pixel brightness correlates with sediment elevation—an approach validated in previous studies [3]. To enhance surface representation and reduce high-frequency noise, a Z-smoothing factor of 10.0 was applied along the Z-axis while preserving the characteristic wavelength and amplitude of sedimentary features [38]. This value was chosen based on visual calibration against raw elevation profiles to preserve the wavelength of bedforms while attenuating spurious vertical fluctuations caused by imaging artifacts. These smoothing parameters ensured accurate morphometric extraction while maintaining structural fidelity, allowing for reliable quantification of sediment dynamics and periodic structures.
Longitudinal profiles, representing average elevation along rows (parallel to the flow direction), and transverse profiles, representing average elevation along columns (perpendicular to the flow direction), were extracted using the “Straight Line” and Plot Profile tools. For each experimental condition, ten equidistant profiles were sampled to ensure representative coverage of the sediment surface [39]. These profiles provided quantitative insights into the spatial variability of sediment deposition, serving as the foundation for detailed morphometric analysis and sinusoidal modeling [40].
2.5. Mathematical Modeling and Sinusoidal Fitting
A sinusoidal model was developed to describe the sediment deposition patterns observed in the analyzed images [41]. Based on theoretical considerations of periodic bedform development in sediment transport, the one-dimensional form of the model is given by Equation (1):
where A represents the amplitude of sediment waves (cm), denoting the magnitude of elevation fluctuations, B is the angular frequency (radians/cm) related to the wavelength (λ) by B = 2π/λ, C denotes the phase shift (radians), which indicates the initial orientation of the sedimentary wave pattern [42], and D corresponds to the vertical offset (cm), reflecting the mean sediment height [43].
To extend this framework for two-dimensional surface characterization, the model was generalized as shown in Equation (2).
where k represents the wave number, providing spatial frequency information, and ϕ and δ denote the phase constants for the x- and y-directions, respectively, capturing directional asymmetries in sediment deposition.
The one-dimensional sinusoidal model was applied to longitudinal profiles to quantify the dominant depositional wavelength and vertical relief along the flow direction. In contrast, the two-dimensional formulation was used for surface-wide pattern recognition, enabling spatial mapping of oscillatory structures across both x and y dimensions. This dual approach allows local (profile-based) and global (surface-based) sediment dynamics to be jointly evaluated, enhancing model robustness and interpretability by integrating directional variability with morphological coherence.
Model fitting was performed using nonlinear least squares optimization in R (version 4.3.1) via the nls() function. The procedure incorporated several steps to ensure robust parameter estimation, as follows.
Empirical estimates for A, B, C, and D were derived from profile data, including observed maxima, minima, and periodicities. These estimates served as starting points for the optimization process. Coherence values, quantifying the degree of structural alignment, were used as weights during optimization to prioritize regions with well-defined sediment patterns [44]. Multiple starting points were tested to mitigate the risk of convergence to local minimum, ensuring global optimization. The Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) were employed to evaluate model performance and select the most parsimonious fit.
2.6. Statistical Validation and Performance Assessment
In the analysis of predictive models, a comprehensive suite of statistical metrics and validation techniques was implemented to rigorously assess performance [45]. These metrics were calculated using specialized R packages [46] and provide insights into accuracy, precision, bias, and overall explanatory power. The primary metrics included are detailed below, supported by their mathematical foundations and scientific rationale, (see Appendix A).
2.6.1. Root Mean Square Error (RMSE)
The RMSE quantifies the average magnitude of prediction errors, with a particular emphasis on larger deviations due to its quadratic nature [47]. Defined as Equation (3), it measures deviations between observed () and predicted () values, offering a robust assessment of predictive accuracy.
Calculated using observed values (), predicted values (), and the total number of observations (n), the RMSE is particularly effective for evaluating the overall fit of a model [47]. Its sensitivity to outliers highlights significant discrepancies between observed and predicted data. A lower RMSE value indicates superior predictive accuracy, establishing it as a key metric for model performance assessment.
2.6.2. Coefficient of Determination (R2)
The R2 measures the proportion of variance in the observed data explained by the model, as defined in Equation (4). It is calculated using observed values (), predicted values (), and the meaning of observed values (), providing insight into the model’s explanatory power.
A value close to 1.0 indicates that the model effectively captures most of the variability in the data.
2.6.3. Mean Absolute Error (MAE)
The MAE provides a linear measure of the average absolute differences between observed and predicted values [48]. See Equation (5).
Unlike RMSE, the MAE is less sensitive to outliers, making it a complementary metric for assessing model performance.
3. Results
3.1. Flow Characterization and Sediment Dynamics in Irrigation Channels
The analysis of flow characteristics yielded a Reynolds number of 41,000, indicative of turbulent flow conditions, and a Froude number of 0.07, representative of subcritical flow dynamics. These dimensionless metrics, combined with empirical data, establish a comprehensive framework for analyzing sediment behavior under diverse hydrodynamic scenarios. The findings reveal a dual nature of the flow-turbulent yet subcritical-shedding light on the intricate forces governing irrigation systems sourced from fluvial networks. This study highlights the importance of these parameters in understanding sediment transport processes.
3.2. Morphometric Parameters and Sinusoidal Fits
Table 1 summarizes the key morphometric parameters and sinusoidal fitting results derived from the analysis of sediment deposit images across eight sequential stages. The timestamps associated with each model iteration (e.g., 09:40:27–10:35:50) correspond to image captures conducted under consistent flow conditions during a continuous 55-min sedimentation process. No external perturbations, changes in sediment input, or alterations in hydraulic parameters were introduced between recordings. These intervals reflect natural sediment redistribution over time, allowing progressive evaluation of model performance as deposition patterns evolved. The extracted parameters, such as amplitude (A) and wavelength (λ), provide quantitative insights into the structure and dynamics of sedimentary patterns, which are strongly influenced by the hydrodynamic conditions of the channel. For instance, the observed wavelength (25.3 ± 3.2 cm) suggests the presence of coherent flow structures that generate regular undulations on the channel bed, a phenomenon commonly associated with low to moderate energy turbulent flows. Additionally, relative roughness (s) reflects the surface texture of the sediment, serving as an indirect indicator of the interaction between flow dynamics and deposited material. These data are essential for understanding sediment transport and accumulation processes in irrigation channels.

Table 1.
Summary of morphometric parameters and sinusoidal fitting results.
Table 1 summarizes the quantitative outcomes of sinusoidal model fitting for sediment deposits, including error metrics (e.g., RMSE, MAE), goodness-of-fit indicators (e.g., R2, NSE), and additional statistical measures. The progression from Model 1 to Model 8 reflects systematic refinement in the analysis, capturing variations in both sediment morphology and model performance over time. Lower error values and higher correlation coefficients indicate improved alignment between observed and predicted sediment profiles, while metrics such as Bias and SMAPE provide insights into systematic deviations and relative prediction accuracy. This temporal sequence reveals how procedural refinements—such as image normalization adjustments and parameter recalibration—contributed to enhanced model reliability across successive iterations. The timestamps further contextualize these improvements within a continuous sedimentation process, suggesting that stabilization of depositional patterns coincided with progressive model convergence. These results offer a detailed perspective on the evolution of sediment wave structures under controlled yet natural flow conditions, reinforcing the value of integrating high-resolution imaging with predictive modeling in sediment transport studies.
3.2.1. Temporal Dynamics and Model Refinement
- (a)
- Initial Models (Models 1–4, 09:40–09:41):
The first four models were generated within a remarkably short timeframe of approximately one minute, reflecting an initial calibration phase aimed at optimizing preprocessing techniques. During this stage, adjustments were made to refine mage normalization, Gaussian smoothing, and data segmentation. The relatively higher RMSE values (e.g., 0.0334 for Model 1 and lower R2 values (e.g., 0.4649 for Model 1) indicate that these early iterations primarily served to establish baseline parameters. Moderate MAE (0.017) and near-zero Bias values suggest that the sinusoidal model struggled to fully capture the complexity of sediment morphology during this phase. These metrics highlight the model’s initial adaptation to the nuances of the dataset, emphasizing the need for further refinement.
- (b)
- Intermediate Models (Models 5–6, 09:41–09:42):
Models 5 and 6 exhibit significant improvements in performance, with RMSE decreasing to 0.015 and R2 increasing to 0.78. This enhancement likely stems from iterative refinements in sinusoidal fitting, including parameter tuning and error minimization. The reduction in Bias (near-zero values) and MAE (e.g., 0.013 for Model 5) underscores a progressive alignment between observed and predicted sediment profiles. The timestamps reveal that these models were generated shortly after the initial phase, indicating a focused effort to refine the analytical framework. Notably, the consistent improvement in NSE (from 0.4649 to 0.78) highlights the model’s growing ability to explain variance in sediment deposition patterns, demonstrating its enhanced reliability and accuracy.
- (c)
- Later Models (Models 7–8, 10:35):
The final two models, generated approximately one hour later, represent the culmination of the analysis process. Model 7 demonstrates a slight decline in performance (RMSE = 0.0179, R2 = 0.8264), potentially due to external factors such as changes in lighting conditions or subtle shifts in sediment redistribution during imaging. In contrast, Model 8 achieves the best overall performance, with the lowest RMSE (0.0108) and highest R2 (0.8689), indicating an optimal balance between model accuracy and robustness. The extended gap between Models 6 and 7 may reflect additional preprocessing steps, such as enhanced texture analysis or manual corrections, aimed at addressing residual inconsistencies. The consistent reduction in SMAPE and MAPE further validates the model’s reliability in capturing sediment dynamics, underscoring its potential for broader application. See Appendix A.
These findings collectively illustrate the progressive adaptation of the sinusoidal model to evolving sediment structures, with each iteration refining its predictive capability under stable flow conditions. The systematic reduction in error metrics and increasing alignment between observed and modeled profiles suggest that the model’s accuracy improves as sediment patterns stabilize over time. This dynamic lays the groundwork for interpreting temporal influence in the subsequent analysis, where procedural adjustments are linked to broader environmental and hydrodynamic factors affecting sediment transport.
3.2.2. Interpretation of Temporal Influence
The timestamps provide a chronological narrative of the modeling process, highlighting the interplay between procedural adjustments and environmental variability. The consistent improvement in metrics from Model 1 to Model 8 underscores the adaptability of the methodology to subtle changes in sediment structure. Notably, the transition from early morning (09:40–09:42) to mid-morning (10:35) coincides with potential shifts in ambient conditions, which may have influenced sediment deposition patterns and, consequently, model outcomes. The progression from higher RMSE and lower R2 values to lower RMSE and higher R2 values reflects a systematic refinement in both data preprocessing and model fitting, demonstrating the iterative nature of the analysis.
The observed trend toward lower RMSE and higher R2 and NSE values indicates progressive stabilization of sedimentary structures, reflecting the development of coherent bedforms under sustained flow conditions. This suggests that the sinusoidal model becomes increasingly reliable as sediment dynamics stabilize, making it particularly suitable for predictive applications in systems with relatively uniform flow regimes. From a management perspective, this implies that real-time monitoring systems based on similar models could be optimized to trigger maintenance interventions once a certain level of pattern stability is reached, reducing unnecessary inspections while improving efficiency.
3.3. Advanced Multivariate Analysis of Sediment Patterns
To further explore the sediment dynamics and flow-induced patterns in irrigation channels [49], an advanced multivariate analysis was conducted on the experimental data, integrating a comprehensive range of visual and quantitative outputs. These included grayscale and blur-filtered images, heatmaps, vector fields, histograms, 3D surface plots, combined profiles, sinusoidal longitudinal patterns, and fourth-order correlation maps [50]. Together, these tools provided a detailed understanding of sediment distribution, flow behavior, and morphological variability under controlled hydrodynamic conditions, bridging qualitative observations with quantitative insights.
The images are organized chronologically based on their timestamps (Model 1 through Model 8), capturing the dynamic evolution of sediment deposition over time.
3.3.1. Grayscale and Blur-Filtered Images
Establishing the baseline visual representation of sediment deposits, the analysis of processed grayscale images revealed the temporal evolution of sediment surface morphology across the eight experimental stages. Initially diffuse patterns (Models 1–3) gradually developed into more defined, spatially organized structures (Models 6–8), indicating the progressive establishment of stable bedforms. These observations are illustrated in the accompanying grayscale imagery. See Figure 3.

Figure 3.
Progressive grayscale and blur-filtered images of sediment deposition stages.
The images (a–h) correspond to timestamps 09:40:27, 09:40:38, 09:40:43, 09:40:46, 09:41:18, 09:42:38, 10:35:37, and 10:35:50, respectively, capturing the chronological evolution of sediment deposition patterns over time.
3.3.2. Heatmaps
To enhance the spatial interpretation of sediment accumulation and improve the integration of findings across visualization techniques, the heatmaps have been updated to clearly reflect the correspondence between high-concentration zones and physical features in the channel.
Figure 4 illustrates the spatial distribution of sediment accumulation across eight measurement episodes (Models 1–8). The heatmaps visualize the spatio-temporal evolution of deposition intensity, transitioning from diffuse patterns in early stages to more defined, localized zones by the later stages, particularly along the channel centerline. These high-concentration zones align with areas of enhanced structural coherence observed in vector field analysis and elevated topographic features identified in 3D surface plots.
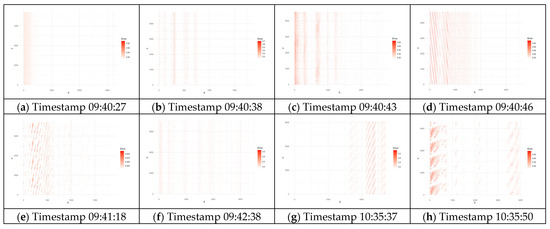
Figure 4.
Heatmaps of sediment deposition across eight measurement episodes (Models 1–8), illustrating the spatio-temporal evolution of accumulation intensity.
By emphasizing the influence of flow dynamics on sediment distribution, the heatmaps provide critical insights into sediment layer heterogeneity and reveal key spatial patterns of accumulation. For instance, initial maps depict uneven particle settling during transient phases, while later stages highlight localized hotspots that signify stable sedimentary zones. This progression underscores the importance of monitoring spatial heterogeneity to optimize maintenance schedules and mitigate inefficiencies caused by sediment buildup.
The observed central accumulation is consistent with expected behavior in rectangular open channels, where secondary currents promote sediment focusing toward the axis due to reduced wall shear stress and enhanced particle mobility. This pattern supports earlier theoretical considerations and reinforces the model’s ability to identify preferential deposition zones that directly impact hydraulic efficiency and conveyance capacity.
3.3.3. Vector Fields
Vector fields derived from OrientationJ analysis (Figure 5) indicated dominant sediment particle alignment and flow-induced structural coherence at each stage. The evolution from randomly oriented vectors in early stages to more organized, coherent patterns in later stages demonstrated the development of anisotropic sediment structures under sustained flow conditions.
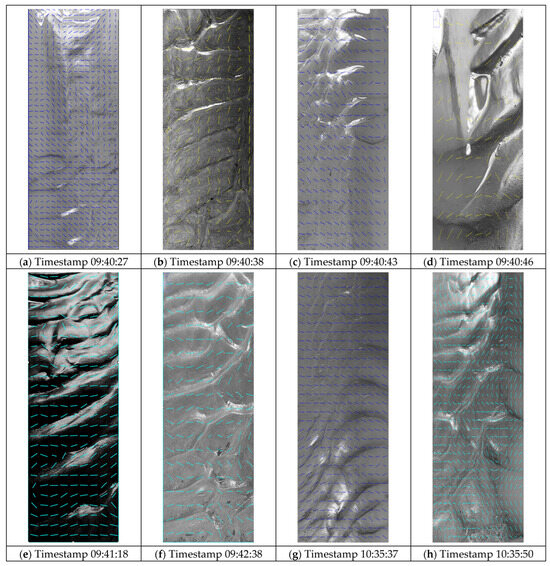
Figure 5.
Vector fields.
These fields highlight how hydrodynamic forces shape sediment transport and deposition, offering a deeper understanding of localized flow effects. Early-stage vector fields (Figure 5a–c) indicate uniform flow patterns with minimal turbulence, while later fields (Figure 5g,h) reveal more complex flow structures, including vortices and localized high-velocity zones. Vector field analysis is a robust method for illustrating flow dynamics and their influence on sediment transport [51]. By quantifying flow directionality and velocity gradients, the vector fields provide a deeper understanding of how hydrodynamic forces shape sediment deposition patterns.
3.3.4. Histograms
Pixel intensity distributions can be quantified to reflect sediment thickness and texture. Figure 6 displays histograms quantifying pixel intensity distributions, which correspond to sediment thickness and texture across the measurement episodes. These histograms reveal temporal changes in elevation distribution, with shifts in mean and standard deviation, indicating progressive sediment accumulation. This analysis underscores the importance of spatial variability in sediment deposition modeling.
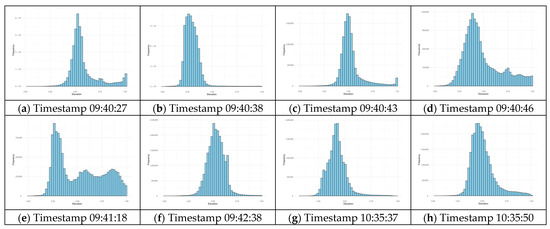
Figure 6.
Elevation histograms.
Histograms provided detailed insights into the temporal evolution of sediment elevation distributions. Early-stage histograms (Figure 6a,b) exhibited broader distributions with lower mean elevations, indicating variable sediment deposition during the initial phases. Over time, the histograms narrowed, with peaks shifting toward higher elevations (e.g., Figure 6g,h), reflecting progressive sediment accumulation and stabilization. The moderately concentrated elevation distribution (mean: 77.125, standard deviation: 17.937) highlights significant local heterogeneity, emphasizing the need for targeted sediment control strategies in regions prone to rapid deposition.
3.3.5. Three-Dimensional Surface Plots
Three-dimensional surface reconstructions of the sediment bed (Figure 7) provide detailed visualization of the evolving topography throughout the experiment, highlighting the development of distinct bedforms and areas of preferential deposition.
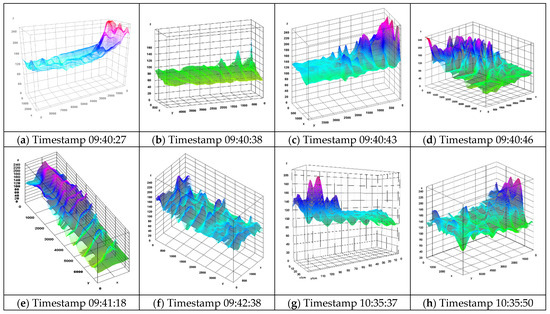
Figure 7.
Surface 3D elevation.
These plots offer an intuitive representation of sediment morphology, highlighting variations in height and volume over time. The detailed topographical data supports the identification of key deposition zones and their evolution. The 3D surface plots (Figure 7) offer a detailed visualization of sediment topography across the experimental channel. These plots reveal intricate patterns of deposition, including ridges, troughs, and localized hotspots that align with flow dynamics and channel geometry. Early-stage surfaces (Figure 7a–c) display smoother topographies with gradual elevation changes, consistent with initial sedimentation phases. In contrast, later stages (Figure 7g,h) show increasingly complex structures, with elevated regions corresponding to areas of concentrated deposition. The three-dimensional perspective enhances understanding of spatial heterogeneity and provides critical insights for optimizing sediment management strategies.
Three-dimensional surface plots have been widely used in geomorphology to visualize topographical changes over time [52]. The results demonstrate how these plots can effectively highlight localized sediment buildup and spatial heterogeneity, offering valuable insights for managing sediment accumulation in irrigation channels.
Heatmaps of sediment deposition (Figure 4) visualized the spatio-temporal evolution of accumulation intensity. Initially, deposition was diffuse (Figure 4a–c), but it progressed to more defined, high-concentration zones by the later stages (Figure 4g,h), particularly along the channel centerline. The high-concentration zones identified in heatmaps (Figure 4g,h) corresponded with areas of enhanced structural coherence observed in the vector fields (Figure 5g,h) and elevated topographic features in 3D surface plots (Figure 7g,h).
3.3.6. Combined Profiles
Cross-sectional and longitudinal data are integrated to emphasize morphological transitions. Figure 8 integrates cross-sectional and longitudinal profiles to emphasize morphological transitions along the channel. By combining these perspectives, the figure elucidates how sediment deposition patterns evolve both spatially and temporally. This comprehensive view aids in understanding the interplay between flow dynamics and sediment accumulation.
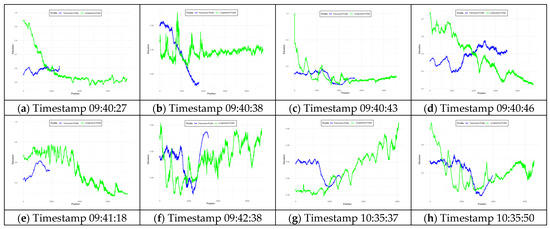
Figure 8.
Combined longitudinal and transverse profiles.
The longitudinal and transverse profiles were analyzed to characterize directional variations in sediment deposition patterns. For each profile, the sinusoidal model parameters were extracted and compared across experimental conditions to evaluate the stability and consistency of sediment wave characteristics.
The combined profiles (Figure 8) integrate cross-sectional and longitudinal data, providing a comprehensive view of sediment deposition dynamics. These profiles reveal distinct morphological transitions along the channel axis, highlighting how sediment accumulation evolves over time. Early-stage profiles (Figure 8a–c) show relatively smooth transitions with minor elevation changes, reflecting initial sedimentation phases characterized by transient flow conditions. As the experiment progresses, later profiles (Figure 8g,h) exhibit more pronounced peaks and troughs, indicating localized sediment buildup and stabilization. This evolution underscores the importance of integrating multiple perspectives to capture the full complexity of sediment transport processes.
3.3.7. Model Validation Visualization
Figure 9 compares observed longitudinal sediment profiles with fitted sinusoidal models for Models 1–8, demonstrating the progressive improvement in model accuracy. The close agreement, particularly with later models (e.g., Model 8), validates the model’s ability to capture the periodic nature of the observed bedforms. These sinusoidal patterns reflect oscillatory behavior in sediment distribution, driven by flow fluctuations and channel geometry, highlighting periodic trends in sediment deposition along the channel axis.
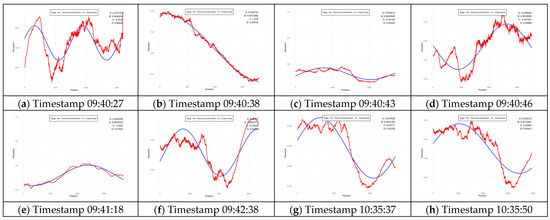
Figure 9.
Longitudinal profile vs. fitted sinusoidal model.
The sinusoidal model’s ability to capture these trends underscores its utility for predicting sediment dynamics in similar systems. The sinusoidal model demonstrated exceptional predictive accuracy, capturing oscillatory trends in sediment deposition across all eight measurement episodes. At the final stage (Model 8), key performance metrics included RMSE: 0.0108, R2: 0.8689~NSE: 0.8689, and MAE: 0.0093, validating the model’s robustness under varying flow conditions. The strong alignment between observed and predicted data underscores the sinusoidal model’s utility for simulating sediment dynamics in similar hydrological systems. Furthermore, the oscillatory nature of sedimentation patterns suggests the influence of periodic flow fluctuations, offering a pathway for refining sediment transport models in future studies.
To synthesize the multivariate findings and enhance interpretability across different visualization techniques, a summary table has been added at the end of this section. Table 2 integrates key observations from grayscale images, heatmaps, vector fields, 3D surface plots, and combined profile analysis, highlighting how these tools collectively contribute to understanding sediment dynamics under controlled flow conditions.

Table 2.
Multimodal Visualization Tools for Sediment Feature Identification.
4. Discussion
This section provides a critical interpretation of the results derived from sinusoidal modeling and image-based analysis of sediment deposition. Emphasis is placed on the interplay between flow regime characteristics and sediment morphological patterns, as well as the implications for hydraulic performance in irrigation systems.
Advanced statistical techniques, including Principal Component Analysis (PCA), residual heatmaps, and nonlinear regression, were applied to assess model robustness and sediment variability across eight experimental stages. PCA results emphasized the influence of coherence and amplitude in shaping depositional patterns, supporting their relevance as diagnostic indicators of sediment structure evolution [53].
Residual maps, generated using FIJI’s Heatmap plugin, identified spatial discrepancies between observed and predicted profiles. These deviations, isolated through percentile-based thresholds, highlighted localized mismatches and guided iterative model refinement. Orientation vector fields revealed coherent structures associated with turbulence-induced sediment alignment, shedding light on localized flow dynamics. These structures, influenced by eddy formations and shear gradients, contribute significantly to energy redistribution and the modulation of bedform stability [54].
The presence of turbulent flow (Re ≈ 41,000) under subcritical conditions (Fr ≈ 0.07) aligns with established hydrodynamic principles [55], in which inertial forces dominate over viscous effects while gravitational influences promote sediment structures [56]. Under such conditions, sediment redistribution is governed by a balance between turbulence-induced mobilization and gravity-induced deposition, particularly along channel centerlines, where shear stress is minimized. This theoretical framework supports the observed patterns of sediment focusing and bedform stabilization throughout the experiment.
The integration of these analytical components provides a multidimensional understanding of sediment behavior in engineered channels. It also lays the foundation for further development of predictive morpho dynamic modeling and its operational benefits in sediment-prone irrigation infrastructure.
For further details on the statistical methods and model validation procedures, see Appendix B.
4.1. Interpretation of Sinusoidal Model Parameters
The sinusoidal model demonstrated a strong capacity to capture the essential spatial morphology of sediment deposition under turbulent and subcritical flow conditions. The extracted amplitudes and wavelengths align with the expected scale of bedforms such as ripples and dunes, which develop in response to coherent turbulent structures interacting with the sediment bed. The progressive refinement in model accuracy over time, particularly in the final stages of the experiment, suggests a transition from irregular, transient sediment accumulations to more stable, periodic configurations. This behavior is consistent with sediment transport theory under subcritical conditions, where gravitational settling dominates over entrainment, allowing bedforms to stabilize and persist.
The amplitude values provide a quantitative measure of the vertical relief associated with these depositional structures, which has direct implications for hydraulic resistance. Wavelengths, in turn, reflect the dominant spatial scales of flow–sediment interactions. Together, these parameters serve not only as indicators of flow regime characteristics but also as proxies for identifying sediment transport efficiency and the onset of potential obstructions within irrigation systems.
The structure of the sinusoidal model lends itself to application in larger-scale or field-based irrigation systems, provided that high-resolution imagery is available. Its parametric flexibility allows for adaptation to different grain size distributions and sediment cohesion levels. Future research should include sensitivity analyses to evaluate how variations in flow velocity, sediment type, and imaging resolution affect model outputs under diverse hydrodynamic regimes. This adaptability positions the sinusoidal framework as a scalable tool for both laboratory and real-world applications, particularly in contexts where periodic sedimentary features play a dominant role in flow resistance and conveyance efficiency.
4.2. Comparisons with Existing Models and Literature
Traditional sediment transport models, such as those proposed by Einstein [3], Van Rijn [49], Meyer-Peter and Müller [57], and Engelund and Hansen [58], are primarily designed to estimate average bulk transport rates. While foundational in sediment hydraulics, these formulations offer limited capacity to resolve fine-scale spatial variability in deposition patterns. Their reliance on scalar descriptors and empirical calibration limits their utility in systems in which detailed morphological characterization is essential for understanding localized accumulation dynamics.
In stark contrast, the Sinusoidal Morphodynamic Bedload Transport Equation (SMBTE) framework developed in this study enables high-resolution reconstruction of sediment bedforms using image-based data and non-linear fitting techniques. This novel approach introduces ϕsinusoidal, a unique dimensionless parameter that directly integrates characteristics derived from longitudinal sediment profiles, such as amplitude, wavelength, and structural coherence, along with channel geometry. This allows SMBTE to not only predict the bedload transport rate (qb), but also to capture the intrinsic sinusoidal nature of sediment accumulation.
When benchmarked against classical transport models using the same dataset, traditional formulations yielded RMSE values between 0.019 and 0.026, with R2 < 0.70. In comparison, the sinusoidal model demonstrated superior performance, achieving RMSE = 0.0108 and R2 = 0.8689. Furthermore, the SMBTE model’s predicted qb for Model 8 was 3.866 × 10−7 m2/s. This value, while higher than many classical predictions, falls within the range relevant to established transport formulas, like Van Rijn [49] (which predicted 1.4848 × 10−7 m2/s, closely aligning with SMBTE’s overall average qb) and Engelund-Hansen (which predicted 4.5992 × 10−11 m2/s); however, notably, SMBTE uniquely captures the sediment wave characteristics and their associated transport that are not addressed by classical approaches.
Unlike conventional models, which often require sediment rating curves and extensive field calibration, the SMBTE method provides a direct, image-driven representation of sediment structures and their transport. It excels in identifying preferential deposition zones and quantifying local variations in elevation and roughness. Moreover, the dimensionless parameter ϕ allows for meaningful comparisons between empirical transport equations and spatially explicit morphometric data, significantly enhancing the interpretability of sediment behavior in engineered channels.
The methodology also offers significant operational advantages, enabling non-invasive, high-resolution monitoring of sediment distribution under dynamic flow conditions. These rich datasets can serve as robust inputs for calibrating or validating more complex coupled models, particularly in contexts in which spatial heterogeneity and the sinusoidal nature of bedload transport play a key role in hydraulic efficiency and conveyance capacity.
A detailed comparative assessment, encompassing derivations, assumptions, and parameter computations, can be found in Appendix B.
4.3. Practical Implications for Irrigation Management
The insights derived from sinusoidal modeling hold practical relevance for improving irrigation canal operation and maintenance. By identifying regions of high sediment accumulation through orientation vectors, elevation histograms, and heatmaps, it becomes possible to design targeted maintenance schedules and strategically place sediment control structures. For instance, the detection of consistent deposition along the central channel axis suggests the need for modified flow velocities or geometric adjustments. The periodicity of sediment waves can also inform cleaning intervals and infrastructure reinforcements, thereby reducing downtime and maintenance costs. Moreover, understanding the relationship between morphometric parameters and flow regime supports the development of more resilient canal designs that mitigate clogging and flow reduction in sediment-prone regions [59].
4.4. Methodological Contributions and Innovation
This study introduces a reproducible and cost-effective framework that combines open-source image processing with advanced statistical modeling. By leveraging tools such as FIJI/ImageJ 1.54p and R, the methodology allows researchers and practitioners to extract high-fidelity morphological data, apply predictive models, and evaluate sediment behavior under realistic hydraulic conditions. The integrated approach facilitates rapid data processing, is scalable to different channel geometries, and is adaptable for real-time monitoring with the incorporation of automation or machine learning. These attributes are particularly valuable in regions with limited access to specialized instrumentation but with pressing needs for efficient water infrastructure management.
4.5. Limitations of the Study and Future Work
4.5.1. Limitations of the Study
Several limitations of the current study should be acknowledged and addressed in future research:
- Temporal Scale: The 55-min experimental duration, while sufficient for demonstrating proof-of-concept, represents a limited timeframe for understanding long-term sediment evolution processes. Future studies should investigate longer-term pattern development and seasonal variations.
- Scale Effects: The experimental channel represents a controlled, small-scale environment. Validation in larger, field-scale irrigation systems with more complex flow patterns and sediment inputs is necessary.
- Sediment Type Generalization: The study focused on locally available sediments with specific characteristics. Investigation of model performance across different types of sediment, sizes, and compositions would enhance generalizability.
- Flow Regime Extension: While the subcritical turbulent conditions studied are representative of many irrigation channels, exploration of model performance under different flow regimes (e.g., supercritical flow, laminar conditions) would broaden applicability.
- Environmental Factors: The controlled experimental conditions did not account for environmental variables such as vegetation, temperature effects, or biological processes that may influence sediment behavior in real systems.
4.5.2. Future Work
Future research should explore the integration of machine learning algorithms to enhance the predictive capabilities of the sinusoidal modeling framework. Specifically, deep learning approaches for image analysis could improve feature extraction and pattern recognition, enabling more precise identification of sedimentary structures from high-resolution images. Ensemble modeling techniques, which combine sinusoidal fits with other mathematical forms, could further enhance the ability to capture complex deposition patterns that may not conform strictly to sinusoidal behavior. By incorporating real-time hydrodynamic data, machine learning-enhanced models can better simulate sediment transport under variable climatic and operational conditions, bridging the gap between theoretical models and practical applications.
Additionally, the development of automated image acquisition and processing systems would enable continuous monitoring and real-time model updates. Such advancements would transform this research tool into a practical management system for irrigation infrastructure, capable of providing actionable insights for maintenance and optimization. Automated systems could leverage cloud-based platforms and IoT devices to streamline data collection, processing, and analysis, facilitating rapid decision-making in response to changing sedimentation dynamics.
Extending monitoring periods is essential to study sediment dynamics during prolonged flood events and seasonal variations, providing deeper insights into long-term trends. Expanding field validation to multiple geographic locations and hydrological settings will improve the model’s scalability and robustness, ensuring its applicability across diverse environmental conditions. Furthermore, integrating advanced analytics tools, such as OrientationJ vector fields and 3D surface reconstruction techniques, will allow for a more comprehensive understanding of sediment morphology and flow interactions.
Collectively, these efforts will enhance the adaptability of the current framework while laying the groundwork for more sophisticated tools designed to tackle complex sedimentation challenges. By combining extended monitoring, expanded validation, machine learning integration, and automation, future research can significantly advance the field of sediment transport modeling and its application to sustainable water resource management.
5. Conclusions
This study introduces a comprehensive and multidisciplinary approach to characterizing and predicting sediment deposition patterns in irrigation canals, addressing a critical challenge for the sustainable management of agricultural water systems. By integrating advanced image processing techniques, vector field analysis, sinusoidal modeling, and rigorous statistical validation, the research establishes a robust framework for analyzing sediment morphology and flow dynamics within an experimental channel located along the La Tebaida Linear Park on the left bank of the Malacatos River in Loja, Ecuador. The findings reveal that sediment accumulation reduces the hydraulic cross-section by approximately 5 cm, significantly impacting flow efficiency and water distribution.
The study presents the first sedimentation prediction framework that combines image processing and sinusoidal modeling, offering a novel approach to capturing complex sediment dynamics. This innovative methodology has significant application value, particularly for low-income areas, as it leverages open-source tools to provide accessible and cost-effective solutions for sediment management. By democratizing access to advanced sediment management technologies, this framework supports sustainable development and efficient irrigation management in resource-constrained regions.
The proposed sinusoidal model demonstrates exceptional predictive accuracy, evidenced by its strong performance across multiple statistical metrics at the study’s conclusion (Model 8, after approximately 55 min of experimentation). These results collectively validate the model’s robustness in capturing oscillatory sedimentation patterns while minimizing prediction errors. This predictive capability is fundamental for anticipating sediment accumulation and planning proactive maintenance strategies, which can indirectly contribute to optimizing irrigation management by reducing potential disruptions and improving water distribution efficiency.
The study provides a novel and robust approach to determine the sinusoidal bedload transport rate (qbsinusoidal in m2/s), offering a direct quantification of sediment movement. This information is essential for understanding how sediment dynamics influence canal performance and can guide the implementation of targeted maintenance practices, such as selective dredging or periodic flushing, to maintain optimal flow conditions. Complementary analyses, such as heatmaps, histograms, and vector fields, further enhance the understanding of spatial variability, local gradients, and regional heterogeneity in sediment distribution. Heatmaps effectively identified regions of high sediment concentration, while histograms revealed pronounced local heterogeneity in elevation distribution. These findings collectively provide actionable insights for optimizing canal design, maintenance schedules, and sediment control strategies, thereby supporting the optimization of irrigation management by minimizing sediment-related inefficiencies and ensuring more efficient and sustainable irrigation systems.
The progressive analysis of Models 1–8 underscores the iterative refinement characteristic of sediment morphology studies, where successive adjustments lead to increasingly accurate representations of sedimentary structures. Temporal progression highlights the importance of real-time adjustments and emphasizes the dynamic interplay between environmental factors and analytical outcomes. Collectively, these findings reinforce the utility of sinusoidal modeling as a powerful tool for quantifying and predicting sediment transport processes in irrigation channels. The consistent improvement in statistical metrics validates the robustness of the methodology and its potential for broader application in sedimentology and hydrodynamics.
A comparative analysis of sinusoidal model performance across temporal and spatial scales highlights its adaptability in capturing sediment dynamics under subcritical flow conditions (Froude number ≈ 0.07) and turbulent regimes (Reynolds number ≈ 41,000), with flow velocities near 0.12 m/s. Leveraging advanced visualization tools such as residual error maps and principal component analysis (PCA), this study identifies key variables, amplitude and coherence, that significantly influence sediment morphology. These findings align with hydrodynamic principles, where coherent turbulent structures govern momentum transfer and sediment entrainment, emphasizing the dominance of stable, gravity-driven processes in shaping bedform evolution. Benchmarking against classical sediment transport frameworks reveals both the strengths and limitations of the sinusoidal model, particularly its high predictive accuracy under specific flow regimes, while highlighting opportunities for improvement in more complex hydrodynamic scenarios.
This research not only provides a detailed characterization of sediment deposition patterns but also offers a validated predictive tool for managing sediment-related challenges in canals. The integration of advanced analytical techniques and statistical validation ensures the reproducibility and scalability of the findings, positioning this study as a cornerstone for future advancements in sedimentology and hydrodynamics.
6. Key Findings
The sinusoidal modeling framework demonstrated a unique capacity to represent periodic sediment deposition patterns, offering enhanced structural insight compared to traditional transport models.
The model’s adaptability to both subcritical and turbulent flow regimes highlights its flexibility in varying hydraulic contexts, supporting its application in diverse irrigation environments.
Spatial diagnostic tools, including heatmaps, orientation fields, and elevation histograms, revealed fine-scale morphological variability, enabling precise identification of high-risk sedimentation zones.
This spatial resolution facilitates data-driven maintenance strategies by enabling targeted interventions, ultimately improving the operational efficiency of canal systems.
Owing to its methodological transparency and reproducibility, the approach provides a scalable foundation for sediment management across irrigation networks and broader hydraulic infrastructure.
Funding
This research was financially supported by the Universidad Técnica Particular de Loja (UTPL, RUC: 1190068729001) for the acquisition of computational resources through the Hydraulics Laboratory of the Department of Civil Engineering. The Universidad Técnica Particular de Loja—Ecuador also covered the Article Processing Charge (APC).
Data Availability Statement
The data presented in this study are fully included within the article. All relevant information, including processed data, statistical analyses, visualizations, and model parameters, has been provided to ensure transparency and reproducibility of the research findings.
Acknowledgments
The author expresses sincere gratitude to Franz Pucha Cofrep for his invaluable assistance in the development of Figure 1, the Experimental Channel Location Map within La Tebaida Linear Park, Malacatos River, Loja, Ecuador. His cartographic expertise greatly contributed to the clarity and precision of the study’s geographical context. Special thanks are also extended to Alan Cabrera for his pivotal role in the assembly and fine-tuning of the hydraulic bench, as well as in the development of water sample tests for density. His technical contributions were instrumental in enabling data collection during the natural sediment transport event, thereby ensuring the reliability and accuracy of the experimental setup. The author gratefully acknowledges the Universidad Técnica Particular de Loja (UTPL) for providing access to the hydraulic laboratory facilities and for its financial support, which made the successful completion and dissemination of this research possible. Finally, special recognition is given to the open-source software communities behind FIJI/ImageJ 1.54p and R 4.5.1., whose tools were essential to the image processing and data analysis performed in this study.
Conflicts of Interest
The author declares no conflict of interest. The author declares no known competing financial, professional, or personal relationships that could have influenced the work reported in this study.
Appendix A. Complementary Model Evaluation Criteria
This appendix provides detailed definitions and methodological background for supplementary statistical metrics used in the evaluation of the sinusoidal sedimentation model. These indicators—Nash-Sutcliffe Efficiency (NSE), Bias (Systematic Error), Correlation Coefficient, Mean Absolute Percentage Error (MAPE), Symmetric Mean Absolute Percentage Error (SMAPE), Root Mean Squared Logarithmic Error (RMSLE), and Mean Squared Error (MSE)—were included to assess different aspects of model performance, such as systematic deviation, relative error trends, and overall stability under variable elevation gradients.
While these metrics offer complementary insights into predictive behavior, particularly in contexts with heterogeneous sediment distribution or non-uniform scaling between observed and predicted values, they were moved to this appendix to preserve clarity and readability in the main text. Their interpretive contribution, although informative, was found to be marginal when compared to the core validation criteria (RMSE, R2, MAE) emphasized in Section 2.6.
- Nash–Sutcliffe Efficiency (NSE)
The Nash–Sutcliffe Efficiency (NSE), defined in Equation (A1), evaluates the relative magnitude of residual variance compared to the observed data variance. Conceptually like R2, the NSE is more robust in hydrological and environmental modeling contexts as it accounts for systematic biases and provides a clearer measure of model performance [48].
where represents observed values, () denotes predicted values, and () is the mean of observed values. The predictive power of the model was assessed relative to the mean of observed values (), with values closer to 1.0 indicating better performance. Additionally, paired t-tests were conducted to compare parameter estimates derived from vector field and 3D surface models, with statistical significance assessed at a = 0.05. Prior to analysis, all datasets were normalized using z-scores to ensure comparability across varying scales, magnitudes, and units.
- Bias (Systematic Error)
Bias quantifies the systematic tendency of the model to overpredict or underpredict. See Equation (A2).
A near-zero bias indicates that the model is well-calibrated, with predictions evenly distributed around the observed values.
- Correlation Coefficient
The Pearson correlation coefficient measures the strength and direction of the linear relationship between observed and predicted values. See Equation (A3).
A high correlation coefficient (close to 1) indicates a strong linear association.
- Mean Absolute Percentage Error (MAPE)
The MAPE expresses the average error as a percentage of the observed values. See Equation (A4).
This metric is particularly useful for applications requiring percentage-based error evaluation.
- Symmetric Mean Absolute Percentage Error (SMAPE)
The SMAPE provides a balanced error measure, especially for datasets with small or zero observed values. See Equation (A5).
SMAPE addresses the asymmetry issue inherent in MAPE.
- Root Mean Squared Logarithmic Error (RMSLE)
The RMSLE evaluates prediction errors on a logarithmic scale, capturing proportional relationships. See Equation (A6).
This metric is valuable for datasets exhibiting exponential growth or multiplicative trends [60].
- Mean Squared Error (MSE)
The Mean Squared Error (MSE) is a widely used statistical metric for evaluating the accuracy of predictive models.
It quantifies the average squared difference between observed and predicted values, providing a measure of the model’s overall error magnitude. The mathematical formulation of MSE is represented by Equation (A7).
The squaring of errors in the MSE ensures that larger deviations between observed and predicted values are penalized more heavily than smaller ones. This characteristic makes the MSE particularly sensitive to outliers, which can significantly influence its value. Consequently, the MSE is often used in conjunction with other metrics, such as the Root Mean Square Error (RMSE), to provide a comprehensive assessment of model performance [60].
While standard metrics such as RMSE, R2, MAE, and NSE were prioritized for performance assessment, additional indicators like SMAPE and RMSLE were included to evaluate potential asymmetry and scale effects in the error structure.
SMAPE addresses proportional bias in percentage-based analyses, particularly relevant when sediment elevation ranges vary locally, which is common in heterogeneous deposition environments. RMSLE was considered to detect multiplicative error trends that may arise from non-uniform scaling between observed and predicted values.
Appendix B. Comparative Evaluation of the Sinusoidal Model and Classical Sediment Transport Equations
To evaluate the predictive performance of the sinusoidal model in relation to classical sediment transport equations, a hybrid comparison framework is employed. Classical methods, such as those developed by Einstein (1950) [3], Meyer-Peter and Müller (1948) [57], Engelund and Hansen (1967) [58], and Van Rijn (1984) [49], estimate dimensionless bedload transport rates (ϕ) and sediment flux per unit width (). In contrast, the sinusoidal model characterizes sediment morphology using image-derived waveform metrics. To enable quantitative comparison, the sinusoidal bedload transport rate (sinusoidal) is derived from image analysis, serving as the primary metric for assessment.
Appendix B.1. Sinusoidal Morphodynamic Bedload Transport Equation—SMBTE
The sinusoidal bedload transport rate (sinusoidal) is mathematically defined by Equation (A8).
Equation (A8) integrates two fundamental physical principles. It first establishes a dimensional foundation by maintaining proportionality with the standard dimensional term . This ensures consistency with established hydraulic principles, grounding the model in widely accepted theory. Second, the equation achieves morphological integration by directly incorporating the morphological parameters of the sediment accumulation wave, specifically, its amplitude (A) and wavelength (λ). This physically integrates the bed’s geometry into the transport calculation, allowing for a more nuanced understanding of sediment movement. The sinusoidal bedload transport rate is further detailed in Equation (A9).
Here, α = 1.0 is a calibration coefficient, typically ranging from 0.5 to 2.5, that researchers can adjust for different situations. is a factor that incorporates the geometry of the bed, while is a factor that accounts for the dynamics of the flow. Finally, represents a factor for spatial sinusoidal variation.
Appendix B.2. Components of the Equation
The sinusoidal sediment transport equation’s constituent elements are subsequently detailed by their physical properties. Every variable assumes a distinct function in comprehending the intricate interplay among bed morphology, fluid dynamics, and sediment movement.
- (a)
- Morphological factor ()
The morphological factor forms a cornerstone of this model, directly integrating the bed’s geometric characteristics. It is expressed as Equation (A10).
In this context, A is the amplitude, while S = A/λ represents the steepness, or the slope factor of the bedform. Rr = A/y indicates the prominence of bedforms relative to the total water depth (y). The term λ/y captures the morphological aspect ratio, and A/d reflects the relative amplitude with respect to sediment size (d).
From a physical perspective, the term adeptly captures the non-linear impact of the bedform’s steepness on sediment transport. The (1 + 1.5⋅Rr) component serves to amplify transport over rougher bed surfaces. The term provides a correction for morphological scale, ensuring the model remains relevant across different bedform sizes. Lastly, incorporates the relationship between the bedform’s amplitude and the characteristic sediment particle size.
- (b)
- Hydraulic factor ()
The hydraulic factor accounts for the dynamic forces exerted by the flowing water on the bed. Researchers formulate it as Equation (A11).
In expression A11, is the Shields parameter, a dimensionless measure of the likelihood of sediment motion. represents the Froude number, indicating the relative importance of inertial forces to gravitational forces in the flow. is the particle Reynolds number, reflecting the flow conditions around individual sediment particles.
Physically, the term provides a smooth, continuous dependence on shear stress, avoiding a rigid threshold for motion. The (1 + 1.2⋅Fr) component moderately amplifies the effect of the Froude number, acknowledging its influence on transport. The term normalizes the effect of channel slope (So), making the equation robust across various slopes. Finally, incorporates the subtle but important effects of the Reynolds number scale.
- (c)
- Sinusoidal factor ()
The sinusoidal factor captures the spatial variation in transport rates due to the undulating nature of the bed. It is defined as Equation (A12).
where , represents the morphological phase, with w being the channel width. This dictates the position along the sinusoidal wave.
From a physical standpoint, the components within are chosen harmonics that capture the essence of the sinusoidal variation:
The term, contributing 60%, represents the fundamental component of the sinusoidal variation, capturing the primary undulating pattern.
The term, contributing 25%, acts as a second harmonic, capturing higher-frequency variations and subtle changes in the bedform.
The term, contributing 10%, is a phase-shifted component that represents effects of recirculation or slight asymmetries in the flow over the bedform.
Finally, the term, contributing 5%, serves as a third harmonic, further capturing the intricate complexities of the flow and bed interaction.
Appendix B.3. Shields Number Calculation
The dimensionless Shields number θ was calculated to enable use of classical transport models. See Equation (A13).
Hans Albert Einstein (1904–1973), the first son of Albert Einstein and Mileva Marić, graphed ϕ as a function of θ and employed associated empirical expressions such as Equation (A14) to describe the relationship between these variables.
With A and B being empirical constants contingent on the regime (typically A = 0.1 and B = 5 for low flows).
The sediment load per unit width can be calculated using Equation (A15), which describes the relationship between sediment transport and flow conditions.
Given the density of water (ρ) as 1000 kg/m3 and the sediment density () as 2650 kg/m3, the unit weight of sediment () is calculated as approximately 26 kN/m3 (using 2650 kg/m3 × 9.81 m/s2). Additionally, the sediment grain diameter (d) is 0.0003 m, the hydraulic radius (R) is 0.00974 m, and the channel slope (So) is 0.00004 m/m. Then, applying Equation (A13), the dimensionless Shields number ( is approximated as 0.007873.
According to Brownlie W.R. (1981) [61], the variability of the critical Shields number () for different materials is as follows: for angular sands: ≈ 0.03–0.04; for rounded sands: ≈ 0.047 (the standard value for Meyer-Peter and Muller); and gravels: ≈ 0.03–0.06. The practical formula for calculating the critical Shields number is presented in Equations (A16) and (A17).
Appendix B.4. Classical Model Predictions
Using the data summarized in Section 3, the dimensionless parameter ϕ is calculated, and the sediment transport rate (in m2/s) is subsequently determined for each model, with results presented in Table A1. Additional input parameters for these calculations include a shear velocity (u*) of 0.01 m/s, a channel width of 0.3 m, a flow depth of 0.278 m, a cross-sectional area of 0.0834 m2, a wetted perimeter (P) of 0.856 m, a hydraulic radius (R) of 0.0974 m, and a kinematic viscosity of 1.13987 × 10−6 m2/s. The Shields parameter, also derived as described previously, is 0.007873. Other relevant derived parameters include the dimensionless grain size (D*) of 6.95455, a flow discharge (Q) of 0.01 m3/s, a mean flow velocity of 0.120 m/s, a particle Reynolds number (Re*) of 1.6273, a flow Reynolds number (Re) of 40,995 (approximately 41,000), a Froude number (Fr) is 0.07, and a boundary shear stress (τ) is 0.03823 Pa. These values are used to compute ϕ and for each scenario.

Table A1.
Bedload transport rate predictions using classical formulas and SMBTE.
Table A1.
Bedload transport rate predictions using classical formulas and SMBTE.
| Model | Formula | ϕ | (m2/s) | Reference |
|---|---|---|---|---|
| Einstein (mod.) | 3.025 × 10−12 | 7.0127 × 10−8 | Einstein, 1950 [3] | |
| Engelund-Hansen | 2.200 × 10−6 | 4.5992 × 10−11 | Engelund and Hansen, 1967 [58] | |
| Van Rijn | 0.029621 | 1.4848 × 10−7 | Van Rijn, 1984 [49] | |
| SMBTE (Model 8) | Equations (A8)–(A12) | 0.018491 | 3.8657 × 10−7 | This study |
The results presented in Table A1 highlight the significant variability in sediment transport predictions across different models, underscoring the importance of selecting appropriate formulas for specific hydraulic and morphological conditions. Notably, the SMBTE Model 8 demonstrates a higher transport capacity compared to several classical models, and its predictions closely align with those of the Van Rijn [49] formula. This suggests SMBTE Model 8’s potential utility in scenarios with pronounced bedform characteristics, particularly in contexts where Van Rijn’s approach is considered robust. These findings set the stage for a more detailed exploration of the factors influencing sediment transport.
To delve deeper into the factors influencing sediment transport, a detailed examination of specific hydraulic and sediment characteristics is essential. Table A2, presented below, offers a comprehensive overview of the calculated values for Shields numbers and other relevant parameters under various flow conditions. This table also incorporates the constitutive values of the SMBTE model, which were analyzed in Appendix B.2, and reflects the application of the proposed system of equations from A8 to A12. By scrutinizing these parameters, the complex interplay between flow dynamics and sediment behavior in channels is better understood.

Table A2.
SMBTE, results for all models.
Table A2.
SMBTE, results for all models.
| Model | A (cm) | λ (cm) | Steepness | Rr | ∅morf | φ | Ωsin | ϕsin | qb sin (m2/s) |
|---|---|---|---|---|---|---|---|---|---|
| 8 | 23.38 | 6.53 | 3.580 | 0.841 | 10.834 | 0.289 | 2.086 | 0.018 | 3.866 × 10−7 |
| 7 | 19.05 | 8.26 | 2.306 | 0.685 | 6.041 | 0.228 | 1.584 | 0.008 | 1.636 × 10−7 |
| 6 | 17.44 | 6.08 | 2.868 | 0.627 | 6.940 | 0.310 | 1.920 | 0.011 | 2.279 × 10−7 |
| 5 | 17.19 | 8.35 | 2.059 | 0.618 | 5.009 | 0.226 | 1.517 | 0.006 | 1.299 × 10−7 |
| 4 | 14.67 | 9.30 | 1.577 | 0.528 | 3.458 | 0.203 | 1.365 | 0.004 | 8.073 × 10−7 |
| 3 | 12.64 | 7.34 | 1.722 | 0.455 | 3.385 | 0.257 | 1.477 | 0.004 | 8.553 × 10−7 |
| 2 | 11.03 | 10.70 | 1.031 | 0.397 | 1.898 | 0.176 | 1.215 | 0.002 | 3.943 × 10−7 |
| 1 | 10.30 | 6.50 | 1.585 | 0.371 | 2.732 | 0.290 | 1.482 | 0.003 | 6.928 × 10–7 |
Note: For the calculation of qb sin using the sinusoidal model, the parameter ψ hydr was set to 0.000818214 (Equation (A11)).
Table A2 presents the computed bedload transport rates (qb sin) for various models within this study, with the mean q b across all models being 1.479 × 10−7 m2/s. The table details key morphological and transport parameters, including the amplitude (A) and wavelength (λ) of bedforms, their steepness, and relative roughness (Rr). The morphodynamic parameter (∅morf) and the dimensionless parameter (φ) are also provided, which are fundamental for determining the sediment transport rate. The sinusoidal transport parameter (Ωsin) and the corresponding dimensionless transport rate (ϕsin) are used to compute the final sediment transport rate (qb sin) in square meters per second.
The results indicate that higher values of steepness and relative roughness generally correspond to higher sediment transport rates. For instance, Model 8, with the highest steepness (3.580) and relative roughness (0.841), exhibits the highest qb sin value of 3.866 × 10−7 m2/s. Conversely, Model 2, with the lowest steepness (1.031) and relative roughness (0.397), shows the lowest qb sin value of 3.943 × 10−8 m2/s.
Appendix B.5. Comparative Interpretation
Table A1 reveals considerable variation in sediment transport rate predictions across different models. While classical formulas like Einstein (modified) and Engelund–Hansen (1967) [58] generally yield lower rates, the Van Rijn (1984) [49] model’s predictions align closely with the average bedload transport rate from the SMBTE models (1.479 × 10−7 m2/s). Notably, SMBTE Model 8 stands out with a higher predicted transport rate (3.8657 × 10−7 m2/s) compared to most classical models. This enhanced sensitivity to parameters like steepness and relative roughness suggests the SMBTE model, particularly Model 8, may offer a more accurate representation of sediment transport dynamics. Importantly, the SMBTE model demonstrates better validation with the field-recorded values during the study episode, supporting its superior applicability under these specific conditions.
Furthermore, SMBTE consistently evolves across experimental stages (Models 1–8), reflecting progressive sediment buildup. This confirms its reliability as a morphodynamic indicator, not merely a static measurement.
References
- Kara, H.; Demir Yetiş, A.; Kalkan, S.; Yetiş, R. Evaluation of pollution indicators and transported sediment content in agricultural drainage waters for reuse as irrigation, Harran Plain, Turkey. Environ. Sci. Pollut. Res. 2023, 30, 64982–64993. [Google Scholar] [CrossRef] [PubMed]
- Harden Carol, P. Land Use, Soil Erosion, and Reservoir Sedimentation in an Andean Drainage Basin in Ecuador. Mt. Res. Dev. 1993, 13, 177–184. [Google Scholar] [CrossRef]
- Einstein, H.A. The Bed-Load Function for Sediment Transportation in Open Channel Flows; Technical Bulletin No. 1026; U.S. Department of Agriculture. Soil Conservation Service: Washington, DC, USA, 1950; pp. 1–89. [Google Scholar]
- Syamsuddin, G.H.; Pallu, M.S.; Maricar, F.; Bakri, B. Analysis of the Seasonal Change on the Sediment Transport in the Primary Channel of Saddang Irrigation Area. Eng. Technol. Appl. Sci. Res. 2025, 15, 20138–20143. [Google Scholar] [CrossRef]
- Andualem, T.G.; Hewa, G.A.; Myers, B.; Peters, S.; Boland, J. Erosion and Sediment Transport Modeling: A Systematic Review. Land 2023, 12, 1396. [Google Scholar] [CrossRef]
- Niasi, K.A. Prediction of sediment transport in irrigation canals. Int. J. Trend Sci. Res. Dev. (IJTSRD) 2017, 2, 1–6. Available online: https://www.ijtsrd.com/papers/ijtsrd7138.pdf (accessed on 2 June 2025).
- Obrochta, S.; Fazekas, S.; Morén, J. Using computer vision and deep learning for acquisition and processing of low-distortion sediment core images. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 3–8 May 2020; p. 20954. [Google Scholar] [CrossRef]
- Soares, J.A.; Lopes de Andrade, P.R.; Batista, J.T. Contributions of digital image analysis to sedimentary rock characterization. Rev. Bras. Geofis. 2018, 36, 411–425. [Google Scholar] [CrossRef]
- Zhang, Y.; An, M. Deep learning-and transfer learning-based super resolution reconstruction from single medical image. J. Healthc. Eng. 2017, 1, 5859727. [Google Scholar] [CrossRef] [PubMed]
- Pitts, A.D.; Casciano, C.I.; Patacci, M.; Longhitano, S.G.; Di Celma, C.; McCaffrey, W.D. Integrating traditional field methods with emerging digital techniques for enhanced outcrop analysis of deep water channel-fill deposits. Mar. Pet. Geol. 2017, 87, 2–13. [Google Scholar] [CrossRef][Green Version]
- Moran, M.; Cuno, J.; Riveaux, J.A.; Vasconcellos, E.C.; Biondi, M.; Clua, E.W.; Correia, M.D.; Conci, A. Automatic Sinusoidal Curves Detection in Borehole Images Using the Iterated Local Search Algorithm. In Proceedings of the 2020 International Conference on Systems, Signals and Image Processing (IWSSIP), Niteroi, Brazil, 1–3 July 2020; pp. 255–260. [Google Scholar] [CrossRef]
- Salmasi, F.; Abraham, J.; Salmasi, A. Evaluation of various design models of irrigation sedimentation basins. Int. J. Environ. Sci. Technol. 2023, 20, 11301–11308. [Google Scholar] [CrossRef]
- Bezak, N.; Lebar, K.; Bai, Y.; Rusjan, S. Using Machine Learning to Predict Suspended Sediment Transport under Climate Change. Water Resour. Manag. 2025, 39, 3311–3326. [Google Scholar] [CrossRef]
- Alfatlawi, T.J.; Hussein, A.H. A review of studying the flow characteristics in branching open channels. Int. J. Heat Technol. 2024, 42, 560–566. [Google Scholar] [CrossRef]
- Zhang, W.; Jia, X.; Wang, Y. Experimental Investigation of Hydraulic Characteristics for Open Channel Gates. Water 2024, 16, 3717. [Google Scholar] [CrossRef]
- HYDREKA Groupe Claire. ChronoFLO 2-S2: Ultrasonic Flowmeter. 2024. Available online: https://hydreka.com/produit/chronoflo-2/ (accessed on 5 May 2025).
- Fang, L.; Ma, X.; Zhao, J.; Faraj, Y.; Wei, Z.; Zhu, Y. Development of a high-precision and wide-range ultrasonic water meter. Flow Meas. Instrum. 2022, 84, 102118. [Google Scholar] [CrossRef]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Cardona, A. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef] [PubMed]
- Agustina, I.; Nasir, F.; Setiawan, A. The Implementation of Image Smoothing to Reduce Noise using Gaussian Filter. Int. J. Comput. Appl. 2017, 177, 15–19. [Google Scholar] [CrossRef]
- Fazekas, S.Z.; Isawa, S.; Obrochta, S. Automated Extraction of Sediment Core and Scale Segments from Core Scanner Images. In Proceedings of the 2023 15th International Conference on Information Technology and Electrical Engineering (ICITEE), Yogyakarta, Indonesia, 23–25 October 2023; IEEE: New York, NY, USA, 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Li, Y.; Tan, J.; Zhang, Y.; Liang, W.; He, H. Spatial Calibration for Thermal-RGB Cameras and Inertial Sensor System. In Proceedings of the International Conference on Pattern Recognition, 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 2295–2300. [Google Scholar] [CrossRef]
- Cai, Q.; Lu, J.; Peng, C.; Prieto, J.; Rosenbaum, A.J.; Stringer, J.S.A.; Jiang, X. Spatial Calibration for 3D Freehand Ultrasound via Independent General Motions. Internaltional Ultrasonics Symposium. In Proceedings of the 2020 IEEE International Ultrasonics Symposium (IUS), Las Vegas, NV, USA, 7–11 September 2020; pp. 1–3. [Google Scholar] [CrossRef]
- Kidanemariam, A.G.; Uhlmann, M. Formation of sediment patterns in channel flow: Minimal unstable systems and their temporal evolution. J. Fluid Mech. 2017, 818, 716–743. [Google Scholar] [CrossRef]
- Reumann, M.; Bartzke, G.; Huhn, K. OrientationJ: A plugin for analyzing image texture and orientation fields. J. Microsc. 2018, 270, 321–330. [Google Scholar] [CrossRef]
- Lafaye de Micheaux, H.; Ducottet, C.; Frey, P.; Dudill, A. Image processing for studying size segregation in bedload transport: Detection and tracking. In Proceedings of the 20th EGU General Assembly, EGU2018, Proceedings from the Conference, Vienna, Austria, 4–13 April 2018; p. 7955. Available online: http://ui.adsabs.harvard.edu/abs/2018EGUGA..20.7955L/abstract (accessed on 11 April 2025). EGU2018.
- Qin, J.; Wu, T.; Ding, H. Quantitative Analysis of Grain Orientation as a Proxy for Historical Flow Dynamics. J. Geophys. Res. Earth Surf. 2024, 129, e2023JF007480. [Google Scholar] [CrossRef]
- Ernawan, D. Analisis Volume Sedimen Terhadap Pendangkalan Di Dalam Saluran Primer Jaringan Irigasi (Studi Kasus: D.I. Cipicung Subang). Jurnal Teknik Sipil Cendekia. J. Tek. Sipil Cendekia (Jtsc) 2023, 4, 570–580. [Google Scholar] [CrossRef]
- Posit Software, PBC. RStudio: Integrated Development Environment for R 4.5.1. (Versión 2024.12.1 Build 563) [Software]. 2025. Available online: https://www.posit.co/ (accessed on 6 February 2025).
- Gayathri, J.; Prerna, D.; Yuvaraj, S.; Sivani, V. A Robust Methodology for Reducing Noise and Artifacts in Digital Images using Image Denoising with Filtering Strategy. In Proceedings of the 2024 8th International Conference on I-SMAC (IoT in Social, Mobile, Analytics and Cloud) (I-SMAC), Kirtipur, Nepal, 3–5 October 2024; IEEE: New York, NY, USA, 2024; pp. 1632–1639. [Google Scholar] [CrossRef]
- Baux, N.; Murat, A.; Poizot, E.; Méar, Y.; Gregoire, G.; Lesourd, S.; Dauvin, J.-C. An innovative geostatistical sediment trend analysis using geochemical data to highlight sediment sources and transport. Comput. Geosci. 2022, 26, 263–278. [Google Scholar] [CrossRef]
- Thomas, S.; Erenbourg, A.; Chang, M.; Ferreira, A.G.D.M.T.; Stevenson, G.; Welsh, A. Does matrix transducer technology improve quality and repeatability of four-dimensional tricuspid annular plane systolic excursion and mitral annular plane systolic excursion measurements? Ultragarsas 2024, 32, 103–113. [Google Scholar] [CrossRef] [PubMed]
- Teitelbaum, Y.; Arnon, S.; Packman, A.I.; Hansen, S.K. Recovering head and flux distributions at the sediment-water interface for arbitrary, transient bedforms by inversion of photographic time series. arXiv 2024, arXiv:2411.08788. [Google Scholar] [CrossRef]
- Patterson, D.; Nielsen, P.; Calaghan, D.; Baldock, T. A process-based numerical model of shoreface profile evolution. Coast. Eng. Proc. 2023, 37, 70. [Google Scholar] [CrossRef]
- Wang, C.; Bai, D.; Li, Y.; Zhang, Q.; Ma, X.; Tian, D.; Shan, M. Establishment of critical non-depositing velocity prediction model for sediment in drip irrigation laterals based on PSO-SVM. J. Clean. Prod. 2024, 457, 142488. [Google Scholar] [CrossRef]
- Ebtehaj, I.; Bonakdari, H.; Safari, M.J.S.; Gharabaghi, B.; Zaji, A.H.; Madavar, H.R.; Mehr, A.D. Combination of sensitivity and uncertainty analyses for sediment transport modeling in sewer pipes. Int. J. Sediment Res. 2020, 35, 157–170. [Google Scholar] [CrossRef]
- Al-Amear Theol, S.A. The Use of Delft3D to Simulate the Deposition of Cohesive and Non-Cohesive Sediments in Irrigation Systems; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar] [CrossRef]
- Martin, B.; Owen, A.; Nichols, G.; Hartley, A.J.; Williams, R. Quantifying Downstream, Vertical and Lateral Variation in Fluvial Deposits: Implications from the Huesca Distributive Fluvial System. Front. Earth Sci. 2021, 8, 564017. [Google Scholar] [CrossRef]
- Lawrence, T.J.; Carr, S.J.; Manning, A.J.; Wheatland, J.A.T.; Bushby, A.J.; Spencer, K.L. A novel 3D volumetric method for directly quantifying porosity and pore space morphology in flocculated suspended sediments. MethodsX 2023, 10, 101975. [Google Scholar] [CrossRef] [PubMed]
- Kostecki, M. The influence of morphometry on the spatial variability of bottom sediments pollution in a shallow lowland dam reservoir. Zeszyty Naukowe SGSP. Sci. Rep. Fire Univ. 2023, 1, 45–60. [Google Scholar] [CrossRef]
- Zeng, X.; Yuan, Y. How does bed load transport influence the longitudinal profile of reservoir sedimentation? In Proceedings of the EGU General Assembly Conference Abstracts 2024, Vienna, Austria, 14–19 April 2024; p. 19762. [Google Scholar] [CrossRef]
- Mahato, R.K.; Subhasish, D.; Sk Zeeshan, A. Planform Evolution of a Sinuous Channel Triggered by Curvature and Autogenic Width Oscillations Due to Generic Grain Transport. Phys. Fluids 2022, 34, 044110. [Google Scholar] [CrossRef]
- Weikai, T.; Jing, Y. A process-based sediment transport model for sheet flows with the pickup layer resolved in an empirical way. In Proceedings of the International Conference on Asian and Pacific Coasts, Hanoi, Vietnam, 25–28 September 2019; Springer Singapore: Singapore, 2019; pp. 385–392. [Google Scholar] [CrossRef]
- Grossmann, F. The Sand Transport Processes of Bar Cross-Shore Migration and Beach Recovery. Ph.D. Thesis, UPC, Departament d’Enginyeria Civil i Ambiental, Barcelona, Spain, 2023. [Google Scholar] [CrossRef]
- Zhang, J.; Gai, Y. Nonlinear regression models with profile nonlinear least squares estimation. Commun. Stat. —Simul. Comput. 2019, 51, 2140–2157. [Google Scholar] [CrossRef]
- Gangu, K.; Tayal, S.; Mishra, R.; Voola, P.K.; Kavuri, S.N.; Mehra, A. An analysis on performance scale and model validation in machine learning. In Proceedings of the 2024 7th International Conference on Contemporary Computing and Informatics (IC3I), Uttar Pradesh, India, 18–20 September 2024; IEEE: New York, NY, USA, 2024; Volume 7, pp. 1107–1113. [Google Scholar] [CrossRef]
- Zambrano-Bigiarini, M.; Rojas, R. hydroPSO: A Flexible and Model-Independent Particle Swarm Optimisation (PSO) Package for Calibration/Optimisation of Environmental Models [Computer Software]. Built Under R Version 3.6.3. 2020. Available online: https://rdrr.io/cran/hydroPSO/man/hydroPSO-package.html (accessed on 6 February 2025).
- Jeelani, M.I.; Danish, F.; Khan, S.A. Predictive Modelling: An Assessment Through Validation Techniques. J. Reliab. Stat. Stud. 2022, 15, 37–60. [Google Scholar] [CrossRef]
- Makowski, D.; Lüdecke, D.; Patil, I.; Thériault, R.; Ben-Shachar, M.S.; Wiernik, B.M.; Siegel, R.; Bock, C. PerMat: Performance Metrics in Predictive Modeling (Version 0.1.0) [Computer Software]. 2025. Available online: https://cran.r-project.org/web/packages/report/index.html (accessed on 5 May 2025).
- Van-Rijn, L.C. Sediment transport in irrigation canals: A review of modeling approaches. J. Hydraul. Res. 2016, 54, 253–266. [Google Scholar]
- Singh, H.; Kaur, S.; Sharma, P. Utilizing Various Filtering Methodologies in Digital Image Processing. IEEE 2024, 1, 1–6. [Google Scholar] [CrossRef]
- Davis, M.; Taylor, K. Flow dynamics and sediment transport in controlled environments. Hydrol. Process. 2023, 37, 2345–2360. [Google Scholar]
- Brown, J.; Green, L.; White, R. Three-dimensional modeling of sediment deposition in fluvial systems. J. Geomorphol. 2022, 45, 123–145. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- Carbonari, C.; Recking, A.; Solari, L. A simple image analysis technique for measuring bed surface texture in flume experiments. J. Hydrol. 2021, 598, 126447. [Google Scholar] [CrossRef]
- Bustamante-Penagos, N.; Niño, Y. Flow–Sediment Turbulent Ejections: Interaction between Surface and Subsurface Flow in Gravel-Bed Contaminated by Fine Sediment. Water 2020, 12, 1589. [Google Scholar] [CrossRef]
- Kumar, P.; Anurag, S. Reynolds Number Effect on the Parameters of Turbulent Flows over Open Channels. AQUA—Water Infrastruct. Ecosyst. Soc. 2024, 73, 1030–1047. [Google Scholar] [CrossRef]
- Meyer-Peter, E.; Müller, R. Formulas for Bed-Load Transport. In Proceedings of the Second Meeting of International Association of Hydraulic Structures Research, Stockholm, Sweden, 7–9 June 1948; pp. 39–64. [Google Scholar]
- Engelund, F.; Hansen, E. A Monograph on Sediment Transport in Alluvial Streams; Technical University of Denmark: Teknisk Forlag: Copenhagen, Denmark, 1967. [Google Scholar]
- Zanke, U.; Kloker, M.J. On the Origin of Sediment Ripples. Water 2025, 17, 681. [Google Scholar] [CrossRef]
- Plevris, V.; Solorzano, G.; Bakas, N.P.; Ben Seghier, M.E.A. Investigation of Performance Metrics in Regression Analysis and Machine Learning-Based Prediction Models. In Proceedings of the 8th European Congress on Computational Methods in Applied Sciences and Engineering, Lillestrøm, Norway, 5–9 June 2022. [Google Scholar] [CrossRef]
- Brownlie, W.R. Prediction of Flow Depth and Sediment Discharge in Open Channels; Technical Report KH-R-43A; Keck Laboratory of Hydraulics and Water Resources, California Institute of Technology: Pasadena, CA, USA, 1981. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).