Multi-Layer and Profile Soil Moisture Estimation and Uncertainty Evaluation Based on Multi-Frequency (Ka-, X-, C-, S-, and L-Band) and Quad-Polarization Airborne SAR Data from Synchronous Observation Experiment in Liao River Basin, China
Abstract
1. Introduction
- (1)
- Compared with multi-spectral data, how do multi-frequency SAR data differ in characterizing vegetation biophysical parameters?
- (2)
- What are the differences in estimating SSM (0–5 cm) using multi-frequency SAR data?
- (3)
- How can multi-frequency SAR data be used to estimate the multi-layer and profile SM (0–50 cm)?
- (4)
- For different types of vegetation, what is the optimal penetration depth for SM estimation?
2. Study Area and Data
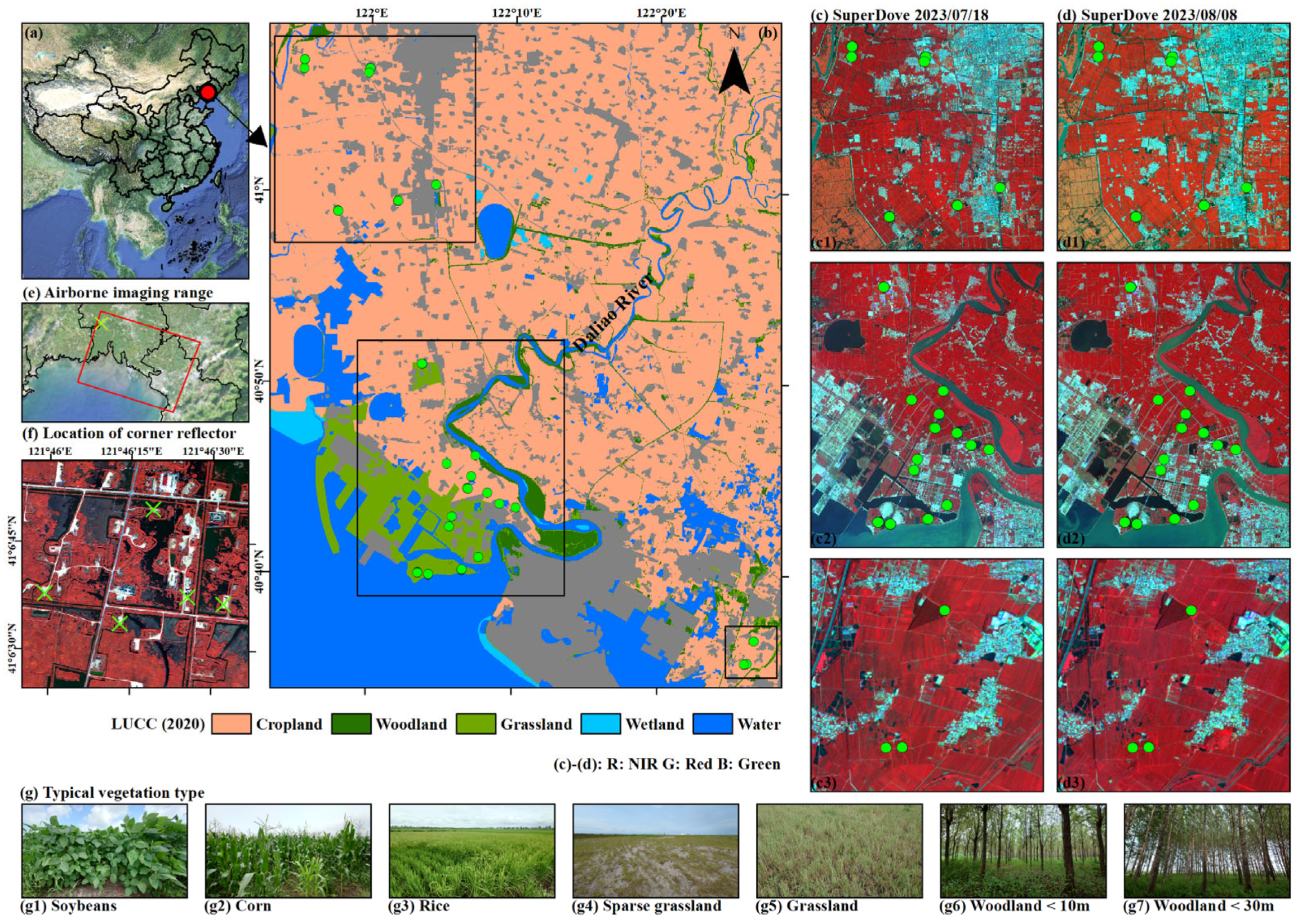
2.1. Liao River Basin
2.2. Xinzhou-60 Airborne Observation Platform
2.3. SuperDove Optical Satellite Data
2.4. Field Sampling Experiment
2.4.1. Vegetation Parameter Sampling
2.4.2. Soil Parameter Sampling
3. Methods
3.1. Technical Process
3.2. Soil Moisture Estimation Model
3.2.1. Water Cloud Model
3.2.2. Gaussian Process Regression Model
3.3. Model Validation Strategies and Accuracy Indices
3.3.1. Model Validation Strategies
3.3.2. Accuracy Indices
4. Results and Discussions
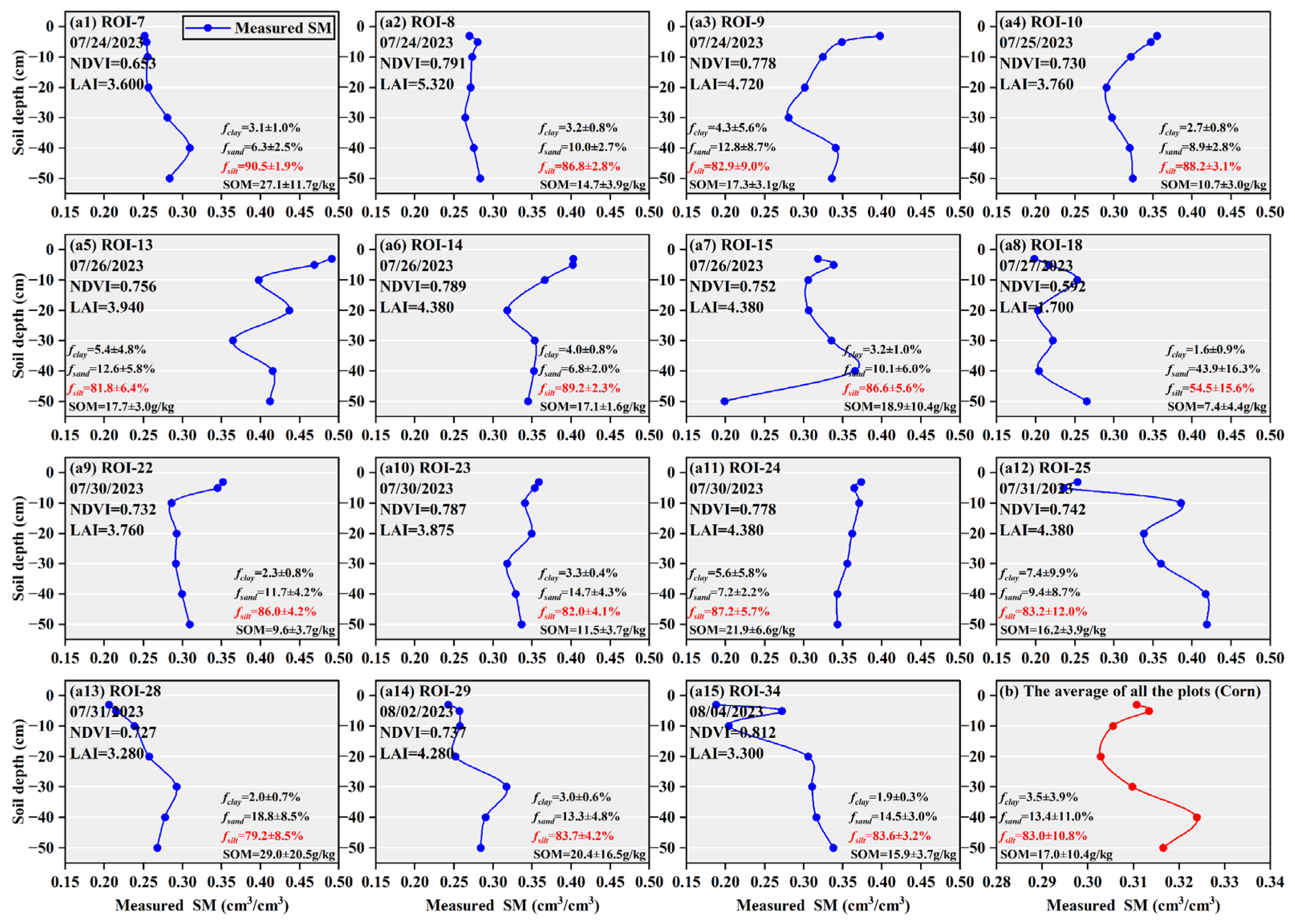
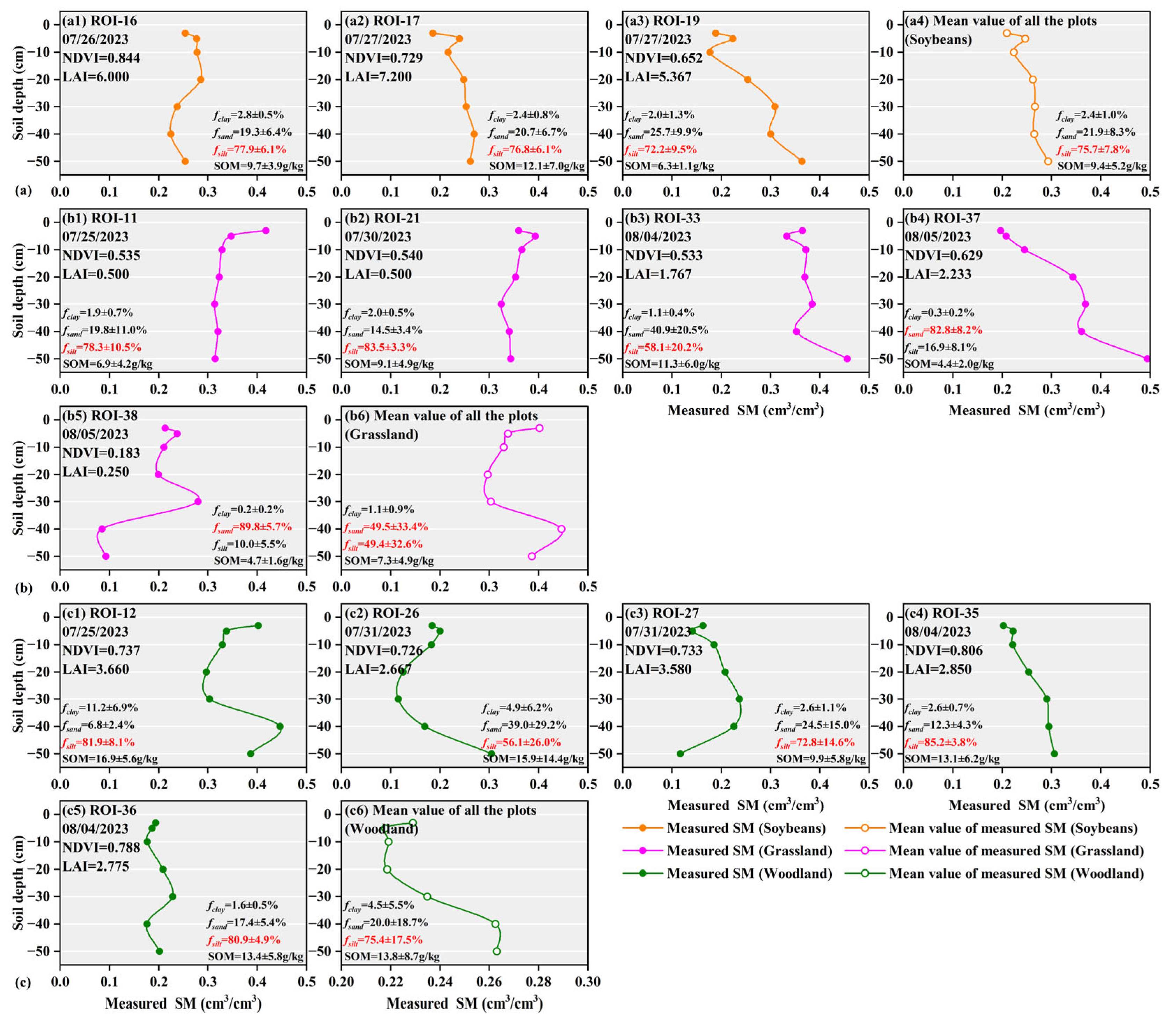
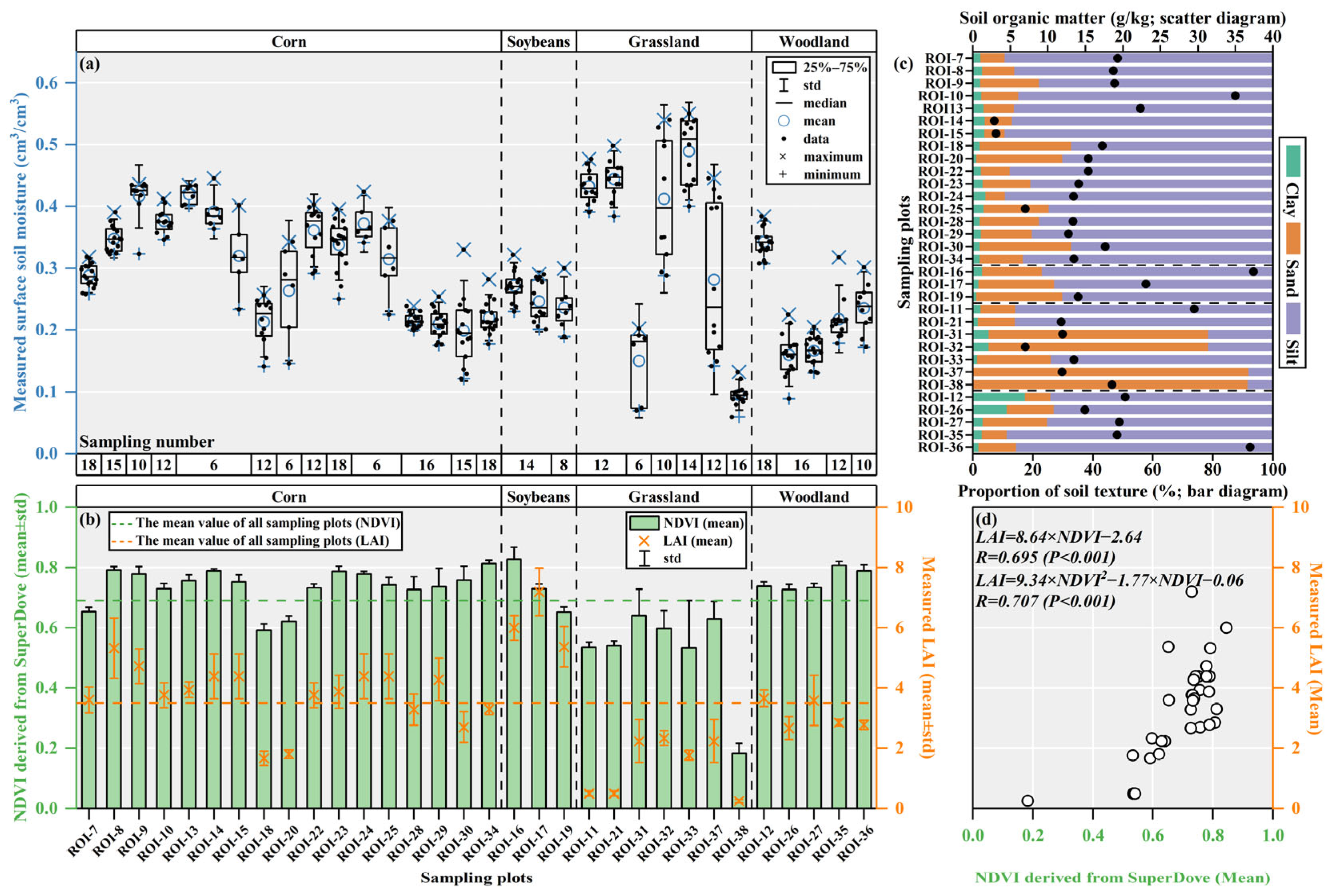
4.1. Analysis of Vegetation and Soil Parameters in the Sampling Plots
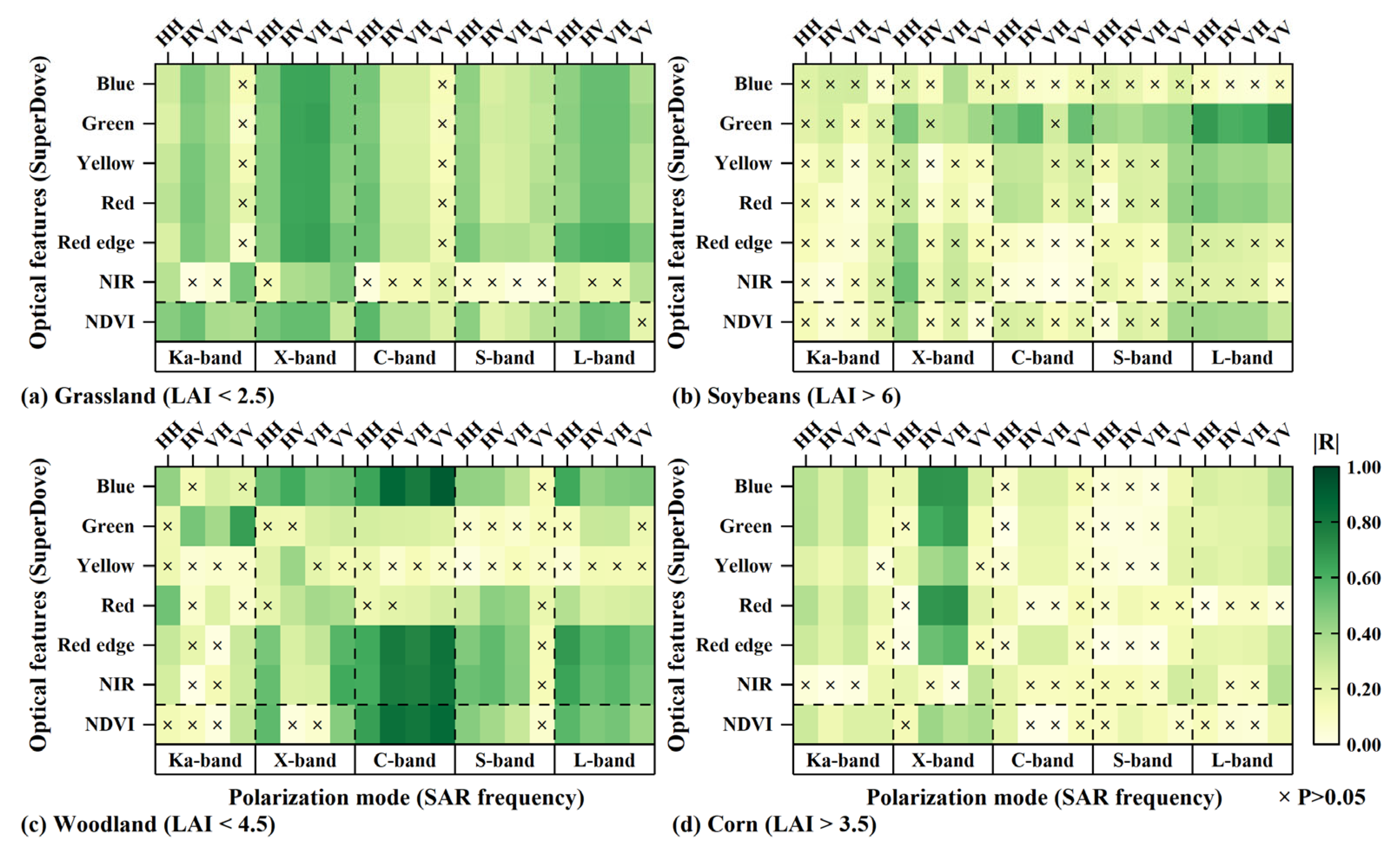
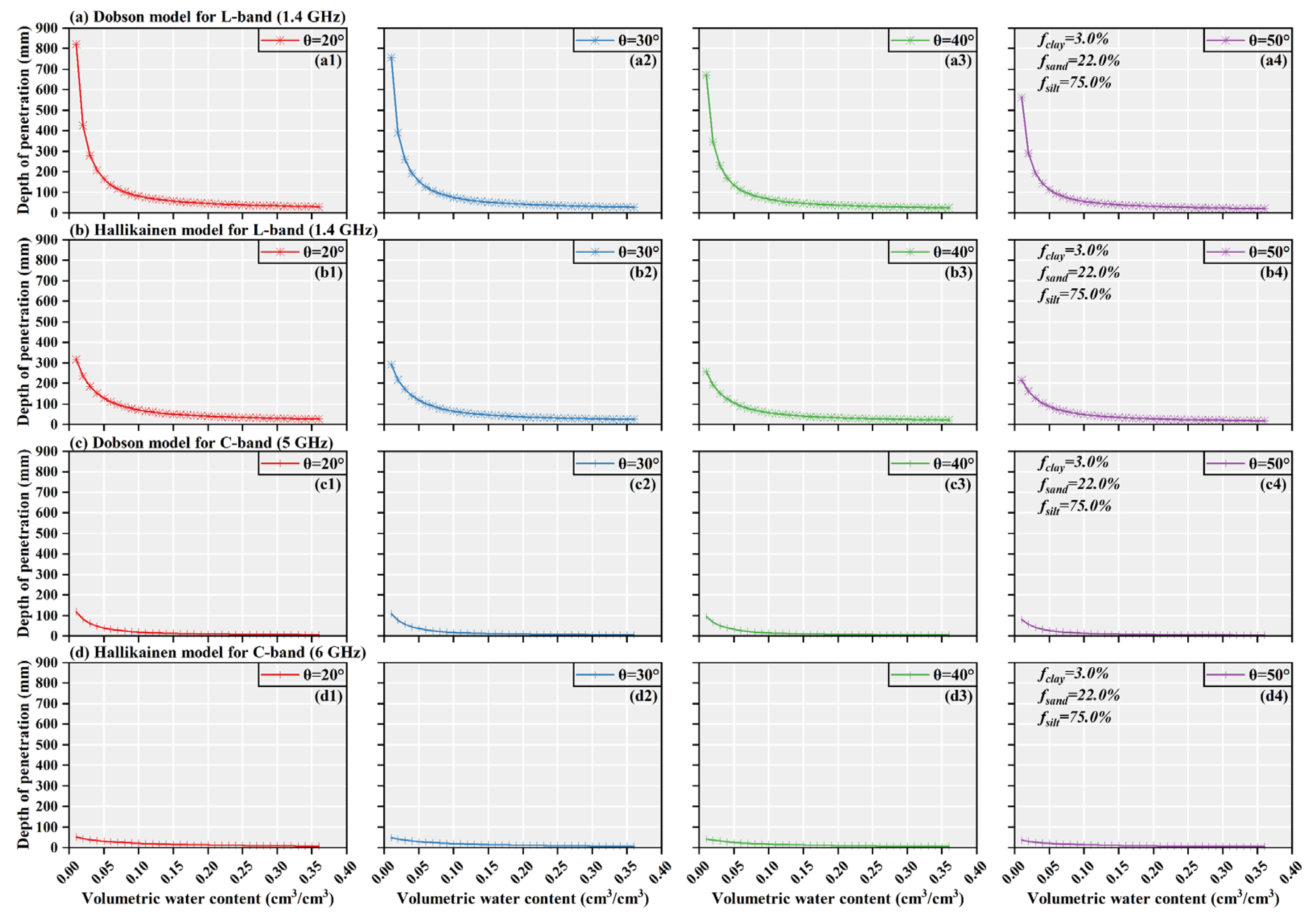
4.2. Theoretical Analysis and Simulation Experiment of Soil Penetration Using the Multi-Frequency SAR Data
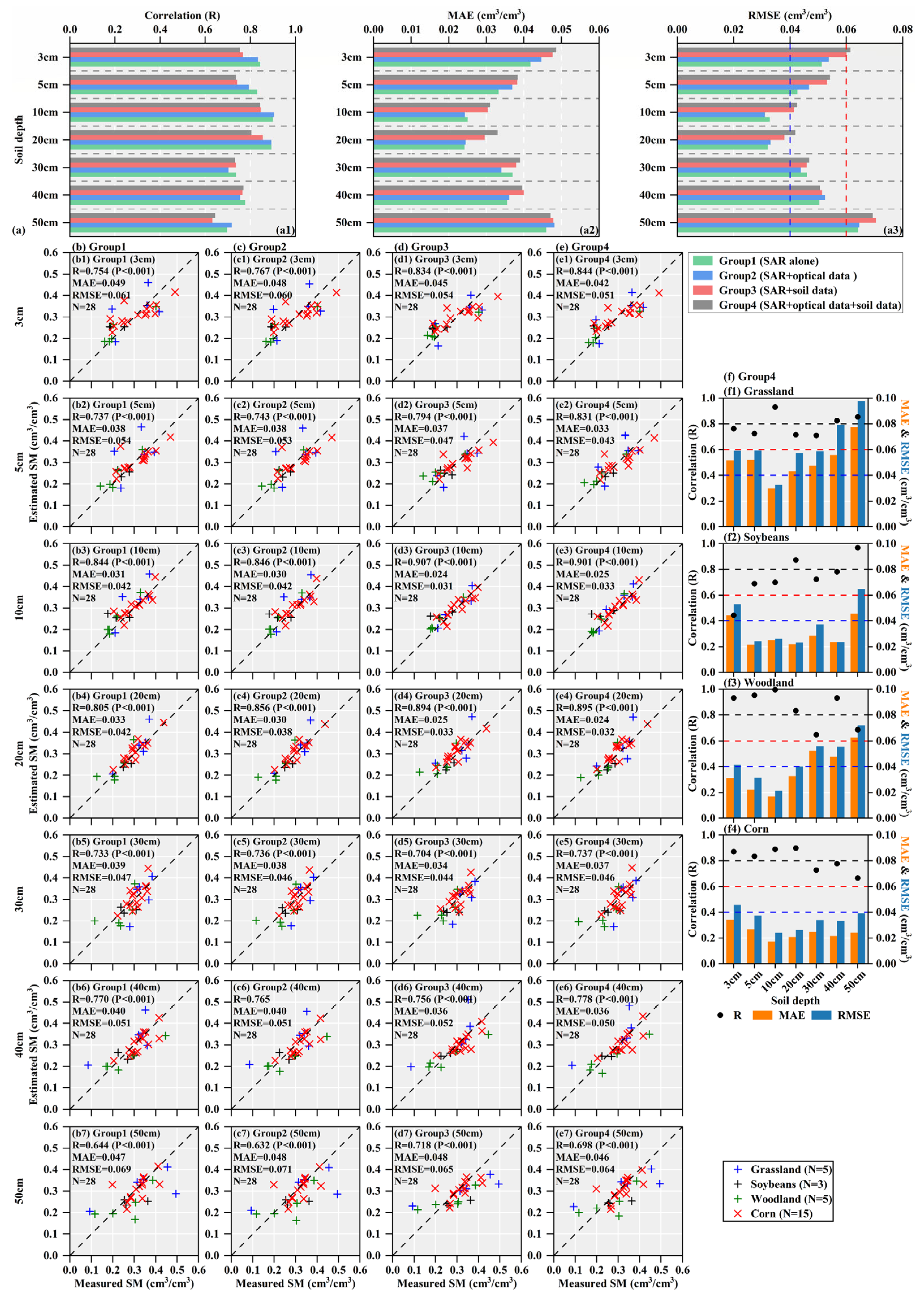
4.3. Estimation Modeling and Validation of Multi-Layer and Profile Soil Moisture Based on the Multi-Frequency SAR Data
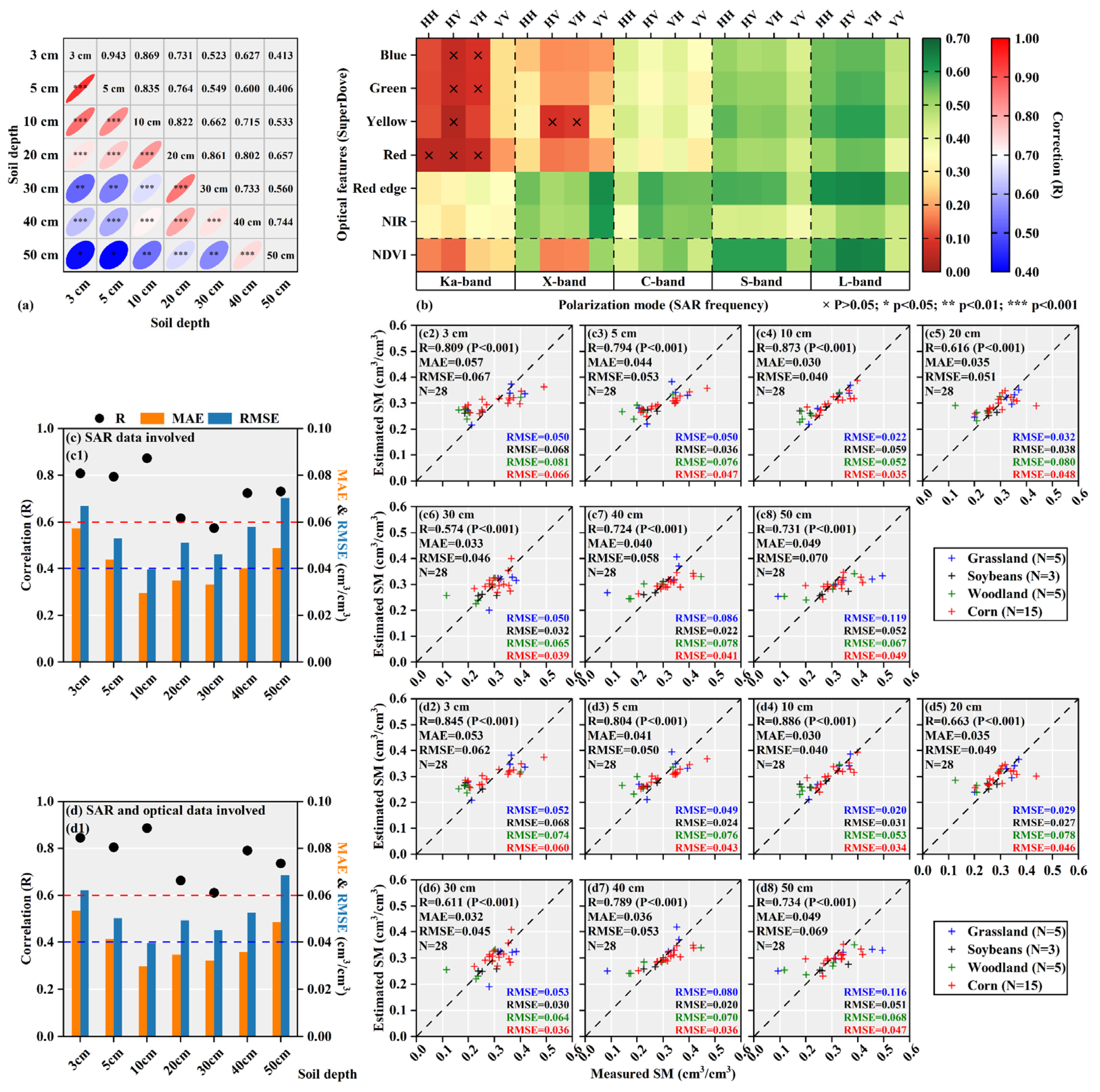
4.3.1. Evaluation of Surface Soil Moisture Estimation Accuracy Based on the Scattering Model and the Regression Model
4.3.2. Evaluation of Multi-Layer and Profile Soil Moisture Estimation Accuracy Based on the Scattering Model
4.3.3. Evaluation of Multi-Layer and Profile Soil Moisture Estimation Accuracy Based on the Regression Model
4.4. Comparison with Other Studies
5. Deficiencies and Prospects
6. Conclusions
- (1)
- The sensitivity of the SAR data to biophysical parameters depends on its frequency, polarization mode, vegetation type, and biomass level. Overall, cross-polarization backscattering coefficients are more sensitive to biophysical parameters than co-polarization coefficients. High-frequency SAR data are more sensitive to low-biomass vegetation, while low-frequency SAR data are more responsive to high-biomass vegetation. Therefore, it is necessary to select appropriate SAR frequencies and polarization modes based on different vegetation types to fully realize the potential of the multi-frequency SAR data in monitoring vegetation growth status.
- (2)
- Due to variations in soil texture distribution and water demand, even when vegetation development in different sampling plots reached similar levels under the same climatic conditions, the SSM at depth 0–5 cm still exhibited significant heterogeneity. Similarly, because of differences between the soil layers, substantial heterogeneity existed in the measured multi-layer and profile SM even within the same vegetation type, including grassland, farmland, and woodland. Therefore, empirical models exhibited insufficient accuracy for fine-scale multi-layer and profile SM estimation.
- (3)
- The WCM based on multi-polarization weighting effectively reduced the adverse impact of vegetation scattering on SSM estimation. Among them, estimation accuracy using the L-band quad-pol SAR data met the monitoring requirement of RMSE < 0.060 cm3/cm3. The estimation accuracy of SSM was mainly influenced by SAR frequency, the dynamic range of SM content, vegetation types, and vegetation cover conditions.
- (4)
- The WCM constrained by multi-polarization weighting and penetration depth weighting fully leveraged the unique soil penetration sensitivity of the multi-frequency SAR data, thereby enabling accurate estimation of the multi-layer and profile SM across different vegetation types. The multi-input multi-output regression model effectively captured the complex relationships between multi-source data, including multi-frequency SAR, multispectral data, and soil physical/geometric parameters, and the measured multi-layer and profile SM, resulting in improved estimation accuracy. Regardless of whether the scattering model or the regression model was used, the overall SM penetration-sensitive depth range based on high-resolution airborne multi-frequency quad-pol SAR data was approximately 10–30 cm, and varied across different vegetation types.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Vegetation Type | Soil Depth | Mean (cm3/cm3) | Standard Deviation | Coefficient of Variation |
|---|---|---|---|---|
| Entirety | 3 cm | 0.285 | 0.092 | 0.322 |
| 5 cm | 0.287 | 0.076 | 0.265 | |
| 10 cm | 0.281 | 0.069 | 0.244 | |
| 20 cm | 0.286 | 0.063 | 0.222 | |
| 30 cm | 0.307 | 0.090 | 0.293 | |
| 40 cm | 0.301 | 0.078 | 0.259 | |
| 50 cm | 0.316 | 0.105 | 0.332 | |
| Corn | 3 cm | 0.311 | 0.086 | 0.276 |
| 5 cm | 0.313 | 0.071 | 0.225 | |
| 10 cm | 0.306 | 0.057 | 0.186 | |
| 20 cm | 0.303 | 0.054 | 0.177 | |
| 30 cm | 0.310 | 0.039 | 0.126 | |
| 40 cm | 0.324 | 0.052 | 0.162 | |
| 50 cm | 0.317 | 0.055 | 0.172 | |
| Soybeans | 3 cm | 0.209 | 0.031 | 0.149 |
| 5 cm | 0.247 | 0.022 | 0.090 | |
| 10 cm | 0.224 | 0.041 | 0.185 | |
| 20 cm | 0.263 | 0.016 | 0.062 | |
| 30 cm | 0.267 | 0.030 | 0.114 | |
| 40 cm | 0.265 | 0.031 | 0.117 | |
| 50 cm | 0.293 | 0.050 | 0.171 | |
| Grassland | 3 cm | 0.310 | 0.089 | 0.286 |
| 5 cm | 0.304 | 0.070 | 0.230 | |
| 10 cm | 0.304 | 0.065 | 0.214 | |
| 20 cm | 0.318 | 0.061 | 0.192 | |
| 30 cm | 0.394 | 0.148 | 0.375 | |
| 40 cm | 0.292 | 0.104 | 0.357 | |
| 50 cm | 0.380 | 0.187 | 0.494 | |
| Woodland | 3 cm | 0.229 | 0.088 | 0.382 |
| 5 cm | 0.218 | 0.065 | 0.301 | |
| 10 cm | 0.219 | 0.057 | 0.261 | |
| 20 cm | 0.219 | 0.057 | 0.261 | |
| 30 cm | 0.235 | 0.066 | 0.283 | |
| 40 cm | 0.262 | 0.102 | 0.390 | |
| 50 cm | 0.263 | 0.094 | 0.356 |
| Estimation Model | Polarization Mode | Accuracy Indices | SAR Frequency | ||||
|---|---|---|---|---|---|---|---|
| Ka-band | X-band | C-band | S-band | L-band | |||
| WCM1 | HH+HV | R | 0.539 | 0.614 | 0.687 | 0.685 | 0.773 |
| MAE | 0.075 | 0.071 | 0.062 | 0.064 | 0.055 | ||
| RMSE | 0.090 | 0.084 | 0.078 | 0.078 | 0.068 | ||
| VV+VH | R | 0.559 | 0.614 | 0.724 | 0.675 | 0.744 | |
| MAE | 0.074 | 0.071 | 0.057 | 0.064 | 0.058 | ||
| RMSE | 0.088 | 0.084 | 0.074 | 0.079 | 0.071 | ||
| HH+HV+VV | R | 0.564 | 0.620 | 0.736 | 0.700 | 0.779 | |
| MAE | 0.073 | 0.071 | 0.058 | 0.063 | 0.055 | ||
| RMSE | 0.088 | 0.084 | 0.073 | 0.076 | 0.068 | ||
| WCM2 | HH+HV | R | 0.669 | 0.708 | 0.787 | 0.795 | 0.840 |
| MAE | 0.066 | 0.061 | 0.051 | 0.050 | 0.046 | ||
| RMSE | 0.079 | 0.075 | 0.066 | 0.065 | 0.059 | ||
| VV+VH | R | 0.672 | 0.718 | 0.809 | 0.773 | 0.825 | |
| MAE | 0.065 | 0.061 | 0.045 | 0.052 | 0.047 | ||
| RMSE | 0.079 | 0.074 | 0.063 | 0.068 | 0.061 | ||
| HH+HV+VV | R | 0.676 | 0.719 | 0.816 | 0.801 | 0.849 | |
| MAE | 0.065 | 0.060 | 0.047 | 0.050 | 0.046 | ||
| RMSE | 0.079 | 0.074 | 0.063 | 0.065 | 0.058 | ||
| GPR model | HH+HV+VV | R | 0.923 | 0.928 | 0.923 | 0.925 | 0.933 |
| MAE | 0.030 | 0.031 | 0.031 | 0.030 | 0.029 | ||
| RMSE | 0.041 | 0.040 | 0.041 | 0.041 | 0.039 | ||
| Estimation Model | Accuracy Indices | Soil Depth | ||||||
|---|---|---|---|---|---|---|---|---|
| 3 cm | 5 cm | 10 cm | 20 cm | 30 cm | 40 cm | 50 cm | ||
| WCM1 | R | 0.809 | 0.794 | 0.873 | 0.616 | 0.574 | 0.724 | 0.731 |
| MAE | 0.057 | 0.044 | 0.030 | 0.035 | 0.033 | 0.040 | 0.049 | |
| RMSE | 0.067 | 0.053 | 0.040 | 0.051 | 0.046 | 0.058 | 0.070 | |
| WCM2 | R | 0.845 | 0.804 | 0.886 | 0.663 | 0.611 | 0.789 | 0.734 |
| MAE | 0.053 | 0.041 | 0.030 | 0.035 | 0.032 | 0.036 | 0.049 | |
| RMSE | 0.062 | 0.050 | 0.040 | 0.049 | 0.045 | 0.053 | 0.069 | |
| Estimation Model | Accuracy Indices | Soil Depth | ||||||
|---|---|---|---|---|---|---|---|---|
| 3 cm | 5 cm | 10 cm | 20 cm | 30 cm | 40 cm | 50 cm | ||
| Group1 | R | 0.754 | 0.737 | 0.844 | 0.805 | 0.733 | 0.770 | 0.644 |
| MAE | 0.049 | 0.038 | 0.031 | 0.033 | 0.039 | 0.040 | 0.047 | |
| RMSE | 0.061 | 0.054 | 0.042 | 0.042 | 0.047 | 0.051 | 0.069 | |
| Group2 | R | 0.767 | 0.743 | 0.846 | 0.856 | 0.736 | 0.765 | 0.632 |
| MAE | 0.048 | 0.038 | 0.030 | 0.030 | 0.038 | 0.040 | 0.048 | |
| RMSE | 0.060 | 0.053 | 0.042 | 0.038 | 0.046 | 0.051 | 0.071 | |
| Group3 | R | 0.834 | 0.794 | 0.907 | 0.894 | 0.704 | 0.756 | 0.718 |
| MAE | 0.045 | 0.037 | 0.024 | 0.025 | 0.034 | 0.036 | 0.048 | |
| RMSE | 0.054 | 0.047 | 0.031 | 0.033 | 0.044 | 0.052 | 0.065 | |
| Group4 | R | 0.844 | 0.831 | 0.901 | 0.895 | 0.737 | 0.778 | 0.698 |
| MAE | 0.042 | 0.033 | 0.025 | 0.024 | 0.037 | 0.036 | 0.046 | |
| RMSE | 0.051 | 0.043 | 0.033 | 0.032 | 0.046 | 0.050 | 0.064 | |
References
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture–climate interactions in a changing climate: A review. Earth Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- SU, S.L.; Singh, D.N.; Baghini, M.S. A critical review of soil moisture measurement. Measurement 2014, 54, 92–105. [Google Scholar] [CrossRef]
- Zuo, Z.; Qiao, L.; Zhang, R.; Chen, D.; Piao, S.; Xiao, D.; Zhang, K. Importance of soil moisture conservation in mitigating climate change. Sci. Bull. 2024, 69, 1332–1341. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A.; et al. ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Wei, J.; Dirmeyer, P.A. Dissecting soil moisture-precipitation coupling. Geophys. Res. Lett. 2012, 39, L19711. [Google Scholar] [CrossRef]
- Koster, R.D.; Suarez, M.J.; Higgins, R.W.; Van den Dool, H.M. Observational evidence that soil moisture variations affect precipitation. Geophys. Res. Lett. 2003, 30, 1241. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Farahmand, A.; Melton, F.S.; Teixeira, J.; Anderson, M.C.; Wardlow, B.D.; Hain, C.R. Remote sensing of drought: Progress, challenges and opportunities. Rev. Geophys. 2015, 53, 452–480. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; D’odorico, P.; Porporato, A.; Ridolfi, L. On the spatial and temporal links between vegetation, climate, and soil moisture. Water Resour. Res. 1999, 35, 3709–3722. [Google Scholar] [CrossRef]
- Li, W.; Migliavacca, M.; Forkel, M.; Denissen, J.M.; Reichstein, M.; Yang, H.; Duveiller, G.; Weber, U.; Orth, R. Widespread increasing vegetation sensitivity to soil moisture. Nat. Commun. 2022, 13, 3959. [Google Scholar] [CrossRef]
- Qian, J.; Yang, J.; Sun, W.; Zhao, L.; Shi, L.; Shi, H.; Dang, C.; Dou, Q. Application potential and spatiotemporal uncertainty assessment of multi-layer soil moisture estimation in different climate zones using multi-source data. J. Hydrol. 2024, 645, 132229. [Google Scholar] [CrossRef]
- Karthikeyan, L.; Mishra, A.K. Multi-layer high-resolution soil moisture estimation using machine learning over the United States. Remote Sens. Environ. 2021, 266, 112706. [Google Scholar] [CrossRef]
- Wang, L.; Qu, J.J. Satellite remote sensing applications for surface soil moisture monitoring: A review. Front. Earth Sci. China 2009, 3, 237–247. [Google Scholar] [CrossRef]
- Xue, S.; Wu, G. Causal inference of root zone soil moisture performance in drought. Agric. Water Manag. 2024, 305, 109123. [Google Scholar] [CrossRef]
- Tian, J.; Zhang, Y.; Guo, J.; Zhang, X.; Ma, N.; Wei, H.; Tang, Z. Predicting root zone soil moisture using observations at 2121 sites across China. Sci. Total Environ. 2022, 847, 157425. [Google Scholar] [CrossRef]
- Li, N.; Skaggs, T.H.; Ellegaard, P.; Bernal, A.; Scudiero, E. Relationships among soil moisture at various depths under diverse climate, land cover and soil texture. Sci. Total Environ. 2024, 947, 174583. [Google Scholar] [CrossRef]
- Sun, P.; Liu, R.; Yao, R.; Shen, H.; Bian, Y. Responses of agricultural drought to meteorological drought under different climatic zones and vegetation types. J. Hydrol. 2023, 619, 129305. [Google Scholar] [CrossRef]
- Qian, J.; Yang, J.; Sun, W.; Zhao, L.; Shi, L.; Shi, H.; Liao, L.; Dang, C.; Dou, Q. Evaluation and improvement of spatiotemporal estimation and transferability of multi-layer and profile soil moisture in the Qinghai Lake and Heihe River basins using multi-strategy constraints. Geoderma 2025, 455, 117222. [Google Scholar] [CrossRef]
- Kim, S.-B.; Liao, T.-H. Robust retrieval of soil moisture at field scale across wide-ranging SAR incidence angles for soybean, wheat, forage, oat and grass. Remote Sens. Environ. 2021, 266, 112712. [Google Scholar] [CrossRef]
- Yadav, V.P.; Prasad, R.; Bala, R.; Vishwakarma, A.K. An improved inversion algorithm for spatio-temporal retrieval of soil moisture through modified water cloud model using C-band Sentinel-1A SAR data. Comput. Electron. Agric. 2020, 173, 105447. [Google Scholar] [CrossRef]
- Balenzano, A.; Mattia, F.; Satalino, G.; Davidson, M.W. Dense temporal series of C-and L-band SAR data for soil moisture retrieval over agricultural crops. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 4, 439–450. [Google Scholar] [CrossRef]
- Shi, H.; Zhao, L.; Yang, J.; Lopez-Sanchez, J.M.; Zhao, J.; Sun, W.; Shi, L.; Li, P. Soil moisture retrieval over agricultural fields from L-band multi-incidence and multitemporal PolSAR observations using polarimetric decomposition techniques. Remote Sens. Environ. 2021, 261, 112485. [Google Scholar] [CrossRef]
- Dorigo, W.; Himmelbauer, I.; Aberer, D.; Schremmer, L.; Petrakovic, I.; Zappa, L.; Preimesberger, W.; Xaver, A.; Annor, F.; Ardö, J. The International Soil Moisture Network: Serving Earth system science for over a decade. Hydrol. Earth Syst. Sci. 2021, 25, 5749–5804. [Google Scholar] [CrossRef]
- Liu, Y.; Qian, J.; Yue, H. Comprehensive evaluation of Sentinel-2 red edge and shortwave-infrared bands to estimate soil moisture. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7448–7465. [Google Scholar] [CrossRef]
- Liu, Y.; Qian, J.; Yue, H. Combined Sentinel-1A with Sentinel-2A to estimate soil moisture in farmland. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 14, 1292–1310. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Richaume, P.; Wigneron, J.P.; Ferrazzoli, P.; Mahmoodi, A.; Al Bitar, A.; Cabot, F.; Gruhier, C.; Juglea, S.E. The SMOS soil moisture retrieval algorithm. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1384–1403. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J. The soil moisture active passive (SMAP) mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Dang, C.; Shao, Z.; Huang, X.; Qian, J.; Cheng, G.; Ding, Q.; Fan, Y. Assessment of the importance of increasing temperature and decreasing soil moisture on global ecosystem productivity using solar-induced chlorophyll fluorescence. Glob. Change Biol. 2021, 28, 2066–2080. [Google Scholar] [CrossRef]
- Chan, S.K.; Bindlish, R.; O’Neill, P.E.; Njoku, E.; Jackson, T.; Colliander, A.; Chen, F.; Burgin, M.; Dunbar, S.; Piepmeier, J. Assessment of the SMAP passive soil moisture product. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4994–5007. [Google Scholar] [CrossRef]
- Peng, J.; Loew, A.; Merlin, O.; Verhoest, N.E. A review of spatial downscaling of satellite remotely sensed soil moisture. Rev. Geophys. 2017, 55, 341–366. [Google Scholar] [CrossRef]
- Karthikeyan, L.; Pan, M.; Wanders, N.; Kumar, D.N.; Wood, E.F. Four decades of microwave satellite soil moisture observations: Part 1. A review of retrieval algorithms. Adv. Water Resour. 2017, 109, 106–120. [Google Scholar] [CrossRef]
- Zhu, L.; Dai, J.; Liu, Y.; Yuan, S.; Qin, T.; Walker, J.P. A cross-resolution transfer learning approach for soil moisture retrieval from Sentinel-1 using limited training samples. Remote Sens. Environ. 2024, 301, 113944. [Google Scholar] [CrossRef]
- Zhao, T.; Hu, L.; Shi, J.; Lü, H.; Li, S.; Fan, D.; Wang, P.; Geng, D.; Kang, C.S.; Zhang, Z. Soil moisture retrievals using L-band radiometry from variable angular ground-based and airborne observations. Remote Sens. Environ. 2020, 248, 111958. [Google Scholar] [CrossRef]
- Colliander, A.; Cosh, M.H.; Misra, S.; Jackson, T.J.; Crow, W.T.; Powers, J.; McNairn, H.; Bullock, P.; Berg, A.; Magagi, R. Comparison of high-resolution airborne soil moisture retrievals to SMAP soil moisture during the SMAP validation experiment 2016 (SMAPVEX16). Remote Sens. Environ. 2019, 227, 137–150. [Google Scholar] [CrossRef]
- Bhogapurapu, N.; Dey, S.; Mandal, D.; Bhattacharya, A.; Karthikeyan, L.; McNairn, H.; Rao, Y.S. Soil moisture retrieval over croplands using dual-pol L-band GRD SAR data. Remote Sens. Environ. 2022, 271, 112900. [Google Scholar] [CrossRef]
- Singh, S.K.; Prasad, R.; Srivastava, P.K.; Yadav, S.A.; Yadav, V.P.; Sharma, J. Incorporation of first-order backscattered power in Water Cloud Model for improving the Leaf Area Index and Soil Moisture retrieval using dual-polarized Sentinel-1 SAR data. Remote Sens. Environ. 2023, 296, 113756. [Google Scholar] [CrossRef]
- Park, S.-E.; Jung, Y.T.; Cho, J.-H.; Moon, H.; Han, S.-h. Theoretical evaluation of water cloud model vegetation parameters. Remote Sens. 2019, 11, 894. [Google Scholar] [CrossRef]
- Zhu, L.; Si, R.; Shen, X.; Walker, J.P. An advanced change detection method for time-series soil moisture retrieval from Sentinel-1. Remote Sens. Environ. 2022, 279, 113137. [Google Scholar] [CrossRef]
- Zhu, L.; Dai, J.; Jin, J.; Yuan, S.; Xiong, Z.; Walker, J.P. Are the current expectations for SAR remote sensing of soil moisture using machine learning over-optimistic? IEEE Trans. Geosci. Remote Sens. 2025, 63, 1–15. [Google Scholar]
- Zheng, X.; Feng, Z.; Li, L.; Li, B.; Jiang, T.; Li, X.; Li, X.; Chen, S. Simultaneously estimating surface soil moisture and roughness of bare soils by combining optical and radar data. Int. J. Appl. Earth Obs. Geoinf. 2021, 100, 102345. [Google Scholar] [CrossRef]
- Reichle, R.H. Data assimilation methods in the Earth sciences. Adv. Water Resour. 2008, 31, 1411–1418. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R. The modern-era retrospective analysis for research and applications, version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Shi, C.; Xie, Z.; Qian, H.; Liang, M.; Yang, X. China land soil moisture EnKF data assimilation based on satellite remote sensing data. Sci. China Earth Sci. 2011, 54, 1430–1440. [Google Scholar] [CrossRef]
- Miralles, D.G.; Holmes, T.; De Jeu, R.; Gash, J.; Meesters, A.; Dolman, A. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef]
- Zhao, T.; Shi, J.; Lv, L.; Xu, H.; Chen, D.; Cui, Q.; Jackson, T.J.; Yan, G.; Jia, L.; Chen, L.; et al. Soil moisture experiment in the Luan River supporting new satellite mission opportunities. Remote Sens. Environ. 2020, 240, 111680. [Google Scholar] [CrossRef]
- Ahmad, S.; Kalra, A.; Stephen, H. Estimating soil moisture using remote sensing data: A machine learning approach. Adv. Water Resour. 2010, 33, 69–80. [Google Scholar] [CrossRef]
- Singh, A.; Gaurav, K. PIML-SM: Physics-informed machine learning to estimate surface soil moisture from multi-sensor satellite images by leveraging swarm intelligence. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–13. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, D.; Jin, Y.; Wan, X.; Ge, Y. Evolution of soil moisture mapping from statistical models to integrated mechanistic and geoscience-aware approaches. Inf. Geogr. 2025, 1, 100005. [Google Scholar] [CrossRef]
- McNairn, H.; Jackson, T.J.; Wiseman, G.; Belair, S.; Berg, A.; Bullock, P.; Colliander, A.; Cosh, M.H.; Kim, S.-B.; Magagi, R. The soil moisture active passive validation experiment 2012 (SMAPVEX12): Prelaunch calibration and validation of the SMAP soil moisture algorithms. IEEE Trans. Geosci. Remote Sens. 2014, 53, 2784–2801. [Google Scholar] [CrossRef]
- Mengen, D.; Montzka, C.; Jagdhuber, T.; Fluhrer, A.; Brogi, C.; Baum, S.; Schüttemeyer, D.; Bayat, B.; Bogena, H.; Coccia, A. The SARSense campaign: Air-and space-borne C-and L-band SAR for the analysis of soil and plant parameters in agriculture. Remote Sens. 2021, 13, 825. [Google Scholar] [CrossRef]
- Zhao, T.; Shi, J.; Entekhabi, D.; Jackson, T.J.; Hu, L.; Peng, Z.; Yao, P.; Li, S.; Kang, C.S. Retrievals of soil moisture and vegetation optical depth using a multi-channel collaborative algorithm. Remote Sens. Environ. 2021, 257, 112321. [Google Scholar] [CrossRef]
- Jackson, T.J.; Le Vine, D.M.; Hsu, A.Y.; Oldak, A.; Starks, P.J.; Swift, C.T.; Isham, J.D.; Haken, M. Soil moisture mapping at regional scales using microwave radiometry: The Southern Great Plains Hydrology Experiment. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2136–2151. [Google Scholar] [CrossRef]
- Tabatabaeenejad, A.; Burgin, M.; Duan, X.; Moghaddam, M. P-Band Radar Retrieval of Subsurface Soil Moisture Profile as a Second-Order Polynomial: First AirMOSS Results. IEEE Trans. Geosci. Remote Sens. 2014, 53, 645–658. [Google Scholar] [CrossRef]
- Hajnsek, I.; Bianchi, R.; Davidson, M.; D’Urso, G.; Gomez-Sanchez, J.; Hausold, A.; Horn, R.; Howse, J.; Loew, A.; Lopez-Sanchez, J. AgriSAR 2006—Airborne SAR and optics campaigns for an improved monitoring of agricultural processes and practices. In Proceedings of the Geophysical Research Abstracts, Vienna, Austria, 15–20 April 2007; p. 04085. [Google Scholar]
- Panciera, R.; Walker, J.P.; Jackson, T.J.; Gray, D.A.; Tanase, M.A.; Ryu, D.; Monerris, A.; Yardley, H.; Rüdiger, C.; Wu, X. The soil moisture active passive experiments (SMAPEx): Toward soil moisture retrieval from the SMAP mission. IEEE Trans. Geosci. Remote Sens. 2013, 52, 490–507. [Google Scholar] [CrossRef]
- Peischl, S.; Walker, J.P.; Rüdiger, C.; Ye, N.; Kerr, Y.H.; Kim, E.; Bandara, R.; Allahmoradi, M. The AACES field experiments: SMOS calibration and validation across the Murrumbidgee River catchment. Hydrol. Earth Syst. Sci. 2012, 16, 1697–1708. [Google Scholar] [CrossRef]
- Kang, J.; Jin, R.; Li, X.; Ma, M. HIWATER: WATERNET Observation Dataset in the Upper Reaches of the Heihe River Basin in 2014; Heihe Plan Science Data Center: Beijing, China, 2015. [Google Scholar]
- Wu, Y.; Ding, C.; Wang, B.; Jiao, Z.; Zhou, L.; Wang, R. Multi-dimensional Imaging with MD-JoSAR Mission in China: Challenges and Opportunities. In Proceedings of the EUSAR 2024; 15th European Conference on Synthetic Aperture Radar, Munich, Germany, 23–26 April 2024; pp. 989–994. [Google Scholar]
- Wang, Z.; Zhao, T.; Shi, J.; Wang, H.; Ji, D.; Yao, P.; Zheng, J.; Zhao, X.; Xu, X. 1-km soil moisture retrieval using multi-temporal dual-channel SAR data from Sentinel-1 A/B satellites in a semi-arid watershed. Remote Sens. Environ. 2023, 284, 113334. [Google Scholar] [CrossRef]
- Dou, Q.; Xie, Q.; Peng, X.; Lai, K.; Wang, J.; Lopez-Sanchez, J.M.; Shang, J.; Shi, H.; Fu, H.; Zhu, J. Soil moisture retrieval over crop fields based on two-component polarimetric decomposition: A comparison of generalized volume scattering models. J. Hydrol. 2022, 615, 128696. [Google Scholar] [CrossRef]
- Li, J.; Wang, S. Using SAR-Derived Vegetation Descriptors in a Water Cloud Model to Improve Soil Moisture Retrieval. Remote Sens. 2018, 10, 1370. [Google Scholar] [CrossRef]
- Attema, E.; Ulaby, F.T. Vegetation modeled as a water cloud. Radio Sci. 1978, 13, 357–364. [Google Scholar] [CrossRef]
- Li, Z.; Yuan, Q.; Yang, Q.; Li, J.; Zhao, T. Differentiable modeling for soil moisture retrieval by unifying deep neural networks and water cloud model. Remote Sens. Environ. 2024, 311, 114281. [Google Scholar] [CrossRef]
- Bao, Y.; Lin, L.; Wu, S.; Kwal Deng, K.A.; Petropoulos, G.P. Surface soil moisture retrievals over partially vegetated areas from the synergy of Sentinel-1 and Landsat 8 data using a modified water-cloud model. Int. J. Appl. Earth Obs. Geoinf. 2018, 72, 76–85. [Google Scholar] [CrossRef]
- Baghdadi, N.; El Hajj, M.; Zribi, M.; Bousbih, S. Calibration of the Water Cloud Model at C-Band for Winter Crop Fields and Grasslands. Remote Sens. 2017, 9, 969. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, T.; Qiu, J.; Zhao, X.; Li, R.; Wang, S. Microwave-based vegetation descriptors in the parameterization of water cloud model at L-band for soil moisture retrieval over croplands. GISci. Remote Sens. 2021, 58, 48–67. [Google Scholar] [CrossRef]
- Hosseini, M.; McNairn, H. Using multi-polarization C-and L-band synthetic aperture radar to estimate biomass and soil moisture of wheat fields. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 50–64. [Google Scholar] [CrossRef]
- Singh, A.; Niranjannaik, M.; Kumar, S.; Gaurav, K. Comparison of different dielectric models to estimate penetration depth of l-and s-band sar signals into the ground surface. Geographies 2022, 2, 734–742. [Google Scholar] [CrossRef]
- Dobson, M.C.; Ulaby, F.T.; Hallikainen, M.T.; El-Rayes, M.A. Microwave dielectric behavior of wet soil-Part II: Dielectric mixing models. IEEE Trans. Geosci. Remote Sens. 1985, 23, 35–46. [Google Scholar] [CrossRef]
- Hallikainen, M.T.; Ulaby, F.T.; Dobson, M.C.; El-Rayes, M.A.; Wu, L.-K. Microwave dielectric behavior of wet soil-part 1: Empirical models and experimental observations. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 25–34. [Google Scholar] [CrossRef]
- Williams, C.; Rasmussen, C. Gaussian processes for regression. Adv. Neural Inf. Process. Syst. 1995, 8, 514–520. [Google Scholar]
- Schulz, E.; Speekenbrink, M.; Krause, A. A tutorial on Gaussian process regression: Modelling, exploring, and exploiting functions. J. Math. Psychol. 2018, 85, 1–16. [Google Scholar] [CrossRef]
- Xue, Z.; Zhang, Y.; Zhang, L.; Li, H. Ensemble Learning Embedded With Gaussian Process Regression for Soil Moisture Estimation: A Case Study of the Continental US. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Qian, J.; Jie, Y.; Weidong, S.; Lingli, Z.; Lei, S.; Chaoya, D. Evaluation and improvement of temporal robustness and transfer performance of surface soil moisture estimated by machine learning regression algorithms. Comput. Electron. Agric. 2024, 217, 108518. [Google Scholar]
- Wu, J.; Chen, X.-Y.; Zhang, H.; Xiong, L.-D.; Lei, H.; Deng, S.-H. Hyperparameter optimization for machine learning models based on Bayesian optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar]
- Wang, H.; Magagi, R.; Goïta, K. Potential of a two-component polarimetric decomposition at C-band for soil moisture retrieval over agricultural fields. Remote Sens. Environ. 2018, 217, 38–51. [Google Scholar] [CrossRef]
- Wang, J.; Wu, F.; Shang, J.; Zhou, Q.; Ahmad, I.; Zhou, G. Saline soil moisture mapping using Sentinel-1A synthetic aperture radar data and machine learning algorithms in humid region of China’s east coast. Catena 2022, 213, 106189. [Google Scholar] [CrossRef]
- Peraza, J.; Rossini, P.R.; Patrignani, A. Mapping mesoscale soil moisture using a model-data fusion approach. J. Hydrol. 2025, 654, 132768. [Google Scholar] [CrossRef]
- Wimalathunge, N.; Bishop, T. A space-time observation system for soil moisture in agricultural landscapes. Geoderma 2019, 344, 1–13. [Google Scholar] [CrossRef]
- Liu, D.; Mishra, A.K.; Yu, Z. Evaluating uncertainties in multi-layer soil moisture estimation with support vector machines and ensemble Kalman filtering. J. Hydrol. 2016, 538, 243–255. [Google Scholar] [CrossRef]
- Singh, A.; Meena, G.K.; Kumar, S.; Gaurav, K. Analysis of the effect of incidence angle and moisture content on the penetration depth of L-and S-band SAR signals into the ground surface. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 4, 197–202. [Google Scholar] [CrossRef]
- Roßberg, T.; Schmitt, M. Comparing the relationship between NDVI and SAR backscatter across different frequency bands in agricultural areas. Remote Sens. Environ. 2025, 319, 114612. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, G.-L.; Song, X.; Li, D.; Zhao, Y.; Yang, J.; Wu, H.; Yang, F. High-resolution and three-dimensional mapping of soil texture of China. Geoderma 2020, 361, 114061. [Google Scholar] [CrossRef]
- Liu, F.; Wu, H.; Zhao, Y.; Li, D.; Yang, J.-L.; Song, X.; Shi, Z.; Zhu, A.X.; Zhang, G.-L. Mapping high resolution National Soil Information Grids of China. Sci. Bull. 2022, 67, 328–340. [Google Scholar] [CrossRef] [PubMed]
- Rasmussen, C.E. Gaussian processes in machine learning. In Proceedings of the Summer School on Machine Learning, Canberra, Australia, 2–14 February 2003; pp. 63–71. [Google Scholar]
- Fluhrer, A.; Jagdhuber, T.; Montzka, C.; Schumacher, M.; Alemohammad, H.; Tabatabaeenejad, A.; Kunstmann, H.; Entekhabi, D. Soil moisture profile estimation by combining P-band SAR polarimetry with hydrological and multi-layer scattering models. Remote Sens. Environ. 2024, 305, 114067. [Google Scholar] [CrossRef]
- Scipal, K. The Biomass mission—ESA’S P-band polarimetric, interferomtric SAR mission. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 3836–3837. [Google Scholar]
- Fluhrer, A.; Jagdhuber, T.; Tabatabaeenejad, A.; Alemohammad, H.; Montzka, C.; Friedl, P.; Forootan, E.; Kunstmann, H. Remote sensing of complex permittivity and penetration depth of soils using P-band SAR polarimetry. Remote Sens. 2022, 14, 2755. [Google Scholar] [CrossRef]
- El Hajj, M.; Baghdadi, N.; Bazzi, H.; Zribi, M. Penetration analysis of SAR signals in the C and L bands for wheat, maize, and grasslands. Remote Sens. 2018, 11, 31. [Google Scholar] [CrossRef]
- Zhu, J.; Liu, G.; Zhao, R.; Ding, X.; Fu, H. ML based approach for inverting penetration depth of SAR signals over large desert areas. Remote Sens. Environ. 2023, 295, 113643. [Google Scholar] [CrossRef]
- Capodici, F.; Maltese, A.; Ciraolo, G.; D’Urso, G.; La Loggia, G. Power sensitivity analysis of multi-frequency, multi-polarized, multi-temporal SAR data for soil-vegetation system variables characterization. Remote Sens. 2017, 9, 677. [Google Scholar] [CrossRef]
- Abdikan, S.; Sekertekin, A.; Madenoglu, S.; Ozcan, H.; Peker, M.; Pinar, M.O.; Koc, A.; Akgul, S.; Secmen, H.; Kececi, M. Surface soil moisture estimation from multi-frequency SAR images using ANN and experimental data on a semi-arid environment region in Konya, Turkey. Soil Tillage Res. 2023, 228, 105646. [Google Scholar] [CrossRef]
- Yao, Z.; Dong, Q.; Song, C.; Jiao, Z.; Wang, B.; Xiang, M. MD-JoSAR Imaging System and Application Based on Multidimensional Joint Spatial Observations. In Proceedings of the 2024 Photonics & Electromagnetics Research Symposium (PIERS), Chengdu, China, 21–25 April 2024; pp. 1–8. [Google Scholar]
- Li, L.; Zhang, F.; Shao, Y.; Wei, Q.; Huang, Q.; Jiao, Y. Airborne SAR radiometric calibration based on improved sliding window integral method. Sensors 2022, 22, 320. [Google Scholar] [CrossRef]
- Ruan, L.; Liu, Z.; Shao, Y.; Xiao, X.; Zhang, T.; Bian, X.; Zhang, N.; Wu, X. Radar Backscattering Characterization of Soil Surface: Comparisons between Backscattering Models and Indoor Microwave Measurements. In Proceedings of the 2023 International Applied Computational Electromagnetics Society Symposium (ACES-China), Hangzhou, China, 15–18 August 2023; pp. 1–3. [Google Scholar]
- Liu, X.; Shao, Y.; Li, K.; Liu, Z.; Liu, L.; Xiao, X. Backscattering Statistics of Indoor Full-Polarization Scatterometric and Synthetic Aperture Radar Measurements of a Rice Field. Remote Sens. 2023, 15, 965. [Google Scholar] [CrossRef]

| Remote Sensing Imaging System | Imaging Band | Wavelength | Spatial Resolution |
|---|---|---|---|
| Xinzhou-60 | Ka-band | 1.0 cm | 0.3 m |
| X-band | 3.1 cm | 0.5 m | |
| C-band | 5.6 cm | ||
| S-band | 10.0 cm | 1.0 m | |
| L-band | 24.0 cm | ||
| SuperDove | Coast blue | 431–452 nm | 3.0 m |
| Blue | 465–515 nm | ||
| Green I | 513–549 nm | ||
| Green II | 547–583 nm | ||
| Yellow | 600–620 nm | ||
| Red | 650–680 nm | ||
| Red edge | 697–713 nm | ||
| NIR | 845–885 nm |
| Sampling Plots | Sampling Phase | Land Cover Type | Vegetation Height | Measured LAI | Airborne SAR Data | Optical Data |
|---|---|---|---|---|---|---|
| ROI-7 | 24 July 2023 | Corn | 220–240 cm | 3.2–4.2 | Route16/24 | 18 July 2023–19 July 2023 (SuperDove) |
| ROI-8 | Corn | 220–250 cm | 3.9–6.5 | |||
| ROI-9 | Corn | 220–260 cm | 3.9–5.4 | |||
| ROI-10 | 25 July 2023 | Corn | 200–210 cm | 3.2–4.4 | Route27/28/31 | |
| ROI-11 | Grassland | 15–50 cm | 0.4–0.6 | |||
| ROI-12 | Woodland (Maple-leaf Forest) | 700–1070 cm | 3.3–4.0 | |||
| ROI-13 | 26 July 2023 | Corn | 250–260 cm | 3.6–4.4 | Route15/29/30 | |
| ROI-14 | Corn | 260–270 cm | 3.5–5.3 | |||
| ROI-15 | Corn | 270–280 cm | 3.5–5.3 | |||
| ROI-16 | Soybeans | 100–120 cm | 6.3–8.3 | |||
| ROI-17 | 27 July 2023 | Soybeans | 100–110 cm | 6.3–8.3 | Route15 | |
| ROI-18 | Corn | 250–260 cm | 1.5–2.0 | |||
| ROI-19 | Soybeans | 105–110 cm | 5.0–6.3 | |||
| ROI-20 | Corn | 205–210 cm | 1.7–2.0 | |||
| ROI-21 (11) | 30 July 2023 | Grassland | 15–50 cm | 0.4–0.6 | Route30/31 | |
| ROI-22 (10) | Corn | 200–210 cm | 3.2–4.4 | |||
| ROI-23 | Corn | 200–220 cm | 3.0–4.5 | |||
| ROI-24 (14) | Corn | 260–270 cm | 3.5–5.3 | |||
| ROI-25 (15) | Corn | 270–280 cm | 3.5–5.3 | |||
| ROI-26 | 31 July 2023 | Woodland (Birch Forest) | 1200–1300 cm | 2.3–4.0 | Route20/26 | |
| ROI-27 | Woodland (Birch Forest) | 1200–1300 cm | 2.6–4.6 | |||
| ROI-28 | Corn | 210–220 cm | 2.3–3.8 | |||
| ROI-29 | Corn | 220–240 cm | 3.5–5.4 | |||
| ROI-30 | 2 August 2023 | Corn | 220–240 cm | 2.0–3.2 | Route12/13/14 | 8 August 2023 (SuperDove) |
| ROI-31 (5) | Grassland | 15–130 cm | 1.4–3.0 | |||
| ROI-32 (5) | Grassland | 15–130 cm | 2.0–2.4 | |||
| ROI-33 | 4 August 2023 | Grassland | 90–100 cm | 1.6–2.0 | ||
| ROI-34 | Corn | 240–250 cm | 3.1–3.6 | |||
| ROI-35 | Woodland (Maple-leaf Forest) | 340–360 cm | 2.7–3.0 | |||
| ROI-36 | Woodland (Birch Forest) | 2400–2500 cm | 2.6–30 | |||
| ROI-37 (5) | 5 August 2023 | Grassland | 15–130 cm | 1.4–3.0 | Route9/10/11 | |
| ROI-38 | Grassland | 5–10 cm | 0.1–0.3 |
| Vegetation Type | Sampling Plot | Soil Sampling (0–5 cm) | Soil Sampling (0–50 cm) | Sampling Phase | Whether Imaging Is Effective? | Radar Incidence Angle | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ka-Band | X-Band | C-Band | S-Band | L-Band | ||||||
| Corn | ROI-7 | √ | √ | 24 July 2023 | √ | √ | √ | √ | √ | 47.13–47.35° |
| ROI-8 | √ | √ | √ | √ | √ | √ | √ | 45.18–45.36° | ||
| ROI-9 | √ | √ | √ | √ | √ | √ | √ | 45.08–45.17° | ||
| ROI-10 | √ | √ | 25 July 2023 | √ | √ | √ | √ | √ | 47.31–47.55° | |
| ROI-13 | √ | √ | 26 July 2023 | √ | √ | √ | √ | √ | 40.60–40.74° | |
| ROI-14 | √ | √ | √ | √ | √ | √ | √ | 46.14–46.16° | ||
| ROI-15 | √ | √ | √ | √ | √ | √ | √ | 46.03–46.05° | ||
| ROI-18 | √ | √ | 27 July 2023 | √ | √ | √ | √ | √ | 38.85–39.16° | |
| ROI-20 | √ | × | √ | √ | √ | √ | √ | 51.02–51.09° | ||
| ROI-22 | √ | √ | 30 July 2023 | √ | √ | √ | √ | √ | 47.29–47.56° | |
| ROI-23 | √ | √ | √ | √ | √ | √ | √ | 44.48–45.12° | ||
| ROI-24 | √ | √ | √ | √ | √ | √ | √ | 46.14–46.17° | ||
| ROI-25 | √ | √ | √ | √ | √ | √ | √ | 46.02–46.05° | ||
| ROI-28 | √ | √ | 31 July 2023 | √ | √ | √ | √ | √ | 45.79–46.16° | |
| ROI-29 | √ | √ | √ | √ | √ | √ | √ | 45.64–46.01° | ||
| ROI-30 | √ | × | 2 August 2023 | √ | √ | √ | √ | √ | 41.97–43.24° | |
| ROI-34 | √ | √ | 4 August 2023 | √ | √ | √ | √ | √ | 45.41–45.89° | |
| Soybeans | ROI-16 | √ | √ | 26 July 2023 | √ | √ | √ | √ | √ | 46.64–47.50° |
| ROI-17 | √ | √ | 27 July 2023 | √ | √ | √ | √ | √ | 41.14–41.80° | |
| ROI-19 | √ | √ | √ | √ | √ | √ | √ | 50.99–51.03° | ||
| Grassland | ROI-11 | √ | √ | 25 July 2023 | √ | √ | √ | √ | √ | 47.51–47.71° |
| ROI-21 | √ | √ | 30 July 2023 | √ | √ | √ | √ | √ | 47.46–47.71° | |
| ROI-31 | √ | × | 2 August 2023 | √ | √ | √ | √ | √ | 41.28–42.07° | |
| ROI-32 | √ | × | √ | √ | √ | √ | √ | 50.88–51.80° | ||
| ROI-33 | √ | √ | 4 August 2023 | √ | √ | √ | √ | √ | 52.04–52.73° | |
| ROI-37 | √ | √ | 5 August 2023 | √ | √ | √ | √ | √ | 41.28–42.12° | |
| ROI-38 | √ | √ | √ | √ | √ | √ | √ | 41.55–42.27° | ||
| Woodland | ROI-12 | √ | √ | 25 July 2023 | √ | √ | √ | √ | √ | 50.11–50.40° |
| ROI-26 | √ | √ | 31 July 2023 | √ | √ | √ | √ | √ | 42.19–42.97° | |
| ROI-27 | √ | √ | √ | √ | √ | √ | √ | 42.57–43.25° | ||
| ROI-35 | √ | √ | 4 August 2023 | √ | √ | √ | √ | √ | 44.58–44.84° | |
| ROI-36 | √ | √ | √ | √ | √ | √ | √ | 47.76–47.99° | ||
| SAR Frequency | Polarization Mode | ||
|---|---|---|---|
| HH Polarization | VV Polarization | HV/VH Polarization | |
| Ka-band | 18.5% | 28.6% | 52.9% |
| X-band | 31.1% | 29.0% | 39.9% |
| C-band | 26.1% | 42.3% | 31.5% |
| S-band | 36.0% | 37.4% | 26.6% |
| L-band | 37.9% | 36.1% | 26.0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, J.; Yang, J.; Sun, W.; Zhao, L.; Shi, L.; Shi, H.; Dang, C.; Dou, Q. Multi-Layer and Profile Soil Moisture Estimation and Uncertainty Evaluation Based on Multi-Frequency (Ka-, X-, C-, S-, and L-Band) and Quad-Polarization Airborne SAR Data from Synchronous Observation Experiment in Liao River Basin, China. Water 2025, 17, 2096. https://doi.org/10.3390/w17142096
Qian J, Yang J, Sun W, Zhao L, Shi L, Shi H, Dang C, Dou Q. Multi-Layer and Profile Soil Moisture Estimation and Uncertainty Evaluation Based on Multi-Frequency (Ka-, X-, C-, S-, and L-Band) and Quad-Polarization Airborne SAR Data from Synchronous Observation Experiment in Liao River Basin, China. Water. 2025; 17(14):2096. https://doi.org/10.3390/w17142096
Chicago/Turabian StyleQian, Jiaxin, Jie Yang, Weidong Sun, Lingli Zhao, Lei Shi, Hongtao Shi, Chaoya Dang, and Qi Dou. 2025. "Multi-Layer and Profile Soil Moisture Estimation and Uncertainty Evaluation Based on Multi-Frequency (Ka-, X-, C-, S-, and L-Band) and Quad-Polarization Airborne SAR Data from Synchronous Observation Experiment in Liao River Basin, China" Water 17, no. 14: 2096. https://doi.org/10.3390/w17142096
APA StyleQian, J., Yang, J., Sun, W., Zhao, L., Shi, L., Shi, H., Dang, C., & Dou, Q. (2025). Multi-Layer and Profile Soil Moisture Estimation and Uncertainty Evaluation Based on Multi-Frequency (Ka-, X-, C-, S-, and L-Band) and Quad-Polarization Airborne SAR Data from Synchronous Observation Experiment in Liao River Basin, China. Water, 17(14), 2096. https://doi.org/10.3390/w17142096









