An Advanced Ensemble Machine Learning Framework for Estimating Long-Term Average Discharge at Hydrological Stations Using Global Metadata
Abstract
1. Introduction
- (1)
- To develop a high-performance Meta Ensemble machine learning model capable of accurately estimating LTA discharge using a diverse set of globally distributed hydrological station metadata.
- (2)
- To systematically compare the performance of the proposed ensemble against various individual models, including a custom-designed neural network and several state-of-the-art gradient boosting machines.
- (3)
- To identify and interpret the key geographical and physical catchment attributes that most significantly influence LTA discharge, using model-agnostic explanation techniques (SHAP).
- (4)
- To demonstrate the potential of this data-driven methodology as a scalable and cost-effective tool for large-scale water resource assessment, especially in ungauged or data-limited regions.
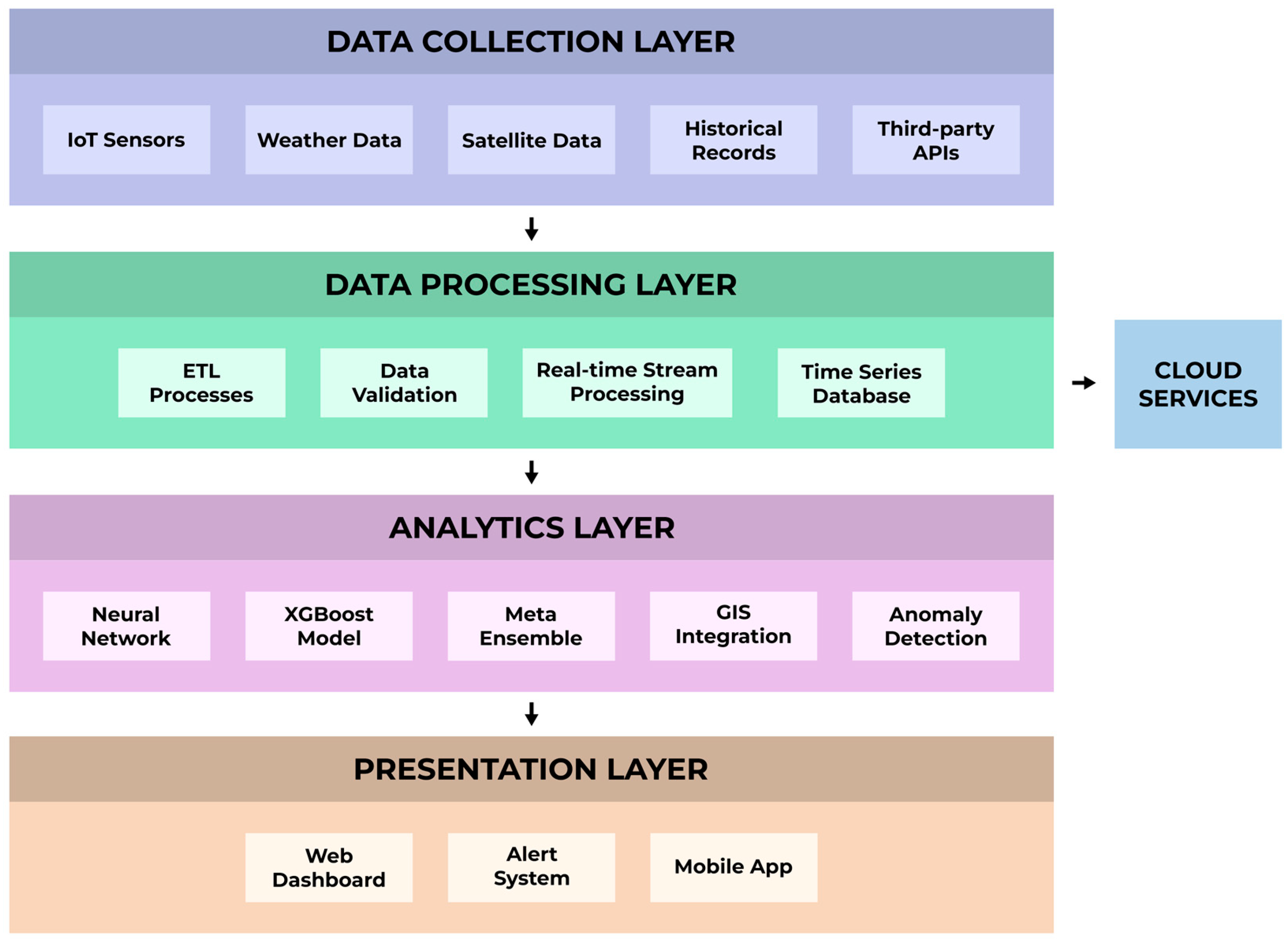
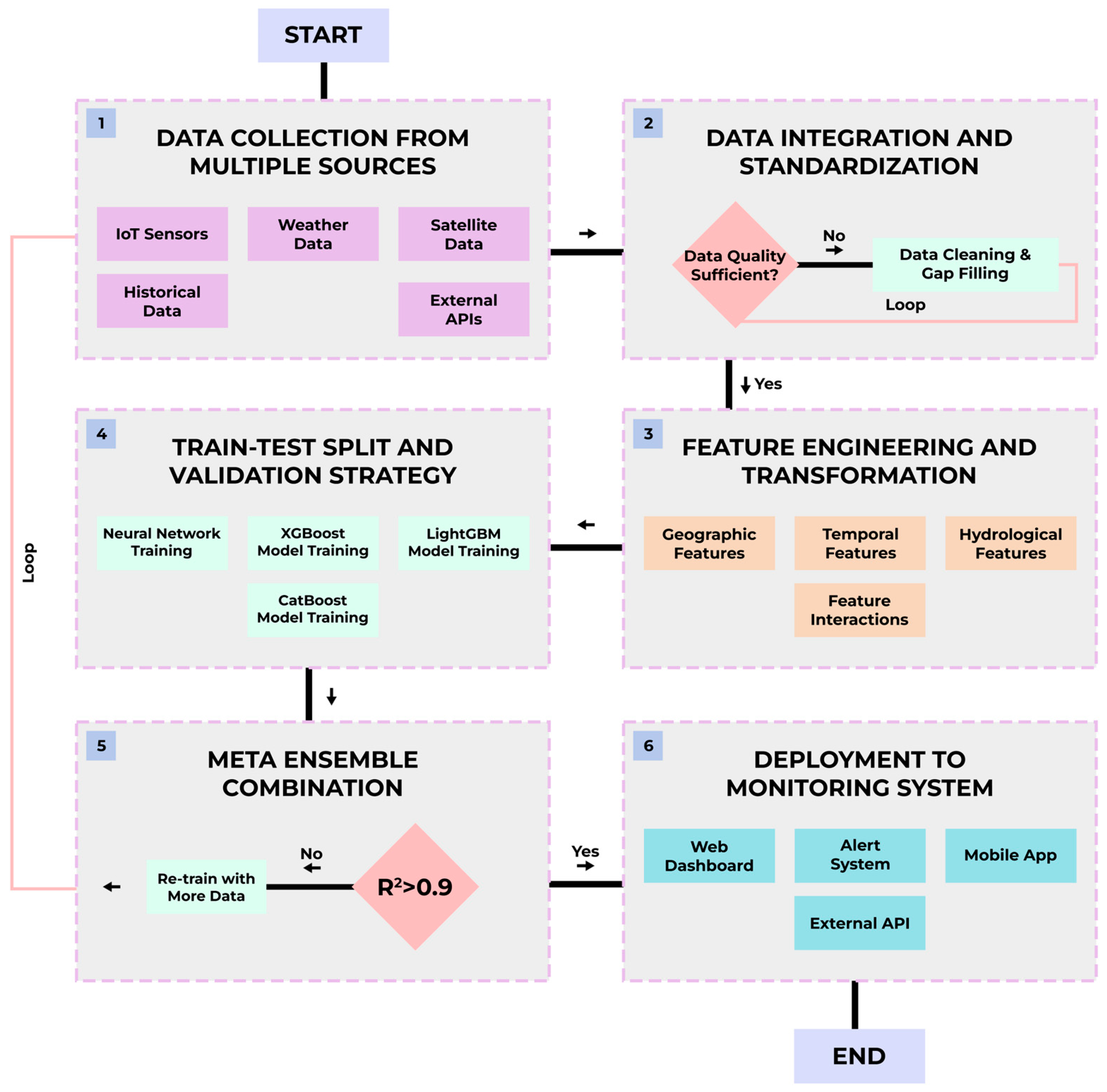
2. Materials and Methods
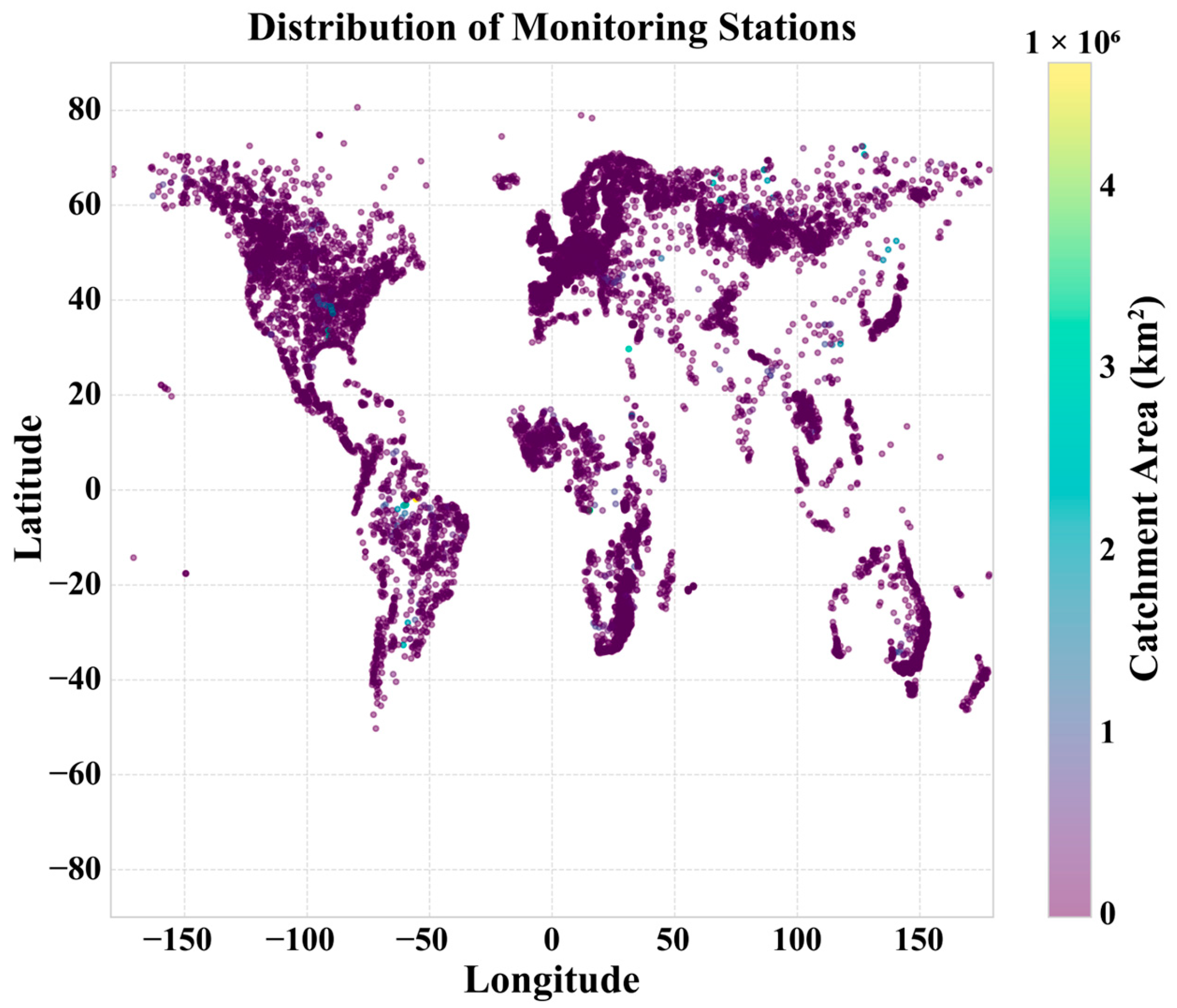
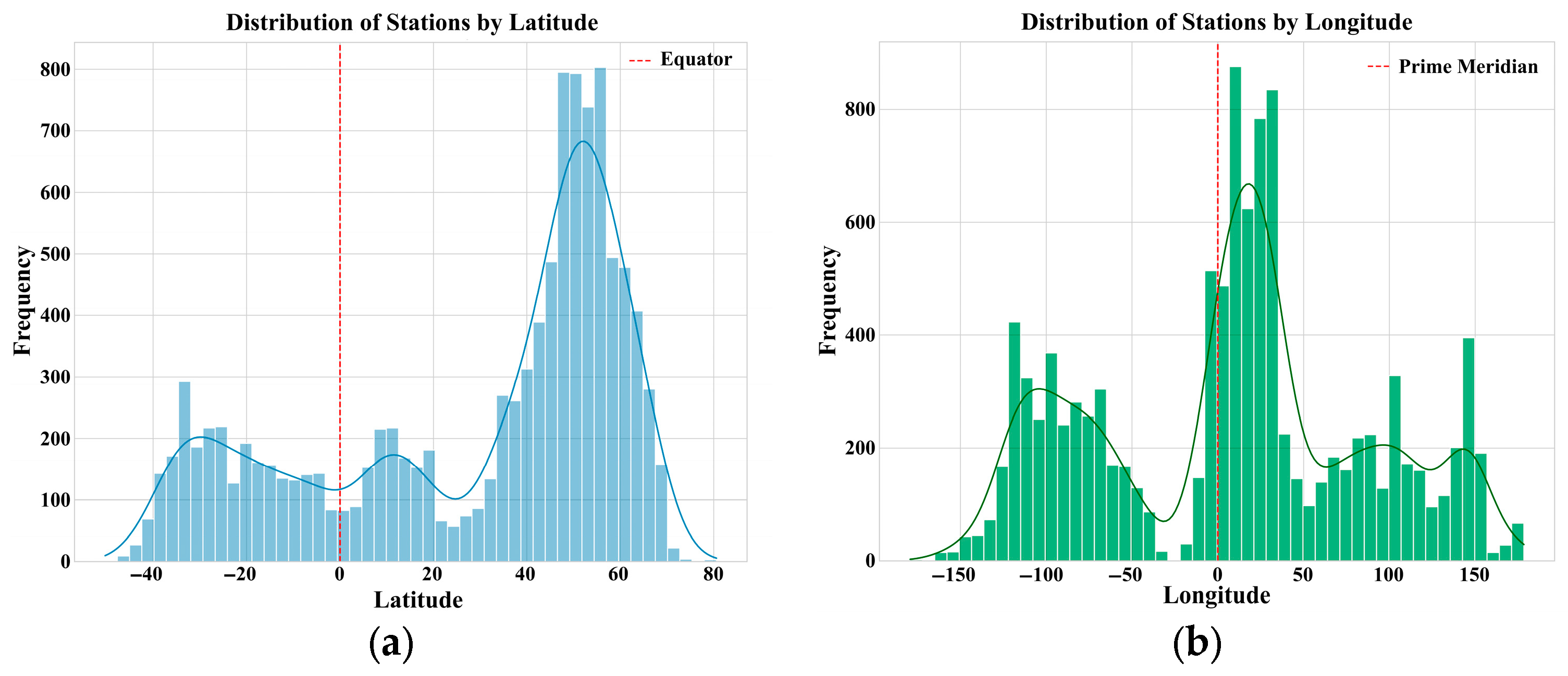
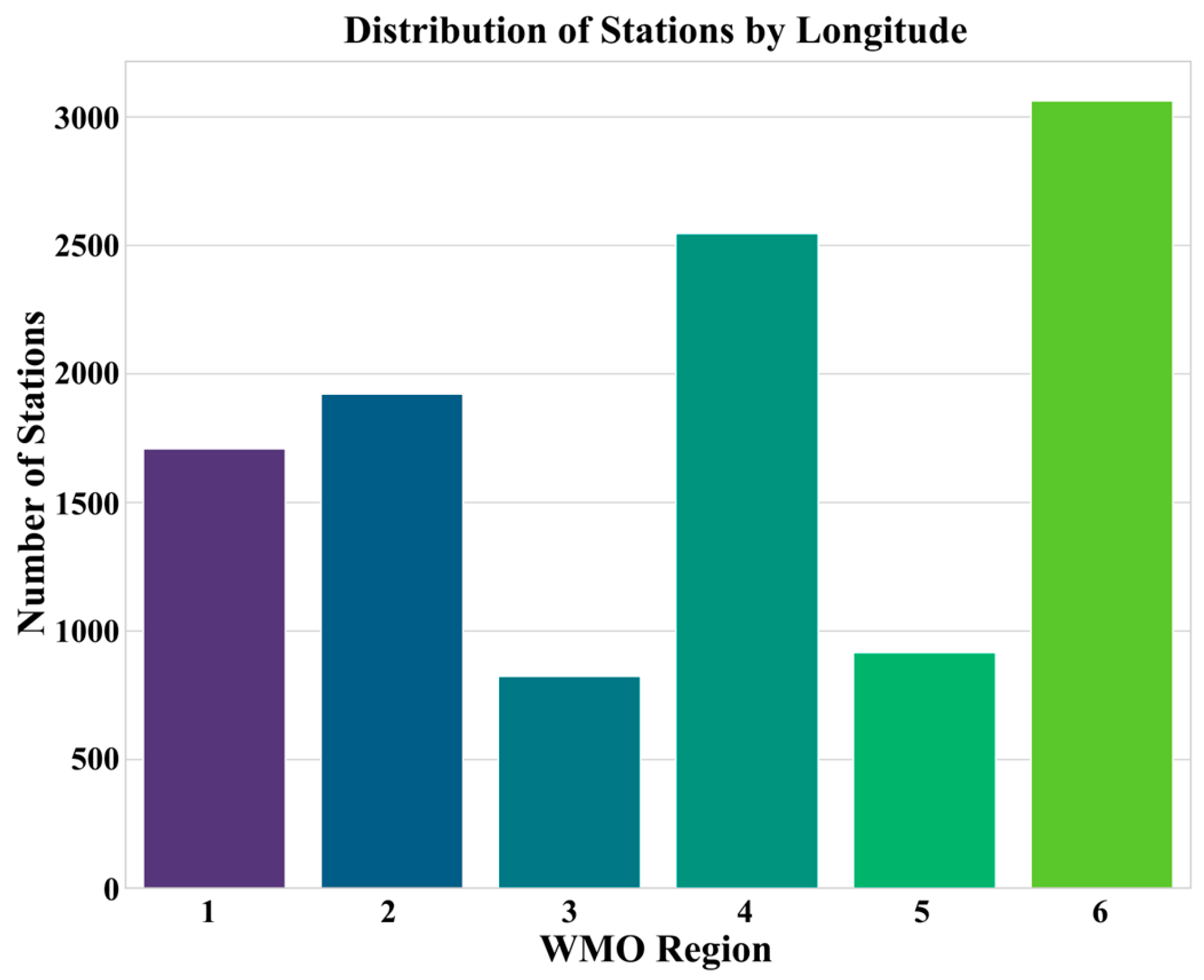
2.1. Data Source and Study Area
2.2. Data Preprocessing and Feature Engineering
2.3. Exploratory Data Analysis and Data Quality
2.4. Feature Selection and Relationship Analysis
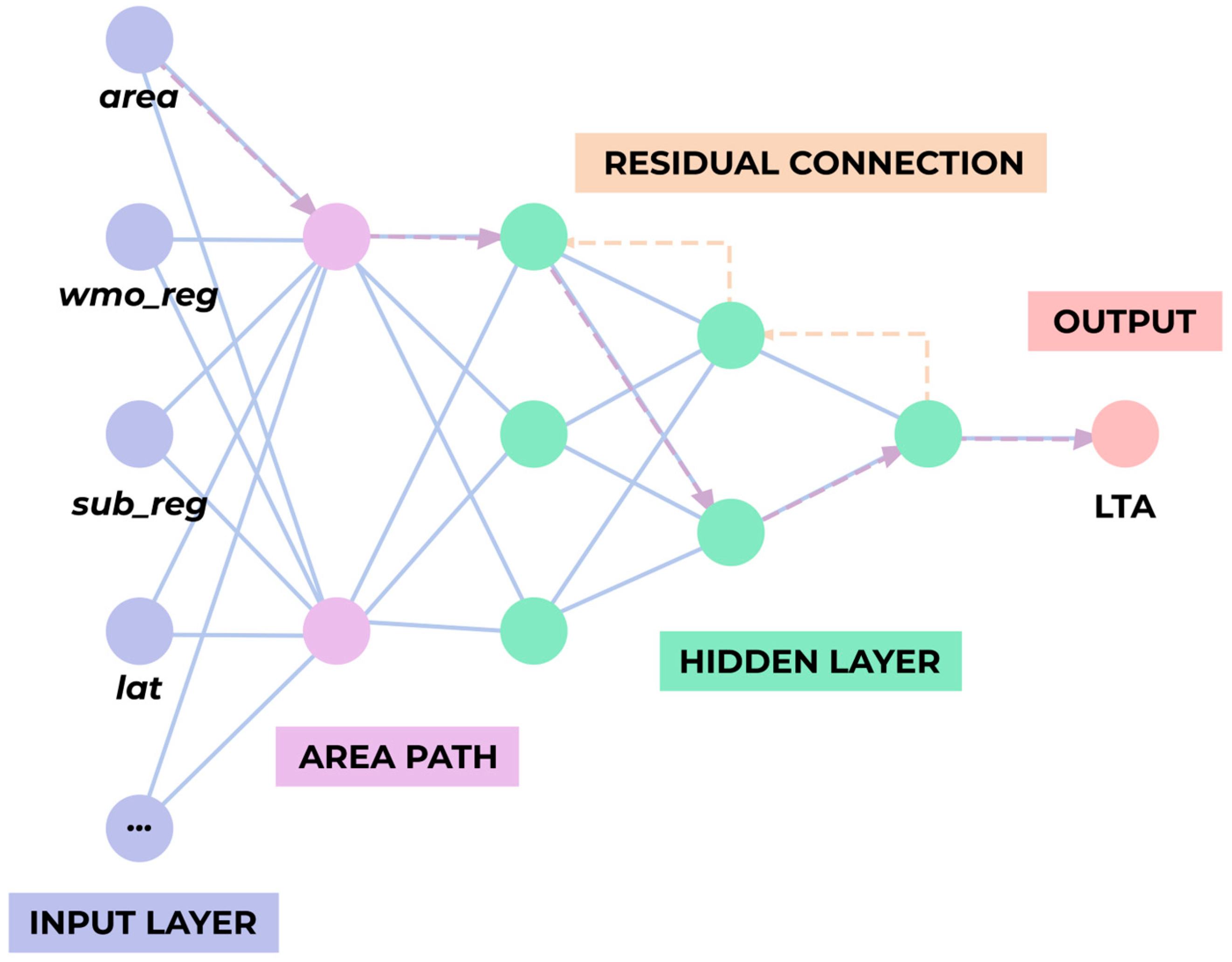
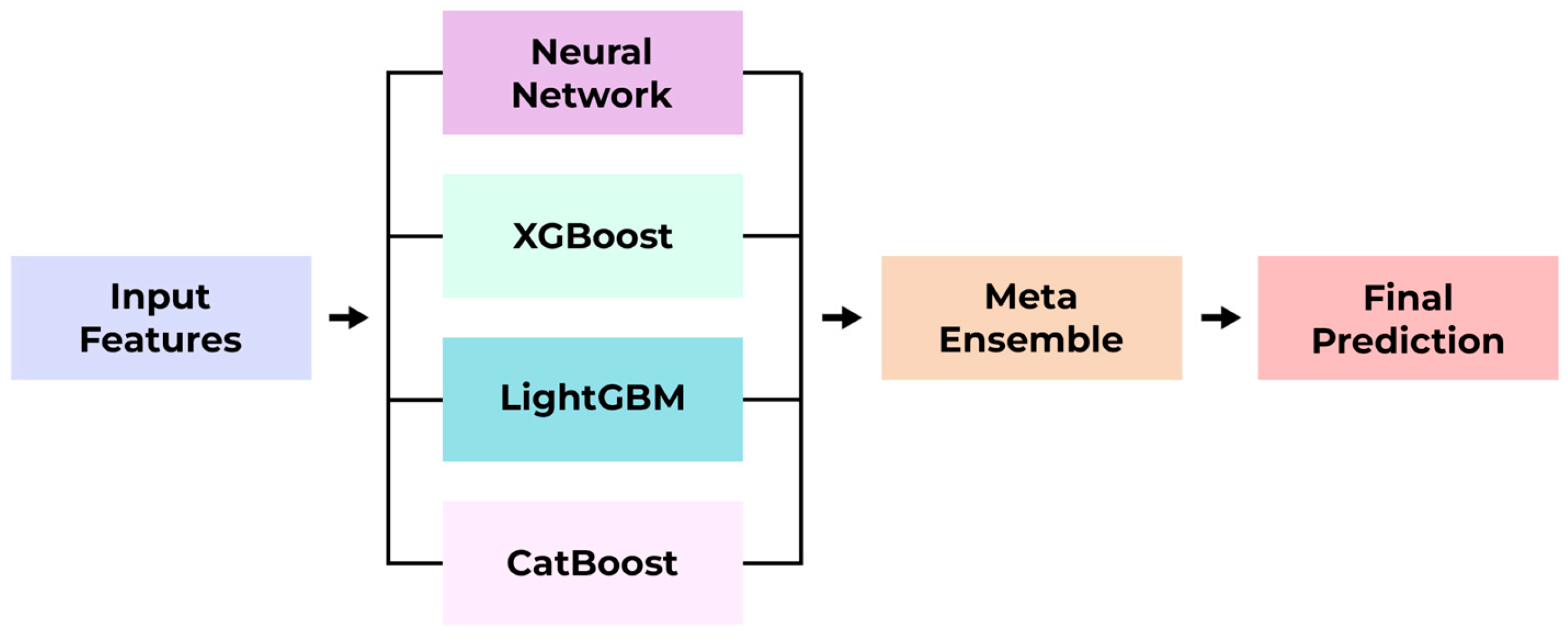
2.5. Predictive Model Development
2.6. Data Preparation for Modeling and Validation Strategy
2.7. Evaluation and Interpretation Methods
3. Results
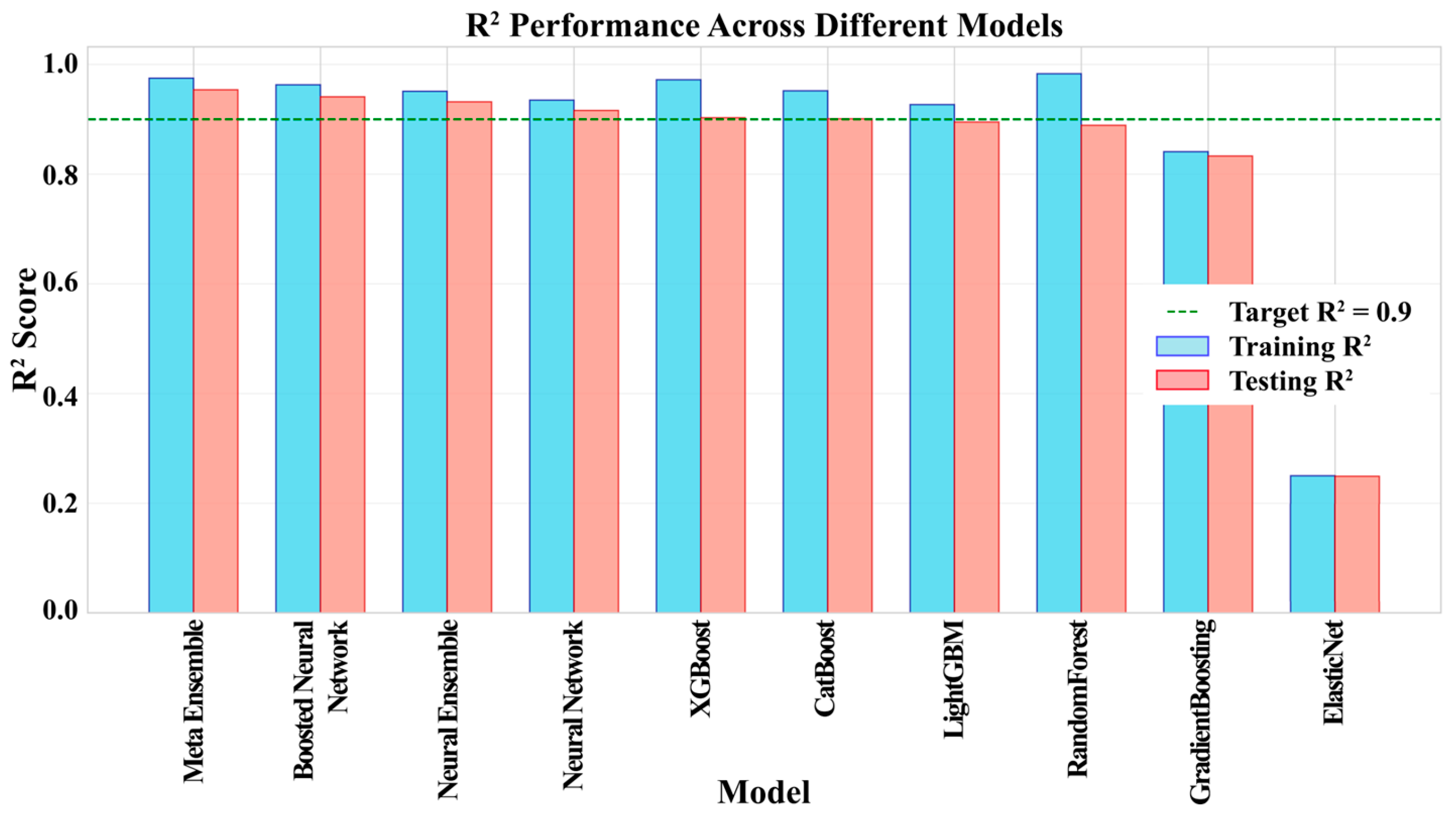
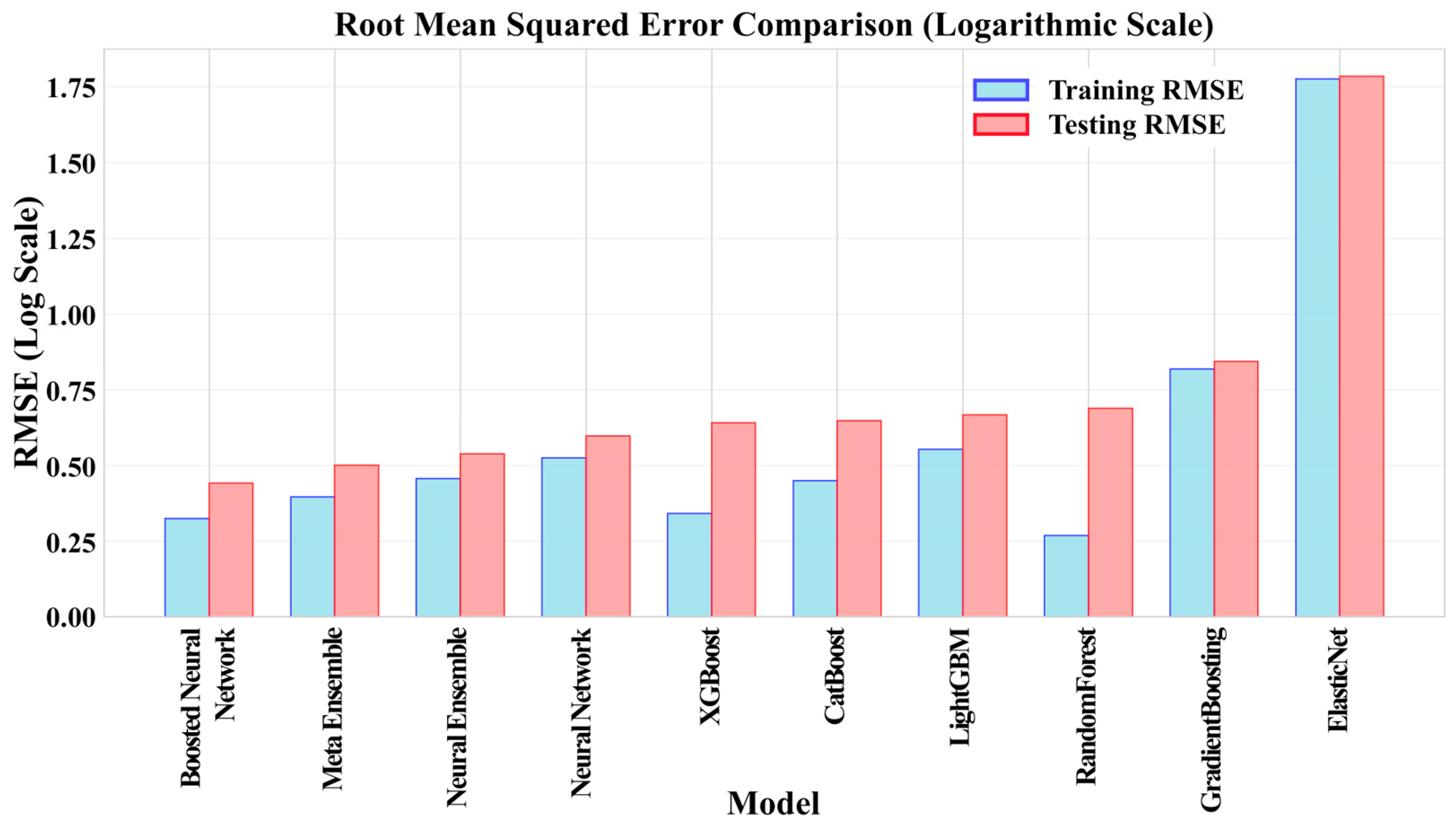
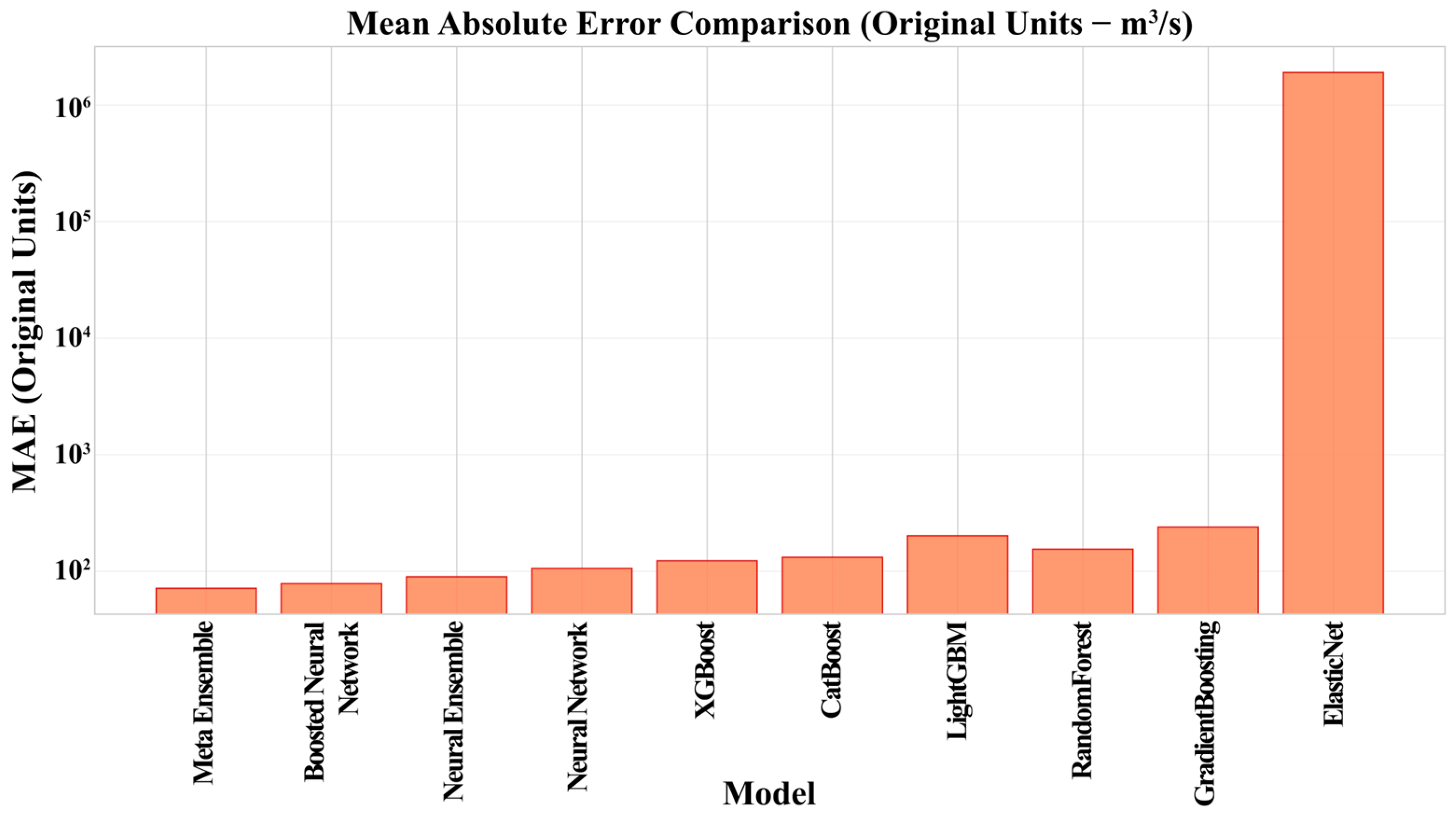
3.1. Comparative Model Performance
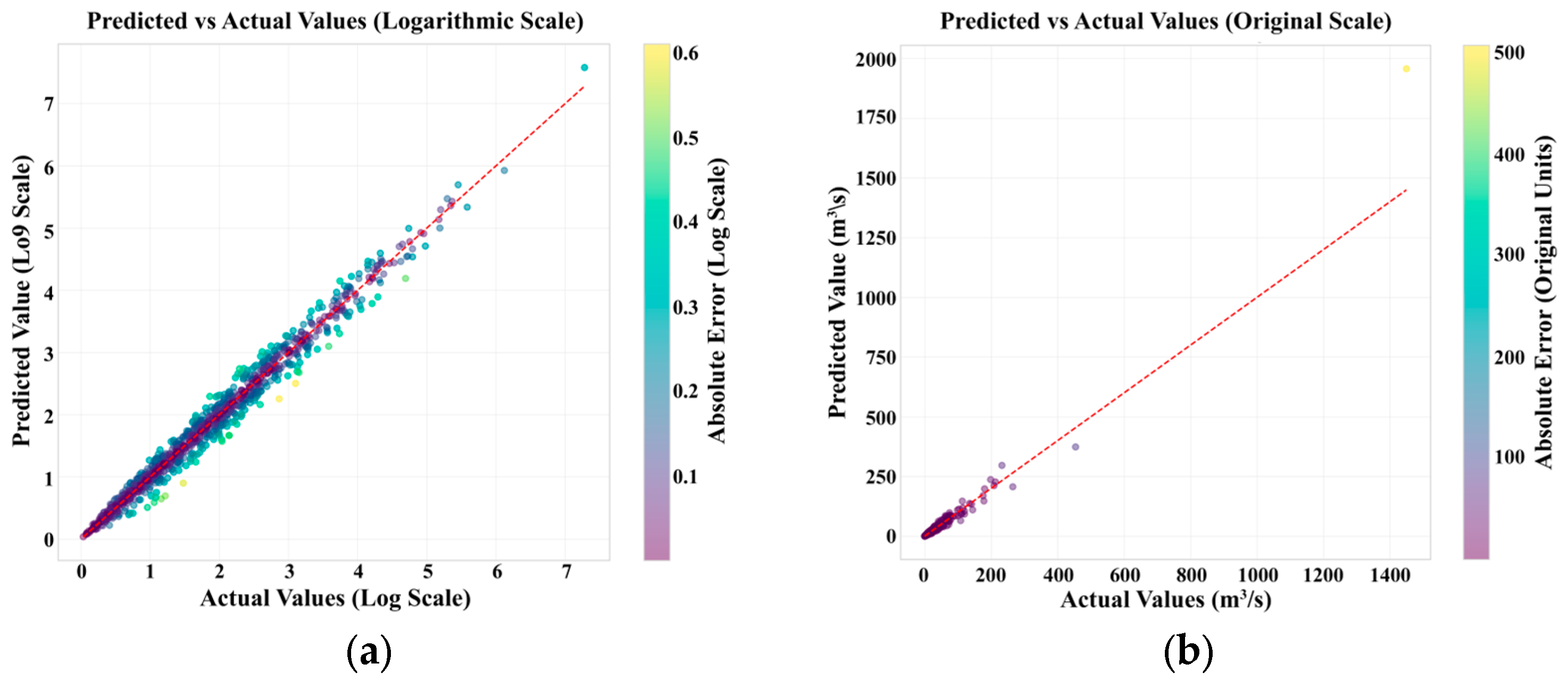
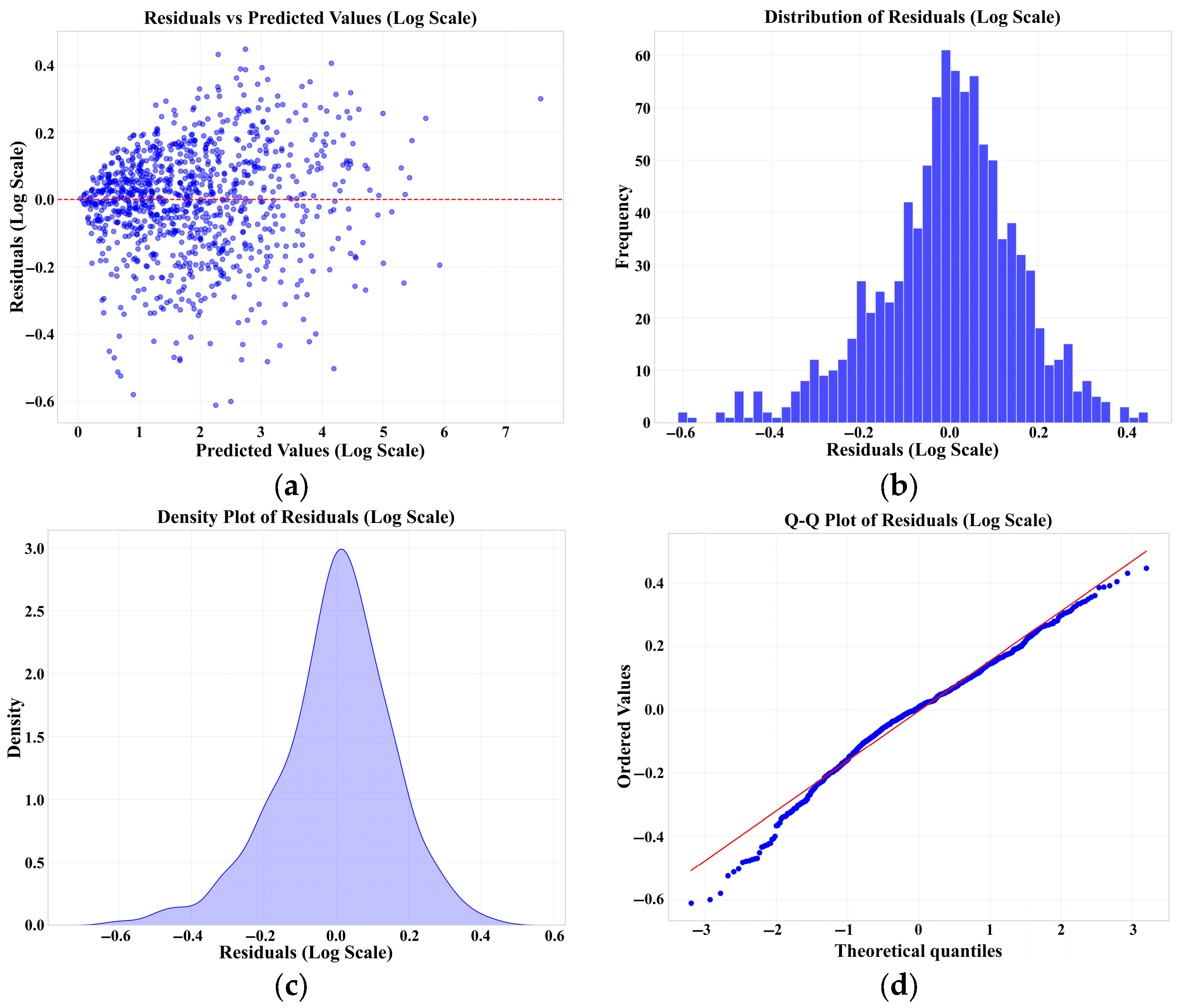
3.2. Final Model Performance and Validation
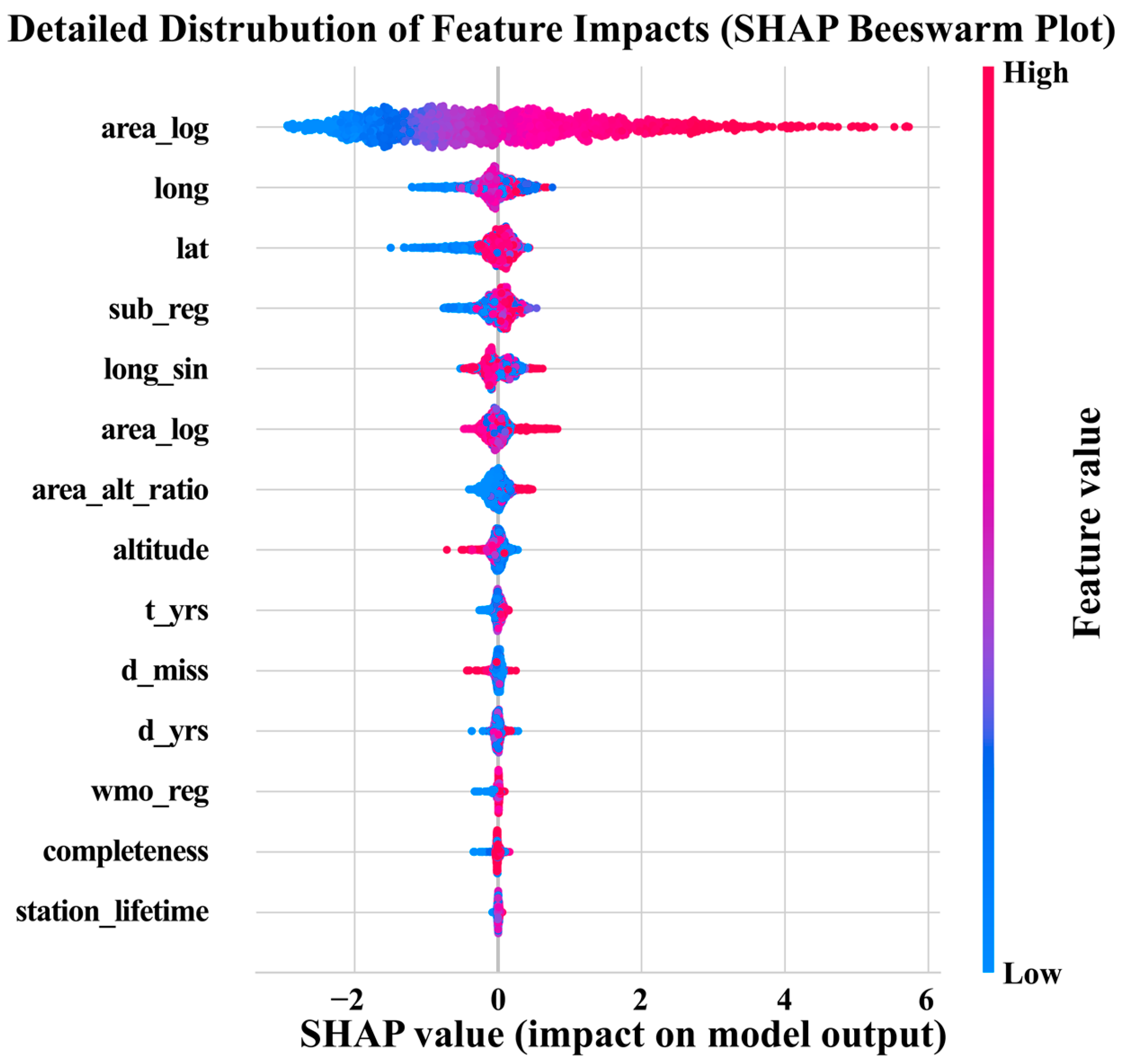
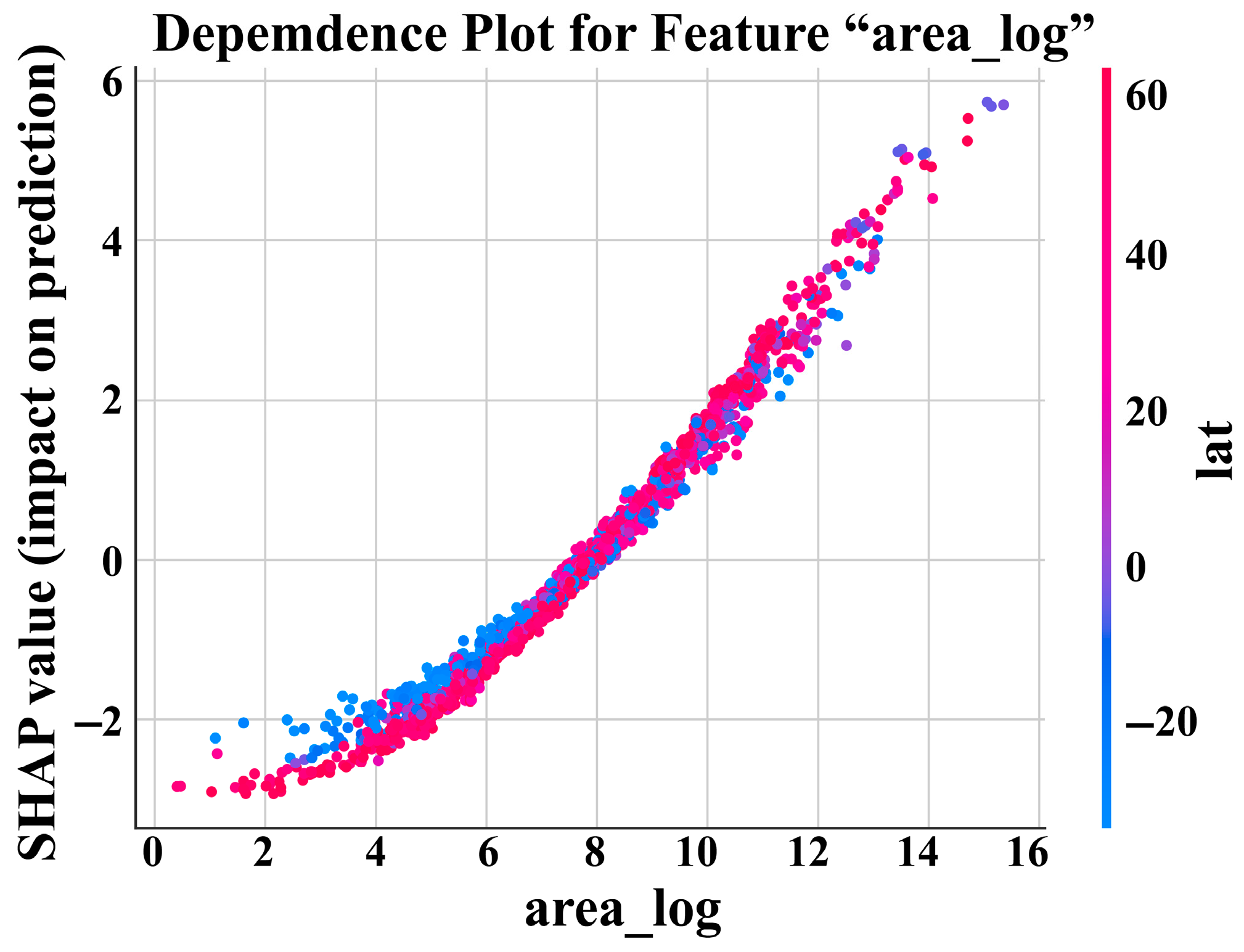
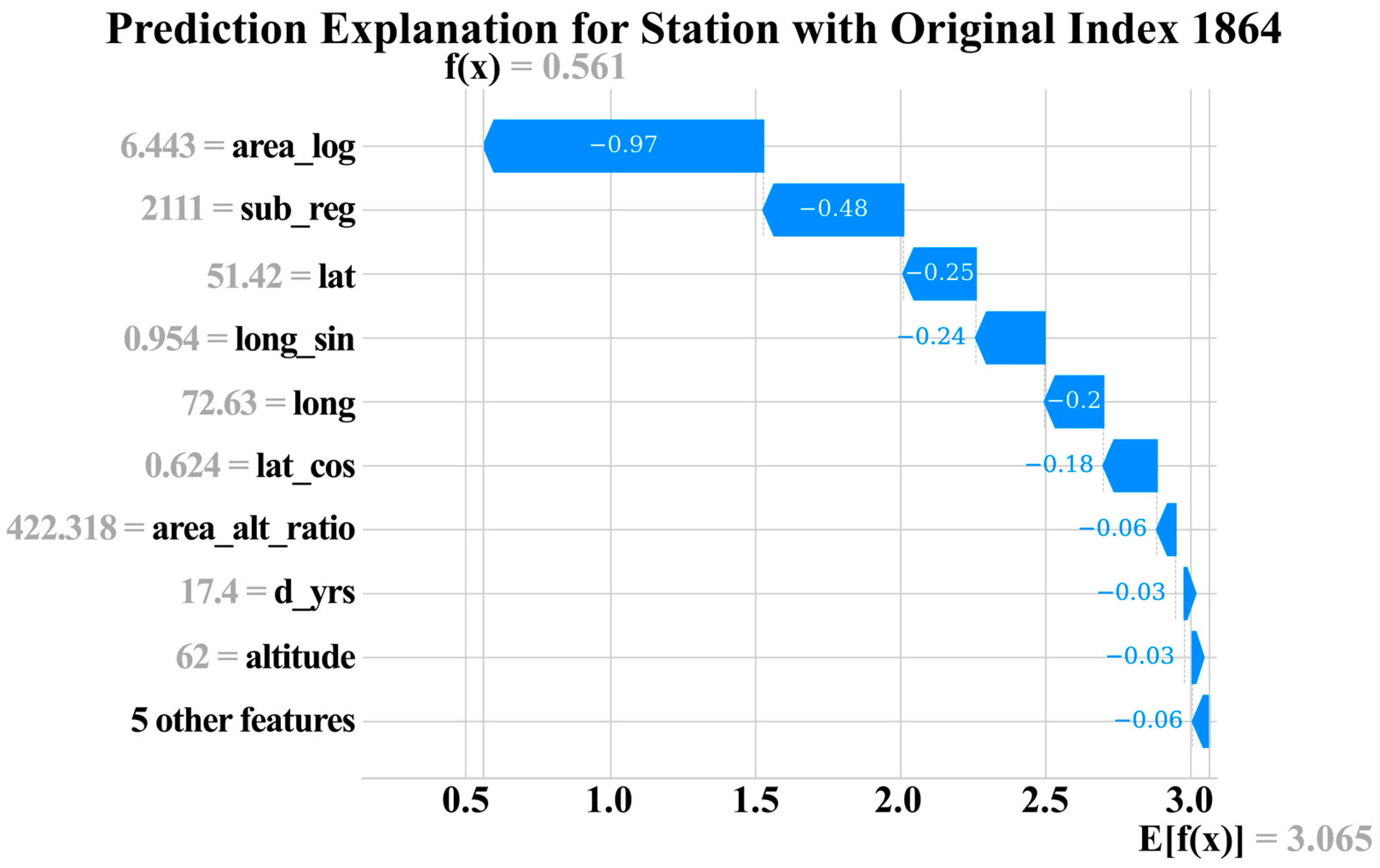
3.3. Model Interpretation and Feature Importance Using SHAP
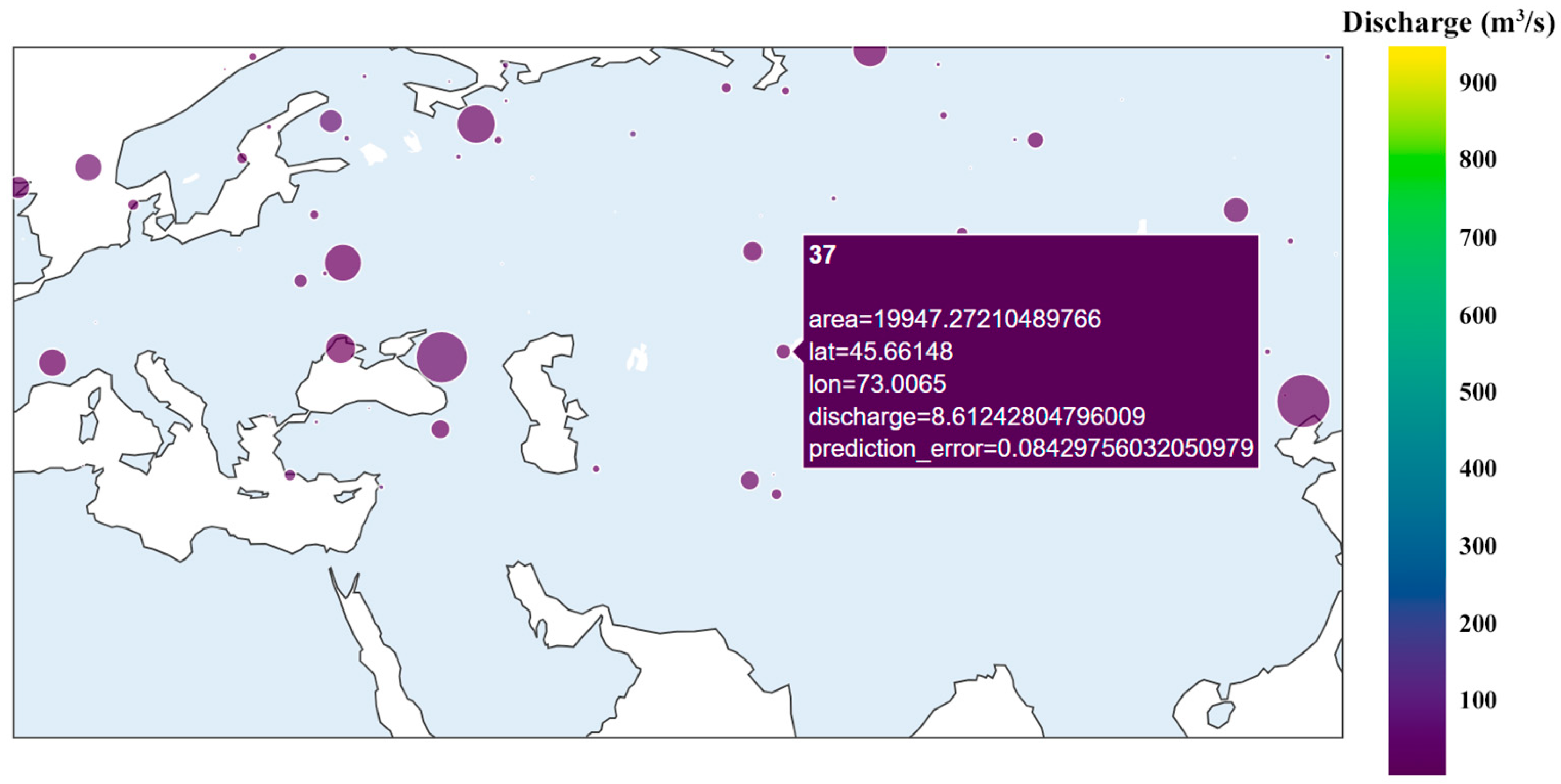
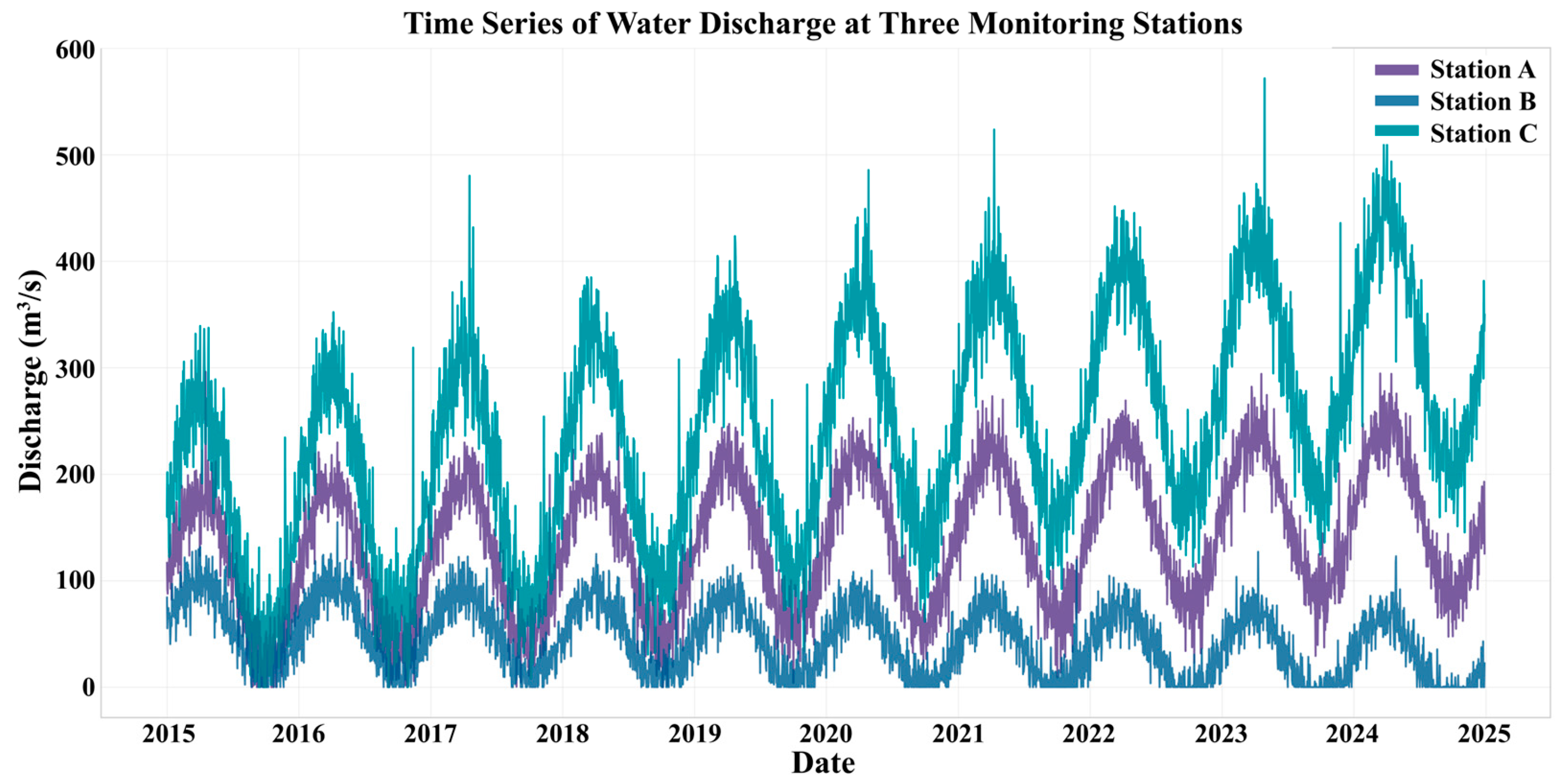
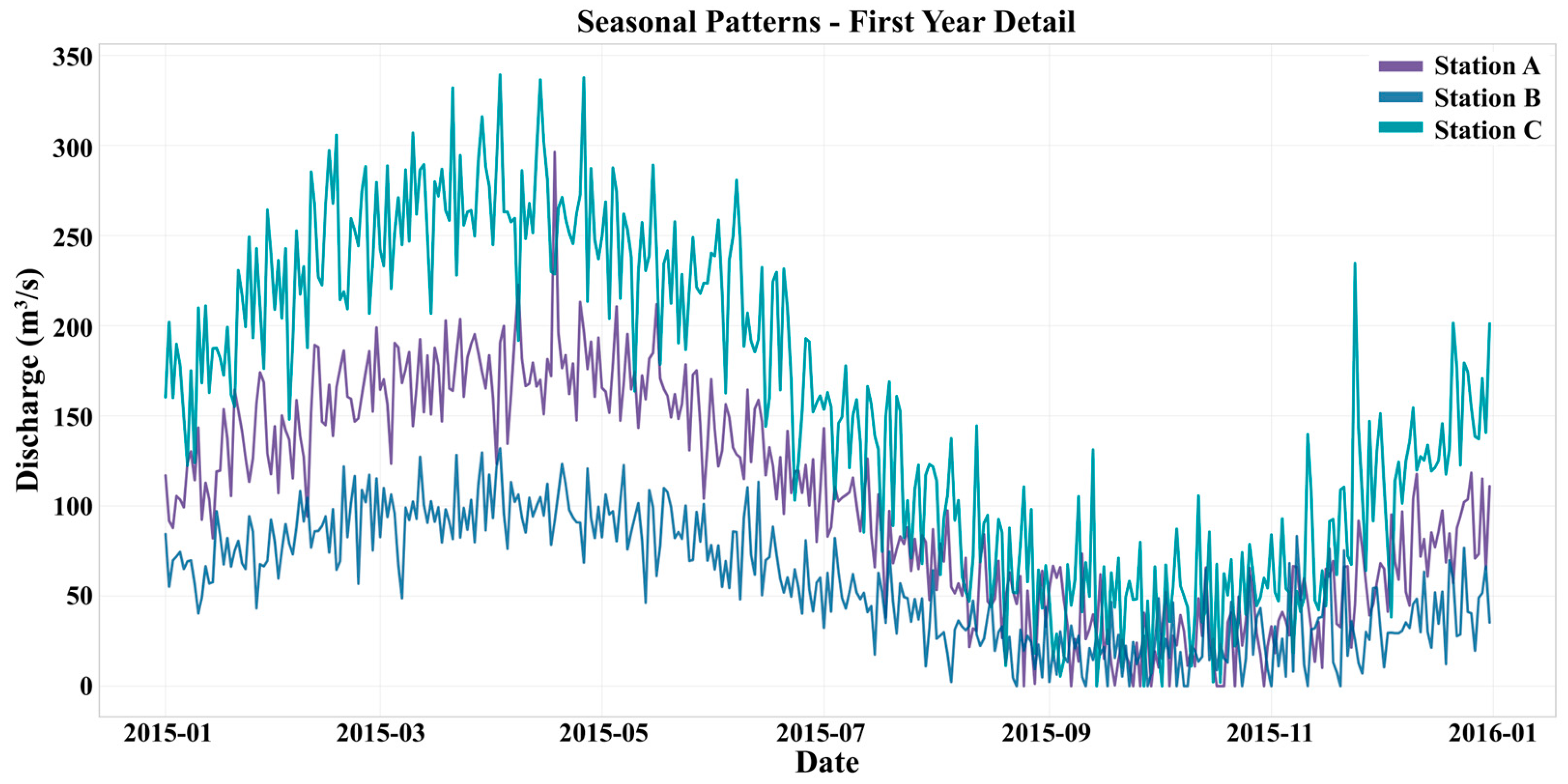
3.4. Example of Time Series Visualization
4. Discussion
4.1. Interpretation of Model Performance and Feature Importance
4.2. Comparison with Existing Research
4.3. Practical Implications and Potential for Operationalization
4.4. Limitations and Future Research Directions
5. Conclusions
- (1)
- The developed Meta Ensemble model, which integrates predictions from an optimized Neural Network and several Gradient Boosting Machines, achieved excellent predictive performance on an independent test set (R2 = 0.954, MAE = 71.3 m3/s). This significantly surpasses the accuracy of both baseline methods and individual advanced models, highlighting the power of hybrid ensembling for this hydrological task.
- (2)
- Model interpretability analysis using SHAP confirmed that the model learned physically plausible relationships. It identified catchment area as the most dominant predictor, with geographical location and regional identifiers playing a crucial secondary role in capturing spatial variability. This provides confidence that the model’s high accuracy is not a “black box” artifact but is grounded in hydrologically meaningful principles.
- (3)
- Rigorous data preprocessing and feature engineering were critical to the model’s success. The logarithmic transformation of the skewed target variable and the creation of interaction, ratio, and transformed geographical features were essential for achieving high performance.
- (4)
- The study demonstrates that it is feasible to build a robust and scalable tool for large-scale water resource assessment using readily available global metadata. This approach offers a valuable, cost-effective alternative to traditional methods, especially for preliminary assessments in ungauged or data-scarce basins.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CNN | Convolutional Neural Network |
| ETL | Extract, Transform, Load |
| IoT | Internet of Things |
| GBM | Gradient Boosting Machine |
| GRDC | Global Runoff Data Centre |
| MAE | Mean Absolute Error |
| NN | Neural Network |
| RMSE | Root Mean Squared Error |
| WMO | World Meteorological Organization |
References
- Zainuddin, A.A.; Hussin, A.A.A.; Annas, A.H.; Bharudin, M.S.; Razak, A.F.; Mahazir, M.N.B.; Puzi, A.A.; Handayan, D.; Raziff, A.R. Selective of IoT Applications for Water Quality Monitoring in Malaysia. Int. J. Percept. Cogn. Comput. 2024, 10, 8–16. [Google Scholar] [CrossRef]
- González, L.; Gonzales, A.; González, S.; Cartuche, A. A Low-Cost IoT Architecture Based on LPWAN and MQTT for Monitoring Water Resources in Andean Wetlands. SN Comput. Sci. 2024, 5, 144. [Google Scholar] [CrossRef]
- Raman, R.; Martin, N. IoT-Enabled Water Pollution Detection for Real-Time Monitoring and Pollution Source Identification with MQTT Protocol. In Proceedings of the 2024 International Conference on Advances in Data Engineering and Intelligent Computing 901 Systems (ADICS), Chennai, India, 18–19 April 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Galletti, A.; Avesani, D.; Bellin, A.; Majone, B. Detailed simulation of storage hydropower systems in large Alpine watersheds. J. Hydrol. 2019, 603, 127125. [Google Scholar] [CrossRef]
- Farabi, M.R.; Sintawati, A. Flood Early Warning System at Jakarta Dam Using Internet of Things (IoT)-Based Real-Time Fishbone Method to Support Industry 4.0. J. Soft Comput. Explor. 2024, 5, 99–106. [Google Scholar] [CrossRef]
- Dahane, A.; Benameur, R.; Naloufi, M.; Souihi, S.; Abreu, T.; Lucas, F.S.; Mellouk, A. IoT Urban River Water Quality System Using Federated Learning via Knowledge Distillation. In Proceedings of the 2024 IEEE International Conference on Communications (ICC 2024), Denver, CO, USA, 9–13 June 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1515–1520. [Google Scholar] [CrossRef]
- Nordling, K.; Fahrenbach, N.L.; Samset, B.H. Climate variability can outweigh the influence of climate mean changes for extreme precipitation under global warming. Atmos. Chem. Phys. 2025, 25, 1659–1684. [Google Scholar] [CrossRef]
- More, K.; Morey, U.; Motade, P.; Muchandi, A.; Motewar, S.; Mukkawar, K. GREEN GUARDIAN: IoT Driven Water Management for Sustainable Agriculture. In Proceedings of the 2024 2nd International Conference on Advances in Computation, Communication and Information Technology (ICAICCIT), Faridabad, India, 28–29 November 2024; IEEE: Piscataway, NY, USA, 2024; Volume 1, pp. 1354–1359. [Google Scholar] [CrossRef]
- Promput, S.; Maithomklang, S.; Panya-isara, C. Design and Analysis Performance of IoT-Based Water Quality Monitoring System using LoRa Technology. TEM J. 2023, 12, 49–54. [Google Scholar] [CrossRef]
- Majone, B.; Avesani, D.; Zulian, P.; Fiori, A.; Bellin, A. Analysis of high streamflow extremes in climate change studies: How do we calibrate hydrological models? Hydrol. Earth Syst. Sci. 2021, 26, 3863–3883. [Google Scholar] [CrossRef]
- Kumar, M.; Singh, T.; Maurya, M.K.; Shivhare, A.; Raut, A.; Singh, P.K. Quality Assessment and Monitoring of River Water Using IoT Infrastructure. IEEE Internet Things J. 2023, 10, 10280–10290. [Google Scholar] [CrossRef]
- Singh, J.; Srivastava, A.; Dalal, V. Designing of Real-time Communication Method to Monitor Water Quality using WSN Based on IoT. Int. J. Recent Innov. Trends Comput. Commun. 2023, 11, 437–446. [Google Scholar] [CrossRef]
- Olatinwo, S.O.; Joubert, T.H. Resource Allocation Optimization in IoT-Enabled Water Quality Monitoring Systems. Sensors 2023, 23, 8963. [Google Scholar] [CrossRef]
- Pires, L.M.; Gomes, J. River Water Quality Monitoring Using LoRa-Based IoT. Designs 2024, 8, 127. [Google Scholar] [CrossRef]
- Nasution, S.F.; Harmadi, H.; Suryadi, S.; Widiyatmoko, B. Development of River Flow and Water Quality Using IoT-based Smart Buoys Environment Monitoring System. J. Ilmu Fisika Univ. Andalas 2023, 16, 1–12. [Google Scholar] [CrossRef]
- Vaidya, R.; Bardekar, A.A. Analysis of Water Quality using IoT. J. Inf. Syst. Eng. Manag. 2025, 10, 1–7. [Google Scholar] [CrossRef]
- Wang, L.; Cuia, S.; Lid, Y.; Huang, H.; Manandhar, B.; Nitivattananon, V.; Fang, X.; Huang, W. A review of the flood management: From flood control to flood resilience. Heliyon 2022, 8, e11763. [Google Scholar] [CrossRef]
- Handini, W.; Widanti, N.; Lestari, S.W.; Haqq, A.R.; Hafizh, A.; Mulyadi, B. Design of Microhydro Power Plant Prototype by Utilizing Irrigation Water in Rice Fields Based on IoT. J. Penelit. Pendidik. IPA 2024, 10, 7144–7150. [Google Scholar] [CrossRef]
- Ashley, M.; David, M.; Iriana, R. Pembuatan Prototype Alat Monitoring Kualitas Air Berbasis Internet of Things (IoT). J. Ilm. Tek. 2024, 3, 92–102. [Google Scholar] [CrossRef]
- Akash, S.; Sahoo, S.; Vijayalakshmi, M. Enhancing High-Density Fish Farming in a Biofloc System Through IoT Driven Monitoring System. In Proceedings of the 2024 8th International Conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 6–8 November 2024; IEEE: Piscataway, NY, USA, 2024; pp. 472–477. [Google Scholar] [CrossRef]
- Nishan, R.K.; Akter, S.; Sony, R.I.; Hoque, M.M.; Anee, M.J.; Hossain, A. Development of an IoT-based multi-level system for real-time water quality monitoring in industrial wastewater. Discov. Water 2024, 4, 43. [Google Scholar] [CrossRef]
- Ghorpade, A.M.; Nanaware, J.D. IoT Based Real Time Dam Water Level Monitoring System. J. Emerg. Technol. Innov. Res. 2020, 7, 266–269. [Google Scholar]
- Souilmi, F.Z.; Ghedda, K.; Fahde, A.; Fihri, F.Z.; Tahraoui, S.; Elasri, F.; Malki, M. Taxonomic diversity of benthic macroinvertebrates along the Oum Er Rbia River (Morocco): Implications for water quality bio-monitoring using indicator species. Biodivers. Conserv. 2019, 27, 137–149. [Google Scholar]
- Ahmed, M.A.; Li, S.S. Machine Learning Model for River Discharge Forecast: A Case Study of the Ottawa River in Canada. Hydrology 2024, 11, 151. [Google Scholar] [CrossRef]
- Adeniyi, O.D.; Odigure, J.O. Water quality monitoring: A case study of water pollution in Minna and its environs in Nigeria. Botswana J. Technol. 2006, 14, 31–35. [Google Scholar] [CrossRef]
- Lee, B.W.; Yoon, J.; Ko, D.; Song, H. Optimization of Structural Scales for Ripraps and Gabions at Seadike Closure. J. Coast. Res. 2024, 116, 6–10. [Google Scholar] [CrossRef]
- Hebbache, M.; Zenati, N.; Belahcene, N.; Messadi, D.; Noureddine, Z. Impact of Hydraulic Developments on the Quality of Surface Water in the Mafragh Watershed, El Tarf, Algeria. Nat. Environ. Pollut. Technol. 2024, 23, 775–783. [Google Scholar] [CrossRef]
- Asadollahi, A.; Magar, B.A.; Poudel, B.; Sohrabifar, A.; Kalra, A. Application of Machine Learning Models for Improving Discharge Prediction in Ungauged Watershed: A Case Study in East DuPage, Illinois. Geographies 2024, 4, 363–377. [Google Scholar] [CrossRef]
- Fuentes-Peñailillo, F.; Ortega-Farías, S.; Acevedo-Opazo, C.; Rivera, M.; Araya-Alman, M. A Smart Crop Water Stress Index-Based IoT Solution for Precision Irrigation of Wine Grape. Sensors 2023, 24, 25. [Google Scholar] [CrossRef]
- Georgantas, I.; Mitropoulos, S.; Katsoulis, S.; Chronis, I.; Christakis, I. Integrated Low-Cost Water Quality Monitoring System Based on LoRa Network. Electronics 2025, 14, 857. [Google Scholar] [CrossRef]
- Wegehenkel, M.; Beyrich, F. Modelling hourly evapotranspiration and soil water content at the grass-covered boundary-layer field site Falkenberg, Germany. Hydrol. Sci. J. 2014, 59, 376–394. [Google Scholar] [CrossRef]
- Majoro, F.; Wali, U.G.; Munyaneza, O.; Naramabuye, F.X.; Mukamwambali, C. On-site and Off-site Effects of Soil Erosion: Causal Analysis and Remedial Measures in Agricultural Land—A Review. RJESTE 2020, 3, 1–19. [Google Scholar] [CrossRef]
- Behney, A.C. The Influence of Water Depth on Energy Availability for Ducks. J. Wildl. Manag. 2020, 84, 436–447. [Google Scholar] [CrossRef]
- Huang, C.; Chang, C.; Chang, C.; Tsai, M. Development of a lightweight convolutional neural network-based visual model for sediment concentration prediction by incorporating the IoT concept. J. Hydroinform. 2023, 25, 2660–2674. [Google Scholar] [CrossRef]
- Dimitriou, E.; Poulis, G.; Papadopoulos, A. Development of a water monitoring network based on open architecture and Internet-of-Things technologies. In Proceedings of the EGU General Assembly 2021, Online, 19–30 April 2021; p. EGU21-13460. [Google Scholar] [CrossRef]
- Hahn, Y.; Kienitz, P.; Wönkhaus, M.; Meyes, R.; Meisen, T. Towards Accurate Flood Predictions: A Deep Learning Approach Using Wupper River Data. Water 2024, 16, 3368. [Google Scholar] [CrossRef]
- Boonrat, P.; Boonrat, P.; Aharari, A. Precision Rehabilitation: IoT-Based Monitoring in Mangrove Ecosystems. In Proceedings of the 2024 IEEE 4th International Conference on Electronic Communications, Internet of Things and Big Data (ICEIB), Taipei, Taiwan, 19–21 April 2024; IEEE: Piscataway, NY, USA, 2024; pp. 145–149. [Google Scholar] [CrossRef]
- Sudibyo, H.; Yuniko, F.T.; Fadel, A.; Lesmana, L.S.; Efendi, R. Sistem Monitoring Budidaya Perikanan Berbasis IoT Fish Feeder Sebagai Implementasi Smart Farming. JOISIE 2024, 8, 236–247. [Google Scholar] [CrossRef]
- Boudville, R.; Tapah, J.B.; Yuzi, A.A.; Johan, N.A.; Daing, M.I.; Aliastar, N.A. Development of IoT-based Headwater Phenomenon Monitoring and Warning System. In Proceedings of the 2024 IEEE 14th International Conference on Control System, Computing and Engineering (ICCSCE), Penang, Malaysia, 23–24 August 2024; IEEE: Piscataway, NY, USA, 2024; pp. 232–236. [Google Scholar] [CrossRef]
- Anda, M.; Fornarelli, R.; Dallas, S.; Schmack, M.; Byrne, J.; Morrison, G.M.; Fox-Reynolds, K. Ultrasonic Smart Metering: Realising the Benefits of Residential Hybrid Water Systems. In WEC2019: World Engineers Convention; Engineers Australia: Melbourne, Australia, 2019; pp. 927–938. [Google Scholar]
- Don, A.A.; Felimar, T.L. Comparative Study of Intrusion Detection Systems against Mainstream Network Sniffing Tools. Int. J. Eng. Technol. 2018, 7, 188–191. [Google Scholar] [CrossRef]
- Mahaasin, H.I.; Kusuma, P.D.; Hasibuan, F.C. Back-end website development for IoT-based automated water dissolved oxygen control. J. Comput. Eng. Progr. Appl. Technol. 2023, 2, 36–43. [Google Scholar] [CrossRef]
- Rajashree, N.; Nithisha, Y.S.; Shaheen, S.; Govardhan, P. An IoT Approach for Monitoring Aqua Culture Using GSM Module. IRE Journals. 2020, 3, 284–288. [Google Scholar]
- Miskon, M.T.; Makmud, M.Z.H.; Zacharee, M.; Abd Rahman, A.B. Real-Time Hardware-In-The-Loop Simulation of IoT-Enabled Mini Water Treatment Plant. In Proceedings of the 2024 IEEE International Conference on Automatic Control and Intelligent Systems (I2CACIS), Shah Alam, Malaysia, 29 June 2024; IEEE: Piscataway, NY, USA, 2024; pp. 319–324. [Google Scholar] [CrossRef]
- Bărbulescu, A.; Zhen, L. Forecasting the River Water Discharge by Artificial Intelligence Methods. Water 2024, 16, 1248. [Google Scholar] [CrossRef]
- Huang, J.; Chen, J.; Huang, H.; Cai, X. Deep Learning-Based Daily Streamflow Prediction Model for the Hanjiang River Basin. Hydrology 2025, 12, 168. [Google Scholar] [CrossRef]
- Abdurrafi, A.; Maulana, D.; Kurniadi, N.T. Optimization Water Conservation Through IoT Sensor Implementation At Smartneasy Nusantara. J. Appl. Intell. Syst. 2023, 8, 432–441. [Google Scholar] [CrossRef]
- Workneh, H.A.; Jha, M.K. Utilizing Deep Learning Models to Predict Streamflow. Water 2025, 17, 756. [Google Scholar] [CrossRef]
- Ziadi, S.; Chokmani, K.; Chaabani, C.; El Alem, A. Deep Learning-Based Automatic River Flow Estimation Using RADARSAT Imagery. Remote Sens. 2024, 16, 1808. [Google Scholar] [CrossRef]
- Liu, W.; Zou, P.; Jiang, D.; Quan, X.; Dai, H. Computing River Discharge Using Water Surface Elevation Based on Deep Learning Networks. Water 2023, 15, 3759. [Google Scholar] [CrossRef]
- Francisco, R.; Matos, J.P. Deep Learning Prediction of Streamflow in Portugal. Hydrology 2024, 11, 217. [Google Scholar] [CrossRef]
- Zhen, L.; Bărbulescu, A. Quantum Neural Networks Approach for Water Discharge Forecast. Appl. Sci. 2025, 15, 4119. [Google Scholar] [CrossRef]
- Almaaitah, T.; Joksimovic, D.; Sajin, T. Real-Time IoT-Enabled Water Management for Rooftop Urban Agriculture Using Commercial Off-the-Shelf Products. Chem. Proc. 2022, 10, 34. [Google Scholar] [CrossRef]
- Rosa, S.L.; Kadir, E.A.; Siswanto, A.; Othmand, M.; Daud, H. Identifying Water Pollution Sources Using Real-Time Monitoring and IoT. Int. J. Adv. Sci. Eng. Inf. Technol. 2022, 12, 2122–2131. [Google Scholar] [CrossRef]
- Chowdurya, M.S.; Emran, T.B.; Ghosh, S.; Pathak, A.; Alam, M.M.; Absar, N.; Andersson, K.; Shahadat, M.; Hossain, S.; Subhasish, H. IoT-Based Real-Time River Water Quality Monitoring System. Procedia Comput. Sci. 2019, 155, 161–168. [Google Scholar] [CrossRef]
- Chaarmart, K.; Jeebkaew, K.; Sripa, S.; Burtyothee, W. Solar Cells Powered Boat for Water Quality Monitoring of Nonghan River Using Wireless Sensor. J. Ind. Technol. Innov. 2024, 3, 254028. [Google Scholar] [CrossRef]
- Youssef, S.B.; Rekhis, S.; Boudriga, N. A Blockchain-Based Secure IoT Solution for Dam Surveillance. In Proceedings of the 2019 IEEE Wireless Communications and Networking Conference (WCNC), Marrakesh, Morocco, 15–18 April 2019; IEEE: Piscataway, NY, USA, 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Dhandre, N.M.; Kamalasekaran, P.D.; Pandey, P. Dam Parameters Monitoring System. In Proceedings of the 2016 7th India International Conference on Power Electronics (IICPE), Patiala, India, 17–19 November 2016; IEEE: Piscataway, NY, USA, 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Sharifi, L.; Kamel, S.; Feizizadeh, B. Monitoring Bioenvironmental Impacts of Dam Construction on Land Use/Cover Changes in Sattarkhan Basin Using Multi-Temporal Satellite Imagery. Iran. J. Energy Environ. 2015, 6, 39–46. [Google Scholar] [CrossRef]
- Chen, S.; Yang, H.; Zheng, H. Intercomparison of Runoff and River Discharge Reanalysis Datasets at the Upper Jinsha River, an Alpine River on the Eastern Edge of the Tibetan Plateau. Water 2025, 17, 871. [Google Scholar] [CrossRef]
- BfG-GRDC Data Download. Available online: https://portal.grdc.bafg.de/applications/public.html?publicuser=PublicUser#dataDownload/StationCatalogue (accessed on 4 May 2025).
- Yong, K.; Li, M.; Xiao, P.; Gao, B.; Zheng, C. Monthly Streamflow Forecasting for the Irtysh River Based on a Deep Learning Model Combined with Runoff Decomposition. Water 2025, 17, 1375. [Google Scholar] [CrossRef]
- Irawan, B.; Fahmi, F.; Zamzami, E.M. Optimizing K-Nearest Neighbor Values Using The Elbow Method. In Proceedings of the 2024 Ninth International Conference on Informatics and Computing (ICIC), Medan, Indonesia, 24–25 October 2024; IEEE: Piscataway, NY, USA, 2024; pp. 1–4. [Google Scholar] [CrossRef]
- Guo, H.; Liu, X.; Zhang, Q. Identifying Daily Water Consumption Patterns Based on K-Means Clustering, Agglomerative Hierarchical Clustering, and Spectral Clustering Algorithms. AQUA 2024, 73, 870–887. [Google Scholar] [CrossRef]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A.A. Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; Volume 31, pp. 4278–4284. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: Piscataway, NY, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Dolhopolov, S.; Honcharenko, T.; Terentyev, O.; Savenko, V.; Rosynskyi, A.; Bodnar, N.; Alzidi, E. Multi-Stage Classification of Construction Site Modeling Objects Using Artificial Intelligence Based on BIM Technology. In Proceedings of the 35th Conference of Open Innovations Association (FRUCT), Tampere, Finland, 24–26 April 2024; FRUCT: Helsinki, Finland, 2024; pp. 179–185. [Google Scholar] [CrossRef]
- Zhang, L.; Jánošík, D. Enhanced Short-Term Load Forecasting with Hybrid Machine Learning Models: CatBoost and XGBoost Approaches. Expert Syst. Appl. 2024, 241, 122686. [Google Scholar] [CrossRef]
- Zhou, Y.; Pan, J.; Shao, G. A Comparative Study of a Two-Dimensional Slope Hydrodynamic Model (TDSHM), Long Short-Term Memory (LSTM), and Convolutional Neural Network (CNN) Models for Runoff Prediction. Water 2025, 17, 1380. [Google Scholar] [CrossRef]
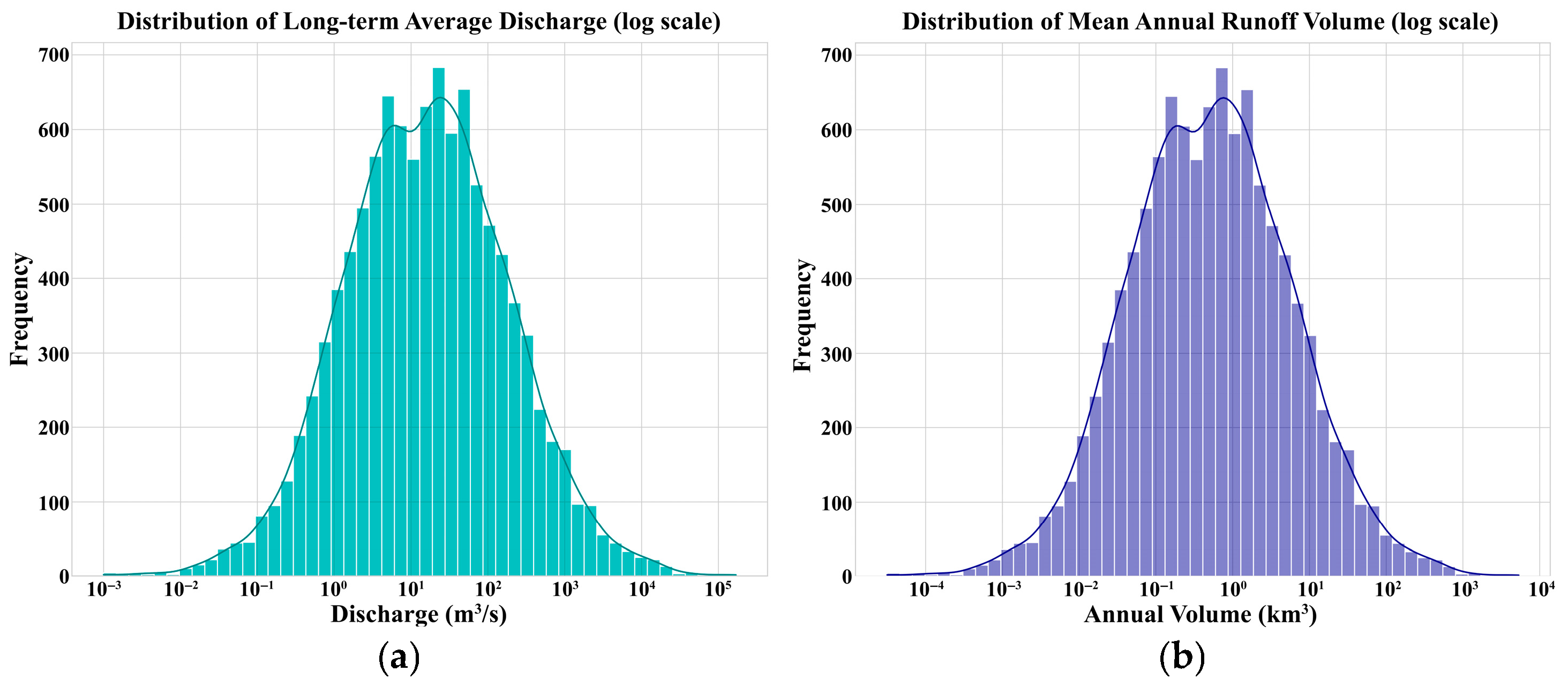
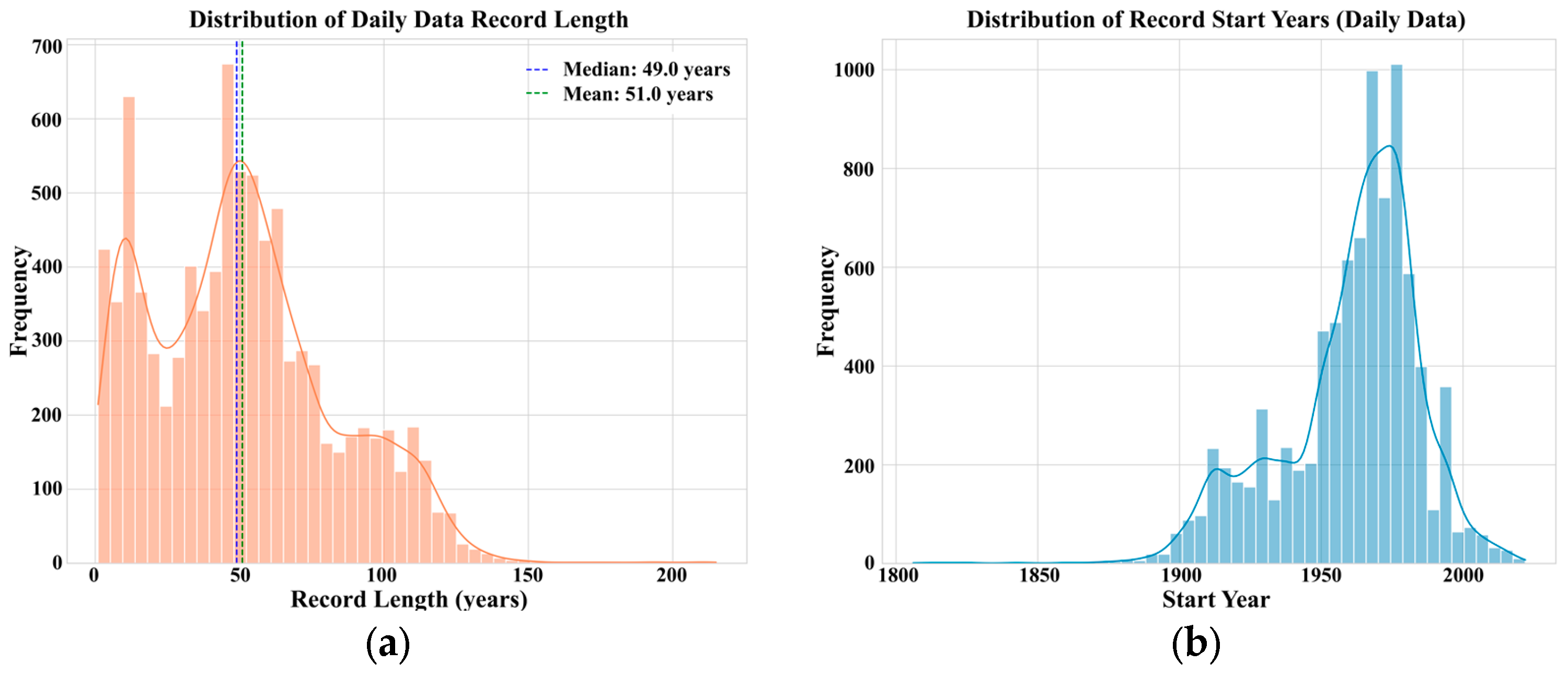
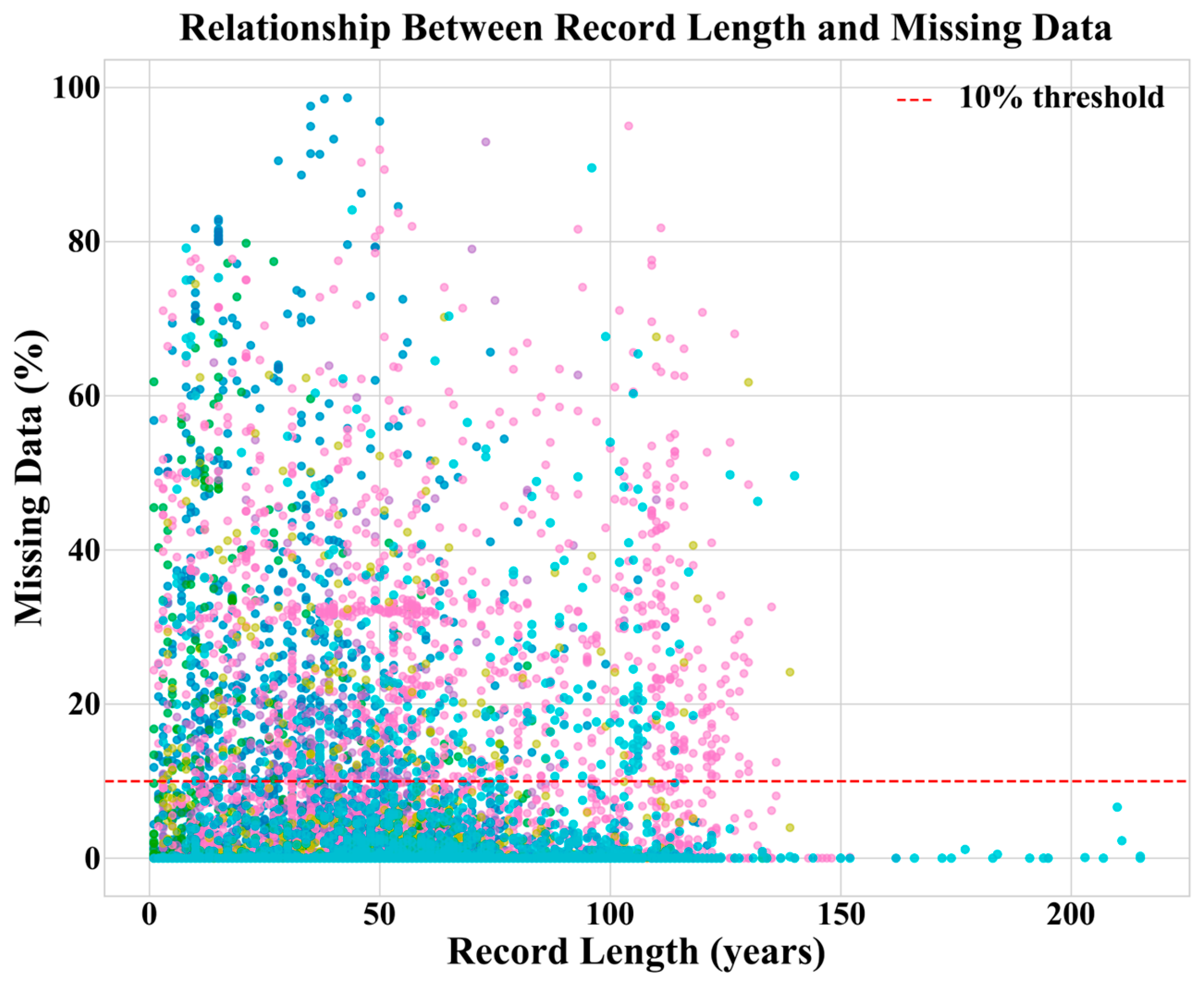
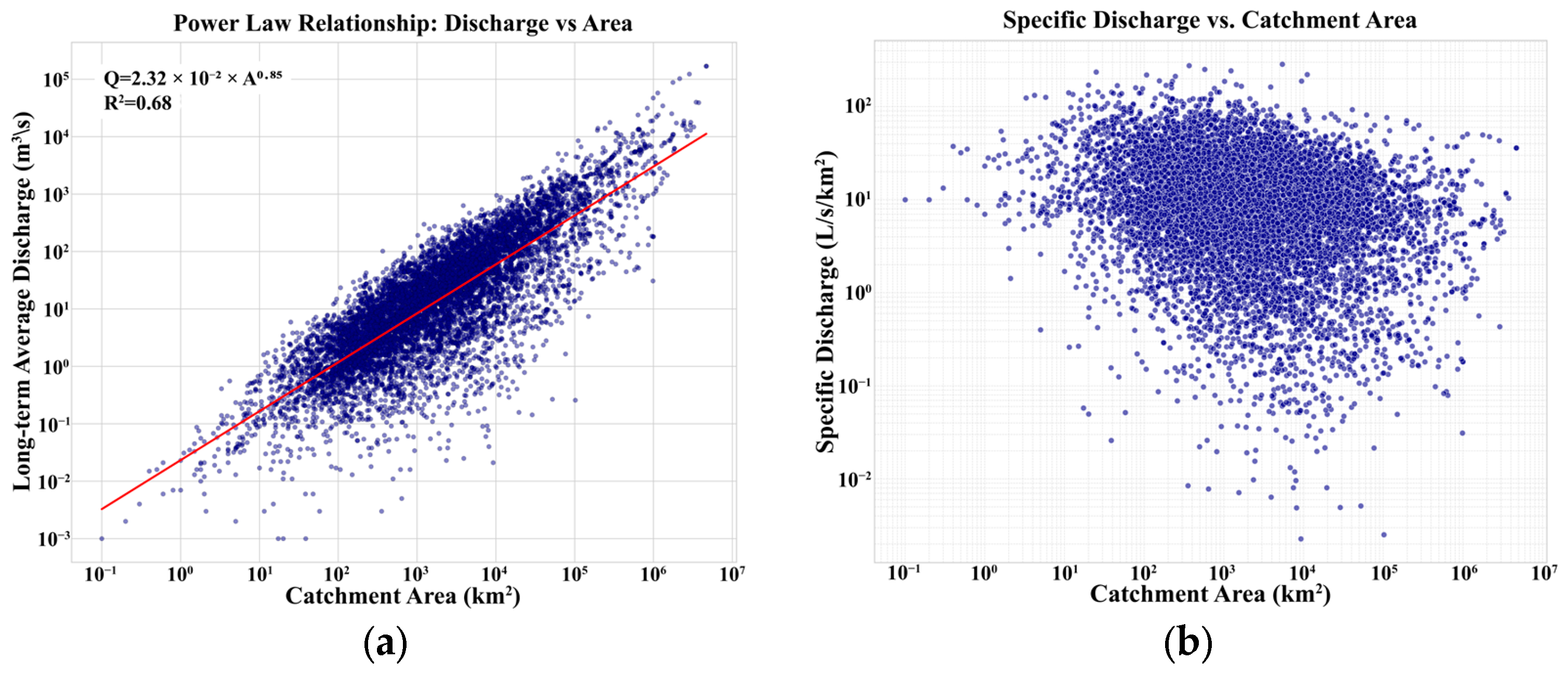
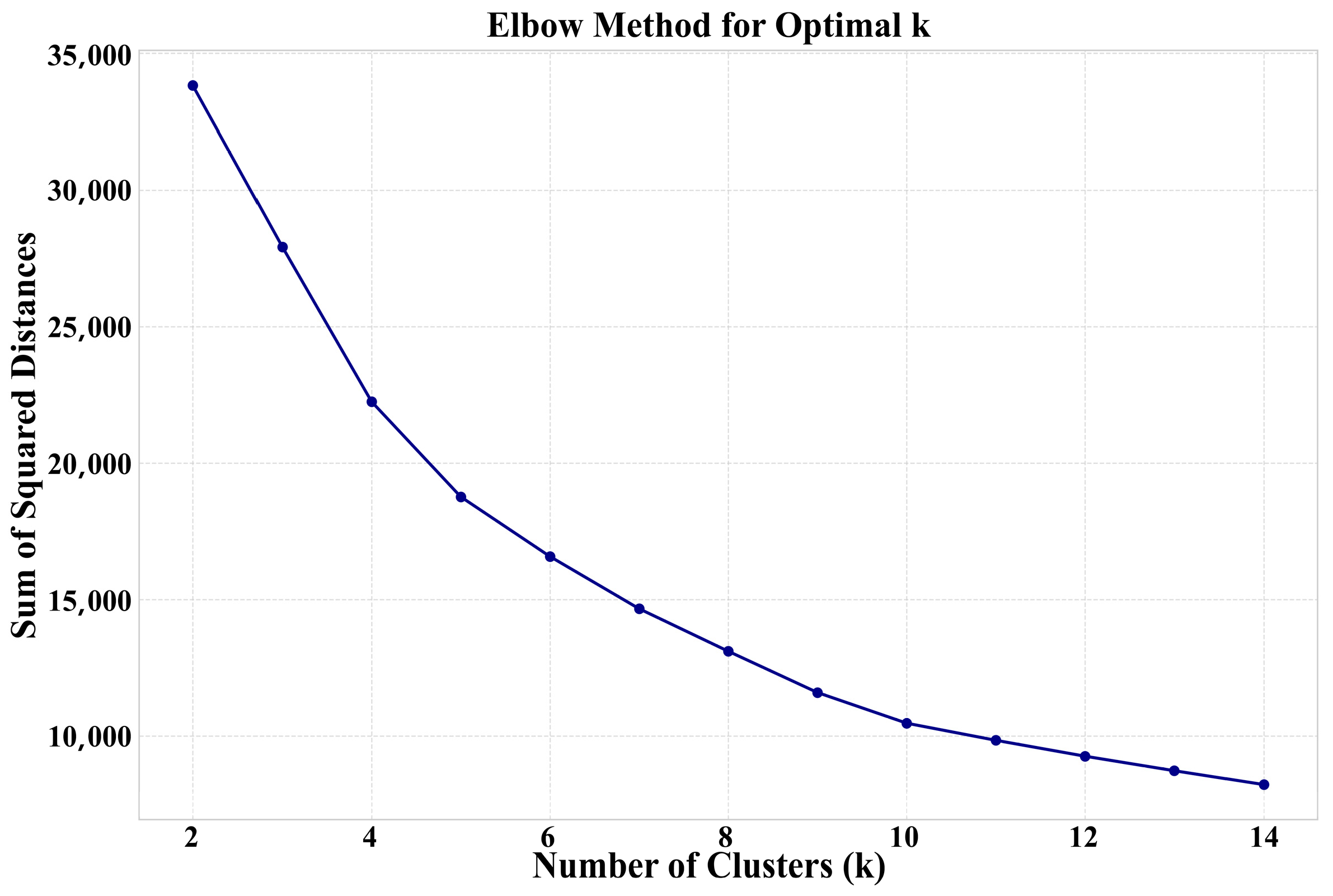

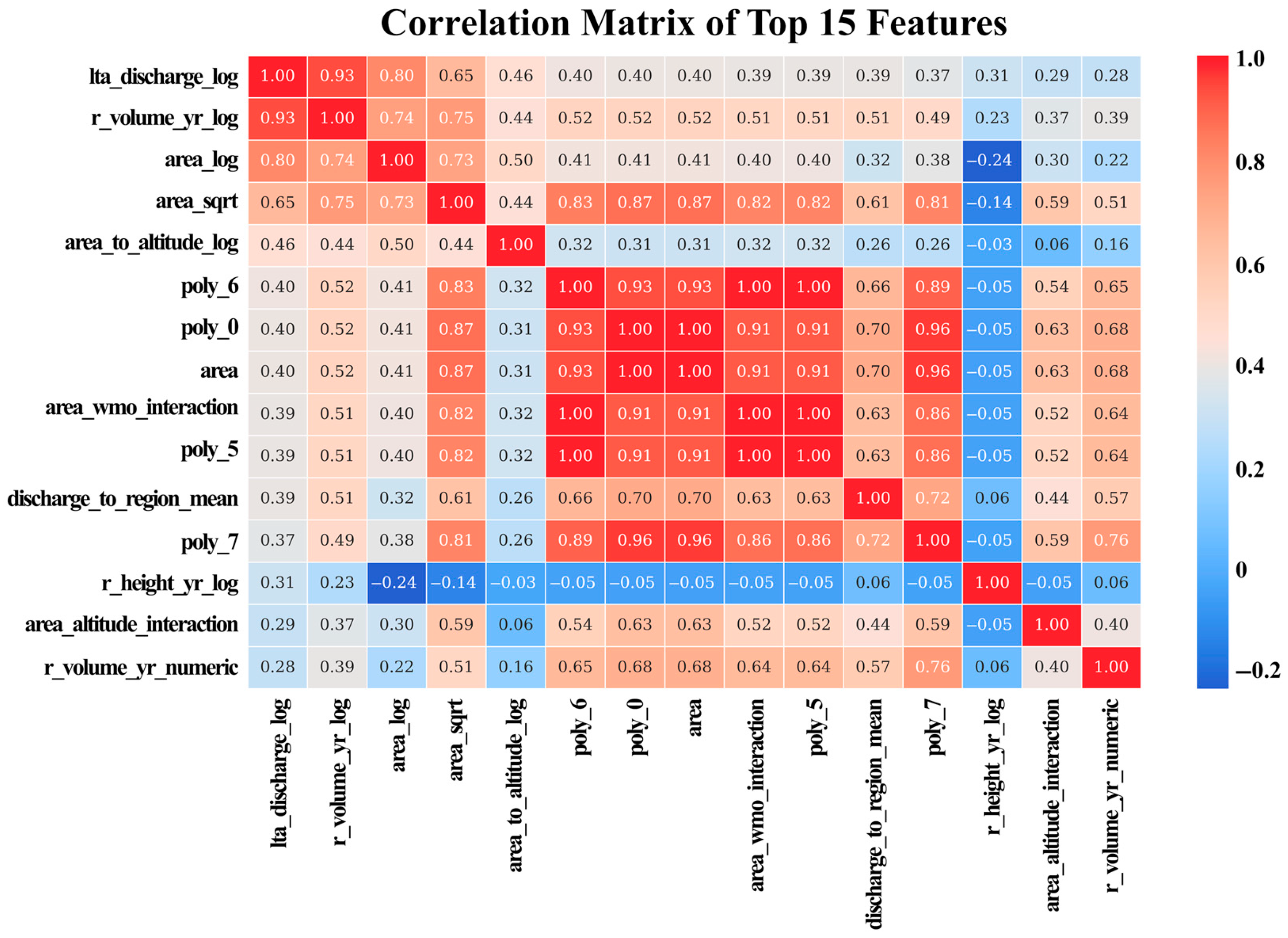
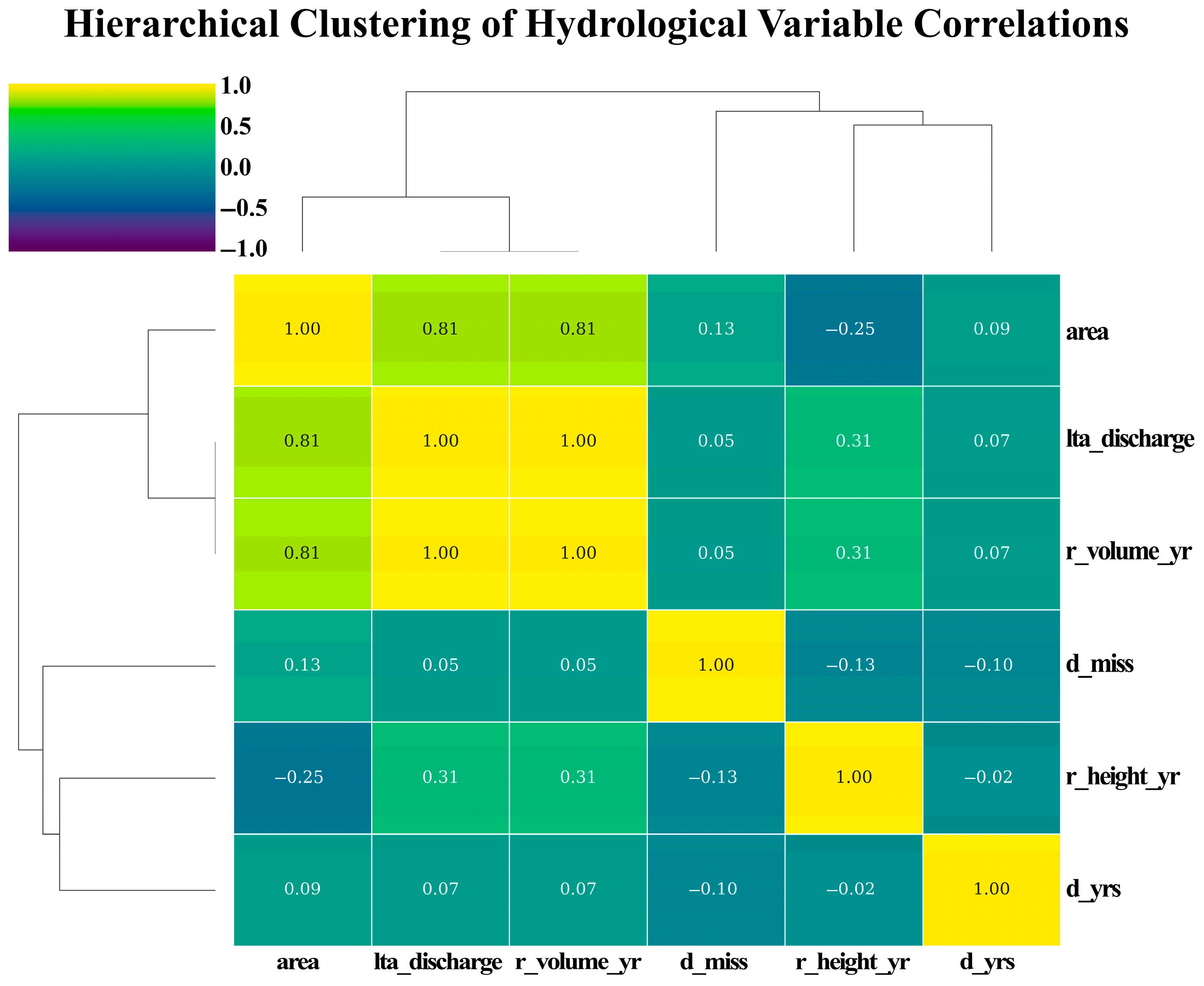
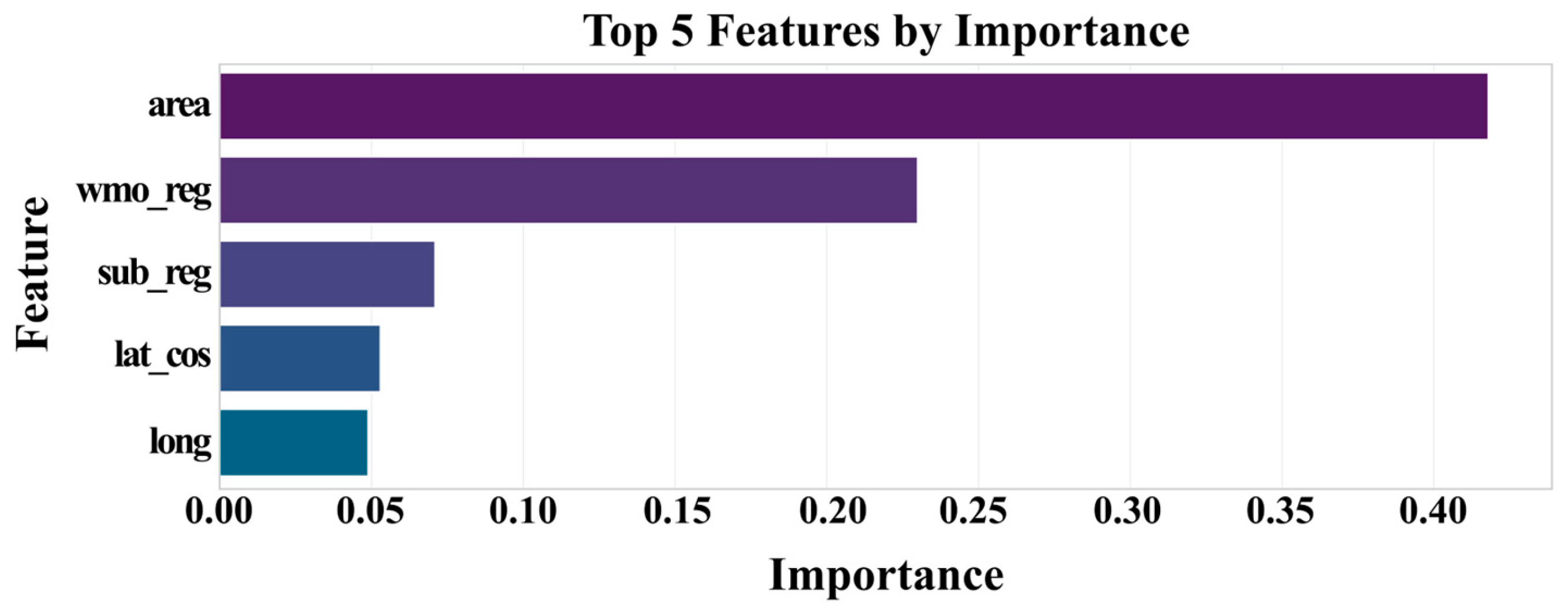
| Category | Feature Name | Description | Data Type |
|---|---|---|---|
| Raw Identifiers & Regional | grdc_no | Unique GRDC station identifier | int64 |
| wmo_reg | WMO region code | int64 | |
| sub_reg | WMO subregion code | int64 | |
| Raw Geographic & Topographic | lat | Latitude | float64 |
| lon | Longitude | float64 | |
| altitude | Altitude of gauge zero | float64 | |
| Raw Catchment | area | Catchment area | float64 |
| Engineered Catchment | area_log | Log-transformed catchment area (log1p) | float64 |
| area_sqrt | Square root of catchment area | float64 | |
| Engineered Geographic | lat_sin | Sine of latitude (radians) | float64 |
| lat_cos | Cosine of latitude (radians) | float64 | |
| long_sin | Sine of longitude (radians) | float64 | |
| long_cos | Cosine of longitude (radians) | float64 | |
| distance_from_equator | Haversine distance from the equator (km) | float64 | |
| Engineered Ratio | area_to_altitude_ratio | Ratio of area to (altitude + 1) | float64 |
| Engineered Interaction | lat_long_interaction | Product of latitude and longitude | float64 |
| area_wmo_interaction | Product of area and WMO region code | float64 | |
| Engineered Temporal | station_lifetime | Duration of station operation (t_end–t_start) | int64 |
| Engineered Regional Context | discharge_to_region_mean | Station LTA discharge relative to WMO region mean discharge | object |
| discharge_to_region_median | Station LTA discharge relative to WMO region median discharge | object | |
| Engineered Polynomial (Degree 2) | poly_0, …, poly_14 | Interaction term from top 5 raw features (e.g., area × wmo_reg) | float64 |
| Model | Train_R2 | Test_R2 | Train_RMSE | Test_RMSE | Train_MAE | Test_MAE |
|---|---|---|---|---|---|---|
| ElasticNet | 0.25 | 0.249 | 1.776 | 1.785 | 449,598.39 | 1,904,236.58 |
| RandomForest | 0.983 | 0.889 | 0.268 | 0.688 | 75.35 | 154.61 |
| GradientBoosting | 0.841 | 0.833 | 0.818 | 0.843 | 173.55 | 239.62 |
| XGBoost | 0.972 | 0.903 | 0.341 | 0.641 | 70.25 | 122.9 |
| LightGBM | 0.72 | 0.895 | 0.553 | 0.667 | 129.61 | 201.36 |
| CatBoost | 0.952 | 0.901 | 0.449 | 0.648 | 95.67 | 131.45 |
| Neural Network | 0.935 | 0.916 | 0.524 | 0.597 | 83.21 | 105.82 |
| Neural Ensemble | 0.951 | 0.932 | 0.456 | 0.538 | 70.46 | 89.73 |
| Boosted Neural Network | 0.963 | 0.941 | 0.396 | 0.501 | 65.78 | 78.41 |
| Meta Ensemble | 0.975 | 0.954 | 0.324 | 0.442 | 62.13 | 71.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neftissov, A.; Biloshchytskyi, A.; Kazambayev, I.; Dolhopolov, S.; Honcharenko, T. An Advanced Ensemble Machine Learning Framework for Estimating Long-Term Average Discharge at Hydrological Stations Using Global Metadata. Water 2025, 17, 2097. https://doi.org/10.3390/w17142097
Neftissov A, Biloshchytskyi A, Kazambayev I, Dolhopolov S, Honcharenko T. An Advanced Ensemble Machine Learning Framework for Estimating Long-Term Average Discharge at Hydrological Stations Using Global Metadata. Water. 2025; 17(14):2097. https://doi.org/10.3390/w17142097
Chicago/Turabian StyleNeftissov, Alexandr, Andrii Biloshchytskyi, Ilyas Kazambayev, Serhii Dolhopolov, and Tetyana Honcharenko. 2025. "An Advanced Ensemble Machine Learning Framework for Estimating Long-Term Average Discharge at Hydrological Stations Using Global Metadata" Water 17, no. 14: 2097. https://doi.org/10.3390/w17142097
APA StyleNeftissov, A., Biloshchytskyi, A., Kazambayev, I., Dolhopolov, S., & Honcharenko, T. (2025). An Advanced Ensemble Machine Learning Framework for Estimating Long-Term Average Discharge at Hydrological Stations Using Global Metadata. Water, 17(14), 2097. https://doi.org/10.3390/w17142097






