Deriving Implicit Optimal Operation Rules for Reservoirs Based on TgLSTM

Abstract

With the continuous improvement of reservoir projects and the advancement of digital twin basin initiatives in China, rapidly and accurately generating long-term practical reservoir operation schedules has become a key priority for stakeholders. This study proposes a Theory-guided Long Short-Term Memory (TgLSTM) model to extract optimal reservoir operation rules accurately and reliably. Concretely, TgLSTM integrates data-fitting accuracy with the physical constraints of an operation, e.g., water level constraints and minimal discharge constraints, to address the low credibility often observed in conventional LSTM networks. Using the Three Gorges Reservoir during the dry season as a case study, a multi-year hydrological series optimized by particle swarm optimization (PSO) was used to train the TgLSTM network and derive optimized operation rules. Results show that TgLSTM efficiently generates operation schemes close to the theoretical optimum, achieving power generations of 4.27 × 10¹⁰ kW·h and 4.19 × 10¹⁰ kW·h in two test years, with deviations of only 4.20% and 2.33%, respectively. Compared to traditional LSTM models, TgLSTM is more reliable as it captures key operational characteristics such as terminal water levels and water level fluctuations, maintaining an average ten-day drawdown depth below 1.5 m—significantly lower than the 7 m fluctuations observed with conventional LSTM. Furthermore, comparative analyses against SwR, BP–ANN, and SVM confirm that TgLSTM offers a moderate performance in absolute metrics but is the best to simulate the constrained reservoir operation.

1. Introduction

With the extensive development of reservoir projects and the advancement of optimization scheduling techniques in China [1], significant progress has been achieved in research on reservoir operation optimization and the extraction of corresponding operation rules [2,3,4]. Operation rules, in a narrow sense, are formulated based on deterministic runoff processes and provide retrospective responses to known hydrological scenarios [5]. However, their applicability to uncertain future inflows remains limited [6,7]. Broadly defined, operation rules are extracted from extensive historical or optimized datasets and aim to support decision-making under uncertainty, thereby offering improved robustness [8,9]. The forms of reservoir operation rules generally include operation charts and operation functions, with the latter further classified into explicit and implicit functions [10]. Machine learning constitutes a type of implicit operation function, capable of learning patterns from historical input–output datasets and generalizing them into practically applicable strategies, thus enabling intelligent responses to future scenarios [11]. For instance, Zhang et al. [12] developed a decision tree-based operation model incorporating factors such as month, monthly inflow, and industrial water supply reliability, which was validated through a case study in a reservoir in Henan Province. Ji et al. [13] proposed a method integrating the Rough Set theory and Support Vector Machine (SVM), where the Rough Set theory was employed to filter the input variables for the SVM model, resulting in superior performance compared to traditional multiple linear regression models, despite some information loss during the discretization of continuous variables. Feng et al. [14] further enhanced rule derivation by first partitioning inputs with k-means clustering and then training a particle swarm-optimized Extreme Learning Machine, which captured complex inflow–storage–release relationships and yielded a high generalization performance. Yang et al. [15] introduced a framework for input data selection in cascade reservoir operations, enabling the dynamic identification of stable decision factors and optimization of operation function parameters. Dai et al. [16] extracted operation rules for upstream reservoirs of the Yangtze River using decision tree and ensemble learning models. While these studies have demonstrated the promising capability of machine learning for enhancing reservoir operation rule extraction, many approaches nevertheless tend to overlook the sequential characteristics inherent in reservoir operations and fail to adequately capture temporal dependencies.

The Artificial Neural Network (ANN) represents a critical branch of machine learning and has been widely applied in geoscience [17,18] and hydrology [19,20]. However, early neural network models were typically shallow, with limited depth, which restricted their ability to capture complex and hierarchical patterns. Following LeCun’s [21] “Go Deeper” principle, deep neural networks with multiple layers were developed, significantly enhancing feature representation capabilities across various fields. However, most deep networks focus on static data, whereas modeling temporal dependencies in sequential data requires specialized architecture. Recurrent Neural Networks (RNNs) were introduced to address this need, maintaining hidden states across time steps to learn temporal patterns. Among them, Long Short-Term Memory (LSTM) networks [22] further improved performance by introducing “forget gates,” “memory gates,” and “output gates,” effectively mitigating the vanishing gradient problem and enabling more accurate sequence modeling. Sun et al. [23] accurately predicted daily reservoir inflow processes using an LSTM network. Zhang et al. [24] compared the performance of the traditional RNN, LSTM, and Gated Recurrent Unit (GRU) models in extracting reservoir operation rules and found that all three demonstrated strong learning capabilities. Han et al. [25] employed a Variational Mode Decomposition (VMD) module as a preprocessing step before applying a GRU model to predict daily reservoir water levels.

Despite these advancements, existing RNN-based methods, including LSTM models, primarily focused on replicating conventional operation patterns without explicitly addressing optimization objectives and often neglected the intrinsic physical constraints governing reservoir systems. These limitations can compromise both the efficiency and the reliability of the extracted operation rules [4,24,25]. Recent research in related fields has explored the integration of physical constraints into neural network frameworks to improve model credibility. For example, Wang [26] proposed an ANN framework incorporating governing equations and initial and final conditions for modeling groundwater flow. Compared with traditional unconstrained networks, this approach better conformed to the physical laws of groundwater movement and produced more credible prediction results. In the context of reservoir operation rules extraction, the absence of physical constraints may lead to unreasonable outcomes, such as rising reservoir levels during supply periods or a failure to meet the minimum ecological and water supply flow requirements, which in turn undermine the credibility of the extracted rules and weaken the reliability of decision support. To address these issues, this study proposes a Theory-guided Long Short-Term Memory (TgLSTM) network for optimized reservoir operation rules extraction, aiming to rapidly and accurately derive optimized and reliable implicit operation rules by embedding physical constraints within the neural network framework. Here, theory-guided means that physical constraints, namely operation regulations, are explicitly coupled in the neural network. The proposed method was applied to the dry season operation of the Three Gorges Reservoir to validate its rationality and reliability.

2. Data and Study Area

The Three Gorges Reservoir is located in Yichang City, Hubei Province, and is situated at the transition zone between the upper and middle-lower reaches of the Yangtze River, as shown in Figure 1. Its average annual discharge is around 451 billion m³. As a cornerstone project in the comprehensive governance and development of the Yangtze River Basin, it controls all upstream inflows and plays a critical role in regulating seasonal flow variations to maximize the reservoir’s beneficial functions. In this study, we assume that the drawdown season is fixed from 1 October to 31 May. The initial water level and end water level are 175 m and 145 m, respectively, according to the regularization rules [27]. The corresponding storage is around 22.1 billion m³, providing massive water resources for hydropower generation, water supply, navigation, and ecological protection [28,29,30].

The long-term runoff series used as inflow is from the Changjiang River Scientific Research Institute. This series can be dated back to 1956. All the data is preprocessed by the institute to ensure accuracy.

3. Model Development

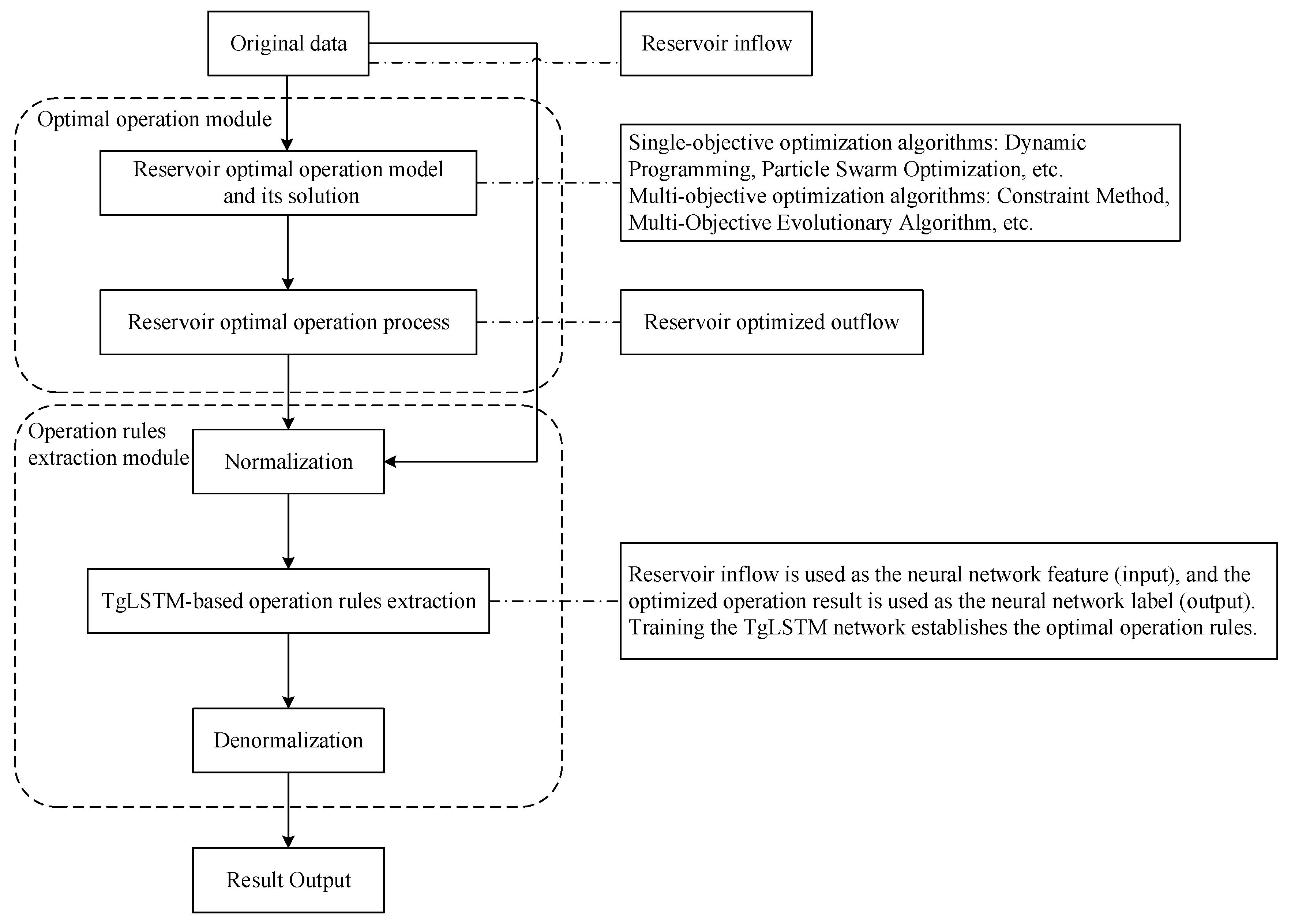
3.1. Optimal Operation Model for Reservoir Power Generation

Considering the operational objectives of the Three Gorges Reservoir during the dry season, this study establishes a reservoir operation optimization model with the maximization of power generation as the primary objective. The water supply and ecological protection tasks are incorporated as constraints [31,32], along with other constraints including the water balance constraint, reservoir water level constraint, release flow constraint, initial and terminal water level constraint, and turbine output constraint. The model operates on a ten-day interval basis, and its mathematical formulation is presented in Equation (1). The operation period spans from 1 October of the current year to 30 June of the subsequent year.

$$\begin{array}{l}\max E={\displaystyle \sum _{i=1}^{n}k{q}_i}{h}_i\Delta t_i\\ s.t.V_{i+1}=V_i+\left(Q_i-q_i\right)\Delta t_i\\ \hspace{1em} \underset{\_}{V} \le V_i \le \overline{V}\\ \hspace{1em} \underset{\_}{q} \le q_i \le \overline{q}\\ \hspace{1em} W_i=k{q}_i{h}_i\le W_C\\ \hspace{1em} V_1=\overline{V}\\ \hspace{1em} V_n=\underset{\_}{V}\end{array}$$

(1)

where $k$ is the hydropower generation efficiency and is fixed at 8.5 in this study; Δt is the time interval used, which is equal to 10 days, as we use a 10-day time step, but varies to 11 or 28 depending on which specific month calculated; $Q_i$ and $q_i$ denote the average inflow and outflow during period i (m³/s); $h_i$ is the average power generation head in period i (m); $V_i$ is the initial reservoir storage at the beginning of period i (m³); $\underset{\_}{V}$, $\overline{V}$, $\underset{¯}{q}$, and $\overline{q}$ represent the lower and upper bounds of the reservoir storage (m³) and release flow (m³/s), respectively; and $W_C$ is the installed capacity of the reservoir (kW).

3.2. Particle Swarm Optimization (PSO)

Particle Swarm Optimization (PSO) [33] is a population-based heuristic algorithm inspired by the foraging behavior of bird flocks. By iteratively updating the positions of individuals based on both their own and the population’s best-known positions, the algorithm converges toward an optimal solution. The update rules are shown in Equations (2) and (3). In reservoir operation optimization problems, constraints are often characterized by high-dimensional nonlinear properties, making constraint handling a critical component in simulation-based optimization [34].

In this study, the constraint-handling mechanism proposed by Yao et al. [35] is adopted, which ensures solution feasibility throughout the search process by projecting infeasible particles onto the feasible region via boundary control at both the population and individual levels.

$$v_i^d=\omega v_i^{d-1}+c_1\left(p_i^{d-1}-x_i^{d-1}\right)+c_2\left(p_g^{d-1}-x_i^{d-1}\right)$$

(2)

$$x_i^d=x_i^{d-1}+\alpha v_i^d$$

(3)

where $v_i^d$ and $x_i^d$ denote the velocity and position of the i-th individual in generation d, respectively; $p_i^{d-1}$ and $p_g^{d-1}$ represent the best historical position of the i-th individual and the global best position of the population in generation $d-1$; $\omega$ is the inertia weight, $c_1$ and $c_2$ are acceleration coefficients, $\alpha$ is the step size, and these four are hyperparameters, which are adjusted to obtain stable optimization results.

3.3. Vanilla Long Short-Term Memory Network

Long Short-Term Memory (LSTM) is one of the most effective models for handling sequential problems. Each LSTM unit transmits not only the cell state but also the hidden state, enabling the updating of the cell state through selective “forgetting” and “retention” mechanisms, subsequently determining the output. The specific computational process is shown in the following equations, and the framework of the LSTM network is illustrated in Figure 2.

$$f_t=\sigma \left(W_f·\left[h_{t-1}, X_t\right]+b_f\right)$$

(4)

$$i_t=\sigma \left(W_i·\left[h_{t-1}, X_t\right]+b_i\right)$$

(5)

$$o_t=\sigma \left(W_o·\left[h_{t-1}, X_t\right]+b_o\right)$$

(6)

$${\tilde{C}}_t=\tanh \left(W_C·\left[h_{t-1}, X_t\right]+b_C\right)$$

(7)

$$C_t=f_t\ast C_{t-1}+i_t\ast {\tilde{C}}_t$$

(8)

$$h_t=o_t\ast \tanh \left(C_t\right)$$

(9)

where $f_t$, $i_t$, and $o_t$ denote the forget gate, input gate, and output gate activations, respectively; $X_t$ is the input to the LSTM unit at time step $t$; $C_t$ and $h_t$ represent the cell state and hidden state of the LSTM unit at time step $t$, respectively; ${\tilde{C}}_t$ denotes the candidate cell state at time step $t$; $W$ and $b$ refer to the weight matrices and bias vectors of the neural network, respectively; and $\sigma$ as well as $\tanh$ denote the sigmoid and hyperbolic tangent activation functions, respectively, with output ranges of (0, 1) and (−1, 1).

In Equation (8), the forget gate controls the extent to which the previous cell state is retained, while the input gate regulates the degree to which the candidate cell state is updated. In Equation (9), the updated cell state is modulated by the output gate to determine the final hidden state. Due to the independent control provided by the forget, input, and output gates, the LSTM network demonstrates outstanding performance in sequential tasks, making it a foundational model for this study.

The LSTM network can be formulated as a parameterized function that maps the input sequence X to the predicted output Y, expressed as:

$$Y=LSTM\left(X;\theta \right)$$

(10)

where $\theta$ denotes the set of trainable parameters. These parameters are typically optimized by minimizing a loss function such as mean squared error (MSE), as shown in Equation (11):

$$loss=MSE={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N{\left(Y_i-{\widehat{Y}}_i\right)}^2}$$

(11)

3.4. Theory-Guided Long Short-Term Memory Network (TgLSTM)

While the MSE captures the overall data-fitting performance, it does not account for domain-specific physical constraints that are critical in real-world reservoir operations. For example, the terminal reservoir level must drop below a flood-limited threshold before the flood season, and the downstream release must satisfy both water supply and ecological flow requirements. When only the MSE is used for training, the resulting LSTM model may produce trajectories that fit the data well but fail to meet these physical constraints. To overcome this limitation, we propose a Theory-guided Long Short-Term Memory (TgLSTM) network, which incorporates prior knowledge in the form of soft constraints into the loss function, thereby guiding the learning process toward physically consistent solutions. The modified loss function is expressed as:

$$los{s}^{\prime }=MSE+{\epsilon }_{1}T{g}_1+{\epsilon }_{2}T{g}_2+{\epsilon }_{3}T{g}_3$$

(12)

where $T{g}_1$, $T{g}_2$, and $T{g}_3$ represent soft constraints related to the terminal water level, fluctuation amplitude, and downstream ecological and supply flow requirements, respectively; ${\epsilon }_1,$ ${\epsilon }_2$, and ${\epsilon }_3$ are the corresponding penalty weights.

In the TgLSTM framework, the reconstructed loss function not only minimizes the prediction error but also incorporates additional penalty terms related to the terminal water level constraint, fluctuation amplitude constraint, and ecological and supply flow constraint. Specifically, the terminal water level constraint arises from the operational requirement that the reservoir water level must drop below the flood-limited level before the flood season. The fluctuation amplitude constraint requires maintaining stable water levels, while the ecological and supply flow constraint demands that downstream releases meet the needs of both ecological systems and water users. These constraints correspond to the penalty terms defined by Equations (13)–(15). Through optimization and training on the augmented loss function, the TgLSTM network is guided to learn the physical constraints implicitly. In principle, when Tg1, Tg2, and Tg3 are all reduced to zero, the TgLSTM model will achieve full compliance with the specified constraints. The constraint terms are defined as follows:

$$T{g}_1=\left(Y_i-{\widehat{Y}}_i\right)\ast T$$

(13)

$$T{g}_2={\displaystyle \frac{1}{N}}{{\displaystyle \sum }}_{i=1}^{N}max\left(\left(X_i-{\widehat{Y}}_i\right),0\right)$$

(14)

$$T{g}_3={\displaystyle \frac{1}{N}}{{\displaystyle \sum }}_{i=1}^{N}max\left(\left({\widehat{Y}}_i-\underset{\_}{Y}\right),0\right)$$

(15)

where $Y_i$ and ${\widehat{Y}}_i$ denote the true value and the predicted value of the reservoir release for the i-th sample, respectively, corresponding to the optimized and TgLSTM-predicted reservoir releases; $T$ is the time step length; $X_i$ is the label of the i-th sample, representing the reservoir inflow; and $\underset{\_}{Y}$ denotes the flow under the ecological and water supply constraint.

3.5. TgLSTM-Based Operation Rules Extraction Model

Evolutionary optimization algorithms typically require repeated iterations to obtain optimal solutions, which can be computationally expensive. In addition, retrospective optimization based on historical inflow data cannot adequately accommodate future uncertain inflow conditions. To address these challenges, this study combines the Particle Swarm Optimization (PSO) algorithm with the Theory-guided Long Short-Term Memory (TgLSTM) network. The objective is to replace traditional evolutionary algorithms with a neural network model capable of providing a reasonable implicit functional form for reservoir operation optimization.

Specifically, the PSO algorithm is first applied to simulate and optimize reservoir storage and release processes based on historical inflow data, thereby generating training data for the TgLSTM neural network. The TgLSTM network is constructed with a sequence length corresponding to the operation period, with the input layer receiving one-dimensional reservoir inflow and the output layer predicting one-dimensional optimized reservoir release. The network is trained to learn and extract the reservoir operation rules for optimization purposes. The overall workflow is illustrated in Figure 3. It is worth noting that, in this study, the PSO algorithm is used only as an example to solve a dry season reservoir operation problem with the objective of maximizing hydropower generation, thereby providing the input (reservoir inflow) and output (optimized reservoir release) data for training the TgLSTM network. Nevertheless, the proposed rule extraction framework is generalizable and can be seamlessly applied to other multi-objective optimization problems and algorithms for broader applications.

4. Application and Validation

4.1. Results and Analysis

Taking the Three Gorges Reservoir as a case study, 62 years of dry season data from 1956 to 2018 were used, with the data processed and reconstructed by the Changjiang River Scientific Research Institute. The optimization results showed that the reservoir maintained a relatively high water level before December and afterward gradually lowered the water level to meet downstream water supply demands, which is consistent with the actual operation patterns of the Three Gorges Reservoir. The optimized average hydropower generated during dry seasons over multiple years reached 4.49 × 10¹⁰ kW·h, which exceeds the historical average generation during dry seasons. Cross-validation was conducted by selecting validation sets at every 10-year interval within the first 60 years to eliminate the influence of runoff variability, while the remaining years were used as the training set to evaluate convergence. The years 2017 and 2018 were used as the testing set for result presentation. The neural network model was trained using the Adam optimizer [36,37], with a learning rate set to 0.001.

The optimized reservoir operation process during dry seasons in the testing years was selected for detailed result analysis, and the comparison of outflow processes is shown in Figure 4. The results demonstrate that the TgLSTM model closely reproduces the optimized release trajectories generated by the PSO algorithm, indicating that the model successfully learned the underlying operation rules from historical data and effectively replicated the optimization process. The corresponding hydropower generated during the dry seasons of 2017 and 2018 reached 4.27 × 10¹⁰ kW·h and 4.19 × 10¹⁰ kW·h, respectively, with deviations of only 4.20% and 2.33% compared to the theoretical optimal generation. In terms of computational efficiency, the TgLSTM model produced predictions within an average time of only 0.002 s, which is significantly shorter than the 75 s required to run the PSO algorithm.

In practical applications, once medium- and long-term runoff forecasts are available, stakeholders can rapidly generate idealized optimized reservoir operation trajectories using the pretrained LSTM model. Compared with traditional optimization algorithms, this approach offers significantly greater timeliness and operational efficiency, while avoiding the reliance on conventional rule curves based on typical hydrological years. Moreover, when runoff forecast uncertainty is considered, traditional interval optimization methods become difficult to implement due to their computational burden. By contrast, the proposed method, while relaxing forecasted inflow constraints, can still flexibly accommodate uncertainty and produce satisfactory operation rules with much lower computational complexity [38,39].

To further verify the ability of the TgLSTM network to enforce the relevant physical constraints in the extracted operation rules, a comparative analysis of the water level trajectories generated by the TgLSTM and conventional LSTM models from the testing dataset was conducted, as shown in Figure 5. In terms of the terminal water level, the trajectories inferred by the TgLSTM model generally maintained higher terminal water levels than those predicted by the conventional LSTM, thereby reducing the risk of violating the dead water level threshold of the Three Gorges Reservoir. This result demonstrates the effectiveness of incorporating the terminal water level constraint (Equation (12)) into the TgLSTM loss function. Compared to the conventional LSTM, which severely underestimated the terminal water level, the proposed TgLSTM model yielded results that were more consistent with practical operational requirements.

Regarding water level fluctuations, the LSTM model exhibited abnormal rises in the early October 2017 period of the testing set, which clearly deviated from actual water supply operation patterns. Additionally, the LSTM-predicted water level experienced a decline exceeding 7 m within a ten-day period at the end of the dry season, which poses a threat to bank slope stability and should be avoided in practical reservoir management [40]. In contrast, no abnormal water level rises were observed in the TgLSTM results during the dry season, and the water level trajectory remained notably smoother, with the average ten-day decline controlled within 1.5 m.

These results demonstrate that the proposed TgLSTM model effectively enhances the network’s ability to respect physical constraints and improves its reliability for practical reservoir operation applications.

4.2. Method Comparison

The performance of the TgLSTM-based method for extracting operation rules was compared with that of traditional approaches, including Stepwise Regression (SwR), Support Vector Machine (SVM), and Backpropagation Artificial Neural Network (BP–ANN). Detailed descriptions of SwR, SVM, and BP–ANN can be found in references [9,41]. Multivariate linear regression was excluded from comparison because all selected models were designed based solely on reservoir inflow as the input variable, thereby making the multivariate approach inapplicable. The comparison results of the four methods are summarized in

Table 1. Performance metrics on different operation extraction models.

	TgLSTM	LSTM	SwR	SVM	BP–ANN
Correlation Coefficient	0.98	0.98	0.97	0.99	0.87
Mean Absolute Error (MAE)	440	394	1090	340	2030
Nash–Sutcliffe Efficiency (NSE)	0.95	0.96	0.86	0.97	0.27
Maximum Ten-Day Water Level Fluctuation (m)	2.08	6.00	6.45	2.82	2.41
Terminal Water Level (m)	143.78	141.96	152.13	149.93	174.85

.

The results indicate that the operation rule extracted by TgLSTM and SVM are comparable and significantly outperforms those derived from BP–ANN and SwR. In both test years, the correlation coefficients between the predicted and true values for TgLSTM and SVM exceeds 0.98, and the MSE is substantially lower than those of BP–ANN and SwR. From the operational trajectories, it can be observed that all four methods effectively capture the strategy of maintaining a high water level in the Three Gorges Reservoir before December. However, as the water supply season commences, requiring increased outflow, only TgLSTM and SVM accurately extract the corresponding operational rules.

When comparing TgLSTM and SVM in more detail, it is noted that SVM requires separate regression modeling for each time interval and does not inherently capture temporal dependencies. Moreover, under reservoir operation constraints, TgLSTM exhibits better performance, maintaining the terminal water level closer to the flood control limit of 145 m and achieving smaller ten-day water level fluctuations.

5. Limitations and Future Work

In this study, we proposed the deep learning model for a fast long-term reservoir operation schedule. However, there are still a few limitations. First, the fixed input–output pair blocks the flexible adjustment of operations. Concretely, the start and end of the operation is fixed, originating from the fixed operation duration from the training samples. Such operation deviates from real-world operations, because the exact fulfill data for the reservoir varies. By far, it is still difficult for RNN models to generate a flexible sequence length. Another issue lies in the predefined weights in Equation (12). In this study, these weights are obtained by trail-and-error. It deserves further investigation to dynamically adjust these weights to avoid negative transfer [42].

6. Conclusions

This study proposed a method for extracting optimized reservoir operation rules using a TgLSTM network. By training the neural network with reservoir operation trajectories optimized through an optimization algorithm, the method accurately captured implicit operation rules and efficiently generated reliable operation schemes. In the test sets, the power generation achieved by the TgLSTM-based scheduling deviated from the theoretical optimum by only 4.20% and 2.33%, respectively, while significantly improving computational efficiency. Compared to traditional machine learning-based methods such as SVM and BP–ANN, the proposed TgLSTM approach comprehensively considers temporal dependencies, regression-fitting accuracy, and the underlying physical constraints of the data. The extracted operation rules are more consistent with actual reservoir operation practices, thereby demonstrating the superiority of the proposed method.

Future research could further enhance the model by increasing the dimensionality of the input data, for example, by incorporating rainfall information and other sources to improve simulation accuracy. Additionally, efforts could be directed towards improving the interpretability of neural networks, aiming to reveal and better understand the quantitative mapping relationships between inflow inputs and optimized outflow outputs.