Physics-Informed Deep Learning for Karst Spring Prediction: Integrating Variational Mode Decomposition and Long Short-Term Memory with Attention
Abstract
1. Introduction
2. Study Area and Data
3. Methodology
3.1. Multi-Scale Signal Decomposition and Data Preparation
3.2. Physics-Informed LSTM Modeling with Attention Mechanism
3.3. Uncertainty Quantification Through Monte Carlo Dropout
4. Results and Discussion
4.1. Multi-Scale Dynamics and Physical Interpretation of IMFs
4.2. Prediction Performance of the Physics-Informed LSTM Framework
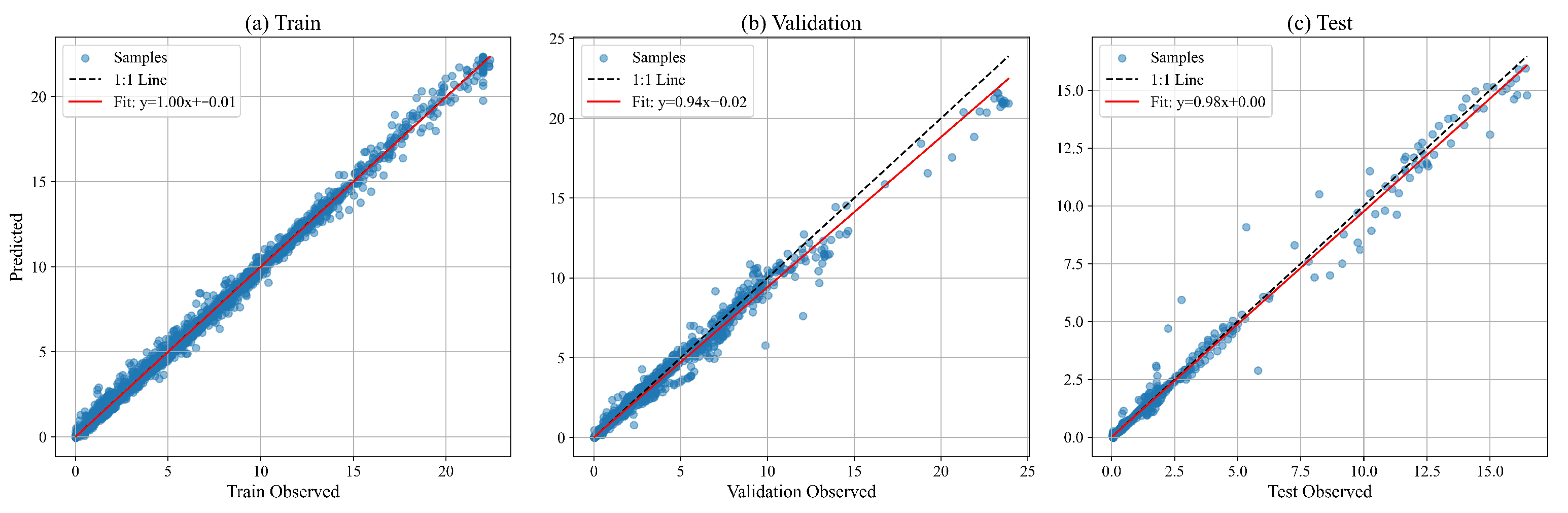
4.2.1. Model Training and Performance
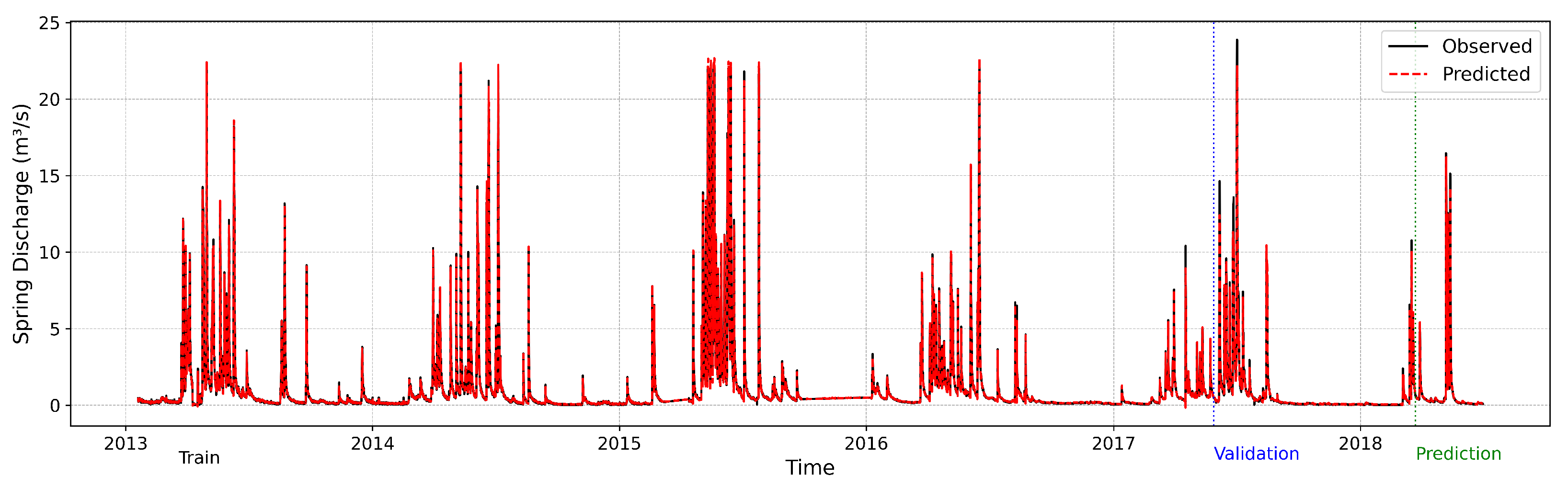
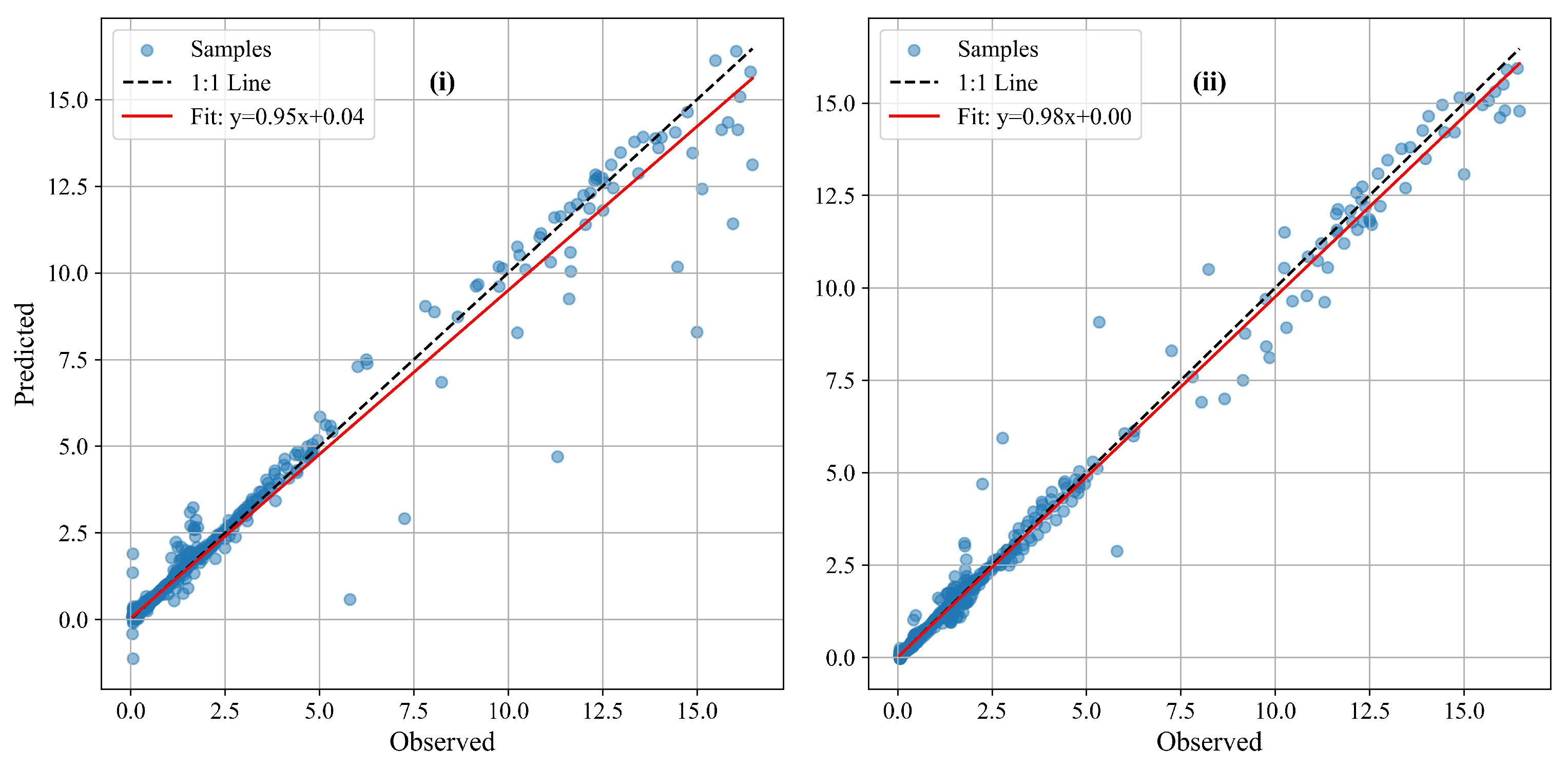
4.2.2. Overall Prediction Performance of the VMD-LSTM Framework
4.2.3. Model Performance Across Hydrological Regimes
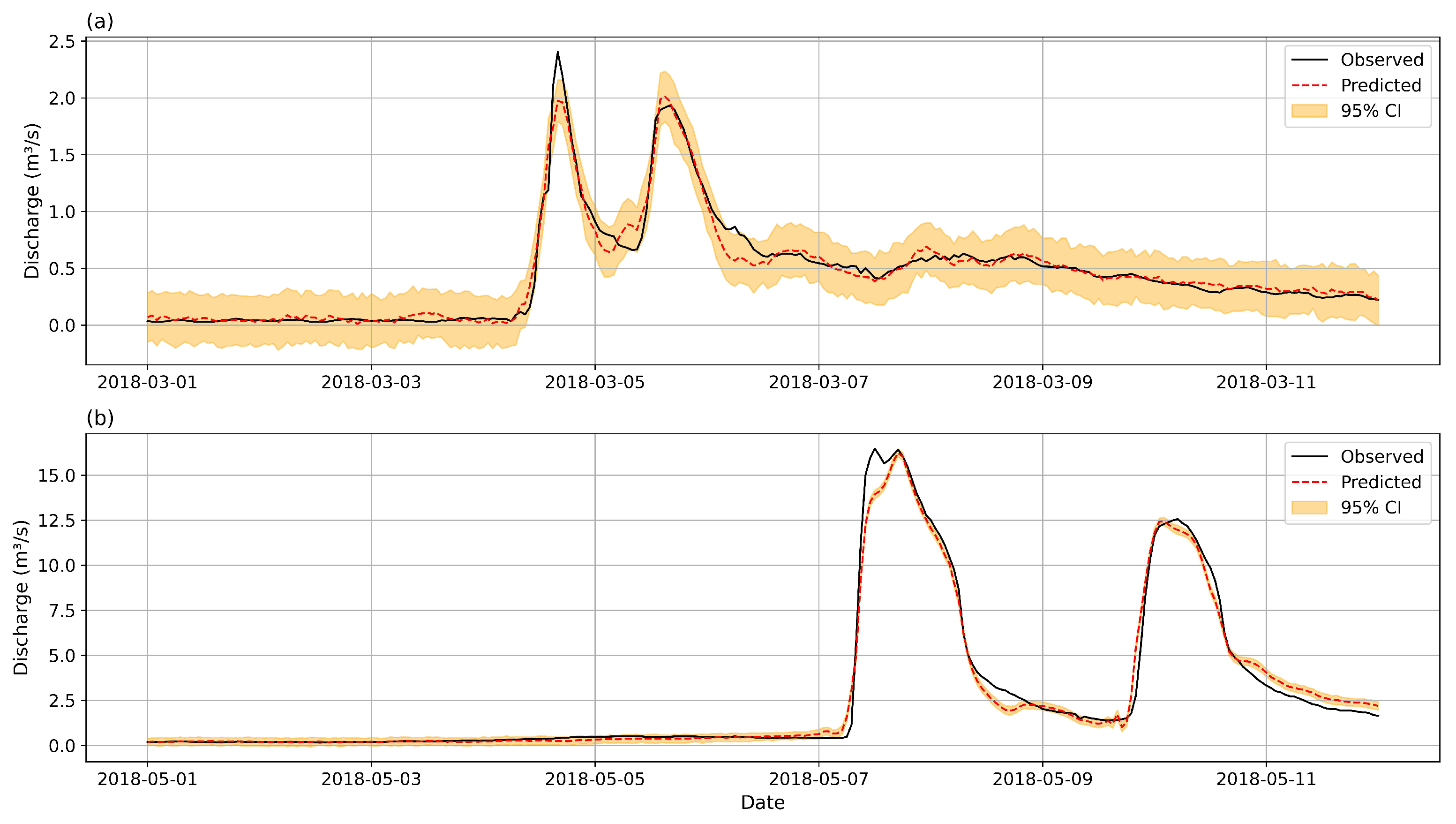
4.3. Uncertainty Quantification
4.4. Comparative Analysis with Benchmark Models
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wali, S.U.; Usman, A.A.; Usman, A.B. Resolving challenges of groundwater flow modelling for improved water resources management: A narrative review. Int. J. Hydrol. 2024, 8, 175–193. [Google Scholar] [CrossRef]
- Hartmann, A.; Goldscheider, N.; Wagener, T.; Lange, J.; Weiler, M. Karst water resources in a changing world: Review of hydrological modeling approaches. Rev. Geophys. 2014, 52, 218–242. [Google Scholar] [CrossRef]
- Goldscheider, N.; Drew, D. (Eds.) Methods in Karst Hydrogeology: IAH International Contributions to Hydrogeology; CRC Press: Boca Raton, FL, USA, 2007; Volume 26, 190p. [Google Scholar]
- Jourde, H.; Wang, X. Advances, challenges and perspective in modelling the functioning of karst systems: A review. Environ. Earth Sci. 2023, 82, 396. [Google Scholar] [CrossRef]
- Chen, Z.; Lucianetti, G.; Hartmann, A. Understanding groundwater storage and drainage dynamics of a high mountain catchment with complex geology using a semi-distributed process-based modelling approach. J. Hydrol. 2023, 625, 130067. [Google Scholar] [CrossRef]
- Willard, J.; Jia, X.; Xu, S.; Steinbach, M.; Kumar, V. Integrating scientific knowledge with machine learning for engineering and environmental systems. ACM Comput. Surv. 2022, 55, 1–37. [Google Scholar] [CrossRef]
- Zhu, L.T.; Chen, X.Z.; Ouyang, B.; Yan, W.C.; Lei, H.; Chen, Z.; Luo, Z.H. Review of machine learning for hydrodynamics, transport, and reactions in multiphase flows and reactors. Ind. Eng. Chem. Res. 2022, 61, 9901–9949. [Google Scholar] [CrossRef]
- Donnelly, J.; Daneshkhah, A.; Abolfathi, S. Physics-informed neural networks as surrogate models of hydrodynamic simulators. Sci. Total Environ. 2024, 912, 168814. [Google Scholar] [CrossRef] [PubMed]
- Fang, L.; Shao, D. Application of long short-term memory (LSTM) on the prediction of rainfall-runoff in karst area. Front. Phys. 2022, 9, 790687. [Google Scholar] [CrossRef]
- Vu, M.T.; Jardani, A.; Massei, N.; Fournier, M. Reconstruction of missing groundwater level data by using Long Short-Term Memory (LSTM) deep neural network. J. Hydrol. 2021, 597, 125776. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Herrnegger, M.; Sampson, A.K.; Hochreiter, S.; Nearing, G.S. Toward improved predictions in ungauged basins: Exploiting the power of machine learning. Water Resour. Res. 2019, 55, 11344–11354. [Google Scholar] [CrossRef]
- Gholizadeh, H.; Zhang, Y.; Frame, J.; Gu, X.; Green, C.T. Long short-term memory models to quantify long-term evolution of streamflow discharge and groundwater depth in Alabama. Sci. Total Environ. 2023, 901, 165884. [Google Scholar] [CrossRef]
- Lange, H.; Sippel, S. Machine Learning Applications in Hydrology. In Forest-Water Interactions; Levia, D.F., Carlyle-Moses, D.E., Iida, S., Michalzik, B., Nanko, K., Tischer, A., Eds.; Springer: Cham, Switzerland, 2020; Volume 240, pp. 233–257. [Google Scholar]
- Le, M.H.; Kim, H.; Adam, S.; Beling, P.; Lakshmi, V. Streamflow Estimation in Ungauged Regions Using Machine Learning: Quantifying Uncertainties in Geographic Extrapolation. Hydrol. Earth Syst. Sci. Discuss. 2022, 2022, 1–24. [Google Scholar]
- De Filippi, F.M.; Sappa, G. The simulation of Bracciano Lake (Central Italy) levels based on hydrogeological water budget: A tool for lake water management when climate change and anthropogenic impacts occur. Environ. Process. 2024, 11, 8. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M.; Matta, E.; Cominola, A.; Xia, X.; Zhang, Q.; Liang, Q.; Hinkelmann, R. Neurocomputing in surface water hydrology and hydraulics: A review of two decades retrospective, current status and future prospects. J. Hydrol. 2020, 588, 125085. [Google Scholar] [CrossRef]
- Wu, M.; Liu, P.; Liu, L.; Zou, K.; Luo, X.; Wang, J.; Xia, Q.; Wang, H. Improving a hydrological model by coupling it with an LSTM water use forecasting model. J. Hydrol. 2024, 636, 131215. [Google Scholar] [CrossRef]
- Lawal, Z.K.; Yassin, H.; Teck, D.; Lai, C.; Idris, A.C. Coastal Wave Modeling and Forecasting with LSTM Optimization for Sustainable Energy Harvesting. 2023. Available online: https://www.preprints.org/manuscript/202304.0282/v2 (accessed on 18 May 2023).
- Tobin, B.W.; Polk, J.S.; Arpin, S.M.; Shelley, A.; Taylor, C. A conceptual model of epikarst processes across sites, seasons, and storm events. J. Hydrol. 2021, 596, 125692. [Google Scholar] [CrossRef]
- Liu, J.; Xu, T.; Lu, C.; Yang, J.; Xie, Y. Variational mode decomposition coupled LSTM with encoder-decoder framework: An efficient method for daily streamflow forecasting. Earth Sci. Inform. 2025, 18, 38. [Google Scholar] [CrossRef]
- Wang, J.; Wang, X.; Lei, X.H.; Wang, H.; Zhang, X.H.; You, J.Y.; Tan, Q.F.; Liu, X.L. Teleconnection analysis of monthly streamflow using ensemble empirical mode decomposition. J. Hydrol. 2020, 582, 124411. [Google Scholar] [CrossRef]
- Renard, B.; Kavetski, D.; Leblois, E.; Thyer, M.; Kuczera, G.; Franks, S.W. Toward a reliable decomposition of predictive uncertainty in hydrological modeling: Characterizing rainfall errors using conditional simulation. Water Resour. Res. 2011, 47, W11516. [Google Scholar] [CrossRef]
- Zhou, R.; Wang, Q.; Jin, A.; Shi, W.; Liu, S. Interpretable multi-step hybrid deep learning model for karst spring discharge prediction: Integrating temporal fusion transformers with ensemble empirical mode decomposition. J. Hydrol. 2024, 645, 132235. [Google Scholar] [CrossRef]
- Zhang, W.; Duan, L.; Liu, T.; Shi, Z.; Shi, X.; Chang, Y.; Wang, G. A hybrid framework based on LSTM for predicting karst spring discharge using historical data. J. Hydrol. 2024, 633, 130946. [Google Scholar] [CrossRef]
- An, L.; Hao, Y.; Yeh, T.-C.J.; Liu, W.; Zhang, B. Simulation of karst spring discharge using a combination of singular spectrum analysis and ensemble empirical mode decomposition with LSTM modeling. Environ. Earth Sci. 2020, 79, 353. [Google Scholar]
- Wang, J.; Zhang, B.; Hao, Y.; Zhang, B.; Zhang, C.; Guo, C.; Zhu, Y. Spring flow prediction model based on VMD and attention mechanism LSTM. In International Conference in Communications, Signal Processing, and Systems; Springer: Singapore, 2023; pp. 111–120. [Google Scholar]
- Wei, X.; Chen, M.; Zhou, Y.; Zou, J.; Ran, L.; Shi, R. Research on optimal selection of runoff prediction models based on coupled machine learning methods. Sci. Rep. 2024, 14, 32008. [Google Scholar] [CrossRef]
- Xu, D.M.; Liao, A.D.; Wang, W.; Tian, W.C.; Zang, H.F. Improved monthly runoff time series prediction using the CABES-LSTM mixture model based on CEEMDAN-VMD decomposition. J. Hydroinform. 2024, 26, 255–283. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, Y.; Feng, J.; Zhang, P.; Cheng, Z. Interpretable spatio-temporal attention LSTM model for flood forecasting. Neurocomputing 2020, 403, 348–359. [Google Scholar] [CrossRef]
- Li, W.; Liu, C.; Xu, Y.; Niu, C.; Li, R.; Li, M.; Tian, L. An interpretable hybrid deep learning model for flood forecasting based on Transformer and LSTM. J. Hydrol. Reg. Stud. 2024, 54, 101873. [Google Scholar] [CrossRef]
- Masih, I.; Maskey, S.; Uhlenbrook, S.; Smakhtin, V. Assessing the impact of areal precipitation input on streamflow simulations using the SWAT Model 1. JAWRA J. Am. Water Resour. Assoc. 2011, 47, 179–195. [Google Scholar] [CrossRef]
- Dai, Z.; Zhang, M.; Nedjah, N.; Xu, D.; Ye, F. A hydrological data prediction model based on LSTM with attention mechanism. Water 2023, 15, 670. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, Y.; Lu, F.; Liu, J.; Zhang, J.; Yin, Z.; Ji, M.; Li, B. Assessing the performance and interpretability of the CNN-LSTM-Attention model for daily streamflow forecasting in typical basins of the eastern Qinghai-Tibet Plateau. Sci. Rep. 2025, 15, 82. [Google Scholar] [CrossRef]
- Zhou, R.; Zhang, Y. Predicting and explaining karst spring dissolved oxygen using interpretable deep learning approach. Hydrol. Process. 2023, 37, e14948. [Google Scholar] [CrossRef]
- Alizadeh, F.; Roushangar, K.; Adamowski, J. Investigating monthly precipitation variability using a multiscale approach based on ensemble empirical mode decomposition. Paddy Water Environ. 2019, 17, 741–759. [Google Scholar] [CrossRef]
- Longyang, Q.; Choi, S.; Tennant, H.; Hill, D.; Ashmead, N.; Neilson, B.T.; Xu, T. An attention-based explainable deep learning approach to spatially distributed hydrologic modeling of a snow dominated mountainous karst watershed. Water Resour. Res. 2024, 60, e2024WR037878. [Google Scholar] [CrossRef]
- Liu, J.; Koch, J.; Stisen, S.; Troldborg, L.; Schneider, R.J. A national scale hybrid model for enhanced streamflow estimation—Consolidating a physically based hydrological model with long short-term memory networks. Hydrol. Earth Syst. Sci. Discuss. 2024, 28, 2871–2893. [Google Scholar] [CrossRef]
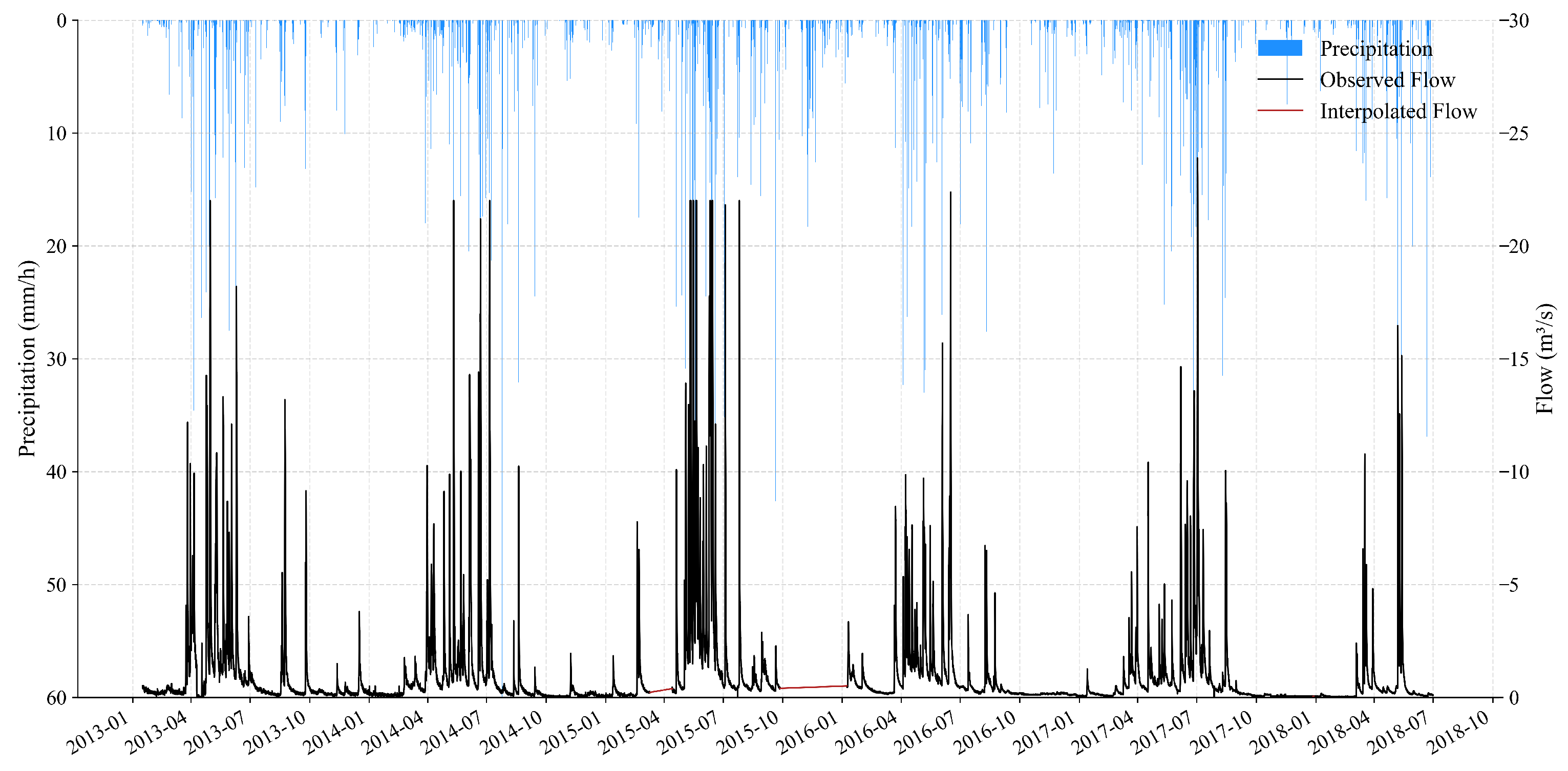
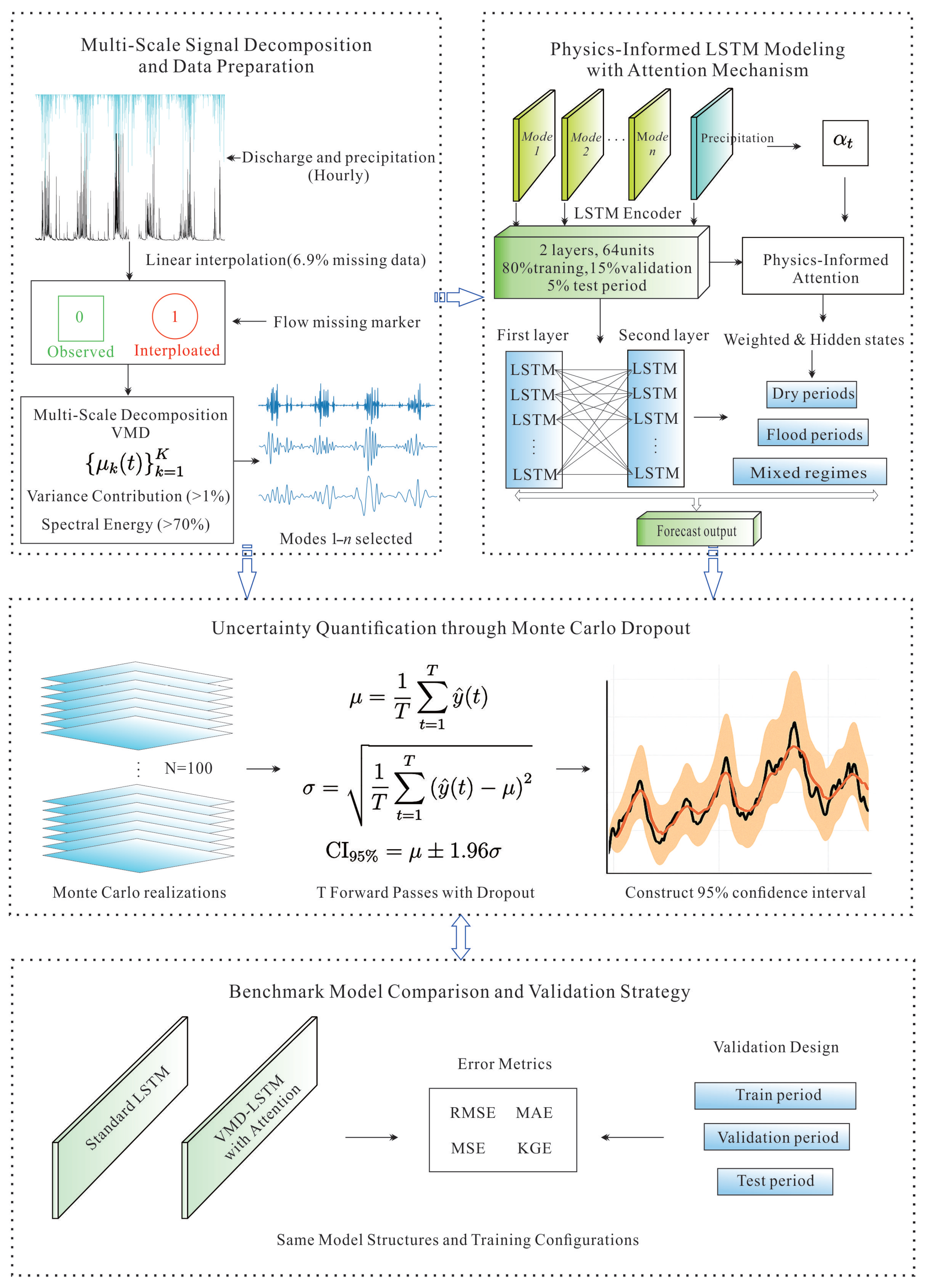
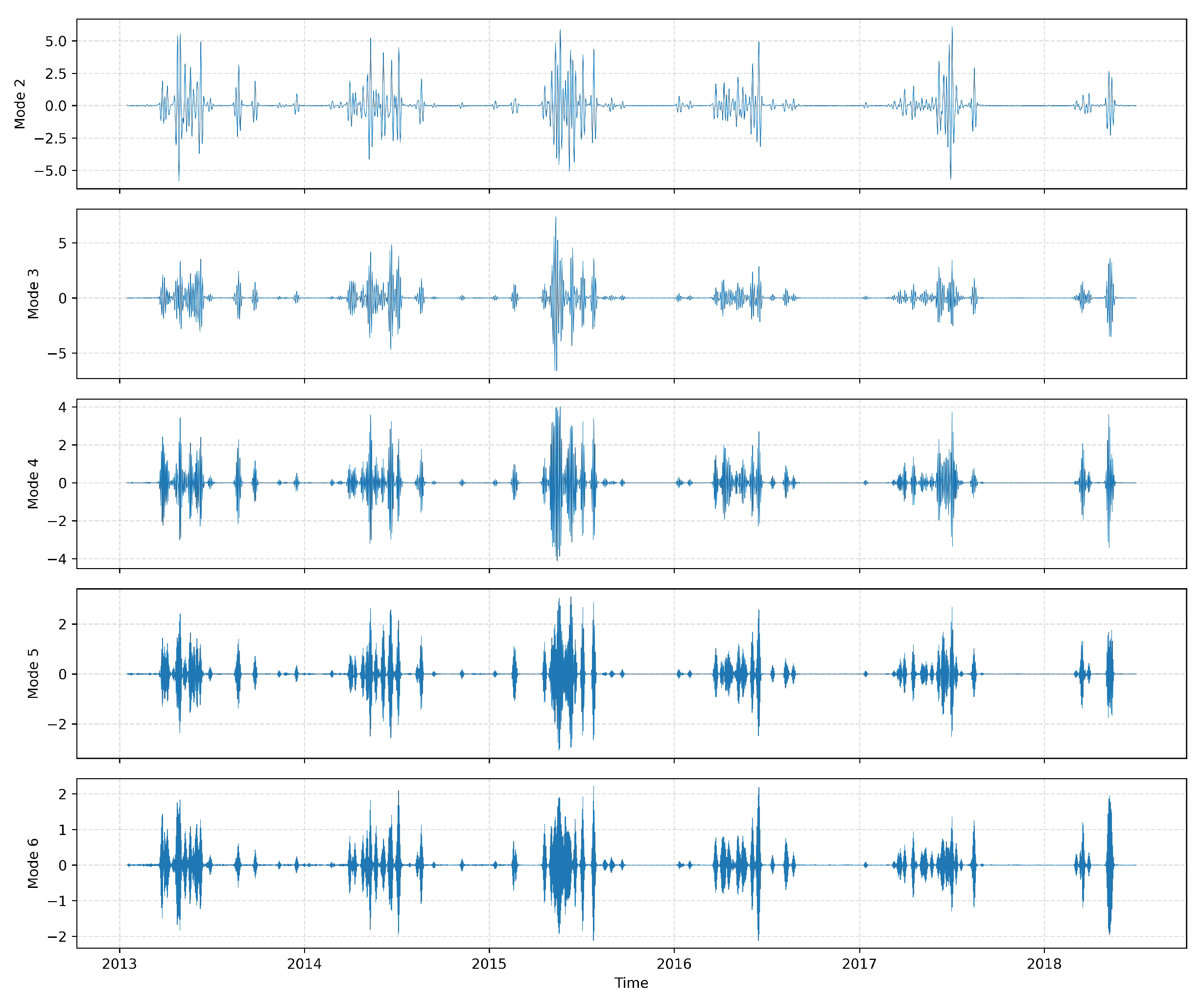



| Mode | Variance Contribution (%) | Dominant Period (h/d) | Preliminary Hydrological Interpretation |
|---|---|---|---|
| Mode1 | 45.86 | 9561.6/398.4 | Interannual variability and seasonal trends |
| Mode2 | 13.99 | 160.4/6.7 | |
| Mode3 | 8.93 | 90.5/3.8 | Medium-scale quickflow response |
| Mode4 | 5.48 | 54.8/2.3 | |
| Mode5 | 2.76 | 37/1.5 | Rapid to intermediate flow processes |
| Mode6 | 1.40 | 30.1/1.3 | |
| Mode7 | 0.76 | 21.6/0.9 | |
| Mode8 | 0.43 | 16.8/0.7 | Variance Contribution < 1% |
| Mode9 | 0.25 | 12.4/0.5 | |
| Mode10 | 0.13 | 9/0.4 | |
| Mode11 | 0.07 | 6.8/0.3 | |
| Mode12 | 0.04 | 5.5/0.2 |
| Metric | Train (i) | Train (ii) | Validation (i) | Validation (ii) | Test (i) | Test (ii) |
|---|---|---|---|---|---|---|
| RMSE | 0.142 | 0.074 | 0.491 | 0.250 | 0.726 | 0.220 |
| MAE | 0.057 | 0.047 | 0.146 | 0.081 | 0.155 | 0.073 |
| NSE | 0.996 | 0.999 | 0.944 | 0.985 | 0.867 | 0.988 |
| KGE | 0.980 | 0.980 | 0.926 | 0.936 | 0.913 | 0.951 |
| Peak_RMSE (5%) | 0.412 | 0.218 | 1.737 | 1.019 | 2.803 | 0.923 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Fazi, S.; Luan, S.; Wang, Z.; Li, C.; Fan, Y.; Yang, Y. Physics-Informed Deep Learning for Karst Spring Prediction: Integrating Variational Mode Decomposition and Long Short-Term Memory with Attention. Water 2025, 17, 2043. https://doi.org/10.3390/w17142043
Zhao L, Fazi S, Luan S, Wang Z, Li C, Fan Y, Yang Y. Physics-Informed Deep Learning for Karst Spring Prediction: Integrating Variational Mode Decomposition and Long Short-Term Memory with Attention. Water. 2025; 17(14):2043. https://doi.org/10.3390/w17142043
Chicago/Turabian StyleZhao, Liangjie, Stefano Fazi, Song Luan, Zhe Wang, Cheng Li, Yu Fan, and Yang Yang. 2025. "Physics-Informed Deep Learning for Karst Spring Prediction: Integrating Variational Mode Decomposition and Long Short-Term Memory with Attention" Water 17, no. 14: 2043. https://doi.org/10.3390/w17142043
APA StyleZhao, L., Fazi, S., Luan, S., Wang, Z., Li, C., Fan, Y., & Yang, Y. (2025). Physics-Informed Deep Learning for Karst Spring Prediction: Integrating Variational Mode Decomposition and Long Short-Term Memory with Attention. Water, 17(14), 2043. https://doi.org/10.3390/w17142043






