Research on an Underwater Target Classification Method Based on the Spatial–Temporal Characteristics of a Flow Field
Abstract
1. Introduction
2. Model Building and Simulation Calculation
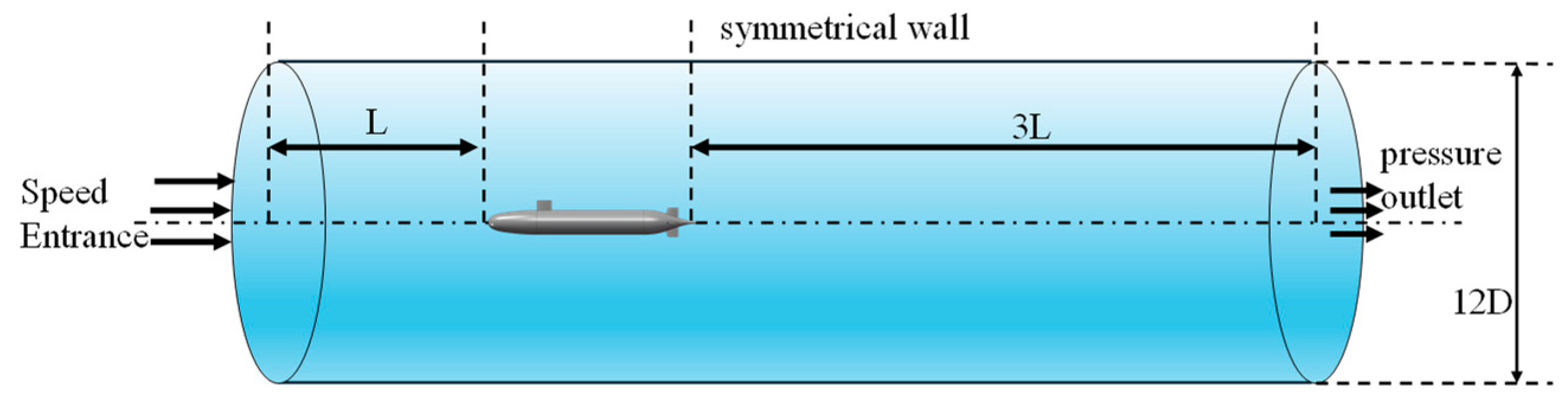
2.1. Model Construction and Description
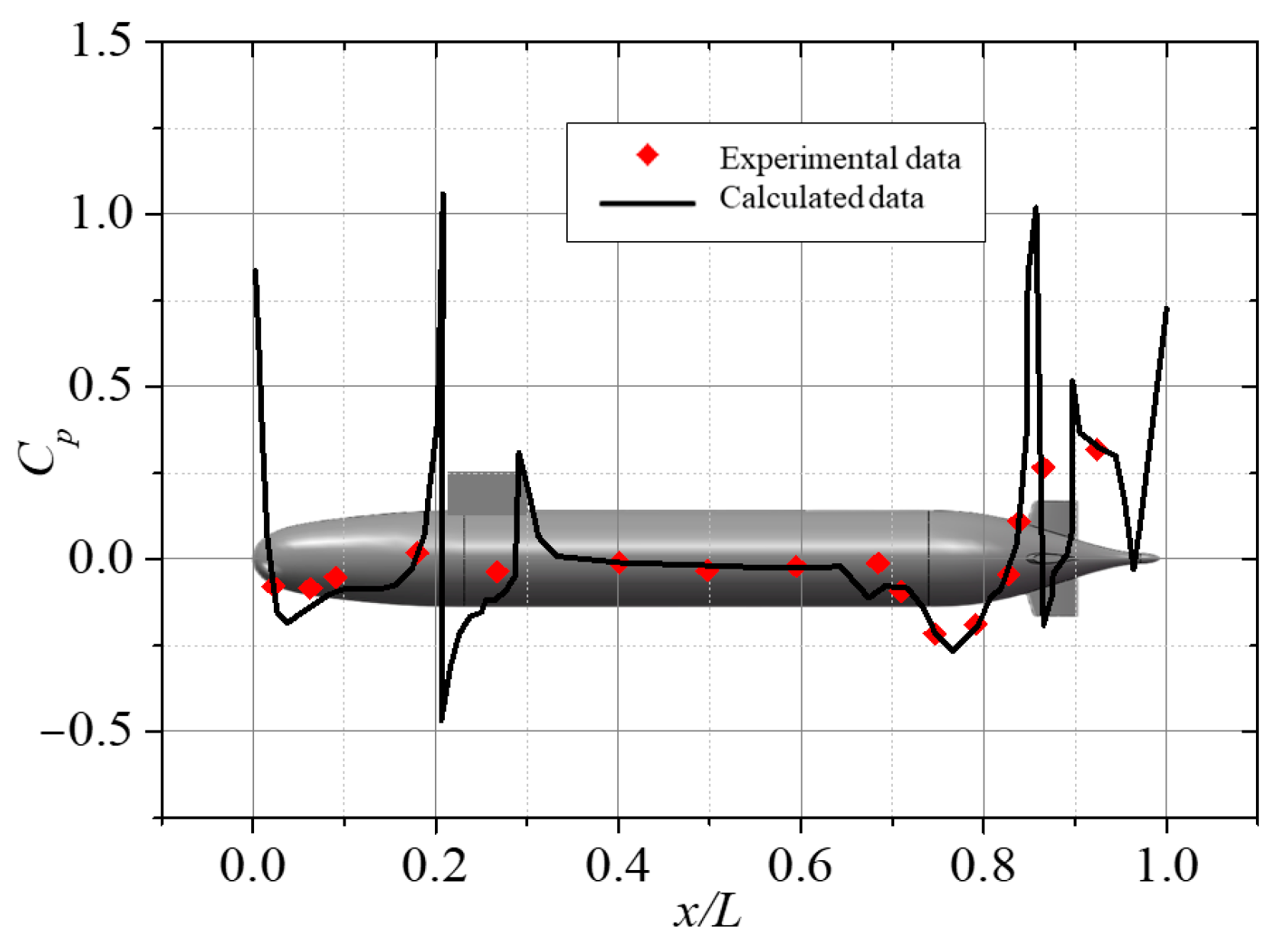
2.2. Calculation Method Validation
3. Characterization of the Flow Field in the Target Sense of Knowledge
3.1. Lateral Line Array and Target Sensing Model Construction
3.2. Flow Field Characterization for Target Structure Identification
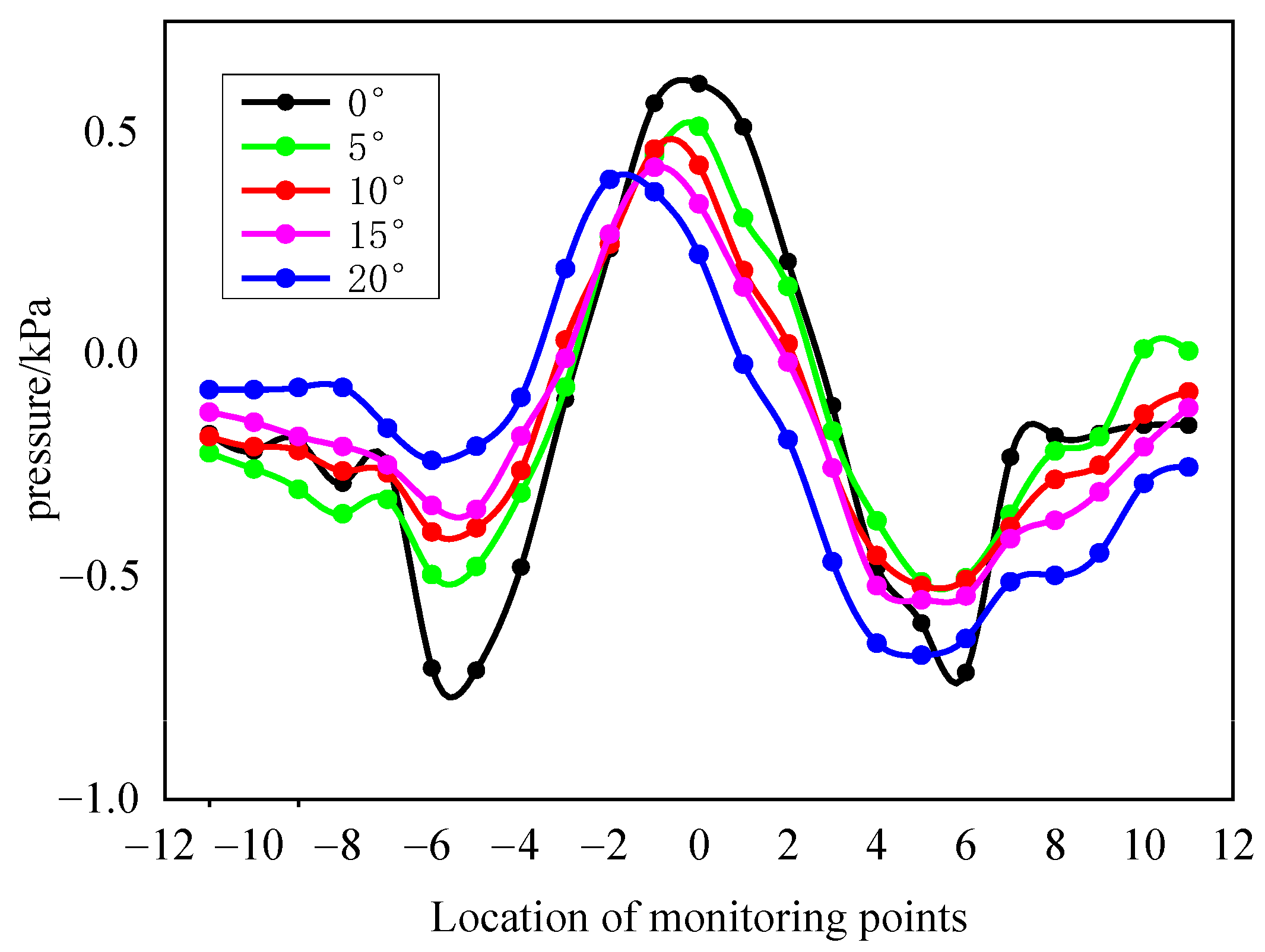
3.3. Flow Field Characterization for Target Attitude Recognition
4. Recognition Result Analysis of Target Perception
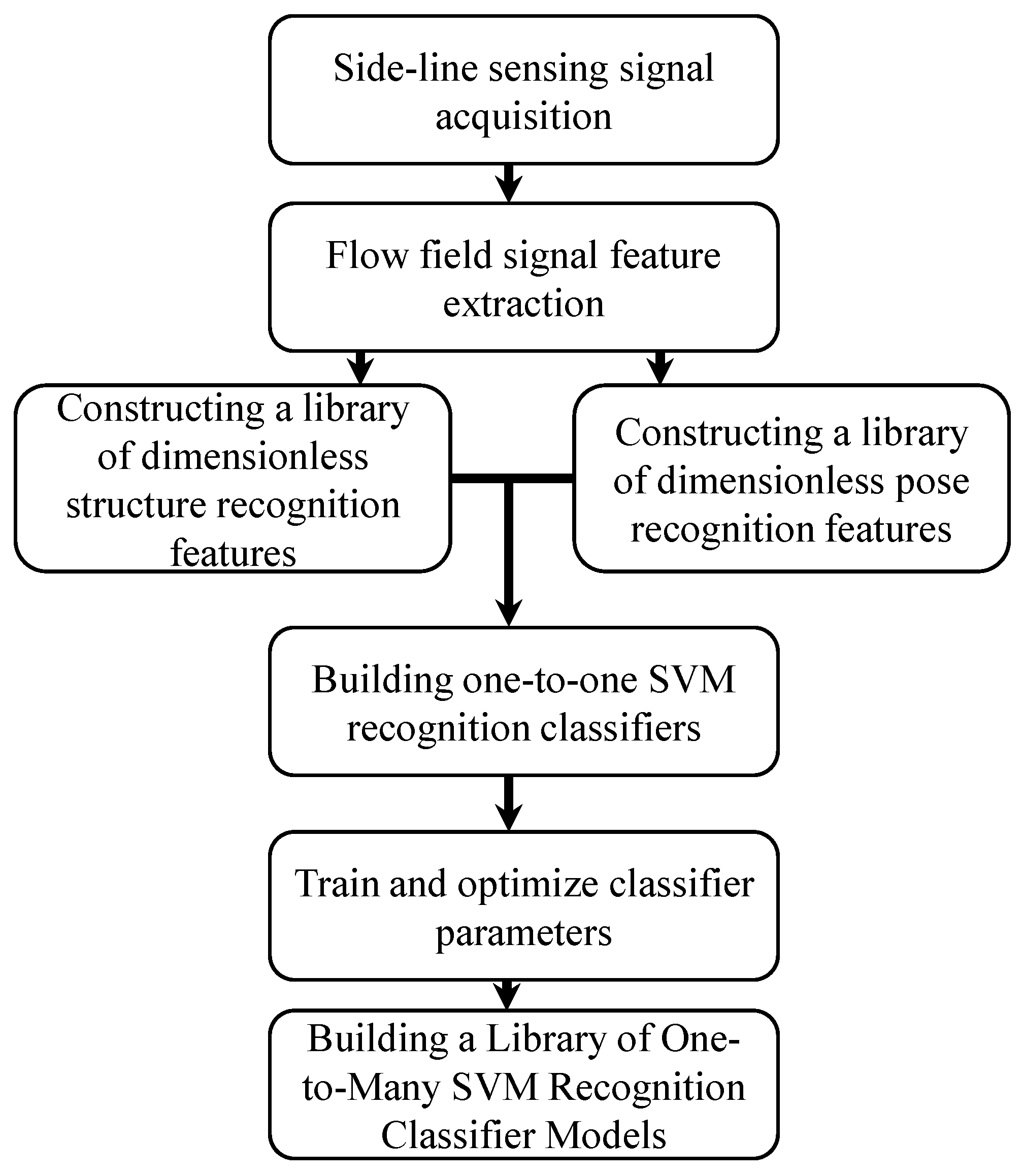
4.1. Model Construction of Target Recognition Classifiers
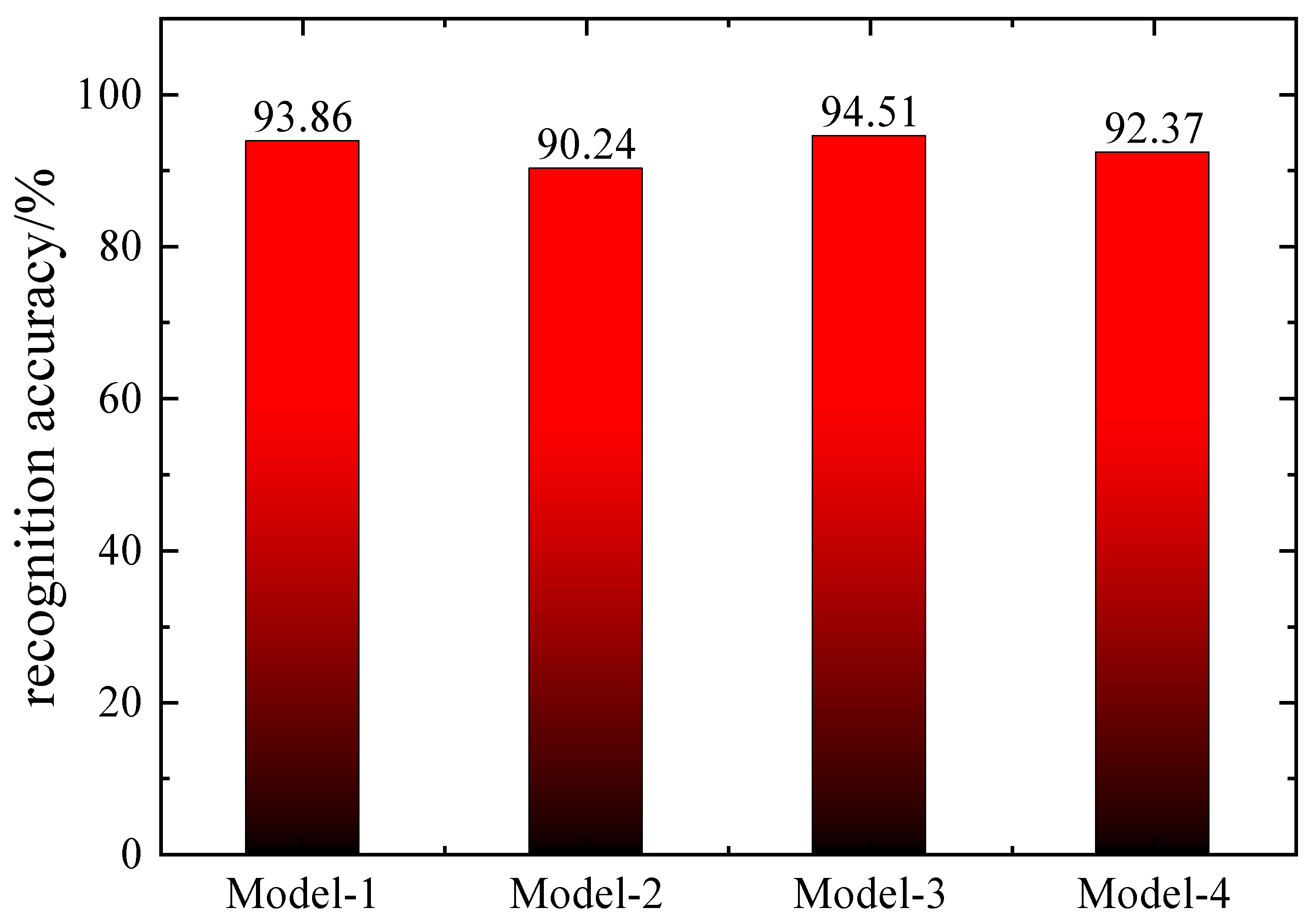
4.2. Analysis of Results of Target Structure Identification
4.3. Analysis of the Results of Target Attitude Recognition
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rashmi, S.N.; Rohit, A.; Domninc, S.; Kumar, A. Image mining application for underwater environment management: A review and research agenda. Int. J. Inf. Manag. Data Insights 2021, 1, 100023. [Google Scholar]
- Zhang, L.Y.; Li, C.Y.; Sun, H.F. Object detection/tracking toward underwater photographs by remotely operated vehicles (ROVs). Future Gener. Comput. Syst. 2022, 126, 163–168. [Google Scholar] [CrossRef]
- Wang, N.; Wang, Y.Y.; Meng, J.E. Review on deep learning techniques for marine object recognition: Architectures and algorithms. Control Eng. Pract. 2022, 118, 104458. [Google Scholar] [CrossRef]
- Bucci, A.; Zacchini, L.; Franchi, M.; Ridolfi, A.; Allotta, B. Comparison of feature detection and outlier removal strategies in a mono visual odometry algorithm for underwater navigation. Appl. Ocean Res. 2022, 118, 102961. [Google Scholar] [CrossRef]
- García-Vega, A.; Fuentes-Pérez, J.F.; Fukuda, S.; Kruusmaa, M.; Sanz-Ronda, F.J.; Tuhtan, J.A. Artificial lateral line for aquatic habitat modelling: An example for lefua echigonia. Ecol. Inform. 2021, 65, 101388. [Google Scholar] [CrossRef]
- Brian, M.M. Lateral line: From water waves to brain waves. Curr. Biol. 2021, 31, 344–347. [Google Scholar]
- Peloggia, J.; Münch, D.; Meneses-Giles, P.; Romero-Carvajal, A.; Lush, M.E.; Lawson, N.D.; McClain, M.; Pan, Y.A.; Piotrowski, T. Adaptive cell invasion maintains lateral line organ homeostasis in response to environmental changes. Dev. Cell 2021, 56, 1296–1312. [Google Scholar] [CrossRef]
- Ahrari, A.; Lei, H.; Sharif, M.A.; Deb, K.; Tan, X. Reliable underwater dipole source characterization in 3D space by an optimally designed artificial line system. Bioinspiration Biomim. 2017, 12, 036010. [Google Scholar] [CrossRef]
- Ashraf, S.; Gao, M.; Chen, Z.; Naeem, H.; Ahmed, T. CED-OR based opportunistic routing mechanism for underwater wireless sensor networks. Wirel. Pers. Commun. 2022, 125, 487–511. [Google Scholar] [CrossRef]
- Zhang, Y.; Zheng, X.D.; Ji, M.J.; Lin, X.; Qiu, J.; Liu, G.J. Orientation recognition of underwater translational target based on fish lateral line perception principle and deep learning. J. Mech. Eng. 2020, 56, 231–239. [Google Scholar]
- Tuhtan, J.A.; Fuentes-Perez, J.F.; Toming, G.; Schneider, M.; Schwarzenberger, R.; Schletterer, M.; Kruusmaa, M. Man-made flows from a fish’s perspective: Autonomous classification of turbulent fishway flows with field data collected using an artificial lateral line. Bioinspiration Biomim. 2018, 13, 046006. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.H.; Wu, J.G.; Qin, Q. A novel obstacle localization method for an underwater robot based on the flow field. J. Mar. Sci. Eng. 2019, 7, 437. [Google Scholar] [CrossRef]
- Lin, X.H.; Wu, J.G.; Wang, X.M.; Zhang, M.G.; Liu, H.T. Research on underwater triangular interference source sensing method based on lateral line sensing mechanism. J. Mech. Eng. 2020, 56, 240–248. [Google Scholar]
- Lin, X.H.; Wu, J.G.; Qin, Q. Robust classification method for underwater targets using the chaotic features of the flow field. J. Mar. Sci. Eng. 2020, 8, 111. [Google Scholar] [CrossRef]
- Liu, G.; Wang, M.; Xu, L.; Incecik, A.; Sotelo, M.A.; Li, Z.; Li, W. A new bionic lateral line system applied to pitch motion parameters perception for autonomous underwater vehicles. Appl. Ocean Res. 2020, 99, 102142. [Google Scholar] [CrossRef]
- Wang, M.; Jin, B.; Liu, G.; Li, Z. The moving vibration source perception using bionic lateral line system and data-driven method. Ocean Eng. 2022, 247, 110463. [Google Scholar] [CrossRef]
- Li, Y.X.; Hu, Q.; Liu, Y.; Yang, Q. Optimized arrangement model and evaluation method of bionic lateral line detection array for underwater vehicles. J. Xi’an Jiaotong Univ. 2021, 55, 34–45. [Google Scholar]
- Ghommem, M.; Bourantas, G.; Wittek, A.; Miller, K.; Hajj, M.R. Hydrodynamic modeling and performance analysis of bio-inspired swimming. Ocean Eng. 2020, 197, 106897. [Google Scholar] [CrossRef]
- Zhang, X.; Shan, X.; Xie, T.; Miao, J.; Du, H.; Song, R. Harbor seal whisker inspired self-powered piezoelectric sensor for detecting the underwater flow angle of attack and velocity. Measurement 2021, 172, 108866. [Google Scholar] [CrossRef]
- Yanagitsuru, Y.R.; Akanyeti, O.; Liao, J.C. Head width influences flow sensing by the lateral line canal system in fishes. J. Exp. Biol. 2018, 221, 180877. [Google Scholar] [CrossRef]
- Zhai, Y.F.; Xiong, M.L.; Wang, C.; Xie, G.M. Progress of underwater bionic lateral line sensing. J. Underw. Unmanned Syst. 2023, 31, 50–67. [Google Scholar]
- Yang, Q.; Hu, Q.; Shan, L.; Jiang, G.; Yao, Y.; Tang, L.; Zhu, Z.; Aabloo, A. A Cavity-Type Pressure Sensor Array with High Anti-Disturbance Performance Inspired by Fish Lateral Line Canal. IEEE Sens. J. 2024, 24, 14050–14058. [Google Scholar] [CrossRef]
- Luo, R.; Li, C.; Wang, F. Underwater motion target recognition using artificial lateral line system and artificial neural network method. Ocean. Eng. 2024, 303, 117757. [Google Scholar] [CrossRef]
- Zhang, N.; Shen, H.C.; Yao, H.Z. Numerical simulation and validation of submarine resistance and flow field and numerical optimization of boat type. Ship Mech. 2005, 9, 13. [Google Scholar]
- Stern, F.; Wilson, R.V.; Coleman, H.W.; Paterson, E.G. Comprehensive Approach to Verification and Validation of CFD Simulations—Part 1: Methodology and Procedures. J. Fluids Eng. 2001, 123, 793–802. [Google Scholar] [CrossRef]
- Lin, X.H.; Wu, J.G.; Qin, Q.; Li, W.M. Research on target-sensing method of underwater robots based on the lateral line mechanism. J. Ship Mech. 2020, 24, 559–569. [Google Scholar]









| Grids | Convergence Type | Rate of Change/% | ||
|---|---|---|---|---|
| Grid-1 | 4.0 | 2.962 | MC | 1.689 |
| Grid-2 | 3.0 | 2.916 | MC | 1.375 |
| Grid-3 | 2.0 | 2.873 | MC | 0.696 |
| Grid-4 | 1.0 | 2.855 | MC | 0.004 |
| Grid-5 | 0.5 | 2.848 | MC | \ |
| Comparative Parameters | Experimental Group | Simulation Group | Relative Error |
|---|---|---|---|
| 0.286 | 0.279 | 2.41% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, X.; Xu, H.; Wang, H.; Sun, P.; Yang, E.; Zan, G. Research on an Underwater Target Classification Method Based on the Spatial–Temporal Characteristics of a Flow Field. Water 2025, 17, 2006. https://doi.org/10.3390/w17132006
Lin X, Xu H, Wang H, Sun P, Yang E, Zan G. Research on an Underwater Target Classification Method Based on the Spatial–Temporal Characteristics of a Flow Field. Water. 2025; 17(13):2006. https://doi.org/10.3390/w17132006
Chicago/Turabian StyleLin, Xinghua, Hang Xu, Hao Wang, Peilong Sun, Enyu Yang, and Guozhen Zan. 2025. "Research on an Underwater Target Classification Method Based on the Spatial–Temporal Characteristics of a Flow Field" Water 17, no. 13: 2006. https://doi.org/10.3390/w17132006
APA StyleLin, X., Xu, H., Wang, H., Sun, P., Yang, E., & Zan, G. (2025). Research on an Underwater Target Classification Method Based on the Spatial–Temporal Characteristics of a Flow Field. Water, 17(13), 2006. https://doi.org/10.3390/w17132006





