Abstract
This study investigated the acoustic modal characteristics of pump tower structures under fluid–structure coupling effects through a finite element analysis. Compared with the dry condition, filling the internal pipelines with liquid causes the first three natural frequencies to decrease by 17.12%, 16.80%, and 19.50%, respectively, while full external immersion (wet mode) further reduces them by 15.60%, 15.10%, and 5.30%. As the liquid level in the surrounding storage tank increases from 0% to 100%, the first-mode frequency falls from 6.07 Hz to 5.13 Hz (a 15.5% reduction), the second-mode from 14.71 Hz to 12.48 Hz (15.1%), and the third-mode from 19.69 Hz to 18.63 Hz (5.5%). Mode-shape distributions remain qualitatively similar across liquid levels, although local deformation magnitudes decrease by up to 21.0% for the first mode and 18.3% for the second mode. These quantitative findings provide a theoretical and technical basis for predicting dynamic responses of pump tower structures in complex fluid environments.
1. Introduction
1.1. Research Background and Significance
The dynamic characteristics of pump tower structures in fluid environments play a crucial role in industrial applications, especially in petroleum, chemical engineering, marine transportation, and energy sectors. Vibrations induced by fluids can compromise equipment stability, potentially resulting in structural damage or safety hazards [1]. Therefore, an in-depth investigation into the modal characteristics of pump towers, particularly considering fluid interactions and liquid level variations, holds significant theoretical and engineering value [2].
1.2. Research Status
With the advancement of computational technologies and finite element methods, the demand for precision in structural dynamic analysis has increased. Traditional modal analyses, often based on dry modes, neglect the influence of surrounding fluids. However, actual working conditions involve internal and external fluid interactions, necessitating wet modal analysis for more accurate dynamic predictions [3]. Research into fluid–structure coupling began early, and recent developments in computational fluid dynamics and finite element methods have significantly enhanced this field. Structural components of hydraulic machinery exhibit different modal behaviors compared to structures in air due to fluid effects, which introduce added mass, damping, and stiffness. Among these, added mass notably dominates the variation in natural frequencies [4]. Wang X. et al. [5] conducted an experimental and numerical study on the buckling behavior of nearly perfect cylindrical shells under axial compression, revealing how geometric imperfections and manufacturing defects reduce the critical loads, and providing correction factors that inform mesh design and numerical validation methods for shell structures. Lu Y. et al. [6] performed a fluid–structure interaction simulation addressing cavitation suppression in submarine propellers under oceanic conditions, uncovering the complex coupling between vapor bubble dynamics and blade vibration; their use of turbulence modeling, dynamic meshing, and fluid–solid boundary treatment offers valuable guidance for defining the coupling interface between internal piping and external fluid domains in pump-tower analyses. In terms of fluid level influence, Chiba [7] systematically studied the relationship between liquid levels and the natural frequencies of cylindrical shells, establishing a quantitative correlation model. Ning Dezhi et al. [8] examined the hydrodynamic behavior of anti-sloshing structures in liquid tanks and demonstrated the nonlinear effect of fluid level on natural frequency. Zhou Ling et al. [9] used LMS Virtual. Lab to analyze the modal properties of multi-stage centrifugal pumps under different fluid conditions. These combined studies validate finite element models through experiments and clarify how liquid level, mesh strategy, turbulence model, and boundary treatment affect low- and high-order modal predictions.
1.3. Research Objectives and Methods
This study focuses on a pump tower structure and employs finite element analysis to examine the impact of fluid presence and liquid level variation on its modal characteristics. Key objectives include
- Analyzing the influence of internal and external fluid on modal behavior via dry and wet modal simulations.
- Investigating the effect of decreasing liquid level on the structure’s natural frequencies and mode shapes.
- Studying variations in the relative positions of identical mode shapes at different liquid levels.
2. Model Development and Validation
2.1. Research Object
The primary object of this study is a tower structure composed mainly of a pipeline system and a pump tower. The pipeline system consists of two pumps and two pipelines, with the pump tower serving as the support and connecting structure. The top of the tower is fixed to a storage tank, which facilitates the inflow and outflow of liquid through the pipeline system.
The pipelines are made of 304L stainless steel, while the pump tower is constructed from aluminum alloy.
The physical properties of the materials used are listed in Table 1:

Table 1.
Material properties.
2.2. Simulation Tools and Methods
2.2.1. Structural Modal Analysis
This paper mainly conducts constrained modal simulation on the finite element model of the pump tower. The modal analysis technique is used to identify the vibration characteristics of the structure. The calculation can be divided into free modal analysis and constrained modal analysis. Among them, constrained modal analysis needs to consider the forces and constraints on the structure under actual working conditions. Therefore, during modeling, reasonable boundary conditions such as loads and supports should be applied to accurately reflect the real working conditions [10]; since the storage tank is directly and fixedly connected to the top of the pump, a fixed constraint is applied to the top of the pump, and a frictionless constraint is applied to the central area of the base [11].
Dry modal analysis (without fluid immersion) and wet modal analysis (with fluid immersion) are studied, respectively. The dry modal calculation uses the Modal module in ANSYS Workbench 2021 R2, and the wet modal calculation uses the Modal Acoustics module [12].
The velocity and pressure of the liquid within the pump tower vary over time, and the flow field is calculated using the CFX module in ANSYS for an unsteady analysis. The computation employs the RNG k–ε turbulence model, with the inlet boundary defined as a pressure inlet and the outlet as a mass flow outlet, and a convergence criterion of 10−5 is set to ensure accuracy.
2.2.2. Mesh Independence Verification
To validate the mesh independence, three mesh schemes (A, B, and C) were compared under dry modal conditions for the first- and second-order natural frequencies. The comparison is summarized in Table 2:

Table 2.
Dry modal frequencies for mesh schemes A, B, and C.
As shown, the frequencies converge as follows: Scheme A → Scheme B → Scheme C. Scheme C’s values of 7.30 Hz and 7.72 Hz serve as the reference converged frequencies. Scheme B differs by only 0.27% (first order) and 0.78% (second order) from Scheme C, both within 1%, indicating sufficient accuracy. Scheme A’s errors (2.05% and 3.89%) are larger and not acceptable. Considering computation time and precision, Scheme B is adopted for all subsequent dry modal analyses.
2.2.3. Experimental Method
In order to ensure the accuracy of the simulation data, this paper compares it with excitation test data from the pump tower.
All experimental data in this study were obtained from laboratory vibration excitation tests conducted on the pump tower structure. A sweep-frequency excitation was applied using an electromagnetic shaker, with the excitation force directly acting on the flange at the bottom of the tower. The shaker model was XYZ-2000 (Hangzhou Zhibo Vibration Technology Co., Ltd., Hangzhou, China), with a maximum excitation force of ±1 kN, operating within a frequency range of 5 Hz to 50 Hz and a sweep rate of 1 Hz/s.
A total of 11 tri-axial accelerometers were arranged as follows: six accelerometers were evenly distributed along the height of the pump tower sidewall to measure vibrations perpendicular to the wall surface; two accelerometers were mounted on the top flange to record horizontal vibrations; and three accelerometers were placed along the outer wall of the internal pipeline—at the inlet, middle, and outlet—to measure radial responses. All sensors used were Kistler 8762B capacitive tri-axial accelerometers (Sinocera Piezotronics, Inc., Yangzhou, China), with a measurement range of ±50 m/s2.
Data acquisition was performed using a NI PXI-1042Q chassis (Pansino Tech, Beijing, China) equipped with NI PXI-4472B data acquisition cards, with a sampling rate set to 5000 Hz to ensure accurate capture of dynamic responses. The collected acceleration signals were processed using Fast Fourier Transform (FFT) to extract the Frequency Response Functions (FRFs) and identify the natural frequencies and corresponding mode shapes, completing the modal parameter identification.
This test configuration and measurement setup provided comprehensive coverage of the critical vibration regions of the pump tower structure and served as a reliable experimental basis for validating the subsequent numerical model.
Figure 1 shows the comparison between the first-order longitudinal and transverse mode shapes of the pump tower and the experimental results. Figure 2 shows the comparison between the second-order longitudinal and transverse mode shapes and the experimental results. In the figures, the left side represents the experimental results, and the right side shows the simulated mode shape cloud diagrams.
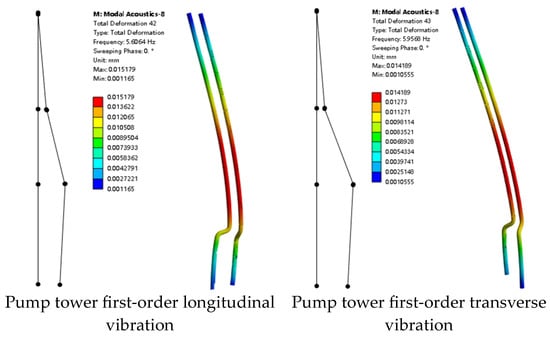
Figure 1.
Comparison of first-order modes.
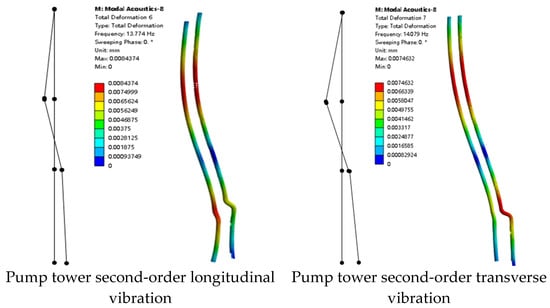
Figure 2.
Comparison of second-order modes.
The natural frequencies of the wet mode of the pump tower and those from experiments are shown in Table 3 below:

Table 3.
Comparison between experimental and simulated frequencies (wet mode).
Based on the above comparison, the following conclusions can be drawn:
The simulated natural frequencies of the wet mode of the pump tower are basically consistent with the experimental results. The error of the first-order mode natural frequency is less than 5%, while the second-order frequency shows a relatively large error, From Table 3, it can be seen that the second-order modal errors in this study are 21.6% and 24.2%, which are higher than the approximately 10% reported in reference [13]. The main reasons for the increased errors may include differences in the selection of model damping parameters, insufficient mesh density, and the treatment of fluid–structure coupling boundaries. The first-order and second-order mode shapes of the pump tower are consistent with the experimental results. The first-order mode is horizontal unidirectional swinging, and the second-order mode is alternating opposite swinging.
3. Modal Analysis of the Pump Tower Structure Under Fluid Effects and the Influence of Liquid Level Variation
3.1. Influence of Internal and External Fluids on the Modal Characteristics of the Pump Tower
When the pump tower operates for the first time or when all the fluid in the storage tank is discharged, there is no liquid inside the pipelines of the pump tower. At this point, performing a finite element analysis on the pump tower structure yields the dry mode.
In a common situation, when the pump tower is operating normally, the internal pipelines are fully filled with liquid, and the entire tower structure is also immersed in the liquid [14]. At this time, the analysis results of the pump tower finite element model represent the wet mode. This section considers the case where the tower structure is fully submerged in liquid.
There is also a relatively special condition: when the pump tower is transferring liquid from the storage tank to the outside under normal operation, the liquid level inside the storage tank gradually drops. When the liquid level reaches the lowest point (i.e., the pump tower is no longer immersed in liquid), there is still some undischarged liquid remaining inside the pipelines. This condition is referred to as zero liquid level.
The finite element models for the three different conditions are shown in Figure 3 below (from left to right: dry mode, zero liquid level, and full liquid level). The dry and wet modal simulations of the pump tower finite element model are performed using the Modal module and the Modal Acoustics module in ANSYS, respectively, to obtain the natural frequencies and mode shapes under the existing structural and boundary conditions.
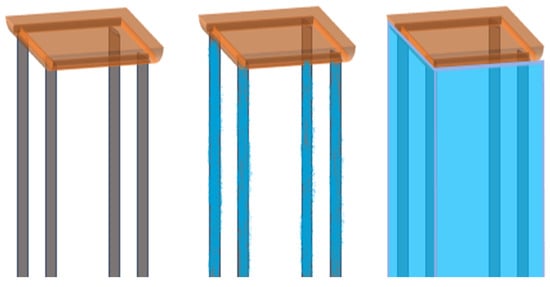
Figure 3.
Finite element models for three different conditions.
According to modal analysis theory, the derivative of natural frequency is proportional to the modal participation factor of the corresponding mode [15,16]. Therefore, when the natural frequency is higher, the corresponding mode’s participation factor is smaller. Thus, the dynamic characteristics of the structure are mainly determined by the lower-order modes, and it is sufficient to calculate only the first few natural frequencies and mode shapes. In this study, the first three modes of the unloading pipeline system of the pump tower are analyzed.
First, a comparison of the mode shape changes in the same mode order under the three conditions is performed. As shown in Figure 4, the first-order mode shapes of the tower structure under the three conditions are basically unchanged. The pipeline exhibits first-order longitudinal vibration along the x-axis direction, and the maximum vibration displacement occurs at the same position in the first-order mode, located in the lower-middle section of the pipeline. This type of vibration may affect the pump’s transport efficiency or cause fatigue damage to the pipeline. However, it is worth noting that the maximum deformation differs significantly. The maximum deformation under the dry mode is 10.51 mm, while in the fully filled pipeline case, it is only 0.017 mm, which is close to the deformation value under the filled condition.
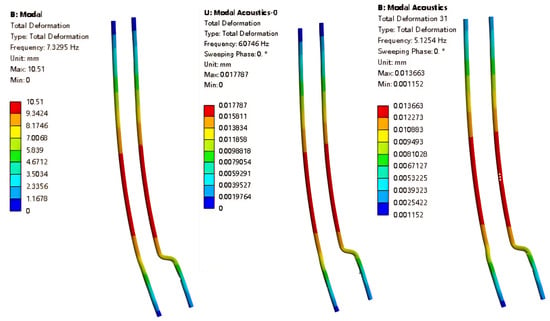
Figure 4.
First-order mode shape cloud maps under three conditions.
As shown in Figure 5, the second-order mode shapes of the tower structure under the three conditions all display second-order transverse vibrations, with structural deformation mainly occurring in the middle of the pipeline. The wave-like deformation of the pipeline is intensified, which may cause local structural fatigue. Under the dry mode, the maximum vibration displacement is 13.289 mm, occurring in the upper-middle part of the pipeline; the maximum vibration displacements under the second and third conditions are 0.009 mm and 0.007 mm, respectively, which are much smaller than those under the dry mode.
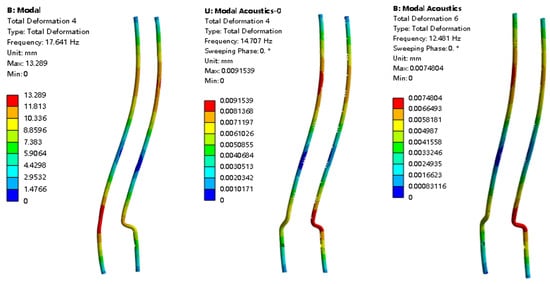
Figure 5.
Second-order mode shape cloud maps under three conditions.
As shown in Figure 6, the third-order mode shape of the tower structure under the three conditions mainly exhibits longitudinal vibration, and the deformation magnitude decreases along the positive z-axis direction. Under the dry mode, the maximum displacement is 9.4321 mm. Excessive deformation at the pump may lead to unstable pump operation, resulting in unbalanced loads, and causing abnormal wear to components such as the pump shaft and impeller.
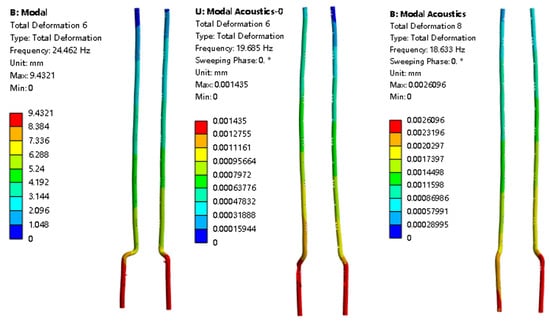
Figure 6.
Third-order mode shape cloud maps under three conditions.
As shown in Figure 7, the variation in the first three mode frequencies of the pump tower system under the three conditions of not being immersed in liquid, zero liquid level, and being submerged in liquid.
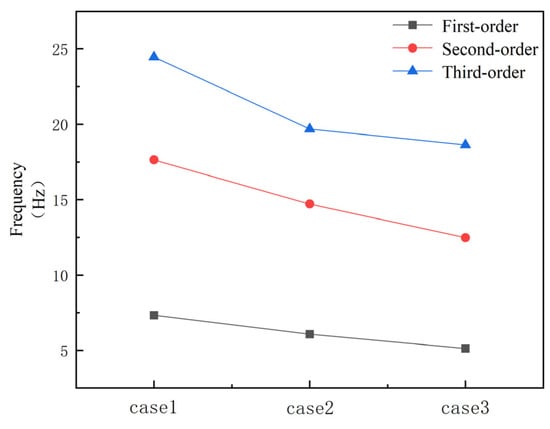
Figure 7.
First three mode frequencies under three conditions.
Based on the analysis of the first three major modes under the above three conditions, the following conclusions can be drawn:
- Compared with external fluid, the internal liquid in the pipeline has a greater influence on the mode shapes, especially the maximum deformation during vibration.
- The internal liquid in the pipeline also has a much greater effect on the decrease in frequency than the external liquid (when the internal pipeline changes from no liquid to full of liquid, the decrease rates of the first three mode frequencies are 17.12%, 16.8%, and 19.5%, respectively; when the liquid level changes from zero to fully immersed, the decrease rates of the first three mode frequencies are 15.6%, 15.1%, and 5.3%, respectively).
3.2. Law of Influence of Liquid Level Drop on Pump Tower Modal Characteristics
When the pump tower is in operation, the liquid in the storage tank increases or decreases, and the liquid level in the tank changes accordingly. The height of the liquid level, that is, the depth to which the tower is immersed, affects the natural frequency of the tower. When the liquid level rises, the added mass from the fluid increases, leading to a decrease in the structural natural frequency; when the liquid level drops, the fluid mass decreases, and the frequency increases. In addition, liquid level changes also affect the modal shapes. Therefore, based on the dry mode model, this study adds fluid bodies to investigate the influence of liquid level variation on modal behavior.
3.2.1. Mode Shape Comparison Analysis
By comparing the first three modes of the tower structure under different liquid levels, the influence of liquid level changes on mode shapes is analyzed. The external water body of the pump tower is divided into 20 height levels. The liquid levels of 0%, 25%, 50%, 75%, and 100% are selected as study cases. The model with liquid level indicators is shown in Figure 8 below:
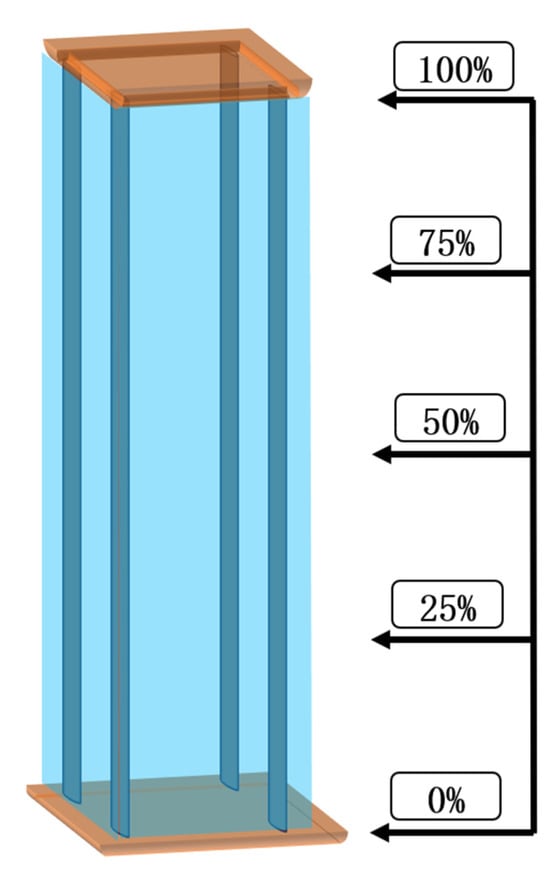
Figure 8.
Liquid level indicator diagram.
As shown in Figure 9 are the first-order mode shape cloud maps under the same mode at five liquid levels, the five subfigures A–E display the modal shapes of the same modal order (for example, first, second, or third order) at five different liquid level heights in the tanks (0%, 25%, 50%, 75%, 100%). The mode shapes do not change with rising liquid level, all showing first-order transverse vibrations, with the maximum deformation occurring in the lower-middle part of the pipeline. From 0% to 100% liquid level, the effect of added mass becomes increasingly significant, and the maximum deformation decreases gradually, with a total reduction rate of 21%.
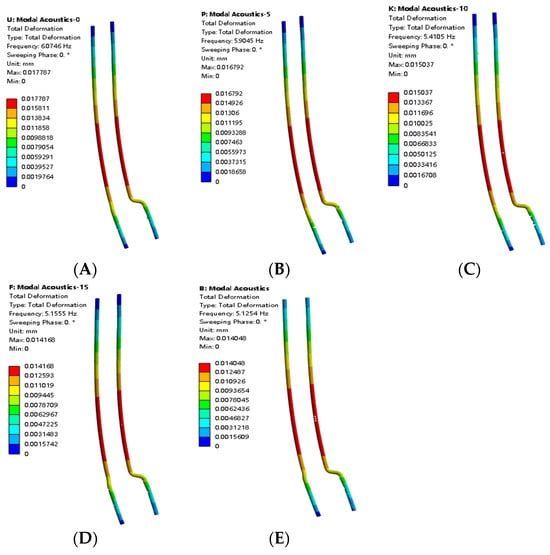
Figure 9.
First-order mode shape cloud maps under different liquid levels. Subfigures (A–E) correspond to 0%, 25%, 50%, 75%, and 100% liquid levels, respectively.
As shown in Figure 10 are the second-order mode shape cloud maps under the same mode at five liquid levels, all displaying second-order transverse vibrations. The maximum deformation at 0% liquid level is 0.0091 mm, and at 100% liquid level is 0.0074 mm, with a total reduction rate of 18.3%.
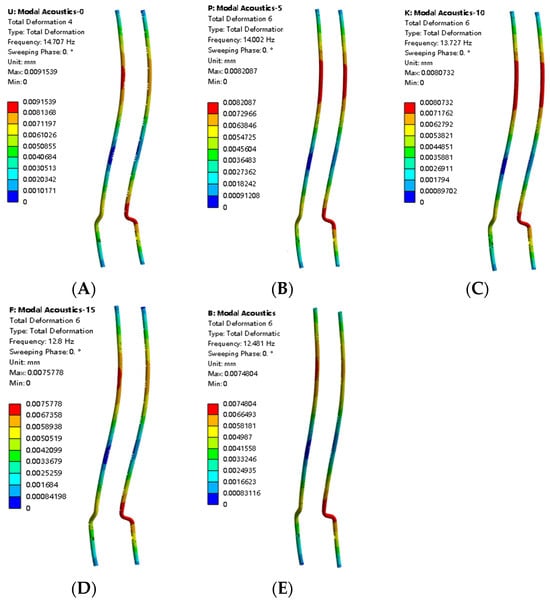
Figure 10.
Second-order mode shape cloud maps under different liquid levels. Subfigures (A–E) correspond to 0%, 25%, 50%, 75%, and 100% liquid levels, respectively.
As shown in Figure 11 are the third-order mode shape cloud maps under the same mode at five liquid levels, all showing second-order longitudinal vibrations, and the deformation decreases gradually from bottom to top. Unlike the previous two cases, at the 0% liquid level, the maximum deformation is only 0.0014 mm, which increases to 0.0026 mm at the 25% liquid level, continues to rise until 50%, and then begins to gradually decline as the liquid level continues to rise.
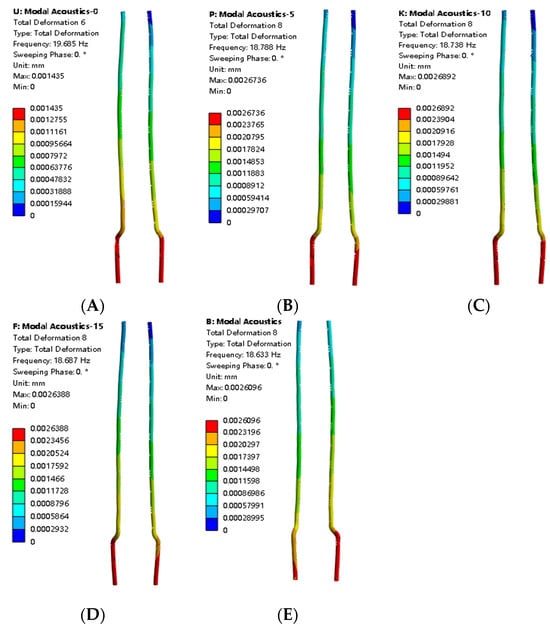
Figure 11.
Third-order mode shape cloud maps under different liquid levels. Subfigures (A–E) correspond to 0%, 25%, 50%, 75%, and 100% liquid levels, respectively.
Overall, the effect of liquid level variation on the same mode shape is minimal. Locally, the maximum deformation varies with liquid level, mostly showing a gradual decrease, though there may be fluctuations.
Figure 11 shows that the third-order mode shape exhibits five distinct contour levels, clearly different from the first and second modes. To confirm that this is not caused by numerical error, we additionally extracted the mode shapes up to the sixth order under the 10% liquid level condition (see Figure 12). The subfigures A–F display different modes of the pump tower under the same liquid level for six consecutive stages. The results show consistent level patterns, indicating that the five-layer distribution is an intrinsic feature of the third mode.

Figure 12.
First six mode shape maps at 50% liquid level. (A) First-order mode shape (B) Second-order mode shape (C) Third-order mode shape (D) Fourth-order mode shape (E) Fifth-order mode shape (F) Sixth-order mode shape.
3.2.2. Influence of Liquid Level on Natural Frequency
This section mainly analyzes the frequency variation in the first three modes under the liquid levels of 0%, 25%, 50%, 75%, and 100%. As shown in Table 4, as the liquid level increases from 0% to 100%, the reduction rates of the first, second, and third mode frequencies are 15.5%, 15.1%, and 5.5%, respectively.

Table 4.
Natural frequency variation in the same mode shape.
By comparing the frequency variation in the same mode under five liquid levels, the following laws are obtained:
- In the range of 50–75% liquid level, the frequency drops the fastest, indicating that the added mass effect of the fluid is most significant in this interval.
- The higher the mode order, the lower the frequency reduction rate caused by the liquid level rise.
3.3. Relative Position Variation in the Same Mode Shape
The pump tower system studied in this paper is actually driven by two pump units. The two pump units, respectively, deliver liquid into two different pipelines.
The pump and pipeline are directly connected by flat flanges fabricated from the same material, with an oil-resistant gasket placed between mating flange faces to ensure sealing integrity. A short section of flexible corrugated hose is installed between the two flanges to compensate for axial and radial misalignment and to absorb vibration. Where necessary, a metallic bellows expansion joint is added at the connection to accommodate thermal expansion and contraction. A sliding support is provided beneath the interface to bear the weight of the pipeline while allowing axial movement, and fixed supports are spaced along the pipeline to stabilize its position. After installation, the flange centerlines are aligned using a laser alignment tool to ensure radial misalignment less than 0.2 mm and axial runout below 0.05 mm, thereby minimizing additional stress and vibration effects.
As indicated earlier, the mode shape variation in the tower structure mainly occurs at the pipeline and pump unit sections [17]. After studying the overall behavior of the pump tower, this section focuses on analyzing the local mode shape variation.
As shown in Figure 13, from left to right are the fourth-order mode shape cloud maps of the tower structure at the liquid levels of 25%, 50%, and 75%, respectively. At the 25% liquid level, the maximum deformation occurs at both pump units, but the deformation at the left pump is significantly smaller than that at the right pump. When the liquid level reaches 50%, the deformation of the left pump slightly decreases, and there is almost no change in the right pump. When the liquid level reaches 75%, the maximum deformation occurs only at the right pump. Under this mode shape, as the liquid level rises, the deformation of the left pump unit due to external forces gradually decreases [18].
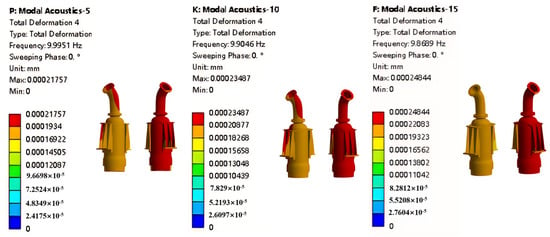
Figure 13.
Fourth-order mode shapes at three liquid levels.
In lower-order modes, no obvious change is observed in the relative deformation positions of the pipeline under the same mode shape as the liquid level increases. However, in the calculated 11th-order mode, a significant change in the relative position of the pipeline is observed.
As shown in Figure 14, these are the cloud maps for the same mode shape at the liquid levels of 50%, 75%, and 100%. At the 50% and 75% levels, the overall deformation of the pipeline is relatively uniform, with deformation gradually decreasing from bottom to top. However, with the rise in the liquid level, the deformation in the upper-middle part of the pipeline becomes more prominent. When the tower structure is fully submerged, the deformation no longer decreases from bottom to top, and the deformation in the upper-middle section significantly increases, becoming the main deformation region.
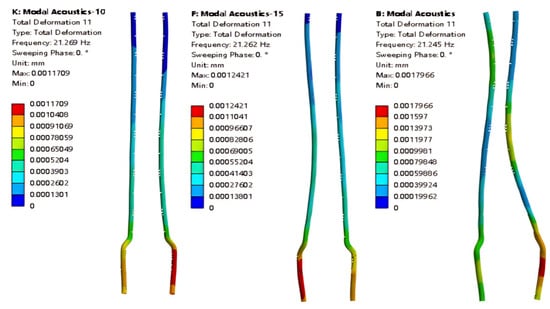
Figure 14.
Eleventh-order mode shapes at three liquid levels.
4. Conclusions
In this paper, based on the fluid–solid coupling effect, the acoustic modal characteristics of a pump tower structure under different liquid levels are studied. Through a finite element analysis and comparison with experimental data, the following main conclusions are drawn:
- Influence of Fluid on the Modal Characteristics of the Pump Tower: the vibration characteristics of the pump tower structure vary significantly under different fluid environments. The internal liquid in the pipeline has a much greater influence on the mode shapes and natural frequencies than the external liquid. By comparing dry and wet modal conditions, it is found that wet modes, which fully consider the added mass and damping effects of the fluid, exhibit significantly lower low-order natural frequencies compared to dry modes. Meanwhile, the mode shapes in wet modes also present smoother and more global deformation distributions.
- Influence of Liquid Level Variation on the Modal Characteristics of the Pump Tower: as the liquid level gradually increases, the natural frequencies of the pump tower show a continuous downward trend. Particularly in the 50% to 75% liquid level range, the effect of fluid added mass is most significant, and the frequency variation in low-order modes (such as the first and second modes) is especially obvious. In addition, liquid level changes also affect the mode shapes, causing slight adjustments in local displacement distributions and deformation magnitudes.
- Influence of Liquid Level on Local Mode Shapes: under varying liquid levels, local mode shapes of the pump tower also change accordingly. Especially in the connection regions between the pump units and pipelines, the amount and location of deformation change with increasing liquid level. Moreover, liquid level variation can lead to the redistribution of vibration energy across different parts of the structure, which may affect the overall vibration coordination and cause local stress concentrations. The higher the mode order, the lower the frequency reduction rate caused by liquid level rise.
Author Contributions
Conceptualization, Y.L. and A.X.; methodology, Y.L.; software, Y.Z.; validation, Y.Z. and Y.L.; formal analysis, Y.Z.; investigation, W.S.; resources, Z.W.; data curation, Y.Z.; writing—original draft preparation, A.X.; writing—review and editing, Y.L.; visualization, W.S.; supervision, Y.L.; project administration, Z.W.; funding acquisition, Z.W. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the Joint Open Research Fund Program of State 381; the Key Laboratory of Hydroscience and Engineering and Tsinghua-Ningxia Yinchuan Joint 382; and the Institute of Internet of Waters on Digital Water Governance (sklhse-2024-Iow07).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ma, F. Structural Analysis of Pump Tower in LNG Carrier Based on Sloshing Dynamic Load. Master’s Thesis, Dalian University of Technology, Dalian, China, 2010. [Google Scholar]
- Sun, C.; Huang, J.; Zhou, Q. Modal Calculation and Influence Law Study of Cylindrical Containers under Fluid Action. Chin. J. Appl. Mech. 2021, 38, 2079–2083. [Google Scholar] [CrossRef]
- Wang, L.; Zhu, L.; Li, J.; Zhao, T.; Sun, W. Vibration Modal Simulation Analysis of Outlet Pipeline of Piston Pump. J. Mech. Eng. Technol. 2023, 12, 177–187. [Google Scholar] [CrossRef]
- Dehkharqani, A.S.; Aidanpä, J.-O.; Engström, F.; Cervantes, M.J. A Review of Available Methods for the Assessment of Fluid Added Mass, Damping, and Stiffness with an Emphasis on Hydraulic Turbines. Appl. Mech. Rev. 2018, 70, 050801. [Google Scholar] [CrossRef]
- Wang, B.; Zhu, S.; Hao, P.; Bi, X.; Du, K.; Chen, B.; Ma, X.; Chao, Y.J. Buckling of quasi-perfect cylindrical shell under axial compression: A combined experimental and numerical investigation. Int. J. Solids Struct. 2018, 130, 232–247. [Google Scholar] [CrossRef]
- Lu, Y.; Guo, Z.; Zheng, Z.; Wang, W.; Wang, H.; Zhou, F.; Wang, X. Underwater propeller turbine blade redesign based on developed inverse design method for energy performance improvement and cavitation suppression. Ocean. Eng. 2023, 277, 114315. [Google Scholar] [CrossRef]
- Chiba, M.; Matsushima, T.; Yamaki, N. Free vibration of a partially liquid-filled cylindrical tank. J. Sound Vib. 1985, 98, 235–255. [Google Scholar]
- Ning, D.; Su, P.; Zhang, C. Hydrodynamic Characteristics of Floater-Type Anti-Sloshing Structure in a 3D Liquid Tank. J. Hebei Univ. Eng. 2018, 40, 154–161. [Google Scholar]
- Zhou, L.; Hou, Y.; Wang, W.; Yang, Y. Numerical modal analysis of multistage centrifugal pump based on LMS Virtual Lab. J. Fluid Mach. 2017, 45, 21–25. [Google Scholar] [CrossRef]
- Chen, S.; Zhou, Y.; Tang, Z.; Lu, S. Modal vibration response of rice combine harvester frame under multi-source excitation. Biosyst. Eng. 2020, 194, 177–195. [Google Scholar] [CrossRef]
- Cao, J.; Luo, Y.; Shi, Y.; Liu, X.; Xu, D.; Wang, Y.; Zhai, L.; Wang, Z. A review of hydro-turbine unit rotor system dynamic behavior: Multi-field coupling of a three-dimensional model. Phys. Fluids 2024, 36, 121304. [Google Scholar] [CrossRef]
- Wang, F. Study on Propeller Acoustic Radiation Under Hull-Propeller Coupling. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2024. [Google Scholar]
- Wang, X.; Li, K.; Bai, C.; Li, Y. Modal analysis of cabin seat structure for large commercial aircraft. Today’s Manuf. Upgrad. 2022, 11, 167–170. [Google Scholar]
- Lu, Y.; Xin, L.; Hu, N.; Zhu, Z.; Xia, W. Influences of floating ice on the water entry process of slender body on the cavity evolution and hydrodynamic characteristics. Phys. Fluids 2025, 37, 42103. [Google Scholar] [CrossRef]
- Wang, X.; Hong, T.; Liu, Y.; Yu, Z.; Guo, J.; Liu, Y. Optimized design for vibration reduction in a residual film recovery machine frame based on modal analysis. Agriculture 2024, 14, 543. [Google Scholar] [CrossRef]
- Liang, Z.; Li, Y.; Xu, L.; Zhao, Z.; Tang, Z. Optimum design of an array structure for the grain loss sensor to upgrade its resolution for harvesting rice in a combine harvester. Biosyst. Eng. 2017, 157, 24–34. [Google Scholar] [CrossRef]
- Zhou, D.; Zhang, N.; Zheng, F.; Gad, M.; Gao, B. Experimental investigation on the effect of the rotor-stator matching mode on velocity pulsation in the centrifugal pump with a vaned diffuser. Nucl. Eng. Technol. 2024, 57, 103255. [Google Scholar] [CrossRef]
- Li, D.; Zhang, N.; Jiang, J.; Gao, B.; Alubokin, A.A.; Zhou, W.; Shi, J. Numerical investigation on the unsteady vortical structure and pressure pulsations of a centrifugal pump with the vaned diffuser. Int. J. Heat Fluid Flow 2022, 98, 109050. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).