Design, Calibration, and Performance Evaluation of a High-Fidelity Spraying Rainfall Simulator for Soil Erosion Research

Abstract

Rainfall simulators are essential tools in soil research, providing a controlled and repeatable approach to studying rainfall-induced erosion. However, the development of high-fidelity rainfall simulators remains a challenge. This study aimed to design, construct, and calibrate a spraying-type rainfall simulator and validate assessment criteria optimized for soil erosion research. The simulator’s design is based on a modified simulator model previously described in the literature and following the defined criteria. The calibration of the simulator was conducted in two phases, on slopes of 0° and 15°, measuring rainfall intensity, drop size, and its spatial distribution, and calculating drop falling velocity, kinetic energy, and momentum. The simulator consists of structural support, a water tank, a water-moving mechanism, a flow regulation system, and sprayers, contributing to its simplicity, cost-effectiveness, durability, rigidity, and stability, ensuring smooth simulator operation. The calibration of the rainfall simulator demonstrated that rainfall intensity increased from 1.4 mm·min⁻¹ to 4.6 mm·min⁻¹ with higher pressure in the hydraulic system (1.0 to 2.0 bar), while spatial uniformity remained within 79–91% across different nozzle configurations. The selected Rain Bird HE-VAN series nozzles proved highly effective in simulating rainfall, achieving drop diameters ranging from 0.8 mm to 1.9 mm, depending on pressure and nozzle type. The rainfall simulator successfully replicates natural rainfall characteristics, offering a controlled environment for investigating soil erosion processes. Drop velocity values varied between 2.5 and 2.9 m·s⁻¹, influencing kinetic energy, which ranged from 0.6 J·min⁻¹·m⁻² to 2.9 J·min⁻¹·m⁻², and impact momentum, which was measured between 0.005 N·s and 0.032 N·s. The simulator design suggests that it is suitable for future applications in both field and laboratory soil erosion research, ensuring repeatability and adaptability for various experimental conditions. Calibration results emphasized the significance of nozzle selection and water pressure adjustments. These factors significantly affect rainfall intensity, drop size, kinetic energy, and momentum, parameters that are critical for accurate erosion modeling.

1. Introduction

Soil erosion studies are vital for understanding and mitigating the detrimental effects of soil degradation, which results in reduced agricultural productivity and increased environmental hazards. Through analyzing soil erosion patterns and dynamics, decision-makers can develop effective land management strategies and promote sustainable practices to conserve soil health and ecosystem sustainability. With the growing pressures of climate change, intensified agriculture, and land use changes, understanding soil erosion dynamics has become increasingly urgent. Rainfall simulators are essential tools for studying soil erosion and investigating the intricate interactions between precipitation and soil. Their applications span various research domains, including soil erosion [1,2,3,4,5], hydrology [6,7], infiltration processes [8,9,10], runoff and sediment transport [11,12,13], slope stability [14,15], and the impact of precipitation on the physical, mechanical, and chemical properties of soil [16]. Data collection methods such as sediment sampling, topographic surveys, and environmental monitoring (temperature, humidity, and wind conditions) further refine analysis. Conducting research on these processes under natural precipitation conditions remains challenging due to uncertainties, time constraints, and high costs. Rainfall simulators provide a controlled experimental environment that enables the precise regulation of precipitation characteristics and environmental conditions (e.g., intensity and drop size), allowing researchers to systematically analyze the factors influencing soil erosion [17,18]. The ability to replicate identical experimental conditions improves comparability across different locations and supports the development, calibration, and validation of mathematical models essential for predictive erosion assessments [19].

Despite their widespread use, the absence of harmonized designs poses challenges for the repeatability and comparability of experimental results across different studies [20,21]. Current rainfall simulators often fail to accurately replicate natural rainfall characteristics, particularly intensity, spatial uniformity, and kinetic energy, limiting the reliability and comparability of erosion predictions [22]. Many existing simulators are either too complex, costly, or limited in their ability to simulate realistic precipitation characteristics [23]. Although existing rainfall simulators have significantly contributed to erosion research, they often fall short in accurately replicating the intensity, spatial uniformity, and kinetic energy of natural rainfall events, particularly under varying pressures. This gap reduces the comparability and applicability of research findings. This study addresses these gaps by developing a cost-effective, versatile, and reproducible rainfall simulator specifically optimized for soil erosion studies. Specifically, this study advances previous simulator designs, e.g., [24], by incorporating adjustable rainfall intensity, improved spatial uniformity, and enhanced control over drop-size distribution. Several key challenges arise in designing and implementing an effective rainfall simulator:

-

Achieving precise control over rainfall parameters—ensuring that rainfall intensity and drop-size distribution highly mimic natural precipitation.

-

Ensuring adaptability across different environments—designing a system that functions effectively in both laboratory and field conditions while maintaining consistent experimental outputs.

-

Balancing complexity and affordability—creating a technically sophisticated system that remains accessible for broader research applications without excessive costs.

Rainfall simulators are broadly categorized into field-based simulators [24,25,26,27,28,29] and laboratory-based simulators [30,31,32,33]. Based on their precipitation generation mechanisms, these simulators further divide into dripping simulators, where raindrops form through gravitational freefall from capillaries [34,35,36,37,38], spraying simulators, where raindrops form under higher water pressure [24,39], and hybrid systems, which combine both processes [40,41,42,43].

Field-based rainfall simulators are influenced by environmental factors such as micromorphology, wind, temperature, and the simulator’s structural constraints (e.g., design dimensions, plot size, and water availability) [44,45]. These factors can hinder the reproducibility of identical experiments of natural rainfall because it is not possible to achieve the real size of the drops with natural terminal speed. However, field-based simulators allow for the study of undisturbed soil samples, producing results that are more representative of natural conditions. In contrast, laboratory-based rainfall simulators provide full control over experimental variables (e.g., temperature, humidity, and wind), enabling highly precise studies of specific parameters [45,46]. As these simulators are stationary, their design accommodates increased structural complexity and larger test plots. Their primary advantage lies in their ability to ensure repeatability under standardized conditions. However, applying laboratory-generated results to real-world environments remains a limitation.

Among rainfall simulators, spraying-type simulators are the most commonly used due to their superior efficiency and capacity for producing rainfall with adjustable intensity and drop size [47]. The selection of a rainfall simulation method depends on the required performance criteria and research objectives. Given the absence of standardized designs, researchers frequently modify or develop custom-built rainfall simulators tailored to their specific studies [15,48]. The construction and operational characteristics of rainfall simulators should be carefully defined, considering factors such as structural simplicity, mobility, fabrication and maintenance costs, water consumption, and precipitation parameters (e.g., intensity, drop size, and kinetic energy). For field-based simulators, additional criteria such as transportability, assembly time, adaptability to different terrain slopes, and usability across various climatic conditions must also be considered [24,49,50,51].

Accurate simulation of rainfall events plays a crucial role in understanding precipitation–soil interactions, which is fundamental for designing sustainable land management strategies [52]. The development of such a simulator not only advances scientific understanding but also holds practical significance by directly informing land management policies and erosion control strategies. Given the increasing threat of soil erosion due to climate change and intensified land use, the development of reliable and cost-effective experimental tools is of utmost importance. This research not only advances fundamental hydrological and geomorphological studies but also provides practical insights for policy-makers and engineers working on soil conservation and watershed management.

Despite significant progress in rainfall simulator technology, achieving high-fidelity replications of natural rainfall characteristics remains a challenge. Rainfall simulators must effectively reproduce rainfall intensity, drop-size distribution, kinetic energy, and spatial uniformity, as these factors are crucial for accurately modeling soil erosion processes [53]. Previous studies, such as [54,55], have highlighted the importance of raindrop characteristics in erosion modeling, demonstrating that variations in drop size, velocity, and impact angle directly influence soil detachment and sediment transport. However, existing rainfall simulators often fail to accurately replicate natural rainfall conditions, particularly under varying hydraulic pressures and wind influences. The ability to control and adjust rainfall intensity, kinetic energy, and drop-size distribution is essential for ensuring realistic soil erosion simulations. Given these gaps in current methodologies, there is a need for a more advanced rainfall simulator that allows for precise control over hydrodynamic parameters while maintaining cost-effectiveness and operational reliability.

This study aims to develop, construct, and calibrate a spraying-type rainfall simulator capable of producing controlled precipitation events for soil erosion research. To achieve these objectives, the present study developed a custom rainfall simulator with precise control over key parameters such as intensity, drop size, and energy. The system was calibrated through standardized and widely accepted measurement techniques, including the flour method for drop-size distribution and pluviometric methods to assess rainfall intensity and spatial uniformity, ensuring high reproducibility and experimental reliability. The simulator’s design ensures high accuracy in rainfall intensity and drop-size distribution, making it suitable for both laboratory and field applications. The generated datasets will contribute to the advancement of predictive erosion models and inform the development of more effective soil conservation strategies, particularly in regions prone to land degradation.

2. Materials and Methods

To meet the objectives of this study and ensure experimental reliability, the development of the rainfall simulator was structured into three sequential phases: design, calibration, and evaluation. The design phase established the technical and functional criteria necessary to simulate rainfall characteristics relevant to soil erosion processes. The calibration phase involved adjusting key operational parameters, such as nozzle type, water pressure, and spatial configuration, to generate controlled, repeatable rainfall under controlled conditions. Finally, the evaluation phase assessed the extent to which the constructed simulator fulfilled the predefined design and performance criteria, with particular attention to rainfall intensity, drop-size distribution, kinetic energy, spatial and temporal uniformity, and overall usability. The overall methodological framework is summarized in Figure 1, which outlines the planning, construction, calibration, and evaluation phases of the simulator development process. These three methodological components are presented in detail in the following subsections.

2.1. Rainfall Simulator Design Criteria

To study the erosive effects of rainfall on soil, a spraying rainfall simulator was designed and calibrated. This study was conducted at a conceptual laboratory scale, without strict geometric scaling of natural slopes or catchments. The setup was specifically designed to ensure precise control over rainfall parameters, such as intensity, drop size, and kinetic energy, under standardized and repeatable conditions. Although the rainfall characteristics were selected to replicate natural precipitation, the spatial configuration of the experimental plots was optimized for controlled analysis rather than field-scale extrapolation.

The rainfall simulator design criteria were formulated explicitly to fulfill the research objectives to accurately simulate rainfall characteristics critical for studying soil erosion. The design was based on fundamental principles of rainfall simulator construction and operation, as established through an extensive review of the scientific and professional literature on simulator designs and performance, studies on rainfall simulator construction and calibration, and research that utilized soil research simulators [11,56,57,58,59]. Additionally, it drew upon scientific work by [24,35,36,60]. The established design criteria were as follows:

-

General criteria (overall design and functionality):

• The rainfall application area must fully cover or exceed the soil plot area to ensure uniform exposure;
• Portability is not required for the intended purpose;
• The rainfall simulator must be usable in both laboratory and field conditions;
• The structure must comply with all applicable operational safety standards;
• The system should allow easy operation, fast calibration, and reliable repeatability of rainfall simulations;
• Maintenance tools and technical support must be readily available and accessible;
• The construction should be mechanically simple, with minimal components, built from durable and affordable materials to ensure longevity and low maintenance needs;
• A supply of clean water and a stable power source must be ensured at all times;
• The working zone must offer enough space for two operators to carry out calibration and handling without obstruction.

-

Specific criteria (technical and performance requirements):

• Simulated rainfall should replicate natural precipitation in terms of intensity, duration, drop size, kinetic energy, and momentum;
• Rainfall uniformity must be achieved in both spatial and temporal distributions across the plot;
• The reservoir must have sufficient capacity for a complete trial or allow continuous refilling during operation;
• The system must enable control of key rainfall parameters via adjustable pressure, nozzle type, and drop height;
• The simulator must include wind protection (e.g., barriers or shields) to prevent the disturbance of the water spray;
• The hydraulic system must be safeguarded against clogging by requiring the use of filtered or clean water.

A stable electric power supply is required to support the operation of pumps and any integrated electronic components. Criteria such as simplicity, durability, and ease of maintenance are essential to ensure reliable long-term use, reduce operational downtime, and facilitate widespread adoption in various research settings. While portability was not a priority in this study, this criterion could constrain field application versatility. Future adaptations could consider more portable designs to broaden applicability.

Additionally, specific criteria for rainfall simulator designs are defined based on the particular requirements of the study, including rainfall factors and soil plot design characteristics. The specified criteria for rainfall factors ensure that the simulated rainfall closely resembles natural rainfall showers observed in Serbia and other climatically similar regions [61,62,63,64]. Rainfall shower simulations are selected due to their greater erosive potential compared to low-intensity rainfall [65,66]. The criteria include the following:

-

Additional specific criteria:

• Rainfall duration ranging from 5 to 30 min;
• Rainfall intensity between 0.5 and 6.0 mm·min⁻¹;
• Drop diameters from 0.5 to 2.5 mm;
• Significant variation in rainfall kinetic energy and momentum;
• Normal distribution of the simulated rainfall factor data.

Soil plot design characteristics mainly relate to a total area of approximately 1 m² (0.9999 m²) for all three plots combined. When placed adjacent to each other, including the edges between them, the covered area increases to approximately 1.2 m² (1.2423 m²), which should be the minimum simulator wetting area. The wetted area of at least 1.2 m² was chosen to comfortably exceed the total plot area (approx. 1.0 m²), ensuring uniform rainfall distribution across plot boundaries, thus avoiding edge effects documented in similar erosion studies.

2.2. Calibration Procedures

The purpose of the calibration was to ensure that the rainfall simulator accurately replicates key rainfall characteristics necessary for soil erosion studies. The two-phase calibration process (Figure 2) determined rainfall intensity, drop size, and spatial uniformity under controlled conditions. Additionally, drop falling velocity, kinetic energy, and impact momentum were derived to assess the physical properties of the simulated rainfall, ensuring compatibility with natural rainfall erosive forces.

The first calibration phase aimed to select optimal nozzle configurations by evaluating rainfall intensity, drop size, and spatial uniformity at a 0° soil plot slope. For the first calibration phase, nozzles were selected based on established criteria for simulator design, specific requirements of soil erosion research, and detailed manufacturer specifications. Key selection parameters included compatibility with moderate operating pressures (1.0–2.0 bar), an adjustable radius of throw, spray angle control, mechanical reliability, and cost-efficiency. The VAN, HE-VAN, and PRO series nozzles were chosen because they offered a practical balance between hydraulic performance and experimental usability. This selection was further validated through preliminary calibration trials and supported by findings from previous scientific studies [24,44], which confirmed that these nozzle types produced raindrops of suitable sizes and kinetic energies for simulating erosive rainfall. Additionally, the drops exhibited a predominantly vertical impact angle, indicating realistic drop behavior under controlled laboratory conditions.

The second calibration phase aimed to validate the selected nozzle configurations at a 15° soil plot slope to ensure accuracy and repeatability under varied experimental conditions. Based on the results from the first phase, specific nozzle types were tested under the same pressure conditions of 1.0, 1.5, and 2.0 bar. Nozzle selection criteria included achieving maximal variation in rainfall intensity and drop diameter while minimizing the number of nozzle sets required, thereby optimizing experimental practicality and efficiency. In the second phase, only rainfall intensity and its uniformity were calibrated, while drop-size values from the first calibration phase were reused to calculate kinetic energy and momentum. Calibration trials were repeated three times, with the mean value adopted for final analysis.

Rainfall intensity and its spatial uniformity were calibrated using the pluviometric method [67], while drop size and its spatial distribution were assessed using the flour method [3,24,68,69]. These methods, widely used in recent rainfall simulator studies [24,69], have demonstrated high reliability for determining raindrop-size distributions. The pluviometric method was employed to evaluate the spatial distribution and uniformity of the rainfall simulator, ensuring that the simulated rainfall closely replicates natural precipitation patterns. The pluviometric method was chosen due to its simplicity, reliability, and accuracy in measuring rainfall spatial uniformity, making it ideal for controlled rainfall experiments. A grid of 90 graduated pluviometers was strategically placed beneath the simulator to measure rainfall intensity and uniformity (Figure 3a). Rainfall intensity was measured over a standardized duration of 10 min and repeated three times per configuration to ensure statistical reliability. The volume of water in each container was measured, recorded, and converted into rainfall intensity, while the Christiansen uniformity coefficient (CUC) was applied to quantitatively evaluate rainfall distribution uniformity, with values greater than 80% indicating acceptable uniformity for reliable erosion experiments. To further ensure accuracy, the water level in the supply tank was measured before and after each trial, allowing for the precise monitoring of water consumption. This comprehensive calibration approach enabled a high-fidelity assessment of rainfall distribution, ensuring that the simulator could accurately replicate rainfall intensities and spatial uniformity for experimental applications.

The flour method is a widely used impact-based technique for measuring raindrop-size distribution (DSD) and uniformity under both natural and simulated rainfall conditions. The flour pellet method was selected due to its practicality, low cost, and proven reliability in precisely measuring raindrop sizes, as validated by previous studies [68,69]. This method involves collecting raindrops in a shallow tray filled with dry flour, where each drop forms an aggregate upon impact. To ensure accurate measurement, the exposure duration typically ranges from 2 to 3 s, allowing sufficient aggregates to form while minimizing overlapping droplets. For the purpose of calibrating raindrop size and spatial distribution, nine ceramic dishes (200 mm in diameter) were evenly placed at the bottom of three soil plots and filled with wheat flour (type 400). A polystyrene plate (1200 × 1000 × 30 mm) was positioned above the dishes, ensuring a uniform flour layer of 20 mm thickness. During rainfall simulation, the protective Styrofoam board was briefly removed to expose the flour to rainfall before being replaced. The collected flour aggregates were then oven-dried at 105 °C for 24 h to solidify their structure. This temperature was selected to ensure complete moisture removal without inducing thermal degradation or collapse of pellet integrity. To minimize breakage during sieving, the aggregates were fully dried and handled gently, and all tests were conducted under stable indoor humidity conditions to prevent premature swelling or disintegration of flour particles. Once dried, the aggregates were sieved through a graded mesh set (3.00, 2.00, 1.40, 1.25, 1.00, 0.71, and 0.50 mm) to classify them by size. Equation (1) from Asseline and Valentin [70] was applied to determine the equivalence between drop size (D_d) and flour pellet size (D_f):

$${\mathrm{D}}_{\mathrm{d}}=0.985·{\mathrm{D}}_{\mathrm{f}}^{1.02}$$

(1)

where D_d is the drop diameter in mm and D_f is the flour ball diameter in mm. This method is favored for its simplicity, cost-effectiveness, and reliability in rainfall simulation experiments, providing an effective means of analyzing raindrop size and distribution (Figure 3b).

Additionally, a dedicated aperture system was installed to facilitate the assessment of the temporal uniformity of rainfall intensity. Rather than incorporating these measurements into the primary calibration phase, the assessment was purposefully scheduled to be conducted immediately before each soil simulation experiment on plots with a 15° slope. This decision was made to better account for real-time fluctuations in water pressure, pump performance, and ambient environmental conditions, which can influence short-term consistency in rainfall delivery. By verifying temporal uniformity just prior to each trial, this approach ensures that the rainfall intensity remains stable and within acceptable thresholds at the moment of experimentation, thereby increasing the reliability and reproducibility of the simulation results.

The calibration of temporal uniformity for simulated rainfall intensity was conducted using a custom frame with three identical nylon troughs. These troughs collected water from the simulated rainfall and directed it through openings at their ends into plastic containers. The frame was positioned on the edges of the plots to ensure proper alignment. Rainfall was collected from the nylon troughs over a 5 min period, with measurements taken at 1 min intervals. During the calibration, an acceptable deviation among measurements is generally considered to be within ±10% of the mean rainfall intensity. According to the Christiansen uniformity coefficient (CU) standard, a uniformity coefficient above 80% is typically deemed acceptable for erosion and hydrological analyses [69,71,72,73,74], which corresponds to a temporal intensity variation below 10%. This threshold ensures that the simulated rainfall remains consistent over time, accurately replicating natural precipitation patterns while minimizing experimental errors. Maintaining deviations within this range accounts for minor fluctuations in water pressure, nozzle performance, and environmental influences, preventing significant inconsistencies in soil erosion and hydrological studies. If deviations in temporal intensity values exceeded 10%, the simulator was adjusted, and the calibration check was repeated (Figure 3c,d).

The calibration of the rainfall simulator in terms of simulated drop fall velocity was determined for d_m50 using the numerical model of Van Boxel [75], with the adopted mean drop fall heights of 600 mm and 470 mm, as determined by soil research criteria, and assuming no initial fall velocity. Drop velocity was estimated using the Van Boxel [75] model, which accounts for gravitational acceleration and air resistance. Although the Van Boxel [75] model assumes no initial velocity, it is acknowledged that spray nozzles may impart a minor initial downward velocity to raindrops. However, this effect is generally considered negligible at typical fall heights used in laboratory simulations, as supported by prior validation studies, e.g., [69,76]. This model was selected because it has been widely validated in previous rainfall simulation studies and provides a realistic approximation of raindrop terminal velocities. Based on the previously measured d_m50, i.e., its drop mass, and the calculated values of fall velocity, the kinetic energy and impact momentum of the drops were calculated using Equations (2) and (3) used previously by Wischmeier and Smith [77], and later by Hudson [78], Morgan [79], and Meshesha et al. [76].

$$\mathrm{K}\mathrm{E}={\displaystyle \frac{1}{2}}·\mathrm{m}·{\mathrm{v}}^2$$

(2)

Here, KE is the kinetic energy of the drop just before impact (J), m is the mass of the drop (kg), and v is the falling velocity of the drop just before impact (m·s⁻¹).

$$\mathrm{M}=\mathrm{m}·\mathrm{v}$$

(3)

Here, M is the momentum of the drop at the moment of impact (N·s), and m is the mass of the drop (kg).

The uniformity of the simulated rainfall factors on the studied surface is expressed by the Christiansen uniformity coefficient (CU) [80] (Equation (4)). The closer the value of the uniformity coefficient CU is to 100%, the better the uniformity of the simulated rainfall [11,12,24].

$$\mathrm{C}\mathrm{U}=1-{\displaystyle \frac{\sum _{\mathrm{t}=1}^{\mathrm{n}}·\left|\begin{array}{c}{\mathrm{R}}_1-{\mathrm{M}}_{\mathrm{X}}\\ \mathrm{M}\mathrm{x}\end{array}\right|}{\mathrm{n}·\mathrm{M}\mathrm{x}}}$$

(4)

Here, CU is the Christiansen uniformity coefficient (%), R1 is the amount of water in each pluviometric container (ml), MX is the mean amount of water in all pluviometric containers (ml), and n is the total number of pluviometric containers (/).

While the calibration process ensured high spatial uniformity and controlled drop-size distribution, minor deviations in kinetic energy due to nozzle spray variation and ambient airflow could introduce slight inconsistencies.

2.3. Criteria Evaluation Method

Evaluation of design-related criteria was based on direct observation during construction, assembly, and trial operation. This included assessing the system’s mechanical simplicity, ease of handling by two operators, structural stability under operational pressure, and the availability and functionality of control components. Additional attention was given to compatibility with clean water and power supply infrastructure, as well as to the ease of maintenance procedures, such as nozzle replacement and hydraulic line leaks. Evaluations of performance-related criteria were based on the systematic use of established measurement procedures during controlled simulations. Quantitative parameters such as rainfall intensity, drop-size distribution, spatial and temporal uniformity, and energy-related characteristics were assessed using the described methods. Each parameter was evaluated against the defined acceptance conditions set forth in the simulator’s design. The evaluation was structured to determine not only whether the simulator produced rainfall characteristics within the expected ranges, but also whether it did so with sufficient consistency, stability, and operational ease to support experimental soil erosion research under laboratory conditions.

3. Results

3.1. Design and Assembly

The rainfall simulator developed for this research was a modified version of the simulator described by Živanović et al. [24]. The modifications aimed to enhance the simulator’s accuracy, reproducibility, and operational efficiency for soil erosion research. It was designed and constructed in accordance with established criteria and comprised the following components:

-

Structural support;

-

Water tank;

-

Water-moving mechanism;

-

Mechanism of water flow regulation, simulator operation, and sprayers.

The structural support was designed for simplicity, durability, and ease of maintenance, utilizing a minimal number of high-quality yet cost-effective components. The frame was constructed using interlocking wooden planks reinforced with steel plates and screws, ensuring mechanical stability under prolonged use. The structural frame measured 1900 × 1900 × 1900 mm (width, length, and height), dimensions chosen to accommodate standardized soil plots while ensuring optimal nozzle coverage. It was designed to be anchored to a wall with the ability to adjust the height of the sprayers on its backside, allowing proper placement of the sprayer, unhindered simulator operation, calibration, and test execution (Figure 4a,b). The structural support was not portable but could be relatively easily mounted on most walls or structures and used in both laboratory and field conditions. The corners of the support featured sprayer holders in the form of plastic clamps (Figure 4c). Steel hooks at the corners held a steel cable that supported a draft shield made of a nylon cover with rivets (Figure 4d). To minimize wind interference and ensure uniform rainfall distribution, three sides of the simulator were enclosed with a nylon barrier, leaving the fourth side with the possibility to open for equipment access (Figure 4a). Additionally, an optional nylon cover was placed over the top and secured with weighted edges, further reducing the impact of airflow variations on raindrop trajectories. This design ensures that external environmental factors do not compromise calibration accuracy (Figure 4b).

The water supply system consisted of a plastic barrel with a total capacity of 200 L, ensuring sufficient water availability for extended simulation trials. The tank was designed to minimize water contamination risks, featuring sealed openings to prevent debris entry. The capacity was chosen based on the expected water consumption per trial, ensuring continuous operation without requiring frequent refills, thereby improving experimental efficiency. The tank was positioned on the ground surface near the simulator. It was required to remain clean and was filled with potable water from a nearby tap connected to the water supply network. The use of clean water and relatively small tank openings minimized the risk of contamination by impurities, which could have otherwise clogged the sprayer filter (Figure 4e).

Water flow was regulated using a Pedrollo PKm 70 electric water pump (San Bonifacio, Verona, Italy) that was selected for its high efficiency and ability to maintain a stable water pressure across varying flow rates. The pump was powered through a standard grid connection, ensuring consistent operation, which was powered by electricity from a nearby power grid connection (Figure 4f). Water flow regulation and simulator operation were manual, controlled through a T-junction with an interconnected system of rubber-reinforced hoses (25.4 mm and 12.7 mm in diameter), valves, couplings, barometers, and sprayers. Valve V1 was used after every simulation to clean the pump before starting a new simulation. Valve V2 primarily regulated pressure, thereby controlling water flow within the hydraulic system, while valve V3 opened and closed the water supply to the sprayers (Figure 4f). A pressure gauge provided feedback on system pressure near the sprayers, allowing for pressure adjustments via valve V2 (Figure 4g).

It should be noted that the nozzle designations have been shortened for easier writing and reference. Thus, the Rain Bird 4 Series VAN nozzle is abbreviated as V4, the 6 Series VAN as V6, the 8 Series HE-VAN as HV8, the 10 Series HE-VAN as HV10, and the HUNTER-6A-PRO ADJUSTABLE NOZZLE as PRO 6A.

The sprayers used in the study were Rain Bird pop-up US400 sprayers with a height of 100 mm. Four sprayers were used, positioned in the corners of the structural support inside plastic holders, ensuring that all sprayers remained at the same height and position, 1550 mm apart, covering a square area of approximately 2.4 m² (2.4025 m²). The wetted area covered by the sprayers (2.4 m²) exceeded the size of the soil plots (1.2 m²) to prevent the formation of dry spots on the plots (Figure 4c). The sprayers were designed to allow for the installation and exchange of nozzle sets.

Five nozzle types were selected based on their ability to generate rainfall intensities and drop sizes representative of natural precipitation, including Rain Bird 4 Series VAN (yellow), Rain Bird 6 Series VAN (orange), Rain Bird 8 Series HE-VAN (dark green), Rain Bird 10 Series HE-VAN (dark blue), and HUNTER-6A-PRO ADJUSTABLE NOZZLE (light blue) [80,81] (Figure 4h). The nozzles featured adjustable horizontal spraying angles ranging from 0° to 360°, allowing flexibility in rainfall distribution. For calibration, the nozzles were set at a 90° angle to achieve optimal spatial coverage and prevent the formation of dry zones. This configuration ensured that rainfall was evenly distributed across the experimental plots, enhancing simulation accuracy (Figure 5). At a pressure of 1.5 bar, the nozzles started spraying at different vertical angles (0° for V4, V6, and PRO 6A to 24–27° for HV8 and HV10), after which the drops of simulated rainfall fell downward under the influence of gravity. Although the nozzles began spraying at 1.5 bar, once spraying was established, the water pressure could be reduced to 1.0 bar without disrupting their operation. After the first calibration phase, three nozzle sets were selected for the second calibration phase, specifically the Rain Bird 4 Series VAN, 6 Series VAN, and 8 Series HE-VAN.

3.2. Calibration and Performance

3.2.1. First Phase of Calibration

The first phase of calibration aimed to evaluate the performance of different nozzle configurations under controlled conditions at a 0° plot slope. The calibration process assessed key rainfall parameters, including intensity, drop size, and spatial uniformity, to determine the optimal nozzle setup for subsequent soil erosion experiments.

Table 1. Water consumption, absolute water losses, and relative water losses for 30 min of simulated rainfall during the first phase of calibration.

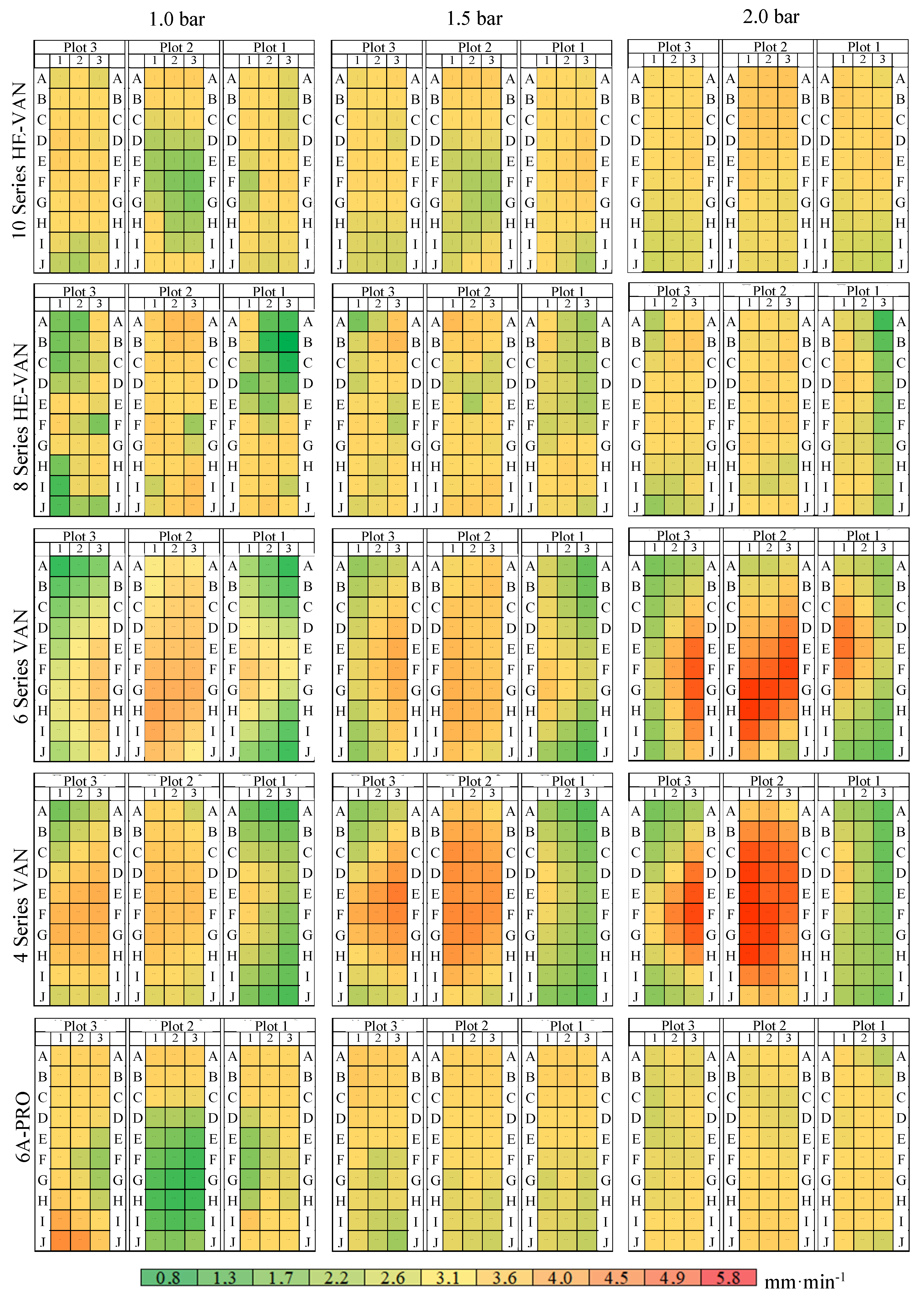
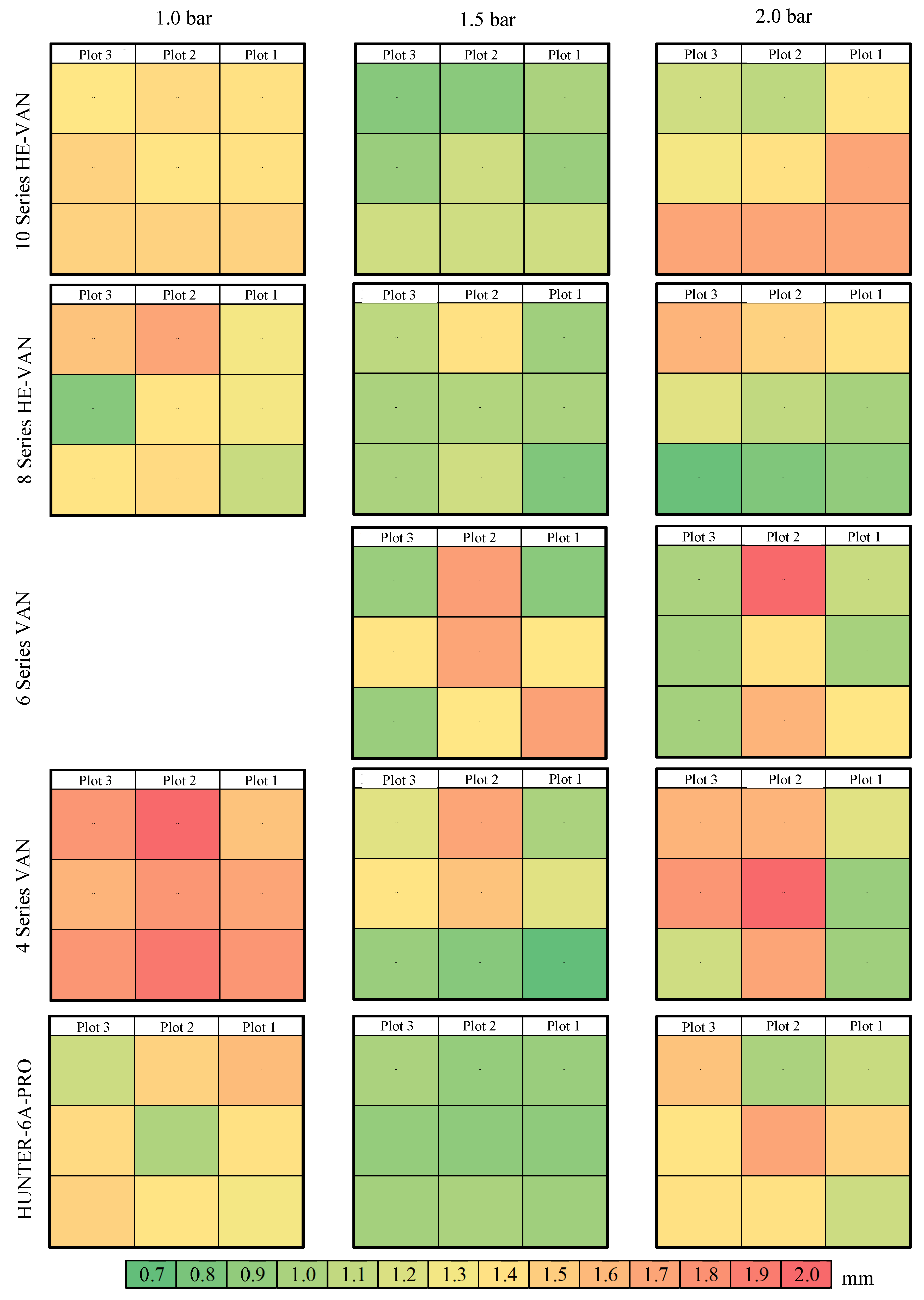
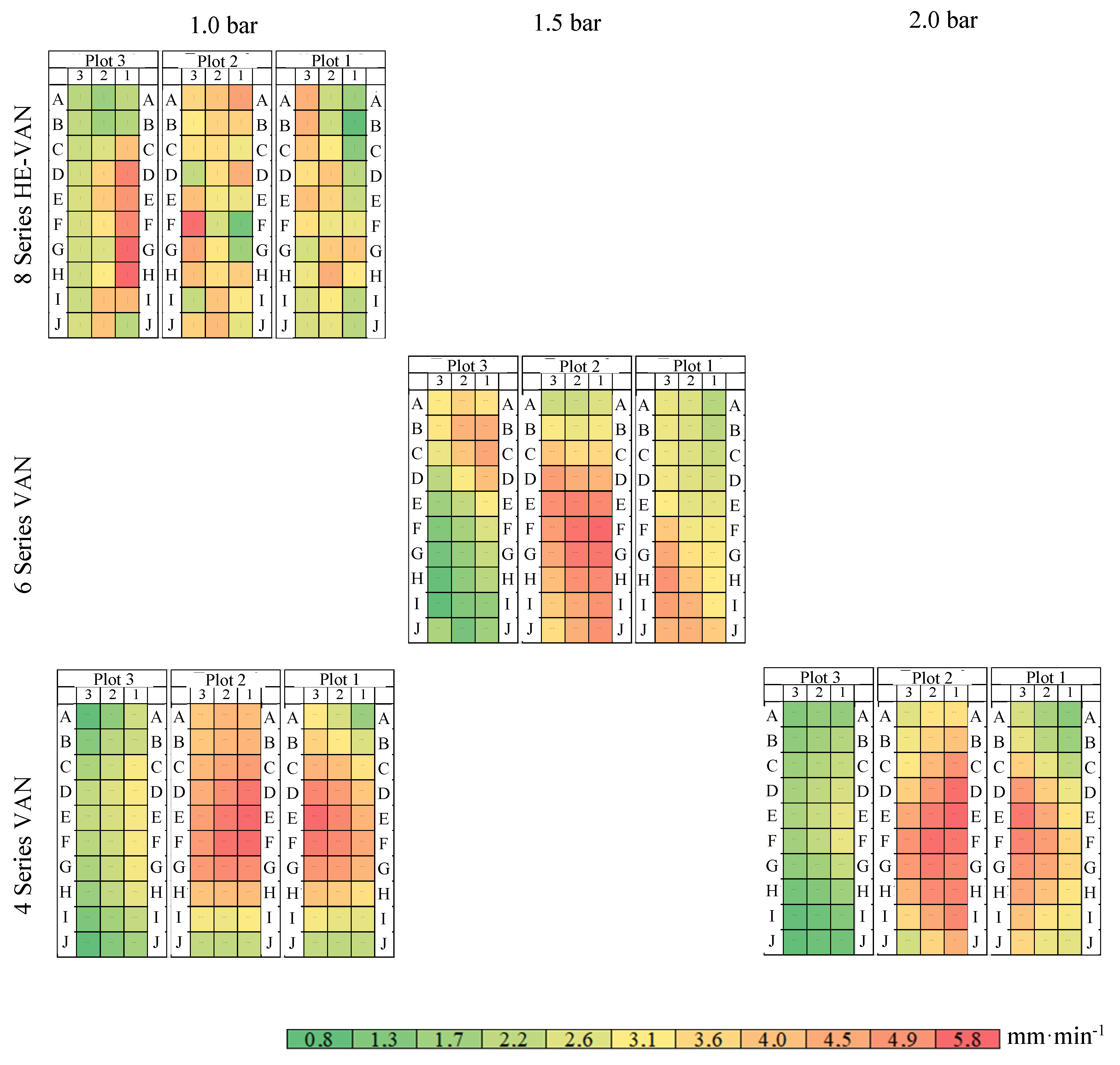
Category			Water Consumption									Absolute Water Losses									Relative Water Losses
Designation			V30min									ΔVLA									ΔVLR
Unit			L									L									%
Pressure	P	bar	1.0			1.5			2.0			1.0			1.5			2.0			1.0			1.5			2.0
Plot Number	PN	/	3	2	1	3	2	1	3	2	1	3	2	1	3	2	1	3	2	1	3	2	1	3	2	1	3	2	1
Nozzle Type	HV10		168			213			264			121			162			198			72			76			75
	HV8		102			138			162			63			88			107			62			64			66
	V6		243			306			372			168			223			272			69			73			73
	V4		234			300			357			164			210			250			70			70			70
	PRO 6A		222			264			321			184			230			276			83			87			86

Note: The fields were color-coded red for the highest values to green for the lowest values, for better visualization of the data. The nozzle designations have been shortened for easier writing and reference. Thus, the Rain Bird 4 Series VAN nozzle is abbreviated as V4, the 6 Series VAN as V6, the 8 Series HE-VAN as HV8, the 10 Series HE-VAN as HV10, and the HUNTER-6A-PRO ADJUSTABLE NOZZLE as PRO 6A.

,

Table 2. Mean intensity and drop diameter of simulated rainfall during the first phase of calibration.

Category			Rainfall Intensity									Drop Diameter
Designation			I									dm50
Unit			mm·min−1									mm
Pressure	P	bar	1.0			1.5			2.0			1.0			1.5			2.0
Plot Number	PN	/	3	2	1	3	2	1	3	2	1	3	2	1	3	2	1	3	2	1
Nozzle Type	HV10		1.6	1.5	1.7	1.9	1.7	1.8	2.3	2.5	2.3	1.2	1.2	1.3	0.9	0.9	0.9	1.5	1.5	1.2
	HV8		1.3	1.6	1.2	1.6	1.8	1.7	2.2	2.0	1.9	1.1	1.3	1.1	0.9	1.0	0.9	1.0	1.0	1.1
	V6		2.2	3.3	2.4	2.5	3.4	2.9	3.0	4.2	3.3				1.2	1.5	1.0	1.0	1.6	0.9
	V4		2.0	2.8	2.8	2.3	3.9	3.3	2.7	4.9	3.6	1.6	1.9	1.6	0.9	1.3	1.0	0.9	1.7	1.4
	PRO 6A		1.3	1.2	1.5	1.2	1.2	1.2	0.8	0.8	0.8	1.3	1.1	1.2	0.8	0.9	0.9	1.1	1.2	1.3

Note: The fields were color-coded red for the highest values to green for the lowest values, for better visualization of the data. The nozzle designations have been shortened for easier writing and reference. Thus, the Rain Bird 4 Series VAN nozzle is abbreviated as V4, the 6 Series VAN as V6, the 8 Series HE-VAN as HV8, the 10 Series HE-VAN as HV10, and the HUNTER-6A-PRO ADJUSTABLE NOZZLE as PRO 6A.

,

Table 3. Coefficient of spatial uniformity of intensity and drop diameter of simulated rainfall during the first phase of calibration.

Category			Coefficient of Spatial Uniformity of Rainfall Intensity									Coefficient of Spatial Uniformity of Drop Diameter
Designation			CU I									CU dm50
Unit			%									%
Pressure	P	bar	1.0			1.5			2.0			1.0			1.5			2.0
Plot Number	PN	/	3	2	1	3	2	1	3	2	1	3	2	1	3	2	1	3	2	1
Nozzle Type	HV10		95	88	93	93	90	95	88	90	90	95	97	96	91	91	94	80	81	87
	HV8		84	84	90	92	90	91	91	94	90	81	87	95	98	90	95	75	81	84
	V6		80	91	82	83	91	85	79	80	75				85	86	76	99	82	90
	V4		84	92	84	86	89	82	86	88	77	95	94	93	89	75	86	81	88	91
	PRO 6A		92	85	76	91	93	88	96	94	97	89	87	89	97	96	98	93	80	87

Note: The fields were color-coded red for the highest values to green for the lowest values, for better visualization of the data. The nozzle designations have been shortened for easier writing and reference. Thus, the Rain Bird 4 Series VAN nozzle is abbreviated as V4, the 6 Series VAN as V6, the 8 Series HE-VAN as HV8, the 10 Series HE-VAN as HV10, and the HUNTER-6A-PRO ADJUSTABLE NOZZLE as PRO 6A.

,

Table 4. The absolute and relative maximum fall velocity of drops during the first phase of calibration.

Category			Absolute Maximum Velocity of a Drop at a Mean Falling Height of 600 mm									Relative Maximum Velocity of a Drop at a Mean Falling Height of 600 mm
Designation			vA									vR
Unit			m·s−1									%
Pressure	P	bar	1.0			1.5			2.0			1.0			1.5			2.0
Plot Number	PN	/	3	2	1	3	2	1	3	2	1	3	2	1	3	2	1	3	2	1
Nozzle Type	HV10		2.9	2.9	2.9	2.7	2.7	2.7	3.0	3.0	2.9	58	62	63	75	73	75	57	57	62
	HV8		2.8	3.0	2.9	2.6	2.8	2.7	2.8	2.8	2.9	68	59	66	77	69	74	72	70	68
	V6					2.9	3.1	2.7	2.8	3.1	2.7				64	58	72	70	54	75
	V4		3.1	3.1	3.1	2.7	2.9	2.8	2.7	3.1	3.0	53	49	53	76	61	68	74	52	58
	PRO 6A		2.9	2.9	3.0	2.6	2.6	2.6	2.8	2.9	2.9	62	66	66	77	77	76	67	62	62

Note: The fields were color-coded red for the highest values to green for the lowest values, for better visualization of the data. The nozzle designations have been shortened for easier writing and reference. Thus, the Rain Bird 4 Series VAN nozzle is abbreviated as V4, the 6 Series VAN as V6, the 8 Series HE-VAN as HV8, the 10 Series HE-VAN as HV10, and the HUNTER-6A-PRO ADJUSTABLE NOZZLE as PRO 6A.

and

Table 5. Kinetic energy and momentum of simulated rainfall during the first phase of calibration.

Category			Kinetic Energy of Rainfall									Rainfall Momentum
Designation			KE									M
Unit			J·min−1·m−2									N·m−2
Pressure	P	bar	1.0			1.5			2.0			1.0			1.5			2.0
Plot Number	PN	/	3	2	1	3	2	1	3	2	1	3	2	1	3	2	1	3	2	1
Nozzle Type	HV10		0.9	0.8	0.9	0.9	0.8	0.8	1.3	1.4	1.2	0.010	0.009	0.010	0.011	0.010	0.010	0.014	0.016	0.014
	HV8		0.6	0.9	0.6	0.7	0.9	0.8	1.0	1.0	1.0	0.007	0.010	0.007	0.009	0.011	0.010	0.013	0.012	0.011
	V6					1.3	2.1	1.4	1.5	2.5	1.5				0.015	0.022	0.017	0.017	0.027	0.018
	V4		1.2	1.7	1.6	1.0	2.1	1.6	1.2	2.9	2.0	0.013	0.018	0.018	0.013	0.024	0.019	0.015	0.032	0.022
	PRO 6A		0.7	0.6	0.9	0.5	0.5	0.5	0.4	0.4	0.4	0.008	0.007	0.010	0.007	0.007	0.007	0.005	0.005	0.005

Note: The fields were color-coded red for the highest values to green for the lowest values, for better visualization of the data. The nozzle designations have been shortened for easier writing and reference. Thus, the Rain Bird 4 Series VAN nozzle is abbreviated as V4, the 6 Series VAN as V6, the 8 Series HE-VAN as HV8, the 10 Series HE-VAN as HV10, and the HUNTER-6A-PRO ADJUSTABLE NOZZLE as PRO 6A.

and Figure 6 and Figure 7 illustrate the results, with color-coded fields highlighting variations in performance across different settings. Five different nozzle sets were used under water pressures of 1.0, 1.5, and 2.0 bar and rainfall at a mean drop height of 600 mm. Simulated rainfall was measured for 10 min, and the water consumption, as well as absolute and relative losses, was extrapolated to represent a 30 min rainfall simulation across three plots (labeled 1, 2, and 3 from right to left). These measurements were conducted to determine the amount of water required for the trials and to assist in the selection of appropriate nozzles. Therefore, the results are presented collectively for all three plots.

The total water consumption averaged 244 L (SD = 79.4 L) and ranged from 102 L for the HV8 nozzle at 1.0 bar to 372 L for the V6 nozzle at 2.0 bar. An increase in pressure from 1.0 to 1.5 bar resulted in a mean water consumption increase of +27% (+50 l; SD = 5.8% or 13.3 l) for all nozzle types. Similarly, increasing the pressure from 1.5 to 2.0 bar increased water consumption by a mean of +21% (+51 l; SD = 2.5% or 16 l) (Table 1). These results highlight the relationship between water pressure and rainfall output, crucial for optimizing nozzle selection.

The absolute water losses averaged 181 L (SD = 65.4 L), ranging from 62 L for the HV8 nozzle at 1.0 bar to 230 L for the PRO 6A nozzle at 1.5 bar. As pressure increased, water losses generally rose, indicating that higher pressures led to greater runoff inefficiencies. While the ratio of losses to water consumption showed minimal variation between 1.0 and 1.5 bar, a significant increase was observed when the pressure was raised from 1.5 to 2.0 bar. These findings underscore the need for optimizing pressure settings to balance water efficiency with rainfall intensity requirements (Table 1).

The relative water losses averaged 73% (SD = 7.4%) and ranged from 62% (62 L) for the HV8 nozzle at 1.0 bar to 87% (276 L) for the PRO 6A nozzle at 2.0 bar (Table 1). An increase in pressure from 1.0 to 1.5 bar resulted in a mean change in relative water losses of +4% (+3 L; SD = 2.4% or 1.8 L). However, with a pressure increase from 1.5 to 2.0 bar, there was no significant change in relative water losses, though slight variations were observed (SD = 1.8% or 1.2 L) (Table 1).

The mean intensity of simulated rainfall across the plots was 2.2 mm·min⁻¹ (SD = 0.9 mm·min⁻¹), with values ranging from 0.8 mm·min⁻¹ for the PRO 6A nozzle at a pressure of 2.0 bar across all three plots to 4.9 mm·min⁻¹ for the V4 nozzle at a pressure of 2.0 bar on plot number 2. With an increase in pressure from 1.0 to 1.5 bar, the mean rainfall intensity increased by 13% (+0.3 mm·min⁻¹, SD = 15.5% or 0.3 mm·min⁻¹). Similarly, when the pressure was raised from 1.5 to 2.0 bar, the intensity increased by 11% (+0.3 mm·min⁻¹, SD = 24.7% or 0.4 mm·min⁻¹) (Table 2). These trends indicate that nozzle type and pressure settings significantly influence rainfall intensity, making them critical calibration factors.

The mean drop diameter was 1.2 mm (SD = 0.3 mm), with values ranging from 0.8 mm for the PRO 6A nozzle at a pressure of 1.5 bar on plot number 3 to 1.9 mm for the V4 nozzle at a pressure of 1.0 bar on plot number 2. When the pressure was increased from 1.0 to 1.5 bar, the mean drop diameter decreased by 28% (−0.4 mm, SD = 7.3% or 0.2 mm). With an increase in pressure from 1.5 to 2.0 bar, the mean drop diameter increased by 24% (+0.2 mm, SD = 23.4% or 0.2 mm) (Table 2). These results highlight the inverse relationship between pressure and drop size, a critical factor in determining rainfall kinetic energy and erosion potential.

The spatial distribution of rainfall intensity and drop diameter across all three plots, evaluated for five different nozzle sets at operating pressures of 1.0, 1.5, and 2.0 bar with a plot inclination of 0°, is graphically represented in Figure 6 and Figure 7. In Figure 6, it can be seen that all the simulated areas have received a similar quantity of rainfall, from 0.8 to 3.1 mm/min, except under 2 bars of pressure, where 4 series van and 6 series van have higher intensities if the rain is over 4 mm/min. In Figure 7, the 4 series van shows the maximum size of the d_m50 drop diameter. Corresponding spatial uniformity coefficients are summarized in Table 3.

On average, the spatial uniformity coefficient of rainfall intensity was 88% (SD = 5.4%), ranging from 75% for the V6 nozzle at 2.0 bar on plot 1 to 97% for the PRO 6A nozzle at the same pressure on the same plot. Increasing the pressure from 1.0 to 1.5 bar improved the uniformity coefficient by a mean of 2.5% (SD = 5.0%), while further increasing the pressure to 2.0 bar reduced it by a mean of 2.0% (SD = 5.9%) (Table 3).

Similarly, the spatial uniformity coefficient of drop diameter averaged 89% (SD = 6.6%), varying from 75% for the V4 and HV8 nozzles at 1.5 and 2.0 bar on plots 2 and 3, respectively, to 99% for the PRO 6A nozzle at 2.0 bar on plot 3. Notably, increasing the pressure from 1.0 to 1.5 bar did not significantly affect the mean uniformity of rainfall intensity, although deviations were considerable (SD = 9.5%). However, increasing the pressure from 1.5 to 2.0 bar decreased uniformity by a mean of 4.5%, with even larger deviations observed (SD = 11.0%) (Table 3).

The absolute maximum velocity of a drop falling from a mean height of 600 mm was 2.9 m·s⁻¹ on average (SD = 0.2 m·s⁻¹). The values ranged from 2.6 m·s⁻¹ for the HV8 nozzle at a pressure of 1.5 bar (on plot 3) and for the PRO 6A nozzle at the same pressure (on all three plots) to 3.1 m·s⁻¹ for the V4 nozzle at a pressure of 1.0 bar (on all three plots), at 2.0 bar on plot 2, and for the V6 nozzle at pressures of 1.5 and 2.0 bar (on plot 2). Increasing the pressure from 1.0 to 1.5 bar decreased the mean drop velocity by 9% (−0.3 m·s⁻¹, SD = 2.4% or 0.1 m·s⁻¹). In contrast, increasing the pressure from 1.5 to 2.0 bar increased water consumption by 5% (+0.1 m·s⁻¹, SD = 5.9% or 0.2 m·s⁻¹) (Table 4).

The relative maximum fall velocity from a mean height of 600 mm was 66% of the terminal velocity on average (SD = 8.0%) and ranged from 49% (for dm₅₀ = 1.9 mm) for the V4 nozzle at a pressure of 1.0 bar (on plot 2) to 77% (for dm₅₀ = 0.8 mm) for the PRO 6A nozzle at a pressure of 1.5 bar (on plot 3) (Table 4). When the pressure increased from 1.0 to 1.5 bar, the relative maximum drop velocity increased by a mean of 22% (SD = 8.6%). However, with an increase in pressure from 1.5 to 2.0 bar, the velocity decreased by a mean of 10% (SD = 10.1%) (Table 4).

Based on the values of the intensity, diameter, and drop falling speed of simulated rainfall, the kinetic energy and momentum of the rainfall were calculated. The kinetic energy of simulated rainfall averaged 1.1 J·min⁻¹·m⁻² (SD = 0.6%) and ranged from 0.4 J·min⁻¹·m⁻² (for dm₅₀ = 0.8–0.9 mm) for the PRO 6A nozzle at a pressure of 1.5 bar across all three plots to 2.9 J·min⁻¹·m⁻² (for dm₅₀ = 0.7 mm) for the V4 nozzle at a pressure of 2.0 bar on plot number 2 (Table 5). With an increase in pressure from 1.0 to 1.5 bar, the kinetic energy of rainfall decreased by a mean of 5%, or less than 0.1 J·min⁻¹·m⁻² (SD = 17.8% or 0.2 J·min⁻¹·m⁻²). However, with an increase in pressure from 1.5 to 2.0 bar, the kinetic energy of rainfall increased by 23% or 0.3 J·min⁻¹·m⁻² (SD = 29.6% or 0.3 J·min⁻¹·m⁻²) (Table 5).

The momentum of simulated rainfall averaged 0.013 N·m⁻² (SD = 0.006% N·s) and ranged from 0.005 N·s (for dm₅₀ = 1.1–1.3 mm) for the PRO 6A nozzle at a pressure of 2.0 bar across all three plots to 0.032 N·s (for dm₅₀ = 1.7 mm) for the V4 nozzle at a pressure of 2.0 bar on plot number 2 (Table 5). With an increase in pressure from 1.0 to 1.5 bar, the momentum of rainfall increased by a mean of 4%, or 0.004 N·m⁻² (SD = 17.4% or 0.002 N·s). Similarly, when the pressure increased from 1.5 to 2.0 bar, the momentum of rainfall increased by 17% or 0.003 N·s (SD = 29.6% or 0.3 N·s) (Table 5).

3.2.2. Second Phase of Calibration

The second phase of calibration was conducted at a 15° slope to assess the impact of surface inclination on rainfall intensity, drop-size distribution, and spatial uniformity. This phase aimed to determine how slope variation influences rainfall behavior and to validate the simulator’s performance under inclined conditions, which better represent natural landscapes. Further calibration was conducted for three different nozzle sets (Rain Bird 4 Series VAN, 6 Series VAN, and 8 Series HE-VAN) at pressures of 1.0, 1.5, and 2.0 bar, with a plot slope of 15° and a mean drop height of 470 mm. Additionally, by measuring the simulated rainfall over a 10 min period, the water consumption, absolute losses, and relative water losses for a 30 min simulated rainfall across all three plots were determined. The total water consumption across the three plots ranged from 102 L for the HV8 nozzle at a pressure of 1.0 bar to 354 L for the V4 nozzle at a pressure of 2.0 bar. Absolute losses varied from 64 L for the HV8 nozzle at 1.0 bar to 262 L for the V4 nozzle at 2.0 bar, while relative water losses ranged from 63% for the HV8 nozzle at 1.0 bar to 78% for the V4 nozzle at 1.5 bar (

Table 6. Water consumption and losses of simulated rainfall during second phase of calibration.

Category			Water Consumption									Absolute Water Losses									Relative Water Losses
Designation			V30min									ΔVLA									ΔVLR
Unit			l									l									%
Pressure	P	bar	1.0			1.5			2.0			1.0			1.5			2.0			1.0			1.5			2.0
Plot Number	PN	/	3	2	1	3	2	1	3	2	1	3	2	1	3	2	1	3	2	1	3	2	1	3	2	1	3	2	1
Nozzle Type	HV8		102									64									63
	V6					309									241									78
	V4		231						354			171						262			73						74

Note: The fields were color-coded red for the highest values to green for the lowest values, for better visualization of the data. The nozzle designations have been shortened for easier writing and reference. Thus, the Rain Bird 4 Series VAN nozzle is abbreviated as V4, the 6 Series VAN as V6, and the 8 Series HE-VAN as HV8.

).

The intensity of simulated rainfall over the plots ranges from 1.4 mm·min⁻¹ for the HV8 nozzle at a pressure of 1.0 bar to 4.6 mm·min⁻¹ for the V4 nozzle at a pressure of 2.0 bar on plot number 2. The spatial distribution of the intensity of simulated rainfall over all three plots, for three different sets of nozzles, at pressures of 1.0, 1.5, and 2.0 bar, and a plot slope of 15°, is presented graphically in Figure 8. The spatial uniformity coefficient is provided in

Table 7. Simulated rainfall intensity and spatial intensity uniformity during second phase of calibration.

Category			Rainfall Intensity									Coefficient of Spatial Uniformity of Rainfall Intensity
Designation			I									CU I
Unit			mm·min−1									%
Pressure	P	bar	1.0			1.5			2.0			1.0			1.5			2.0
Plot Number	PN	/	3	2	1	3	2	1	3	2	1	3	2	1	3	2	1	3	2	1
Nozzle Type	HV8		1.4	1.5	1.5							82	84	79
	V6					2.6	2.9	2.3							91	90	83
	V4		2.5	2.7	1.8				3.7	4.6	2.3	84	88	85				79	83	84

Note: The fields were color-coded red for the highest values to green for the lowest values, for better visualization of the data. The nozzle designations have been shortened for easier writing and reference. Thus, the Rain Bird 4 Series VAN nozzle is abbreviated as V4, the 6 Series VAN as V6, and the 8 Series HE-VAN as HV8.

. The spatial uniformity coefficient of intensity ranges from 79% for the HV8 and V4 nozzles at pressures of 1.0 and 2.0 bar, on plots 1 and 3, to 91% for the V6 nozzle at a pressure of 1.5 bar on plot number 3 (Table 7). The observed reduction in mean intensity suggests that surface inclination influences the distribution and infiltration dynamics of simulated rainfall, which is critical for erosion process modeling.

The mean drop diameter, spatial distribution, and uniformity of diameter distribution were adopted from the calibration results at a slope of 0°, at the corresponding pressures and nozzle types (Table 2 and Table 3 and Figure 7).

The absolute maximum drop falling velocity from a mean height of 470 mm ranges from 2.5 m·s⁻¹ for the V6 and V4 nozzles at pressures of 1.5 and 2.0 bar on plots 1 and 3 to 2.8 m·s⁻¹ for the V4 nozzle at pressures of 1.0 and 2.0 bar on all three plots. The relative maximum drop falling velocity from a mean height of 470 mm ranges from 44% (for d_m50 1.9 mm) for the V4 nozzle at a pressure of 1.0 bar on plot number 2 to 68% (for d_m50 0.9 mm) for the V4 nozzle at a pressure of 2.0 bar on plot number 3 (

Table 8. The absolute and relative maximum fall velocity of drops during the second phase of calibration.

Category			Absolute Maximum Velocity of a Drop at a Mean Falling Height of 470 mm									Relative Maximum Velocity of a Drop at a Mean Falling Height of 470 mm
Designation			vA									vR
Unit			m·s−1									%
Pressure	P	bar	1.0			1.5			2.0			1.0			1.5			2.0
Plot Number	PN	/	3	2	1	3	2	1	3	2	1	3	2	1	3	2	1	3	2	1
Nozzle Type	HV8		2.6	2.7	2.6							62	54	60
	V6					2.6	2.7	2.5							58	51	66
	V4		2.8	2.8	2.8				2.5	2.8	2.7	49	44	48				68	46	52

Note: The drop diameter and spatial distribution of simulated rainfall are adopted from first-phase measurements. The fields were color-coded red for the highest values to green for the lowest values, for better visualization of the data. The nozzle designations have been shortened for easier writing and reference. Thus, the Rain Bird 4 Series VAN nozzle is abbreviated as V4, the 6 Series VAN as V6, and the 8 Series HE-VAN as HV8.

).

Based on the values of intensity, diameter, and drop fall velocity of simulated rainfall, the kinetic energy and momentum of the rainfall were calculated. The kinetic energy of simulated rainfall ranges from 0.6 J·min⁻¹·m⁻² (for d_m50 0.9 mm) for the HV8 nozzle at a pressure of 1.0 bar on plots 3 and 1 to 2.3 J·min⁻¹·m⁻² (for d_m50 1.7 mm) for the V4 nozzle at a pressure of 2.0 bar on plot number 2. The momentum of simulated rainfall ranges from 0.008 N·m⁻² (for d_m50 0.9–1.0 mm) for the HV8 nozzle at a pressure of 1.0 bar on all three plots to 0.027 N·m⁻² (for d_m50 1.7 mm) for the V4 nozzle at a pressure of 2.0 bar on plot number 2 (

Table 9. Kinetic energy and momentum of simulated rainfall during the second phase of calibration.

Category			Kinetic Energy of Rainfall									Rainfall Momentum
Designation			KE									M
Unit			J·min−1·m−2									N·m−2
Pressure	P	bar	1.0			1.5			2.0			1.0			1.5			2.0
Plot Number	PN	/	3	2	1	3	2	1	3	2	1	3	2	1	3	2	1	3	2	1
Nozzle Type	HV8		0.6	0.7	0.6							0.008	0.008	0.008
	V6					1.1	1.3	0.9							0.014	0.016	0.012
	V4		1.2	1.3	0.9				1.4	2.3	1.0	0.015	0.016	0.011				0.019	0.027	0.013

Note: The fields were color-coded red for the highest values to green for the lowest values, for better visualization of the data. The nozzle designations have been shortened for easier writing and reference. Thus, the Rain Bird 4 Series VAN nozzle is abbreviated as V4, the 6 Series VAN as V6, and the 8 Series HE-VAN as HV8.

).

3.3. Evaluation of Design and Performance Criteria

The constructed rainfall simulator was evaluated against the predefined design and performance criteria described in Section 2.1. The evaluation focused on both structural adequacy and hydraulic functionality, with supporting data presented in Figure 4a–g and Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9. The simulator was conceptually based on the design described by Živanović et al. [24], but it was independently developed and modified to meet specific experimental needs, including reduced wetted area, adjustable drop height, and the use of different nozzle types.

The structural framework (Figure 4a–d) exhibited mechanical stability, ease of assembly, and operational rigidity throughout the trials. The vertical supports, nozzle platforms, and anchoring systems were simple to construct and provided sufficient resistance to external disturbances, including airflow. The frame demonstrated satisfactory rigidity, suggesting its suitability for both laboratory and field applications. The working zone offered adequate space for two operators to perform adjustments and calibration without obstruction, fulfilling ergonomic and operational requirements.

The simulator was designed and assembled using standardized components and basic tools, ensuring easy maintenance and wide applicability without the need for specialized support. Operational safety was also taken into account, as the structure maintained stability under high flow rates and included protective components (e.g., secure tank lids and spray angle containment) to prevent unintended exposure to high-pressure jets or electrical components.

The adjustable drop height and sprayer angle control mechanisms functioned properly; however, when raised above 1.3 m, sprayers occasionally projected beyond the defined wetted area (Figure 4b), especially due to the lateral spray pattern of the nozzles. This lateral dispersion partially limited application precision on compact plots (~1.0 m²), indicating the need for improved spray containment or nozzle shielding.

The simulator’s configuration exceeded the minimum wetted area required to uniformly cover the three adjacent soil plots (~1.2 m² total), thus eliminating edge effects. While portability was not required for this study, the modular design allows for partial disassembly, which may facilitate transport in future applications.

The water tank (Figure 4e) allowed convenient refilling and included a secure lid that prevented contamination of the hydraulic system. However, the volume was insufficient to support 30 min simulations at 1.0, 1.5, and 2.0 bar using V4 and V6 nozzles. The tank was not equipped for automated refill, which would be beneficial for long-duration tests. The water-moving mechanism and flow regulation system (Figure 4f) were found to be reliable, with no observable malfunctions or pressure instability during operation. Still, the manometer (Figure 4g) had a 0–10 bar scale and lacked sufficient resolution in the operational range of 0.5–2.0 bar. A 0–3 bar gauge would be more appropriate for precision control.

Sprayer filters were effective in preventing blockages from impurities, confirming their importance for system maintenance. The simulator relied on a clean water source and stable power supply, which were maintained throughout all trials. Wind shielding with nylon barriers minimized lateral spray deflection and stabilized drop trajectories. It contributed to spatial uniformity and fulfilled design stability criteria. The solution proved effective for controlled laboratory conditions.

Regarding rainfall simulation characteristics, the system achieved target values for all critical factors. Rainfall intensity ranged from 0.60 to 5.80 mm·min⁻¹, and durations up to 30 min were supported by system capacity under specific nozzle-pressure configurations. Drop diameters (dm₅₀) varied between 0.85 and 1.90 mm, remaining within the target range of 0.5–2.5 mm. Kinetic energy and momentum increased with pressure, demonstrating the simulator’s ability to produce rainfall with significant erosive potential. Although the distribution of rainfall factors was not formally tested for normality in this section, simulation results across trials showed consistent spatial and temporal patterns, suggesting uniformity aligned with normal distribution assumptions.

In summary, the structural and hydraulic components fulfilled both general and specific design objectives, including spatial and temporal uniformity, adjustable rainfall parameters, and safety compliance. Nonetheless, improvements such as splash shields, larger tanks, more precise manometers, and potential field-portability enhancements are recommended for future iterations.

4. Discussion

4.1. Discussion of Structural Design Performance

The rainfall simulator’s structural design met key requirements for laboratory-based erosion research, particularly in terms of simplicity, durability, and modularity (Figure 4a–d). The frame demonstrated sufficient rigidity under operational conditions, including airflow disturbances, confirming its suitability for repeated trials. However, the observed lateral overspray at higher drop heights—especially beyond 1.3 m (Figure 4b)—compromised spatial containment, indicating the need for improved nozzle directionality or installation of splash shields. The water tank design (Figure 4e) enabled straightforward refilling and effective contamination prevention via its lid. Still, during trials at 1.0, 1.5, and 2.0 bar using V4 and V6 nozzles, its volume proved insufficient for 30 min simulations, necessitating either shorter trials or continuous refill mechanisms (as evidenced in Table 1). This constraint could be resolved by enlarging the reservoir or implementing an automated water supply system. Flow regulation components (Figure 4f) performed reliably, but the manometer (Figure 4g) lacked adequate resolution in the operational pressure range (0.5–2.0 bar), as its 0–10 bar scale impeded fine control. For future setups, a narrower-range pressure gauge (e.g., 0–3 bar) would improve calibration precision and operational feedback. Despite these drawbacks, the simulator fulfilled its structural objectives. Recommended improvements include increasing tank volume, refining nozzle spray geometry, and integrating pressure instrumentation better suited to low-pressure hydraulic systems. These adaptations would enhance performance consistency, particularly in spatially constrained or high-pressure scenarios.

4.2. Discussion of Simulated Rainfall Performance

The calibration results confirmed that the rainfall simulator achieved the desired control over intensity, drop size, energy, and spatial uniformity across multiple trials and configurations (Table 2, Table 3, Table 4 and Table 5, Table 8 and Table 9; Figure 6 and Figure 7). Intensity values ranged from 0.60 to 5.80 mm·min⁻¹, aligning well with the predefined design interval (Table 2), and drop diameters (dm₅₀) were within the target range of 0.5–2.5 mm (Table 2), ensuring representativeness for erosive rainfall. The simulated rainfall intensities selected in this study corresponded to a realistic range typically observed during moderate-to-high-rainfall storm events. This facilitated a controlled investigation of their effects on sediment detachment and transport. Such repeatable and quantifiable intensity values are advantageous for the mechanistic understanding of erosion dynamics. However, it should be noted that these simulations do not encompass long-term rainfall variability and are not intended for direct extrapolation to field-scale erosion rates. Interestingly, a non-linear trend in drop diameter was observed, with a decrease at 1.5 bar followed by an increase at 2.0 bar (Table 2). This pattern may reflect droplet coalescence effects or hydrodynamic limitations of the nozzles at higher pressures, which have been reported in previous simulation studies. Performance consistency was validated by the repeatability of hydrodynamic parameters under identical configurations (Table 6, Table 7, Table 8 and Table 9). However, slight deviations in drop size and energy were noted at inclined settings, where the mean kinetic energy and momentum declined (Table 6 and Table 7) due to reduced drop height and altered impact dynamics. These findings underscore the importance of slope-specific recalibration in studies involving inclined surfaces. Spatial uniformity was generally high under flat conditions (CUC = 88.3%) but declined to 77.8% at 15° slope (Table 3), demonstrating slope sensitivity typical of simulators without adaptive nozzle controls. The observed reduction in CUC at a 15° slope may result from altered droplet trajectories caused by the inclined plot geometry, where the direction of fall no longer intersects the surface perpendicularly. Additionally, the slope modifies the dispersion pattern of splash droplets, favoring downslope displacement and reducing uniform distribution across the plot. Visual wetting patterns and splash behavior corroborated these results (Figure 7 and Figure 8), reinforcing the need for slope-calibrated nozzle arrangements in complex terrain simulations. Drop velocities exceeded 75% of terminal velocity in multiple trials (Table 4), enhancing the simulator’s ability to replicate erosive force dynamics. Corresponding kinetic energy values reached 2.27 J·m⁻²·min⁻¹ and a momentum of 0.027 N·m⁻² under the highest-pressure configurations (Table 5), confirming that the simulator produced rainfall capable of initiating detachment processes. While KE values derived from the Van Boxel [75] model may be underestimated due to the assumption of zero initial fall velocity, this does not affect the validity of relative comparisons between nozzle configurations, which remain robust for comparative purposes in erosion studies. Absolute and relative water losses (Table 1) showed that while absolute losses rose with pressure, relative losses remained relatively stable, indicating scalable performance, though improved spray containment could reduce wastage. Nozzle selection proved critical: HE-VAN nozzles delivered lower absolute losses but did not consistently improve relative efficiency (Table 1), confirming the need for tailored nozzle use depending on the specific experimental objective. Finally, Figure 7 and Figure 8 illustrate that drop distribution and cumulative rainfall patterns were consistent with realistic storm events, providing visual affirmation of the simulator’s reproducibility. Nonetheless, fine-tuning nozzle configurations and enhancing pressure regulation could further improve spatial homogeneity and control over drop kinetics, especially for advanced erosion modeling.

4.3. Limitations and Future Development

While the simulator performed well overall, certain limitations were identified. While the selected intensities allowed for the precise analysis of sediment response under defined conditions, the simulations do not encompass the full spectrum of natural rainfall variability. As such, the results are not intended for direct extrapolation to long-term or large-scale field scenarios. One methodological constraint of this study is its limited applicability to large-scale natural terrains due to the lack of geometric scaling. While rainfall dynamics were realistically reproduced, the experimental results are not directly transferable to watershed-scale erosion modeling without further scaling validation. However, the simulator itself, owing to its modular design and structural rigidity, is suitable for use in both laboratory and field environments, particularly for plot-scale process studies. Calibration trials were conducted at only two slope angles (0° and 15°), which limited the applicability of the findings to steeper slopes. The simulator exhibited overspray when nozzles were elevated beyond a certain height, leading to potential inaccuracies in spatial rainfall distribution and increased water losses. Temperature and evaporation, which influenced rainfall behavior in natural settings, were not accounted for during simulations, potentially reducing the realism of the results. Absolute and relative water losses increased at higher pressures, affecting the accuracy of the simulations. Conservative assumptions regarding drop fall velocity may have led to an underestimation of kinetic energy and erosive potential, impacting the accuracy of soil erosion modeling.

Although the present study does not directly estimate the R-factor used in empirical models such as USLE, the measured rainfall parameters, intensity, drop size, kinetic energy, and momentum represent key components of rainfall erosivity and may serve as a foundation for future efforts to develop empirical relationships under controlled conditions. However, these data are primarily intended for use in physical modeling and controlled experimental studies, where precise replication of rainfall characteristics is essential for investigating soil erosion processes.

Future development trends toward adjustment and improvement of the simulator largely depend on research requirements. Some directions that could have guided its further improvement and development included extending calibration to cover a wider range of slopes, from shallow to steep, to better mimic real-world conditions and assess the simulator’s performance on varied terrains. Simulating natural environmental factors such as wind, temperature, and evaporation would have enhanced the realism and applicability of the results. Incorporating sensors for the real-time monitoring of rainfall parameters, such as drop velocity, kinetic energy, and momentum, would have improved data accuracy. Evaluating the durability and reliability of the simulator under prolonged use, including its resistance to wear and malfunctions, would have demonstrated its long-term operational effectiveness.

5. Conclusions

This study successfully designed, constructed, and calibrated a spray-type rainfall simulator optimized for soil erosion research. The results highlight the importance of carefully considering design and calibration parameters to achieve reliable simulations for soil erosion research. Addressing key limitations of existing simulators, the developed system provides controlled, repeatable, and customizable rainfall conditions suitable for both laboratory and field applications. The careful selection of nozzles, water pressure regulation, and spatial distribution mechanisms ensures that the simulator can accurately replicate the characteristics of natural rainfall that are necessary for investigating erosion processes.

In addition to its practical implementation, this research contributes to the advancement of experimental methodologies in hydrological and soil studies. The simulator’s ability to produce adjustable rainfall intensities, droplet size distributions, and kinetic energy makes it a valuable tool for future studies on rain-induced soil erosion, infiltration dynamics, and sediment transport modeling. In addition, the structured calibration approach, which integrates pluviometric and flour-based methods, provides a robust framework for optimizing rainfall simulations in different research settings.

Despite the progress, further improvements could improve the control of temporal uniformity and adaptability to different environmental conditions. Future developments may focus on refining the wind protection, expanding the range of adjustable parameters, and integrating automated feedback mechanisms for real-time calibration. By offering a cost-effective and scientifically rigorous approach to precipitation simulation, this research supports ongoing efforts in erosion mitigation, watershed management, and soil conservation strategies, ultimately contributing to more sustainable land use planning and environmental protection.