A Stochastic Multisite Bias Correction Method for Hydro-Meteorological Impact Studies
Abstract
1. Introduction
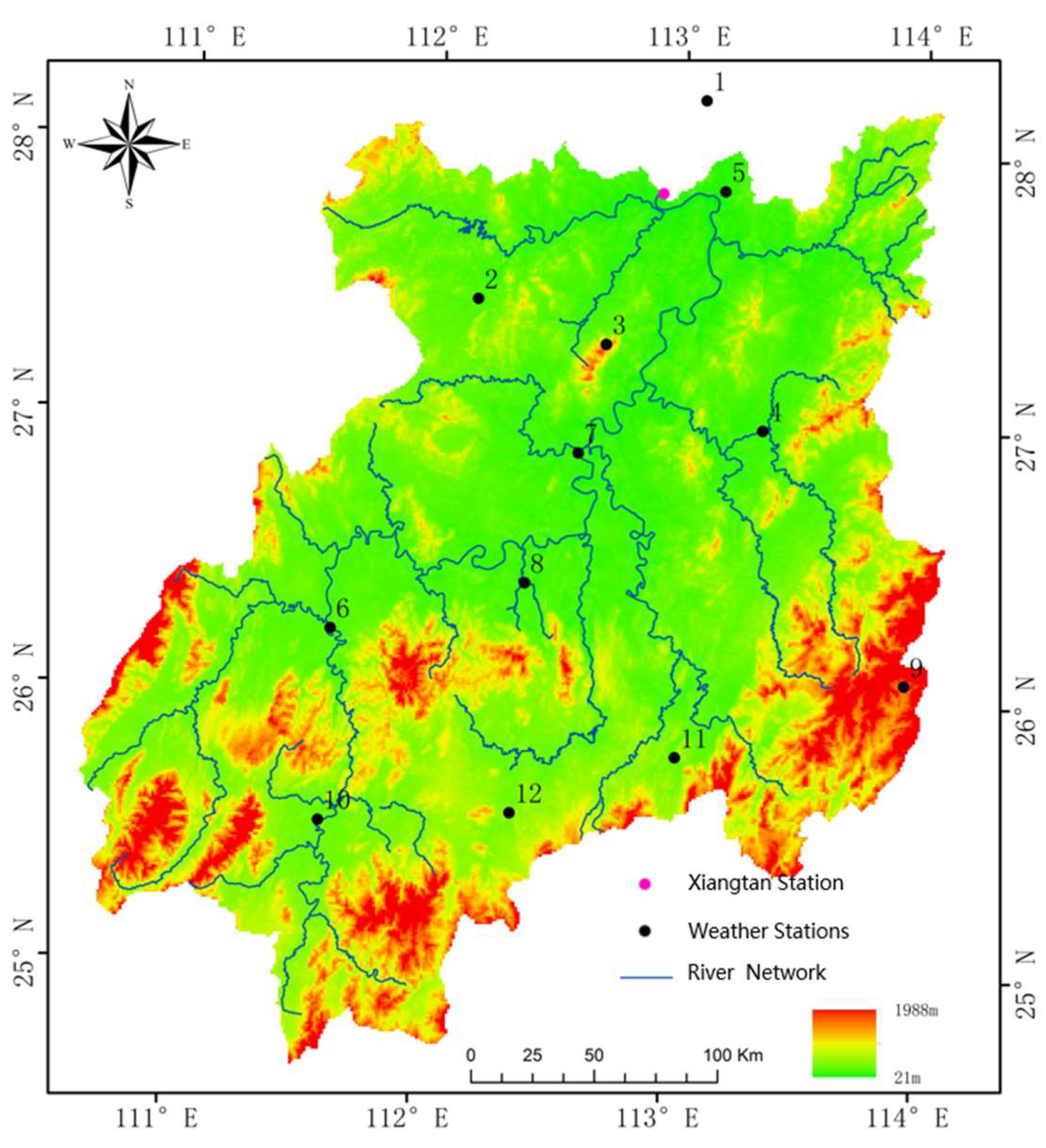
2. Study Area and Data
3. Methodology
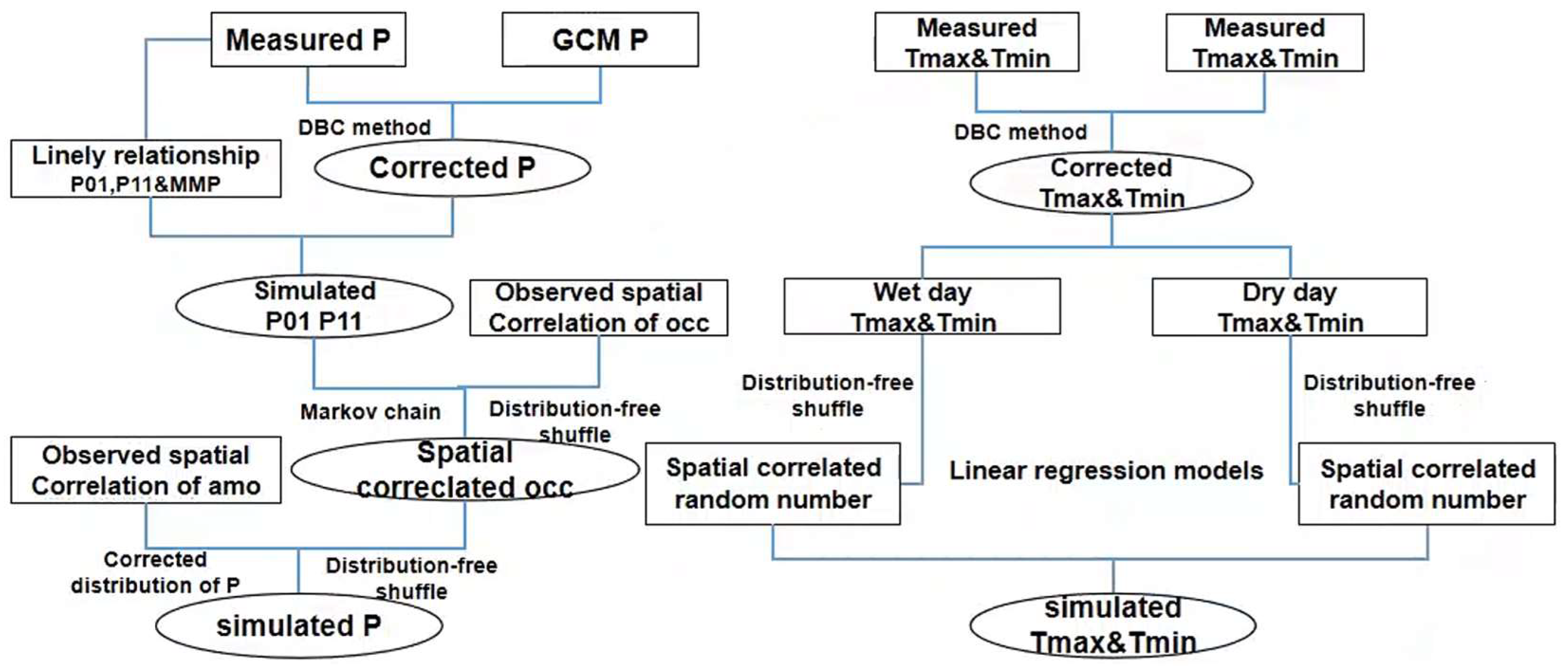
3.1. Bias Correction Method
3.1.1. Simulating of Distribution
- (1)
- For each month, a threshold is set for the precipitation series simulated by the climate model to ensure that the wet-day frequency in the simulation in the historical period matches that of the observation. This threshold is then applied to precipitation series of simulations in the future period to determine the weather state.
- (2)
- The bias of the simulated series relative to the observation in terms of the empirical distribution represented by the 1st to 100th percentiles during the historical period is calculated as the correction factor. The same bias is removed from the empirical distribution of precipitation and temperature in the future. The calculation formula for correcting simulated precipitation is as follows:
3.1.2. Simulation of Precipitation Occurrence
3.1.3. Simulation of Spatial Correlation
- (1)
- Calculate the n × n spatial correlation matrix [C] for precipitation occurrence, where n represents the number of stations. To ensure the matrix is positive definite, set any elements in its eigenvalue vector that are less than 0 to 0.0001, then recompose these eigenvalues into the correlation matrix [C].
- (2)
- Perform Cholesky decomposition on [C], resulting in [C] = [P][P’], where [P] is a lower triangular matrix and [P’] is its transpose. For any random matrix [X] multiplied by [P], the resulting matrix [D] will exhibit the same spatial correlation structure as [C].
- (3)
- The spatially correlated random number matrix [D], together with the simulated precipitation transition probability parameters, is used to generate a precipitation occurrence sequence with spatial correlation.
3.1.4. The Stochastic Multisite Bias Correction Method
- (1)
- According to the four-point regression method [50], the linear relationship between the precipitation transition probabilities and the mean monthly precipitation is constructed monthly.
- (2)
- The DBC method is employed to correct the distributions of precipitation and temperature, from which the corrected mean monthly precipitation is obtained.
- (3)
- Spatial correlation matrices for observations (precipitation amount, precipitation occurrence, maximum temperature, minimum temperature) are calculated every month. By employing the distribution-free shuffle algorithm, the Cholesky decomposition is performed on these spatial correlation matrices. Multiply the decomposed lower triangular matrices by random number matrices, resulting in random number matrices that maintain the same spatial correlation as the observation.
- (4)
- Using the downscaled precipitation transition probabilities from step (2) and the spatially correlated random number matrix of precipitation occurrence in step (3), the first-order two-state Markov chain is employed to simulate the precipitation occurrence at each station.
- (5)
- The spatial correlation matrix of the precipitation amount from step (3) is normalized and multiplied by the spatially correlated random number matrix of the precipitation occurrence, yielding a spatial correlation matrix for the wet-day precipitation amount. The generated wet-day precipitation amounts are sampled from the corrected precipitation of the DBC method, according to the random number ranks in the correlation matrix. Finally, an overall scaling procedure is applied to ensure the water balance of the monthly total precipitation amount.
- (6)
- The temperature series are divided into wet-day maximum temperature/minimum temperature and dry-day maximum temperature/minimum temperature. Based on this categorization, a regression model for temperature is established. The spatially correlated random numbers computed in step (3) are input into the linear regression model to generate the temperature series.
3.2. Hydrological Modeling
3.3. Data Analysis
4. Results
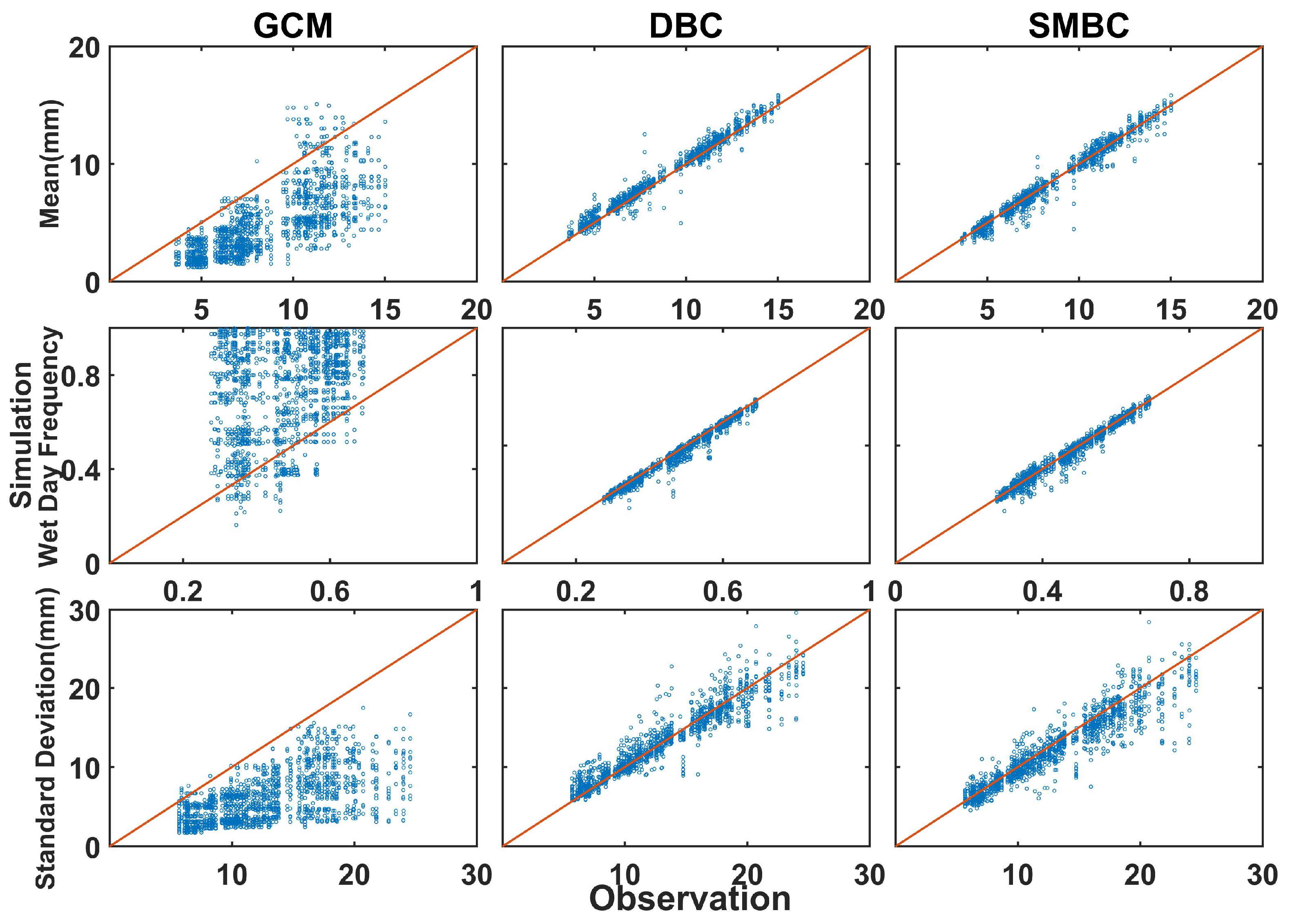
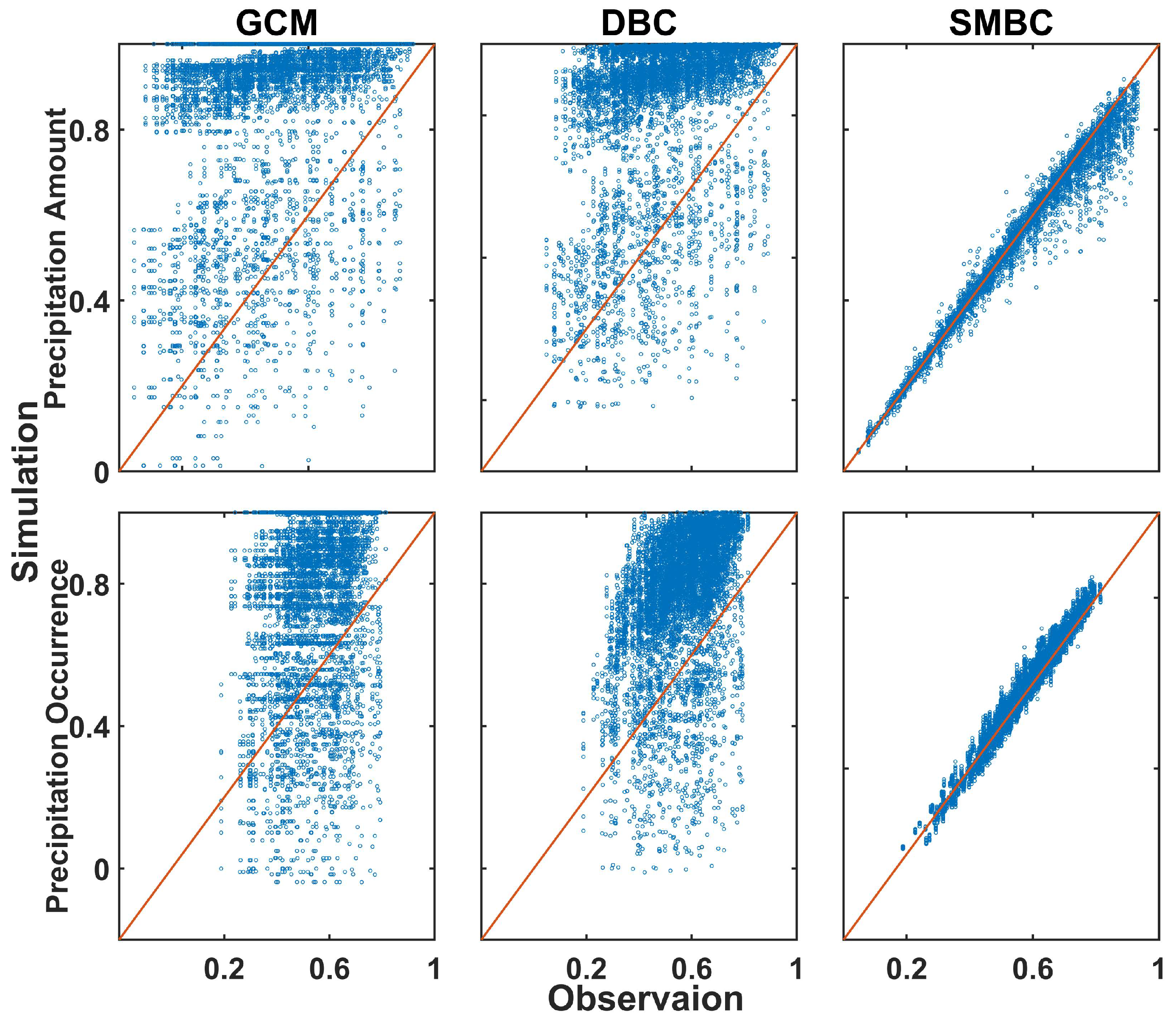
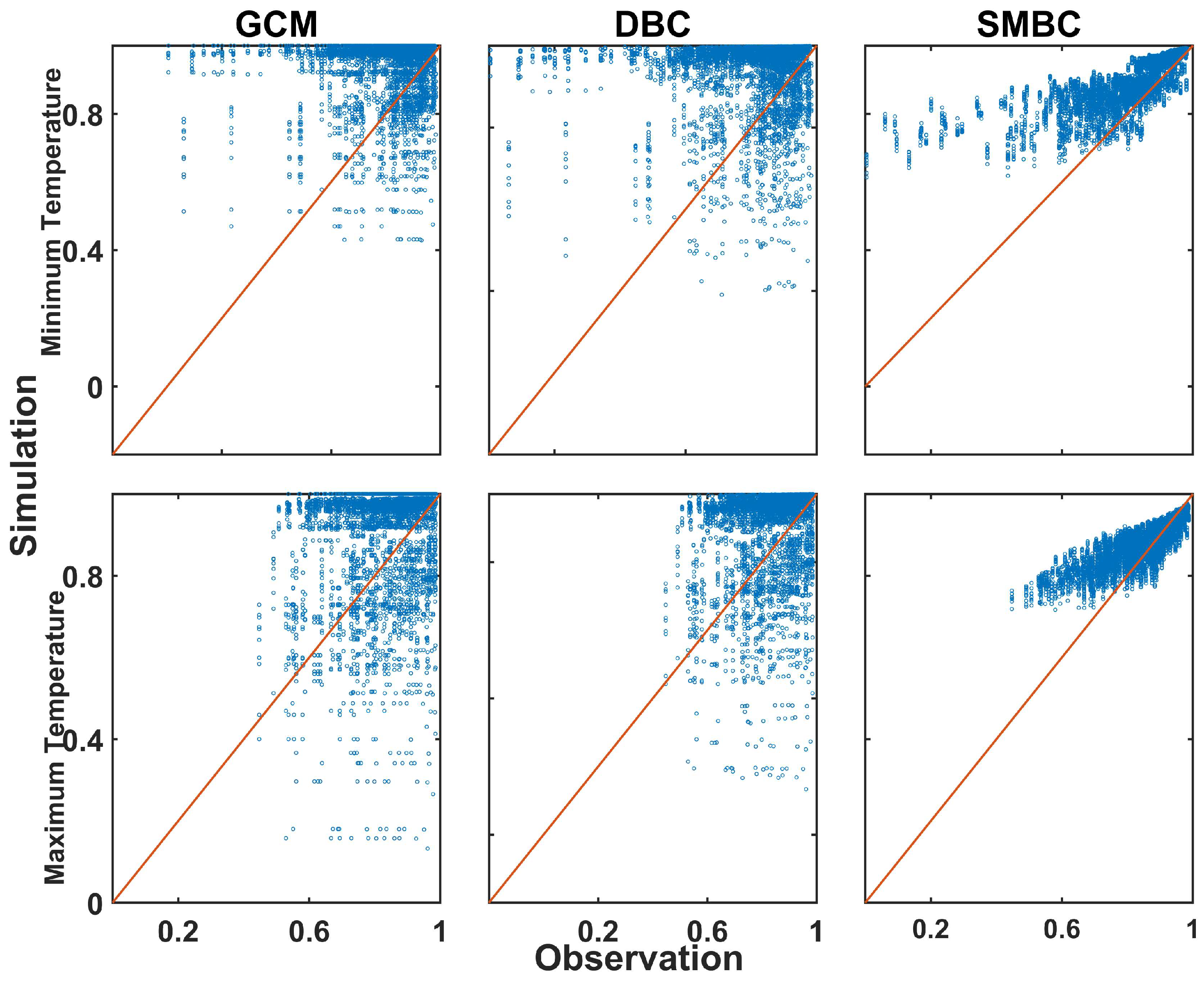
4.1. SMBC and DBC in Meteorological Correction
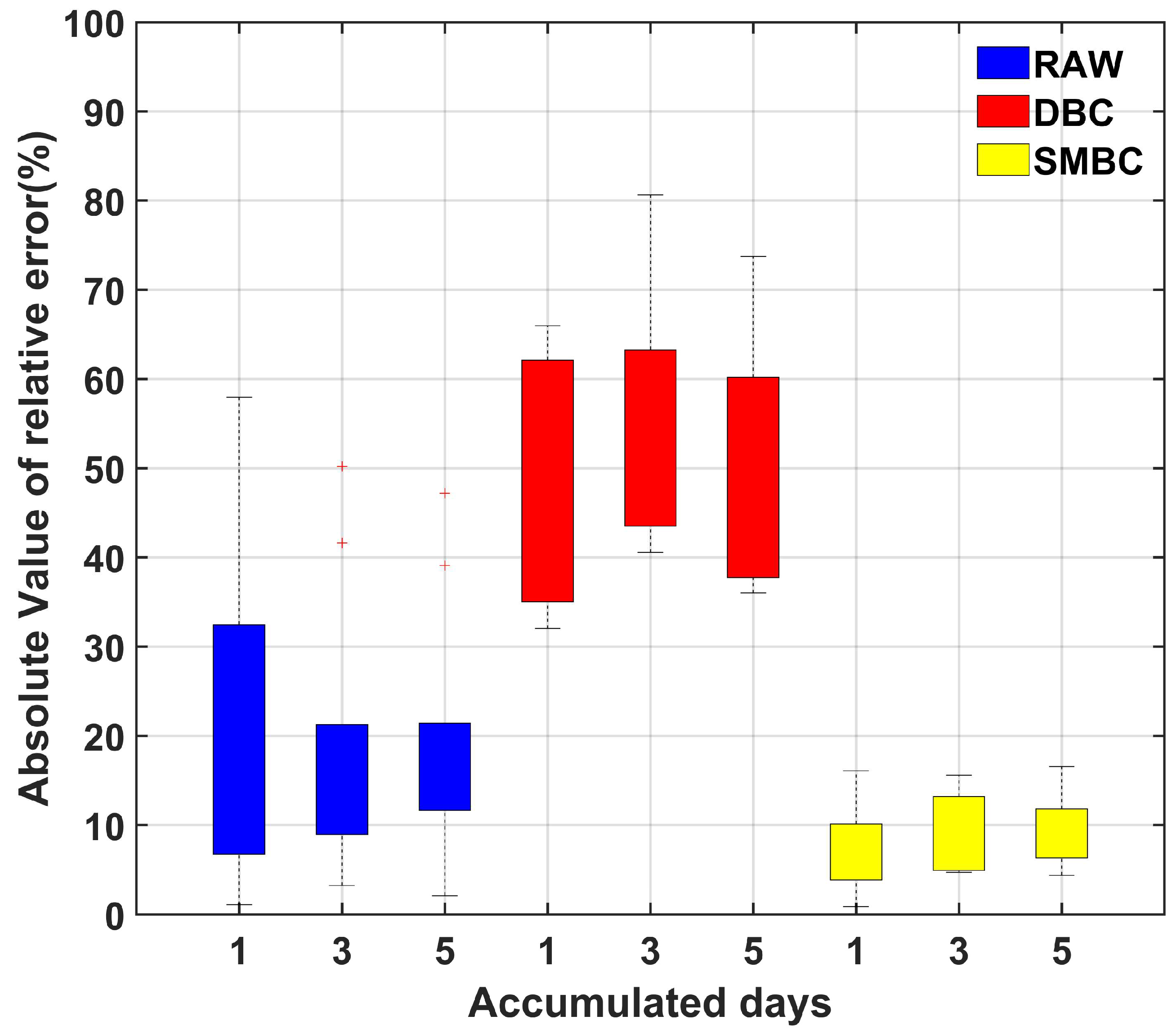
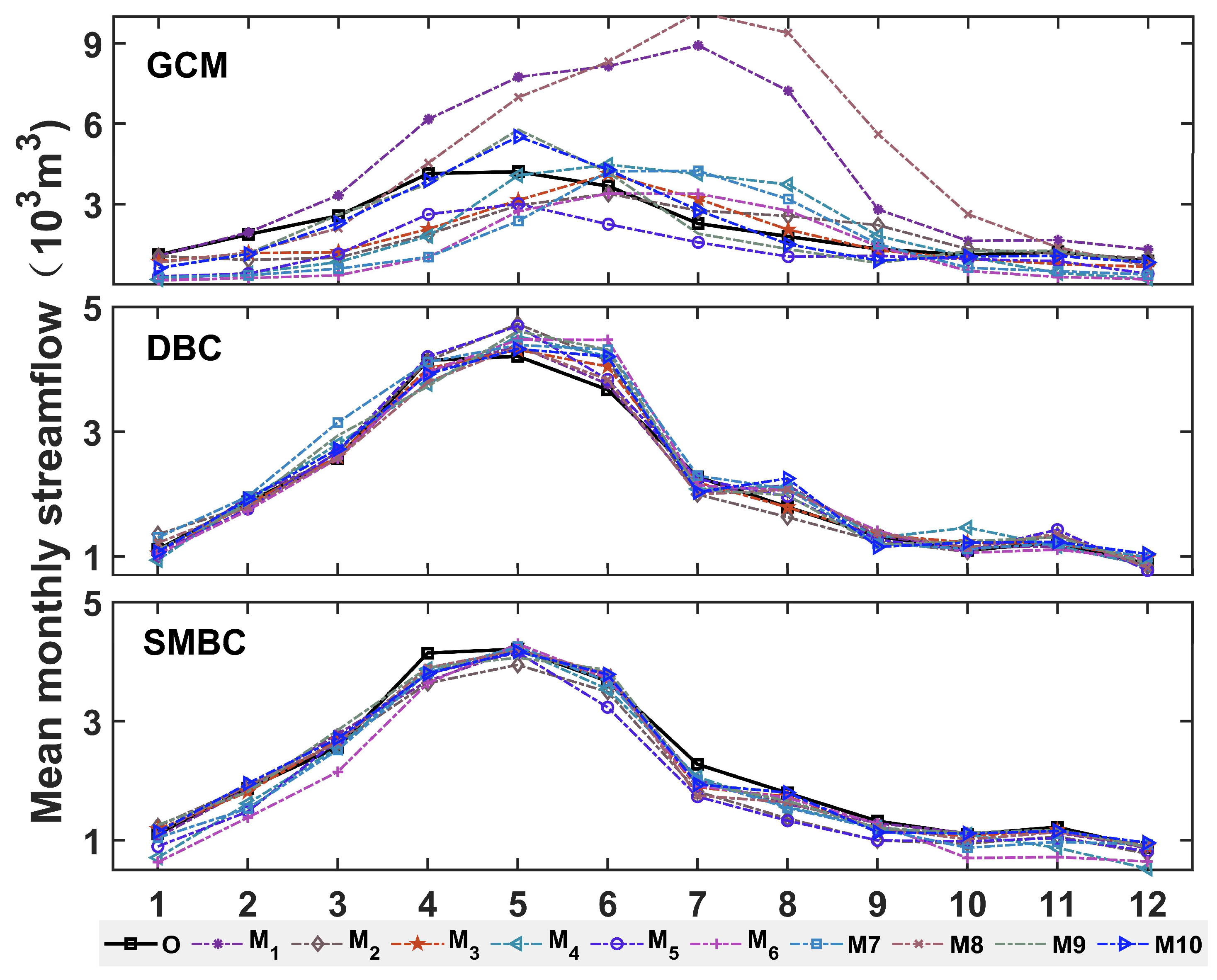
4.2. SMBC and DBC in Hydrological Simulation
5. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ali, Z.; Hamed, M.M.; Muhammad, M.K.I.; Shahid, S. A novel approach for evaluation of CMIP6 GCMs in simulating temperature and precipitation extremes of Pakistan. Int. J. Clim. 2024, 44, 592–612. [Google Scholar] [CrossRef]
- Iqbal, Z.; Shahid, S.; Ahmed, K.; Ismail, T.; Ziarh, G.F.; Chung, E.-S.; Wang, X. Evaluation of CIMP6 GCM rainfall in mainland Southeast Asia. Atmos. Res. 2021, 254, 105525. [Google Scholar] [CrossRef]
- Su, T.; Chen, J.; Cannon, A.J.; Xie, P.; Guo, Q. Multi-site bias correction of climate model outputs for hydro-meteorological impact studies: An application over a watershed in China. Hydrol. Process. 2020, 34, 2575–2598. [Google Scholar] [CrossRef]
- Goswami, P.; Saha, S.; Das, L.; Banerjee, S. Evaluation of CMIP6 GCMs performance and future projection for the Boro and Kharif seasons over the new alluvial zones of West Bengal. J. Agrometeorol. 2024, 26, 168–173. [Google Scholar] [CrossRef]
- Lorenzo, M.; Meucci, A.; Liu, J.; Syktus, J.; Thatcher, M.; Young, I. From global to regional-scale CMIP6-derived wind wave extremes: A single-GCM HighResMIP and CORDEX downscaling experiment in South-East Australia. Clim. Dyn. 2025, 63, 97. [Google Scholar] [CrossRef]
- Maraun, D. Bias Correction, Quantile Mapping, and Downscaling: Revisiting the Inflation Issue. J. Clim. 2013, 26, 2137–2143. [Google Scholar] [CrossRef]
- Nahar, J.; Johnson, F.; Sharma, A. Addressing Spatial Dependence Bias in Climate Model Simulations: An Independent Component Analysis Approach. Water Resour. Res. 2018, 54, 827–841. [Google Scholar] [CrossRef]
- Maraun, D.; Widmann, M.; Gutiérrez, J.M.; Kotlarski, S.; Chandler, R.E.; Hertig, E.; Wibig, J.; Huth, R.; Wilcke, R.A. VALUE: A framework to validate downscaling approaches for climate change studies. Earth’s Future 2014, 3, 1–14. [Google Scholar] [CrossRef]
- Guo, Q.; Chen, J.; Zhang, X.; Shen, M.; Chen, H.; Guo, S. A new two-stage multivariate quantile mapping method for bias correcting climate model outputs. Clim. Dyn. 2019, 53, 3603–3623. [Google Scholar] [CrossRef]
- Klein, W.H.; Glahn, H.R. Forecasting Local Weather by Means of Model Output Statistics. Bull. Am. Meteorol. Soc. 1974, 55, 1217–1227. [Google Scholar] [CrossRef]
- Wilby, R.L.; Dawson, C.W.; Barrow, E.M. sdsm—A decision support tool for the assessment of regional climate change impacts. Environ. Model. Softw. 2002, 17, 145–157. [Google Scholar] [CrossRef]
- Song, Y.H.; Chung, E.S.; Shahid, S. The New Bias Correction Method for Daily Extremes Precipitation over South Korea using CMIP6 GCMs. Water Resour. Manag. 2022, 36, 5977–5997. [Google Scholar] [CrossRef]
- Amunugama, M.; Tanaka, Y.; Suzuyama, K.; Ogata, T. WRF Dynamical Downscaling for High-Intensity Typhoons of D4PDF. In Proceedings of the International Conference on Asian and Pacific Coasts, Kyoto, Japan, 14–17 November 2023; Springer: Singapore, 2024; pp. 243–253. [Google Scholar] [CrossRef]
- Navarro-Racines, C.; Tarapues, J.; Thornton, P.; Jarvis, A.; Ramirez-Villegas, J. High-resolution and bias-corrected CMIP5 projections for climate change impact assessments. Sci. Data 2020, 7, 7. [Google Scholar] [CrossRef] [PubMed]
- Doury, A.; Somot, S.; Gadat, S. On the suitability of a convolutional neural network based RCM-emulator for fine spatio-temporal precipitation. Clim. Dyn. 2024, 62, 8587–8613. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 456, 12–29. [Google Scholar] [CrossRef]
- Jaiswal, R.; Mall, R.K.; Singh, N.; Kumar, T.V.L.; Niyogi, D. Evaluation of Bias Correction Methods for Regional Climate Models: Downscaled Rainfall Analysis Over Diverse Agroclimatic Zones of India. Earth Space Sci. 2022, 9, e2021EA001981. [Google Scholar] [CrossRef]
- Xavier, A.C.F.; Martins, L.L.; Rudke, A.P.; de Morais, M.V.B.; Martins, J.A.; Blain, G.C. Evaluation of Quantile Delta Mapping as a bias-correction method in maximum rainfall dataset from downscaled models in So Paulo state (Brazil). Int. J. Climatol. 2022, 42, 175–190. [Google Scholar] [CrossRef]
- Chen, J.; Arsenault, R.; Brissette, F.P.; Zhang, S. Climate Change Impact Studies: Should We Bias Correct Climate Model Outputs or Post-process Impact Model Outputs? Water Resour. Res. 2021, 57, e2020WR028638. [Google Scholar] [CrossRef]
- Voropay, N.; Ryazanova, A.; Dyukarev, E. High-resolution bias-corrected precipitation data over South Siberia, Russia. Atmos. Res. 2021, 254, 105528. [Google Scholar] [CrossRef]
- Maraun, D. Nonstationarities of regional climate model biases in European seasonal mean temperature and precipitation sums. Geophys. Res. Lett. 2012, 39, L06706. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Zhang, X.J.; Chen, H.; Guo, S.; Zhao, Y. Bias correcting climate model multi-member ensembles to assess climate change impacts on hydrology. Clim. Change 2019, 153, 361–377. [Google Scholar] [CrossRef]
- Han, X.; Mehrotra, R.; Sharma, A. Measuring the spatial connectivity of extreme rainfall. J. Hydrol. 2020, 590, 125510. [Google Scholar] [CrossRef]
- Li, X.; Vladan, B. A new scheme for multivariate, multisite weather generator with inter-variable, inter-site dependence and inter-annual variability based on empirical copula approach. Clim. Dyn. 2018, 52, 2247–2267. [Google Scholar] [CrossRef]
- Yao, N.; Ye, J.; Wang, S.; Yang, S.; Lu, Y.; Zhang, H.; Yang, X. Bias correction of the hourly satellite precipitation product using machine learning methods enhanced with high-resolution WRF meteorological simulations. Atmos. Res. 2024, 310, 107637. [Google Scholar] [CrossRef]
- Iqbal, Z.; Shahid, S.; Ahmed, K.; Wang, X.; Ismail, T.; Gabriel, H.F. Bias correction method of high-resolution satellite-based precipitation product for Peninsular Malaysia. Theor. Appl. Climatol. 2022, 148, 1429–1446. [Google Scholar] [CrossRef]
- Meema, T.; Wattanasetpong, J.; Wichakul, S. Integrating machine learning and zoning-based techniques for bias correction in gridded precipitation data to improve hydrological estimation in the data-scarce region. J. Hydrol. 2025, 646, 132356. [Google Scholar] [CrossRef]
- Pan, B.; Hsu, K.; AghaKouchak, A.; Sorooshian, S. Improving precipitation estimation using convolutional neural network. Water Resour. Res. 2019, 55, 2301–2321. [Google Scholar] [CrossRef]
- Huang, B.; Liu, Z.; Duan, Q.; Rajib, A.; Yin, J. Unsupervised deep learning bias correction of CMIP6 global ensemble precipitation predictions with cycle generative adversarial network. Environ. Res. Lett. 2024, 19, 094003. [Google Scholar] [CrossRef]
- Hu, Y.; Yin, F.; Zhang, W. Deep learning-based precipitation bias correction approach for Yin–He global spectral model. Meteorol. Appl. 2021, 28, e2032. [Google Scholar] [CrossRef]
- Xu, L.; Chen, N.; Chen, Z.; Zhang, C.; Yu, H. Spatiotemporal forecasting in earth system science: Methods, uncertainties, predictability and future directions. Earth-Sci. Rev. 2021, 222, 103828. [Google Scholar] [CrossRef]
- Ebert-Uphoff, I.; Hilburn, K. Evaluation, tuning and interpretation of neural networks for working with images in meteorological applications. Bull. Am. Meteorol. Soc. 2020, 101, E2149–E2170. [Google Scholar] [CrossRef]
- Chen, J.; Chen, H.; Guo, S. Multisite precipitation downscaling using a stochastic weather generator. Clim. Dyn. 2018, 50, 1975–1992. [Google Scholar] [CrossRef]
- Li, X.; Babovic, V. Multisite multivariate downscaling of global climate model outputs: An integrated framework combining quantile mapping, stochastic weather generator and Empirical Copula approaches. Clim. Dyn. 2018, 52, 5775–5799. [Google Scholar] [CrossRef]
- Nguyen, V.D.; Merz, B.; Hundecha, Y.; Haberlandt, U.; Vorogushyn, S. Comprehensive evaluation of an improved large-scale multi-site weather generator for Germany. Int. J. Climatol. 2021, 41, 4933–4956. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, J.; You, Y.; Wang, Y.; Xu, Y.-P.; Guo, Y.-X. A new multisite multi-variable stochastic model with inter-site and inter-variable correlations, low-frequency attributes and stochasticity: A case study in the lower Yellow River basin. J. Hydrol. 2021, 599, 126365. [Google Scholar] [CrossRef]
- Verdin, A.; Rajagopalan, B.; Kleiber, W.; Podestá, G.; Bert, F. A conditional stochastic weather generator for seasonal to multi-decadal simulations. J. Hydrol. 2018, 556, 835–846. [Google Scholar] [CrossRef]
- Ben Alaya, M.A.; Chebana, F.; Ouarda, T.B.M.J. Multisite and multi-variable statistical downscaling using a Gaussian copula quantile regression model. Clim. Dyn. 2015, 47, 1383–1397. [Google Scholar] [CrossRef]
- Hnilica, J.; Hanel, M.; Puš, V. Multisite bias correction of precipitation data from regional climate models. Int. J. Climatol. 2017, 37, 2934–2946. [Google Scholar] [CrossRef]
- Franois, B.; Thao, S.; Vrac, M. Adjusting spatial dependence of climate model outputs with cycle-consistent adversarial networks. Clim. Dyn. 2021, 57, 3323–3353. [Google Scholar] [CrossRef]
- François, B.; Vrac, M.; Cannon, A.J.; Robin, Y.; Allard, D. Multivariate bias corrections of climate simulations: Which benefits for which losses? Earth Syst. Dyn. 2020, 11, 537–562. [Google Scholar] [CrossRef]
- Liu, H.; Chen, J.; Zhang, X.-C.; Xu, C.-Y.; Hui, Y. A Markov Chain-Based Bias Correction Method for Simulating the Temporal Sequence of Daily Precipitation. Atmosphere 2020, 11, 109. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Chaumont, D.; Braun, M. Performance and uncertainty evaluation of empirical downscaling methods in quantifying the climate change impacts on hydrology over two North American river basins. J. Hydrol. 2013, 479, 200–214. [Google Scholar] [CrossRef]
- Mpelasoka, F.; Chiew, F. Influence of rainfall scenario construction methods on runoff projections. J. Hydrometeorol. 2009, 10, 1168–1183. [Google Scholar] [CrossRef]
- Schmidli, J.; Frei, C.; Vidale, P.L. Downscaling from GCM precipitation: A benchmark for dynamical and statistical downscaling methods. Int. J. Climatol. J. R. Meteorol. Soc. 2006, 26, 679–689. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Chaumont, D.; Braun, M. Finding appropriate bias correction methods in downscaling precipitation for hydrologic impact studies over North America. Water Resour. Res. 2013, 49, 4187–4205. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Caya, D. Remaining error sources in bias-corrected climate model outputs. Clim. Change 2020, 162, 563–582. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, X.J.; Brissette, F.P. Assessing scale effects for statistically downscaling precipitation with GPCC model. Int. J. Climatol. 2013, 34, 708–727. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Zhang, X.J. A multisite stochastic weather generator for daily precipitation and temperature. Trans. Asabe 2014, 57, 1375–1391. [Google Scholar] [CrossRef]
- Zhang, X. Verifying a temporal disaggregation method for generating daily precipitation of potentially nonstationary climate change for site-specific impact assessment. Int. J. Climatol. 2013, 33, 326–342. [Google Scholar] [CrossRef]
- Iman, R.L.; Conover, W.J. A distribution-free approach to inducing rank correlation among input variables. Commun. Stat.-Simul. Comput. 1982, 11, 311–334. [Google Scholar] [CrossRef]
- Brissette, F.P.; Khalili, M.; Leconte, R. Efficient stochastic generation of multisite synthetic precipitation data. J. Hydrol. 2007, 345, 121–133. [Google Scholar] [CrossRef]
- Arnold, J.G.; Williams, J.R.; Maidment, D.R. Continuous-Time Water and Sediment-Routing Model for Large Basins. J. Hydraul. Eng. 1995, 121, 171–183. [Google Scholar] [CrossRef]
- Hui, Y.; Chen, J.; Xu, C.; Xiong, L.; Chen, H. Bias nonstationarity of global climate model outputs: The role of internal climate variability and climate model sensitivity. Int. J. Climatol. 2018, 39, 2278–2294. [Google Scholar] [CrossRef]
- Cannon, A.J. Probabilistic Multisite Precipitation Downscaling by an Expanded Bernoulli-Gamma Density Network. J. Hydrometeorol. 2008, 9, 1284–1300. [Google Scholar] [CrossRef]
- Van de Velde, J.; Demuzere, M.; De Baets, B.; Verhoest, N.E.C. Impact of bias nonstationarity on the performance of uni-and multivariate bias-adjusting methods: A case study on data from Uccle, Belgium. Hydrol. Earth Syst. Sci. 2022, 26, 2319–2344. [Google Scholar] [CrossRef]
- Vidrio-Sahagún, C.T.; He, J.; Pietroniro, A. Improved correction of extreme precipitation through explicit and continuous nonstationarity treatment and the metastatistical approach. Water Resour. Res. 2025, 61, e2024WR037721. [Google Scholar] [CrossRef]
- Ayugi, B.; Zhihong, J.; Zhu, H.; Ngoma, H.; Babaousmail, H.; Rizwan, K.; Dike, V. Comparison of CMIP6 and CMIP5 Models in Simulating Mean and Extreme Precipitation over East Africa. Int. J. Climatol. 2021, 41, 6474–6496. [Google Scholar] [CrossRef]
- Yu, T.; Chen, W.; Gong, H.; Feng, J.; Chen, S. Comparisons between CMIP5 and CMIP6 models in simulations of the climatology and interannual variability of the East Asian summer Monsoon. Clim. Dyn. 2022, 60, 2183–2198. [Google Scholar] [CrossRef]
- Zhu, H.; Jiang, Z.; Li, J.; Li, W.; Sun, C.; Li, L. CMIP6 Inspire More Confidence in Simulating Climate Extremes over China? Adv. Atmos. Sci. 2020, 37, 1119–1132. [Google Scholar] [CrossRef]
- Fan, X.; Miao, C.; Duan, Q.; Shen, C.; Wu, Y. The performance of CMIP6 versus CMIP5 in simulating temperature extremes over the global land surface. J. Geophys. Res. Atmos. 2020, 125, e2020JD033031. [Google Scholar] [CrossRef]
- Lei, Y.; Chen, J.; Xiong, L. A comparison of CMIP5 and CMIP6 climate model projections for hydrological impacts in China. Hydrol. Res. 2023, 54, 330–347. [Google Scholar] [CrossRef]



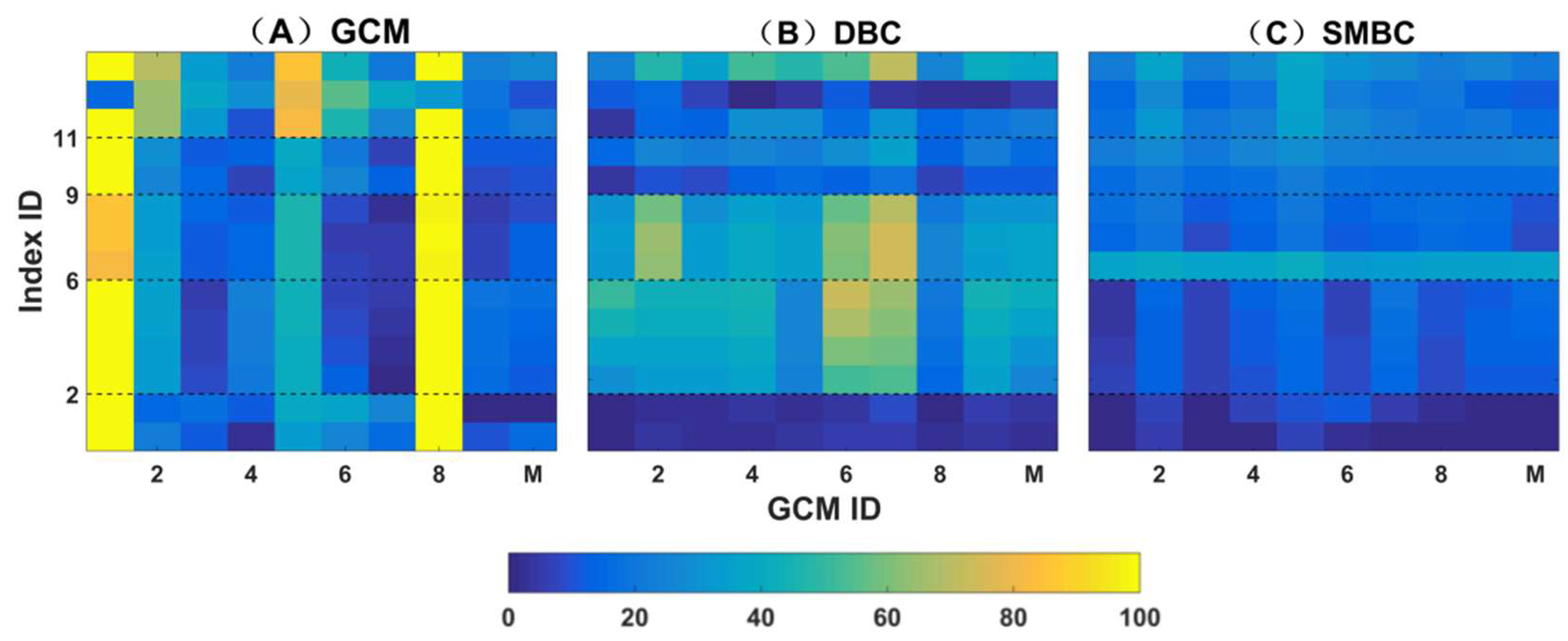
| Mean Value Index ID | Description |
|---|---|
| 1 | Annual mean flow (m3/s) |
| 2 | Mean flow in the rainy season (Apr. to Jul.) (m3/s) |
| Extreme Value Index ID | Description |
| 3 | Ten-year return period streamflow (m3/s) |
| 4 | Twenty-year return period streamflow (m3/s) |
| 5 | Fifty-year return period streamflow (m3/s) |
| 6 | Hundred-year return period streamflow (m3/s) |
| 7 | Annual maximum flow of one day (m3/s) |
| 8 | Annual maximum flow in intervals of consecutive three days (m3/s) |
| 9 | Annual maximum flow in intervals of five consecutive days (m3/s) |
| 10 | Annual flow of 90th quantile (m3/s) |
| 11 | Annual flow of 95th quantile (m3/s) |
| 12 | An extreme streamflow process is the consecutive days when QN > Q90 (day) |
| 13 | Number of extreme streamflow processes (times) |
| 14 | Total streamflow of extreme streamflow processes (m3) |
| The Number of GCMs | Mean Daily Precipitation (mm) | Wet-Day Frequency | Standard Deviation (mm) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| GCM | DBC | SMBC | GCM | DBC | SMBC | GCM | DBC | SMBC | |
| M1 | 2.56 | 0.26 | 0.21 | 0.42 | 0.01 | 0.01 | 4.99 | 0.91 | 1.02 |
| M2 | 4.9 | 0.26 | 0.37 | 0.44 | 0.01 | 0.01 | 9.36 | 1.07 | 1.94 |
| M3 | 3.6 | 0.27 | 0.2 | 0.21 | 0.01 | 0.01 | 6.24 | 0.77 | 0.95 |
| M4 | 3.97 | 0.31 | 0.37 | 0.22 | 0.02 | 0.02 | 7.04 | 0.8 | 0.98 |
| M5 | 5.51 | 0.29 | 0.43 | 0.36 | 0.01 | 0.02 | 9.41 | 0.96 | 1.8 |
| M6 | 4.91 | 0.52 | 0.56 | 0.23 | 0.02 | 0.02 | 8.19 | 1.58 | 1.55 |
| M7 | 4.59 | 0.5 | 0.41 | 0.24 | 0.02 | 0.01 | 7.59 | 1.57 | 1.24 |
| M8 | 2.3 | 0.24 | 0.22 | 0.32 | 0.01 | 0.01 | 4.46 | 0.76 | 1.08 |
| M9 | 2.7 | 0.44 | 0.27 | 0.15 | 0.02 | 0.01 | 5.48 | 0.81 | 0.86 |
| M10 | 2.58 | 0.46 | 0.26 | 0.15 | 0.02 | 0.01 | 5.04 | 1.06 | 1.11 |
| The Number of GCMs | Precipitation Occurrence | Precipitation Amount | ||||
|---|---|---|---|---|---|---|
| GCM | DBC | SMBC | GCM | DBC | SMBC | |
| M1 | 0.37 | 0.34 | 0.01 | 0.27 | 0.22 | 0.02 |
| M2 | 0.39 | 0.38 | 0.01 | 0.38 | 0.29 | 0.02 |
| M3 | 0.38 | 0.36 | 0.01 | 0.32 | 0.25 | 0.02 |
| M4 | 0.38 | 0.36 | 0.02 | 0.32 | 0.26 | 0.02 |
| M5 | 0.36 | 0.34 | 0.01 | 0.25 | 0.22 | 0.02 |
| M6 | 0.38 | 0.36 | 0.02 | 0.33 | 0.26 | 0.01 |
| M7 | 0.38 | 0.36 | 0.02 | 0.33 | 0.25 | 0.02 |
| M8 | 0.38 | 0.35 | 0.02 | 0.27 | 0.23 | 0.02 |
| M9 | 0.39 | 0.37 | 0.01 | 0.32 | 0.26 | 0.02 |
| M10 | 0.39 | 0.37 | 0.01 | 0.33 | 0.26 | 0.02 |
| The Number of GCMs | Maximum Temperature | Minimum Temperature | ||||
|---|---|---|---|---|---|---|
| GCM | DBC | SMBC | GCM | DBC | SMBC | |
| M1 | 0.12 | 0.12 | 0.05 | 0.16 | 0.15 | 0.09 |
| M2 | 0.17 | 0.17 | 0.05 | 0.18 | 0.18 | 0.09 |
| M3 | 0.13 | 0.12 | 0.05 | 0.16 | 0.16 | 0.08 |
| M4 | 0.13 | 0.12 | 0.05 | 0.16 | 0.15 | 0.08 |
| M5 | 0.12 | 0.12 | 0.05 | 0.15 | 0.14 | 0.08 |
| M6 | 0.13 | 0.12 | 0.05 | 0.16 | 0.15 | 0.08 |
| M7 | 0.13 | 0.12 | 0.05 | 0.16 | 0.15 | 0.08 |
| M8 | 0.12 | 0.12 | 0.05 | 0.15 | 0.15 | 0.08 |
| M9 | 0.12 | 0.11 | 0.05 | 0.15 | 0.15 | 0.08 |
| M10 | 0.12 | 0.11 | 0.05 | 0.15 | 0.15 | 0.09 |
| Wet Days | Dry days | |||||
|---|---|---|---|---|---|---|
| GCM | DBC | SMBC | GCM | DBC | SMBC | |
| M1 | 0.51 | 0.04 | 0.01 | 0.34 | 0.06 | 0.01 |
| M2 | 0.52 | 0.07 | 0.01 | 0.35 | 0.07 | 0.01 |
| M3 | 0.28 | 0.05 | 0.01 | 0.14 | 0.06 | 0.01 |
| M4 | 0.27 | 0.05 | 0.02 | 0.17 | 0.07 | 0.02 |
| M5 | 0.43 | 0.05 | 0.02 | 0.28 | 0.06 | 0.02 |
| M6 | 0.27 | 0.05 | 0.02 | 0.2 | 0.08 | 0.03 |
| M7 | 0.3 | 0.05 | 0.01 | 0.19 | 0.07 | 0.01 |
| M8 | 0.41 | 0.05 | 0.01 | 0.24 | 0.06 | 0.01 |
| M9 | 0.21 | 0.05 | 0.01 | 0.11 | 0.08 | 0.01 |
| M10 | 0.21 | 0.05 | 0.01 | 0.11 | 0.08 | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Gu, Y.; Geng, L.; Liu, H. A Stochastic Multisite Bias Correction Method for Hydro-Meteorological Impact Studies. Water 2025, 17, 1807. https://doi.org/10.3390/w17121807
Liu H, Gu Y, Geng L, Liu H. A Stochastic Multisite Bias Correction Method for Hydro-Meteorological Impact Studies. Water. 2025; 17(12):1807. https://doi.org/10.3390/w17121807
Chicago/Turabian StyleLiu, Han, Yicheng Gu, Leihua Geng, and Heng Liu. 2025. "A Stochastic Multisite Bias Correction Method for Hydro-Meteorological Impact Studies" Water 17, no. 12: 1807. https://doi.org/10.3390/w17121807
APA StyleLiu, H., Gu, Y., Geng, L., & Liu, H. (2025). A Stochastic Multisite Bias Correction Method for Hydro-Meteorological Impact Studies. Water, 17(12), 1807. https://doi.org/10.3390/w17121807





