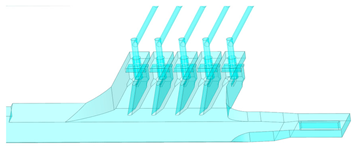
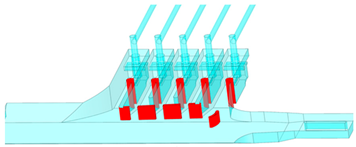
Abstract
The flow pattern in a pumping station intake basin has a significant influence on the inlet conditions of the pumping machine. For the purpose of solving the problems of flow disorder and the uneven flow velocity distribution in the intake basin of a lateral-inlet pumping station with a truncated-type canal, this study takes a flood discharge pumping station as an example and then studies and analyzes the flow pattern in the inlet pool of a lateral-inlet pumping station with a truncated-type canal. The Revit2018 modeling software is used to establish a three-dimensional model, CFD fluid calculation software is used to simulate the fluid, and the reliability of the numerical simulation results is verified using physical model tests. This paper proposes a new type of separated guide wall rectification measure, which is combined with a guide pier and other optimization measures to improve the flow of the inlet pool and is composed of a variety of programs. The results show that the optimization scheme of a “closed flow guide wall and flow guide pier” is the most effective. Compared with the original scheme, the lateral flow velocity distribution ratio and the mean square error (MSE) are reduced, while the axial flow velocity uniformity is increased by 52.24% and the axial flow velocity weighted average angle is increased by 5.92°. The optimal spacing of the dividing deflector wall is investigated using the response surface methodology, and further optimization of the scheme results in a further increase of 2.23% in the flow uniformity.
1. Introduction
Today, urban land is increasingly in demand, so the lateral water inlet arrangement form, which can more effectively save land-use area, is adopted for pumping stations. If the inlet direction of a pool is axially inclined to the direction of flow from a river, the water flow will be deflected at a large angle in the front pool of the pumping station, making it prone to unfavorable flow conditions, such as backflow and eddies [1,2]. Urban rivers are limited to narrower land and often form truncated rivers; that is, one end of the river is open, and the other end has a closed layout form. In order to save land-use area, the design of urban pumping station projects is based on topography, and diversion sections are shortened or even deleted [3]. The water enters from the open end of the river without passing through the diversion channel, and it enters directly into the front basin and the intake basin of the pumping station at the side. When more than one unit is operating simultaneously, it is easy for a backflow and eddy to form in front of the intake basin separated by the pier, and the flow velocity distribution in each intake basin is relatively uneven. Poor inlet conditions and poor flow will seriously affect the efficiency of the pumping machine, so it is important to analyze the flow in the intake basin of the pumping station. In the pumping station, before the pool and the intake pool, reasonable optimization measures should be implemented to help the intake pool flow state become more stable, which can improve the pumping machine’s water intake conditions, effectively improving the pumping station’s water intake efficiency [4,5].
Historically, research on pumping station flow improvement has mainly relied on isometrically scaled-down physical model tests to simulate the operation of prototype projects. In the last century, scientists have analyzed the flow regimes of pumping stations more qualitatively using physical model tests and quantitatively measured the flow velocity at selected model sections manually using flow meters. With the development of computer technology, DPIV technology has been widely used in hydraulic model testing. Computation of the DPIV using the laws of fluid dynamics can quickly lead to the real-time implementation of flow reconstruction and visualization, improving the qualitative analysis of vector fields and quantitative measurement feasibility [6,7]. In recent years, with the development and gradual maturity of computational fluid dynamics (CFD) technology, the use thereof to conduct research on hydraulic models has gradually become mainstream. Many studies are based on traditional theoretical analyses and experimental measurements, which provide a solid theoretical foundation for the development of CFD [8,9,10]. Many scholars have used CFD for pumping stations before pools and inlet pools with poor flow and hydraulic characteristics in a large number of studies, and in their mathematical models, they propose various rectification measures for combination. Thereby, they conduct a comparative selection of better measures in the physical model for verification, which can undoubtedly greatly reduce the cost of materials and time [11,12]. Rajendran and Constantinescu et al. [13], in order to verify the accuracy of a three-dimensional turbulence numerical simulation model of a water pump inlet, conducted tests on an indoor model. The tests were conducted using particle image velocimetry for data acquisition, and it was found that the expected number, location, and structure of the vortices were basically the same as in the physical model tests, although the numerical model test results were usually larger, indicating that the turbulence model was still deficient in simulating the flow. Chen Zhang [14] conducted a flow analysis of the front pool of a lateral-inlet pumping station with an asymmetric pumping machine and optimized the flow regime of the front pool by using different forms of guide pier arrangement. The flow uniformity and weighted flow mean angle were adopted as evaluation indices, and the orthogonal experimental method was used to determine the optimal design parameters for the guide piers. The results showed that the flow regime of the pumping station forebay had been effectively optimized. In the rectification of the pumping station forebay flow, in the face of more complex flow conditions, the use of a combination of rectification measures can often achieve better results. Fan Yang [15] used a variety of optimization measures to rectify the flow in a pool upstream of a parallel pumping station to solve the problem of a poor flow pattern. Physical and numerical models were used to verify the results, and the results showed that the combination of rectifying bottom cans and open-hole deflector walls was the most effective measure. Jinghong Li [16] conducted a numerical study on the hydraulic characteristics of a lateral-inlet multiple-forebay pumping station, taking the largest urban water supply pumping station in Asia as an example, where the flow was rectified by a combination of guide pillars, inlet grids, and bottom cans. Different flow distributions of different units were designed to make the model reduce the hydraulic losses and improve the flow uniformity, and the flow pattern was found to be effectively improved through numerical verification of the physical models. Some scholars have studied sediment deposition in the forebays of pumping stations and concluded that the efficiency of sediment deposition there is strongly related to the diffusion angle of the forebay [17,18]. Luo, C. [19] conducted a study on the vortex distribution in the forebay of a lateral pumping station with a Y-shaped channel. He introduced the entropy generation theory to analyze the energy changes in the anti-vortex base plate and found that the main sources of energy loss in the base plate were water flow impact and vortices. Olszewski, P. [20] used a genetic algorithm to optimize a control scheme and validated it through model testing. These tests show that sensors and a programmable controller can significantly reduce the energy consumption of a multi-pump system.
For similar lateral-intake pumping stations with a short diversion channel or no diversion channel, most of the current rectification measures are installed in front of the intake pool’s curved guide pier or in front of a pool in the arrangement of a Y-shaped guide pier. These rectification measures have a relatively good effect on improving the flow pattern in the forebay and the intake basin of the pumping station. However, through physical modeling tests, it was found that similar correction measures are not very effective for pumping station projects with a small forebay under the truncated channel. In the intake pool in front of an arc-shaped flow guide pier, it is easy for the water flow to follow the arc-shaped flow guide pier’s bending angle at the pier mouth to form a small area and a relatively high-flow-velocity vortex, thus affecting the flow pattern of the entire intake pool. In this study, taking a flood pumping station as an example, a lateral-intake pumping station under the truncated channel of a river intake pool is used to study and analyze the flow pattern. A combination of physical model tests and numerical simulations was utilized for comparative validation. The three-dimensional model is constructed by using the Revit modeling software, CFD fluid calculation software is used to simulate the fluid, and the numerical simulation results are verified using physical model testing. A new type of separated guide wall rectification measure is proposed in combination with a guide pier and other optimization measures to improve the inlet pool flow state and comparative analysis. The analysis process is shown in Figure 1.
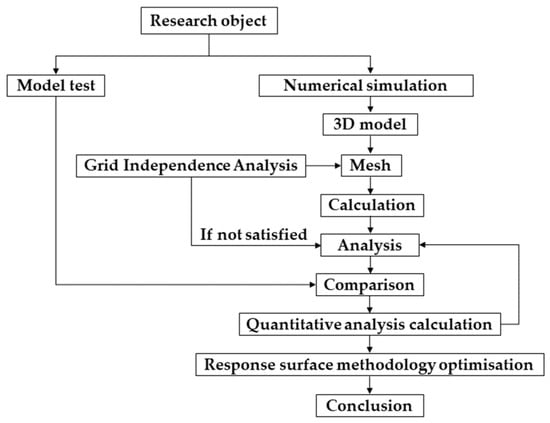
Figure 1.
Analysis flowchart.
The innovation of this study is its proposal of a new type of divided flow guide wall combined with a flow guide pier for flow rectification. The uniformity of the flow distribution in the inlet basin is optimized by the flow guide pier, and the flow distribution in each inlet basin is controlled by the separated flow guide wall. This study proposes a variety of evaluation indices to compare different optimization schemes and select the optimal scheme. The response surface method is used to determine the spacing between the partition walls to further optimize the scheme. The results of this study can provide some ideas and methodological guidance for the optimization of the flow of similar lateral-inlet pumping stations with a small or no forebay in the diversion channel.
2. Physical Model Test and Numerical Simulation
2.1. Project Overview
This study takes a flood discharge gate station hub project as the research background; the design flow rate is about 22.5 m3/s. The primary function of urban drainage pumping stations is to manage emergency stormwater drainage in their respective jurisdictions. During the rainy season or flood season, when substantial precipitation is observed in a city, the urban drainage pumping station is activated. This ensures the effective removal of excess water, thereby safeguarding the well-being of the populace and the integrity of their possessions. During the non-flooding season, the drainage pumping station also undertakes certain ecological functions, such as accelerating the flow of water, improving the water environment, promoting the biodiversity of the water body, and improving the quality of urban water. The scope of the model test includes the upstream river channel, the sewage cleaning machine bridge, the slope, the front pool, and the intake pool. The pumping station adopts five sets of vertical submersible pumps, numbered as #1–#5, and the design flow rate of a single pump unit is 4.5 m3/s. This pumping station project is a medium-sized pumping station, and it has a lateral-inlet arrangement due to the constraints of the project site and the control regulations. Figure 2 shows a layout diagram of the lateral-inlet water pumping station within the engineering test simulation scope.
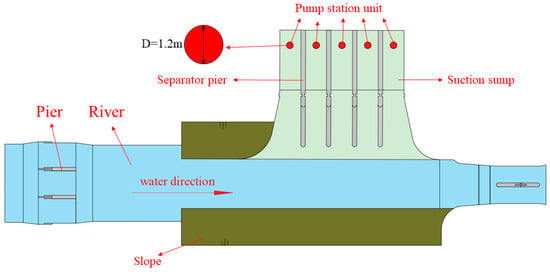
Figure 2.
Engineering plane diagram.
2.2. Physical Model
2.2.1. Similarity Criterion
In accordance with the parameters delineated in this study on the subject of pumping station engineering, it is imperative that similarity conditions and criteria are observed during model tests in order to ensure that the two flow systems, the model and the prototype, are sufficiently similar. In general, three basic conditions must be met to simulate water movement between the model and the prototype, namely, geometric similarity, kinematic similarity, and dynamic similarity.
The geometric similarity scale mainly includes the length scale, area scale, and volume scale, as shown in Equation (1). A summary of the physical meaning of the symbols utilised in this paper can be found in the Appendix A (Table A1).
respectively, represent the length, area, and volume. The subscripts respectively, represent the scale, prototype, and model.
The principle of kinematic similarity is shown in Equation (2).
respectively, represent the time and flow rate.
The principle of dynamic similarity is shown in Equation (3).
respectively, represent mass, water density, and gravity.
In order to simulate the pumping station operation process in and out of the pool and the river part of the water flow, the model water flow must be in the resistance square area, and the model must meet the requirements of the depth of water; the combination of the above factors implies the use of the geometric scale . The following values can be obtained via calculation:
Flow velocity similarity scale:
Flow quantity similarity scale:
Roughness similarity scale:
Bathymetric similarity scale:
In order to ensure that the roughness of each part of the model is similar to that of the prototype, it is necessary to use different modeling materials for different parts of the model. The prototype was made from reinforced concrete. PVC boards were chosen to make the river and tank parts of the model, and acrylic boards were used to make the forebay and inlet pool parts of the model. The roughness met the requirements of the test.
2.2.2. Model Layout
The physical model includes a flume, river, forebay, inlet pool, vortex elimination plate, electromagnetic flowmeter, and recirculation pump. The layout of the model is shown in Figure 3.
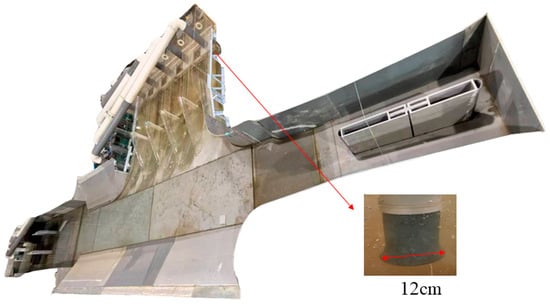
Figure 3.
Physical model layout.
The physical model is characterized by the utilization of an internal circulating water flow system, whereby pipes are employed to establish a connection between the outlet and the inlet. Foam plates are fitted to the model inlet tank to reduce turbulence in the water flow. In order to regulate and quantify the flow rate of each pump, a system of valves, electromagnetic flow meters, and circulating power pumps is employed. In order to meet the requirements of the test, it is necessary to form each pump in isolation, thereby creating a circulation system that is subject to individual control.
In order to ensure the credibility of the test data, this study adopts a wireless rotating paddle tachometer and its supporting automatic acquisition system (as shown in Figure 4) and a DPIV HD flow field measurement system to measure the flow velocity; the two are used to corroborate each other (as shown in Figure 5). This wireless rotating paddle tachometer is a photoelectric rotating paddle tachometer; the counter records the number of pulses N per unit time, which is converted into a flow velocity value by the counting circuit or microprocessor. The wireless rotating paddle flowmeter acquisition system is capable of synchronously measuring the flow velocity at 20 measurement points, achieving simultaneous multi-point flow measurement and reducing the influence of measurement errors. The relationship between the flow velocity signal and the pulse frequency is determined by a rate determination curve. The rate curve approximates a set of straight lines and can be expressed as the following linear equation:
where represents the flow rate (cm/s); represents the frequency of the flow rate signal (r/s); represents the slope of the calibration curve; and is a coefficient related to resistance (cm/s).

Figure 4.
Wireless rotating paddle flow meter.
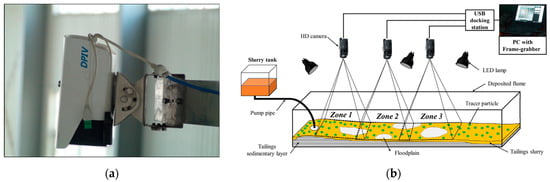
Figure 5.
The DPIV HD flow field measurement system: (a) high-definition webcam; (b) schematic diagram of the DPIV measurement principle.
The DPIV HD flow field measurement system is a large-area flow field measurement system based on particle image velocimetry technology. The system involves a 10 million pixel HD webcam connected to a computer through a wireless network, and it uses an advanced digital image processing algorithm combined with the basic theory of fluid dynamics to synchronously collect large-range and multi-channel flow field data with high measurement efficiency and accuracy.
The DPIV system utilized in this study diverges from the conventional PIV system in that it exclusively measures the surface flow field. Therefore, particles with a strong tracer and good reflectivity suspended on the surface of the flow field are selected for the purpose of simulating the movement of water flow. During the test, the particles are uniformly scattered into the flow field from the inlet. Instantaneous-exposure images are continuously captured with the aid of a high-definition camera in order to obtain the particle velocity and vector direction through the image processing system. In the context of six acquisitions, a time interval of 10 s is observed, with a correlation window set to 64 pixels and a correlation time of 100 ms. In order to guarantee the precision of the test results, a minimum of three to five measurements were obtained for each set of tests. The image of the area encompassed by the camera is presented in Figure 6.

Figure 6.
Image of the area covered by the camera: (a) camera 1; (b) camera 2.
2.3. Numerical Simulation
Due to the limitations of the site or test equipment, only the test data of fixed measurement points could be collected in the actual physical model test, and it was difficult to collect the flow velocity and other data of the model profile, so it was necessary to establish a numerical model to simulate the physical model so that they could complement and verify each other. The numerical model was not limited by the site and cost; it was easy to compare various correction measures to select the optimal scheme, and it was more convenient to collect the test data at any point of the model and verify the accuracy of the test data of the physical model.
2.3.1. Geometric Model
In this study, REVIT is used to construct a three-dimensional model of a lateral-inlet pumping station of a truncated-type river without a diversion channel, and the model structure is shown in Figure 7 [21].
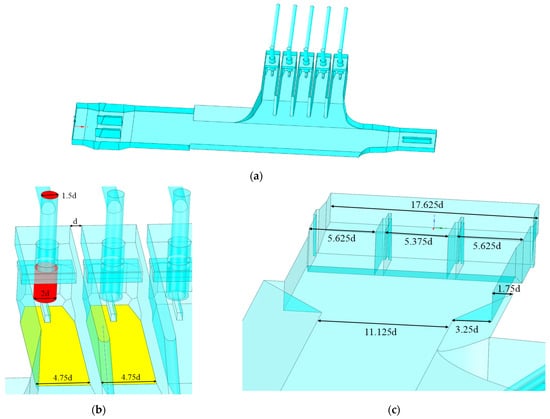
Figure 7.
Three-dimensional model of the numerical simulation: (a) overall model diagram; (b) partial detail diagram 1; (c) partial detail diagram 2.
The setting of boundary conditions must be determined after the model is built. In this study, we refer to the articles of Caishui [22] for the boundary condition setting. We set the inlet boundary for the velocity inlet boundary, the outlet boundary for the free outflow; in the division of the grid, these are coded as the inlet and outlet. The side and bottom of the model and the wall of the outlet pipe are set as non-slip fixed boundaries. The solver is set based on pressure, the velocity format is set to absolute velocity, and the time type is steady state. The viscous model was a realizable K-epsilon model, the wall function was a standard wall function (SWF), and the solution method was simpleC pressure–velocity coupling.
2.3.2. Governing Equations and Turbulent Flow Models
Considering that in actual simulations, the heat exchange of an incompressible fluid in a short period of time has a negligible effect on the modeled flow rate, while the 3D hydrodynamic model is principally governed by the mass continuity equation and the momentum equation.
The mass continuity equation is
The momentum equation is
In Equations (5) and (6), and are the velocity vectors in all directions; and represent each coordinate axis; is the density of the fluid; is time; is the static pressure of turbulent kinetic energy; is the effective viscosity coefficient of the fluid; and is the gravity component in the i direction.
Turbulence models are more difficult to simulate due to their three-dimensionality, instability, and other characteristics, so selecting a more appropriate turbulence model can reduce the error caused by a simulation [23]. The k-ε model is widely used in hydraulic models, especially in the simulation of flow regimes in pumping station forebays and inlet pools. This turbulence model is based on the concept of eddy viscosity and solves for the turbulent kinetic energy k, as well as turbulent eddy dissipation [24]. The Standard k-ε model is a more basic two-equation model that has the advantage of being more widely applicable. However, it can deviate significantly from reality when modeling complex flows [25]. In the Realizable k-ε model, the turbulent viscous coefficients are calculated using an improved methodology that enables the derivation of dissipation rate equations using the exact transport equations for the fluctuating component vorticity. Compared with the Standard k-ε model, the Realizable k-ε model derives a modified transport equation for the dissipation rate using the exact equation for the rise and fall of the mean square vorticity, which enables more accurate simulation of rotationally homogeneous shear flows, jets, mixed-layer free flows, channel and boundary–layer flows, and separated flows [26]. Additionally, a flow case with a high strain rate and significant streamline curvature is simulated with high accuracy by the Realizable k-ε model.
Different turbulence models have different areas of application, so a comprehensive approach is necessary when selecting an appropriate turbulence model to ensure the accuracy of the simulation. When selecting a turbulence model, factors such as calculation accuracy and the characteristics of the fluid being simulated should be considered. This paper presents a model test study that reveals a wide range of de-flow and backflow phenomena in the project’s forebay and inlet pool. The Realizable k-ε model is highly accurate in simulating such problems and has, therefore, been selected for use in this study. Equations (7) and (8) show the k and ε equations in the Realizable k-ε model.
where is the turbulent kinetic energy due to the mean velocity gradient; is the turbulent kinetic energy due to buoyancy; is the dissipation due to the pulsating expansion of the compressible velocity turbulence; and is the turbulence Prandtl number.
2.3.3. Grid Independence Analysis
In the process of numerical simulation, the quality of the mesh has a significant impact on the simulation results, so it is necessary to analyze the mesh for irrelevance and convergence. In general, the smaller the mesh size, the greater the potential for capturing more details of turbulent flows. As the difference between the numerical simulation solution and the real solution becomes smaller and smaller, it can be concluded that the numerical simulation solution has converged to meet the accuracy requirements. In this study, the absolute difference of the total hydraulic loss of the computational model is used to verify the independence of the grid, and the hydraulic loss when using different grid numbers in the original working conditions is used for comparison; the number of grids is reasonable when the value of the hydraulic loss tends to be stable [27]. The hydraulic loss is calculated using Equation (7).
where represents the total pressure at the inlet; represents the total pressure at the outlet; is the density of water; and is the acceleration of gravity. Surface integration is performed on the inlet and outlet sections. The total inlet and outlet pressures are then calculated using Fluent’s own module, and the hydraulic loss is calculated using Equation (9). The results are shown in Figure 8. It can be found that when the number of grids is greater than 5 million, the change in the hydraulic loss is not greater than 1%. At this time, it can be considered that the calculation results are not related to the grid. The algorithm used to delimit the mesh is the patch conformal method, which utilizes tetrahedra for meshing. For the test, a grid size of 0.2 m was selected, and the number of grids was 5,223,898. The grid division diagram is shown in Figure 9.
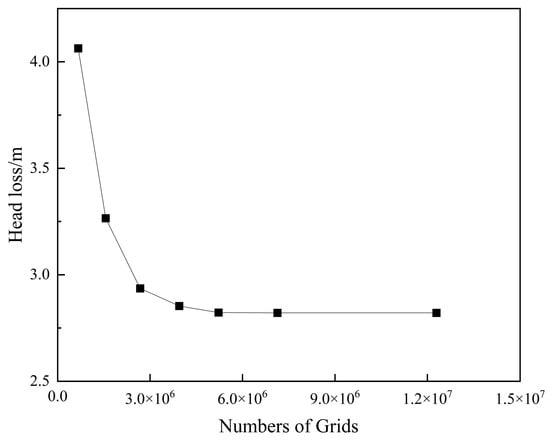
Figure 8.
Hydraulic loss diagram under different grid conditions.

Figure 9.
Grid division diagram.
2.3.4. Verification of the Numerical Simulation’s Reliability
In order to verify the reliability of the numerical simulation results, the test scheme with the original working conditions was selected for the numerical simulation to compare the results with the test results of the physical model. Using the DPIV measurement system to measure the surface flow velocity of the physical model and using tecplot for post-processing, a flow field cloud diagram is shown in Figure 10. This is basically consistent with the numerical model.
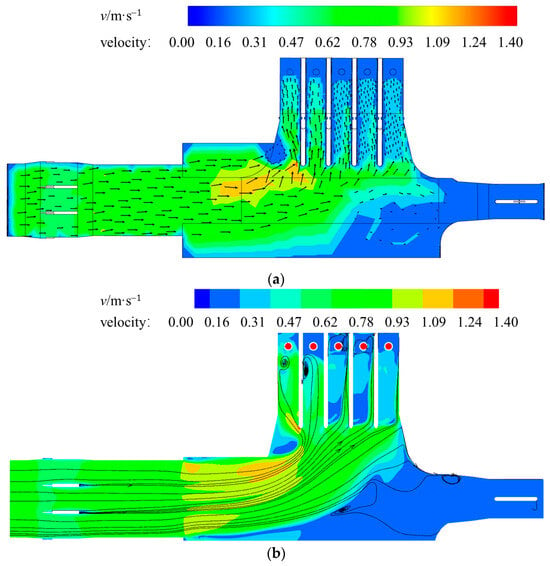
Figure 10.
Planar flow field cloud chart: (a) planar flow field cloud for the physical model test; (b) planar flow field cloud for the numerical simulation test.
The DPIV measurement system utilized in this study is capable of quantifying the extent of the surface flow field in terms of the area of decanting and refluxing with relative ease. However, it does not yield highly detailed data for comparison purposes when compared with numerical modeling. To further provide quantitative data support for the accuracy of numerical simulation data, a vertical cross-section in the inlet pool was selected to measure the average flow velocity in the physical model. A schematic representation of the selected section and vertical line of measurement is shown in Figure 11.
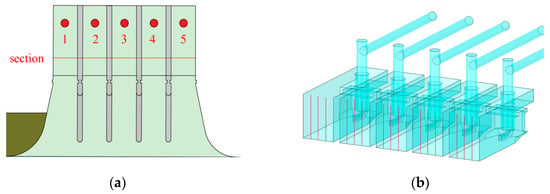
Figure 11.
Schematic representation of the selected section and vertical line of measurement: (a) plan view of the location of the section; (b) 3D figure of the vertical line of the measurement point.
Three measurement points were selected horizontally in the cross-section of each inlet pool, and the axial flow velocity at the measurement points was used as the discriminating index. The flow velocity at a depth of 20 cm from the surface of the water was designated as the surface flow velocity, the flow velocity at 0.6 times the depth of the water was selected as the middle flow velocity, and the flow velocity at a depth of 10 cm from the bottom was selected as the bottom flow velocity. The measurement of flow velocity was conducted at varying water depths at each measurement point using a wireless rotating paddle flow meter. In the numerical model, the same measurement points with the same cross-section in the same location, as in the physical model, were selected to compare the data differences, and it can be seen in Figure 12 that the numerical simulation data and the physical model test data basically match, i.e., the credibility of the data in this study is guaranteed.
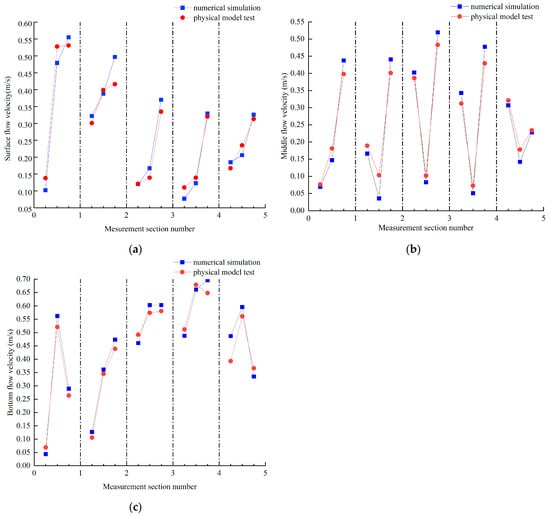
Figure 12.
Comparison of flow velocities at gauging points: (a) comparison of flow velocities at surface gauging points; (b) comparison of flow velocities at middle gauging points; (c) comparison of flow velocities at bottom gauging points.
As previously indicated for the river cross-section, as illustrated in the designated Figure 13, a total of five measurement points were selected for the purpose of data comparison.
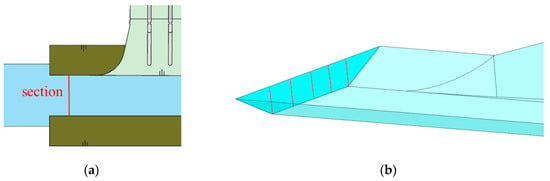
Figure 13.
Schematic representation of a selected section and vertical line of measurement: (a) plan view of the location of the section; (b) 3D figure of the vertical line of the measuring point.
The results of the comparison of the measured data are presented in Figure 14.
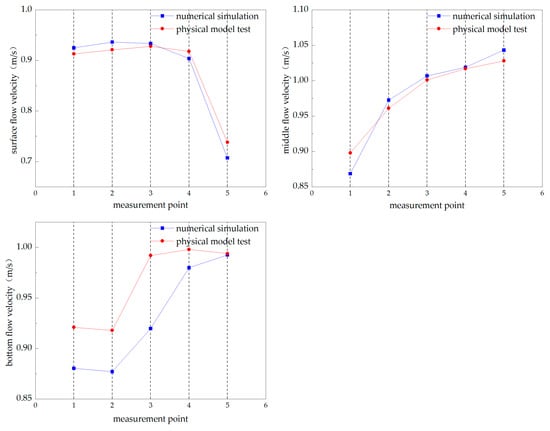
Figure 14.
Comparison of the measured data.
In order to quantitatively analyze and validate the reliability of the numerical simulations, the root mean square error was introduced to analyze the data.
In this study, represents the data obtained from the numerical simulation, and represents the data obtained from actual measurement. The intake pool cross-section is characterized by a total of 15 measurement points, with three distinct water depths. Consequently, the total number of measurements for the intake pool cross-section is 45. The river cross-section contains a total of five measurement points, each with three distinct water depths. Consequently, the total number of measurements for the river cross-section is 15. The RMES values for the intake pool cross-section and the river cross-section were calculated to be 0.0347 and 0.0274, indicating that they can be considered to have a high degree of fit.
3. Analysis and Discussion
3.1. Optimizing Program Design
In the physical model test, this study employed a mid-level flow field tracer fluid, as illustrated in Figure 15, to enable a more intuitive observation of the model flow regime. The model flow pattern is analyzed using numerical simulations, which are combined to propose optimization measures (as shown in Figure 10).
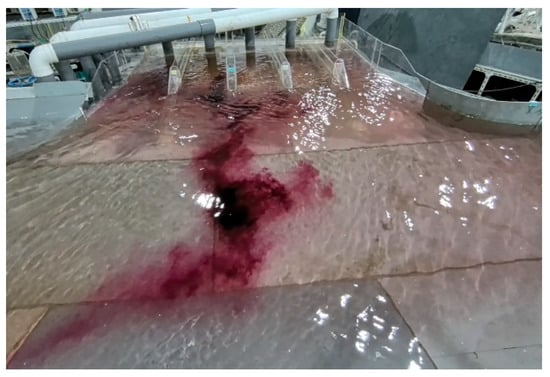
Figure 15.
Mid-level flow field tracer fluid.
Because the deflection angle in front of inlet pool No. 1 is too large to form a counterclockwise vortex, a wide range of backflow is formed in the truncated end of the river (as shown in Figure 16). The distribution of the flow velocity in each inlet pool is extremely uneven; the flow velocity in the fourth and fifth inlet pools is much smaller than that in the first and second inlet pools, and there is a small eddy distribution in each inlet pool with turbulent flow patterns. Usually, for similar lateral-inlet pumping stations, a common rectification program is the use of a curved guide pier or Y-shaped guide pier, but the physical model test showed that for the small pumping station in a city’s truncated-type channel used in this study, this type of rectification measure cannot solve the problem of uneven flow velocity in the inlet pool, and the phenomenon of water flow against the wall cannot be improved [28,29].
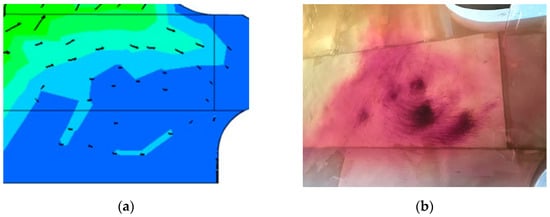
Figure 16.
Comparison of a large reflux in the forebay: (a) numerical modeling of large reflux ranges; (b) areas of reflux shown by tracer sand.
In this study, a new type of separating diagonal deflector wall is designed to solve the problem of the uneven distribution of the flow velocity in each inlet pool; the deflector wall and the horizontal axis have an angle of 5°, parallel to the flow line of the river, which allows the water to flow into the fifth inlet pool when the flow direction is smoother to reduce the reflux in inlet pool #5. The dividing pier between inlet pools #1 and #2 and the dividing pier between inlet pools #4 and #5 were each lengthened to connect to the deflector wall. This was to prevent the flow in each inlet pool from bypassing the separation piers and affecting the flow regime in the adjacent inlet pool. To solve the problem of large-area backflow in the river area (as shown in Figure 16), this study proposes placing a curved flow-guiding pier in the backflow area. This will increase the flow rate in intake pool #5, resulting in a more even distribution of flow rates across the various intake pools. The specific design and arrangement of the deflector walls and curved deflector pier are shown in Figure 17.
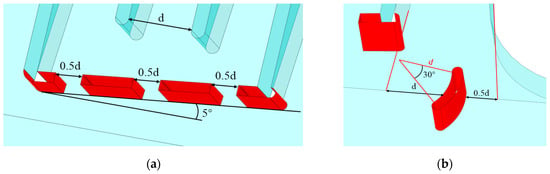
Figure 17.
Specific design and arrangement: (a) deflector walls; (b) curved deflector pier.
In order to solve the phenomenon of water flow close to the wall of the separation pier, in the horizontal section of each inlet pool, a fan-shaped flow-guiding pier was placed at the opening end (as shown in scheme 1 in Table 1). In the test of optimization scheme 1, it was found that the distribution of the flow velocity in the inlet pool was more uniform with the optimization of the separating guide wall, and the model flow pattern was optimized (as shown in Section 3.2.2 and Section 3.3). Further optimization was conducted on the basis of scheme 1, where all the separation piers were connected to the guide wall to reduce the lateral flow velocity in each inlet pool, and the arrangement of the guide piers was optimized (as shown under scheme 2 in Table 1).

Table 1.
Optimization measures of scheme 1 and scheme 2.
3.2. Hydraulic Characteristic Analysis
3.2.1. Original Scheme
As illustrated in the model surface flow field cloud in Figure 10, the lateral-inlet pumping station generates a counterclockwise vortex in front of inlet pool 1. This is due to the excessive angle of deflection of the water flow, which is sideways into the water. The water will initially flow through the mouth of inlet pool 2, where the lateral flow velocity is influenced by bypassing the separation pier. It will then enter inlet pool 1, forming a range of counterclockwise vortices with a smaller flow velocity in front of inlet pool 1. As illustrated by the cloud diagram, the surface flow velocity of each inlet pool is unevenly distributed, with the surface flow velocity of inlet pool 1 and inlet pool 2 significantly exceeding that of inlet pool 4 and inlet pool 5. This phenomenon can be attributed to the formation of a stagnant zone at the closed end of the truncated-type channel. This stagnant zone has the capacity to affect the flow velocity of inlet pool 4 and inlet pool 5 and to form a larger and slower reflux zone in proximity to the stagnant zone. In order to more intuitively analyze the flow pattern of the inlet pool, this study selects a longitudinal profile in the inlet pool for comparative observation, and the location of the profile is selected as shown in Figure 18.
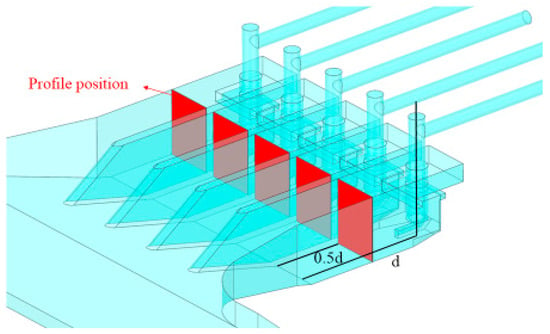
Figure 18.
Selection of the profile position.
Figure 19 provides a cloud diagram of the model’s sectional flow field. As is apparent in the figure, the inlet pool has a large area in the Y-axis direction with a flow velocity of 0, which represents the inlet pool in the lower and middle layers. This demonstrates the existence of a large range of backflow area and shows how the operation of the vertical submersible pumping machine causes adverse effects by reducing the efficiency of the pumping unit. Simultaneously, the second, third, fourth, and fifth inlet pools exhibit a phenomenon of paste wall water flow. This is attributable to the configuration of the pumping station, which is designed for lateral water intake. When the angle is excessively large, the water flow into the inlet pool is substantial, resulting in water flow close to the separation pier. The vertical submersible pumps in the pump are positioned above the installation height, which leads to the development of a large area of reflux.
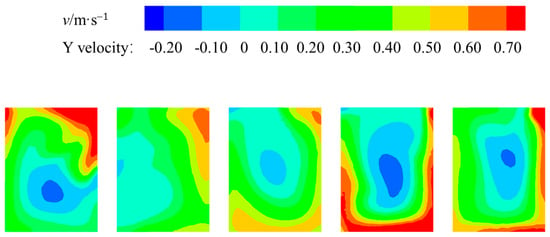
Figure 19.
Original scheme of the cloud diagram of the model sectional flow field.
3.2.2. Optimization Scheme 1
As demonstrated in Figure 20 by the cloud diagram of the model profile flow field of optimization scheme 1, the optimization of scheme 1 resulted in a substantial enhancement of the model flow state. The reflux area of each inlet pool is reduced, and the flow velocity distribution is more balanced. It is determined that the first and fifth inlet pools, which constitute a substantial segment of the reflux area, have been eradicated. However, the presence of a minor reflux area in the separation pier indicates that the curvature of the diversion pier is excessive. Consequently, it is necessary to optimize the geometric design. In comparison with the original conditions, the return area is reduced by more than 50%. The flow of water is concentrated in the middle of the water depth, which is higher than the installation height of the pump. This time, the adverse flow has less of an impact on the efficiency of the pumping unit.
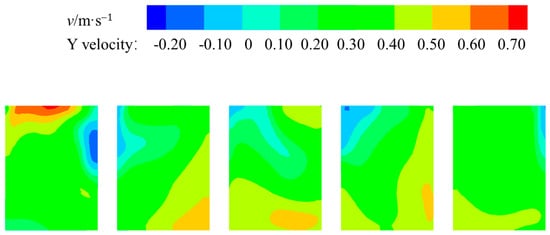
Figure 20.
Cloud diagram of the model sectional flow field with scheme 1.
3.2.3. Optimization Scheme 2
Figure 21 depicts a cloud diagram of the model profile flow field with optimization scheme 2, which is based on scheme 1 in order to optimize the geometric design of the guide pier. As demonstrated by the figure, subsequent to the optimization of scheme 2, the model of the upper flow is significantly enhanced in comparison with scheme 1. The water in the inlet pool is rendered more stable, and the pump unit exhibits minimal effect on the upper surface of the water in the vicinity of the side wall or separation pier, within a confined range of reflux area. Simultaneously, the axial flow velocity distribution of the inlet pool is found to be more uniform. The flow rate of the vertical axial pump is influenced by the model from the surface to the bottom of the uniform expansion, resulting in a more stable flow pattern and reduced hydraulic loss.
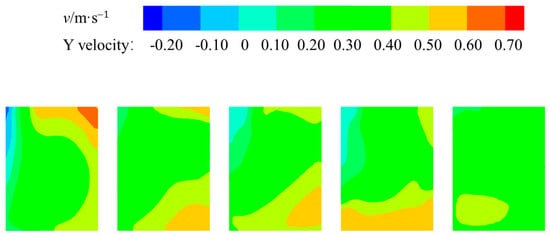
Figure 21.
Cloud diagram of the model sectional flow field with scheme 2.
3.3. Quantitative Evaluation of the Optimization Effect
3.3.1. Transverse Velocity Distribution Ratio
In the course of the study of the hydraulic characteristics of the inlet pool of the lateral pumping station, due consideration should be provided to the lateral flow velocity in the inlet pool. It is evident that an increase in the lateral velocity will result in an increase in the lateral bias flow, which, in turn, will cause a larger hydraulic loss. The objective of this study is to facilitate a comparison between the original working condition model and the optimization model. In order to achieve this, the same position cross-section is compared, with the flow velocity distribution ratio S being used for the purpose of evaluation. The calculation of the flow velocity distribution ratio S is achieved through the following formula:
, , and represent the flow velocity in the , , and directions, respectively. In this study, 100 points were selected from the upper profile of each inlet pool (Figure 18) in the middle water depth (0.6 times the water depth) on average, and their lateral flow velocities were extracted (as shown in Figure 22).
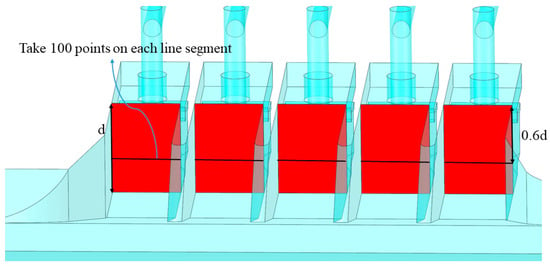
Figure 22.
Selection of the locations of the flow points.
The total flow velocity was subsequently calculated, and the average lateral flow velocity distribution ratio of each inlet pool was determined. As illustrated in Figure 23, the distribution of the lateral flow velocity for the various schemes is presented.
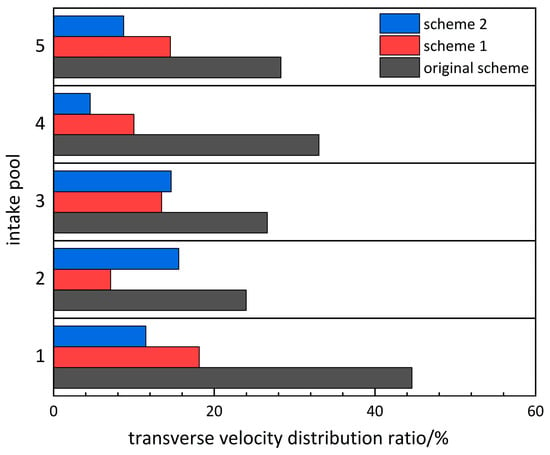
Figure 23.
Transverse velocity distribution ratio.
As demonstrated by the figure, it can be observed that the lateral flow velocity of each inlet pool is reduced after optimization. The lateral flow velocity distribution ratio is observed to be the largest at inlet pools #2 and #5. Through the optimization of the two pools, a comparison is made with the best results, and it is evident that the lateral flow velocity is reduced by more than 50%, signifying that the guide wall and curved guide pier play pivotal roles in optimizing the flow pattern. It is imperative to ensure a more uniform flow of water into the intake basin. The lateral flow velocity distribution ratios of the original working condition of the model, scheme 1, and scheme 2 in the combined calculation are 31.302%, 12.644%, and 10.997%, respectively. It can be concluded that the horizontal flow velocity distribution ratio is smaller under scheme 2, leading to reduced hydraulic losses. This finding suggests that the optimization of the fan-shaped flow deflector piers in scheme 2 generally result in a positive enhancement of the flow regime in the inlet pools in comparison with scheme 1. The increase in the lateral flow velocity distribution ratio for scheme 2 in comparison with scheme 1 in intake pools #3 and #4 suggests that the optimization of the fan-shaped guide piers exerts a detrimental effect on intake pools #3 and #4.
3.3.2. Axial Velocity Weighted Average Angle and Axial Velocity Uniformity
In this study, the axial velocity weighted average angle and axial velocity uniformity are utilized to evaluate the uniformity of the flow rate distribution in the selected cross-section. The magnitude of flow uniformity is directly proportional to the uniform distribution of flow velocity across the cross-section. A uniformly distributed flow rate can ensure a smoother water inlet experience for the pumping unit, thereby reducing hydraulic losses and enhancing the unit’s operational efficiency. The magnitude of flow uniformity is directly proportional to the uniform distribution of flow velocity across the cross-section. The following formula [30] is employed to calculate this magnitude:
is the uniformity of the axial velocity distribution; is the axial velocity at each characteristic point of the flow (m/s); is the number of nodes; and is the average axial velocity of each sectional unit (m/s). The mean angle of axial flow is defined as the angle between the direction of axial flow and the selected profile. It has been established that values closer to 90° correspond to a smoother axial velocity. The following formula [30] can be utilized to calculate its value:
In this study, 1000 points in the cross-section (Figure 22) at 0.6 times the depth of water were selected for the purpose of calculating and analyzing the axial flow uniformity and the weighted average angle of axial flow in the inlet pool under the different schemes. Due to the reflux of a substantial scale and extensive area in the inlet pool in the original condition, the flow uniformity in the original condition is calculated to be 17.50%, and the weighted average angle is 77.17°. In the optimized scheme, the flow uniformity is increased by 45.03%, and the weighted average angle is increased by 5.52°. These changes result in a more stable water flow and a more even distribution of flow velocity. The axial flow uniformity is shown to be further enhanced under optimization scheme 2 when compared with scheme 1. An improvement of 7.21% is observed in this regard. However, the flow-weighted average angle does not appear to be significantly improved. Table 2 illustrates the relevant data.

Table 2.
The axial velocity uniformity and axial velocity weighted average angle.
3.4. Optimal Scheme Determination
The experimental study and subsequent data analysis conducted in this study have led to the conclusion that scheme 2 is the most effective optimization scheme. In order to verify and compare the optimization effect of each scheme in more detail, the cross-sectional flow pattern of the suction port of the pumping unit in schemes 1 and 2 is now compared with the original scheme, as shown in Figure 24.
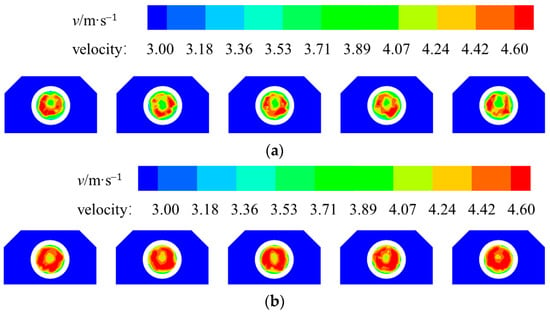
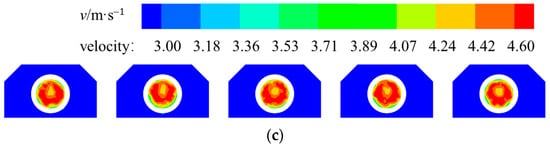
Figure 24.
Cross-sectional flow velocity cloud at the inhalation inlet: (a) flow pattern with the original scheme; (b) flow pattern with scheme 1; (c) flow pattern with scheme 2.
As illustrated in Figure 24, under the original conditions, the distribution of flow velocity within the pump unit’s suction port section exhibits significant unevenness. As can be seen in Figure 25, the region of high flow velocity is mainly distributed between 0.3r and 0.8r. This is particularly evident in the proximity to the side wall, where the flow velocity is notably diminished. Consequently, the inlet flow state is found to be deficient.
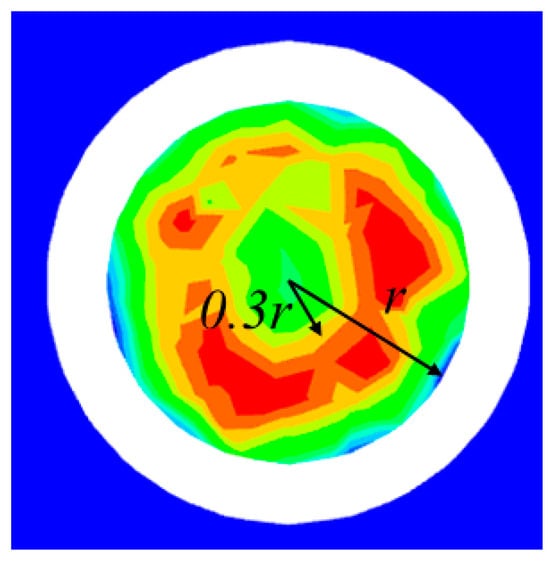
Figure 25.
Distribution of flow velocity at the pump port section in original condition.
In optimization scheme 1, the flow pattern of the pump inlet section is effectively improved, the flow velocity distribution of the section is more uniform, and the area of low flow velocity at the side wall and the center of the section is reduced. In optimization scheme 2, the flow pattern of the section is further optimized, and the area of low flow velocity at the side wall is reduced, which has no effect on the normal operation of the pump unit. The flow velocity within the designated section is found to be uniformly distributed, with a range from 4.2 m/s to 4.6 m/s. A comparison with the flow velocity distribution of the original scheme also reveals that, after optimization, the improved flow pattern results in reduced hydraulic losses in the model and increased average flow velocity in the diameter of the pumping unit. The flow rates for the original condition and optimized scenarios 1 and 2 were derived by surface-integrating the five pump suction port sections using the Fluent calculation module, resulting in values of 21.218 m3/s, 22.209 m3/s, and 22.223 m3/s, respectively. This also proves the validity of the optimized solution and the superiority of optimized solution 2 over optimized solution 1.
In order to quantitatively analyze the uniformity of the flow velocity distribution in the cross-section, this study takes 100 measurement points from the suction inlet cross-section of each pumping unit and judges the uniformity of the flow velocity distribution in the suction inlet of pumping units with the different schemes by calculating the mean square error of the flow velocities. The mean square error can be calculated using Equation (10).
is the mean square error; is the number of measurement points; is the velocity of the measurement points; and is the theoretical average velocity. can be calculated using Equation (11).
The mean square error value of 2.047 for the original condition indicates that the uniformity of the flow velocity distribution is poor in each inhalation port section. The mean square error of optimization scheme 1 is 1.595, which indicates that the flow velocity distribution is more uniform with the optimization of scheme 1. The of scheme 2 is 1.426, which is smaller than the values of optimization scheme 1 and the original condition. This finding suggests that the cross-sectional flow velocity distribution is the most uniform and that optimization is the most effective for scheme 2.
3.5. Response Surface Methodology to Optimize Parameter Design
The flow regime in the model inlet pool is effectively improved with the optimization of scheme 2. In order to further optimize the flow regime, the spacing of the deflector walls is quantitatively analyzed. In this section, the effect of the spacings L1, L2, and L3 of the separated guide walls on the flow regime of the flow field is investigated using the response surface method based on scheme 2. The Box–Behnken method is utilized for the experimental design. Prior to this, the range of values for each spacing must be determined. This is achieved through numerical and physical model tests. The range of values for each spacing is as follows: L1 (160 cm–180 cm); L2 (160 cm–180 cm); and L3 (180 cm–200 cm). The flow uniformity is utilized to quantitatively characterize the rectification effect at varying spacing values, and the range of flow vector points is selected as outlined in Section 3.3.2. Table 3 displays the simulation results.

Table 3.
Results of the numerical calculations for each scheme.
Subsequent to the completion of the calculation, the results are analyzed, and polynomial regression equations of axial flow uniformity and the length of each interval of the compartmentalized deflector wall are established using the Design-Expert13 software. In this study, the second-order equation is selected for fitting, and the corresponding surface regression equation is shown in Equation (12).
The regression equation was analyzed using the analysis of variance (ANOVA) method, and the results are displayed in Table 4. The p-value is a measure of the significance of the model, and it enables the validity of the results to be tested. In the context of statistical analysis, the model’s p-value is a crucial metric that indicates the significance of the model’s results. When the p-value is less than 0.05, it is indicative of a significant model. The surface model p-value, as indicated in the table, is 0.0004 less than 0.05, which is less than the critical value of 0.05. This indicates that the model is significant and of high quality. The model’s predicted R2 value is 0.801, and its adjusted R2 value is 0.9601. The difference between these values is less than 0.2, indicating a high degree of consistency.

Table 4.
Analysis of variance in the response surface regression equation.
The effect of the change in the length of the separated guide wall interval on the flow velocity uniformity is analyzed, taking L1 and L2 as an example, and its interaction with the flow velocity uniformity is shown in Figure 26. It is evident that the flow uniformity exhibits an increase followed by a decrease in conjunction with the rise in L1 and L2. The rate of increase associated with L1 is marginally higher than that observed for L2. The optimal parameters for the spacing of the dividing deflector wall can be determined through iterative calculations, yielding . The predicted value of the uniformity of flow velocity under this configuration is = 71.795%. In order to ascertain the validity of this scenario, a numerical simulation was conducted. The resultant simulated value was found to be = 71.97%, with an error margin of less than 1% when compared with the predicted value. It can, therefore, be concluded that the simulation satisfies the accuracy requirement. The response surface method was utilized to ascertain the optimal parameters for each spacing of the separated deflector wall, and it was established that the flow uniformity was enhanced by 2.23% in comparison with scheme 2. Furthermore, the flow pattern was refined.
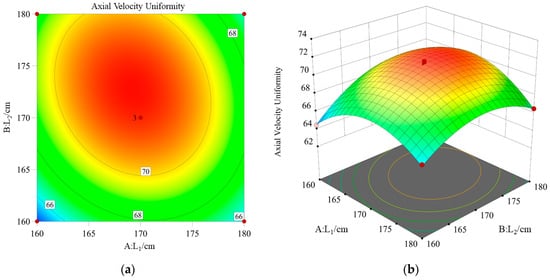
Figure 26.
The effect of guide wall spacing on axial flow uniformity: (a) response surface; (b) response contour cloud map.
4. Conclusions
The optimization of the flow pattern in the inlet pool of a pumping station has been demonstrated to reduce head loss, thereby enhancing the operational efficiency of the pumping unit. This, in turn, has been shown to reduce losses, leading to a reduction in the operating cost of the pumping station. This study employs a dual-pronged approach integrating physical model tests and numerical model tests. The former is utilized to validate the reliability of the latter. In this study, a series of optimization measures composed of different optimization schemes are proposed for a lateral-inlet pumping station in a truncated-type river in an inlet pool with a bad flow state. The flow field cloud diagram, lateral flow velocity distribution ratio, axial flow velocity uniformity, axial flow velocity weighted average angle, and flow velocity mean square error in the suction port section of the pumping machine under different schemes are obtained through numerical modeling calculations. Through comparison of the advantages and disadvantages of each scheme, the final optimization scheme is confirmed. The response surface method is then used to further optimize the final scheme. The following conclusions can be drawn.
- In the absence of optimization measures for the original conditions, the pumping station inlet pool is subject to undesirable flow conditions, including bias flow and return flow. Furthermore, the flow velocity distribution is characterized by significant unevenness. This will increase the head loss, affect the pumping unit’s intake efficiency, reduce the efficiency of the pumping station, and shorten the working life of the pumping unit.
- Scheme 1 and scheme 2 have been shown to be effective in improving the flow pattern in the inlet pool of the pumping station. However, it is optimized scheme 2 that has been demonstrated to have a superior rectification effect. The lateral flow velocity distribution ratio of the pumping station under scheme 2 is reduced by 20.305%, the axial flow uniformity is improved by 52.24%, the weighted mean axial flow angle is improved by 5.92°, and the mean square error MSE is reduced by 0.621. This indicates that the rectification effect of scheme 2 is superior to that of scheme 1. In this study, the response surface method is employed to ascertain the optimal distribution of the separation distance of the separation pier under the optimized scheme 2. The flow uniformity is enhanced by 2.23% in comparison with scheme 2, and the inlet pool exhibits a superior rectification effect. The flow uniformity is enhanced by 2.23% in comparison with scheme 2, and the flow pattern in the inlet pool is further optimized.
- This study puts forward a series of evaluation indices that are of great significance for the qualitative and quantitative analysis of flow patterns in hydraulic tests. It is evident that, in flow analysis, the pumping station inlet pool and the front pool play a significant role in guiding the selection of different optimization schemes. A comparison between these selection schemes provides a substantial amount of powerful data support. The design stage of pumping stations is often constrained by limitations relating to the available urban land, as well as numerous environmental factors. This study proposes a novel guide wall and guide pier amalgamation rectification strategy. In a lateral-intake pumping station inlet pool in a truncated-type river, the rectification effect is enhanced by poor flow patterns. The rectification of similar pumping stations with a small forebay or no forebay provides a certain degree of guidance.
- This study is founded upon a project simulation. The rectification scheme that has been proposed has geometric parameters designed for special characteristics, and it is necessary for these to be combined with the geometric parameters of a pumping station in similar cases. The same is true for the flow rate or flow direction in the corresponding empirical formulas. Subsequent studies could examine the interactions between various optimization features, such as the angle between the deflector wall and the main flow line, the curvature of the fan-shaped deflector piers, and the direction of the interval segments of the separating deflector wall.
Author Contributions
Conceptualization, R.J. and B.X.; methodology, R.J. and B.X.; software, R.J.; validation, R.J., Y.L., and Z.S.; formal analysis, R.J.; investigation, R.J.; resources, R.J.; data curation, R.J.; writing—original draft preparation, R.J.; writing—review and editing, R.J.; visualization, R.J.; supervision, B.X.; project administration, R.J.; funding acquisition, B.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant no. 51541912), Postgraduate Research and Practice Innovation Program of Jiangsu Province (grant no. KYCX24_3762).
Data Availability Statement
The article above contains all of the data that can be disclosed. The disclosure of more detailed data is prohibited by the terms and conditions of privacy agreements.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Table A1 offers a concise synopsis of the physical significance and units of the symbols that are present in the article.

Table A1.
Description of main symbols.
Table A1.
Description of main symbols.
| Symbol | Physical Meaning | Unit |
|---|---|---|
| length | m | |
| area | m2 | |
| volume | m3 | |
| scale | / | |
| prototype | / | |
| model | / | |
| time | s | |
| flow rate | m3/s | |
| gravity | N | |
| water density | Kg/m3 | |
| mass | Kg | |
| similarity scale | / | |
| roughness | / | |
| flow rate | cm/s | |
| flow rate signal frequency | r/s | |
| curve slope | / | |
| coefficient | cm/s | |
| velocity vector | / | |
| coordinate axis | / | |
| static pressure | pa | |
| effective viscosity coefficient | / | |
| gravity component | / | |
| , | turbulent kinetic energy | / |
| dissipation | / | |
| turbulence Prandtl number | / | |
| gravity | N/Kg | |
| hydraulic loss | m | |
| mean square error | / | |
| velocity | m/s | |
| uniformity | / | |
| axial velocity | m/s | |
| angle of axial flow | ° | |
| root mean square error | / |
References
- Nasr, A.; Yang, F.; Zhang, Y.Q.; Wang, T.L.; Hassan, M. Analysis of the Flow Pattern and Flow Rectification Measures of the Side-Intake Forebay in a Multi-Unit Pumping Station. Water 2021, 13, 2025. [Google Scholar] [CrossRef]
- Xi, W.; Lu, W.G.; Wang, C.; Liu, J.F. Analysis of Pumping Station Inlet Characteristics Based on Vorticity. Int. J. Simul. Model. 2022, 21, 453–464. [Google Scholar] [CrossRef]
- Alvez, A.; Espinosa, P.; Castillo, R.; Iglesias, K.; Bañales-Seguel, C. An Urgent Dialogue between Urban Design and Regulatory Framework for Urban Rivers: The Case of the Andalien River in Chile. Water 2022, 14, 3444. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, H.; Zhang, X.; Han, L.; Wang, R.; Wen, Q.; Ding, L. Numerical Simulation of the Impact of Unit Commitment Optimization and Divergence Angle on the Flow Pattern of Forebay. Int. J. Heat Technol. 2015, 33, 91–96. [Google Scholar] [CrossRef]
- Song, W.; Pang, Y.; Shi, X.; Xu, Q. Study on the Rectification of Forebay in Pumping Station. Math. Probl. Eng. 2018, 2018, 1–16. [Google Scholar] [CrossRef]
- Tsai, Y.S.; Chang, Y.M.; Chang, Y.J.; Chen, Y.M. Phase-Resolved Piv Measurements of the Flow between a Pair of Corotating Disks in a Cylindrical Enclosure. J. Fluids Struct. 2007, 23, 191–206. [Google Scholar] [CrossRef]
- Chen, T.D. An Affine-Model-Based Technique for Fast Dpiv Computation. Image Vis. Comput. 2006, 24, 407–410. [Google Scholar]
- Wijesooriya, K.; Mohotti, D.; Lee, C.K.; Mendis, P. A Technical Review of Computational Fluid Dynamics (Cfd) Applications on Wind Design of Tall Buildings and Structures: Past, Present and Future. J. Build. Eng. 2023, 74, 106828. [Google Scholar] [CrossRef]
- Blocken, B. Computational Fluid Dynamics for Urban Physics: Importance, Scales, Possibilities, Limitations and Ten Tips and Tricks Towards Accurate and Reliable Simulations. Build. Environ. 2015, 91, 219–245. [Google Scholar] [CrossRef]
- Al-Obaidi, A.R. Evaluation and Investigation of Hydraulic Performance Characteristics in an Axial Pump Based on Cfd and Acoustic Analysis. Processes 2024, 12, 129. [Google Scholar] [CrossRef]
- Choi, J.-W.; Choi, Y.-D.; Kim, C.-G.; Lee, Y.-H. Flow Uniformity in a Multi-Intake Pump Sump Model. J. Mech. Sci. Technol. 2010, 24, 1389–1400. [Google Scholar] [CrossRef]
- Dimas Athanassios, A.; Andreas, P.V. Effect of Cross-Flow Velocity at Forebay on Swirl in Pump Suction Pipe: Hydraulic Model of Seawater Intake at Aliveri Power Plant in Greece. J. Hydraul. Eng. 2012, 138, 812–816. [Google Scholar] [CrossRef]
- Rajendran, V.P.; Constantinescu, S.G.; Patel, V.C. Experimental Validation of Numerical Model of Flow in Pump-Intake Bays. J. Hydraul. Eng.-ASCE 1999, 125, 1119–1125. [Google Scholar] [CrossRef]
- Zhang, C.; Yan, H.; Jamil, M.T.; Yu, Y. Improvement of the Flow Pattern of a Forebay with a Side-Intake Pumping Station by Diversion Piers Based on Orthogonal Test Method. Water 2022, 14, 2663. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, Y.; Liu, C.; Wang, T.; Jiang, D.; Jin, Y. Numerical and Experimental Investigations of Flow Pattern and Anti-Vortex Measures of Forebay in a Multi-Unit Pumping Station. Water 2021, 13, 935. [Google Scholar] [CrossRef]
- Li, J.; Zhou, J.; Xu, H.; Feng, J.; Tong, H.; Chen, Y.; Qian, S. Undesired Flows in Lateral-Intake Multiple Forebays and Their Hydraulic Implications: Case Study for Asia’s Largest Urban Water Supply Pumping Station. Eng. Appl. Comput. Fluid Mech. 2024, 18, 2380304. [Google Scholar] [CrossRef]
- Wang, H.D.; Xu, D.; Ding, C.F.; Ran, Q.H.; Yuan, S.Y.; Tang, H.W. Numerical and Experimental Study on Water-Sediment Flow in a Lateral Pumping Station Forebay. Phys. Fluids 2024, 36, 095162. [Google Scholar] [CrossRef]
- Qiao, Q.; Wang, H.D.; Huang, L.X.; Jing, H.F.; Wang, B.Y. Impact of Inlet Flow Velocity on Sediment Reduction in Pump Station Forebays. Phys. Fluids 2024, 36, 115183. [Google Scholar] [CrossRef]
- Luo, C.; Zhang, L.; Wang, T.L.; Liu, H.; Cheng, L.; Lu, M.Z.; Jiao, W.X. Vortex Energy Behaviors in the Forebay of Lateral Pumping Station for Y-Type Channel. Phys. Fluids 2024, 36, 075162. [Google Scholar] [CrossRef]
- Olszewski, P. Genetic Optimization and Experimental Verification of Complex Parallel Pumping Station with Centrifugal Pumps. Appl. Energy 2016, 178, 527–539. [Google Scholar] [CrossRef]
- Banaszek, A.; Losiewicz, Z.; Jurczak, W. Corrosion Influence on Safety of Hydraulic Pipelines Installed on Decks of Contemporary Product and Chemical Tankers. Pol. Marit. Res. 2018, 25, 71–77. [Google Scholar] [CrossRef]
- Caishui, H.O.U. Three-Dimensional Numerical Analysis of Flow Pattern in Pressure Forebay of Hydropower Station. Procedia Eng. 2012, 28, 128–135. [Google Scholar] [CrossRef]
- Shaheed, R.; Mohammadian, A.; Gildeh, H.K. A Comparison of Standard K–Ε and Realizable K–Ε Turbulence Models in Curved and Confluent Channels. Environ. Fluid Mech. 2019, 19, 543–568. [Google Scholar] [CrossRef]
- Wang, H.D.; Li, C.G.; Lu, S.J.; Yang, C.; Huang, L.X. Numerical and Experimental Study on Vortex Optimization in the Forebay of a Sandy River. Phys. Fluids 2023, 35, 085128. [Google Scholar] [CrossRef]
- Liu, J.Y.; Heidarinejad, M.; Pitchurov, G.; Zhang, L.H.; Srebric, J. An Extensive Comparison of Modified Zero-Equation, Standard K-Ε, and Les Models in Predicting Urban Airflow. Sustain. Cities Soc. 2018, 40, 28–43. [Google Scholar] [CrossRef]
- Lateb, M.; Masson, C.; Stathopoulos, T.; Bédard, C. Comparison of Various Types of K-Ε Models for Pollutant Emissions around a Two-Building Configuration. J. Wind Eng. Ind. Aerodyn. 2013, 115, 9–21. [Google Scholar] [CrossRef]
- Zhan, J.-M.; Wang, B.-C.; Yu, L.-H.; Li, Y.-S.; Tang, L. Numerical Investigation of Flow Patterns in Different Pump Intake Systems. J. Hydrodyn. 2012, 24, 873–882. [Google Scholar] [CrossRef]
- Xu, B.; Liu, J.F.; Lu, W.G. Optimization Design of Y-Shaped Settling Diversion Wall Based on Orthogonal Test. Machines 2022, 10, 91. [Google Scholar] [CrossRef]
- Zhou, J.R.; Zhao, M.M.; Wang, C.; Gao, Z.J. Optimal Design of Diversion Piers of Lateral Intake Pumping Station Based on Orthogonal Test. Shock Vib. 2021, 2021, 6616456. [Google Scholar] [CrossRef]
- Chen, Y.-X.; Xi, B.; Chen, Z.; Shen, S. Study on the Hydraulic Characteristics of an Eccentric Tapering Outlet Pressure Box Culvert in a Pumping Station. Processes 2023, 11, 1598. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).