Application of LSTM and Climate Index for Prediction of Meteorological Drought in South Korea
Abstract
1. Introduction
2. Materials and Methods
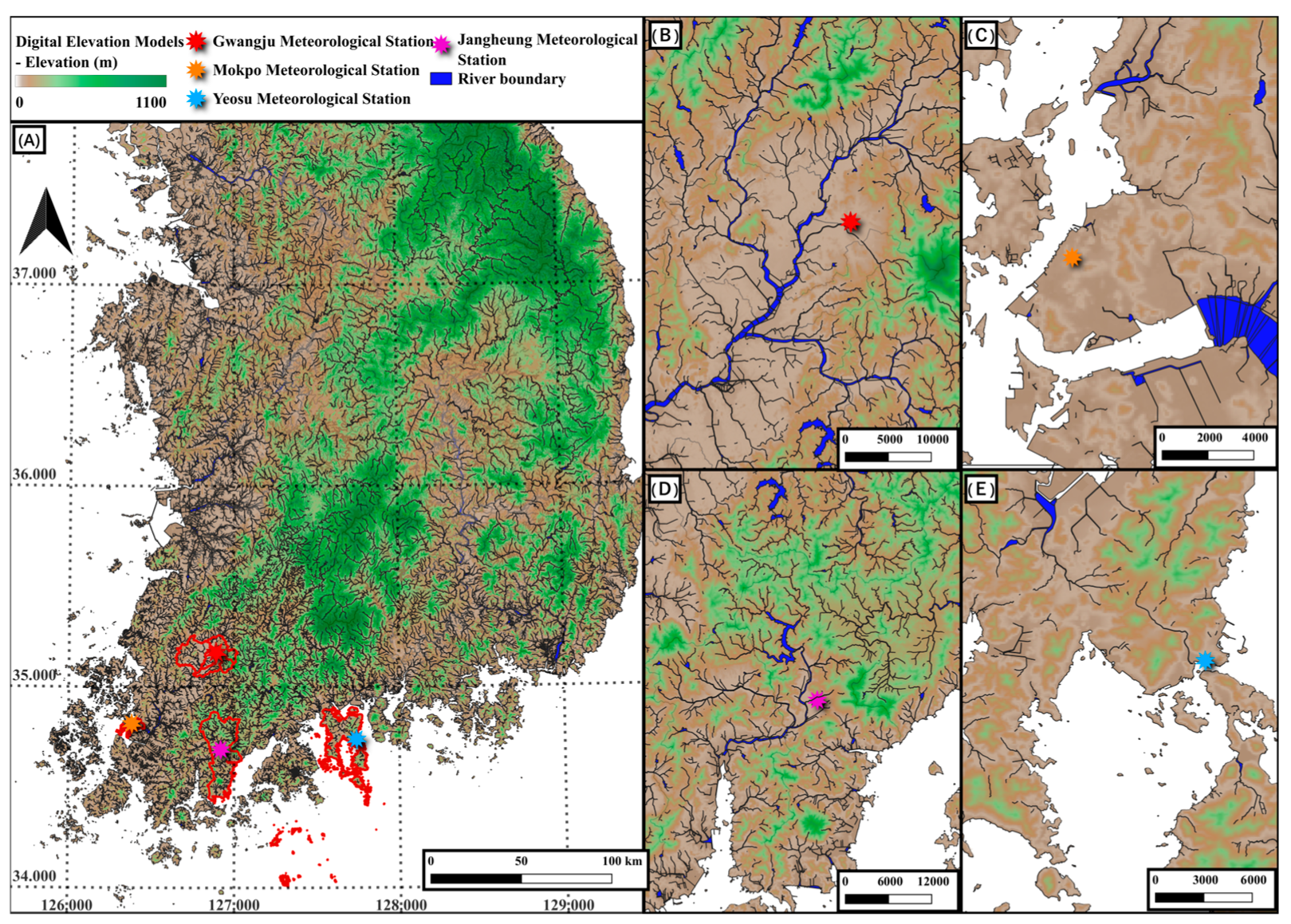
2.1. Study Area Information
2.2. Datasets
2.2.1. Data Information
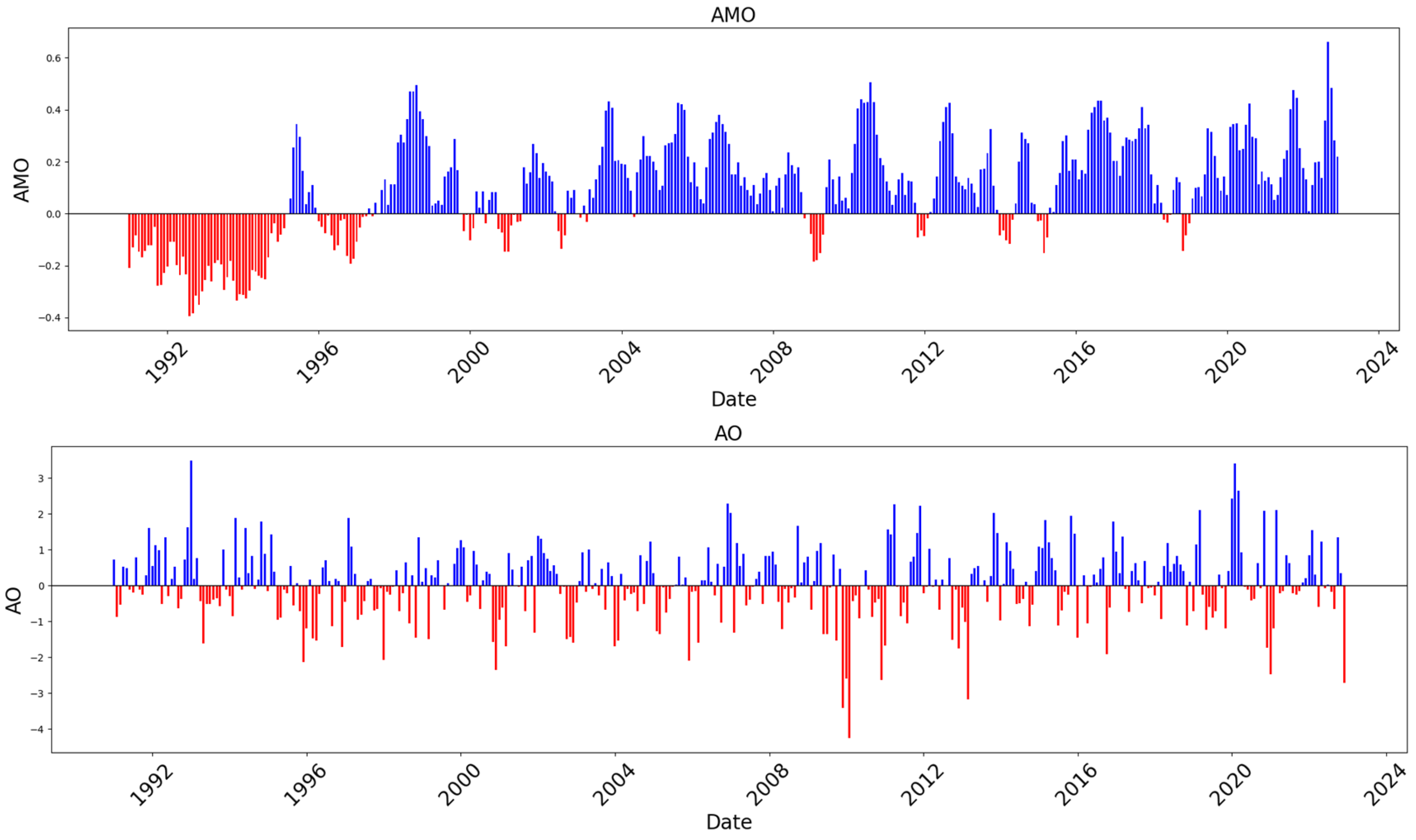
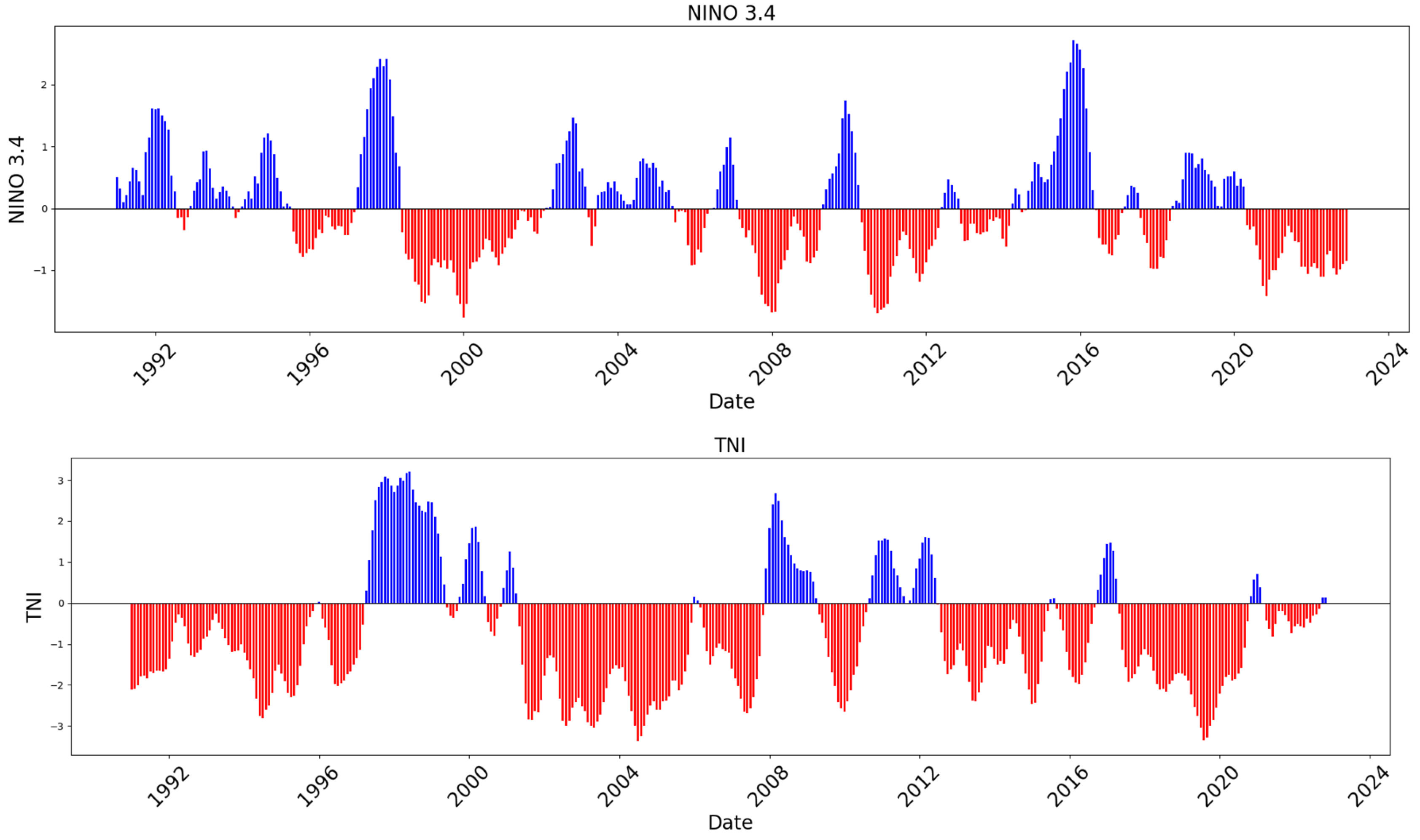
2.2.2. Climate Index
2.3. LSTM Algorithm
Evaluation Metrics
3. Results and Discussions
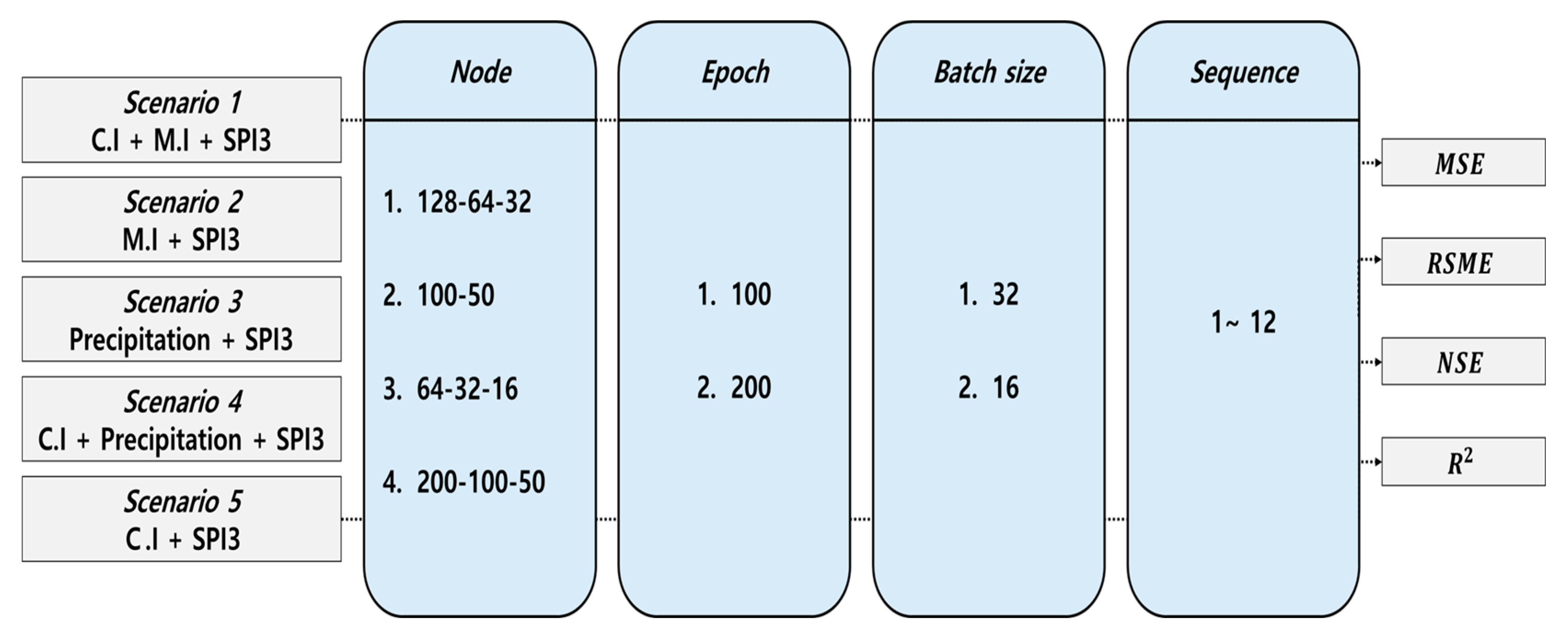
3.1. Algorithm Optimization
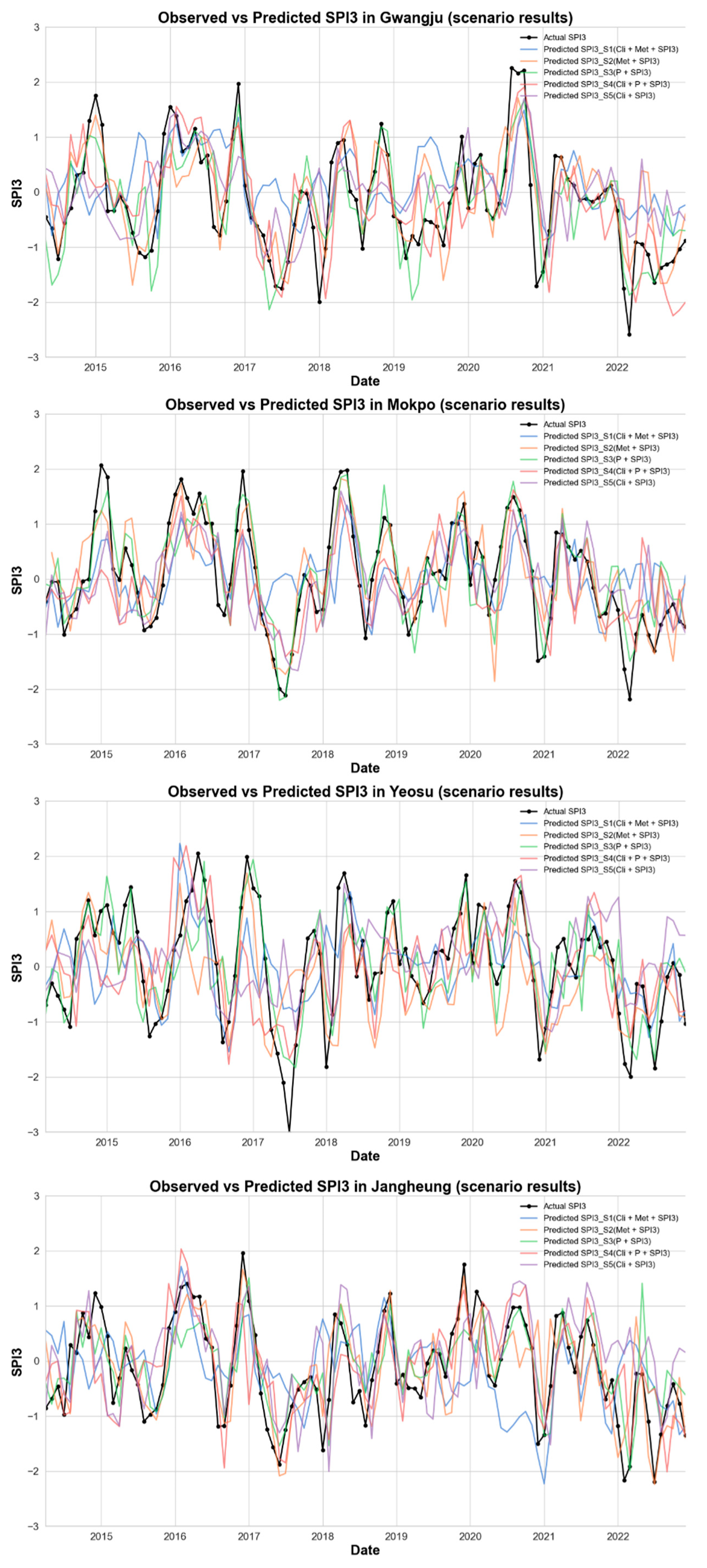
3.2. Drought Index Prediction
3.3. Prediction Results of Seasonal Variability of SPI
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zittis, G.; Hadjinicolaou, P.; Lelieveld, J. Role of soil moisture in the amplification of climate warming in the eastern Mediterranean and the Middle East. Clim. Res. 2014, 59, 27–37. [Google Scholar] [CrossRef]
- Samuel, A.L. Some studies in machine learning using the game of checkers. IBM J. Res. Dev. 1959, 3, 210–229. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biol. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Langley, P.; Iba, W.; Thompson, K. An analysis of Bayesian classifiers. In Proceedings of the AAAI’92: Proceedings of the Tenth National Conference on Artificial Intelligence, San Jose, CA, USA, 12–16 July 1992; Volume 90, pp. 223–228. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hearst, M.A.; Dumais, S.T.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef]
- Johnson, S.C. Hierarchical clustering schemes. Psychometrika 1967, 32, 241–254. [Google Scholar] [CrossRef]
- McInnes, L.; Healy, J.; Melville, J. Umap: Uniform manifold approximation and projection for dimension reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar] [CrossRef]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Feng, P.; Wang, B.; Li Liu, D.; Yu, Q. Machine learning-based integration of remotely-sensed drought factors can improve the estimation of agricultural drought in South-Eastern Australia. Agric. Syst. 2019, 173, 303–316. [Google Scholar] [CrossRef]
- Rahmati, O.; Falah, F.; Dayal, K.S.; Deo, R.C.; Mohammadi, F.; Biggs, T.; Bui, D.T. Machine learning approaches for spatial modeling of agricultural droughts in the south-east region of Queensland Australia. Sci. Total Environ. 2020, 699, 134230. [Google Scholar] [CrossRef] [PubMed]
- Tyagi, S.; Zhang, X.; Saraswat, D.; Sahany, S.; Mishra, S.K.; Niyogi, D. Flash drought: Review of concept, prediction and the potential for machine learning, deep learning methods. Earth’s Future 2022, 10, e2022EF002723. [Google Scholar] [CrossRef]
- Mokhtar, A.; Jalali, M.; He, H.; Al-Ansari, N.; Elbeltagi, A.; Alsafadi, K.; Rodrigo-Comino, J. Estimation of SPEI meteorological drought using machine learning algorithms. IEEE Access 2021, 9, 65503–65523. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, Z.Y.; Xu, L.J.; Ou, C.Q. Meteorological drought forecasting based on a statistical model with machine learning techniques in Shaanxi province, China. Sci. Total Environ. 2019, 665, 338–346. [Google Scholar] [CrossRef]
- Karbasi, M.; Jamei, M.; Malik, A.; Kisi, O.; Yaseen, Z.M. Multi-steps drought forecasting in arid and humid climate environments: Development of integrative machine learning model. Agric. Water Manag. 2023, 281, 108210. [Google Scholar] [CrossRef]
- IPCC. Summary for Policymakers. In Climate Change 2013: The Physical Science Basis, Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK, 2013; p. 15. [Google Scholar]
- Shamshirband, S.; Hashemi, S.; Salimi, H.; Samadianfard, S.; Asadi, E.; Shadkani, S.; Chau, K.W. Predicting standardized streamflow index for hydrological drought using machine learning models. Eng. Appl. Comput. Fluid Mech. 2020, 14, 339–350. [Google Scholar] [CrossRef]
- Belayneh, A.; Adamowski, J. Drought forecasting using new machine learning methods. J. Water Land Dev. 2013, 18, 3–12. [Google Scholar] [CrossRef]
- Kim, C.; Kim, C.S. Comparison of the performance of a hydrologic model and a deep learning technique for rainfall-runoff analysis. Trop. Cyclone Res. Rev. 2021, 10, 215–222. [Google Scholar] [CrossRef]
- K-water. Drought White Paper on the Yeongsan & Sumjin River Basin (2022–2023); K-water: Daejeon, Republic of Korea, 2023; p. 139. [Google Scholar]
- Korea Meteorological Administration (KMA). Precipitation Data. Available online: https://data.kma.go.kr (accessed on 23 January 2024).
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; Volume 17, pp. 179–183. [Google Scholar]
- Kim, G.S.; Lee, J.W. Evaluation of drought indices using drought records. J. Korea Water Resour. Assoc. 2011, 44, 639–652. [Google Scholar] [CrossRef]
- National Oceanic and Atmospheric Administration (NOAA). Climate Indices. Available online: https://www.ncei.noaa.gov (accessed on 23 January 2024).
- Nye, J.A.; Baker, M.R.; Bell, R.; Kenny, A.; Kilbourne, K.H.; Friedland, K.D.; Wood, R. Ecosystem effects of the Atlantic multidecadal oscillation. J. Mar. Syst. 2014, 133, 103–116. [Google Scholar] [CrossRef]
- Rigor, I.G.; Wallace, J.M.; Colony, R.L. Response of sea ice to the Arctic Oscillation. J. Clim. 2002, 15, 2648–2663. [Google Scholar] [CrossRef]
- Yu, J.Y.; Kao, H.Y. Decadal changes of ENSO persistence barrier in SST and ocean heat content indices: 1958–2001. J. Geophys. Res. Atmos. 2007, 112, 13106. [Google Scholar] [CrossRef]
- Wolter, K.; Timlin, M.S. El Niño/Southern Oscillation behaviour since 1871 as diagnosed in an extended multivariate ENSO index (MEI. ext). Int. J. Climatol. 2011, 31, 1074–1087. [Google Scholar] [CrossRef]
- Stenseth, N.C.; Ottersen, G.; Hurrell, J.W.; Mysterud, A.; Lima, M.; Chan, K.S.; Ådlandsvik, B. Studying climate effects on ecology through the use of climate indices: The North Atlantic Oscillation, El Nino Southern Oscillation and beyond. Proc. Biol. Sci. 2003, 270, 2087–2096. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Stepaniak, D.P. Indices of el Niño evolution. J. Clim. 2001, 14, 1697–1701. [Google Scholar] [CrossRef]
- Linkin, M.E.; Nigam, S. The North Pacific Oscillation–west Pacific teleconnection pattern: Mature-phase structure and winter impacts. J. Clim. 2008, 21, 1979–1997. [Google Scholar] [CrossRef]
- Glantz, M.H.; Ramirez, I.J. Reviewing the Oceanic Niño Index (ONI) to enhance societal readiness for El Niño’s impacts. Int. J. Disaster Risk Sci. 2020, 11, 394–403. [Google Scholar] [CrossRef]
- Ge, Y.; Luo, D. Impacts of the different types of El Niño and PDO on the winter sub-seasonal North American zonal temperature dipole via the variability of positive PNA events. Clim. Dyn. 2023, 60, 1397–1413. [Google Scholar] [CrossRef]
- Kwok, R.; Comiso, J.C. Southern Ocean climate and sea ice anomalies associated with the Southern Oscillation. J. Clim. 2002, 15, 487–501. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Shea, D.J. Atlantic hurricanes and natural variability in 2005. Geophys. Res. Lett. 2006, 33, 12704. [Google Scholar] [CrossRef]
- Hassanzadeh, Y.; Ghazvinian, M.; Abdi, A.; Baharvand, S.; Jozaghi, A. Prediction of short and long-term droughts using artificial neural networks and hydro-meteorological variables. arXiv 2020, arXiv:2006.02581. [Google Scholar] [CrossRef]
- Yalçın, S.; Eşit, M.; Çoban, Ö. A new deep learning method for meteorological drought estimation based-on standard precipitation evapotranspiration index. Eng. Appl. Artif. Intell. 2023, 124, 106550. [Google Scholar] [CrossRef]

| Meteorological Data | Date (Resolution) | Sources |
|---|---|---|
| Average temperature | 1991–2022 (Monthly) | KMA |
| Average local atmospheric pressure | 1991–2022 (Monthly) | KMA |
| Average sea-surface atmospheric pressure | 1991–2022 (Monthly) | KMA |
| Average water vapor pressure | 1991–2022 (Monthly) | KMA |
| Average dew point temperature | 1991–2022 (Monthly) | KMA |
| Average relative humidity | 1991–2022 (Monthly) | KMA |
| Total precipitation per month | 1991–2022 (Monthly) | KMA |
| Average wind speed | 1991–2022 (Monthly) | KMA |
| Total daily flow | 1991–2022 (Monthly) | KMA |
| Average cloudiness | 1991–2022 (Monthly) | KMA |
| Average ground temperature | 1991–2022 (Monthly) | KMA |
| Sunshine rate | 1991–2022 (Monthly) | KMA |
| Scenario 1 | ||||||||
| Stations | Nodes | Batch size | Epochs | Sequence | MSE | RMSE | NSE | |
| Gwangju | 100-50 | 16 | 100 | 12 | 0.442 | 0.665 | 0.143 | 0.529 |
| Mokpo | 128-64-32 | 16 | 200 | 11 | 0.277 | 0.526 | 0.399 | 0.709 |
| Yeosu | 200-100-50 | 16 | 200 | 10 | 0.430 | 0.656 | 0.322 | 0.570 |
| Jangheung | 200-100-50 | 16 | 100 | 11 | 0.358 | 0.598 | 0.263 | 0.533 |
| Scenario 2 | ||||||||
| Stations | Nodes | Batch size | Epochs | Sequence | MSE | RMSE | NSE | |
| Gwangju | 128-64-32 | 16 | 100 | 7 | 0.274 | 0.523 | 0.543 | 0.699 |
| Mokpo | 64-32-16 | 16 | 100 | 12 | 0.229 | 0.479 | 0.425 | 0.760 |
| Yeosu | 200-100-50 | 16 | 100 | 7 | 0.374 | 0.612 | 0.255 | 0.620 |
| Jangheung | 64-32-16 | 32 | 100 | 2 | 0.354 | 0.595 | 0.528 | 0.530 |
| Scenario 3 | ||||||||
| Stations | Nodes | Batch size | Epochs | Sequence | MSE | RMSE | NSE | |
| Gwangju | 64-32-16 | 32 | 100 | 8 | 0.298 | 0.546 | 0.579 | 0.675 |
| Mokpo | 64-32-16 | 16 | 100 | 5 | 0.200 | 0.447 | 0.770 | 0.781 |
| Yeosu | 128-64-32 | 32 | 100 | 7 | 0.347 | 0.589 | 0.628 | 0.647 |
| Jangheung | 100-50 | 32 | 100 | 2 | 0.316 | 0.562 | 0.578 | 0.580 |
| Scenario 4 | ||||||||
| Stations | Nodes | Batch size | Epochs | Sequence | MSE | RMSE | NSE | |
| Gwangju | 200-100-50 | 16 | 200 | 2 | 0.534 | 0.731 | 0.331 | 0.356 |
| Mokpo | 128-64-32 | 16 | 200 | 4 | 0.407 | 0.638 | 0.473 | 0.551 |
| Yeosu | 64-32-16 | 16 | 100 | 2 | 0.570 | 0.755 | 0.297 | 0.406 |
| Jangheung | 100-50 | 16 | 100 | 2 | 0.451 | 0.671 | 0.342 | 0.401 |
| Scenario 5 | ||||||||
| Stations | Nodes | Batch size | Epochs | Sequence | MSE | RMSE | NSE | |
| Gwangju | 128-64-32 | 32 | 200 | 5 | 0.617 | 0.786 | 0.149 | 0.309 |
| Mokpo | 200-100-50 | 32 | 100 | 5 | 0.521 | 0.722 | 0.360 | 0.430 |
| Yeosu | 100-50 | 32 | 100 | 9 | 0.695 | 0.834 | 0.049 | 0.303 |
| Jangheung | 200-100-50 | 16 | 200 | 2 | 0.695 | 0.833 | 0.067 | 0.077 |
| Station | Seasons | MSE | RMSE | NSE | |
|---|---|---|---|---|---|
| Mokpo | Spring | 0.281 | 0.530 | 0.638 | 0.638 |
| Summer | 0.365 | 0.604 | 0.493 | 0.493 | |
| Fall | 0.256 | 0.506 | 0.678 | 0.678 | |
| Winter | 0.367 | 0.606 | 0.702 | 0.702 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.; Han, H. Application of LSTM and Climate Index for Prediction of Meteorological Drought in South Korea. Water 2025, 17, 1801. https://doi.org/10.3390/w17121801
Park S, Han H. Application of LSTM and Climate Index for Prediction of Meteorological Drought in South Korea. Water. 2025; 17(12):1801. https://doi.org/10.3390/w17121801
Chicago/Turabian StylePark, Soonchan, and Heechan Han. 2025. "Application of LSTM and Climate Index for Prediction of Meteorological Drought in South Korea" Water 17, no. 12: 1801. https://doi.org/10.3390/w17121801
APA StylePark, S., & Han, H. (2025). Application of LSTM and Climate Index for Prediction of Meteorological Drought in South Korea. Water, 17(12), 1801. https://doi.org/10.3390/w17121801







