Statistical and Physical Significance of Homogeneous Regions in Regional Flood Frequency Analysis
Abstract
1. Introduction
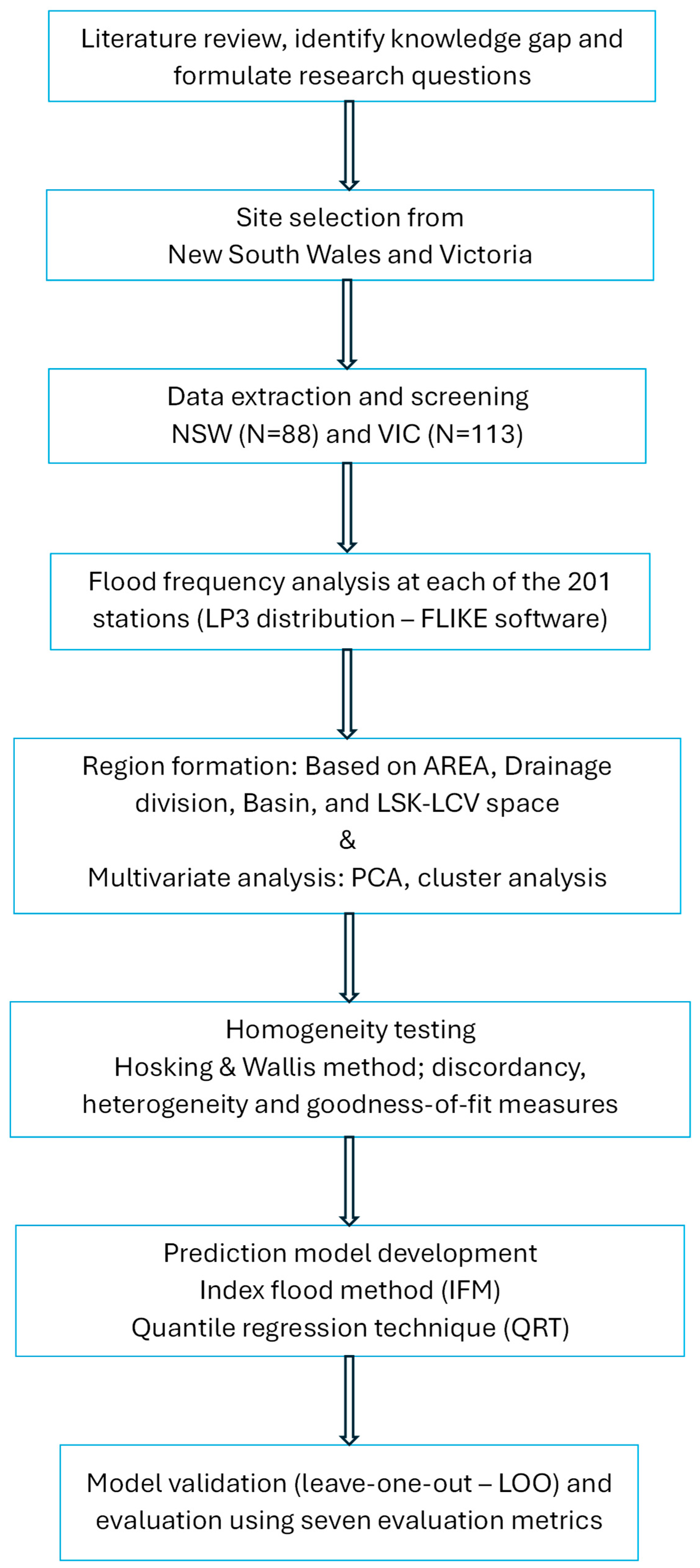
2. Data and Methodology
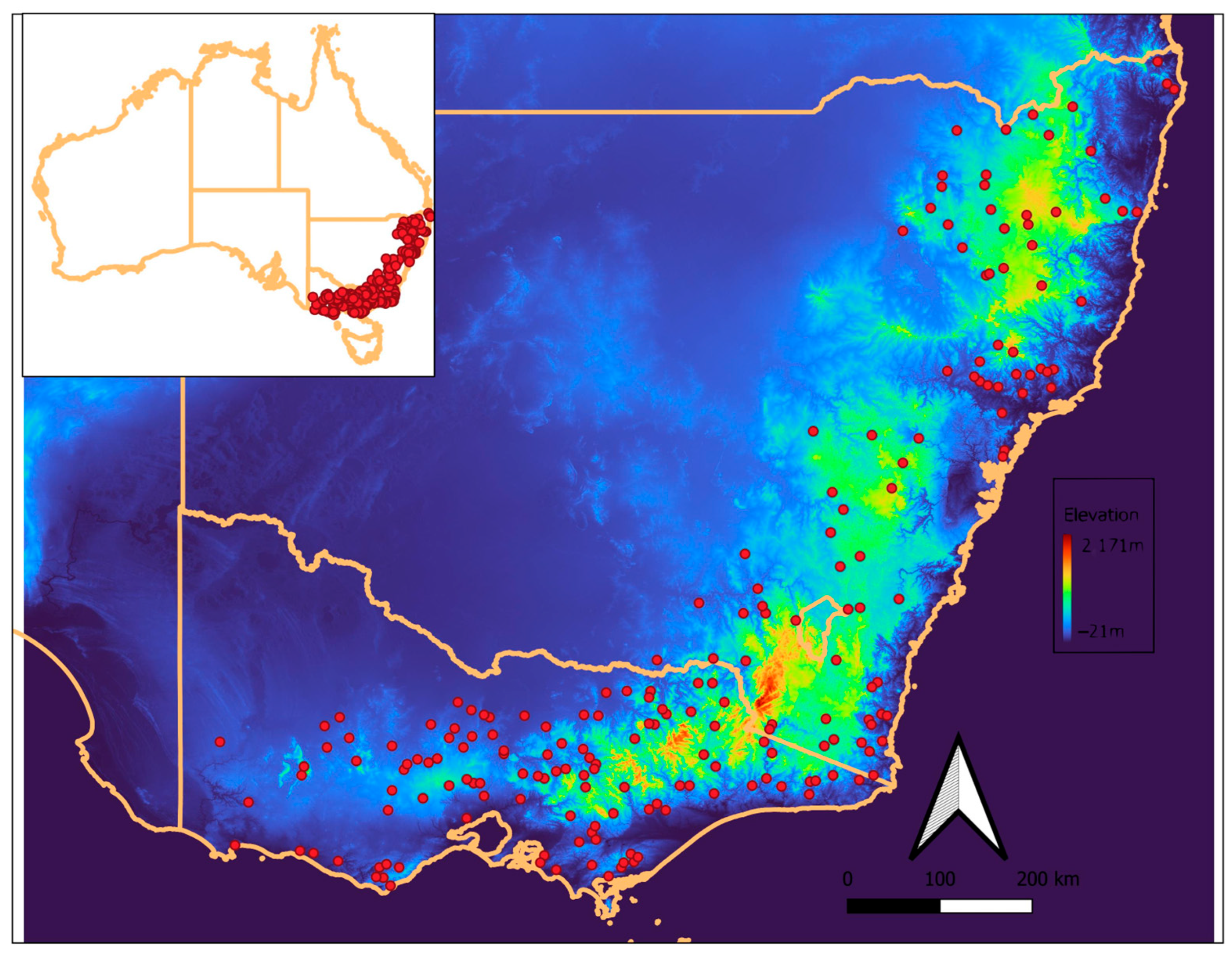
2.1. Study Area
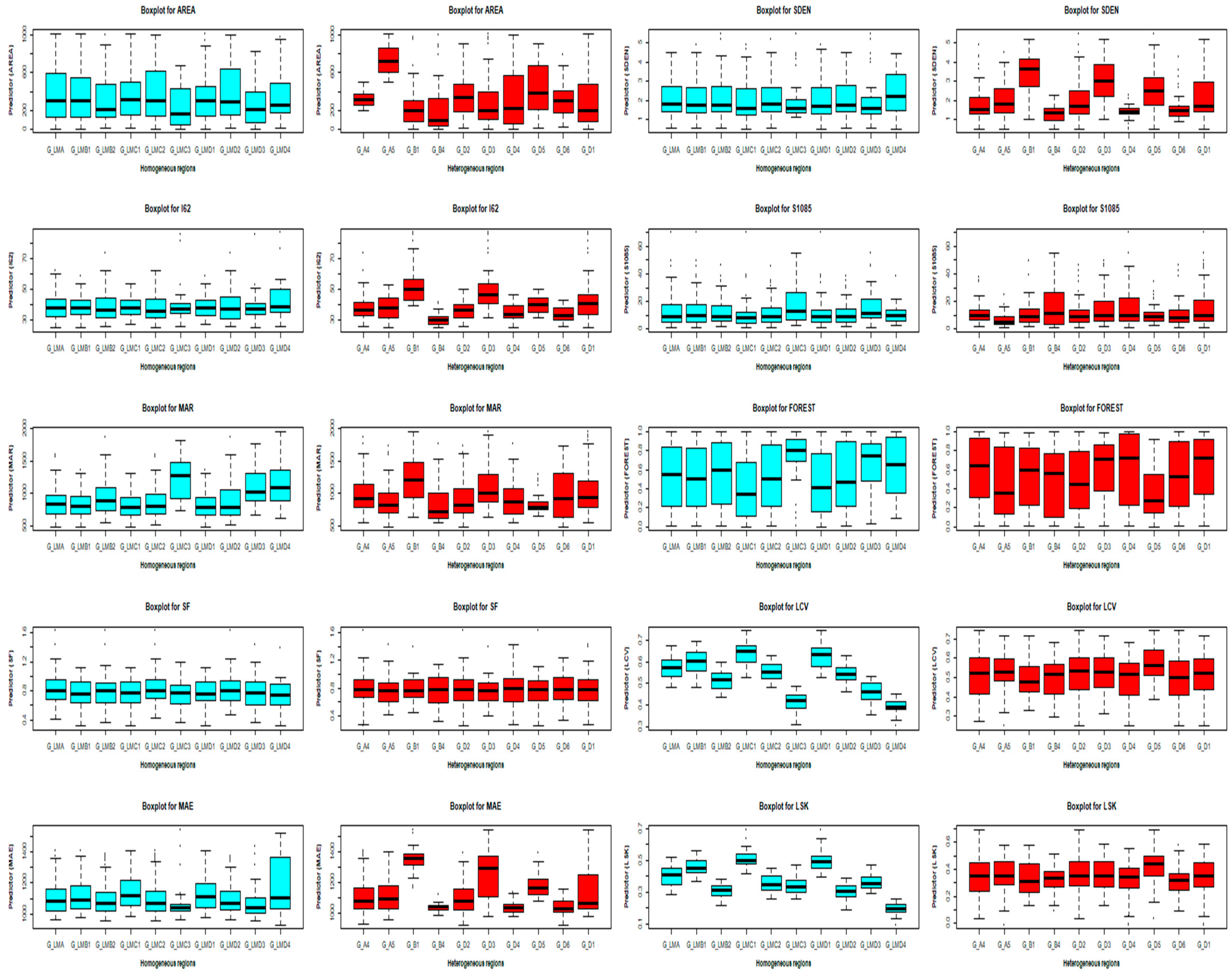
2.2. Exploratory Data Analysis
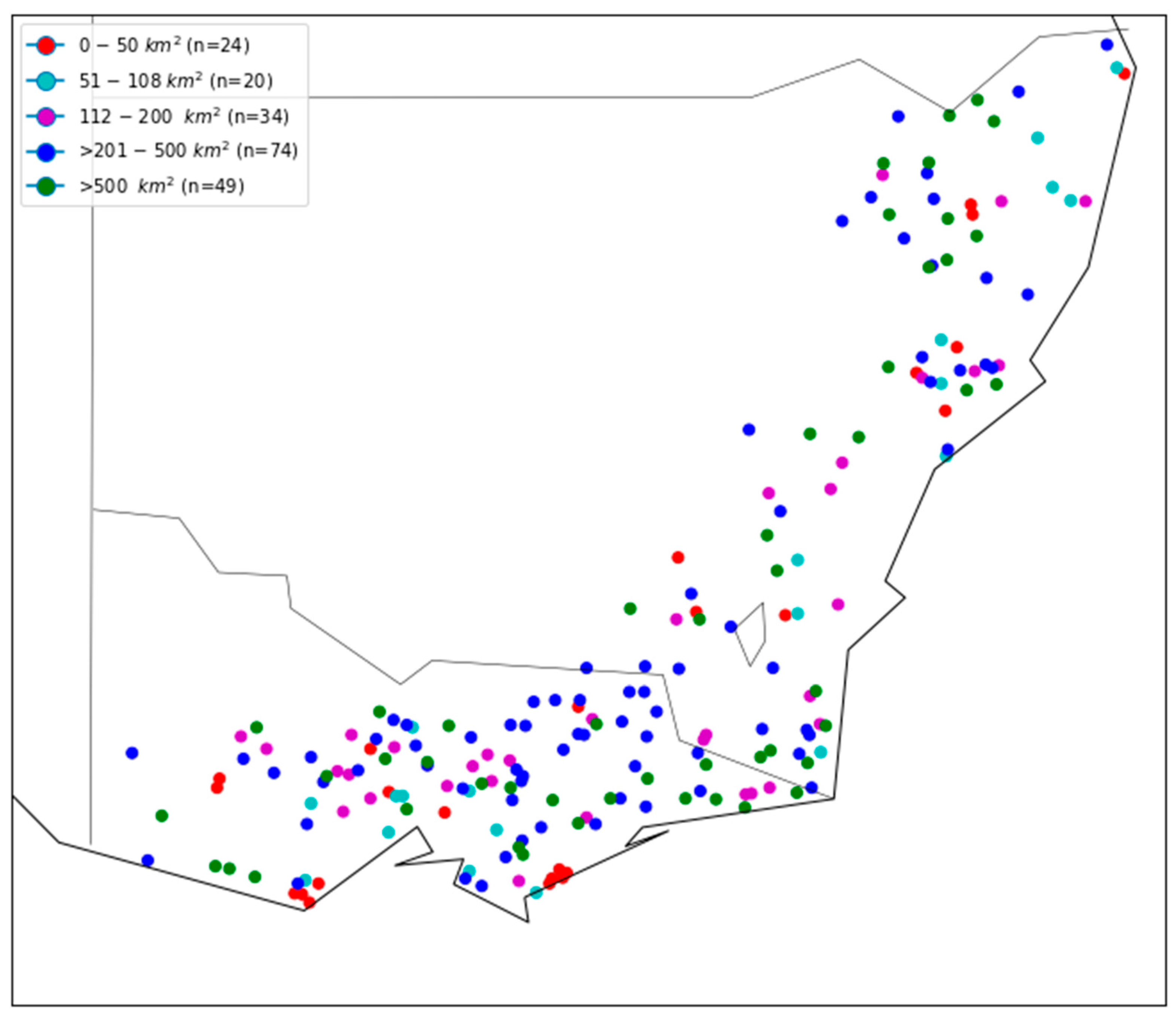
Catchment and Climate Characteristics
2.3. Formation of Regions and Testing for Homogeneity
2.3.1. Homogeneous Region Identification
2.3.2. Testing Homogeneity
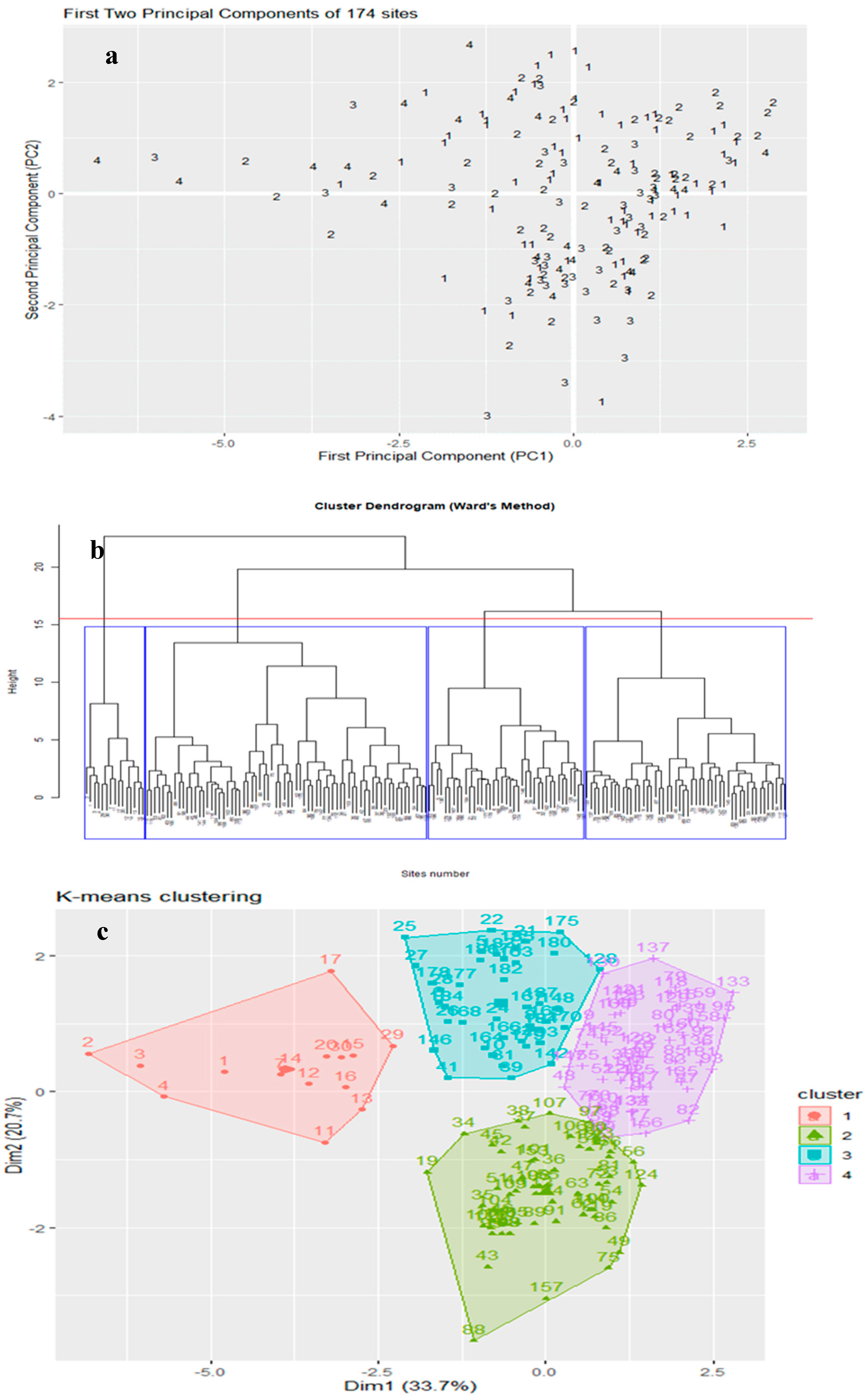
2.3.3. Multivariate Statistical Analysis
Principal Component Analysis (PCA)
Cluster Analysis
2.3.4. Prediction Model Development
2.3.5. Validation Approach and Evaluation Criteria
3. Results
3.1. Discordancy and Homogeneity Assessment of the Formed Regions
3.2. Prediction Model Evaluation
3.2.1. Degree of Heterogeneity vs. Absolute Median Relative Error
3.2.2. Model Evaluation Adopting Evaluation Statistics
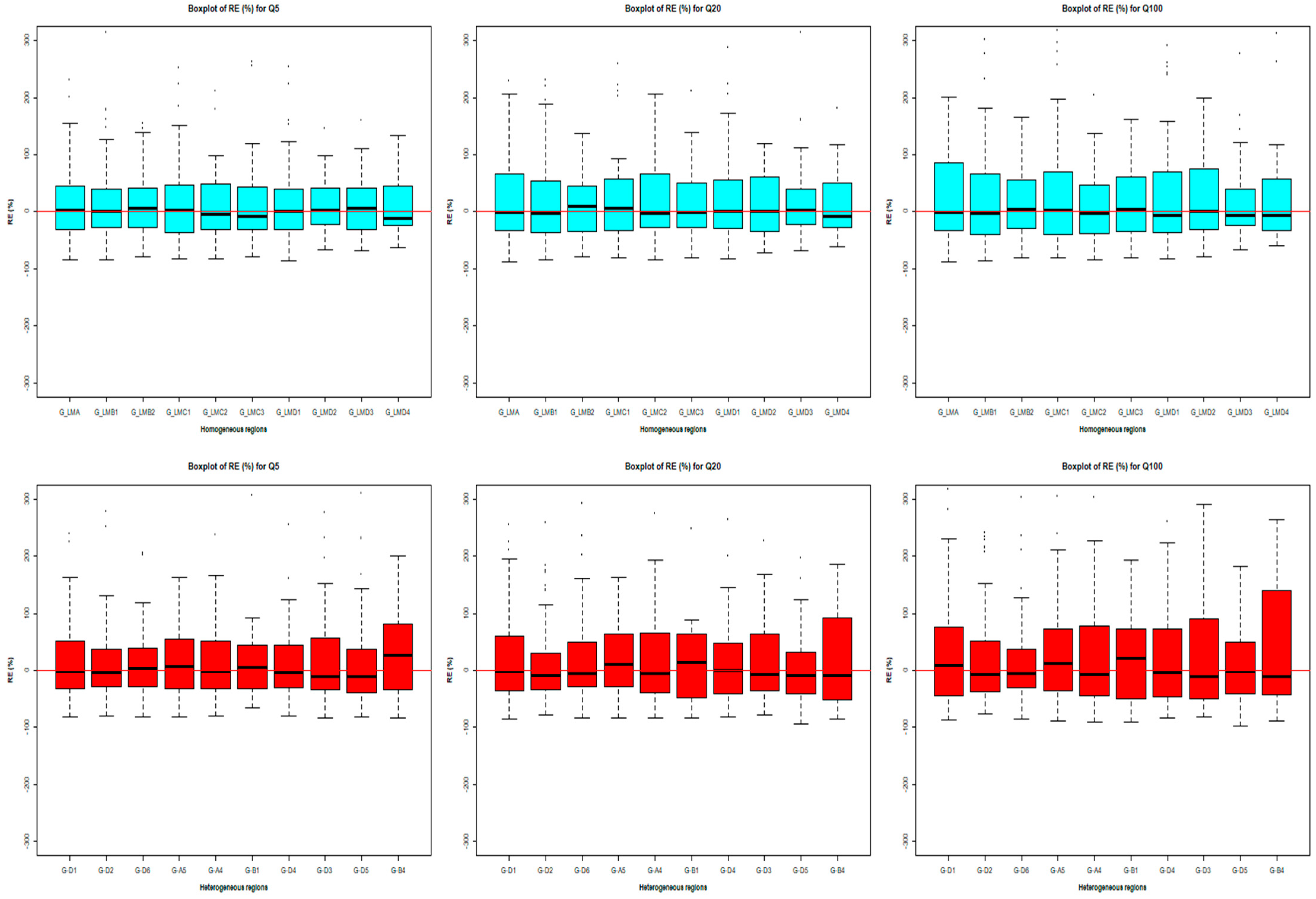
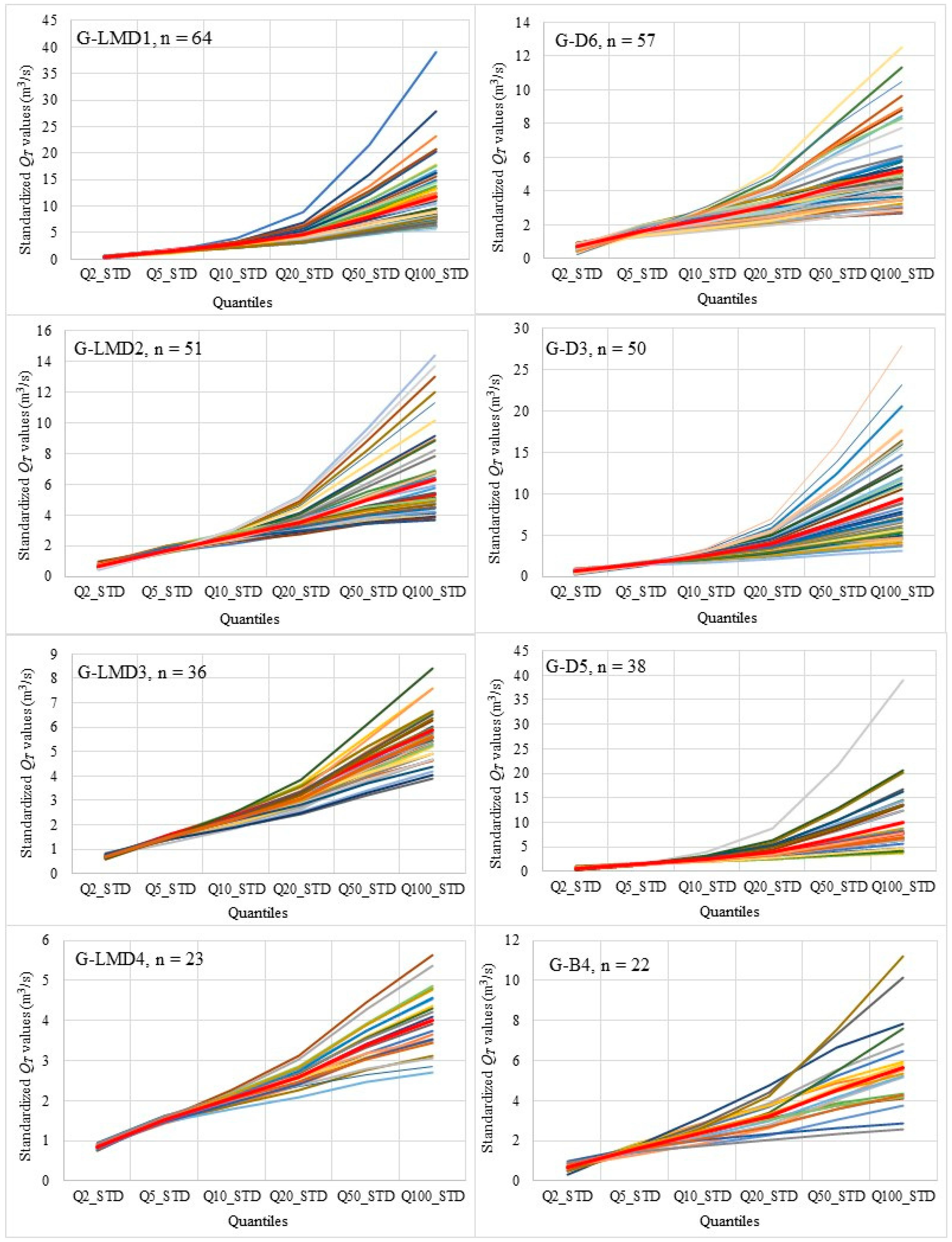
3.2.3. Comparison of Standardized Flood Frequency Curves Between the Homogeneous and Heterogeneous Regions
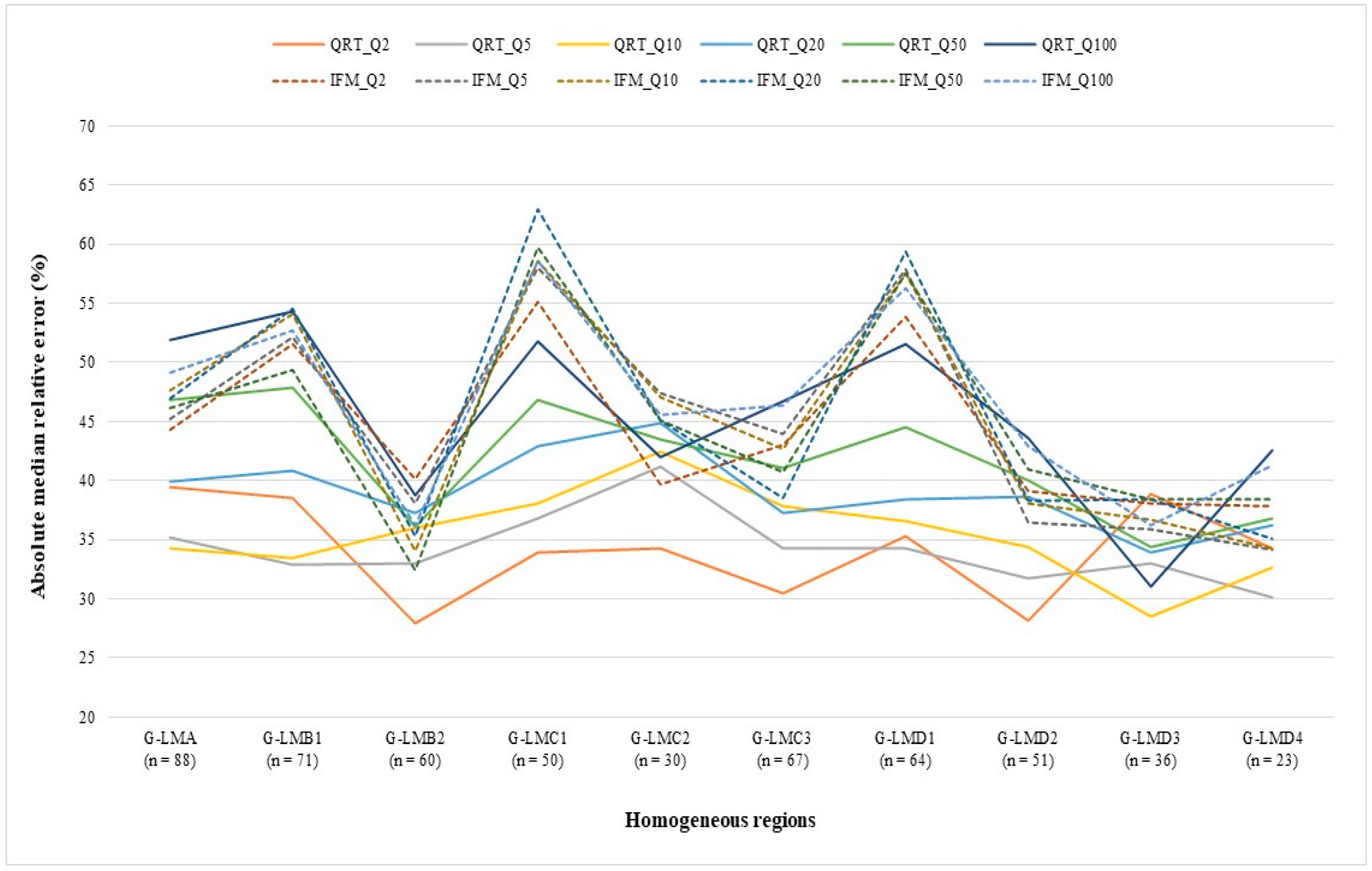
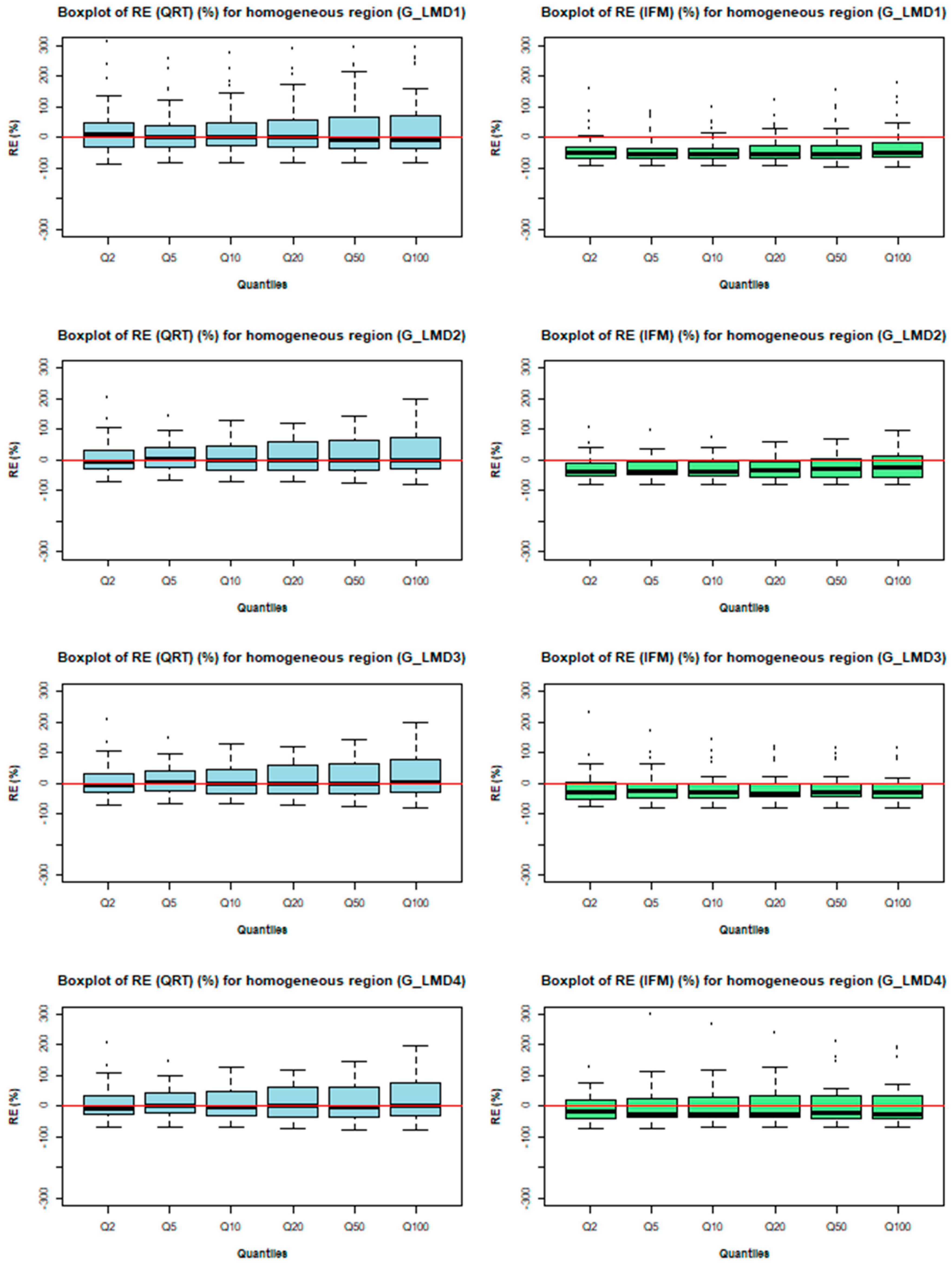
3.3. Comparison of Quantile Regression Technique (QRT) and Index Flood Method (IFM)
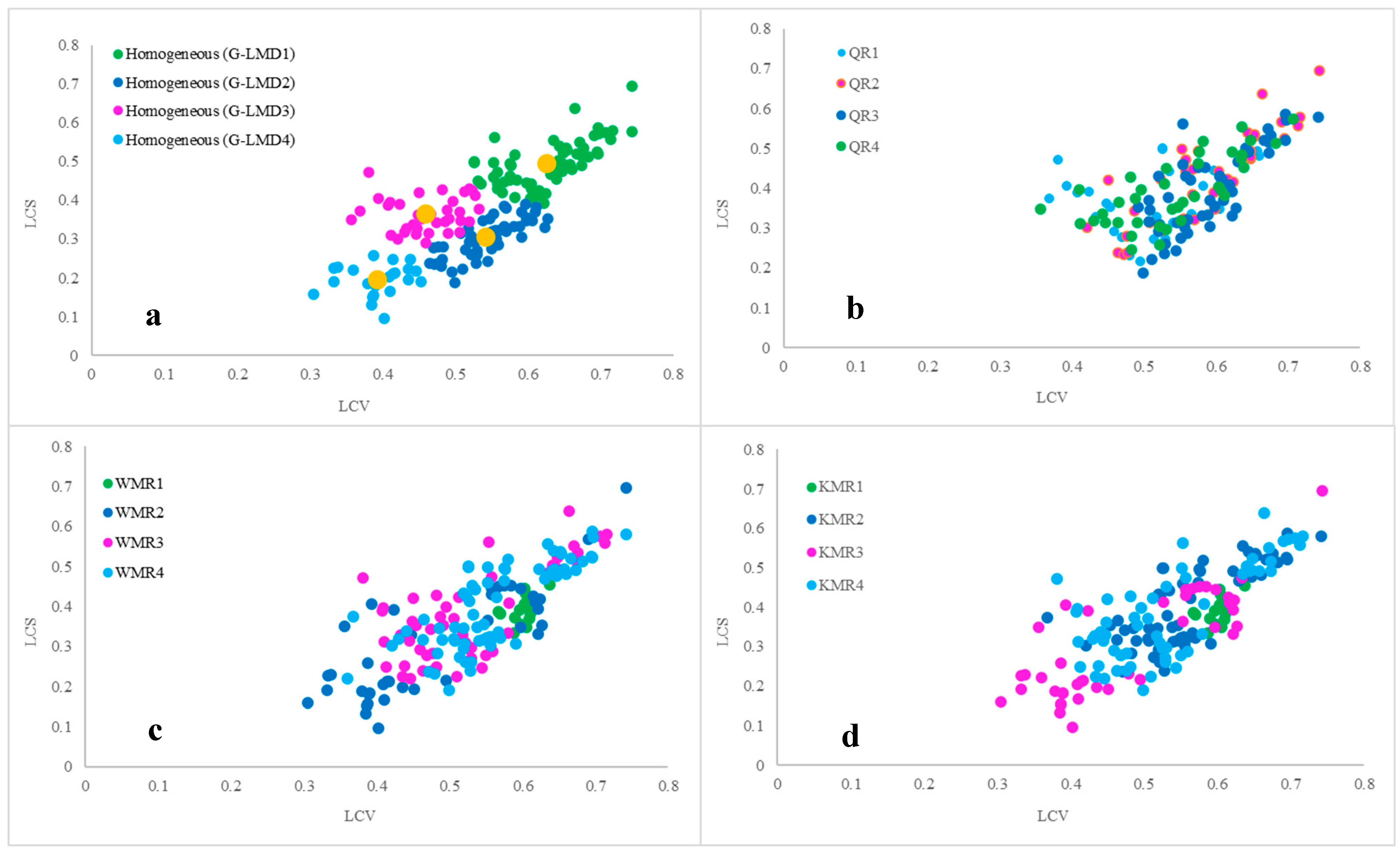
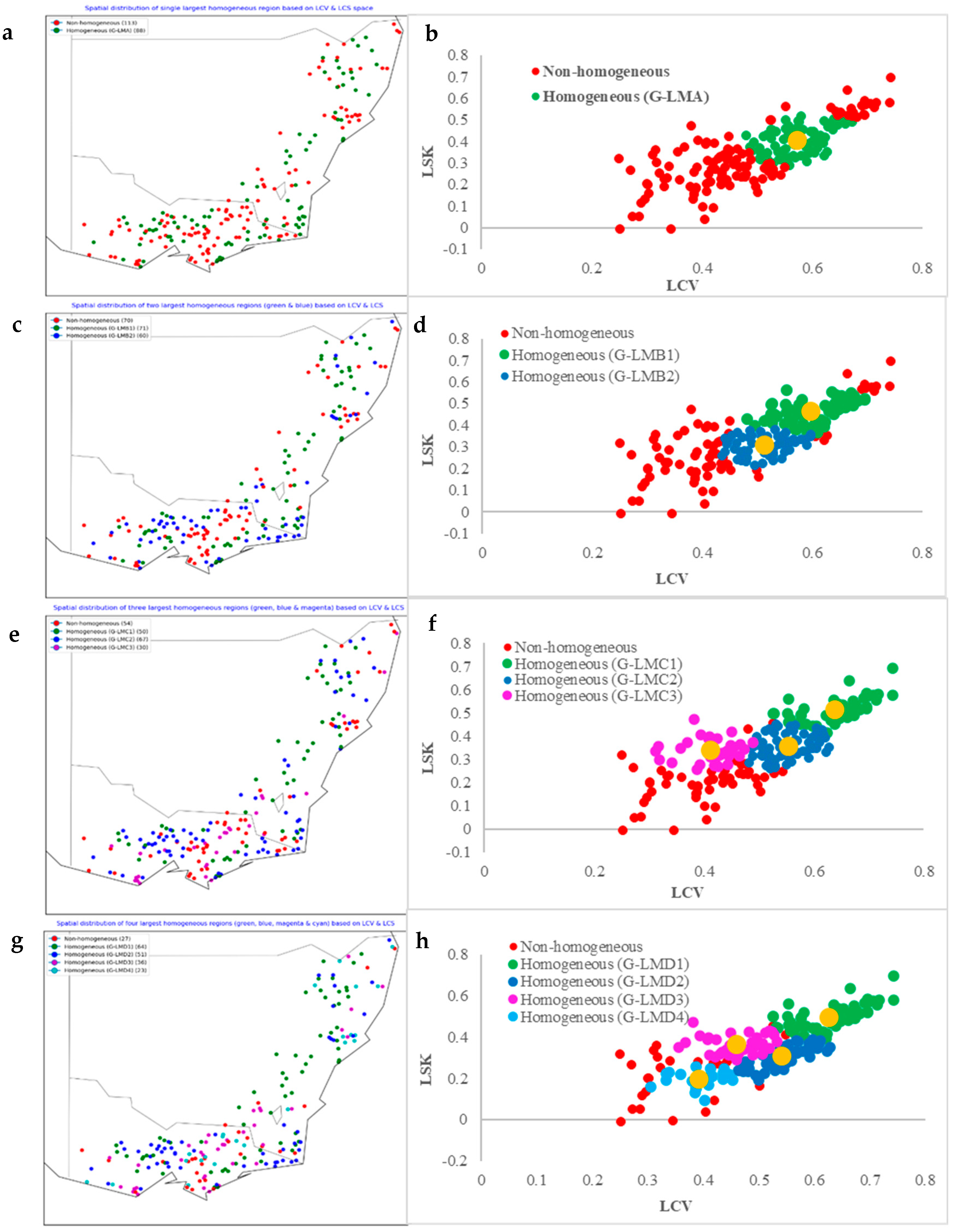
3.4. Coherence of Group Formation Between Flood Data and Catchment Data Space
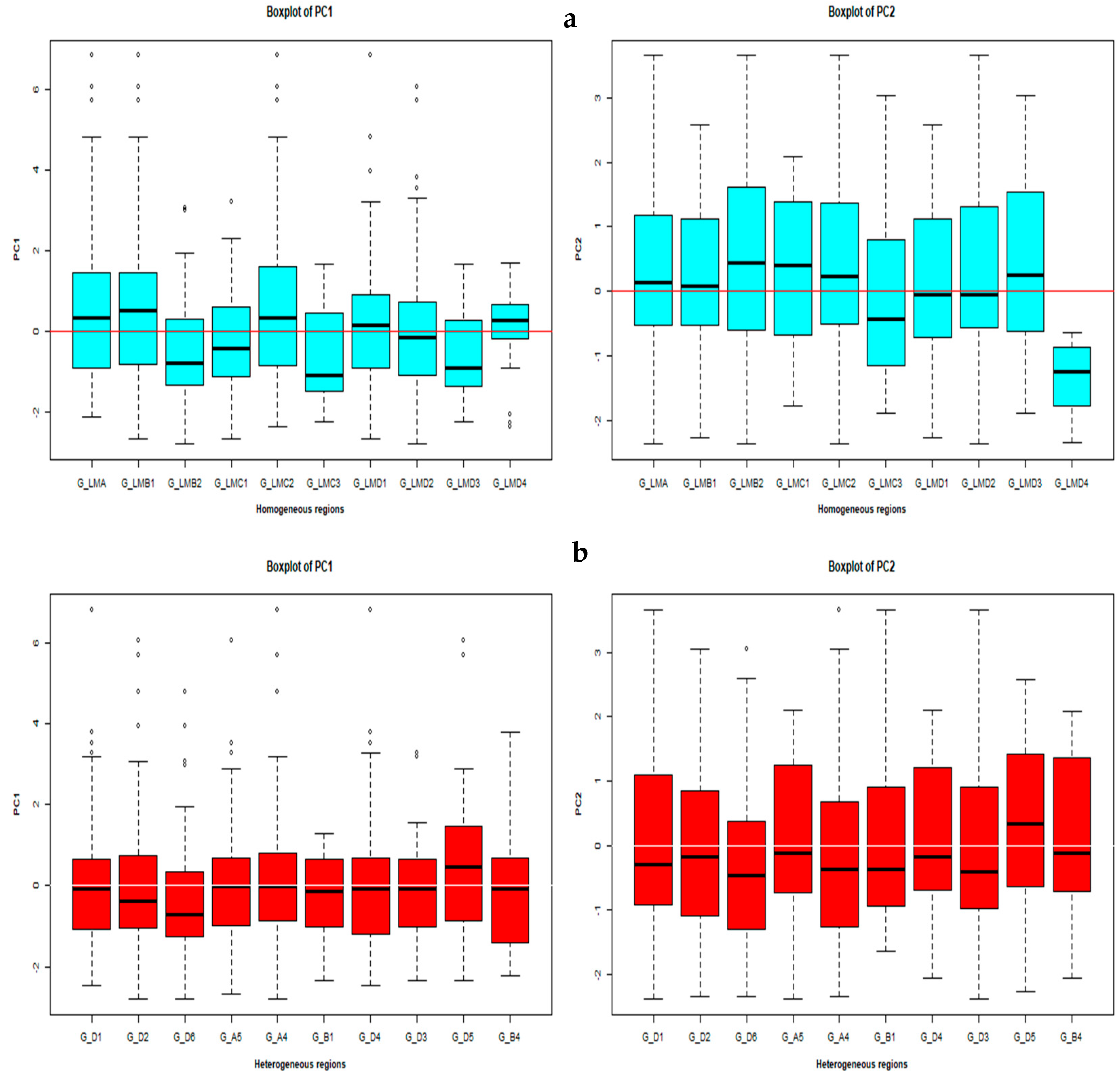
3.5. Physical and Geographical Interpretation in Terms of Degree of Homogeneity and Heterogeneity
3.5.1. Physical Interpretation of Catchment Characteristics
3.5.2. Geographical Coherence of Assumed Homogeneous Regions
4. Discussion
5. Conclusions
- The Pearson Type III (PE3) and Generalized Pareto (GPA) distributions are the best-fit regional distributions in southeast Australia.
- For the homogeneous regions (formed in the L-moments space), the variation in estimated model accuracy is smaller for the IFM than the QRT, but the QRT generally outperforms the IFM with lower AMRE values.
- There is a weak association between the flood characteristics data space (L-moments of AMF data) and catchment characteristics data space in southeast Australia.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Endendijk, T.; Botzen, W.; de Moel, H.; Aerts, J.; Slager, K.; Kok, M. Flood Vulnerability curves and household flood damage mitigation measures: An econometric analysis of survey data. In Proceedings of the EGU23, the 25th EGU General Assembly, Vienna, Austria, 23–28 April 2023. Copernicus Meetings. [Google Scholar]
- FitzGerald, G.; Du, W.; Jamal, A.; Clark, M.; Hou, X.Y. Flood fatalities in contemporary Australia (1997–2008). Emerg. Med. Australas. 2010, 22, 180–186. [Google Scholar] [CrossRef]
- Li, Z.; Gao, S.; Chen, M.; Gourley, J.J.; Hong, Y. Spatiotemporal characteristics of US floods: Current status and forecast under a future warmer climate. Earth’s Future 2022, 10, e2022EF002700. [Google Scholar] [CrossRef]
- Rhodes, C. Flood Damage Costs Beyond Buildings—A Lake Champlain Case Study; US Geological Survey: Reston, VA, USA, 2023. [Google Scholar]
- Quesada-Román, A.; Ballesteros-Cánovas, J.A.; Granados-Bolaños, S.; Birkel, C.; Stoffel, M. Improving regional flood risk assessment using flood frequency and dendrogeomorphic analyses in mountain catchments impacted by tropical cyclones. Geomorphology 2022, 396, 108000. [Google Scholar] [CrossRef]
- Mangukiya, N.K.; Sharma, A. Alternate pathway for regional flood frequency analysis in data-sparse region. J. Hydrol. 2024, 629, 130635. [Google Scholar] [CrossRef]
- Sharifi Garmdareh, E.; Vafakhah, M.; Eslamian, S.S. Regional flood frequency analysis using support vector regression in arid and semi-arid regions of Iran. Hydrol. Sci. J. 2018, 63, 426–440. [Google Scholar] [CrossRef]
- Srinivas, V.V.; Tripathi, S.; Rao, A.R.; Govindaraju, R.S. Regional flood frequency analysis by combining self-organizing feature map and fuzzy clustering. J. Hydrol. 2008, 348, 148–166. [Google Scholar] [CrossRef]
- Stedinger, J.R.; Griffis, V.W. Flood frequency analysis in the United States: Time to update. J. Hydrol. Eng. 2008, 13, 199–204. [Google Scholar] [CrossRef]
- Kumar, R.; Goel, N.K.; Chatterjee, C.; Nayak, P.C. Regional flood frequency analysis using soft computing techniques. Water Resour. Manag. 2015, 29, 1965–1978. [Google Scholar] [CrossRef]
- Mengistu, T.D.; Feyissa, T.A.; Chung, I.M.; Chang, S.W.; Yesuf, M.B.; Alemayehu, E. Regional Flood Frequency Analysis for Sustainable Water Resources Management of Genale–Dawa River Basin, Ethiopia. Water 2022, 14, 637. [Google Scholar] [CrossRef]
- Ouarda, T.B.; Girard, C.; Cavadias, G.S.; Bobée, B. Regional flood frequency estimation with canonical correlation analysis. J. Hydrol. 2001, 254, 157–173. [Google Scholar] [CrossRef]
- Ouarda, T.B.; Bâ, K.M.; Diaz-Delgado, C.; Cârsteanu, A.; Chokmani, K.; Gingras, H.; Quentin, E.; Trujillo, E.; Bobée, B. Intercomparison of regional flood frequency estimation methods at ungauged sites for a Mexican case study. J. Hydrol. 2008, 348, 40–58. [Google Scholar] [CrossRef]
- Guru, N. Implication of partial duration series on regional flood frequency analysis. Int. J. River Basin Manag. 2024, 22, 167–186. [Google Scholar] [CrossRef]
- Dalrymple, T. Flood-Frequency Analyses, Manual of Hydrology: Part 3; USGPO: Washington, DC, USA, 1960. [Google Scholar]
- Hosking, J.R.M.; Wallis, J.R. Some statistics useful in regional frequency analysis. Water Resour. Res. 1993, 29, 271–281. [Google Scholar] [CrossRef]
- Griffis, V.; Stedinger, J. The use of GLS regression in regional hydrologic analyses. J. Hydrol. 2007, 344, 82–95. [Google Scholar] [CrossRef]
- Mostofi Zadeh, S.; Burn, D.H. A Super Region Approach to Improve Pooled Flood Frequency Analysis. Can. Water Resour. J./Rev. Can. Des Ressour. Hydr. 2019, 44, 146–159. [Google Scholar] [CrossRef]
- Han, X.; Ouarda, T.B.M.J.; Rahman, A.; Haddad, K.; Mehrotra, R.; Sharma, A. A Network Approach for Delineating Homogeneous Regions in Regional Flood Frequency Analysis. Water Resour. Res. 2020, 56, e2019WR025910. [Google Scholar] [CrossRef]
- Burn, D.H. Delineation of groups for regional flood frequency analysis. J. Hydrol. 1988, 104, 345–361. [Google Scholar] [CrossRef]
- Viglione, A.; Laio, F.; Claps, P. A comparison of homogeneity tests for regional frequency analysis. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Bates, B.C.; Rahman, A.; Mein, R.G.; Weinmann, P.E. Climatic and physical factors that influence the homogeneity of regional floods in southeastern Australia. Water Resour. Res. 1998, 34, 3369–3381. [Google Scholar] [CrossRef]
- Sabrina, A.; Rahman, A. Development of a kriging-based regional flood frequency analysis technique for South-East Australia. Nat. Hazards 2022, 114, 2739–2765. [Google Scholar]
- Zalnezhad, A.; Rahman, A.; Vafakhah, M.; Samali, B.; Ahamed, F. Regional Flood Frequency Analysis Using the FCM-ANFIS Algorithm: A Case Study in South-Eastern Australia. Water 2022, 14, 1608. [Google Scholar] [CrossRef]
- Ahmed, A.; Khan, Z.; Rahman, A. Searching for homogeneous regions in regional flood frequency analysis for Southeast Australia. J. Hydrol. Reg. Stud. 2024, 53, 101782. [Google Scholar] [CrossRef]
- Rahman, A. Flood Estimation for Ungauged Catchments: A Regional Approach using Flood and Catchment Characteristics. Ph.D. Thesis, Department of Civil Engineering, Monash University, Victoria, Australia, 1997. [Google Scholar]
- Rahman, A.S.; Khan, Z.; Rahman, A. Application of independent component analysis in regional flood frequency analysis: Comparison between quantile regression and parameter regression techniques. J. Hydrol. 2020, 581, 124372. [Google Scholar] [CrossRef]
- Rahman, A.; Haddad, K.; Kuczera, G.; Weinmann, E. Regional Flood Methods. In Australian Rainfall and Runoff: A Guide to Flood Estimation; Chapter 3, Book 3; Ball J, B.M., Nathan, R., Weeks, W., Weinmann, E., Retallick, M., Testoni, I., Eds.; Geoscience Australia, Commonwealth of Australia, Engineers Australia: Symonston, Australia, 2019. [Google Scholar]
- Taylor, M.; Haddad, K.; Zaman, M.; Rahman, A. Regional flood modelling in Western Australia: Application of regression based methods using ordinary least squares. In Proceedings of the 19th International Congress on Modelling and Simulation—Sustaining Our Future: Understanding and Living with Uncertainty, MODSIM2011, Perth, WA, USA, 12–16 December 2011; pp. 3803–3810. [Google Scholar]
- Zalnezhad, A.; Rahman, A.; Nasiri, N.; Haddad, K.; Rahman, M.M.; Vafakhah, M.; Samali, B.; Ahamed, F. Artificial Intelligence-Based Regional Flood Frequency Analysis Methods: A Scoping Review. Water 2022, 14, 2677. [Google Scholar] [CrossRef]
- Rahman, A.S.; Rahman, A. Application of Principal Component Analysis and Cluster Analysis in Regional Flood Frequency Analysis: A Case Study in New South Wales, Australia. Water 2020, 12, 781. [Google Scholar] [CrossRef]
- Gado, T.A.; Nguyen, V.T.V. Comparison of homogenous region delineation approaches for regional flood frequency analysis at ungauged sites. J. Hydrol. Eng. 2016, 21. [Google Scholar] [CrossRef]
- Ward Jr, J.H. Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Malekinezhad, H.; Nachtnebel, H.P.; Klik, A. Comparing the index-flood and multiple-regression methods using L-moments. Phys. Chem. Earth Parts A/B/C 2011, 36, 54–60. [Google Scholar] [CrossRef]
- Murtagh, F.; Legendre, P. Ward’s hierarchical agglomerative clustering method: Which algorithms implement Ward’s criterion? J. Classif. 2014, 31, 274–295. [Google Scholar] [CrossRef]
- Farsadnia, F.; Rostami Kamrood, M.; Moghaddam Nia, A.; Modarres, R.; Bray, M.T.; Han, D.; Sadatinejad, J. Identification of homogeneous regions for regionalization of watersheds by two-level self-organizing feature maps. J. Hydrol. 2014, 509, 387–397. [Google Scholar] [CrossRef]
- Sharghi, E.; Nourani, V.; Soleimani, S.; Sadikoglu, F. Application of different clustering approaches to hydroclimatological catchment regionalization in mountainous regions, a case study in Utah State. J. Mt. Sci. 2018, 15, 461–484. [Google Scholar] [CrossRef]
- Acreman, M.C.; Sinclair, C.D. Classification of drainage basins according to their physical characteristics; an application for flood frequency analysis in Scotland. J. Hydrol. 1986, 84, 365–380. [Google Scholar] [CrossRef]
- Ahani, A.; Mousavi Nadoushani, S.S.; Moridi, A. A ranking method for regionalization of watersheds. J. Hydrol. 2022, 609, 127740. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, Y.; Zhang, X.; Ma, Q.; Ren, L. Mapping homogeneous regions for flash floods using machine learning: A case study in Jiangxi province, China. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102717. [Google Scholar] [CrossRef]
- Baidya, S.; Singh, A.; Panda, S.N. Flood frequency analysis. Nat. Hazards 2020, 100, 1137–1158. [Google Scholar] [CrossRef]
- Kuczera, G. Comprehensive at-site flood frequency analysis using Monte Carlo Bayesian inference. Water Resour. Res. 1999, 35, 1551–1557. [Google Scholar] [CrossRef]
- Kuczera, G.; Franks, S.W. At-Site Flood Frequency Analysis. In Australian Rainfall and Runoff: A Guide to Flood Estimation; Chapter 3, Book 3; Ball J, B.M., Nathan, R., Weeks, W., Weinmann, E., Retallick, M., Testoni, I., Eds.; Geoscience Australia: Symonston, Australia, 2019. [Google Scholar]
- Franks, S.W.; Kuczera, G. Flood frequency analysis: Evidence and implications of secular climate variability, New South Wales. Water Resour. Res. 2002, 38, 20-21–20-27. [Google Scholar] [CrossRef]
- Rahman, A.S.; Rahman, A.; Zaman, M.A.; Haddad, K.; Ahsan, A.; Imteaz, M. A study on selection of probability distributions for at-site flood frequency analysis in Australia. Nat. Hazards 2013, 69, 1803–1813. [Google Scholar] [CrossRef]
- Bobée, B.; Mathier, L.; Perron, H.; Trudel, P.; Rasmussen, P.F.; Cavadias, G.; Bernier, J.; Nguyen, V.T.V.; Pandey, G.; Ashkar, F.; et al. Presentation and review of some methods for regional flood frequency analysis. J. Hydrol. 1996, 186, 63–84. [Google Scholar]
- Rahman, A. A quantile regression technique to estimate design floods for ungauged catchments in south-east Australia. Australas. J. Water Resour. 2005, 9, 81–89. [Google Scholar] [CrossRef]
- Rahman, A.; Haddad, K.; Zaman, M.; Kuczera, G.; Weinmann, P.E. Design Flood Estimation in Ungauged Catchments: A Comparison Between the Probabilistic Rational Method and Quantile Regression Technique for NSW. Australas. J. Water Resour. 2011, 14, 127–139. [Google Scholar] [CrossRef]
- Thomas, D.; Benson, M.A. Generalization of Streamflow Characteristics from Drainage-Basin Characteristics; US Government Printing Office: Washington, DC, USA, 1970. [Google Scholar]
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: New York, NY, USA, 1997. [Google Scholar]
- Ouarda, T.B.M.J. Handbook of Applied Hydrology, Second Edition, Chapter 77, Regional Flood Frequency Modeling; Regional Flood Frequency Modeling, ed. V.P.S. (Editor-in-Chief); McGraw-Hill Education: New York, NY, USA, 2017. [Google Scholar]
- Cunnane, C. Methods and merits of regional flood frequency analysis. J. Hydrol. 1988, 100, 269–290. [Google Scholar] [CrossRef]
- Potter, K.W.; Lettenmaier, D.P. A comparison of regional flood frequency estimation methods using a resampling method. Water Resour. Res. 1990, 26, 415–424. [Google Scholar] [CrossRef]
- GREH, G.D.R.E.H.S. Inter-comparison of regional flood frequency procedures for Canadian rivers. J. Hydrol. 1996, 186, 85–103. [Google Scholar]
- Aissia, B.; Chebana, F.; Ouarda, T.; Bruneau, P.; Barbet, M.; Équipement, H.-Q. Bivariate index flood model for a northern case study. Hydrol. Sci. J. 2015, 60, 247–268. [Google Scholar] [CrossRef]
- Chebana, F.; Ouarda, T.B. Index flood-based multivariate regional frequency analysis. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Formetta, G.; Over, T.; Stewart, E. Assessment of Peak Flow Scaling and Its Effect on Flood Quantile Estimation in the United Kingdom. Water Resour. Res. 2021, 57, e2020WR028076. [Google Scholar] [CrossRef]
- Kader, F.; Derbas, A.; Haddad, K.; Rahman, A. Regional flood estimation for NSW: Comparison of quantile regression and parameter regression techniques. In Proceedings of the 21st International Congress on Modelling and Simulation: Partnering with Industry and the Community for Innovation and Impact through Modelling, MODSIM 2015—Held jointly with the 23rd National Conference of the Australian Society for Operations Research and the DSTO Led Defence Operations Research Symposium, DORS 2015, Queensland, Australia, 29 November–4 December 2015; Modelling and Simulation Society of Australia and New Zealand Inc. (MSSANZ): Perth, WA, Australia, 2015; pp. 2179–2185. [Google Scholar]
- Requena, A.I.; Chebana, F.; Mediero, L. A complete procedure for multivariate index-flood model application. J. Hydrol. 2016, 535, 559–580. [Google Scholar] [CrossRef]
- Šimková, T. L-moment homogeneity test in trivariate regional frequency analysis of extreme precipitation events. Meteorol. Appl. 2018, 25, 11–22. [Google Scholar] [CrossRef]
- Mosaffaie, J. Comparison of two methods of regional flood frequency analysis by using L-moments. Water Resour. 2015, 42, 313–321. [Google Scholar] [CrossRef]
- Haddad, K.; Rahman, A.; A Zaman, M.; Shrestha, S. Applicability of Monte Carlo cross validation technique for model development and validation using generalised least squares regression. J. Hydrol. 2013, 482, 119–128. [Google Scholar] [CrossRef]
- Haque, M.M.; Rahman, A.; Haddad, K.; Kuczera, G.; Weeks, W. Development of a regional flood frequency estimation model for Pilbara, Australia. In Proceedings of the 21st International Congress on Modelling and Simulation: Partnering with Industry and the Community for Innovation and Impact through Modelling, MODSIM 2015—Held jointly with the 23rd National Conference of the Australian Society for Operations Research and the DSTO led Defence Operations Research Symposium, DORS 2015, Queensland, Australia, 29 November–4 December 2015; Modelling and Simulation Society of Australia and New Zealand Inc. (MSSANZ): Perth, WA, Australia, 2015; pp. 2172–2178. [Google Scholar]
- Saf, B. Regional Flood Frequency Analysis Using L-Moments for the West Mediterranean Region of Turkey. Water Resour. Manag. 2008, 23, 531–551. [Google Scholar] [CrossRef]
- Rosbjerg, D.; Bloschl, G.; Burn, D.; Castellarin, A.; Croke, B.; Di Baldassarre, G.; Iacobellis, V.; Kjeldsen, T.R.; Kuczera, G.; Merz, R. Prediction of floods in ungauged basins. In Runoff Prediction in Ungauged Basins: Synthesis Across Processes, Places and Scales; Cambridge University Press: Cambridge, UK, 2013; pp. 189–225. [Google Scholar]
- Tramblay, Y.; Khedimallah, A.; Sadaoui, M.; Benaabidate, L.; Boulmaiz, T.; Boutaghane, H.; Dakhlaoui, H.; Hanich, L.; Ludwig, W.; Meddi, M. Regional flood frequency analysis in North Africa. J. Hydrol. 2024, 630, 130678. [Google Scholar] [CrossRef]
- Singh, A.K.; Chavan, S.R. An approach to regional flood frequency analysis for general peak discharge distribution datasets. J. Hydrol. 2025, 650, 132493. [Google Scholar] [CrossRef]
- Desai, S.; Ouarda, T.B. Regional hydrological frequency analysis at ungauged sites with random forest regression. J. Hydrol. 2021, 594, 125861. [Google Scholar] [CrossRef]
- Rahman, A.; Haddad, K.; Rahman, A.S.; Haque, M. Australian Rainfall and Runoff Revision Project 5: Regional Flood Methods: Database Used to Develop ARR RFFE Technique: Stage 3 Report; Engineers Australia: Barton, Australia, 2015. [Google Scholar]
- Haddad, K.; Rahman, A. Regional flood frequency analysis in eastern Australia: Bayesian GLS regression-based methods within fixed region and ROI framework—Quantile Regression vs. Parameter Regression Technique. J. Hydrol. 2012, 430–431, 142–161. [Google Scholar] [CrossRef]
- Alexandre, D.A.; Chaudhuri, C.; Gill-Fortin, J. Continental Scale Regional Flood Frequency Analysis: Combining Enhanced Datasets and a Bayesian Framework. Hydrology 2024, 11, 119. [Google Scholar] [CrossRef]
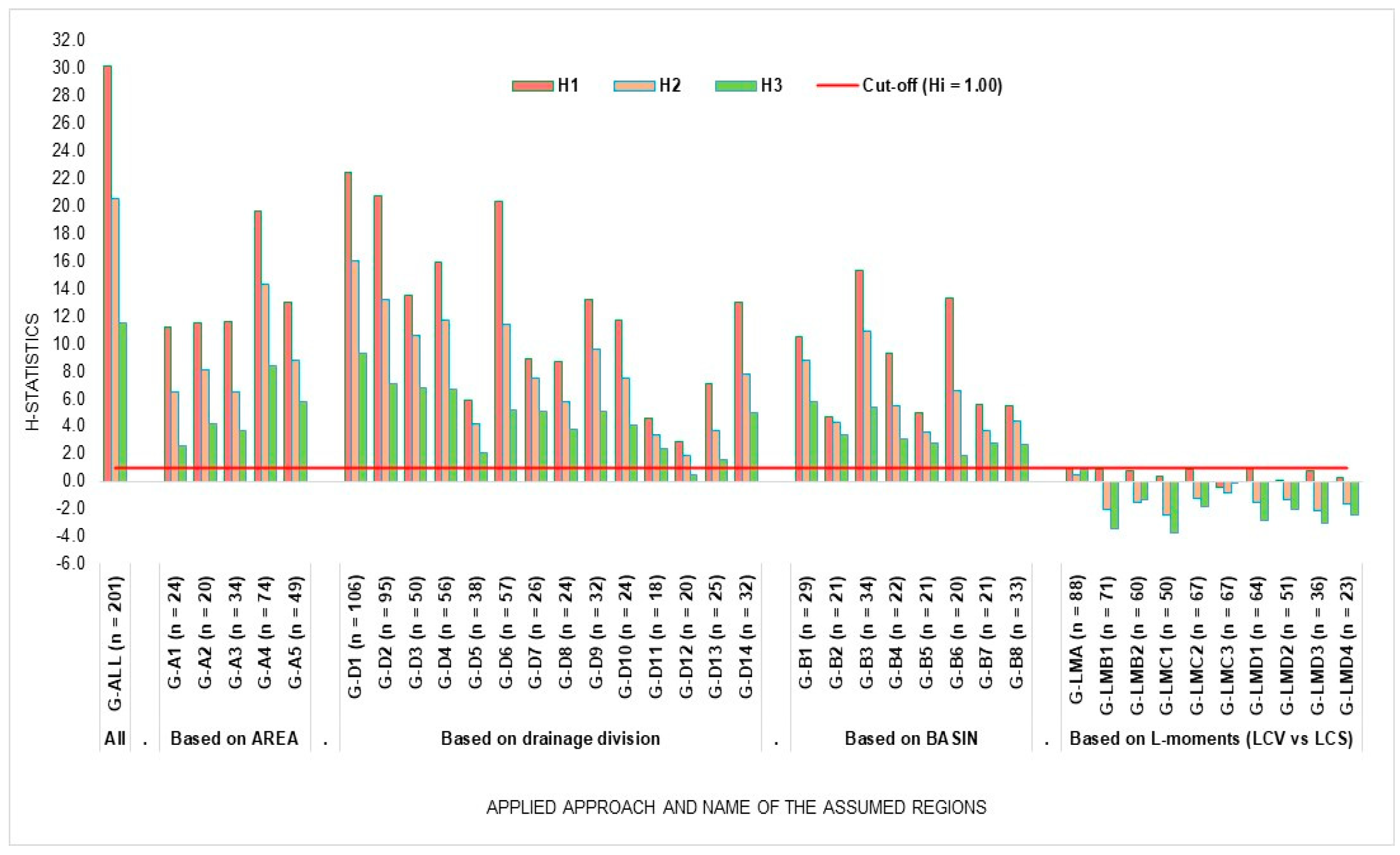
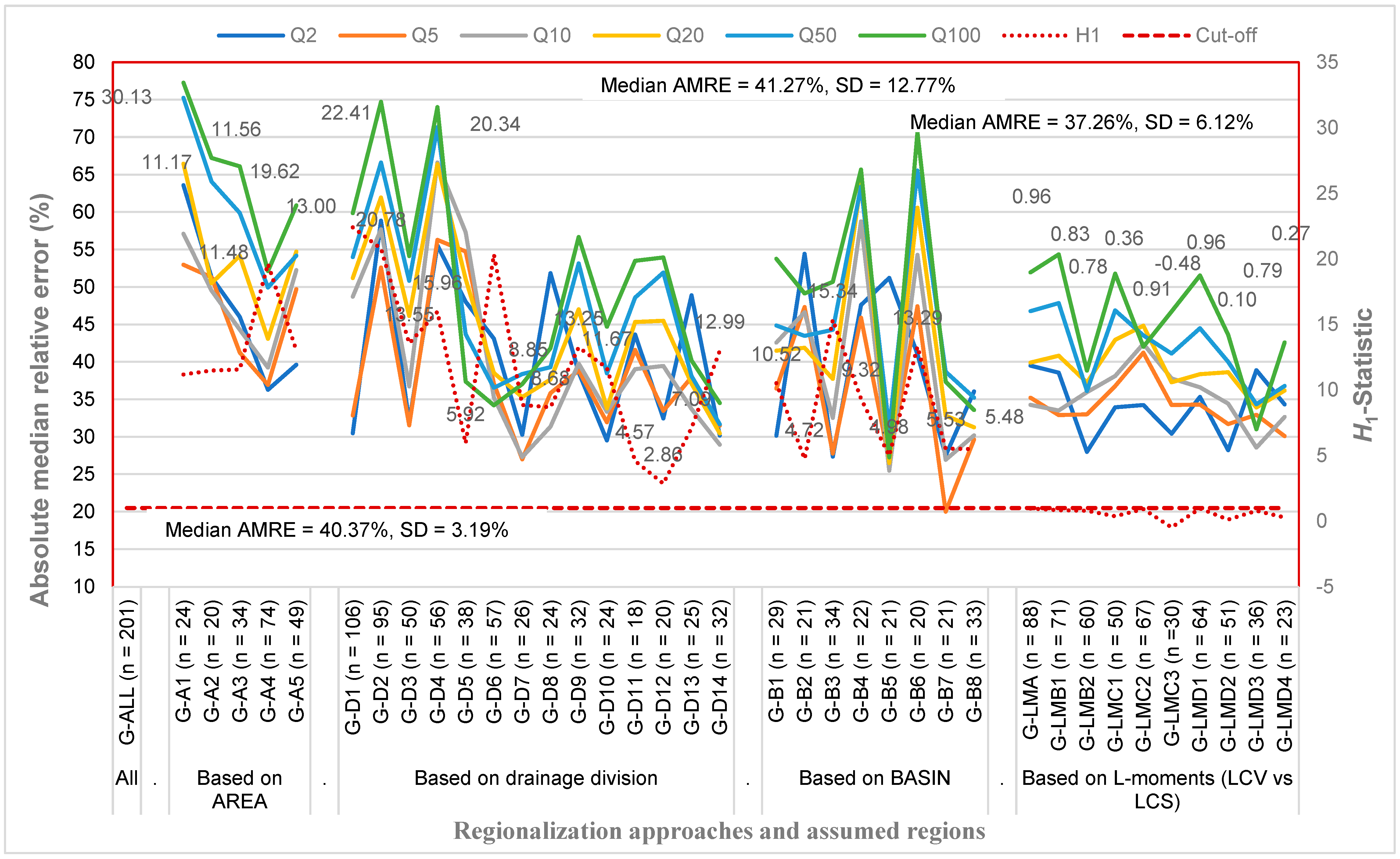
| Regionalization Approaches | Description | Region Notation | Site No. (n) | Site Covered (%) | Di-Values (≥3.00) | Hi-Statistics | Z-Statistics | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lowest | Highest | H1 | H2 | H3 | GLO | GEV | GNO | PE3 | GPA | |||||
| All stations | Placing 201 stations in a region | G-ALL | 201 | 100 | 3.26 | 6.43 | 30.13 | 20.58 | 11.51 | 17.18 | 12.98 | 7.59 | −1.77 | 0.02 |
| Based on AREA | ≤50 km2 | G-A1 | 24 | 12 | 3.72 | 11.17 | 6.51 | 2.53 | 6.72 | 5.43 | 3.51 | 0.19 | 1.30 | |
| 51–108 km2 | G-A2 | 20 | 10 | 3.04 | 3.49 | 11.48 | 8.12 | 4.13 | 5.10 | 3.88 | 2.22 | −0.66 | 0.06 | |
| 112–200 km2 | G-A3 | 34 | 17 | 3.34 | 11.56 | 6.47 | 3.72 | 7.88 | 5.95 | 3.80 | 0.07 | 0.23 | ||
| 201–500 km2 | G-A4 | 74 | 37 | 3.30 | 4.63 | 19.62 | 14.36 | 8.42 | 9.15 | 6.60 | 3.44 | −2.05 | −1.19 | |
| >500 km2 | G-A5 | 49 | 24 | 4.97 | 13.00 | 8.76 | 5.78 | 8.89 | 6.84 | 4.07 | −0.74 | 0.44 | ||
| Based on drainage division | Drainage division “2” | G-D1 | 106 | 53 | 3.34 | 5.36 | 22.41 | 16.03 | 9.25 | 14.50 | 11.19 | 7.16 | 0.17 | 1.15 |
| Drainage division “4” | G-D2 | 95 | 47 | 3.05 | 7.18 | 20.78 | 13.23 | 7.13 | 9.36 | 6.82 | 3.37 | −2.61 | −1.13 | |
| Drainage division “2” within NSW | G-D3 | 50 | 25 | 4.64 | 13.55 | 10.56 | 6.76 | 10.03 | 8.05 | 5.14 | 0.12 | 1.69 | ||
| Drainage division “2” within VIC | G-D4 | 56 | 28 | 3.41 | 4.13 | 15.96 | 11.74 | 6.71 | 10.03 | 7.43 | 4.77 | 0.16 | −0.15 | |
| Drainage division “4” within NSW | G-D5 | 38 | 19 | 3.06 | 4.10 | 5.92 | 4.14 | 2.07 | 3.83 | 2.85 | 0.57 | −3.36 | −0.83 | |
| Drainage division “4” within VIC | G-D6 | 57 | 28 | 3.16 | 5.80 | 20.34 | 11.41 | 5.22 | 9.83 | 7.14 | 4.54 | 0.01 | −0.58 | |
| Drainage division “2” within northern NSW | G-D7 | 26 | 13 | - | - | 8.85 | 7.46 | 5.11 | 6.91 | 5.23 | 3.21 | −0.30 | 0.13 | |
| Drainage division “2” within southern NSW | G-D8 | 24 | 12 | 4.47 | 8.68 | 5.77 | 3.81 | 8.22 | 6.94 | 4.62 | 0.62 | 2.56 | ||
| Drainage division “2” within eastern VIC | G-D9 | 32 | 16 | 3.60 | 13.25 | 9.57 | 5.10 | 7.43 | 5.57 | 3.49 | −0.14 | 0.05 | ||
| Drainage division “2” within western VIC | G-D10 | 24 | 12 | 3.00 | 11.67 | 7.49 | 4.11 | 7.00 | 5.11 | 3.47 | 0.61 | −0.16 | ||
| Drainage division “4” within northern NSW | G-D11 | 18 | 9 | 3.33 | 4.57 | 3.38 | 2.36 | 3.98 | 3.33 | 1.75 | −0.97 | 0.86 | ||
| Drainage division “4” within southern NSW | G-D12 | 20 | 10 | - | - | 2.86 | 1.88 | 0.50 | 1.47 | 0.80 | −0.69 | −3.25 | −1.66 | |
| Drainage division “4” within eastern VIC | G-D13 | 25 | 12 | - | - | 7.09 | 3.66 | 1.59 | 4.44 | 2.35 | 0.95 | −1.51 | −3.21 | |
| Drainage division “4” within western VIC | G-D14 | 32 | 16 | 3.11 | 6.45 | 12.99 | 7.76 | 4.98 | 9.63 | 7.84 | 5.56 | 1.60 | 2.34 | |
| Based on basin | Basin (‘201’, ‘203’, ‘204’, ’206’, ‘207’, ’208’, ’209’, ‘210’) | G-B1 | 29 | 14 | - | - | 10.52 | 8.79 | 5.79 | 7.13 | 5.39 | 3.32 | −0.27 | 0.15 |
| Basin (‘211’, ‘212’, ‘215’, ‘218’, ‘219’, ‘220’, ‘221’) | G-B2 | 21 | 10 | 3.20 | 4.72 | 4.27 | 3.40 | 9.30 | 7.90 | 5.82 | 2.23 | 3.40 | ||
| Basin (‘222’, ‘223’, ‘224’, ‘225’, ‘226’, ‘227’) | G-B3 | 34 | 17 | 3.14 | 15.34 | 10.94 | 5.35 | 5.73 | 4.04 | 2.01 | −1.53 | −1.07 | ||
| Basin (‘229’, ‘230’, ‘231’, ‘232’, ‘233’, ‘234’, ‘235’, ‘236’, ‘237’, ‘238’) | G-B4 | 22 | 11 | - | - | 9.32 | 5.51 | 3.05 | 6.97 | 5.34 | 3.66 | 0.75 | 0.59 | |
| Basin (‘401’, ‘402’, ‘403’, ‘404’) | G-B5 | 21 | 10 | - | - | 4.98 | 3.54 | 2.72 | 4.86 | 3.04 | 1.62 | −0.85 | −1.95 | |
| Basin (‘405’) | G-B6 | 20 | 10 | 3.79 | 13.29 | 6.58 | 1.84 | 4.78 | 2.87 | 1.52 | −0.84 | −2.26 | ||
| Basin (‘406’, ‘407’, ‘410’) | G-B7 | 21 | 10 | - | - | 5.53 | 3.64 | 2.74 | 6.07 | 4.91 | 3.01 | −0.28 | 1.05 | |
| Basin (‘411’, ‘412’, ‘415’, ‘416’, ‘418’, ‘419’, ‘421’) | G-B8 | 33 | 16 | 3.39 | 5.48 | 4.39 | 2.70 | 4.62 | 3.84 | 1.71 | −1.95 | 0.74 | ||
| Based on LCV and LSK space | Single largest homogeneous region | G-LMA | 88 | 44 | 5.35 | 0.96 | 0.50 | 0.86 | 13.95 | 11.90 | 7.92 | 1.06 | 4.72 | |
| Two largest homogeneous regions | G-LMB1 | 71 | 65 | 3.35 | 4.79 | 0.83 | −2.02 | −3.41 | 8.08 | 7.02 | 3.64 | −2.14 | 2.52 | |
| G-LMB2 | 60 | 3.02 | 0.78 | −1.56 | −1.33 | 16.81 | 13.30 | 10.35 | 5.20 | 3.55 | ||||
| Three largest homogeneous regions | G-LMC1 | 50 | 73 | 4.91 | 0.36 | −2.41 | −3.76 | 5.16 | 4.59 | 1.70 | −3.16 | 1.59 | ||
| G-LMC2 | 67 | 3.25 | 3.36 | 0.91 | −1.20 | −1.81 | 3.66 | 1.99 | 0.13 | −3.09 | −2.98 | |||
| G-LMC3 | 30 | 3.23 | −0.48 | −0.84 | −0.11 | 16.76 | 13.99 | 10.42 | 4.23 | 5.45 | ||||
| Four largest homogeneous regions | G-LMD1 | 64 | 87 | 3.07 | 4.80 | 0.96 | −1.52 | −2.86 | 6.98 | 6.19 | 2.83 | −2.85 | 2.36 | |
| G-LMD2 | 51 | - | - | 0.10 | −1.37 | −2.02 | 19.62 | 16.30 | 13.58 | 8.82 | 7.11 | |||
| G-LMD3 | 36 | 3.88 | 0.79 | −2.16 | −3.01 | 4.41 | 2.83 | 0.64 | −3.15 | −2.16 | ||||
| G-LMD4 | 23 | 3.08 | 0.27 | −1.66 | −2.43 | 8.84 | 5.28 | 4.50 | 2.85 | −2.93 | ||||
| Evaluation Criteria | QT | All | Based on AREA | Based on BASIN | Based on L-Moments (LCV vs. LSK) | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| G-ALL | G-A1 | G-A2 | G-A3 | G-A4 | G-A5 | G-B1 | G-B2 | G-B3 | G-B4 | G-B5 | G-B6 | G-B7 | G-B8 | G-LMA | G-LMB1 | G-LMB2 | G-LMC1 | G-LMC2 | G-LMC3 | G-LMD1 | G-LMD2 | G-LMD3 | G-LMD4 | ||
| AMRE | Q2 | 39.49 | 63.57 | 51.29 | 46.00 | 36.27 | 39.61 | 30.46 | 58.84 | 31.96 | 55.55 | 48.02 | 43.09 | 30.27 | 51.84 | 39.49 | 38.55 | 27.98 | 33.92 | 34.23 | 30.41 | 35.31 | 28.21 | 38.87 | 34.32 |
| Q5 | 37.80 | 52.96 | 51.29 | 41.25 | 36.93 | 49.70 | 32.84 | 52.59 | 31.52 | 56.28 | 54.72 | 37.11 | 26.98 | 35.82 | 35.22 | 32.90 | 32.99 | 36.76 | 41.22 | 34.23 | 34.30 | 31.68 | 32.94 | 30.09 | |
| Q10 | 36.98 | 57.09 | 49.51 | 44.29 | 39.22 | 52.24 | 48.69 | 57.69 | 36.73 | 66.61 | 57.30 | 35.26 | 27.29 | 31.34 | 34.25 | 33.50 | 35.95 | 38.10 | 42.40 | 37.78 | 36.59 | 34.41 | 28.55 | 32.65 | |
| Q20 | 41.24 | 66.45 | 50.50 | 54.16 | 43.08 | 54.71 | 51.19 | 61.94 | 46.11 | 66.38 | 51.06 | 38.52 | 35.29 | 37.63 | 39.89 | 40.81 | 37.23 | 42.94 | 44.82 | 37.28 | 38.36 | 38.62 | 33.91 | 36.18 | |
| Q50 | 43.04 | 75.25 | 64.06 | 59.89 | 49.92 | 54.17 | 53.97 | 66.60 | 50.81 | 71.31 | 43.69 | 36.54 | 38.38 | 39.29 | 46.77 | 47.85 | 36.11 | 46.86 | 43.53 | 41.11 | 44.49 | 39.99 | 34.34 | 36.78 | |
| Q100 | 45.34 | 77.27 | 67.21 | 66.10 | 52.09 | 60.87 | 59.84 | 74.70 | 54.12 | 73.99 | 37.37 | 34.19 | 37.02 | 41.81 | 51.93 | 54.34 | 38.81 | 51.77 | 42.01 | 46.73 | 51.53 | 43.60 | 30.99 | 42.59 | |
| MSE | Q2 | 2514.73 | 401.48 | 1465.38 | 1823.47 | 2877 | 6770 | 5380 | 11,839 | 1493 | 314 | 7621 | 1648 | 206 | 1717 | 1712 | 820 | 2326 | 736 | 2902 | 1736 | 696 | 2365 | 3095 | 3592 |
| Q5 | 13,166.85 | 4380.66 | 5373.60 | 19,734.92 | 141,92 | 36,263 | 25,387 | 121,274 | 7202 | 3125 | 56852 | 12,797 | 1223 | 8141 | 15,615 | 8780 | 13,864 | 7781 | 18,165 | 11,708 | 6840 | 13,760 | 17,213 | 10,520 | |
| Q10 | 36,474.56 | 39,183.65 | 14,464.86 | 87,771.38 | 35,444 | 103,510 | 73,838 | 485,875 | 18,771 | 10,417 | 78,074 | 31,879 | 2836 | 27,302 | 51,647 | 33,843 | 38,813 | 29,589 | 47,928 | 33,542 | 25,244 | 46,210 | 40,808 | 18,951 | |
| Q20 | 94,459.31 | 222,126.95 | 38,891.46 | 306,740.34 | 801,88 | 278,231 | 204313 | 1,856,370 | 44,676 | 26,355 | 80,394 | 58,223 | 6080 | 89,060 | 147,390 | 108,650 | 98,994 | 96,021 | 108,083 | 88,894 | 80,540 | 143,457 | 81,729 | 31,368 | |
| Q50 | 309,516.46 | 1,429,884.04 | 132,519.97 | 1,247,388.99 | 216,832 | 952,076 | 726,152 | 11,728,100 | 128,854 | 69,605 | 86,694 | 99,656 | 16,226 | 377,765 | 511,950 | 426,355 | 308,162 | 392,278 | 271,005 | 297,021 | 327,252 | 546,552 | 175,799 | 56,678 | |
| Q100 | 722,328.06 | 4,760,233.15 | 309,416.08 | 3,155,874.16 | 440,854 | 2,273,787 | 1,787,504 | 50,031,260 | 274,128 | 128,601 | 106,835 | 134,021 | 33,252 | 1,026,171 | 1,210,574 | 1,091,092 | 676,944 | 1,044,854 | 501,192 | 691,407 | 875,336 | 1,340,578 | 291,266 | 85,604 | |
| RMSE | Q2 | 50.15 | 20.04 | 38.28 | 42.70 | 53.64 | 82.28 | 73.35 | 108.81 | 38.64 | 17.73 | 87.30 | 40.60 | 14.36 | 41.44 | 41.38 | 28.63 | 48.23 | 27.12 | 53.87 | 41.67 | 26.38 | 48.63 | 55.64 | 59.94 |
| Q5 | 114.75 | 66.19 | 73.30 | 140.48 | 119.13 | 190.43 | 159.33 | 348.24 | 84.86 | 55.90 | 238.44 | 113.12 | 34.98 | 90.23 | 124.96 | 93.70 | 117.74 | 88.21 | 134.78 | 108.20 | 82.71 | 117.30 | 131.20 | 102.57 | |
| Q10 | 190.98 | 197.95 | 120.27 | 296.26 | 188.27 | 321.73 | 271.73 | 697.05 | 137.01 | 102.06 | 279.42 | 178.55 | 53.26 | 165.23 | 227.26 | 183.97 | 197.01 | 172.01 | 218.93 | 183.14 | 158.88 | 214.97 | 202.01 | 137.66 | |
| Q20 | 307.34 | 471.30 | 197.21 | 553.84 | 283.17 | 527.48 | 452.01 | 1362.49 | 211.37 | 162.34 | 283.54 | 241.29 | 77.98 | 298.43 | 383.91 | 329.62 | 314.63 | 309.87 | 328.76 | 298.15 | 283.80 | 378.76 | 285.88 | 177.11 | |
| Q50 | 556.34 | 1195.78 | 364.03 | 1116.87 | 465.65 | 975.74 | 852.15 | 3424.63 | 358.96 | 263.83 | 294.44 | 315.68 | 127.38 | 614.63 | 715.51 | 652.96 | 555.12 | 626.32 | 520.58 | 545.00 | 572.06 | 739.29 | 419.28 | 238.07 | |
| Q100 | 849.90 | 2181.80 | 556.25 | 1776.48 | 663.97 | 1507.91 | 1336.98 | 7073.28 | 523.57 | 358.61 | 326.86 | 366.09 | 182.35 | 1013.00 | 1100.26 | 1044.55 | 822.77 | 1022.18 | 707.95 | 831.51 | 935.59 | 1157.83 | 539.69 | 292.58 | |
| BIAS | Q2 | −9.53 | 1.95 | −4.49 | −3.11 | −10.69 | −14.87 | −1.19 | −4.77 | −4.00 | 0.69 | 13.60 | 6.91 | −0.51 | −3.90 | −6.60 | −3.33 | −9.12 | −3.37 | 4.67 | −5.71 | −3.17 | −7.32 | −3.60 | 2.58 |
| Q5 | −20.05 | 11.93 | −6.62 | 1.92 | −22.53 | −33.48 | −3.93 | 6.31 | −9.05 | 5.14 | 38.47 | 17.62 | −1.60 | −4.06 | −20.98 | −10.89 | −20.82 | −9.72 | 15.63 | −16.75 | −10.10 | −17.69 | −6.26 | 1.24 | |
| Q10 | −33.25 | 35.29 | −9.07 | 12.21 | −35.30 | −54.46 | −8.99 | 46.25 | −16.06 | 10.98 | 37.54 | 27.87 | −2.72 | −5.98 | −39.96 | −22.48 | −32.62 | −18.65 | 27.79 | −31.10 | −20.13 | −30.58 | −8.42 | −0.71 | |
| Q20 | −54.95 | 84.52 | −14.31 | 29.21 | −53.97 | −86.77 | −18.68 | 157.56 | −27.56 | 18.27 | 23.64 | 38.88 | −4.17 | −12.96 | −70.42 | −42.92 | −48.03 | −34.68 | 44.17 | −53.78 | −37.49 | −50.94 | −10.85 | −3.56 | |
| Q50 | −105.44 | 217.69 | −29.53 | 63.48 | −93.06 | −158.96 | −43.39 | 579.62 | −53.76 | 28.89 | −3.76 | 53.31 | −6.65 | −37.93 | −138.35 | −93.15 | −76.03 | −75.99 | 73.34 | −103.19 | −79.87 | −95.21 | −14.91 | −8.77 | |
| Q100 | −169.16 | 401.23 | −51.45 | 98.56 | −138.97 | −248.34 | −76.41 | 1375.82 | −86.32 | 36.63 | −26.68 | 63.62 | −8.85 | −77.51 | −220.83 | −159.53 | −104.73 | −133.30 | 102.11 | −161.54 | −135.94 | −147.16 | −19.10 | −13.95 | |
| RBIAS | Q2 | 22.24 | 396.41 | 40.60 | 26.60 | 21.75 | 20.11 | 15.81 | 61.28 | 11.83 | 36.06 | 83.04 | 48.34 | 8.72 | 36.78 | 18.83 | 19.18 | 13.13 | 28.15 | 41.89 | 16.32 | 25.32 | 10.09 | 19.12 | 26.48 |
| Q5 | 21.41 | 143.52 | 25.59 | 22.07 | 21.57 | 21.49 | 14.02 | 88.51 | 16.88 | 36.50 | 126.99 | 58.18 | 14.34 | 21.88 | 20.34 | 20.19 | 12.38 | 29.65 | 47.21 | 14.25 | 28.67 | 8.89 | 18.86 | 23.20 | |
| Q10 | 23.55 | 103.03 | 26.32 | 26.38 | 24.60 | 24.51 | 18.68 | 114.99 | 21.74 | 43.45 | 110.31 | 64.74 | 16.90 | 20.94 | 21.81 | 22.78 | 12.67 | 30.26 | 50.66 | 13.85 | 30.34 | 9.72 | 18.05 | 22.70 | |
| Q20 | 26.91 | 96.27 | 30.90 | 33.26 | 28.92 | 28.45 | 25.54 | 150.41 | 27.05 | 51.65 | 82.72 | 69.92 | 19.31 | 23.15 | 23.80 | 26.07 | 13.31 | 31.41 | 54.27 | 14.10 | 31.98 | 11.22 | 17.00 | 23.03 | |
| Q50 | 32.76 | 110.88 | 41.81 | 45.26 | 36.11 | 34.94 | 37.05 | 215.27 | 34.74 | 63.48 | 52.10 | 75.67 | 22.76 | 28.87 | 27.31 | 31.45 | 14.77 | 34.27 | 59.14 | 15.44 | 34.69 | 14.15 | 15.62 | 24.44 | |
| Q100 | 38.13 | 133.48 | 53.75 | 56.29 | 42.51 | 40.80 | 47.40 | 282.46 | 41.11 | 73.15 | 37.18 | 79.77 | 25.73 | 34.66 | 30.66 | 36.34 | 16.35 | 37.60 | 63.04 | 17.22 | 37.44 | 17.03 | 14.73 | 26.11 | |
| RRMSE | Q2 | 0.15 | 0.15 | 0.10 | 0.07 | 0.16 | 0.14 | 0.01 | 0.05 | 0.08 | 0.03 | 0.28 | 0.16 | 0.02 | 0.06 | 0.11 | 0.07 | 0.11 | 0.08 | 0.10 | 0.08 | 0.08 | 0.08 | 0.07 | 0.02 |
| Q5 | 0.13 | 0.39 | 0.06 | 0.02 | 0.14 | 0.13 | 0.01 | 0.02 | 0.08 | 0.10 | 0.37 | 0.20 | 0.02 | 0.02 | 0.12 | 0.08 | 0.11 | 0.07 | 0.17 | 0.09 | 0.07 | 0.08 | 0.06 | 0.01 | |
| Q10 | 0.13 | 0.71 | 0.05 | 0.07 | 0.14 | 0.13 | 0.02 | 0.09 | 0.09 | 0.14 | 0.25 | 0.23 | 0.02 | 0.02 | 0.13 | 0.09 | 0.11 | 0.07 | 0.22 | 0.10 | 0.08 | 0.09 | 0.05 | 0.00 | |
| Q20 | 0.15 | 1.15 | 0.06 | 0.11 | 0.15 | 0.13 | 0.03 | 0.21 | 0.10 | 0.16 | 0.12 | 0.25 | 0.02 | 0.03 | 0.15 | 0.10 | 0.12 | 0.08 | 0.26 | 0.12 | 0.09 | 0.10 | 0.05 | 0.01 | |
| Q50 | 0.18 | 1.87 | 0.07 | 0.16 | 0.17 | 0.15 | 0.04 | 0.45 | 0.13 | 0.18 | 0.01 | 0.27 | 0.03 | 0.04 | 0.18 | 0.13 | 0.13 | 0.09 | 0.31 | 0.15 | 0.10 | 0.12 | 0.05 | 0.02 | |
| Q100 | 0.21 | 2.52 | 0.09 | 0.18 | 0.19 | 0.17 | 0.05 | 0.76 | 0.16 | 0.18 | 0.08 | 0.27 | 0.03 | 0.06 | 0.20 | 0.15 | 0.14 | 0.11 | 0.35 | 0.17 | 0.12 | 0.14 | 0.05 | 0.02 | |
| RMSNE | Q2 | 0.93 | 17.97 | 1.52 | 1.00 | 0.86 | 0.80 | 0.75 | 1.99 | 0.57 | 0.97 | 3.11 | 1.53 | 0.52 | 1.08 | 0.83 | 0.76 | 0.59 | 1.04 | 1.55 | 0.75 | 0.95 | 0.55 | 0.84 | 1.05 |
| Q5 | 0.95 | 5.47 | 0.99 | 0.81 | 0.88 | 0.93 | 0.70 | 2.74 | 0.72 | 1.09 | 5.15 | 1.93 | 0.76 | 0.82 | 0.86 | 0.81 | 0.54 | 1.15 | 1.73 | 0.65 | 1.14 | 0.48 | 0.82 | 0.94 | |
| Q10 | 1.03 | 3.19 | 1.00 | 0.93 | 1.01 | 1.03 | 0.80 | 3.50 | 0.83 | 1.27 | 4.44 | 2.10 | 0.88 | 0.84 | 0.90 | 0.90 | 0.55 | 1.11 | 1.86 | 0.61 | 1.17 | 0.50 | 0.80 | 0.91 | |
| Q20 | 1.13 | 2.60 | 1.13 | 1.13 | 1.18 | 1.14 | 0.95 | 4.49 | 0.93 | 1.46 | 3.23 | 2.22 | 0.97 | 0.95 | 0.95 | 1.00 | 0.56 | 1.08 | 2.01 | 0.60 | 1.18 | 0.53 | 0.77 | 0.91 | |
| Q50 | 1.29 | 3.05 | 1.44 | 1.48 | 1.44 | 1.30 | 1.22 | 6.35 | 1.07 | 1.72 | 1.89 | 2.35 | 1.07 | 1.15 | 1.05 | 1.18 | 0.59 | 1.10 | 2.21 | 0.61 | 1.18 | 0.60 | 0.74 | 0.94 | |
| Q100 | 1.42 | 3.90 | 1.78 | 1.80 | 1.66 | 1.43 | 1.49 | 8.38 | 1.17 | 1.93 | 1.29 | 2.44 | 1.14 | 1.34 | 1.14 | 1.33 | 0.63 | 1.16 | 2.37 | 0.64 | 1.20 | 0.67 | 0.72 | 0.98 | |
| R2 | Q2 | 0.72 | 0.73 | 0.81 | 0.71 | 0.51 | 0.59 | 0.93 | 0.55 | 0.86 | 0.79 | 0.82 | 0.75 | 0.93 | 0.73 | 0.70 | 0.70 | 0.82 | 0.75 | 0.80 | 0.81 | 0.74 | 0.89 | 0.85 | 0.92 |
| Q5 | 0.73 | 0.72 | 0.86 | 0.69 | 0.53 | 0.57 | 0.93 | 0.52 | 0.83 | 0.80 | 0.85 | 0.67 | 0.88 | 0.84 | 0.69 | 0.69 | 0.83 | 0.72 | 0.78 | 0.82 | 0.71 | 0.88 | 0.85 | 0.93 | |
| Q10 | 0.72 | 0.69 | 0.87 | 0.67 | 0.54 | 0.57 | 0.90 | 0.50 | 0.79 | 0.78 | 0.87 | 0.63 | 0.85 | 0.87 | 0.69 | 0.67 | 0.83 | 0.71 | 0.78 | 0.82 | 0.69 | 0.88 | 0.86 | 0.93 | |
| Q20 | 0.70 | 0.66 | 0.87 | 0.66 | 0.54 | 0.58 | 0.87 | 0.48 | 0.75 | 0.75 | 0.88 | 0.60 | 0.81 | 0.87 | 0.69 | 0.66 | 0.83 | 0.69 | 0.77 | 0.82 | 0.68 | 0.87 | 0.86 | 0.93 | |
| Q50 | 0.68 | 0.62 | 0.86 | 0.64 | 0.54 | 0.57 | 0.81 | 0.46 | 0.70 | 0.72 | 0.89 | 0.57 | 0.78 | 0.85 | 0.69 | 0.64 | 0.82 | 0.67 | 0.76 | 0.81 | 0.66 | 0.86 | 0.87 | 0.93 | |
| Q0 | 0.66 | 0.59 | 0.84 | 0.63 | 0.53 | 0.57 | 0.76 | 0.45 | 0.67 | 0.70 | 0.89 | 0.54 | 0.76 | 0.84 | 0.68 | 0.63 | 0.81 | 0.65 | 0.76 | 0.80 | 0.65 | 0.84 | 0.88 | 0.93 | |
| Evaluation Criteria | QT | Based on L-Moments (LCV vs. LSK) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| G-LMA | G-LMB1 | G-LMB2 | G-LMC1 | G-LMC2 | G-LMC3 | G-LMD1 | G-LMD2 | G-LMD3 | G-LMD4 | ||
| AMRE | Q2 | 44.34 | 51.55 | 40.09 | 55.11 | 39.70 | 43.04 | 53.87 | 39.12 | 38.07 | 37.81 |
| Q5 | 45.16 | 52.16 | 38.08 | 58.02 | 47.36 | 43.98 | 57.91 | 36.42 | 35.88 | 34.14 | |
| Q10 | 47.61 | 54.07 | 34.08 | 58.57 | 47.01 | 42.62 | 57.50 | 38.07 | 36.74 | 34.21 | |
| Q20 | 46.94 | 54.50 | 35.30 | 62.98 | 45.05 | 38.53 | 59.35 | 38.27 | 38.38 | 35.07 | |
| Q50 | 46.15 | 49.34 | 32.45 | 59.78 | 45.14 | 40.76 | 57.52 | 41.00 | 38.44 | 38.42 | |
| Q100 | 49.08 | 52.68 | 36.22 | 58.53 | 45.60 | 46.40 | 56.26 | 42.90 | 36.17 | 41.25 | |
| MSE | Q2 | 2856 | 1352 | 4017 | 1457 | 1923 | 3055 | 1326 | 4408 | 2766 | 3866 |
| Q5 | 25535 | 14,548 | 22,134 | 15,881 | 6937 | 22,212 | 14,187 | 25,240 | 13,691 | 14,161 | |
| Q10 | 84,987 | 53,586 | 58,871 | 58,805 | 13,523 | 68,967 | 52,290 | 78,829 | 31,159 | 29,867 | |
| Q20 | 238,889 | 162,588 | 138,274 | 180,426 | 23,432 | 186,568 | 159,991 | 219,196 | 61,011 | 57,210 | |
| Q50 | 796,207 | 589,607 | 378,756 | 670,029 | 43,527 | 599,810 | 591,596 | 725,082 | 129,700 | 122,138 | |
| Q100 | 1,811,742 | 1,424,691 | 757,186 | 1,656,379 | 65,925 | 1,327,169 | 1,455,826 | 1,623,676 | 215,182 | 204,411 | |
| RMSE | Q2 | 53.44 | 36.77 | 63.38 | 38.17 | 43.85 | 55.27 | 36.42 | 66.39 | 52.60 | 62.18 |
| Q5 | 159.80 | 120.61 | 148.77 | 126.02 | 83.29 | 149.04 | 119.11 | 158.87 | 117.01 | 119.00 | |
| Q10 | 291.52 | 231.49 | 242.63 | 242.50 | 116.29 | 262.62 | 228.67 | 280.77 | 176.52 | 172.82 | |
| Q20 | 488.76 | 403.22 | 371.85 | 424.77 | 153.07 | 431.93 | 399.99 | 468.18 | 247.00 | 239.19 | |
| Q50 | 892.30 | 767.86 | 615.43 | 818.55 | 208.63 | 774.47 | 769.15 | 851.52 | 360.14 | 349.48 | |
| Q100 | 1346.01 | 1193.60 | 870.16 | 1287.00 | 256.76 | 1152.03 | 1206.58 | 1274.24 | 463.88 | 452.12 | |
| BIAS | Q2 | −29.58 | −24.15 | −31.14 | −25.54 | −7.95 | −29.66 | −24.32 | −34.24 | −17.32 | −16.46 |
| Q5 | −89.83 | −77.62 | −74.30 | −86.00 | −14.76 | −80.45 | −80.18 | −85.58 | −39.54 | −34.90 | |
| Q10 | −160.31 | −143.76 | −118.40 | −163.06 | −20.41 | −136.24 | −150.26 | −144.48 | −60.40 | −54.61 | |
| Q20 | −259.15 | −240.23 | −174.50 | −277.86 | −26.71 | −211.12 | −253.56 | −225.31 | −85.37 | −79.81 | |
| Q50 | −447.24 | −430.99 | −270.92 | −509.77 | −36.15 | −347.52 | −460.10 | −374.67 | −125.64 | −122.18 | |
| Q100 | −646.25 | −639.47 | −364.04 | −767.95 | −44.17 | −486.44 | −688.11 | −527.84 | −162.38 | −161.59 | |
| RBIAS | Q2 | −33.05 | −40.22 | −21.91 | −45.23 | 6.97 | −28.03 | −43.58 | −26.47 | −16.55 | 6.58 |
| Q5 | −33.50 | −40.80 | −22.60 | −47.28 | 7.09 | −29.74 | −45.07 | −27.91 | −17.38 | 4.35 | |
| Q10 | −32.83 | −39.31 | −22.39 | −46.49 | 7.80 | −29.90 | −44.11 | −27.44 | −17.67 | 3.98 | |
| Q20 | −30.99 | −37.05 | −21.59 | −44.77 | 8.87 | −28.90 | −42.21 | −25.81 | −17.89 | 4.37 | |
| Q50 | −26.55 | −32.78 | −19.32 | −41.16 | 10.60 | −25.59 | −38.22 | −21.65 | −17.97 | 5.93 | |
| Q100 | −21.53 | −28.41 | −16.58 | −37.33 | 12.20 | −21.46 | −33.91 | −16.85 | −17.80 | 7.87 | |
| RRMSE | Q2 | 0.50 | 0.54 | 0.39 | 0.61 | 0.17 | 0.43 | 0.58 | 0.39 | 0.35 | 0.14 |
| Q5 | 0.52 | 0.55 | 0.39 | 0.60 | 0.16 | 0.44 | 0.58 | 0.38 | 0.36 | 0.16 | |
| Q10 | 0.54 | 0.56 | 0.40 | 0.60 | 0.16 | 0.46 | 0.59 | 0.41 | 0.37 | 0.18 | |
| Q20 | 0.55 | 0.57 | 0.42 | 0.61 | 0.16 | 0.48 | 0.59 | 0.44 | 0.38 | 0.20 | |
| Q50 | 0.58 | 0.59 | 0.45 | 0.61 | 0.15 | 0.50 | 0.60 | 0.48 | 0.38 | 0.23 | |
| Q100 | 0.59 | 0.60 | 0.47 | 0.61 | 0.15 | 0.52 | 0.60 | 0.51 | 0.39 | 0.25 | |
| RMSNE | Q2 | 0.57 | 0.55 | 0.45 | 0.62 | 1.13 | 0.53 | 0.60 | 0.45 | 0.60 | 0.86 |
| Q5 | 0.55 | 0.56 | 0.43 | 0.60 | 1.13 | 0.49 | 0.59 | 0.43 | 0.55 | 0.77 | |
| Q10 | 0.55 | 0.57 | 0.43 | 0.60 | 1.15 | 0.48 | 0.59 | 0.43 | 0.53 | 0.73 | |
| Q20 | 0.55 | 0.59 | 0.43 | 0.60 | 1.20 | 0.47 | 0.60 | 0.44 | 0.52 | 0.72 | |
| Q50 | 0.56 | 0.61 | 0.44 | 0.61 | 1.27 | 0.48 | 0.61 | 0.46 | 0.50 | 0.73 | |
| Q100 | 0.59 | 0.63 | 0.47 | 0.62 | 1.33 | 0.50 | 0.64 | 0.49 | 0.50 | 0.76 | |
| R2 | Q2 | 0.70 | 0.70 | 0.82 | 0.75 | 0.80 | 0.81 | 0.74 | 0.89 | 0.85 | 0.92 |
| Q5 | 0.69 | 0.69 | 0.83 | 0.72 | 0.78 | 0.82 | 0.71 | 0.88 | 0.85 | 0.93 | |
| Q10 | 0.69 | 0.67 | 0.83 | 0.71 | 0.78 | 0.82 | 0.69 | 0.88 | 0.86 | 0.93 | |
| Q20 | 0.69 | 0.66 | 0.83 | 0.69 | 0.77 | 0.82 | 0.68 | 0.87 | 0.86 | 0.93 | |
| Q50 | 0.69 | 0.64 | 0.82 | 0.67 | 0.76 | 0.81 | 0.66 | 0.86 | 0.87 | 0.93 | |
| Q100 | 0.68 | 0.63 | 0.81 | 0.65 | 0.76 | 0.80 | 0.65 | 0.84 | 0.88 | 0.93 | |
| Comparison in % (n) | LCV-LSK Space [% (n)] | Total (n) | ||||
|---|---|---|---|---|---|---|
| G-LMD1 | G-LMD2 | G-LMD3 | G-LMD4 | |||
| PC1 vs. PC2 space | QR1 | 25 (16) | 19.61 (10) | 19.44 (7) | 0 (0) | 33 |
| QR2 | 26.56 (17) | 21.57 (11) | 8.33 (3) | 65.22 (15) | 46 | |
| QR3 | 25 (16) | 29.41 (15) | 38.89 (14) | 34.78 (8) | 53 | |
| QR4 | 23.44 (15) | 29.41 (15) | 33.33 (12) | 0 (0) | 42 | |
| Ward’s Method | WMR1 | 9.38 (6) | 17.65 (9) | 0 (0) | 0 (0) | 15 |
| WMR2 | 18.75 (12) | 9.8 (5) | 11.11 (4) | 78.26 (18) | 39 | |
| WMR3 | 21.88 (14) | 29.41 (15) | 47.22 (17) | 17.39 (4) | 50 | |
| WMR4 | 50 (32) | 43.14 (22) | 41.67 (15) | 4.35 (1) | 70 | |
| K-means clustering | KMR1 | 9.38 (6) | 17.65 (9) | 0 (0) | 0 (0) | 15 |
| KMR2 | 40.63 (26) | 37.25 (19) | 38.89 (14) | 0 (0) | 59 | |
| KMR3 | 18.75 (12) | 11.76 (6) | 11.11 (4) | 82.61 (19) | 41 | |
| KMR4 | 31.25 (20) | 33.33 (17) | 50 (18) | 17.39 (4) | 59 | |
| Total | 100 (64) | 100 (51) | 100 (36) | 100 (23) | 174 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, A.; Rahman, A.; Rafi, R.S.M.H.; Khan, Z.; Mannan, H. Statistical and Physical Significance of Homogeneous Regions in Regional Flood Frequency Analysis. Water 2025, 17, 1799. https://doi.org/10.3390/w17121799
Ahmed A, Rahman A, Rafi RSMH, Khan Z, Mannan H. Statistical and Physical Significance of Homogeneous Regions in Regional Flood Frequency Analysis. Water. 2025; 17(12):1799. https://doi.org/10.3390/w17121799
Chicago/Turabian StyleAhmed, Ali, Ataur Rahman, Ridwan S. M. H. Rafi, Zaved Khan, and Haider Mannan. 2025. "Statistical and Physical Significance of Homogeneous Regions in Regional Flood Frequency Analysis" Water 17, no. 12: 1799. https://doi.org/10.3390/w17121799
APA StyleAhmed, A., Rahman, A., Rafi, R. S. M. H., Khan, Z., & Mannan, H. (2025). Statistical and Physical Significance of Homogeneous Regions in Regional Flood Frequency Analysis. Water, 17(12), 1799. https://doi.org/10.3390/w17121799







