Evaluating Drought Mitigation Measures for Wetland Management with DEMATEL: A Case Study Report of the Koviljsko–Petrovaradinski Rit Wetland in Serbia
Abstract
1. Introduction
2. Research Methods
2.1. DEMATEL
2.2. Conformity
2.3. Spearman’s Rank Correlation Coefficient
3. Study Area and Problem Description
3.1. The Problem to Be Solved by DEMATEL Methodology
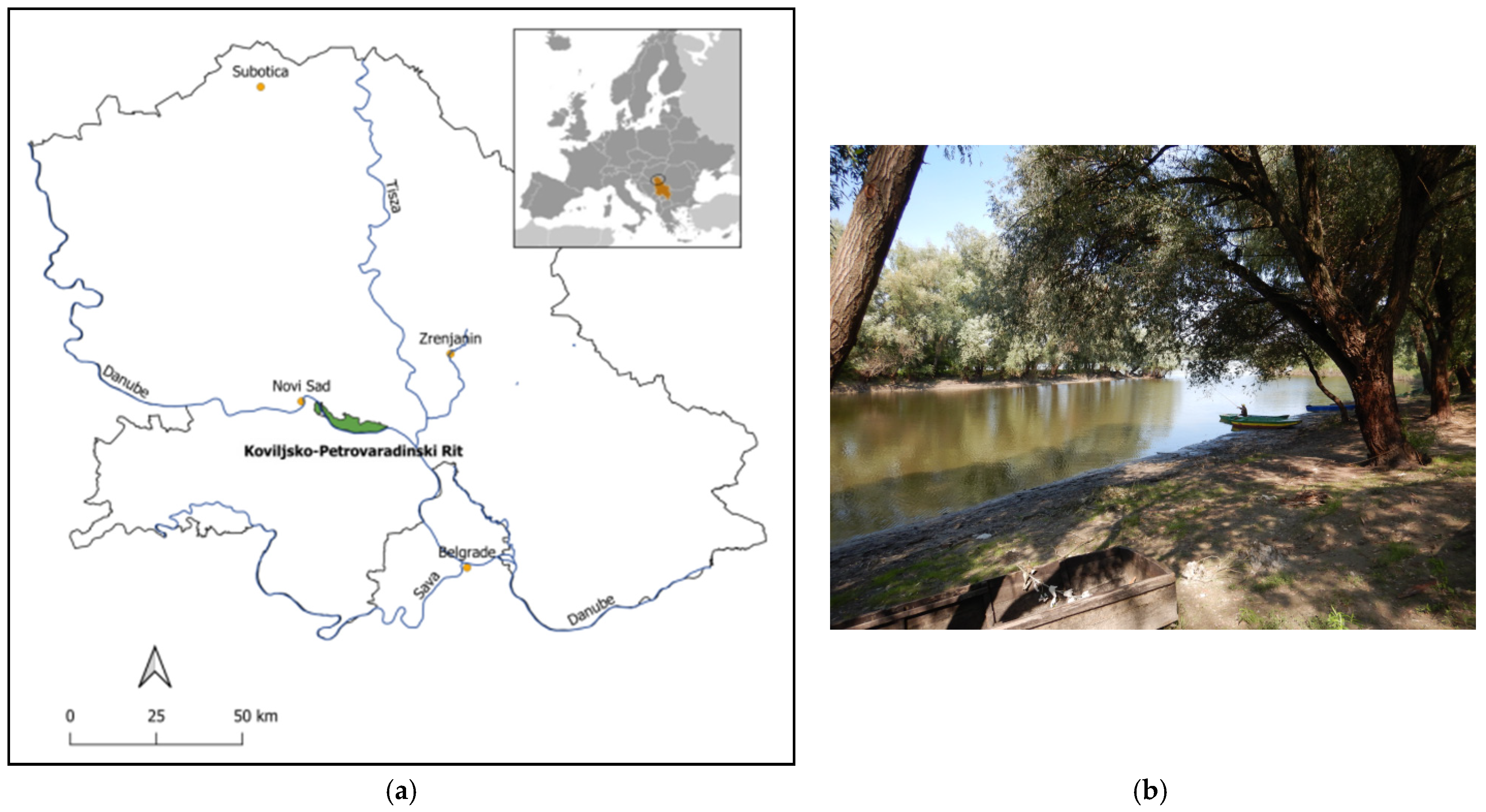
3.2. Description of Selected Measures and Participating Experts
| Expert | Background/ Academic Degree | Professional Activity | Field of Expertise |
| E1 | M.Sc. | public institution | environmental engineering |
| E2 | M.Sc. | public institution | environmental engineering |
| E3 | M.Sc./PhD cand. | academia | water management/environment |
| E4 | M.Sc./PhD cand. | academia | agriculture/water management |
| E5 | Professor | academia | academia/water management |
| E6 | Professor | academia | academia/water management |
| E7 | B.Sc. | public institution | environmental engineering |
| E8 | M.Sc. | public enterprise/private co. | forestry engineering |
| E9 | M.Sc. | public enterprise/private co. | forestry engineering |
| E10 | Dr. | public enterprise | water management |
| E11 | Ph.D. | public enterprise | water management |
| E12 | Professor | academia | academia/civil engineering |
| Measure | Description | |
| M1 | Floodplain restoration | Rewatering and restoration of wetlands, conservation of mires, near-natural widening of the water body, reforestation, promotion of near-natural floodplain development, reduction in sealing, rain seepage facilities, green roofs, restoration of former inundation areas, preserving retention areas, conversion of arable land to permanent pasture, and demolishing of flood-sensitive facilities [12]. |
| M2 | Habitat improvement | Removal of bed or bank consolidation, introduction of large wood or stones, creation of gravel spawning grounds, allowing erosion of the shores, re-meandering, reactivating primary floodplains, connecting tributaries or cut-off meanders, fish protection, sediment management, creation of shallow water zones and typical bank structures, and de-sludging [12]. |
| M3 | Prevention or control of the adverse impacts of invasive species | Promotion of autochthonous plant communities, combat of ecosystem-damaging neobiota, and protection of native species [12]. |
| M4 | Policy changes | Improvements in the legislative system and enforcement in the area of nature protection, implementation of national and international environmental legislation efforts, conducting of regular evaluations, and improvement in strategies and adaptation measures [10]. |
| M5 | Environmental education and awareness campaign | Raising public awareness of water-saving behavior; awareness raising and support of strong public education and training programs will require major investments in monitoring, research, technology transfer, and education [10]. |
| M6 | Streamlining the decision-making process | Improvements in communication and coordination between different sectors. |
| M7 | Application of nature-based solutions | Promotion of nature-based solutions as a sustainable way of reducing drought risk. |
4. DEMATEL Application
- The standard DEMATEL methodology, as described in Steps 1–5, is applied to each group member. Corresponding priority (weight) vectors are calculated using Formula (7).
- Individual direct-relation matrices in principle can be aggregated into a group matrix in three ways: (a) additively; (b) using the rough numbers method; and (c) geometrically. In this study, the standard DEMATEL methodology is applied to the group direct-relation matrix in the same manner as in the previous step, and the corresponding group priority vector is derived by additive aggregation.
- Conformity coefficients and Spearman’s rank correlation coefficients are computed for each group member to identify potential outliers.
- All results are collected and discussed.
4.1. DEMATEL Results by Individuals
4.2. DEMATEL Results for the Group
4.3. Weights of Measures
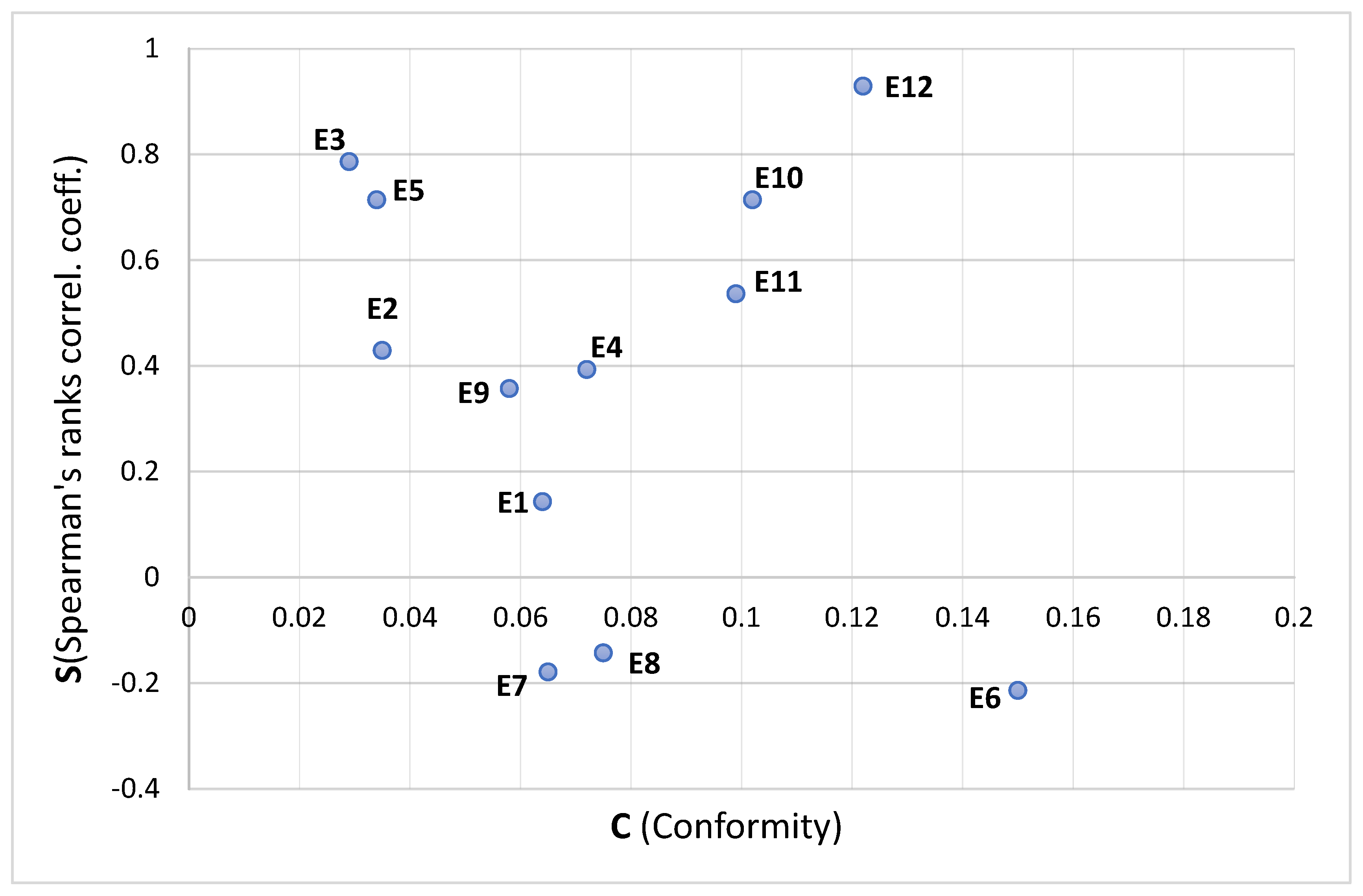
4.4. Analysis of Experts’ Correlation with Group Decision
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- EPA. Available online: https://www.epa.gov/cwa-404/how-wetlands-are-defined-and-identified-under-cwa-section-404 (accessed on 1 February 2024).
- Mitsch, W.J.; Gosselink, J.G. Wetlands, 2nd ed.; Wiley: New York, NY, USA, 1993; p. 920. [Google Scholar]
- Bongaarts, J. Summary for policymakers of the global assessment report on biodiversity and ecosystem services of the Intergovernmental Science-Policy Platform on Biodiversity and Ecosystem Services. Popul. Dev. Rev. 2019, 45, 680–681. [Google Scholar] [CrossRef]
- Junk, W.J.; An, S.; Finlayson, C.M.; Gopal, B.; Květ, J.; Mitchell, S.A.; Mitsch, W.J.; Robarts, R.D. Current state of knowledge regarding the world’s wetlands and their future under global climate change: A synthesis. Aquat. Sci. 2013, 75, 151–167. [Google Scholar] [CrossRef]
- Gxokwe, S.; Dube, T.; Mazvimavi, D.; Grenfell, M. Using cloud computing techniques to monitor long-term variations in ecohydrological dynamics of small seasonally-flooded wetlands in semi-arid South Africa. J. Hydrol. 2022, 612, 128080. [Google Scholar] [CrossRef]
- Ballut-Dajud, G.A.; Sandoval Herazo, L.C.; Fernández-Lambert, G.; Marín-Muñiz, J.L.; López Méndez, M.C.; Betanzo-Torres, E.A. Factors affecting wetland loss: A review. Land 2022, 11, 434. [Google Scholar] [CrossRef]
- Davidson, N.C. How much wetland has the world lost? Long-term and recent trends in global wetland area. Mar. Freshw. Res. 2014, 65, 934–941. [Google Scholar] [CrossRef]
- Li, Z.T.; Li, M.; Xia, B.C. Spatio-temporal dynamics of ecological security pattern of the Pearl River Delta urban agglomeration based on LUCC simulation. Ecol. Indic. 2020, 114, 106319. [Google Scholar] [CrossRef]
- Xu, X.; Chen, M.; Yang, G.; Jiang, B.; Zhang, J. Wetland ecosystem services research: A critical review. Glob. Ecol. Conserv. 2020, 22, 01027. [Google Scholar] [CrossRef]
- ICPDR. Available online: http://www.icpdr.org/main/climate-change-adaptation-measures-toolbox (accessed on 14 February 2024).
- INTEREG. Available online: https://www.interreg-danube.eu/approved-projects/danube-floodplain/outputs/ (accessed on 9 February 2024).
- Hornung, L.K.; Podschun, S.A.; Pusch, M. Linking ecosystem services and measures in river and floodplain management. Ecosyst. People 2019, 15, 214–231. [Google Scholar] [CrossRef]
- Stäps, J.; Gericke, A.; Lungu, A.; Stammel, B. (Eds.) Ecosystem Services in Floodplains and Their Potential to Improve Water Quality—A Manual for the IDES Tool, Eichstätt/Berlin/Bucharest, Germany, 2022. [CrossRef]
- Chen, V.Y.C.; Lin, J.C.L.; Tzeng, G.H. Assessment and improvement of wetlands environmental protection plans for achieving sustainable development. Environ. Res. 2019, 169, 280–296. [Google Scholar] [CrossRef]
- Fonseca, K.; Espitia, E.; Breuer, L.; Correa, A. Using fuzzy cognitive maps to promote nature-based solutions for water quality improvement in developing-country communities. J. Clean. Prod. 2022, 377, 134246. [Google Scholar] [CrossRef]
- Mazzuto, G.; Stylios, C.; Ciarapica, F.E.; Bevilacqua, M.; Voula, G. Improved Decision-Making through a DEMATEL and Fuzzy Cognitive Maps-Based Framework. Math. Probl. Eng. 2022, 2022, 2749435. [Google Scholar] [CrossRef]
- Mourhir, A. Scoping review of the potentials of fuzzy cognitive maps as a modeling approach for integrated environmental assessment and management. Environ. Model. Softw. 2021, 135, 104891. [Google Scholar] [CrossRef]
- Castro, C. Systems-thinking for environmental policy coherence: Stakeholder knowledge, fuzzy logic, and causal reasoning. Environ. Sci. Policy 2022, 136, 413–427. [Google Scholar] [CrossRef]
- Schön, F.; Domínguez, A.; Achkar, M. Urban wetlands, their dynamics and management strategies from the perspective of Environmental Geography. Geogr. J. 2022, 188, 415–428. [Google Scholar] [CrossRef]
- Gabus, A.; Fontela, E.; Gabus, S. World Problems, an Invitation to Further Thought Within the Framework of DEMATEL; Battelle Geneva Research Center: Geneva, Switzerland, 1972; Volume 1. [Google Scholar]
- Aksakal, E.; Dağdeviren, M.; Yüksel, I. A new Hybrid Approach to intern problems: Ahp and Dematel. In Proceedings of the International Symposium on the Analytic Hierarchy Process, Sorrento, Italy, 15–18 June 2011. [Google Scholar]
- Du, Y.W.; Li, X.X. Hierarchical DEMATEL method for complex systems. Expert Syst. Appl. 2021, 167, 113871. [Google Scholar] [CrossRef]
- Gandhi, S.; Mangla, S.K.; Kumar, P.; Kumar, D. A combined approach using AHP and DEMATEL for evaluating success factors in implementation of green supply chain management in Indian manufacturing industries. Int. J. Logist.-Res. Appl. 2016, 19, 537–561. [Google Scholar] [CrossRef]
- Srdjevic, B.; Lakicevic, M. Causality and Importance of Sustainable Forestry Goals: Strategic and Tactical Assessment by DEMATEL and AHP. Forests 2023, 14, 77. [Google Scholar] [CrossRef]
- Yazdi, M.; Khan, F.; Abbassi, R.; Rusli, R. Improved DEMATEL methodology for effective safety management decision-making. Saf. Sci. 2020, 127, 104705. [Google Scholar] [CrossRef]
- Si, S.L.; You, X.Y.; Liu, H.C.; Zhang, P. DEMATEL technique: A systematic review of the state-of-the-art literature on methodologies and applications. Math. Probl. Eng. 2018, 2018, 3696457. [Google Scholar] [CrossRef]
- Srđević, Z.; Srđević, B.; Suvočarev, K.; Galamboš, L. Hybrid constructed wetland selection as a group decision-making problem. Water Resour. Manag. 2020, 34, 295–310. [Google Scholar] [CrossRef]
- Srdjevic, B.; Srdjevic, Z. Evaluating groundwater ponds for urban drinking water supply under uncertainty. Water Supply 2022, 22, 7643–7655. [Google Scholar] [CrossRef]
- Forman, E.; Peniwati, K. Aggregating individual judgments and priorities with the analytic hierarchy process. Eur. J. Oper. Res. 1998, 108, 165–169. [Google Scholar] [CrossRef]
- Tsai, C.H.; Lee, Y.C.; Yen, T.M. Using Importance-Performance Analysis and Decision Making Trial and Evaluation Laboratory to Enhance Order-Winner Criteria–a Study of Computer Industry. Inf. Technol. J. 2008, 7, 396–408. [Google Scholar]
- Dalalah, D.; Al-Tahat, M.; Bataineh, K. Mutually dependent multi-criteria decision making. Fuzzy Inf. Eng. 2012, 4, 195–216. [Google Scholar] [CrossRef]
- Golany, B.; Kress, M. A multicriteria evaluation of methods for obtaining weights from ratio-scale matrices. Eur. J. Oper. Res. 1993, 69, 210–220. [Google Scholar] [CrossRef]
- Sušnik, A.; Gregorič, G.; Szalai, S.; Bokal, S.; Srđević, Z. Making drought management in the Danube region efficient and operative: Drought risk in the Danube region project (DriDanube). Vodoprivreda 2018, 50, 349–354. [Google Scholar]
- Srđević, Z.; Stammel, B.; Ionescu, C.; Galamboš, L.; Srđević, B.; Grabić, J.; Ždero, S.; Ilić, M.; Benka, P.; Antonić, N. Stakeholders in the Koviljsko-Petrovaradinski Rit special nature reserve near Novi Sad, Serbia: Who are they and how to involve them in the processes of identification and integration of ecosystem services important for improving the Danube water quality? (In Serbian: Stejkholderi u specijalnom rezervatu prirode Koviljsko-petrovaradinski rit kod Novog Sada: Ko su i kako ih uključiti u procese identifikacije i integracije ekosistemskih usluga važnih za poboljšanje kvaliteta vode Dunava?). Vodoprivreda 2021, 53, 241–248. [Google Scholar]


| Description | Numerical |
|---|---|
| No influence | 0 |
| Small influence | 1 |
| Medium influence | 2 |
| Significant influence | 3 |
| Extremely significant influence | 4 |
| Factors | F1 | F2 | … | Fn |
|---|---|---|---|---|
| F1 | 0 | 3 | … | 4 |
| F2 | 4 | 0 | … | 1 |
| … | 1 | 2 | … | 2 |
| Fn | 0 | 3 | … | 0 |
| Measures | M1 | M2 | M3 | M4 | M5 | M6 | M7 |
|---|---|---|---|---|---|---|---|
| M1 floodplain restoration | 0 | 3 | 4 | 4 | 3 | 3 | 4 |
| M2 habitat improvement | 4 | 0 | 4 | 4 | 3 | 3 | 4 |
| M3 control invasive species | 3 | 3 | 0 | 4 | 4 | 3 | 4 |
| M4 policy changes | 4 | 4 | 4 | 0 | 4 | 4 | 4 |
| M5 education and awareness | 3 | 3 | 3 | 3 | 0 | 3 | 3 |
| M6 streamlining the d-m pr. | 3 | 3 | 3 | 3 | 4 | 0 | 4 |
| M7 app. of nat. based sol. | 4 | 4 | 4 | 4 | 3 | 3 | 0 |
| Expert | Measures Cause(+)/Effect(−) Relations | ||||||
|---|---|---|---|---|---|---|---|
| M1 Floodplain Restoration | M2 Habitat Improv. | M3 Control Inv. Species | M4 Policy Changes | M5 Education/ Awareness | M6 Streamlining Dm Process | M7 App. of Nat. Based Solut. | |
| E1 enviro | Cause (+) | Cause (+) | Cause (+) | Cause (+) | Effect (−) | Effect (−) | Cause (+) |
| E2 enviro | Effect (−) | Effect (−) | Effect (−) | Effect (−) | Cause (+) | Cause (+) | Cause (+) |
| E3 water | Effect (−) | Effect (−) | Effect (−) | Effect (−) | Cause (+) | Cause (+) | Cause (+) |
| E4 agric | Effect (−) | Effect (−) | Effect (−) | Cause (+) | Cause (+) | Cause (+) | Effect (−) |
| E5 acade | Effect (−) | Effect (−) | Effect (−) | Cause (+) | Cause (+) | Cause (+) | Cause (+) |
| E6 acade | Effect (−) | Effect (−) | Effect (−) | Cause (+) | Cause (+) | Cause (+) | Effect (−) |
| E7 enviro | Cause (+) | Cause (+) | Effect (−) | Cause (+) | Effect (−) | Cause (+) | Effect (−) |
| E8 forest | Cause (+) | Cause (+) | Cause (+) | Cause (+) | Effect (−) | Effect (−) | Effect (−) |
| E9 forest | Effect (−) | Effect (−) | Effect (−) | Effect (−) | Cause (+) | Cause (+) | Cause (+) |
| E10 water | Cause (+) | Cause (+) | Cause (+) | Effect (−) | Effect (−) | Effect (−) | Cause (+) |
| E11 water | Effect (−) | Effect (−) | Effect (−) | Cause (+) | Cause (+) | Cause (+) | Effect (−) |
| E12 water | Effect (−) | Effect (−) | Effect (−) | Cause (+) | Cause (+) | Cause (+) | Effect (−) |
| No. of Causes (+) | 4 | 4 | 3 | 8 | 8 | 9 | 6 |
| No. of Effects (−) | 8 | 8 | 9 | 4 | 4 | 3 | 6 |
| Measures | Group | ||||||
|---|---|---|---|---|---|---|---|
| M1 | M2 | M3 | M4 | M5 | M6 | M7 | |
| M1 | 0.00 | 3.42 | 2.42 | 2.00 | 1.92 | 1.75 | 2.67 |
| M2 | 2.67 | 0.00 | 2.75 | 2.00 | 1.58 | 1.75 | 2.50 |
| M3 | 2.08 | 3.08 | 0.00 | 2.33 | 1.67 | 1.67 | 1.83 |
| M4 | 2.08 | 2.17 | 2.42 | 0.00 | 2.75 | 2.67 | 2.33 |
| M5 | 3.17 | 3.08 | 2.58 | 2.00 | 0.00 | 3.25 | 2.75 |
| M6 | 2.75 | 2.83 | 2.58 | 1.92 | 3.17 | 0.00 | 3.00 |
| M7 | 3.08 | 3.42 | 2.75 | 2.33 | 2.08 | 1.92 | 0.00 |
| Measures | Group | ||||||
|---|---|---|---|---|---|---|---|
| M1 | M2 | M3 | M4 | M5 | M6 | M7 | |
| M1 | 0.87 | 1.15 | 0.98 | 0.82 | 0.82 | 0.81 | 0.96 |
| M2 | 0.95 | 0.92 | 0.95 | 0.78 | 0.77 | 0.77 | 0.91 |
| M3 | 0.89 | 1.04 | 0.77 | 0.76 | 0.74 | 0.74 | 0.85 |
| M4 | 1.01 | 1.12 | 1.01 | 0.73 | 0.89 | 0.88 | 0.98 |
| M5 | 1.18 | 1.30 | 1.14 | 0.94 | 0.85 | 1.00 | 1.12 |
| M6 | 1.14 | 1.26 | 1.11 | 0.92 | 0.99 | 0.82 | 1.10 |
| M7 | 1.10 | 1.23 | 1.07 | 0.89 | 0.89 | 0.88 | 0.91 |
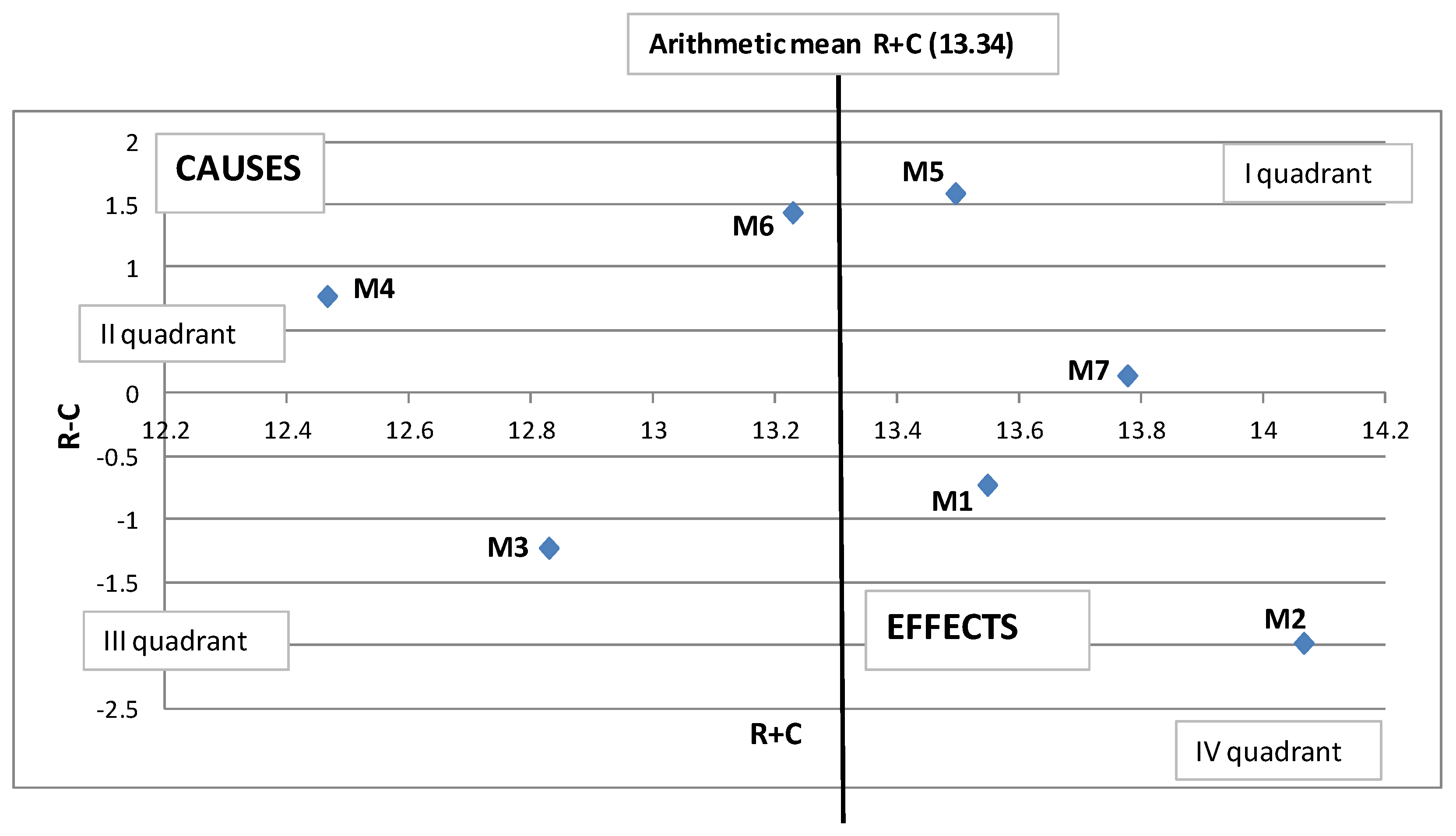
| Measures | Group | ||||
|---|---|---|---|---|---|
| Rg | Cg | Rg + Cg | Rg − Cg | E/C | |
| M1 | 6.41 | 7.14 | 13.55 | −0.73 | effect |
| M2 | 6.04 | 8.02 | 14.067 | −1.98 | effect |
| M3 | 5.80 | 7.03 | 12.83 | −1.23 | effect |
| M4 | 6.62 | 5.85 | 12.46 | 0.77 | cause |
| M5 | 7.54 | 5.95 | 13.50 | 1.59 | cause |
| M6 | 7.33 | 5.90 | 13.23 | 1.44 | cause |
| M7 | 6.96 | 6.82 | 13.78 | 0.14 | cause |
| Expert | Weights of Measures | ||||||
|---|---|---|---|---|---|---|---|
| M1 | M2 | M3 | M4 | M5 | M6 | M7 | |
| E1 | 0.148 (4) | 0.155 (1) | 0.139 (5) | 0.150 (3) | 0.151 (2) | 0.133 (6) | 0.124 (7) |
| E2 | 0.136 (5) | 0.148 (3) | 0.133 (7) | 0.135 (6) | 0.153 (1) | 0.149 (2) | 0.145 (4) |
| E3 | 0.143 (4) | 0.156 (1) | 0.141 (6) | 0.124 (7) | 0.142 (5) | 0.147 (2) | 0.146 (3) |
| E4 | 0.151 (3) | 0.152 (1) | 0.143 (6) | 0.144 (5) | 0.152 (2) | 0.147 (4) | 0.111 (7) |
| E5 | 0.144 (3) | 0.161 (1) | 0.134 (6) | 0.136 (5) | 0.149 (2) | 0.134 (7) | 0.142 (4) |
| E6 | 0.111 (7) | 0.175 (1) | 0.155 (3) | 0.157 (2) | 0.136 (5) | 0.151 (4) | 0.115 (6) |
| E7 | 0.142 (5) | 0.143 (4) | 0.145 (3) | 0.154 (1) | 0.133 (6) | 0.133 (7) | 0.151 (2) |
| E8 | 0.149 (2) | 0.147 (3) | 0.157 (1) | 0.147 (4) | 0.127 (7) | 0.140 (5) | 0.134 (6) |
| E9 | 0.144 (4) | 0.141 (5) | 0.138 (6) | 0.115 (7) | 0.156 (1) | 0.154 (2) | 0.152 (3) |
| E10 | 0.132 (6) | 0.162 (2) | 0.138 (4) | 0.103 (7) | 0.152 (3) | 0.134 (5) | 0.179 (1) |
| E11 | 0.141 (5) | 0.148 (4) | 0.114 (6) | 0.114 (7) | 0.168 (1) | 0.149 (3) | 0.167 (2) |
| E12 | 0.148 (4) | 0.179 (1) | 0.086 (7) | 0.123 (6) | 0.150 (3) | 0.142 (5) | 0.172 (2) |
| Group | 0.145 (3) | 0.151 (1) | 0.137 (6) | 0.133 (7) | 0.145 (4) | 0.142 (5) | 0.147 (2) |
| Expert | Conformity (Manhattan Distance) (CONF) | Spearman’s Ranks Correlation Coefficient (S) |
|---|---|---|
| E1 | 0.064 (5) | 0.143 (9) |
| E2 | 0.035 (3) | 0.429 (6) |
| E3 | 0.029 (1) | 0.786 (2) |
| E4 | 0.072 (7) | 0.393 (7) |
| E5 | 0.034 (2) | 0.714 (3) |
| E6 | 0.150 (12) | −0.214 (12) |
| E7 | 0.065 (6) | −0.179 (11) |
| E8 | 0.075 (8) | −0.143 (10) |
| E9 | 0.058 (4) | 0.357 (8) |
| E10 | 0.102 (10) | 0.714 (4) |
| E11 | 0.099 (9) | 0.536 (5) |
| E12 | 0.122 (11) | 0.929 (1) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Srđević, Z.; Srđević, B.; Ilić Paunić, M.; Ždero, S.; Galamboš, L.; Bošnjak, T.; Pantelić, S. Evaluating Drought Mitigation Measures for Wetland Management with DEMATEL: A Case Study Report of the Koviljsko–Petrovaradinski Rit Wetland in Serbia. Water 2025, 17, 1777. https://doi.org/10.3390/w17121777
Srđević Z, Srđević B, Ilić Paunić M, Ždero S, Galamboš L, Bošnjak T, Pantelić S. Evaluating Drought Mitigation Measures for Wetland Management with DEMATEL: A Case Study Report of the Koviljsko–Petrovaradinski Rit Wetland in Serbia. Water. 2025; 17(12):1777. https://doi.org/10.3390/w17121777
Chicago/Turabian StyleSrđević, Zorica, Bojan Srđević, Milica Ilić Paunić, Senka Ždero, Laslo Galamboš, Tanja Bošnjak, and Sanja Pantelić. 2025. "Evaluating Drought Mitigation Measures for Wetland Management with DEMATEL: A Case Study Report of the Koviljsko–Petrovaradinski Rit Wetland in Serbia" Water 17, no. 12: 1777. https://doi.org/10.3390/w17121777
APA StyleSrđević, Z., Srđević, B., Ilić Paunić, M., Ždero, S., Galamboš, L., Bošnjak, T., & Pantelić, S. (2025). Evaluating Drought Mitigation Measures for Wetland Management with DEMATEL: A Case Study Report of the Koviljsko–Petrovaradinski Rit Wetland in Serbia. Water, 17(12), 1777. https://doi.org/10.3390/w17121777






