Quantitative Assessment of the Reliability of Water Treatment Plant as an Example of Anthropotechnical System
Abstract
1. Introduction
2. Materials and Methods
2.1. Reliability Indicators
- Mean failure-free operating time Tp [d]—expected value of the random variable T’p, defining the system (or element) operating time between two successive failures. This can be determined using Formula (1) or it can be calculated based on operating data with Formula (2) [11]:
- -
- E(T’p)—expected value of a random variable T’p;
- -
- t—observation time [d];
- -
- f(t)—probability density of a random variable T’p;
- -
- k—number of periods of failing objects operation;
- -
- z—number of periods of non-destructive objects operation;
- -
- tpi—value of the i-th operating time of the failing objects.
- Average renewal time To [d]—expected value of the random variable T’o defining the renewal time. This can be calculated using Formula (3), or it can be calculated based on the operating data with Formula (4) [11]:
- -
- E(T’o)—expected value of a random variable T’o;
- -
- fo(t)—probability density of a random variable T’o;
- -
- no—number of repairs in the analyzed time period;
- -
- toi—duration of i-th repair.
- Failure intensity index λ(t)—determines the number of failures per unit of time [1/d]. It is determined using Formula (5), or it can be calculated based on operating data with Formulas (6) and (7) [11]:
- -
- Tp—the average value of the operating time between successive failures is equal to E(T’p) [d];
- -
- n(t,t + Δt)—total number of failures in a time interval Δt;
- -
- N—number of tested elements;
- -
- Δt—observation time, [d].
- Renewal intensity index µ(t)—determines the number of failures removed per unit of time. It can be determined using Formula (8), or it can be calculated based on operating data with Formulas (9) and (10) [11]:
- -
- Po(t)—probability of renewal of the system;
- -
- fo(t)—probability density of a random variable T’o;
- -
- To—the average value of the system renewal equals to E(T’o) [d];
- -
- n(t,t + Δt)—the number of all elements whose renewal was completed in the time interval t + Δt;
- -
- N—number of tested elements;
- -
- Δt—observation time, [d].
- Reliability index Kg—determines the probability that the system will be in an efficient state in a given time interval. It can be determined using Formula (11), or it can be calculated based on operating data with Formula (12) [11]:
- -
- µ—renewal intensity index [1/d];
- -
- λ—failure intensity index [1/d];
- -
- Tp—mean failure-free operating time [d];
- -
- To—mean time to repair [d].
2.2. Reliability Structures
- Serial structure—used if the failure of any element causes the failure of the entire system. The Kg reliability index for the serial structure is equal to the product of the reliability indexes of the individual system elements. It is calculated using Formula (13):
- -
- Kgi—reliability index of the i-th element of the system [-];
- -
- n—number of elements.
- Threshold structure—used if failure to “k” of “m” homogeneous system elements causes failure to the entire system. It is called threshold structure of the “m-k of m” type. For the threshold structure, the reliability index Kg is calculated according to Formula (14):
- -
- k—number of damaged elements;
- -
- kp—permissible number of damaged elements;
- -
- m—number of all elements;
- -
- Kg0—single element reliability index [-];
- -
- Kp0—single element unreliability index [-].
- Parallel structure—used if the failure of the entire system occurs as a result of the failure of all system elements at the same time. The Kg reliability index of the parallel structure is described by Formula (15):
- -
- Kgi—reliability index of the i-th element of the system [-];
- -
- n—number of elements.
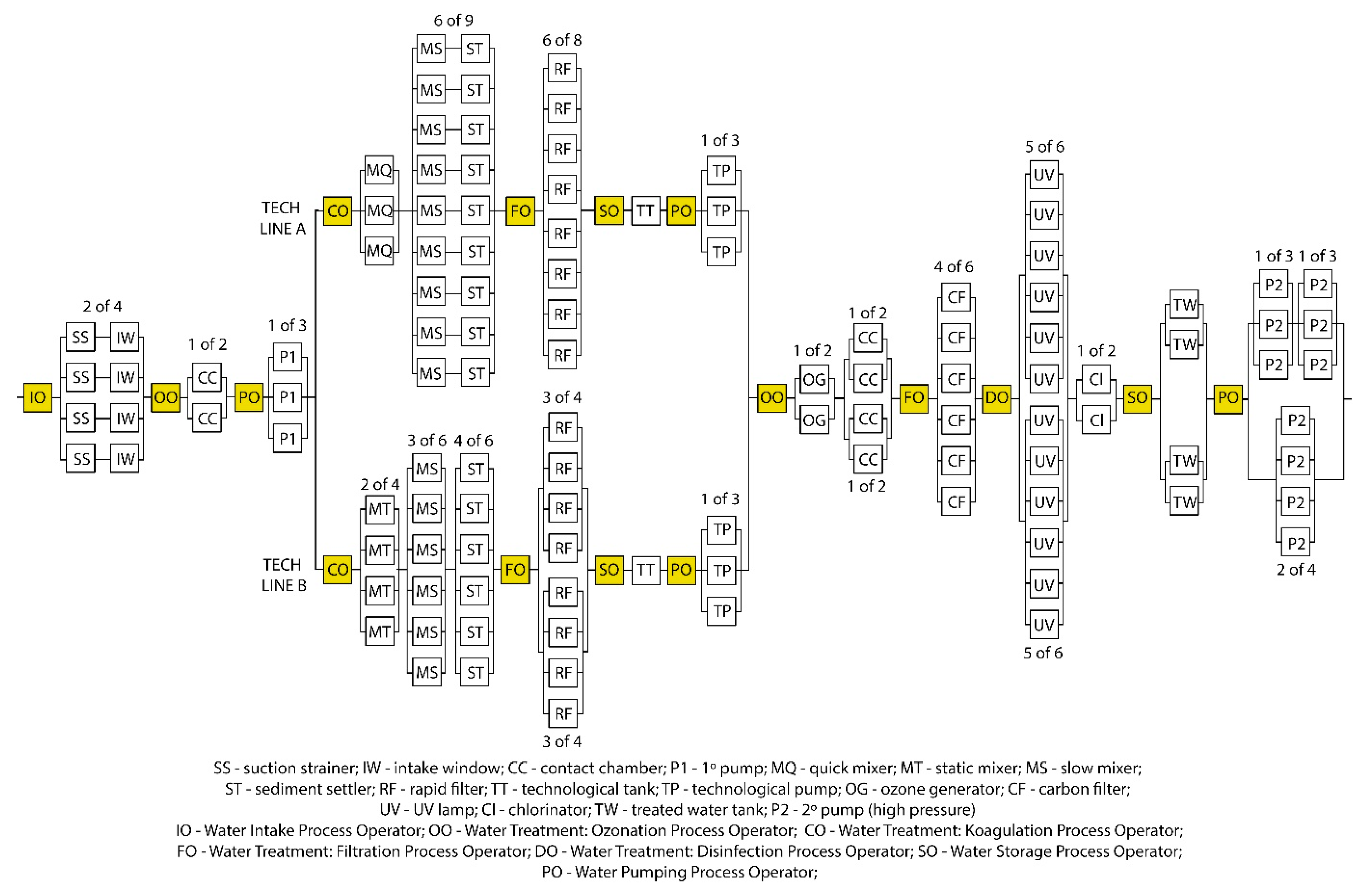
2.3. Anthropotechnical Reliability Structures and Indicators
- -
- HEP—human error probability.
2.4. Reliability Requirements for Water Supply Systems
- -
- Technical and economic—they mainly concern industrial water recipients, for whom the lack of water supply means interruptions in production or reduced efficiency; deterioration of product quality; damage to technical equipment, causing financial losses;
- -
- Health and sanitary—these mainly concern households and public utility buildings. Lack of or interruptions in water supply pose a threat to maintaining appropriate sanitary conditions in the place where people live. Inadequate water quality can also be a source of epidemics;
- -
- Psychological and social—lack of or long-term interruptions in water supply affect the quality of people’s lives, causing social tensions that can lead to riots. This aspect is particularly observed during crisis situations;
- -
- Catastrophic—these may be related to the effects mentioned above, but their scale is very large, posing a threat to human health and life.
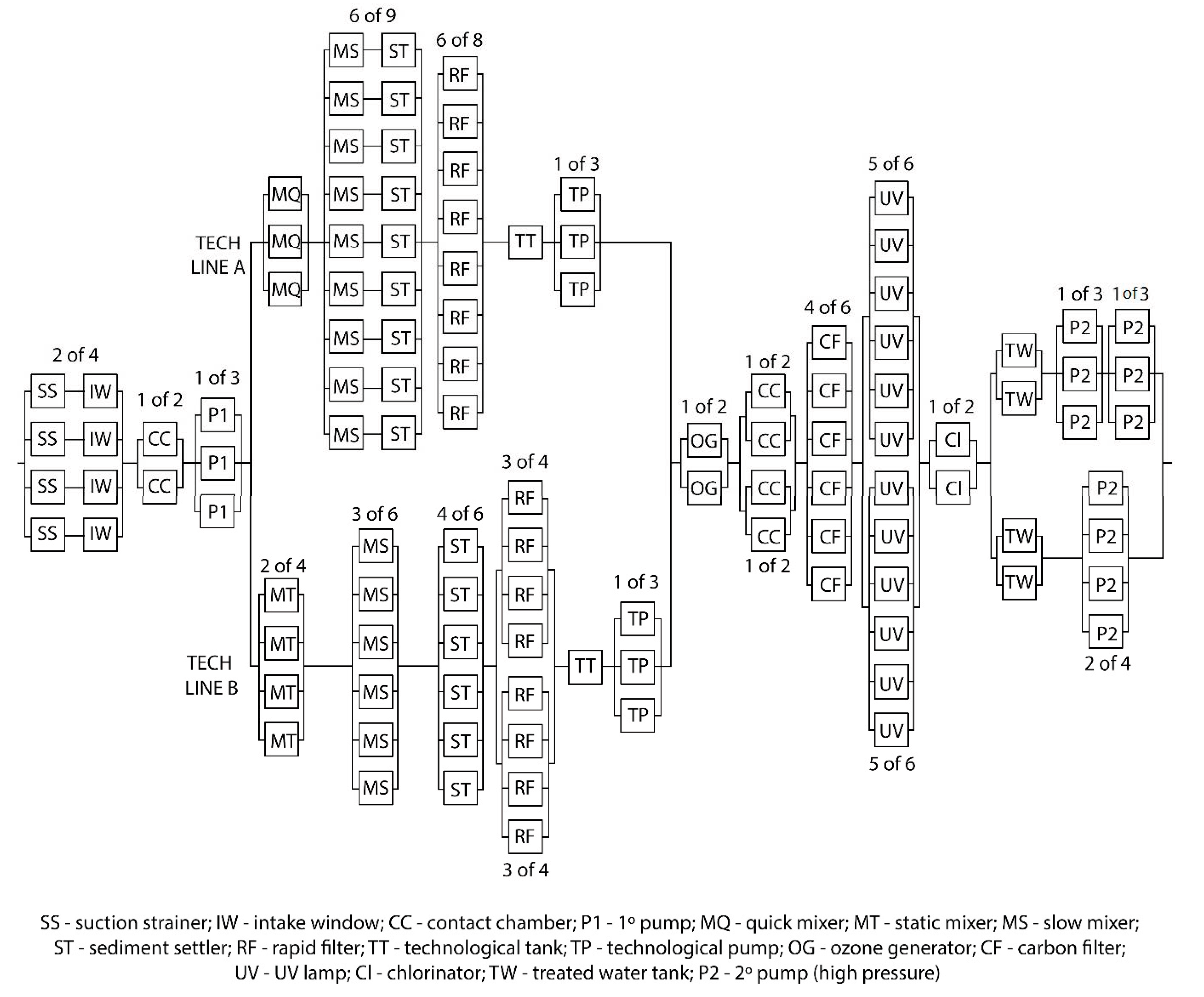
2.5. Research Object
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| COCOM | Contextual Control Model |
| CREAM | Cognitive Reliability and Error Analysis Method |
| HEP | Human Error Probability |
| HRA | Human Reliability Assessment |
| WSS | Water Supply System |
| WTP | Water Treatment Plant |
References
- Hollnagel, E. Cognitive Reliability and Error Analysis Method—CREAM; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Helmreich, R.L. On error management: Lessons from aviation. BMJ 2000, 320, 781–785. [Google Scholar] [CrossRef] [PubMed]
- Kariuki, S.G.; Löwe, K. Integrating human factors into process hazard analysis. Reliab. Eng. Syst. 2007, 92, 1764–1773. [Google Scholar] [CrossRef]
- Reason, J. Human error: Models and management. BMJ 2000, 320, 768. [Google Scholar] [CrossRef] [PubMed]
- Ren, J.; Jenkinson, I.; Wang, J.; Xu, D.L.; Yang, J.B. A methodology to model causal relationships on offshore safety assessment focusing on human and organizational factors. J. Saf. Res. 2008, 39, 87–100. [Google Scholar] [CrossRef]
- Tang, Y.; Wu, S.; Miao, X.; Pollard, S.J.T.; Hrudey, S.E. Resilience to evolving drinking water contamination risks: A human error prevention perspective. J. Clean. Prod. 2013, 57, 228–237. [Google Scholar] [CrossRef]
- Wu, S.; Hrudey, S.; French, S.; Bedford, T.; Soane, E.; Pollard, S. A role for human reliability analysis (HRA) in preventing drinking water incidents and securing safe drinking water. Water Res. 2009, 43, 3227–3238. [Google Scholar] [CrossRef]
- Rak, J.; Tchórzewska-Cieślak, B. The concept of reliability and safety of the operator’s work in the water supply system. Instal 2019, 2, 44–48. (In Polish) [Google Scholar]
- Tchórzewska-Cieślak, B. Water supply system reliability management. Environ. Prot. Eng. 2009, 35, 29–35. [Google Scholar]
- Tchórzewska-Cieślak, B.; Rak, J.; Pietrucha-Urbanik, K.; Piegdoń, I.; Boryczko, K.; Szpak, D.; Żywiec, J. Water supply safety assessment considering the water supply system resilience. Desalin. Water Treat. 2023, 288, 26–361. [Google Scholar] [CrossRef]
- Kwietniewski, M.; Roman, M.; Kłoss-Trębaczkiewicz, H. Reliability of Water and Sewage Systems; Arkady: Warsaw, Poland, 1993. (In Polish) [Google Scholar]
- Fujiwara, O.; Chen, H.-J. Reliability analysis of water supply systems integrating with treatment plant operations. Reliab. Eng. Syst. 1993, 42, 47–53. [Google Scholar] [CrossRef]
- Boccafoschi, A.; Rejtano, B. Reliability analysis of water supply systems by the entropy and equivocation theory. In Integrating Water Systems Proceedings of the 10th International on Computing and Control for the Water Industry, Sheffield, UK, 1–3 September 2009; Boxall, J., Maksimovic, C., Eds.; CRC Press: London, UK, 2009. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, B.; Li, Y.; Fu, G. Exploring the relationships among reliability, resilience, and vulnerability of water supply using many-objective analysis. J. Water Resour. Plan. Manag. 2017, 143, 04017044. [Google Scholar] [CrossRef]
- Islam, M.S.; Sadiq, R.; Rodriguez, M.; Najjaran, H.; Hoorfar, M. Reliability assessment for water supply systems under uncertainties. J. Water Resour. Plan. Manag. 2014, 140, 468–479. [Google Scholar] [CrossRef]
- Szpak, D.; Tchórzewska-Cieslak, B. Analysis and assessment of water treatment plant reliability. J. KONBiN 2017, 41, 21–38. Available online: https://www.scopus.com/record/display.uri?eid=2-s2.0-85033442378&origin=resultslist&sort=r-f&src=s&sot=b&sdt=b&s=TITLE-ABS-KEY%28Analysis+and+assessment+of+water+treatment+plant+reliability%29&sessionSearchId=459a90dd5b23bfb18b867be438ee5700 (accessed on 18 May 2025). [CrossRef]
- Piegdon, I.; Tchorzewska-Cieslak, B.; Szpak, D.; Szlachta, A. Analysis of selected reliability indicators of water supply network. J. KONBiN 2018, 47, 45–651. [Google Scholar] [CrossRef]
- Silva Monte, M.B.; Teixeira De Almeida Filho, A. A reliability-based approach to maximize availability in a water supply system. IEEE Lat. Am. Trans. 2015, 13, 3807–3812. [Google Scholar] [CrossRef]
- Vreeburg, J.H.G.; van den Hoven Th, J.J.; Hoogsteen, K.J. Quantitative method to determine reliability of water supply systems. Water Supply 1994, 12. Available online: https://www.scopus.com/record/display.uri?eid=2-s2.0-0028757782&origin=resultslist&sort=r-f&src=s&sot=b&sdt=b&s=TITLE-ABS-KEY%28Quantitative+method+to+determine+reliability+of+water+supply+systems%29&sessionSearchId=459a90dd5b23bfb18b867be438ee5700 (accessed on 18 May 2025).
- Ren, K.; Huang, S.; Huang, Q.; Wang, H.; Leng, G.; Fang, W.; Li, P. Assessing the reliability, resilience and vulnerability of water supply system under multiple uncertain sources. J. Clean. Prod. 2020, 252, 119806. [Google Scholar] [CrossRef]
- Chai, Y.; Liu, H. Reliability analysis of conventional island water supply system. In Proceedings of the 4th International Conference on Mechanical, Control and Computer Engineering, ICMCCE, Hohhot, China, 25–27 October 2019. [Google Scholar] [CrossRef]
- Chen, B.P.-T.; Chen, C.-S. Feasibility assessment of a water supply reliability index for water resources project planning and evaluation. Water 2019, 11, 1977. [Google Scholar] [CrossRef]
- Muttiah, R.S.; Wurbs, R.A. Modeling the impacts of climate change on water supply reliabilities. Water Int. 2002, 27, 407–419. [Google Scholar] [CrossRef]
- Halmova, D.; Melo, M. Climate change impact on reservoir water supply reliability. In Climate Variability and Change—Hydrological Impacts—Proceedings of the Fifth FRIEND World Conference, Havana, Cuba, 27 November–1 December 2006; IAHS: Wallingford, UK, 2006; Volume 308. [Google Scholar]
- Jihyeon, J.; Kook, W.D. Assessment of water supply reliability under climate stress scenarios. J. Korea Water Resour. Assoc. 2024, 57, 409–419. [Google Scholar]
- Rak, J.; Tchórzewska-Cieślak, B.; Żywiec, J. Human Reliability Factor in Water Supply Systems. Instal 2019, 3, 40–43. (In Polish) [Google Scholar]
- Rak, J.; Tchórzewska-Cieślak, B.; Żywiec, J. New segment of water system operator reliability indicator estimators. Instal 2019, 4, 40–43. (In Polish) [Google Scholar]
- Boryczko, K.; Szpak, D.; Żywiec, J.; Tchórzewska-Cieślak, B. The Use of a Fault Tree Analysis (FTA) in the Operator Reliability Assessment of the Critical Infrastructure on the Example of Water Supply System. Energies 2022, 15, 4416. [Google Scholar] [CrossRef]
- Żywiec, J.; Tchórzewska-Cieślak, B.; Rak, J. Safety of the Water Supply System from the System Operator Perspective. In Proceedings of CEE 2023; Blikharskyy, Z., Koszelnik, P., Lichołai, L., Nazarko, P., Katunský, D., Eds.; Lecture Notes in Civil Engineering; Springer: Cham, Switzerland, 2024; Volume 438, pp. 551–561. [Google Scholar] [CrossRef]
- Żywiec, J.; Tchórzewska-Cieślak, B.; Sokolan, K. Assessment of Human Errors in the Operation of the Water Treatment Plant. Water 2024, 16, 2399. [Google Scholar] [CrossRef]
- Tu, J.; Lin, W.; Lin, Y. A Bayes-SLIM based methodology for human reliability analysis of lifting operations. Int. J. Ind. Ergon. 2015, 45, 48–54. [Google Scholar] [CrossRef]
- Borgheipour, H.; Mohammadfam, I.; Narenji, M.A. Assessing and Comparing Human Errors in Technical operations in Petroleum Wells using Extended CREAM Technique. J. Occup. Hyg. 2017, 9, 132–141. [Google Scholar]
- Lin, Y.; Pan, X.; He, C. Human Reliability Analysis in Carrier-based Aircraft Recovery Procedure based on CREAM. In Proceedings of the 2015 First International Conference on Reliability Systems Engineering (ICRSE), Beijing, China, 21–23 October 2015. [Google Scholar] [CrossRef]
- Lin, Q.L.; Wang, D.J.; Lin, W.G.; Liu, H.C. Human reliability assessment for medical devices based on failure mode and effects analysis and fuzzy linguistic theory. Saf. Sci. 2014, 62, 248–256. [Google Scholar] [CrossRef]
- Zheng, X.; Bolton, M.L.; Daly, C.; Biltekoff, E. The development of a next-generation human reliability analysis: Systems analysis for formal pharmaceutical human reliability (SAFPH). Reliab. Eng. Syst. 2020, 202, 106927. [Google Scholar] [CrossRef]
- Aalipour, M.; Ayele, Y.Z.; Barabadi, A. Human reliability assessment (HRA) in maintenance of production process: A case study. Int. J. Syst. Assur. Eng. Manag. 2016, 7, 229–238. [Google Scholar] [CrossRef]
- Akyuz, E.; Celik, M. A methodological extension to human reliability analysis for cargo tank cleaning operation on board chemical tanker ships. Saf. Sci. 2015, 75, 146–155. [Google Scholar] [CrossRef]
- Sezer, S.I.; Akyuz, E.; Arslan, O. An extended HEART Dempster–Shafer evidence theory approach to assess human reliability for the gas freeing process on chemical tankers. Reliab. Eng. Syst. 2022, 220, 108275. [Google Scholar] [CrossRef]
- Xi, Y.T.; Yang, Z.L.; Fang, Q.G.; Chen, W.J.; Wang, J. A new hybrid approach to human error probability quantification–applications in maritime operations. Ocean Eng. 2017, 138, 45–54. [Google Scholar] [CrossRef]
- Fruggiero, F.; Fera, M.; Lambiase, A.; Di Pasquale, V. Linking Human Factors to Assess Human Reliability. In Human-Friendly Robotics 2019, HFR 2019. Springer Proceedings in Advanced Robotics, Modena, Italy, 24–25 October 2019; Ferraguti, F., Villani, V., Sabattini, L., Bonfè, M., Eds.; Springer: Cham, Switzerland, 2020; Volume 12. [Google Scholar] [CrossRef]


| Water Supply System Category | Coverage of Total Water Demand [%] | C [1/year] | T0 [h] | Kg | |
|---|---|---|---|---|---|
| I | Large (>50,000 recipients) | 0–70 | ≤0.02 | ≤24 | ≥0.9999453 |
| 71–99 | ≤2 | ≤24 | ≥0.9945206 | ||
| 100 | ≤3 | ≤24 | ≥0.9917809 | ||
| II | Average (500–50,000 recipients) | 0–70 | ≤0.2 | ≤24 | ≥0.9994542 |
| 71–99 | ≤3 | ≤24 | ≥0.9917809 | ||
| 100 | ≤6 | ≤24 | ≥0.9835617 | ||
| III | Small (<500 recipients) | 0–70 | ≤1 | ≤24 | ≥0.9972603 |
| 71–99 | ≤6 | ≤24 | ≥0.9835617 | ||
| 100 | ≤12 | ≤24 | ≥0.9671233 | ||
| Symbol | Object | Kg |
|---|---|---|
| SS | Suction strainer | 0.999 |
| IW | Intake window | 0.9992 |
| CC | Contact chamber | 0.9970 |
| P1 | 1° pump | 0.9681 |
| MQ | Quick mixer | 0.9891 |
| MT | Static mixer | 0.998 |
| MS | Slow mixer | 0.9729 |
| ST | Sediment settler | 0.9986 |
| RF | Rapid filter | 0.9846 |
| TT | Technological water tank | 0.9910 |
| TP | Technological pump | 0.9890 |
| OG | Ozone generator | 0.9980 |
| CF | Carbon filter | 0.9980 |
| UV | UV lamp | 0.9870 |
| Cl | Chlorinator | 0.9985 |
| TW | Treated water tank | 0.9892 |
| P2 | 2° pump (high pressure) | 0.9905 |
| Object | Kg (For Single Element) | Reliability Structure Type | Kg (For Reliability Structure) | Object | Kg (For Single Element) | Reliability Structure Type | Kg (For Reliability Structure) |
|---|---|---|---|---|---|---|---|
| TECH LINE A | TECH LINE B | ||||||
| MQ | 0.9891 | parallel | 0.9999 | MT | 0.998 | threshold 2 of 4 | 0.992 |
| MS | 0.9729 | series | 0.9715 | MS | 0.9729 | threshold 3 of 6 | 0.9999 |
| ST | 0.9986 | ST | 0.9986 | threshold 4 of 6 | 0.9999 | ||
| MS + ST | 0.9715 | threshold 6 of 9 | 0.9999 | RF | 0.9846 | threshold 3 of 4 | 0.9989 |
| RF | 0.9846 | threshold 6 of 8 | 0.9998 | RF + RF | 0.9989 | pararell | 0.9999 |
| TT | 0.991 | - | 0.991 | TT | 0.991 | - | 0.991 |
| TP | 0.989 | threshold 1 of 3 | 0.9999 | TP | 0.989 | threshold 1 of 3 | 0.9999 |
| TECH LINE A (total) | - | series | 0.9905 | TECH LINE B (total) | - | series | 0.9827 |
| Object | Kg (For Single Element) | Reliability Structure Type | Kg (For Reliability Structure) | ||||
| SS | 0.999 | series | 0.9982 | ||||
| IW | 0.9992 | ||||||
| SS + IW | 0.9982 | threshold 2 of 4 | 0.9999 | ||||
| CC | 0.997 | threshold 1 of 2 | 0.9999 | ||||
| P1 | 0.9681 | threshold 1 of 3 | 0.9999 | ||||
| TECH LINE A + TECH LINE B | - | parallel | 0.9998 | ||||
| OG | 0.998 | threshold 1 of 2 | 0.9999 | ||||
| CC | 0.997 | threshold 1 of 2 | 0.9999 | ||||
| CC + CC | 0.9999 | parallel | 0.9999 | ||||
| CF | 0.998 | threshold 4 of 6 | 0.9999 | ||||
| UV | 0.987 | threshold 5 of 6 | 0.9976 | ||||
| UV + UV | 0.9976 | parallel | 0.9999 | ||||
| Cl | 0.9985 | threshold 1 of 2 | 0.9999 | ||||
| TW | 0.9892 | parallel | 0.9998 | ||||
| P2 | 0.9905 | threshold 1 of 3 | 0.9999 | ||||
| TW + P2 + P2 | - | series | 0.9996 | ||||
| P2 | 0.9905 | threshold 2 of 4 | 0.9999 | ||||
| TW + P2 + P2 | - | series | 0.9997 | ||||
| TW + P2 + P2 + TW + P2 | - | parallel | 0.9999 | ||||
| WTP (total) | - | series | 0.9988 | ||||
| Symbol | Object | Kg | ||
|---|---|---|---|---|
| Min | Average | Max | ||
| IO | Water Intake Process Operator | 0.9287 | 0.9864 | 0.9993 |
| OO | Water Treatment—Ozonation Process Operator | 0.9493 | 0.9863 | 0.9994 |
| CO | Water Treatment—Coagulation Process Operator | 0.9433 | 0.9868 | 0.9995 |
| FO | Water Treatment—Filtration Process Operator | 0.9287 | 0.9853 | 0.9993 |
| DO | Water Treatment—Disinfection Process Operator | 0.9423 | 0.9879 | 0.9994 |
| PO | Water Pumping Operator | 0.9254 | 0.9863 | 0.9992 |
| SO | Water Storage Operator | 0.9357 | 0.9861 | 0.9995 |
| Object | Kg (For Single Element) | Reliability Structure Type | Kg (For Reliability Structure) | Object | Kg (For Single Element) | Reliability Structure Type | Kg (For Reliability Structure) |
|---|---|---|---|---|---|---|---|
| TECH LINE A | TECH LINE B | ||||||
| CO | 0.9868 | - | 0.9868 | CO | 0.9868 | - | 0.9868 |
| MQ | 0.9891 | parallel | 0.9999 | MT | 0.998 | threshold 2 of 4 | 0.992 |
| MS | 0.9729 | series | 0.9715 | MS | 0.9729 | threshold 3 of 6 | 0.9999 |
| ST | 0.9986 | ST | 0.9986 | threshold 4 of 6 | 0.9999 | ||
| MS + ST | 0.9715 | threshold 6 of 9 | 0.9999 | CO + MT + MS + ST | - | series | 0.9787 |
| CO + MQ + MS + ST | - | series | 0.9866 | FO | 0.9853 | - | 0.9853 |
| FO | 0.9853 | - | 0.9853 | RF | 0.9846 | threshold 3 of 4 | 0.9989 |
| RF | 0.9846 | threshold 6 of 8 | 0.9998 | RF + RF | 0.9989 | parallel | 0.9999 |
| FO + RF | - | series | 0.9851 | OF + RF + RF | - | series | 0.9852 |
| SO | 0.9861 | - | 0.9861 | SO | 0.9861 | - | 0.9861 |
| TT | 0.991 | - | 0.991 | TT | 0.991 | - | 0.991 |
| SO + TT | - | series | 0.9772 | SO + TT | - | series | 0.9772 |
| PO | 0.9863 | - | 0.9863 | PO | 0.9863 | - | 0.9863 |
| TP | 0.989 | threshold 1 of 3 | 0.9999 | TP | 0.989 | threshold 1 of 3 | 0.9999 |
| PO + TP | - | series | 0.9862 | PO + TP | - | series | 0.9862 |
| TECH LINE A (total) | - | series | 0.9366 | TECH LINE B (total) | series | 0.9292 | |
| Object | Kg (for Single Element) | Reliability Structure Type | Kg (for Reliability Structure) | ||||
| IO | 0.9864 | - | 0.9864 | ||||
| SS | 0.999 | series | 0.9982 | ||||
| IW | 0.9992 | ||||||
| SS + IW | 0.9982 | threshold 2 of 4 | 0.9999 | ||||
| IO + SS + IW | - | series | 0.9863 | ||||
| OO | 0.9863 | - | 0.9863 | ||||
| CC | 0.997 | threshold 1 of 2 | 0.9999 | ||||
| OO + CC | - | series | 0.9862 | ||||
| PO | 0.9863 | - | 0.9863 | ||||
| P1 | 0.9681 | threshold 1 of 3 | 0.9999 | ||||
| PO + P1 | - | series | 0.9862 | ||||
| TECH LINE A + TECH LINE B | - | parallel | 0.9955 | ||||
| OO | 0.9863 | - | 0.9863 | ||||
| OG | 0.998 | threshold 1 of 2 | 0.9999 | ||||
| CC | 0.997 | threshold 1 of 2 | 0.9999 | ||||
| CC + CC | 0.9999 | parallel | 0.9999 | ||||
| OO + OG + CC + CC | - | series | 0.9861 | ||||
| FO | 0.9853 | - | 0.9853 | ||||
| CF | 0.998 | threshold 4 of 6 | 0.9999 | ||||
| FO + CF | - | series | 0.9852 | ||||
| DO | 0.9879 | - | 0.9879 | ||||
| UV | 0.987 | threshold 5 of 6 | 0.9976 | ||||
| UV + UV | 0.9976 | parallel | 0.9999 | ||||
| Cl | 0.9985 | threshold 1 of 2 | 0.9999 | ||||
| DO + UV + UV + Cl | - | series | 0.9877 | ||||
| SO | 0.9861 | - | 0.9861 | ||||
| TW | 0.9892 | parallel | 0.9998 | ||||
| TW + TW | 0.9998 | parallel | 0.9999 | ||||
| SO + TW + TW | - | series | 0.986 | ||||
| PO | 0.9863 | - | 0.9863 | ||||
| P2 | 0.9905 | threshold 1 of 3 | 0.9999 | ||||
| P2 + P2 | 0.9999 | series | 0.9998 | ||||
| P2 | 0.9905 | threshold 2 of 4 | 0.9999 | ||||
| P2 + P2 + P2 | - | parallel | 0.9999 | ||||
| PO + P2 + P2 + P2 | - | series | 0.9862 | ||||
| WTP (total) | - | series | 0.8910 | ||||
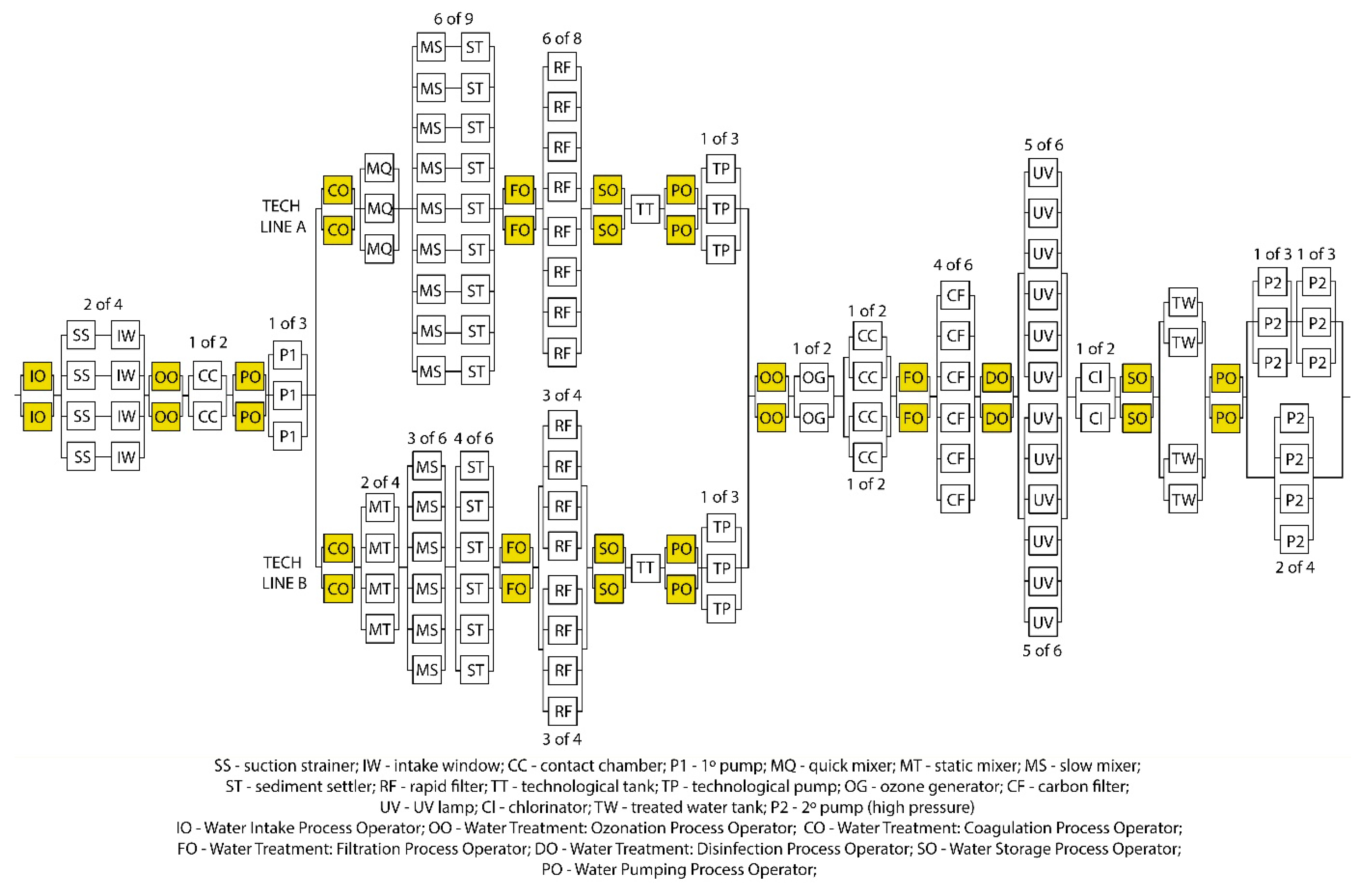
| Object | Kg (For Single Element) | Reliability Structure Type | Kg (For Reliability Structure) | Object | Kg (For Single Element) | Reliability Structure Type | Kg (For Reliability structure) |
|---|---|---|---|---|---|---|---|
| TECH LINE A | TECH LINE B | ||||||
| CO | 0.9868 | parallel | 0.9998 | CO | 0.9868 | parallel | 0.9868 |
| MQ | 0.9891 | parallel | 0.9999 | MT | 0.998 | threshold 2 of 4 | 0.992 |
| MS | 0.9729 | series | 0.9996 | MS | 0.9729 | threshold 3 of 6 | 0.9999 |
| ST | 0.9986 | ST | 0.9986 | threshold 4 of 6 | 0.9999 | ||
| MS + ST | 0.9715 | threshold 6 of 9 | 0.9999 | CO + MT + MS + ST | - | series | 0.9787 |
| CO + MQ + MS + ST | - | series | 0.9866 | FO | 0.9853 | parallel | 0.9853 |
| FO | 0.9853 | parallel | 0.9998 | RF | 0.9846 | threshold 3 of 4 | 0.9989 |
| RF | 0.9846 | threshold 6 of 8 | 0.9998 | RF + RF | 0.9989 | parallel | 0.9999 |
| FO + RF | - | series | 0.9996 | OF + RF + RF | - | series | 0.9852 |
| SO | 0.9861 | parallel | 0.9998 | SO | 0.9861 | parallel | 0.9861 |
| TT | 0.991 | - | 0.991 | TT | 0.991 | - | 0.991 |
| SO + TT | - | series | 0.9908 | SO + TT | - | series | 0.9772 |
| PO | 0.9863 | parallel | 0.9998 | PO | 0.9863 | parallel | 0.9863 |
| TP | 0.989 | threshold 1 of 3 | 0.9999 | TP | 0.989 | threshold 1 of 3 | 0.9999 |
| PO + TP | - | series | 0.9997 | PO + TP | - | series | 0.9862 |
| TECH LINE A (total) | - | series | 0.9897 | TECH LINE B (total) | - | series | 0.9819 |
| Object | Kg (For Single Element) | Reliability Structure Type | Kg (For Reliability Structure) | ||||
| IO | 0.9864 | parallel | 0.9998 | ||||
| SS | 0.999 | series | 0.9982 | ||||
| IW | 0.9992 | ||||||
| SS + IW | 0.9982 | threshold 2 of 4 | 0.9999 | ||||
| IO + SS + IW | - | series | 0.9997 | ||||
| OO | 0.9863 | parallel | 0.9998 | ||||
| CC | 0.997 | threshold 1 of 2 | 0.9999 | ||||
| OO + CC | - | series | 0.9997 | ||||
| PO | 0.9863 | parallel | 0.9998 | ||||
| P1 | 0.9681 | threshold 1 of 3 | 0.9999 | ||||
| PO + P1 | - | series | 0.9997 | ||||
| TECH LINE A + TECH LINE B | - | parallel | 0.9998 | ||||
| OO | 0.9863 | parallel | 0.9998 | ||||
| OG | 0.998 | threshold 1 of 2 | 0.9999 | ||||
| CC | 0.997 | threshold 1 of 2 | 0.9999 | ||||
| CC + CC | 0.9999 | parallel | 0.9999 | ||||
| OO + OG + CC + CC | - | series | 0.9996 | ||||
| FO | 0.9853 | parallel | 0.9998 | ||||
| CF | 0.998 | threshold 4 of 6 | 0.9999 | ||||
| FO + CF | - | series | 0.9997 | ||||
| DO | 0.9879 | parallel | 0.9998 | ||||
| UV | 0.987 | threshold 5 of 6 | 0.9976 | ||||
| UV + UV | 0.9976 | parallel | 0.9999 | ||||
| Cl | 0.9985 | threshold 1 of 2 | 0.9999 | ||||
| DO + UV + UV + Cl | - | series | 0.9996 | ||||
| SO | 0.9861 | parallel | 0.9998 | ||||
| TW | 0.9892 | parallel | 0.9998 | ||||
| TW + TW | 0.9998 | parallel | 0.9999 | ||||
| SO + TW + TW | - | series | 0.9997 | ||||
| PO | 0.9863 | parallel | 0.9998 | ||||
| P2 | 0.9905 | threshold 1 of 3 | 0.9999 | ||||
| P2 + P2 | 0.9999 | series | 0.9998 | ||||
| P2 | 0.9905 | threshold 2 of 4 | 0.9999 | ||||
| P2 + P2 + P2 | - | parallel | 0.9999 | ||||
| PO + P2 + P2 + P2 | - | series | 0.9997 | ||||
| WTP (total) | - | series | 0.9972 | ||||
| Scenario | Decrease in Operator Reliability Index Kg | WTP Reliability Index Kg | |
|---|---|---|---|
| Single Operator | Doubled Operator | ||
| 1 | 1% | 0.8646 | 0.9944 |
| 2 | 5% | 0.7640 | 0.9676 |
| 3 | 10% | 0.6496 | 0.9024 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Żywiec, J.; Tchórzewska-Cieślak, B.; Rak, J. Quantitative Assessment of the Reliability of Water Treatment Plant as an Example of Anthropotechnical System. Water 2025, 17, 1742. https://doi.org/10.3390/w17121742
Żywiec J, Tchórzewska-Cieślak B, Rak J. Quantitative Assessment of the Reliability of Water Treatment Plant as an Example of Anthropotechnical System. Water. 2025; 17(12):1742. https://doi.org/10.3390/w17121742
Chicago/Turabian StyleŻywiec, Jakub, Barbara Tchórzewska-Cieślak, and Janusz Rak. 2025. "Quantitative Assessment of the Reliability of Water Treatment Plant as an Example of Anthropotechnical System" Water 17, no. 12: 1742. https://doi.org/10.3390/w17121742
APA StyleŻywiec, J., Tchórzewska-Cieślak, B., & Rak, J. (2025). Quantitative Assessment of the Reliability of Water Treatment Plant as an Example of Anthropotechnical System. Water, 17(12), 1742. https://doi.org/10.3390/w17121742








